
All Solutions
Section 9-6: Techniques for Solving Equations and Inequalities
#### (a)
$i) x=dfrac{1}{2}, 2,$or $dfrac{7}{2}$
$ii) x=-1$ or $2$
#### (b)
$i) dfrac{1}{2} < x dfrac{7}{2}$
$ii) -1 < x < 2$
#### (c)
$i) xleq dfrac{1}{2}$; $2leq xleq dfrac{7}{2}$
$ii) xleq -1$ or $xgeq 2$
#### (d)
$i) dfrac{1}{2}leq x leq 2$ or $xgeq dfrac{7}{2}$
$ii) -1leq x leq 2$
$3=2^{2x}$
Try $x=1:3=2^2$
$3=4$ To high
Try $x=0.5:3=2^1$
$3=2$ Too low
Try $0.6:3=2^{1.2}$
$3=2.3$ Too low
Try $0.8:3=2^{1.6}$
$3=3.03$
So, $x=0.8$
$0=sin(0.25x^2)$
Try $x=0$: $0=sin0$
$0=0$ Correct
Try $x=2$: $0=sin(0.25(4))$
$0=0.84$ Too high
Try $x=3$: $0=sin(0.25(9))$
$0=0.78$ Too high
Try $x=3.5$: $0=sin(0.25(12.25))$
$0=0.08$ Close
Try $x=3.6$: $0=sin(0.25(12.96))$
$0=-0.1$
So, $x=0$ and $3.5$
$3x=0.5x^3$
Try $x=-2: 3(-2)=0.5(-2)^3$
$-6=-4$
Try $x=-3: 3(-3)=0.5(-3)^3$
$-9=-13.5$
Try $x=-2.5: 3(-2.5)=0.5(-2.5)^3$
$-7.5=-7.8$
Try $x=-2.4: 3(-2.4)=0.5(-2.4)^3$
$-7.2=-6.9$
So, $x=-2.4$
$cos x=x$
Try $x=0$: $cos 0=0$
$1=0$
Try $0.5$ : $cos0.5=0.5$
$0.8=0.5$
Try $0.6$: $cos 0.6=0.6$
$0.8=0.6$
Try $0.7$: $cos0.7=0.7$
$0.76=0.7$
So, $x=0.7$
$x=-1.3$ or $1.8$
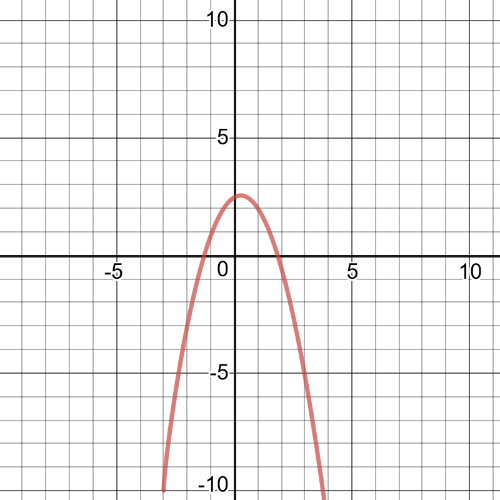
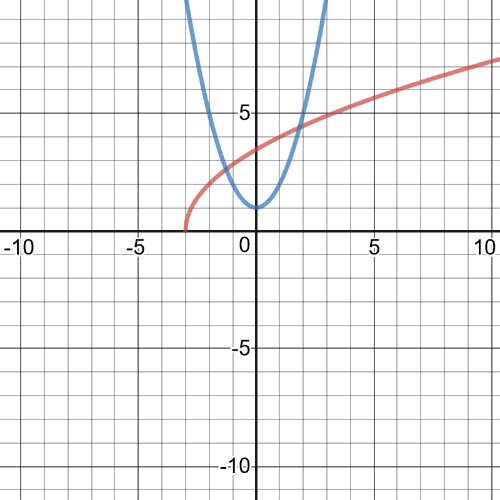
$f(x)<g(x): 1.3< x g(x): 0 < x < 1.3$ or $1.6 < x < 3$
$5sec{x}=-x^2$
We can try $x=2$: $5sec2=-2^2 Rightarrow -12=-4$
We can try $x=2.5$: $5sec2.5=-2.5^2 Rightarrow -6.24=-6.25$
$textbf{So}$, $x=2.5$
#### (b)
$sin^3{x}=sqrt{x}-1$
We can try $x=2$: $sin^32=sqrt{2}-1Rightarrow 0.75=0.41$
Now, we can try $x=2.2$: $sin^32.2=sqrt{2.2}-1 Rightarrow 0.53=0.48$
$textbf{So}$, $x=2.2$
#### (c)
$5^x=x^5$
We can try $x=1$: $5^1=1^5 Rightarrow 5=1$
Now, we can try $x=2$: $5^2=2^5 Rightarrow 25=32$
We can try $x=1.9$: $5^1.9=1.9^5 Rightarrow 21.28=24.76$
We can try $x=1.8$: $5^1.8=1.8^5 Rightarrow 18.12=18.9$
$textbf{So}$, $x=1.8$.
$cos{x}=dfrac{1}{x}$
We can try $x=-2$: $cos-2=dfrac{1}{-2} Rightarrow -0.42=-0.5$
We can try $x=-2.1$: $cos-2.1=dfrac{1}{-2.1} Rightarrow -0.5=-0.58$
$$
textbf{So, $x=-2.1$.}
$$
#### (e)
$log{x}=(x-10)^2+1$
We can try $x=9$: $log9=(9-10)^2+1 Rightarrow 0.95=0$
We can try $x=10$: $log10=(10-10)^2+1 Rightarrow 1=1$
$textbf{So, $x=10$}$.
#### (f)
$sin(2pi{x})=-4x^2+16x-12$
We can try $x=0$: $sin0=-4(0)^2+16cdot0-12 Rightarrow 0=-12$
We can try $x=1$: $sin1=-4(1)^2+16cdot1-12 Rightarrow 0=0$
We can try $x=3$: $sin6pi=-4(3)^2+16cdot3-12 Rightarrow 0=0$
$textbf{So, $x=1$ or $x=3$}$.
#### (a)
$x=1.81$ or $x=0.48$
#### (b)
$x=-1.38$ or $x=1.6$
#### (c)
$x=-1.38$ or $x=1.30$
#### (d)
$x=-0.8$ or $x=0.8$
#### (e)
$x=0.21$ or $x=0.74$
#### (f)
$x=0$ or $x=0.18$ or $x=0.38$ or $x=1$
$y=-3x^2$
$y=-3(0.7)^2$
$y=-1.47$
So, the coordinates are $(0.7, -1.5)$.
We can use graphing calculator to estimate the solution, and according to it, we can conclude that $textbf{solution is}$ $t=15$.
So, they will be $textbf{about the same in}$ $1997+15$ or $2012.$
$textbf{(a)}$ $xin(-0.57,1)$
$textbf{(b)}$ $xin[0,0.58]$
$textbf{(c)}$ $xin(-infty,0)$
$textbf{(d)}$ $xin(0.17,0.83)$
$textbf{(e)}$ $xin(0.35,1.51)$
$textbf{(f)}$ $xin(0.1,0.5)$
$textbf{(b)}$ $xin[0,0.58]$
$textbf{(c)}$ $xin(-infty,0)$
$textbf{(d)}$ $xin(0.17,0.83)$
$textbf{(e)}$ $xin(0.35,1.51)$
$textbf{(f)}$ $xin(0.1,0.5)$
$acos(-1.2)=b(-1.2)^3+6$
$acos(-0.7)=b(-0.7)^3+6$
$0.36a=-1.728b+6$
$0.76a=-0.343b+6$
$dfrac{-1.728b+6}{0.36}=dfrac{-0.343b+6}{0.76}$
$-1.31328b+4.56=-0.12348b+2.16$
$-1.1898b=-2.4$
$b=2$
So, we have that $a=dfrac{-1.728cdot2+6}{0.36}=7$
$textbf{Finally, we have that}$ $a=7, b=2$.
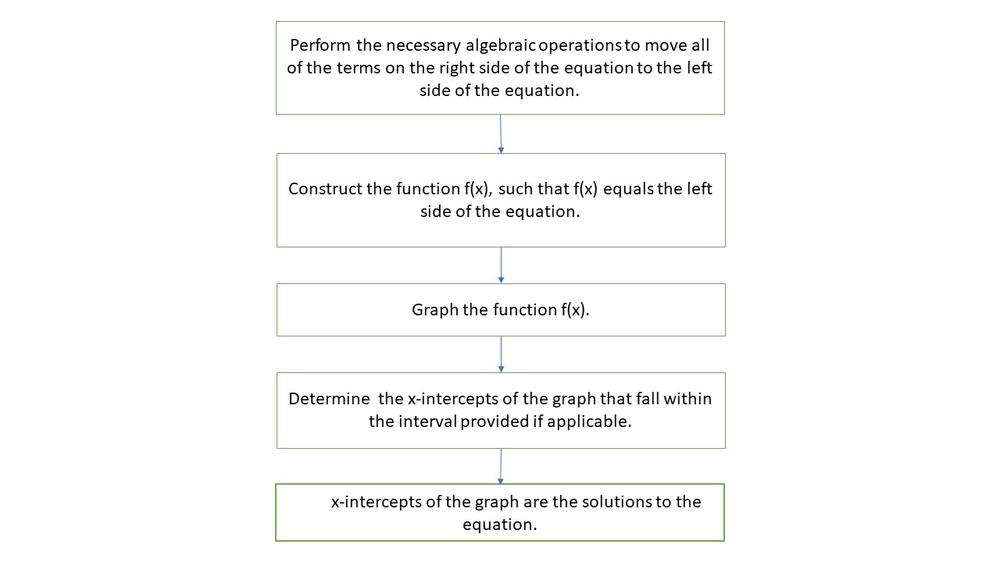
$x=0pm2n, x=-0.67pm2n$, or $x=0.62pm2n, ninBbb{I}$.
$xin(2n,2n+1), ninBbb{I}$.

