
All Solutions
Page 542: Further Your Understanding
$(f div g)(x)=dfrac{5}{x}, xne0$
#### (b)
$(f div g)(x)=dfrac{4x}{2x-1}, xnedfrac{1}{2}$
#### (c)
$(fdiv g)(x)=dfrac{4x}{x^2+4}$
#### (d)
$(fdiv g)(x)=dfrac{(x+2)(sqrt{x-2})}{x-2}, x>2$
#### (e)
$(fdiv g)(x)=dfrac{8}{1+left(dfrac{1}{2} right)^x}$
#### (f)
$(fdiv g)(x)=dfrac{x^2}{log(x)}, x>0$
1(a):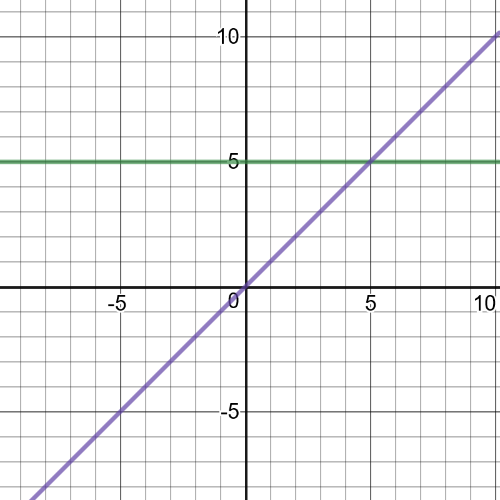
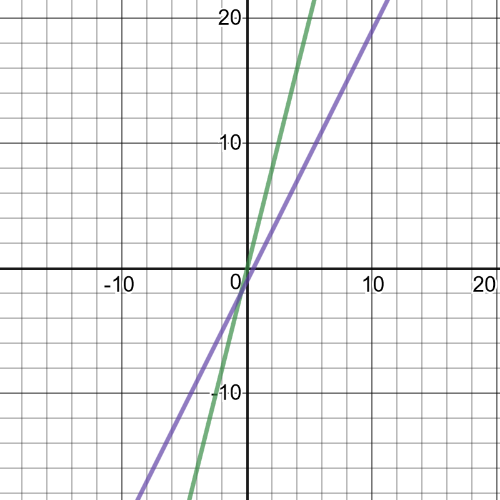
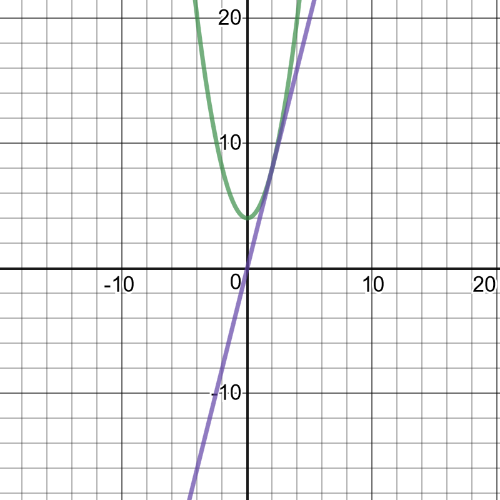
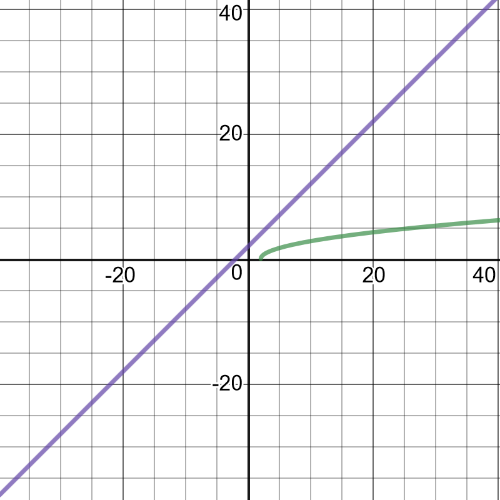
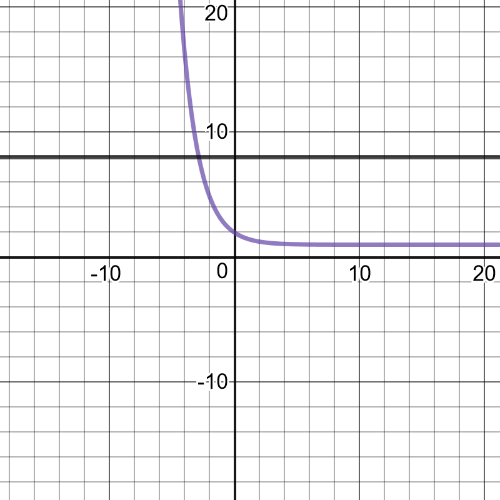
1(a): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$
1(b): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$
1(c): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$
1(d): domain of $f: left{xinBbb{R} right}$; domain of $g:left{ xinBbb{R}|xgeq 2right}$
1(e): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$
1(f): domain of $f: left{xinBbb{R} right}$; domain of $g:left{xinBbb{R}|x > 0 right}$
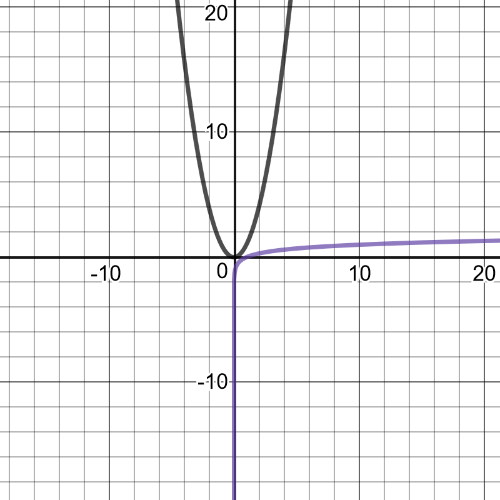
1(a):
1(a): domain of $(fdiv g): left{xinBbb{R}|xne 0 right}$
1(b): domain of $(fdiv g): left{ xinBbb{R}|xne dfrac{1}{2}right}$
1(c): domain of $(fdiv g): left{xinBbb{R} right}$
1(d): domain of $(fdiv g): left{xinBbb{R}|x > 2 right}$
1(e): domain of $(fdiv g): left{xinBbb{R} right}$
1(f): domain of $(fdiv g): left{xin Bbb{R}|x > 0 right}$
$dfrac{260}{1+24(0.9)^t}=dfrac{260}{1+24(0.9)^{20}}=66$cm
textbf{The rate of change is $left[66-(260 div 25) right] div 20$ or $2.798$ cm/day.
}
#### (b)
The maximum height is $260$, so half of $260$ is $130$ cm.
$130=dfrac{260}{1+24(0.9)^t}$
$130+3120(0.9)^t=260$
$3120(0.9)^t=130$
$(0.9)^t=130 div 3120$
$tlog0.9=log(130 div 3120)$
$t=30$ days
#### (c)
$left(dfrac{260}{1+24(0.9)^{30.1}}-dfrac{260}{1+24 (0.9)^{30}} right)div 0.1= 6.848$ cm/day
#### (d)
It slows down and eventually comes to zero.This is seen on the graph as it becomes horizontal at the top.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

