We would like to prove that $color{#4257b2}dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}=cos x$. First, we will simplify the left side and see it will equal the left side or not.

We note that the left side is $color{#4257b2}dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}$ but we know that the Pythagorean identity $color{#4257b2}sin^{2}x+cos^{2}x=1$, so we can use this identity to replace $color{#4257b2}1$ from the numerator by $color{#4257b2}sin^{2}x+cos^{2}x$

$$
begin{align*}
dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}&=dfrac{sin^{2}x+cos^{2}x-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}
\ \
&=dfrac{cos^{2}x-sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}
end{align*}
$$

Now we can factor the term $color{#4257b2}cos^{2}x-sin^{2}x$.

$$
begin{align*}
dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}&=dfrac{cos^{2}x-sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}
\ \
&=dfrac{left(cos x-sin xright)left(cos x+sin xright)}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}
\ \
&=dfrac{left(cos x-sin xright)cancel{left(cos x+sin xright)}}{cancel{cos x+sin x}}+2sin dfrac{x}{2}cos dfrac{x}{2}
\ \
&=cos x-sin x+2sin dfrac{x}{2}cos dfrac{x}{2}
end{align*}
$$

Now we can use the double angle formula for the sine function where
$color{#4257b2}sin x=2sin dfrac{x}{2}cos dfrac{x}{2}$.

$$
begin{align*}
dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}&=cos x-sin x+2sin dfrac{x}{2}cos dfrac{x}{2}
\ \
&=cos x-sin x+sin x
\ \
&=cos xcancel{-sin x}+cancel{sin x}
\ \
&=cos x
end{align*}
$$

So the left side can be simplified to $color{#4257b2}cos x$ which equals the right side, so we proved that $color{#4257b2}dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}=cos x$.

$$
color{#c34632}dfrac{1-2sin^{2}x}{cos x+sin x}+2sin dfrac{x}{2}cos dfrac{x}{2}=cos x
$$

We would like to solve the equation $color{#4257b2}cos 2x+2sin^{2}x-3=-2$, where $color{#4257b2}0 leq x leq 2pi$. First, we can use the double angle formula for the cosine function where $color{#4257b2}cos 2x=1-2sin^{2}x$.

$$
cos 2x+2sin^{2}x-3=-2
$$

$$
1-2sin^{2}x+2sin^{2}x-3=-2
$$

$$
1cancel{-2sin^{2}x}+cancel{2sin^{2}x}-3=-2
$$

$$
1-3=-2
$$

$$
-2=-2
$$

We note that the equation doesn’t contain the variable $color{#4257b2}x$ which means that the equation is independent on the variable $color{#4257b2}x$, so this equation has infinite no of solutions in the interval $color{#4257b2}0 leq x leq 2pi$ which means that all the interval is the solution of the equation.

$$
text{color{#c34632}Infinite no of solutions over the interval $0 leq x leq 2pi$}
$$

(a) We would like to solve the equation $color{#4257b2}cos x=dfrac{sqrt{3}}{2}$, where $color{#4257b2}0 leq x leq 2pi$. First, we can take $color{#4257b2}cos^{-1}$ for each side to find the values of $color{#4257b2}x$.

$$
cos x=dfrac{sqrt{3}}{2}
$$

$$
cos^{-1}left(cos xright)=cos^{-1}left(dfrac{sqrt{3}}{2}right)
$$

$$
x=cos^{-1}left(dfrac{sqrt{3}}{2}right)
$$

$$
x=dfrac{pi}{6}
$$

Note that $color{#4257b2}dfrac{pi}{6}$ is a special angle which we know the value of the cosine function of it where $color{#4257b2}cos dfrac{pi}{6}=dfrac{sqrt{3}}{2}$.

Now we found the related acute angle for the equation $color{#4257b2}cos x=dfrac{sqrt{3}}{2}$, so the next step is to know in which quadrants the solutions are exist. We note that $color{#4257b2}cos x=dfrac{sqrt{3}}{2}$ which means that it is positive, so the solutions are in quadrant $1$ and quadrant $4$ where the cosine ratio is positive in these quadrants. Now we can use the related acute angle to find the solutions of the equation.

$$
x=dfrac{pi}{6} text{or} x=2pi-dfrac{pi}{6}
$$

$$
x=dfrac{pi}{6} text{or} x=dfrac{11pi}{6}
$$

So the solutions of the equation are $boxed{ x=dfrac{pi}{6} } text{or} boxed{ x=dfrac{11pi}{6} }$

(b) We would like to solve the equation $color{#4257b2}tan x=-sqrt{3}$, where $color{#4257b2}0 leq x leq 2pi$. First, we can take $color{#4257b2}tan^{-1}$ for each side to find the values of $color{#4257b2}x$.

$$
tan x=-sqrt{3}
$$

$$
tan^{-1}left(tan xright)=tan^{-1}left(-sqrt{3}right)
$$

$$
x=tan^{-1}left(-sqrt{3}right)
$$

Now we will calculate $color{#4257b2}tan^{-1}left(sqrt{3}right)$ to find the related acute angle.

$$
x=dfrac{pi}{3}
$$

Note that $color{#4257b2}dfrac{pi}{3}$ is a special angle which we know the value of the tangent function of it where $color{#4257b2}tan dfrac{pi}{3}=sqrt{3}$.

Now we found the related acute angle for the equation $color{#4257b2}tan x=-sqrt{3}$, so the next step is to know in which quadrants the solutions are exist. We note that $color{#4257b2}tan x=-sqrt{3}$ which means that it is negative, so the solutions are in quadrant $2$ and quadrant $4$ where the tangent ratio is negative in these quadrants. Now we can use the related acute angle to find the solutions of the equation.

$$
x=pi-dfrac{pi}{3} text{or} x=2pi-dfrac{pi}{3}
$$

$$
x=dfrac{2pi}{3} text{or} x=dfrac{5pi}{3}
$$

So the solutions of the equation are $boxed{ x=dfrac{2pi}{3} } text{or} boxed{ x=dfrac{5pi}{3} }$

(c) We would like to solve the equation $color{#4257b2}sin x=-dfrac{sqrt{2}}{2}$, where $color{#4257b2}0 leq x leq 2pi$. First, we can take $color{#4257b2}sin^{-1}$ for each side to find the values of $color{#4257b2}x$.

$$
sin x=-dfrac{sqrt{2}}{2}
$$

$$
sin^{-1}left(sin xright)=sin^{-1}left(-dfrac{sqrt{2}}{2}right)
$$

$$
x=sin^{-1}left(-dfrac{sqrt{2}}{2}right)
$$

Now we will calculate $color{#4257b2}sin^{-1}left(dfrac{sqrt{2}}{2}right)$ to find the related acute angle.

$$
x=dfrac{pi}{4}
$$

Note that $color{#4257b2}dfrac{pi}{4}$ is a special angle which we know the value of the sine function of it where $color{#4257b2}sin dfrac{pi}{4}=dfrac{sqrt{2}}{2}$.

Now we found the related acute angle for the equation $color{#4257b2}sin x=-dfrac{sqrt{2}}{2}$, so the next step is to know in which quadrants the solutions are exist. We note that $color{#4257b2}sin x=-dfrac{sqrt{2}}{2}$ which means that it is negative, so the solutions are in quadrant $3$ and quadrant $4$ where the sine ratio is negative in these quadrants. Now we can use the related acute angle to find the solutions of the equation.

$$
x=pi+dfrac{pi}{4} text{or} x=2pi-dfrac{pi}{4}
$$

$$
x=dfrac{5pi}{4} text{or} x=dfrac{7pi}{4}
$$

So the solutions of the equation are $boxed{ x=dfrac{5pi}{4} } text{or} boxed{ x=dfrac{7pi}{4} }$

$$
text{color{#c34632}(a) $x=dfrac{pi}{6}$ {color{Black}text{or}} $x=dfrac{11pi}{6}$
\
\
\
Large{color{#c34632}(b) $x=dfrac{2pi}{3}$ {color{Black}text{or}} $x=dfrac{5pi}{3}$}
\
\
\
Large{color{#c34632}(c) $x=dfrac{5pi}{4}$ {color{Black}text{or}} $x=dfrac{7pi}{4}$}}
$$

We would like to find the values $color{#4257b2}a$ and $color{#4257b2}b$ in the quadratic trigonometric equation $color{#4257b2}a cos^{2}x+b cos x-1=0$ if we know that this equation has the solutions $color{#4257b2}dfrac{pi}{3}, pi$ and $color{#4257b2}dfrac{5pi}{3}$. First, Since we know the solutions of the equation, so we can substitute the first two solutions in the equation and find two equations in the two variables $color{#4257b2}a$ and $color{#4257b2}b$ and then solve them to find the values of them.

For the solution $color{#4257b2}dfrac{pi}{3}$

$$
a cos^{2}x+b cos x-1=0
$$

$$
a cos^{2}dfrac{pi}{3}+b cos dfrac{pi}{3}-1=0
$$

$$
acdot left(dfrac{1}{2}right)^{2}+b cdot left(dfrac{1}{2}right)-1=0
$$

Note that $color{#4257b2}dfrac{pi}{3}$ is a special angle which we know the value of the cosine function of it where $color{#4257b2}cos dfrac{pi}{3}=dfrac{1}{2}$.

$$
dfrac{1}{4} a+dfrac{1}{2} b-1=0
$$

$$
dfrac{1}{4} a+dfrac{1}{2} b=1
$$

Now we can multiply the two sides by $4$.

$$
a+2b=4 (1)
$$

Now we found the first equation which relates the two variables $color{#4257b2}a$ and $color{#4257b2}b$, so the next step is to substitute the solution $color{#4257b2}pi$ in the trigonometric equation to find the second equation.

For the solution $color{#4257b2}pi$

$$
a cos^{2}x+b cos x-1=0
$$

$$
a cos^{2}pi+b cos pi-1=0
$$

$$
acdot left(-1right)^{2}+b cdot (-1)-1=0
$$

Note that $color{#4257b2}pi$ is a special angle which we know the value of the cosine function of it where $color{#4257b2}cos pi=-1$.

$$
acdot 1- b-1=0
$$

$$
a-b-1=0
$$

$$
a=b+1 (2)
$$

Now we found two equations in the two variables $color{#4257b2}a$ and $color{#4257b2}b$, so we can solve these equations to find the values of $color{#4257b2}a$ and $color{#4257b2}b$. To solve these equations we can substitute the equation (2) in the equation (1) to find the value of $color{#4257b2}b$.

$$
a+2 b=4 (1), a=b+1 (2)
$$

$$
(b+1)+2b=4
$$

$$
3b+1=4
$$

$$
3b=4-1
$$

$$
3b=3
$$

$$
dfrac{3b}{3}=dfrac{3}{3}
$$

$$
boxed{ b=1 }
$$

Now we can substitute the value of $color{#4257b2}c$ in equation (2) to find the value of $color{#4257b2}a$.

$$
a=b+1
$$

$$
a=1+1
$$

$$
boxed{ a=2 }
$$

$$text{color{#c34632}a=2 {color{Black$text{and}} $b=1$}}$

Since we know that the depth of the ocean can be modeled by the function $color{#4257b2}d(t)=4+2sinleft(dfrac{pi}{6} tright)$ where $color{#4257b2}0 leq t leq 24$, so to determine when the depth of water is $color{#4257b2}3 text{m}$ we can substitute $color{#4257b2}d=3$ in the function to determine the time.

$$
d(t)=4+2sinleft(dfrac{pi}{6} tright)
$$

$$
3=4+2sinleft(dfrac{pi}{6} tright)
$$

Now we can subtract $color{#4257b2}4$ from each side to make the sine function in the right side alone.

$$
-1=2sinleft(dfrac{pi}{6} tright)
$$

Now we can divide the two sides by $color{#4257b2}2$.

$$
sin left(dfrac{pi}{6} tright)=-dfrac{1}{2}
$$

Now we can take $color{#4257b2}sin^{-1}$ for each side to find the related acute angle.

$$
sin^{-1}left[sin left(dfrac{pi}{6} tright)right]=sin^{-1}left(-dfrac{1}{2}right)
$$

$$
dfrac{pi}{6} t=sin^{-1}left(-dfrac{1}{2}right)
$$

Note that $color{#4257b2}sin^{-1}left(sin thetaright)$, so $color{#4257b2}sin^{-1}left[sin left(dfrac{pi}{6} tright)right]=dfrac{pi}{6} t$. Now we can calculate $color{#4257b2}sin^{-1}left(dfrac{1}{2}right)$ to determine the related acute angle.

$$
dfrac{pi}{6} t=dfrac{pi}{6}
$$

Note that $color{#4257b2}dfrac{pi}{6}$ is a special angle which we know the value of the sine function of it where $color{#4257b2}sin dfrac{pi}{6}=dfrac{1}{2}$.

Now we found the related acute angle for the equation $color{#4257b2}sin left(dfrac{pi}{6} tright)=-dfrac{1}{2}$, so the next step is to know in which quadrants the solutions are exist. we note that $color{#4257b2}sin left(dfrac{pi}{6} tright)=-dfrac{1}{2}$ which means that it is negative, so the solutions are in quadrant $3$ and quadrant $4$. Now we can use the related acute angle to find these solutions.

$$
dfrac{pi}{6} t=pi+dfrac{pi}{6} text{or} dfrac{pi}{6} t=2pi-dfrac{pi}{6}
$$

$$
dfrac{pi}{6} t=dfrac{7pi}{6} text{or} dfrac{pi}{6} t=dfrac{11pi}{6}
$$

But we know that the period of the sine function is $color{#4257b2}2pi$, so we can add $color{#4257b2}2 n pi$ to each side in the two solutions we found in the last step to find the general solution of $color{#4257b2}dfrac{pi}{6} t$ where $color{#4257b2}n$ is any integer number.

$$
dfrac{pi}{6} t=dfrac{7pi}{6}+2 n pi text{or} dfrac{pi}{6} t=dfrac{11pi}{6}+2n pi
$$

Now to find the values of $color{#4257b2}t$ we can substitute $color{#4257b2}n=0, 1, dots$ and we will stop when the value of $color{#4257b2}t$ is not exist in the interval $color{#4257b2}0 leq t leq 24$

at $color{#4257b2}n=0$

$$
dfrac{pi}{6} t=dfrac{7pi}{6}+2 (0) pi text{or} dfrac{pi}{6} t=dfrac{11pi}{6}+2 (0) pi
$$

$$
dfrac{pi}{6} t=dfrac{7pi}{6} text{or} dfrac{pi}{6} t=dfrac{11pi}{6}
$$

Now we can multiply the two sides by $color{#4257b2}dfrac{6}{pi}$.

$$
left(dfrac{6}{pi}right)left(dfrac{pi}{6} tright)=left(dfrac{6}{pi}right)left(dfrac{7pi}{6}right) text{or} left(dfrac{6}{pi}right)left(dfrac{pi}{6} tright)=left(dfrac{6}{pi}right)left(dfrac{11pi}{6}right)
$$

$$
boxed{ t=7 } text{or} boxed{ t=11 }
$$

at $color{#4257b2}n=1$

$$
dfrac{pi}{6} t=dfrac{7pi}{6}+2 pi text{or} dfrac{pi}{6} t=dfrac{11pi}{6}+2 pi
$$

$$
dfrac{pi}{6} t=dfrac{19pi}{6} text{or} dfrac{pi}{6} t=dfrac{23pi}{6}
$$

Now we can multiply the two sides by $color{#4257b2}dfrac{6}{pi}$.

$$
left(dfrac{6}{pi}right)left(dfrac{pi}{6} tright)=left(dfrac{6}{pi}right)left(dfrac{19pi}{6}right) text{or} left(dfrac{6}{pi}right)left(dfrac{pi}{6} tright)=left(dfrac{6}{pi}right)left(dfrac{23pi}{6}right)
$$

$$
boxed{ t=19 } text{or} boxed{ t=23 }
$$

Note that we will not substitute $color{#4257b2}n=2$ because in this case the value of $color{#4257b2}t$ will not be exist in the interval $color{#4257b2}0 leq t leq 24$.

So the values of $color{#4257b2}t$ when the depth of the water is $color{#4257b2}3 text{m}$ are $color{#4257b2}t=7, t=11, t=19$ and $color{#4257b2}t=23$ which means that these times will be at $color{#4257b2}7 text{Am}, 11 text{Am}, 7 text{Pm}$ and $color{#4257b2}11 text{Pm}$ because we consider the day when $color{#4257b2}t=0$ represents midnight.

$$text{color{#c34632}7 text{Am}, 11 text{Am}, 7 text{Pm} {color{Black$text{and}} $11 text{Pm}$}}$

We would like to find the value of $color{#4257b2}cos dfrac{11pi}{4}$. First, we know that
$color{#4257b2}dfrac{11pi}{4}=pi+dfrac{7pi}{4}$, so we can rewrite the cosine function using this fact.

$$
cos dfrac{11pi}{4}=cos left(pi+dfrac{7pi}{4}right)
$$

Note that we rewrite $color{#4257b2}dfrac{11pi}{4}=pi+dfrac{7pi}{4}$ because we know the values of the sine and cosine of $color{#4257b2}pi$, as well as the sine and cosine of $color{#4257b2}dfrac{7pi}{4}$. Now we note that our function is a cosine function with two sum angles, so we can use the addition formula for the cosine function where $color{#4257b2}cos (a+b)=cos acos b-sin asin b$.

$$
begin{align*}
cos dfrac{11pi}{4}&=cos left(pi+dfrac{7pi}{4}right)
\ \
&=cos picos dfrac{7pi}{4}-sin pisin dfrac{7pi}{4}
\ \
&=(-1)cdot left(dfrac{sqrt{2}}{2}right)-(0)cdot left(-dfrac{sqrt{2}}{2}right)
\ \
&=-dfrac{sqrt{2}}{2}+0
\ \
&=-dfrac{sqrt{2}}{2}
end{align*}
$$

So we found the cosine of $color{#4257b2}dfrac{11pi}{4}$ by knowing the sine and cosine of $color{#4257b2}pi$, as well as the sine and cosine of $color{#4257b2}dfrac{7pi}{4}$ by applying the addition formula for the cosine function and the value it is $boxed{ -dfrac{sqrt{2}}{2} }$

$$
color{#c34632}cos dfrac{11pi}{4}=-dfrac{sqrt{2}}{2}
$$

We would like to solve the equation $color{#4257b2}3sin x+2=1.5$, where $color{#4257b2}0 leq x leq 2pi$. First, we can subtract $color{#4257b2}2$ from each side to make $color{#4257b2}sin x$ in the left side alone.

$$
3sin x+2=1.5
$$

$$
3sin x=1.5-2=-0.5
$$

Now we can divide the two sides by $color{#4257b2}3$

$$
dfrac{3sin x}{3}=dfrac{-0.5}{3}
$$

$$
sin x=-dfrac{1}{6}
$$

Now we can take $color{#4257b2}sin^{-1}$ for each side to find the values of $color{#4257b2}x$.

$$
sin^{-1}left(sin xright)=sin^{-1}left(-dfrac{1}{6}right)
$$

$$
x=sin^{-1}left(-dfrac{1}{6}right)
$$

Now we will calculate $color{#4257b2}sin^{-1}left(dfrac{1}{6}right)$ to find the related acute angle.

$$
x=0.17 text{radians}
$$

Now we found the related acute angle for the equation $color{#4257b2}sin x=-dfrac{1}{6}$, so the next step is to know in which quadrants the solutions are exist. We note that $color{#4257b2}sin x=-dfrac{1}{6}$ which means that it is negative, so the solutions are in quadrant $3$ and quadrant $4$ where the sine ratio is negative in these quadrants. Now we can use the related acute angle to find the solutions of the equation.

$$
x=pi+0.17=3.31 text{radians} text{or} x=2pi-0.17=6.12 text{radians}
$$

So the solutions of the equation are $boxed{ x=3.31 text{radians} } text{or} boxed{ x=6.12 text{radians} }$

$$
text{color{#c34632}(a) $x=3.31 text{radians}$ {color{Black}text{or}} $x=6.12 text{radians}$}
$$

Since we would like to determine the value of $color{#4257b2}sin left(alpha-betaright)$ and $color{#4257b2}cos left(alpha+betaright)$, so we need to know the values of $color{#4257b2}sin alpha, cos alpha, sin beta$ and $color{#4257b2}cos beta$ and then substitute in the subtraction formula of the sine function and the addition formula of the cosine function. We note that $color{#4257b2}tan alpha=0.75$ and $color{#4257b2}tan beta=2.4$, so we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to find the value of $color{#4257b2}sec alpha$ and $color{#4257b2}sec beta$.

$$
1+tan^{2}alpha=sec^{2}alpha
$$

$$
1+left(0.75right)^{2}=sec^{2}alpha
$$

$$
1+dfrac{9}{16}=sec^{2}alpha
$$

$$
sec^{2}alpha=1+dfrac{9}{16}=dfrac{25}{16}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}sec alpha$.

$$
sec alpha=pm sqrt{dfrac{25}{16}}=pm dfrac{5}{4}
$$

But we know that the angle $color{#4257b2}alpha$ is acute angle which means that it is in quadrant $1$, so the value of $color{#4257b2}sec alpha$ is positive.

$$
sec alpha=dfrac{5}{4}
$$

But we know that $color{#4257b2}sec alpha=dfrac{1}{cos alpha}$, so we can use this identity in our equation.

$$
dfrac{1}{cos alpha}=dfrac{5}{4}
$$

$$
boxed{ cos alpha=dfrac{4}{5} }
$$

Now we have the value of $color{#4257b2}cos alpha$ and $color{#4257b2}tan alpha$, so we can use the identity $color{#4257b2}tan alpha=dfrac{sin alpha}{cos alpha}$ to find the value of $color{#4257b2}sin alpha$.

$$
tan alpha=dfrac{sin alpha}{cos alpha}
$$

$$
sin alpha=tan alphacos alpha
$$

$$
sin alpha=left(0.75right)cdot left(dfrac{4}{5}right)
$$

$$
boxed{ sin alpha=dfrac{3}{5} }
$$

Now we found the value of $color{#4257b2}sin alpha$ and $color{#4257b2}cos alpha$, so the next step is to find the value of $color{#4257b2}sin beta$ and $color{#4257b2}cos beta$ by the same way.

$$
1+tan^{2}beta=sec^{2}beta
$$

$$
1+left(2.4right)^{2}=sec^{2}beta
$$

$$
1+dfrac{144}{25}=sec^{2}beta
$$

$$
sec^{2}beta=1+dfrac{144}{25}=dfrac{169}{25}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}sec beta$.

$$
sec beta=pm sqrt{dfrac{169}{25}}=pm dfrac{13}{5}
$$

But we know that the angle $color{#4257b2}beta$ is acute angle which means that it is in quadrant $1$, so the value of $color{#4257b2}sec beta$ is positive.

$$
sec beta=dfrac{13}{5}
$$

But we know that $color{#4257b2}sec beta=dfrac{1}{cos beta}$, so we can use this identity in our equation.

$$
dfrac{1}{cos beta}=dfrac{13}{5}
$$

$$
boxed{ cos beta=dfrac{5}{13} }
$$

Now we have the value of $color{#4257b2}cos beta$ and $color{#4257b2}tan beta$, so we can use the identity $color{#4257b2}tan beta=dfrac{sin beta}{cos beta}$ to find the value of $color{#4257b2}sin beta$.

$$
tan beta=dfrac{sin beta}{cos beta}
$$

$$
sin beta=tan betacos beta
$$

$$
sin beta=left(2.4right)cdot left(dfrac{5}{13}right)
$$

$$
boxed{ sin beta=dfrac{12}{13} }
$$

Now we found the value of $color{#4257b2}sin alpha, cos alpha, sin beta$ and $color{#4257b2}cos beta$, so to find $color{#4257b2}sin left(alpha-betaright)$ and $color{#4257b2}cos left(alpha+betaright)$ we can use the subtraction formula of the sine function where $color{#4257b2}sin (a-b)=sin acos b-cos asin b$ and we can use the addition formula of the cosine function where $color{#4257b2}cos (a+b)=cos acos b-sin asin b$.

$$
begin{align*}
sinleft(alpha-betaright)&=sin alphacos beta-cos alphasin beta
\ \
&=left(dfrac{3}{5}right)cdot left(dfrac{5}{13}right)-left(dfrac{4}{5}right)left(dfrac{12}{13}right)
\ \
&=dfrac{15}{65}-dfrac{48}{65}
\ \
&=boxed{ -dfrac{33}{65} }
end{align*}
$$

$$
begin{align*}
cosleft(alpha+betaright)&=cos alphacos beta-sin alphasin beta
\ \
&=left(dfrac{4}{5}right)cdot left(dfrac{5}{13}right)-left(dfrac{3}{5}right)left(dfrac{12}{13}right)
\ \
&=dfrac{20}{65}-dfrac{36}{65}
\ \
&=boxed{ -dfrac{16}{65} }
end{align*}
$$

Large{$text{color{#c34632}$sin left(alpha-betaright)=-dfrac{33}{65}$ $cos left(alpha+betaright)=-dfrac{16}{65}$}$

Since we would like to determine the value of $color{#4257b2}sin 2x, cos 2x, cos dfrac{x}{2}$ and $color{#4257b2}sin 3x$, so we need to know the values of $color{#4257b2}sin x$ and $color{#4257b2}cos x$ and then substitute in the formula of each function of them. We note that $color{#4257b2}sin^{2}x=dfrac{4}{9}$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to find the value of $color{#4257b2}cos x$.

$$
sin^{2}x+cos^{2}x=1
$$

$$
dfrac{4}{9}+cos^{2}x=1
$$

$$
cos^{2}x=1-dfrac{4}{9}=dfrac{5}{9}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}cos x$.

$$
cos x=pm sqrt{dfrac{5}{9}}=pm dfrac{sqrt{5}}{3}
$$

But we know that $color{#4257b2}dfrac{pi}{2} leq x leq pi$ is acute angle which means that it is in quadrant $2$, so the value of $color{#4257b2}cos x$ is negative.

$$
boxed{ cos alpha=-dfrac{sqrt{5}}{3} }
$$

Since we know that $color{#4257b2}sin^{2}x=dfrac{4}{9}$, so to find the value of $color{#4257b2}sin x$ we can take the square root for each side.

$$
sin^{2}x=dfrac{4}{9}
$$

$$
sin x=pm sqrt{dfrac{4}{9}}=pm dfrac{2}{3}
$$

But we know that $color{#4257b2}dfrac{pi}{2} leq x leq pi$ is acute angle which means that it is in quadrant $2$, so the value of $color{#4257b2}sin x$ is negative.

$$
boxed{ sin alpha=dfrac{2}{3} }
$$

Now we found the value of $color{#4257b2}sin x$ and $color{#4257b2}cos x$, so we can solve each requirement as follows:

(a) We would like to find the value of $color{#4257b2}sin 2x$, so we can use the double angle formula of the sine function where $color{#4257b2}sin 2x=2sin xcos x$.

$$
begin{align*}
sin 2x&=2sin xcos x
\ \
&=2cdot left(dfrac{2}{3}right)cdot left(-dfrac{sqrt{5}}{3}right)
\ \
&=-dfrac{4sqrt{5}}{9}=-0.9938
end{align*}
$$

So the value of $color{#4257b2}sin 2x$ is $boxed{ -0.9938 }$

(b) We would like to find the value of $color{#4257b2}cos 2x$, so we can use the double angle formula of the cosine function where $color{#4257b2}cos 2x=cos^{2}x-sin^{2}x$.

$$
begin{align*}
cos 2x&=cos^{2}x-sin^{2}x
\ \
&=left(-dfrac{sqrt{5}}{3}right)^{2}-left(dfrac{2}{3}right)^{2}
\ \
&=dfrac{5}{9}-dfrac{4}{9}
\ \
&=dfrac{1}{9}=0.1111
end{align*}
$$

So the value of $color{#4257b2}cos 2x$ is $boxed{ 0.1111 }$

(c) We would like to find the value of $color{#4257b2}cos dfrac{x}{2}$, so we can use the double angle formula of the cosine function where $color{#4257b2}cos x=2cos^{2}dfrac{x}{2}-1$.

$$
cos x=2cos^{2}dfrac{x}{2}-1
$$

$$
-dfrac{sqrt{5}}{3}=2cos^{2}dfrac{x}{2}-1
$$

Now we can add $color{#4257b2}1$ to each side.

$$
-dfrac{sqrt{5}}{3}+1=2cos^{2}dfrac{x}{2}-1+1
$$

$$
dfrac{3-sqrt{5}}{3}=2cos^{2}dfrac{x}{2}
$$

Now we can divide the two sides by $2$.

$$
cos^{2}dfrac{x}{2}=dfrac{3-sqrt{5}}{6}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}cos dfrac{x}{2}$.

$$
cos dfrac{x}{2}=pm sqrt{dfrac{3-sqrt{5}}{6}}
$$

$$
cos dfrac{x}{2}=pm 0.3568
$$

But we that $color{#4257b2} dfrac{pi}{2} leq x leq pi$, so to know in which quadrant the angle $color{#4257b2}dfrac{x}{2}$ relates we can divide each side by $2$.

$$
dfrac{pi}{2} leq x leq pi
$$

$$
dfrac{pi}{4} leq dfrac{x}{2} leq dfrac{pi}{2}
$$

So the angle $color{#4257b2}dfrac{x}{2}$ in quadrant $1$ where the cosine function is positive in this quadrant, so $color{#4257b2}cos dfrac{x}{2}$ is positive.

$$
boxed{ cos dfrac{x}{2}=0.3568 }
$$

(d) We would like to find the value of $color{#4257b2}sin 3x$, First, we can rewrite $color{#4257b2}sin 3x$ as $color{#4257b2}sin left(2x+xright)$ to make our function is sine function with two sum angles. Now we can use the addition formula of the sine function where $color{#4257b2}sin (a+b)=sin acos b+cos asin a$.

$$
begin{align*}
sin (2x+x)&=sin 2xcos x+cos 2xsin x
\ \
&=left(-dfrac{4sqrt{5}}{9}right)cdot left(-dfrac{sqrt{5}}{3}right)+left(dfrac{1}{9}right)cdot left(dfrac{2}{3}right)
\ \
&=dfrac{20}{27}+dfrac{2}{27}
\ \
&=dfrac{22}{27}=0.8148
end{align*}
$$

So the value of $color{#4257b2}sin 3x$ is $boxed{ 0.8148 }$

Large{$text{$text{color{#c34632}(a) $sin 2x=-0.9938$ (c) $cos dfrac{x}{2}=0.3568$
\
\
Large{color{#c34632}(b) $cos 2x=0.1111$ (d) $sin 3x=0.8148$}$}$

We would like to use the graph of $color{#4257b2}f(x)=cos x$ to estimate the solution of each equation in the interval $color{#4257b2}-2pi leq x leq 2pi$.

(a) Since we need to estimate the solutions of the equation $color{#4257b2}2-14cos x=-5$ using the graph of the $color{#4257b2}f(x)=cos x$, we need to simplify this equation and make the function $color{#4257b2}cos x$ in the left side alone and then use the graph of it to find the solutions.

$$
2-14cos x=-5
$$

We can subtract $2$ from each side

$$
2-14cos x-2=-5-2
$$

$$
cancel{2}-14cos xcancel{-2}=-7
$$

$$
-14cos x=-7
$$

Now we can divide the two sides by $-14$.

$$
dfrac{-14cos x}{-14}=dfrac{-7}{-14}
$$

$$
cos x=dfrac{1}{2}
$$

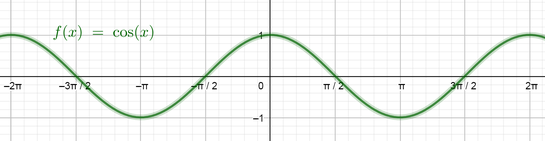
Now our equation consists of the function $color{#4257b2}cos x$ in the left side and the number $color{#4257b2}dfrac{1}{2}$ in the right side, so to find the solutions using the graph of $color{#4257b2}f(x)=cos x$ we can graph the line $color{#4257b2}y=dfrac{1}{2}$ on the same plane of the graph of the cosine function and then find the points where the graph intersects the line and the solutions will be the values of $color{#4257b2}x$ at these points.

We note that the graph $color{#4257b2}f(x)=cos x$ intersects the line $color{#4257b2}y=dfrac{1}{2}$ at the points $color{#4257b2}A, B, C$ and $color{#4257b2}D$, so the solutions will be the values of $color{#4257b2}x$ at these points and these solutions are $color{#4257b2}-dfrac{5pi}{3}, -dfrac{pi}{3}, dfrac{pi}{3}$ and $color{#4257b2}dfrac{5pi}{3}$.

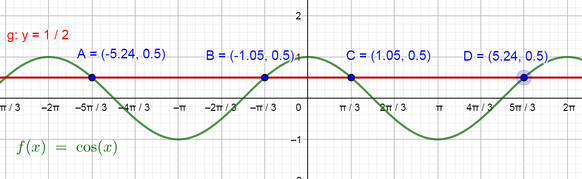
So the solutions of the equation are $color{#4257b2}x=left{-dfrac{5pi}{3}, -dfrac{pi}{3}, dfrac{pi}{3}, dfrac{5pi}{3}right}$

(b) Since we need to estimate the solutions of the equation $color{#4257b2}9-22cos x-1=19$ using the graph of the $color{#4257b2}f(x)=cos x$, we need to simplify this equation and make the function $color{#4257b2}cos x$ in the left side alone and then use the graph of it to find the solutions.

$$
9-22cos x-1=19
$$

$$
8-22cos x=19
$$

We can subtract $8$ from each side

$$
8-22cos x-8=19-8
$$

$$
-22cos x=11
$$

Now we can divide the two sides by $-22$.

$$
dfrac{-22cos x}{-22}=dfrac{11}{-22}
$$

$$
cos x=-dfrac{1}{2}
$$

Now our equation consists of the function $color{#4257b2}cos x$ in the left side and the number $color{#4257b2}-dfrac{1}{2}$ in the right side, so to find the solutions using the graph of $color{#4257b2}f(x)=cos x$ we can graph the line $color{#4257b2}y=-dfrac{1}{2}$ on the same plane of the graph of the cosine function and then find the points where the graph intersects the line and the solutions will be the values of $color{#4257b2}x$ at these points.

We note that the graph $color{#4257b2}f(x)=cos x$ intersects the line $color{#4257b2}y=-dfrac{1}{2}$ at the points $color{#4257b2}A, B, C$ and $color{#4257b2}D$, so the solutions will be the values of $color{#4257b2}x$ at these points and these solutions are $color{#4257b2}-dfrac{4pi}{3}, -dfrac{2pi}{3}, dfrac{2pi}{3}$ and $color{#4257b2}dfrac{4pi}{3}$.

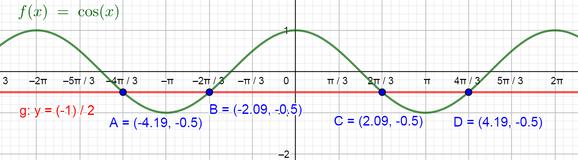
So the solutions of the equation are $color{#4257b2}x=left{-dfrac{4pi}{3}, -dfrac{2pi}{3}, dfrac{2pi}{3}, dfrac{4pi}{3}right}$

(c) Since we need to estimate the solutions of the equation $color{#4257b2}2+7.5cos x=-5.5$ using the graph of the $color{#4257b2}f(x)=cos x$, we need to simplify this equation and make the function $color{#4257b2}cos x$ in the left side alone and then use the graph of it to find the solutions.

$$
2+7.5cos x=-5.5
$$

We can subtract $2$ from each side

$$
2+7.5cos x-2=-5.5-2
$$

$$
7.5cos x=-7.5
$$

Now we can divide the two sides by $7.5$.

$$
dfrac{7.5cos x}{7.5}=dfrac{-7.5}{7.5}
$$

$$
cos x=-1
$$

Now our equation consists of the function $color{#4257b2}cos x$ in the left side and the number $color{#4257b2}-1$ in the right side, so to find the solutions using the graph of $color{#4257b2}f(x)=cos x$ we can graph the line $color{#4257b2}y=-1$ on the same plane of the graph of the cosine function and then find the points where the graph intersects the line and the solutions will be the values of $color{#4257b2}x$ at these points.

We note that the graph $color{#4257b2}f(x)=cos x$ intersects the line $color{#4257b2}y=-1$ at the points $color{#4257b2}A$ and $color{#4257b2}B$, so the solutions will be the values of $color{#4257b2}x$ at these points and these solutions are $color{#4257b2}-pi$ and $color{#4257b2}pi$.

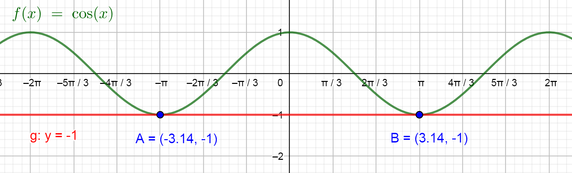
So the solutions of the equation are $color{#4257b2}x=left{-pi, piright}$

$$
text{color{#c34632}(a) $x=left{-dfrac{5pi}{3}, -dfrac{pi}{3}, dfrac{pi}{3}, dfrac{5pi}{3}right}$
\
\
\
Large{color{#c34632}(b) $x=left{-dfrac{4pi}{3}, -dfrac{2pi}{3}, dfrac{2pi}{3}, dfrac{4pi}{3}right}$}
\
\
\
Large{color{#c34632}(c) $x=left{-pi, piright}$}}
$$