
All Solutions
Section 6-3: Exploring Graphs of the Primary Trigonometric Functions
$y=sin theta$ and $y=costheta$ have the same period, axis,amplitude, maximum value,minimum value,domain and range. They have different $y-$ and $theta-$intercepts.
#### (b)
$y=sin theta$ and $y=tan theta$ have no characteristics in common except for theri $y-$ intercept and zeros.
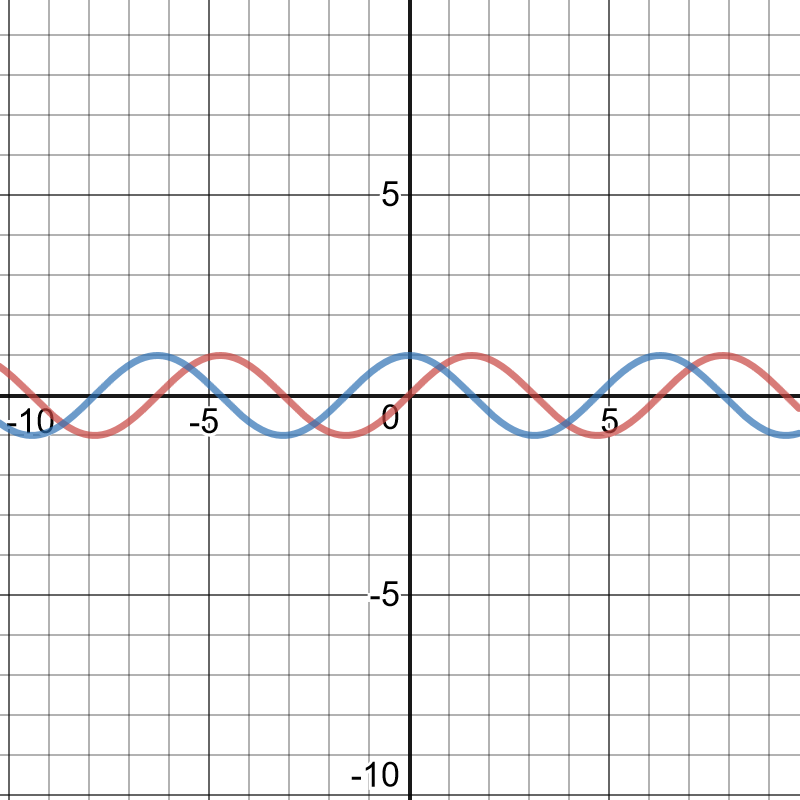
$theta=-5.50$
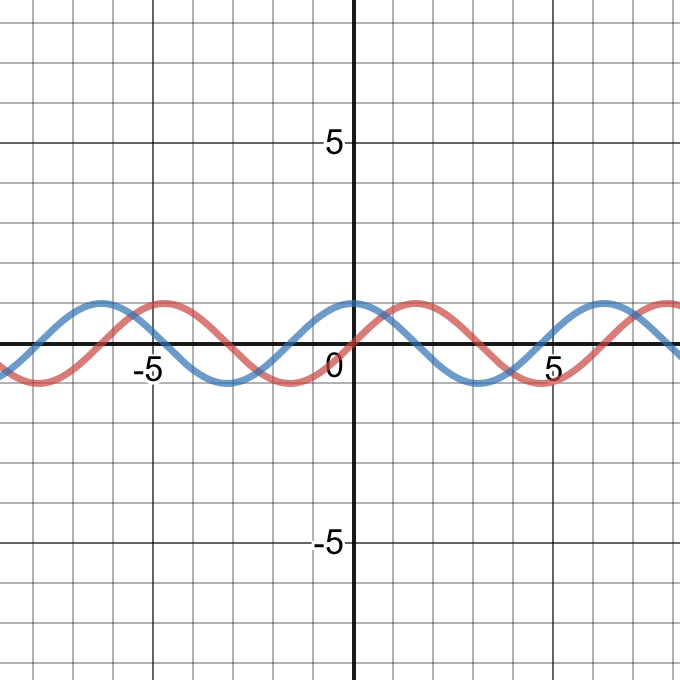
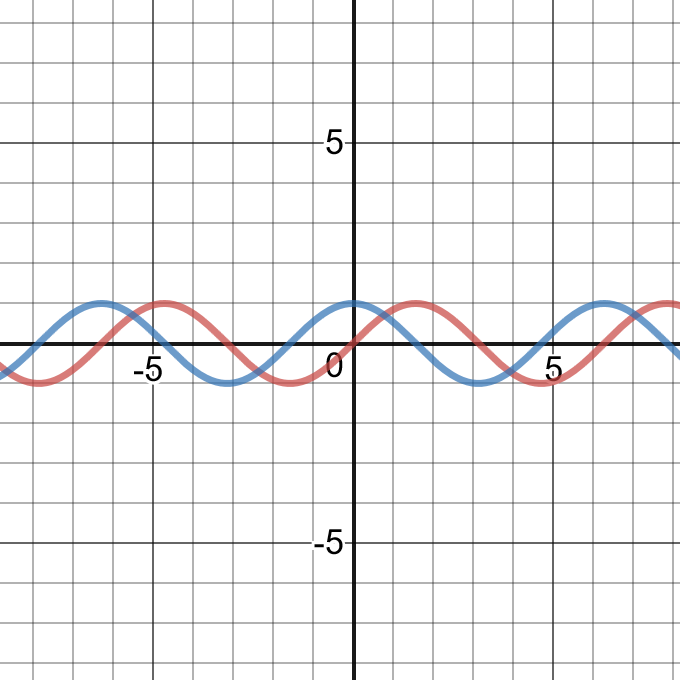
i) The graph of $y=sin theta$ intersects the $theta$-axis at $0, pmpi, pm2pi,…$
$t_{n}=npi, nin I$
ii) The maximum value occurs at $dfrac{pi}{2}$ and every $2pi$, since the period is $2pi$.
$t_{n}=dfrac{pi}{2}+2npi, nin I$
iii) The minimum value occurs at $dfrac{3pi}{2}$ and every $2pi$, since the period is $2pi$.
$t_{n}=dfrac{3pi}{2}+2npi, nin I$
The graph of $y=cos theta$ intersects the $theta-$axis at $pmdfrac{pi}{2}, pm dfrac{3pi}{2}$,…
$t_{n}=dfrac{pi}{2}+npi, nin I$
#### (b)
The maximum values occur at $0$ and every $2pi$, since the period is $2pi$.
$t_{n}=2npi,nin I$
#### (c)
The minimum value occurs at $pi$ and every $2pi$, since the period is $2pi$.
$t_{n}=-pi+2npi, nin I$
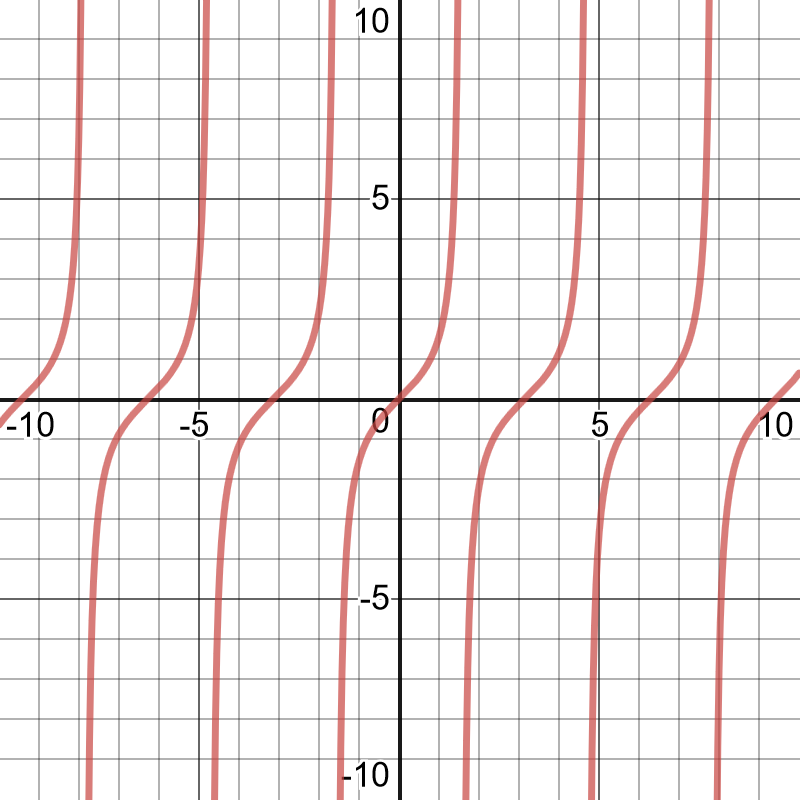
The graph of $y=tan theta$ intersects the $theta$-axis at $0,pmpi,pm2pi,..$
$t_{n}=npi, nin I$
#### (b)
The graph of $y=tan theta$ has vertical asymptotes at $pmdfrac{pi}{2},pmdfrac{3pi}{2}$,…
$t_{n}=dfrac{pi}{2}+npi$, $nin I$
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

