
All Solutions
Section 6-2: Radian Measure and Angles on the Cartesian Plane
$dfrac{3pi}{4}$ is located in the second quadrant.The related angle is $dfrac{pi}{4}$, and $sin$ is positive in the second quadrant.
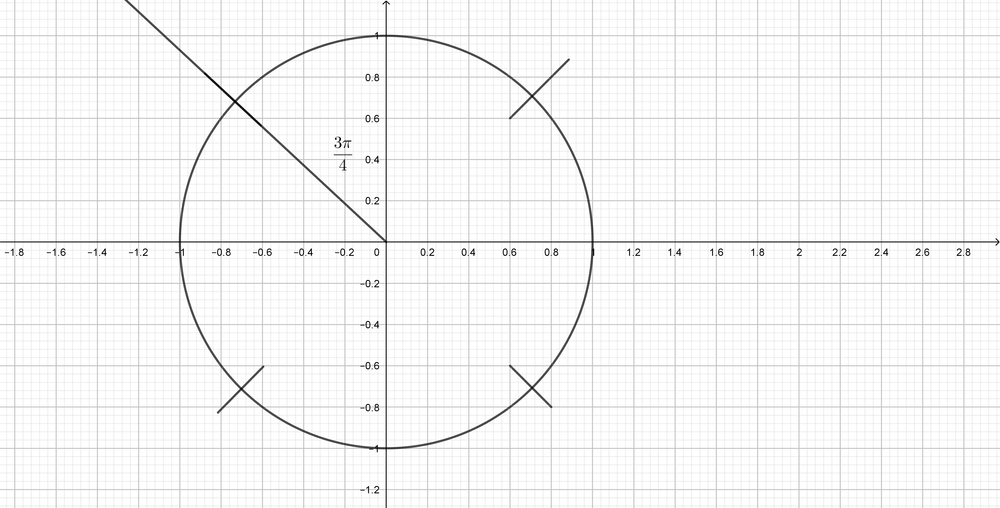
$dfrac{5pi}{3}$ is located in the fourth quadrant.The related angle is $dfrac{pi}{3}$, and $cos$ is positive in the fourth quadrant.
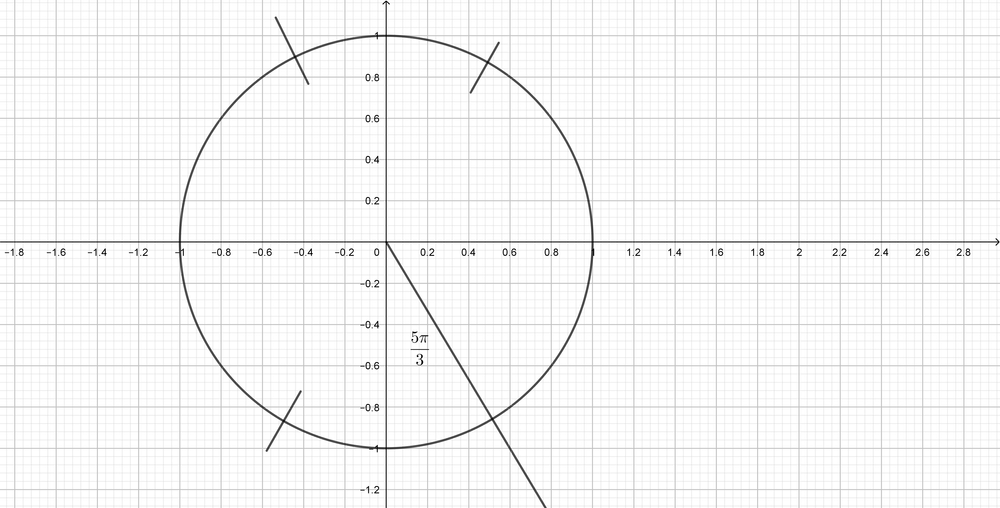
$dfrac{4pi}{3}$ is located in the third quadrant.The related angle is $dfrac{pi}{3}$, and $tan$ is positive in the third quadrant.
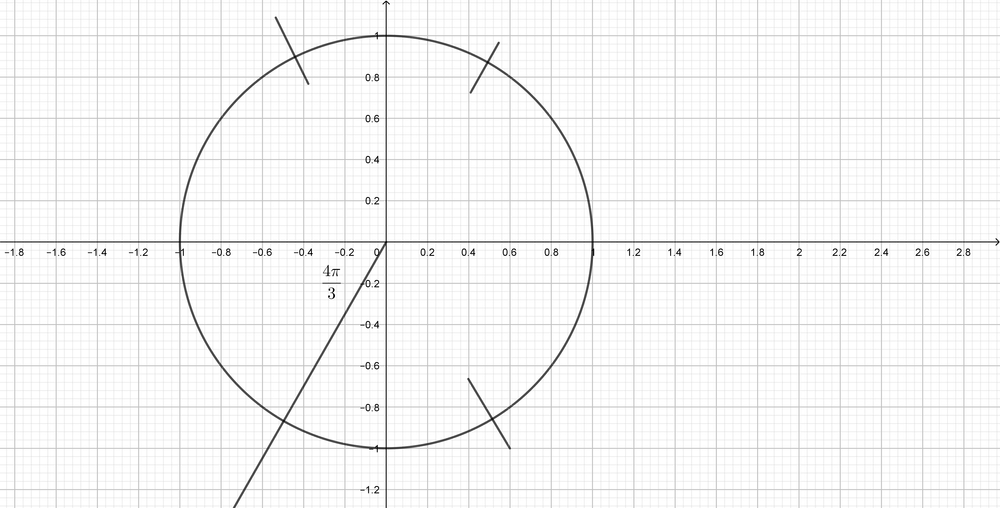
$dfrac{5pi}{6}$ is located in the second quadrant.The related angle is $dfrac{pi}{6}$, and $sin$ is negative in the second quadrant.
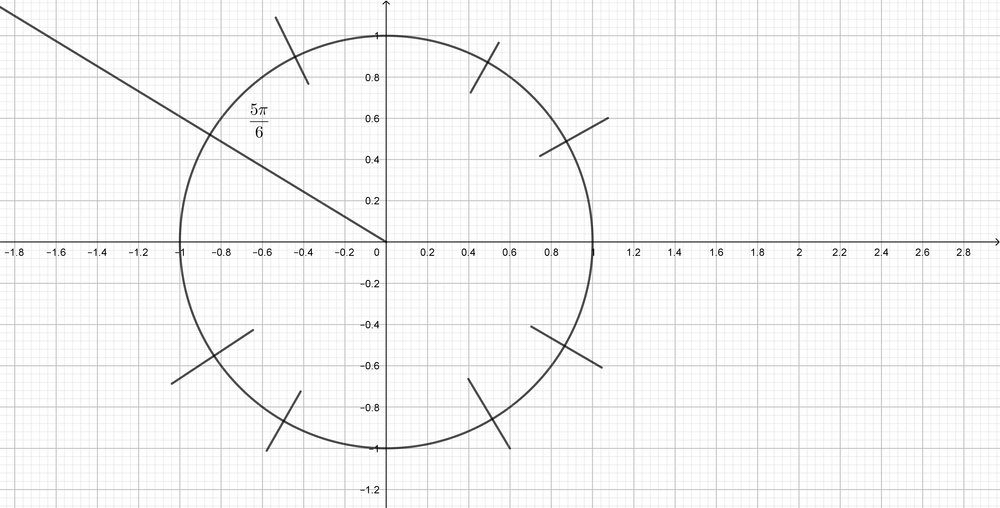
$dfrac{2pi}{3}$ is located in the second quadrant.The related angle is $dfrac{pi}{3}$, and $cos$ is negative in the second quadrant.
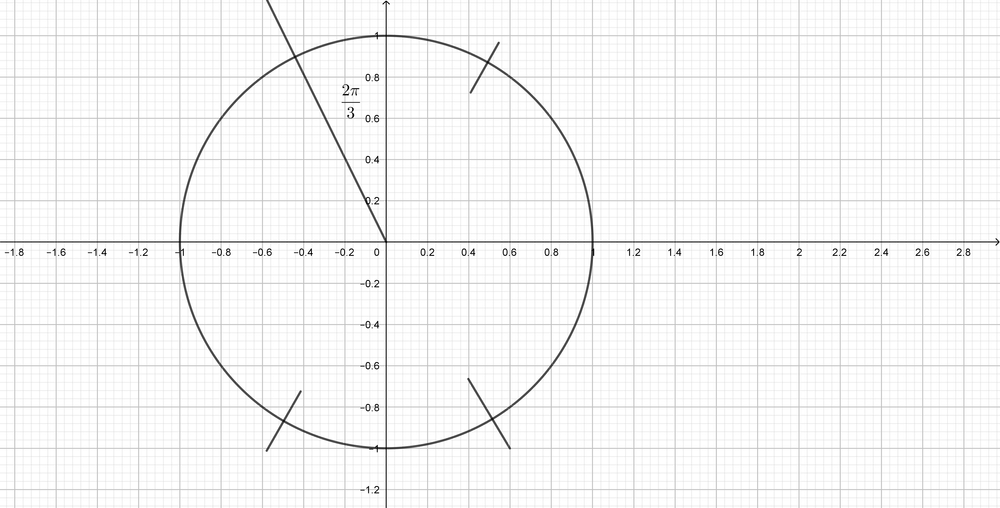
$dfrac{7pi}{4}$ is located in the fourth quadrant.The related angle is $dfrac{pi}{4}$, and $cot$ is negative in the fourth quadrant.
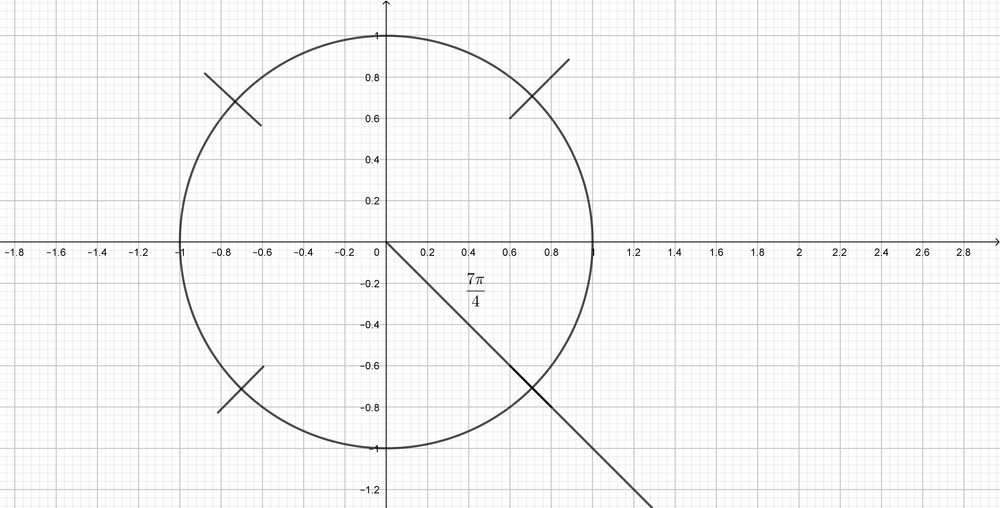
(ii) $r^2=6^2+8^2=36+64=100 Rightarrow r=10$
(iii) $sin theta=dfrac{4}{5}, cos theta=dfrac{3}{5}, tan theta=dfrac{4}{3}, csc theta=dfrac{5}{4}, sec theta=dfrac{5}{3}, cot theta=dfrac{3}{4}$
(iv) $sin^{-1}(dfrac{4}{5})=0.93 Rightarrow theta=0.93$
(i)
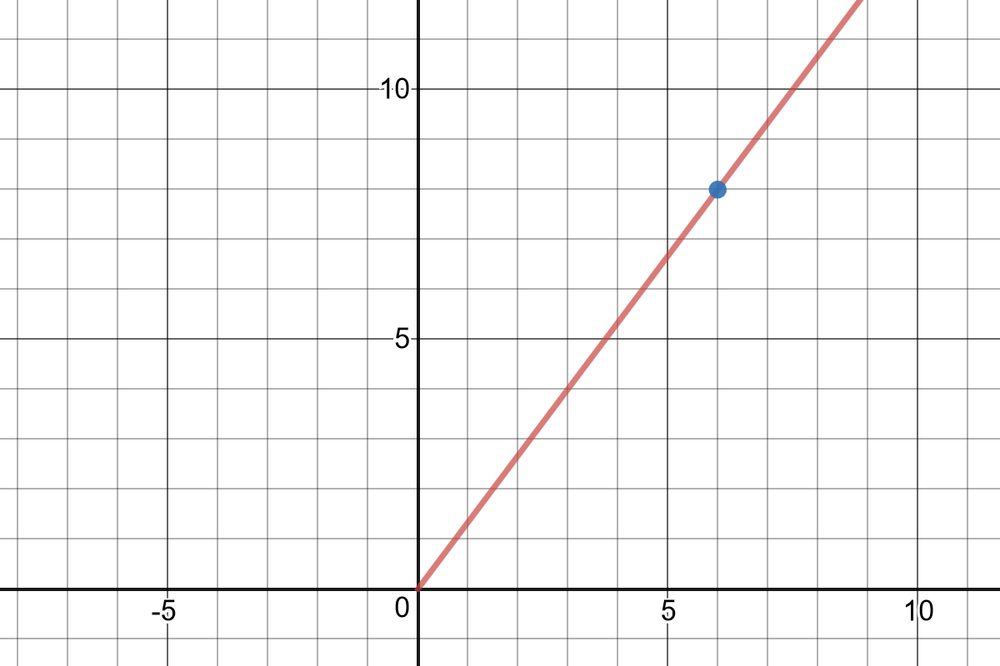
(ii) $r^2=(-12)^2+(-5)^2=144+25=169 Rightarrow r=13$
(iii) $sin theta=-dfrac{5}{13}, cos theta=-dfrac{12}{13}, tan theta=dfrac{5}{12}, csc theta=-dfrac{13}{5}, sec theta=-dfrac{13}{12}$,
$cot theta=dfrac{12}{5}$
(iv) $sin^{-1}(-dfrac{5}{13})=-0.395 Rightarrow theta=pi+0.395=3.54$
(i)
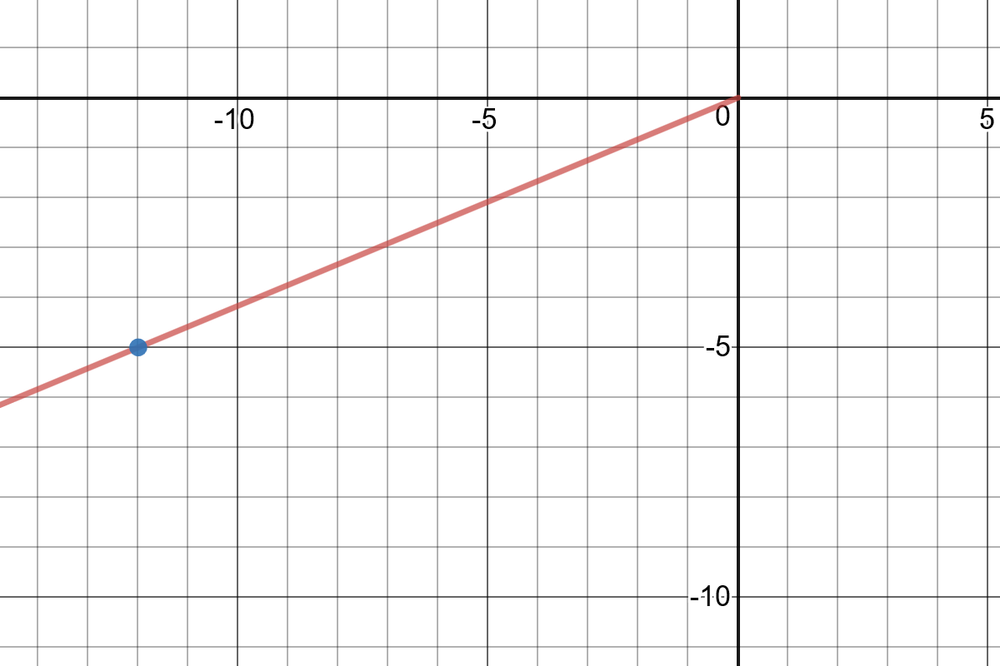
(ii) $r^2=4^2+(-3)^2=16+9=25 Rightarrow r=5$
(iii) $sin theta=-dfrac{3}{5}, cos theta=dfrac{4}{5}, tan theta=-dfrac{3}{4}, csc theta=-dfrac{5}{3}, sec theta=dfrac{5}{4}, cot theta=-dfrac{4}{3}$
(iv) $sin^{-1}(-dfrac{3}{5})=-0.64 Rightarrow theta=2pi-0.64=5.64$
(i)
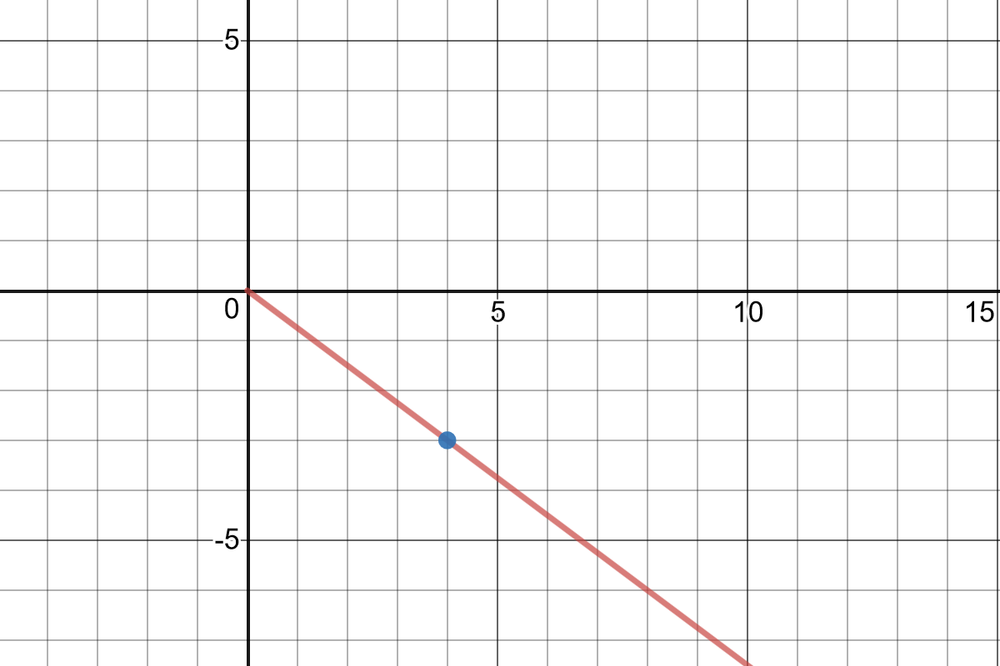
(ii) $r^2=0^2+5^2=0+25=25 Rightarrow r=5$
(iii) $sin theta=dfrac{5}{5}=1, cos theta=dfrac{0}{5}=0, tan theta=dfrac{5}{0}=$undefined,
$csc theta=dfrac{5}{5}=1, sec theta=dfrac{5}{0}=$undefined, $cot theta=dfrac{0}{5}=0$
(iv) $sin^{-1}(1)=1.57 Rightarrow theta=dfrac{pi}{2}$
(i)
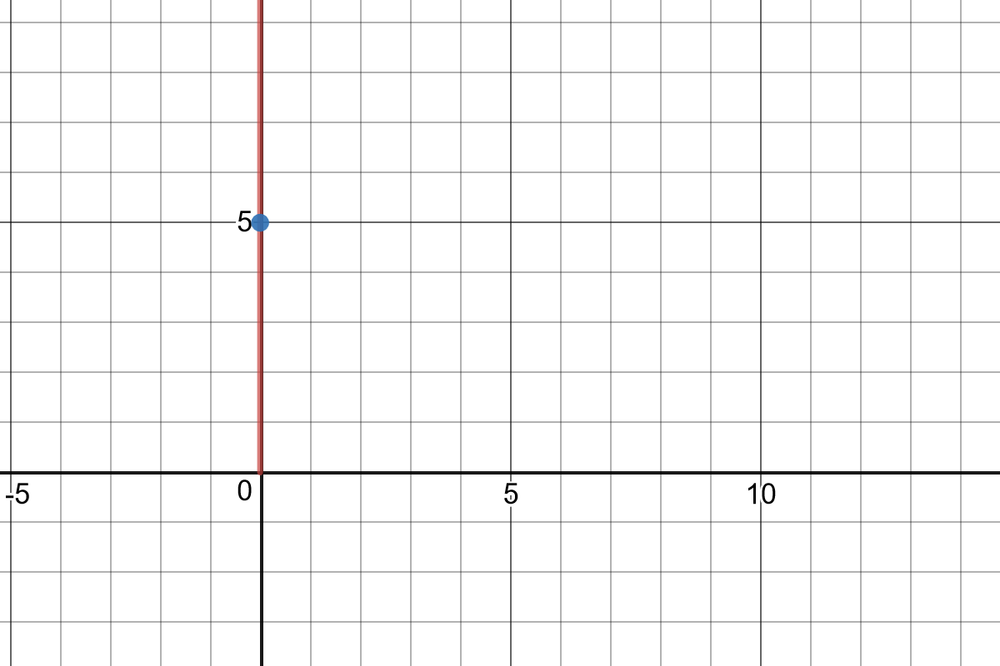
$x=0$, $y=-1, r=1$
$sinleft(-dfrac{pi}{2} right)=-1, cosleft(-dfrac{pi}{2} right)=0$,
$tanleft(-dfrac{pi}{2} right)=undefined, cscleft(-dfrac{pi}{2} right)=-1$
$secleft(-dfrac{pi}{2} right)=undefined, cotleft(-dfrac{pi}{2} right)=0$
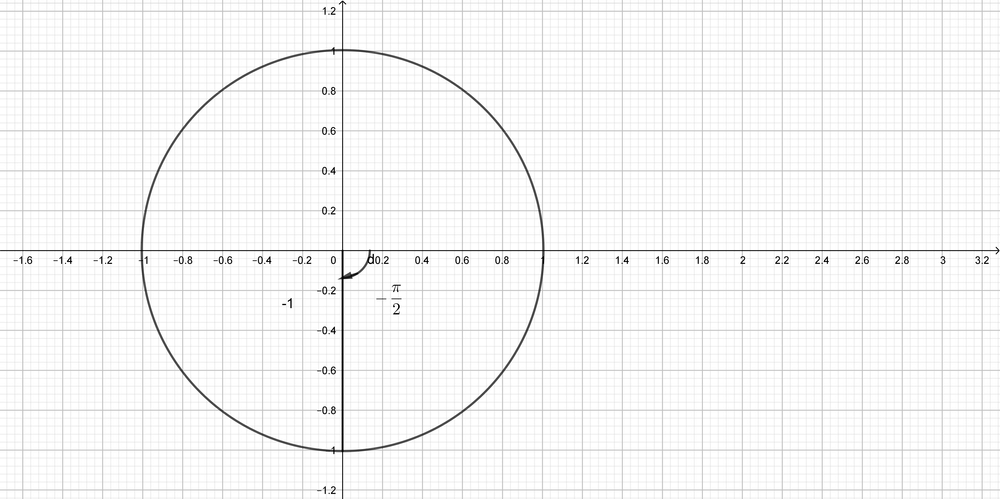
$x=-1, y=0, r=1$
$sin(-pi)=0, cos(-pi)=-1, tan(-pi)=0$,
$csc(-pi)=undefined, sec(-pi)=-1$,
$$
cot(-pi)=undefined
$$
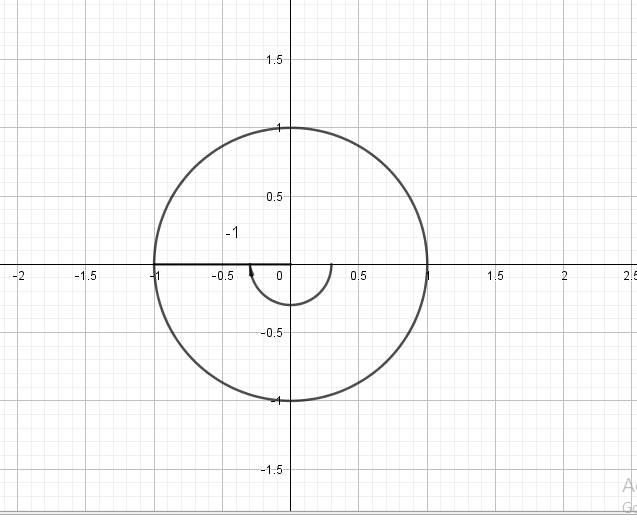
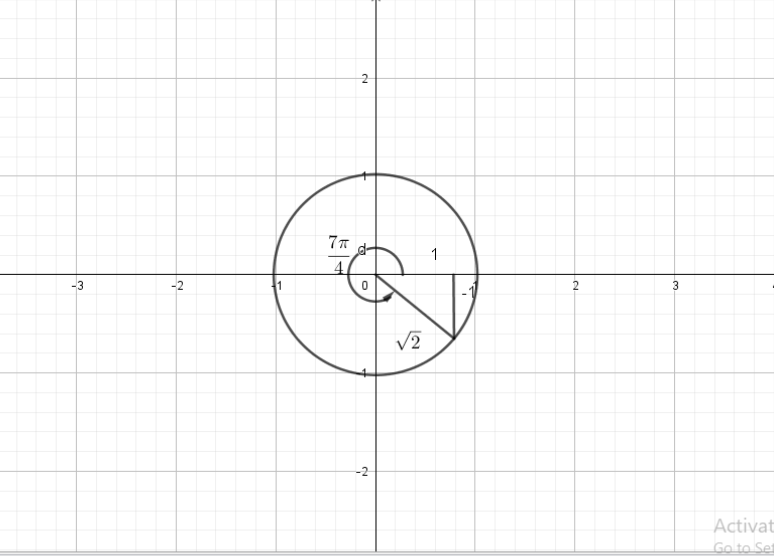
$x=1, y=-1, r=sqrt{2}$
$sinleft( dfrac{7pi}{4}right)=-dfrac{sqrt{2}}{2},cosleft(dfrac{7pi}{4} right)=dfrac{sqrt{2}}{2}$,
$tanleft( dfrac{7pi}{4}right)=-1, cscleft(dfrac{7pi}{4} right)=-sqrt{2}$,
$secleft(dfrac{7pi}{4} right)=sqrt{2}, cotleft(dfrac{7pi}{4} right)=-1$
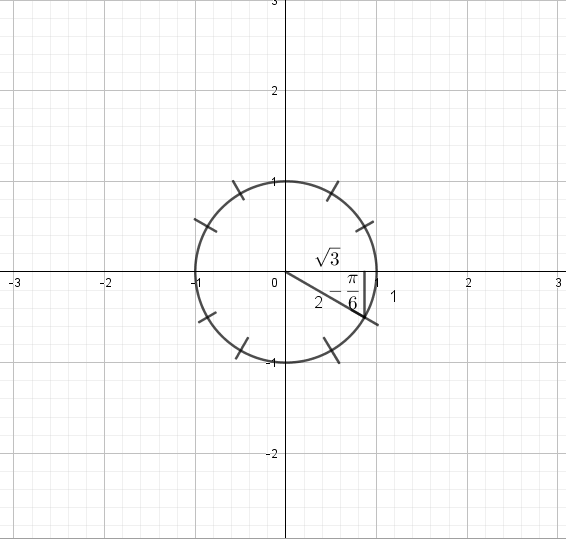
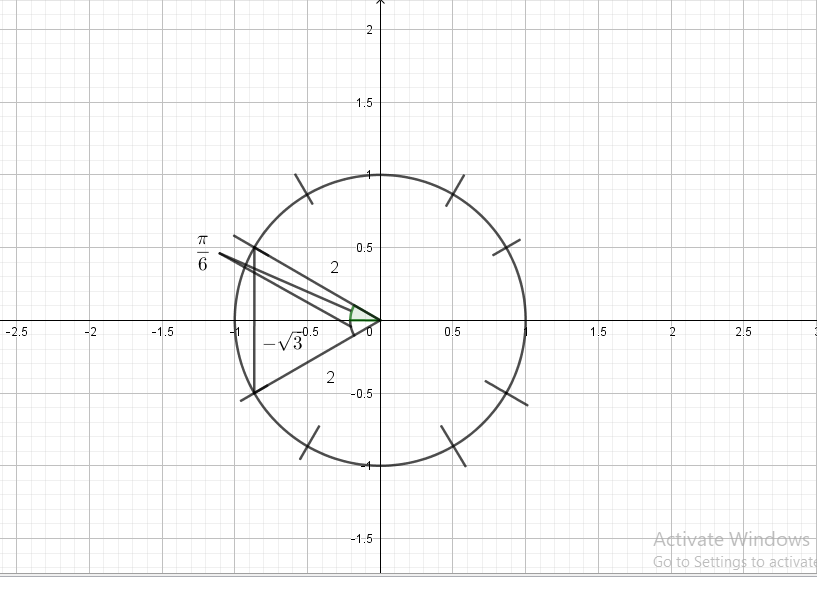
$x=sqrt{3}, y=-1, r=2$
$sinleft(-dfrac{pi}{6} right)=-dfrac{1}{2},cosleft(-dfrac{pi}{6} right)=dfrac{sqrt{3}}{2}$,
$tanleft(-dfrac{pi}{6} right)=-dfrac{sqrt{3}}{3}, cscleft(-dfrac{pi}{6} right)=-2$,
$secleft(-dfrac{pi}{6} right)=dfrac{2sqrt{3}}{3}, cotleft(-dfrac{pi}{6} right)=-sqrt{3}$
This is an the second quadrrant where sine is positive. Sine is also positive in the first quadrant.
So, an equivalent expression would be $sindfrac{pi}{6}$.
#### (b)
This is in the fourth quadrant where cosine is positive.Cosine is also positive in the first quadrant.
So, an equivalent expression would be cos$dfrac{pi}{3}$.
#### (c)
This is in the fourth quadrant where cotangent is negative. Cotangent is also negative in the second quadrant.So, an equivalent expression would be cot$dfrac{3pi}{4}$
#### (d)
This is in the third quadrant where secant is negative. Secant is also negative in the second quadrant.
So, an equivalent expression would be sec$dfrac{5pi}{6}$.
$$
sin(dfrac{2pi}{3})=dfrac{sqrt{3}}{2}
$$
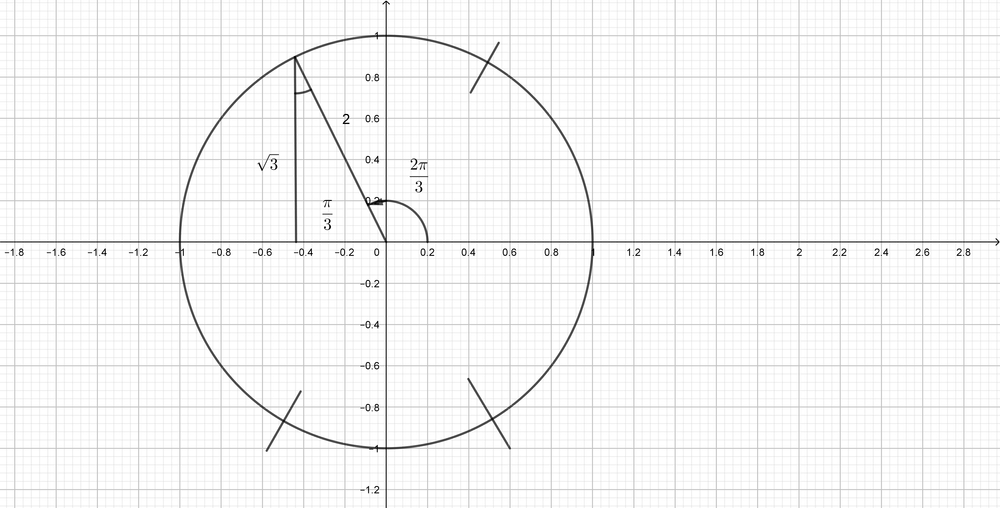
$$
cos(dfrac{5pi}{4})=-dfrac{1}{sqrt{2}}=-dfrac{sqrt{2}}{2}
$$

$$
tan(dfrac{11pi}{6})=dfrac{-1}{sqrt{3}}=-dfrac{sqrt{3}}{3}
$$
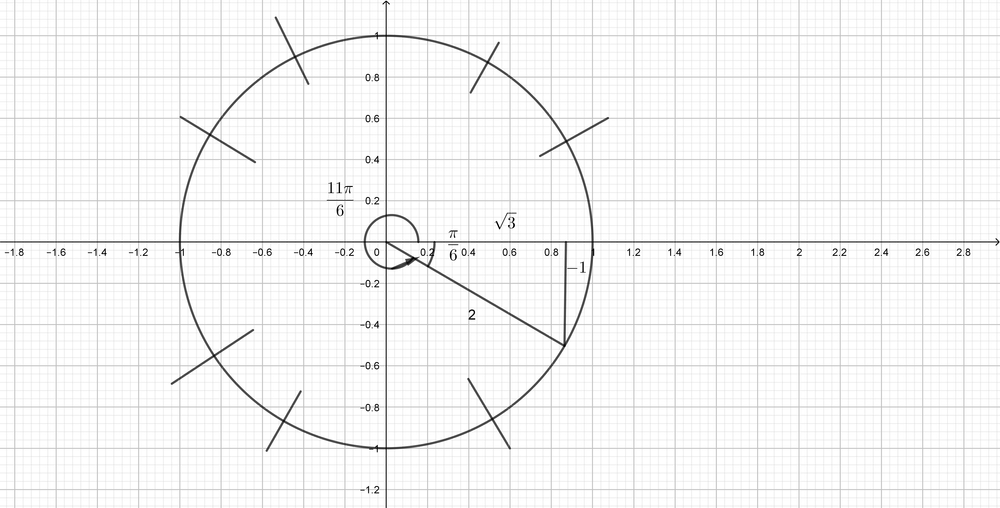
$$
sin(dfrac{7pi}{4})=dfrac{-1}{sqrt{2}}=-dfrac{sqrt{2}}{2}
$$

$$
csc(dfrac{5pi}{6})=dfrac{2}{1}=2
$$
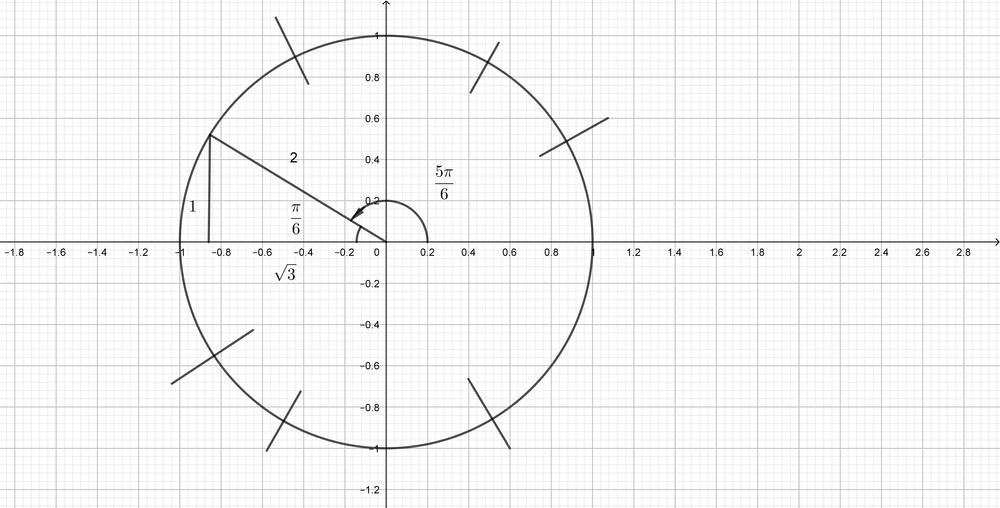
$$
sec(dfrac{5pi}{3})=dfrac{2}{1}=2
$$

$costheta=-dfrac{1}{2}$
$theta=dfrac{2pi}{3}, dfrac{4pi}{3}$
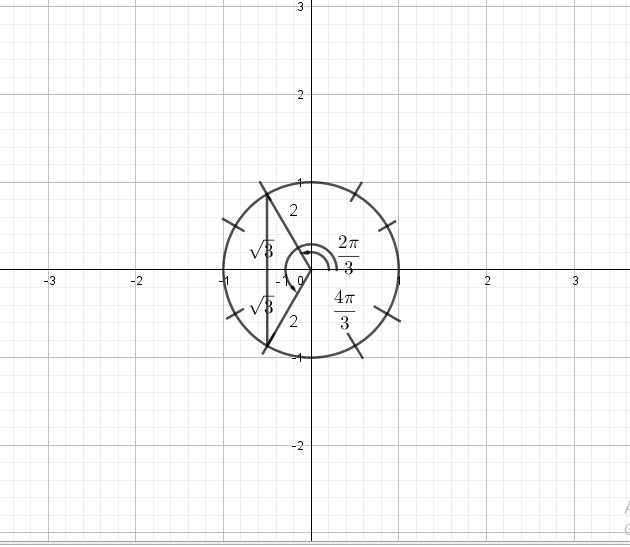
$costheta=dfrac{sqrt{3}}{2}$
$theta=dfrac{pi}{6}, dfrac{11pi}{6}$
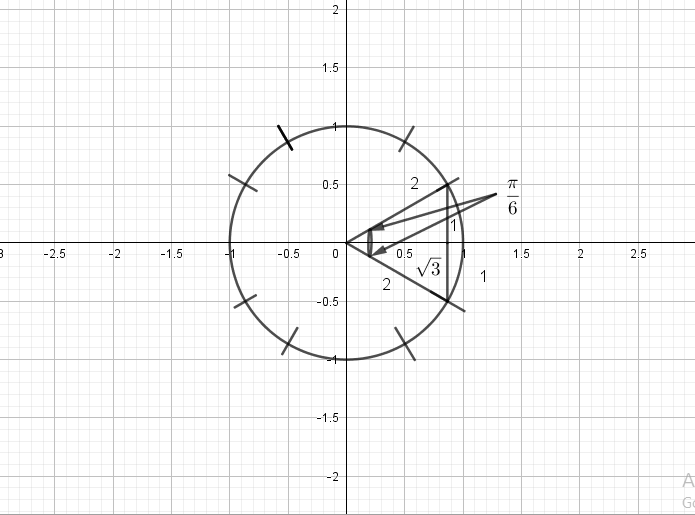
$-dfrac{sqrt{2}}{2}=-dfrac{1}{sqrt{2}}$
$costheta=-dfrac{1}{sqrt{2}}$
$theta=dfrac{3pi}{4},dfrac{5pi}{4}$
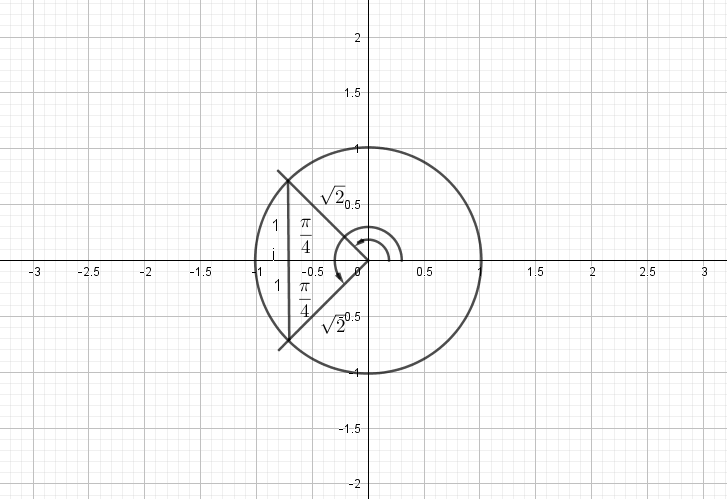
$costheta=-dfrac{sqrt{3}}{2}$
$theta=dfrac{5pi}{6}, dfrac{7pi}{6}$
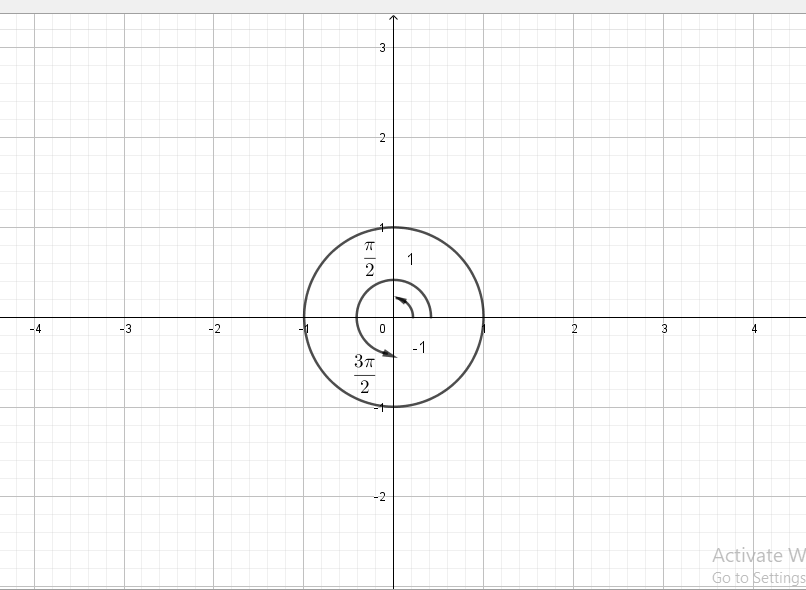
$costheta=0$
$theta=dfrac{pi}{2}, dfrac{3pi}{2}$
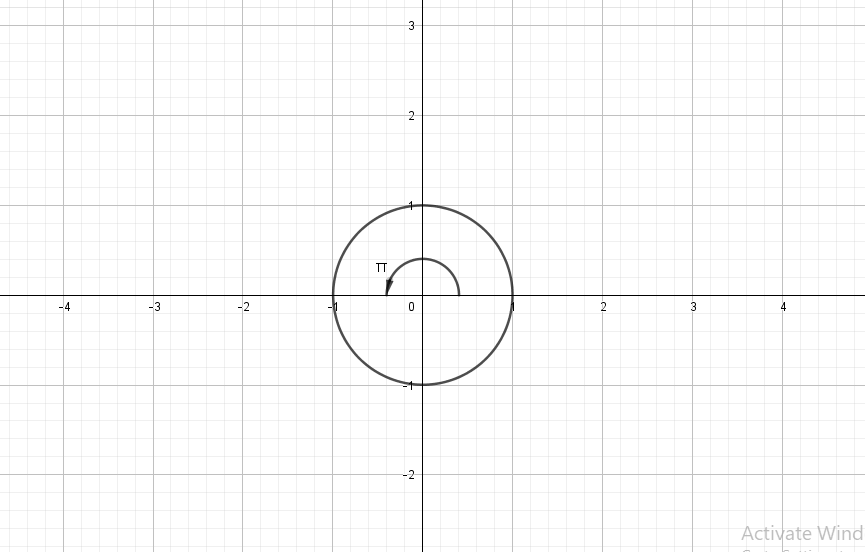
$costheta=-1$
$$
theta=pi
$$
$(-7,8)$ is in the second quadrant.
$tan^{-1}left(dfrac{8}{-7} right)=-0.852$
$theta=pi-0.852=2.29$
#### (b)
$(12,2)$ is in the first quadrant.
$tan^{-1}left(dfrac{2}{12} right)=0.17$
$theta=0.17$
#### (c)
$(3, 11)$ is in the first quadrant.
$tan^{-1}left(dfrac{11}{3} right)=1.30$
$theta=1.30$
$(-4, -2)$ is in the third quadrant.
$tan^{-1}left(dfrac{-2}{-4} right)=0.464$
$theta=pi+0.464=3.61$
#### (e)
$(9,10)$ is in the first quadrant.
$tan^{-1}left(dfrac{10}{9} right)=0.84$
$theta=0.84$
#### (f)
$(6, -1)$ is in the fourth quadrant.
$tan^{-1}left(dfrac{-1}{6} right)=-0.165$
$theta=2pi-0.165=6.12$
This is in the second quadrant where cosine is negative.Cosine is also negative in the third quadrant.
So, an equivalent expression would be $cosdfrac{5pi}{4}$.
#### (b)
This is in the fourth quadrant where tangent is negative. Tangent is also negative in the second quadrant. So, an equivalent expression would be $tandfrac{5pi}{6}$
#### (c)
This is in the fourth quadrant where cosecant is negative. Cosecant is also negative in the third quadrant. So, an equivalent expression would be $cscdfrac{4pi}{3}$.
#### (d)
This is in the second quadrant where cotangent is negative.Cotangent is also negative in the fourth quadrant. So, an equivalent expression would be $cotdfrac{5pi}{3}$
#### (e)
This is in the fourth quadrant where sine is negative. Sine is also negative in the third quadrant.
So, an equiavalent expression would be $sindfrac{7pi}{6}$.
#### (f)
This is in the fourth quadrant where secant is positive.Secant is also positive in the first quadrant.
So, an equivalent expression would be $secdfrac{pi}{4}$.
$theta=sin^{-1}left(dfrac{3.4}{5} right)=0.748$
$pi-0.748=2.39$

$sin(0.8584)=dfrac{4.2}{x}$
$x=dfrac{4.2}{sin(0.8584)}=5.55$cm

$dfrac{10 sec}{60 sec}=dfrac{r rad}{2pi rad}$
$r=1.05 rad$
$cos(1.05)=dfrac{x}{9}$
$x=9cos(1.05)$
$x=4.5 cm$

It lies in the second or third quadrant because cosine is negative in these quadrants.
#### (b)
$x=-5, r=13, y=?$
$13^2-(-5)^2=y^2$
$169-25=y^2$
$144=y^2$
$12=y$
$sintheta=dfrac{12}{13}$ or $-dfrac{12}{13}$,
$tantheta=dfrac{12}{5}$ or $-dfrac{12}{5}$,
$sectheta=-dfrac{13}{5}$,
$csctheta=dfrac{13}{12}$ or $-dfrac{13}{12}$
$cottheta=dfrac{5}{12}$ or $-dfrac{5}{12}$
#### (c)
$sintheta=dfrac{12}{13}$
$theta=sin^{-1}left(dfrac{12}{13} right)$
$theta=1.176$
In the second quadrant, $pi-1.176=1.97.$
In the second quadrant, $pi+1.176=4.32.$
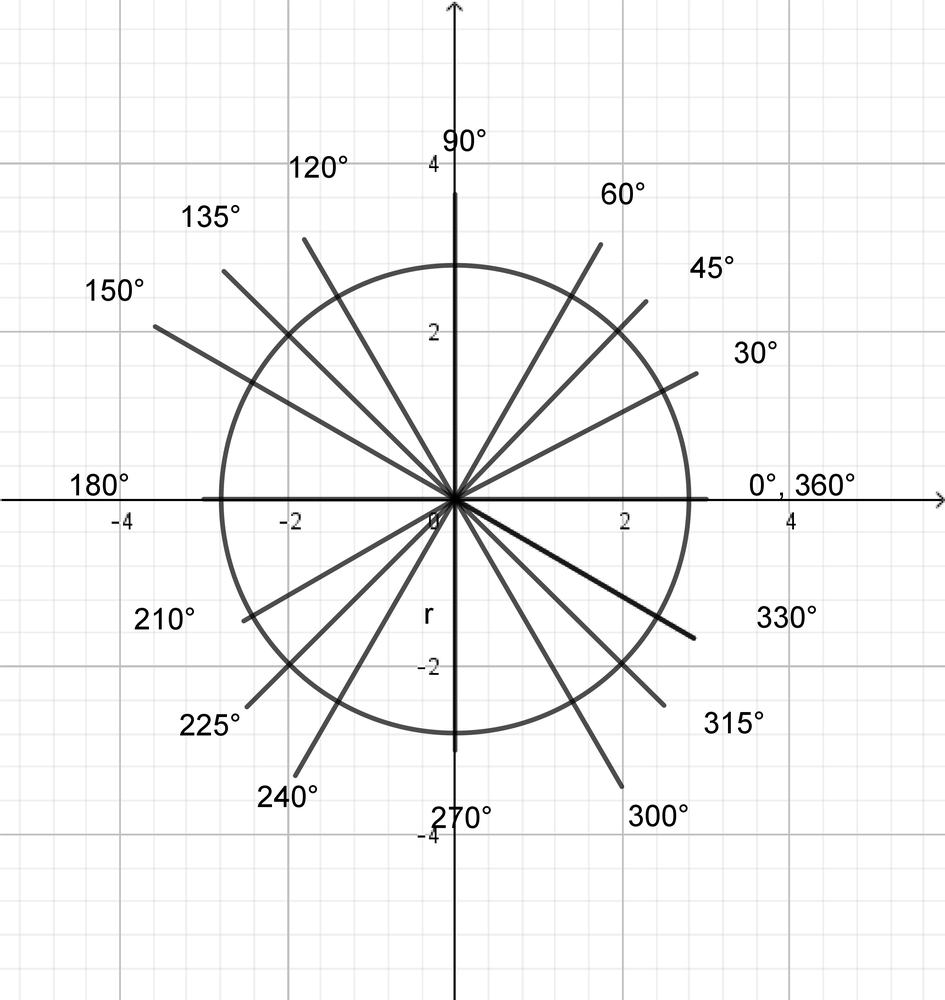
$30^{circ}=30^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{pi}{6} radians$;
$45^{circ}=45^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{pi}{4} radians$;
$60^{circ}=60^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{pi}{3} radians$;
$90^{circ}=90^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{pi}{2} radians$;
$120^{circ}=120^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{2pi}{3} radians$;
$135^{circ}=135^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{3pi}{4} radians$;
$150^{circ}=150^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{5pi}{6} radians$;
$180^{circ}=180^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=pi radians$;
$210^{circ}=210^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{7pi}{6} radians$;
$225^{circ}=225^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{5pi}{4} radians$;
$240^{circ}=240^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{4pi}{3} radians$;
$270^{circ}=270^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{3pi}{2} radians$
$300^{circ}=300^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{5pi}{3} radians;$
$315^{circ}=315^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{7pi}{4} radians$;
$330^{circ}=330^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{11pi}{6} radians;$
$360^{circ}=360^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=2pi radians$
$=2left(-dfrac{1}{2} right)^2 -1$
$=2left(dfrac{1}{4} right)-1=-dfrac{1}{2}$
$left(sin^2dfrac{11pi}{6} right)-left( cos^2dfrac{11pi}{6}right)$
$=left(-dfrac{1}{2} right)^2-left(dfrac{sqrt{3}}{2} right)^2=dfrac{1}{4}-dfrac{3}{4}=-dfrac{1}{2}$
$2left(sin^2left(dfrac{11pi}{6} right) right)-1=left(sin^2dfrac{11pi}{6} right)-left(cos^2dfrac{11pi}{6} right)$
$AB=dfrac{8}{sinleft( dfrac{pi}{6}right)}$
$AB=16$
$(AD)^2=8^2+8^2$
$(AD)^2=64+64$
$(AD)^2=128$
$(AD)=sqrt{128}=8sqrt{2}$
$sin D=dfrac{8}{8sqrt{2}}=dfrac{sqrt{2}}{2}$;
$cos D=dfrac{8}{8sqrt{2}}=dfrac{sqrt{2}}{2}$;
$tan D=dfrac{8}{8}=1$
The first and second quadrants both have a positive y-value.
The first quadrant has a positive y-value, and the fourth quadrant has a negative y-value.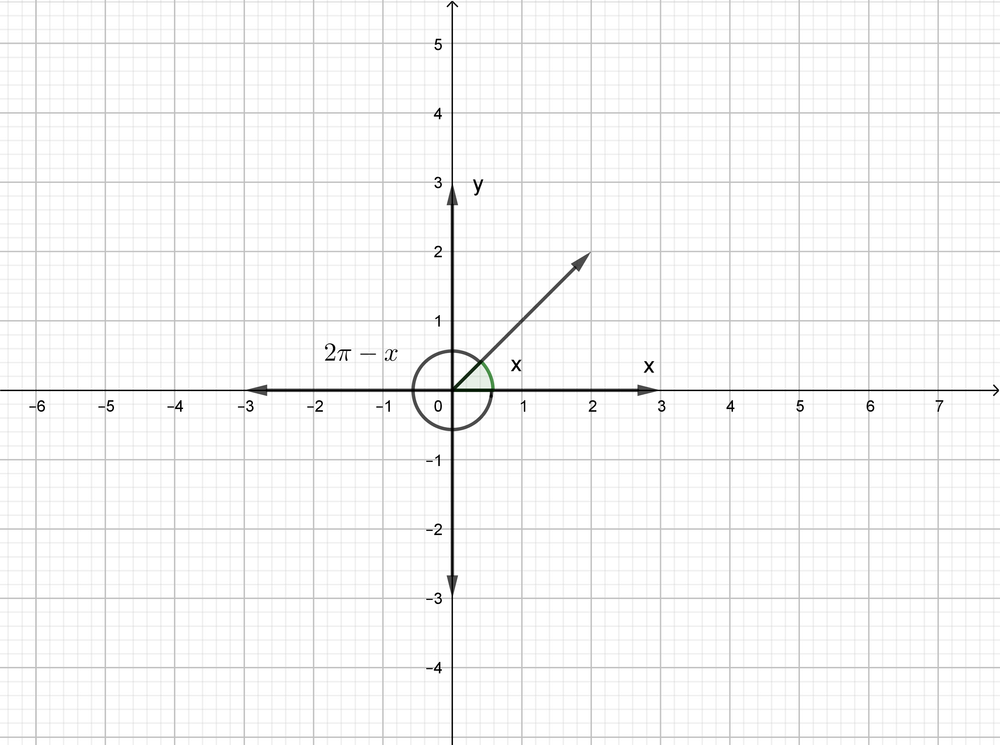
The first quadrant has a positive x-value, and the second quadrant has a negative x-value.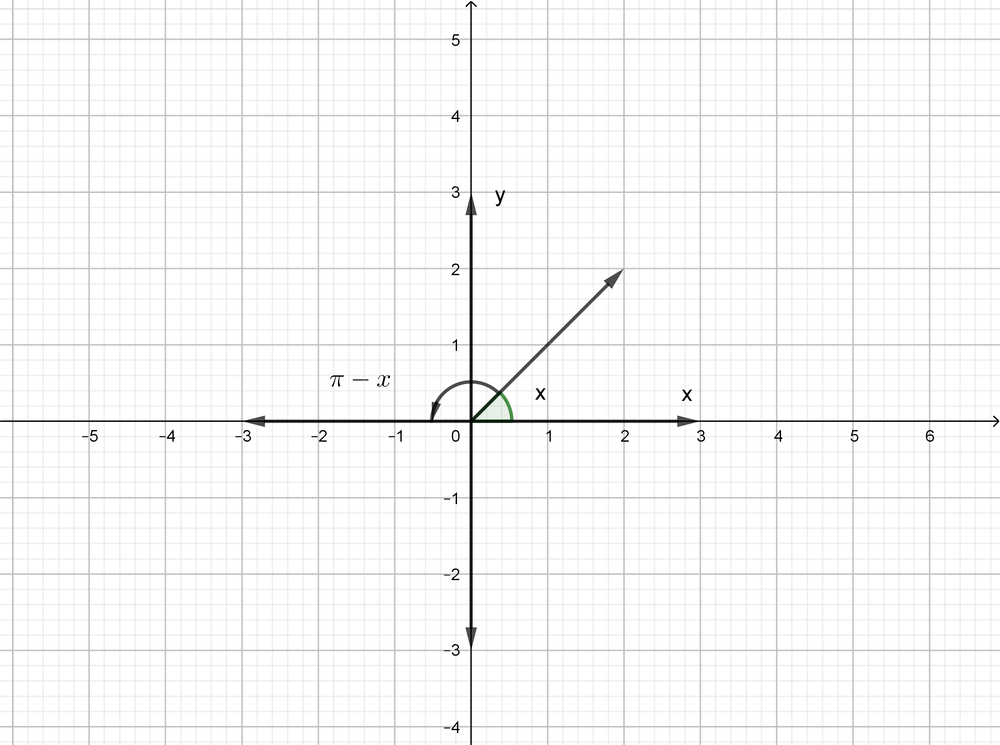
The first quadrant has a positive x-value and a positive y-value, and the third quadrant has a negative x-value and a negative y-value.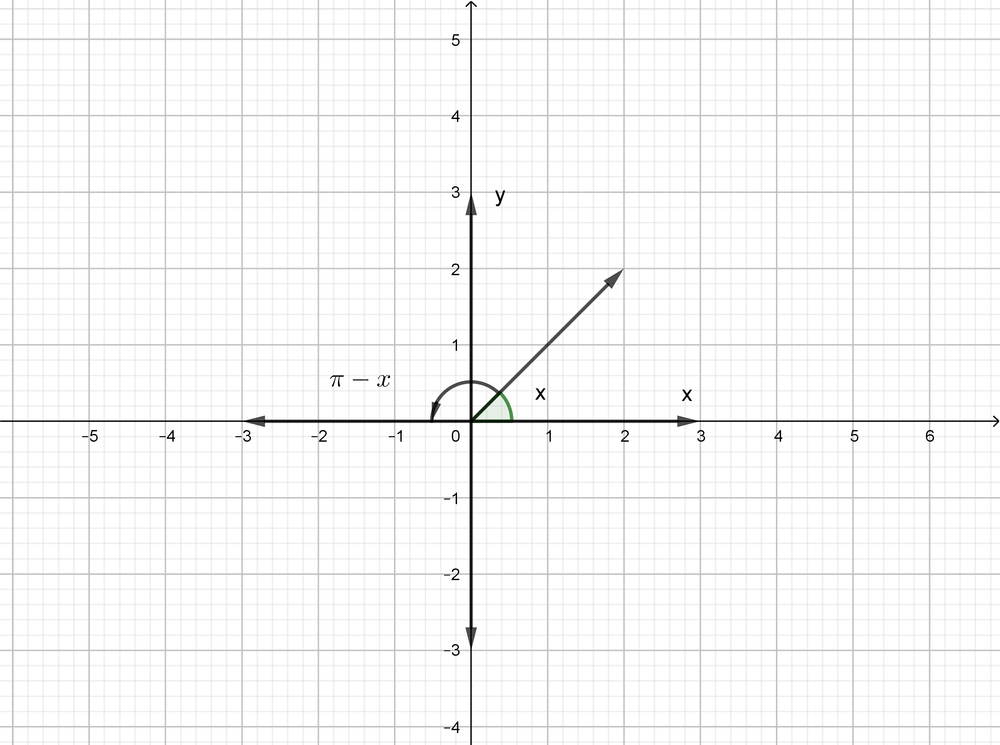
$a=tan^{-1}left(dfrac{3}{3sqrt{3}} right)$
$a=30^{circ}$
$tan c=dfrac{4sqrt{3}}{4}$
$c=tan^{-1}left(dfrac{4sqrt{3}}{4} right)$
$c=60^{circ}$
$b=180^{circ}-30^{circ}-60^{circ}=90^{circ}$
$sin 90^{circ}=1$
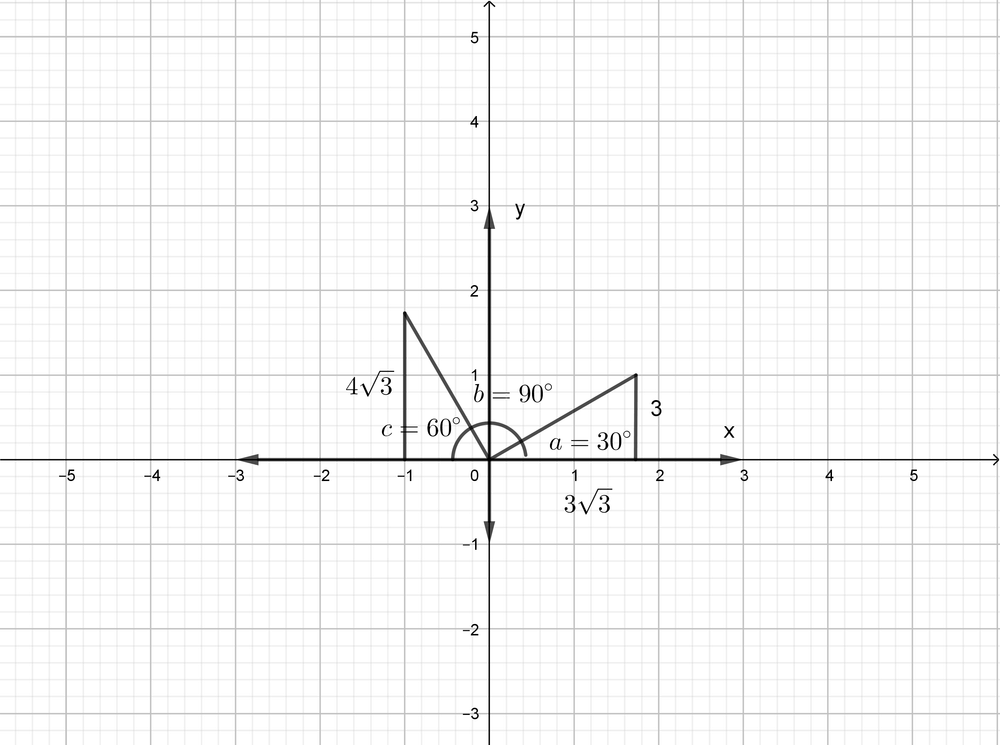

$a=tan^{-1}(dfrac{1}{1})$
$a=45^circ$
$tan c=dfrac{7}{7sqrt{3}}$
$c=tan^{-1}(dfrac{7}{7sqrt{3}})$
$c=30^circ$
$b=180^circ-30^circ=105^circ$
$cos 150^circ=-0.26$
$sin theta cot theta-cos^2 theta=-dfrac{1}{2}(-sqrt{3})-(-dfrac{sqrt{3}}{2})^2=dfrac{sqrt{3}}{2}-dfrac{3}{4}=dfrac{2sqrt{3}-3}{4}$

