$pi radians$;

$cancel{pi radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=180^{circ}$

#### (b)

$dfrac{pi}{2} radians$;

$dfrac{cancel{pi}}{2}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=90^{circ}$

#### (c)

$-pi radians$;

$-cancel{pi radians}timesleft( dfrac{180^{circ}}{cancel{pi radians}}right)=-180^{circ}=180^{circ}$

#### (d)

$-dfrac{3pi}{2} radians=dfrac{pi}{2} radians$;

$-dfrac{3cancel{pi}}{2} cancel{ radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=-270^{circ}$

$-2pi radians$;

$-2cancel{pi radians}timesleft( dfrac{180^{circ}}{cancel{pi radians}}right)=-360^{circ}$

#### (f)

$dfrac{3pi}{2} radians$;

$dfrac{3cancel{pi}}{2}cancel{radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=270^{circ}$

#### (g)

$-dfrac{4cancel{pi}}{3}cancel{radians}timesleft( dfrac{180^{circ}}{cancel{pi radians}}right)=-240^{circ}$

#### (h)

$dfrac{2pi}{3} radians$;

$dfrac{2cancel{pi}}{3}timesleft( dfrac{180^{circ}}{cancel{pi radians}}right)=120^{circ}$

$75^circ=75^circ(dfrac{pi radians}{180^circ})=dfrac{5pi}{12} radians$

#### (b)

$200^circ=200^circ(dfrac{pi radians}{180^circ})=dfrac{10pi}{9} radians$

#### (c)

$400^circ=400^circ(dfrac{pi radians}{180^circ})=dfrac{20pi}{9} radians$

#### (d)

$320^circ=320^circ(dfrac{pi radians}{180^circ})=dfrac{16pi}{9} radians$

$dfrac{5pi}{3}=dfrac{5pi}{3}timesleft(dfrac{180^{circ}}{pi radians} right)=300^{circ}$

#### (b)

$0.3pi=0.3pitimesleft(dfrac{180^{circ}}{pi radians} right)=54^{circ}$

#### (c)

$3=3timesleft(dfrac{180^{circ}}{pi radians} right)=171.89^{circ}$

#### (d)

$dfrac{11pi}{4}=dfrac{11pi}{4}timesleft(dfrac{180^{circ}}{pi radians} right)=495^{circ}$

$5=dfrac{x^{circ}}{360^{circ}}(2pi)(2.5)$

$1800=(x)(2pi)(2.5)$

$114.6^{circ}=x$

$114.6^{circ}=^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=2 radians$

#### (b)

$200^{circ}=200^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=dfrac{10 pi}{9} radians$

$x=dfrac{dfrac{10pi}{9}}{2pi}(2pi)(2.5)$

$x=dfrac{5}{9}(2pi)(2.5)$

$x=dfrac{25pi}{9}$ cm

$3.5=3.5timesleft( dfrac{180^{circ}}{pi radians}right)=200.5^{circ}$

$x=dfrac{200.5^{circ}}{360^{circ}}(2pi)(8)$

$x=28$ cm

#### (b)

$300^{circ}=300^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{5pi}{3} radians$

$x=dfrac{dfrac{5pi}{3}}{2pi}(2pi)(8)$

$x=dfrac{5}{6}(2pi)(8)$

$x=dfrac{40pi}{3}$ cm

$90^{circ}=90^{circ}timesleft( dfrac{pi radians }{180^{circ}}right)=dfrac{pi}{2} radians$

#### (b)

$270^{circ}=270^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=dfrac{3 pi}{2} radians$

#### (c)

$-180^{circ}=-180^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=-pi=pi radians$

#### (d)

$45^{circ}=45^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{pi}{4} radians$

#### (e)

$-135^{circ}=-135^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=-dfrac{3pi}{4}=dfrac{5pi}{4} radians$

#### (f)

$60^{circ}=60^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=dfrac{pi}{3} radians$

#### (g)

$240^{circ}=240^{circ}timesleft( dfrac{pi radians}{180^{circ}}right)=dfrac{4pi}{3} radians$

#### (h)

$-120^{circ}=-120^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=-dfrac{2pi}{3}=dfrac{4pi}{3}radians$

$dfrac{2pi}{3}=dfrac{2pi}{3}timesleft( dfrac{180^{circ}}{pi radians}right)=120^{circ}$

#### (b)

$-dfrac{5pi}{3}=-dfrac{5pi}{3}timesleft( dfrac{180^{circ}}{pi radians}right)=-300^{circ}=60^{circ}$

#### (c)

$dfrac{pi}{4}=dfrac{pi}{4}timesleft(dfrac{180^{circ}}{pi radians} right)=45^{circ}$

#### (d)

$-dfrac{3pi}{4}=-dfrac{3pi}{4}timesleft( dfrac{180^{circ}}{pi radians}right)=-135^{circ}=225^{circ}$

#### (e)

$dfrac{7pi}{6}=dfrac{7pi}{6}timesleft( dfrac{180^{circ}}{pi radians}right)=210^{circ}$

#### (f)

$-dfrac{3pi}{2}=-dfrac{3pi}{2}timesleft( dfrac{180^{circ}}{pi radians}right)=-270^{circ}=90^{circ}$

#### (g)

$dfrac{11pi}{6}=dfrac{11pi}{6}timesleft( dfrac{180^{circ}}{pi radians}right)=330^{circ}$

#### (h)

$-dfrac{9pi}{2}=-dfrac{9pi}{2}timesleft( dfrac{180^{circ}}{pi radians}right)=-810^{circ}=-90^{circ}=270^{circ}$

$x=dfrac{dfrac{19pi}{20}}{2pi}(2pi)(65)$

$x=dfrac{19}{40}(2pi)(65)$

$x=dfrac{2470pi}{40}$

$x=dfrac{247pi}{4}m$

#### (b)

$1.25=1.25timesleft(dfrac{180^{circ}}{pi radians} right)=143.2^{circ}$

$x=dfrac{143.2^{circ}}{360^{circ}}(2pi)(65)$

$x=162.5$m

#### (c)

$150^{circ}=150^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=dfrac{5pi}{6} radians$

$x=dfrac{dfrac{5pi}{6}}{2pi}(2pi)(65)$

$x=dfrac{5}{12}(2pi)(65)$

$x=dfrac{325pi}{6} cm$

b) $x=162.5$m

c) $x=dfrac{325pi}{6} cm$

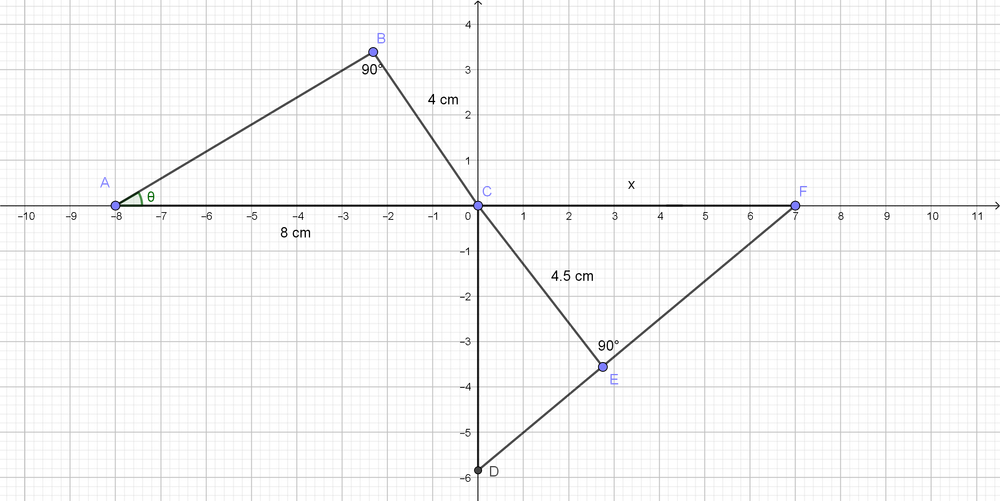
$angle BCA=dfrac{pi}{2}-dfrac{pi}{6}=dfrac{pi}{3}$

Because they are vertical angles,

$angle BCA=angle DCF, angle DCF=angle DCE+angle ECF$

$dfrac{pi}{3}=dfrac{pi}{12}+angle ECF$

$angle ECF=dfrac{pi}{3}-dfrac{pi}{12}$

$angle ECF=dfrac{pi}{4}$

Since $angle ECF=dfrac{pi}{4}$, $x=sqrt{2}(CE)=4.5sqrt{2}$ cm.

It rotates $4$ times per min. So it rotates once every $15$ seconds.

$omega=dfrac{2pi radians}{15 s}=0.418 88 radians/s$

#### (b)

Radius=$3$m

Revolutions, $n=(4 rev/min)(5 min)=20 rev$

distance travelled$=20(2pi)(3)=377.0$m

$omega=1.2pi rad/s(60 s/min)=72pi rad/min$

$72pi rad/minleft(dfrac{180^{circ}}{pi radians} right)=12 960^{circ}$

In one minute, the wheel rotates $12 960^{circ}$. So, Revolutions,

$n=12 960^{circ}div360^{circ}=36$

#### (b)

The wheel travels $(9.6pi)(6)=57.6pi$ metres in a minute.

$57.6pi=36(2pi)(r)$

$0.8m=r$

The angular velocity of piece $A$ is equal to piece $B$ because they rotate at same speed around the centre.

#### (b)

The velocity of piece $A$ is greater than piece $B$ because the radius od $A$ is greater than the radius of $B$.

#### (c)

The percentage would stay the same.

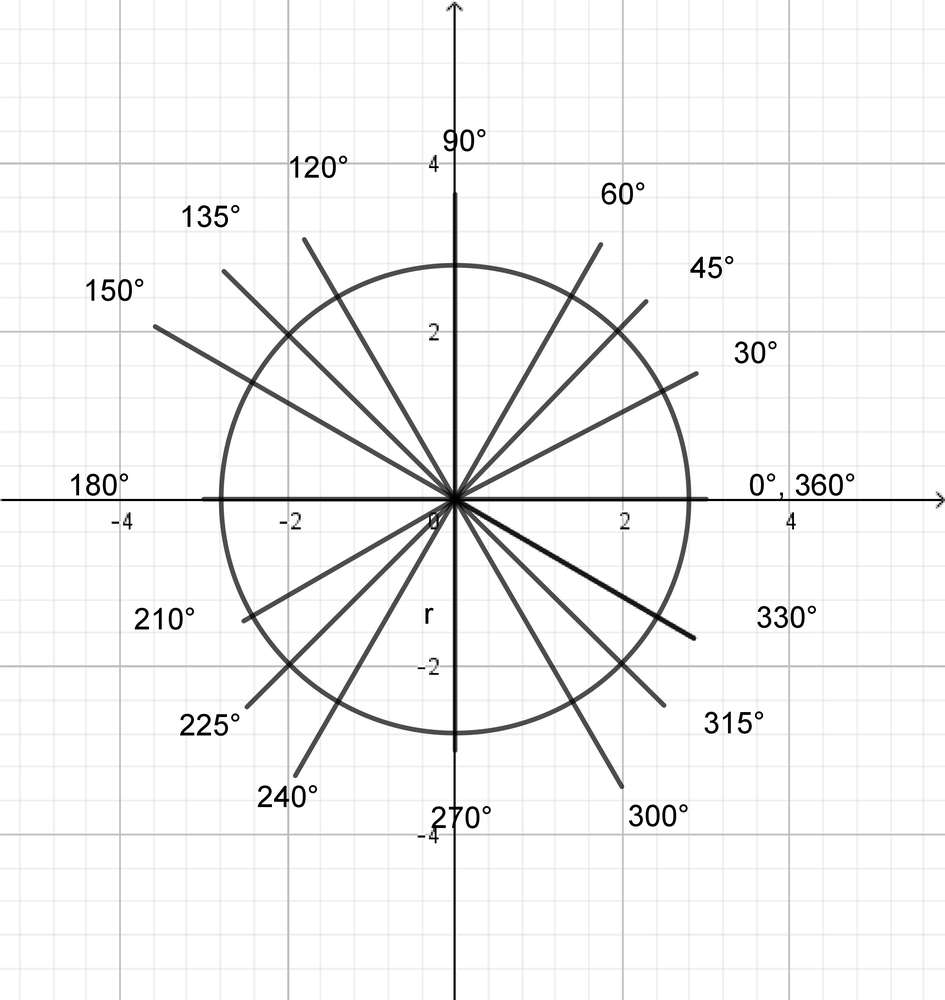
$30^{circ}=30^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=dfrac{pi}{6} radians;$

$45^${circ}$=45^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{pi}$
{4} radians;$\$60^${circ}$=60^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{pi}{3}$ radians;$\$90^${circ}$=90^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{pi}{2}$ radians;$\$120^${circ}$=120^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{2pi}{3}$ radians;$\$135^${circ}$=135^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{3pi}{4}$ radians;$\$150^${circ}$=150^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{5pi}{6}$ radians;$\$180^${circ}$=180^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= pi radians;$\$210^${circ}$=210^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{7pi}{6}$ radians;$\$225^${circ}$=225^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{5pi}{4}$ radians;$\$240^${circ}$=240^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{4pi}{3}$ radians;$\$270^${circ}$=270^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)=$dfrac{3pi}{2}$ radians;$\$300^${circ}$=300^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{5pi}{3}$ radians;$\$315^${circ}$=315^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{7pi}{4}$ radians;$\$330^${circ}$=330^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= $dfrac{11pi}{6}$ radians;$\$360^${circ}$=360^${circ}$timesleft($dfrac{pi radians}{180^{circ}}$ right)= 2pi radians;$

Circle B: $dfrac{dfrac{pi}{7}}{2pi}(17)=7.62$ cm

Circle C: $dfrac{dfrac{pi}{5}}{2pi}(2pi)(14)=8.80$ cm

So, from smallest to largest, the order of the ares would be Circle B, Circle A, and Circle C.

$64pi cmtimesleft(dfrac{1 m}{100 cm} right)timesleft(dfrac{1 km}{1000 m} right)=0.000 64pi km$

Revolutions$=dfrac{675 km}{0.000 64 pi km}=1 054 687.5$

$6 hr 45 min=765 mintimesleft(dfrac{60 s}{1 min} right)=45 900 s$

Rev/sec$=dfrac{1 054 687.5 rev}{45 900 s}=23 rev/s$

$23 rev times 360^{circ}=8280^{circ} / s$

$8280^{circ} /s=8280^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=144.5$ radians/s