
All Solutions
Page 161: Practice Questions
$$y=2x^3+3x^2-2x-5.
$$
Note that any other coefficient is allowed.
$$y=5x^4-2x^2-3.
$$
Note that any other coefficient is allowed, as well as the terms with $x^3$ or $x$.
$$y=12x^6-5x.
$$
Note that any other coefficient is allowed, as well as the terms with $x^5$, $x^4$, $x^3$, $x^2$, or constant term.
$$y=3x^5-x^3+2x^2-7x+4.
$$
Note that any other coefficient is allowed, as well as the terms with $x^4$ instead of the chosen.
$$
color{#4257b2}text{(a)} f(x)=-11x^3+x^2-2
$$
The end behavior is as $(xrightarrowpminfty)$ and $(yrightarrow-infty)$
$$
color{#4257b2}text{(b)} f(x)=70x^2-67
$$
The end behavior is as $(xrightarrowpminfty)$ and $(yrightarrowinfty)$
$$
color{#4257b2}text{(c)} f(x)=x^3-1000
$$
The end behavior is as $(xrightarrow-infty, yrightarrow-infty)$ and $(xrightarrowinfty, yrightarrowinfty)$
$$
color{#4257b2}text{(d)} f(x)=-13x^4-4x^3-2x^2+x+5
$$
The end behavior is as $(xrightarrow-infty, yrightarrowinfty)$ and $(xrightarrowinfty, yrightarrow-infty)$
text{color{Brown}(a) The end behavior is as $(xrightarrowpminfty)$ and $(yrightarrow-infty)$
\ \
(b) The end behavior is as $(xrightarrowpminfty)$ and $(yrightarrowinfty)$
\ \
(c) The end behavior is as $(xrightarrow-infty, yrightarrow-infty)$ and $(xrightarrowinfty, yrightarrowinfty)$
\ \
(d) The end behavior is as $(xrightarrow-infty, yrightarrowinfty)$ and $(xrightarrowinfty, yrightarrow-infty)$}
$$
$$
color{#4257b2}text{(a)} f(x)=6x^3+2x
$$
The turning point is most $n-1$ as follows:
$$
n=3 n-1=3-1=2 text{Even number}
$$
This equation may have zero or two turning point.
$$
color{#4257b2}text{(b)} f(x)=-20x^6-5x^3+x^2-17
$$
The turning point is most $n-1$ as follows:
$$
n=6 n-1=6-1=5 text{Odd number}
$$
This equation may have one or three or five turning point.
$$
color{#4257b2}text{(c)} f(x)=22x^4-4x^3+3x^2-2x+2
$$
The turning point is most $n-1$ as follows:
$$
n=4 n-1=4-1=3 text{Odd number}
$$
This equation may have one or three turning point.
$$
color{#4257b2}text{(d)} f(x)=-x^5+x^4-x^3+x^2-x+1
$$
The turning point is most $n-1$ as follows:
$$
n=5 n-1=5-1=4 text{Even number}
$$
This equation may have zero or two or four turning point.
text{color{Brown}(a) Even number (b) Odd number
\ \
(c) Odd number (d) Even number}
$$
$$
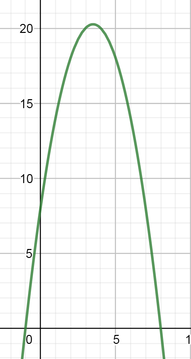
color{#4257b2}text{(a)} f(x)=-(x-8)(x+1)
$$
Use distributive property as follows:
$$
-[x(x+1)-8(x+1)]=-[x^2+x-8x-8]
$$
$$
-x^2-x+8x+8
$$
$$
-x^2+7x+8
$$
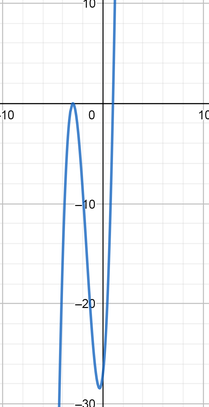
color{#4257b2}text{(b)} f(x)=3(x+3)(x+3)(x-1)
$$
Use distributive property as follows:
$$
3x[(x+3)(x-1)]+9[(x+3)(x-1)]
$$
$$
3x[x^2+2x-3]+9[x^2+2x-3]
$$
$$
3x^3+6x^2-9x+9x^2+18x-27
$$
Rearrange the tiles to group like terms as follows:
$$
3x^3+15x^2+9x-27
$$
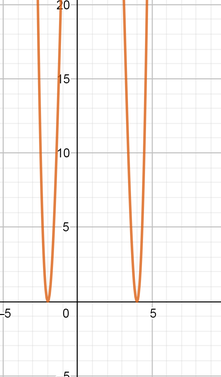
color{#4257b2}text{(c)} f(x)=(x+2)(x-4)(x+2)(x-4)
$$
$$
(x+2)^2(x-4)^2
$$
$$
[x^2+4x+4][x^2-8x+16]
$$
Use distributive property as follows:
$$
x^2[x^2-8x+16]+4x[x^2-8x+16]+4[x^2-8x+16]
$$
$$
x^4-8x^3+16x^2+4x^3-32x^2+64x+4x^2-32x+64
$$
Rearrange the tiles to group like terms as follows:
$$
x^4+(-8x^3+4x^3)+(16x^2-32x^2+4x^2)+(64x-32x)+64
$$
$$
x^4-4x^3-12x^2+32x+64
$$
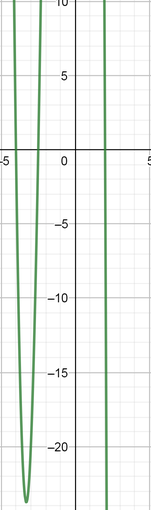
color{#4257b2}text{(d)} f(x)=-4(2x+5)(x-2)(x+4)
$$
$$
-4(2x+5)[(x-2)(x+4)]
$$
$$
(-8x-20)[x^2+2x-8]
$$
Use distributive property as follows:
$$
-8x[x^2+2x-8]-20[x^2+2x-8]
$$
$$
-8x^3-16x^2+64x-20x^2-40x+160
$$
Rearrange the tiles to group like terms as follows:
$$
-8x^3+(-16x^2-20x^2)+(64x-40x)+160
$$
$$
-8x^3-36x^2+24x+160
$$
text{color{Brown}(a) $-x^2+7x+8$
\ \
(b) $3x^3+15x^2+9x-27$
\ \
(c) $x^4-4x^3-12x^2+32x+64$
\ \
(d) $-8x^3-36x^2+24x+160$}
$$
$y=k(x+14)(x-13)(x+15)(x-16)$ cant determined.
The $x$ intercepts the shape of the function near each zero.
text{color{Brown}The $x$ intercepts the shape of the function near each zero.}
$$
$$
color{#4257b2}x=2
$$
Standard function is $y=a(x+x_{1})$
$$
y=a(x-2)
$$
Substitute the value of $x=7, y=5000$ as follows:
$$
5000=a(7-2) 5000=5a
$$
$$
a=dfrac{5000}{5} a=1000
$$
$$
y=1000(x-2)
$$
$$
color{#4257b2}x=-3, -3
$$
Standard function is $y=a(x+x_{1})(x+x_{2})$
$$
y=a(x+3)(x+3)
$$
Substitute the value of $x=7, y=5000$ as follows:
$$
5000=a(7+3)(7+3) 5000=100a
$$
$$
a=dfrac{5000}{100} a=50
$$
$$
y=50(x+3)(x+3)
$$
color{#4257b2}x=5
$$
Standard function is $y=a(x+x_{1})$
$$
y=a(x-5)
$$
Substitute the value of $x=7, y=5000$ as follows:
$$
5000=a(7-5) 5000=2a
$$
$$
a=dfrac{5000}{2} a=2500
$$
$$
y=2500(x-5)
$$
text{color{Brown}$y=1000(x-2)$
\ \
$y=50(x+3)(x+3)$
\ \
$y=2500(x-5)$}
$$
$$
color{#4257b2}text{(a)} y=-25[3(x+4)]^4-60
$$
$$
a=-25 k=3 d=-4 c=-60
$$
$$
color{#4257b2}text{(b)} y=8left[dfrac{3}{4} xright]^4+43
$$
$$
a=8 k=dfrac{3}{4} c=43
$$
$$
color{#4257b2}text{(c)} y=(-13x+26)^4+13
$$
$$
k=-13 d=-26 c=13
$$
$$
color{#4257b2}text{(d)} y=dfrac{8}{11}(-x)^4-1
$$
$$
a=dfrac{8}{11} k=-1 c=-1
$$
text{color{Brown}(a) $a=-25 k=3 d=-4 c=-60$
\ \
(b) $a=8 k=dfrac{3}{4} c=43$
\ \
(c) $k=-13 d=-26 c=13$
\ \
(d) $a=dfrac{8}{11} k=-1 c=-1$}
$$
text{color{#4257b2}Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^3$}
$$
The center point of the parent function $f(x)=x^3$ is equal $(0, 0)$, and the center point of transformed function is equal $(-4, -2)$, so the function transformed by the following terms:
** Vertically translated by $(2)$ units down on the $(y)$ axis.
** Horizontal translated by $(-4)$ units to the left side on the $(x)$ axis.
** Vertically stretched by factor of $(5)$ and reflected to the $(x)$ axis.
$$
f(x)=-5(x+4)^3-2
$$
text{color{Brown}$$f(x)=-5(x+4)^3-2$$}
$$

