
All Solutions
Page 91: Further Your Understanding
Here we have $textbf{graph of this function and a series of secant lines}$ which we can use to estimate the slope of the tangent when $x=2$.
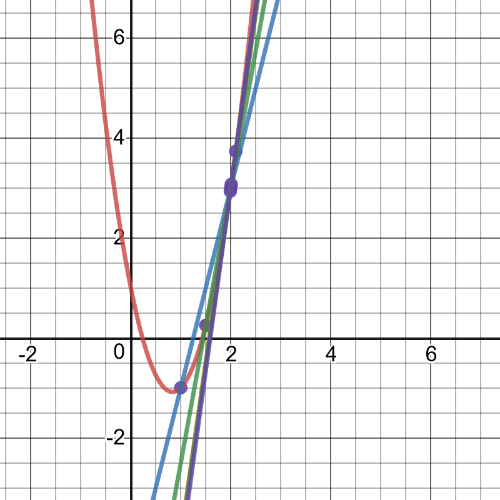
$textbf{slope}$ = $dfrac{f(x)-f(2)}{x-2}$
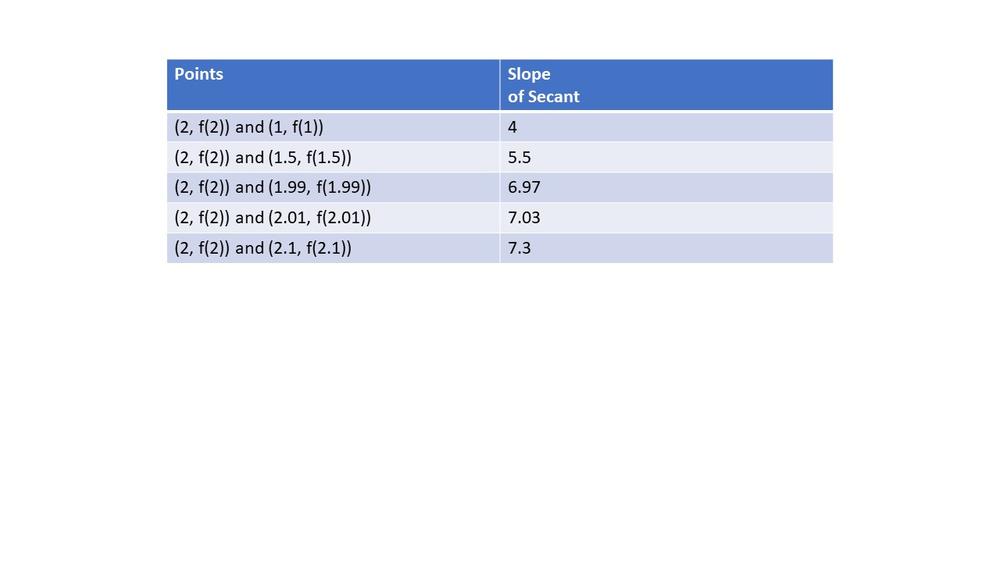
Here we have $textbf{graph of this function and a series of secant lines}$ which we can use to estimate the slope of the tangent when $x=2$.
$textbf{slope}$ = $dfrac{f(x)-f(2)}{x-2}$
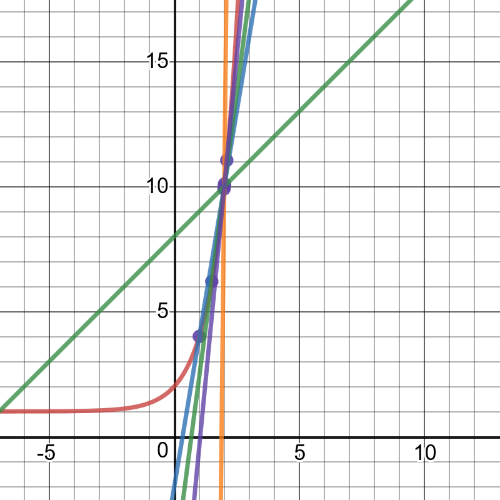
Here we have $textbf{graph of this function and a series of secant lines}$ which we can use to estimate the slope of the tangent when $x=2$.
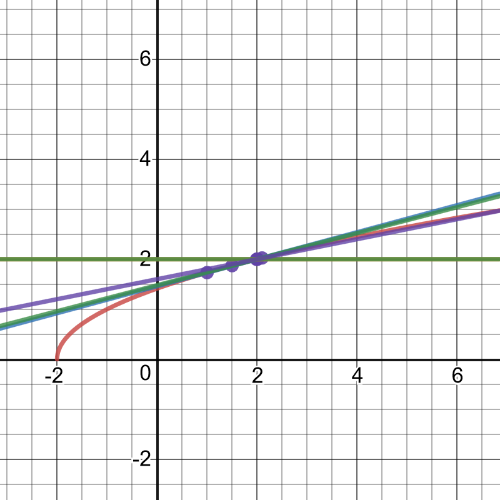
$textbf{slope}$ = $dfrac{f(x)-f(2)}{x-2}$
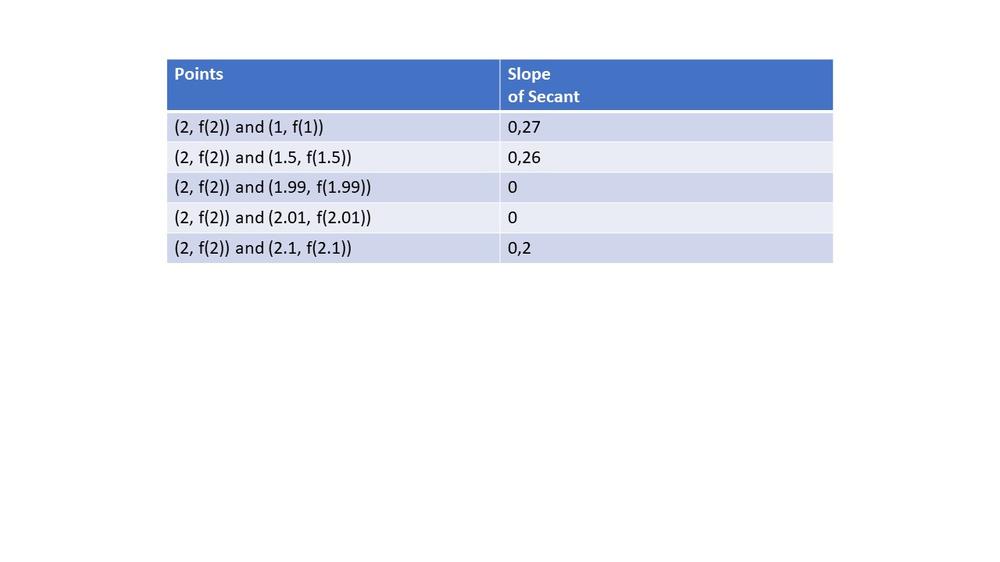
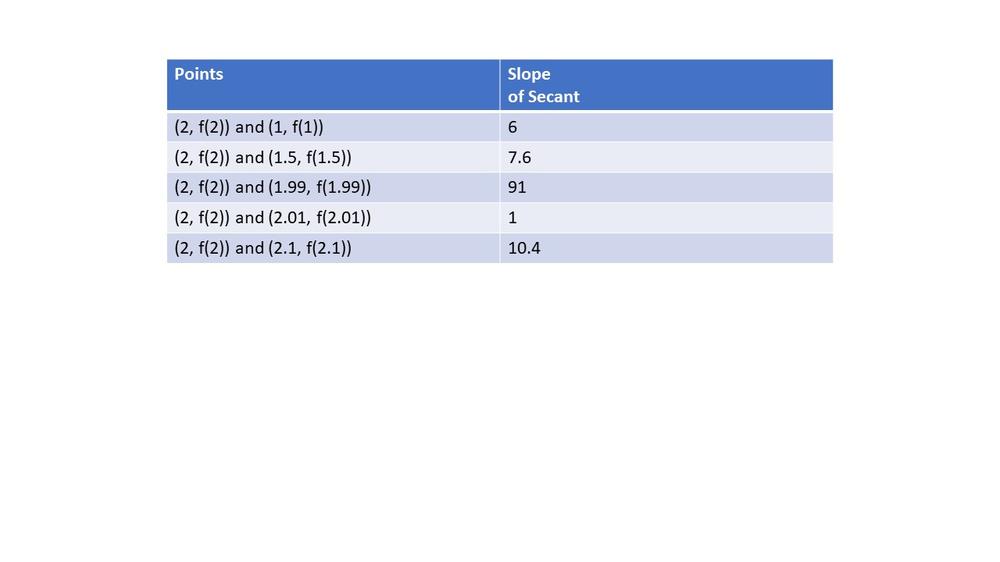
Here we have $textbf{graph of this function and a series of secant lines}$ which we can use to estimate the slope of the tangent when $x=2$.Here, we can see that all secant lines are all equivalent to the given function.
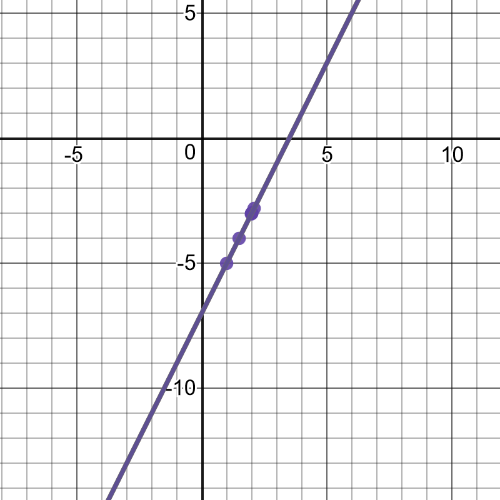
$textbf{slope}$ = $dfrac{f(x)-f(2)}{x-2}$
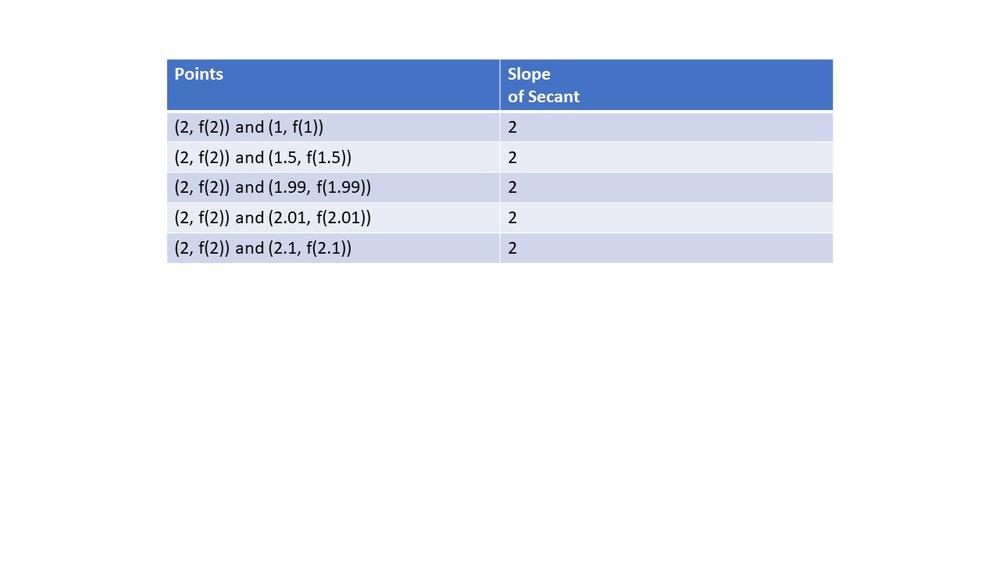
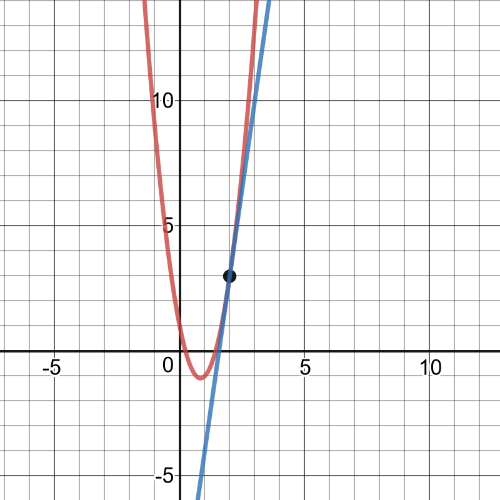
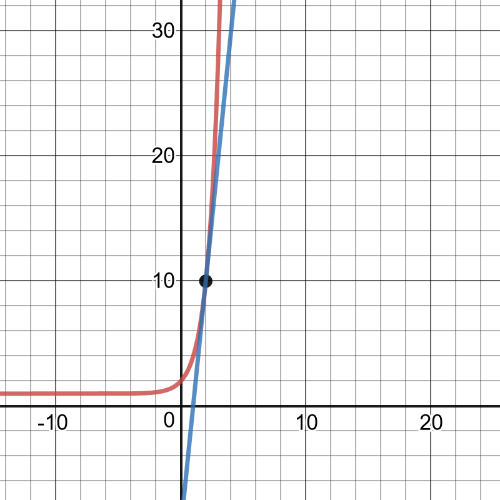
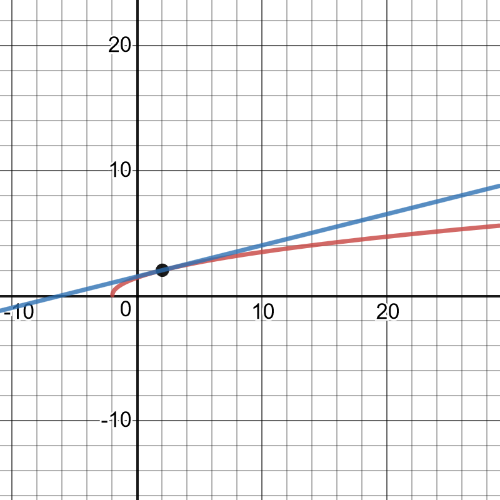
Here we have that tangent line in $x=2$ is equivalent to the function:
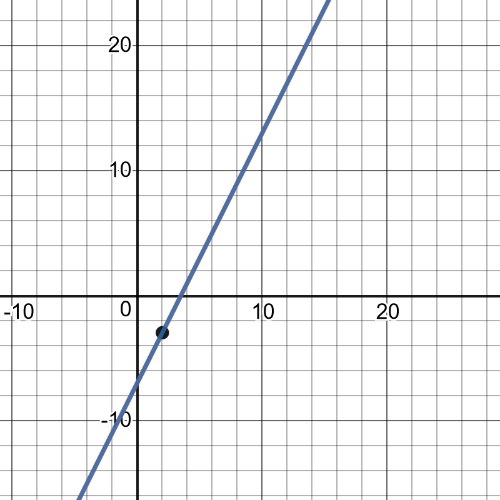
Set A
For the function $f(x)=-x^2+6x-4$ in $x=3$, we can find slope of the tangent in this point as derivative of this function in $x=3$.
So, the derivative of this function is:
$f'(x)=-2x+6$
$textbf{And the slope of tangent in point $x=3$ is}$ $f'(3)=-2cdot3+6=0$
For the function $g(x)=sin{x}$ in $x=3$, we can find slope of the tangent in this point as derivative of this function in $x=dfrac{pi}{2}$.
So, the derivative of this function is:
$g'(x)=cos{x}$
$textbf{And the slope of tangent in point $x=dfrac{pi}{2}$ is}$ $g'(dfrac{pi}{2})=cos{dfrac{pi}{2}}=0$
For the function $h(x)=-x^2+4x+11$ in $x=-2$, we can find slope of the tangent in this point as derivative of this function in $x=-2$.
So, the derivative of this function is:
$h'(x)=2x+4$
$textbf{And the slope of tangent in point $x=-2$ is}$ $h'(-2)=2cdot4+4=0$
For the function $j(x)=5$ in $x=1$, we can find slope of the tangent in this point as derivative of this function in $x=1$.
So, the derivative of this function is:
$j'(x)=0$
$textbf{And the slope of tangent in point $x=1$ is}$ $j'(1)=0$
For the function $f(x)=3x^2+2x-1$ in $x=2$, we can find slope of the tangent in this point as derivative of this function in $x=2$.
So, the derivative of this function is:
$f'(x)=6x+2$
$textbf{And the slope of tangent in point $x=2$ is}$ $f'(2)=6cdot2+2=14$
For the function $g(x)=2^x+3$ in $x=1$, we can find slope of the tangent in this point as derivative of this function in $x=1$.
So, the derivative of this function is:
$g'(x)=2^xln{2}$
$textbf{And the slope of tangent in point $x=1$ is}$ $g'(1)=2^1ln2=2ln2$
For the function $h(x)=5x+4$ in $x=3$, we can find slope of the tangent in this point as derivative of this function in $x=3$.
So, the derivative of this function is:
$h'(x)=5$
$textbf{And the slope of tangent in point $x=3$ is}$ $h'(3)=5$
For the function $j(x)=sin{x}$ in $x=dfrac{pi}{3}$, we can find slope of the tangent in this point as derivative of this function in $x=dfrac{pi}{3}$.
So, the derivative of this function is:
$j'(x)=cos{x}$
$textbf{And the slope of tangent in point $x=dfrac{pi}{3}$ is}$ $j'(dfrac{pi}{3})=cos{dfrac{pi}{3}}=dfrac{1}{2}$
For the function $f(x)=3x^2+2x-1$ in $x=-1$, we can find slope of the tangent in this point as derivative of this function in $x=-1$.
So, the derivative of this function is:
$f'(x)=6x+2$
$textbf{And the slope of tangent in point $x=-1$ is}$ $f'(-1)=6cdot({-1})+2=-4$
For the function $g(x)=-2^x+3$ in $x=0$, we can find slope of the tangent in this point as derivative of this function in $x=0$.
So, the derivative of this function is:
$g'(x)=-2^xln2$
$textbf{And the slope of tangent in point $x=0$ is}$ $g'(0)=-2^0ln2=-ln2$
For the function $h(x)=-3x+5$ in $x=2$, we can find slope of the tangent in this point as derivative of this function in $x=2$.
So, the derivative of this function is:
$hf'(x)=-3$
$textbf{And the slope of tangent in point $x=2$ is}$ $h'(2)=-3$
For the function $j(x)=sin{x}$ in $x=2dfrac{pi}{3}$, we can find slope of the tangent in this point as derivative of this function in $x=2dfrac{pi}{3}$.
So, the derivative of this function is:
$j'(x)=cos{x}$
$textbf{And the slope of tangent in point $x=2dfrac{pi}{3}$ is}$ $j'(2dfrac{pi}{3})=cos{2dfrac{pi}{3}}=-dfrac{1}{2}$
Set A
All the slopes of the tangents at this set are $textbf{equivalent to}$ $0$.
Set B
All the slopes of the tangents at this set are $textbf{positive.}$
Set C
All the slopes of the tangents at this set are $textbf{negative.}$
Here we have $textbf{graph}$ of given data:
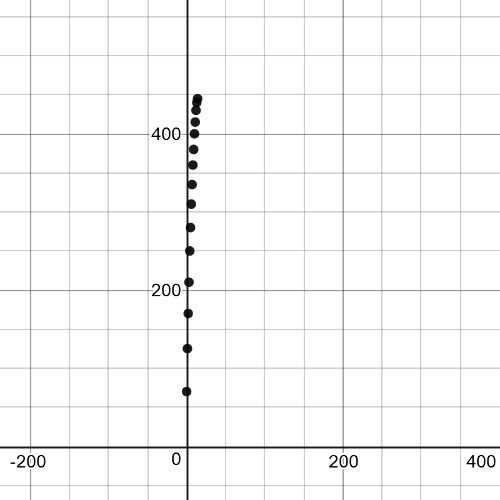
Here we have $textbf{a curve of best fit and the tangent line at}$ $x=5$:
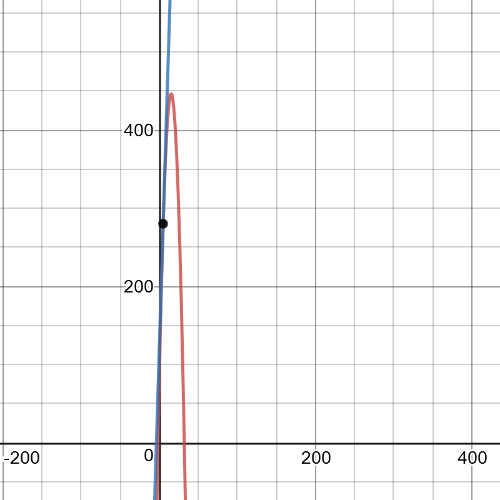
We have that the slope of the tangent line in $x=5$ is $32.47$.We got this value using quadriatic regression to estimate given data and derivative in $x=5$.
#### (d)
Here we have that $textbf{the instantaneous rate of change in temperature}$ at
exactly 5 min using a centred interval from the table of values is:
$dfrac{Delta{T}}{Delta{x}}=dfrac{310-250}{6-4}=30$
#### (e)
We have that slope of tangent line is a little bit bigger than instaneous rate of change in temperature in same point, $x=5$.
subsection*{(a)}
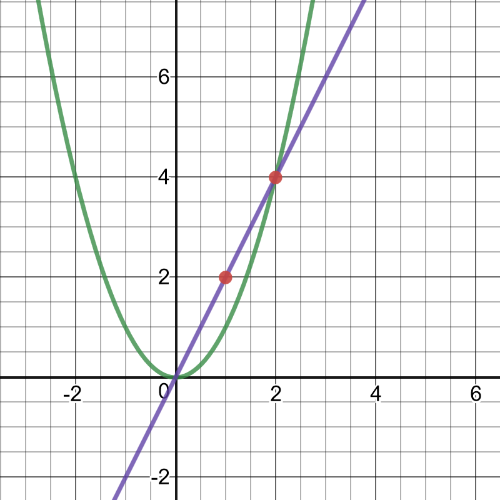subsection*{(b)}
$$
f'(x)=2x,
$$
is the function of the slope of the tangent of the curve $y=x^2$ at any point $x$.
Now, from part b), we know that the slope of the tangent line is $2$. Substituting in the tangent slope equation, we get:
$$begin{aligned}
2x&=2\
x&=1.
end{aligned}$$
Finally, we know that the point of tangency must lie on the curve, which means we can substitute the $x$ coordinate in the equation of the curve to obtain the $y$ coordinate, i.e.,
$$
y=x^2=1^2=1.
$$
Therefore, we can conclude that the point of tangency with the same slope as the secant line is at $(1,1)$.

