
All Solutions
Page 62: Chapter Self-Test
$textbf{This relation is a function}$, because its graph passes vertical line test.
#### (b)
$textbf{Its domain and range}$ is following set:
$D=R=Bbb{R}$
$textbf{Possible parent function}$ could be a function $y=x^2$.
#### (b)
Here we have graph of $textbf{possible function $y=x^2-2$}$:
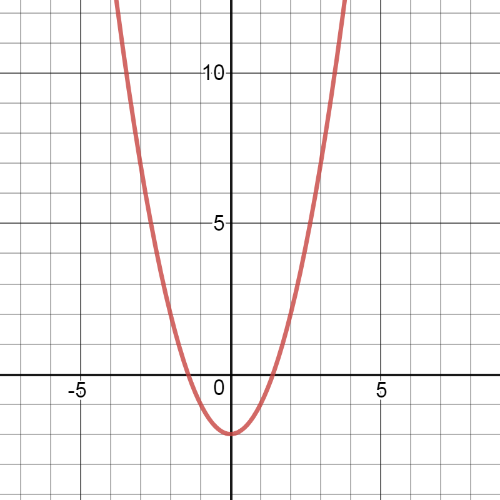
$textbf{The transformation}$ which is made here is $textbf{translation 2 units down}$.
$$
f(-x)=left|3(-x) right|+(-x)^2=left|-3x right|+x^2=left|3x right|+x^2=f(x)
$$
f(-x)=left|3(-x) right|+(-x)^2=left|-3x right|+x^2=left|3x right|+x^2=f(x)
$$
Function $y=x^2$:
This function is $textbf{decreasing}$ on $left(-infty,0 right)$ and $textbf{increasing}$ on $left[0,infty right)$, it has $textbf{one zero}$ in $x=0$ and it is $textbf{even}$ function.
Function $y=2^x$:
This function is $textbf{increasing}$ on its domain, $textbf{it has no zeros}$ and this fuction is $textbf{neither function}$.
On the following picture is $textbf{graph}$ of this transfpremd function:
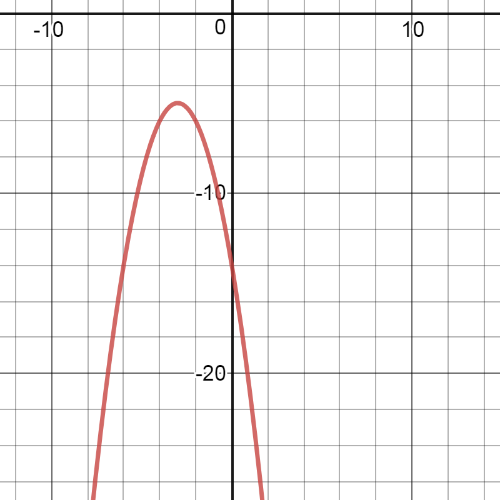
$$
y=left|dfrac{1}{2}x right|+1
$$
y=left|dfrac{1}{2}x right|+1
$$
First, we will transform a little given function:
$3f(-x+1)+2=3f(-(x-1))+2$,
so we have following transformation of coordinates of given point:
$left(3,5 right)rightarrowleft(-1cdot3,3cdot5 right)=left(-3,15 right)$
$left(-3,15 right)rightarrowleft(-3+1,15+2 right)=left(-2,17 right)$
So, $textbf{corresponding point}$ is $left(-2,17 right)$.
#### (b)
Here we have actually $textbf{inverse function}$, so transformation is:
$$
left(3,5 right)rightarrowleft(5,3 right)
$$
$y=-2(x+1)=-2x-2$
$x=-2y-2$
$-2y=x+2$
$y=-dfrac{1}{2}(x+2)$
So, $textbf{inverse function}$ is $y=dfrac{1}{2}(x+2)$
How we have in this task that $125000$>50000$$, we have tax,$x$, of$12%$, so, the solution is next:\$x=$dfrac{12cdot125000}{100}$=15000
$$
\
textbf{So, the tax is} $15000
$$
#### (b)
$textbf{Function which describes this model os tax policy}$ would be following:
$$
f(x)=begin{cases}
dfrac{5}{100}x & xleq50000\\
dfrac{12}{100}x & x>50000\
end{cases}
$$
(b)$f(x)=
$$
begin{cases}
dfrac{5}{100}x & xleq50000\\
dfrac{12}{100}x & x>50000\
end{cases}
$$
$
Here we have $textbf{graph}$ of this function:
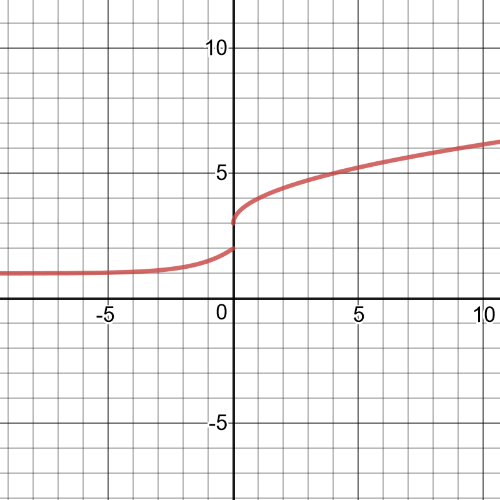
This function is $textbf{discontinuous}$ on its entire domain because all the pieces of the function not join together at the endpoints of the given intervals.
#### (c)
This function is $textbf{increasing}$ on its entire domain.We can see that from the graph of this function from part $(a)$.
#### (d)
$textbf{The domain}$ of this function is set $D=Bbb{R}$ and $textbf{range}$ is set $R=left(0,infty right)$.
(d)$D=Bbb{R}$, $R=left(0,infty right)$

