All Solutions
Section 1-2: Exploring Absolute Value
$$
begin{align*}
abs{-5}&=5\
abs{20}&=20\
abs{-15}&=15\
abs{12}&=12\
abs{-25}&=25.
end{align*}$$
Arranging these results in ascending order, we obtain
$$
5,12,15,20,25,
$$
or, as they were given in the exercise
$$
abs{-5},abs{12}, abs{-15},abs{20}, abs{-25}.$$
$$abs{-22}=22.$$
$$-abs{-35}=-(35)=-35.$$
$$abs{-5-13}=abs{-18}=18.$$
$$abs{4-7}+abs{-10+2}=abs{-3}+abs{-8}=3+8=11.$$
$$dfrac{abs{-8}}{-4}=dfrac{8}{-4}=-2.$$
$$dfrac{abs{-22}}{abs{-11}}+dfrac{-16}{abs{-4}}=dfrac{22}{11}+dfrac{-16}{4}=2-4=-2.$$
$$
begin{equation*}
left|x right|>3
end{equation*}
$$
$$
begin{equation*}
left|x right|leq8
end{equation*}
$$
$$
begin{equation*}
left|x right|geq1
end{equation*}
$$
$$
begin{equation*}
left|xright|ne5
end{equation*}
$$




$$
begin{equation*}
left|x right|leq3
end{equation*}
$$
$$
begin{equation*}
left|x right|>2
end{equation*}
$$
$$
begin{equation*}
left|x right|geq2
end{equation*}
$$
$$
begin{equation*}
left|x right|<4
end{equation*}
$$
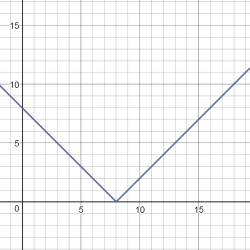
We note that the graphs of these two functions coincide.
#### (b)
We have that, according to definition of absolute value is:
$$
begin{equation*}
g(x)=left|-x+8 right|=left|-(x-8) right|=left|x-8 right|=f(x)
end{equation*}
$$
So, from the previous equality, we see that $f(x)$ and $g(x)$ are the same functions, so and their graphs are the same.
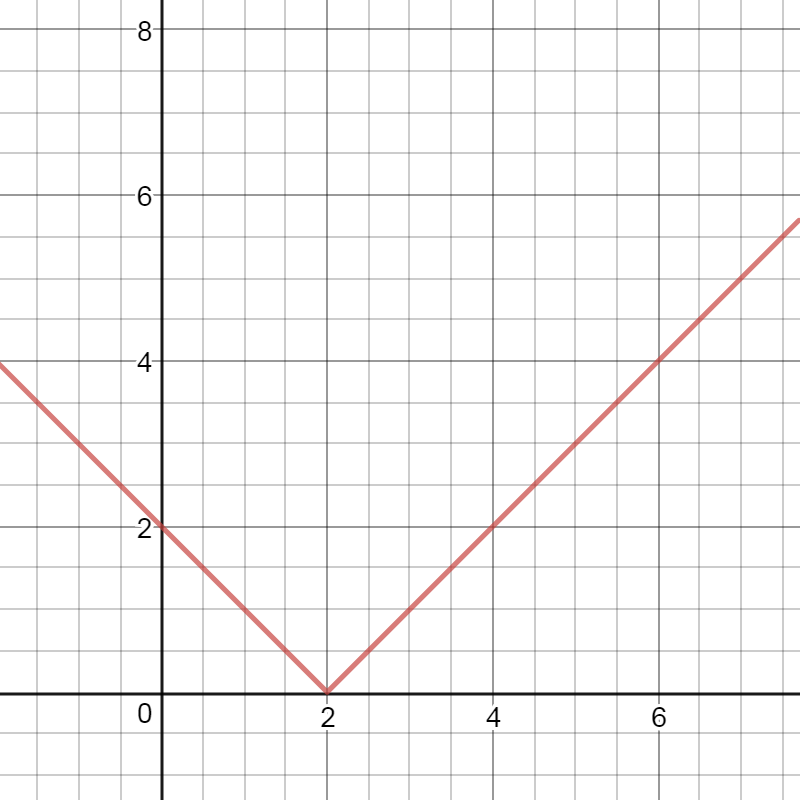
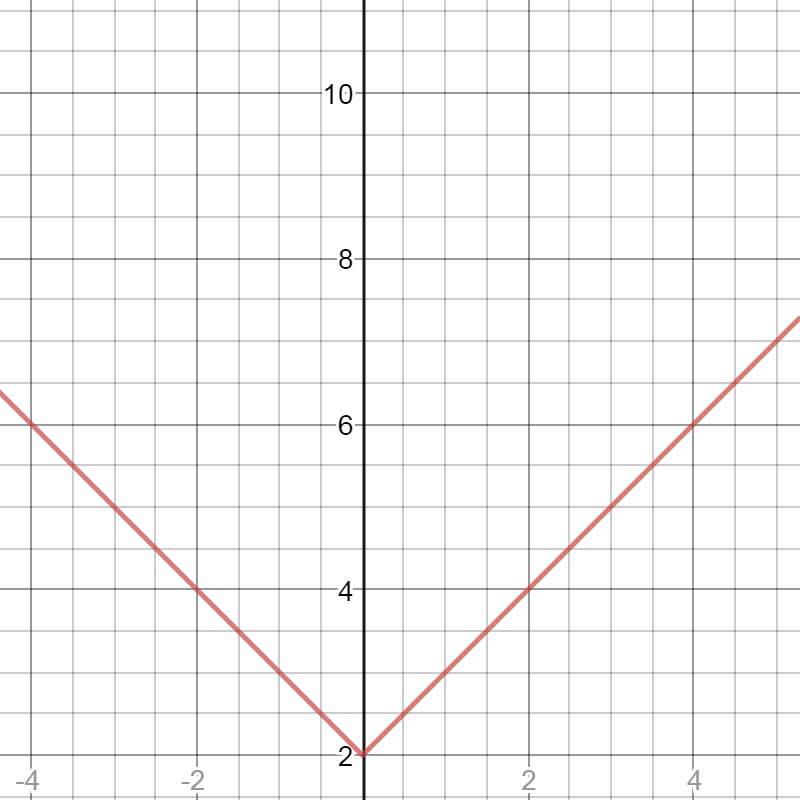
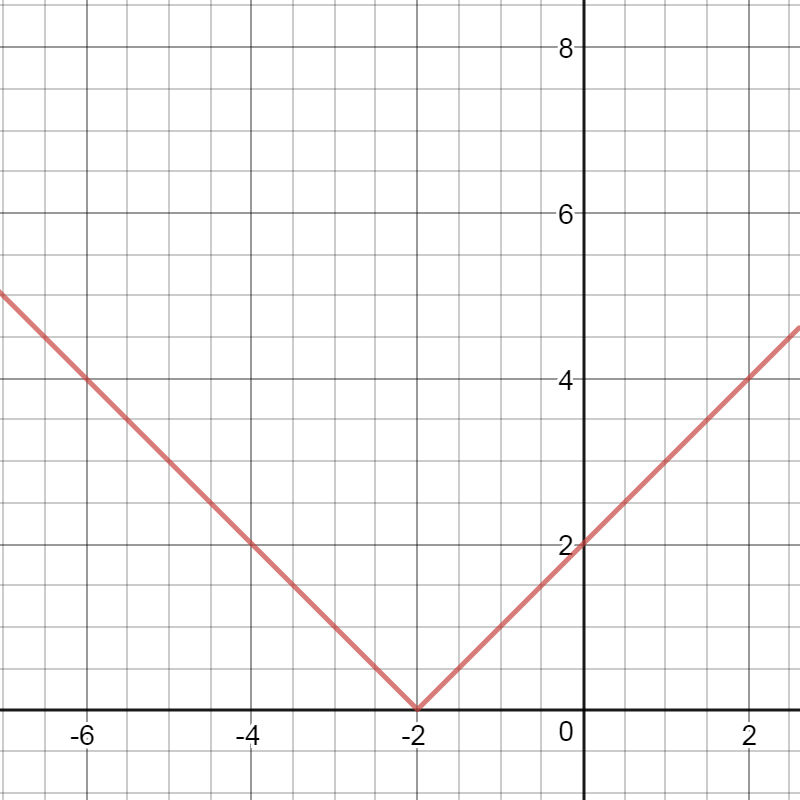
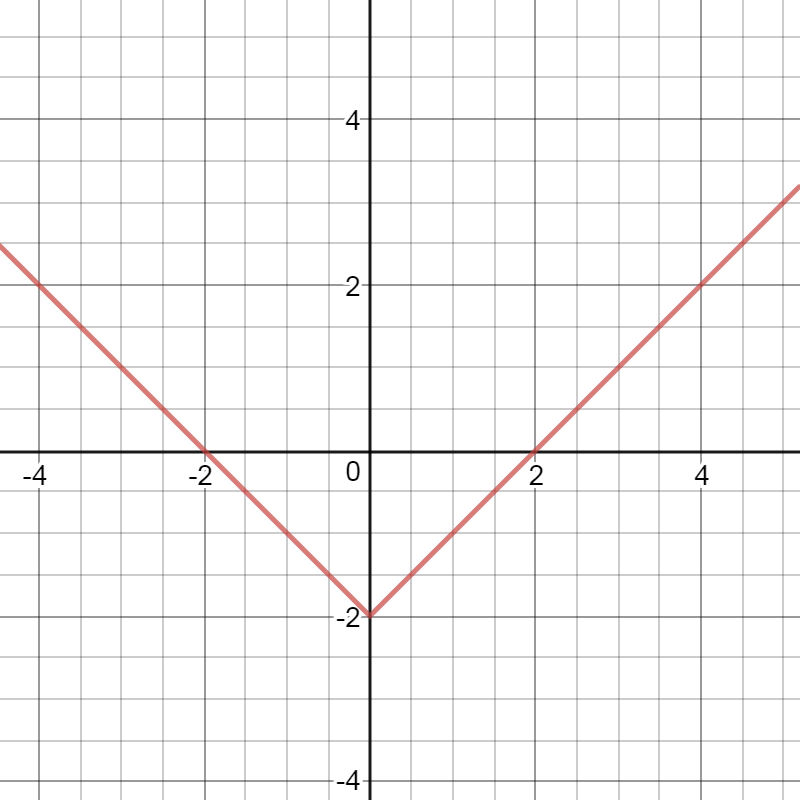
And the graphics of the functions $b$ and $d$ differ in the fact that the themes of the graphics are moved to 2, that is, in -2 on the y-axis, respectively
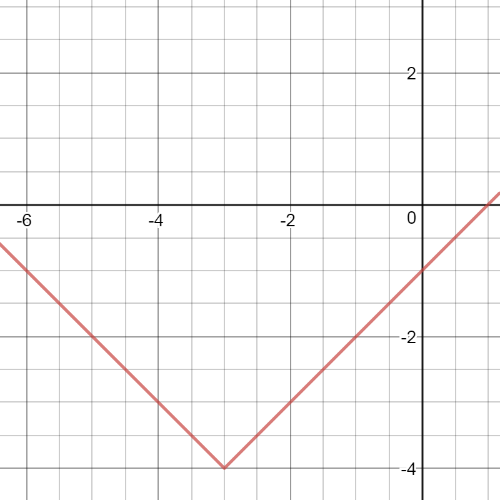
So, the graph of the functions given in this task will have $textbf{topics}$ in point (-3.-4), analogous to the previous consideration, as can be seen from the graph below.