All Solutions
Page 71: Questions
$$
angle ITR=angle NGA=180text{textdegree}-90text{textdegree}-28text{textdegree}=62text{textdegree}
$$
Since all three pair of angles are congruent and two pairs of sides are congruent, the third pair of sides also have to be equivalent.
The rigid transformations needed will be a rotation and a translation.
b.
$$
triangle IRT cong triangle NAG
$$
There are multiple correct congruence statements, by reordering the letters in one triangle name and then applying the same reordering to the other triangle name.
b. $triangle IRT cong triangle NAG$
$angle N$ is in between the side of length 15 and the side of length 12, the same is true for $angle W$ and thus $angle N$ is congruent with $angle W$.
$angle P$ is in between the side of length 12 and the side of length 6, the same is true for $angle V$ and thus $angle P$ is congruent with $angle V$.
The congruence statement then becomes:
$$
triangle MNPcong triangle UWV
$$
b. A rotation of 180$text{textdegree}$ about $P$ and a translation is sufficient.
b. A rotation of 180$text{textdegree}$ about $P$ and a translation is sufficient.
$$
triangle NLRcong triangle BAC
$$
triangle NLRcong triangle BAC
$$
$$
SAS: triangle ABC cong triangle FED
$$
You would need a rotation and a translation to map one triangle on the other.
b. Not congruent, because the indicated angle in the first triangle lies between the known sides, but not in the second triangle.
c. Using the vertical angles and alternate interior angles are equivalent:
$$
ASA: triangle MNXcong triangle ZYX
$$
You would need a rotation about $X$ at 180$text{textdegree}$ counterclockwise.
d.
$$
RHS: triangle ACD cong triangle ABD
$$
You would need a reflection about $AD$.
e. Using alternate interior angles are equivalent:
$$
AAS: triangle EFHcong triangle GHF
$$
You would need a rotation and a translation to map one triangle on the other.
f. Not congruent, because the indicated angle in the first triangle lies between the known sides, but not in the second triangle.
b. Not congruent
c. Congruent
d. Congruent
e. Congruent
f. Not congruent
SSS: three pairs of corresponding sides are congruent
SAS: two pairs of corresponding sides are congruent and the included angles are also congruent
ASA: two pairs of corresponding angles are congruent and the corresponding sides between them are congruent.
AAS: two pairs of corresponding angles are congruent and a pair of corresponding sides not in between the angle are congruent.
HL: The hypotenuse and a leg of both right triangles are congruent.
$$
ASA: triangle ABDcong triangle CBD
$$
b. The two triangles are congruent, because they have two pairs of sides of the same lengths and the included angles have the same measure.
$$
SAS: triangle DBCcong triangle ACB
$$
c. Vertical pairs and alternate interior angles are equivalent, which implies that we have three pairs of equivalent angles in the two triangles. However, the side $CD$ in $triangle CDE$ corresponds with side $AC$ in $triangle ABC$, which are not necessarily equally long (similarly, side $BC$ and side $CE$ are not necessarily equally long) and thus we cannot determine whether the two triangles are congruent.
d. The two triangles are congruent, because they have two angles of the same measure and a pair of non-included corresponding sides of equal length.
$$
AAS: triangle ADBcong triangle BCA
$$
e. Cannot be determined, because we do not know if there is a pair of corresponding sides that are congruent.
f. The two triangles are congruent, because they have three pairs of sides of the same lengths.
$$
SSS: triangle SQRcong triangle HGK
$$
b. SAS
c. Cannot be determined
d. AAS
e. Cannot be determined
f. SSS
b. Square with length 6
c. Hexagon
d.
b. Square with side length 6
c. Hexagon
d. Answers could vary. For example, circle
$$
Slope AB: dfrac{6-4}{1+3}=dfrac{1}{2}
$$
$$
Slope BC: dfrac{-2-6}{5-1}=dfrac{-8}{4}=-2
$$
$$
Slope CD: dfrac{-4+2}{1-5}=dfrac{1}{2}
$$
$$
Slope DA: dfrac{4+4}{-3-1}=-2
$$
Since parallel lines have the same slope and perpendicular lines have slopes whose product is $-1$, we then know that the shape is a rectangle.
b. The coordinates are $(4,3),(6,-1),(-2-5),(-4,-1)$ (interchange the $x$- and $y$-values and change the new $y$-values of sign).
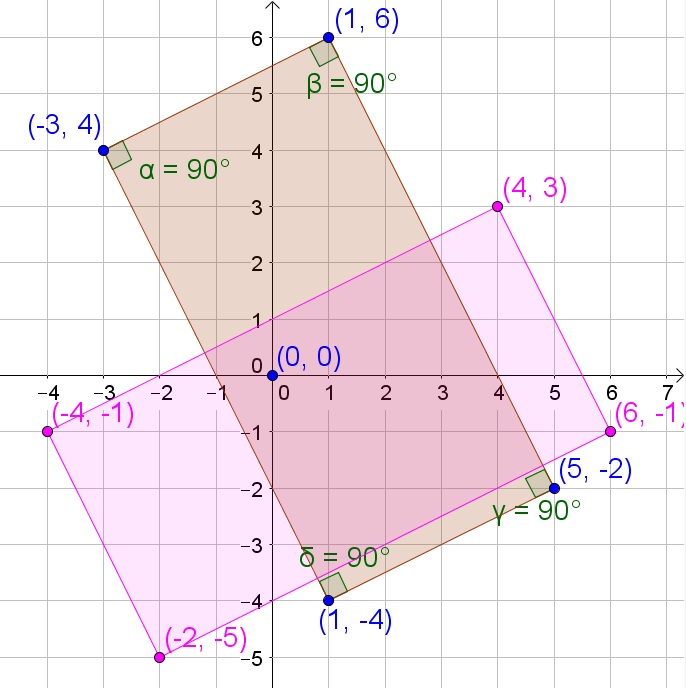
b. $(4,3),(6,-1),(-2-5),(-4,-1)$
$$
AREA=dfrac{(5+8)4}{2}=26
$$
Determine the length of the left side using the Pythagorean theorem:
$$
sqrt{1^2+4^2}=sqrt{1+16}=sqrt{17}
$$
The perimeter is the sum of all sides:
$$
PERIMETER=sqrt{17}+5+8+sqrt{20}=13+sqrt{17}+sqrt{20}
$$
Perimeter: $13+sqrt{17}+sqrt{20}$
$$
Maximum: 8+5=13ft
$$
$$
Minimum: 8-5=3ft
$$
Thus the length of the third side is between 3 ft and 13 ft.
b.
$$
AB=DF
$$
$$
BC=DE
$$
$$
AC=EF
$$
$$
Downarrow SSS
$$
$$
triangle ABCcong triangle FDE
$$
PQ=ST
$$
$$
mangle P = mangle T=120text{textdegree}
$$
$$
mangle QRP = mangle SRTtext{ (vertical angles) }
$$
$$
Downarrow AAS
$$
$$
triangle PQRcong triangle TSR
$$
$$
UV=XY
$$
$$
VW=YZ
$$
$$
UW=XZ
$$
$$
angle Ucong angle X
$$
$$
angle Vcong angle Y
$$
$$
angle Wcong angle Z
$$
$$
AC=CA
$$
$$
mangle B = mangle D
$$
$$
mangle BAC= mangle DCAtext{ (alternate interior angles) }
$$
$$
Downarrow AAS
$$
$$
triangle ABCcong triangle CDA
$$
b. Not congruent, because the triangles have three pair of congruent angles, while a pair of corresponding sides do not have an equal length.
d.
$$
MP=QR=13
$$
$$
KL=PR=12 text{ Using pythagorean theorem}
$$
$$
mangle KLM= mangle QRP=90text{textdegree}
$$
$$
Downarrow SAS
$$
$$
triangle KLMcong triangle RPQ
$$
b. Not congruent
c. Not congruent
d. Congruent
$$
SE=ME
$$
$$
SY=MY
$$
$$
YE=YE
$$
$$
Downarrow SSS
$$
$$
triangle SYEcong triangle MYE
$$
$$
Downarrow
$$
$$
angle Scong angle M
$$
b. Yes
$$
dfrac{(8-1-1+4)3}{2}=dfrac{30}{2}=15
$$
The area of a rectangle is the product of the length and the width of the rectangle:
$$
8cdot 2=16
$$
Thus the total area is then the sum of the subareas:
$$
15+16=31
$$
$$
dfrac{5cdot 3}{2}=7.5
$$
$$
dfrac{4cdot 2}{2}=4
$$
The area of a rectangle is the product of the length and the width of the rectangle:
$$
6cdot 5=30
$$
Thus the total area is then the sum of the subareas:
$$
7.5+4+30=41.5
$$
b. 41.5
$$
34x-10x=-8+80
$$
Simplify;
$$
24x=72
$$
Divide both sides of the equation by 24:
$$
x=3
$$
$$
4x-4x=10+5
$$
Simplify
$$
0x=15
$$
This is not possible, since zero cannot equal 15 and thus the equation has no solutions.
$$
3x-15+6x+2=41
$$
Group like terms:
$$
3x+6x=41+15-2
$$
Simplify:
$$
9x=54
$$
Divide both sides of the equation by 9:
$$
x=6
$$
$$
-2x-8+6=-3
$$
Group like terms:
$$
-2x=-3+8-6
$$
Simplify:
$$
-2x=-1
$$
Divide both sides of the equation by $-2$:
$$
x=dfrac{1}{2}
$$
b. No solutions
c. $x=6$
d. $x=dfrac{1}{2}$
a. We need to find two numbers whose product is 15 and whose sum is 8, this is true for 5 and 3. Thus 5 and 3 need to be filled in the left and right cells (order is not important).
b. Upper: $3cdot 1=3$ and Lower: $3+1=4$
c. Right: $dfrac{10}{5}=2$ and Lower: $5+2=7$
d. Upper: $dfrac{1}{2}cdot dfrac{1}{3}=dfrac{1}{6}$ and Lower: $dfrac{1}{2}+dfrac{1}{3}=dfrac{3}{6}+dfrac{2}{6}=dfrac{5}{6}$
b. 3 and 4
c. 2 and 7
d. $frac{1}{6}$ and $frac{5}{6}$
$$
5x+7=9x-63
$$
Group like terms:
$$
5x-9x=-63-7
$$
Simplify:
$$
-4x=-70
$$
Divide both sides of the equation by $-4$:
$$
x=17.5
$$
Determine the angles:
$$
5x+7=5(17.5)+7=94.5text{textdegree}
$$
$$
9x-63=9(17.5)-63=94.5text{textdegree}
$$
$$
12x-14=5x+21
$$
Group like terms:
$$
12x-5x=21+14
$$
Simplify:
$$
7x=35
$$
Divide both sides of the equation by $7$:
$$
x=5
$$
Determine the angles:
$$
12x-14=12(5)-14=46text{textdegree}
$$
$$
5x+21=5(5)+21=46text{textdegree}
$$
$$
20x+34=20(5)+34=134text{textdegree}
$$
b. $x=5text{textdegree}$, Angles are 46$text{textdegree}$, 46$text{textdegree}$, and 134$text{textdegree}$
a. If angles are congruent, then they are vertical angles.
b. The original statement is true, but the converse is not true. Because vertical angles are congruent and alternate interior angles are an example of congruent angles that are not vertical angles.
b. The original statement is true, but the converse is not true.
a. Yes, this arrow is true because the statement after the arrow is a property of congruent triangles.
b. All pairs of corresponding sides are congruent $Rightarrow$ Triangles congruent
The converse is also true (SSS).
c. Yes, this arrow is true because the statement after the arrow is a property of congruent triangles.
d. All pairs of corresponding angles are congruent $Rightarrow$ Triangles congruent
The converse is not true because we do not know if the two triangles have at least one pair of corresponding sides that are congruent.
e. The area of a polygon is $b cdot h$ $Rightarrow$ the polygon is a rectangle
The converse is not true, because the area of a parallelogram is also $bcdot h$ while a parallelogram is not a rectangle.
b. Yes
c. Yes
d. No
d. No
a. If a polygon is a square, then the polygon is a rhombus. TRUE
Converse: If a polygon is a rhombus, then the polygon is a square FALSE because a rhombus does not necessarily have four right angles.
b. If a triangle is isosceles, then the triangle is equilateral. FALSE, because an isosceles triangle has two equally long sides, while an equilateral triangles has three equilly long sides.
Converse: If a triangle is equilateral, then the triangle is isosceles. TRUE
c. If two parralel lines cut by a transversal, then the same-side interior angles are supplementary. TRUE, because of the same-side interior angles theorem
Converse: If the same-side interior angles of two lines who are cut by a transversal are supplementary, then the two lines are parallel. TRUE
b. False (converse is true)
c. True (converse is true)
For example, If a polygon is a square, then the polygon is a rhombus.
Converse: If a polygon is a rhombus, then the polygon is a square.
Knowing that a statement is true or false, gives no information about the converse being true or false.
a. If the ground is wet, then it rains. FALSE (you could have sprayed water on the ground yourself)
b. If a polygon is a rectangle, then the polygon is a square. FALSE A rectangle does not have four equal sides.
c. If a polygon hs four 90$text{textdegree}$ angles, then the polygon is a rectangle. FALSE The polygon could have 5 angles.
d. If a polygon is a triangle, then it has three angles. TRUE
e. If vertical angles are congruent, then two lines intersect. TRUE, this follows from the definition of vertical angles.
b. False
c. False
d. True
e. True
$$
180text{textdegree}-75text{textdegree}-35text{textdegree}=70text{textdegree}
$$
Supplementary angles:
$$
x=180text{textdegree}-70text{textdegree}=110text{textdegree}
$$
$$
180text{textdegree}-140text{textdegree}=40text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$ and the base angles of an isosceles triangle are equal:
$$
2x=180text{textdegree}-40text{textdegree}=140text{textdegree}
$$
Thus:
$$
x=70text{textdegree}
$$
$$
180text{textdegree}-148text{textdegree}=32text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$:
$$
x=180text{textdegree}-32text{textdegree}-100text{textdegree}=48text{textdegree}
$$
$$
180text{textdegree}-36text{textdegree}=144text{textdegree}
$$
Thus:
$$
dfrac{144}{2}text{textdegree}=72text{textdegree}
$$
Supplementary angles:
$$
x=180text{textdegree}-72text{textdegree}=108text{textdegree}
$$
b. 70$text{textdegree}$
c. 48$text{textdegree}$
d. 108$text{textdegree}$
b.
$$
a+b=x
$$
c. $c$ and $x$ are supplmentary angles:
$$
x=180text{textdegree} -c
$$
The sum of all angles in a triangle is equal to $180text{textdegree}$:
$$
c=180text{textdegree}-a-b
$$
Then we obtain:
$$
x=180text{textdegree} -180text{textdegree}+a+b=a+b
$$
d. The measure of the exterior angle is equal to the sum of the measure of the remote interior angles.
b. $a+b=x$
c. Use that $c$ and $x$ are supplementary angles and thus the sum of all angles in a triangle is equal to $180text{textdegree}$
d. The measure of the exterior angle is equal to the sum of the measure of the remote interior angles.
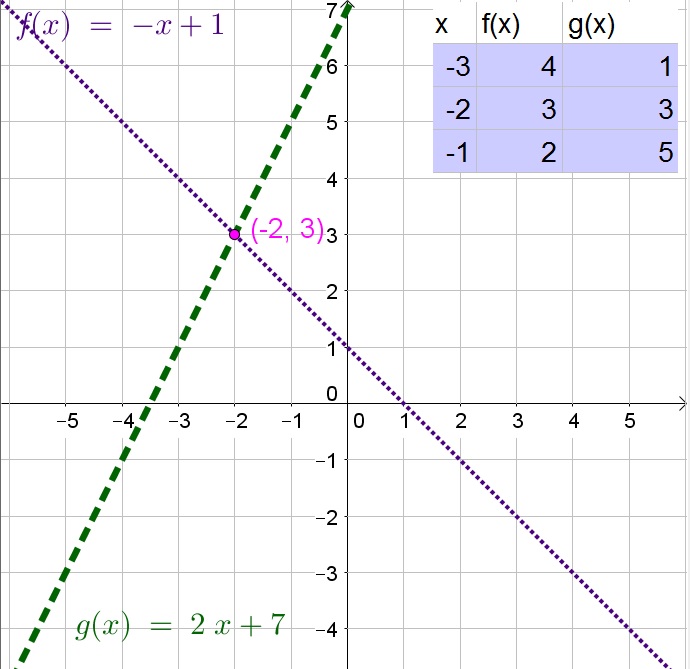
$$
2y=-2x+2
$$
$$
y=2x+7
$$
Add the two equations:
$$
3y=9
$$
Divide both sides of the equation by 3:
$$
y=3
$$
Determine $x$:
$$
3=-x+1
$$
Add $x$ to both sides of the equation:
$$
3+x=1
$$
Subtract three from both sides of the equation:
$$
x=-2
$$
Thus the solution is $(-2,3)$.
(-2,3)
$$
$$
sqrt{8^2+6^2}=sqrt{100}=10
$$
Then by SAS we know that the two triangles are congruent.
b. Congruent because of AAS.
c. Not congruent, because the pair of congruent angles does not lie in between the two pairs of corresponding congruent sides.
d. Congruent, because of SAS.
b. Congruent
c. Not congruent
d. Congruent
a. Upper: $(-4)cdot (-7)=28$ and Lower: $-4-7=-11$
b. We need to find two numbers whose product is $-12$ and whose sum is 4, this is true for 6 and $-2$. Thus 6 and $-2$ need to be filled in the left and right cells (order is not important).
c. Right: $dfrac{-8}{1/2}=-16$ and Lower: $dfrac{1}{2}-16=-dfrac{31}{2}$
d. Upper: $dfrac{1}{2}cdot dfrac{1}{5}=dfrac{1}{10}$ and Lower: $dfrac{1}{2}+dfrac{1}{5}=dfrac{5}{10}+dfrac{2}{10}=dfrac{7}{10}$
b. 6, $-2$
c. $-16$, $-frac{31}{2}$
d. $frac{1}{10}$, $frac{7}{10}$

a. The lines that are crossed by a transversal are parallel$Rightarrow x$ and $y$ are supplementary.
b. $x$ and $y$ are supplementary $Rightarrow$ The lines that are crossed by a transversal are parallel
This is true.
c. Assume that same-side interior angles are supplementary but that the lines are not parallel. If the lines are not parallel, then there exists a point where the two lines intersect, let us call this point A. But then we have created a triangle with angles $x$ and $y$ and $angle A$. Since the sum of the angles in a triangle is 180$text{textdegree}$:
$$
x+y+angle A =180text{textdegree}
$$
Since $x$ and $y$ are supplementary:
$$
180text{textdegree}+angle A=180text{textdegree}
$$
Subtract 180$text{textdegree}$ from both sides of the equation:
$$
angle A=0text{textdegree}
$$
But the angle of the triangle cannot be zero, thus we have obtained a contradiction and thus the lines must be parallel.
b. Yes
c. Derive $angle A=0text{textdegree}$
b. The sum of the angles in a triangle is 180$text{textdegree}$:
$$
mangle BED=180text{textdegree}-100text{textdegree}-80text{textdegree}=0text{textdegree}
$$
c. This example does not exist, because an angle of a triangle cannot be zero.
b. $mangle BED=0text{textdegree}$
c. This example doesn’t exist
$$
mangle YBA=180text{textdegree}-x
$$
b. Assume that $overleftrightarrow{BY}$ and $overleftrightarrow{AZ}$ are not parallel.
c.
$$
mangle BAZ=x
$$
$$
mangle YBA=180text{textdegree}-x
$$
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are not parallel}
$$
$$
Downarrow
$$
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{intersect in a point } C
$$
$$
Downarrow
$$
$$
ABC is a triangle
$$
$$
Downarrow
$$
$$
mangle BAZ+mangle YBA+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
180text{textdegree}+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
mangle C=0text{textdegree}
$$
$$
CONTRADICTIONRightarrow overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are parallel}
$$
b. Assume that $overleftrightarrow{BY}$ and $overleftrightarrow{AZ}$ are not parallel.
c. Assume that the lines are not parallel and derive a contradiction.
d. If the same-side interior angles of two lines with a transversal are supplementary, then the lines are parallel.
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are not parallel}
$$
$$
Downarrow
$$
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{intersect in a point } C
$$
$$
Downarrow
$$
$$
ABCtext{ is a triangle}
$$
$$
Downarrow
$$
$$
mangle BAZ+mangle YBA+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
180text{textdegree}+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
mangle C=0text{textdegree}
$$
$$
CONTRADICTIONRightarrow overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are parallel}
$$
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are not parallel}
$$
$$
Downarrow
$$
$$
overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{intersect in a point } C
$$
$$
Downarrow
$$
$$
ABC is a triangle
$$
$$
Downarrow
$$
$$
mangle BAZ+mangle YBA+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
180text{textdegree}+mangle C=180text{textdegree}
$$
$$
Downarrow
$$
$$
mangle C=0text{textdegree}
$$
$$
CONTRADICTIONRightarrow overleftrightarrow{BY}text{ and }overleftrightarrow{AZ}text{ are parallel}
$$
If alternate interior angles are congruent, then the lines are parallel.
b. Prove by assuming that the lines are not parallel and deriving a contradiction.
c. If corresponding angles are congruent, then the lines are parallel.
If alternate interior angles are congruent, then the lines are parallel.
If the corresponding angles are congruent, then the lines are parallel.
If alternate interior angles are congruent, then the lines are parallel.
For example, $y=1$ and $y=2$ are parallel lines and they cannot have a point of intersection because 1 is never equal to 2.
$$
14(3)=(5)x
$$
Simplify:
$$
42=5x
$$
Divide both sides of the equation by 5:
$$
8.4=x
$$
$$
10(11)=(5)m
$$
Simplify:
$$
110=5m
$$
Divide both sides of the equation by 5:
$$
22=m
$$
$$
(t-2)(8)=(7)12
$$
Simplify:
$$
8t-16=84
$$
Add 16 to both sides of the equation:
$$
8t=100
$$
Divide both sides of the equation by 8:
$$
t=12.5
$$
$$
3(x+1)=(5)x
$$
Simplify:
$$
3x+3=5x
$$
Subtract $3x$ from both sides of the equation:
$$
3=2x
$$
Divide both sides of the equation by 2:
$$
1.5=x
$$
b. $m=22$
c. $t=12.5$
d. $x=1.5$
$$
triangle DEFcong triangle LJK
$$
Because $70text{textdegree}+60text{textdegree}+50text{textdegree}=180text{textdegree}$ and $DE=JL$ which are the sides between the angles of 70$text{textdegree}$ and of 50$text{textdegree}$.
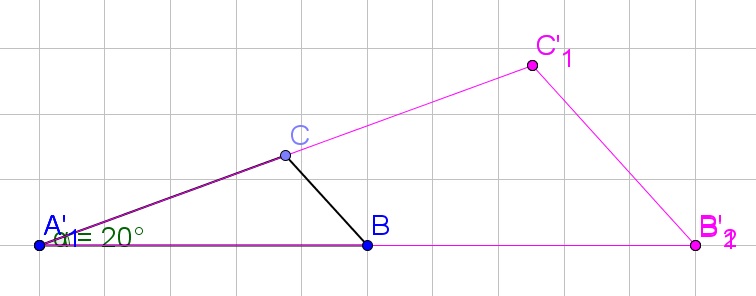
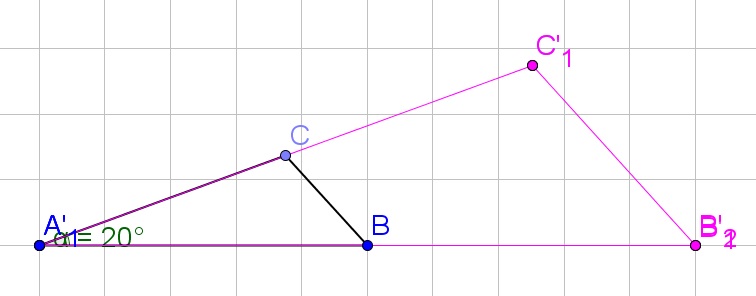
b. A reflection, rotation and translation will be needed.
b. Use reflection, rotation, and translation
The area of a rectangle is the product of the length and the width:
$$
4cdot 3=12
$$
The area of a triangle is product of the base and the height divided by 2:
$$
h=sqrt{10^2-6^2}=sqrt{64}=8 text{Pythagorean identity}
$$
$$
dfrac{bcdot h}{2}=dfrac{12cdot 8}{2}=48
$$
The total area is then the sum of the subareas:
$$
A=12+48=60
$$
The perimeter is the sum of the lengths of all sides:
$$
P=10+10+4+3+4+3+4=38
$$
Perimeter 38
$$
mangle ADB=180text{textdegree}-11text{textdegree}-90text{textdegree}=79text{textdegree}
$$
$$
mangle BDC=180text{textdegree}-90text{textdegree}-68text{textdegree}=22text{textdegree}
$$
Since longer sides are opposite larger angles, we then know that $overline{AB}$ is longer than $overline{BC}$.
overline{AB}
$$
$$
{ab, ac, ad, ae, bc, bd, be, cd, ce, de}
$$
We did not forget any songs because we worked alphabetically.
b. Yes, every combination is equally likely and this is important because else the songs would not be chosen randomly.
c. We note that the songs $a$, $b$, and $d$ all have the word Mama in its title. Moreover, 3 of the 10 pairs of songs in part (a) contain two letters out of $a$, $b$, and $d$ (that is, the pairs of songs $ab$, $ad$, and $bd$).
$$
dfrac{3}{10}=0.3=30%
$$
d. We note that the songs $a$, $b$, and $d$ all have the word Mama in its title. Moreover, 9 of the 10 pairs of songs in part (a) contain either $a$, $b$, or $d$ (since the only pair of songs not containing one of these letters is $ce$).
$$
dfrac{9}{10}=0.9=90%
$$
e. Because the probability of (d) includes the probability of (c), because if at least one song contains mama, then either both songs contain mama or exactly one of the songs contains mama.
b. Yes
c. $dfrac{3}{10}=0.3=30%$
d. $dfrac{9}{10}=0.9=90%$
e. Because the probability of (d) includes the probability of (c)
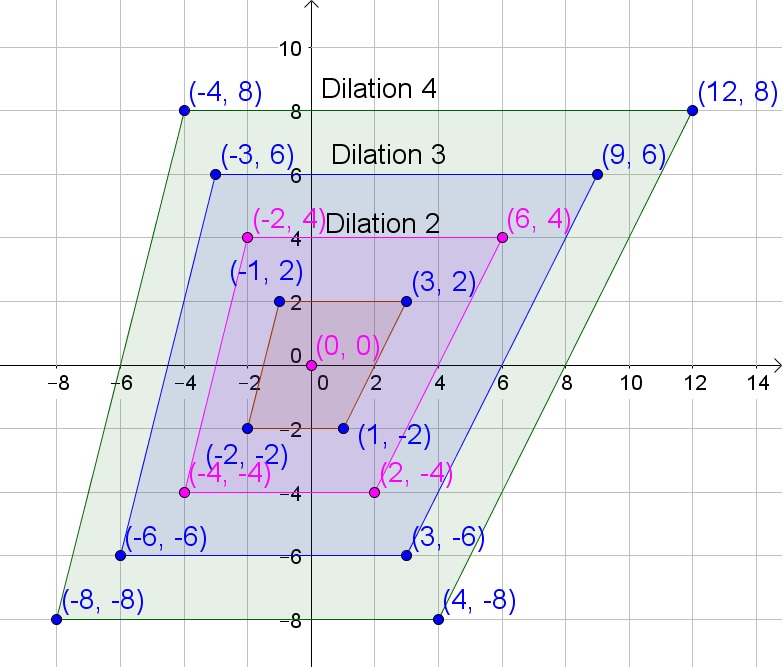
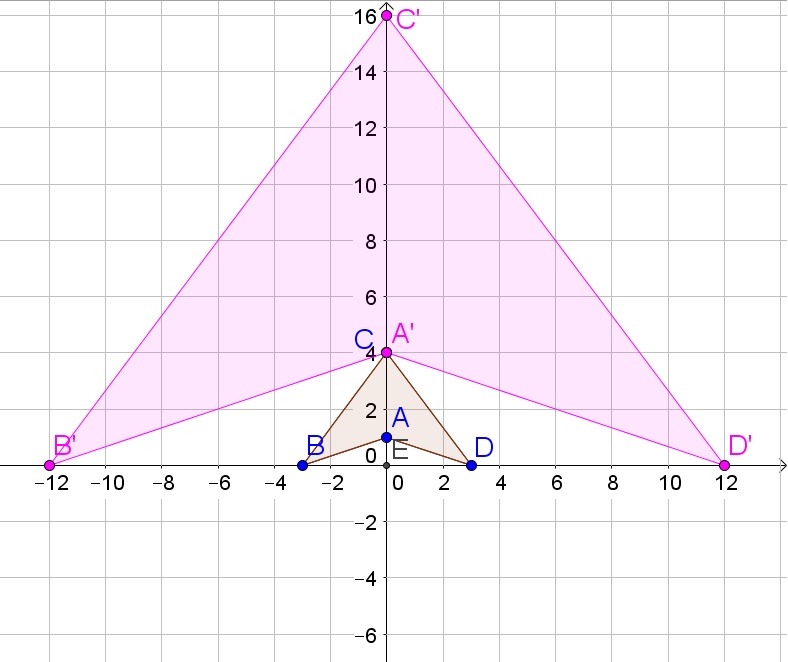
The lengths of the sides of the quadrilaterals are multiplied by the dilation factor, so are the coordinates of the vertices.
c. The shape of the quadrilaterals remain the same after the dilation. Moreover, the angle measure of all angles remain the same before and after dilation.
The lengths of the sides of the quadrilaterals are multiplied by the dilation factor.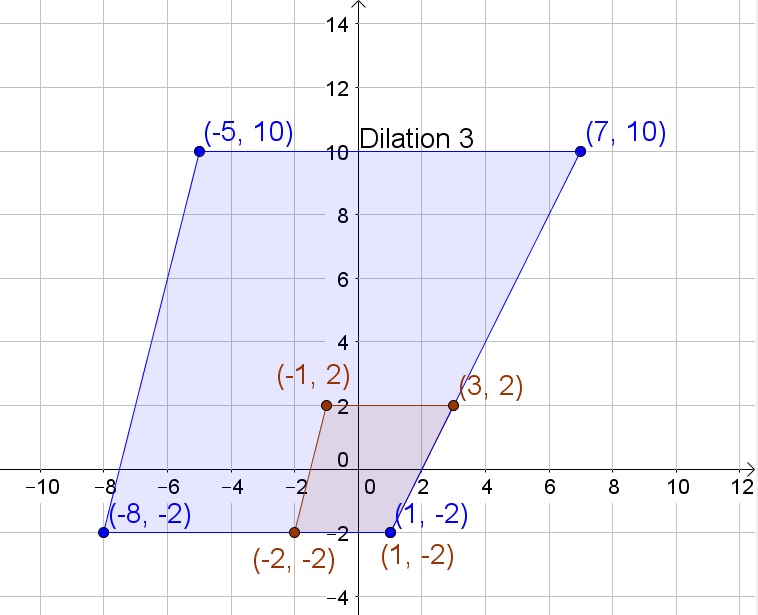
b. Larger/smaller figure, Similar in shape
c. Yes
b. (G) is difference from the other triangles because its obtuse angle is less obtuse than the other triangles obtuse angles.
b. (G)
b. $D$ has to correspond with $C$; $O$ has to correspond to $T$ and $G$ has to correspond with $A$. Thus (ii) is the correct statement.
b. (ii)
The lengths of the sides are multiplied by the dilation factor.
$$
AB=sqrt{(3-0)^2+(4-0)^2}=sqrt{25}=5
$$
$$
BC=sqrt{(3-3)^2+(4-0)^2}=sqrt{16}=4
$$
$$
AC=sqrt{(3-0)^2+(0-0)^2}=sqrt{9}=3
$$
b. The side lengths of the enlarged triangle is the product of the dilation factor and the side lengths of the original triangle.
$$
A’B’=2cdot 5=10
$$
$$
B’C’=2cdot 4=8
$$
$$
A’C’=2cdot 3=6
$$
c. The perimeter is the sum of all sides:
$$
10+8+6=24
$$
The area of a triangle is the product of the base and the height, divided by 2:
$$
AREA=dfrac{8cdot 6}{2}=24
$$
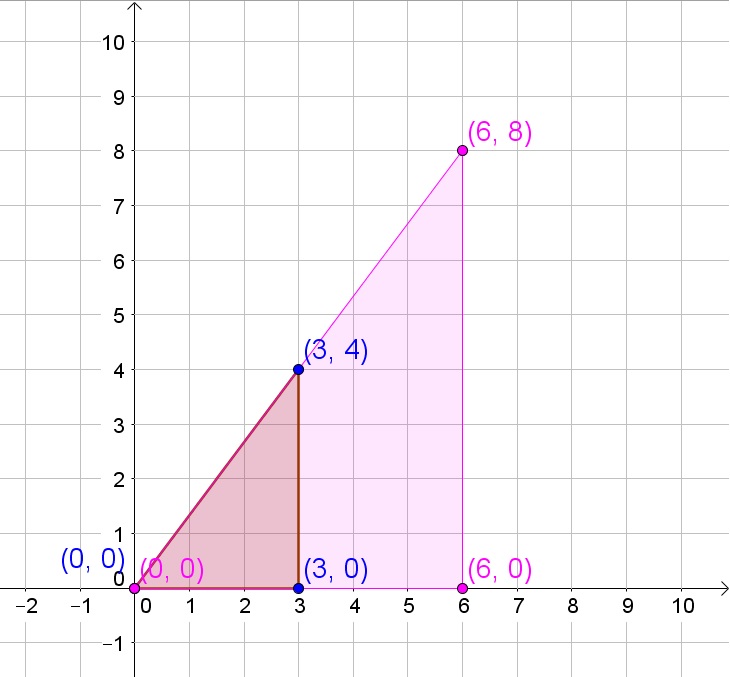
b. 10, 8, 6
c. Perimeter 24 and Area 24
b. If a rectangle has base $x$ and height $3y$, then the perimeter of the rectangle is $3xy$. FALSE, because the perimeter of a rectangle isthe sum of all sides: $x+x+3y+3y=2x+6y$.
Thus the correct statement is then: If a rectangle has base $x$ and height $3y$, then the perimeter of the rectangle is $2x+6y$.
c. If a rectangle has base $2$ft and height $3$ft, then the area of the rectangle is $864$ square inches. TRUE, because the area of a rectangle is the product of the base and the height.
b. False
c. True
$$
dfrac{(10cdot h)}{2}=25
$$
Multiply both sides of the equatoin by 2:
$$
10h=50
$$
Divide both sides of the equation by 10:
$$
h=5
$$
Determine the sides of the triangle using the Pythagorean theorem:
$$
sqrt{h^2+6^2}=sqrt{25+36}=sqrt{61}
$$
$$
sqrt{h^2+4^2}=sqrt{25+16}=sqrt{41}
$$
The perimeter is then the sum of all sides:
$$
6+4+sqrt{61}+sqrt{41}=10+sqrt{61}+sqrt{41}
$$
Perimeter=$10+sqrt{61}+sqrt{41}$ft
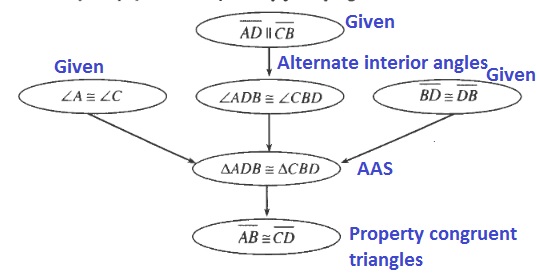
AC=DF
$$
$$
mangle A=mangle D
$$
$$
AB=DE
$$
$$
Downarrow SAS
$$
$$
triangle ABC cong triangle DEF
$$
$$
(x+5)(x+3)=x^2+5x+3x+15=x^2+8x+15
$$
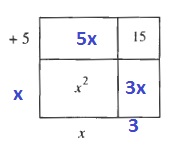
$$
(x+5)(2x+3)=2x^2+10x+3x+15=2x^2+13x+15
$$
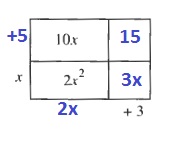
b. $(x+5)(2x+3)=2x^2+13x+15$
$$
2x+x+x=180text{textdegree}
$$
Combine like terms:
$$
4x=180text{textdegree}
$$
Divide both sides of the equation by 4:
$$
x=45text{textdegree}
$$
$$
y=180text{textdegree}-71text{textdegree}=109text{textdegree}
$$
b. $y=109text{textdegree}$
$overline{A’B’}$ corresponds with $overline{AB}$
b. $C’B’=2CB$ and $A’B’=AB$, thus the lengths of the sides are multiplied by the dilation factor.
c. Because the point about which you dilated is $A$ and it lies on $overline{AB}$ and $overline{AC}$, but not on $overline{BC}$.
d. No, because you would need to add the length of the original sides itself, which is different for each side.
e. 4 times because $AB=5$, the length of the other side is then the product of the dilation factor 4 and the original length:
$$
B”C”=4cdot 4=16
$$
$overline{A’B’}$ corresponds with $overline{AB}$
b. $C’B’=2CB$ and $A’B’=AB$
c. Because the point about which you dilated is $A$ and it lies on $overline{AB}$ and $overline{AC}$, but not on $overline{BC}$.
d. No
e. $B”C”=16$
$$
dfrac{24}{8}=dfrac{18}{6}=3
$$
b. Yes, the ratios are both equal to $dfrac{4}{3}$ (see part (a)).
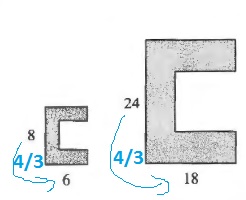
$$
x=8cdot 12=96
$$
d. We note that the height has been multiplied by $dfrac{1}{4}$ (to reduce the height of 8 to the height of 2) and thus the scale factor is $dfrac{1}{4}$.
e. If the scale factor is 1, then the figure remains the same and we will thus obtain two congruent figures.
b. Yes
c. $x=96$ cm
d. $frac{1}{4}$
e. Congruent figures
b.
$$
dfrac{4}{10}=dfrac{x}{x+9}
$$
Use cross multiplication:
$$
4x+36=10x
$$
Subtract $4x$ from both sides of the equation:
$$
36=6x
$$
Divide both sides of the equation by 6:
$$
6=x
$$
c.
$$
dfrac{4}{x}=dfrac{10}{x+9}
$$
Use cross multiplication:
$$
4x+36=10x
$$
Subtract $4x$ from both sides of the equation:
$$
36=6x
$$
Divide both sides of the equation by 6:
$$
6=x
$$
e. $dfrac{4}{10}=dfrac{2}{5}$ (see (b))
f. Parallel lines
b. $x=6$
c. $x=6$
d. 15, 6
e. $frac{2}{5}$
f. Parallel lines
$$
dfrac{15}{6}=dfrac{20}{8}=2.5
$$
b. Use the Pythagorean theorem:
$$
sqrt{15^2+20^2}=sqrt{625}=25
$$
$$
sqrt{6^2+8^2}=sqrt{100}=10
$$
The ratio is then:
$$
dfrac{25}{10}=2.5
$$
Thus we note that the ratio remains unchanged.
c. You will need a dilation, rotation, and translation.
b. Yes
c. You will need a dilation, rotation, and translation.
b. Temperature will increase gradually when being heated, thus the graph should slope slowly upwards and thus graph 3 is the best option.
c. River miles traveled increases and thus the only graph left for (c) is graph 1 (since graph (3) belongs to part (b)).
b. Graph 3
c. Graph 1
b. Using the Pythagorean theorem:
$$
5^2+12^2=169=13^2neq 14^2
$$
Thus the hypotenuse should be 13 in stead of 14.
c. Since two sides of the triangle are equal, the base angles are also equal. Summing up all angles we then obtain:
$$
65text{textdegree}+65text{textdegree}+55text{textdegree}=185text{textdegree}neq 180text{textdegree}
$$
Thus this is not possible, because the sum of all angles in a triangle should be equal to 180$text{textdegree}$.
b. Hypotenuse should be 13 instead of 14
c. The sum of all angles in a triangle should be equal to 180$text{textdegree}$.
a. Right: $dfrac{-98}{7}=-14$ and Lower: $7-14=-7$
b. Upper: $dfrac{3}{2}cdot dfrac{3}{2}=dfrac{9}{4}$ and Lower: $dfrac{3}{2}+dfrac{3}{2}=dfrac{6}{2}=3$
c. Left: $dfrac{5/4}{-5/2}=-dfrac{1}{2}$ and Lower: $-dfrac{1}{2}-dfrac{5}{2}=-dfrac{6}{2}=-3$
d. Right: $0+10=10$ and Upper: $(-10)cdot (10)=-100$
b. $frac{9}{4}$ and 3
c. $-frac{1}{2}$ and $-3$
d. 10 and $-100$
b. Since the playlist contains 2 country songs out of 5 songs:
$$
dfrac{2}{5}=0.4=40%
$$
c. Since the playlist contains 3 “Mama” songs out of 5 songs:
$$
dfrac{3}{5}=0.6=60%
$$
d. Since the playlist contains 1 Hank Tumbleweed out of 5 songs:
$$
dfrac{1}{5}=0.2=20%
$$
e. Since the playlist contains 4 not R&B songs out of 5 songs:
$$
dfrac{4}{5}=0.8=80%
$$
b. 40%
c. 60%
d. 20%
e. 80%
b. The two triangles are similar.
c. Perform a dilation with factor $dfrac{1}{2}$ to the larger triangle and then translated onto the smaller triangle.
b. It is not possible to create two triangles with the same angle measures that are not similar.
b. No
c. You might need rotations, dilations, transformations, and reflections.
$$
mangle I=180text{textdegree}-68text{textdegree}-87text{textdegree}=25text{textdegree}
$$
$$
mangle E=180text{textdegree}-25text{textdegree}-87text{textdegree}=68text{textdegree}
$$
Thus we note that the corresponding angle measures are all equal and thus the triangle are similar.
b.Two, because the third angle will follow from the fact that the sum of all angles in a triangle is 180$text{textdegree}$. Abreviated we will refer to this as AA.
b. Two, AA
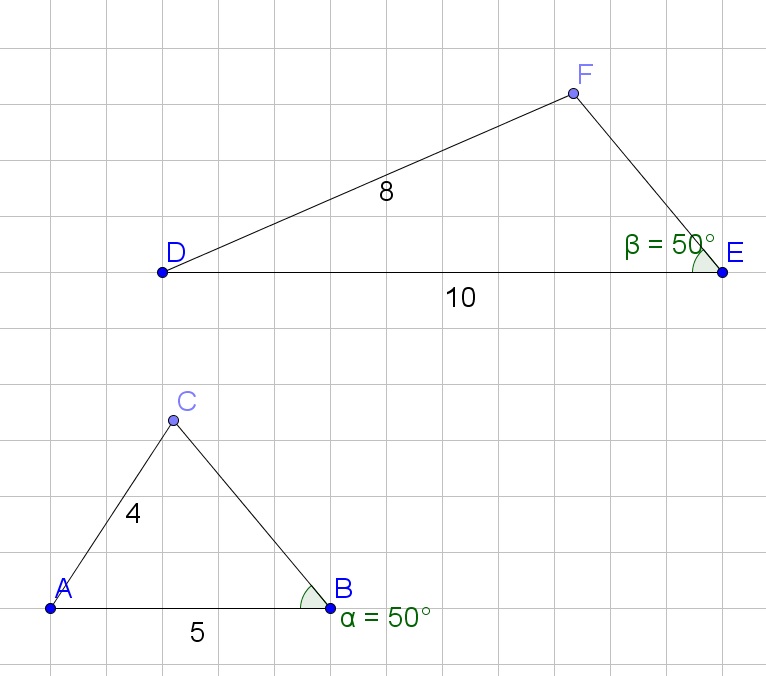
d. Let us abbreviate it as $SAS$.
b. No
c. Two triangles are similar if they have two pairs of corresponding sides that are proportional and the included angles are congruent.
d. $SAS$
b. It is not possible to find triangles with proportional sides that are not similar.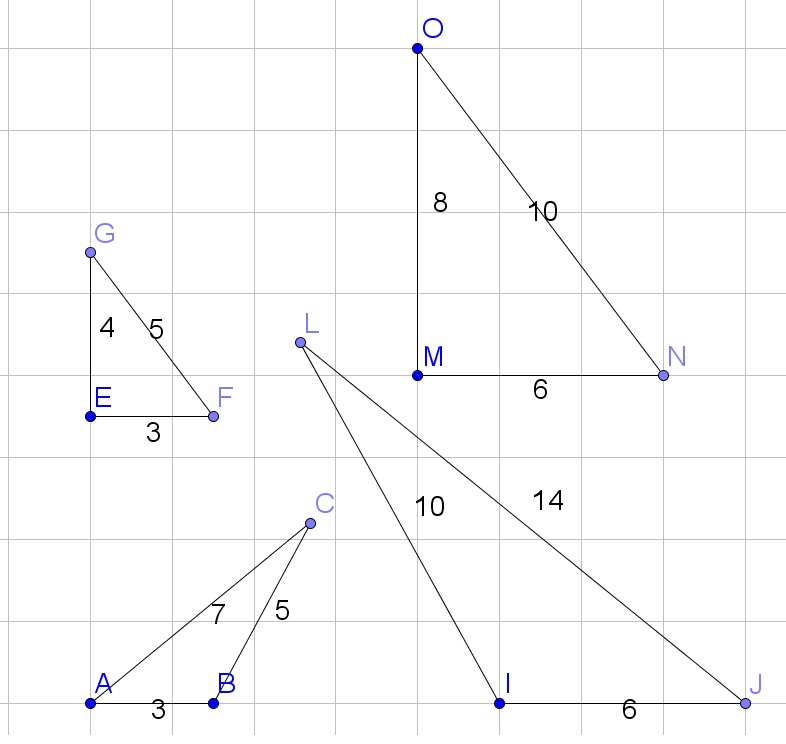
b. No
c. Three valid triangle similarity conditions: AA, SAS, SSS.
b. Yes
c. AA, SAS, SSS
$$
mangle P=180text{textdegree}-32text{textdegree}-52text{textdegree}=96text{textdegree}
$$
Thus we then know that the triangles are similar because of AA.
b. Similar because of SAS, and the common ratio of the sides is
$$
dfrac{64}{20}=dfrac{44.8}{14}=3.2
$$
c. Similar because of AA (top angle is the same angle in both triangles)
d. Not similar because the ratios of the sides are not equal:
$$
dfrac{211.2}{58.5}=3.6neq dfrac{202.4}{44}=4.6neq dfrac{90}{18}=5
$$
b. Similar
c. Similar
d. Not similar
SAS: If two pair of corresponding sides are proportional and the included angles are congruent, then the two triangles are similar.
SSS: If three pair of corresponding sides are proportional, then the two triangles are similar.
b. Similar, because of SSS. A dilation about the left vertex and a translation will be sufficient.
c. Not similar because the sides are not proportional:
$$
dfrac{33}{11}=3text{ and } dfrac{20}{8}=2.5text{ and }dfrac{15}{6}=2.5
$$
d. Not similar, because the two triangles cannot have two pairs of congruent angles.
b. Similar
c. Not similar
d. Not similar
a.
$$
(2y)(x+4)=2xy+8y
$$
b.
$$
(x+8)(x+5)=x^2+8x+5x+40=x^2+13x+40
$$
c.
$$
(x-4)(2z-3y+5)=2xz-3xy+5x-8z+12y-20
$$
d.
$$
(x+1)(x+6)=x^2+6x+x+6=x^2+7x+6
$$
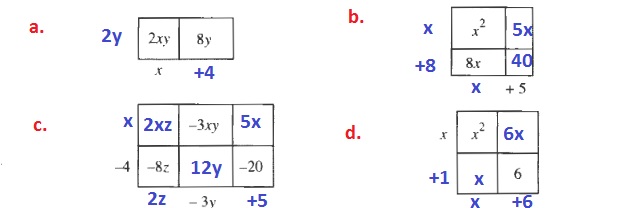
b. $x^2+13x+40$
c. $2xz-3xy+5x-8z+12y-20$
d. $x^2+7x+6$
a. If a triangle is isosceles, then the base angles of the triangle are congruent. TRUE (property isosceles triangles)
b. If the sum of the angles in a polygon is 180$text{textdegree}$, then the polygon is a triangle. TRUE (triangles are the only polygons whose angles sum up to 180$text{textdegree}$)
c. If my mom is happy, then I have cleaned my room. FALSE (Your mom could be happy for another reason)
b. True
c. False
$$
h=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12
$$
The area of a trapezium is the sum of its bases, multiplied by the height divided by 2:
$$
dfrac{(12+18+5)12}{2}=210
$$
210
$$
a.
$$
ABCDsim EVOL
$$
b.
$$
RIGHTsim RONGW
$$
c.
$$
triangle DOGsim triangle ACT
$$
$$
ABCDsim EVOL
$$
b.
$$
RIGHTsim RONGW
$$
c.
$$
triangle DOGsim triangle ACT
$$
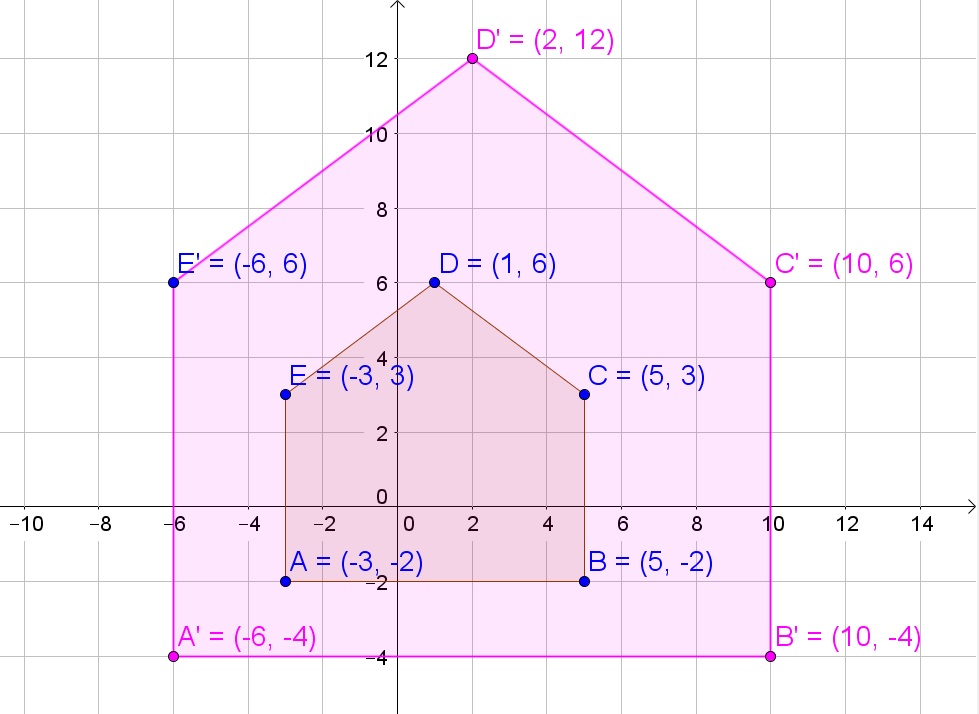
c. The perimeter is the sum of all sides:
$$
P_1=3+8+3+sqrt{4^2+3^2}+sqrt{4^2+3^2}=3+8+3+5+5=24
$$
$$
P_2=6+16+6+sqrt{8^2+6^2}+sqrt{8^2+6^2}=6+16+6+10+10=48
$$
The area is the sum of the area of the triangle (roof) and the area of the rectangle:
$$
A_1=3cdot 8+dfrac{8cdot 3}{2}=24+12=36
$$
$$
A_2=6cdot 16+dfrac{16cdot 6}{2}=96+48=144
$$
b. Coordinates of every point are multiplied by dilation factor
c. Original figure: Perimeter 24 and area 36
Enlarged figure: Perimeter 48 and area 144
$$
180text{textdegree}-60text{textdegree}-40text{textdegree}=80text{textdegree}
$$
Thus we then know that the triangles are NOT similar because they have two pairs of angles that are not congruent.
b. Determine the missing angle using that the sum of all angles in a triangle is 180$text{textdegree}$:
$$
180text{textdegree}-45text{textdegree}-50text{textdegree}=85text{textdegree}
$$
Similar because of AA.
c. Similar because the ratios of the sides are equal and thus SSS:
$$
dfrac{12}{8}=dfrac{14}{7}=dfrac{12}{6}=2
$$
b. Similar
c. Similar
$$
dfrac{AC}{BC}=dfrac{DF}{EF}
$$
$$
dfrac{AB}{BC}=dfrac{DE}{EF}
$$
dfrac{AC}{BC}=dfrac{DF}{EF}
$$
$$
dfrac{AB}{BC}=dfrac{DE}{EF}
$$
b. A rotation and a translation will be sufficient.
c. A dilation of factor 2 and a rotation and a translation will be suffiicient.
d. A dilation of factor $dfrac{1}{2}$, a rotation, a reflection and a translation will all be needed.
b. Rotation and translation
c. Dilation, rotation, translation
d. Dilation, rotation, reflection, translation
$$
-dfrac{2}{5}x-2=-dfrac{2}{5}x+1
$$
Group like terms:
$$
-dfrac{2}{5}x+dfrac{2}{5}x=1+2
$$
Simplify:
$$
0x=3
$$
This last equation has no solution because 0 never equals 3. You can also see that the system has no solutions, because the lines are parallel (have the same slope).
b. Since one of the angles of the triangle is 90$text{textdegree}$, then the sum of the other two angles need to be 90$text{textdegree}$ too. Since both sides have length 18, the angle opposite the side of length 18 needs to be equal to the angle opposite the other side of length 18. This then means that $x$ must be equal than 45$text{textdegree}$.
c. Since one of the angles of the triangle is 90$text{textdegree}$, then the sum of the other two angles need to be 90$text{textdegree}$ too. Since 2 is less than 8, the angle opposite the side of length 2 needs to be smaller than the angle opposite the side of length 8. This then means that $x$ must be more than 45$text{textdegree}$.
b. Equal
c. More
$$
(3x^2-4x^2)+(x-x)+(-2-(-5))
$$
Combine like terms:
$$
-1x^2+0x+3
$$
Simplify:
$$
-x^2+3
$$
-x^2+3
$$
$$
dfrac{16}{12}=dfrac{12}{9}=dfrac{4}{3}
$$
b. Not similar, because two of the corresponding sides have doubled in length (that is, the longest sides and the shortest sides), but the third one has not.
c. Similar because of AA (right angle is the same angle in both triangles)
b. Not similar
c. Similar
$$
JK=sqrt{12^2+9^2}=sqrt{144+81}=sqrt{225}=15
$$
b. It is not possible to determine $overline{VT}$ because we do not know the length of the corresponding side $overline{SN}$.
c. Using that the lengths of corresponding sides in the triangles have the same propertions:
$$
dfrac{x+11}{11}=dfrac{2.5+9}{9}
$$
Multiply both sides of the equation by 11:
$$
x+11=dfrac{126.5}{9}
$$
Subtract 11 from both sides of the equation:
$$
x=dfrac{126.5}{9}-11approx 3
$$
b. Not possible
c. $dfrac{126.5}{9}-11$
$$
angle Q=angle X
$$
$$
dfrac{DQ}{XZ}=1
$$
$$
dfrac{PQ}{XY}=1
$$
$$
Downarrow SAS
$$
$$
triangle QDPsim triangle XZY
$$
b. Yes, because the ratios are 1.
c. If two triangles are congruent, then they are also similar. This follows directly from the transformations, since a congruence only uses rotations, reflections and translations, while a similarity uses rotations, reflections, translations and dilations.
d. Triangles are congruent $Rightarrow$ Triangles are similar
b. Yes
c. If two triangles are congruent, then they are also similar.
c. Triangles are congruent $Rightarrow$ Triangles are similar
$$
angle R=angle C
$$
$$
dfrac{RN}{CT}=2
$$
$$
dfrac{RU}{CA}=2
$$
$$
Downarrow SAS
$$
$$
triangle RUNsim triangle CAT
$$
b. They are both correct, because Leesa and Charles have the same letters that correspond (and to our solution from (a)).
c. No because the triangles use a dilation of factor $2$ to transform one triangle into another and congruence does not use dilations.
d.
$$
AT=dfrac{12.3}{2}=6.15
$$
$$
angle U=angle A=103text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$:
$$
angle N=angle T=180text{textdegree}-103text{textdegree}-47text{textdegree}=30text{textdegree}
$$
b. Both are correct
c. No
d. 6.15, 103$text{textdegree}$, 30$text{textdegree}$
$$
dfrac{6}{5}=dfrac{4.8}{4}=dfrac{3.6}{3}=1.2
$$
b. Similar because of AA
c. Not able to determine, since only one pair of side lengths and one pair of angle measures have been given.
b. AA
c. Not possible to determine
$$
angle y =angle x = 48text{textdegree}
$$
Using reflection properties:
$$
angle z =angle x = 48text{textdegree}
$$
angle y =angle z = 48text{textdegree}
$$
angle B =angle E = 90text{textdegree}
$$
$$
angle C=angle Ctext{ (common angle)}
$$
$$
Downarrow AA
$$
$$
triangle ABC sim triangle DEC
$$
$$
32=acdot b^0=a
$$
$$
4=acdot b^3=32cdot b^3
$$
Thus we know $a=32$, divide both sides of the last equation by 32:
$$
dfrac{1}{8}=b^3
$$
Take the 3th root of both sides of the equation:
$$
dfrac{1}{2}=b
$$
Thus the equation then becomes:
$$
f(x)=32left( dfrac{1}{2}right)^x
$$
f(x)=32left( dfrac{1}{2}right)^x
$$
$$
8”+13”=21”
$$
$$
13”-8”=5”
$$
Thus the length of the third side is between 5” and 21”.
$$
dfrac{2}{5}=0.4=40%
$$
b. No, because the songs are played without repeating and thus there is less chance of the second song being a country song if we know that the first song was already a country song.
c. There will be 1 out of the remaining 2 songs that will be by Sapphire:
$$
dfrac{1}{2}=0.5=50%
$$
d. Since writing a letter is 1 out of 3 possibilities and taking bus 41 is 1 out of 4 possibilities:
$$
dfrac{1}{3}cdot dfrac{1}{4}=dfrac{1}{12}approx 8.3%
$$
Since writing a letter is 1 out of 3 possibilities and taking bus 55 is 1 out of 4 possibilities:
$$
dfrac{1}{3}cdot dfrac{1}{4}=dfrac{1}{12}approx 8.3%
$$
b. No
c. $frac{1}{2}=0.5=50%$
d. $frac{1}{12}=8.3%$, $frac{1}{12}=8.3%$
b. Yes
b. Yes
$$
triangle AEIsim triangle AGH
$$
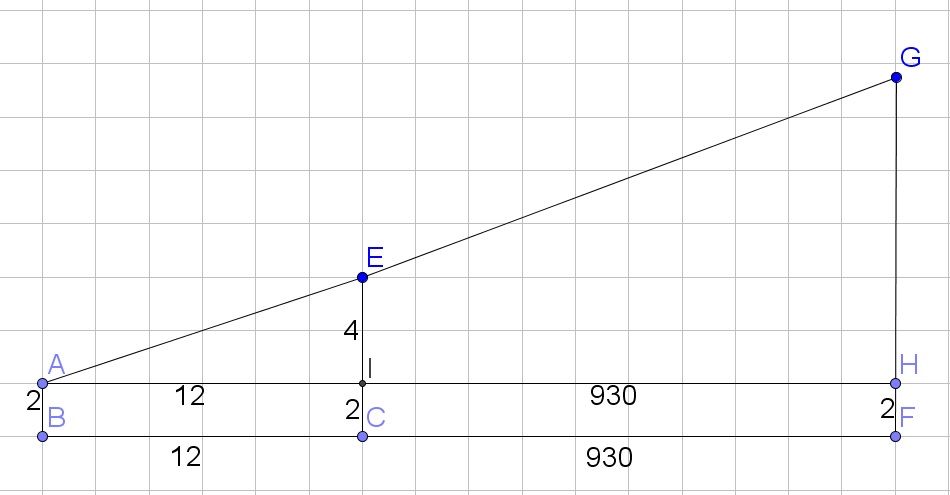
$$
dfrac{x}{930+12}=dfrac{4}{12}
$$
Simplify:
$$
dfrac{x}{942}=dfrac{4}{12}
$$
Multiply both sides of the equation by 942:
$$
x=dfrac{4cdot 942}{12}=314
$$
Finally, adding the 2 ft to the height as well, we obtain that the total height of 314 ft + 2 ft = 316 ft.
$$
angle B=angle E=9text{textdegree}
$$
$$
angle A=angle D=74text{textdegree}
$$
$$
Downarrow AA
$$
$$
triangle ABCsim triangle DEF
$$
b. Yes, because of AAS (two pair of angles are congruent and a pair of sides is congruent)
b. Yes, AAS
a. If the cat runs away frightened, then it has knocked over the lamp. FALSE (the cat could be frightened because of a different reason)
b. If the probability of getting a 3 is $dfrac{1}{6}$, then a six-sided dice is rolled. FALSE (it could also be drawing a number out of a bowl containing the numbers 1 to 6 once each).
c. If a triangle has a right angle, then the triangle has a 90$text{textdegree}$ angle. TRUE A right angle is a 90$text{textdegree}$ angle.
b. False
c. True
a.
$$
(x+3)(2x+1)=2x^2+6x+x+3=x^2+7x+3
$$
b.
$$
2x(x+5)=2x^2+10x
$$
c.
$$
x(2x+y)=2x^2+xy
$$
d.
$$
(2x+5)(x+y+2)=2x^2+2xy+4x+5x+5y+10=2x^2+2xy+9x+5y+10
$$

b. $2x^2+10x$
c. $2x^2+xy$
d. $2x^2+2xy+9x+5y+10$
$$
16cdot 9 = 144 text{cm}^2
$$
The perimeter is the sum of the lengths of all sides:
$$
P=16+10+16+10=52text{ cm}
$$
$$
A=dfrac{(25+44.67)20}{2}=696.7 text{m}^2
$$
The perimeter is the sum of the lengths of all sides:
$$
P=25+24+44.67+21=114.67text{ m}
$$
$$
Total: 9cdot 12=108text{ cm}^2
$$
$$
Left: 7cdot 3=21text{ cm}^2
$$
$$
Right: 5cdot 3=15text{ cm}^2
$$
The area of the shape is then the area of the total rectangle decreased by the two rectangles that have been cutout:
$$
A=108-21-15=72text{ cm}^2
$$
The perimeter is the sum of the lengths of all sides:
$$
P=12+2+3+5+3+2+9+7+3+2=48text{ cm}
$$
$$
dfrac{(23+11)8}{2}=136text{ ft}^2
$$
The area of a rectangle is the product of the length and the width:
$$
2cdot 3=6text{ ft}^2
$$
The area of the shape is then the area of the trapezium decreased by tje area of the rectangle:
$$
A=136′-6’=130text{ ft}^2
$$
The perimeter is the sum of the lengths of all sides:
$$
P=10’+4’+2’+3’+2’+4’+10’+23’=58′
$$
b. Area 696.7 m$^2$ and Perimeter 114.67 m
c. Area 72 cm$^2$ and Perimeter 48 cm
d. Area 130 ft$^2$ and Perimeter 58′
a.
$$
dfrac{n}{2}=dfrac{112}{7}
$$
Multiply both sides of the equation by 2:
$$
n=dfrac{112cdot 2}{7}=32
$$
b.
$$
dfrac{m}{7}=dfrac{49}{23}
$$
Multiply both sides of the equation by 7:
$$
m=dfrac{49cdot 7}{23}=dfrac{343}{23}approx 15
$$
b. $m=dfrac{343}{23}approx 15$
b.Yes, Eliana is correct.
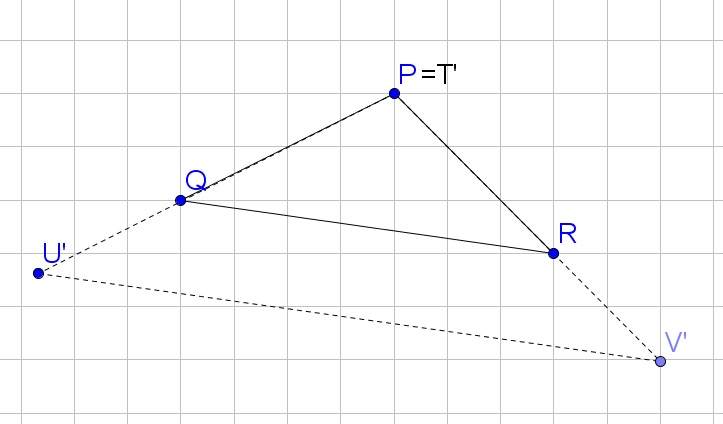
d. The scale factor is $dfrac{UV}{QR}$ (or you can use any pair of corresponding sides)
e. Yes, because the diagram has only been rotated and nothing has been changed about the lengths of the sides of the triangles.
b. Yes
c. Parallel
d. $frac{UV}{QR}$
e. Yes
$$
4(5+x)=5(6)
$$
Use distributive property:
$$
20+4x=30
$$
Subtract 20 from both sides of the equation:
$$
4x=10
$$
Divide both sides of the equation by 4:
$$
x=2.5
$$
b. Janelle use the propertions of the two sides instead of the sides of the triangles.
c. Kamraan should add that $overline{DE}$ and $overline{BC}$ are parallel. He wants to proof that the proportions of both sides are equal:
$$
dfrac{a}{b}=dfrac{c}{d}
$$
d. By similar triangles we know:
$$
dfrac{a+b}{a}=dfrac{c+d}{c}
$$
e. Rewrite the expression:
$$
dfrac{a}{a}+dfrac{b}{a}=dfrac{c}{c}+dfrac{d}{c}
$$
Simplify:
$$
1+dfrac{b}{a}=1+dfrac{d}{c}
$$
Subtract 1 from both sides of the equation:
$$
dfrac{b}{a}=dfrac{d}{c}
$$
b. Proportions of the two sides
c. $frac{a}{b}=frac{c}{d}$
d. $frac{a+b}{a}=frac{c+d}{c}$
e. $frac{b}{a}=frac{d}{c}$
b.
$$
dfrac{a}{b}=dfrac{c}{d}
$$
c.
$$
angle M=angle Mtext{ (same angle)}
$$
$$
dfrac{a+b}{a}=dfrac{a}{a}+dfrac{b}{a}=1+dfrac{d}{c}=dfrac{c}{c}+dfrac{d}{c}=dfrac{d+c}{c}
$$
$$
Downarrow SAS
$$
$$
triangle MSNsim triangle MVT
$$
d. Since $triangle MSNsim triangle MVT$, we know that the corresponding angles $angle V$ and $angle S$ are equal and thus the lines $overleftrightarrow{VT}$ and $overleftrightarrow{SN}$are parallel.
b. $dfrac{a}{b}=dfrac{c}{d}$
c. Yes (Use SAS)
d. $angle V$ and $angle S$ are equal
$$
dfrac{12}{8}=dfrac{9}{6}=dfrac{6}{4}=1.5
$$
b. Multiply each length by the scale factor:
$$
D’E’=12cdot dfrac{2}{3}=8
$$
$$
D’F’=6cdot dfrac{2}{3}=4
$$
$$
E’F’=9cdot dfrac{2}{3}=6
$$
c. The triangle are congruent because the two triangles have three pairs of congruent sides.
d. It remains to rotate and translate $triangle D’E’F’$ to make it overlap $triangle ABC$ and thus we then know that the two triangles are similar (since only dilations, rotations and translations were used).
e. Yes, but then you need to dilate the larger triangle over factor $dfrac{1}{k}$.
b. 8, 4, 6
c. Congruent
d. Rotate and translate
e. Yes
SAS: If two pairs of corresponding sides are proportional and the included angles are congruent, then the two triangles are similar.
SSS: If three pairs of corresponding sides are proportional, then the two triangles are similar.
$$
dfrac{15}{5}=dfrac{12}{4}=dfrac{6}{2}=3
$$
However, the triangles are not congruent since the ratios are not equal to 1.
b. Determine the missing angles using that the sum of all angles in a triangle is 180$text{textdegree}$:
$$
180text{textdegree}-48text{textdegree}-20text{textdegree}=112text{textdegree}
$$
Thus we then know that the three pairs of angles are equivalent and one of the pair of sides is also equivalent, thus the triangles are congruent by ASA and are also similar (since congruent triangles are also similar triangle).
c. Determine the missing sides using the Pythagorean theorem:
$$
12^2+5^2=169=13^2
$$
Thus we then know that one pair of angles are equivalent and three pair of sides are also equivalent, thus the triangles are congruent by SAS and are also similar (since congruent triangles are also similar triangle).
d. Similar because of AA. Not congruent because the known lengths of the sides are not of corresponding sides.
b. Similar, Congruent
c. Similar, Congruent
d. Similar, not congruent
b. No, because a frog or grass (or something else) can also be green.
c. No, the first statements says that if you have a tree, then it is green. While the second statement says the converse: if a thing is green, then it is a tree.
b. No
c. Yes
a.
$$
dfrac{x}{12}=dfrac{10}{6}
$$
Multiply both sides of the equation by 12:
$$
x=dfrac{10cdot 12}{6}=20
$$
b.
$$
dfrac{w}{7}=dfrac{39}{3}
$$
Multiply both sides of the equation by 7:
$$
w=dfrac{39cdot 7}{3}=91
$$
b. $w=91$
b. No, because after you have drawn one ace from the deck, the deck will now contain one less ace and thus the probability for drawing another ace will be smaller.
c. Yes, because having blue eyes is not influenced by having blonde hair.
d. Yes, because winning the state championship is not influence by raining.
e. No, because after your friend has taking a diet soda, the cooler will now contain one less diet soda and thus the probability for drawing the same type of diet soda will be smaller.
b. No
c. Yes
d. Yes
e. No
a.
$$
(2x+1)(2x+1)=4x^2+2x+2x+1=4x^2+4x+1
$$
b.
$$
(2x)(4x)=8x^2
$$
c.
$$
2(3x+5)=6x+10
$$
d.
$$
y(2x+y+3)=2xy+y^2+3y
$$
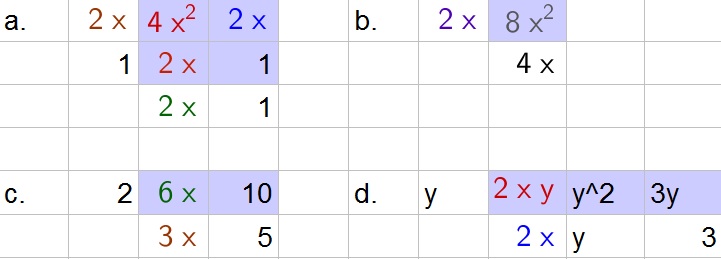
b. $8x^2$
c. $6x+10$
d. $2xy+y^2+3y$

