All Solutions
Page 371: Questions
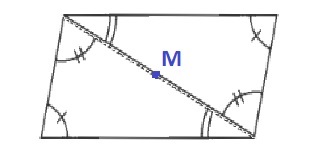
c. Opposite angles of a parallelogram are congruent.
We need to copy the given triangle and its markings and make it a quadrilateral that looks like a parallelogram.
*How can we rotate the triangle to make a quadrilateral that looks like a parallelogram?*
One of the three possible quadrilaterals that we draw is shown below.

$$smalltext{Figure 1. A quadrilateral formed by rotating the triangle.}$$
We need to give a convincing argument that the quadrilateral that we drew is a parallelogram using its angles.
*What theorem about angles can we use to prove that the quadrilateral is a parallelogram?*
Again, with the diagonal as the transversal, the two angles with two arc marks are congruent alternate interior angles so by the theorem above, the top and bottom sides of the quadrilateral are parallel.
Because the quadrilateral has two pairs of parallel sides, then it is a parallelogram.
We need to determine other properties of a parallelogram using the congruent triangles.
*What other parts of the congruent triangles can we use?*
Because the quadrilateral is formed by rotating a triangle about the midpoint of one of its side, then the opposite sides are congruent. So, we can conclude that the opposites sides of a parallelogram are congruent.
In part (a), we picked a side, determined its midpoint, and rotated the triangle about it to form a quadrilateral. In party (b), we used a theorem about congruent alternate interior angles formed by a transversal intersecting two lines to conclude that the quadrilateral has two pairs of parallel sides. In part (c), we used the remaining corresponding congruent parts of the two congruent triangles to determine other properties of a parallelogram.
$$
overleftrightarrow{AB}//overleftrightarrow{DC}
$$
$$
overleftrightarrow{AD}//overleftrightarrow{BC}
$$
$$
Downarrow
$$
$$
angle ADBcong angle CBD ( text{alternate interior angles })
$$
$$
angle ABDcong angle CDB ( text{alternate interior angles })
$$
$$
overline{BD}cong overline{DB}(text{ shared side})
$$
$$
Downarrow ASA
$$
$$
triangle ABDcong triangle CDB
$$
b.
$$
Downarrow
$$
$$
overline{AB}cong overline{DC}
$$
$$
overline{AD}cong overline{BC}
$$
b. Kip has made a kite, because adjacent sides of the quadrilateral have equal lengths.
c. The quadrilateral has two congruent angles, but the other angles are not congruent.
d. The diagonal is the line of symmetry of the kite.
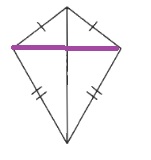
c.
$$
overline{FG}cong overline{GH} (text{ Given })
$$
$$
angle FGJcong angle HGJ(text{ Given})
$$
$$
overline{GJ}cong overline{GJ} (text{ Shared side })
$$
$$
Downarrow SAS
$$
$$
triangle FGJcong triangle HGJ
$$
d.
$$
Downarrow
$$
$$
angle FJGcong angle HJG
$$
$$
Downarrow
$$
$$
mangle FJG=m angle HJG=90text{textdegree} (text{ Supplementary angles})
$$
b. If a quadrilateral has two consecutive right angles, then it has at least one pair of parallel sides.
c. Same-sides interior angles are supplementary ($mangle M+mangle P=90text{textdegree}+90text{textdegree}=180text{textdegree}$), thus $overleftrightarrow{MN}//overleftrightarrow{PO}$.
d. No, the right angles could also be opposite each other and then you obtain the form of a kite (which is not a trapezoid).
b. If a quadrilateral has two consecutive right angles, then it has at least one pair of parallel sides.
c. Same-sides interior angles are supplementary
d. No
Same-sides interior angles are supplementary ($mangle Q+mangle T=90text{textdegree}+90text{textdegree}=180text{textdegree}$), thus $overleftrightarrow{QR}//overleftrightarrow{ST}$.
Thus the rectangle has two pair of parallel sides and thus the rectangle is also a parallelogram.
If a quadrilateral has two consecutive right angles, then the quadrilateral is a right trapezoid.
The diagonals of a kite intersect at a right angle.
A parallelogram has two pair of parallel sides.
overline{AD}cong overline{BC} ( text{given })
$$
$$
angle ABDcong angle CDB ( text{alternate interior angles })
$$
$$
overline{BD}cong overline{DB}(text{ shared side})
$$
$$
Downarrow SAS
$$
$$
triangle ABDcong triangle CDB
$$
Corresponding sides of congruent triangles are equally long:
$$
6x+6=8x+2
$$
Subtract $8x$ from both sides of the equation:
$$
-2x+6=2
$$
Subtract 6 from both sides of the equation:
$$
-2x=-4
$$
Divide both sides of the equation by $-2$:
$$
x=2
$$
x=2
$$
*What properties of parallelograms might be useful in our proof?*
* Opposite sides of a parallelogram are congruent.
* Opposite angles of a parallelogram are congruent.
The diagonals of the parallelogram divide it into triangles so the following triangle congruence theorems may also prove useful:
* **SAS:** If two triangles have two pairs of congruent sides and the included angles are also congruent, then the triangles are congruent.
* **SSS:** If two triangles have three pairs of congruent sides, then the triangles are congruent.
* **ASA:** If two triangles have two pairs of congruent angles and the included sides are also congruent, then the triangles are congruent.
* **AAS:** If two triangles have two pairs of congruent angles and a pair of non-included sides are also congruent, then the triangles are congruent.
Before we start the proof, let’s make a plan on how to go from our Given statement to our Prove statement.
Since we are trying to prove that segments are congruent, let’s use the congruent opposite sides parallelogram property to label all the pairs of sides we know must be congruent. Also, label the congruent angles. Recall that vertical angles are congruent and alternate interior angles created by parallel lines must also be congruent.
Note that we can label our diagram in two different ways, depending on what pair of triangles we want to use in our proof:

$$text{Figure 1: }triangle WXMtext{ and }triangle YMZ$$

$$text{Figure 2: }triangle WZMtext{ and }triangle YXZ$$
Notice for both Figure $1$ and Figure $2$ that we have all three pairs of congruent angles and a pair of congruent sides so we can use either AAS or ASA to prove the triangles are congruent. However, in the given flowchart, only one oval can be for congruent alternate interior angles so we will need to specifically use AAS to fill in the given flowchart proof.
We can choose to use either figure for our proof.
Our plan for both versions of the proof is:
1. State our given.
2. Use the definition of a parallelogram to state a pair of lines are parallel.
3. Use the Alternate Interior Angles Theorem to prove a pair of angles are congruent.
4. Use the Vertical Angles Theorem to prove a second pair of angles are congruent.
5. Use the congruent opposite sides of a parallelogram property to prove a pair of sides are congruent.
6. State a pair of triangles are congruent using AAS.
7. Conclude the two pairs of sides are congruent since they are congruent parts of congruent triangles.
**Proof for Figure $boldsymbol{1}$:**

**Proof for Figure $boldsymbol{2}$:**

First, we recalled some of the basic properties of parallelograms and the triangle congruence theorems. Then we decided which of these was useful for our proof. After applying the appropriate properties to our diagram, we made a plan on how to go from the Given statement to the Prove statement. Using our plan, we then constructed a two-column proof.
a.
$$
dfrac{9+15}{2}=dfrac{24}{2}=12
$$
b.
$$
dfrac{27+3}{2}=dfrac{30}{2}=15
$$
c.
$$
dfrac{10+21}{2}=dfrac{31}{2}=15.5
$$
b. 15
c. 15.5
b. Rational, because the expression contains only fractions and no roots or other irrational numbers.
c. Irrational, because $sqrt{11}$ cannot be simplified.
d. Irrational, because $sqrt[3]{9}$ cannot be simplified.
b. Rational
c. Irrational
d. Irrational
$$
f(x)=(x+2)^2-1
$$
f(x)=(x+2)^2-1
$$
$$
P(high-fiber)=dfrac{2}{12}=dfrac{1}{6}approx 0.167=16.7%
$$
b. $frac{1}{6}approx 0.167=16.7%$
$$
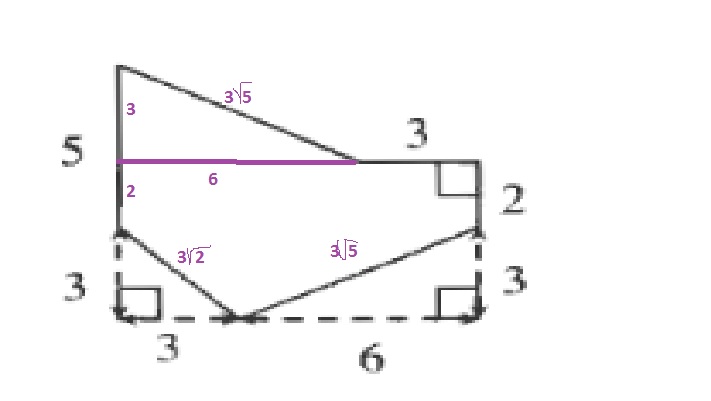
AREA=dfrac{3cdot 6}{2}+9cdot 5-dfrac{3cdot 3}{2}-dfrac{6cdot 3}{2}=45-4.5=40.5
$$
The perimeter is the sum of all lengths of the sides:
$$
PERIMETER=5+3sqrt{5}+3+2+3sqrt{5}+3sqrt{2}=10+6sqrt{5}+3sqrt{2}
$$
Perimeter $10+6sqrt{5}+3sqrt{2}$
$$
x=sqrt{10^2-8^2}=sqrt{36}=6
$$
$$
x=BC=AD=10
$$
$$
tan{35text{textdegree}}=dfrac{11}{x}
$$
Multiply both sides by $x$:
$$
xtan{35text{textdegree}}=11
$$
Divide both sides of the equation by $tan{35text{textdegree}}$:
$$
x=dfrac{11}{tan{35text{textdegree}}}approx 15.7
$$
b. $x=10$
c. $x=15.7$
d. Cannot be determined
angle ADB cong angle CBD (text{Given})
$$
$$
overline{BD} cong overline{DB} (text{Same side})
$$
$$
angle ABDcong angle CDB (text{alternate interior angles})
$$
$$
Downarrow ASA
$$
$$
triangle ABD cong triangle CDB
$$
$$
Downarrow
$$
$$
overline{AD} cong overline{CB}
$$
$$
15x^2+39x-18=3(5x^2+13x-6)
$$
Factor further:
$$
15x^2+39x-18=3(5x-2)(x+3)
$$
$$
6t^2-26t+8=2(3t^2-13t+4)
$$
Factor further:
$$
6t^2-26t+8=2(3t-1)(t+4)
$$
$$
6x^2-24=6(x^2-4)
$$
Factor further using difference of squares:
$$
6x^2-24=6(x-2)(x+2)
$$
b. $2(3t-1)(t+4)$
c. $6(x-2)(x+2)$
$$
x=6sqrt{3}
$$
$$
y=2cdot 6=12
$$
x=6sqrt{3}
$$
$$
y=12
$$
a.
$$
125^{2/3}=(sqrt[3]{125})^2=sqrt[3]{5^3})^2=5^2=25
$$
b.
$$
16^{1/2}=sqrt{16}=sqrt{4^2}=4
$$
c.
$$
16^{-1/2}=dfrac{1}{16^{1/2}}=dfrac{1}{sqrt{16}}=dfrac{1}{4}
$$
d.
$$
left( dfrac{1}{81}right)^{1/4}=sqrt[4]{dfrac{1}{81}}=dfrac{sqrt[4]{1}}{sqrt[4]{81}}=dfrac{1}{sqrt[4]{3^4}}=dfrac{1}{3}
$$
b. 4
c. $frac{1}{4}$
d. $frac{1}{3}$
$$
y=ab^t
$$
with $y$ the value of the car and $t$ the time.
$a$ is the initial value and thus $a=35,000$.
Using the information we then obtain:
$$
21,494=35,000(b)^3
$$
Divide both sides of the equation by 35,000:
$$
dfrac{21,494}{35,000}=(b)^3
$$
Take the cube root of both sides of the equation:
$$
0.85approx sqrt[3]{dfrac{21,494}{35,000}}=b
$$
Replace $a$ in the general equation $y=ab^t$ with 35,000 and $b$ with 0.85:
$$
y=35,000(0.85)^t
$$
$$
100%-0.85=100%-85%=15%
$$
y=35,000(0.85)^t
$$
Depreciation rate: 15%
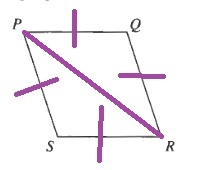
c.
$$
overline{PR}cong overline{RP}(text{ Same side})
$$
$$
overline{SR}cong overline{QP}(text{ Sides of rhombus have equal length})
$$
$$
overline{SP}cong overline{QR}(text{ Sides of rhombus have equal length})
$$
$$
Downarrow SSS
$$
$$
triangle RSP cong triangle PQR
$$
d.
$$
Downarrow
$$
$$
angle PRS cong angle RPQ
$$
$$
angle SPRcong angle QRP
$$
$$
Downarrow
$$
$$
overleftrightarrow{PQ}// overleftrightarrow{RS}(text{ alternate interior angles are congruent})
$$
$$
overleftrightarrow{PS}// overleftrightarrow{QR}(text{ alternate interior angles are congruent})
$$
c.
$$
angle PTScong angle RTQ(text{ Vertical angles})
$$
$$
overline{PS}cong overline{QR}(text{ Sides of rhombus have equal length})
$$
$$
angle TPScong angle TRQ (triangle PQRcong triangle RSP (SSS))
$$
$$
Downarrow AAS
$$
$$
triangle PTScong triangle RTQ
$$
$$
Downarrow
$$
$$
PT=TR
$$
$$
QT=TS
$$
Opposite sides of rhombi are parallel.
$$
left( dfrac{x_1+x_2}{2}, dfrac{y_1+y_2}{2}right)
$$
Thus for these two points:
$$
M=left( dfrac{0+0}{2}, dfrac{3+11}{2}right)=(0,7)
$$
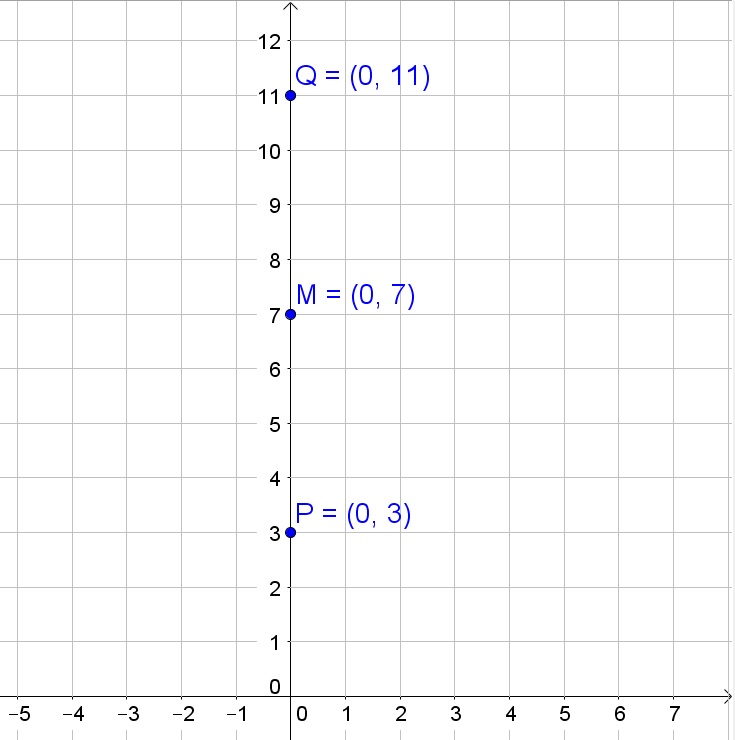
(0,7)
$$
$$
(x-5)^2=0
$$
Take the square root of both sides of the equation:
$$
x-5=0
$$
Add 5 to both sides of the equation:
$$
x=5
$$
$$
0=(3x-1)(x+6)
$$
Zero product property:
$$
3x-1=0text{ or } x+6=0
$$
Solve each equation to $x$:
$$
3x=1text{ or } x=-6
$$
$$
x=dfrac{1}{3}text{ or } x=-6
$$
$$
3x^2-2x-5=0
$$
Factorize:
$$
(x+1)(3x-5)=0
$$
Zero product property:
$$
x+1=0text{ or } 3x-5=0
$$
Solve each equation to $x$:
$$
x=-1text{ or } 3x=5
$$
$$
x=-1text{ or } x=dfrac{5}{3}
$$
$$
(4x-3)(4x+3)=0
$$
Zero product property:
$$
4x-3=0text{ or } 4x+3=0
$$
Solve each equation to $x$:
$$
4x=3text{ or } 4x=-3
$$
$$
x=dfrac{3}{4}text{ or } x=-dfrac{3}{4}
$$
b. $x=frac{1}{3}$ and $x=-6$
c. $x=-1$ and $x=frac{5}{3}$
d. $x=frac{3}{4}$ and $x=-frac{3}{4}$
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
with $a$ the coefficient of $x^2$, $b$ the coefficient of $x$ and $c$ the constant term.
Then we obtain:
$$
x=dfrac{-17pm sqrt{17^2-4(3)(-6)}}{2(3)}=dfrac{-17pm 19}{6}=dfrac{1}{3}text{ or }-6
$$
a.
$$
p+q=(2+5i)+(3-4i)=(2+3)+(5i-4i)=5+i
$$
b.
$$
p-q=(2+5i)-(3-4i)=(2-3)+(5i+4i)=-1+9i
$$
c.
$$
pq=(2+5i)(3-4i)=6+15i-8i-20i^2=6+7i+20=26+7i
$$
b. $-1+9i$
c. $26+7i$
$$
80%cdot 80%=0.8cdot 0.8=0.64=64%
$$
b. Since each flip is independent of the other flip, the probability is the product of each probability:
$$
80% cdot 20%=0.8cdot 0.2=0.16=16%
$$
b. 16%
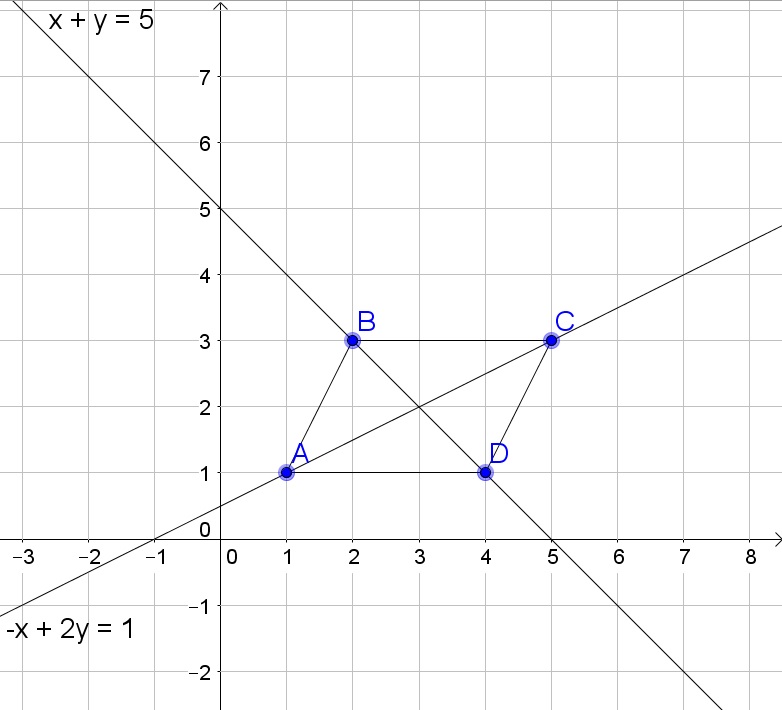
$$
mangle DAB=mangle BCD=tan^{-1}dfrac{2}{1}approx 63text{textdegree}
$$
c. The equation of a line thourgh two points $(x_1,y_1)$ and $(x_2,y_2)$ is:
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$
Then we obtain
$$
AC: y-1=dfrac{3-1}{5-1}(x-1)=dfrac{1}{2}(x-1)
$$
$$
BD: y-3=dfrac{3-1}{2-4}(x-4)=-dfrac{1}{2}(x-4)
$$
We then note that there slopes are $dfrac{1}{2}$ and $-dfrac{1}{2}$. Since the product of the slopes does not equal $-1$, the diagonals are not perpendicular.
d. On the graph we note that the intersection is $(3,2)$.
b. 63$text{textdegree}$
c. No
d. $(3,2)$
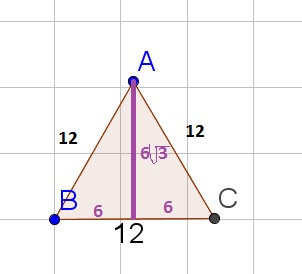
$$
AREA=dfrac{12cdot 6sqrt{3}}{2}=36sqrt{3}
$$
36sqrt{3}
$$
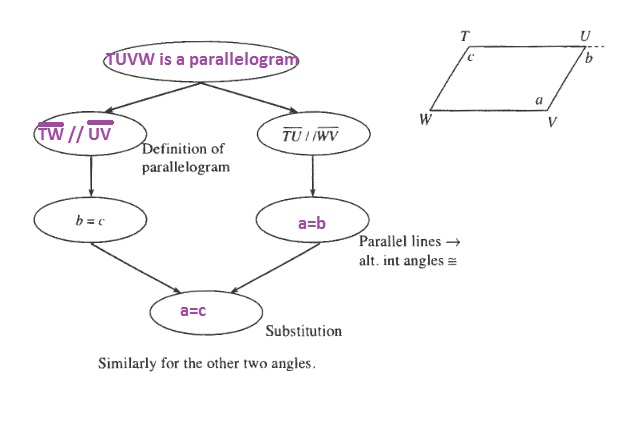
$$
overline{TW}//overline{UV}
$$
$$
a=b
$$
$$
a=c
$$

3. Definition of a parallelogram
4. If lines are parallel, then the corresponding angles are equivalent.
5. $a=b$
6. $a=c$

2. $mangle AMP=mangle BMP$
3. $AM=BM$
4. $PM=PM$, Common side
5. $triangle AMPcong triangle BMP$, SAS
6. $AP=BP$
A point of the perpendicular bisector of a segment is equidistant from both end points of the segment.


b. Use SAS
The two-column proof contains the statements in the first column and the reasons in the second column. This proof contains more explanations than a flow chart, however, it is harder to see which statements follow from which statements than in a flow chart.
We are given the following diagram:

$$text{Figure 1: Given Diagram}$$
*What angle relationships do we have when lines intersect or are cut by a transversal?*
* **Supplementary angles:** Two or more angles are supplementary if their angle measures add to $180^circ$. Angles that form a straight line are supplementary.
* **Vertical Angles Theorem:** If two angles are vertical angles (which are non-adjacent angles created by two intersecting lines), then they are congruent.
When two parallel lines are cut by a transversal, we also have the following additional angle relationships:
* **Corresponding Angles Theorem:** If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
* **Alternate Interior Angles Theorem:** If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
* **Same Side Interior Angles Theorem:** If two parallel lines are cut by a transversal, then the same-side interior angles are supplementary.
Before we start the proof, let’s make a plan on how to go from our Given statement to our Prove statement.
It is given that $overline{AD}paralleloverline{EH}$ and $overline{BF}paralleloverline{CG}$. We then know from Figure $1$ that:
* $a=b$ since they are alternate interior angles for $overline{AD}$ and $overline{EH}$ and
* $b=c$ since they are corresponding angles for $overline{BF}$ and $overline{CG}$.
We can also see from Figure $1$ that $c=d$ since they are vertical angles.
Notice we have $a=b=c=d$ so we know by the repeated use of the Substitution Property (or Transitive Property) that $a=d$.
Our plan for the proof is then:
1. State our givens.
2. Use the Alternate Interior Angles Theorem to prove $a$ and $b$ are equal.
3. Use the Corresponding Angles Theorem to prove $b$ and $c$ are equal.
4. Use the Vertical Angles Theorem to prove $c$ and $d$ are equal.
5. Use the Substitution Property to combine $a=b$ and $b=c$ to get $a=c$ and then to combine $a=c$ and $c=d$ to get $a=d$.
| Statements| Reasons|
|–|–|
| 1. $overline{AD}paralleloverline{EH}$|1. Given |
| 2. $a=b$|2. Alternate Interior Angles Theorem |
|3. $overline{BF}paralleloverline{CG}$ |3. Given |
| 4. $b=c$|4. Corresponding Angles Theorem |
| 5. $a=c$|5. Substitution |
| 6. $c=d$|6. Vertical Angles Theorem |
| 7. $a=d$|7. Substitution |
First, we recalled some of the angle relationships created by intersecting lines and parallel lines cut by a transversal. Then we decided which of these relationships was useful for our proof. After applying the appropriate theorems and properties to our diagram, we made a plan on how to go from the Given statement to the Prove statement. Using our plan, we then constructed a two-column proof.
$$
M'(0,0), A'(6,0), X'(6,4.5)
$$
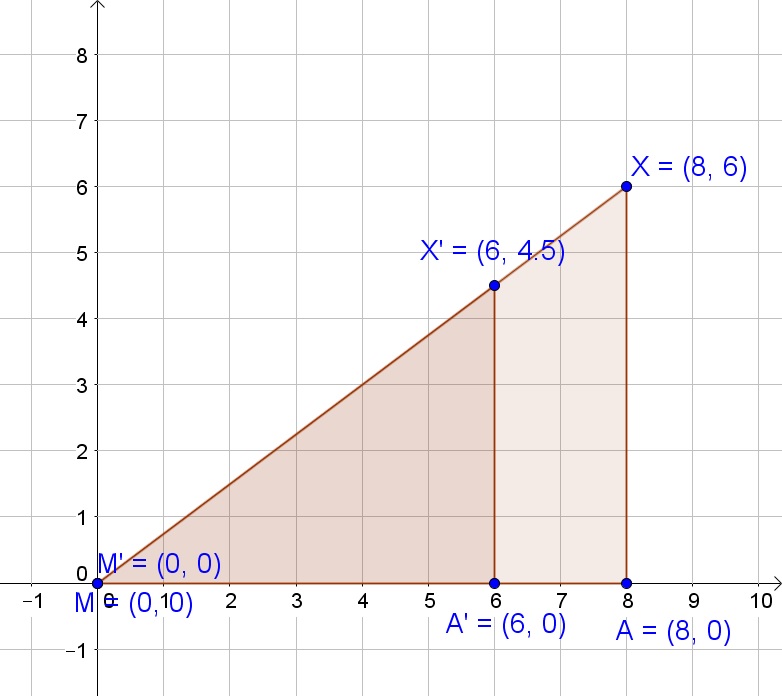
$$
dfrac{MA’}{MA}=dfrac{6}{8}=dfrac{3}{4}
$$
$$
dfrac{MX’}{MX}=dfrac{7.5}{10}=dfrac{3}{4}
$$
c. The difference in the $x$-coordinates of JK is 6 and the difference in $y$-coordinates is 8, then U is the coordinates of J increased by $dfrac{1}{4}$ the difference in distance:
$$
U=left( 11+dfrac{1}{4}cdot 6, 7+dfrac{1}{4}cdot 8right)=(11+1.5,7+2)=(12.5,9)
$$
b. (i) $frac{3}{4}$ (ii) $frac{3}{4}$
c. $(12.5,9)$
$$
theta=sin^{-1}dfrac{70}{100}approx 44.4text{textdegree}
$$
Thus the correct answer is B.
$$
7=x^2-4x+4
$$
Factorize:
$$
7=(x-2)^2
$$
Take the square root of both sides of the equation:
$$
pm sqrt{7}=x-2
$$
Add 2 to both sides of the equation:
$$
2pm sqrt{7}=x
$$
Thus the roots are $x=2pm sqrt{7}$
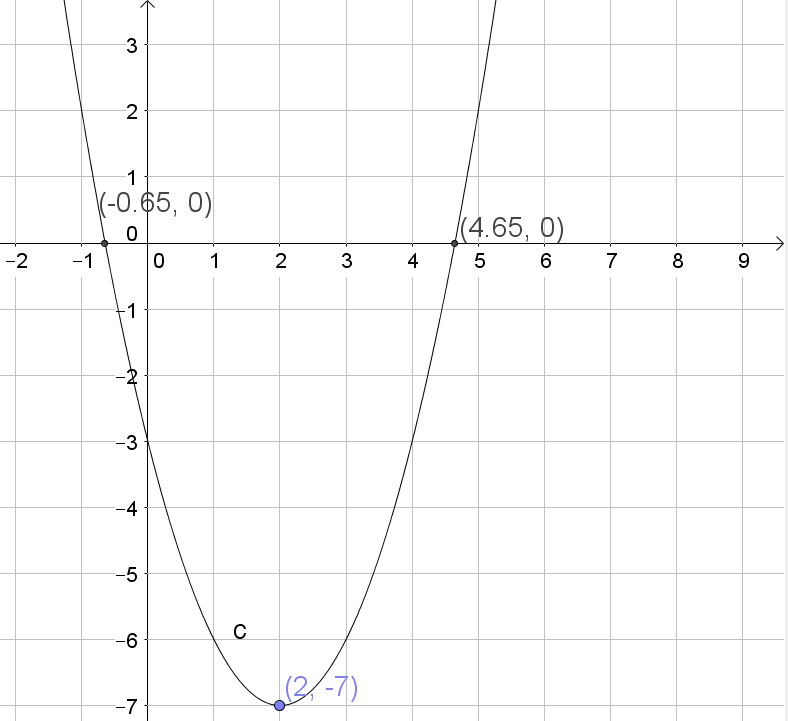
$x$-intercepts: $(2pm sqrt{7}, 0)$
$y$-intercept: $(0,-3)$
$$
4^{3/2}=(4^2)^{3/4}=16^{3/4}=4^x
$$
The powers should be equal:
$$
x=dfrac{3}{2}
$$
$$
2^1=(2^{3})^{1/3}=8^{1/3}=4^x=(2^2)^x=2^{2x}
$$
The powers should be equal:
$$
2x=1
$$
Divide both sides of the equation by 2:
$$
x=dfrac{1}{2}
$$
$$
3^{4x}=9^2=(3^2)^2=3^4
$$
The powers should be equal:
$$
4x=4
$$
Divide both sides of the equation by 4:
$$
x=1
$$
$$
2^{-x}=(2^{-1})^{x}=left( dfrac{1}{2}right)^{x}=4=2^2
$$
The powers should be equal:
$$
-x=2
$$
Divide both sides of the equation by $-1$:
$$
x=-2
$$
b. $x=frac{1}{2}$
c. $x=1$
d. $x=-2$
The longest line segment in a triangle is the diagonal, whose length can be determined using the Pythagorean theorem:
$$
sqrt{(5sqrt{2})^2+(5sqrt{2})^2}=sqrt{50+50}=sqrt{100}=10
$$
Thus the longest line is 10 units long.
$$
4x-2+x=90
$$
Add 2 to both sides of the equation:
$$
5x=92
$$
Divide both sides of the equation by 5:
$$
x=dfrac{92}{5}=18.4
$$
$$
2m+3+m+9+m-1=180
$$
Combine like terms:
$$
4m+11=180
$$
Subtract 11 from both sides of the equation:
$$
4m=169
$$
Divide both sides of the equation by 4:
$$
m=dfrac{169}{4}=42.25
$$
$$
7k-6=3k+18
$$
Subtract $3k$ from both sides of the equation:
$$
4k-6=18
$$
Add 6 to both sides of the equation:
$$
4k=24
$$
Divide both sides of the equation by 4:
$$
k=6
$$
$$
dfrac{x}{8}=dfrac{16}{13}
$$
Multiply both sides of the equation by 8:
$$
x=dfrac{16cdot 8}{13}=dfrac{128}{13}approx 9.8
$$
b. $m=42.25text{textdegree}$
c. $k=6text{textdegree}$
d. $x=9.8$



b. If the base angles of a trapezoid are congruent, then the non-parallel side lengths are equal.
c.
b. If the base angles of a trapezoid are congruent, then the non-parallel side lengths are equal.
c. Use AA
The diagonal that bisects the rhombus divides the rhombus in two congruent triangles.
If the base angles of a triangle are congruent, then the triangle is isosceles.
The diagonals of rectangles are congruent.
b. HR needs to be half the length of AK, because SR is half of SK. Then we also know that SH is half the length of SA and SH is equal to HA.
c. Since SR has to be half SK:
$$
SR=dfrac{20}{2}=10
$$
Determine SH using the Pythagorean theorem:
$$
HA=SH=sqrt{10^2-8^2}=sqrt{36}=6
$$
b. $HR$ is half the length of $AK$, $SH$ is half the length of $SA$, $SH$ has an equal length of $HA$
c. 6
b. True, because the sum of all angles of a quadrilateral is 360$text{textdegree}$ and thus each angle has to be 90$text{textdegree}$.
c. True, because a rhombus has two pair of parallel sides.
d. False, for example a non-square rectangle is also a parallelogram and its diagonals will not bisect the angles.
b. True
c. True
d. False
$$
y=77+3x
$$
$$
y=92-2x
$$
Subtract the two equations:
$$
0=-15+5x
$$
Add 15 to both sides of the equation:
$$
15=5x
$$
Divide both sides of the equation by 5:
$$
3=x
$$
Determine $y$:
$$
y=77+3x=77+3(3)=77+9=86
$$
Thus 3 hours from now it will be 86$text{textdegree}$ F in both towns.
Let $x$ be 0:
$$
0=x^2+3x+2
$$
Factorize:
$$
0=(x+1)(x+2)
$$
Zero product property:
$$
x+1=0text{ or }x+2=0
$$
Solve each equation to $x$:
$$
x=-1text{ or }x=-2
$$
Thus the $x$-intercepts then have to be $x=-1$ and $x=-2$.
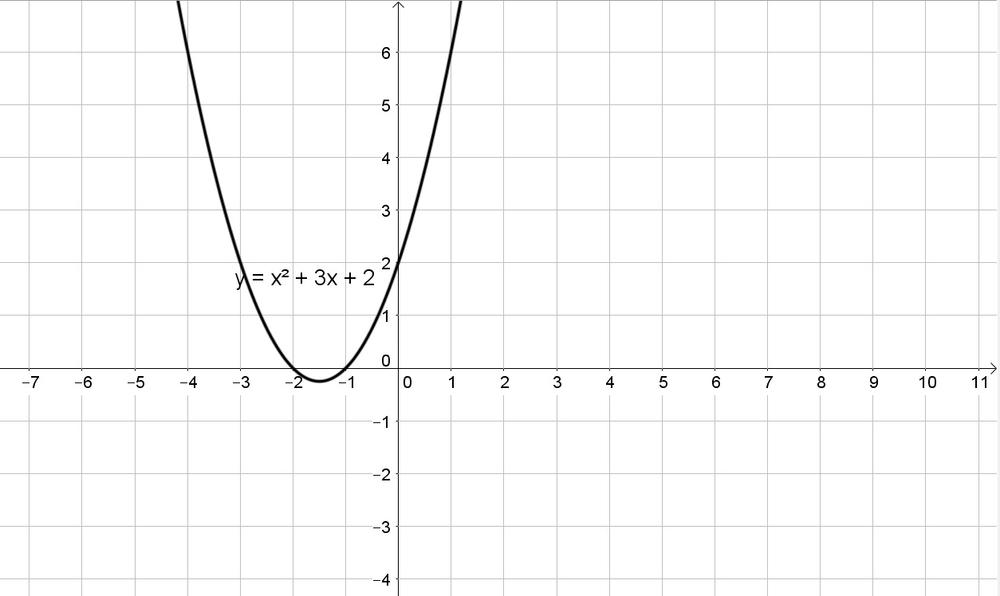
$y$-intercept: $(0,2)$
$$
AB=2DE
$$
Moreover these two sides seem to be parallel
b. The midsegment of a triangle is half as long as the parallel third side of the triangle.
c. The triangles are similar:
$$
angle C=angle C(text{ shared angle})
$$
$$
dfrac{CD}{CA}=dfrac{1}{2}(overline{DE}text{ is the midsegment })
$$
$$
dfrac{CE}{CB}=dfrac{1}{2}(overline{DE}text{ is the midsegment })
$$
$$
Downarrow SAS
$$
$$
triangle ABC sim triangle DEC
$$
d. The ratio is $dfrac{1}{2}$, as determined in the proof. Then we obtain:
$$
dfrac{DE}{AB}=dfrac{1}{2}
$$
e. Since the two triangles are similar:
$$
angle Dcong angle A
$$
Since they are corresponding angles, the lines then have to be parallel.
b. Midsegment is half as long as the parallel third side of the triangle.
c. Use SAS
d. $frac{1}{2}$
e. $angle Dcong angle A$
b. Yes, because they are corresponding sides in the pair of corresponding triangles.
c. Use cross multiplication and interchange the left and right sides of the equations.
d. We replace the squares with the expressions found in (c).
e. Use distributive property
f.
$$
DB+DC=BC
$$
Thus the expression then becomes:
$$
BC(BC)
$$
g. Because the product of twice the same factor is the square of that factor.
b. Yes
c. Cross multiplication
d. Replace squares
e. Distributive property
f. $BC$, $BC(BC)$
g. Product of twice the same factor is the square of that factor.
$$
left( dfrac{x_1+x_2}{2}, dfrac{y_1+y_2}{2}right)
$$
Thus for these two points:
$$
M=left( dfrac{-4+8}{2}, dfrac{-2+4}{2}right)=(2,1)
$$
b. Add the difference in coordinates multiplied by the given factor to the coordinates of $A$ to obtain the points:
$$
(i) left( -4+dfrac{1}{3}(8+4),-2+dfrac{1}{3}(4+2)right)=(0,0)
$$
$$
(ii) left( -4+dfrac{3}{4}(8+4),-2+dfrac{3}{4}(4+2)right)=(5,2.5)
$$
$$
(iii) left( -4+dfrac{1}{3}(8+4),-2+dfrac{1}{3}(4+2)right)=(0,0)
$$
$$
(iv) left( -4+dfrac{d}{c}(8+4),-2+dfrac{d}{c}(4+2)right)=left( -4+dfrac{12d}{c},-2+dfrac{6d}{c}right)
$$
c. You dilate star B with the given factor and center star A.
d. By determining the difference in the coordinates of the two given points and then adding the product of the fraction and the difference(s) to the corresponding coordinates (of the point where you start).
b. (i) $(0,0)$ (ii) $(5,2.5)$ (iii) $(0,0)$, (iv) $left(-4+frac{12d}{c}, -2+frac{6d}{c}right)$
c. You dilate star B with the given factor and center star A.
d. By determining the difference in the coordinates of the two given points and then adding the product of the fraction and the difference(s) to the corresponding coordinates (of the point where you start).
The Pythagorean theorem states: $a^2+b^2=c^2$.
AB=CD(text{Given})
$$
$$
AC=CA(text{ Same side})
$$
$$
angle BACcong angle DCA(text{Alternate interior angles })
$$
$$
Downarrow SAS
$$
$$
triangle BACcong triangle DCA
$$
$$
Downarrow
$$
$$
angle BCAcong angle DAC
$$
$$
Downarrow
$$
$$
overline{BC}//overline{AD}
$$
$$
(3x-2)(2x+5)=0
$$
Zero product property:
$$
3x-2=0text{ or } 2x+5=0
$$
Solve each equation to $x$:
$$
3x=2text{ or } 2x=-5
$$
$$
x=dfrac{2}{3}text{ or } x=-dfrac{5}{2}
$$
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
with $a$ the coefficient of $x^2$, $b$ the coefficient of $x$ and $c$ the constant term.
Then we obtain:
$$
x=dfrac{-11pm sqrt{11^2-4(6)(-10)}}{2(6)}=dfrac{-11pm 19}{12}=dfrac{2}{3}text{ or }-dfrac{5}{2}
$$
$$
(2+i)(3-5i)-(1-4i)^2=6+3i-10i-5i^2-(1-8i+16i^2)
$$
$$
=5+i-21i^2=5+i+21=26+i
$$
26+i
$$
$$
70%cdot 70%=0.7cdot 0.7=0.49=49%
$$
b. Since each flip is independent of the other flip, the probability is the product of each probability:
$$
70% cdot 30%=0.7cdot 0.3=0.21=21%
$$
b. 21%
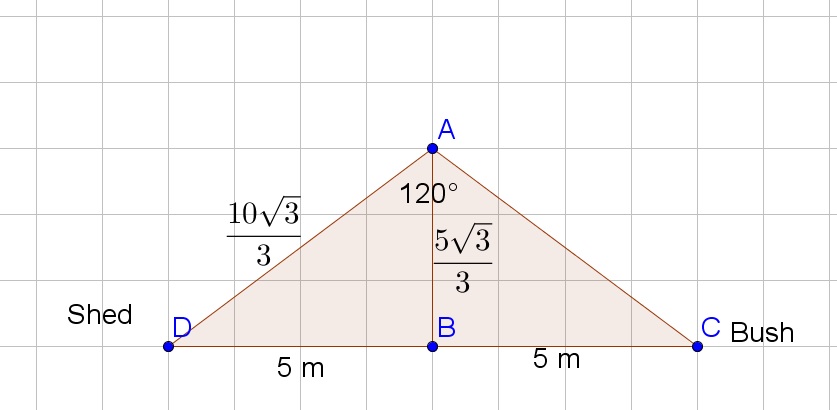
$$
dfrac{10sqrt{3}}{3}approx 5.77 ft
$$
$$
4x^2-20x+25=(2x-5)^2
$$
$$
x=frac{-bpm sqrt{b^2-4ac}}{2a}
$$
Determine the roots of the given equation using the quadratic formula:
$$
begin{align*}
x&=frac{-11pm sqrt{11^2-4(1)(-2)}}{2(1)}
\ &=frac{-11pm sqrt{129}}{2}
end{align*}
$$
The factorization of a quadratic equation is $(x-d)(x-e)$ when $d$ and $e$ are the roots of the equation.
$$
left(x-frac{-11+sqrt{129}}{2}right)left(x-frac{-11-sqrt{129}}{2}right)
$$
$$
3x^2-12x=3x(x-4)
$$
$$
10x^2-35x-20=5(2x^2-7x-4)
$$
Factor further:
$$
10x^2-35x-20=5(2x+1)(x-4)
$$
b. $left(x-frac{-11+sqrt{129}}{2}right)left(x-frac{-11-sqrt{129}}{2}right)$
c. $3x(x-4)$
d. $5(2x+1)(x-4)$
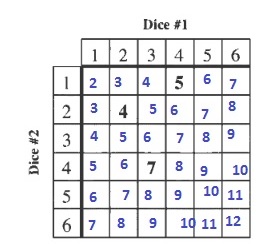
c. 1 way out of the 5.
d. The probability is the number of favorable outcomes divided by the number of possible outcomes.
$$
P=dfrac{1}{5}=0.2=20%
$$
e. The probability is the number of favorable outcomes divided by the number of possible outcomes.
$$
P=dfrac{6}{10}=dfrac{3}{5}=0.6=60%
$$
b. 5 ways
c. 1 way
d. $frac{1}{5}=0.2=20%$
e. $frac{3}{5}=0.6=60%$
$$
P=dfrac{6+34}{6+34+30+170}=dfrac{40}{240}=dfrac{1}{6}approx 0.167=16.7%
$$
b. The probability is the number of favorable outcomes divided by the number of possible outcomes.
$$
P=dfrac{6}{30+6}=dfrac{1}{6}approx 0.167=16.7%
$$
c. Yes, because the probability of a student being on the student council given that the student eats at the cafeteria is equal to the probability of a student being on the student council.
d. No, because these two events can happen at the same time (a student can be on the student council and eat at the cafeteria).
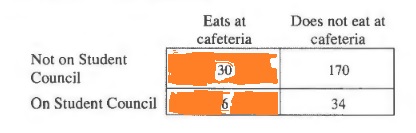
b. $frac{1}{6}approx 0.167=16.7%$
c. Yes
d. No
b. Yes, because there are more students with long hair wearing jeans, then there are students who do not have long hair and wear jeans.
c. Yes, they are associated (not independent) because knowing if a student wears jeans has changed our opinion.
d. No, because they can occur at the same time.
b. Yes
c. Yes
d. No
b. Yes, because the two events cannot happen at the same time, since their intersection contains 0 outcomes.
b. Yes, 0
Two events are $textbf{independent}$, if the probability that one event occurs in no way affects the probability of the other event occurring.
Two events are $textbf{disjoint}$ or $textbf{mutually exclusive}$, if the events cannot occur at the same time.
Two events are $textbf{disjoint}$ or $textbf{mutually exclusive}$, if the events cannot occur at the same time.
$$
P=dfrac{2cdot 2}{5cdot 4}=dfrac{4}{20}=dfrac{1}{5}=0.2=20%
$$
b. The probability of not finding the ring is 100%=1 decreased by the probability of finding the ring (since the events are complements of each other):
$$
100%-20%=80%
$$
c. No, because the area of the shaded region has not changed in respect to the area of the original region.
b. 80%
c. No
*What angle relationships do we have when lines intersect or are cut by a transversal?*
* **Corresponding Angles Theorem:** If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
* **Alternate Interior Angles Theorem:** If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
* **Same Side Interior Angles Theorem:** If two parallel lines are cut by a transversal, then the same-side interior angles are supplementary.
* **SAS:** If two triangles have two pairs of congruent sides and the included angles are also congruent, then the triangles are congruent.
* **SSS:** If two triangles have three pairs of congruent sides, then the triangles are congruent.
* **ASA:** If two triangles have two pairs of congruent angles and the included sides are also congruent, then the triangles are congruent.
* **AAS:** If two triangles have two pairs of congruent angles and a pair of non-included sides are also congruent, then the triangles are congruent.
Before we start the proof, let’s make a plan on how to go from our Given statement to our Prove statement.
It is given that $overline{BC}paralleloverline{EF}$, $overline{AB}paralleloverline{DE}$, and $AF=DC$. Let’s start by labeling the given diagram with all of the congruent alternate interior angles and congruent segments. Recall that a segment is congruent to itself by the Reflexive Property so we can also label $FC$ with tick marks to emphasize this:

$$text{Figure 1: Labeled diagram}$$
From Figure $1$, we can now see that the two triangles have two pairs of congruent angles and a pair of congruent included sides (the bases of the triangles). Therefore, we also know the triangles must be congruent.
Our plan for the proof is then:
1. State our givens.
2. Use the Alternate Interior Angles Theorem to prove the two pairs of angles of congruent.
3. Use the Segment Addition Postulate to prove the bases of the triangles are congruent.
4. Use ASA to prove the triangles are congruent.
5. Conclude the segments are congruent since the triangles are congruent.
| Statements| Reasons|
|–|–|
|1. $overline{BC}paralleloverline{EF}$ | 1. **Given**|
|2. $mangle BCF=mangle EFC$ | 2. **Alternate Interior Angles Theorem**|
|3. $overline{AB}paralleloverline{DE}$| 3. **Given**|
|4. $mangle BAC=mangle EFD$| 4. **Alternate Interior Angles Theorem**|
|5. $AF=DC$|5. **Given**|
|6. $boldsymbol{FC=FC}$|6. Reflexive Property|
|7. $AF+FC=FC+DC$| 7. Addition Property of Equality|
|8. $AC=DC$|8. Segment addition|
|9. $triangle ABCcongtriangle DEF$|9. **ASA**|
|10. $boldsymbol{overline{BC}congoverline{EF}}$|10. $cong;triangletext{s}rightarrowcongtext{ parts}$|
First, we recalled some of the angle relationships created by parallel lines cut by a transversal and the triangle congruence theorems. Then we decided which of these theorems were useful for our proof. After applying the appropriate theorems to our diagram, we made a plan on how to go from the Given statement to the Prove statement. Using our plan, we then constructed a two-column proof.
$$
left( dfrac{x_1+x_2}{2}, dfrac{y_1+y_2}{2}right)
$$
Then we obtain that $E=(6.5,5)$ (as on the graph).
b. We note that E lies $dfrac{3}{8}$ from A to B.
c.
$$
E=left( 2+dfrac{3}{8}(14-2), 2+dfrac{3}{8}(10-2)right)=(6.5,5)
$$
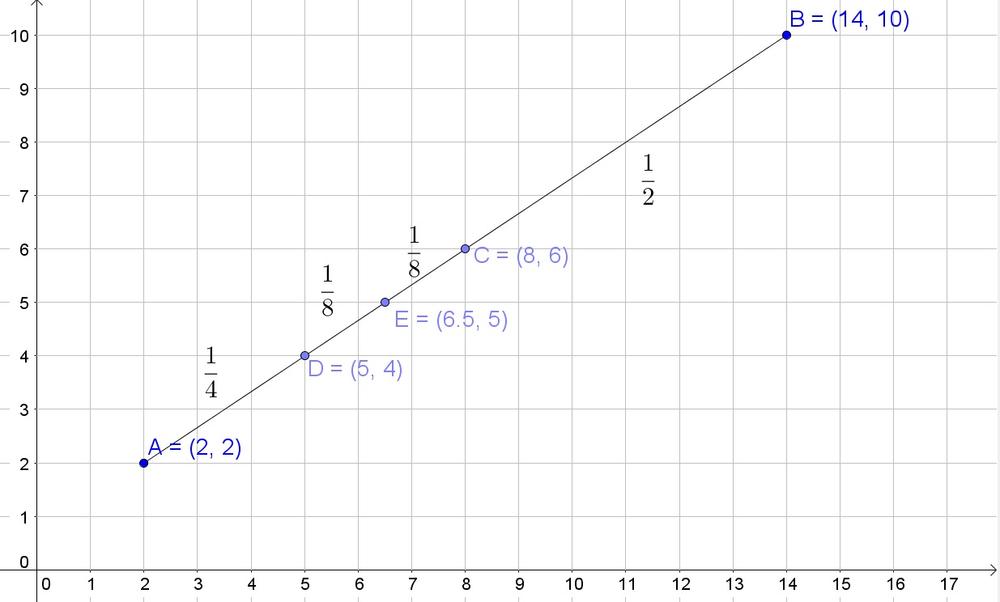
b. $frac{3}{8}$
c. $(6.5,5)$
a. A possible function is then:
$$
y=left( x-dfrac{3}{4}right)(x+2)=x^2+dfrac{5}{4}x-dfrac{3}{2}
$$
b. A possible function is then:
$$
y=(x+sqrt{5})(x-sqrt{5})=x^2-5
$$
b. $y=x^2-5$
b. True
c. True, because if it has three right angles, then the forth angle is also a right angle (using (b)) and thus the quadrilateral is a rectangle.
d. False, the diagonals of a rectangle also bisect each other.
b. True
c. True
d. False
$$
AREA=dfrac{2cdot 11}{2}+dfrac{5cdot 10}{2}=11+25=36ft^2
$$
The perimeter is the sum of the lengths of all sides:
$$
5+10+11+2=28ft
$$
b. The area of a triangle is the product of the base and the height divided by 2. The area of a square is one of its sides squared
$$
AREA=dfrac{20cdot 20}{2}+20^2=200+400=600cm^2
$$
The perimeter is the sum of the lengths of all sides:
$$
20+20+20+20+20+(20sqrt{2}-20)=80+20sqrt{2}cm
$$
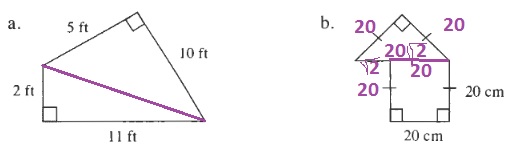
b. Area 600 cm$^2$ and Perimeter $80+20sqrt{2}$ cm
$a$ is the initial value and thus $a=2$.
Using the information we then obtain:
$$
0.45=2(b)^8
$$
Divide both sides of the equation by 2:
$$
0.225=(b)^8
$$
Take the 8throot of both sides of the equation:
$$
0.83approx sqrt[8]{0.225}=b
$$
Thus the equation then becomes:
$$
y=2(0.83)^t
$$
b. The approximate hourly multiplier is 0.83 and the hourly percent of decrease is then:
$$
100%-0.83=100%-83%=17%
$$
c. Evaluate the function at $x=-2$:
$$
y=2(0.83)^{-2}=2.9
$$
Thus about 2.9 grams.
b. $17%$
c. 2.9 grams.
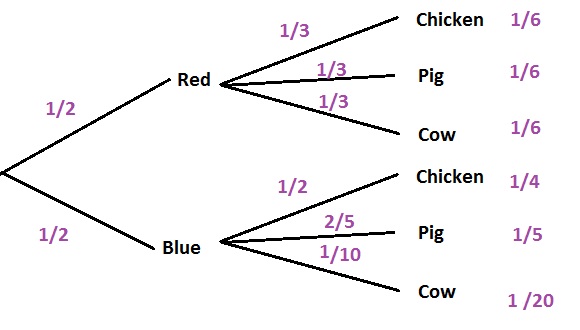
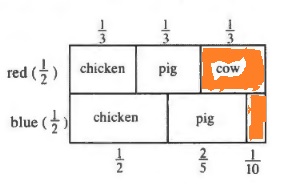
$$
P(cow)=dfrac{1}{6}+dfrac{1}{20}=dfrac{13}{60}approx 0.217=21.7%
$$
c.Add the probabilities that result in a cow counter:
$$
P(cow)=dfrac{1}{2}cdot dfrac{1}{3}+dfrac{1}{2}cdot dfrac{1}{10}=dfrac{13}{60}approx 0.217=21.7%
$$
$$
P(text{ red given cow})=dfrac{10}{10+1}=dfrac{10}{11}approx 0.909=90.9%
$$
e. No, because the probability of red given cow is not equal to the probability of red (50%).
f. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(text{ blue given pig})=dfrac{4}{10+4}=dfrac{2}{7}approx 0.286=28.6%
$$
b. $frac{13}{60}approx 0.217=21.7%$
c. $frac{13}{60}approx 0.217=21.7%$
d. $frac{10}{11}approx 0.909=90.9%$
e. No
f. $frac{2}{7}approx 0.286=28.6%$
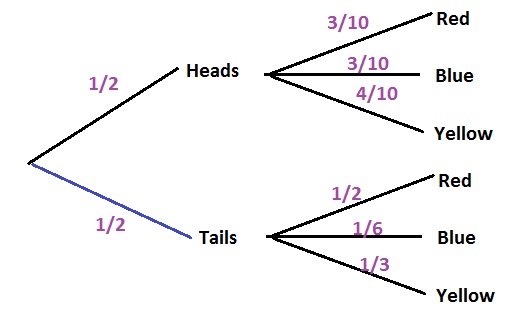
$$
P(text{ heads given blue})=dfrac{3}{4}=0.75=75%
$$
b. $frac{3}{4}=0.75=75%$
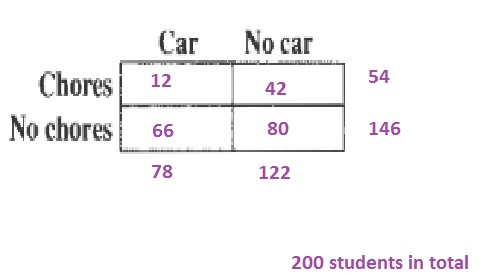
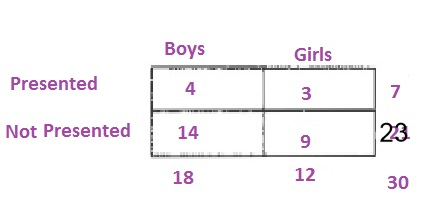
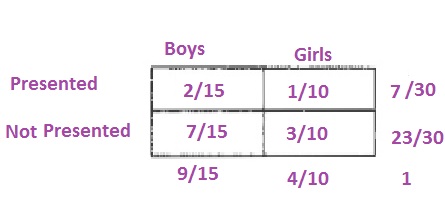
d. Add the probabilities from the table in (b):
$$
dfrac{4}{10}+dfrac{2}{15}=dfrac{16}{30}approx 0.533=53.3%
$$
e. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{3}{7}approx 0.429=42.9%
$$
b. Table
c. $frac{2}{15}approx 0.133=13.3%$
d. $frac{8}{15}approx 0.533=53.3%$
e. $frac{3}{7}approx 0.429=42.9%$
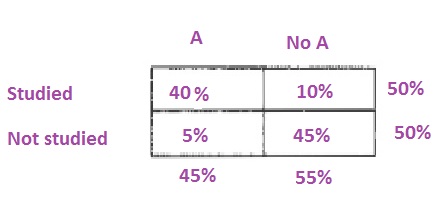
c. The probability is the number of favorable events divided by the number of possible events:
$$
dfrac{40%}{45%}=dfrac{0.4}{0.45}=dfrac{8}{9}approx 0.889=88.9%
$$
b. 45%
c. $frac{8}{9}approx 0.889=88.9%$
$$
dfrac{120}{920}=dfrac{3}{23}approx 0.13=13%
$$
b. The probability is the number of favorable events divided by the number of possible events:
$$
dfrac{12,000}{20,000}=dfrac{3}{5}=0.6=60%
$$
c. Yes, because if they were not associated, the probabilities in (a) and (b) had to be equal.
b. $frac{3}{5}=0.6=60%$
c. Yes
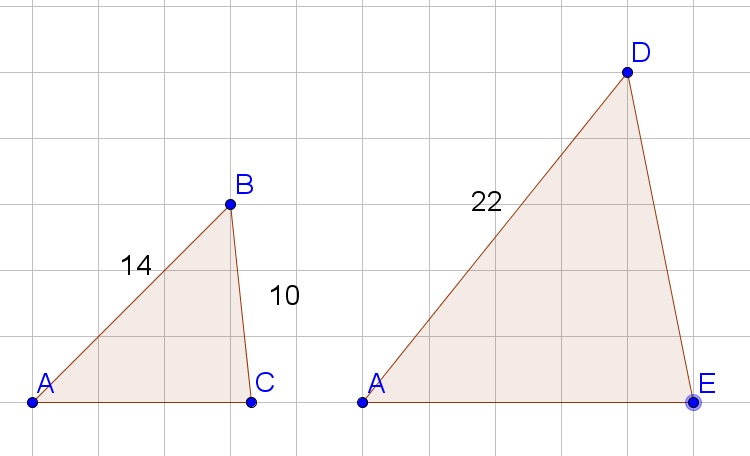
$$
dfrac{10}{14}=dfrac{x}{22}
$$
Multiply both sides of the equation by 22:
$$
15.7approx dfrac{10cdot 22}{14}=x
$$
overline{DE}=15.7
$$
$$
3x-2=2x+17
$$
a.
$$
36x^2-a^2=(6x-a)(6x+a)
$$
b.
$$
16x^4-81=(4x^2-9)(4x^2+9)=(2x-3)(2x+3)(4x^2+9)
$$
b. $(2x-3)(2x+3)(4x^2+9)$
Radicals can be described by the following expression:
$$begin{gather}
^nsqrt{a^m} = a^{frac{m}{n}}
end{gather}$$
We evaluate the expression $27^{frac{1}{3}}$ using the property of radicals. We are to find the value of $a$ as shown in Eq (1) as follows:
$$begin{aligned}
&= ^nsqrt{a^m} = a^{frac{m}{n}} \
&= 27^{frac{1}{3}} \
&= ^3 sqrt{27} \
& text{ we know that: }27 = 3^3 \
&= ^3 sqrt{3^3}\
&= boxed{3}
end{aligned}$$
Hence, the expression yields the value $boxed{3}$
We evaluate the expression $16^{frac{1}{4}}$ using the property of radicals. We are to find the value of $a$ as shown in Eq (1) as follows:
$$begin{aligned}
&= ^nsqrt{a^m} = a^{frac{m}{n}} \
&= 16^{frac{1}{4}} \
&= ^4 sqrt{16} \
& text{ we know that: }16 = 2^4 \
&= ^4 sqrt{2^4}\
&= boxed{2}
end{aligned}$$
Hence, the expression yields the value $boxed{2}$
We evaluate the expression $49^{frac{1}{2}}$ using the property of radicals. We are to find the value of $a$ as shown in Eq (1) as follows:
$$begin{aligned}
&= ^nsqrt{a^m} = a^{frac{m}{n}} \
&= 49^{frac{1}{2}} \
&= ^2 sqrt{49} \
& text{ we know that: }49 = 7^2 \
&= ^2 sqrt{7^2}\
&= boxed{7}
end{aligned}$$
Hence, the expression yields the value $boxed{7}$
We evaluate the expression $1000^{frac{1}{3}}$ using the property of radicals. We are to find the value of $a$ as shown in Eq (1) as follows:
$$begin{aligned}
&= ^nsqrt{a^m} = a^{frac{m}{n}} \
&= 1000^{frac{1}{3}} \
&= ^3 sqrt{1000} \
& text{ we know that: }1000 = 10^3 \
&= ^3 sqrt{10^3}\
&= boxed{10}
end{aligned}$$
Hence, the expression yields the value $boxed{10}$
b. $2$
c. $7$
d. $10$
b. Let $x$ be the number of new gym memberships sold and $y$ the amount earned.
c. Let $x$ be the day of the month and $y$ the amount in the savings account.
$$
dfrac{236}{236+274}=dfrac{236}{510}approx 0.463=46.3%
$$
b. Yes,because if somebody has brought a laptop it is more likely that they are traveling for business.
b. Yes
$$
x^2-8x+7=(x-7)(x+1)
$$
$$
y^2-2y-15=(y-5)(y+3)
$$
$$
7x^2-63=7(x^2-9)
$$
Factorize the difference of squares ($a^2-b^2=(a-b)(a+b)$):
$$
7x^2-63=7(x-3)(x+3)
$$
$$
3x^2+10x+8=(3x+4)(x+2)
$$
b. $(y-5)(y+3)$
c. $7(x-3)(x+3)$
d. $(3x+4)(x+2)$
Two exponents with the same base can be evaluated using the following property:
$$begin{gather}
x^n + x^m = x^{(n+m)}
end{gather}$$
On the other hand, radicals can be described by the following expression:
$$begin{gather}
^nsqrt{a^m} = a^{frac{m}{n}}
end{gather}$$
Evaluate the expression:
$6x^{frac{2}{3}}y^{frac{1}{4}}cdot x^{-1}y^{frac{1}{2}}$
Given that $x=27$ and $y=16$
We first plug-in the values of $x$ and $y$ as follows:
$$begin{aligned}
&= 6x^{frac{2}{3}}y^{frac{1}{4}}cdot x^{-1}y^{frac{1}{2}} \
&= 6 cdot27^{frac{2}{3}} cdot 16^{frac{1}{4}}cdot 27^{-1} cdot 16^{frac{1}{2}} \
end{aligned}$$
$$begin{aligned}
&= 6 cdot27^{frac{2}{3}} cdot 16^{frac{1}{4}}cdot 27^{-1} cdot 16^{frac{1}{2}} \
&= 6 cdot (27^{frac{2}{3}} cdot 27^{-1}) cdot (16^{frac{1}{4}}cdot 16^{frac{1}{2}}) \
end{aligned}$$
$$begin{aligned}
&= 6 cdot (27^{frac{2}{3}} cdot 27^{-1}) cdot (16^{frac{1}{4}}cdot 16^{frac{1}{2}}) \
&= 6 cdot (27^{(frac{2}{3} -1)}) cdot (16^{frac{1}{4}+frac{1}{2}}) \
&= 6 cdot (27^{(frac{2}{3} -frac{3}{3})}) cdot (16^{frac{1}{4}+frac{2}{4}}) \
&= 6 cdot (27^{-frac{1}{3}}) cdot (16^{frac{3}{4}}) \
end{aligned}$$
$$begin{aligned}
&= 6 cdot (27^{-frac{1}{3}}) cdot (16^{frac{3}{4}}) \
^nsqrt{a^m} &= a^{frac{m}{n}} \
&= 6 cdot left(frac{1}{^3sqrt{27}} right) cdot (^4sqrt{16^3}) \
& text{ we know that: $27= 3^3$ and $16 = 2^4$} \
&= 6 cdot left(frac{1}{^3sqrt{3^3}} right) cdot (^4sqrt{(2^4)^3}) \
&= 6 cdot left(frac{1}{3}right) cdot (2^3) \
&= 6 cdot frac{1}{3} cdot 8 \
&= boxed{16}
end{aligned}$$
The expression $6x^{frac{2}{3}}y^{frac{1}{4}}cdot x^{-1}y^{frac{1}{2}}$ when $x=27$ and $y=16$ yields the value $16$
$$
4x+28+x+19+3x+13=180
$$
Combine like terms:
$$
8x+60=180
$$
Subtract 60 from both sides of the equation:
$$
8x=120
$$
Divide both sides of the equation by 8:
$$
x=15
$$
$$
6k+3=3k+18
$$
Subtract $3k$ from both sides of the equation:
$$
3k+3=18
$$
Subtract 3 from both sides of the equation:
$$
3k=15
$$
Divide both sides of the equation by 3:
$$
k=5
$$
$$
4t+13=8t-23
$$
Subtract $4t$ from both sides of the equation:
$$
13=4t-23
$$
Add 23 to both sides of the equation:
$$
36=4t
$$
Divide both sides of the equation by 4:
$$
9=t
$$
Adjacent angles of a parallelogram are supplementary:
$$
w=180-(4t+13)=180-4(9)-13=131
$$
$$
sin{35.5text{textdegree}}=dfrac{x/2}{43}
$$
Multiply both sides of the equation by 86:
$$
50approx 86sin{35.5text{textdegree}}=x
$$
b. $k=5$
c. $t=9text{textdegree}$ and $w=131text{textdegree}$
d. $x=50$
$$
Fr^2=GmM
$$
Divide both sides of the equation by $F$:
$$
r^2=dfrac{GmM}{F}
$$
Take the square root of both sides of the equation:
$$
r=sqrt{dfrac{GmM}{F}}
$$
$$
dfrac{tau}{rF}=sin{theta}
$$
Take the inverse sine of both sides of the equation:
$$
sin^{-1}{dfrac{tau}{rF}}=theta
$$
Interchange left and right side of the equation:
$$
theta =sin^{-1}{dfrac{tau}{rF}}
$$
b. $theta=sin^{-1}frac{tau}{rF}$
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
Evaluate for the given points:
$$
sqrt{(5-1)^2+(2-6)^2}=sqrt{16+16}=sqrt{32}=4sqrt{2}
$$
b. ABB’A’ is a trapezium and the area of a trapezium is the sum of the bases multiplied by the height, divided by 2:
$$
AREA=dfrac{(2+10)4}{2}=24
$$
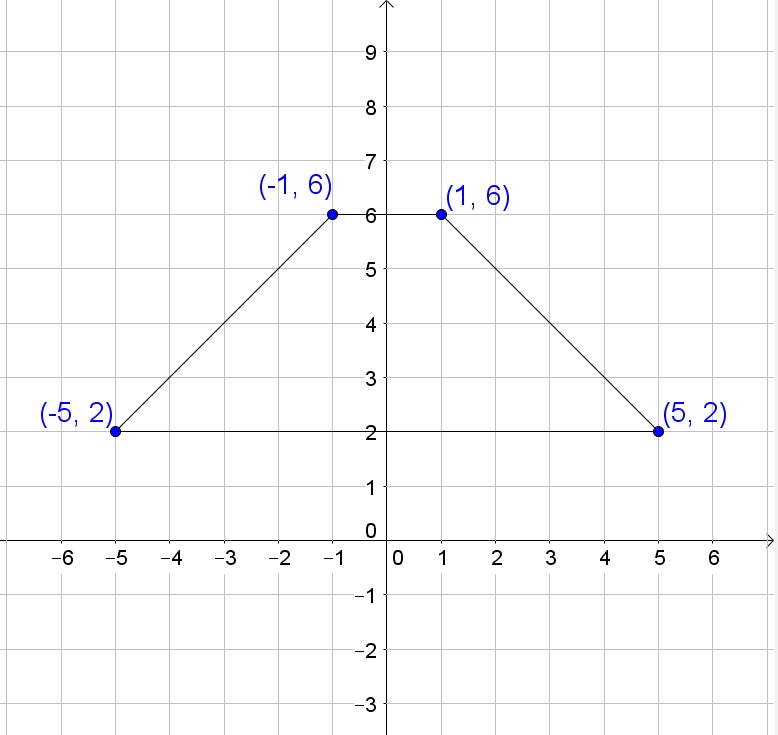
b. 24
$$
x+4=pm 7
$$
Subtract 4 from both sides of the equation:
$$
x=-4pm 7=3text{ or }-11
$$
$$
sqrt{x+2}=4
$$
Square both sides of the equation:
$$
x+2=16
$$
Subtract 2 from both sides of the equation:
$$
x=14
$$
$$
dfrac{2}{x}=dfrac{10}{10}=1
$$
Multiply both sides of the equation by $x$:
$$
2=x
$$
$$
5(2x-1)=15
$$
Divide both sides of the equation by 5:
$$
2x-1=3
$$
Add 1 to both sides of the equation:
$$
2x=4
$$
Divide both sides of the equation by 2:
$$
x=2
$$
b. $x=14$
c. $x=2$
d. $x=2$
c. Add the corresponding probabilities:
$$
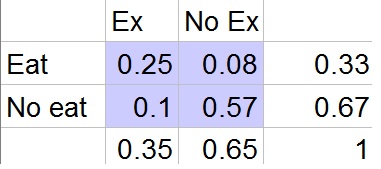
0.25+0.08+0.1=0.43=43%
$$
d. Yes, because the relationship between EAT and EX in the column is higher than either column/row being No.
b. $0.25=25%$
c. $0.43=43%$
d. Yes
$$
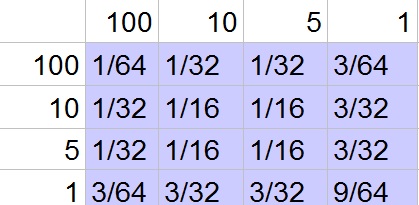
P(win)=dfrac{1}{64}+dfrac{1}{16}+dfrac{1}{16}+dfrac{9}{64}=dfrac{9}{32}approx 28.125=28.125%
$$
c. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(100|win)=dfrac{1/64}{9/32}=frac{1}{18}approx 0.055=5.5%
$$
d.
$$
P(100|win)=dfrac{P(100text{ and }win)}{P(win)}=dfrac{1/64}{9/32}=dfrac{1}{18}approx 0.055=5.5%
$$
b. $frac{9}{32}approx 0.28125=28.125%$
c. $frac{1}{18}approx 0.055=5.5%$
d. $frac{1}{18}approx 0.055=5.5%$
$$
P(Atext{ given }B)=dfrac{P(Atext{ and }B)}{P(B)}
$$
Multiply both sides of the equation by $P(B)$ and interchange the left and right side of the equation:
$$
P(Atext{ and }B)=P(B)cdot P(Atext{ given }B)
$$
b. If $A$ and $^B$ are independent:
$$
P(Atext{ given }B)=P(A)
$$
c. Substitute $P(AgivenB)$ with $P(A)$ in the equation of (a):
$$
P(Atext{ and }B)=P(B)cdot P(A)
$$
d. Yes, when determining the probability of two events at the same time (which were independent).
b. $P(Atext{ given }B)=P(A)$
c. $P(Atext{ and }B)=P(B)cdot P(A)$
d. Yes
$$
P(AgivenB)=dfrac{P(AandB)}{P(A)}=dfrac{72/240}{180/240}=dfrac{2}{5}=0.4=40%
$$
While we know that:
$$
P(A)=dfrac{180}{240}=dfrac{3}{4}=0.75=75%
$$
Thus we note that $P(Agiven B)neq P(A)$ and thus the two events are associated.
$$
P(text{ heads and truth})=dfrac{1}{2}cdot dfrac{1}{6}=dfrac{1}{12}approx 0.083=8.3%
$$
b.
$$
P(heads)=P(text{ heads and truth})+P(text{ heads and lie})
$$
$$
=dfrac{1}{12}+dfrac{1}{2}cdot dfrac{5}{6}=dfrac{1}{12}+dfrac{5}{12}=dfrac{1}{2}=0.5=50%
$$
c. Since the events are independent:
$$
P(truth|heads)=P(truth)=dfrac{1}{6}=0.167=16.7%
$$
d. Independent because flipping a coin and rolling a dice is independent (they cannot influence each other).
b. $frac{1}{2}=0.5=50%$
c. $frac{1}{6}approx 0.167=16.7%$
d. Independent
$$
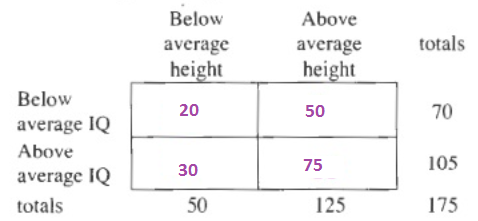
70cdot dfrac{50}{175}=20
$$
The remaining numbers can be found by makings sure the totals at the right and bottom are correct.
$$
P(red)=100%-x=1-x
$$
b.

$$
P(same color)=(1-x)^2+x^2
$$
d. Use the multiplication rule:
$$
P(blue|same color)=dfrac{P(BLUE and SAME COLOR)}{P(BLUE)}=dfrac{x^2}{x}=x
$$
b. Area model
c. $(1-x)^2+x^2$
d. $x$
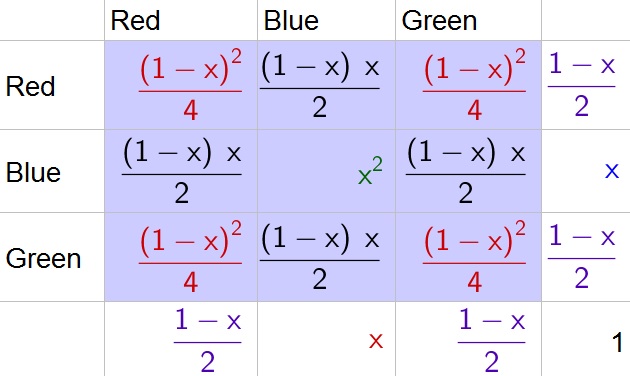
$$
P(green)+P(red)=100%-x=1-x
$$
Since green and red have equal probability:
$$
P(green)=P(red)=dfrac{1-x}{2}
$$
b.
$$
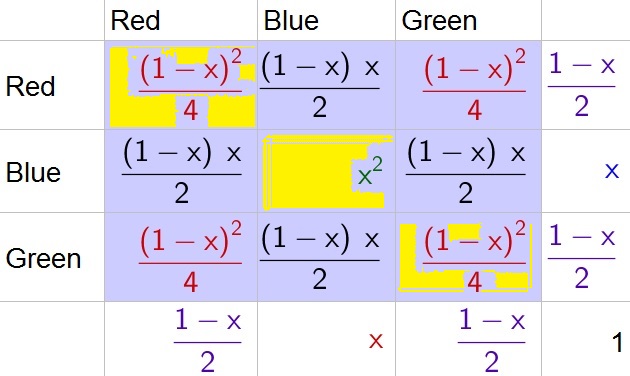
P(same color)=dfrac{(1-x)^2}{4}+x^2+dfrac{(1-x)^2}{4}=dfrac{(1-x)^2}{2}+x^2
$$
e. Use the multiplication rule:
$$
P(blue|same color)=dfrac{P(BLUE and SAME COLOR)}{P(SAME COLOR)}=dfrac{x^2}{dfrac{(1-x)^2}{2}+x^2}
$$
b. Model
c. Shaded region
d. $frac{(1-x)^2}{2}+x^2$
e. $frac{x^2}{frac{(1-x)^2}{2}+x^2}$
The addition rule: P(A or B)=P(A)+P(B)-P(A and B)
The multiplication rule: P(A given B)=P(A and B)/P(B)
Other version multiplication rule: P(A and B)=P(A)P(A given B)
Independence rule: P(A given B)=P(A)
Other independence rule: P(A and B)=P(A)P(B)
The multiplication rule: P(A given B)=P(A and B)/P(B)
Other version multiplication rule: P(A and B)=P(A)P(A given B)
Independence rule: P(A given B)=P(A)
Other independence rule: P(A and B)=P(A)P(B)
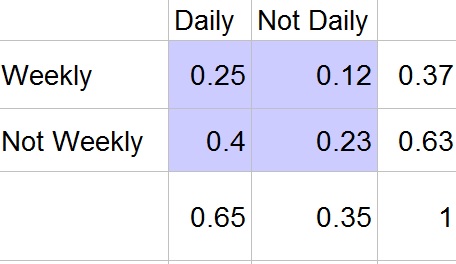
$$
P(either)=0.25+0.12+0.4=0.77=77%
$$
c. Use the multiplication rule:
$$
P(daily|either)=dfrac{P(DAILYand EITHER)}{P(EITHER)}=dfrac{0.65}{0.77}approx 0.844=84.4%
$$
c. 0.77=77%
c. 0.844=84.4%
$$
P(FineArts|academic)=dfrac{P(FINEARTSand ACADEMIC)}{P(ACADEMIC)}=dfrac{8/768}{128/768}=dfrac{8}{128}=dfrac{1}{16}=0.0625=6.25%
$$
Compare with the probability of the fine arts alone:
$$
P(FineArts)=dfrac{48}{768}=dfrac{1}{16}=0.0625=6.25%
$$
We note that the two probabilities are equal and thus Dr. G has nothing to worrty about because the two events are independent.
$$
10.25=x^2+7x+12.25
$$
Factorize:
$$
10.25=(x+3.5)^2
$$
Take the square root of both sides of the equation:
$$
pm 0.5sqrt{41}=pm sqrt{10.25}=x+3.5
$$
Subtract 3.5 from both sides of the equation:
$$
-0.3text{ or } -6.7approx -3.5pm 0.5sqrt{41}=x
$$
Thus the solutions are $x=-3.5pm 0.5sqrt{41}$.
The $y$-intercept is $y=2$ and the vertex is $(-3.5,-10.25)$ which is a minimum.
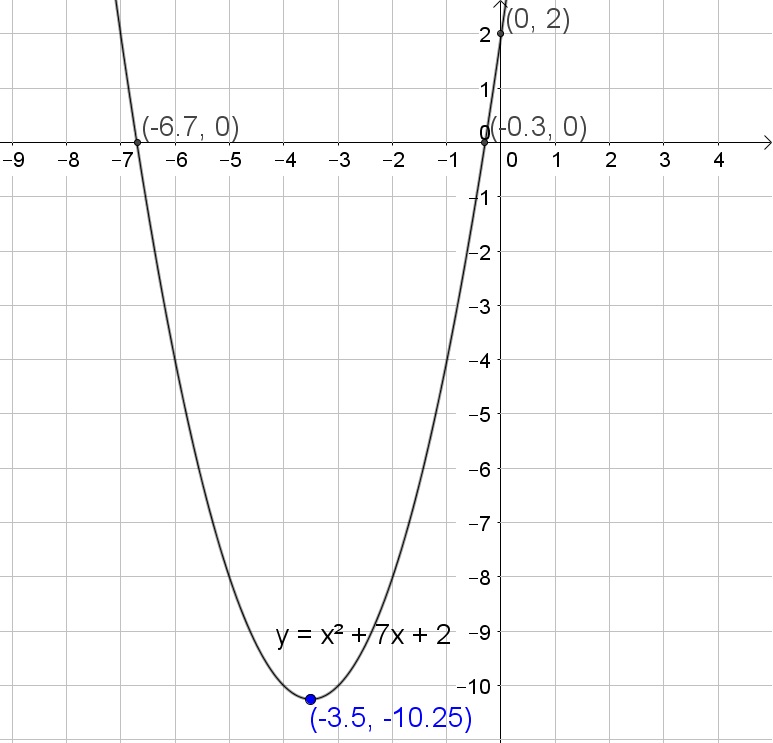
$y$-intercept: $(0,2)$
Minimum
$$
2^{2z}=(2^2)^z=4^z=2^3
$$
The powers have to be equal:
$$
2z=3
$$
Divide both sides of the equation by 2:
$$
z=dfrac{3}{2}
$$
$$
2^{10z}=(2^2)^{5z}=4^{5z}=8^{z+2}=(2^3)^{z+3}=2^{3(z+3)}
$$
The powers have to be equal:
$$
10z=3z+9
$$
Subtract $3z$ from both sides of the equation:
$$
7x=9
$$
Divide both sides of the equation by 7:
$$
z=dfrac{9}{7}
$$
$$
3^z=81^2=(3^4)^2=3^8
$$
The powers have to be equal:
$$
z=8
$$
$$
5^{(z+1)/3}=25^z=(5^2)^z=5^{2z}
$$
The powers have to be equal:
$$
dfrac{1}{3}z+dfrac{1}{3}=2z
$$
Subtract $dfrac{1}{3}z$ from both sides of the equation:
$$
dfrac{1}{3}=dfrac{5}{3}z
$$
Multiply both sides of the equation by $dfrac{3}{5}$:
$$
dfrac{1}{5}=z
$$
b. $z=frac{9}{7}$
c. $z=8$
d. $z=frac{1}{5}$
$$
AC=sqrt{(6-3)^2+(4-0)^2}=5=sqrt{(2-6)^2+(7-4)^2}=BC
$$
and the slope of $overline{AC}$is $dfrac{4-0}{6-3}=dfrac{4}{3}$ while the slope of $overline{BC}$ is $dfrac{2-6}{7-4}=-dfrac{3}{4}$, then we know that $overline{AC}$ and $overline{BC}$ are perpendicular (since the product of the slopes is $-1$).
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
mangle A=tan^{-1}dfrac{5}{5}=tan^{-1}1=45text{textdegree}
$$
c. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{45text{textdegree}}=dfrac{5}{5}=1
$$
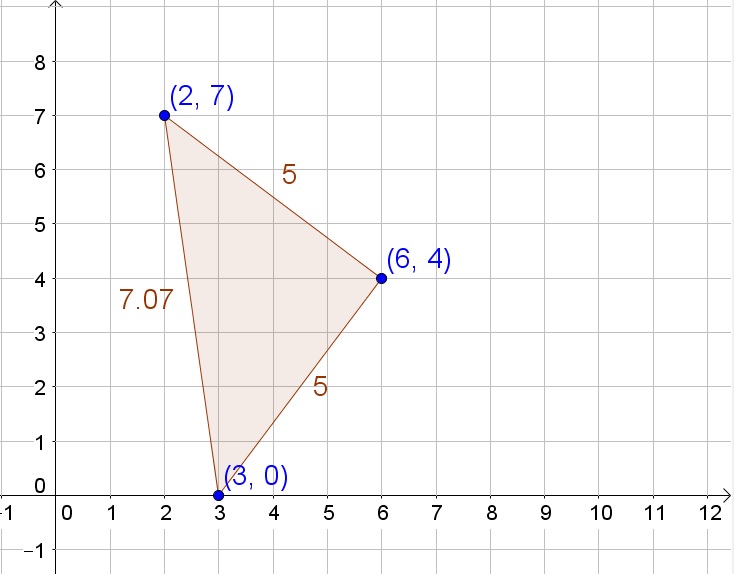
b. 45$text{textdegree}$
c. 1
$$
P(able)=dfrac{9+3}{9+3+36+12}=dfrac{12}{60}=dfrac{1}{5}=0.2=20%
$$
b. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(music AND able)=dfrac{3}{60}=dfrac{1}{20}=0.05=5%
$$
c. Use the multiplication rule:
$$
P(able GIVEN music)=dfrac{P(musicANDable)}{P(able)}=dfrac{39/60}{0.2}=0.13=13%
$$
Since this probability is not equal to $P(able)$ we then know that the events are NOT independent.
b. $frac{1}{20}=0.05=5%$
c.Not independent
BC=CD
$$
$$
AB=CE(text{ Pythagorean theorem})
$$
$$
angle Bcong angle C
$$
$$
Downarrow SAS
$$
$$
triangle ABCcong triangle ECD
$$
Since corresponding sides of congruent triangles are equal:
$$
x=41-9=32
$$
x=32
$$
$$
x=-dfrac{b}{2a}=-dfrac{5}{2(-1)}=dfrac{5}{2}=2.5
$$
The maximum value is then the corresponding $y$-value:
$$
y=-(2.5)^2+5(2.5)+6=12.25
$$
Thus we note that this maximum is higher than the maximum on the graph ($y=2$).
y=-x^2+5x+6
$$
$$
49=x^2+8x+16
$$
Factorize:
$$
49=(x+4)^2
$$
Take the square root of both sides of the equation:
$$
pm 7=x+4
$$
Subtract 4 from both sides of the equation:
$$
3text{ or }-11=-4pm 7=x
$$
$$
x^2-2x+1=-4
$$
Factorize:
$$
(x-1)^2=-4
$$
Take the square root of both sides of the equation:
$$
x-1=2i
$$
Add 1 to both sides of the equation:
$$
x=1+2i
$$
$$
x^2-7x+12.25=15.25
$$
Factorize:
$$
(x-3.5)^2=15.25
$$
Take the square root of both sides of the equation:
$$
x-3.5=pm sqrt{15.25}=pm 0.5sqrt{61}
$$
Add 3.5 to both sides of the equation:
$$
x=3.5pm 0.5sqrt{61}
$$
b. $x=1+2i$
c. $x=3.5pm 0.5sqrt{61}$
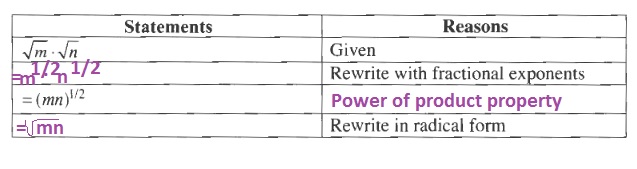
m^{1/2}n^{1/2}
$$
Power of product property
$$
sqrt{mn}
$$
$$
-5y=15x+10
$$
$$
2x+5y=16
$$
Add the two equations:
$$
2x=16+15x+10
$$
Subtract $15x$ from both sides of the equation:
$$
-13x=26
$$
Divide both sides of the equation by $-13$:
$$
x=-2
$$
Determine $y$:
$$
y=-3x-2=-3(-2)-2=6-2=4
$$
Thus the solution is $(-2,4)$.
(-2,4)
$$

