All Solutions
Page 211: Questions
a.
$$
(x+4)(x+y+1)=xy+4y+x^2+6x+8
$$
b.
$$
(6x-1)(3x+2)=18x^2+12x-3x-2=18x^2+9x-2
$$
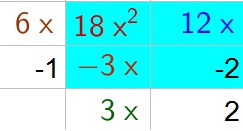
b. $(6x-1)(3x+2)=18x^2+12x-3x-2=18x^2+9x-2$
The area of the rectangle is the product of the length and the width of the rectangle. The area is also the sum of the subareas:
a.
$$
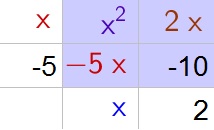
2x^2+7x+6=(2x+3)(x+2)
$$
b.
$$
6x^2+7x+2=(3x+2)(2x+1)
$$
c. Not possible, since the first term is $x^2$ both factor should contain $x$ and since the last term is 1 both factors should contain 1, but as you can see in the area model we then obtain the polynomial $x^2+2x+1$.
d.
$$
2xy+y^2+6x+3y=(2x+y)(y+3)
$$
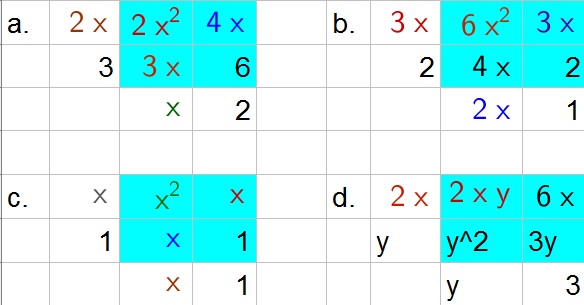
b. $(3x+2)(2x+1)$
c. Not factorable
d. $(2x+y)(y+3)$
a.
$$
(1+3x)(2x+5)=6x^2+17x+5
$$
b.
$$
(-2+5x)(y+3)=-2y-6+5xy+15x
$$
c.
$$
(-3+4x)(3x+4)=12x^2+7x-12
$$
Strategy: find the greatest common factors in every row and column and write these at the beginning of the row or the bottom of the column.
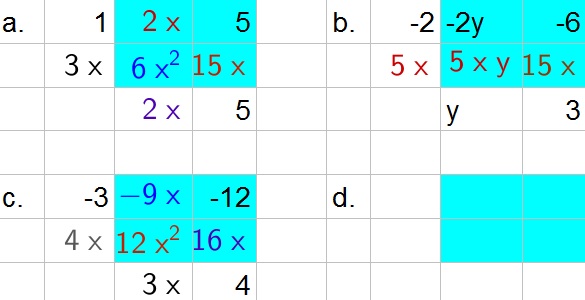
b. $(-2+5x)(y+3)=-2y-6+5xy+15x$
c. $(-3+4x)(3x+4)=12x^2+7x-12$
b. No, because we note that the the 2-by-2 area model in (b) does not fit this property due to the other variable $y$ being present.
b. No
a.
$$
(2x-3)(4x+1)=8x^2-12x+2x-3=8x^2-10x-3
$$
b.
$$
(4x-8)(4x-8)=16x^2-32x-32x+64=16x^2-64x+64
$$

b. $16x^2-64x+64$
$$
(-1+2x)(x+3y-5)=-11x-3y+5+2x^2+6xy
$$
(-1+2x)(x+3y-5)=-11x-3y+5+2x^2+6xy
$$
$$
4(x+2)
$$
b. The greatest common factor is 5:
$$
5(2x+5y+1)
$$
c. The greatest common factor is $2x$:
$$
2x(x-4)
$$
d. The greatest common factor is $3x$:
$$
3x(3xy+4+y)
$$
b. $5(2x+5y+1)$
c. $2x(x-4)$
d. $3x(3xy+4+y)$
$$
tan{17text{textdegree}}=dfrac{9.0}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{17text{textdegree}}=9.0
$$
Divide both sides of the equation by $tan{17text{textdegree}}$:
$$
x=dfrac{9.0}{tan{17text{textdegree}}}approx 29.4cm
$$
The hypotenuse can then be calculated by the Pythagorean theorem:
$$
c=sqrt{9.0^2+29.4^2}=sqrt{945.36}approx 30.7cm
$$
The perimeter is then the sum of all sides:
$$
9.0cm+30.7cm+29.4cm=69.1cm
$$
b. No function, because if you would draw a vertical line, then the graph will intersect it twice.
c. Function, because every $x$-value has exactly one corresponding $y$-value.
d. Function, because every $x$-value has exactly one corresponding $y$-value.
b. No function
c. Function
d. Function
$$
P(text{ student is female })=100%-P(male)=100%-25%=75%
$$
b. The probability of both events is the product of the probability of each event:
$$
P(maletext{ and } not walk)=P(male)cdot P(not walk)=25% cdot (100%-40%)=0.25cdot 0.6=0.15=15%
$$
c. Addition rule: $P(Atext{ or }B)=P(A)+P(B)-P(Atext{ and }B)$:
$$
P(walktext{ or } not walk)=P(walk)+P(not walk)-P(walktext{ and } not walk)=40%+60%-0%=100%
$$
d. (b) uses AND and is thus an intersection, (c) uses OR and is thus a union.
b. 15%
c. 100%
c. Union
a.
$$
(-7+2x)(5x-2)=10x^2-39x+14
$$
b. The bottom left corner contains the product of two terms and the upper right corner contains the product of two terms.
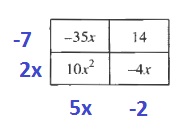
b. Yes
A quadratic expression in the form: $ax^2 + bx + c$, can be represented as a product of two binomial expressions as follows:
$$begin{gather}
ax^2 + bx + c &= (dx+e)(fx+g)
end{gather}$$
We are to use algebra tiles to obtain the factors of the expression $2x^2 + 5x +3$. We first obtain the factors of the expression using Eq (1) as follows:
$$begin{aligned}
ax^2 + bx + c &= (dx+e)(fx+g) \
2x^2 +5x+3 &= (2x+3)(x+1) \
2x^2 +5x+3 &= 2x^2 + 3x + 2x + 3 \
2x^2 +5x+3 &= 2x^2 +5x+3
end{aligned}$$

We the determine the area as a product as follows:
$$begin{aligned}
A_1 &= text{length} times text{width} \
&= (2x + 3) times (x+1) \
&= 2x^2+ 3x + 2x + 3 \
&= boxed{2x^2+5x +3}
end{aligned}$$
We are to use algebra tiles to obtain the factors of the expression $3x^2 + 10x +8$. We first obtain the factors of the expression using Eq (1) as follows:
$$begin{aligned}
ax^2 + bx + c &= (dx+e)(fx+g) \
3x^2 + 10x +8 &= (3x+4)(x+2) \
3x^2 + 10x +8 &= 3x^2 + 4x + 6x + 8 \
3x^2 + 10x +8&= 3x^2 +10x+8
end{aligned}$$

We then determine the area as a product as follows:
$$begin{aligned}
A_2 &= text{length} times text{width} \
&= (3x+4) times (x+2) \
&= 3x^2+ 4x + 6x + 8 \
&= boxed{3x^2+10x +8}
end{aligned}$$
We are to use algebra tiles to obtain the factors of the expression $2x^2 + 7x +6$. From Casey’s pattern for diagonals, we know that the product of the diagonals should be equal. Hence, we obtain the two values that would be equal to the product of the given diagonal as follows:
$$begin{aligned}
D_1 &= D_2 \
D_1 &= 2x^2 times 6 \
D_1 &= 12x^2 \
D_2 &= 3x times 4x \
D_2 &= 12x^2
end{aligned}$$
Hence, the missing values are $3x$ and $4x$
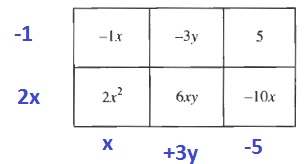
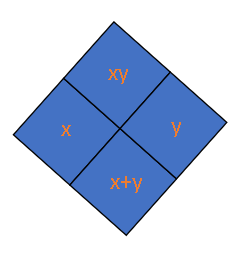
We know that a diamond problem has the form:

From the values in part (c), we set $x=3x$ and $y=4x$.

We then illustrate the area model using the values from part (c) as follows:

We then determine the area as a product as follows:
$$begin{aligned}
A_4 &= text{length} times text{width} \
&= (2x+3) times (x+2) \
&= 2x^2+ 4x + 3x + 6 \
&= boxed{2x^2+7x +6}
end{aligned}$$
A diamond problem has the form:
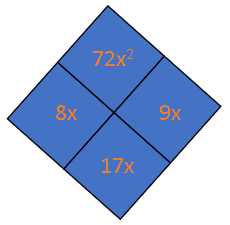
From the expression $6x^2 +17x +12$, we obtain the area model using the diamond problem to obtain the factors of the expression.
We first place the first and last term of the expression inside the diagonal as follows:

We then determine the missing values using Casey’s pattern

$$begin{aligned}
D_1 &= D_2 \
D_1 &= 6x^2 times 12 \
D_1 &= 72x^2 \
D_2 &= 8x times 9x \
D_2 &= 72x^2
end{aligned}$$
Hence, the missing values are $8x$ and $9x$
$$begin{aligned}
6x^2 +17x +12 &= (3x+4) (2x+3) \
6x^2 +17x +12 &= (3x cdot 2x) + 8x + 9x + 12 \
6x^2 +17x +12 &= 6x^2 + 17x + 12
end{aligned}$$
Therefore, the factors $(3x+4)(2x+3)$ yields the expression $6x^2 +17x +12$
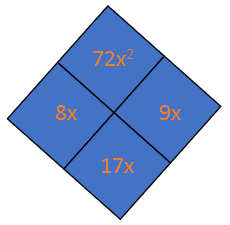
Given the trinomial $6x^2 + 17x + 12$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 6x^2 times 12 \
D_1 &= 72x^2 \
D_2 &= 8x times 9x \
D_2 &= 72x^2
end{aligned}$$
Hence, the missing values in the area model are $8x$ and $9x$
A diamond problem has the form:

The product $(xy)$ goes on the top, while the sum $(x+y)$ goes on the bottom.
We set-up the diamond problem by setting $x=8x$ and $y=9y$. The diamond problem is solved as follows:

Using the area model in part (c), we obtain the area of the rectangle as a product as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (3x+4) times (2x+3) \
&= (3x cdot 2x) + 8x + 9x + 12 \
&= boxed{6x^2 + 17x + 12}
end{aligned}$$
Given the trinomial $x^2 + 9x +18$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= x^2 times 18 \
D_1 &= 18x^2 \
D_2 &= 6x times 3x \
D_2 &= 18x^2
end{aligned}$$
Hence, the missing values in the area model are $3x$ and $6x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (x+6) times (x+3) \
&= x^2 + 6x + 3x + 18 \
&= x^2 + 9x+18
end{aligned}$$
Therefore, the factors $boxed{(x+6)(x+3)}$ yields the expression $x^2+9x+18$
Given the trinomial $4x^2 + 17x -15$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 4x^2 times (-15) \
D_1 &= -60x^2 \
D_2 &= 20x times (-3x) \
D_2 &= -60x^2
end{aligned}$$
Hence, the missing values in the area model are $20x$ and $-3x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (x+5) times (4x-3) \
&= 4x^2 + 20x – 3x -15 \
&= 4x^2 + 17x-15
end{aligned}$$
Therefore, the factors $boxed{(x+5)(4x-3)}$ yields the expression $4x^2 + 17x-15$
Given the trinomial $4x^2 – 8x +3$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 4x^2 times 3 \
D_1 &= 12x^2 \
D_2 &= -2x times -6x \
D_2 &= 12x^2
end{aligned}$$
Hence, the missing values in the area model are $-2x$ and $-6x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (2x-1) times (2x-3) \
&= 4x^2 – 2x – 6x +3 \
&= 4x^2 – 8x+3
end{aligned}$$
Therefore, the factors $boxed{(2x-1)(2x-3)}$ yields the expression $4x^2 – 8x+3$
Given the trinomial $3x^2 + 5x -3$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 3x^2 times (-3) \
D_1 &= -9x^2 \
D_2 &= -3x times 3x \
D_2 &= -9x^2
end{aligned}$$
Hence, the missing values in the area model are $-3x$ and $3x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (x+1) times (x-1) \
&= x^2 +x – x -1 \
&= x^2 – 1
end{aligned}$$
The result obtained is not equal to the original expression.
b. $(4x-3)(x+5)$
c. $(2x-1)(2x-3)$
d. Cannot be factored
$$begin{aligned}
ax^2+bx+c
end{aligned}$$
$$begin{aligned}
8x^2+2x-45
end{aligned}$$

| | |product|sum |
|–|–|–|–|
|-1 |360 |-360 |359 |
|-2 |180 |-360 |178 |
|-3 |120 |-360 |117 |
|-4 |90 |-360 |86 |
|-5 |72 |-360 |67 |
|-6 |60 |-360 |54 |
|-8 |45 |-360 |37 |
|-9 |40 |-360 |31 |
|-10 |36 |-360 |26 |
|-12 |30 |-360 |18 |
|-15 |24 |-360 |9 |
|-18 |20 |-360 |2 |
$$begin{aligned}
(2x+5)(4x-9)
end{aligned}$$
Given the trinomial $x^2 + 9x +18$, we place the first and last term of the expression in the area model as follows:

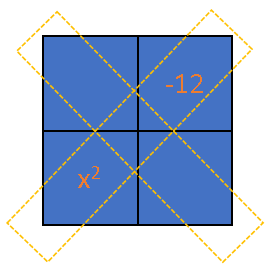
$$begin{aligned}
D_1 &= D_2 \
D_1 &= x^2 times (-12) \
D_1 &= -12x^2 \
D_2 &= 2x times (-6x) \
D_2 &= -12x^2
end{aligned}$$
Hence, the missing values in the area model are $2x$ and $-6x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (x-6) times (x+2) \
&= x^2 – 6x + 2x -12 \
&= x^2 – 4x-12
end{aligned}$$
Therefore, the factors $boxed{(x-6)(x+2)}$ yields the expression $x^2-4x-12$
Given the trinomial $2x^2 – 9x -5$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 2x^2 times (-5) \
D_1 &= -10x^2 \
D_2 &= x times (-10x) \
D_2 &= -10x^2
end{aligned}$$
Hence, the missing values in the area model are $x$ and $-10x$
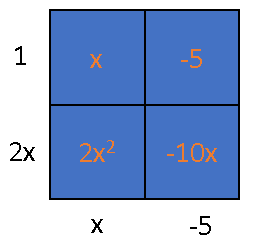
We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (x-5) times (2x+1) \
&= 2x^2 – 10x + x -5 \
&= 2x^2 – 9x-5
end{aligned}$$
Therefore, the factors $boxed{(x-5)(2x+1)}$ yields the expression $2x^2-9x-5$
Given the trinomial $4x^2 +4x +1$, we place the first and last term of the expression in the area model as follows:


$$begin{aligned}
D_1 &= D_2 \
D_1 &= 4x^2 times 1 \
D_1 &= 4x^2 \
D_2 &= 2x times 2x \
D_2 &= 4x^2
end{aligned}$$
Hence, the missing values in the area model are $2x$ and $2x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (2x+1) times (2x+1) \
&= 4x^2 +2x +2x+1 \
&= 4x^2 + 4x+1
end{aligned}$$
Therefore, the factors $boxed{(2x+1)(2x+1)}$ yields the expression $4x^2+4x+1$
Given the trinomial $3x^2 +10x -8$, we place the first and last term of the expression in the area model as follows:
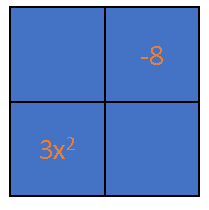

$$begin{aligned}
D_1 &= D_2 \
D_1 &= 3x^2 times (-8) \
D_1 &= -24x^2 \
D_2 &= 12x times (-2x) \
D_2 &= -24x^2
end{aligned}$$
Hence, the missing values in the area model are $12x$ and $-2x$

We obtain the area of the rectangle be getting the product of the length and width as follows:
$$begin{aligned}
A &= text{length} times text{width} \
&= (3x-2) times (x+4) \
&= 3x^2 +12x -2x-8 \
&= 3x^2 + 10x-8
end{aligned}$$
Therefore, the factors $boxed{(x+4)(3x-2)}$ yields the expression $3x^2+10x-8$
b. $(2x-1)(x+5)$
c. $(2x+1)(2x+1)$
d. $(3x-2)(x+4)$
$$
tan{68text{textdegree}}=dfrac{x}{15}
$$
Multiply both sides of the equation by $15$:
$$
37.1approx 15tan{68text{textdegree}}=x
$$
Add the height of Mary’s eyes with respect to the ground to the found height:
$$
37.1’+32’=69.1′
$$

a.
$$
EV=9cdot dfrac{1}{12}+4cdot dfrac{11}{12}=dfrac{9}{12}+dfrac{44}{12}=dfrac{53}{12}approx 4.42
$$
b.
$$
EV=12cdot 1=12
$$
b. 12
$$
angle E=angle Gtext{ alternate interior angles}
$$
$$
angle H=angle Ftext{ alternate interior angles}
$$
$$
Downarrow AA
$$
$$
triangle EHZsim triangle GFZ
$$
b. Corresponding sides of similar triangles are proportional:
$$
dfrac{x}{20}=dfrac{x+2}{24}
$$
Use cross multiplication:
$$
24x=20(x+2)
$$
Use distributive property:
$$
24x=20x+40
$$
Subtract $20x$ from both sides of the equation:
$$
4x=40
$$
Divide both sides of the equation by $4$:
$$
x=10
$$
b. $x=10$
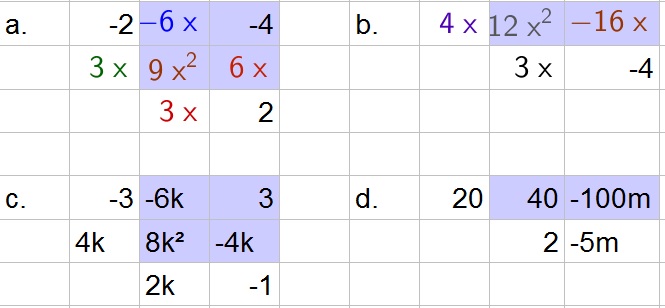
a.
$$
x^2+6x+9=(x+3)(x+3)
$$
b.
$$
2x^2+5x+3=(2x+3)(x+1)
$$
c. Not possible to factor using only integers.
d.
$$
3m^2+m-14=(3m+7)(m-2)
$$

b. $(2x+3)(x+1)$
c. Not favorable
c. $(3m+7)(m-2)$
a. We note that a term of the form $a^2-b^2$ can be factored as $(a-b)(a+b)$:
$$
9x^2=(3x-2)(3x+2)
$$
b. Factor out the greatest common factor:
$$
12x^2-16x=4x(3x-4)
$$
c.
$$
8k^2-10k+3=(4k-3)(2k-1)
$$
d. Factor out the greatest common factor:
$$
40-100m=20(2-5m)
$$
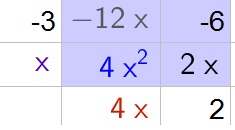
b. $4x(3x-4)$
c. $(4k-3)(2k-1)$
d. $20(2-5m)$
$$
4x^2-10x-6=(x-3)(4x+2)
$$
However, you can also factor out 2 from the last factor:
$$
4x^2-10x-6=2(x-3)(x+1)
$$
Thus we note that it was possible to find more than one factorization.

$$
(x+7+3x+1)(x-2+2x+1)=x^2+5x-14+2x^2+15x+7+3x^2-5x-2+6x^2+5x+1
$$
Combine like terms:
$$
(4x+8)(3x-1)=12x^2+20x-8
$$
(4x+8)(3x-1)=12x^2+20x-8
$$
a.
$$
k^2-12k+20=(k-10)(k-2)
$$
b.
$$
6x^2+17x-14=(3x-2)(2x+7)
$$
c.
$$
x^2-8x+16=(x-4)(x-4)=(x-4)^2
$$
d.
$$
9m^2-1=(3m-1)(3m+1)
$$
e. Each expression is quadratic because they contain the square of a variable.
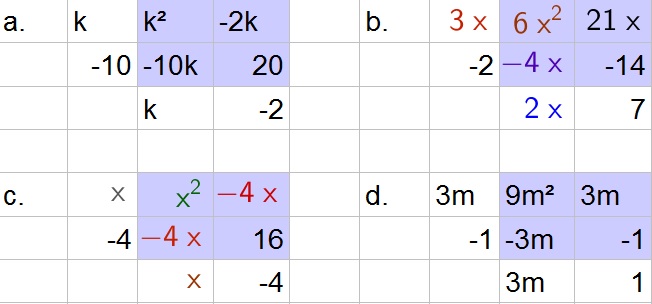
b. $(3x-2)(2x+7)$
c. $(x-4)^2$
d. $(3m-1)(3m+1)$
e. All are quadratic (due to the square in each expression)
$$
tan{80text{textdegree}}=dfrac{x}{58}
$$
Multiply both sides of the equation by $58$:
$$
329approx 58tan{80text{textdegree}}=x
$$
Add the eye level to the height: $329+1.5=330.5m$
$$
dfrac{x+5}{5}=dfrac{10}{4}
$$
Multiply both sides of the equation by 5:
$$
x+5=dfrac{10cdot 5}{4}=12.5
$$
Subtract 5 from both sides of the equation:
$$
x=7.5
$$
x=7.5
$$
a.
$$
dfrac{14+10}{9+14+10+7}=dfrac{24}{40}=dfrac{3}{5}=0.6=60%
$$
b. Let $x$ be the total number of fish:
$$
dfrac{18}{x}=30%=0.3
$$
Multiply both sides of the equation by $x$:
$$
18=0.3x
$$
Divide both sides of the equation by 0.3:
$$
60=x
$$
Thus there are 60 fish in total.
b. 60 fish
a. Upper: $dfrac{1}{2}cdot dfrac{1}{2}=dfrac{1}{4}$ and Lower: $dfrac{1}{2}+dfrac{1}{2}=1$
b. Upper: $dfrac{1}{3}cdot dfrac{3}{4}=dfrac{1}{4}$ and Lower: $dfrac{1}{3}+dfrac{3}{4}=dfrac{4}{12}+dfrac{9}{12}=dfrac{13}{12}$
c. Upper: $xcdot x=x^2$ and Lower: $x+x=2x$
d. Upper: $acdot b=ab$ and Lower: $a+b$
b. $frac{1}{4}$, $frac{13}{12}$
c. $x^2$, $2x$
d. $ab$, $a+b$
$$
(3x^3-3x^3)+(-2x^2-5x^2)+(4-(-2))
$$
Simplify:
$$
-7x^2+6
$$
a. Terms are separated by a + (or -) sign and thus the (simplified) expression contains 2 terms.
b. We note that the expression contains no $x$ term and thus the coefficient is 0.
b. 0
a.
$$
9x^2-12x+4=(3x-2)(3x-2)=(3x-2)^2
$$
b.
$$
81m^2-1=(9m-1)(9m+1)
$$
c.
$$
x^2-11x+28=(x-7)(x-4)
$$
d.
$$
3n^2+9n+6=(3n+3)(3n+2)
$$

b. $(9m-1)(9m+1)$
c. $(x-7)(x-4)$
d. $(3n+3)(3n+2)$
$$
3n^2+9n+6=(3n+3)(n+2)
$$
You could also factor out the 3 in the first factor:
$$
3n^2+9n+6=3(n+1)(n+2)
$$
b. Because the expression has a greatest common factor that is not 1.
c. (i) More than one, because 2 is the greatest compmon factor
(ii) Not more than one, because 1 is the greatest common factor
(iii) More than one, because 5 is the greatest compmon factor
(iv) Not more than one, because 1 is the greatest common factor
b. Greatest common factor is not 1.
c. (i) More than 1 (ii) Not more than 1 (iii) More than 1 (iv) Not more than 1
$$
10x^2+25x-15=5(2x^2+5x-3)
$$
b.
$$
10x^2+25x-15=5(2x^2+5x-3)=5(2x-1)(x+3)
$$
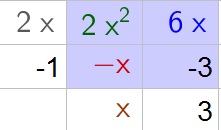
b. $5(2x-1)(x+3)$
$$
5x^2+15x-20=5(x^2+3x-4)
$$
Factor further using an area model:
$$
5x^2+15x-20=5(x^2+3x-4)=5(x-1)(x+4)
$$
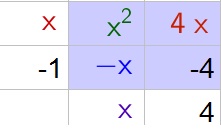
$$
3x^3-6x^2-45x=3x(x^2-2x-15)
$$
Factor further using an area model:
$$
3x^3-6x^2-45x=3x(x^2-2x-15)=3(x-5)(x+3)
$$
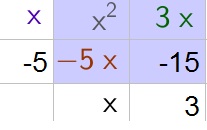
$$
2x^2-50=2(x^2-25)
$$
Factor further using an area model:
$$
2x^2-50=2(x^2-25)=2(x-5)(x+5)
$$
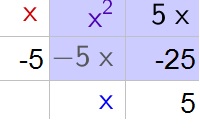
$$
x^2y-3xy-10y=y(x^2-3x-10)
$$
Factor further using an area model:
$$
x^2y-3xy-10y=y(x^2-3x-10)=y(x-5)(x+2)
$$
b. $3(x-5)(x+3)$
c. $2(x-5)(x+5)$
d. $y(x-5)(x+2)$
$$
7+(-3)=4
$$
$$
7-(-3)=10
$$
$$
4+9=13
$$
$$
4-9=-5
$$
b. Because adding two integers will be an integer too (it cannot become a rational number) and subtracting two integers will also be an integer.
c. The integers are closed under multiplication, because the product of two integers is an integer too. The integers are NOT closed under division, because the division of some integers will result in a rational number.
$$
2cdot 7=14
$$
$$
3cdot 4=12
$$
$$
4div 2=dfrac{4}{2}=2
$$
$$
4div 3=dfrac{4}{3}
$$
b. Adding/subtracting two integers always results in an integer
c. Yes, No
a.
$$
2x^2+3x-5=(2x+5)(x-1)
$$
b.
$$
x^2-x-6=(x-3)(x+2)
$$
c.
$$
3x^2+13x+4=(3x+1)(x+4)
$$
d. Not possible, it would however be possible it the coefficient of $x$ would be $-5$ in stead of 5.
e.
$$
7x^2-7x-42=(7x-21)(x+2)=7(x-3)(x+2)
$$
f.
$$
6x^2+26x+8=(6x+2)(x+4)=2(3x+1)(x+4)
$$

b. $(x-3)(x+2)$
c. $(3x+1)(x+4)$
d. Not factorable
e. $(7x-21)(x+2)$
f. $(6x+2)(x+4)$
If you add two odd numbers, then the sum is even and thus the set of odd numbers is not closed under addition.
$$
dfrac{x}{10}=dfrac{30}{12}=2.5
$$
Multiply both sides of the equation by 10:
$$
x=25
$$
b. The area of a rectangle is the product of the length and the width:
$$
First: 10cdot 4=40
$$
$$
Second: 25cdot 10=250
$$
The area of a triangle isthe product of the base and the height divided by 2:
$$
First: dfrac{4cdot 8}{2}=16
$$
$$
Second: dfrac{10cdot 20}{2}=100
$$
The total area is then the sum of the subareas:
$$
First: 40+16=56
$$
$$
Second: 250+100=350
$$
b. First polygon 56 and Second polygon 350
$$
dfrac{x+13}{13}=dfrac{8+5}{8}=dfrac{13}{8}
$$
Multiply both sides of the equation by 13:
$$
x+13=dfrac{169}{8}
$$
Subtract 13 from both sides of the equation:
$$
x=dfrac{65}{8}=8.125
$$
$$
dfrac{x}{8}=dfrac{8}{6}=dfrac{4}{3}
$$
Multiply both sides of the equation by 8:
$$
x=dfrac{32}{3}
$$
b. Cannot be determined
c. $x=frac{32}{3}$
$$
4cdot 3=12
$$
b. Yes, because every main dish has an equal chance of being chosen and every dessert has an equal chance of being chosen.
c. The probability is the number of favorable outcomes divided by the total number of possible outcomes.
The probability to pick a menu without meat is then:
$$
dfrac{2}{4}cdot dfrac{3}{3}=dfrac{6}{12}=dfrac{1}{2}=0.5=50%
$$
The probability to pick a menu with chocalate is then:
$$
dfrac{4}{4}cdot dfrac{2}{3}=dfrac{2}{3}approx 0.667=66.7%
$$
b. Yes
c. $frac{1}{2}=0.5=50%$, $frac{2}{3}approx 0.667=66.7%$
If an expression of the form $a^2-2ab+b^2$ then the factorization is $(a-b)^2$.
If an expression of the form $a^2+2ab+b^2$ then the factorization is $(a+b)^2$.
a. $x^2-49=(x-7)(x+7)$
b. $x^2+2x-24=(x+6)(x-4)$
c. $x^2-10x+25=(x-5)(x-5)=(x-5)^2$
d. $9x^2+12x+4=(3x+2)(3x+2)=(3x+2)^2$
e. $5x^2-4x-1=(x-1)(5x+1)$
f. $4x^2-25=(2x-5)(2x+5)$
g. $x^2-6x+9=(x-3)(x-3)=(x-3)^2$
h. $x^2-36=(x-6)(x+6)$
i. $7x^2-20x-3=(7x+1)(x-3)$
j. $4x^2+20x+25=(2x+5)(2x+5)=(2x+5)^2$
k. $x^2+4$ not factorable
l. $9x^2-1=(3x-1)(3x+1)$
b. $(x+6)(x-4)$
c. $(x-5)^2$
d. $(3x+2)^2$
e. $(x-1)(5x+1)$
f. $(2x-5)(2x+5)$
g. $(x-3)^2$
h. $(x-6)(x+6)$
i. $(7x+1)(x-3)$
j. $(2x+5)^2$
k. Not factorable
l. $(3x-1)(3x+1)$
If an expression is of the form $a^2-2ab+b^2$ then the factorization is $(a-b)^2$.
If an expression is of the form $a^2+2ab+b^2$ then the factorization is $(a+b)^2$.
If an expression is of the form $x^2+(a+b)x+(ab)$ then the factorization is $(x+a)(x+b)$.
a. $25x^2-1=(5x-1)(5x+1)$
b. $x^2-5x+36=(x-9)(x+4)$
c. $x^2+8x+16=(x+4)^2$
d. $9x^2-12x+4=(3x-2)^2$
e. This expression does not contain one of the patterns and is also not factorable.
f. $9x^2-100=(3x-10)(3x+10)$
b. $(x-9)(x+4)$
c. $(x+4)^2$
d. $(3x-2)^2$
e. Not factorable
f. $(3x-10)(3x+10)$
a.
$$
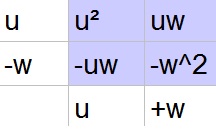
u^2-x^2=(u-w)(u+w)
$$
$$
u^2+2uw+w^2=(u+w)(u+w)=(u+w)^2
$$
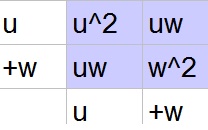
b. $u^2+2uw+w^2=(u+w)(u+w)=(u+w)^2$
$$
(x^2+4x+8)+(4x^2+3x+7)=5x^2+7x+15
$$
$$
(4x+8)+(3x+7)=7x+15
$$
If you subtract two polynomials, you obtain another polynomial and thus the set of polynomials is closed under subtraction:
$$
(x^2+4x+8)-(4x^2+3x+7)=-3x^2+x+1
$$
$$
(4x+8)+(3x+7)=x+1
$$
b. Because the sum and difference of polynomial will always remain of the same form and will thus remain a polynomial.
b. Because the sum and difference of polynomial will always remain of the same form and will thus remain a polynomial.
If an expression is of the form $a^2-2ab+b^2$ then the factorization is $(a-b)^2$.
If an expression is of the form $a^2+2ab+b^2$ then the factorization is $(a+b)^2$.
If an expression is of the form $x^2+(a+b)x+(ab)$ then the factorization is $(x+a)(x+b)$.
The special products have the following forms:
$$begin{gather}
(a^2-b^2) = (a+b)(a-b) \
(a^2+2ab+b^2) = (a+b)^2 \
(a^2-2ab+b^2) = (a+b)^2
end{gather}$$
We factor the polynomial $x^2-64$ using Eq (1) as follows:
$$begin{aligned}
(a^2-b^2) &= (a+b)(a-b) \
x^2 – 64 &= (x+b)(x-b) \
x^2 – 64 &= (x+8)(x-8) \
end{aligned}$$
Hence, the factors $(x+8)(x-8)$ yields the polynomial $x^2-64$
We factor the polynomial $x^2-6x+9$ using Eq (3) as follows:
$$begin{aligned}
(a^2-2ab+b^2) &= (a-b)^2 \
x^2 – 6x+9 &= (x-b)^2 \
x^2 – 6x+9 &= (x-3)^2 \
end{aligned}$$
Hence, the factors $(x-3)(x-3)$ yields the polynomial $x^2 – 6x+94$
We factor the polynomial $4x^2+4x+1$ using Eq (2) as follows:
$$begin{aligned}
(a^2+2ab+b^2) &= (a+b)^2 \
4x+4x+1 &= (2x+b)^2 \
4x+4x+1 &= (2x+1)^2 \
end{aligned}$$
Hence, the factors $(2x+1)(2x+1)$ yields the polynomial $4x+4x+1$
We factor the polynomial $4x^2-49$ using Eq (1) as follows:
$$begin{aligned}
(a^2-b^2) &= (a+b)(a-b) \
4x^2 – 49 &= (2x+b)(2x-b) \
4x^2 – 49 &= (2x+7)(2x-7) \
end{aligned}$$
Hence, the factors $(2x+7)(2x-7)$ yields the polynomial $4x^2 – 49$
b. $(x-3)(x-3)$
c. $(2x+1)(2x+1)$
d. $(2x-7)(2x+7)$
$$begin{aligned}
W=2,3,5,7,11,13,17,….
end{aligned}$$
$$begin{aligned}
2+3&=5enspacetext{textcolor{#4257b2}{(prime number)}}\
2+5&=7enspacetext{textcolor{#4257b2}{(prime number)}}\
2+7&=9enspacetext{textcolor{#4257b2}{(not a prime number)}}\
end{aligned}$$
The Pythagorean theorem can be used to determine the relationship between the sides of the triangle. This can be described by the expression:
$$begin{gather}
c^2 = a^2 + b^2
end{gather}$$
We are given with the following figure:

Determine the area and perimeter of the figure
We determine the area of the figure by separating the figure into two parts: triangle and rectangle. We first calculate for the area of the rectangle as follows:
$$begin{aligned}
A_{text{square}} &= text{length} times text{width} \
&= 16.0 times 18.0 \
&= 288 text{ m}^2
end{aligned}$$
$$begin{aligned}
h &= 24.0 – 18.0 \
h &= 6.0
end{aligned}$$
$$begin{aligned}
tan theta &= frac{text{opposite}}{text{adjacent}} \
text{opposite} &= text{adjacent} cdot tan theta \
b &= h cdot tan theta \
b &= (6.0) cdot tan (20^circ) \
b &= 2.18 text{ m}
end{aligned}$$
$$begin{aligned}
A_{text{triangle}} &= frac{1}{2}bh \
&= frac{1}{2} (2.18) cdot (6.0) \
&= boxed{6.54 text{ m}^2}
end{aligned}$$
$$begin{aligned}
A_{text{total}} &= A_{text{square}} + A_{text{triangle}} \
&= 288+ 6.54 \
&= boxed{294.54 text{ m}^2}
end{aligned}$$
We can determine the perimeter of the figure by adding the lengths of the sides of the figure. We already have the values of the three sides of the figure, we still have to determine the other two sides on the top.
$$begin{aligned}
l &= 16.0 – b_{text{triangle}} \
&= 16.0 – 2.8 \
&= 13.2 text{ m}
end{aligned}$$
$$begin{aligned}
c^2 &= a^2 + b^2 \
c &= sqrt{a^2 + b^2} \
c &= sqrt{b^2 + h^2} \
c &= sqrt{(2.8)^2 + (6.0)^2} \
c &=6.62 text{ m}
end{aligned}$$
Hence, the length of the remaining side is $6.62 text{ m}$
$$begin{aligned}
P &= 24.0 + 16.0 + 18.0 + 6.62 + 13.2 \
& boxed{P = 77.82 text{ m}}
end{aligned}$$
The perimeter of the figure is $77.82 text{ m}$
$P = 77.82 text{ m}$
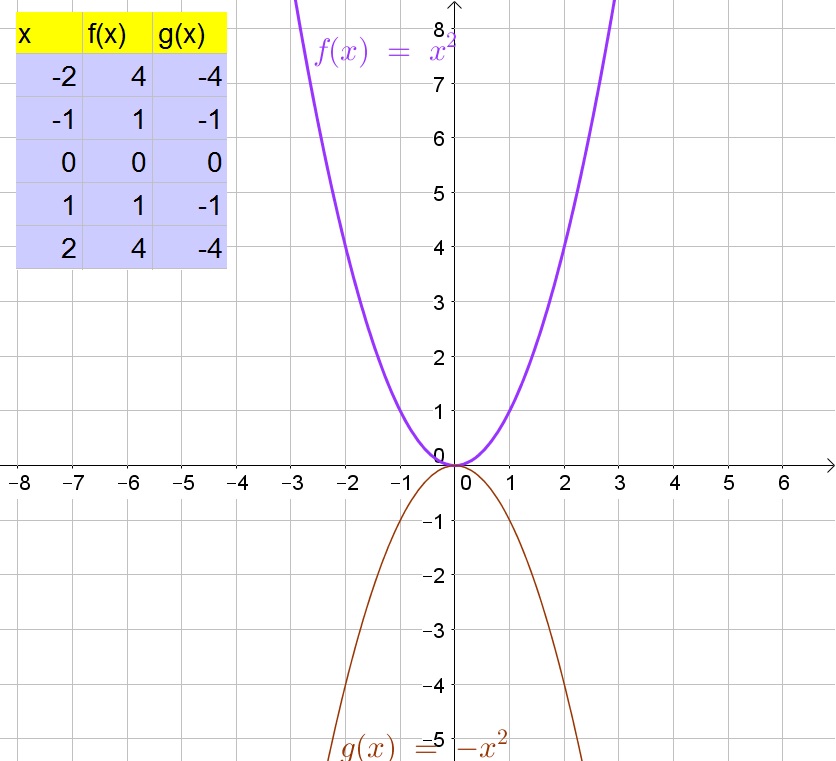
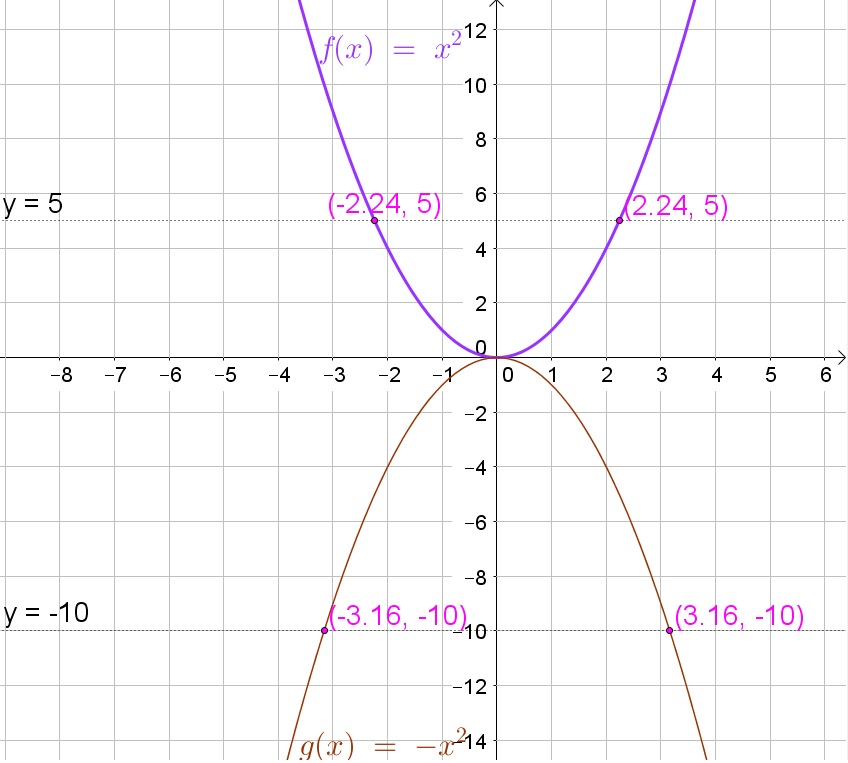
d. On the graph we note $xapprox pm 2.24$.
e. On the graph we note $xapprox pm 3.16$.
b. Use the addition rule:
$$
P(Atext{ or B})=P(A)+P(B)-P(Atext{ and }B)=dfrac{12}{36}+dfrac{9}{36}-dfrac{1}{36}=dfrac{20}{36}=dfrac{5}{9}approx 0.555=55.5%
$$
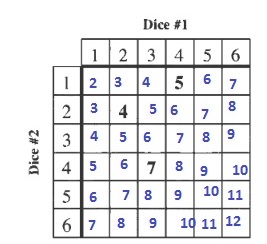
b. 55.5%
b. Isosceles triangle
c. Not possible
d. Equilateral triangle
$$
Delta y=sqrt{6^2-3^2}=sqrt{27}=3sqrt{3}approx 5.2
$$
METHOD 2: The tangent ratio is the opposite side divided by the afjacent rectangular side:
$$
tan{60text{textdegree}}=dfrac{Delta y}{3}
$$
Multiply both sides of the equation by 3:
$$
5.2approx 3tan{60text{textdegree}}=Delta y
$$
b. The ratios must be equal, because the triangle are similar (SAS).
$$
dfrac{Delta x}{hypotenuse}=dfrac{1}{2}=dfrac{3}{6}=dfrac{1}{2}
$$
c. The ratio of $Delta x$ to the hypotenuse should be equal to $dfrac{1}{2}$:
$$
dfrac{BC}{7}=dfrac{1}{2}
$$
Multiply both sides of the equation by 7:
$$
BC=dfrac{7}{2}
$$
Determine $AC$ using the Pythagorean theorem:
$$
AC=sqrt{7^2-left( dfrac{7}{2}right)^2}=sqrt{dfrac{147}{4}}=dfrac{sqrt{147}}{2}
$$
b. $frac{1}{2}$
c. $BC=frac{7}{2}$ and $AC=frac{sqrt{147}}{2}$
$$
sin{60text{textdegree}}approx 0.866
$$
$$
cos{60text{textdegree}}=0.5
$$
b. The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{23text{textdegree}}=dfrac{a}{15}
$$
Multiply both sides of the equation by 15:
$$
5.86approx 15sin{23text{textdegree}}=a
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{37text{textdegree}}=dfrac{b}{8}
$$
Multiply both sides of the equation by 8:
$$
4.81approx 8cos{37text{textdegree}}=b
$$
b. Sine ratio, $a=5.86$
b. $b=4.81$
$$
sin{31.5text{textdegree}}=dfrac{Delta y}{100}
$$
Multiply both sides of the equation by 100:
$$
52.25approx 100sin{31.5text{textdegree}}=Delta y
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{31.5text{textdegree}}=dfrac{Delta x}{100}
$$
Multiply both sides of the equation by 100:
$$
85.26approx 100cos{31.5text{textdegree}}=Delta x
$$
Delta yapprox 52.25ft
$$
$$
Delta xapprox 85.26ft
$$
$$
cos{17text{textdegree}}=dfrac{3}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcos{17text{textdegree}}=3
$$
Divide both sides of the equation by $cos{17text{textdegree}}$:
$$
x=dfrac{3}{cos{17text{textdegree}}}approx 3.14
$$
$$
sin{25text{textdegree}}=dfrac{x}{9}
$$
Multiply both sides of the equation by 9:
$$
3.8approx 9sin{25text{textdegree}}=x
$$
$$
tan{45text{textdegree}}=dfrac{x}{5}
$$
Multiply both sides of the equation by 5:
$$
5=5tan{45text{textdegree}}=x
$$
$$
tan{62text{textdegree}}=dfrac{5}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{62text{textdegree}}=5
$$
Divide both sides of the equation by $tan{62text{textdegree}}$:
$$
x=dfrac{5}{tan{62text{textdegree}}}approx 2.66
$$
$$
sin{34text{textdegree}}=dfrac{13}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{34text{textdegree}}=13
$$
Divide both sides of the equation by $sin{34text{textdegree}}$:
$$
x=dfrac{13}{sin{34text{textdegree}}}approx 23.25
$$
$$
cos{20text{textdegree}}=dfrac{10}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcos{20text{textdegree}}=10
$$
Divide both sides of the equation by $cos{20text{textdegree}}$:
$$
x=dfrac{10}{cos{20text{textdegree}}}approx 10.64
$$
b. $x=3.8$
c. $x=5$
d. $x=2.66$
e. $x=23.25$
f. $x=10.64$
The sine ratio is the opposite side divided by the hypotenuse.
The tangent ratio is the opposite side divided by the adjacent rectangular side.
The Pythagorean theorem states that the sum of the squares of the legs is equal to the square of the hypotenuse:
$$
a^2+b^2=c^2
$$
$$
sin{47text{textdegree}}=dfrac{y}{11}
$$
Multiply both sides of the equation by 11:
$$
8.04approx 11sin{47text{textdegree}}=y
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{47text{textdegree}}=dfrac{x}{11}
$$
Multiply both sides of the equation by 11:
$$
7.5approx 11cos{47text{textdegree}}=x
$$
yapprox 8.04
$$
$$
xapprox 7.5
$$
$$
sin{theta}=dfrac{b}{a}
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side.
$$
tan{theta}=dfrac{a}{b}
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse.
$$
cos{theta}=dfrac{a}{b}
$$
b. $tan{theta}=dfrac{a}{b}$
c. $cos{theta}=dfrac{a}{b}$
a. $6x^2+5x-6=(3x-2)(2x+3)$
b. $8x^2-50=2(4x^2-25)=2(2x-5)(2x+5)$
c. $2x^3+2x^2-112x=2x(x^2+x-56)=2x(x+8)(x-7)$
d. $9x^2-24x+16=(3x-4)(3x-4)=(3x-4)^2$
b. $2(2x-5)(2x+5)$
c. $2x(x+8)(x-7)$
d. $(3x-4)^2$
$$
ED=EF
$$
b. Let us first determine the height of the triangle. We note that the height is the opposite side of the angle 54$text{textdegree}$ in a right triangle. The sine ratio is the length of the opposite side divided by the length of the hypotenuse in a right triangle.
$$
sin(54text{textdegree})=frac{text{Height}}{DE}
$$
Solve the equation to the height:
$$
begin{align*}
text{Height}&=DEcdot sin (54text{textdegree})=9sin (54text{textdegree})approx 7.2812
end{align*}
$$
Next, we determine $x$ using the Pythagorean theorem $a^2+b^2=c^2$ (where $x$ is half the length of $overline{DF}$).
$$
begin{align*}
x&=sqrt{ED^2-text{Height}^2}=sqrt{9^2-7.2812^2}approx 5.2900
end{align*}
$$
Finally, the length of $overline{DF}$ is twice $x$:
$$
DF=2x=2(5.2900)=10.5800
$$
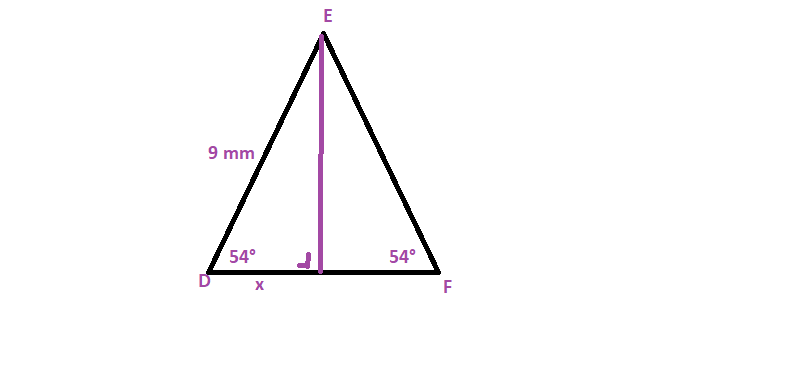
b. $DF=10.5800$ mm
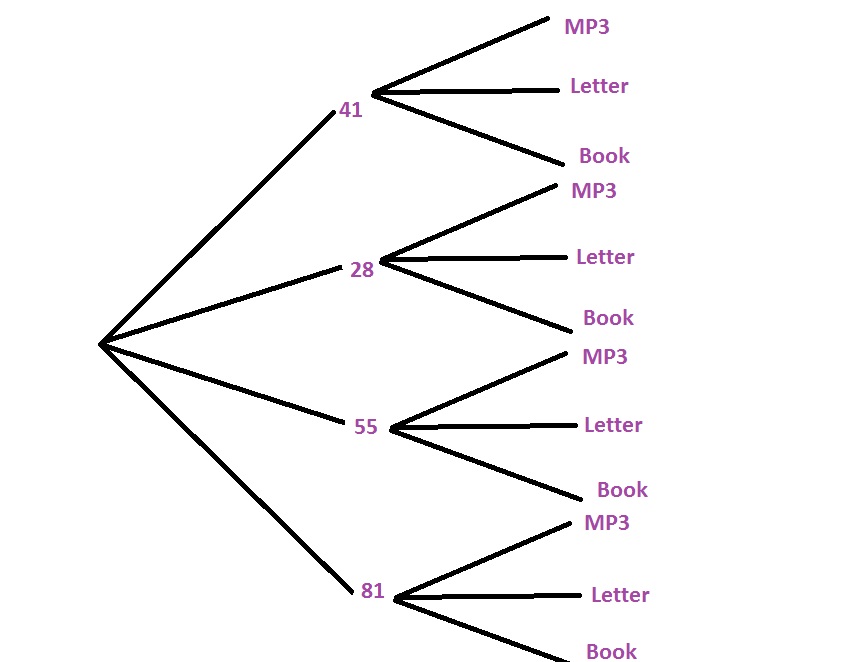
(i)
$$
P(odd)=dfrac{3}{4}=0.75=75%
$$
(ii)
$$
P(text{Not letter})=dfrac{2}{3}approx 0.667=66.7%
$$
(iii)
$$
P(28text{ and }book)=dfrac{1}{4}cdot dfrac{1}{3}=dfrac{1}{12}approx 0.083=8.3%
$$
(iv)
$$
P(text{Not read})=dfrac{2}{3}approx 0.667=66.7%
$$
c. No, because the activities were randomly chosen.
b.
(i) $frac{3}{4}=0.75=75%$
(ii) $frac{2}{3}approx 0.667=66.7%$
(iii) $frac{1}{12}approx 0.083=8.3%$
(iv) $frac{2}{3}approx 0.667=66.7%$
c. No
$$
dfrac{2}{4}=frac{1}{2}=0.5=50%
$$
b. $frac{1}{2}=0.5=50%$
$$
sin{28text{textdegree}}=dfrac{x}{19}
$$
Multiply both sides of the equation by 19:
$$
8.92approx 19sin{28text{textdegree}}=x
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{45text{textdegree}}=dfrac{8}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{45text{textdegree}}=8
$$
Divide both sides of the equation by $tan{45text{textdegree}}$
$$
x=dfrac{8}{tan{45text{textdegree}}}=8
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{61text{textdegree}}=dfrac{18}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcos{61text{textdegree}}=18
$$
Divide both sides of the equation by $cos{61text{textdegree}}$:
$$
x=dfrac{18}{cos{61text{textdegree}}}approx 37.13
$$
$$
sin{25text{textdegree}}=dfrac{6}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{25text{textdegree}}=6
$$
Divide both sides of the equation by $sin{34text{textdegree}}$:
$$
x=dfrac{6}{sin{25text{textdegree}}}approx 14.2
$$
e. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{60text{textdegree}}=dfrac{8}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcos{60text{textdegree}}=8
$$
Divide both sides of the equation by $cos{60text{textdegree}}$:
$$
x=dfrac{8}{cos{60text{textdegree}}}=16
$$
f. The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{30text{textdegree}}=dfrac{x}{42}
$$
Multiply both sides of the equation by 42:
$$
21=42sin{30text{textdegree}}=x
$$
h. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{73text{textdegree}}=dfrac{x}{3}
$$
Multiply both sides of the equation by $3$:
$$
0.88approx 3cos{73text{textdegree}}=x
$$
i. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{42text{textdegree}}=dfrac{x}{12}
$$
Multiply both sides of the equation by $12$:
$$
10.8approx 12tan{42text{textdegree}}=x
$$
b. $x=8$
c. $x=37.13$
d. $x=14.2$
e. $x=16$
f. $x=21$
g. Triangle doesn’t exist
h. $x=0.88$
i. $x=10.8$
b.
$$
x=dfrac{29}{sin{25text{textdegree}}}approx 68.62
$$
c. Because Ziv used the other angle in the triangle and the cosine is the adjacent rectangular side divided by the hypotenuse.
d. METHOD 1: The sine ratio is the opposite side divided by the hypotenuse.
$$
sin{53text{textdegree}}=dfrac{y}{5}
$$
Multiply both sides of the equation by 5:
$$
3.99approx 5sin{53text{textdegree}}=y
$$
METHOD 2: The sum of all angles in a triangle is 180$text{textdegree}$:
$$
180text{textdegree}-53text{textdegree}-90text{textdegree}=37text{textdegree}
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse.
$$
cos{37text{textdegree}}=dfrac{y}{5}
$$
Multiply both sides of the equation by 5:
$$
3.99approx 5cos{37text{textdegree}}=y
$$
b. 68.62
c. Because Ziv used the other angle in the triangle and the cosine is the adjacent rectangular side divided by the hypotenuse.
d. $y=3.99$
$$
tan{theta}=dfrac{9}{9}=1
$$
We then know that $theta=45text{textdegree}$.
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{theta}=dfrac{1}{5}
$$
We then know that $theta=11text{textdegree}$.
c. The cosine ratio is the opposite side divided by the adjacent rectangular side:
$$
cos{theta}=dfrac{5}{10}=dfrac{1}{2}
$$
We then know that $theta=60text{textdegree}$.
b. $theta=11text{textdegree}$
c. $theta=60text{textdegree}$
You decide which one to choose based on which sides are given or based on which side has been given plus which side you are looking for.
The cosine ratio is the adjacent rectangular side divided by the hypotenuse.
The sine ratio is the opposite side divided by the hypotenuse.
The tangent ratio is the opposite side divided by the adjacent rectangular side.
The cosine ratio is the adjacent rectangular side divided by the hypotenuse.
The sine ratio is the opposite side divided by the hypotenuse.
The tangent ratio is the opposite side divided by the adjacent rectangular side.
$$
sin{22text{textdegree}}=dfrac{x}{17}
$$
Multiply both sides of the equation by 17:
$$
6.37approx 17sin{22text{textdegree}}=x
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{49text{textdegree}}=dfrac{7}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{49text{textdegree}}=7
$$
Divide both sides of the equation by $tan{49text{textdegree}}$:
$$
x=dfrac{7}{tan{49text{textdegree}}}
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{60text{textdegree}}=dfrac{x}{6}
$$
Multiply both sides of the equation by $6$:
$$
3=6cos{60text{textdegree}}=x
$$
d. The sum of all angles in a triangle is 180$text{textdegree}$:
$$
180text{textdegree}-90text{textdegree}-60text{textdegree}=30text{textdegree}
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{30text{textdegree}}=dfrac{x}{6}
$$
Multiply both sides of the equation by $6$:
$$
3=6sin{30text{textdegree}}=x
$$
b. $x=frac{7}{tan 49text{textdegree}}$
c. $x=3$
d. $x=3$
b.
$$
cos{29text{textdegree}}=dfrac{y}{42}
$$
Multiply both sides of the equation by $42$:
$$
36.73approx 42cos{29text{textdegree}}=y
$$
b. $y=36.73$
$$
dfrac{m}{22}=dfrac{15}{10}
$$
Multiply both sides of the equation by 22:
$$
m=dfrac{15cdot 22}{10}=33
$$
Determine the other side:
$$
dfrac{n}{24}=dfrac{15}{10}
$$
Multiply both sides of the equation by 24:
$$
n=dfrac{15cdot 24}{10}=36
$$
b. The area of a rectangle is the product of the length and the width. The area of a triangle is the product of the base and the height divided by 2. Determine then the area of both figure by determining the area of the rectangle and decrease the area by the area of the missing triangles:
$$
FIRST: 22cdot 24-dfrac{24cdot 10}{2}-dfrac{5cdot 12}{2}=528-120-30=378
$$
$$
SECOND: 378cdot left(dfrac{15}{10}right)^2=850.5
$$
The perimeter is the sum of all sides (determine the missing side lengths using the Pythagorean theorem):
$$
FIRST=22+19+13+26=80
$$
$$
SECOND=80cdot dfrac{15}{10}=120
$$
b. First figure: Area 378 and perimeter 80
Second figure: Area 850.5 and perimeter 120
a.
$$
xy-6x-18+3y=(x+3)(y-6)
$$
b.
$$
2xy-3y+2x-3=(2x-3)(y+1)
$$
c.
$$
12y+14x-8xy-21=(3-2x)(4y-7)
$$
d. Place terms that both contain an $x$ term in the same row (or column) and the same for terms that contain both a $y$ term, the remaining term then is place in the remaining cell.
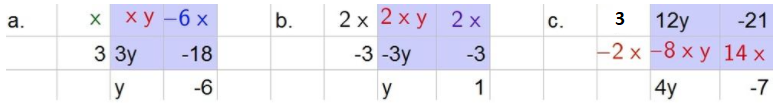
b. $(2x-3)(y+1)$
c. $(3-2x)(4y-7)$
d. lace terms that both contain an $x$ term in the same row (or column) and the same for terms that contain both a $y$ term, the remaining term then is place in the remaining cell.
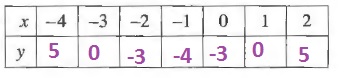
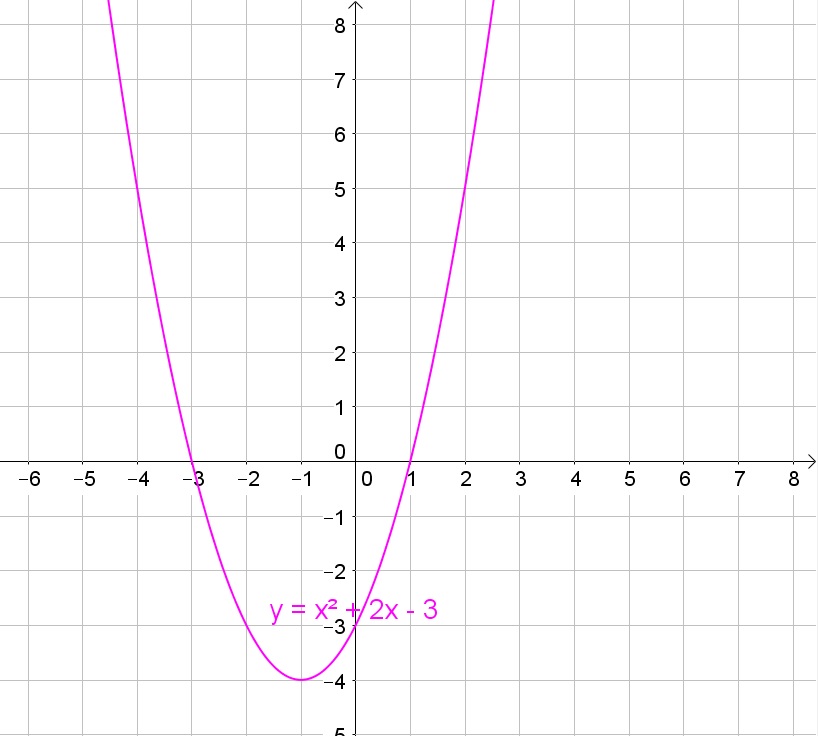
$y$-intercept $(0,-3)$
a.
$$
EV=4cdot dfrac{1}{2}-7cdot dfrac{1}{2}=dfrac{4}{2}-dfrac{7}{2}=-dfrac{3}{2}=-1.5
$$
b. The expected winings (or losings) is the product of the expected value andthe number of flips:
$$
8cdot left( -dfrac{3}{2}right)=-12
$$
b. Loss of $12
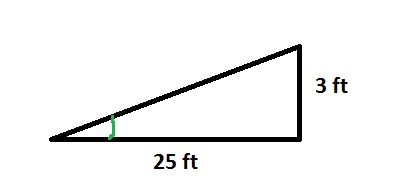
$$
cos^{-1}{dfrac{8}{16}}=60text{textdegree}
$$
c. The tangent is the opposite side divided by the adjacent rectangular side:
$$
x=tan^{-1}left( dfrac{3}{25}right)=6.84text{textdegree}
$$
Thus we note that the ramp will not meet the state building code.
d. The tangent is the opposite side divided by the adjacent rectangular side:
$$
tan{4.76text{textdegree}}=dfrac{3}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{4.76text{textdegree}}=3
$$
Divide both sides of the equation by $tan{4.76text{textdegree}}$:
$$
x=dfrac{3}{tan{4.76text{textdegree}}}approx 36
$$
Thus the ramp should start about 36 ft from the building.
b. Yes
c. 6.84$text{textdegree}$
d. 36 ft
$$
mangle B =sin^{-1}left( dfrac{14}{15}right)approx 69text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$:
$$
mangle A=180text{textdegree}-69text{textdegree}-90text{textdegree}=21text{textdegree}
$$
mangle B =69text{textdegree}
$$
$$
mangle A=21text{textdegree}
$$
$$
theta=cos^{-1}{dfrac{12}{24}}=cos^{-1}{dfrac{1}{2}}=60text{textdegree}
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
theta=tan^{-1}{dfrac{8}{8}}=tan^{-1}{1}=45text{textdegree}
$$
c. The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{57text{textdegree}}=dfrac{7}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{57text{textdegree}}=7
$$
Divide both sides of the equation by $sin{57text{textdegree}}$:
$$
x=dfrac{7}{sin{57text{textdegree}}}approx 8.35
$$
b. $theta=45text{textdegree}$
c. $x=8.35$
The tangent ratio is the opposite side divided by the adjacent rectangular side.
The sine ratio is the opposite side divided by the hypotenuse.
b. If one angle of a right triangle has the sine ratio $dfrac{a}{b}$, then the complementary angle has a cosine ratio of $dfrac{a}{b}$.
If one angle of a right triangle has the cosine ratio $dfrac{a}{b}$, then the complementary angle has a sine ratio of $dfrac{a}{b}$.
$$
angle A=cos^{-1}{dfrac{5}{13}}approx 67text{textdegree}
$$
METHOD 2: The sine ratio is the opposite side divided by the hypotenuse:
$$
angle A=sin^{-1}{dfrac{12}{13}}approx 67text{textdegree}
$$
If an expression is of the form $a^2-2ab+b^2$ then the factorization is $(a-b)^2$.
If an expression is of the form $a^2+2ab+b^2$ then the factorization is $(a+b)^2$.
If an expression is of the form $x^2+(a+b)x+(ab)$ then the factorization is $(x+a)(x+b)$.
a. Difference of squares: $4x^2-49=(2x)^2-7^2=(2x-7)(2x+7)$
b. $2x^2+11x+12=(2x+3)(x+4)$
c. Not possible
d. Perfect square trinomial: $9x^2+6x+1=(3x)^2+2(3x)(1)+1^2=(3x+1)^2$
e. $xy-4y+2x-8=y(x-4)+2(x-4)=(y+2)(x-4)$
f. Difference of squares: $x^4-16=(x^2-4)(x^2+4)=(x-2)(x+2)(x^2+4)$
b. $(2x+3)(x+4)$
c. Not possible
d. $(3x+1)^2$
e. $(y+2)(x-4)$
f. $(x-2)(x+2)(x^2+4)$
$$
7-y=dfrac{15}{4}
$$
Subtract 7 from both sides of the equation:
$$
-y=-dfrac{13}{4}
$$
Multiply both sides of the equation by $-1$:
$$
y=dfrac{13}{4}
$$
b. Use cross multiplication:
$$
3(y-2)=6y
$$
Use distributive property:
$$
3y-6=6y
$$
Subtract $3y$ from both sides of the equation:
$$
-6=3y
$$
Divide both sides of the equation by $3$:
$$
-2=y
$$
$$
dfrac{1dfrac{3}{4}}{4dfrac{1}{2}}=dfrac{1.75}{4.5}=dfrac{7}{18}
$$
The growth per year is then the product of the number of months and the grow ratio:
$$
12cdot dfrac{7}{18}=dfrac{84}{18}=dfrac{14}{3}=4dfrac{2}{3}
$$
d. Corresponding sides of similar triangles are proportional:
$$
dfrac{x}{4}=dfrac{x+8}{12}
$$
Use cross multiplication:
$$
12x=4(x+8)
$$
Use distributive property:
$$
12x=4x+32
$$
Subtract $4x$ from both sides of the equation:
$$
8x=32
$$
Divide both sides of the equation by $8$:
$$
x=4
$$
b. $y=-2$
c. $4frac{2}{3}$
d. $x=4$
$$
P(blemishwalktext{ or }dent)=P(blemish)+P(dent)-P(blemishtext{ and }dent)=4%+dfrac{1}{2}%-dfrac{1}{2}%=4%
$$
Thus the probability that the refrigerator has a defect is 4%, and thus 4 in 100 refrigerators will have a defect, which is reasonably small.
The Pythagorean theorem can be used to determine the relationship between the sides of the triangle. This can be described by the expression:
$$begin{gather}
c^2 = a^2 + b^2
end{gather}$$
David and Emily’s scenario can be illustrated by the following figure:

Determine (a) the length of the rope between David and carabiner above Emily and (b) the
The length of the rope between David and the carabiner above Emily is equal to the value of $x$ in the figure. Using the trigonometric identity: $cos theta = frac{text{adjacent}}{text{hypotenuse}}$, the hypotenuse side of the triangle represents $x$ while the adjacent side is the distance of David from the wall. We calculate for the value of $x$ as follows:
$$begin{aligned}
cos theta &= frac{text{adjacent}}{text{hypotenuse}} \
cos (55^circ) &= frac{20}{x} \
x &= frac{20}{cos (55^circ)} \
& boxed{x = 34.87 text{ ft}}
end{aligned}$$
Therefore, the length of the rope between David and carabiner above Emily is $34.87 text{ ft}$
We take note that the total length of the rope is $48 text{ ft}$. We determine the length of the rope between Emily and the carabiner above her by subtracting the total length of the rope by $x$ as follows:
$$begin{aligned}
y &= l_text{rope} – x \
y &= 48 – 34.87 \
& boxed{y = 13.13 text{ ft}}
end{aligned}$$
We use this value as the distance between Emily and the highest point of the rope (location of the carabiner).
$$begin{aligned}
tan theta &= frac{text{opposite}}{text{adjacent}} \
tan theta &= frac{b}{20.0} \
b &= 20.0 cdot tan theta \
b &= (20.0) cdot tan (55^circ) \
& boxed{b = 28.56 text{ ft}}
end{aligned}$$
$$begin{aligned}
h_{text{wall}} &= b + 3 \
h_{text{wall}} &= 28.56 + 3 \
& boxed{h_{text{wall}} = 31.56 text{ ft}}
end{aligned}$$
$$begin{aligned}
h_{text{Emily}} &= h_{text{wall}} – y \
&= 31.56 – 13.13 \
&= boxed{18.43 text{ ft}}
end{aligned}$$
Therefore, Emily has climbed $18.43 text{ ft}$ above the ground.
$h_{text{Emily}} = 18.43 text{ ft}$
$$
sin{60text{textdegree}}=dfrac{70}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{60text{textdegree}}=70
$$
Divide both sides of the equation by $sin{60text{textdegree}}$:
$$
x=dfrac{70}{sin{60text{textdegree}}}approx 81ft
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{60text{textdegree}}=dfrac{70}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{60text{textdegree}}=70
$$
Divide both sides of the equation by $tan{60text{textdegree}}$:
$$
x=dfrac{70}{tan{60text{textdegree}}}approx 40ft
$$
b. About 40 ft
$$
tan{10text{textdegree}}=dfrac{x}{185}
$$
Multiply both sides of the equation by $185$:
$$
33approx 185tan{10text{textdegree}}=x
$$
The height of Emily is then $33+6=39$ ft (add the height of Nathan’s eyes).
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{25text{textdegree}}=dfrac{x}{185}
$$
Multiply both sides of the equation by $185$:
$$
86approx 185tan{25text{textdegree}}=x
$$
The height of Emily is then $86+6=91$ ft (add the height of Nathan’s eyes).
The distance climbed is then the difference with the previous height: 91ft$-$39ft=52ft.
c. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
theta=tan^{-1}{dfrac{91+32}{185}}approx 34text{textdegree}
$$
b. About 91 ft
c. About 34$text{textdegree}$
$$
sin{36text{textdegree}}=dfrac{x}{9}
$$
Multiply both sides of the equation by $9$:
$$
5.3approx 9sin{36text{textdegree}}=x
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{36text{textdegree}}=dfrac{l}{9}
$$
Multiply both sides of the equation by $9$:
$$
7.3approx 9cos{36text{textdegree}}=x
$$
The area of a trapezium is then the product of the bases multiplied by the height, divided by 2:
$$
AREA=dfrac{(8+8+5.3)7.3}{2}=77.745
$$
Thus the area is 77.745 square meter $approx 837$ square ft.
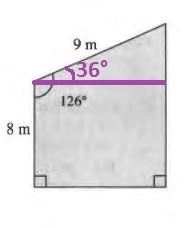
$$
dfrac{837}{150}=5.58approx 6
$$
Thus he will need 6 cans.
b. 6 cans
$$begin{aligned}
d_1&=18 ftenspacetext{(distance from David to wall base)}\
d_2&=185 ftenspacetext{(distance from Nathan to wall base)}\
end{aligned}$$
$$begin{aligned}
theta_1&=text{angle from David waist to the ground}\
theta_2&=text{angle of sight of Nathan to Emily}\
y&=text{height from carabiner to the ground}\
y_1&=text{height from Emily to David’s waist}\
y_2&=text{height from Emily to Nathan’s eyes}\
h&=text{distance of rope from David’s waist to Emily}\
h_1&=text{distance from Nathan’s eyes to Emily}\
end{aligned}$$

$$begin{aligned}
tantheta_2&=dfrac{y_2}{d_2}\
tantheta_2&=dfrac{y_2}{185}
end{aligned}$$
$$begin{aligned}
theta_1&=180degree-90degree-6degree\
theta_1&=84degree
end{aligned}$$
$$begin{aligned}
tan84degree&=dfrac{y_1}{d_1}\
tan84degree&=dfrac{y-3}{18}\
end{aligned}$$
$$begin{aligned}
tan84degree(18)&=y-3\
171.26&=y-3\
171.26+3&=y\
174.26&=y
end{aligned}$$
$$begin{aligned}
y_2&=y-6\
y_2&=174.26-6\
y_2&=168.26
end{aligned}$$
$$begin{aligned}
tantheta_2&=dfrac{y_2}{185}\
end{aligned}$$
$$begin{aligned}
tantheta_2&=dfrac{168.26}{185}\
tantheta_2&=0.909\
theta_2&=arctan(0.909)\
theta_2&=42.29degree
end{aligned}$$
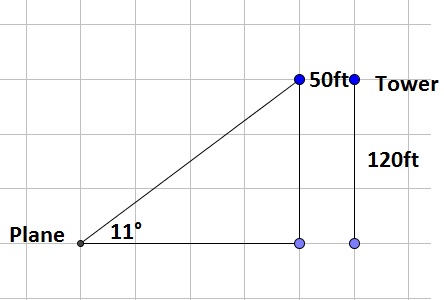
$$
tan{11text{textdegree}}=dfrac{120}{x}
$$
Multiply both sides of the equation by $x$:
$$
xtan{11text{textdegree}}=120
$$
Divide both sides of the equation by $tan{11text{textdegree}}$:
$$
x=dfrac{120}{tan{11text{textdegree}}}approx 617
$$
The minimum distance is then $x$ increase by the clearance needed:
$$
617+50=667ft
$$
$$
180text{textdegree}-90text{textdegree}-67text{textdegree}=23text{textdegree}
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse.
$$
cos{23text{textdegree}}=dfrac{18}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcos{23text{textdegree}}=18
$$
Divide both sides of the equation by $cos{23text{textdegree}}$:
$$
x=dfrac{18}{cos{23text{textdegree}}}approx dfrac{18}{0.921}approx 19.55
$$
b. The sine ratio of an angle is equal to the cosine ratio of the complementary angle:
$$
sin{67text{textdegree}}=cos{23text{textdegree}}approx 0.921
$$
b. $sin{67text{textdegree}}=cos{23text{textdegree}}approx 0.921$
$$
2x^2-2x-4=2(x^2-x-2)
$$
Factor further:
$$
2x^2-2x-4=2(x^2-x-2)=2(x+1)(x-2)
$$
$$
4(x^2-6x+9)
$$
Use $a^2-2ab+b^2=(a-b)^2$:
$$
4(x-3)^2
$$
b. $4(x-3)^2$
b. The $x$-intercepts are the intersections of the graph with the $x$-axis and thus are at $x=-2$ and $x=4$.
c. The lowest point on the graph is at $(1,-9)$.
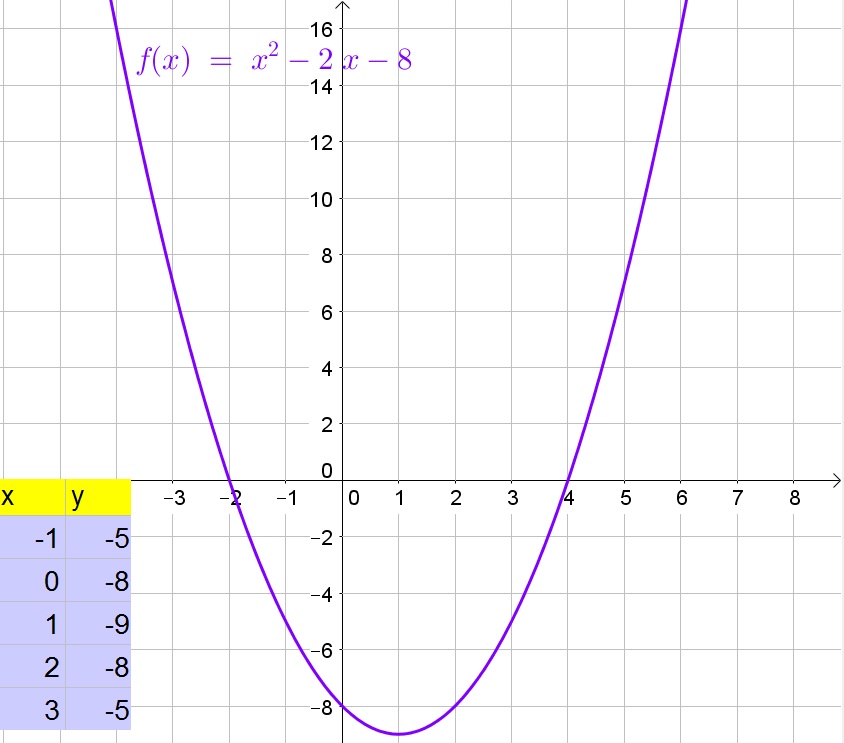
b. $x=-2$ and $x=4$
c. $(1,-9)$
$$
36cdot dfrac{1}{3}=12
$$
Thus there are 12 boys in the class.
b. f the probability of selecting a boy is $dfrac{1}{3}$, then two thirds of the students in the class should be girls and thus there are twice as much girls as boys:
$$
2cdot 12=24
$$
Thus there are 24 girls in the class.
c. Since the total probability is 100%=1, the probability of selecting a girl is 1 decreased by the probability of selecting a boy:
$$
P(girl)=1-P(boy)=1-dfrac{1}{3}=dfrac{2}{3}
$$
d. If the probability of selecting a boy is $dfrac{1}{3}$, then one third of the students in the class should be boys:
$$
24cdot dfrac{1}{3}=8
$$
Thus the class has 8 boys and 16 girls. After one boy has been selected, we can then choose 7 boys out of 23 students:
$$
P(2^{nd} boy)=dfrac{7}{23}
$$
b. 24 girls
c. $dfrac{2}{3}$
d. $dfrac{7}{23}$
a. We need to find two numbers whose product is $-80$ and whose sum is 2. Those numbers are then 10 and $-8$. These numbers should be filled in in the left and right cell but the order does not matter.
b. We need to find two numbers whose product is $12$ and whose sum is $-7$. Those numbers are then $-4$ and $-3$. These numbers should be filled in in the left and right cell but the order does not matter.
c. We need to find two numbers whose product is $0$ and whose sum is 7. Those numbers are then 0 and $7$. These numbers should be filled in in the left and right cell but the order does not matter.
d. We need to find two numbers whose product is $-81$ and whose sum is 0. Those numbers are then $-9$ and $9$. These numbers should be filled in in the left and right cell but the order does not matter.
e. We need to find two numbers whose product is $6x^2$ and whose sum is $5x$. Those numbers are then $3x$ and $2x$. These numbers should be filled in in the left and right cell but the order does not matter.
f. We need to find two numbers whose product is $-7x^2$ and whose sum is $-6x$. Those numbers are then $-7x$ and $x$. These numbers should be filled in in the left and right cell but the order does not matter.
b. $-4$ and $-3$
c. 0 and 7
d. $-9$ and 9
e. $3x$ and $2x$
f. $-7x$ and $x$

