All Solutions
Page 429: Questions
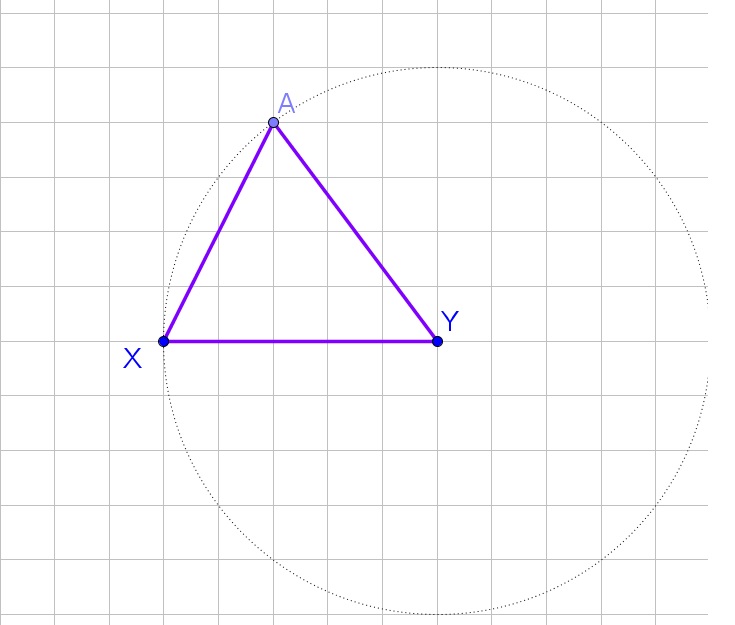
Using the details provided, the constructed equilateral triangle is shown in **Step 3**.
See illustration below.
See illustration below.

See illustration below of isosceles right triangle.

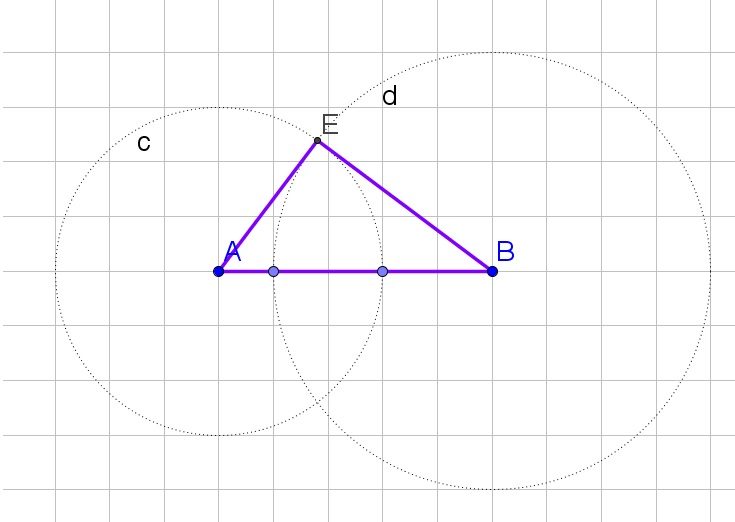
b. Draw a circle from both endpoints of a side of the traingle with equal width, then connect the intersections with a line. Repeat this for every side of the triangle, the intersections of these three lines is then the centroid.
c. The centroid is the center of balance of the triangle.
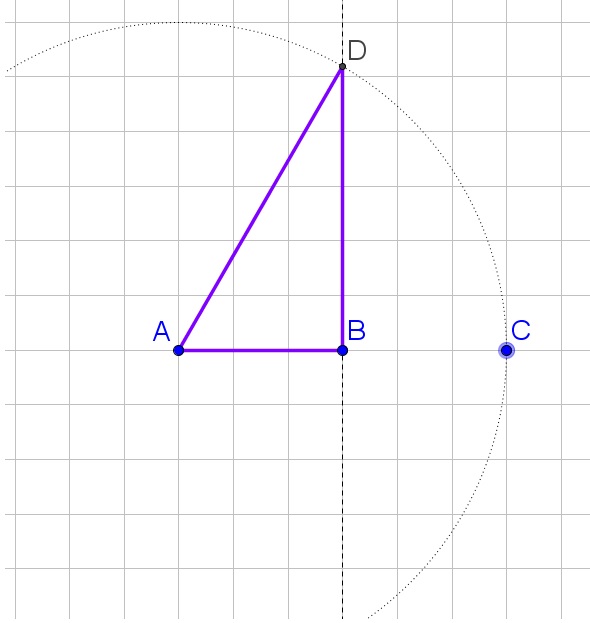
b. Determine the perpendicular bisector from each side of the triangle, their intersection then lies an equal distance from each vertex.
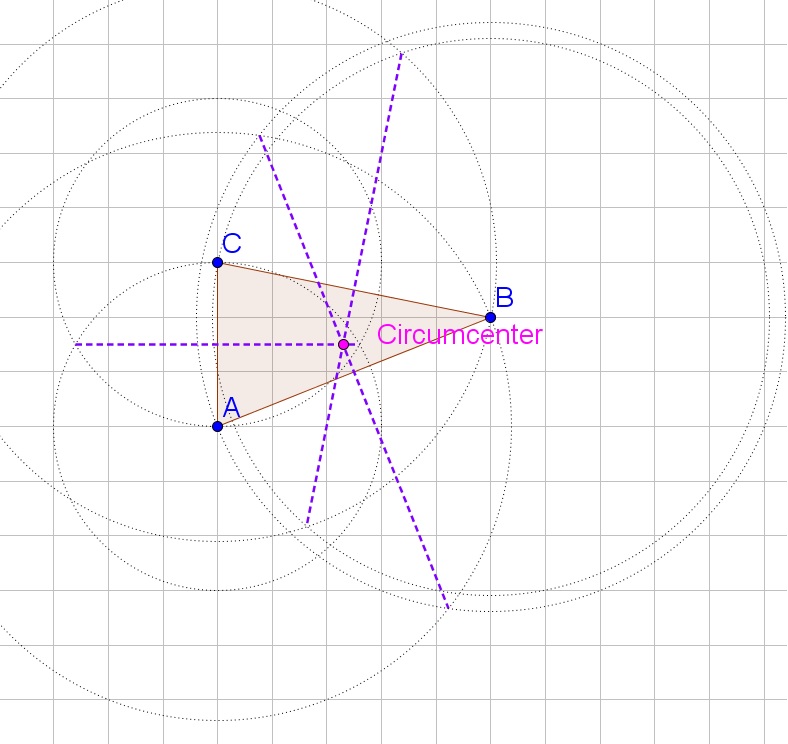
d.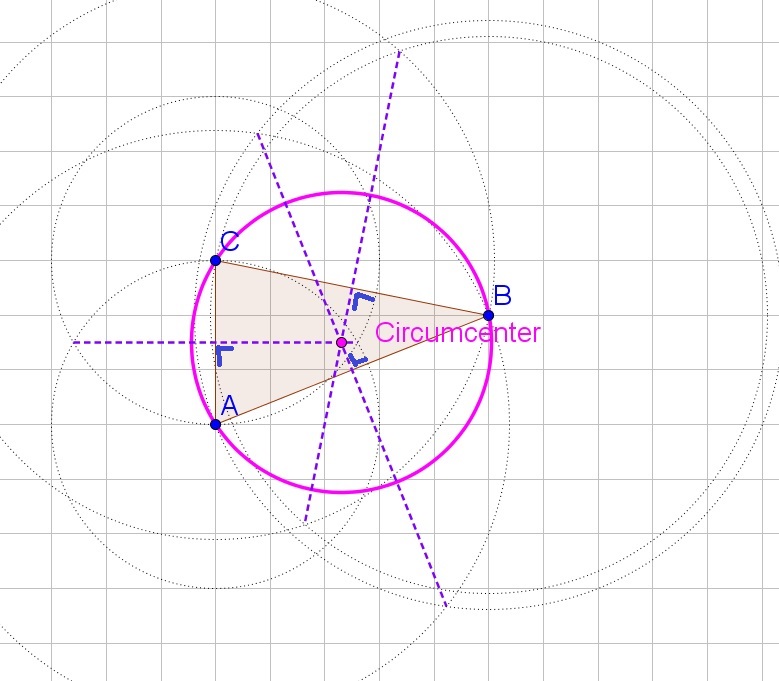
b. Determine the perpendicular bisector from each side of the triangle, their intersection then lies an equal distance from each vertex.
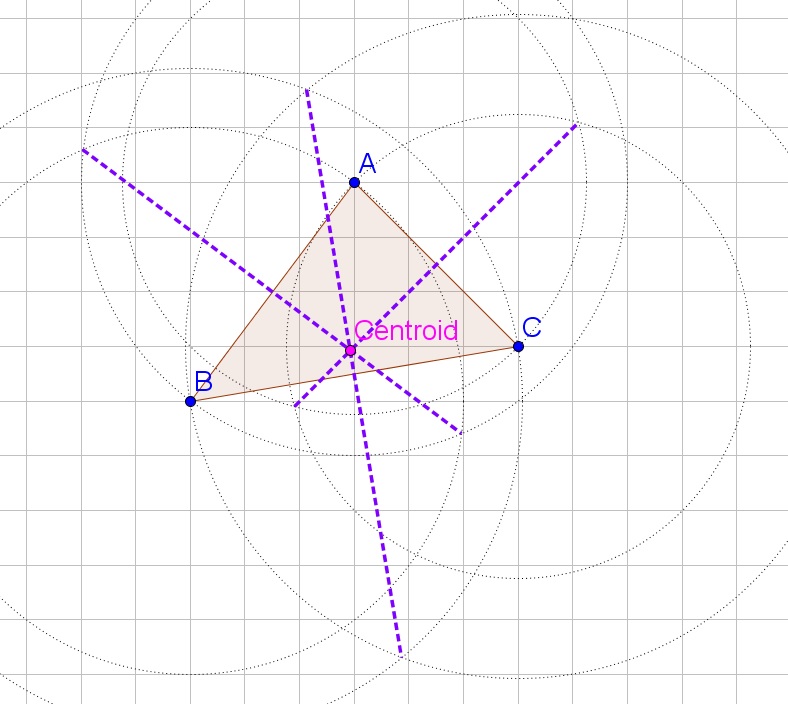
c. Draw the circle with center the circumcenter and radius the distance to each vertex.
d. Graph
b. Determine the bisector of $angle B$, this bisector contains all points that are equally distant from both sides.
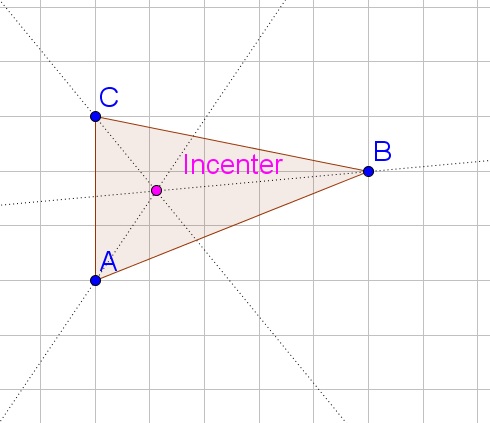
e. The insribed circle then has center the incenter and radius the distance from the incenter to the intersection of the perpendicular lines from (d) with the corresponding sides.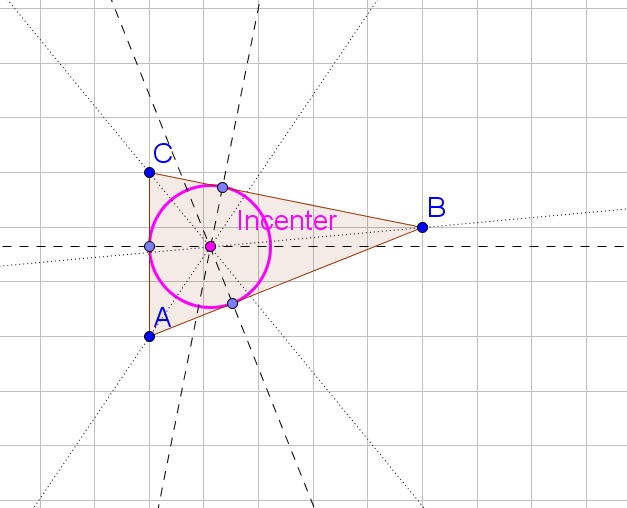
b. Determine the bisector of $angle B$, this bisector contains all points that are equally distant from both sides.
c. The three bisectors intersect at one point, the incenter.
d. Determine the perpendicular line to each side of the triangle that goes through the incenter.
e. The insribed circle then has center the incenter and radius the distance from the incenter to the intersection of the perpendicular lines from (d) with the corresponding sides.
b. $overline{FE}$ is parallel to $overline{BC}$ and is have the length of $overline{BC}$.
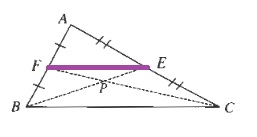
$$
angle FPEcong angle CPB text{Vertical angles}
$$
$$
angle PFEcong angle PCB text{Alternate interior angles}
$$
$$
angle FEPcong angle CBPtext{Alternate interior angles}
$$
$$
Downarrow AAA
$$
$$
triangle FPE sim triangle CPB
$$
d. Since the midline of a triangle is half the length of the side of the triangle it is parallel to:
$$
dfrac{EF}{BC}=dfrac{EP}{BP}=dfrac{BP}{BE}=dfrac{1}{2}
$$
e. Yes, because the same properties for midlines will be true and thus we would be able to prove it again.
f. Since the medians always have ratio $dfrac{1}{2}$ to a point $P$, this means that this point $P$ is the intersection of all three medians.
b. Equal length
c. Use AAA
d. $frac{1}{2}$
e. Yes
f. Since the medians always have ratio $dfrac{1}{2}$ to a point $P$, this means that this point $P$ is the intersection of all three medians.
$$
AC=DC(text{Given})
$$
$$
angle ABC cong angle DCB(text{Given})
$$
$$
BC=CB(text{Same side})
$$
$$
Downarrow SAS
$$
$$
triangle ABCcong triangle DCB
$$
$$
Downarrow
$$
$$
overline{AC}cong overline{DB}
$$
b. No, because you only needed to know that they were congruent.
b. No
$$
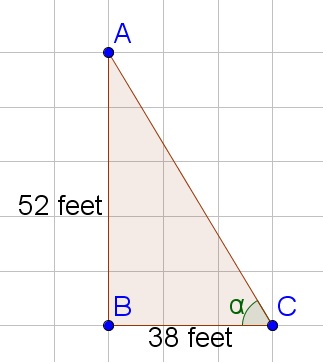
alpha=tan^{-1}dfrac{52}{38}approx 54text{textdegree}
$$
$$
left( dfrac{x_1+x_2}{2}, dfrac{y_1+y_2}{2}right)
$$
Thus the coordinates of $M$ are then:
$$
M=left( dfrac{-3+6}{2}, dfrac{-1+11}{2}right)=(1.5,5)
$$
b. The point $P$ is the coordinates of $A$ increased by $dfrac{2}{3}$ the difference between the coordinates of $A$ and $B$:
$$
P=left( -3+dfrac{2}{3}(6-(-3)), -1+dfrac{2}{3}(11-(-1))right)=(3,7)
$$
c. The equation of a line through two points $(x_1,y_1)$ and $(x_2,y_2)$ is:
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$
Thus the equation of this line then becomes:
$$
y+1=dfrac{11+1}{6+3}(x+3)
$$
Or simplified:
$$
y+1=dfrac{4}{3}(x+3)
$$
d. Determine the distance using the distance formula: $sqrt{(x_2-x-1)^2+(y_2-y_1)^2}$
$$
sqrt{(6+3)^2+(11+1)^2}=sqrt{225}=15
$$
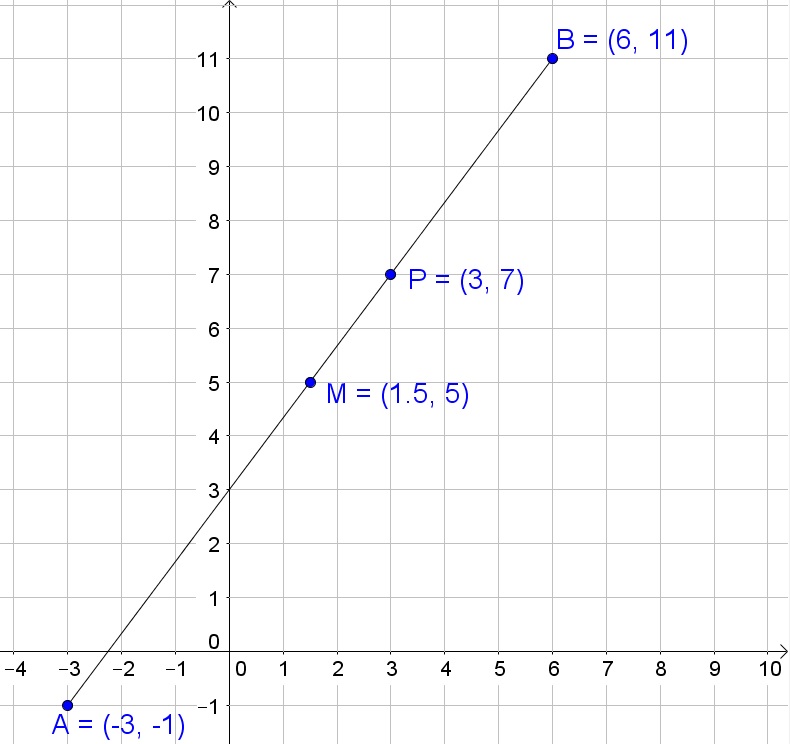
b. $(3,7)$
c. $y+1=frac{4}{3}(x+3)$
d. 15
b. Expand the brackets:
$$
49+x^2=x^2+2x+1
$$
Subtract $x^2$ from both sides of the equation:
$$
49=2x+1
$$
Subtract 1 from both sides of the equation:
$$
48=2x
$$
Divide both sides of the equation by 2:
$$
24=x
$$
The perimeter is then the sum of lengths of all sides:
$$
7+x+x+1=7+24+24+1=56
$$
b. 56
$$
64x^2-y^2=(8x-y)(8x+y)
$$
$$
12x^2-xy-6y^2=(3x+2y)(4x-3y)
$$
$$
4x^2+12x+9=(2x+3)^2
$$
b. $(3x+2y)(4x-3y)$
c. $(2x+3)^2$
d. Not possible to factorize further
b. Since the altitude is also the bisector:
$$
mangle DAB=dfrac{36text{textdegree}}{2}=18text{textdegree}
$$
Since the altitude is also the median:
$$
BD=dfrac{BC}{2}=dfrac{8}{2}=4
$$
c. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
tan{18text{textdegree}}=dfrac{AD}{4}
$$
Multiply both sides of the equation by 4;
$$
1.3approx 4tan{18text{textdegree}}=AD
$$
d. The area of a triangle is the product of the base and the height divided by 2:
$$
AREA=dfrac{8cdot 1.3}{2}=5.2
$$
b. 18$text{textdegree}$, 4
c. 1.3
d. 5.2
$$
180text{textdegree}-48text{textdegree}-72text{textdegree}=60text{textdegree}
$$
The measure of the exterior angle is the sum of the two opposite angle measures of the triangle:
$$
a=72text{textdegree}+60text{textdegree}=132text{textdegree}
$$
$$
b=48text{textdegree}+60text{textdegree}=108text{textdegree}
$$
$$
c=48text{textdegree}+72text{textdegree}=120text{textdegree}
$$
The sum of all exterior angle measures is then:
$$
132text{textdegree}+108text{textdegree}+120text{textdegree}=360text{textdegree}
$$
b. Squares, equilateral triangles and regular polygons are always similar.
$$
sqrt{11^2+17^2}=sqrt{121+289}=sqrt{410}
$$
The perimeter is then the sum of the lengths of the sides of the triangle:
$$
11+17+sqrt{410}=28+sqrt{410}approx 48
$$
b. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
theta_1 = tan^{-1}dfrac{11}{17}approx 33text{textdegree}
$$
$$
theta_2 = tan^{-1}dfrac{17}{11}approx 57text{textdegree}
$$
b. 33$text{textdegree}$, 57$text{textdegree}$
a.
$$
(sqrt{3x})^3=(3x)^{3/2}
$$
b.
$$
sqrt[x]{81}=(sqrt[x]{81})^1=81^{1/x}
$$
c.
$$
(sqrt[3]{17})^x=(17)^{x/3}
$$
b. $81^{1/x}$
c. $17^{x/3}$
$$
frac{x}{3.2}=frac{x^2}{7.5}
$$
Multiply both sides of the equation by 240:
$$
75x=32x^2
$$
Subtract $75x$ from both sides of the equation:
$$
0=32x^2-75x
$$
Factorize:
$$
0=x(32x-75)
$$
Zero product property:
$$
x=0text{ or }32x-75=0
$$
Solve each equation to $x$:
$$
x=0text{ or }32x=75
$$
$$
x=0text{ or }x=dfrac{75}{32}
$$
$$
4(x-2)+3(-x+4)=-2(x-3)
$$
Use distributive property:
$$
4x-8-3x+12=-2x+6
$$
Add $2x$ to both sides of the equation:
$$
3x+4=6
$$
Subtract 4 from both sides of the equation:
$$
3x=2
$$
Divide both sides of the equation by 3:
$$
x=dfrac{2}{3}
$$
$$
2x^2+7x-15=0
$$
Factorize:
$$
0=(2x-3)(x+5)
$$
Zero product property:
$$
2x-3=0text{ or }x+5=0
$$
Solve each equation to $x$:
$$
2x=3text{ or }x=-5
$$
$$
x=dfrac{3}{2}text{ or }x=-5
$$
$$
3x^2-2x=-1
$$
Add 1 to both sides of the equation:
$$
3x^2-2x+1=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{2pm sqrt{(-2)^2-4(3)(1)}}{2(3)}=dfrac{2pm 2sqrt{2}i}{6}=dfrac{1pm sqrt{2}i}{3}
$$
b. $x=frac{2}{3}$
c. $x=frac{3}{2}$ or $x=-5$
d. $x=frac{1pm sqrt{2}i}{3}$
Complex numbers can be written in the form:
$$begin{gather}
a + bi
end{gather}$$
where $a$ and $b$ are real numbers
We consider that $i^2 = -1$. Using this concept, we multiply the following expression as follows:
$$begin{aligned}
&= (9i)(2i) \
&= 18i^2 \
& i^2 = -1 \
&= 18 (-1) \
&= boxed{-18}
end{aligned}$$
The expression $(9i)(2i)$ yields the value $-18$ and it has no imaginary component
We consider that $i^2 = -1$. Using this concept, we multiply the following expression using the FOIL method as follows:
$$begin{aligned}
&= (2+i)(5-i) \
&= (2 cdot 5) + (5i) + (-2i) – (i^2) \
&= 10 + 3i -i^2 \
& i^2 = -1 \
&= 10 + 3i -(-1) \
&= boxed{11 + 3i}
end{aligned}$$
The expression $(2+i)(5-i)$ yields the value $11+3i$
We consider that $i^2 = -1$. Using this concept, we multiply the following expression as follows:
$$begin{aligned}
&= (3-i)(13i) \
&= (3 cdot 13i) + (-i cdot 13i) \
&= 39i – 13i^2 \
& i^2 = -1 \
&= 39i – 13(-1) \
&= boxed{13 + 39i}
end{aligned}$$
The expression $(3-i)(3i)$ yields the value $11+3i$
b. $11+3i$
c. $13+39i$
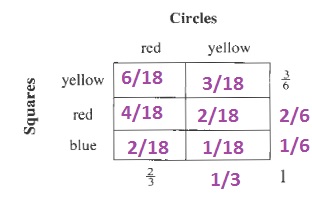
$$
P(win)=dfrac{2}{18}=dfrac{1}{9}approx 0.111=11.1%
$$
c. Use the multiplication rule:
$$
P(winGIVENblue)=dfrac{P(winANDblue)}{P(blue)}=dfrac{2/18}{1/6}=dfrac{2}{3}approx 0.667=66.7%
$$
b. $frac{1}{9}approx 0.111=11.1%$
c. $frac{2}{3}approx 0.667=66.7%$
$$
3cdot 180text{textdegree}=540text{textdegree}
$$

$$
(100-2)180text{textdegree}=(98)180text{textdegree}=17640text{textdegree}
$$
c. We note that the sum of a $n$-gon is a multiple of 180$text{textdegree}$ and moreover is $(n-2)$ times 180$text{textdegree}$.
b. 17640$text{textdegree}$
c. $(n-1)180text{textdegree}$
$$
6x=720text{textdegree}
$$
Divide both sides of the equation by 6:
$$
x=120text{textdegree}
$$
b. We know that the sum of all interior angles of an octagon is $6cdot 180text{textdegree}=1080text{textdegree}$ (see previous exercise) and since all angles are equal we then obtain:
$$
8x=1080text{textdegree}
$$
Divide both sides of the equation by 8:
$$
x=135text{textdegree}
$$
c. We know that the sum of all interior angles of a 100-gon is $98cdot 180text{textdegree}=17640text{textdegree}$ (see previous exercise) and since all angles are equal we then obtain:
$$
100x=17640text{textdegree}
$$
Divide both sides of the equation by 100:
$$
x=176.4text{textdegree}
$$
d. Yes, We know that the sum of all interior angles of a $n$-gon is $(n-2)cdot 180text{textdegree}$ (see previous exercise) and since all angles are equal we then obtain:
$$
nx=(n-2)cdot 180text{textdegree}
$$
Divide both sides of the equation by $n$:
$$
x=dfrac{n-2}{n}cdot 180text{textdegree}
$$
b. $x=135text{textdegree}$
c. $x=176.4text{textdegree}$
d. $x=frac{n-2}{n}cdot 180text{textdegree}$
b. We know that the interior angle of a regular hexagon is 120$text{textdegree}$ (see previous exercise) and supplementary angles sum up to 180$text{textdegree}$:
$$
a=180text{textdegree}-120text{textdegree}=60text{textdegree}
$$
c. Since there are 6 angles:
$$
6cdot 60text{textdegree}=360text{textdegree}
$$
We note that the sum is 360$text{textdegree}$, which is normal because if you would lie all angles with the center at the same point, you would get a full 360$text{textdegree}$ angle.
d. The exterior angles are always the complement of the interior angles and always sum up to 360$text{textdegree}$.
e. The sum of all exterior angles of a regular polygon is 360$text{textdegree}$.
f. Yes, this will be true for all polygons.
g. Since the sum of all exterior angles is 360$text{textdegree}$ and since the regular $n$-gon has $n$ angles, the measure of one exterior angle is:
$$
dfrac{360text{textdegree}}{n}
$$
b. 60$text{textdegree}$
c. 360$text{textdegree}$
d. Exterior angles are complement of interior angles
e. 360$text{textdegree}$
f. Yes
g. $frac{360text{textdegree}}{n}$
Sum of the interior angles of a $n$-gon:
$$
(n-2)cdot 180text{textdegree}
$$
Interior angle of a $n$-gon:
$$
dfrac{n-2}{n}cdot 180text{textdegree}
$$
Sum of exterior angles of a $n$-gon: 360$text{textdegree}$
Exterior angle of a $n$-gon:
$$
dfrac{360text{textdegree}}{n}
$$
$$
(n-2)cdot 180text{textdegree}
$$
Interior angle of a $n$-gon:
$$
dfrac{n-2}{n}cdot 180text{textdegree}
$$
Sum of exterior angles of a $n$-gon: 360$text{textdegree}$
Exterior angle of a $n$-gon:
$$
dfrac{360text{textdegree}}{n}
$$
$$
5x=360text{textdegree}
$$
Divide both sides of the equation by 5:
$$
x=72text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$:
$$
2y+72text{textdegree}=180text{textdegree}
$$
Subtract 72$text{textdegree}$ from both sides of the equation:
$$
2y=108text{textdegree}
$$
Divide both sides of the equation:
$$
y=54text{textdegree}
$$
x=72text{textdegree}
$$
$$
y=54text{textdegree}
$$
$$
10x=360text{textdegree}
$$
Divide both sides of the equation by 10:
$$
x=36text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$ and the base angles of a isosceles triangle are congruent:
$$
2y+36text{textdegree}=180text{textdegree}
$$
Subtract 36$text{textdegree}$ from both sides of the equation:
$$
2y=144text{textdegree}
$$
Divide both sides of the equation:
$$
y=72text{textdegree}
$$
b. The area is the sum of the areas of all triangles:
$$
AREA=10cdot 14.5=145in^2
$$
b. 145in$^2$
overline{BC}cong overline{DC}(text{Given})
$$
$$
angle Acong angle E(text{Given})
$$
$$
angle ACBcong angle ECD(text{Vertical angles})
$$
$$
Downarrow AAS
$$
$$
triangle ABCcong triangle EDC
$$
$$
Downarrow
$$
$$
overline{AB}cong overline{ED}
$$
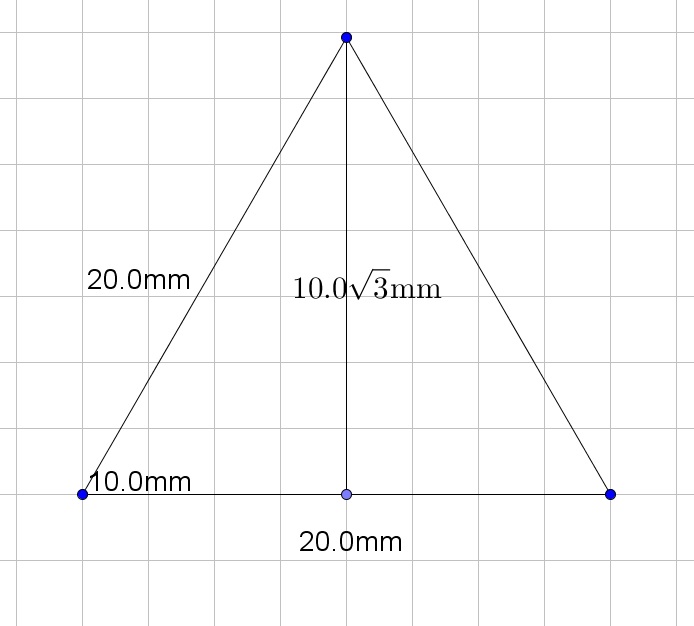
$$
AREA=dfrac{20cdot 10sqrt{3}}{2}=100sqrt{3}mm
$$
100sqrt{3}mm
$$
Two triangles are said to be similar when their corresponding angles are congruent and their corresponding sides are proportional.
The triangle LMN can be illustrated as follows:

We can observe that since all the sides of the triangle are equal, it $bigtriangleup$ LMN is an equilateral triangle. Another property of this triangle is that all three interior angles of are equal, such that $angle LMN = angle MNL = angle NLM = 60^circ$
The figure for the triangle in part a is shown below:

From the figure, we observe that all the interior angles of the triangle in part a is equal to $60^circ$. Since all its interior angles are equal to each other, this triangle is an equilateral triangle. Also, this property can also be observed in $bigtriangleup$ LMN. Moreover, from the AAA (angle-angle-angle) similarity theorem, if two triangles have the same interior angle, then the two triangles are said to be similar. Hence, this triangle is similar to $bigtriangleup$ LMN.
The triangle in part b can be illustrated as follows:

From the figure, we observe that all three sides of the triangle share equal lengths, hence, it is an equilateral triangle. From the SSS (side-side-side) similarity theorem, if the three sides of two triangles are proportional, then the two triangles are similar.
$$begin{aligned}
& frac{text{side of triangle in Part b}}{text{side of $bigtriangleup$ LMN}} \
frac{a}{2} &=boxed{ frac{a}{2} }\
frac{a}{2} &=boxed{ frac{a}{2} }\
frac{a}{2} &=boxed{ frac{a}{2} }\
end{aligned}$$
From the results, we observe that this triangle is proportional to $bigtriangleup$ LMN, hence, this triangle is similar to $bigtriangleup$ LMN.
The triangle in part c can be illustrated as follows:

From the figure, we observe that all three sides of the triangle are equal and each having a length of $2$. From the SSS (side-side-side) similarity theorem, if the three sides of two triangles are proportional, then the two triangles are similar. Since this triangle share the same length of the sides in $bigtriangleup$ LMN, hence, this triangle is similar to $bigtriangleup$ LMN.
The triangle in part d can be illustrated as follows:

From the figure, we observe that all three sides of the triangle share equal lengths, hence, it is an equilateral triangle. From the SSS (side-side-side) similarity theorem, if the three sides of two triangles are proportional, then the two triangles are similar.
$$begin{aligned}
& frac{text{side of triangle in Part d}}{text{side of $bigtriangleup$ LMN}} \
frac{5}{2} &=boxed{ frac{5}{2} }\
frac{5}{2} &=boxed{ frac{5}{2} }\
frac{5}{2} &=boxed{ frac{5}{2} }\
end{aligned}$$
From the results, we observe that this triangle is proportional to $bigtriangleup$ LMN, hence, this triangle is similar to $bigtriangleup$ LMN.
Since one half of the diagonal is 6, the diagonal is 12. Determine the side of the square $x$ using the Pythagorean theorem:
$$
2x^2=x^2+x^2=12^2=144
$$
Divide both sides of the equation by 2:
$$
x^2=72
$$
Take the square root of both sides of the equation:
$$
x=sqrt{72}=6sqrt{2}
$$
The area of a square is then the length of one of its sides squared:
$$
(6sqrt{2})^2=36cdot 2=72
$$
Since the diagonals in a square intersect at a right angle and since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{6cdot 6}{2}=18
$$
Since the square contains 4 of these triangles:
$$
AREA=4cdot 18=72
$$
The area of a regular hexagon is
$$
A=dfrac{3sqrt{3}}{2}a^2
$$
with $a$ the length of the side, thus the area of this hexagon is:
$$
A=dfrac{3sqrt{3}}{2}8^2=96sqrt{3}
$$
Determine the height of one triangle using the Pythagorean theorem:
$$
sqrt{8^2-4^2}=sqrt{48}=4sqrt{3}
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{8cdot 4sqrt{3}}{2}=16sqrt{3}
$$
Since the square contains 6 of these triangles:
$$
AREA=6cdot 16sqrt{3}=96sqrt{3}
$$
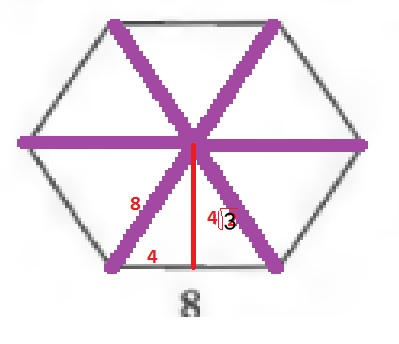
b. $96sqrt{3}$
The other method we used is divided by the regular polygon is congruent triangles and then determine the area of one triangle after which you can determine the total area of a polygon. This is possible to use for other regular polygons.
$$
x=11sin{70text{textdegree}}approx 10.3
$$
$$
y=11cos{70text{textdegree}}approx 3.8
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{7.6cdot 10.3}{2}=39.14
$$
Since the square contains 9 of these triangles:
$$
AREA=9cdot 39.14=352.26
$$
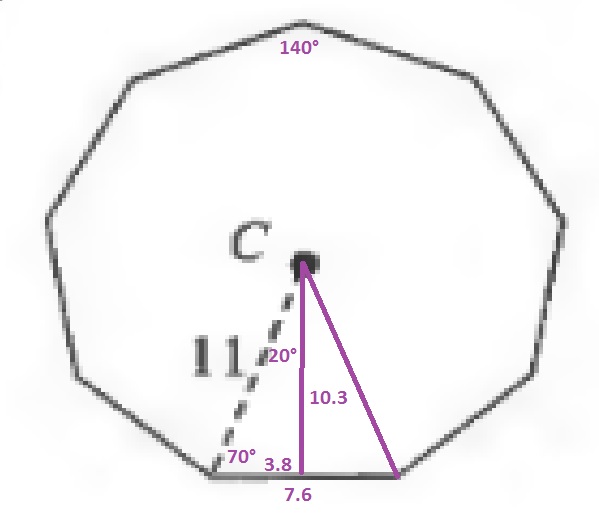
$$
x=dfrac{5}{tan{72text{textdegree}}}approx 1.6
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{3.2cdot 5}{2}=8
$$
Since the square contains 10 of these triangles:
$$
AREA=10cdot 8=80
$$
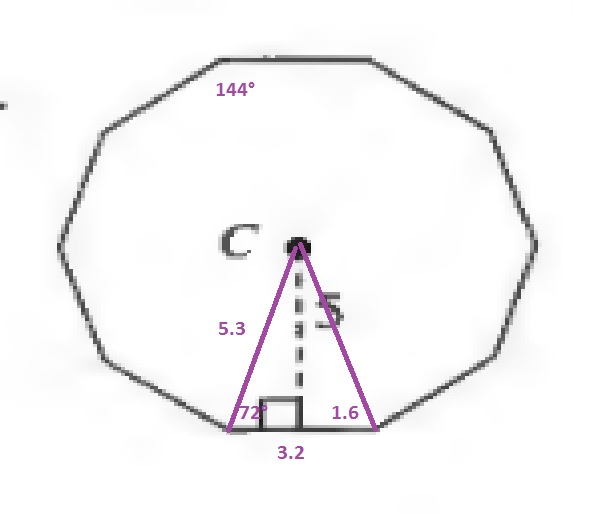
$$
x=2tan{60text{textdegree}}=2sqrt{3}
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{4cdot 2sqrt{3}}{2}=4sqrt{3}
$$
Since the square contains 6 of these triangles:
$$
AREA=6cdot 4sqrt{3}=24sqrt{3}
$$
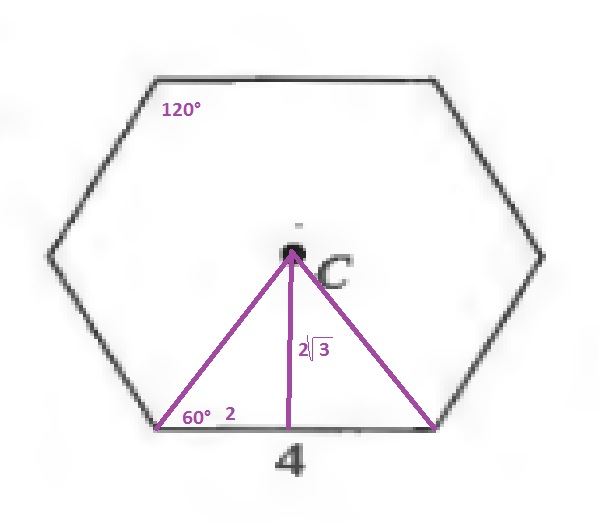
b. 80
c. 24$sqrt{3}$
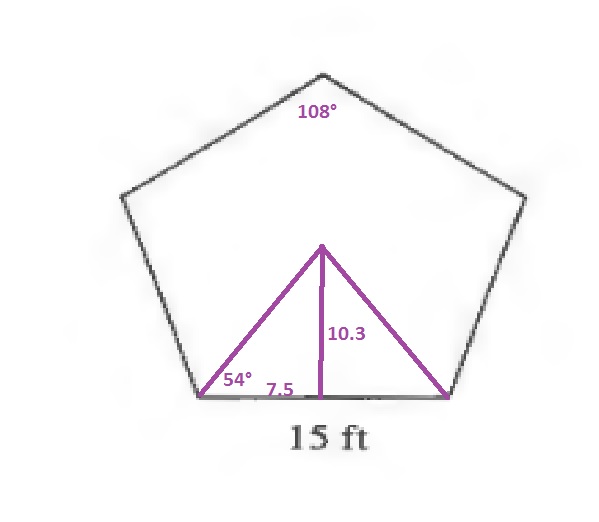
$$
x=7.5tan{54text{textdegree}}approx 10.3
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{15cdot 10.3}{2}=77.25ft^2
$$
Since the square contains 5 of these triangles:
$$
AREA=5cdot 77.25ft^2=386.25ft^2
$$
Divide the total area by the square feet per bag and round this number up to obtain the number of bags needed:
$$
dfrac{386.25}{150}= 2.575approx 3
$$
Thus she will need about 3 bags.
$$
x=2sin{67.5text{textdegree}}approx 1.8
$$
$$
y=2cos{67.5text{textdegree}}approx 0.8
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{1.6cdot 1.8}{2}=1.44
$$
Since the polygon contains 8 of these triangles:
$$
AREA=8cdot 1.44=11.52ft^2
$$
b. The cost is the product of the cost per foot and the perimeter of the hexagon:
$$
$48.99cdot (8cdot 1.6)approx $627.07
$$
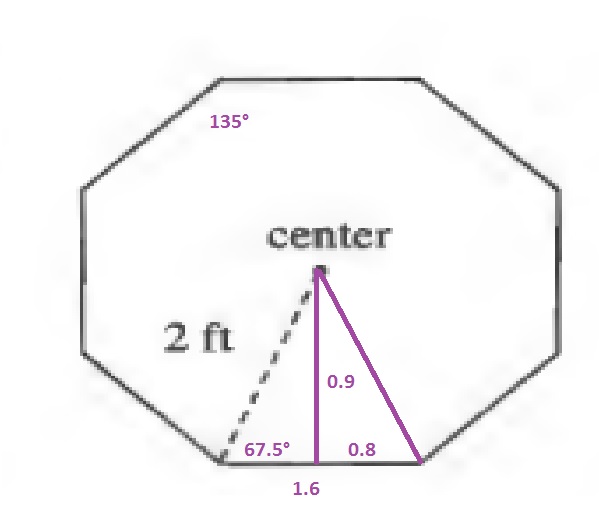
b. $$627.07$
Divide the $n$-gon into $n$ congruent triangles. Determine the base and the height of the triangle using the sine, cosine and tangent ratios and that the angles of a regular $n$-gon are $dfrac{n-2}{n}180text{textdegree}$. Then determine the area of one triangle. Finally multiply the area of one triangle by $n$ to obtain the area of the regular polygon.
$$
dfrac{n-2}{n}180text{textdegree}=135text{textdegree}
$$
Multiply both sides of the equation by $n$:
$$
(n-2)180=135n
$$
Use distributive property:
$$
180n-360=135n
$$
Subtract $135n$ from both sides of the equation:
$$
45n-360=0
$$
Add 360 to both sides of the equation:
$$
45n=360
$$
Divide both sides of the equation by 45:
$$
n=8
$$
Thus the regular polygon has 8 sides.
This method was more efficient, however for regular polygons with more sides the other method is easier to use.
a.
$$
tan{C}=dfrac{AB}{BC}
$$
b.
$$
sin{C}=dfrac{AB}{AC}
$$
c.
$$
tan{A}=dfrac{BC}{AB}
$$
d.
$$
cos{C}=dfrac{BC}{AC}
$$
e.
$$
cos{A}=dfrac{AB}{AC}
$$
f.
$$
sin{A}=dfrac{BC}{AC}
$$
b. $dfrac{AB}{AC}$
c. $dfrac{BC}{AB}$
d. $dfrac{BC}{AC}$
e. $dfrac{AB}{AC}$
f. $dfrac{BC}{AC}$
triangle ABC cong triangle EDF
$$
$$
Downarrow
$$
$$
angle D=angle B (text{Congruent triangles means that corresponding angles are congruent})
$$
$$
Downarrow
$$
$$
triangle DBGtext{isosceles} (text{if the base angles of a triangle are congruent, then the triangle is isosceles})
$$
a.
$$
(3+2i)(4+i)=12+8i+3i+2i^2=12+11i-2=10+11i
$$
b.
$$
(2+3i)(2-3i)=4+6i-6i-9i^2=4+9=13
$$
c.
$$
(5-2i)(5+2i)=25-10i+10i-4i^2=25+4=29
$$
d.
$$
(a+bi)(a-bi)=a^2+abi-abi-b^2i^2=a^2+b^2
$$
b. $13$
c. 29
d. $a^2+b^2$
Subtract 8 from both sides of the equation:
$$
x^2+3x-18=0
$$
Factorize:
$$
(x+6)(x-3)=0
$$
Zero product property:
$$
x+6=0text{ or }x-3=0
$$
Solve each equation to $x$:
$$
x=-6text{ or }x=3
$$






b. $x=0$
c. $x=pm 4$
d. $x=pm 5$
e. $x=3$ and $x=7$
f. $x=4$ and $x=-10$
$$
AREA=12cdot 8+6cdot 4+9cdot 8=192cm^2
$$
The perimeter is the sum of the lengths of all sides:
$$
PERIMETER=20+12+8+6+4+3+8+9=70cm
$$
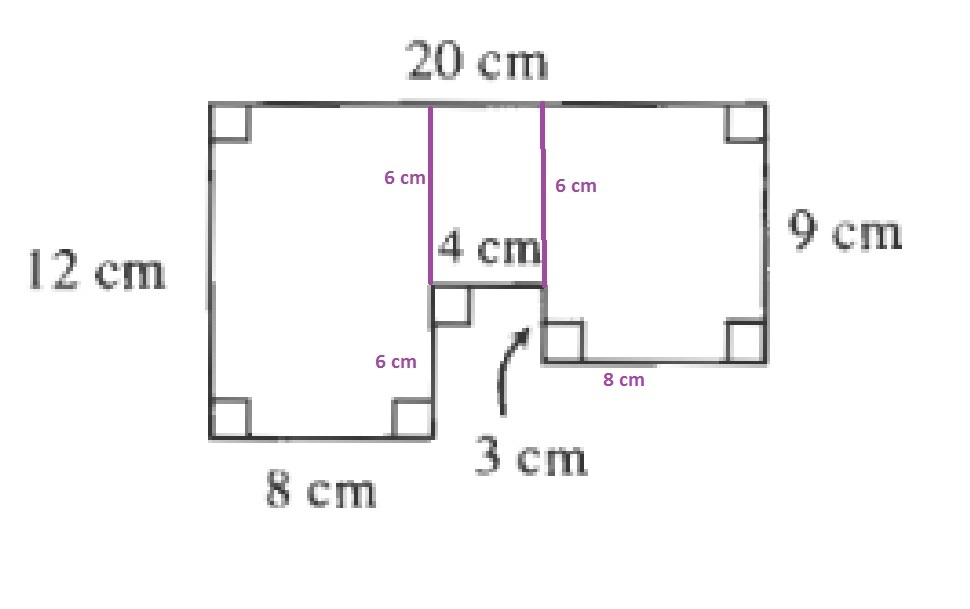
$$
PERIMETER=5cdot 70=350cm
$$
The area is multiplied by the scale factor squared:
$$
AREA=5^2cdot 192=4800cm^2
$$
c. The perimeter has been multiplied by the scale factor.
d. The area has been multiplied by the scale factor squared.
b. Perimeter 350 cm and Area 4800 cm$^2$.
c. Multiply by scale factor
d. Multiply by square factor squared
$$
x=3tan{75text{textdegree}}approx 11.2
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{6cdot 11.2}{2}=33.6cm^2
$$
Since the square contains 12 of these triangles:
$$
AREA=12cdot 33.6cm^2=403.2cm^2
$$
b. Thus three of the triangles are left:
$$
3cdot 33.6=100.8cm^2
$$
b. 100.8cm$^2$
$$
sqrt{(10-4)^2+(9-1)^2}=sqrt{100}=10
$$
b. The point $P$ is the coordinates of $A$ increased by $dfrac{3}{4}$ the difference between the coordinates of $A$ and $B$:
$$
P=left( 4+dfrac{3}{4}(10-4), 1+dfrac{3}{4}(9-1)right)=(8.5,7)
$$
c. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
angle CAB=tan^{-1}dfrac{4}{3}approx 53text{textdegree}
$$
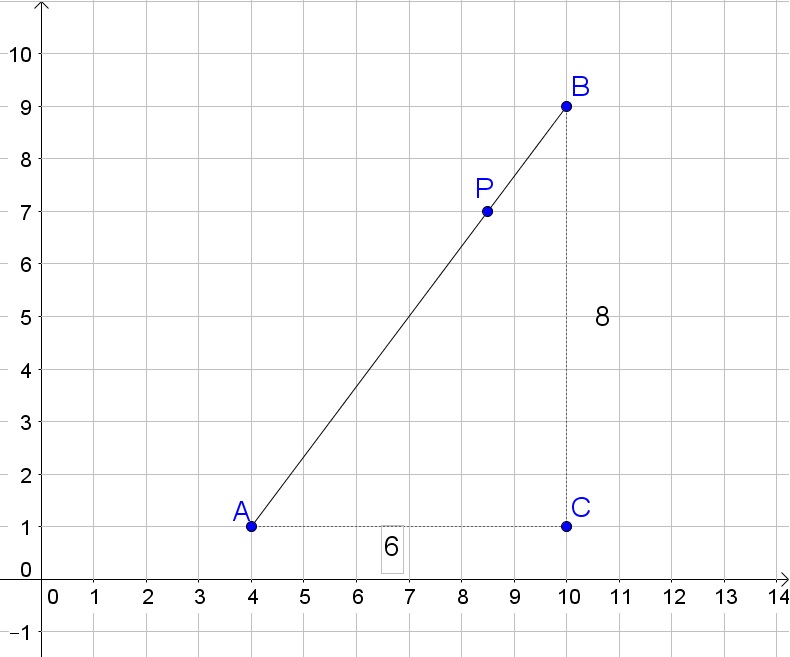
b. $(8.5,7)$
c. 53$text{textdegree}$
$$
begin{align*}
P(text{Green Fang})&=64%=0.64
\ P(text{Alarm})&=28%=0.28
\ P(text{Green Fang and Alarm})&=22%=0.22
end{align*}
$$
a. The probability of having neither system is 100% decreased by having either system (do not forget to add those that have both, because they will have been subtracted twice):
$$
begin{align*}
&P(text{neither})
\ &=100%-P(text{Green Fang or Alarm})
\ &=1-(P(text{Green Fang})+P(text{Alarm})-P(text{Green Fang and Alarm}))
\ &=1-P(text{Green Fang})-P(text{Alarm})+P(text{Green Fang and Alarm})
\ &=1-0.64-0.28+0.22
\ &=0.30
\ &=30%
end{align*}
$$
$$
begin{align*}
&P(text{Green Fang or Alarm})
\ &=P(text{Green Fang})+P(text{Alarm})-P(text{Green Fang and Alarm})
\ &=0.64+0.28-0.22
\ &=0.70
end{align*}
$$
A car had Green Fang and was not protected by an alarm system, when the car had Green Fang or an alarm, but did not have an alarm.
$$
begin{align*}
&P(text{Green Fang and No alarm})
\ &=P(text{Green Fang or Alarm})-P(text{Alarm})
\ &=0.70-0.28
\ &=0.42
\ &=42%
end{align*}
$$
Since 22% had both Green Fang and an alarm system, the two events “Green Fang” and “Alarm system” can occur at the same time and thus the events are $textbf{not disjoint}$.
$$
begin{align*}
P(text{Green Fang and Alarm})&=0.22=22%
\ P(text{Green Fang})cdot P(text{Alarm})&=0.64cdot 0.28=0.1792=17.92%
end{align*}
$$
Since $P(text{Green Fang and Alarm})neq P(text{Green Fang})cdot P(text{Alarm})$, the events are not independent and thus there is an association between Green Fang and Alarm. Moreover, the percentage of both events occurring (22%) is very close to the percentage of alarm systems (28%) and thus Green Fang appears to be associated with having an alarm.
b. $0.42=42%$
c. No
d. Green Fang appears to be associated with having an alarm.
$$
x=10tan{72text{textdegree}}approx 30.78
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{20cdot 30.78}{2}=307.8units^2
$$
Since the square contains 10 of these triangles:
$$
AREA=10cdot 307.8units^2=3,078units^2
$$
$$
64^{1/3}=sqrt[3]{64}=sqrt[3]{4^3}=4
$$
b. Power of product property, power of power property and negative exponent property:
$$
(4x^2y^5)^{-2}=4^{-2}(x^{2})^{-2}(y^5)^{-2}=dfrac{1}{4^2}x^{-4}y^{-10}=dfrac{1}{16x^4y^{10}}
$$
c. Add the powers of corresponding variables
$$
(2x^2y^{-3})(3x^{-1}y^5)=(2)(3)x^{2-1}y^{-3+5}=6xy^2
$$
b. $frac{1}{16x^4y^{10}}$
c. $6xy^2$
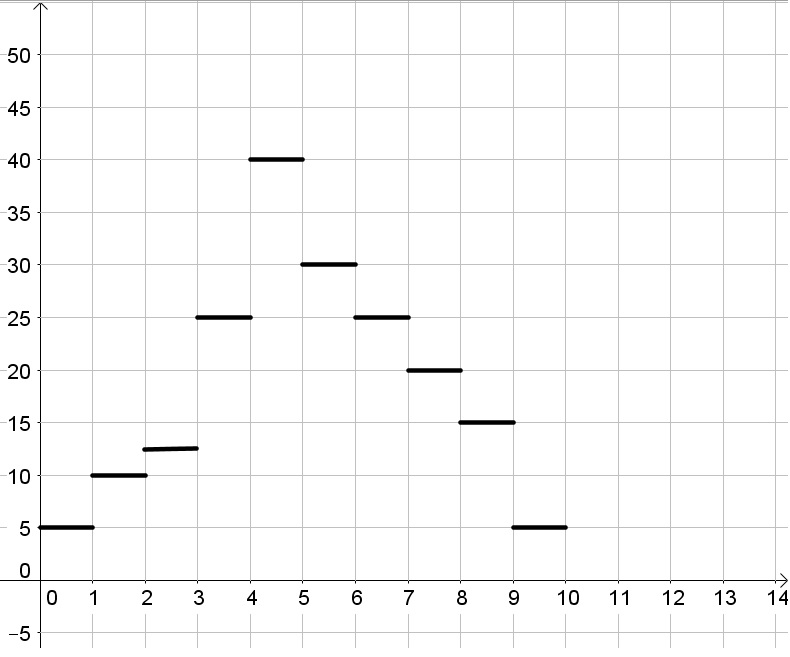
b. The number of shoppers per hour differs and is always an integer.
c. The temperature decreases gradually.
b. Since each dimension was doubled, the area of the flag will be quadrupled and thus the cost will be 4 times more:
$$
4cdot $2=$8
$$
c. Yes, the number of materials needed has been quadrupled.
d. If each dimension has been multiplied by 3, then the area will be multiplied by the square of this scale factor:
$$
3^2cdot $2=$18
$$
If each dimension has been multiplied by 4, then the area will be multiplied by the square of this scale factor:
$$
4^2cdot $2=$32
$$
b. $$8$
c. Yes
d. $$18$, $$32$
If the area has been enlarged $n$ times, then the dimensions have been enlarged $sqrt{n}$ times.
If the linear scale factor is $r$, then the area of the new shape is $r^2$ times larger.
$$
5^2cdot 17mm^2=425mm^2
$$
b. The linear scale factor is 4 since the length has been multiplied by 4. The area is then divided by the scale factor squared:
$$
dfrac{1}{4^2}cdot 656un^2=41un^2
$$
c. Yes, the linear scale factor is $dfrac{2}{3}$ (since the sides have been multiplied by the factor), the ratios of thee areas is then the factor squared:
$$
dfrac{4}{9}
$$
d. No, the price should have been one forth (since the area has been decreased to one forth of the original) and thus the price should have been $200.
b. 41 un$^2$
c. Yes, $frac{2}{3}$, $frac{4}{9}$
d. No
Determine the height of the triangle using the tangent ratio:
$$
x=5tan{60text{textdegree}}approx 8.7
$$
$$
x=15tan{60text{textdegree}}approx 26
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{5cdot 8.7}{2}=21.75
$$
$$
dfrac{15cdot 26}{2}=195
$$
Since the square contains 6 of these triangles:
$$
AREA=6cdot 21.75=130.5
$$
$$
AREA=6cdot 195=1170
$$
Then we note that $9cdot 130.5approx 1170$
$$
AREA=5cdot 2 +4cdot 4+dfrac{4cdot 4}{2}=34
$$
The perimeter is the sum of the lengths of all sides:
$$
2+5+2+3+4+4+4sqrt{2}=20+4sqrt{2}
$$
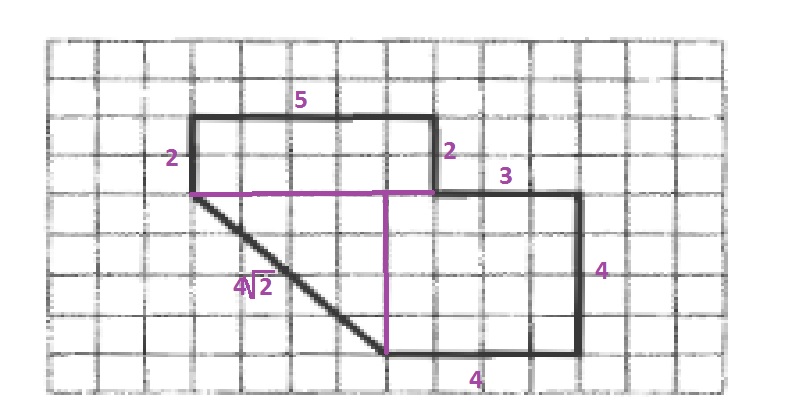
$$
AREA=3^2cdot 34=306
$$
The perimeter will be multiplied by the scale factor:
$$
PERIMETER=3cdot (20+4sqrt{2})=60+12sqrt{2}
$$
c. The ratio of the perimeter is the scale factor, while the ratio of the areas is the scale factor squared.
b. Area 306, Perimeter $60+12sqrt{2}$
c. Scale factor, Scale factor squared.
$$
180text{textdegree}-20text{textdegree}=160text{textdegree}
$$
b. Since the interior angle is given by $dfrac{n-2}{n}180text{textdegree}$ we obtain:
$$
dfrac{n-2}{n}180text{textdegree}=160text{textdegree}
$$
Multiply both sides of the equation by $n$:
$$
(n-2)180=160n
$$
Use distributive property:
$$
180n-360=160n
$$
Subtract $160n$ from both sides of the equation:
$$
20n-360=0
$$
Add 360 to both sides of the equation:
$$
20n=360
$$
Divide both sides of the equation by 20:
$$
n=18
$$
Thus the regular polygon has 18 sides.
b. 18 sides
$$
x=2tan{60text{textdegree}}=2sqrt{3}
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{4cdot 2sqrt{3}}{2}=4sqrt{3}
$$
Since the hexagon contains 6 of these triangles:
$$
AREA=6cdot 4sqrt{3}=24sqrt{3}
$$
Thus the area of the square also has to be $24sqrt{3}$. Using the Pythagorean theorem determine the length of the side:
$$
x=sqrt{dfrac{(24sqrt{3})^2}{2}}=sqrt{864}=12sqrt{6}
$$
12sqrt{6}
$$
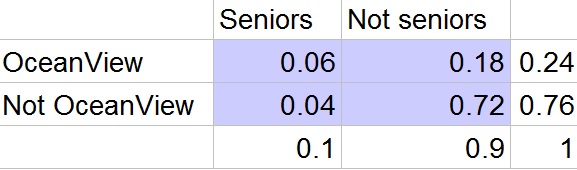
$$
P=dfrac{0.06}{0.24}=dfrac{1}{4}=0.25=25%
$$
c. Yes, because the probability of a student being a senior given that he lives in ocean view, is not equal to the probability of being a senior.
c. $0.25=25%$
c. Yes
b. For example 5,5,1 are possible lengths for a triangle.
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-7pm sqrt{7^2-4(1)(k)}}{2(1)}=dfrac{-7pm sqrt{49-4k}}{2}
$$
The expression is then factorable if
$$
49-4kgeq 0
$$
Dubtract 49 from both sides of the inequality:
$$
-4kgeq -49
$$
Divide both sides of the equation by $-4$:
$$
kleq 12.25
$$
Thus for $k=0$ till $k=12$ the expression is factorable.The probability is then the number of favorable outcomes divided by the number of possible outcomes:
$$
P=dfrac{13}{21}approx 0.619=61.9%
$$
a.
$$
x=0
$$
b.
$$
x-1=0Rightarrow x=1
$$
c.
$$
x+7=0Rightarrow x=-7
$$
b. $x=1$
c. $x=-7$
b. Since the dimensions have been multiplied by 2, the area is multiplied by $2^2=4$ and thus the cost will be:
$$
4 cdot $0.45=$1.80
$$
c. Divide the new cost by the original cost:
$$
dfrac{$7.20}{$0.45}=16
$$
Thus the area has been enlarged 16 times and the dimensions have then been enlarged $sqrt{16}=4$ times:
$$
4cdot 4 intimes 4cdot 5 in=16intimes 20in
$$
b. $$1.80$
c. 16 in. $times$ 20 in.
b. The ratio of the sides is $frac{4}{6}=dfrac{2}{3}$ which is also equal to the ratio of the perimeters.
c. The ratio of the sides is $frac{5}{40}=dfrac{1}{8}$ and this is also the ratio of the perimeters.
d. The ratio of the perimeters of similar figures is equal to the linear scale factor.
b. $2.54^2=6.4516$ square centimers in one square inch. The area is the scale factor squared, just as we did here.
c. The price per square centimeter is then the original price divided by the number of square centimeters in one square inch:
$$
dfrac{$0.45}{6.4516}approx$0.07
$$
Thus we note that this is more than in the online print shop.
b. 6.4516 square cm, The area is the scale factor squared.
c. $$0.07$, More
$$
3cdot (8+4+5+10+13+4)=3cdot 44=132cm^2
$$
If the linear scale factor of the similar figures is $r$, then the ratio of the perimeters of the similar figures is also $r$, while the ratio of the areas of the similar figures is $r^2$.
$$
dfrac{3}{4}
$$
b. The perimeter of figure B is the perimeter of figure A multiplied by the linear scale factor:
$$
pr
$$
c. The area of figure B is the product of the area of figure A multiplied by the linear scale factor squared:
$$
ar^2
$$
b. $pr$
c. $ar^2$
$$
x=0.5tan{60text{textdegree}}approx 0.866
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{1cdot 0.866}{2}=0.433
$$
Since the hexagon contains 6 of these triangles:
$$
AREA=6cdot 0.433=2.598yd^2
$$
b.
$$
2.598yd^2=9cdot 2.598ft^2=23.382ft^2
$$
Divide the area by the area per packet:
$$
dfrac{23.382}{10}=2.3382<3
$$
Thus we need 3 packet of wildflowers.
b. 3 packets
$$
x+x+125+125+90=540
$$
Combine like terms:
$$
2x+340=540
$$
Subtract 340 from both sides of the equation:
$$
2x=200
$$
Divide both sides of the equation by 2:
$$
x=100
$$
$$
6x+18=2x+30
$$
Subtract $2x$ from both sides of the equation:
$$
4x+18=30
$$
Subtract 18 from both sides of the equation:
$$
4x=12
$$
Divide both sides of the equation by 4:
$$
x=3
$$
b. $x=3$
$$
dfrac{8cdot 4sqrt{3}}{2}=16sqrt{3}approx 27.7
$$
b. Since the perimeter of the square will be 24, the length of one of its sides will be 6. The area of a square is one of its sides squared:
$$
6^2=36
$$
Thus we note that the area of the square is larger than the area of the triangle.
c. Since the perimeter of the hexagon will be 24, the length of one of its sides will be 4. The area of a hexagon is then:
$$
dfrac{3sqrt{3}}{2}cdot 4^2=24sqrt{3}approx 41.6
$$
Thus we note that the area of the hexagon is larger than the area of the triangle and the square.
d. The greatest area will be obtained by a circle (because the regular $n$-gons will be approximate a circle as $n$ increases).
b. 36, Larger
c. 41.6, Larger
d. Circle
b. Still the second spinner, for the same reason.
b. Second spinner
b. $x$ are the values that are 50 units away from $-7$ and thus $x=-57$ and $x=43$.
c. $x$ are the values that are 12 units away from 10 and thus $x=-2$ and $x=22$.
d. This is impossible, because the absolute value (and the distance) is never negative.
e. You need to use the absolute value:
$$
|42-117|text{ or } |117-42|
$$
f. Add the absolute value signs:
$$
|x-47|=21text{ or }|47-x|=21
$$
g. (i)
$$
|x-4|=12
$$
(ii)
$$
|x+9|=15
$$
b. $x=-57$ and $x=43$
c. $x=-2$ and $x=22$
d. Impossible
e. $|42-117|$ or $|117-42|$
f. $|x-47|=21$ or $|47-x|=21$
g. (i) $|x-4|=12$ (ii) $|x+9|=15$
b. A circle
c. Yes, the number is $pi$ which is used in the calculation of the area and perimeter of a circle.
b. A circle
c. Yes
b. The ratio of their circumference is 3 (since this is the ratio of their radii). The ratio of their areas is then $3^2=9$.
c. The area is the product of the area of the original circle and the scale factor squared:
$$
r=3Rightarrow A=3^2pi=9pi
$$
$$
r=10Rightarrow A=10^2pi=100pi
$$
Thus in general:
$$
A=r^2pi
$$
d. The circumcenter is the product of the circumcenter of the original circle and the scale factor:
$$
r=3Rightarrow A=6pi
$$
$$
r=7Rightarrow A=14pi
$$
Thus in general:
$$
C=2rpi
$$
b. $3$, 9
c. $9pi$, $100pi$, $r^2pi$
d. $6pi$, $14pi$, $2rpi$
The area of a circle with radius 1 is $pi$, while its circumcenter is $2pi$.
All circles are similar. If the radius is $r$, then the area is $A=pi r^2$ and the circumference is $C=2pi r$.
All circles are similar. If the radius is $r$, then the area is $A=pi r^2$ and the circumference is $C=2pi r$.
a.
$$
A=pi r^2=pi 10^2=100pi units^2
$$
b.
$$
r=dfrac{d}{2}=dfrac{7}{2}=3.5
$$
$$
C=2pi r=2pi (3.5)=7pi units
$$
c.
$$
r^2 pi=A=121piRightarrow r^2=121Rightarrow r=11 units
$$
Thus the diamater is then 22 units.
d.
$$
2pi r=C=20pi Rightarrow r=10
$$
Then the area is:
$$
A=pi r^2=100pi
$$
b. $7pi$ units
c. 22 units
d. $100pi$
$$
dfrac{60}{360}
$$
The shaded part of the circle is then the part of the entire circle that is not white. The total circle is 100% or 1, thus the shaded part is then 1 decreased by the white part of the circle.
$$
1-dfrac{60}{360}=dfrac{360-60}{360}=dfrac{300}{360}
$$
which is answer B.
The sum of all exterior angles is 360$text{textdegree}$, thus the measure of an exterior angle is then:
$$
theta=dfrac{360text{textdegree}}{30}=12text{textdegree}
$$
Since interior angles and exterior angles are supplementary, the angle of interior angles is then:
$$
180text{textdegree}-12text{textdegree}=168text{textdegree}
$$
An interior angle of an $n$-gon is
$$
dfrac{n-2}{n}cdot 180text{textdegree}
$$
Repalce $n$ with 30:
$$
dfrac{28}{30}cdot 180text{textdegree}=168text{textdegree}
$$
$$
n=dfrac{360text{textdegree}}{18text{textdegree}}=20
$$
b. Divide the 20-gon into 20 congruent triangles. Determine the height of the triangle using the tangent ratio:
$$
x=1tan{81text{textdegree}}approx 6.3
$$
Since the area of a triangle is the product of the base and height divided by 2, the area of one of the smaller triangles is:
$$
dfrac{2cdot 6.3}{2}=6.3
$$
Since the area contains 20 of these triangles:
$$
AREA=20cdot 6.3=126units^2
$$
b. 126 units$^2$
*How can we prove two right triangles are congruent?*
If two right triangles have congruent hypotenuses and a pair of congruent legs, then the right triangles are congruent.
Before we start the proof, let’s make a plan on how to go from our Given statement to our Prove statement.
It is given that $overline{AB}perpoverline{DE}$ and $overline{DE}$ is a diameter of the circle. Let’s start by labeling the given diagram with all of the congruent segments. Recall that all radii of a circle must be congruent. Also, a segment is congruent to itself by the Reflexive Property so we can label $FC$ with tick marks to emphasize this:

$$text{Figure 1: Labeled diagram}$$
From Figure $1$, we can now see that the right triangles $triangle ACF$ and $triangle BCF$ have congruent hypotenuses and a pair of congruent legs.
Our plan for the proof is then:
1. State our givens.
2. Use the definition of $perp$ lines to list the right angles.
3. Use the Reflexive Property to conclude $overline{FC}congoverline{FC}$.
4. Use the HL $cong$ theorem to state the triangles are congruent.
5. Use the definition of congruence to conclude $overline{AF}$ and $overline{FB}$ are congruent.
| Statements| Reasons|
|–|–|
|1. $overline{AB}perpoverline{DE}$ and $overline{DE}$ is a diameter of $odot C$.|1. **Given**|
|2. $angle AFC$ and $angle BFC$ are right angles. |2. **Definition of $boldsymbol{perp}$ lines**|
|3. $overline{FC}congoverline{FC}$|3. **Reflexive Property**|
|4. $overline{AC}congoverline{BC}$|4. Definition of a circle (radii must be equal)|
|5. $boldsymbol{triangle ACFcongtriangle BCF}$|5. HL $cong$|
|6. $overline{AF}congoverline{FB}$|6. $boldsymbol{congtriangletextbf{s}rightarrowcongtextbf{ parts}}$
First, we recalled the triangle congruence theorem we have for right triangles. Then we applied applicable definitions and properties to the given diagram to find congruent segments. Next, we made a plan on how to go from the Given statement to the Prove statement. Using our plan, we then constructed a two-column proof.
$$
tan{54text{textdegree}}=dfrac{27}{AB}
$$
Multiply both sides of the equation by $AB$:
$$
ABtan{54text{textdegree}}=27
$$
Divide both sides of the equation by $tan{54text{textdegree}}$:
$$
AB=dfrac{27}{tan{54text{textdegree}}}approx 19.62
$$
Thus the correct answer is D.
a.
$$
x=0
$$
b.
$$
x+2=0Rightarrow x=-2
$$
c.
$$
x-5=0Rightarrow x=5
$$
b. $x=-2$
c. $x=5$
$$
A=pi 10^2=100pi
$$
The circumference of a circle is $C=2pi r$:
$$
C=2pi (10) =20pi
$$
b. A 45$text{textdegree}$ angle means that she eats $dfrac{45}{360}=dfrac{1}{8}$th of the pizza:
$$
A=dfrac{pi 8^2}{8}=8pi
$$
$$
C=dfrac{2pi (8)}{8}=2pi
$$
c. A 72$text{textdegree}$ angle means that she eats $dfrac{72}{360}=dfrac{1}{5}$th of the pizza:
$$
A=dfrac{pi 10^2}{5}=20pi
$$
$$
C=dfrac{2pi (10)}{5}=4pi
$$
d. A 30$text{textdegree}$ angle means that the arc has length $dfrac{30}{360}=dfrac{1}{12}$th of the original arc:
$$
C=dfrac{2pi (6)}{12}=pi
$$
e. A 20$text{textdegree}$ angle means that the area is $dfrac{20}{360}=dfrac{1}{18}$th of the original arc:
$$
A=dfrac{pi 10^2}{18}=dfrac{50}{9}pi
$$
b. $8pi$, $2pi$
c. $20pi$, $4pi$
d. $pi$
e. $frac{50}{9}pi$
b. Since the area of a circle is $A=pi r^2$, we then obtain:
$$
A=dfrac{theta}{360text{textdegree}}pi r^2
$$
$$
C_1=dfrac{2pi (3)}{12}=dfrac{pi}{2}
$$
$$
C_2=dfrac{2pi (5)}{12}=dfrac{5pi}{6}
$$
b. The ratio is:
$$
dfrac{C_1}{r}=dfrac{pi/2}{3}=dfrac{pi}{6}
$$
c. The ratio is:
$$
dfrac{C_2}{r}=dfrac{5pi/6}{5}=dfrac{pi }{6}
$$
We note that this ratio is equal to the ratio in (b).
d. The ratio is:
$$
dfrac{C}{r}=dfrac{2pi (100)/12}{100}=dfrac{pi}{6}
$$
e. Because the radian mesuare is also an angle measure like the degree measure, and thus both measures will represent the same angle.
b. $frac{pi}{6}$
c. $frac{pi}{6}$
d. $frac{pi}{6}$
e. Same angle
$$
A_1=dfrac{1}{10}pi 14^2=19.6pi in^2
$$
The area of one square piece is (1 foot = 12 inches):
$$
A_2=dfrac{12^2}{8}=dfrac{144}{8}=18in^2
$$
Thus a fair price would then be:
$$
dfrac{18}{19.6pi } $2.00approx $0.58
$$
b. The circumcenter of a circular piece is:
$$
C_1=dfrac{1}{10}2pi (14)=2.8pi inapprox 8.8in
$$
The circumcenter of a pizza piece is:
$$
C_2=dfrac{4cdot 12}{12}=4in
$$
Thus a circular piece is advised.
c. No, because somebody will always have the corner piece.
b. Circular piece
c. No
The area of the sector is $dfrac{theta}{360text{textdegree}}$th of the area of the full circle.
$$
A=dfrac{theta}{360text{textdegree}}pi r^2
$$
The arc of the sector is $dfrac{theta}{360text{textdegree}}$th of the arc of the full circle.
$$
text{Arc length}=dfrac{theta}{360text{textdegree}}2pi r
$$
A=dfrac{theta}{360text{textdegree}}pi r^2
$$
$$
text{Arc length}=dfrac{theta}{360text{textdegree}}2pi r
$$
$$
A=dfrac{theta}{360text{textdegree}}pi r^2
$$
The arc of the sector is $dfrac{theta}{360text{textdegree}}$th of the arc of the full circle.
$$
C=dfrac{theta}{360text{textdegree}}2pi r
$$
a. Then we obtain:
$$
A=dfrac{120text{textdegree}}{360text{textdegree}}pi 5^2=dfrac{25pi }{3}cm^2
$$
$$
C=dfrac{120text{textdegree}}{360text{textdegree}}2pi (5)=dfrac{10pi}{3}cm
$$
b. The diameter is 6 inches, thus the radius is 3 inches (since the radious is half the diameter).
$$
A=dfrac{180text{textdegree}}{360text{textdegree}}pi 3^2=dfrac{9pi }{2}=dfrac{9}{2}pi in^2
$$
$$
C=dfrac{180text{textdegree}}{360text{textdegree}}2pi (3)=dfrac{6pi}{2}=3pi in
$$
b. $3pi$ in, $frac{9}{2}pi$ in$^2$
$$
x+x+x=180text{textdegree}
$$
Combine like terms:
$$
3x=180text{textdegree}
$$
Divide both sides of the equation by 3:
$$
x=60text{textdegree}
$$
$$
130text{textdegree}+46text{textdegree}+102text{textdegree}+x=360text{textdegree}
$$
Combine like terms:
$$
278text{textdegree}+x=360text{textdegree}
$$
Subtract 278$text{textdegree}$ from both sides of the equation:
$$
x=82text{textdegree}
$$
$$
10x+8x-16+12x-8+7x+2+9x+4+6x+10=720text{textdegree}
$$
Combine like terms:
$$
52x-8=720text{textdegree}
$$
Add 8 to both sides of the equation:
$$
52x=728text{textdegree}
$$
Divide both sides of the equation by 52:
$$
x=14text{textdegree}
$$
$$
x+123text{textdegree}+113text{textdegree}+97text{textdegree}+90text{textdegree}=540text{textdegree}
$$
Combine like terms:
$$
x+423text{textdegree}=540text{textdegree}
$$
Subtract 423$text{textdegree}$ from both sides of the equation:
$$
x=117text{textdegree}
$$
b. $x=82text{textdegree}$
c. $x=14text{textdegree}$
d. $x=117text{textdegree}$
$$
2pi r=C=24cm
$$
Divide both sides of the equation by $2pi$:
$$
r=dfrac{24}{2pi}cm
$$
Thus the greatest area is a circle with radius $dfrac{24}{2pi}$ cm.
$$
2pi r=C=18pi cm
$$
Divide both sides of the equation by $2pi$:
$$
r=dfrac{18pi }{2pi}cm=9cm
$$
Thus the greatest area is a circle with radius $9$ cm.
b. Circle with radius 9 cm
a.
$$
C=2pi (14)=28pi units
$$
$$
A=pi (14)^2=196 pi units^2
$$
b.
$$
C=2pi (5)=10pi units
$$
$$
A=pi (5)^2=25pi units^2
$$
c.
$$
2pi r=C=100pi units
$$
Divide both sides of the equation by $2pi$:
$$
r=50 units
$$
The area is then:
$$
A=pi (50)^2=2500pi units^2
$$
d.
$$
2pi r=C
$$
Divide both sides of the equation by $2pi$:
$$
r=dfrac{C}{2pi}
$$
The area is then:
$$
A=pi left(dfrac{C}{2pi}right)^2=dfrac{pi C^2}{4pi^2}=dfrac{C^2}{4pi}
$$
b. $10pi$ units, $25pi$ units$^2$
c. 2500$pi$ units$^2$
d. $frac{C^2}{4pi}$
$$
P(blue)=100%-40%-10%=50%
$$
b.
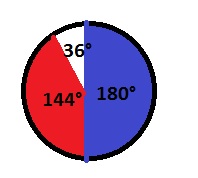
b. Sketch
c. No
$$
cos{58.5text{textdegree}}=dfrac{x}{7}
$$
b. The cosine of an angle is equal to the sine of the complementary angle:
$$
sin{31.5text{textdegree}}=dfrac{x}{7}
$$
Multiply both sides of the equation by 7:
$$
3.654=7(0.522)approx 7sin{31.5text{textdegree}}=x
$$
b. $x=3.654$
b. No, the solutions are complex. Subtract 4 from both sides of the equation:
$$
(x-11)^2=-4
$$
Take the square root of both sides of the equation:
$$
x-11=pm sqrt{-4}
$$
Add 11 to both sides of the equation:
$$
x=11pm sqrt{-4}=11pm 2i
$$
b. No, there are no real solutions but there are complex solutions.
a.
$$
C=2pi (93,000,000)=186,000,000pi milesapprox 584,336,233 miles
$$
b. It takes eath one year to complete an orbit, determine the number of hours in a year:
$$
365 cdot 24=8760 hours
$$
The speed is the distance divided by the time:
$$
dfrac{186,000,000pi}{8760}approx 21,233pi mphapprox 66,705 mph
$$
b. 66,705 mph
$$
A=dfrac{theta}{360text{textdegree}}pi r^2
$$
Determine the area of the largest circle sector:
$$
A=dfrac{120text{textdegree}}{360text{textdegree}}pi (20)^2=dfrac{400pi}{3}in^2
$$
Determine the area of the smallest circle sector:
$$
A=dfrac{120text{textdegree}}{360text{textdegree}}pi (5)^2=dfrac{25pi}{3}in^2
$$
Determine the difference in areas:
$$
dfrac{400pi}{3}-dfrac{25pi}{3}=dfrac{375pi}{3}=125pi in^2approx 393 in^2
$$
125pi in^2approx 393 in^2
$$
$$
A=pi 1.5^2=2.25piapprox 7 in^2
$$
The area of a square is the length of its side squared:
$$
A=12^2=144in^2
$$
Thus the amount of cookie dough wasted is then:
$$
144in^2-16cdot 7in^2approx 31in^2
$$
The amount of cookie dough wasted for a few other diameters is:
$$
144in^2-1cdot pi(6)^2in^2approx 31in^2
$$
$$
144in^2-4cdot pi(3)^2in^2approx 31in^2
$$
$$
144in^2-9cdot pi(2)^2in^2approx 31in^2
$$
Thus we note that the radius of the cookies does not change the amount of cookie dough wasted.
$$
C=dfrac{theta}{360text{textdegree}}2pi r
$$
a. The radian measure of a circle with radius 5 is:
$$
dfrac{C}{r}=dfrac{dfrac{45text{textdegree}}{360text{textdegree}}2pi (5)}{5}=dfrac{pi}{4}
$$
The radian measure of a circle with radius 1 is:
$$
dfrac{C}{r}=dfrac{dfrac{45text{textdegree}}{360text{textdegree}}2pi (1)}{1}=dfrac{pi}{4}
$$
b. We note that the angle measure is:
$$
dfrac{2pi theta}{360text{textdegree}}=dfrac{pi}{3}
$$
Divide both sides of the equation by $pi$:
$$
dfrac{ theta}{180text{textdegree}}=dfrac{1}{3}
$$
Multiply both sides of the equation by 180$text{textdegree}$:
$$
theta=dfrac{180text{textdegree}}{3}=60text{textdegree}
$$
b. 60$text{textdegree}$
$$
2cdot dfrac{pi}{2}=pi
$$
pi
$$
$$
A=pi 30^2=900piapprox 2,827 ft^2
$$
The area of a rectangle is the product of the length and the width:
$$
A=55cdot 60=3300 ft^2
$$
The amount of grass that needs to be ordered is then:
$$
2,827ft^2+3,300ft^2=6,127ft^2
$$
b. The circumcenter of a circle is $C=2pi r$:
$$
C=2pi (30)=60piapprox 189ft^2
$$
The total perimeter is then:
$$
189+55+55=299ft
$$
The cost of the fence is then:
$$
299cdot $8=$2,392
$$
c. The area of the new design is the product of the area of the original design with the square of the linear scale factor:
$$
A=2^2cdot 6,127=24,508ft^2
$$
The perimeter of the new design is the product of the perimeter of the original design with the linear scale factor:
$$
P=2cdot 299=598 ft
$$
b. $$2392$
c. 24,580 ft$^2$, 598 ft
$$138degree+106degree+m+13degree+120degree+133degree+m+m-9degree=900degree$$
$$501degree+3m=900degree$$
Subtract 501° from both sides of the equation:
$$3m=399degree$$
Divide both sides of the equation by 3:
$$m=133degree$$
$$x+x+64degree=180degree$$
Subtract 64° from both sides of the equation:
$$2x=116degree$$
Divide both sides of the equation by 2:
$$x=58degree$$
The sum of all angles in a pentagon is 540°:
$$64degree+58degree+90degree+96degree+k+88degree=540degree$$
Combine like terms:
$$396degree+k=540degree$$
Subtract 396° from both sides of the equation:
$$k=144degree$$
$$135degree+2y+3y+180degree=540degree$$
Combine like terms:
$$5y+315degree=540degree$$
Subtract 315° from both sides of the equation:
$$5y=225degree$$
Divide both sides of the equation by 5:
$$y=45degree$$
b. $k=144degree$
c. $y=45degree$
$$
sqrt{5^2+3^2}=sqrt{34}
$$
The perimeter is the sum of all lengths of the sides:
$$
5’+8’+5’+sqrt{34}’=(18+sqrt{34})’
$$
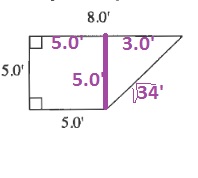
$$
tan {35text{textdegree}}=dfrac{x}{10}
$$
Multiply both sides of the equation by 10:
$$
7.00approx 10tan{35text{textdegree}}=x
$$
$$
x=cos^{-1}{dfrac{60}{120}}=60text{textdegree}
$$
$$
sin{45text{textdegree}}=dfrac{5}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{45text{textdegree}}=5
$$
Divide both sides of the equation by $sin{45text{textdegree}}$:
$$
x=dfrac{5}{sin{45text{textdegree}}}approx 7
$$
$$
sin{42text{textdegree}}=dfrac{x}{500}
$$
Multiply both sides of the equation by 500:
$$
335approx 500sin{42text{textdegree}}=x
$$
Thus the kite is about 335 ft above the ground.
b. $x=7.00$
c. $x=60text{textdegree}$
d. $x=7$
e. $x=335$ ft
a.
$$
x+4=0Rightarrow x=-4
$$
b.
$$
x+27=0Rightarrow x=-27
$$
c.
$$
x-40=0Rightarrow x=40
$$
d.
$$
x+32=0Rightarrow x=-32
$$
b. $x=-27$
c. $x=40$
d. $x=-32$
$$
P(A, C, and E)=P(A)cdot P(C)cdot P(E)=dfrac{3}{4}cdot dfrac{1}{2}cdot dfrac{1}{3}=dfrac{1}{8}=0.125=12.5%
$$
b. The combinations that have at least one vowel are:
ACE, ACF, ACG, ADE, ADF, ADG, BCE, BDE
Note that all combinations that start with an A will have equal probability and the combinations that start with B also have an equal probability:
$$
P(vowel)=6cdot P(ACE)+2cdot P(BCE)=6cdot dfrac{1}{8}+2cdot dfrac{1}{4}cdot dfrac{1}{2}cdot dfrac{1}{3}=dfrac{3}{4}+dfrac{1}{12}=dfrac{5}{6}approx 0.833=83.3%
$$
b. $frac{5}{6}approx 0.833=83.3%$
$$
thetatext{ radians}=dfrac{theta cdot 360text{textdegree}}{2pi}
$$
a.
$$
2pi text{ radians}=dfrac{2pi 360text{textdegree}}{2pi}=360text{textdegree}
$$
b.
$$
dfrac{pi}{6} text{ radians}=dfrac{pi/6cdot 360text{textdegree}}{2pi}=30text{textdegree}
$$
c.
$$
dfrac{pi}{3} text{ radians}=dfrac{pi/3cdot 360text{textdegree}}{2pi}=60text{textdegree}
$$
d.
$$
dfrac{pi}{4} text{ radians}=dfrac{pi/4cdot 360text{textdegree}}{2pi}=45text{textdegree}
$$
b. 30$text{textdegree}$
c. 60$text{textdegree}$
d. 45$text{textdegree}$

