All Solutions
Page 599: Questions
$$
S=2(6)+2(8)+2(12)=52
$$
The volume is equal to the number of blocks in the figure and since each layer contains 12 blocks:
$$
V=2(12)=24
$$
Volume 24
b. The surface area is the sum of the area of each surface:
$$
S=2cdot dfrac{3cdot 4}{2}+9cdot 4+9cdot 3+9cdot 5=120cm^2
$$
c. The volume of the triangular prism is the area of the base surface multiplied by the height:
$$
V=dfrac{3cdot 4}{2}cdot 9=54cm^3
$$
b. 120 cm$^2$
c. 54 cm$^3$
Determine the area of the regular hexagon that is the base:
$$
A=dfrac{3sqrt{3}}{2}a^2=dfrac{3sqrt{3}}{2}(4)^2=6sqrt{3}in
$$
The surface area is the sum of the areas of each surface:
$$
S=2(6sqrt{3})+6(4cdot 7)=12sqrt{3}+168in^2
$$
The volume is the product of the area of the base and the height:
$$
V=6sqrt{3}cdot 7=42sqrt{3}in^3
$$
Volume $42sqrt{3}$ in$^3$
$$
A=2pi (5)cdot 8=80pi units^2
$$
The surface area is the sum of the areas of each surface:
$$
S=2(pi 5^2)+80pi=130pi units^2
$$
The volume is the product of the area of the base and the height:
$$
V=pi 5^2 cdot 8=200pi units^3
$$
Surface area $130pi$ units$^2$
b. No, the volume would remain the same.
c. The volume of the cylinder is then the product of the area of the base and the height:
$$
V=pi 5^2cdot 8=200pi units^3
$$
b. No
c. 200$pi$ units$^3$
$$
V=pi 1^2cdot 3=3pi ft^3approx 9.42ft^3
$$
Determine the number of gallons:
$$
dfrac{9.42}{0.1337}approx 70 gallons
$$
Thus we note that the tank can only contain 70 gallons and thus the tank will not provide enough water.
$$
A=dfrac{3sqrt{3}}{2}a^2=dfrac{3sqrt{3}}{2}(14)^2=294sqrt{3}cm^2
$$
The volume is the product of the area of the base and the height:
$$
h=dfrac{V}{A}=dfrac{2546.13}{294sqrt{3}}approx 5cm
$$
The surface area is the sum of the areas of each surface:
$$
S=2(294sqrt{3})+6(14cdot 5)=588sqrt{3}+420cm^2
$$
Surface area $588sqrt{3}+420$cm$^2$
$$
triangle ADEsim triangle ABC
$$
and the linear scale factor is $dfrac{1}{2}$.
The area of the smaller triangle is then the area of the larger triangle multiplied by the linear scale factor squared:
$$
A=96cdot dfrac{1}{2^2}=24units^2
$$
24units^2
$$
$$
dfrac{DE}{4}=dfrac{10}{16-10}
$$
Multiply both sides of the equation by $4$:
$$
DE=dfrac{10(4)}{6}=6dfrac{2}{3}
$$
The diameter is then:
$$
DC=DE+EC=6dfrac{2}{3}+4=10dfrac{2}{3}
$$
Since the radius is half the diameter:
$$
r=5dfrac{1}{3}
$$
5dfrac{1}{3}
$$
b. By dilating the circle(s) about $P$.
c. The arc length is
$$
dfrac{theta}{360text{textdegree}}(2pi r)=dfrac{60text{textdegree}}{360text{textdegree}}(2pi 14)=dfrac{14}{3}pi
$$
b. By dilating the circle(s) about $P$.
c. $=dfrac{14}{3}pi$
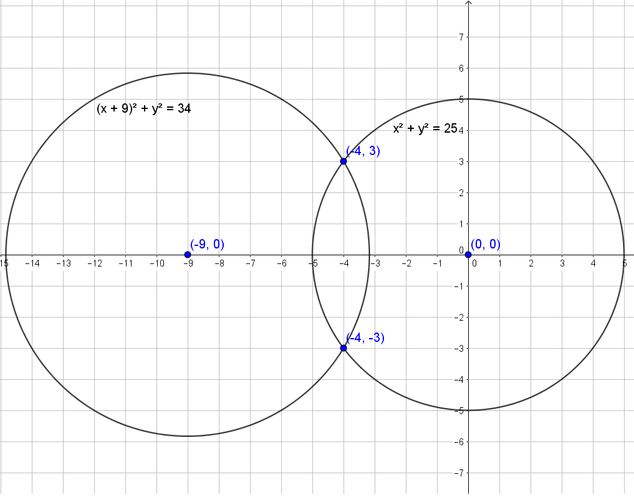
$(x+9)^2+y^2=34$ is a circle with center $(-9,0)$ and radius $sqrt{34}approx 5.831$
On the graph, we note that the intersection of the two graphs is
$$
(-4,pm 3)
$$
$$
(x+9)^2-x^2=34-25
$$
Simplify:
$$
18x+81=9
$$
Subtract 81 from both sides of the equation:
$$
18x=-72
$$
Divide both sides of the equation by 18:
$$
x=-4
$$
Determine $y$:
$$
y^2=25-x^2=25-(-4)^2=25-16=9
$$
Take the square root of both sides of the equation:
$$
y=pm 3
$$
Thus the solutions are $(-4, pm 3)$.
(-4, pm 3)
$$
$$
5^4=(5^2)^2=25^2=125^{x+1}=(5^3)^{x+1}=5^{3(x+1)}
$$
The powers have to be equal:
$$
4=3(x+1)
$$
Divide both sides of the equation by 3:
$$
dfrac{4}{3}=x+1
$$
Subtract 1 from both sides of the equation:
$$
dfrac{1}{3}=x
$$
$$
dfrac{x}{5}+dfrac{x-1}{3}=2
$$
Multiply both sides of the equation by 15:
$$
3x+5(x-1)=30
$$
Use distributive property:
$$
3x+5x-5=30
$$
Add 5 to both sides of the equation:
$$
8x=35
$$
Divide both sides of the equation by 8:
$$
x=dfrac{35}{8}=4.375
$$
$$
(x-2)^2=25
$$
Take the square root of both sides of the equation:
$$
x-2=pm 5
$$
Add 2 to both sides of the equation:
$$
x=2pm 5=7text{ or }-3
$$
$$
3^{2x}=(3^2)^x=9^x=left( dfrac{1}{3}right)^{x+3}=(3^{-1})^{x+3}=3^{-(x+3)}
$$
The powers have to be equal:
$$
2x=-(x+3)
$$
Add $x$ to both sides of the equation:
$$
3x=-3
$$
Divide both sides of the equation by 3:
$$
x=-1
$$
b. $x=frac{35}{8}$
c. $x=7$ and $x=-3$
d. $x=-1$
The sine ratio is the opposite side of the angle divided by the hypotenuse:
$$
sin theta =dfrac{2}{8}=dfrac{1}{4}
$$
Solve to $theta$ using the $sin^{-1}$ command on your calculator:
$$
theta = sin^{-1}dfrac{1}{4}approx 14.48text{textdegree}
$$
The angle of the ladder is then double as big (see figure):
$$
2theta approx 28.96text{textdegree}approx 29text{textdegree}
$$
Or in radians: $0.5054$.
Radian: 0.0504
b.

b. Graph
c. Ratio $1/R^3$
d. 1000, $r^3$
Build the solid using wooden boxes with the dimensions $1times1times1$.
If each of the dimensions of the solid is enlarged by the linear scale factor of $2$, then each dimension of the solid is doubled, resulting in a solid with the dimensions of $2times2times6$.
If you would build the solid from the part **B**, you would need $7$ more solids of the dimensions $1times1times3$. You need to add one solid on top of the existing solid, add two more solids laterally to the first two solids, and then add four more solids in front of the first two solids to make a solid with the dimensions of $2times2times6$.
If the solid of the dimensions $1times1times3$ would be enlarged by the linear scale factor of $3$, then the resulting solid would have a dimension of $3times3times9$. Its volume can be calculated using the formula $V=abc$.
$$begin{aligned}
V&=3cdot3cdot9\
V&=81
end{aligned}$$
If the volume of the initial solid is $3$, then the volume of the resulting solid is $27$ times larger.

$$begin{aligned}
dfrac{v_n}{v_o}=r^3cdottext{(original volume)}
end{aligned}$$
where
$r$ – is the linear scale factor.
$v_o$ – is the original volume.
$v_n$ – is the new volume
$$begin{aligned}
text{original volume}&=1times1times3\
text{original volume}&=3medspacetext{units}^3
end{aligned}$$
$$begin{aligned}
dfrac{v_n}{v_o}cdottextcolor{#4257b2}{(v_o)}&=r^3cdottextcolor{#4257b2}{(v_o)}\
v_n&=r^3cdot v_o
end{aligned}$$
$$begin{aligned}
v_n&=(3)^3cdot(3)\
v_n&=81medspacetext{units}^3
end{aligned}$$
$$
320cdot 1.5^3=1080
$$
Thus the medium tub should hold 1,080 kernels of popcorn.
If the linear scale factor is 2, then the volume increases by $2^3=8$ times.
If the linear scale factor is $r$, then the volume increases by $r^3$ times.
$$
2^3cdot 3=8cdot 3=24text{breaths}
$$
We thus require 24 breaths in total.
However, she already made 3 breaths and thus $24-3=21$ additional breaths are required.
$$
B=pi r^2=pi 6^2=36pi in^2
$$
The surface area is then the sum of all areas of the surfaces:
$$
S=2(36pi)+(2pi (6))(9)=72pi +108pi = 180pi in^2
$$
b. The volume of the cylinder is the product of the area of the base and the height:
$$
V=pi 6^2cdot 9=324pi in^3
$$
c. If the linear scale factor is 3, then the volume is multiplied by the scale factor cubed:
$$
V=3^3cdot 324pi = 8,748pi in^3
$$
$$
V=pi 6^2cdot 9=324pi in^3
$$
We know that 12 in = 1 ft:
$$
V=dfrac{324pi}{12^3}=dfrac{3pi}{16}ft^3
$$
dfrac{3pi}{16}ft^3
$$
$$
180text{textdegree}-135text{textdegree}=45text{textdegree}
$$
The exterior angle is 360$text{textdegree}$ divided by the number of sides $n$ and thus:
$$
n=dfrac{360text{textdegree}}{45text{textdegree}}=8
$$
Thus the number of sides is 8.
$$
B=2(1+sqrt{2})a^2=2(1+sqrt{2})25^2=1250+1250sqrt{2}in^2
$$
The volume is then the area of the base multiplied by the height:
$$
V=(1250+1250sqrt{2})10=12500+12500sqrt{2}ft^3approx 30,178ft^3
$$
b. 30,178 ft$^3$
$$
OX=sqrt{20^2-15^2}=sqrt{175}=5sqrt{7}
$$
The area of the circle is the product of $pi$ and the radius squared:
$$
A=pi (sqrt{175})^2=175pi cm^2
$$
$$
theta = sin^{-1}dfrac{15}{20}approx 49text{textdegree}
$$
The area of the circle sector is then:
$$
A=dfrac{theta}{360text{textdegree}}pi r^2=dfrac{49text{textdegree}}{360text{textdegree}}175pi approx 75cm^2
$$
$$
A=dfrac{5sqrt{7}cdot 15}{2}-75approx 24 cm^2
$$
b. 75 cm$^2$
d. 24 cm$^2$
$$
y=(x^2+3x+2.25)+4-2.25
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
y=(x+1.5)^2+1.75
$$
$$
0=(x+1.5)^2+1.75
$$
Subtract 1.75 from both sides of the equation:
$$
-1.75=(x+1.5)^2
$$
Take the square root of both sides of the equation:
$$
pm 0.5sqrt{7}i=pm sqrt{-1.75}=x+1.5
$$
Subtract 1.5 from both sides of the equation:
$$
-1.5pm 0.5sqrt{7}i=x
$$
Thus we note that the solutions are complex, because the graph does not intersect the $x$-axis.
x=-1.5pm 0.5sqrt{7}i
$$
Graph doesn’t intersect $x$-axis
$$
P=7+7+7sqrt{2}=14+7sqrt{2}mmapprox 24mm
$$
$$
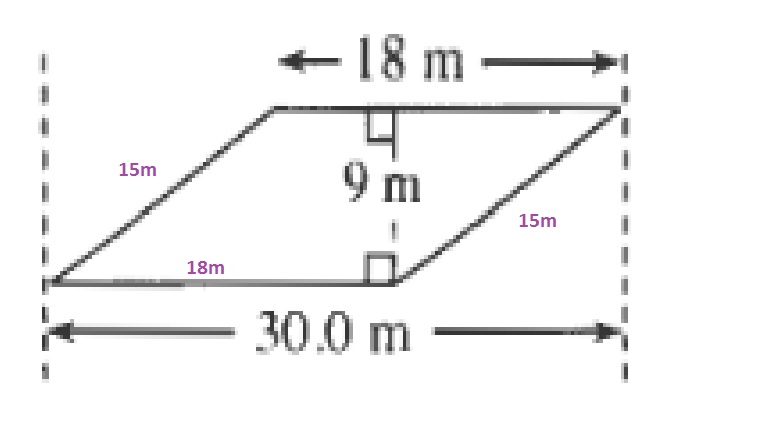
P=18+15+18+15=66m
$$
$$
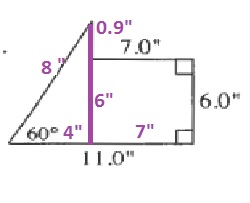
P=8+11+6+7+0.9=32.9ft
$$
b. 66 m
c. 32.9 ft
$$
(1,-3)
$$
b. Use the Pythagorean theorem:
$$
sqrt{(x-1)^2+(y+2)^2}
$$
c. The distance is the difference in $y$-values:
$$
y-4
$$
d.
$$
sqrt{(x-1)^2+(y+2)^2}=y+4
$$
Square both sides of the equation:
$$
(x-1)^2+(y+2)^2=y^2+8y+16
$$
Subtract $y^2$ from both sides of the equation:
$$
(x-1)^2+4y+4=8y+16
$$
Subtract $4y$ from both sides of the equation:
$$
(x-1)^2+4=4y+16
$$
Subtract 16 from both sides of the equation:
$$
(x-1)^2-12=4y
$$
Divide both sides of the equation by $4$:
$$
dfrac{1}{4}(x-1)^2-3=y
$$
Thus the equation of the parabola $y=dfrac{1}{4}(x-1)^2-3$.
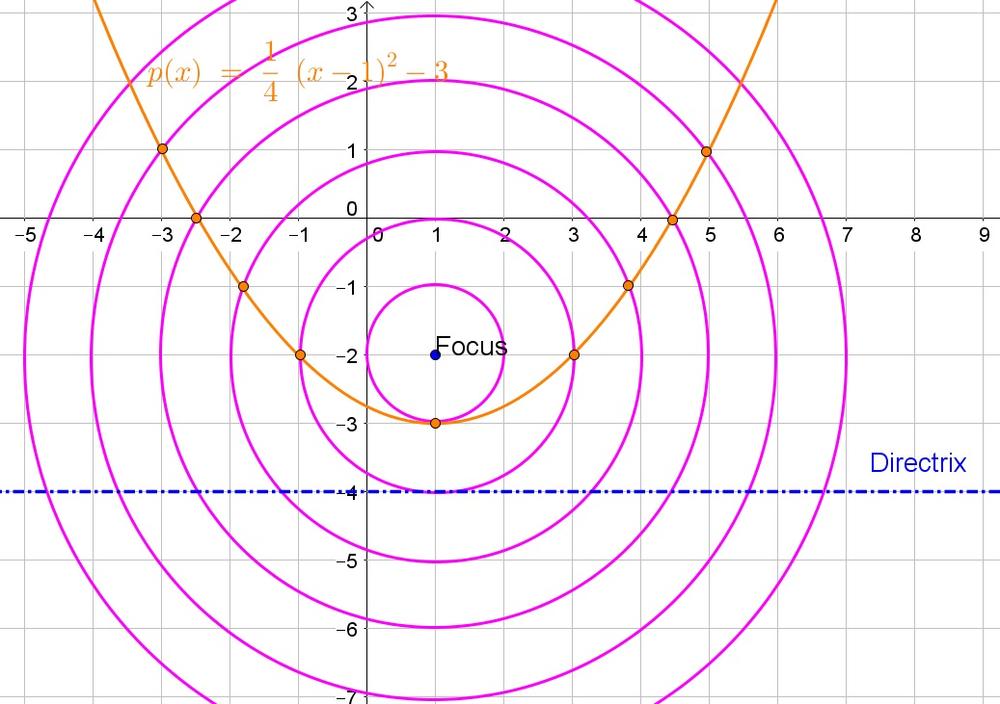
b. $sqrt{(x-1)^2+(y-2)^2}$
c. $y-4$
d. $y=frac{1}{4}(x-1)^2-3$
$$
1.5pintscdot 4^2=24pints=3gallons
$$
$$
14pounds cdot 4^3=896pounds
$$
b. 896 pounds
$$
V=20cdot 12,000cdot dfrac{5^3}{4^3}=468,750gallons
$$
Determine the difference in volume:
$$
Delta V=468,750-20cdot 12,000=228,750gallons
$$
c.
$$
V=dfrac{12,000}{7.48}approx 1,604 ft^3
$$
d.
$$
V=dfrac{1,604}{3.28^3}approx 45m^3
$$
e. In (d) you needed to divide by the cubed factor and in (c) not, this is because the factor was given in feet and the units were given in cubic feet.
b. Standard tanks
c. 1,604 ft$^3$
d. 45 m$^3$
e. Cubed factor
$$
V=9.5cdot 12cdot dfrac{1}{3}=38ft^3
$$
Since 1 ft = 3 yards:
$$
V=dfrac{38}{3^3}=dfrac{38}{27}approx 1.4 text{yards}^3
$$
Her error was thus that she did not write the inches in feet to determine the volume.
b. The surface area is the sum of the areas of the surfaces:
$$
S=3+1+4+2+2+4+4+4=24
$$
The surface area of the bigger solid is then the product of the surface area and the linear scale factor squared:
$$
S=24cdot 2^2=96
$$
The ratio of the surface areas is then the linear scale factor squared: 4.
c. The volume is the number of blocks in the solid:
$$
V=6
$$
The volume of the bigger solid is then the product of the volume and the linear scale factor cubed:
$$
S=6cdot 2^3=48
$$
The ratio of the volumes is then the linear scale factor cubed: 8.
b. 24, 4, $2^2$
c. 6
$$
(n-2)180text{textdegree}
$$
Thus if $n=1002$:
$$
(1002-2)180text{textdegree}=(1000)180text{textdegree}=180,000text{textdegree}
$$
$$
B=dfrac{45text{textdegree}}{360text{textdegree}}(pi 2^2)=dfrac{pi}{2}ft^2
$$
The volume of the solid is then the product of the area of the base and the height:
$$
V=dfrac{pi}{2}cdot 4=2pi ft^3
$$
2pi ft^3
$$
$$
dfrac{IG}{6}=dfrac{9}{8}
$$
Multiply both sides of the equation by 6:
$$
IG=dfrac{9cdot 6}{8}=6.75
$$
6.75
$$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
The given circle has center $(0,0)$ and radius $3$, thus the equation is:
$$
x^2+y^2=3^2
$$
$$
1^2+(sqrt{5})^2=1+5=6neq 9=3^2
$$
Thus the point does NOT lie on the circle.
b. Replace $y$ with $sqrt{5}$:
$$
x^2+5=x^2+(sqrt{5})^2=3^2=9
$$
Subtract 5 from both sides of the equation:
$$
x^2=4
$$
Take the square root of both sides of the equation:
$$
x=pm 2
$$
c. Given that the radius is 3, we know that $(3,0)$, $(-3,0)$ and $(0,-3)$ are also on the circle.
b. $x=pm 2$
c. $(3,0)$, $(-3,0)$, $(0,-3)$
$$
s=sqrt[3]{27}=sqrt[3]{3^3}=3
$$
b. 2 yards
$$
f(x)=45x
$$
Since there cannot be a nonnegative number of participants, the domain contains only the nonnegative integers:
$$
mathbb{N}
$$
b. The profit is the revenue decreased by the cost:
$$
p(x)=45x-1200
$$
Let $p(x)$ be zero:
$$
0=45x-1200
$$
Add 1200 to both sides of the equation:
$$
1200=45x
$$
Divide both sides of the equation by 45:
$$
27approx x
$$
Thus Jamie makes a profit if she has at least 27 participants per month.
b. 27 participants
Soray should buy tent A because it will have a greater volume than tent B.
b. Each layer is a rectangular prism.
c. The volumes are identical (because the layers have only been moved around)
d. You need three copies of the pyramid to assemble a cube. Thus you calculate the volume of a pyramid by dividing the volume of the prism by 3.
e. Yes, because all pyramids and corresponding prisms have the same shapes.
b. Each layer is a rectangular prism.
c. The volumes are identical.
d. You need three copies of the pyramid to assemble a cube.
e. Yes
$$
V_A=dfrac{5cdot 6}{2}cdot 6=90in^3
$$
$$
V_B=dfrac{1}{3}dfrac{3sqrt{3}}{2}cdot 4^2cdot 6=48sqrt{3}approx 83in^3
$$
Determine the base areas:
$$
B_A=6cdot 6=36in^2
$$
$$
B_B=dfrac{3sqrt{3}}{2}cdot 4^2=24sqrt{3}approx 42in^2
$$
Determine the surface area:
$$
S_A=36+2cdot dfrac{5cdot 6}{2}+2cdot sqrt{34}cdot 6=66+12sqrt{34}approx 136in^2
$$
$$
S_B=24sqrt{3}+6cdot dfrac{4sqrt{52}}{2}approx 128in^2
$$
The volume of the first tent is bigger, thus you should buy this tent.
The slant height and height are both sides of a rectangular triangle, thus the Pythagorean theorem can be used to determine the other.
The volume of a circle is the product of the area of the base and the height, while the surface area contains the area of two circles and the area of a rectangle with length the circumference of a circle.
The volume of a pyramid is one-third of the product of the area of the base and the height, while the surface area is the sum of the area of the surfaces.
$$
sqrt{96^2+220^2}=sqrt{57,616}approx 240
$$
The area of one of its upstanding surface is then:
$$
S=dfrac{240cdot 96}{2}=11,520 m^2
$$
The total surface area (without the base) is then:
$$
4S=4(11,520 )=46,080 m^2
$$
The number of gallons needed is then:
$$
dfrac{46,080 }{250}=184.32approx 184
$$
Thus about 184 gallons are needed.
$$
V=7cdot 13cdot 12=1,092in^3approx 0.632 ft^3
$$
b. Determine the number of gallons:
$$
0.632cdot 7.48=4.727gallons
$$
b. 4.727 gallons
$$
dfrac{500pi}{4pi}=125
$$
The ratio of the heights is the cubic root of the ratio of the volumes:
$$
sqrt[3]{125}=sqrt[3]{5^3}=5
$$
$$
mangle C=moverarc{PQ}=360text{textdegree}-314text{textdegree}=46text{textdegree}
$$
The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
CP=dfrac{5}{tan{46text{textdegree}}}=4.83
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
CR=dfrac{5}{sin{46text{textdegree}}}approx 6.95
$$
Then we obtain:
$$
x=CR-CQ=CR-CP=6.95-4.83=2.12
$$
$$
dfrac{x}{2}=7sin{102text{textdegree}}approx 6.85
$$
Multiply both sides of the equation by 2:
$$
xapprox 13.7
$$
b. $x=13.7$
b. On the graph we note that $(0,-4)$ is a point and thus $f(0)=-4$.
c. On the graph we note that $(-3.8,4)$ and $(2.8,4)$ are points and thus $x=-3.8$ and $x=2.8$.
d. On the graph we note that $(-2,0)$ and $(2,0)$ are points and thus $x=-2$ and $x=2$.
b. $-4$
c. $x=-3.8$ and $x=2.8$
d. $x=-2$ and $x=2$
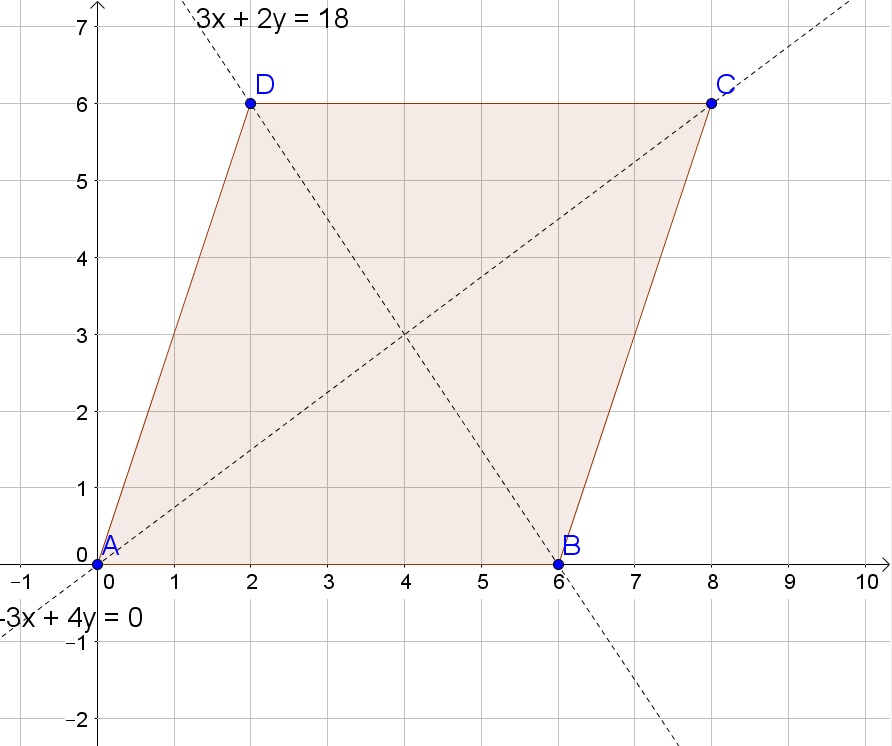
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$
Thus we then obtain for the line $overline{AC}$:
$$
y=dfrac{4}{3}x
$$
and for line $overline{BD}$:
$$
y=-dfrac{3}{2}(x-6)
$$
b. $y=frac{4}{3}x$, $y=-frac{3}{2}(x-6)$.
$$
300x=3900
$$
Divide both sides of the equation by 300:
$$
x=13
$$
$$
18x=10x+24
$$
Subtract $10x$ from both sides of the equation:
$$
8x=24
$$
Divide both sides of the equation by 8:
$$
x=3
$$
$$
(x-5)(x+5)leq 0
$$
Since the function $y=(x-5)(x+5)$ opens upwards:
$$
-5leq x leq 5
$$
$$
3x-24
$$
Add 2 to both sides of the equation:
$$
3×6
$$
Divide both sides of the equation by 3:
$$
x2
$$
b. $x=3$
c. $-5leq xleq 5$
d. $x2$
$$
3V=pi r^2 h
$$
Divide both sides of the equation by $pi r^2$:
$$
dfrac{3V}{pi r^2}=h
$$
Interchange left and right sides of the equation:
$$
h=dfrac{3V}{pi r^2}
$$
$$
2K=mv^2
$$
Divide both sides of the equation by $m$:
$$
dfrac{2K}{m}=v^2
$$
Take the square root of both sides of the equation (and note that a negative velocity is impossible):
$$
sqrt{dfrac{2K}{m}}=v
$$
Interchange left and right sides of the equation:
$$
v=sqrt{dfrac{2K}{m}}
$$
b. $v=sqrt{frac{2K}{m}}$
$$
B=6^2=36units^2
$$
The volume of the pyramid is the product of the area of the base and the height divided by 3:
$$
V=dfrac{36cdot 4}{3}=48units^3
$$
$$
s=sqrt{3^2+4^2}=sqrt{25}=5units
$$
Determine the area of the triangle:
$$
A=dfrac{6cdot 5}{2}=15units^2
$$
Determine the surface area:
$$
S=B+4A=36+4(15)=96units^2
$$
Surface area 96 units$^2$
$$
h=0.5sin{88.2text{textdegree}}approx 0.5
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{1cdot 0.5}{2}=0.25
$$
Since the polygon is made up out of 100 triangles, the area of the polygon is:
$$
100cdot 0.25=25units^2
$$
25units^2
$$
$$
Vcdot 9^3=729V
$$
$$
B=pi 3^2=9pi ft^2
$$
The volume of the cylinder is the product of the area of the base and the height:
$$
V=9pi cdot 4=36pi ft^3approx 113ft^3
$$
36pi ft^3
$$
$$
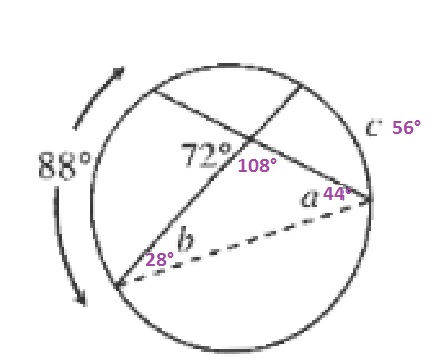
a=dfrac{88text{textdegree}}{2}=44text{textdegree}
$$
The exterior angle is equal to the sum of the angles of the triangle with the exception of the corresponding interior angle:
$$
b=72text{textdegree}-44text{textdegree}=28text{textdegree}
$$
The meausre of the arc is twice the measure ofthe inscribed angle:
$$
c=2(28text{textdegree})=56text{textdegree}
$$
b. No
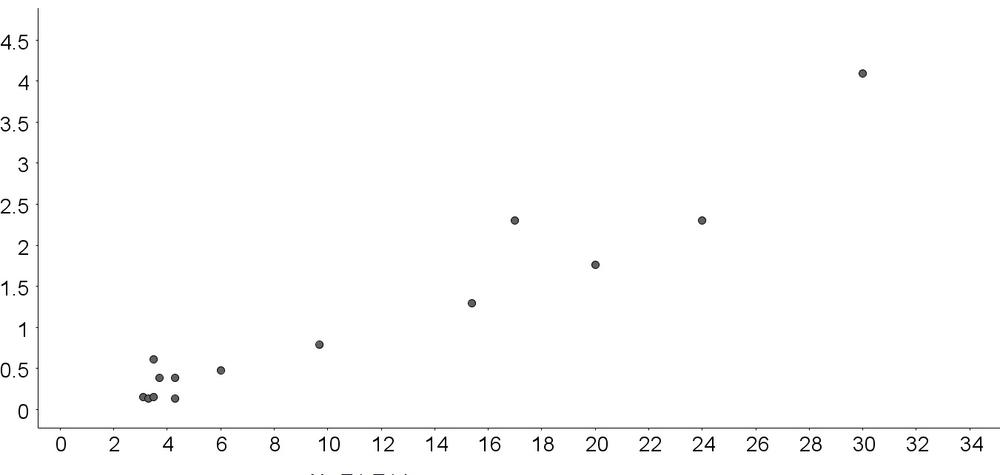
c. Quadratic: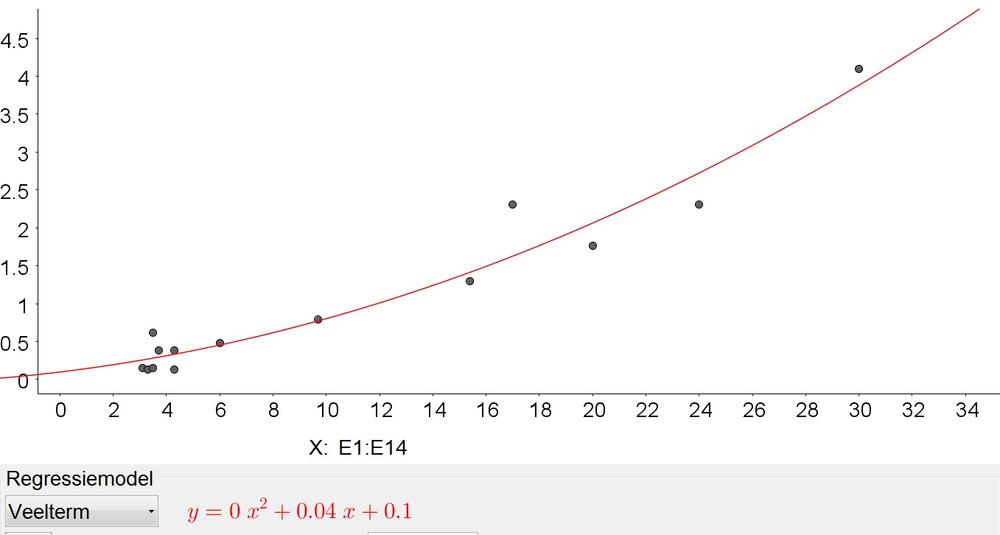
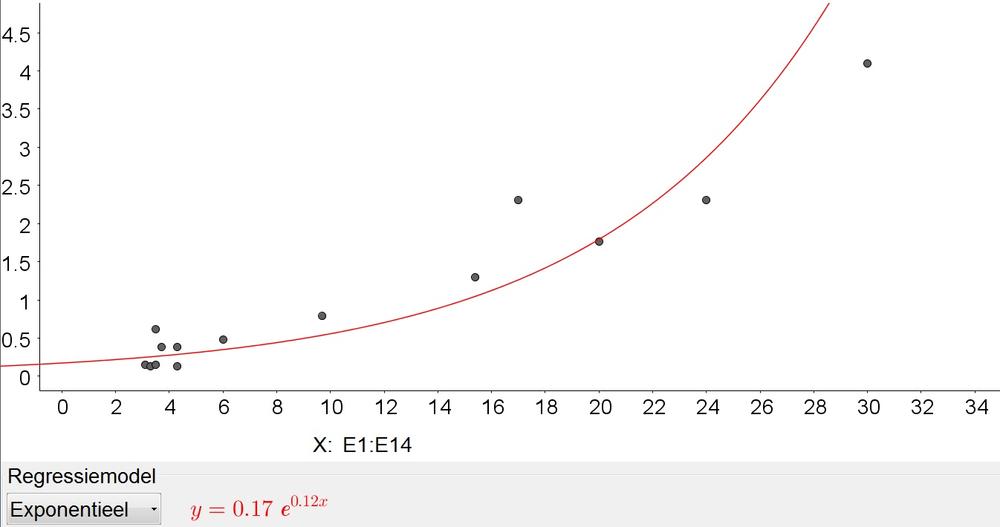
$$
2,100,000=0.00279x^2+0.04x+0.1Rightarrow xapprox 27,428in
$$
$$
2,100,000=0.17e^{0.12x}Rightarrow xapprox 136in
$$
We note that the exponential model gives a more reaqonable diagonal.
e. The area of the screen, because it will represent the pixels better than the diagonal.
b. Quadratic
c. $y=0.00729x^2+0.04x+0.1$, $y=0.17e^{0.12x}$
d. 2,428 in, 136 in
e. Area of the screen
$$
0=(x+2)^2-1-dfrac{1}{2}x-2
$$
Simplify:
$$
0=x^2+dfrac{7}{2}x+1
$$
Multiply both sides of the equation by 2:
$$
0=2x^2+7x+2
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-7pm sqrt{7^2-4(2)(2)}}{2(2)}=-dfrac{7}{4}pm dfrac{sqrt{33}}{4}
$$
Determine $y$:
$$
y=dfrac{1}{2}x+2=-dfrac{7}{8}pm dfrac{sqrt{33}}{8}+2=dfrac{9}{8}pm dfrac{sqrt{33}}{8}
$$
Thus the solutions are $left( -dfrac{7}{4}pm dfrac{sqrt{33}}{4}, dfrac{9}{8}pm dfrac{sqrt{33}}{8}right)$
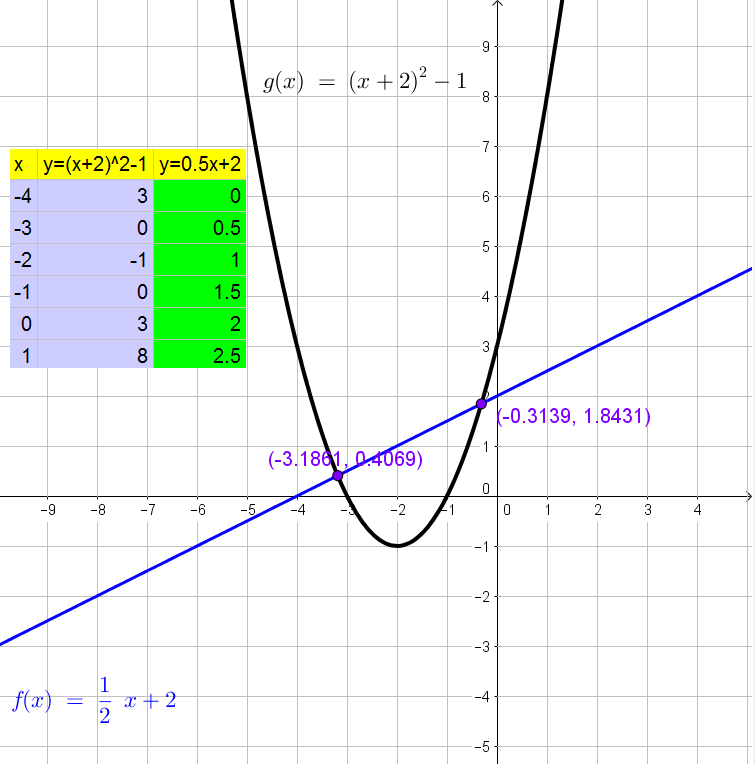
left( -dfrac{7}{4}pm dfrac{sqrt{33}}{4}, dfrac{9}{8}pm dfrac{sqrt{33}}{8}right)
$$
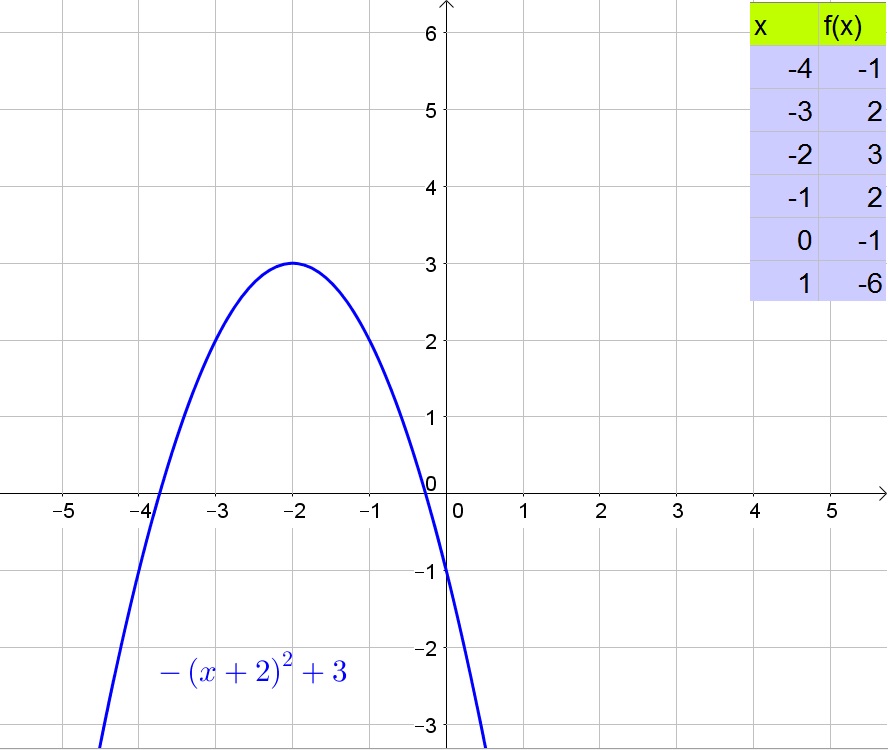
$$
0=-(x+2)^2+3
$$
Add $(x+2)^2$ to both sides of the equation:
$$
(x+2)^2=3
$$
Take the square root of both sides of the equation:
$$
x+2=pm sqrt{3}
$$
Subtract 2 from both sides of the equation:
$$
x=-2pm sqrt{3}
$$
Thus the domain should be $[-2-sqrt{3},-2+ sqrt{3}]$.
b. $[-2-sqrt{3}, -2+sqrt{3}]$
c. 3
d. Balloon is launched at $x=-2+sqrt{3}$, lands at $-2-sqrt{3}$, and reaches its maximum height of 3 at $x=-2$.
a.
$$
V=dfrac{14cdot 6 cdot 19}{3}=532
$$
b.
$$
V=dfrac{dfrac{3sqrt{3}}{2} 10^2cdot 36}{3}=1800sqrt{3}approx 3,118
$$
c.
$$
V=dfrac{dfrac{9cdot 4}{2} cdot 13}{3}=78
$$
b. 3,118
c. 78
b.
$$
V=dfrac{Bcdot h}{3}=dfrac{pi r^2 h}{3}
$$
c. Replace $r$ with 8 (radius is half the diameter of 16) and $h$ with 12:
$$
V=dfrac{pi 8^2 (12)}{3}=256pi approx 804mm^3
$$
b. $dfrac{pi r^2 h}{3}$
c. $804mm^3$
$$
A_L=dfrac{2pi r}{2pi l}pi l^2=pi r l = pi rsqrt{r^2+h^2}
$$
A_l=pi rsqrt{r^2+h^2}
$$
$$
V=dfrac{pi 2^2 sqrt{6^2-2^2}}{3}=dfrac{16pi sqrt{2}}{3} approx 7.5in^3
$$
The lateral surface area of a cone is:
$$
A_L=pi r l=pi (2)(6)=12pi approx 38in^2
$$
Lateral surface area 38 in$^2$
$$
V=dfrac{Bcdot h}{3}=dfrac{pi r^2h}{3}
$$
The lateral surface area of a cone is:
$$
A_L=pi rl = pi rsqrt{r^2+h^2}
$$
and the surface area of the cone is then the sum of the lateral surface area increased by the area of the base.
$$
V=dfrac{7cdot 24}{2}cdot 12=1008in^3
$$
Note that the 24 is the length of the missing side (height of the triangle and 7,24,25 is a Pythagorean triple).
Determine the surface area:
$$
S=2cdot dfrac{7cdot 24}{2}+7cdot 12+24cdot 12+25cdot 12=840in^2
$$
$$
V=dfrac{pi 5^2cdot 12}{3}=100piapprox 314m^3
$$
Determine the surface area:
$$
S=pi r sqrt{r^2+h^2}+pi r^2
$$
$$
=pi (5)sqrt{12^2+5^2}+pi 5^2=65pi+25pi=90piapprox 283 m^2
$$
b. Volume 314 m$^3$, Surface area 283 m$^2$
$$
V=pi r^2 h=pi 1.5^2 (7)=15.75pi approx 49cm^3
$$
Determine the volume of the missing cylinder:
$$
V=pi r^2 h=pi 0.5^2 (7)=1.75pi approx 5.8cm^3
$$
Determine the difference in volumes that obtain the volume of the cylinder with the hole:
$$
V=15.75pi-1.75pi=14piapprox 44cm^3
$$
$$
B=2(1+sqrt{2})a^2=2(1+sqrt{2})2^2approx 19ft^2
$$
Determine the volume of the prism:
$$
V=Bcdot h=19cdot 7=133ft^3
$$
b. 133 ft$^3$
$$
V=12^3=1728in^3
$$
The surface area contains 6 squares:
$$
S=6A=6(12^2)=864in^2
$$
b. Since 12 inches = 1 foot. The volume of a cube is the length of its side cubed:
$$
V=1^3=1ft^3
$$
The surface area contains 6 squares:
$$
S=6A=6(1^2)=6ft^2
$$
b. Volume 1 ft$^3$, Surface area 6ft$^2$
$$
108=dfrac{27h}{3}
$$
Simplify:
$$
108=9h
$$
Divide both sides of the equation by 9:
$$
12=h
$$
Thus the height is 12 inches.
$$
b=dfrac{21text{textdegree}}{2}=10.5text{textdegree}
$$
The exterior angle is equal to the sum of the angles of the triangle with the exception of the corresponding interior angle:
$$
a=62text{textdegree}-10.5text{textdegree}=51.5text{textdegree}
$$
The measure of the arc is twice the measure of the inscribed angle:
$$
x=c=2(51.5text{textdegree})=103text{textdegree}
$$
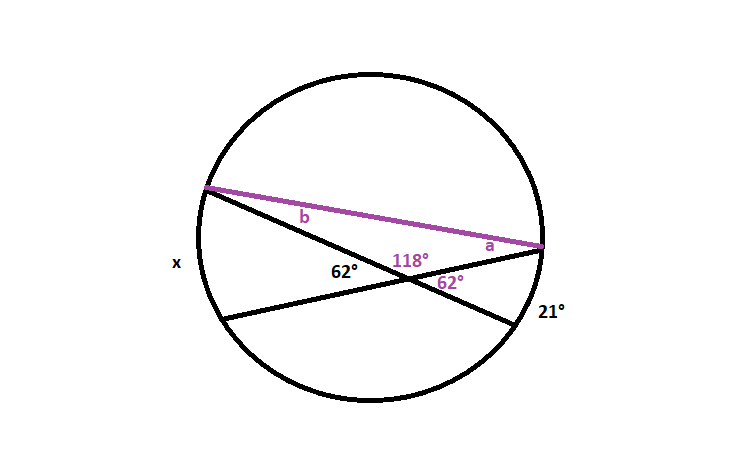
x=103text{textdegree}
$$
$$
x^2+(-x)^2=8
$$
Simplify:
$$
2x^2=8
$$
Divide both sides of the equation by 2:
$$
x^2=4
$$
Take the square root of both sides of the equation:
$$
x=pm 2
$$
Determine $y$:
$$
y=-x=-(pm 2)=mp 2
$$
Thus the solutions are $(pm 2, mp 2)$.
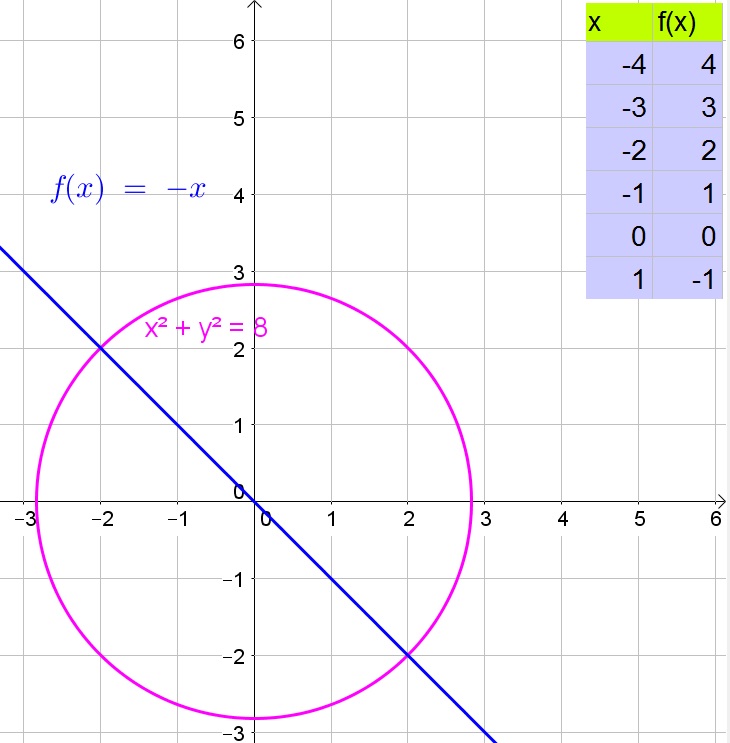
(pm 2, mp 2)
$$
angle Dcong angle F (text{both are 90text{textdegree} because of tangent lines})
$$
$$
DE=EF(text{ both are the radius of the circle})
$$
$$
EA=EA(text{Shared side})
$$
$$
Downarrow text{Pythagorean theorem}
$$
$$
AD=sqrt{EA^2+DE^2}=sqrt{EA^2+EF^2}=AF
$$
$$
100%+5%=105%=1.05
$$
b. Thus we need to value of the house 6 years ago:
$$
175,000(1.05)^{-6}approx $130,588
$$
c. $a$ is the initial value and thus is $130,588$ and $b$ is the multiplier:
$$
f(t)=130,588(1.05)^t
$$
b. $$130,588$
c. $133,588(1.05)^t$
b. a Soccer ball, a globe, the sun
c. Semi-spheres (which are half of a sphere), circles and ellipses (which are the cross sections of a sphere),.
b. Answers could vary
c. Semi-spheres, circles, ellipses
The area of the United States will also be needed to be able to the determine the percent of the Earth’s surface.
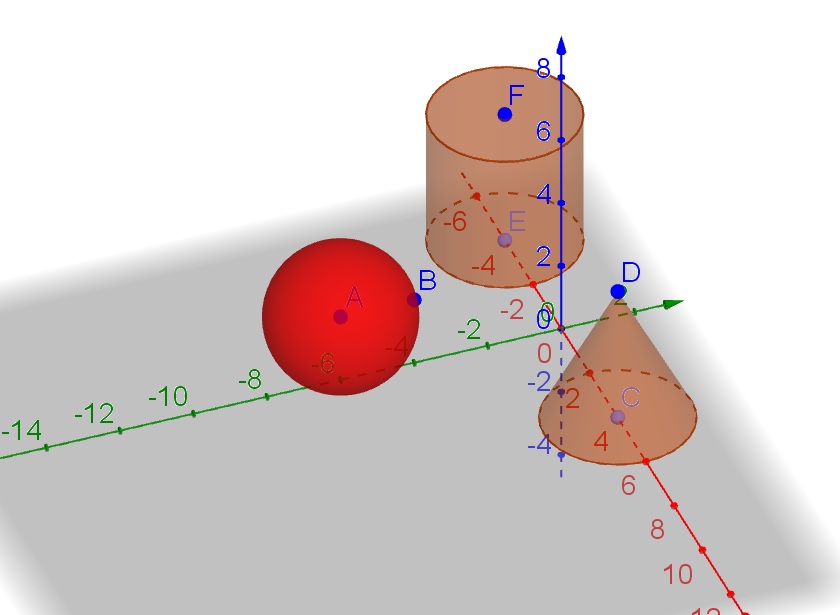
c. Let $V$ be the volume of the sphere:
$$
V=V_{cilinder}-V_{cone}=pi r^2 (2r)-dfrac{pi r^2 (2r)}{3}=dfrac{2pi r^2(2r)}{3}=dfrac{4pi r^3}{3}
$$
$$
V=frac{4pi r^3}{3}
$$
$$
S=S_L :_{cilinder}=2pi r h=2pi r (2r)=4pi r^2
$$
4pi r^2
$$
$$
S=4pi r^2=4pi (4000)^2=64,000,000pi mi^2
$$
70% of earth is covered in water:
$$
70% cdot 64,000,000pi=44,800,000pi approx 140,743,350mi^2
$$
$$
dfrac{3,537,438}{64,000,000pi}approx 0.0176=1.76%
$$
$$
V=dfrac{4pi r^3}{3}=dfrac{4pi 4000^3}{3}approx 26,808,527,310 mi^3
$$
1.76%
26,808,527,310 mi$^3$
$$
V=dfrac{4pi r^3}{3}
$$
and its surface area is:
$$
S=4pi r^2
$$
$$
S=4pi r^2=4pi 4^2=64pi approx 201cm^2
$$
Determine the volume:
$$
V=dfrac{4pi r^3}{3}=dfrac{4pi 4^3}{3}=dfrac{256pi}{3}approx 268cm^3
$$
Volume 268 cm$^3$
$$
dfrac{n-2}{n}180text{textdegree}=dfrac{20-2}{20}180text{textdegree}=162text{textdegree}
$$
$$
180text{textdegree}-157.5text{textdegree}=22.5text{textdegree}
$$
The number of sides is then 360$text{textdegree}$ divided by the exterior angle:
$$
dfrac{360text{textdegree}}{22.5text{textdegree}}=16
$$
Thus the polygon has 16 sides.
$$
h=2.5tan{67.5text{textdegree}}approx 6
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{5cdot 6}{2}=15
$$
Since the octagon is made up out of 8 triangles, the area of the octagon is:
$$
8cdot 15=120cm^2
$$
b. 16 sides
c. 120 cm$^2$
B. True. The measure of the arc is equal to the measure of the central angle on the arc.
C. Not necessarily true
D. True, The measure of the arc is double the measure of the inscribed angle on the arc.
E. True, twice the radius is the diameter.
$$
r=frac{text{Diameter}}{2}=frac{12}{2}:6
$$
Determine the volume of the cylinder:
$$
V=pi r^2 h=pi 6^2 (14.5)=522pi approx 1640 in^3
$$
Determine the volume in gallons:
$$
dfrac{1640 }{231}approx 7gallons
$$
$$
(x-i)(x-i)=x^2-ix-ix+i^2=x^2-2ix-1
$$
b. Use distributive property and $i^2=-1$:
$$
(x-2i)(x-2i)=x^2-2ix-2ix+4i^2=x^2-4ix-4
$$
c. Factorize and use $i^2=-1$:
$$
x^2-6ix-9=x^2-6ix+9i^2=(x-3i)(x-3i)=(x-3i)^2
$$
b. $x^2-4ix-4$
c. $(x-3i)^2$
$$
S=pi 6^2+2pi (6)cdot 11+pi (6)sqrt{6^2+7^2}=36pi +132pi +6sqrt{85}pi=(168+6sqrt{85})piapprox 702m^2
$$
b. The volume is made up of a cylinder and a cone:
$$
V=pi 6^2 (11)+dfrac{pi 6^2 (7)}{3}=396pi+84pi=480piapprox 1,508m^3
$$
b. 1,508 m$^3$
$$
y=(x^2+8x+16)+10-16
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
y=(x+4)^2-6
$$
Thus the vertex is $(-4,-6)$ and from the original equation we note that $y=10$ is the $y$-intercept.
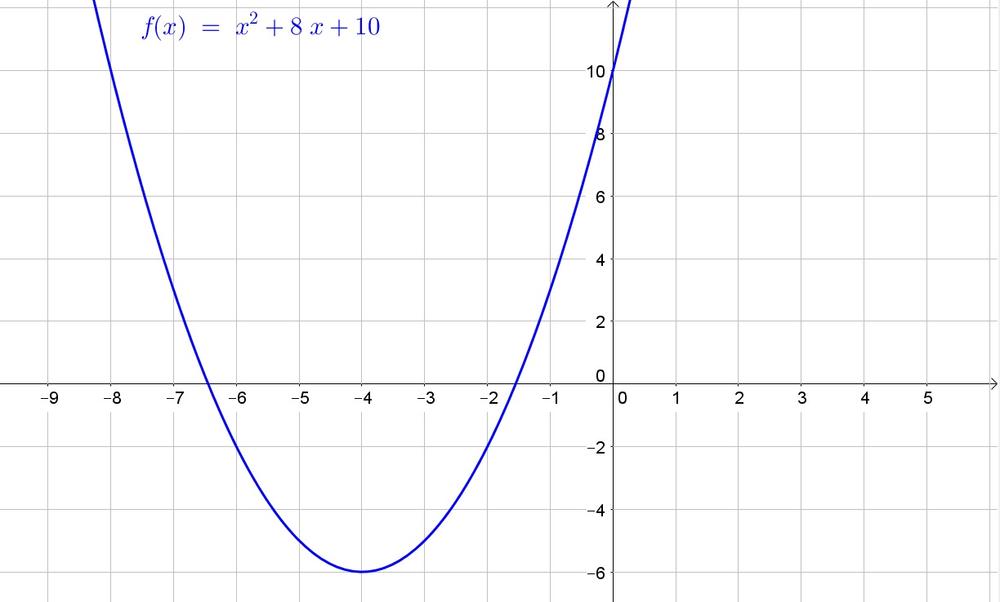
$y$-intercept: $y=10$
$$
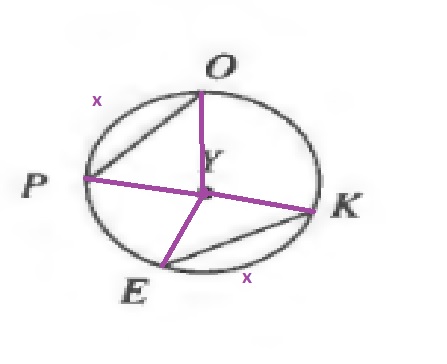
angle OYPcong angle KYE(text{Equal arcs})
$$
$$
OY=YK (text{Both are the radius of the circle})
$$
$$
PY=YE (text{Both are the radius of the circle})
$$
$$
Downarrow SAS
$$
$$
triangle OYP cong triangle KYE
$$
$$
Downarrow
$$
$$
overline{PO}cong overline{EK}
$$