All Solutions
Page 545: Questions
b. Since 6,8,10 is a Pythagorean triple, we then know that $y=8$ and $y=-8$ are possible $y$-values.
c. Since 3,4,5 is a Pythagorean triple, we then know that $y=4$ and $y=-4$ are possible $y$-values.
d. Using the Pythagorean theorem:
$$
x^2+y^2=10^2=100
$$
e. Yes, it workd for all points that lie a distance of 10 from the center of the origin.
b. $y=8$ and $y=-8$
c. $y=4$ and $y=-4$
d. $x^2+y^2=100$
e. Yes
$$
x^2+y^2=4^2=16
$$
b. Replace the radius 4 with $r$:
$$
x^2+y^2=r^2
$$
c. Yes, it is a circle with radius 6 centered at the origin:
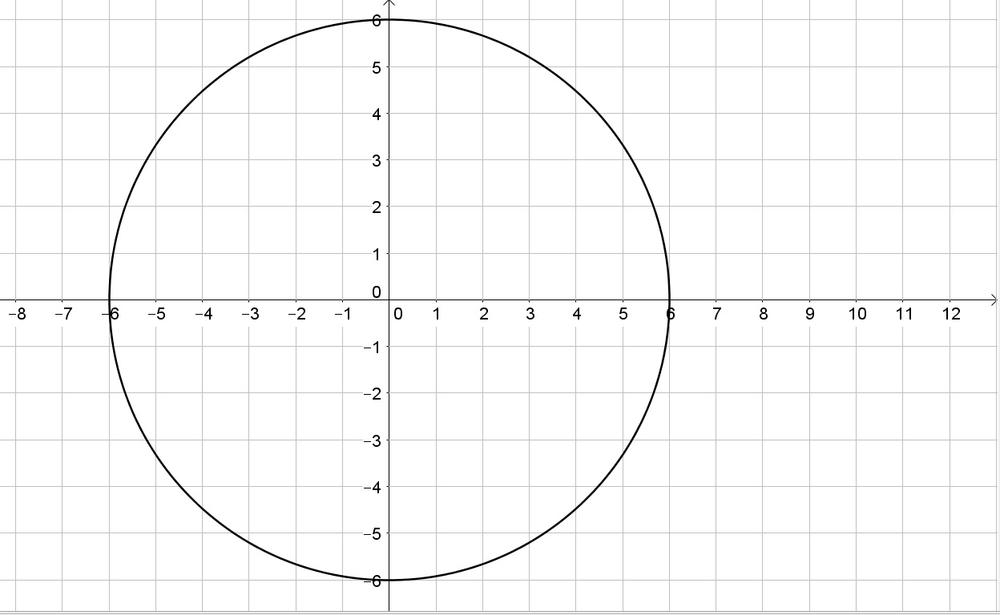
b. $x^2+y^2=r^2$
c. Yes
d. Origin
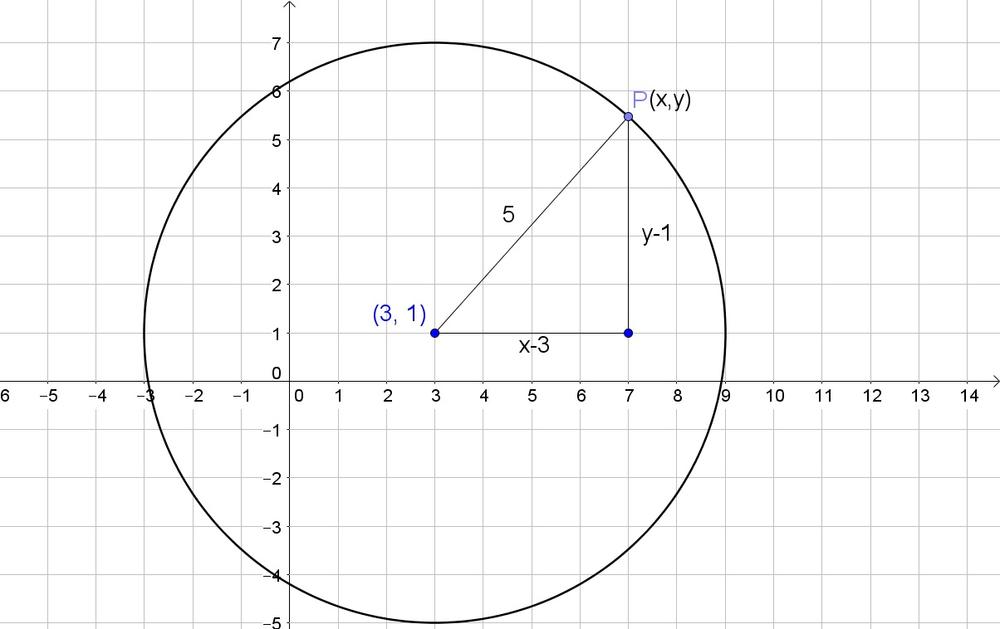
c. Use the Pythagorean theorem:
$$
(x-3)^2+(y-1)^2=5^2
$$
d. (1)
$$
(x-2)^2+(y-7)^2=1^2
$$
(2)
$$
(x-3)^2+(y-3)^2=2^2
$$
(3) The circle is then centered at the origin with radius 5:
$$
x^2+y^2=5^2
$$
(4)
$$
(x+2)^2+(y-1)^2=3^2
$$
b. $y-1$, $x-3$
c. $(x-3)^2+(y-1)^2=5^2$
d.
(1) $(x-2)^2+(y-7)^2=1^2$
(2) $(x-3)^2+(y-3)^2=2^2$
(3) $x^2+y^2=5^2$
(4) $(x+2)^2+(y-1)^2=3^2$
b. Use the substitution method and replace $y$ with $x+2$ in the second equation:
$$
(x+2)^2+(x+2+3)^2=9
$$
Rewrite the equation:
$$
x^2+4x+4+x^2+10x+25=9
$$
Subtract 9 from both sides of the equation:
$$
x^2+14x+20=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-14pm sqrt{14^2-4(1)(20)}}{2(1)}=-7pm sqrt{29}
$$
Determine $y$:
$$
y=x+2=-7pm sqrt{29}+2=-5pm sqrt{29}
$$
Thus the solutions are $(-7pm sqrt{29},-5pm sqrt{29})$.
c. A line can intersect a circle at most twice and thus we have found all points of intersections.
b. $(-7pm sqrt{29}, -5pm sqrt{29})$
c. A line can intersect a circle at most twice.
The equation of a circle with center $(x_1,y_1)$ and radius $r$ is:
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
$$
7cdot 6=42
$$
b. The bottom surface has 7 surfaces (and the upper surface thus too), while the sides of one layer has 14 surfaces:
$$
2cdot 7+6cdot 14=98
$$
c. (1) Volume 20 and surface area 58
(2) Volume 24 and surface area 60
(3) Volume
$$
3cdot 4cdot 5=60
$$
and surface area
$$
2cdot 3cdot 5+2cdot 3cdot 4+2cdot 4cdot 5=30+24+40=94
$$
b. 98 units$^3$
c. (1) 20 units$^3$ and 58 units$^2$
(2) 24 units$^3$ and 60 units$^2$
(3) 60 units$^3$ and 94 units$^2$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
a. Since the circle has center the origin and radius 3:
$$
x^2+y^2=3^2=9
$$
b. The radius is $sqrt{81}=9$:
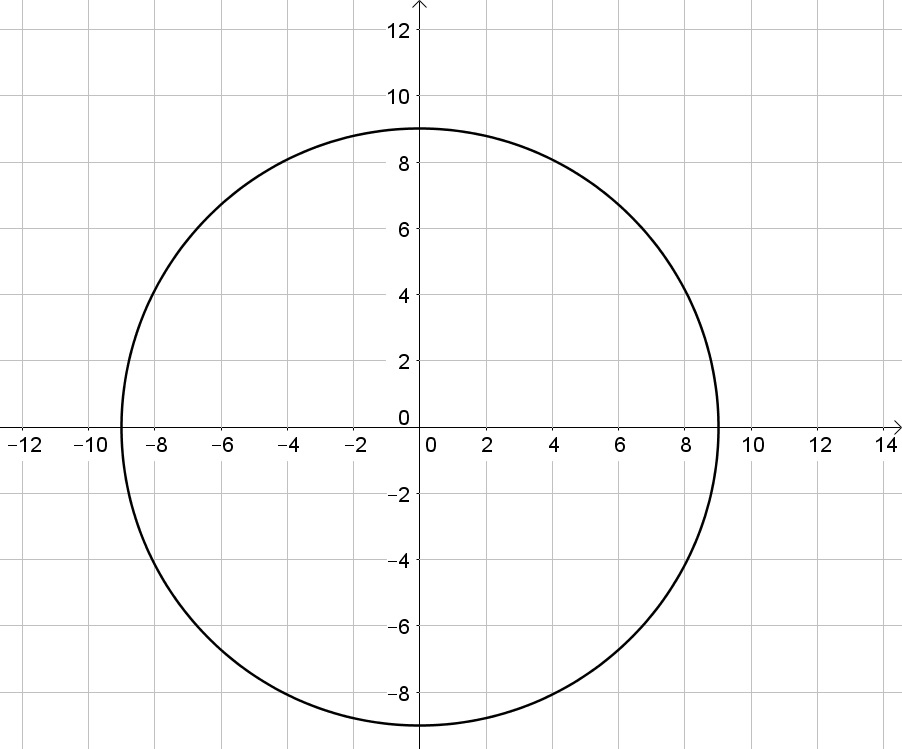
x^2+y^2=9
$$
Factorize:
$$
y=2(x^2+6x)-7
$$
Add and subtract 18 from both sides of the equation:
$$
y=2(x^2+6x+9)-7-18
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
y=2(x+3)^2-25
$$
Thus the vertex is $(-3,-25)$.
Determine the $x$-intercepts by letting $y=0$:
$$
0=2(x+3)^2-25
$$
Add 25 to both sides of the equation:
$$
25=2(x+3)^2
$$
Divide both sides of the equation by 2:
$$
dfrac{25}{2}=(x+3)^2
$$
Take the square root of both sides of the equation:
$$
pm dfrac{5sqrt{2}}{2}=pm sqrt{dfrac{25}{2}}=x+3
$$
Subtract 3 from both sides of the equation:
$$
-3pm dfrac{5sqrt{2}}{2}=x
$$
Thus the $x$-intercepts are $x=-3pm dfrac{5sqrt{2}}{2}$.
b.
b. Sketch
c. Together
$$
y=2x+3
$$
Interchange $x$ and $y$:
$$
x=2y+3
$$
Subtract 3 from both sides of the equation:
$$
x-3=2y
$$
Divide both sides of the equation by 2:
$$
dfrac{1}{2}(x-3)=y
$$
Interchange the left and right side of the equation and replace $y$ with $f^{-1}(x)$:
$$
f^{-1}(x)=dfrac{1}{2}(x-3)
$$
Thus we note that Kent was not correct.
$$
77cm cdot 53cm=4,081cm^2
$$
The area of the billboard is then the product of the area of the painting and the linear scale factor squared:
$$
20^2cdot 4,081cm^2=1,632,400cm^2
$$
$$
3x-26+2x+70+5x-10+3x+2x+56=540
$$
Combine like terms:
$$
15x+90=540
$$
Subtract 90 from both sides of the equation:
$$
15x=450
$$
Divide both sides of the equation by 15:
$$
x=30
$$
$$
3x-26=3(30)-26=64text{textdegree}
$$
$$
2x+70=2(30)+70=130text{textdegree}
$$
$$
5x-10=5(30)-10=140text{textdegree}
$$
$$
3x=3(30)=90text{textdegree}
$$
$$
2x+56=2(30)+56=116text{textdegree}
$$
Then we note that 4 out of 5 angles is greater than or equal to 90$text{textdegree}$:
$$
P=dfrac{4}{5}=0.8=80%
$$
$$
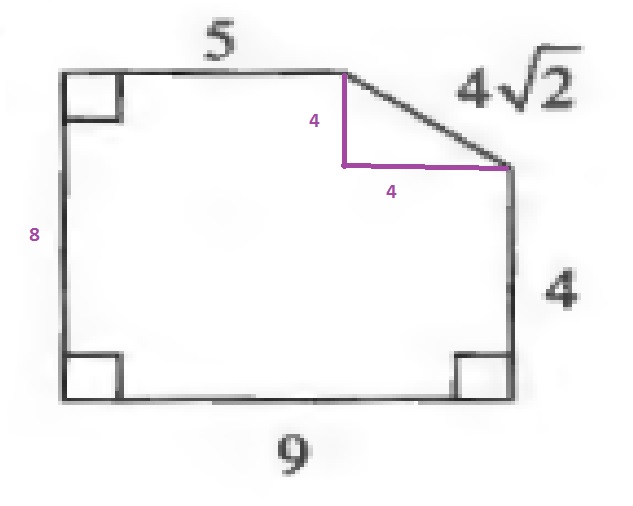
A=8cdot 9-dfrac{4cdot 4}{2}=72-8=64
$$
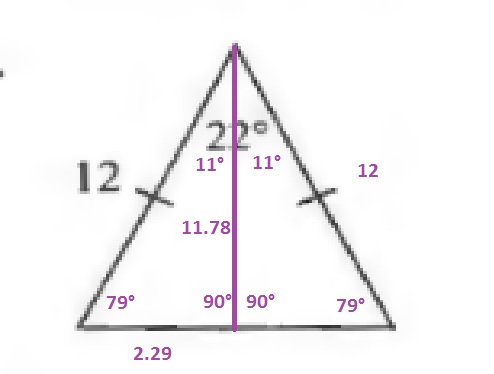
$$
h=12sin{79text{textdegree}}approx 11.78
$$
$$
dfrac{b}{2}=12cos{79text{textdegree}}approx 2.29Rightarrow bapprox 4.58
$$
The area of a triangle is the product of the base and the height divided by 2:
$$
A=dfrac{4.58cdot 11.78}{2}approx 27
$$
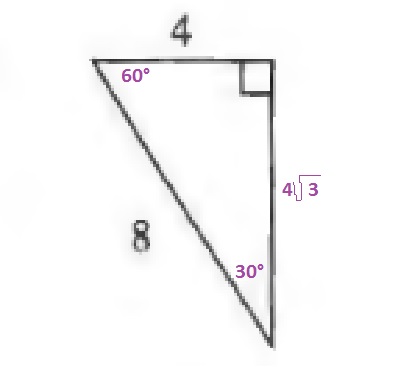
$$
sqrt{8^2-4^2}=sqrt{48}=4sqrt{3}
$$
The area of a triangle is the product of the base and the height divided by 2:
$$
A=dfrac{4cdot 4sqrt{3}}{2}=8sqrt{3}
$$
b. 27
c. $8sqrt{3}$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
a.
$$
(x-3)^2+(y-1)^2=5^2
$$
b. Use $(apm b)^2=a^2pm 2ab+b^2$:
$$
x^2-6x+9+y^2-2y+1=25
$$
Subtract 25 from both sides of the equation:
$$
x^2+y^2-6x-2y-15=0
$$
c. You can change it back using the method for complete the square (for $x$ and for $y$).
b. $x^2+y^2-6x-2y-15=0$
c. Method for complete the square
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
a. To complete the square containing the $x$ terms needs 4 units, while the square containing the $y$ terms needs 1 unit.
b. Thus we need to add 5 units in total.
c. We need to add 5 units to both sides of the equation.
d. Then we obtain:
$$
(x^2+4x+4)+(y^2+2y+1)=11+5
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
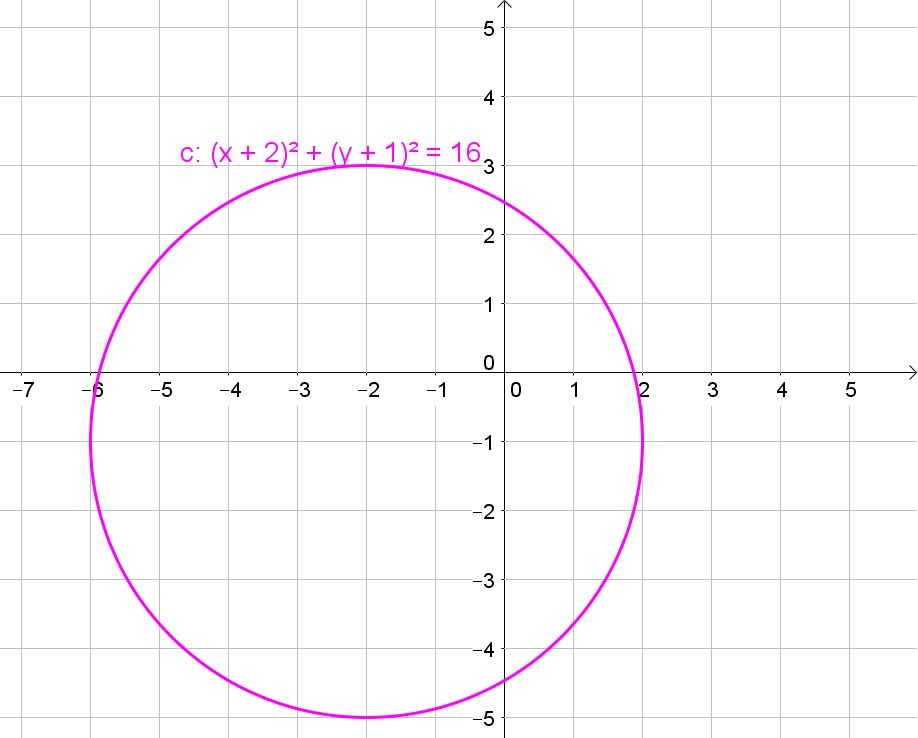
$$
(x+2)^2+(y+1)^2=16=4^2
$$
Thus the equation is a circle with center $(-2,-1)$ and radius 4.
b. Add 5 units in total
c. Add 5 units to both sides of the equation
c. $(x+2)^2+(y+1)^2=16$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
Add 3 to both sides of the given equation:
$$
x^2-4x+y^2-6y=3
$$
Add 13 to both sides of the equation:
$$
(x^2-4x+4)+(y^2-6y+9)=3+13
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
$$
(x-2)^2+(y-3)^2=16=4^2
$$
Thus the equation is a circle with center $(2,3)$ and radius 4.
$$
12x-12=0
$$
Add 12 to both sides of the equation:
$$
12x=12
$$
Divide both sides of the equation by 12:
$$
x=1
$$
Now we need to find the corresponding $y$-values, however this cannot be done directly because the equations contain terms $y^2$ and $y$.
$$
(x+2)^2+(y-3)^2=25
$$
$$
(x-4)^2+(y-3)^2=25
$$
Subtract the two equations:
$$
(x+2)^2-(x-4)^2=0
$$
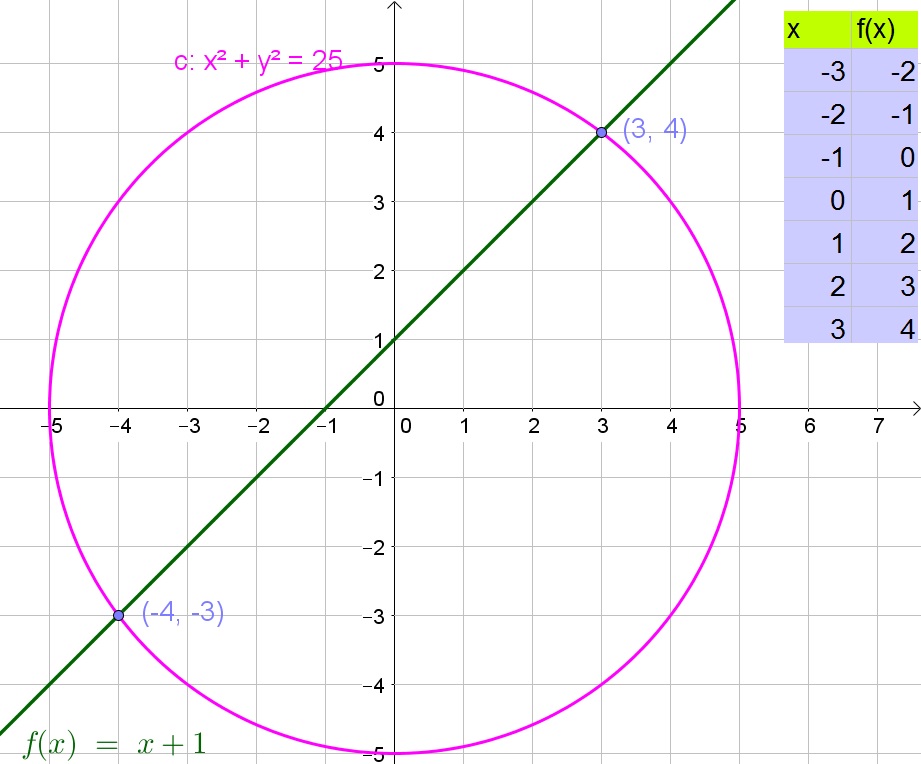
Then we note that $x=1$ is a solution.
Determine the corresponding $y$-value:
$$
(y-3)^2=25-(1-4)^2=25-9=16
$$
Take the square root of both sides of the equatino:
$$
y-3=pm 4
$$
Add 3 to both sides of the equation:
$$
y=3pm 4=7text{ or }-1
$$
Thus the solutions are $(1,7)$ and $(1,-1)$.
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
Subtract 9 from both sides of the given equation:
$$
x^2-8x+y^2+6y=-9
$$
Add 25 to both sides of the equation:
$$
(x^2-8x+16)+(y^2+6y+9)=-9+25
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
$$
(x-4)^2+(y+3)^2=16=4^2
$$
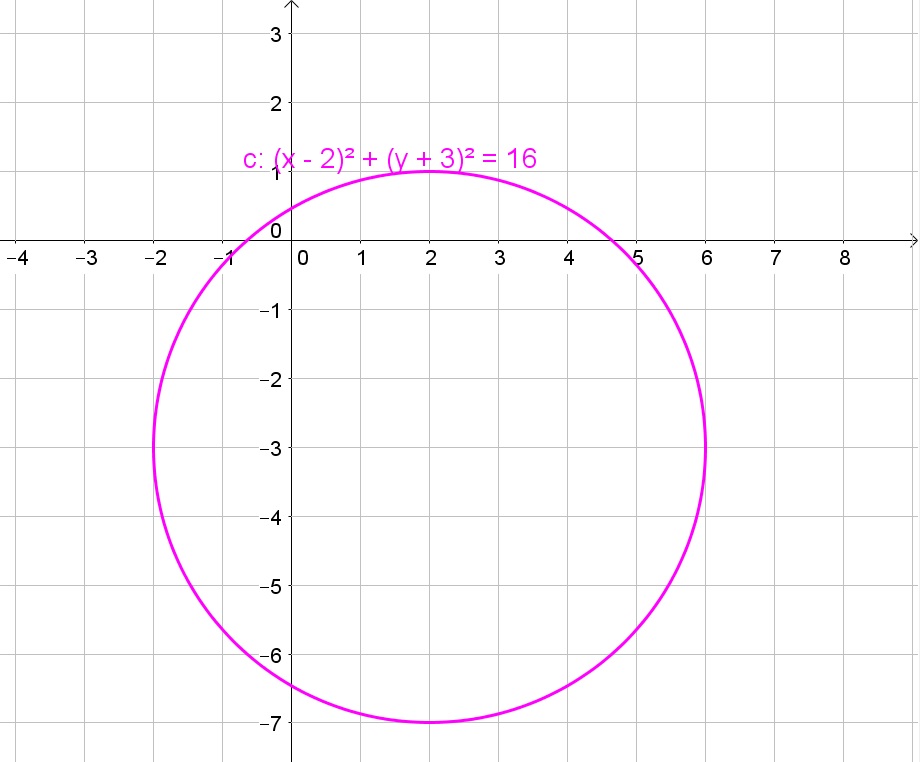
Thus the equation is a circle with center $(4,-3)$ and radius 4.
$$
(x-3)(x+1)<0
$$
Thus the roots are $x=3$ and $x=-1$. Since the function $y=x^2-2x-3$ opens upwards, we then know:
$$
-1<x<3
$$
$$
x^2+4x-3=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-4pm sqrt{4^2-4(1)(-3)}}{2(1)}=-2pm sqrt{7}
$$
$$
(x-4)(x+9)<0
$$
Thus the roots are $x=4$ and $x=-9$. Since the function $y=x^2+5x-36$ opens upwards, we then know:
$$
-9<x<4
$$
$$
x=dfrac{3pm sqrt{(-3)^2-4(1)(13.75)}}{2(1)}=dfrac{3pm sqrt{-46}}{2}=dfrac{3}{2}pm dfrac{sqrt{46}}{2}i
$$
b. $x=-2pm sqrt{7}$
c. $-9<x<4$
d. $x=frac{3}{2}pm frac{sqrt{46}}{2}i$
$$
0=2x^2-x-15
$$
Factorize:
$$
0=(2x+5)(x-3)
$$
Zero product property:
$$
2x+5=0text{ or }x-3=0
$$
Solve each equation to $x$:
$$
2x=-5text{ or }x=3
$$
$$
x=-dfrac{5}{2}text{ or }x=3
$$
b. Same shape, Same $x$-intercept, reflected about the $x$-axis
a.
$$
3+i-(5+6i)=(3-5)+(i-6i)=-2-5i
$$
b.
$$
8i+16+2i=16+(8i+2i)=16+10i
$$
c.
$$
(20+5i)-(-5i)=20+(5i-(-5i))=20+10i
$$
b. $16+10i$
c. $20+10i$
$$
V=16^3=4,096units^3
$$
The surface area contains six squares:
$$
S=6cdot 16^2=1,536units^2
$$
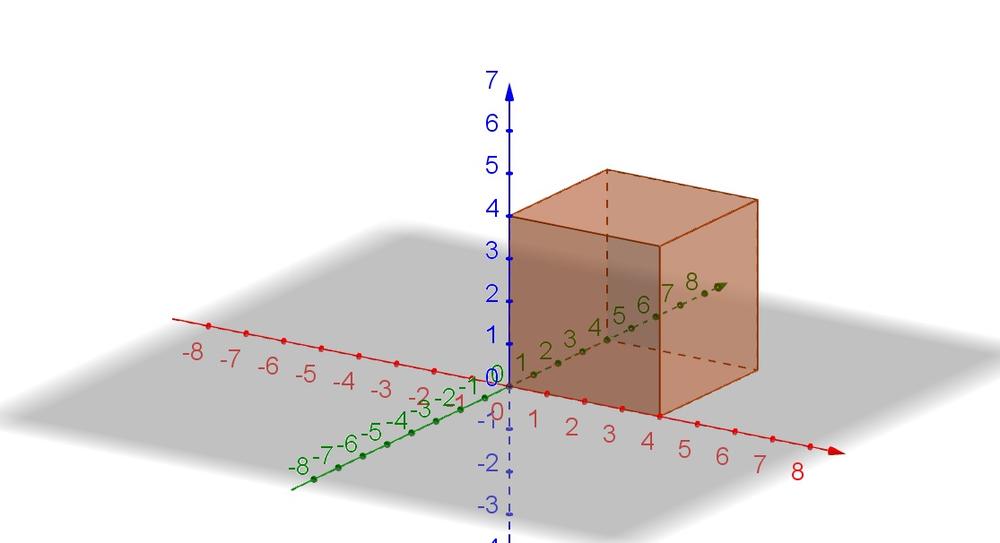
Surface area 1;536 units$^2$
$$
P(2blue)=P(blue)cdot P(blue)=dfrac{5}{6}cdot dfrac{5}{6}=dfrac{25}{36}approx 0.694=69.4%
$$
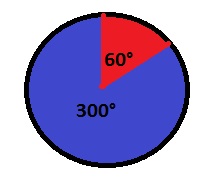
c. The area of a circle sector with central angle $theta$ is $dfrac{theta}{360text{textdegree}}pi r^2$:
$$
A=dfrac{300text{textdegree}}{360text{textdegree}}pi 7^2=dfrac{245pi}{6} cm^2
$$
d. The central angle of the purple area is 90$text{textdegree}$ and the area of the yellow area is 240$text{textdegree}$. Since the total spinner is 360$text{textdegree}$, the central angle of the green region is then:
$$
360text{textdegree}-240text{textdegree}-90text{textdegree}=30text{textdegree}
$$
b. $frac{25}{36}approx 0.694=69.4%$
c. $frac{245 pi}{6}$ cm$^2$
d. 30$text{textdegree}$
$$
4x^2-12x=4x(x-3)
$$
$$
3y^2+6y+3=3(y^2+2y+1)
$$
Factor the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
3y^2+6y+3=3(y+1)^2
$$
$$
2m^3+7m^2+3m=m(2m^2+7m+3)
$$
Factor further:
$$
2m^3+7m^2+3m=m(2m+1)(m+3)
$$
$$
3x^2+4x-4=(3x-2)(x+2)
$$
b. $3(y+1)^2$
c. $m(2m+1)(m+3)$
d. $(3x-2)(x+2)$
b. Yes, The curve (parabola) lies with vertex between F and the line and opens away from the line $l$.
b. Yes
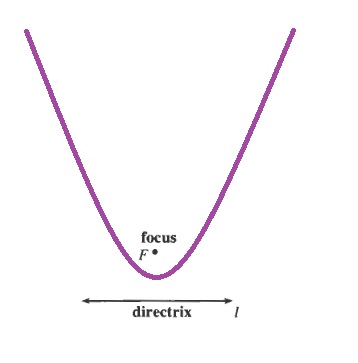
c. The closer the focus lies to the directrix, the narrower the parabola is, the further away the focus lies to the directrix, the wider the parabola is.
d. A parabola is defined geometrically as the set of all points that lie an equal distance from a line (the directrix) and a point (the focus).
b. All points on the parabola lie an equal distance away from both the focus and the directrix.
c. The closer the focus lies to the directrix, the narrower the parabola is, the further away the focus lies to the directrix, the wider the parabola is.
d. A parabola is defined geometrically as the set of all points that lie an equal distance from a line (the directrix) and a point (the focus).
c. No, there is only one point.
d.
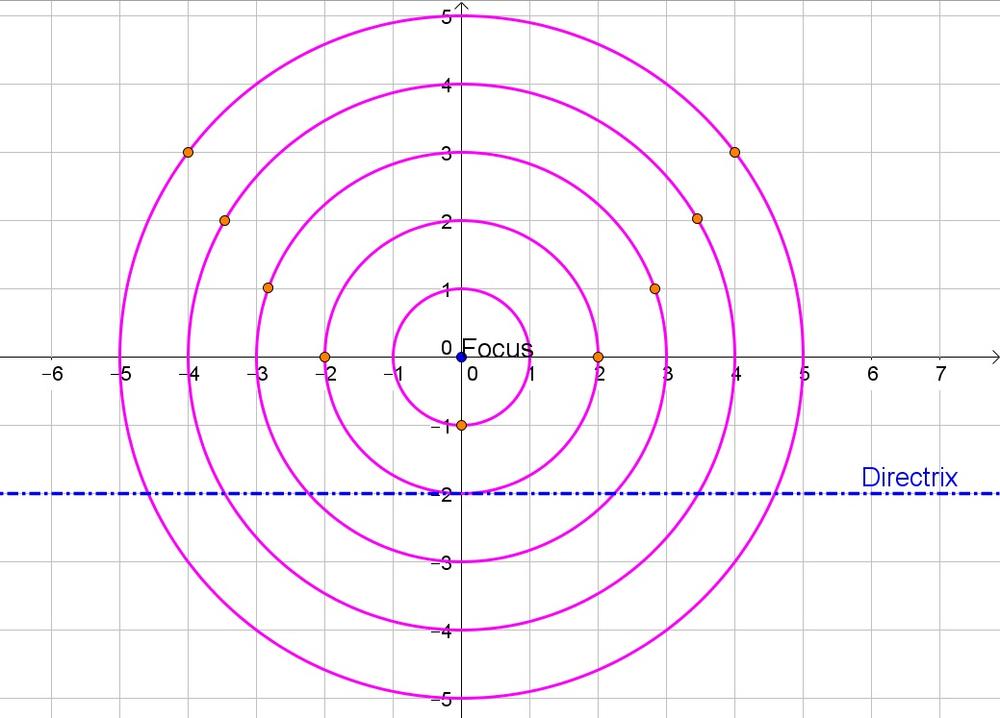
b. $R$ is three circles from the focus
c. No
d. Sketch
The focus is never on the parabola and the parabola never intersects the directrix.
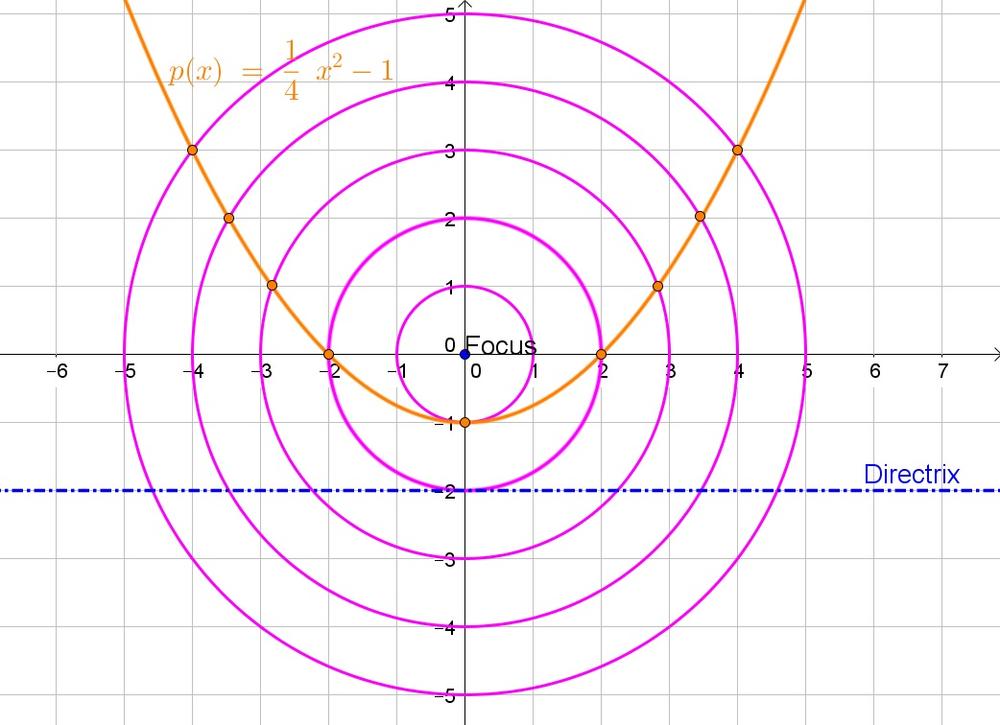
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=sqrt{(x-0)^2+(y-0)^2}=sqrt{x^2+y^2}
$$
c. $y=-2$
d. The distance is the difference in $y$-coordinates: $y+2$.
e. Since every point is an equal distance from the focus and the directrix:
$$
sqrt{x^2+y^2}=y+2
$$
Square both sides of the equation:
$$
x^2+y^2=y^2+4y+4
$$
Subtract $y^2$ from both sides of the equation:
$$
x^2=4y+4
$$
Subtract 4 from both sides of the equation:
$$
x^2-4=4y
$$
Divide both sides of the equation by:
$$
dfrac{1}{4}x^2-1=y
$$
Thus the equation of the parabola is $y=dfrac{1}{4}x^2-1$.
b. $sqrt{x^2+y^2}$
c. $y=-2$
d. $y+2$
e. $y=frac{1}{4}x^2-1$
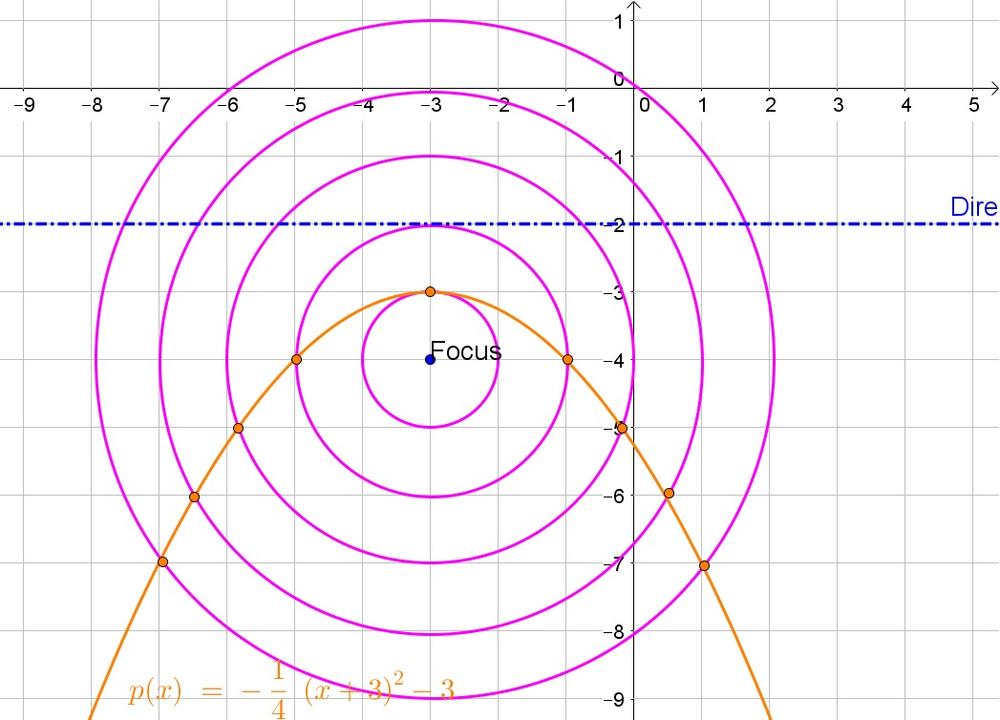
$$
sqrt{(x+3)^2+(y+4)^2}=y+2
$$
Square both sides of the equation:
$$
(x+3)^2+(y+4)^2=y^2+4y+4
$$
Expand:
$$
x^2+6x+9+y^2+8y+16=y^2+4y+4
$$
Subtract $y^2$ from both sides of the equation:
$$
x^2+6x+25+8y=4y+4
$$
Subtract $8y$ from both sides of the equation:
$$
x^2+6x+25=-4y+4
$$
Subtract 4 from both sides of the equation:
$$
x^2+6x+21=-4y
$$
Divide both sides of the equation by $-4$:
$$
-dfrac{1}{4}(x^2+6x+21)=y
$$
Thus the equation of the parabola is $y=-dfrac{1}{4}(x^2+6x+21)$.
$$
y=-dfrac{1}{4}(x^2+6x+9)-dfrac{21}{4}+dfrac{9}{4}
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
y=-dfrac{1}{4}(x+3)^2-3
$$
b. $y=-frac{1}{4}(x^2+6x+21)$
c. $y=-frac{1}{4}(x+3)^2-3$
$$
8x+20-11=4x-3
$$
Subtract $4x$ from both sides of the equation:
$$
4x+9=-3
$$
Subtract 9 from both sides of the equation:
$$
4x=-12
$$
Divide both sides of the equation by 4:
$$
x=-3
$$
$$
20m-10=19m
$$
Subtract $20m$ of both sides of the equation:
$$
-10=-m
$$
Divide both sides of the equation by $-1$:
$$
10=m
$$
$$
(3p-2)(p+4)=0
$$
Zero product property:
$$
3p-2=0text{ or }p+4=0
$$
Solve each equation to $p$:
$$
3p=2text{ or }p=-4
$$
$$
p=dfrac{2}{3}text{ or }p=-4
$$
$$
x+2=25
$$
Subtract 2 from both sides of the equation:
$$
x=23
$$
b. $m=10$
c. $p=frac{2}{3}$ or $p=-4$
d. $x=23$
Let $x$ be the time in years and $y$ the total amount of money.
Then we obtain:
$$
f(x)=left{ begin{matrix} 200 & 0leq xleq 0.25\ 200(1+0.02)^{x-0.25} & 0.25<xleq 5.25end{matrix}right.
$$
f(x)=left{ begin{matrix} 200 & 0leq xleq 0.25\ 200(1+0.02)^{x-0.25} & 0.25<xleq 5.25end{matrix}right.
$$
$$
15.4in^2=dfrac{15.4}{12^2}ft^2approx 0.107ft^2
$$
Thus you get more pizza from the square pizza and thus you should order the slice of the square pizza.
$$
dfrac{360text{textdegree}}{5}=72text{textdegree}
$$
Thus we then also know that the two base angles of the isosceles triangles are 72$text{textdegree}$. Since the sum of all angles in a triangle is 180$text{textdegree}$, we then know that the vertex angles are:
$$
180text{textdegree}-72text{textdegree}-72text{textdegree}=36text{textdegree}
$$
b. The first model seems the best, because the function keep decreasing but will not become negative and will not increase again.
c. Replace $x$ with 10, 20 and 30:
$$
y=16+10(0.95)^{10}approx 22
$$
$$
y=16+10(0.95)^{20}approx 20
$$
$$
y=16+10(0.95)^{30}approx 18
$$
d. The distance that the athletes run, does not determine the intensity of the training and thus the plan will not work for everybody.
b. First model
c. 22, 20, 18
d. Plan will not work for everybody
a.
$$
(x+i)(x-i)=x^2+ix-ix-i^2=x^2-i^2=x^2+1
$$
b.
$$
(x+2i)(x-2i)=x^2+2xi-2xi-4i^2=x^2-4i^2=x^2+4
$$
c. Use the difference of squares:
$$
x^2+25=x^2-(-25)=x^2-(25i^2)=x^2-(5i)^2=(x-5i)(x+5i)
$$
b. $x^2+4$
c. $(x-5)(x+5i)$
$$
mangle A=30text{textdegree}
$$
$$
0.5=sin{A}=dfrac{BC}{AB}=dfrac{BC}{10}
$$
Multiply both sides of the equation by 10:
$$
5=BC
$$
$$
cos{B}=sin{A}=0.5
$$
$$
AC=sqrt{10^2-5^2}=sqrt{75}=5sqrt{3}
$$
b. 5
c. 0.5
d. $5sqrt{3}$
$$
22=51-29<x<51+29=80
$$
the length needs to be more than 22 and less than 80, which means that (C) is the only possible answer.
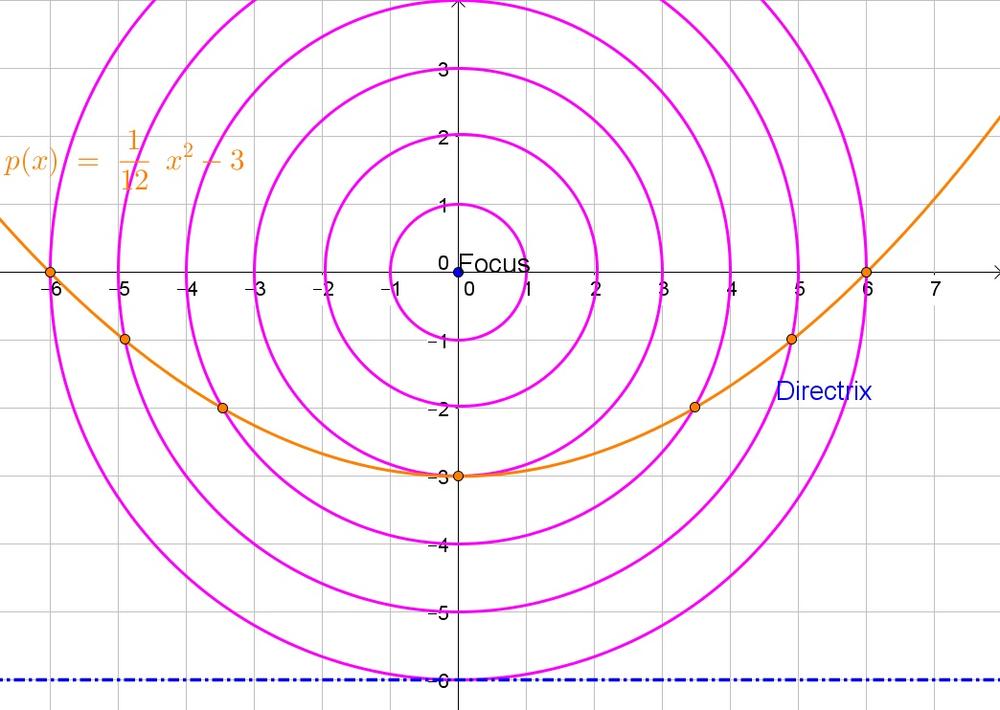
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=sqrt{(x-0)^2+(y-0)^2}=sqrt{x^2+y^2}
$$
b. The distance is the difference in $y$-coordinates: $y+6$.
c. Since every point is an equal distance from the focus and the directrix:
$$
sqrt{x^2+y^2}=y+6
$$
Square both sides of the equation:
$$
x^2+y^2=y^2+12y+36
$$
Subtract $y^2$ from both sides of the equation:
$$
x^2=12y+36
$$
Subtract 36 from both sides of the equation:
$$
x^2-36=12y
$$
Divide both sides of the equation by:
$$
dfrac{1}{12}x^2-3=y
$$
Thus the equation of the parabola is $y=dfrac{1}{12}x^2-3$.
b. $y+6$
c. $y=frac{1}{12}x^2-3$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
a. The center is $(2,-3)$ and the radius is 5.
b. Add 6 to both sides of the given equation:
$$
x^2+2x+y^2+6y=6
$$
Add 10 to both sides of the equation:
$$
(x^2+2x+1)+(y^2+6y+9)=6+10
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
$$
(x+1)^2+(y+3)^2=16=4^2
$$
Thus the equation is a circle with center $(-1,-3)$ and radius 4.
b. $(-1,-3)$, 4
$$
y=dfrac{x}{3}-2
$$
Interchange $x$ and $y$:
$$
x=dfrac{y}{3}-2
$$
Add 2 to both sides of the equation:
$$
x+2=dfrac{y}{3}
$$
Multiply both sides of the equation by 3:
$$
3(x+2)=y
$$
Interchange the left and right side of the equation and replace $y$ with $f^{-1}(x)$:
$$
f^{-1}(x)=3(x+2)=3x+6
$$
$$
y=dfrac{1}{2}x+5
$$
Interchange $x$ and $y$:
$$
x=dfrac{1}{2}y+5
$$
Subtract 5 from both sides of the equation:
$$
x-5=dfrac{1}{2}y
$$
Multiply both sides of the equation by 2:
$$
2(x-5)=y
$$
Interchange the left and right side of the equation and replace $y$ with $g^{-1}(x)$:
$$
g^{-1}(x)=2(x-5)=2x-10
$$
b. $g^{-1}(x)=2x-10$
Since the area is double every 20 minutes, the area is multiplied by $2^6=64$ in 2 hours (as there are six 20-minute periods in 2 hours).
b.
$$
1(2)^{-0.5}
$$
$$
1(2^{1/20})^{-10}
$$
$$
1(2^3)^{1/6}
$$
b. $1(2)^{-0.5}$
b. Let $g(x)$ be 0:
$$
0=x^2+9
$$
Subtract 9 from both sides of the equation:
$$
-9=x^2
$$
Take the square root of both sides of the equation:
$$
pm 3i = pm sqrt{-9}=x
$$
Thus the roots are $x=pm 3i$ and we can then write:
$$
x^2+9=(x-3i)(x+3i)
$$
b. $x^2+9=(x-3i)(x+3i)$
$$
x-3=dfrac{11}{4}
$$
Add 3 to both sides of the equation:
$$
x=dfrac{11}{4}+3=dfrac{23}{4}
$$
$$
x=pm sqrt{-10}=pm sqrt{10}i
$$
$$
3x^2=18
$$
Divide both sides of the equation by 3:
$$
x^2=6
$$
Take the square root of both sides of the equation:
$$
x=pm sqrt{6}
$$
b. $x=pm sqrt{10}i$
c. $x=pm sqrt{6}$
d. No solutions
$$
a=dfrac{360text{textdegree}}{3}=120text{textdegree}
$$
while we know that the interior angle of a regular pentagon is $b=108text{textdegree}$. Thus $a$ is greater.
$$
a=sin^{-1}dfrac{8}{12}approx 42text{textdegree}
$$
The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
b=cos^{-1}dfrac{8}{12}approx 48text{textdegree}
$$
Thus $b$ is greater.
b. Not enough information
c. $b$
d. $a$
e. Same
$$
dfrac{360text{textdegree}}{18text{textdegree}}=20
$$
$$
dfrac{360text{textdegree}}{24text{textdegree}}=15
$$
$$
dfrac{360text{textdegree}}{28text{textdegree}}approx 12.857
$$
$$
dfrac{360text{textdegree}}{40text{textdegree}}=9
$$
Thus we note that C cannot be the measure of an exterior angle of a regular polygon.
$$
1.85cdot 10=18.5ft
$$
The diameter is twice the radius:
$$
2cdot 18.5ft=37ft
$$
Thus the diameter dos not appear larger than 45 ft.
b. 18.5 ft, 45 ft, No
b. Let us call the larger arc $overset{frown}{AXB}$.
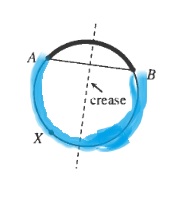
b. Let us call the larger arc $overset{frown}{AXB}$.
c. If the minor and major arc have the same length, then the points $A$ and $B$ lie on direct opposite sides of the circle and thus the chord is then the diameter of the circle.
$$
overline{AD}cong overline{BD}(text{Given})
$$
$$
overline{AC}cong overline{BC}(text{Radius circle})
$$
$$
overline{CD}cong overline{CD}(text{Common side})
$$
b. However then we know that $mangle ADC=mangle BDC$. Since $C$ does not lie in the center we know that at least one of these angle is less than 90$text{textdegree}$ and thus
$$
mangle ADC+mangle BDC<180text{textdegree}
$$
But this then means that $overline{AB}$ cannot be a chord of the circle which is a contradiction. Thus the center must lie on th perpendicular bisector.
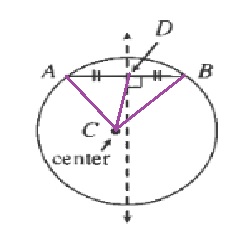
b. $mangle ADC+mangle BDC<180text{textdegree}$
b. Draw the perpendicular bisector of two different chords, their intersection is then the center of the circle.
$$
x=sqrt{5^2-4^2}=sqrt{9}=3
$$
Thus the chord lies 3 units away from the center.
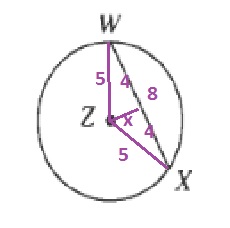
$$
mangle ABC=180text{textdegree}-35text{textdegree}-35text{textdegree}=110text{textdegree}
$$
$angle ABC$ and $angle CBD$ are supplementary angles:
$$
mangle CBD=180text{textdegree}-mangle ABC=180text{textdegree}-110text{textdegree}=70text{textdegree}
$$
$$
mangle ABC=180text{textdegree}-mangle CBD=180text{textdegree}-100text{textdegree}=80text{textdegree}
$$
Triangle $ABC$ is isosceles since two of its sides are the radius of the circle. Thus the base angles of the triangle are congruent and the sum of all angles in a triangle is 180$text{textdegree}$:
$$
mangle A=dfrac{180text{textdegree}-80text{textdegree}}{2}=50text{textdegree}
$$
$$
mangle CBD=180text{textdegree}-x-x=180text{textdegree}-2x
$$
$angle ABC$ and $angle CBD$ are supplementary angles:
$$
mangle CBD=180text{textdegree}-mangle ABC=180text{textdegree}-(180text{textdegree}-2x)=2x
$$
(b) 50$text{textdegree}$
(c) $2x$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
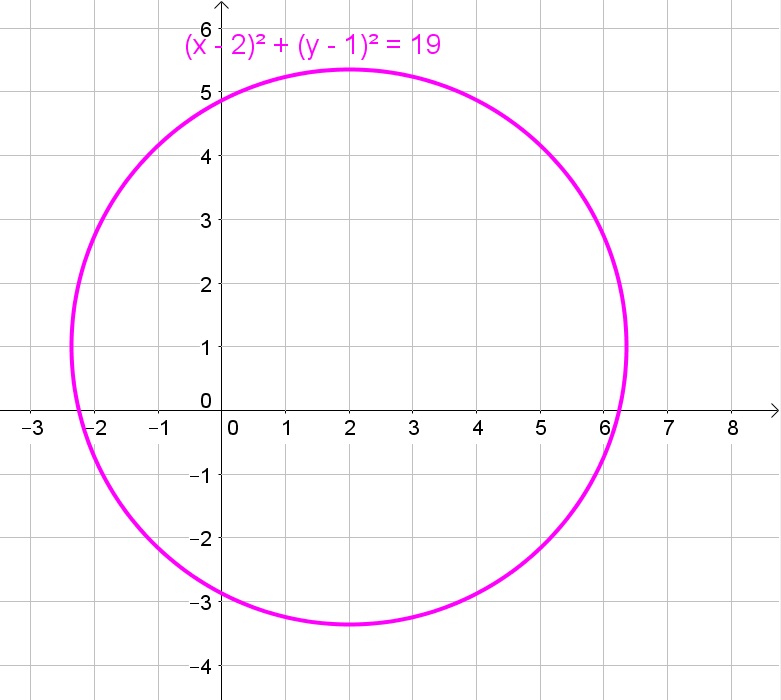
a. The circle has center $(0,0)$ and radius 4.5:
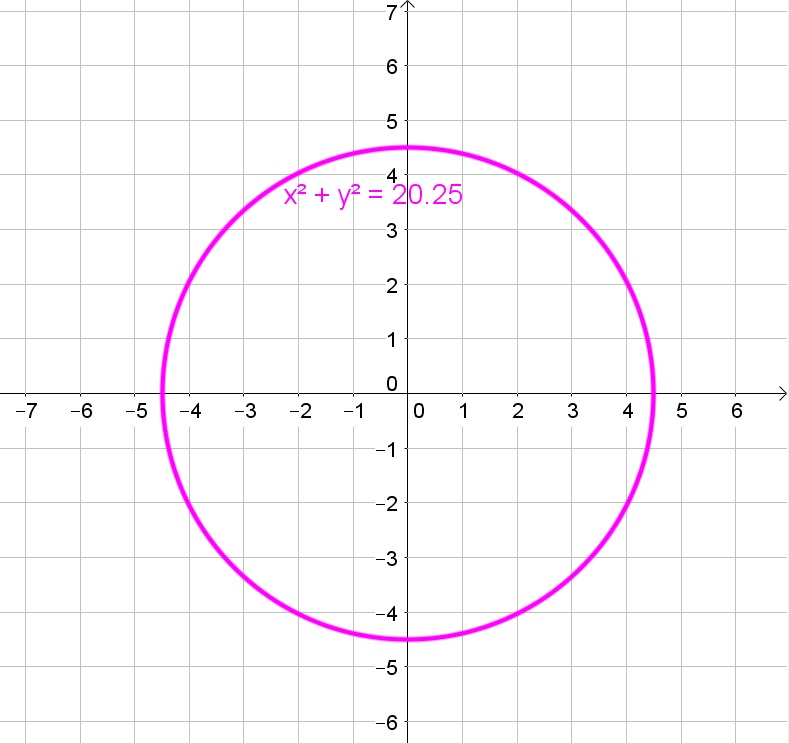
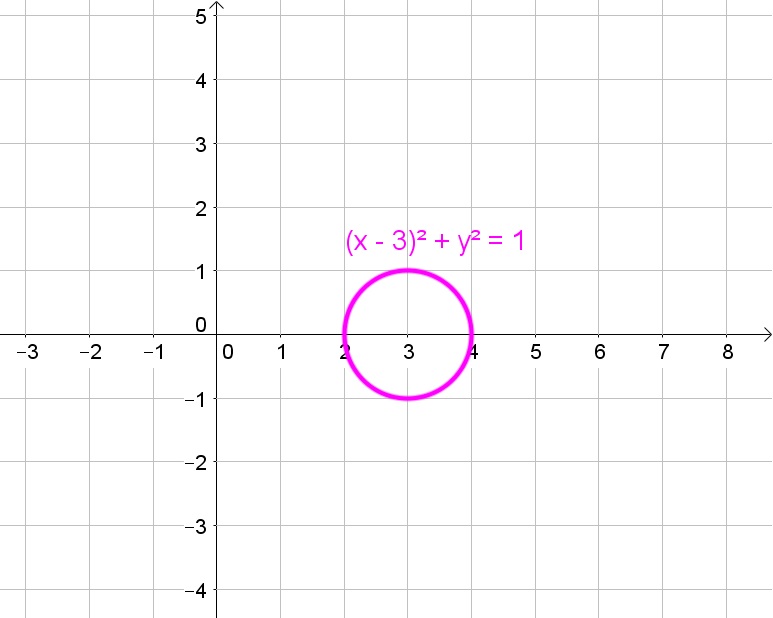
$$
(x^2-4x+4)+(y^2-2y+1)=15+4
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
$$
(x-2)^2+(y-1)^2=19
$$
Thus the equation is a circle with center $(2,1)$ and radius $sqrt{19}approx 4.36$.
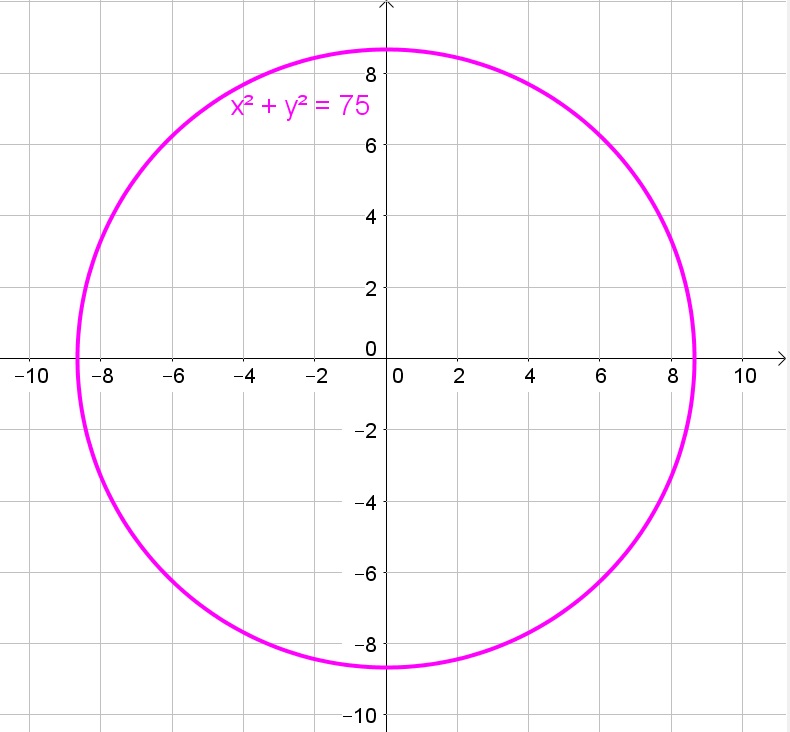
b. $(0,0)$, $sqrt{75}$
c. $(3,0)$, 1
d. $(2,1)$, $sqrt{19}$
$$
dfrac{312}{13}=24
$$
Thus the tower is 24 layers tall.
$$
x^2+dfrac{9}{16}x^2=25
$$
Combine like terms:
$$
dfrac{25}{16}x^2=25
$$
Multiply both sides of the equation by $dfrac{16}{25}$:
$$
x^2=16
$$
Take the square root of both sides of the equation:
$$
x=pm 4
$$
Determine $y$
$$
y=dfrac{3}{4}(pm 4)=pm 3
$$
Thus the solutions are then $(pm 4,pm 3)$
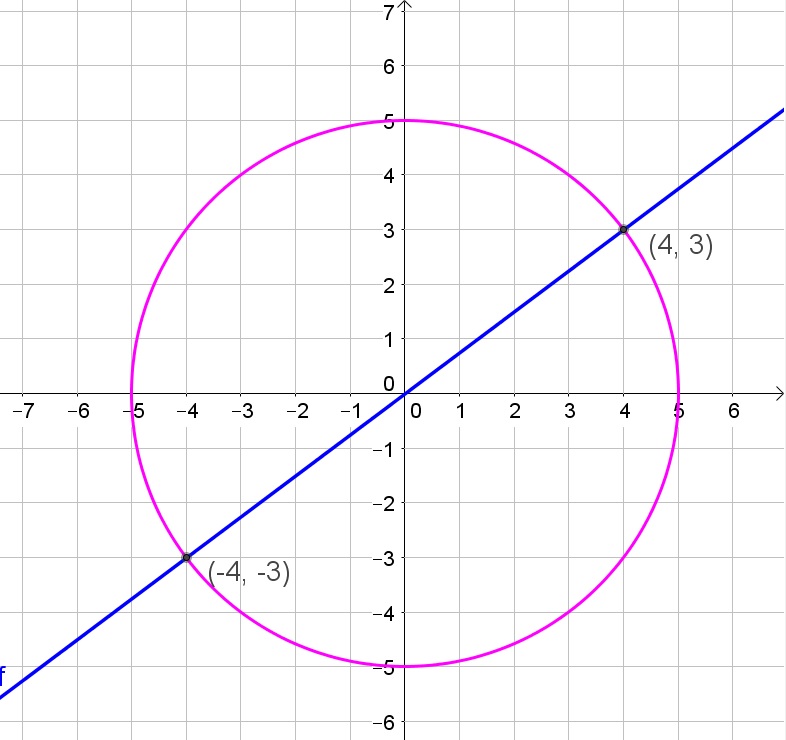
(pm 4,pm 3)
$$
b. The average rate of change is the difference in value divided by the difference in months:
$$
A=dfrac{1060-1040}{6-4}=10
$$
$$
B=dfrac{1061.50-1040.60}{6-4}=10.45
$$
$$
C=dfrac{1036-1016}{6-4}=10
$$
c. Investment B, because in the long run the exponential always wins over the linear and quadratic.
A: linear with 10 per month
B: exponential with 1%
C: Quadratic
b. 10, 10.45, 10
c. B
$$
dfrac{4}{5}x-2=7
$$
Add 2 to both sides of the equation:
$$
dfrac{4}{5}x=9
$$
Multiply both sides of the equation by $dfrac{5}{4}$:
$$
x=dfrac{35}{4}
$$
$$
3x^2=300
$$
Divide both sides of the equation by 3:
$$
x^2=100
$$
Take the square root of both sides of the equation:
$$
x=pm 10
$$
$$
dfrac{4x-1}{2}=dfrac{x+5}{3}
$$
Multiply both sides of the equation by 6:
$$
12x-3=2x+10
$$
Subtract $2x$ from both sides of the equation
$$
10x-3=10
$$
Add 3 to both sides of the equation:
$$
10x=13
$$
Divide both sides of the equatino by 10:
$$
x=dfrac{13}{10}=1.3
$$
$$
x^2-4x+6=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{4pm sqrt{(-4)^2-4(1)(6)}}{2(1)}=2pm sqrt{2}i
$$
b. $x=pm 10$
c. $x=frac{13}{10}=1.3$
d. $s=2pm sqrt{2}i$
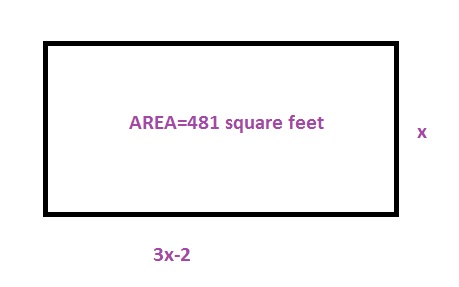
$$
x(3x-2)=481
$$
The perimeter is the sum of all sides:
$$
2x+2(3x-2)=100
$$
c. Rewrite the equations:
$$
3x^2-2x-481=0
$$
$$
8x-4=100
$$
Solve the second equation. Add 4 to both sides of the equation:
$$
8x=104
$$
Divide both sides of the equation by 8:
$$
x=13
$$
Check if it is also a solution of the first equation:
$$
3(13)^2-2(13)-481=0
$$
Thus we then know that the width is 13ft and the length is:
$$
l=3x-2=3(13)-2=37ft
$$
b. $x(3x-2)=481$, $2x+2(3x-2)=100$
c. 13 ft by 37 ft
M text{ is the midpoint of }overline{KQ}
$$
$$
Downarrow
$$
$$
overline{KM}=overline{MQ}
$$
$$
angle KML cong angle QMP(text{Vertical angles})
$$
$$
angle L cong angle P(text{Given})
$$
$$
Downarrow AAS
$$
$$
triangle KML cong triangle QMP
$$
$$
Downarrow
$$
$$
overline{KL}cong overline{QP}
$$
$$
theta=tan^{-1}dfrac{127ml}{1000mm}approx 7text{textdegree}
$$
b. Since alternate intior angles of parallel lines are congruent, we then know that the central angle is about $7text{textdegree}$
c. The circumference of $theta=7text{textdegree}$ is 500 and thus the circumference of the earth (which is 360$text{textdegree}$) is then:
$$
dfrac{360text{textdegree}}{7text{textdegree}}cdot 500approx 25,714mi^2
$$
d. Since the circumference is also $C=2pi r$:
$$
r=dfrac{C}{2pi}=dfrac{25,714}{2pi}approx 4,093mi
$$
b. 7$text{textdegree}$
c. 25,714 mi$^2$
d. 4,903 mi
$$
moverset{frown}{SU}=40text{textdegree}
$$
The major arc is then:
$$
moverset{frown}{SZU}=360text{textdegree}-40text{textdegree}=320text{textdegree}
$$
b. The arce length is the product of the measure of the arc to the entire circle and the circumference of a circle($C=2pi r$):
$$
dfrac{40text{textdegree}}{360text{textdegree}}cdot (2pi (12))=dfrac{8}{3}piapprox 7.11
$$
b. $frac{8}{3}pi approx 7.11$
$$
mangle F=mangle G=mangle H
$$
b. Both angles intercept the same arc $overset{frown}{WY}$ and we note that the measure of the central angle is double the measure of the inscribed angle.
$$
x=dfrac{118text{textdegree}}{2}=59text{textdegree}
$$
$$
x=2cdot 41text{textdegree}=82text{textdegree}
$$
$$
x=180text{textdegree} (=2cdot 90text{textdegree})
$$
$$
y=2cdot 78text{textdegree}=156text{textdegree}
$$
The sum of all angles in a triangle is also equal to 180$text{textdegree}$:
$$
z=2cdot (180text{textdegree}-78text{textdegree}-90text{textdegree})=2cdot 12text{textdegree}=24text{textdegree}
$$
$$
x=56text{textdegree}
$$
The inscribed angle is half the central angle:
$$
y= dfrac{56text{textdegree}}{2}=28text{textdegree}
$$
$$
x=114text{textdegree}
$$
The inscribed angle is half the central angle:
$$
y= dfrac{114text{textdegree}}{2}=57text{textdegree}
$$
$$
x=2cdot 28text{textdegree}=56text{textdegree}
$$
The inscribed angles of the same arc is are congruent:
$$
y= 56text{textdegree}
$$
b. 82$text{textdegree}$
c. 180$text{textdegree}$, 156$text{textdegree}$, 24$text{textdegree}$
d. 56$text{textdegree}$, 28$text{textdegree}$
e. 114$text{textdegree}$, 57$text{textdegree}$
f. 56$text{textdegree}$, 56$text{textdegree}$
The measure of an arc is equal to the measure of the central angle.
The inscribed angle is half the central angle on the same arc.
The inscribed angle is half the measure of the arc.
The inscribed angle is half the central angle on the same arc.
The inscribed angle is half the measure of the arc.
$$
mangle D=mangle C=64text{textdegree}
$$
$$
moverset{frown}{BF}=2mangle C=2cdot 64text{textdegree}=128text{textdegree}
$$
$$
mangle E=mangle C=64text{textdegree}
$$
$$
moverset{frown}{CBF}=180text{textdegree}
$$
$$
mangle BAF=2mangle BCF=2cdot 64text{textdegree}=128text{textdegree}
$$
$$
mangle BAC = 180text{textdegree}-mangle BAF=180text{textdegree}-128text{textdegree}=52text{textdegree}
$$
b. 128$text{textdegree}$
c. 64$text{textdegree}$
d. 180$text{textdegree}$
e. 128$text{textdegree}$
f. 52$text{textdegree}$
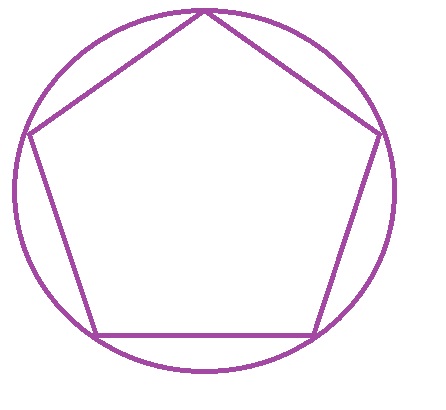
$$
mangle EDC = dfrac{5-2}{5}180text{textdegree}=108text{textdegree}
$$
$$
mangle BOC=180text{textdegree}-108text{textdegree}=72text{textdegree}
$$
$$
moverset{frown}{EBC}=2cdot 72text{textdegree}=144text{textdegree}
$$
b. 108$text{textdegree}$
c. 72$text{textdegree}$
d. 144$text{textdegree}$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
a. The circle has center $(-5,0)$ and radius $sqrt{10}approx 3.16$
$$
x^2-6x+y^2-2y=5
$$
Add 10 to both sides of the equation:
$$
(x^2-6x+9)+(y^2-2y+1)=5+10
$$
Factorize the perfect square trinomials ($a^2pm 2ab+b^2=(apm b)^2$):
$$
(x-3)^2+(y-1)^2=15
$$
Thus the equation is a circle with center $(3,1)$ and radius $sqrt{15}approx 3.87$.
b. $(3,1)$, $sqrt{15}approx 3.87$
$$
16-2x=3x
$$
Add $2x$ to both sides of the equation:
$$
16=5x
$$
Divide both sides of the equation by 5:
$$
3.2=dfrac{16}{5}=x
$$
$$
-10x+2-3=-10x
$$
Add $10x$ to both sides of the equation:
$$
-1=0
$$
Thus is impossible because $-1$ does not equal 0 and thus the equation has no solutions.
$$
(x+11)(x-3)=0
$$
Zero product property:
$$
x+11=0text{ or }x-3=0
$$
Solve each equation to $x$:
$$
x=-11text{ or }x=3
$$
$$
frac{2}{3}x-12=180
$$
Multiply both sides of the equation by 3:
$$
2x-36=540
$$
Add 36 to both sides of the equation:
$$
2x=576
$$
Divide both sides of the equation by 2:
$$
x=288
$$
b. No solution
c. $x=-11$ or $x=3$
d. $x=288$
$$
y=7x-2
$$
Interchange $x$ and $y$:
$$
x=7y-2
$$
Add 2 to both sides of the equation:
$$
x+2=7y
$$
Divide both sides of the equation by 7:
$$
dfrac{1}{7}(x+2)=y
$$
Interchange the left and right side of the equation and replace $y$ with $f^{-1}(x)$:
$$
f^{-1}(x)=dfrac{1}{7}(x+2)
$$
$$
f^{-1}(x)=dfrac{1}{7}(5+2)=dfrac{1}{7}(7)=1
$$
b. $f^{-1}(x)=1$
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=sqrt{(x-0)^2+(y-0)^2}=sqrt{x^2+y^2}
$$
b. The distance is the difference in $y$-coordinates: $y-4$.
c. Since every point is an equal distance from the focus and the directrix:
$$
sqrt{x^2+y^2}=y-4
$$
Square both sides of the equation:
$$
x^2+y^2=y^2-8y+16
$$
Subtract $y^2$ from both sides of the equation:
$$
x^2=-8y+16
$$
Subtract 16 from both sides of the equation:
$$
x^2-16=-8y
$$
Divide both sides of the equation by $-8$:
$$
-dfrac{1}{8}x^2+2=y
$$
Thus the equation of the parabola is $y=-dfrac{1}{8}x^2+2$.
b. $y-4$
c. $y=-frac{1}{8}x^2+2$
The area is the product of the length and the width:
$$
9cdot 15=135units^2
$$
The perimeter is the sum of all sides:
$$
9+15+9+15=48units
$$
REDUCED RECTANGLE
The area is the product of the area of the original rectangle and the scale factor squared:
$$
135cdot dfrac{1}{3^2}=15units^2
$$
The perimeter is the product of the perimeter of the original rectangle and the scale factor:
$$
48cdot dfrac{1}{3}=16units
$$
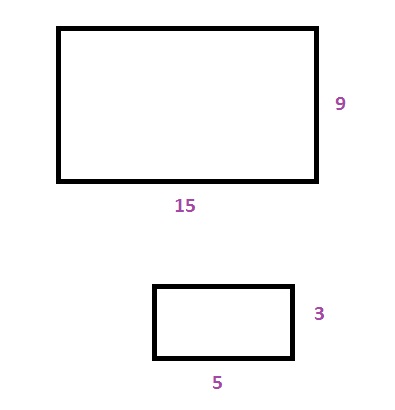
Reduced rectangle: 15 units$^2$, 16 units
$$
C(x)=300+7x
$$
b. Let $P(x)$ be the profit (which is also the revenue decreased by the cost):
$$
P(x)=50x-(300+7x)=43x-300
$$
c.
$$
P(x)=100
$$
Replace the function with its expression:
$$
43x-300=100
$$
Add 300 to both sides of the equation:
$$
43x=400
$$
Divide both sides of the equation by 43:
$$
x=dfrac{400}{43}approx 9.3
$$
Thus she will require at least 10 guests to make a profit of at least $100.
b. $P(x)=43x-300$
c. 10 guests
$$
mangle P=dfrac{180text{textdegree}}{2}=90text{textdegree}
$$
b. $overline{QR}$ would be the diameter of the circle, since $angle QCR$ (with $C$ the center of the circle) is 180$text{textdegree}$.
c. No, because it is still an inscribed angle on the same arc.
Determine the diameter using the Pythagorean theorem:
$$
text{Diameter}=sqrt{8^2+6^2}=sqrt{100}=10
$$
The radius is half the diameter:
$$
begin{align*}
text{Radius}&=frac{text{Diameter}}{2}=frac{10}{2}=5
end{align*}
$$
The area of a circle is the product of $pi$ and the square radius. The radiis half the diameter.
$$
A=pi r^2=pi 5^2=25pi
$$
b. Diameter circle
c. No
d. 25$pi$ units$^2$
$$
moverset{frown}{BAD}=2cdot 100text{textdegree}=200text{textdegree}
$$
The sum of the minor and major arc is 360$text{textdegree}$:
$$
moverset{frown}{BCD}=360text{textdegree}-moverset{frown}{BAD}=360text{textdegree}-200text{textdegree}=160text{textdegree}
$$
The insribed angle of the arc is half the measure of the arc:
$$
x=dfrac{160text{textdegree}}{2}=80text{textdegree}
$$
$$
moverset{frown}{BAD}=2y
$$
The sum of the minor and major arc is 360$text{textdegree}$:
$$
moverset{frown}{BCD}=360text{textdegree}-moverset{frown}{BAD}=360text{textdegree}-2y
$$
The insribed angle of the arc is half the measure of the arc:
$$
x=dfrac{360text{textdegree}-2y}{2}=180text{textdegree}-y
$$
Thus $x$ and $y$ are always supplementary.
b. Yes
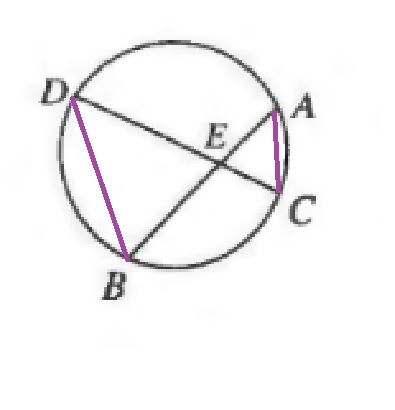
c. They have to be similar, because they have two pair of congruent angles (AA).
d. Corresponding sides of similar triangles have the same proportions:
$$
dfrac{DE}{EB}=dfrac{AE}{EC}
$$
Replace the sides with their known lengths:
$$
dfrac{8}{6}=dfrac{4}{EC}
$$
Use cross multiplication:
$$
8EC=4(6)
$$
Divide both sides of the equation by 8:
$$
EC=dfrac{24}{8}=3
$$
b. Equally large
c. Similar
d. 3
$$
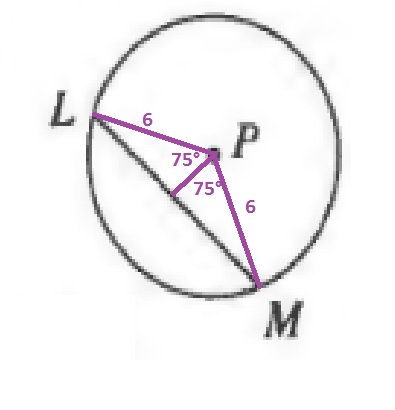
sin{75text{textdegree}}=dfrac{x}{6}
$$
Multiply both sides of the equation by 6:
$$
5.8approx 6sin{75text{textdegree}}=x
$$
The length of the chord is then:
$$
LM=2cdot 5.8=11.6units
$$
$$
x=sin^{-1}{dfrac{3}{5}}approx 37text{textdegree}
$$
The length of the arc is then:
$$
moverset{frown}{LM}=2cdot 37text{textdegree}=74text{textdegree}
$$
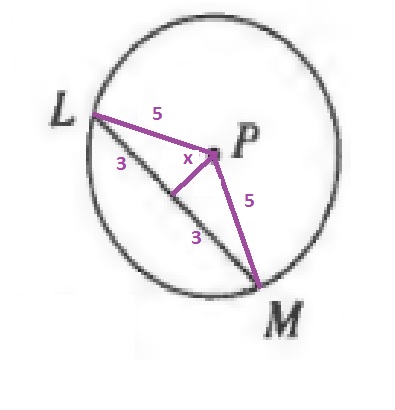
b. 74$text{textdegree}$
$$
dfrac{x}{6}=dfrac{2}{3}
$$
Multiply both sides of the equation by 6:
$$
x=dfrac{2cdot 6}{3}=4
$$
$$
moverset{frown}{RT}=mangle ROT=180text{textdegree}
$$
Since $S$ is the inscribed angle on $overset{frown}{RT}$:
$$
mangle S=90text{textdegree}
$$
The cosine is the adjacent rectangular side divided by the hypotenuse:
$$
x=cos^{-1}dfrac{r}{2r}=cos^{-1}dfrac{1}{2}=60text{textdegree}
$$
$$
moverset{frown}{EF}=2cdot 52text{textdegree}=104text{textdegree}
$$
The arc of the total circle is 360$text{textdegree}$:
$$
x=moverset{frown}{FG}=360text{textdegree}-104text{textdegree}-131text{textdegree}=125text{textdegree}
$$
b. 60$text{textdegree}$
c. 125$text{textdegree}$
The measure of an arc of which the diameter forms the central angle is 180$text{textdegree}$ and the inscribed angle on the arc is then 90$text{textdegree}$.
Opposite angles of a quadrilateral inscribed in a circle are supplementary.
Two chords of a circle that intersect, create two similar triangles.
You can determine the length of the chord, radius, distance to the center or the central angle using the sine/cosine/tangent ratios.
Opposite angles of a quadrilateral inscribed in a circle are supplementary.
Two chords of a circle that intersect, create two similar triangles.
You can determine the length of the chord, radius, distance to the center or the central angle using the sine/cosine/tangent ratios.
$$
moverset{frown} instead of overarc{AD}=2x=56text{textdegree}
$$
b. Since $overline{AB}$ is the diameter, we know that $mangle D=90text{textdegree}$. Then we can determine $AB$ using the Pythagorean theorem:
$$
AB=sqrt{5^2+(5sqrt{3})^2}=sqrt{100}=10
$$
Then we know that the radius is 5. The area of a circle is $pi$ multiplied by the radius squared:
$$
A=pi r^2=pi 5^2=25pi
$$
c. Since $overline{AB}$ is the diameter, we know that $mangle D=90text{textdegree}$. Since the inscribed angle on an arc is half the measure of the arc:
$$
x=dfrac{100text{textdegree}}{2}=50text{textdegree}
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
BD=2(8)sin{50text{textdegree}}approx 12.26
$$
b. 25$pi$
c. 12.26
b. 6, a chord connects two points on the circle.
c. 2, a semicircle is half the circle and thus the endpoints form a diameter of the circle.
d. 1, an inscribed angle is an angle inside a circle that lies on the circle.
e. 4, a minor arc is an arc that is less than half a circle.
f. 5, a central angle is an angle with center at the center of the origin.
b. 6
c. 2
d. 1
e. 4
f. 5
$$
6cdot 4cdot 5+6cdot 10cdot 3=120+180=300cm^3
$$
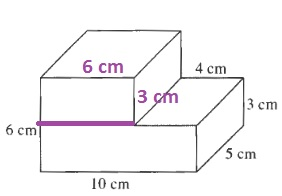
300cm^3
$$
$$
x=y
$$
b. The central angles is double the inscribed angle on the same arc:
$$
y=2x
$$
c. The ratios of intersecting chords are proportional:
$$
dfrac{3}{x}=dfrac{5}{y}
$$
d. Opposite angles of a quadrilateral inscribed in a circle are supplementary:
$$
x+y=180text{textdegree}
$$
b. $y=2x$
c. $frac{3}{x}=frac{5}{y}$
d. $x+y=180text{textdegree}$
$$
16x^2-16x-96leq 0
$$
Factorize:
$$
16(x-3)(x+2)leq 0
$$
Since the function $y=16(x-3)(x+2)$ opens upwards and since $x=3$ and $x=-2$ are its roots:
$$
-2leq xleq 3
$$
$$
x-1=pm 3
$$
Add 1 to both sides of the equation:
$$
x=1pm 3=4text{ or }-2
$$
$$
(x+5)(x-4)<0
$$
Since the function $y=(x+5)(x-4)$ opens upwards and since $x=-5$ and $x=4$ are its roots:
$$
-5<x<4
$$
$$
2(x^2-3x)=-5
$$
Add 4.5 to both sides of the equation:
$$
2(x^2-3x+2.25)=-0.5
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
2(x-1.5)^2=-0.5
$$
Divide both sides of the equation by 2:
$$
(x-1.5)^2=-0.25
$$
Take the square root of both sides of the equation:
$$
x-1.5=pm sqrt{-0.25}=pm 0.5i
$$
Add 1.5 to both sides of the equation:
$$
x=1.5pm 0.5i
$$
b. $x=4$ and $x=-2$
c. $-5<x<4$
d. $x=1.5pm 0.5i$
$$
0=x^2-2x+4
$$
Subtract 3 from both sides of the equation:
$$
-3=x^2-2x+1
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
-3=(x-1)^2
$$
Take the square root of both sides of the equation:
$$
sqrt{3}i=sqrt{-3}=x-1
$$
Add 1 to both sides of the equation:
$$
1pm sqrt{3}i=x
$$
Determine $y$:
$$
y=x-5=1pm sqrt{3}i-5=-4pm sqrt{3}i
$$
Thus the solutions are $(1pm sqrt{3}i, -4pm sqrt{3}i)$
$$
0=2x^2+2x-4
$$
Factorize:
$$
0=2(x+2)(x-1)
$$
Zero product property
$$
x+2=0text{ or }x-1=0
$$
Solve each equation to $x$:
$$
x=-2text{ or }x=1
$$
Determine $y$:
$$
y=x-5=-2-5=-7
$$
$$
y=x-5=1-5=-4
$$
Thus the solutions are $(-2,-7)$ and $(1,-4)$.
b. $(-2,-7)$ and $(1,-4)$
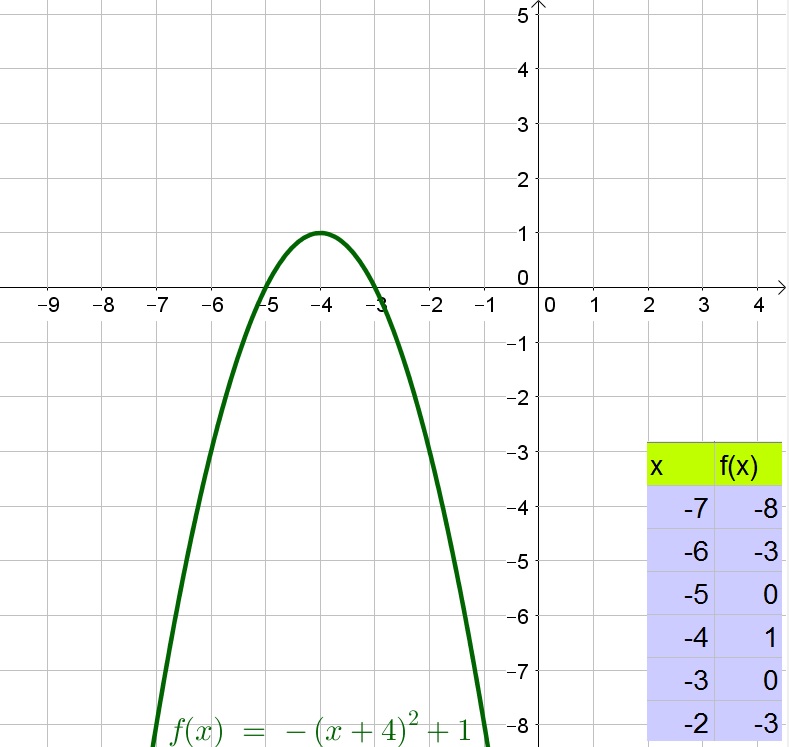
c. The maximum value is the $y$-value of the vertex and thus is $y=1$.
b. $x<-4$
c. $y=1$
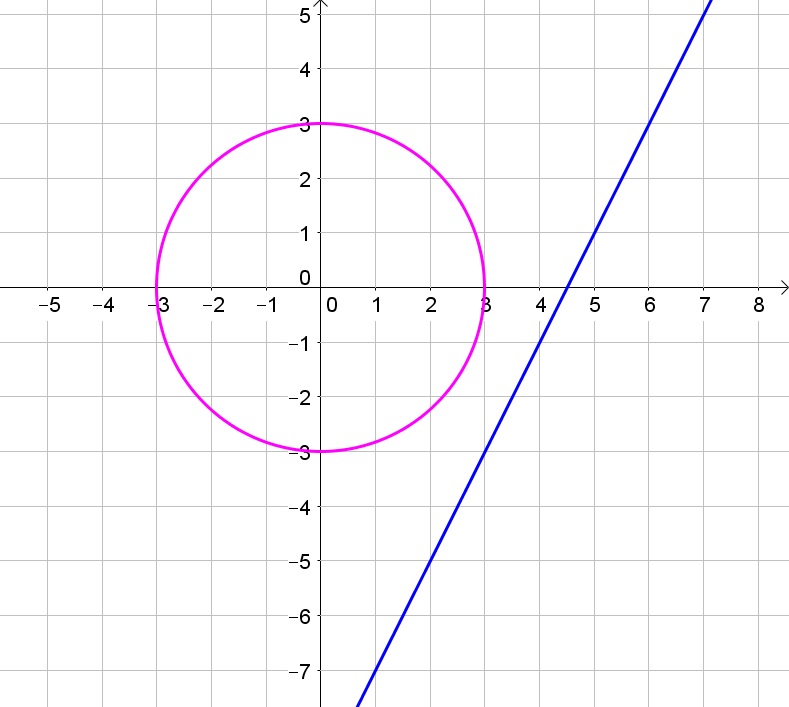
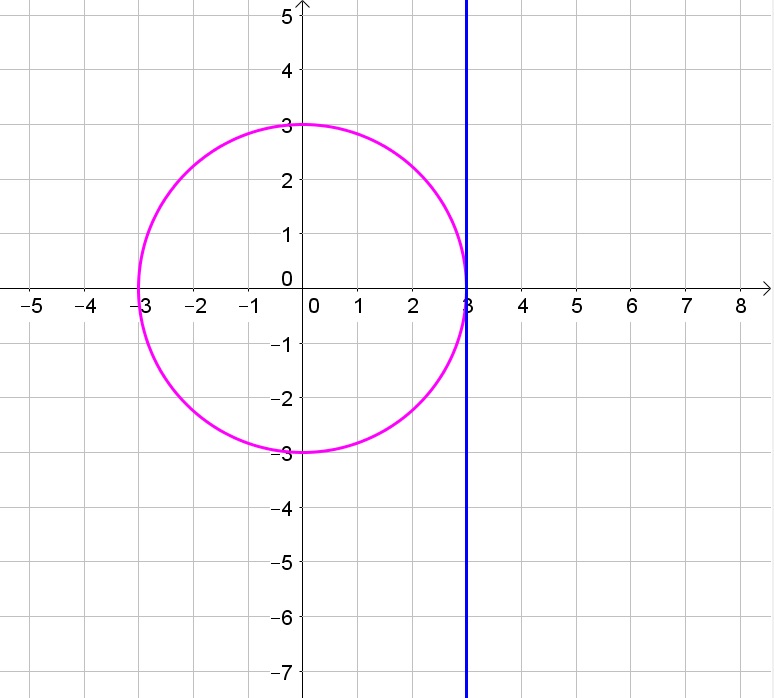
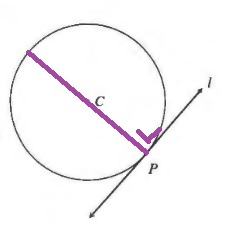
b. Possible
c. Possible
d. Not possible
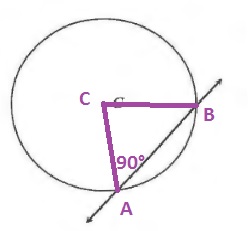
c. Yes, because the base angles of an isosceles triangle are congruent. But since the sum of all angles in a triangle is 180$text{textdegree}$, we then know that this is impossible.
d. This means that $overline{AB}$ cannot be a secant line of the circle.
b. Yes
c. Yes
d. $overline{AB}$ cannot be a secant line of the circle
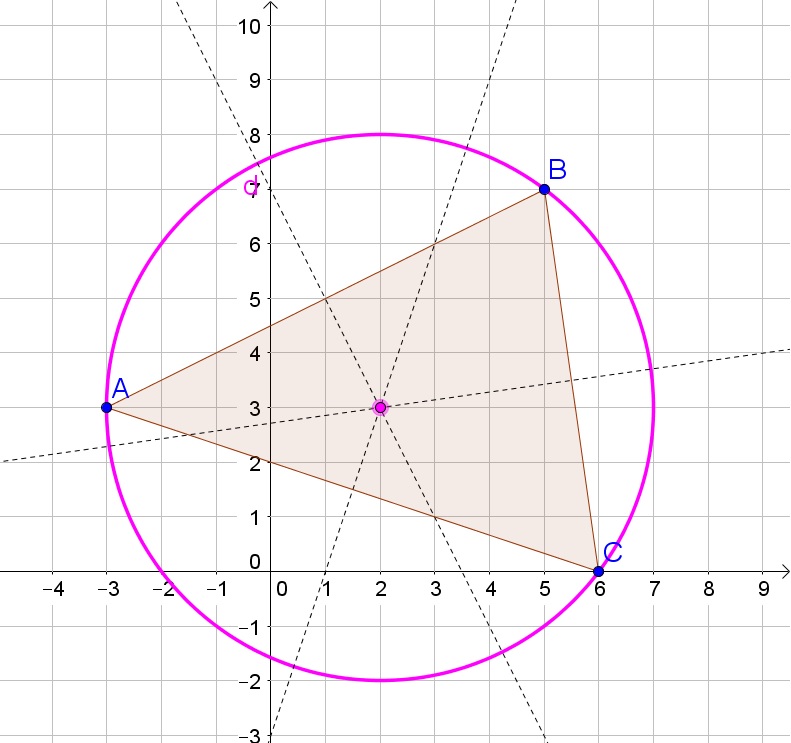
c. At the center of the circle and thus at $(2,3)$. Because the center of the circle is an equal distance away from all three cities.
b. 5, Circumcenter
c. $(2,3)$
$$
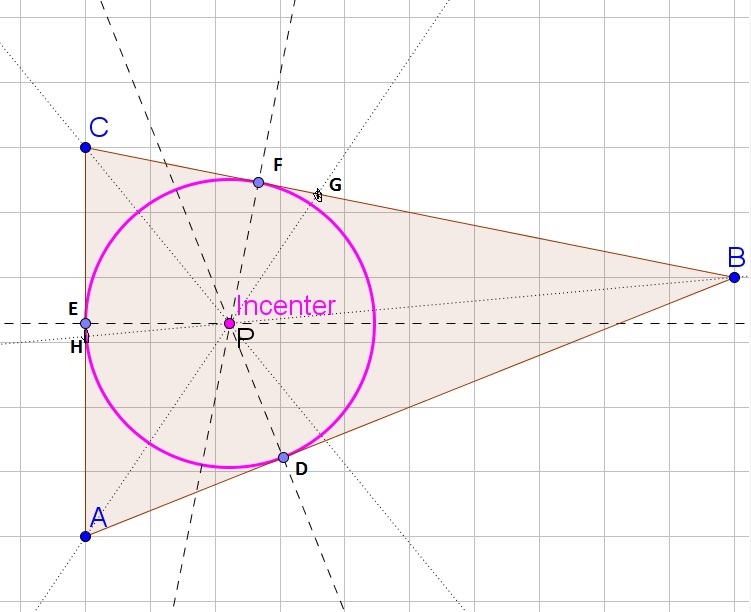
overline{AP}cong overline{AP}(text{Same side})
$$
$$
angle EAPcong angle DAP (text{$overline{AG}$ is the bisector of $angle BAC$})
$$
$$
angle PEAcong angle PDA (text{Right angles})
$$
$$
Downarrow AAS
$$
$$
triangle PEA cong triangle PDA
$$
$$
Downarrow
$$
$$
PE=PD
$$
$$
overline{BP}cong overline{BP}(text{Same side})
$$
$$
angle PBDcong angle PBF(text{$overline{BH}$ is the bisector of $angle ABC$})
$$
$$
angle PDBcong angle PFB(text{Right angles})
$$
$$
Downarrow AAS
$$
$$
triangle PDBcong triangle PFB
$$
$$
Downarrow
$$
$$
PF=PD
$$
Each side of the triangle is then also tangent, because it touches the circle in exactly one point and we know that $overline{PD}$ is perpendicular to $overline{AB}$ (similar to the other sides).
$$
CP=sqrt{6^2-5^2}=sqrt{11}approx 3.32
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
mangle C=sin^{-1}dfrac{5}{6}=56text{textdegree}
$$
$$
moverset{frown}{GD}=360text{textdegree}-40text{textdegree}-210text{textdegree}=110text{textdegree}
$$
$$
moverset{frown}{OR}=360text{textdegree}-40text{textdegree}-110text{textdegree}-180text{textdegree}=30text{textdegree}
$$
$$
moverset{frown}{RGO}=360text{textdegree}-30text{textdegree}=330text{textdegree}
$$
$$
BC=sqrt{34^2-16^2}=sqrt{900}=30
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
moverset{frown}{BC}=2mangle A=2sin^{-1}dfrac{30}{34}approx 124text{textdegree}
$$
b. 330$text{textdegree}$
c. 124$text{textdegree}$
$$
ER=AB=sqrt{39^2-6^2}=sqrt{1485}=3sqrt{165}approx 38.5
$$
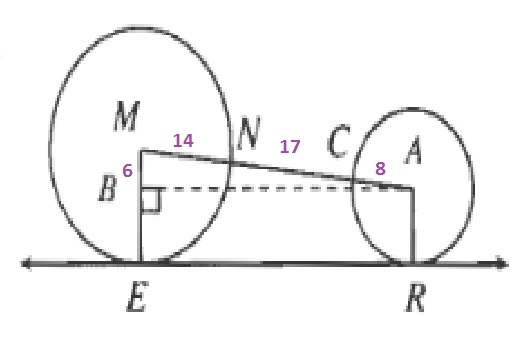
ERapprox 38.5 ft
$$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
Thus the given circle is a circle with center $(0,3)$ and radius 5.
The $x$-intercepts are the intersections with the $x$-axis and thus are $x=pm 4$. The $y$-intercepts are the intersections with the $y$-axis and thus are $y=-2$ and $y=8$.
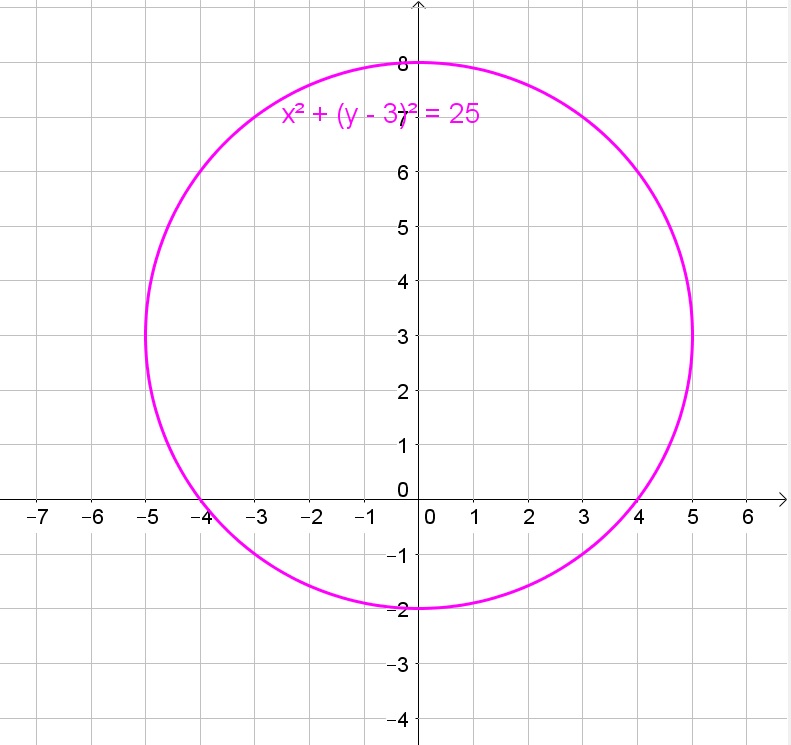
$y$-intercepts: $y=-2$ and $y=8$
$$
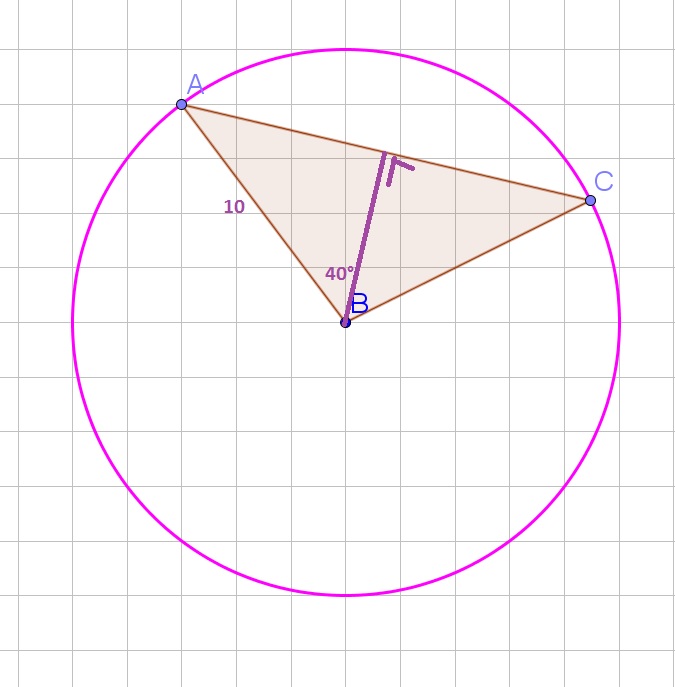
dfrac{AC}{2}=10sin{40text{textdegree}}approx 6.43
$$
Multiply both sides of the equation by 2:
$$
ACapprox 12.86
$$
$$
dfrac{GK}{3}=dfrac{6}{9}
$$
Multiply both sides of the equation by $3$:
$$
GK=dfrac{6cdot 3}{9}=2
$$
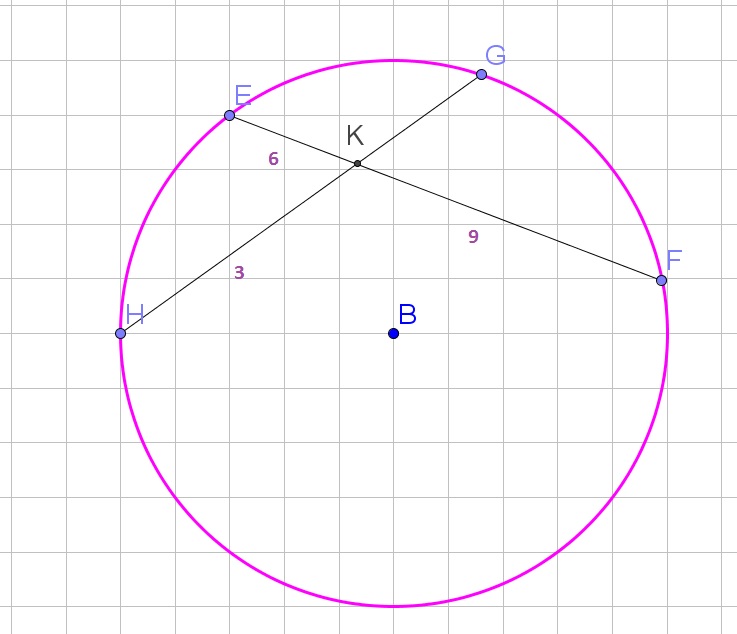
b. 2
$$
dfrac{360text{textdegree}}{9}=40text{textdegree}
$$
b. Inscribed angles on the same arc are congruent:
$$
mangle C = mangle B=97text{textdegree}
$$
The measure of the arc is double the measure of the inscribed angle on the same arc:
$$
moverset{frown}{AD}=2cdot 97text{textdegree}=194text{textdegree}
$$
c. The measure of the arc is equal to the measure of the central angle over the same arc:
$$
moverset{frown}{AB}=125text{textdegree}
$$
The length of the chord is the ratio of the measure of the arc to that of the circle multiplied by the circumference of a circle ($2pi r$):
$$
dfrac{125text{textdegree}}{360text{textdegree}}cdot 2pi 8=5.56piapprox 17.45
$$
b. 194$text{textdegree}$
c. 17.45
$$
x+3=sqrt{26^2-10^2}=sqrt{576}=24
$$
Subtract 3 from both sides of the equation:
$$
x=21
$$
x=21
$$
b. If $x=0$, then $y=-2$ and $a=1$ thus the function opens downwards, then graph 3 is the only possible graph.
c. If $x=0$, then $y=2$, then graph 1 is the only possible graph.
b. 3
c. 1
$$
V=pi 3^2cdot 2=18pi
$$
The volume of the remaining piece is then the product of the found volume and the ratio of the angle to the angle of a full circle:
$$
V=dfrac{45text{textdegree}}{360text{textdegree}}cdot 18pi=dfrac{9}{4}pi in^3approx 7in^3
$$
dfrac{9}{4}pi in^3approx 7in^3
$$
$$
2x+3x+4x+5x=360text{textdegree}
$$
Combine like terms:
$$
14x=360text{textdegree}
$$
Divide both sides of the equation by 14:
$$
x=dfrac{180}{7}text{textdegree}approx 26text{textdegree}
$$
dfrac{180}{7}text{textdegree}approx 26text{textdegree}
$$
See illustration below

See illustration below.

$$begin{aligned}
angle{DEF}+90degree+90degree+90degree&=360degree\
angle{DEF}+270degree&=360degree\
angle{DEF}&=360degree-270degree\
angle{DEF}&=90degree
end{aligned}$$
See illustration below.

$$begin{aligned}
angle{D}&=dfrac{1}{2}overset{largefrown}{DF}\
end{aligned}$$
where $overset{largefrown}{DF}$ is the arc angle from point $D$ and $F$.
$$begin{aligned}
overset{largefrown}{DF}&=angle{DEF}\
overset{largefrown}{DF}&=90degree
end{aligned}$$
$$begin{aligned}
angle{D}&=dfrac{1}{2}overset{largefrown}{DF}\
angle{D}&=dfrac{1}{2}(90degree)\
angle{D}&=45degree
end{aligned}$$
$$begin{aligned}
angle{F}&=angle{D}\
angle{F}&=45degree
end{aligned}$$
See illustration below.

$$begin{aligned}
costheta&=dfrac{r}{r+overline{AX}}
end{aligned}$$
$$begin{aligned}
cosdfrac{angle{DEF}}{2}&=dfrac{r}{r+overline{AX}}
end{aligned}$$
$$begin{aligned}
cosdfrac{90degree}{2}&=dfrac{4000}{4000+overline{AX}}\
cos45degree&=dfrac{4000}{4000+overline{AX}}\
end{aligned}$$
$$begin{aligned}
cos45degree(4000+overline{AX})&=dfrac{4000}{4000+overline{AX}}cdot(4000+overline{AX})\
cos45degree(4000+overline{AX})&=4000\
end{aligned}$$
$$begin{aligned}
dfrac{cos45degree(4000+overline{AX})}{cos45degree}&=dfrac{4000}{cos45degree}\
4000+overline{AX}&=dfrac{4000}{0.707}\
4000+overline{AX}&=5656.854
end{aligned}$$
$$begin{aligned}
4000+overline{AX}-textcolor{#4257b2}{4000}&=5656.854-textcolor{#4257b2}{4000}\
overline{AX}&=1656.854medspacetext{miles}
end{aligned}$$
$$
angle B=dfrac{180text{textdegree}}{2}=90text{textdegree}
$$
c.
$$
angle B=dfrac{180text{textdegree}}{2}=90text{textdegree}
$$
When $angle B$ is a right angle, we thus obtain that $overline{AB}$ is tangent to the circle at $B$.
$$
text{color{white} jmlirjtet mjretm lijretm lrejtj erjtl jrljtlr jlktjrl jtrlj ljr litelrj tlretm ermthmre hmtlrel thmrleht hlirht lhr}
$$
b. Yes
c. Graph
d. 90$text{textdegree}$
$$
mangle A=180text{textdegree}-moverset{frown}{BD}=moverset{frown}{BZD}-180text{textdegree}
$$
b.
$$
moverset{frown}{BD}=mangle BCD=180text{textdegree}-angle A=180text{textdegree}-x
$$
$$
moverset{frown}{BZD}=360text{textdegree}-moverset{frown}{BD}=360text{textdegree}-(180text{textdegree}-x)=180text{textdegree}+x
$$
c.
$$
x=moverset{frown}{BZD}-180text{textdegree}=180text{textdegree}-moverset{frown}{BD}
$$
Thus $angle A$ and $moverset{frown}{BD}$ are supplementary, while $moverset{frown}{BZD}$ is 180$text{textdegree}$ increased by $angle A$.
d.
$$
x=moverset{frown}{BZD}-180text{textdegree}=180text{textdegree}-moverset{frown}{BD}
$$
b. $moverset{frown}{BZD}=180text{textdegree}+x$
c. Supplementary angles
d. $x=moverset{frown}{BZD}-180text{textdegree}=180text{textdegree}-moverset{frown}{BD}$
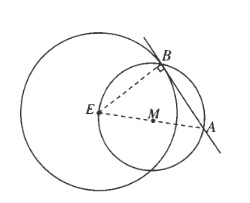
If you need to determine the tangent line through a given point, then you determine the midpoint between the center of the circle and the point. Draw a circle through this midpoint that goes through the point and its intersections with the other circles are then the points at which the tangent lines are.
$$
x=90text{textdegree}+180text{textdegree}=270text{textdegree}
$$
$$
tan{24text{textdegree}}=dfrac{7}{y}
$$
Multiply both sides of the equation by $y$:
$$
ytan{24text{textdegree}}=7
$$
Divide both sides of the equation by $tan{48text{textdegree}}$:
$$
y=dfrac{7}{tan{24text{textdegree}}}approx 15.72
$$
We also need to determine the value of $x$, which is one of the angles in the quadrilateral with two right angles and an angle of $48text{textdegree}$.
Since a right angle is $90text{textdegree}$ and the sum of all angles in a quadrilateral needs to be equal to $360text{textdegree}$:
$$
begin{align*}
x&=360text{textdegree}-90text{textdegree}-90text{textdegree}-48text{textdegree}=132text{textdegree}
end{align*}
$$
$$
dfrac{x}{6}=dfrac{3}{x+2}
$$
Use cross multiplication:
$$
x^2+2x=18
$$
Subtract 18 from both sides of the equation:
$$
x^2+2x-18=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-2pm sqrt{2^2-4(1)(-18)}}{2(1)}=-1pm sqrt{19}
$$
Only a positive length makes sence:
$$
x=-1+sqrt{19}
$$
b. $y=15.72$, $x=132text{textdegree}$
c. $-1+sqrt{19}$
$$
(x-x_1)^2+(y-y_1)^2=r^2
$$
Thus the equation of this circle is then
$$
(x-4)^2+(y-2)^2=3^2
$$
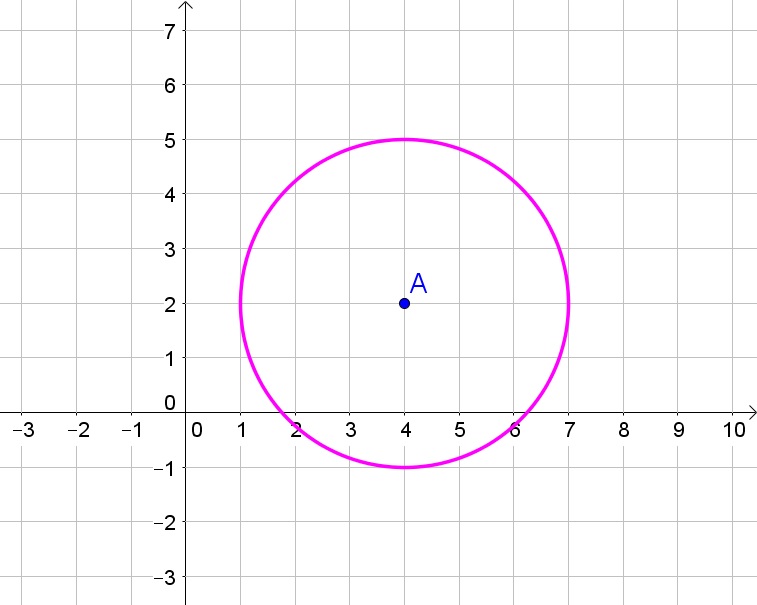
(x-4)^2+(y-2)^2=3^2
$$
$$
mangle QSO=dfrac{360text{textdegree}-180text{textdegree}-80text{textdegree}}{2}=dfrac{100text{textdegree}}{2}=50text{textdegree}
$$
$$
mangle QPO=mangle QSO=50text{textdegree}
$$
$$
mangle ONS=180text{textdegree}-63text{textdegree}-50text{textdegree}=67text{textdegree}
$$
$$
moverarc{PS}=2mangle SON=2(63text{textdegree})=126text{textdegree}
$$
$$
moverarc{PQ}=180text{textdegree}-126text{textdegree}=54text{textdegree}
$$
$$
mangle PQN = 63text{textdegree}
$$
b. 50$text{textdegree}$
c. 67$text{textdegree}$
d. 126$text{textdegree}$
e. 54$text{textdegree}$
f. 63$text{textdegree}$
$$
AB=sqrt{5^2+12^2}=sqrt{169}=13
$$
$$
r=dfrac{13}{2}=6.5
$$
$$
mangle ABC=tan^{-1}dfrac{12}{5}approx 67text{textdegree}
$$
$$
moverarc{AC}=2(67text{textdegree})=134text{textdegree}
$$
b. 6.5
c. 67$text{textdegree}$
d. 134$text{textdegree}$
$$
(x-5)(x+2)=0
$$
Zero product property:
$$
x-5=0text{ or }x+2=0
$$
Solve each equation to $x$:
$$
x=5text{ or }x=-2
$$
$$
3x^2-4x+10=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{4pm sqrt{(-4)^2-4(3)(10)}}{2(3)}=dfrac{2}{3}pm dfrac{sqrt{26}}{3}i
$$
$$
(x-8)(x-1)=0
$$
Zero product property:
$$
x-8=0text{ or }x-1=0
$$
Solve each equation to $x$:
$$
x=8text{ or }x=1
$$
$$
y^2-2y-15=0
$$
Factorize:
$$
(x-5)(x+3)=0
$$
Zero product property:
$$
x-5=0text{ or }x+3=0
$$
Solve each equation to $x$:
$$
x=5text{ or }x=-3
$$
b. $x=frac{2}{3}pm frac{sqrt{26}}{3}i$
c. $x=8$ or $x=1$
d. $x=5$ or $x=-3$
$$
dfrac{1}{4}x+2=12
$$
Subtract 2 from both sides of the equation:
$$
dfrac{1}{4}x=10
$$
Multiply both sides of the equation by 4:
$$
x=40
$$
Thus it will take 40 hours.
$$
h=5sin{72text{textdegree}}approx 4.76
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{10cdot 4.76}{2}=23.8
$$
Since the decagon is made up out of 10 triangles, the area of the decagon is:
$$
10cdot 23.8=238units^2
$$
238units^2
$$
$$
mangle PSR=360text{textdegree}-140text{textdegree}=220text{textdegree}
$$
The sum of all angles in a quadrilateral is 360$text{textdegree}$:
$$
mangle Q=360text{textdegree}-220text{textdegree}-40text{textdegree}-35text{textdegree}=65text{textdegree}
$$

