All Solutions
Page 701: Closure Activity
There would be a total of $12$ balls in the jar.
$$begin{aligned}
&= 5 text{ red} + 4 text{ white} + 3 text{ blue} \
&= 12 text{ balls} \
end{aligned}$$
$$begin{aligned}
P &= frac{4}{12} cdot frac{3}{11} cdot frac{2}{10}\\
&= 0.0182
end{aligned}$$
$$begin{aligned}
P &= frac{(_5C_2)(_4C_1)}{_{12}C_3} \\
&= frac{frac{5!}{2!cdot3!} cdot frac{4!}{1!cdot3!}}{frac{12!}{3!cdot9!}}\\
&= frac{10cdot 4}{220}\\
&= 0.1818
end{aligned}$$
$$begin{aligned}
P &= left(frac{5}{12} cdot frac{4}{11} cdot frac{3}{10} right) + left(frac{4}{12} cdot frac{3}{11} cdot frac{2}{10} right) + left(frac{3}{12} cdot frac{2}{11} cdot frac{1}{10} right) \\
&= frac{1}{22} + frac{1}{55} + frac{1}{220}\\
&= frac{3}{44} approx 0.0682 \
end{aligned}$$
b. $0.1818$
c. $0.0682$
Use the binomial coefficients to solve the problem. If there are $8$ people present and the position of person $K$ is fixed, then the number of possibilities for this case is $(8-1)!$ or $7!$ because $7$ people don’t have a fixed position and can have different seats. Also, person $K$ can sit on one or the other side of the aisle and this also must be included in the calculations. Therefore, the total number of possibilities is $2cdot7!$.
If there are two people with $K$ and three people with $S$ and none of them have a fixed position, then the number of possibilities is $8!$. Also, since some people have the same initial, we need to eliminate the possibilities that will repeat. if two people have the initial $K$, and three people have the initial $S$, then we need to reduce the number of possibilities by $2!cdot3!$. The total number of possibilities is $frac{8!}{2!cdot3!}$.
**B.** $hspace{4pt}dfrac{8!}{2!cdot3!}$
a. Since Nora is very particular with the order of the scoops, we will use permutation.
$$begin{aligned}
_{23}P_3 &= frac{23!}{(23-3)!} \\
&= frac{23!}{20!} \\
&= 10626 \
end{aligned}$$
$$begin{aligned}
_{23}C_3 &= frac{23!}{20! cdot 3!} \
&= 1771\
end{aligned}$$
$$begin{aligned}
&= 1 cdot 22 cdot 22 \
&= 484\
end{aligned}$$
$$begin{aligned}
&= 4 cdot 19 cdot 19\
&= 1444\
end{aligned}$$
b. $1771$
c. $484$
d. $1444$
Calculate the surface areas of both boxes.
The measures of the cylindric box are:
$$begin{aligned}
h&=10\
d&=6\
d&=2r\
2r&=6\r&=3
end{aligned}$$
Calculate the surface area of the cylindrical box:
$$begin{aligned}
S&=2rpi(r+h)\
&=2cdot3pi(3+10)\
&=6picdot13\
&=78pi\
&approxboxed{245 text{ in}^2}
end{aligned}$$
The measures of the cylindrical box are:
$$begin{aligned}
a= 5 quad b=6quad c=9
end{aligned}$$
Calculate the surface area of the rectangular box:
$$begin{aligned}
S&= 2ab+2ac+2bc\
&=2cdot5cdot6+2cdot5cdot9+2cdot6cdot9\
&=60+90+108\
&=boxed{258text{ in}^2}
end{aligned}$$
Conclude that the cylindrical box has a lesser surface area than the rectangular box.
Determine the amount of ribbon necessary to wrap the present in the way demonstrated on the figure.
Calculate the amount of ribbon for the cylindrical box first.
Notice that one of the ribbons is present in the middle of the box. The amount of ribbon for this loop can be calculated as the perimeter of the circle using the formula $2rpi$.
$$begin{aligned}
P_1&=2rpi\
&=2cdot3pi\
&=6pi
end{aligned}$$
The other two loops can be calculated using the formula $2h+2d$ as the loops encircle the box twice by height and twice by diameter.
$$begin{aligned}
P_2&=2h+2d\
&=2cdot10+2cdot6\
&=32
end{aligned}$$
Finally, calculate the total amount of ribbon to wrap the cylindrical box.
$$begin{aligned}
P_{total}&=P_1+2P_2\
&=6pi+2cdot32\
&=18.85+64\
&approxboxed{83text{ in}} \
end{aligned}$$
$$begin{aligned}
P_1&=2a+2b\
&=2cdot5+2cdot6\
&=22\
\
P_2&=2b+2c\
&=2cdot6+2cdot9\
&=30\
\
P_3&=2a+2c\
&=2cdot5+2cdot9\
&=28\
\
end{aligned}$$
Calculate the total amount of ribbon needed to wrap the rectangular box as a sum of all three perimeters.
$$begin{aligned}
P_{total}&=P_1+P_2+P_3\
&=22+30+28\
&=boxed{80text{ in}}
end{aligned}$$
Conclude that the lesser amount of ribbon is needed to tie the loops around the rectangular box than the cylindrical box.
a.
[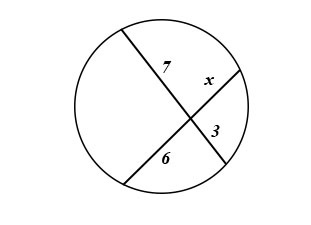](https://postimg.cc/8FxghpPX)
$$begin{aligned}
6 cdot x &= 7 cdot 3 \
6 x &= 21 \
frac{6 x}{6} &= frac{21}{6} \
x &= 3.5 \
end{aligned}$$
[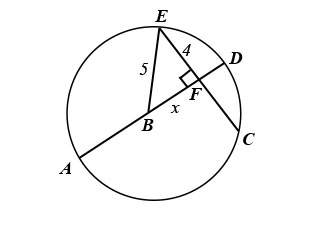](https://postimg.cc/Rq7xHzrG)
$$begin{aligned}
z^2 &= x^2+ y^2 \
5^2 &= x^2+ 4^2 \
25-16 &= x^2\
sqrt{9} &= sqrt{x^2}\
3 &= x
end{aligned}$$
[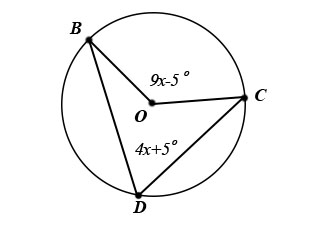](https://postimg.cc/crTqFMLn)
$$begin{aligned}
2(4x+5) &= 9x-5 \
8x+10 &= 9x-5 \
8x-9x &= -5-10 \
-1 cdot -x &= -15 cdot -1 \
x &= 15
end{aligned}$$
[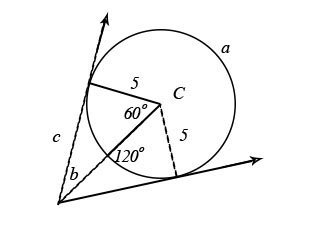](https://postimg.cc/DSn7pwhS)
$$begin{aligned}
a &= 360-120 \
&= 240^circ
end{aligned}$$
$$begin{aligned}
b &= frac{1}{2}(240-120) \
&= frac{120}{2}\
&= 60^circ
end{aligned}$$
Solve for $c$ using the $30^circ-60^circ-90^circ$ triangle theorem.
$$begin{aligned}
c &= 5sqrt{3} \
end{aligned}$$

where
$h=3$ ft
$b=2$ ft
$l=3$ ft
$x=y$ – sides of base triangle
$$begin{aligned}
A_s&=2A_b+P_bl
end{aligned}$$
where,
$A_s$ – surface area
$A_b$ – base area
$P_b$ – perimeter of the base
$l$ – height of small size tent
$$begin{aligned}
A_b&=dfrac{1}{2}bh\
A_b&=dfrac{1}{2}(2)(3)\
A_b&=3medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
x^2&=3^2+left(dfrac{2}{2}right)^2\
x^2&=9+1\
x^2&=10\
x&=sqrt{10}\
x&=3.162=y
end{aligned}$$
$$begin{aligned}
P_b&=x+y+b\
P_b&=3.162+3.162+2\
P_b&=8.324medspacetext{ft}
end{aligned}$$
$$begin{aligned}
A_s&=2A_b+P_bl\
A_s&=2(3)+8.324(3)\
A_s&=6+24.972\
A_s&=30.972medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
V&=dfrac{1}{2}(b)(h)(l)
end{aligned}$$
$$begin{aligned}
V&=dfrac{1}{2}(2)(3)(3)\
V&=dfrac{1}{2}(18)\
V&=9medspacetext{ft}^3
end{aligned}$$
$$begin{aligned}
r^3&=dfrac{V_f}{V}
end{aligned}$$
where
$V_f$ – volume of full size tent
$V$ – volume of small size tent
$r$ – linear scale factor
$$begin{aligned}
r^3&=dfrac{72}{9}\
r^3&=8
end{aligned}$$
$$begin{aligned}
sqrt[3]{r^3}&=sqrt[3]{8}\
r&=2
end{aligned}$$
$$begin{aligned}
l_f&=lcdot 2
end{aligned}$$
where
$l_f$ – height of full size tent
$$begin{aligned}
l_f&=3(2)\
l_f&=6medspacetext{ft}
end{aligned}$$
$$begin{aligned}
dfrac{A_{sf}}{A_s}&=r^2
end{aligned}$$
where
$A_{sf}$ – surface area of full size tent
$A_s$ – surface area of small size tent
$r$ – scale factor
$$begin{aligned}
dfrac{A_{sf}}{30.972}&=(2)^2\
dfrac{A_{sf}}{30.972}&=4
end{aligned}$$
$$begin{aligned}
dfrac{A_{sf}}{30.972}cdottextcolor{#4257b2}{(30.972)}&=4cdottextcolor{#4257b2}{(30.972)}\
A_{sf}&=123.89medspacetext{ft}^2
end{aligned}$$
Calculate the surface area of the smaller tent. The tent has the shape of a three-sided prism. Notice that the sides of the tent form a triangle. The base of the triangle has the length $a=2$ and the height $h=3$. Use these data to calculate the area of the single side of the tent.
$$begin{aligned}
A_1&=frac{1}{2}acdot h\
&=frac{1}{2}cdot2cdot3\
&=3 text{ ft}^2
end{aligned}$$
To calculate the surface area of the rectangular-shaped sizes of the tent, we lack the length of the other sides of the triangle-shaped side of the tent. Notice that the side we lack, the half of the base of the triangle, and the height of the triangle form a right triangle. This triangle is demonstrated in the figure below.

The side we need to calculate the length for is the hypotenuse of this right triangle. Use the Pythagorean Principle to calculate the length of the hypotenuse.
$$begin{aligned}
x^2&=h^2+left(frac{a}{2}right)^2\
&=3^2+1^2\
&=10\
x&=sqrt{10}\
&=3.162 text{ ft}
end{aligned}$$
$$begin{aligned}
M&= (a+x+x)cdot b\
&=(2+3.162+3.162)cdot3\
&=8.324cdot3\
&=24.97\
&approx25 text{ ft}^2
end{aligned}$$
Finally, calculate the entire surface area of the tent by adding two times the area $A_1$ to the value of $M$.
$$begin{aligned}
SA_1&=2A_1+M\
&=2cdot3+25\
&=boxed{31 text{ ft}^2}
end{aligned}
Calculate the volume of the smaller tent.
Use the formula for the volume of the three-sided prism to calculate the volume of the tent. Multiply the surface area of the triangle-shaped side with the length of the tent, as demonstrated below:
$$begin{aligned}
V&=A_1cdot b\
&=3cdot 3\
&=boxed{9 text{ ft}^3}
end{aligned}$$
Calculate the height of the full-sized tent given the data on its volume. In other words, find the value of the parameter $h$ for the full-sized tent.
First, calculate the linear scale factor ($l$) for the enlargement of the tent. If the linear scale factor is calculated using the volume, it needs to be cubed.
$$begin{aligned}
V_2&=l^3V_1\
72&=l^3cdot9\
l^3&=8\
l&=2
end{aligned}$$
If the linear scale factor is $2$, then the height of the large tent is calculated by multiplying the height of the small tent by the linear scale factor.
$$begin{aligned}
h_2&=h_1cdot l\
&=3cdot2\
&=boxed6
end{aligned}$$
Calculate the surface size of the larger tent.
Use the linear scale factor and the surface area of the smaller tent to calculate the surface area of the larger tent. When changing the area according to the linear scale factor, the linear scale factor is squared.
$$begin{aligned}
SA_2&=l^2cdot SA_1\
&=2^2cdot 31\
&approxboxed{124 text{ ft}^2}\
end{aligned}
Calculate the volume of the stadium. The given data is that the stadium has a radius $r=200$ ft and a height $h=150$ ft.
It is stated in the text of the exercise that the roof of the stadium has a shape of half of the sphere. The formula for the volume of the sphere is $V=frac{4}{3}r^3pi$. Therefore, the formula for the volume of the half-sphere is:
$$begin{aligned}
V&=frac{1}{2}cdotfrac{4}{3}r^3pi\
&=frac{4}{6}r^3pi\
&=frac{2}{3}r^3pi\
end{aligned}$$
Combine the formulas for the volume of the cylinder and the volume of the sphere to solve the problem.
$$begin{aligned}
V&=V_{cyinder}+frac{1}{2}V_{sphere}\
&=r^2pi h+frac{1}{2}cdotfrac{4}{3}r^3pi\
&=200^2picdot150+frac{2}{3}cdot200^3pi\
&=6000000pi+5333333.333pi\
&=pi(6000000+5333333.333)\
&=11333333.333pi\
&=boxed{35604716.74 text{ ft}^3}
end{aligned}$$
Calculate the surface area of the stadium by combining the formulas for the surface area of the cylinder side and half the surface area of the sphere since the dome of the stadium represents half the sphere.
$$begin{aligned}
SA_{total}&=SA_{cylinder side}+frac{1}{2}SA_{sphere}\
&=2rpi h+frac{1}{2}cdot4r^2pi\
&=2cdot200pi cdot150+2cdot200^2pi\
&=60000pi +80000pi\
&=pi(60000+80000)\
&=140000pi\
&=439822.97\
&approxboxed{440000 text{ ft}^2}
end{aligned}$$
$SAapprox440000 text{ ft}^2$
$$begin{aligned}
V_{st}&=V_c+V_s\
end{aligned}$$
where
$V_{st}$ – volume of the stadium
$V_c$ – volume of the cylinder
$V_s$ – volume of the sphere
$$begin{aligned}
V_s&=dfrac{dfrac{4}{3}pi r^3}{2}\
&=dfrac{4}{3}pi r^3cdotdfrac{1}{2}&text{(Transposition Method)}\
&=dfrac{4}{6}pi r^3\
&=dfrac{2}{3}pi r^3\
end{aligned}$$
$$begin{aligned}
V_c&=pi r^2h\
end{aligned}$$
For $V_c$.
$$begin{aligned}
V_c&=pi r^2h\
&=(3.1416)(200)^2(150)\
&=18849555.92medspacetext{ft}^3
end{aligned}$$
$$begin{aligned}
V_s&=dfrac{2}{3}pi r^3\
&=dfrac{2}{3}(3.1416)(200)^3\
&=16755160.82medspacetext{ft}^3
end{aligned}$$
$$begin{aligned}
V_{st}&=V_c+V_s\
&=18849555.92+16755160.82\
&=35604716.74medspacetext{ft}^3
end{aligned}$$
$$begin{aligned}
SA_{st}&=SA_c+SA_s
end{aligned}$$
where
$SA_{st}$ – surface area of the stadium
$S_c$ – surface area of the cylinder
$S_s$ – surface area of the sphere

$$begin{aligned}
SA_c&=2pi r^2+2pi rh\
end{aligned}$$
$$begin{aligned}
SA_c&=2pi r^2+2pi rh\
SA_c&=pi r^2+pi r^2+2pi rh\
SA_c&=2pi rh&& blue*
end{aligned}$$
$blue*$ The upper and bottom base area of the cylinder is eliminated from the equation.
$$begin{aligned}
SA_c&=2pi rh\
&=2(3.1416)(200)(150)\
&=188495.55medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
SA_s&=dfrac{4pi r^2}{2}\
&=2pi r^2
end{aligned}$$
$$begin{aligned}
SA_s&=2pi r^2\
&=2(3.1416)(200)^2\
&=251327.41medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
SA_{st}&=SA_c+SA_s\
&=188495.55+251327.41\
&=439822.96medspacetext{ft}^2
end{aligned}$$

