All Solutions
Page 644: Questions
$$
7cdot 7 cdot 7 cdot 7=7^4=2,401
$$
b. We need to make four decisions about the digits (one for each digit) and each digit has 7 choices.
c. There will be 4 branch points (one each for the digit) and 7 branches at each point. Note that these answers contain the same integers as the answers of Nick’s.
d. There are 7 choices for each decision and thus the number of possibilities are:
$$
7cdot 7 cdot 7 cdot 7=7^4=2,401
$$
e. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{1}{2,401}approx 0.0004=0.04%
$$
b. 4 decision, 7 choices each
c. 4, 7
d. 2,401
e. 0.0004=0.04%
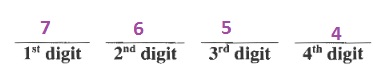
$$
7times 6times 5times 4=840
$$
Thus in total, there are 840 possible passwords if you can’t repeat numbers.
$$
9cdot 8 cdot 7=504
$$
b. There are 9 choices for each digit:
$$
9cdot 9 cdot 9 =9^3=729
$$
c. The similarities is that the same digits are possible and the same number of digits are needed. The difference is that in (a) the digits cannot be repeated, while in (b) the same digits can be repeated.
b. 729
c. Digits cannot be repeated vs. Digits can be repeated.
$$
6cdot 5 cdot 4cdot 3 cdot 2 cdot 1=720
$$
b. For the first period there is 1 choice, the second 5, the third 4, etc.:
$$
1cdot 5 cdot 4cdot 3 cdot 2 cdot 1=120
$$
c. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{120}{720}=dfrac{1}{6}approx 0.167=16.7%
$$
d. The number of possibilities of having first-period pre-calculus and second-period physics:
$$
1cdot 1 cdot 4 cdot 3 cdot 2cdot 1=24
$$
The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{24}{720}=dfrac{1}{30}approx 0.033=3.3%
$$
b. 720
c. $frac{1}{6}approx 0.167=16.7%$
d. $frac{1}{30}approx 0.033=3.3%$
b. 6! is the same as the number of possible schedules.
c. 6! means the product of all integers between 1 and 6, which is exactly how we calculated the number of different schedules.
d. Because
$$
4!=4cdot 3 cdot 2cdot 1
$$
which is the same way we would calculate the number of possible ways to arrange the letters of MATH(since if you picked the first letter, there are three possibilities left for the second, then two possibilities left for the third and one possibility for the forth).
b. 6!
c. Product of all integers from 1 to 6.
d. $4!=4cdot 3cdot 2cdot 1$.
a.
$$
dfrac{10!}{8!}=10cdot 9 = 90
$$
b.
$$
dfrac{70!}{68!}=70cdot 69 = 4,830
$$
c.
$$
dfrac{7!}{4!3!}=dfrac{7cdot 6cdot 5}{3cdot 2 cdot 1} = 35
$$
d.
$$
dfrac{20!}{18!2!}=dfrac{20cdot 19}{2 cdot 1} = 190
$$
b. 4,830
c. 35
d. 190
$$
4!=4cdot 3 cdot 2 cdot 1=24
$$
b.
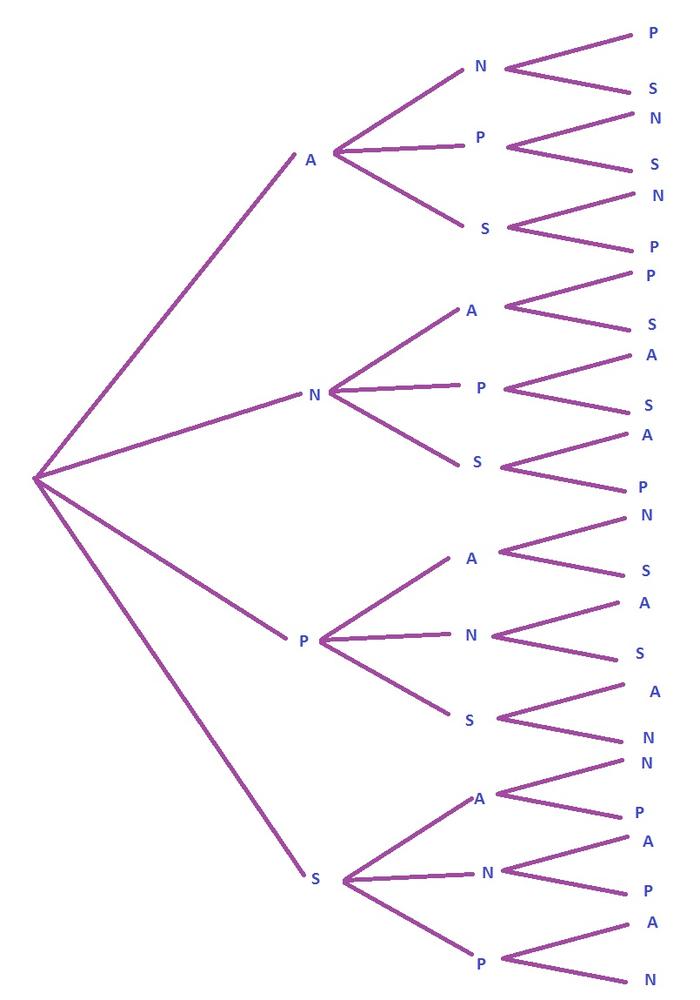
$$
P(word)=dfrac{4}{24}=dfrac{1}{6}approx 0.167=16.7%
$$
b. Tree diagram
c. $frac{1}{6}approx 0.167=16.7%$
$$
5!=5cdot 4cdot 3 cdot 2 cdot 1=120
$$
120
$$
$$
dfrac{8}{k}=dfrac{k}{18}
$$
Use cross multiplication:
$$
144=k^2
$$
Take the square root of both sides of the equation and take into account that a negative length is not possible:
$$
12=k
$$
$$
z=360text{textdegree}-50text{textdegree}=310text{textdegree}
$$
The sine ratio is the opposite side divided by the hypotenuse:
$$
r=dfrac{5}{sin{25text{textdegree}}}approx 11.83
$$
b. $r=11.83$
$$
dfrac{n-2}{n}180text{textdegree}
$$
Replace $n$ with 8:
$$
dfrac{n-2}{n}180text{textdegree}=dfrac{6}{8}180text{textdegree}=135text{textdegree}
$$
$$
r=dfrac{40}{2pi}=dfrac{20}{pi}
$$
The surface area of the sphere is then:
$$
S=4pi r^2=4pi dfrac{20^2}{pi^2}=dfrac{1600}{pi}approx 509ft^2
$$
Determine the volume of the sphere:
$$
V=dfrac{4pi r^3}{3}=dfrac{4pi 20^3}{3pi^3}=dfrac{32000}{3pi^2}approx 1,081ft^3
$$
$$
C=sqrt[3]{2}cdot 40approx 50ft
$$
b. 50 ft
$$
0=x^2-5x-6
$$
Factorize:
$$
0=(x-6)(x+1)
$$
Zero product property:
$$
x-6=0text{ or }x+1=0
$$
Solve each equation to $x$:
$$
x=6text{ or }x=-1
$$
Determine $y$:
$$
y=2x+8=2(6)+8=20
$$
$$
y=2x+8=2(-1)+8=6
$$
Thus the solutions are $(6,20)$ and $(-1,6)$.
b. In the graph we note a quadratic pattern.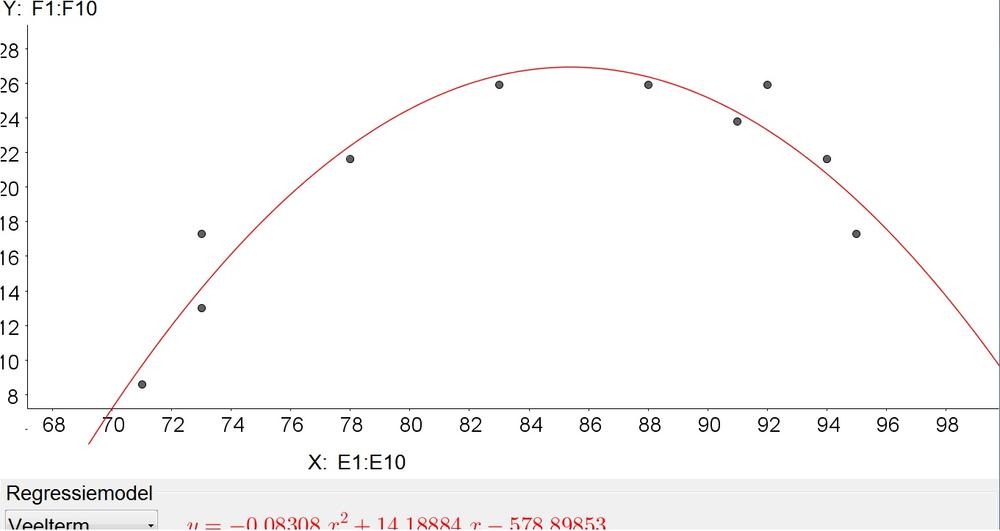
$$
y=-0.08308x^2+14.18884x-578.89853
$$
Evaluate at $x=95$:
$$
y=-0.08308(95)^2+14.18884(95)-578.89853=19.24427
$$
Thus the attendance is about 19.24427 thousand or 19,244.
b. Quadratic
c. 19,244
$$
10cdot 9 cdot 8 cdot 7=5,040
$$
b. The product of the integer 1 to 6 are missing (and thus 6!).
c. You can thus rewrite this as:
$$
dfrac{10!}{6!}=10cdot 9 cdot 8 cdot 7=5,040
$$
b. Product of 1 to 6, 6!
c. $frac{10!}{6!}$
$$
dfrac{52!}{(52-4)!}=dfrac{52!}{48!}=52cdot 51cdot 50cdot 49=6,497,400
$$
b. Repetition is not allowed and tus we need a permutation:
$$
7!=5,040
$$
c. Repetition is not allowed and tus we need a permutation:
$$
dfrac{36!}{(36-3)!}=dfrac{36!}{3!}=36cdot 35cdot 34=42,840
$$
d. Repetition is not allowed and tus we need a permutation:
$$
35cdot 35 cdot 34=41,650
$$
e. Repetition is allowed:
$$
36cdot 36cdot 36=36^3=46,656
$$
b. 5,040 ways
c. 42,840 ways
d. 41,650 ways
e. 46,656 ways
b. The list of candidates will be longer than the list of applications, because the order matters with president/vice/secratary but it does not matter with the applications (group of applicant 1,2 and 3 is the same as the group of applicant 3,2 and 1).
c. The second situation is a permutation, because the tiles cannot be repeated.
d. Order is important and there cannot be repetition. In general, if you have to pick k from p:
$$
_pP_k=dfrac{p!}{(p-k)!}
$$
b. List of candidates will be longer
c. Second situation is permutation
d. $_pP_k=frac{p!}{(p-k)!}$
b.
$$
_nP_r=dfrac{n!}{(n-r)!}
$$
c. (i)
$$
_7P_4=dfrac{7!}{(7-4)!}=7cdot 6 cdot 5cdot 4=840
$$
(ii)
$$
_{52}P_4=dfrac{52!}{(52-4)!}=52cdot 51 cdot 50cdot 49=6,497,400
$$
(iii)
$$
_{16}P_7=dfrac{16!}{(16-7)!}=16cdot 15 cdot 14cdot 13cdot 12cdot 11 cdot 10=57,657,600
$$
b. $_nP_r=frac{n!}{(n-r)!}$
c. (i) 840 (ii) 6,497,400 (iii) 57,657,600
$$
_4P_4=dfrac{4!}{(4-4)!}=4!=24
$$
b. Since two of the letters are the same, every combination appears twice and thus there are only 12 combinations.
c. Since three letters are identical, there are only 4 possibilities (since A can be in the first to forth place while the remaining places are S).
d.
$$
(b) dfrac{4!}{(4-2)!}=dfrac{4!}{2!}
$$
$$
(c)dfrac{4!}{(4-1)!}=dfrac{4!}{3!}
$$
e. If a letter is repeated $k$ times, then divide the number of arrangements by $k!$ (as there are $k!$ ways to order $k$ elements).
b. 12 ways, two letters are the same
c. 4 ways
d. (b) $frac{4!}{2!}$ (c) $frac{4!}{3!}$
e. Divide the number of arrangements by $k!$
$$
_7P_7=dfrac{7!}{(7-7)!}=7!=5,040
$$
b. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{1}{5,040}approx 0.0002=0.02%
$$
b. 0.0002=0.02%
$$
_{12}P_3=dfrac{12!}{(12-3)!}=dfrac{12!}{9!}=12cdot 11 cdot 10=1,320
$$
b. See (a)
$$
DB=sqrt{AB^2+AD^2}=sqrt{4^2+3^2}=sqrt{25}=5
$$
The minimal distance from point $B$ to the hot tub is then $DB$ decreased by the radius:
$$
DB-r=5-3=2ft
$$
$$
V=dfrac{Bcdot h}{3}=dfrac{(12cdot 7)cdot 21}{2}=882 units^3
$$
$$
f(x)=(x^2+6x+9)+11-9
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x+3)^2+2
$$
b. The vertex is $(-3,2)$.
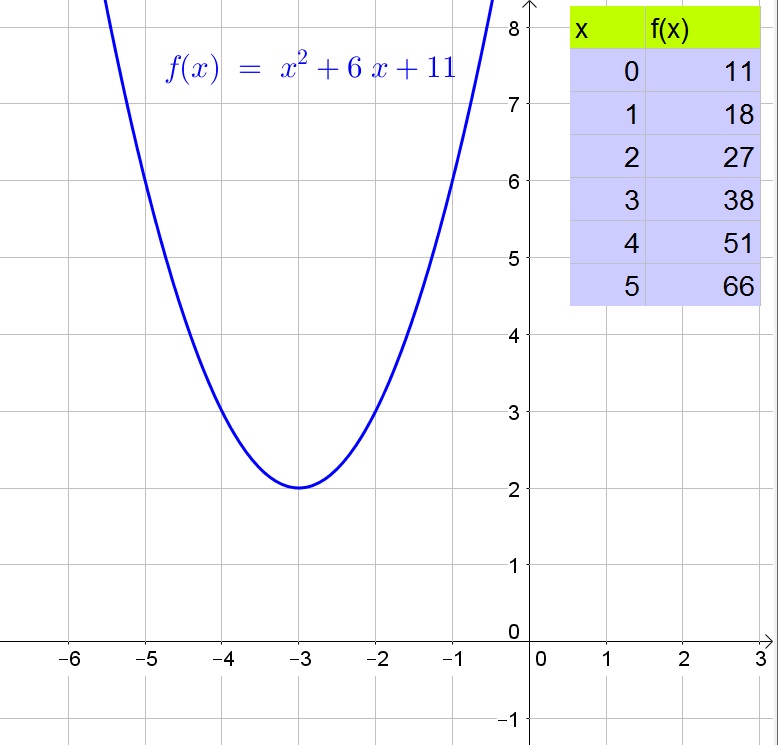
b. $(-3,2)$
c. No real solutions
$$
sqrt{4^2+2^2}=sqrt{20}=2sqrt{5}
$$
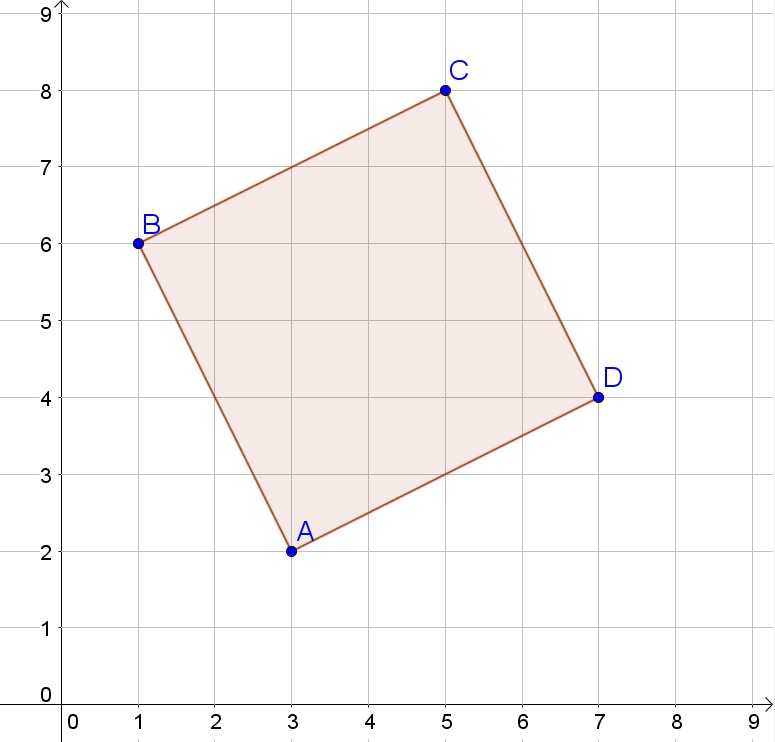
$$
C’=(-5,-8)
$$
The reflection then changes the sign of the $y$-coordinate:
$$
D”=(-7,4)
$$
b. $C’=(-5,-8)$, $D”=(-7,4)$
$$
y=-f(x)=-x^2
$$
b. The graph is the graph of $f(x)=x^2$ translated right by 3 units:
$$
y=f(x-3)=(x-3)^2
$$
c. The graph is the graph of $f(x)=x^2$ translated down by 3 units:
$$
y=f(x)-3=x^2-3
$$
d. The graph is the graph of $f(x)=x^2$ stretched horizontally by factor $dfrac{1}{4}$:
$$
y=f(2x)=(2x)^2=4x^2
$$
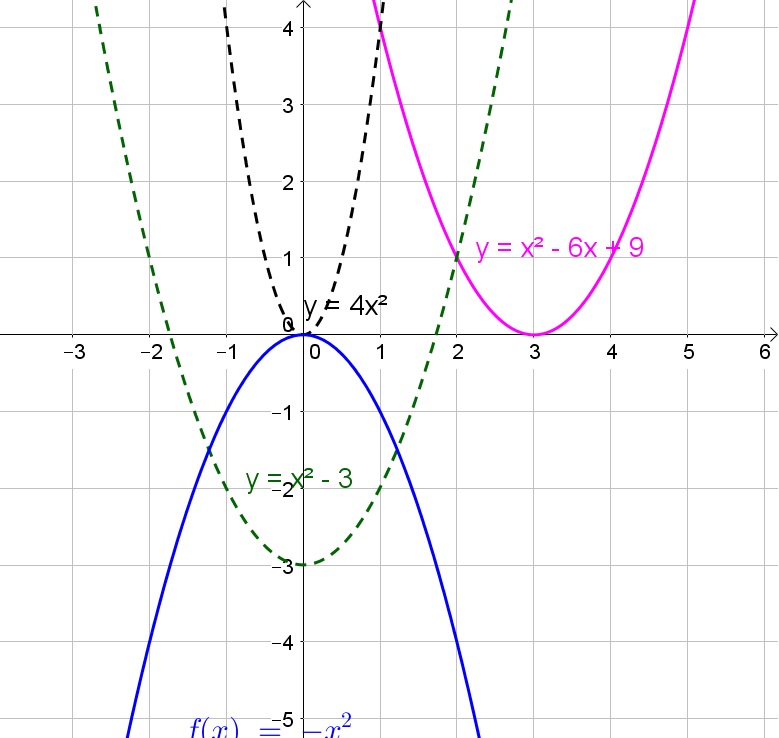
b. Translated to the right by 3 units
c. Translated down by 3 units
d. Stretched horizontally by factor $frac{1}{4}$.
\
\
b. If$x$is the number of years and$y$ the population of a town, then the function described that the initial population of the town is 25,000 and yearly the population decreases by 17%.
$$
_5P_3=dfrac{5!}{(5-3)!}=5cdot 4=20
$$
b. Using the initials of their names, we obtain the possibilities:
ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE
Thus we note that there are 10 possibilities.
c. (i)
$$
_6P_3=dfrac{6!}{(6-3)!}=6cdot 5cdot 4=120
$$
(ii) Using the initials of their names, we obtain the possibilities:
ABC, ABD, ABE, ABF, ACD, ACE, ACF, ADE, ADF, AEF, BCD, BCE, BCF, BDE, BDF, BEF, CDE, CDF, CEF, DEF
Thus we note that there are 20 possibilities.
d. (i)
$$
_6P_4=dfrac{6!}{(6-4)!}=6cdot 5=30
$$
(ii)
$$
4!=4cdot 3 cdot 2 cdot 1 = 24
$$
b. 10 possibilities
c. 20 possibilities.
d. (i) 30 (ii) 24
b. The permutation is divided by the factorial of the number of items you choose.
c. We would expect the combinations to be half the permutations, because every combination will appear twice in the list of permutations:
$$
_6P_2=dfrac{6!}{(6-2)!}=6cdot 5 cdot 4 cdot 3=360
$$
$$
_6C_2=dfrac{6!}{(6-2)!2!}=dfrac{360}{2}=180
$$
d.
$$
_nC_r=dfrac{n!}{(n-r)!r!}=frac{_nP_r}{r!}
$$
b. The permutation is divided by the factorial of the number of items you choose.
c. 360 ways, 180 ways, Yes
d. $_nC_r=dfrac{n!}{(n-r)!r!}=frac{_nP_r}{r!}$
$$
_{20}C_4=dfrac{20!}{(20-4)!4!}=dfrac{20cdot 19cdot 18cdot 17}{4cdot 3cdot 2cdot 1}=4,845
$$
b. The formula has been derived from the formula of permutations, thus basically we first determine the number of permutations and then divided by $r!$ which eliminates the duplicate possibilities in the permutations.
b. Formula has been derived from formula of permutations.
$$
_{56}C_6=dfrac{56!}{(56-6)!6!}=dfrac{56cdot 55cdot 54cdot 53cdot 52cdot 51}{6cdot 5cdot 4cdot 3cdot 2cdot 1}=32,468,436
$$
b. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(win)=dfrac{1}{32,468,436}=0.00000003=0.000003%
$$
b. 0.00000003=0.000003%
$$
_{52}C_5=dfrac{52!}{(52-5)!5!}=dfrac{52cdot 51cdot 50cdot 49cdot 48}{ 5cdot 4cdot 3cdot 2cdot 1}=2,598,960
$$
b. Order is not important and repetition is not possible, thus we need to use a combination:
$$
_{13}C_5=dfrac{13!}{(13-5)!5!}=dfrac{13cdot 12cdot 11cdot 10cdot 9}{ 5cdot 4cdot 3cdot 2cdot 1}=1,287
$$
Since there are four different suits, the total number of possibilities is:
$$
4cdot 1,287=5,148
$$
b. 5,148 hands
$$
_{10}P_2=dfrac{10!}{(10-2)!}=10cdot 9=90
$$
Order is not important and repetition is not possible, for the other three committee members:
$$
_{8}C_3=dfrac{8!}{(8-3)!3!}=dfrac{8cdot 7cdot 6}{ 3cdot 2cdot 1}=56
$$
$textbf{Fundamental counting principle}$: If the first event could occur in $m$ ways and the second event could occur in $n$ ways, then the number of ways that the two events could occur in sequence is $mcdot n$.
$$
_{10}P_2cdot _8C_3=90cdot 56=5040
$$
Thus there are 5040 ways.
$$
0!=1
$$
b. $_8P_8$ means picking 8 items out of 8 and thus we should have:
$$
_8P_8=8!
$$
But since we also know:
$$
_8P_8=dfrac{8!}{(8-8)!}=dfrac{8!}{0!}
$$
We then need $0!=1$.
c. $dfrac{3!}{3}=2!$, $dfrac{2!}{2}=1!$, $dfrac{1!}{1}=0!$ and thus we then obtain that
$$
0!=dfrac{1!}{1}=dfrac{1}{1}=1
$$
b. Picking 8 items out of 8, 8!
c. $0!=frac{1!}{1}$
$$
_nP_r=dfrac{n!}{(n-r)!}
$$
A combination is defined as:
$$
_nC_r=dfrac{n!}{(n-r)!r!}
$$
a.
$$
_{10}P_8=dfrac{10!}{(10-8)!}=10cdot 9cdot 8cdot 7cdot 6 cdot 5cdot 4cdot 3=1,814,400
$$
b.
$$
_{10}C_8=dfrac{10!}{(10-8)!8!}=dfrac{10cdot 9}{2cdot 1}=45
$$
c.
$$
_{6}C_1=dfrac{6!}{(6-1)!1!}=dfrac{6}{1}=6
$$
b. 45
c. 6
$$
dfrac{700}{5.6}=125=5^3
$$
Determine the ratios of the surface area:
$$
dfrac{500}{20}=25=5^2
$$
Thus we note that the two nuggets are similar with linear scale factor 5.
b. The ratio of their lengths is equal to the linear scale factor and thus is 5.
b. 5
$$
D=b^2-4ac=7^2-4(6)(-20)=49+480=529>0
$$
Since the discriminant is positive, the graph of the equation has two $x$-intercepts and two real roots.
$$
D=b^2-4ac=(-8)^2-4(1)(16)=64-64=0
$$
Since the discriminant is zero, the graph of the equation has one $x$-intercept and one real root.
$$
D=b^2-4ac=1^2-4(2)(3)=1-24=-23<0
$$
Since the discriminant is negative, the graph of the equation has zero $x$-intercepts and two complex roots.
b. One $x$-intercept, One real root.
c. Zero $x$-intercepts, Two complex roots
d. One $x$-intercept, One real root.
A pentagon has 5 vertices and thus this pentagon has sides of 4mm. Divide the pentagon into 5 congruent triangles. Determine the height of these triangles using the tangent ratio:
$$
h=2tan{54text{textdegree}}approx 2.75
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{2.75cdot 4}{2}=5.5
$$
Since the pentagon is made up out of 5 triangles, the area of the pentagon is:
$$
5cdot 5.5=27.5mm^2
$$
$$
V=dfrac{Bcdot h}{3}=dfrac{27.5cdot 7}{3}approx 64mm^3
$$
Determine the surface area:
$$
S=27.5+5cdot dfrac{4cdot sqrt{3.4^2+7^2}}{2}approx 90 mm^2
$$
$$
5m+1=3m+9
$$
Subtract $3m$ from both sides of the equation:
$$
2m+1=9
$$
Subtract 1 from both sides of the equation:
$$
2m=8
$$
Divide both sides of the equation by 2:
$$
m=4
$$
$$
3x-9=2(x+4)
$$
Use distributive property:
$$
3x-9=2x+8
$$
Subtract $2x$ from both sides of the equation:
$$
x-9=8
$$
Add 9 to both sides of the equation:
$$
x=17text{textdegree}
$$
$$
p^2=(p-2)^2+6^2
$$
Rewrite:
$$
p^2=p^2-4p+4+36
$$
Subtract $p^2$ from both sides of the equation:
$$
0=-4p+40
$$
Add $4p$ to both sides of the equation:
$$
4p=40
$$
Divide both sides of the equation by 4:
$$
p=10
$$
$$
2t+9+5t+8t-10+3t+1=360
$$
Combine like terms:
$$
18t=360
$$
Divide both sides of the equation by 18:
$$
t=20text{textdegree}
$$
b. $x=17text{textdegree}$
c. $p=10$
d. $t=20text{textdegree}$
$$
A=pi r^2=pi 5^2=25pi approx 79
$$
B. The area of a square is the square of the side lengths.
$$
A=s^2=9^2=81
$$
C. The area of a trapezium is the sum of the length of the bases, multiplied by the height, and divided by 2.
$$
A=dfrac{(8+10)9}{2}=81
$$
D. The area of a rhombus is the product of the side length and the height.
$$
A=9cdot 8=72
$$
Thus we note that D has the least area.
$$
y=f(x)-3
$$
b. The graph has been translated to the right by 2 units and then is $h=2$ and $k=0$:
$$
y=f(x-2)
$$
b. $y=f(x-2)$
$$
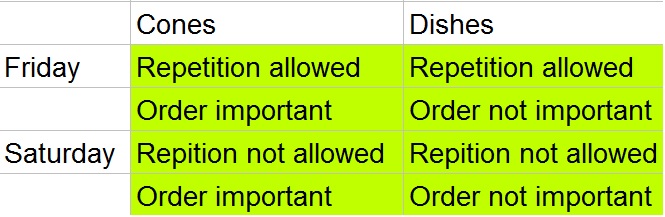
5cdot 5cdot 5=5^3=125
$$
On Friday, repetition is allowed and order is not important in dishes:
AAA, AAB, AAC, AAD, AAE, ABB, ABC, ABD, ABE, ACC, ACD, ACE, ADD, ADE, AEE, BBB, BBC, BBD, BBE, BCC, BCD, BCE, BDD, BDE, BEE, CCC, CCD, CCE, CDD, CDE, CEE, DDD, DDE, DEE, EEE
Thus we note that there are then 25 possibilities.
$$
_5P_3=dfrac{5!}{3!}=5cdot 4=20
$$
On Saturday, repetition is not allowed and order is NOT important in dishes:
$$
_5C_3=dfrac{5!}{(5-3)!3!}=dfrac{5cdot 4}{2cdot 1}=10
$$
$$
5cdot 5cdot 5=5^3=125
$$
$$
_5P_3=dfrac{5!}{3!}=5cdot 4=20
$$
On Saturday, repetition is not allowed and order is NOT important in dishes, COMBINATION:
$$
_5C_3=dfrac{5!}{(5-3)!3!}=dfrac{5cdot 4}{2cdot 1}=10
$$
AAA, AAB, AAC, AAD, AAE, ABB, ABC, ABD, ABE, ACC, ACD, ACE, ADD, ADE, AEE, BBB, BBC, BBD, BBE, BCC, BCD, BCE, BDD, BDE, BEE, CCC, CCD, CCE, CDD, CDE, CEE, DDD, DDE, DEE, EEE
Thus we note that there are then 25 possibilities.
$$
text{color{white} jmlirjtet mjretm lijretm lrejtj erjtl jrljtlr jlktjrl jtrlj ljr litelrj tlretm ermthmre hmtlrel thmrleht hlirht lhr}
$$
b. 25 ways
$$
_7P_3=dfrac{7!}{(7-3)!}=7cdot 6cdot 5=210
$$
If order is not important and if repetition is allowed, the problem involves the Fundamental Counting Principle.
If order is important and if repetition is not allowed, then the problem involves permutations.
If order is not important and if repetition is not allowed, then the problem involves combinations.
$$
_8C_3=dfrac{8!}{(8-3)!3!}=dfrac{8cdot 7cdot 6}{3cdot 2cdot 1}=56
$$
$$
_{10}C_3=dfrac{10!}{(10-3)!3!}=dfrac{10cdot 9cdot 8}{3cdot 2cdot 1}=120
$$
$textbf{Fundamental counting principle}$: If the first event could occur in $m$ ways and the second event could occur in $n$ ways, then the number of ways that the two events could occur in sequence is $mcdot n$.
$$
begin{align*}
_8C_3cdot _{10}C_3&=56cdot 120=6720
end{align*}
$$
Thus there are $6720$ possibilities in total.
$$
_4P_1=dfrac{4!}{(4-1)!1!}=4
$$
$$
_7P_1=dfrac{7!}{(7-1)!1!}=7
$$
$$
_1P_1=dfrac{1!}{(1-1)!1!}=1
$$
$$
_2P_1=dfrac{2!}{(2-1)!1!}=2
$$
$$
_3P_1=dfrac{3!}{(3-1)!1!}=3
$$
$textbf{Fundamental counting principle}$: If the first event could occur in $m$ ways and the second event could occur in $n$ ways, then the number of ways that the two events could occur in sequence is $mcdot n$.
$$
begin{align*}
_4P_1cdot _7P_1cdot _1P_1cdot _2P_1cdot _3P_1&=4cdot 7cdot 1cdot 2cdot 3=168
end{align*}
$$
Thus there are $168$ possibilities in total.
$$
_{22}P_3=dfrac{22!}{(22-3)!}=22cdot 21cdot 20=9,240
$$
b. No, because a combination was not used since order is important.
c. Repetition is allowed and order is important, thus use the Fundamental Counting Principle:
$$
22cdot 22cdot 22=22^3=10,648
$$
d. Thus for the first number you would have 22 possibilities, the second number 21 possibilities and the last number also 21 possibilities (since the first number is possible again):
$$
22cdot 21cdot 21=9,702
$$
b. No
c. 10,648 mathematical combinations
c. 9,702 choices
$$
x=180text{textdegree}-91text{textdegree}-12text{textdegree}=77text{textdegree}
$$
$$
(18+BC)^2=BC^2+24^2
$$
Rewrite:
$$
324+36BC+BC^2=BC^2+576
$$
Subtract $BC^2$ from both sides of the equaton:
$$
36BC+324=576
$$
Subtract 324 from both sides of the equation:
$$
36BC=252
$$
Divide both sides of the equation by 36:
$$
BC=7
$$
The area of the circle is then:
$$
A=pi r^2=pi 7^2=49pi approx 154
$$
$$
dfrac{x}{6}=dfrac{10}{2x}
$$
Use cross multiplication:
$$
2x^2=60
$$
Divide both sides of the equation by 2:
$$
x^2=30
$$
Take the square root of both sides of the equation:
$$
x=pm sqrt{30}
$$
Only a positive length makes sense:
$$
x=sqrt{30}
$$
b. $A=154$
c. $x=sqrt{30}$
$$
r=109cdot 4000=436,000mi
$$
b. The radius of the sun is greater than (and almost double) the distance between Earth and the Moon.
c. The ratio of the volume of the sun to the earth is the linear scale factor cubed:
$$
109^3=1,295,029
$$
Thus the earth fits about 1,295,029 times inside the Sun.
b. Radius of sun is greater than distance between Earth and Moon.
c. 1,295,029 times.
$$
f(x)=(x^2-6x+9)+5-9
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x-3)^2-4
$$
Thus the vertex is $(3,4)$.
Since $a=1$ is positive, the graphs opens upwards and thus the vertex is a minimum. The range is then:
$$
[4,+infty)
$$
$$
0=(x-3)^2-4
$$
Add 4 to both sides of the equation:
$$
4=(x-3)^2
$$
Take the square root of both sides of the equation:
$$
pm 2 =x-3
$$
Add 3 to both sides of the equation:
$$
5text{ or } 1=3pm 2=x
$$
The function is then positive on $(-infty, 1)$ and $(5,+infty)$.
b. Domain $mathbb{R}$, Range $[4,+infty)$
c. Minimum
d. $(-infty, 1)$ and $(5, +infty)$
$$
0=x^2-2x+5
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{2pmsqrt{(-2)^2-4(1)(5)}}{2(1)}=1pm 2i
$$
Determine $y$:
$$
y=2x=2(1pm 2i)=2pm 4i
$$
Thus the solutions are $(1pm 2i, 2pm 4i)$.
b. The graphs do not intersect.
$$
tan{45text{textdegree}}=dfrac{1}{1}=1
$$
b. The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{45text{textdegree}}=dfrac{1}{sqrt{2}}=dfrac{sqrt{2}}{2}
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{45text{textdegree}}=dfrac{1}{sqrt{2}}=dfrac{sqrt{2}}{2}
$$
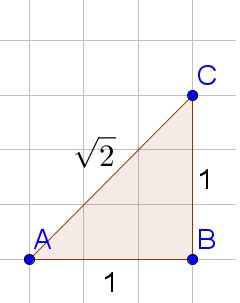
b. $frac{sqrt{2}}{2}$
c. $frac{sqrt{2}}{2}$
b) The sheep’s grazing region is the entire field if she is free, and her grazing region is a circle of radius of $20$ ft if she is restrained as described in the exercise.
c) In order to calculate the probability for both cases, we need to calculate the following:
$1.$ The number of bites she eats in the given time.
$2.$ The area of the field available to the sheep.
$3.$ The number of possible bites in the available area.
$4.$ The ratio between the number of bites the sheep will eat in the given period of time and the total number of bites available (this is the probability we need to calculate).

$$begin{aligned}
A_M&=dfrac{270degree}{360degree}pi r^2\
A_M&=0.75(3.1416)(20)^2\
A_M&=942.48medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
A_R&=A_M+A_P\
A_R&=942.48+left(dfrac{90degree}{360degree}cdotpicdot(10)^2right)\
A_R&=942.48+78.54\
A_R&=1021.02medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot A_R\
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot 1021.02medspacetext{ft}^2\
text{Total bites}&approx40841medspacetext{bites}
end{aligned}$$
$$begin{aligned}
text{bites per day}&=dfrac{1medspacetext{bite}}{3medspacetext{mins}}cdotdfrac{60medspacetext{mins}}{1medspacetext{hr}}cdotdfrac{6medspacetext{hr}}{text{day}}\
text{bites per day}&=120dfrac{text{bites}}{text{day}}
end{aligned}$$
$$begin{aligned}
P_W&=dfrac{text{bites per day}}{text{total bites in area of Zoe can roam}}\
end{aligned}$$
where
$P_W$ – probability of Zoe can eat locoweed in one day.
$$begin{aligned}
P_W&=dfrac{120}{40841}\
P_W&=0.00294
end{aligned}$$

$$begin{aligned}
A_R&=dfrac{270degree}{360degree}cdotpi r^2
end{aligned}$$
where
$A_R$ – area of the region that Zoe can roam.
$$begin{aligned}
A_R&=0.75cdot(3.1416)(10)^2\
A_R&=235.62medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot A_R\
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot235.62medspacetext{ft}^2\
text{Total bites}&approx9425medspacetext{bites}
end{aligned}$$
$$begin{aligned}
text{bites per day}&=dfrac{1medspacetext{bite}}{3medspacetext{mins}}cdotdfrac{60medspacetext{mins}}{1medspacetext{hr}}cdotdfrac{6medspacetext{hr}}{text{day}}\
text{bites per day}&=120dfrac{text{bites}}{text{day}}
end{aligned}$$
$$begin{aligned}
P&=dfrac{text{bites per day}}{text{total bites}}\
P&=dfrac{120}{9425}\
P&=0.0127
end{aligned}$$

$$begin{aligned}
r^2&=(20)^2+y^2\
y^2&=r^2-(20)^2\
y^2&=(30)^2-(20)^2\
y^2&=900-400\
y^2&=500
end{aligned}$$
$$begin{aligned}
sqrt{y^2}&=sqrt{500}\
y&=22.36medspacetext{ft}
end{aligned}$$
$$begin{aligned}
A_{triangle{BXY}}&=dfrac{1}{2}y(20)\
A_{triangle{BXY}}&=dfrac{1}{2}(22.36)(20)\
A_{triangle{BXY}}&=223.6medspacetext{ft}
end{aligned}$$
$$begin{aligned}
angle{BA}&=90degree-angle{BX}
end{aligned}$$
$$begin{aligned}
sinangle{BX}&=dfrac{y}{r}\
sinangle{BX}&=dfrac{22.36}{30}\
sinangle{BX}&=0.745\
angle{BX}&=arcsin0.745\
angle{BX}&=48.16degree
end{aligned}$$
$$begin{aligned}
angle{BA}&=90degree-angle{BX}\
angle{BA}&=90degree-48.16degree\
angle{BA}&=41.84degree
end{aligned}$$
$$begin{aligned}
A_R&=A_{triangle{BXY}}+Atext{(sector YBA)}\
A_R&=223.6+dfrac{angle{BA}}{360degree}pi r^2\
A_R&=223.6+dfrac{41.84degree}{360degree}cdot(3.1416)(30)^2\
A_R&=223.6+0.116(2827.44)\
A_R&=223.6+327.98\
A_R&=551.58medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot A_R\
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot551.58medspacetext{ft}^2\
text{Total bites}&approx22063medspacetext{bites}
end{aligned}$$
$$begin{aligned}
P&=dfrac{text{bites per day}}{text{total bites}}\
P&=dfrac{120}{22063}\
P&=0.00544
end{aligned}$$

$$begin{aligned}
A_{triangle{CEF}}&=dfrac{1}{2}(10)(20)\
A_{triangle{CEF}}&=100medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
tantheta&=dfrac{20}{10}\
tantheta&=2\
theta&=arctan2\
theta&=63.43degree
end{aligned}$$
$$begin{aligned}
overline{CF}&=sqrt{20^2+10^2}\
overline{CF}&=sqrt{400+100}\
overline{CF}&=sqrt{500}\
overline{CF}&=22.36medspacetext{ft}
end{aligned}$$
$$begin{aligned}
overline{FG}&=r-overline{CF}\
overline{FG}&=30-22.36\
overline{FG}&=7.64medspacetext{ft}
end{aligned}$$

$$begin{aligned}
A_R&=A_F+A_{triangle{CEF}}+A_{text{sector}GS}+(A_{text{sector}ST}-A_{ABTC})\
A_R&=left(dfrac{theta}{360degree}cdotpi overline{FG}^2right)+100+left(dfrac{270degree-theta}{360degree}cdotpi r^2right)+left[dfrac{90degree}{360degree}cdotpi r^2-(30)(10)right]\
A_R&=left(dfrac{63.43degree}{360degree}cdot pi (7.64)^2right)+100+left(dfrac{270degree-63.43degree}{360degree}cdotpi (30)^2right)+left[dfrac{90degree}{360degree}cdot pi (30)^2-(30)(10)right]\
A_R&=32.31+100+1622.29+left[706.86-(300)right]\
A_R&=1754.6+406.86\
A_R&=2161.46medspacetext{ft}^2
end{aligned}$$
$$begin{aligned}
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot A_R\
text{Total bites}&=40dfrac{text{bites}}{text{ft}^2}cdot2161.46medspacetext{ft}^2\
text{Total bites}&approx86458medspacetext{bites}
end{aligned}$$
$$begin{aligned}
P&=dfrac{text{bites per day}}{text{total bites}}\
P&=dfrac{120}{86458}\
P&=0.00139
end{aligned}$$
There are $5$ French books and $3$ Spanish books to be placed in a shelf, given that each language must remain together. Determine the number of ways these books can be arranged.
We first determine the number of ways we can arrange the five French books using permutations. There are $5$ French books so we start with $5$ choices for the first slot, then $4$ choices on the second slot, and so on. We obtain the number of ways we can place the French books as follows:
$$begin{aligned}
5 times 4 times 3 times 2 times 1 = 120 text{ ways}
end{aligned}$$
This expression can also be represented as a factorial form: $5!$
$$begin{aligned}
3 times 2 times 1 = 6 text{ ways}
end{aligned}$$
This expression can also be represented as a factorial form: $3!$
$$begin{aligned}
&= 5! times 3! times 2! \
&= boxed{1440 text{ ways}}
end{aligned}$$
There are $1440 text{ ways}$ to arrange the books
Francis and John’s distance can be described by the the following equation:
$$begin{gather}
x_f = x_o + at
end{gather}$$
where $x_f$ is the distance traveled after time $t$, $x_o$ is the initial distance in front of the starting line, and $a$ is the running speed
$x_{o,F} = 2 text{ m}$
$x_{o,J} =5 text{ m}$
$a_{F} = 1 frac{text{m}}{text{s}}$
$a_{J} = 0.75 frac{text{m}}{text{s}}$
Determine the time, $t$ when Francis will catch up to John
We can determine the time when Francis will catch up to John by finding the value of $t$ such that the final distance covered by the two are equal. We determine the expression for this scenario using Eq (1) as follows:
$$begin{aligned}
x_{f,F} &= x_{o,F} + a_{F} t \
x_{f,J} &= x_{o,J} + a_J t \
x_{o,F} + a_{F} t &= x_{o,J} + a_J t
end{aligned}$$
$$begin{aligned}
x_{o,F} + a_{F} t &= x_{o,J} + a_J t \
2 + 1t &= 5 + 0.75t \
2 + t &= 5 + 0.75t \
t – 0.75t &= 5 – 2 \
0.25t &= 3 \
t &= frac{3}{0.25} \
&= boxed{12 text{ s}}
end{aligned}$$
Francis will be able to catch up to John after $12 text{ s}$
We are given with the following equation that describes the scenario:
$$begin{gather}
y = -16x^2 + 64x + 80
end{gather}$$
where $y$ is the height travelled by the ball in feet, and $x$ is the time travelled in seconds
We determine how how is the ball when thrown from the edge of the cliff. We determine the value of the height when $x=0$ using Eq (1) as follows:
$$begin{aligned}
y &= -16x^2 + 64x + 80 \
y &= -16(0)^2 + 64(0) + 80 \
&= boxed{80 text{ feet}}
end{aligned}$$
This means that the ball is thrown initially from the edge of the cliff at a height of $80 text{ feet}$
Next, we obtain the height of the ball after $x=3 text{ s}$ and $x=0.5 text{ s}$ after it is thrown using Eq (1) as follows:
$$begin{aligned}
y_3 &= -16x^2 + 64x + 80 \
y_3 &= -16(3)^2 + 64(3) + 80 \
&= -144 +192 +80 \
&= boxed{128 text{ feet}}
end{aligned}$$
After $3 text{ s}$, the ball is at a height $128 text{ feet}$
y_{0.5} &= -16x^2 + 64x + 80 \
y_{0.5} &= -16(0.5)^2 + 64(0.5) + 80 \
&= -4 +32 +80 \
&= boxed{108 text{ feet}}
end{aligned}$$
After $0.5 text{ s}$, the ball is at a height $108 text{ feet}$
When the ball hits the ground, the height of the ball will be equal to $0 text{ ft}$. We determine the time, $x$ when this happens by setting $y=0$. We solve for the value of $x$ for this scenario using Eq (1) as follows:
$$begin{aligned}
y &= -16x^2 + 64x+ 80 \
0 &= -16x^2 + 64x+ 80 \
0 &= frac{-16x^2}{-16} + frac{64x}{-16} + frac{80}{-16} \
0 &= x^2 -4x +5 \
0 &= (x-5)(x+1) \
x &= {-1,5 }
end{aligned}$$
Based from the results, the ball hits the ground at the time, $x = {-1,5 }$, we know that having a negative time for the scenario cannot happen, hence, we consider the positive value of $x$. Hence, the ball will hit the ground when $boxed{x=5}$
The domain of the function is $[0,5]$, this means that the possible values for the time ranges from $x=0$ to $x=5$. Any value does it not included in this range is not considered a solution of the equation or does not represent the scenario.
See illustration below.

$$begin{aligned}
angle{a}&=dfrac{1}{2}(overset{frown}{BC})\
end{aligned}$$
$$begin{aligned}
(angle{a})<(angle{b})
end{aligned}$$
Let $x$ = remaining angle
$$begin{aligned}
62degree+70degree+x&=180degree\
x&=180degree-62degree-70degreemedspacetext{(Transposition Method)}\
x&=48degree
end{aligned}$$
$$begin{aligned}
a>b
end{aligned}$$
$$begin{aligned}
a&=dfrac{sqrt{3}}{4}cdot6^2\
a&=15.59
end{aligned}$$
$$begin{aligned}
b&=4^2\
b&=16
end{aligned}$$

$$begin{aligned}
x&=dfrac{12-0}{2}\
x&=6
end{aligned}$$
$$begin{aligned}
h=dfrac{sqrt{3}}{2}a
end{aligned}$$
where $a$ is the length of one side of the triangle.
$$begin{aligned}
a&=x_B-x_A\
a&=12-0\
a&=12
end{aligned}$$
$$begin{aligned}
y&=dfrac{sqrt{3}}{2}a\
y&=dfrac{sqrt{3}}{2}(12)\
y&=6sqrt{3}
end{aligned}$$

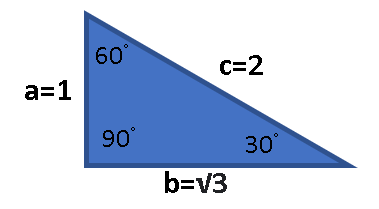
The length of the sides $30^circ-60^circ-90^circ$ triangle or right triangle can be described using the Pythagorean theorem:
$$begin{gather}
c^2 = a^2 + b^2
end{gather}$$
$c=2 text{ units}$
Sketch and label the triangle and determine the values of the following: (a.) $tan 30^circ$, (b.) $sin 30^circ$, (c.) $cos 30^circ$, and determine if the relationship of $sin 60^circ$ and $cos 30^circ$ is the same for any pair of acute angles in a right triangle
We assume that one side of the triangle has a value of $1 text{ unit}$. From the Pythagorean theorem we determine the value of the sides as follows:
$$begin{aligned}
c^2 = a^2 + b^2 \
2^2 &= 1^2 + b^2 \
4 &= 1 + b^2 \
4-1 &= b^2 \
b^2 &= 3 \
b &= sqrt{3} \
end{aligned}$$
The length of each side of the right triangle are the following values: $c=2$, $a=1$, and $b=sqrt{3}$
[](https://postimg.cc/06b1zPhF)
We obtain the value of $tan 30^circ$. We know that the trigonometric identity for $tan$ is $tan theta= frac{text{opposite}}{text{adjacent}}$. Hence, by using the length of the opposite and adjacent sides we can determine the value of $tan theta$.
We verify the value of $tan 30^circ$ using this property as follows:
$$begin{aligned}
tan 30^circ &= boxed{0.58} \
tan 30^circ &= frac{text{opposite}}{text{adjacent}} \
&= frac{1}{sqrt{3}} \
&= boxed{0.58}
end{aligned}$$
Next, we obtain the value of $sin 30^circ$. We know that the trigonometric identity for $sin$ is $sin theta= frac{text{opposite}}{text{hypotenuse}}$. Hence, by using the length of the opposite and adjacent sides we can determine the value of $sin theta$.
We verify the value of $sin 30^circ$ using this property as follows:
$$begin{aligned}
sin 30^circ &= frac{1}{2} = boxed{0.5} \
sin 30^circ &= frac{text{opposite}}{text{hypotenuse}} \
&= frac{1}{2} \
&= boxed{0.5}
end{aligned}$$
Next, we obtain the value of $cos 30^circ$. We know that the trigonometric identity for $cos$ is $cos theta= frac{text{adjacent}}{text{hypotenuse}}$. Hence, by using the length of the opposite and adjacent sides we can determine the value of $cos theta$.
We verify the value of $cos 30^circ$ using this property as follows:
$$begin{aligned}
cos 30^circ &= frac{sqrt{3}}{2} = boxed{0.87} \
cos 30^circ &= frac{text{adjacent}}{text{hypotenuse}} \
&= frac{sqrt{3}}{2} \
&= boxed{0.87}
end{aligned}$$
We obtain the value of $sin 60^circ$ and $cos 30^circ$ from the diagram as follows:
$$begin{aligned}
sin 60^circ &= frac{text{opposite}}{text{hypotenuse}} \
&= frac{sqrt{3}}{2} \
cos 30^circ &= frac{text{adjacent}}{text{hypotenuse}} \
&= frac{sqrt{3}}{2} \
end{aligned}$$
We observe the the two have the same values.
$$begin{aligned}
sin 30^circ &= frac{text{opposite}}{text{hypotenuse}} \
&= frac{1}{2} \
cos 60^circ &= frac{text{adjacent}}{text{hypotenuse}} \
&= frac{1}{2} \
end{aligned}$$
We observe the the two have the same values. Hence, this relationship holds true for any pair of acute angles in a right triangle.
The daily compounded interest can be described by the equation:
$$begin{gather}
f(t) = a times left(1+frac{r}{365} right)^{tcdot 365}
end{gather}$$
First Equations Bank: $f(t)= a(1.04)^t$
You Figure Bank: $r = 3.9%$
Determine what type of account will Sofia choose
We can determine which bank should Sofia choose by getting which bank produced the highest interest gained from her deposit. We assume that Sofia invested an initial amount of $$ 10000$, we determine the amount after $t=5 text{ yrs}$ from First Equations Bank as follows:
$$begin{aligned}
f(t)&= a(1.04)^t \
f(5)&= 10000 cdot (1.04)^5 \
&= boxed{12166.53}
end{aligned}$$
$$begin{aligned}
f(t) &= a times left(1+frac{r}{365} right)^{tcdot 365} \
f(t) &= 10000 times left(1+frac{0.039}{365} right)^{5cdot 365} \
&= boxed{12152.98}
end{aligned}$$
Let
$x$ = new volume
$y$ = original volume
$$begin{aligned}
x=r^3cdot y
end{aligned}$$
where $r$ is linear scale factor.
$$begin{aligned}
702&=r^3cdot 26
end{aligned}$$
$$begin{aligned}
dfrac{702}{26}&=dfrac{r^3cdot 26}{26}\
27&=r^3
end{aligned}$$
$$begin{aligned}
sqrt[3]{27}&=sqrt[3]{r^3}\
3&=r
end{aligned}$$
Determine how many ways Mike can make the ten layers in a glass serving pan.
We use permutations to determine the number of ways Mike can arrange the ten layers. We consider that in the first slot, there are $10$ choices, in the second slot, there are $9$ choices and so on. The number of ways for the layers to be arranged is as follows:
$$begin{aligned}
& 10 times 9 times 8 times 7 times 6 times 5 times 4 times 3 times 2 times 1 = boxed{3628800 text{ ways}}
end{aligned}$$
This expression can be expressed as $10!$
$$begin{aligned}
3 times 2 times 1 = boxed{6 text{ ways}}
end{aligned}$$
$$begin{aligned}
& frac{10!}{3! 2} = boxed{302400 text{ ways}}
end{aligned}$$
$$begin{aligned}
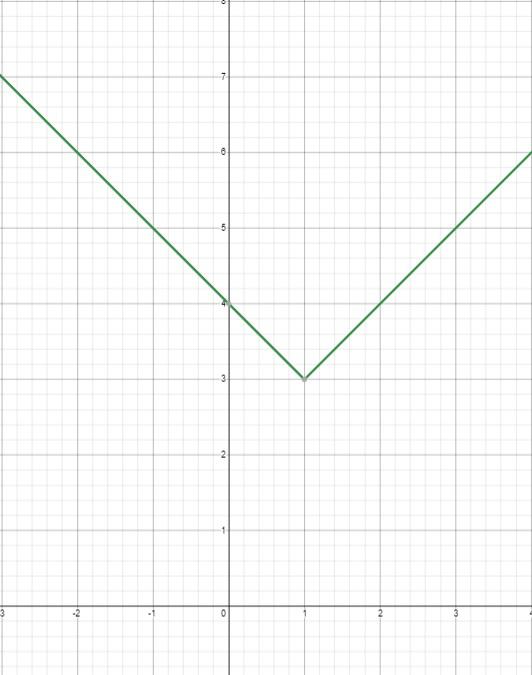
y=a|x-h|+k
end{aligned}$$
where $(h, k)$ is the vertex of the graph.
$$begin{aligned}
y=|x-1|enspacetext{(where $a$ = 1, $h$ = 1 and $k$ = 0)}
end{aligned}$$
The vertex of the graph is $(1,0)$.
3.)

$$begin{aligned}
y=|x|+3enspacetext{($a$ = 1, $h$ = 0 and $k$ = 3)}
end{aligned}$$
The vertex of the graph is $(0,3)$.
1.)

$$begin{aligned}
y=|x-1|+3enspacetext{($a$ = 1, $h$ = 1 and $k$ = 3)}
end{aligned}$$
The vertex of the graph is $(1,3)$.
2.)
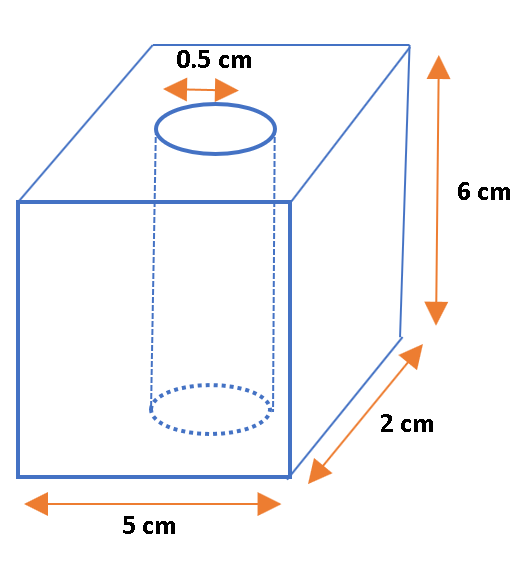
The volume of a rectangular prism can be obtained using:
$$begin{gather}
V_{prism} = lwh
end{gather}$$
On the other hand, the volume of a cylinder can be calculated using:
$$begin{gather}
V_{cylinder} = pi r^2 h
end{gather}$$
We consider the figure with the dimensions:
[](https://postimg.cc/zVpg5YW4)
We determine the volume of the solid by getting the volume of the prism and subtracting the volume of the hole (cylinder). We first obtain for the expression for the volume of the solid using Eq (1) and Eq (2) as follows:
$$begin{aligned}
V_{solid} &= V_{prism} – V_{cylinder} \
V_{solid} &= lwh – (pi r^2 h) \
end{aligned}$$
$$begin{aligned}
V_{solid} &= l w h – (pi r^2 h) \
&= (5) cdot (2) cdot (6) – (pi (0.5)^2 (6)) \
&= 60 – (4.71) \
&= boxed{55.28 text{ cm}^3}
end{aligned}$$
The volume of the solid is $55.28 text{ cm}^3$
This geometric figure can represent multiple things. It can be a pencil sharpener, a trash bin, or even a pen holder. Depending on how we use it, we can model the geometric figure in such a way that we vary its dimension to fit its use.
First observe the upper triangle, which has an angle of $80°$. Properly label its sides and vertices, like shown in the figure.

Use the Law of Cosines to verify if the length of the side $a$ really is $5$ given the measures of the other sides and the angle $A$.
$$begin{aligned}a=5, b=7, c= 4, A=80°end{aligned}$$
$$begin{aligned}
a^2&=b^2+c^2-2bccos A\
5^2&=7^2+4^2-2cdot7cdot4cos(80°)\
25&=49+16-56cdot0.173648\
25&=65-9.72\
25&ne55.27
end{aligned}$$
This is proof that the triangle in the figure cannot have the given measures.
Repeat the procedure for the other given triangle.

$$begin{aligned}a=5, b=4, c= 7, A=80°end{aligned}$$
$$begin{aligned}
a^2&=b^2+c^2-2bccos A\
5^2&=4^2+7^2-2cdot4cdot7cos(50°)\
25&=16+49-56cdot0.64279\
25&=65-25.996\
25&ne29.0
end{aligned}$$
Look at the given figure. It is made of two triangles.

Calculate the value of the angle $x$ if you know that the sum of the angles in the triangle equals $180°$.
$$begin{aligned}
x+40°+50°&=180°\
x&=180°-40°-50°\
x&=90°
end{aligned}$$
The angle symmetrical to the angle $x$ should also have a measure of $90°$, it cannot possibly have a measure of $80°$.
The given is an isosceles triangle since the line from the upper vertex passing through the bottom side of the triangle bisects the bottom side into two equal halves. We know that an isosceles triangle has both its arms equal. Therefore, one of the arms cannot possibly have a length of $10$, while the other arm has a length of $12$.
The given is an isosceles triangle since the arms of the triangle have the same length. We know that the angles the arms of an isosceles triangle enclose with the third side of the triangle must have an equal measure. Therefore, in no way can one of these angles have a measure of $50°$ while the other angle has a measure of $60°$.
We are given a geometric figure comprised of two identical right triangles. We know that because each of these right triangles has a right angle and they have another identical angle (labeled with the lines). Since we know that the sum of the angles in any triangle is $180°$, if two angles have equal measures for two angles, they also must have equal measures of the third triangle. Therefore, it is impossible that one right triangle has a leg with a measure of $13$, while the same leg of the other triangle has a measure of $14$ because the measures of the angles would not be the same.
Solve the equation by completing the square.
$$begin{aligned}
x^2-6x+11 &= 0 \
x^2-6x+11-11 &= 0-11 \
x^2-6x+ left(frac{6}{2} right)^2 &= -11 \
x^2-6x+ 3^2 &= -11+3^2 \
x^2-6x+9 &= -11+9 \
(x-3)^2 &= -2 \
end{aligned}$$
$$begin{aligned}
(x-3)^2 &= -2 \
sqrt{(x-3)^2} &= sqrt{-2} \
x-3 &= pm sqrt {-2} \
x-3+3 &= pm sqrt {-2}+3 \
x &= 3 pm sqrt {-2} \
end{aligned}$$
Compute for the area of the Moon.
$$begin{aligned}
A &= pi r^2 \
&= pi (1080)^2 \
&= pi cdot 1166400 \
&= 3664353.67 \
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of Asia}}\\
&= frac{17212048.1}{3664353.6} \\
&= boxed{4.69}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of Africa}}\\
&= frac{11608161.4}{3664353.6} \\
&= boxed{3.17}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of North America}}\\
&= frac{9365294.0}{3664353.6} \\
&= boxed{2.56}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of South America}}\\
&= frac{6879954.4}{3664353.6} \\
&= boxed{1.88}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of Antarctica}}\\
&= frac{5100023.4}{3664353.6} \\
&= boxed{1.39}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of Europe}}\\
&= frac{3837083.3}{3664353.6} \\
&= boxed{1.05}
end{aligned}$$
$$begin{aligned}
text{Ratio} &= frac{text{Area of the Moon}}{text{Area of Australia/Oceania}}\\
&= frac{2967967.3}{3664353.6} \\
&= boxed{0.81}
end{aligned}$$
Solve for $x$ by substituting $y$.
$$begin{aligned}
x^2 + y^2 &= 9 \
x^2 + (2)^2 &= 9 \
x^2 + 4 &= 9 \
x^2 + 4 -4 &= 9-4 \
sqrt{x^2} &= sqrt{5} \
x &= pm sqrt{5}\
end{aligned}$$
$$begin{aligned}
x^2+y^2 &= r^2 \
end{aligned}$$
becomes
$$begin{aligned}
x^2+y^2 &= 9 \
x^2+y^2 &= 3^2 \
end{aligned}$$
The circle is centered at $(0,0)$ and has radius $3$.
With the details you know, you can conclude that a horizontal line intersects the circle at two points.
$$begin{aligned}
(sqrt{5},2) text{ and } (-sqrt{5}, 2)
end{aligned}$$
Let’s assume that the house is located at the point $H(0,0)$ and the school and the practice field at the point $S(2,0)$.
Also, if the person is located three miles from the school, his distance from the school can be described by an equation of a circle with the origin at point $S$ with the radius of $3$, or
$$begin{aligned}
(x-p)^2+(y-q)^2&=r^2\
(x-2)^2+(y-0)^2&=3^2\
(x-2)^2+y^2&=9
end{aligned}$$

$$begin{aligned}
(x-2)^2+y^2&=9\
(x-2)^2+0&=9\
(x-2)^2&=9\
x-2&=pm3 quad*\
x&=2pm3\
x_1&=boxed{5}\
x_2&=boxed{-1}
end{aligned}$$
$*$Take square root of both sides.
Therefore, the person is located either on the point $A(-1,0)$ or the point $B(5,0)$ at the moment of the call.

Conclude that the person is located either one mile or five miles from his home at the moment of the phone call.
Using the points, graph a scatterplot.
[](https://postimg.cc/k2t85Hy6)
A linear model will best fit the data.
[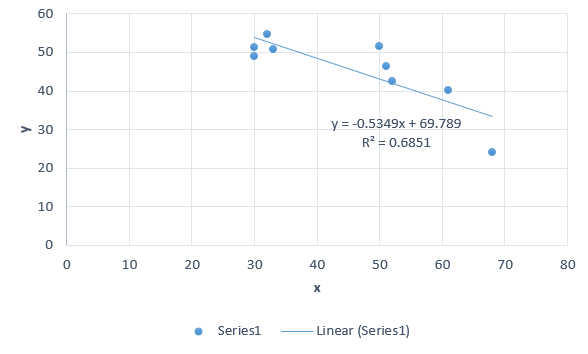](https://postimg.cc/fJ1t1Khw)
The linear model for the data is:
$$begin{aligned}
y = 69.789 -0.5349x\
end{aligned}$$
The intercepts of the model are:
$$begin{aligned}
beta_0 = 69.789 text{ and } beta_1=-0.5349\
end{aligned}$$
Meaning,
– The first intercept cannot be interpreted since the value of $x$ will never be equal to zero.
– The stadium revenue decreases by $-0.5349$ for every thousand seat increase in the stadium capacity.
No, the interpretation of the intercepts doesn’t make sense. Usually, establishments are created with a huge seating capacity because they can generate larger revenues than small seating capacity places.
From the data, the university should build a stadium with a capacity of $32$ thousand seats because it produces the largest revenue, $54.7$ million dollars.
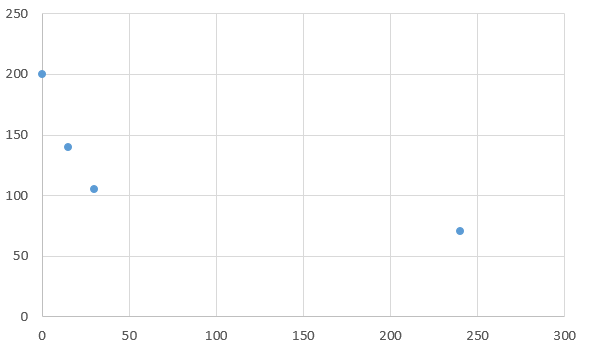
Using a graphing calculator, plot the points to create a scatterplot.
|$x$ |$0$ |$15$ |$30$ |$240$ |
|–|–|–|–|–|
|$y$ |$200$ |$140$ |$105$ |$70$ |
Graph:
[](https://postimg.cc/219VD7Wc)
Based on the graph, a linear function can be used.
Scatter plot with line regression line.
[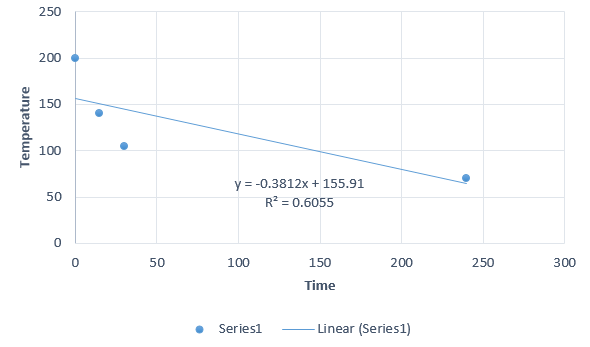](https://postimg.cc/GTBRwVWz)
The linear model for the data is:
$$begin{aligned}
y = 155.91 -0.3812x\
end{aligned}$$
$$begin{aligned}
beta_0 = 155.91 text{ and } beta_1=-0.3812\
end{aligned}$$
Meaning,
– When the tea is poured instantly $(t=0)$, the temperature is equal to $155.91^circ F$.
– The temperature of the tea decreases by $0.3812$ for every minute increase in the time.
If Carol will put the tea outside, time and temperature will still have an indirect relationship. If the time increases, the temperature of the tea decreases as well, but in a much faster way. That is because external factor like the temperature of the surrounding adds to the cooling time.
Preeti Work Done in a day.
$$begin{aligned}
20medspacetext{cranes per hour x $6$ hours}&=120medspacetext{cranes per day}
end{aligned}$$
$$begin{aligned}
end{aligned}$$
$$begin{aligned}
120medspacetext{cranes x $6$ days}&=720medspacetext{cranes}
end{aligned}$$
$$begin{aligned}
6+8+12&=26medspacetext{cranes(3 hours)}cdot2&=52medspacetext{cranes per day}\
end{aligned}$$
$$begin{aligned}
52medspacetext{cranes x $6$ days}&=312medspacetext{cranes}
end{aligned}$$
$$begin{aligned}
720+312&=1032medspacetext{cranes}
end{aligned}$$
Start by making a table of points for person $P$ given the data in the previous exercise. Label the number of hours with the variable $x$ and the numbers of manufactured cranes with the variable $y$.
$$begin{array}{|c|c|}
hline
x & y \
hline
0 & 0\
hline
1 & 20\
hline
2 & 40\
hline
2.25 & 40\
hline
3.25 & 60\
hline
4.25 & 80\
hline
4.5 & 80\
hline
5.5 & 100\
hline
6.5 & 120\
hline
end{array}$$

Note that this is a linear dependency, so perform the linear regression to obtain the model.

the linear model describing the work of person $P$ is described by the function $f(x)=18.14x+1.03$.
$$begin{aligned}
f(5)&=18.14cdot5+1.03\
&=91.73\
&approx92
end{aligned}$$
Start by making a table of points for person $A$ given the data in the previous exercise. Label the number of hours with the variable $x$ and label the numbers of manufactured cranes in that time with the variable $y$. Make an assumption that person $A$ will take a $30$ minutes break after $3$ hours as person $A$ is more inexperienced in making cranes than person $P$. Also, make an assumption that person $A$ is a quick learner and will be able to continue making $12$ cranes per hour after the break.
$$begin{array}{|c|c|}
hline
x & y \
hline
0 & 0\
hline
1 & 6\
hline
2 & 14\
hline
3 & 26\
hline
3.5 & 26\
hline
4.5 & 38\
hline
5.5 & 50\
hline
6.5 & 62\
hline
end{array}$$

Observe that the model for person $A$ is also linear.

The linear model describing the work of person $A$ is $g(x)=9.58x-3.38$.
My model was made under the assumption that person A is a quick learner and that he will be able to continue manufacturing $12$ cranes per hour after the first three hours. Also, I didn’t want to assume that he will improve much more than that because person P is an experienced crane maker and he does not exceed making $20$ cranes per hour. Therefore, this assumption about the efficiency of person A after three hours seems the most logical to me.
$$begin{aligned}
g(5)&=9.58cdot5-3.38\
&=44.52\
&approx45
end{aligned}$$
Use the obtained models to determine the time needed to make $1000$ cranes. In other words, determine the value of $x$ for which the statement $f(x)+g(x)=1000$.
$$begin{aligned}
f(x)+g(x)&=1000\
18.14x+1.03+9.58x-3.38&=1000\
27.72x&=1000-1.03+3.38\
27.72x&=1002.35\
x&=36.15\
x&approx36
end{aligned}$$
According to the models, it will take them approximately $36$ hours to finish the project of making $1000$ cranes.
The accuracy of this prediction is based upon the assumptions made about the efficiency of the work performed by person $A$.
In my opinion, this is not a reasonable amount of time to work in $6$ days during the spring break because the spring break should be a time to relax, not manufacturing paper cranes for half of the day.
The number of *petit fours* the chef can make from all the fillings is:
$$begin{aligned}
_8C_3 &= frac{8!}{5! cdot 3!} \\
&= frac{8cdot 7 cdot 6cdot5cdot4cdot3cdot2cdot1}{(5cdot4cdot3cdot2cdot1)(3cdot2cdot1)}\\
&=boxed{56}
end{aligned}$$
The number of *petit fours* with raspberry and custard the chef can make is:
$$begin{aligned}
_6C_1 &= frac{6!}{5! cdot 1!} \\
&= frac{6cdot5cdot4cdot3cdot2cdot1}{(5cdot4cdot3cdot2cdot1)(1)}\\
&=boxed{6}
end{aligned}$$
The number of apricot-filled *petit fours* is:
$$begin{aligned}
_7C_2 &= frac{7!}{5! cdot 2!} \\
&= frac{7cdot6cdot5cdot4cdot3cdot2cdot1}{(5cdot4cdot3cdot2cdot1)(2cdot1)}\\
&= 21
end{aligned}$$
filling is:
$$begin{aligned}
P&= frac{text{number of apricot-filled petit four}}{text{total number of petit four}} times 100 \\
&= frac{_7C_2}{56} times 100\\
&= frac{21}{56} times 100\\
&= 0.375 times 100\\
&= boxed{37.5%}
end{aligned}$$
b. $6$
c. $37.5%$
Since there are no duplicate letters, here’s how to solve it:
$$begin{aligned}
&= 5! \
&= 5 cdot 4 cdot 3 cdot 2 cdot 1 \
&= boxed{120}
end{aligned}$$
Since there is 1 duplicate letter, here’s how to solve it:
$$begin{aligned}
&= frac{5!}{2} \\
&= frac{5 cdot 4 cdot 3 cdot 2 cdot 1}{2} \\
&= frac{120}{2} \\
&= boxed{60}
end{aligned}$$
Since there are 2 duplicate letters, here’s how to solve it:
$$begin{aligned}
&= frac{5!}{2 cdot 2} \\
&= frac{5 cdot 4 cdot 3 cdot 2 cdot 1}{4} \\
&= frac{120}{4} \\
&= boxed{30}
end{aligned}$$
The formula in getting the number of sides of a polygon is:
$$begin{aligned}
s &= (n-2)cdot180 \
end{aligned}$$
where
$s$ = the sum of the interior angles
$n$ = number of sides of a polygon
Using the formula, substitute the values.
$$begin{aligned}
s &= (n-2) cdot 180 \
2160 &= (n-2) cdot 180 \
frac{2160}{180} &= frac{(n-2) cdot 180}{180} \
12+2 &= n-2+2 \
boxed{14} &= n \
end{aligned}$$
Graph $triangle ABC$ first.
[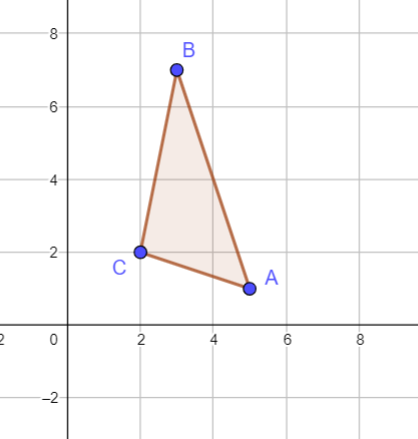](https://postimg.cc/njxMx4ZN)
[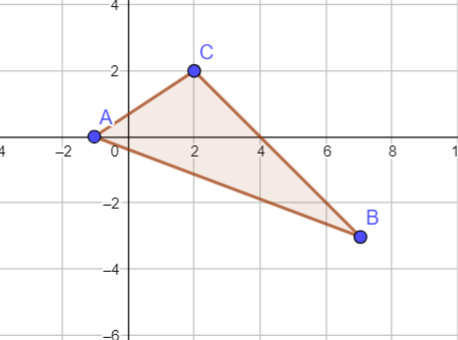](https://postimg.cc/DJ7fH7PT)
Notice that point $B$ is now on the coordinate $boxed{(7,-3)}$.
Solve the quadratic equations below.
a. $x^2+8 = -6x$
$$begin{aligned}
x^2+8 &= -6x \
x^2+8+6x &= -6x+6x \
x^2+8+6x &= 0 \
(x+2)(x+4) &= 0 \
end{aligned}$$
Thus, $boxed{x=-2}$ and $boxed{x=-4}$
Get the factors of the equation.
$$begin{aligned}
3x^2-7x+4 &= 0 \
(3x-4)(x-1) &= 0 \
end{aligned}$$
Then solve for $x$ in the first factor,
$$begin{aligned}
3x-4 &= 0 \
3x-4+4 &= 0+4 \
frac{3x}{3} &= frac{4}{3} \
x &= frac{4}{3} \
end{aligned}$$
Thus,
$boxed{x=frac{4}{3}}$ and $boxed{x=1}$
Solve for $x$ in the second factor.
$$begin{aligned}
-2x+3&=0 \
-2x+3-3&=0-3 \
frac{-2x}{-2} &= frac{-3}{-2} \
x &= frac{3}{2} \
end{aligned}$$
Thus,
$boxed{x= frac{3}{2}}$ and $boxed{x=-5}$
b. $x=frac{4}{3}$ and $x=1$
c. $x= frac{3}{2}$ and $x=-5$
Remember that the measure of the intercepted arc is equal to the measure of the central angle.
$$begin{aligned}
text{if } moverset{largefrown}{AB} = 60^circ text{ then, } mangle C = 60^circ
end{aligned}$$
[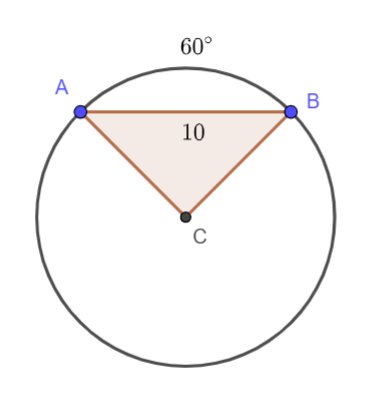](https://postimg.cc/cvx3bs5n)
$$begin{aligned}
overline{AC} = overline{BC}
end{aligned}$$
Thus, $triangle ABC$ is an isosceles triangle with congruent base angles.
$$begin{aligned}
mangle A = mangle B
end{aligned}$$
$$begin{aligned}
mangle A + mangle B + mangle C &= 180^circ \
mangle A + mangle B + 60^circ &= 180^circ \
mangle A + mangle B + 60^circ -60^circ &= 180^circ -60^circ\
mangle A + mangle B &= 120^circ\
end{aligned}$$
Since $mangle A = mangle B$, then divide $120^circ$ to $2$.
$$begin{aligned}
mangle A = mangle B = 60^circ
end{aligned}$$
Now compute for the area of the circle.
$$begin{aligned}
A &= pi r^2 \
&= pi (10)^2 \
&= pi cdot 100 \
&= boxed{314.16 text{ units}^2} \
end{aligned}$$
Draw the square-based pyramid.
[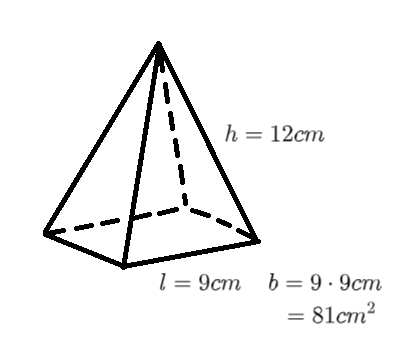](https://postimg.cc/GH6LBRZy)
$$begin{aligned}
Volume &= frac{1}{3}bh \
&= frac{1}{3}(81text{ cm}^2)(12text{ cm}) \
&= boxed{324 text{ cm}^3}
end{aligned}$$
Here’s an illustration of the smaller pyramid.
[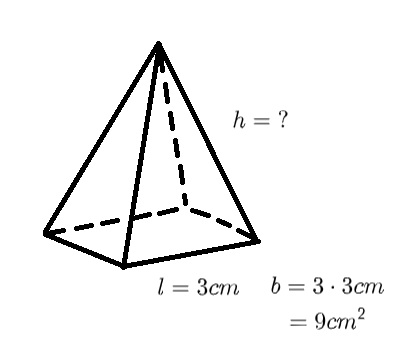](https://postimg.cc/bs74X3yK)
$$begin{aligned}
V &= frac{1}{3}bh \
12 &= frac{9}{3} cdot h \
12 &= 3h \
frac{12}{3} &= frac{3h}{3} \
boxed{4 text{ cm}} &= h
end{aligned}$$
a. The longest time recorded was the last throw with $t=1.25s$, and the ball has still not reached the ground. Thus, the **last throw** is when the ball stayed in the air longer.
$$begin{aligned}
overline{v} &= frac{triangle text{height}}{triangle text{time}} \
&= frac{5.5-1.5}{0.25-0} \
&= frac{4}{0.25} \
&= boxed{16 ft/s} \
end{aligned}$$
b. $16 ft/s$
c. second throw
Since the batting orders of nine starting baseball players don’t have any conditions, it can be solved using simple factorial.
$$begin{aligned}
&= 9! \
&= 9cdot8cdot7cdot6cdot5cdot4cdot3cdot2cdot1 \
&= boxed{362,880}
end{aligned}$$
a. Multiply the number of Beethoven symphonies to Mozart concerto to get the number of ways the local radio station KALG can play two pieces.
$$begin{aligned}
9 cdot 27 = boxed{243 text{ ways}}
end{aligned}$$
$$begin{aligned}
9 cdot 27 cdot 15 = boxed{3645 text{ ways}}
end{aligned}$$
b. $3645$ ways
Exponential Functions are expressed as:
$$begin{aligned}
y &= i(1 pm r)^t
end{aligned}$$
where:
$y =$ final amount
$i =$ initial amount
$r =$ rate (in percent)
$1 pm r =$ multiplier
$t =$ time
a. Based on the discussion above, the starting point is $20$ and the multiplier is $1.06$.
|$x$ |$-1$ |$0$ |$1$ |
|–|–|–|–|
|$y$ |$19.87$ |$20$ |$21.2$ |
Sketch the graph using the points from the table of values.
[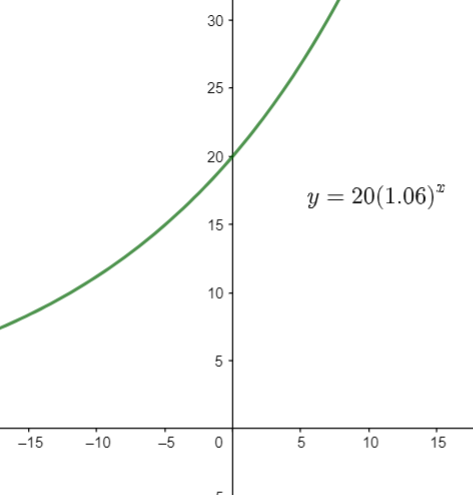](https://postimg.cc/8J6rxwQF)

Equate the equations to each other to solve for the values of $x$.
$$begin{aligned}
2x+9 &= x^2-2x-3 \
2x+9 – x^2+2x+3 &= x^2-2x-3+ (-x^2+2x+3) \
– x^2+4x+11 &= 0 \
end{aligned}$$
factoring out,
$$begin{aligned}
– x^2+4x+11 &= 0 \
(x+2)(x-6) &= 0
end{aligned}$$
Thus, $boxed{x=-2}$ and $boxed{x=6}$.
For $x=-2$,
$$begin{aligned}
y &= 2x+9 \
&= 2(-2)+9 \
&= -4+9 \
&= boxed{5} \
end{aligned}$$
$$begin{aligned}
y &= 2x+9 \
&= 2(6)+9 \
&= 12+9 \
&= boxed{21} \
end{aligned}$$
$x=6$
$y=5$
$y=21$
a. Since there are $5$ inscribed angles in the circle, the measure of angle $a$ is computed by dividing the measurement of the whole circle into $5$. Then, divide by $2$.
$$begin{aligned}
mangle a &= frac{360^circ}{5} \\
&= 72^circ\\
&= frac{72^circ}{2}\\
&= boxed{36^circ}\
end{aligned}$$
$$begin{aligned}
mangle b &= 180^circ – 72^circ \
&= boxed{108^circ}
end{aligned}$$
$$begin{aligned}
mangle c &= mangle b \
108^circ &= 108^circ \
&= boxed{108^circ}
end{aligned}$$
$$begin{aligned}
mangle d &= 180^circ – 108^circ \
&= boxed{72^circ}
end{aligned}$$
The volume of a rectangular prism is computed as:
$$begin{aligned}
V = lcdot wcdot h
end{aligned}$$
a. Draw a diagram of the block.
[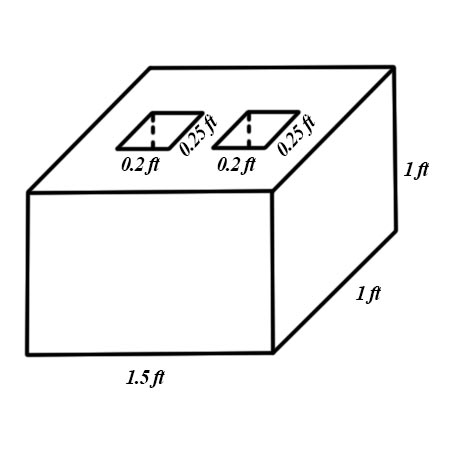](https://postimg.cc/hzNYBXCs)
$$begin{aligned}
V_{inner} &= lcdot wcdot h \
&= 0.25 text{ ft} cdot 1 text{ ft} cdot 0.2 text{ ft}\
&= 0.05 text{ ft}^3
end{aligned}$$
Multiply by $2$ since there are two prisms.
$$begin{aligned}
V_{inner} &= 0.05 text{ ft}^3 \
&= 2 times 0.05 text{ ft}^3 \
&= 0.1 text{ ft}^3
end{aligned}$$
$$begin{aligned}
V_{outer} &= lcdot wcdot h \
&= 1.5 text{ ft} cdot 1 text{ ft} cdot 1 text{ ft}\
&= 1.5 text{ ft}^3
end{aligned}$$
$$begin{aligned}
V &= V_{outer} – V_{inner} \
&= 1.5 text{ ft}^3 – 0.1text{ ft}^3 \
&= boxed{1.4 text{ ft}^3}
end{aligned}$$
a. To solve for the area and perimeter of the resulting triangle, multiply the previous results to $2$.
$$begin{aligned}
A_1 &= A_0 cdot 2 \
&= 36 text{ units}^2 cdot 2 \
&= boxed{72 text{ units}^2}
end{aligned}$$
$$begin{aligned}
P_1 &= P_0 cdot 2 \
&= 42 text{ units} cdot 2 \
&= boxed{84 text{ units}}
end{aligned}$$
$$begin{aligned}
A_2 &= A_1 cdot frac{1}{3} \
&= 72 text{ units}^2 cdot frac{1}{3} \
&= boxed{24 text{ units}^2}
end{aligned}$$
$$begin{aligned}
P_2 &= P_1 cdot frac{1}{3} \
&= 84 text{ units} cdot frac{1}{3} \
&= boxed{28 text{ units}}
end{aligned}$$
b. $A=24 text{ units}^2$ and $P=28 text{ units}$

$$begin{aligned}
c^2&=a^2+b^2\
end{aligned}$$
$$begin{aligned}
c^2&=1^2+left(dfrac{1}{2}right)^2\
c^2&=dfrac{5}{4}\
c&=sqrt{dfrac{5}{4}}\
c&=sqrt{dfrac{5}{(2)^2}}\
c&=dfrac{sqrt{5}}{2}
end{aligned}$$

$$begin{aligned}
x&=dfrac{1}{2}+dfrac{sqrt{5}}{2}\
x&=dfrac{1+sqrt{5}}{2}approx1.618
end{aligned}$$

$$begin{aligned}
text{ratio}&=dfrac{text{larger dimension}}{text{smaller dimension}}\
text{ratio}&=dfrac{1}{dfrac{sqrt{5}}{2}-dfrac{1}{2}}\
text{ratio}&=dfrac{1}{dfrac{sqrt{5}-1}{2}}\
text{ratio}&=1cdot{dfrac{2}{sqrt{5}-1}medspacetext{(Transposition Method)}}\
text{ratio}&=dfrac{2}{sqrt{5}-1}\
text{ratio}&=1.618
end{aligned}$$
See the rectangle below.

$$begin{aligned}
text{scale factor}&=dfrac{1+x}{1+left(dfrac{sqrt{5}}{2}-dfrac{1}{2}right)}\
text{scale factor}&=dfrac{1+left(dfrac{sqrt{5}}{2}+dfrac{1}{2}right)}{1+left(dfrac{sqrt{5}}{2}-dfrac{1}{2}right)}\
end{aligned}$$
$$begin{aligned}
text{scale factor}&=dfrac{2.618}{1.618}\
text{scale factor}&=1.618
end{aligned}$$
$$begin{aligned}
text{ratio}&=dfrac{dfrac{sqrt{5}}{2}+dfrac{1}{2}}{1}=dfrac{sqrt{5}}{2}+dfrac{1}{2}\
text{ratio}&=dfrac{1+sqrt{5}}{2}\
end{aligned}$$
$$begin{aligned}
text{ratio}&=dfrac{1+sqrt{5}}{2}\
text{ratio}&=dfrac{1+2.236}{2}\
text{ratio}&=1.618
end{aligned}$$
See figure below.

$$begin{aligned}
phi&=dfrac{w}{h}\
1.618&=dfrac{267}{h}\
h&=dfrac{267}{1.618}\
h&approx165medspacetext{cm}
end{aligned}$$

$$begin{aligned}
text{ratio}&=dfrac{1}{dfrac{sqrt{5}}{2}-dfrac{1}{2}}\
text{ratio}&=dfrac{1}{0.618}\
text{ratio}&=1.618=phi
end{aligned}$$

$$begin{aligned}
c^2&=a^2+b^2\
c^2&=0.618^2+0.309^2\
c^2&=0.477\
c&=sqrt{0.477}\
c&=0.691
end{aligned}$$
$$begin{aligned}
text{ratio}&=dfrac{0.618}{0.691-0.309}\
text{ratio}&=dfrac{0.618}{0.382}\
text{ratio}&=1.618=phi
end{aligned}$$
Calculate the radius of the right decagon if the length of its side is $1$.
Keep in mind that there are two radii of the right decagon:
1. Incircle radius, $r_1=frac{1}{2}sqrt{5+2sqrt5}cdot a$
2. Circumcircle radius, $r_o=frac{1+sqrt5}{2}cdot a$,
where the parameter $a$ represents the length of the side for the right decagon.
Calculate each if $a=1$.
$$begin{aligned}
r_i&=frac{1}{2}sqrt{5+2sqrt5}cdot 1\
&=1.534\
\
r_o&=frac{1+sqrt5}{2}cdot 1\
&=1.618
end{aligned}$$
Conclude that the circumcircle radius or the radius of the outer circle of this decagon has the radius that is equal to the golden ratio, $phi$.
Calculate the angles of the golden triangle inside this right decagon.
We know that the $r_o=1.618$ for this right decagon.
Use the formula $r_o=frac{a}{2sin(alpha/2)}$, where $a$ represents the side length of the decagon (and the base of the golden triangle), whereas $alpha$ represents the angle of the golden triangle in the middle of the decagon.
$$begin{aligned}
r_o&=dfrac{a}{2sin(alpha/2)}\
1.618&=dfrac{1}{2sin(alpha/2)}\
2sin(alpha/2)cdot1.618&=1\
3.236sin(alpha/2)&=1\
sin(alpha/2)&=frac{1}{3.236}\
frac{alpha}{2}&=sin^{-1}{frac{1}{3.236}}\
frac{alpha}{2}&=18°\
alpha&=boxed{36°}
end{aligned}$$
$$begin{aligned}
alpha+2beta&=180°\
36°+ 2beta&=180°\
2beta&=180°-36°\
2beta&=144°\
beta&=boxed{72°}
end{aligned}$$
Check the ratio of $overline{AC} text{ to }overline{BC}$ and the ratio of $overline{AB} text{ to }overline{BD}$ in the given pentagram.
Use the ruler to measure the length of the lines in question and then divide them to get their ratio. Then determine if the obtained ratios correspond to the golden ratio.
Try to calculate the following expression as close as possible.
$sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt{1+}sqrt{1+sqrt{1+}cdots}}}}}$
First, calculate $sqrt1$. The result is $1$.
Then, calculate $sqrt{1+sqrt1}$.
$$begin{aligned}
sqrt{1+sqrt1}&=sqrt{1+1}\
&=sqrt2\
&=1.41
end{aligned}$$
Calculate $sqrt{1+sqrt{1+sqrt1}}$.
$$begin{aligned}
sqrt{1+sqrt{1+sqrt1}}&=sqrt{1+sqrt{1+1}}\
&=sqrt{1+sqrt{2}}\
&=sqrt{1+1.414}\
&=sqrt{2.414}\
&=1.55
end{aligned}$$
Now skip a few and proceed to calculate $sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt1}}}}}$
$$begin{aligned}
&sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt1}}}}}\
&=sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt{1+1}}}}}\
&=sqrt{1+sqrt{1+sqrt{1+sqrt{1+sqrt{2}}}}}\
&=sqrt{1+sqrt{1+sqrt{1+sqrt{1+1.41}}}}\
&=sqrt{1+sqrt{1+sqrt{1+sqrt{2.41}}}}\
&=sqrt{1+sqrt{1+sqrt{1+1.552}}}\
&=sqrt{1+sqrt{1+sqrt{2.552}}}\
&=sqrt{1+sqrt{1+1.597}}\
&=sqrt{1+sqrt{2.597}}\
&=sqrt{1+1.612}\
&=sqrt{2.612}\
&=1.616
end{aligned}$$
Conclude that the more the expression diverges to infinity, the result converges to the golden ratio.
Observe the properties of $phi$.
First, determine what happens with the inverse of $phi$.
Let’s examine the ratio of two high Fibonacci that gives a good approximation of the golden ratio, for example, $55$ and $89$.
Their ratio is $frac{89}{55}=1.61818$.
Now, take the inverse of this number.
$$begin{aligned}
dfrac{1}{1.61818}=0.618
end{aligned}$$
Therefore, we get the relation $1+dfrac{1}{phi}=phi$.
This is not true for other irrational numbers. Examine $piapprox3.14$.
$$begin{aligned}
1+frac{1}{pi}approx1.32\
pine1.32
end{aligned}
$$begin{aligned}
phi^2&=1.61818cdot1.61818\
phi^2&=2.618\
end{aligned}$$
Therefore, we get the relation $1+phi=phi^2$.
This relation is also not true for other irrational numbers.
$$begin{aligned}
1+pi&=pi^2\
1+3.14&=9.87\
4.14&ne9.87
end{aligned}$$
Solve the system of equations graphically.
Make a table of values for the first equation.
$$begin{array}{|c|c|}
hline
x & y \
hline
-3 & 8\
hline
-2 & 3\
hline
-1 & 0\
hline
0 & -1\
hline
1 & 0\
hline
2 & 3\
hline
3 & 8\
hline
end{array}$$
Make a table of values for the second equation.
$$begin{array}{|c|c|}
hline
x & y \
hline
-3 & -3\
hline
-2 & -2\
hline
-1 & -1\
hline
0 & 0\
hline
1 & 1\
hline
2 & 2\
hline
3 & 3\
hline
end{array}$$


$$begin{aligned}
x&=x^2-1\
x^2-x-1&=0
end{aligned}$$
Solve the quadratic equation using the Quadratic Formula.
$$begin{aligned}
a=1, b=-1, c=-1
end{aligned}$$
$$begin{aligned}
x_{1,2}&= frac{-bpmsqrt{b^2-4ac}}{2a}\
&= frac{-(1)pmsqrt{(-1)^2-4cdot1cdot(-1)}}{2cdot1}\
&= frac{1pmsqrt{1+4}}{2}\
&= frac{1pmsqrt{5}}{2}\
x_1&=frac{1+sqrt{5}}{2} \
x_1&approx 1.618\
x_2&approx-0.618
end{aligned}$$
Then, from the second equation,
$$begin{aligned}
y_1&=1.618\
y_2&=-0.618
end{aligned}$$
Conclude that the solutions to the given system of inequalities are $A(phi, phi)$ and $left(-frac{1}{phi}, -frac{1}{phi} right)$.
It is correct to say that the Fibonacci sequence follows the golden ratio, meaning that as the sequence diverges to infinity, the closer the ratio of two subsequent terms of the sequence converges to the golden ratio.
As for the golden spiral, the numbers constituting the Fibonacci spiral are a close approximation of the golden spiral, but it is NOT exactly a golden spiral. The golden spiral is created by creating a series of golden rectangles. The golden rectangles are created by expanding the previous rectangle by the golden ratio, whereas the Fibonacci spiral is created by creating a series of rectangles with length and width as the subsequent terms of the Fibonacci sequence, with the characteristics of getting closer to the golden ratio as they get bigger, but at the lower numbers, they do not greate a golden ratio.
This is true. As the Fibonacci spiral diverges to infinity, it basically becomes a golden spiral because the ratio of the subsequent terms of the Fibonacci sequence converges to the golden ratio.
License plates of the first type can be computed as:
$$begin{aligned}
T_1&= 26 cdot 26 cdot 26 cdot 10 cdot 10 cdot10 \
&= 17,576,000 \
end{aligned}$$
$$begin{aligned}
T_2 &= 9 cdot 26 cdot 26 cdot 26 cdot 10 cdot 10 cdot10 \
&= 158,184,000 \
end{aligned}$$
$$begin{aligned}
T &= 158,184,000-17,576,000 \
&= boxed{140,608,000 text{ more plates}}
end{aligned}$$
$$begin{aligned}
T &= 9 cdot 1 cdot 1 cdot 1 cdot 1 cdot 10 cdot10 \
&= 900 \
end{aligned}$$
$$begin{aligned}
P(INT2) &= frac{900}{158,184,000} \\
&= boxed{frac{1}{175,760}}\
end{aligned}$$
a. The number of *petit four* they can make is computed as:
$$begin{aligned}
&= _{12}C_4 + _{12}C_3 \\
&= frac{12!}{8! cdot 4!} + frac{12!}{9! cdot 3!} \\
&= 495 + 220\
&= boxed{715}
end{aligned}$$
$$begin{aligned}
&= _{10}C_2 \
&= frac{10!}{8! cdot 2!} \
&= 45
end{aligned}$$
$$begin{aligned}
P &= frac{_{10}C_2}{715} times 100\\
&= frac{45}{715} times 100 \\
&= 0.0629 times 100 \
&= boxed{6.29%}
end{aligned}$$
Illustrate the bigger pyramid.
[](https://postimg.cc/GH6LBRZy)
$$begin{aligned}
V_1 &= frac{1}{3}bh \
&= frac{1}{3}(81text{ cm}^2)(12text{ cm}) \
&= boxed{324 text{ cm}^3}
end{aligned}$$
[](https://postimg.cc/7C3NCNyJ)
$$begin{aligned}
V_2 &= frac{1}{3}bh \
&= frac{1}{3}(9text{ cm}^2)(3text{ cm}) \
&= boxed{9 text{ cm}^3}
end{aligned}$$
$$begin{aligned}
V &= V_1-V_2 \
&= 324text{ cm}^3- 9 text{ cm}^3 \
&= boxed{315 text{ cm}^3}
end{aligned}$$
The equation of a circle can be described by the following:
$$begin{gather}
(x-h)^2 + (y-k)^2 = r^2
end{gather}$$
We are given with the following system of equations:
$$begin{cases}
x^2+ y^2 = 20 \
(x-6)^2 + y^2 = 32
end{cases}$$
We observe from Eq (1) that both equations represent equations of a circle. Hence, when the graph of the two circles intersect, there would be two points of intersection. However, if the two circles do not intersect, then there will be no point of intersection.
$$begin{aligned}
x^2 + y^2 &= 20 \
y^2 &= 20 -x^2
end{aligned}$$
$$begin{aligned}
(x-6)^2 + y^2 &= 32 \
y^2 &= 20 -x^2 \
(x-6)^2 + (20-x^2) &= 32 \
(x^2 -12x + 36) + (20-x^2) &= 32 \
-12x + 56 &= 32 \
-12x &= 32 – 56 \
x &= frac{32-56}{-12} \
&= boxed{2}
end{aligned}$$
$$begin{aligned}
x^2 + y^2 &= 20 \
x &= 2 \
y^2 &= 20 – x^2 \
y^2 &= 20 – (2)^2 \
y^2 &= 16 \
y &= boxed{pm 4}
end{aligned}$$
The graph of the system of equations can be illustrated as follows:
[](https://postimg.cc/56mL9TCc)
From the graph, we observe that our prediction in part a is correct. The system of equations intersect twice.
We know that there are $52$ playing cards in a deck. Dillon was able to select $4$ cards from the deck (including one ace). Determine the probability of getting an ace for the fifth card.
$$begin{aligned}
A &= 4 – 1 \
A &= boxed{3} \
B &= 52 – 4 \
B &= boxed{48}
end{aligned}$$
$$begin{aligned}
&= frac{A}{B} \
&= frac{3}{48} \
&= frac{1}{16}
end{aligned}$$
There probability is $boxed{text{A.} frac{1}{16}}$
$$begin{aligned}
ax^2+bx+c=0
end{aligned}$$
where
$a, b, c$ – are the coefficients.
$$begin{aligned}
a&=5\
c&=20\
end{aligned}$$
$$begin{aligned}
b^2-4ac&=0&text{textcolor{#4257b2}{discriminant}}
end{aligned}$$
$$begin{aligned}
b^2-4ac&=0\
b^2&=4ac&text{textcolor{#4257b2}{Transposition Method}}\
b^2&=4(5)(20)\
b^2&=400\
b&=sqrt{400}\
b&=20
end{aligned}$$
$$begin{aligned}
b&>20medspacetext{(two real solutions)}\
b&=20medspacetext{(one real solution)}\
b&<20medspacetext{(no real solution)}\
end{aligned}$$
$$begin{aligned}
bgeq20
end{aligned}$$

Let
$x$ = circumference of the circle
$A$ = area of the circle
$r$ = radius of the circle
$d$ = diameter of the circle
$$begin{aligned}
x&=2pi r\
A&=pi r^2
end{aligned}$$
$$begin{aligned}
overline{AF}=overline{DE}=2r
end{aligned}$$
$$begin{aligned}
r&=overline{CX}+2\
r-2&=overline{CX}
end{aligned}$$
$$begin{aligned}
(overline{CX})^2&=r^2+4^2-2(r)(4)costheta\
(r-2)^2&=r^2+16-8rcostheta\
r^2-4r+4&=r^2+16-8rcostheta\
r^2-4r+4-r^2-16&=-8rcosthetaenspacetext{textcolor{#4257b2}{(Transposition Method)}}\
-4r-12&=-8rcostheta\
-4(r+3)&=-8rcostheta
end{aligned}$$
$$begin{aligned}
dfrac{-4(r+3)}{-4}&=dfrac{-8rcostheta}{-4}\
r+3&=2rcostheta\
dfrac{r+3}{2r}&=costheta\
cos^{-1}left(dfrac{r+3}{2r}right)&=theta
end{aligned}$$
$$begin{aligned}
theta_1&=180degree-90degree-theta\
theta_1&=90degree-cos^{-1}left(dfrac{r+3}{2r}right)
end{aligned}$$
$$begin{aligned}
sintheta_1&=dfrac{overline{AB}}{overline{AF}}\
sinleft[90degree-cos^{-1}left(dfrac{r+3}{2r}right)right]&=dfrac{7}{2r}
end{aligned}$$
$$begin{aligned}
sin(A-B)&=sin Acos B-cos Asin B
end{aligned}$$
$$begin{aligned}
sinleft[90degree-cos^{-1}left(dfrac{r+3}{2r}right)right]
&=sin90degreecosleft[cos^{-1}left(dfrac{r+3}{2r}right)right]-cos90degreesinleft[cos^{-1}left(dfrac{r+3}{2r}right)right]\
&=1cdot left(dfrac{r+3}{2r}right)-0cdotsinleft[cos^{-1}left(dfrac{r+3}{2r}right)right]\
&=dfrac{r+3}{2r}
end{aligned}$$
$$begin{aligned}
sinleft[90degree-cos^{-1}left(dfrac{r+3}{2r}right)right]&=dfrac{7}{2r}\
dfrac{r+3}{2r}&=dfrac{7}{2r}
end{aligned}$$
$$begin{aligned}
dfrac{r+3}{2r}cdot(2r)&=dfrac{7}{2r}cdot(2r)\
r+3&=7\
end{aligned}$$
$$begin{aligned}
r+3-textcolor{#4257b2}{3}&=7-textcolor{#4257b2}{3}\
r&=4
end{aligned}$$
$$begin{aligned}
x&=2pi r\
x&=2(3.1416)(4)\
x&=25.133
end{aligned}$$
$$begin{aligned}
A&=pi r^2\
A&=(3.1416)(4)^2\
A&=50.266
end{aligned}$$
Determine the value of the parameters $a, b$ if it is given that the exponential function passes through the given points. Substitute the variables $x$ and $f(x)$ from the given equation with the coordinates of the given points to get the system of equations.
$$
left{
begin{array}{cc}
6=ab^1 \
30.375=ab^5
end{array}
right.$$
Divide the second equation by the first equation to obtain the value of the parameter $b$.
$$begin{aligned}
frac{30.375}{6}&=frac{ab^5}{ab}\
b^4&=frac{81}{16}\
b&=pmfrac{3}{2}
end{aligned}$$
Calculate the possible value of the parameter $a$ using the first equation.
$$begin{aligned}
acdotfrac{3}{2}&=6\
a&=6cdotfrac{2}{3}\
a_1&=4\
\
acdotfrac{-3}{2}&=6\
a&=6cdotfrac{-2}{3}\
a_2&=-4\
end{aligned}$$
Therefore, the possible exponential functions that pass through the given points are:
– $f(x)=4cdotleft(dfrac{3}{2}right)^x$
– $f(x)=-4cdotleft(-dfrac{3}{2}right)^x$
Beware! The base of an exponential function $(b)$ has to be a **POSITIVE** real number. Therefore, the expression under the number two is **NOT** and exponential function because its base is not a positive number.
The parameter $b$ is the base of the exponential function. It tells is us on which side of the coordinate plane the graph of the exponential function is located, relative to the $x$-axis. If the base of the exponential function is a positive real number greater than $1$, the exponential function is growing, whereas the exponential function is decaying if the value of the base is in the interval $0<b<1$.
Exponential functions can describe a multitude of things, for example to follow the growth of a population of animals in real-time.
For point $(1,6)$.
$$begin{aligned}
y&=ab^x\
6&=ab^1\
6&=ab\
dfrac{6}{b}&=a
end{aligned}$$
$$begin{aligned}
y&=ab^x\
30.375&=ab^5
end{aligned}$$
$$begin{aligned}
30.375&=left(dfrac{6}{b}right)b^5\
30.375&=6b^4\
end{aligned}$$
$$begin{aligned}
dfrac{30.375}{6}&=dfrac{6b^4}{6}\
5.0625&=b^4\
end{aligned}$$
$$begin{aligned}
sqrt[4]{5.0625}&=sqrt[4]{b^4}\
1.5&=b
end{aligned}$$
$$begin{aligned}
a&=dfrac{6}{b}\
a&=dfrac{6}{1.5}\
a&=4
end{aligned}$$
$$begin{aligned}
y=4(1.5)^x
end{aligned}$$
A train has $8$ cars comprising of $2$ first-class, $5$ second-class, and $1$ restaurant car. We determine the number of ways these cars can be linked together.
Since there are a total of $8$ cars, we can obtain the number of ways these cars can be linked as follows:
$$begin{aligned}
8 times 7 times 6 times 5 times 4 times 3 times 2 times 1 &= 8!
end{aligned}$$
$$begin{aligned}
2 times 1 &= 2!
end{aligned}$$
$$begin{aligned}
5 times 4 times 3 times 2 times 1 &= 5!
end{aligned}$$
$$begin{aligned}
&= frac{8!}{5! 2!} \
&= frac{40320}{240} \
&= boxed{168}
end{aligned}$$
Hence, there are $168$ ways that we can link the cars.
Arik charges $$5.00$ when driving for less than $3$ miles, and charges additional $$1.50$ per mile for driving more than $3$ miles. We determine the piecewise function of Arik’s earning using these information as follows:
$$f(x)=
begin{cases}
5 & 0 < x <3 \
5 + 1.5x & 3 le x
end{cases}$$
where $x$ is the number of miles driven
The price per galloon of gas is $$3.00$ and Arik’s mileage is $28 frac{text{mi}}{text{gal}}$. While his car’s maintenance cost is $$ 0.60$ per mile. We obtain the following function for Arik’s fuel and maintenance cost per mile driven:
$$begin{gather}
f(x)=
-frac{3x}{28} – 0.60x
end{gather}$$
where $x$ is the number of miles driven
We create the new piecewise function that represents Arik’s profit by combining the profit (part a) and cost (part b) functions as follows:
$$f(x)=
begin{cases}
5 & 0 < x 0
end{cases}$$
$$begin{aligned}
x &= 2.5 \
f(x) &= 5 -frac{3x}{28} – 0.60x \
f(2.5) &= 5 – frac{3cdot 2.5}{28} – 0.60(2.5) \
&= 5 -1.23 \
&= boxed{3.77}
end{aligned}$$
Arik’s predicted profit when he drives for $2.5$ miles is $$3.77$
$$begin{aligned}
x &= 10 \
f(x) &= (5+1.5x) -frac{3x}{28} – 0.60x \
f(10) &= (5+1.5 (10)) + left(- frac{3cdot 10}{28} – 0.60(10) right) \
&= (20) + (-7.07) \
&= boxed{13.93}
end{aligned}$$
Arik’s predicted profit when he drives for $10$ miles is $$13.93$
We are given with the following house plan:
[](https://postimg.cc/rKrq2nfS)
Determine the area of the diagram
We determine the area of the diagram by separating the diagram into $3$ rectangles and $1$ triangle. We illustrate these sections as follows:
[](https://postimg.cc/G9pkKYX0)
$$begin{aligned}
sin theta &= frac{text{opposite}}{text{hypotenuse}} \
sin 60^circ &= frac{text{opposite}}{30} \
text{opposite} &= 30 sin (60^circ) \
&= 25.98 \
&approx boxed{26 text{ mm}}
end{aligned}$$
$$begin{aligned}
cos theta &= frac{text{adjacent}}{text{hypotenuse}} \
cos 60^circ &= frac{text{adjacent}}{30} \
text{adjacent} &= 30 cos (60^circ) \
&= boxed{15 text{ mm}} \
end{aligned}$$
$$begin{aligned}
A_t &= frac{1}{2}bh \
&= frac{1}{2} (15) cdot (26) \
&= boxed{195 text{ mm}^2}
end{aligned}$$
$$begin{aligned}
L_r &= frac{51 – L_t}{3} \
&= frac{51-15}{3} \
&= boxed{12}
end{aligned}$$
$$begin{aligned}
A_r &= l cdot h \
&= (12) cdot (26) \
&= boxed{192 text{ mm}^2}
end{aligned}$$
$$begin{aligned}
A_s &= l^2 \
&= (12)^2 \
&= boxed{144 text{ mm}^2}
end{aligned}$$
$$begin{aligned}
A_{total} &= 3 A_r + A_t – A_s \
&= 3 (192) + (195) – (144) \
&= boxed{627 text{ mm}^2}
end{aligned}$$
The area of the diagram is $627 text{ mm}^2$
If the diagram is enlarged by $400%$, this means that the total area of the diagram is increased by $4$ times. We calculate for the new area as follows:
$$begin{aligned}
A_{new} &= A_{total} cdot 4 \
&= 627 cdot 4 \
&= boxed{2508 text{ mm}^2}
end{aligned}$$
The new area when the diagram is enlarged will be $2508 text{ mm}^2$
b. $2508 text{ mm}^2$
Compute the volume of the cylinder.
[](https://postimg.cc/phzmjw6q)
$$begin{aligned}
V_1 &= pi r^2h \
&= pi cdot (38 text{ units})^2 cdot 71text{ units} \
&= pi cdot 1444 text{ units}^2 cdot 71text{ units} \
&= 322,088.65 text{ units}^3 \
end{aligned}$$
[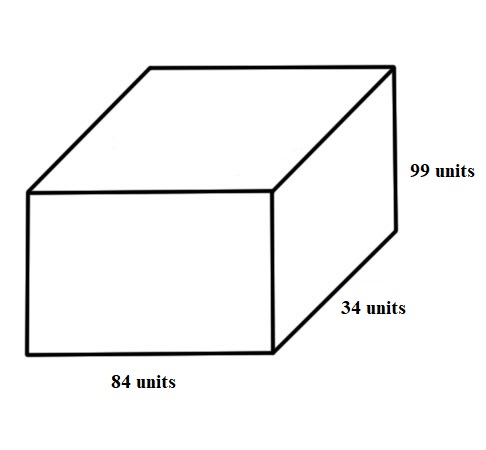](https://postimg.cc/VrqqjGGB)
$$begin{aligned}
V_1 &= lwh \
&= 84text{ units} cdot 34 text{ units} cdot 99text{ units} \
&= 282,744 text{ units}^3 \
end{aligned}$$

$$begin{aligned}
x+x+theta&=180degree
end{aligned}$$
$$begin{aligned}
x+x+106degree&=180degree\
2x+106degree&=180degree
end{aligned}$$
$$begin{aligned}
2x+106degree-textcolor{#4257b2}{106degree}&=180degree-textcolor{#4257b2}{106degree}\
2x&=74degree
end{aligned}$$
$$begin{aligned}
dfrac{2x}{textcolor{#4257b2}{2}}&=dfrac{74degree}{textcolor{#4257b2}{2}}\
x&=37degree
end{aligned}$$
$$begin{aligned}
x+67degree&=180degree&text{Eq. 1}\
5y+(3y-16degree)&=180degree&text{Eq. 2}
end{aligned}$$
$$begin{aligned}
x+67degree-textcolor{#4257b2}{67degree}&=180degree-textcolor{#4257b2}{67degree}\
x&=113degree
end{aligned}$$
$$begin{aligned}
5y+3y-16degree&=180degree\
8y-16degree&=180degree
end{aligned}$$
$$begin{aligned}
8y-16degree+textcolor{#4257b2}{16degree}&=180degree+textcolor{#4257b2}{16degree}\
8y&=196degree
end{aligned}$$
$$begin{aligned}
dfrac{8y}{textcolor{#4257b2}{8}}&=dfrac{196degree}{textcolor{#4257b2}{8}}\
y&=24.5degree
end{aligned}$$
$$begin{aligned}
sin60degree&=dfrac{x}{28}\
0.866&=dfrac{x}{28}\
end{aligned}$$
$$begin{aligned}
0.866cdot(28)&=dfrac{x}{28}cdot(28)\
24.249&=x
end{aligned}$$
Take note that area of triangle is.
$$begin{aligned}
A&=dfrac{1}{2}bh
end{aligned}$$
where,
$b$ = base length.
$h$ = height of the triangle.

$$begin{aligned}
A_s&=dfrac{1}{2}cdot (b)cdot(x)\
96&=dfrac{1}{2}cdot(8)cdot(x)\
96&=4x
end{aligned}$$
$$begin{aligned}
dfrac{96}{textcolor{#4257b2}{4}}&=dfrac{4x}{textcolor{#4257b2}{4}}\
24medspacetext{units}&=x
end{aligned}$$
The given is a right triangle with the hypotenuse of $28$ and the measure of one of its acute angles is $60°$. Determine the length of the leg opposing the angle of $60°$.
Use right-angle trigonometry to solve the problem.
$$begin{aligned}
sinalpha&=frac{text{Opposing Leg}}{text{Hypotenuse}}\
sin60°&=frac{x}{28}\
x&=sin60°cdot28\
x&=boxed{24.25}
end{aligned}$$
Conclude that it is possible to determine the value of the variable $x$ for this triangle.
The given is a right triangle with a hypotenuse that has a measure of $17$ and one leg that has a measure of $19$. Calculate the value of the other leg.
This triangle can not exist because the hypotenuse has to be the longest side of the right triangle.
Prove this using the Pythagorean Principle, as demonstrated below:
$$begin{aligned}
a=19, b=x, c=17
end{aligned}$$
$$begin{aligned}
c^2&=a^2+b^2\
b^2&=c^2-a^2\
b&=sqrt{c^2-a^2}\
b&=sqrt{17^2-19^2}\
b&=sqrt{289-361}\
b&=sqrt{-72}\
end{aligned}$$
This equation is not solvable outside the complex numbers.
The given is a triangle with the base of $8$ and the area of $96$. Calculate the value of the variable $x$ representing the height of this triangle.
Use the formula $A=dfrac{1}{2}acdot h$, where the parameter $a$ represents the base of the triangle, and the parameter $h$ represents the height of the triangle, perpendicular to the base of the triangle, to solve this problem.
$$begin{aligned}
A&=frac{1}{2}acdot h\
96&=frac{1}{2}cdot8cdot x\
4x&=96\
x&=frac{96}{4}\
x&=boxed{24}
end{aligned}$$
Conclude that it is possible to calculate the value of the variable $x$ for this triangle.

$$begin{aligned}
sinangle{A}&=dfrac{overline{BC}}{overline{AC}}\
sin42degree&=dfrac{7}{overline{AC}}
end{aligned}$$
$$begin{aligned}
sin42degreecdot(overline{AC})&=dfrac{7}{overline{AC}}cdot(overline{AC})\
sin42degreeoverline{AC}&=7
end{aligned}$$
$$begin{aligned}
dfrac{sin42degreeoverline{AC}}{sin42degree}&=dfrac{7}{sin42degree}\
overline{AC}&=10.46medspacetext{mm}
end{aligned}$$
$$begin{aligned}
sinalpha&=frac{text{Opposing Leg}}{text{Hypotenuse}}\
sin42°&=frac{7}{x}\
x&=frac{7}{sin42°}\
x&approxboxed{10.46}
end{aligned}$$
The hypotenuse of this right triangle has a length of about $10.46$ cm. This is given as the option **B**.
The standard form of the quadratic equation is $ax^2+bx+c=0$.
Use the $x$-intercept form of the quadratic equations to solve the problem.
$$begin{aligned}x^2-x(x_1+x_2)+ (x_1cdot x_2)=0 end{aligned}$$
If the $x$-intercepts of this quadratic equation are $x_1=-3$ and $x_2=2$, then:
$$begin{aligned}
x^2-x(x_1+x_2)+ (x_1cdot x_2)&=0\
x^2-x(-3+2)+ (-3cdot2)&=0\
x^2-xcdot(-1)-6&=0\
x^2+x-6&=0
end{aligned}$$
$$begin{aligned}
a=1, b=1, c=-6
end{aligned}$$
$$begin{aligned}
x_{1,2}&= frac{-bpmsqrt{b^2-4ac}}{2a}\
&= frac{-1pmsqrt{1^2-4cdot1cdot(-6)}}{2cdot1}\
&= frac{-1pmsqrt{1+24}}{2}\
&= frac{-1pmsqrt{25}}{2}\
x_{1,2}&= frac{-1pm5}{2}\
x_1&=2 \
x_2&=-3
end{aligned}$$
If the $x$-intercepts of this quadratic equation are $x_1=-3$ and $x_2=frac{1}{2}$, then:
$$begin{aligned}
x^2-x(x_1+x_2)+ (x_1cdot x_2)&=0\
x^2-x(-3+0.5)+ (-3cdot0.5)&=0\
x^2-xcdotleft(-frac{5}{2}right)+left(-frac{3}{2}right)&=0\
x^2+frac{5}{2}x-frac{3}{2}&=0\
end{aligned}$$
$$begin{aligned}
a=1, b=2.5, c=-1.5
end{aligned}$$
$$begin{aligned}
x_{1,2}&= frac{-bpmsqrt{b^2-4ac}}{2a}\
&= frac{-2.5pmsqrt{2.5^2-4cdot1cdot(-1.5)}}{2cdot1}\
&= frac{-2.5pmsqrt{6.25+6}}{2}\
&= frac{-2.5pmsqrt{12.25}}{2}\
x_{1,2}&= frac{-2.5pm3.5}{2}\
x_1&=frac{1}{2} \
x_2&=-3
end{aligned}$$
$$begin{aligned}
y=a(x-b)(x-c)
end{aligned}$$
where
$a$ – leading coefficient
$(b, 0) (c, 0)$ – $x$-intercepts
$$begin{aligned}
y&=a[x-(-3)][x-2]\
y&=a(x+3)(x-2)
end{aligned}$$
$$begin{aligned}
y&=1(x+3)(x-2)\
y&=x^2-2x+3x-6\
y&=x^2+x-6
end{aligned}$$
$$begin{aligned}
y&=a(x-b)(x-c)\
y&=aleft[x-(-3)right] left(x-dfrac{1}{2}right)\
y&=a(x+3)left(x-dfrac{1}{2}right)\
end{aligned}$$
$$begin{aligned}
y&=2(x+3)left(x-dfrac{1}{2}right)\
y&=(x+3)left(2x-1 right)\
y&=2x^2-x+6x-3\
y&=2x^2+5x-3
end{aligned}$$
a. The number of possible Judicial Boards are:
$$begin{aligned}
_{900}C_{12} &= frac{900!}{888! cdot 12!}\\
&= boxed{5.47758 times 10^{26}}
end{aligned}$$
$$begin{aligned}
_{899}C_{11} &= frac{899!}{888! cdot 11!}\\
&= boxed{7.30343 times 10^{24}}
end{aligned}$$
$$begin{aligned}
P&= frac{_{899}C_{11} }{_{900}C_{12}} times 100\\
&= frac{7.30343 times 10^{24}}{5.47758 times 10^{26}} times 100\\
&= boxed{1.33%}
end{aligned}$$
b. $7.30343 times 10^{24}$
c. $1.33%$
Illustrate the pyramid.
[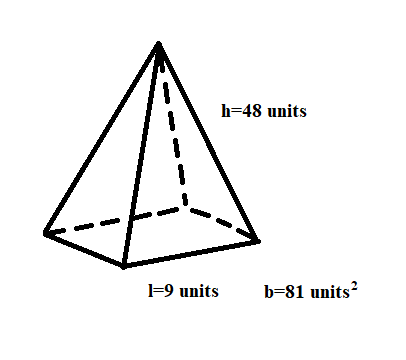](https://postimg.cc/cgdRcqK1)
$$begin{aligned}
V &= frac{1}{3} cdot l cdot w cdot h \
&= frac{1}{3} cdot 9 text{ units} cdot 9 text{ units} cdot 48 text{ units} \
&= frac{1}{3} cdot 3888 text{ units}^3\
&= boxed{1296 text{ units}^3}
end{aligned}$$
Remember how to convert a radical expression into its exponential form.
$$begin{aligned}
sqrt[n]{a^x} &= a^{frac{x}{n}}
end{aligned}$$
Convert the following radical expression in exponent form.
a.
$$begin{aligned}
sqrt[3]{10} &= 10^{frac{1}{3}}
end{aligned}$$
$$begin{aligned}
sqrt{15} &= 15^{frac{1}{2}}
end{aligned}$$
$$begin{aligned}
sqrt[4]{18^3} &= 18^{frac{3}{4}}
end{aligned}$$
$$begin{aligned}
frac{1}{sqrt{5}} &= frac{1}{5^{frac{1}{2}}}
end{aligned}$$

$$begin{aligned}
angle{ADB}&=overset{largefrown}{AB}\
angle{ADB}&=32degree
end{aligned}$$
$$begin{aligned}
theta+theta+32degree&=180degree\
2theta+32degree&=180degree
end{aligned}$$
$$begin{aligned}
2theta+32degree-(32degree)&=180degree-32degree\
2theta&=148degree
end{aligned}$$
$$begin{aligned}
dfrac{2theta}{2}&=dfrac{148degree}{2}\
theta&=74degree
end{aligned}$$
$$begin{aligned}
dfrac{r}{sintheta}&=dfrac{9}{sinangle{ADB}}\
dfrac{r}{sin74degree}&=dfrac{9}{sin32degree}\
dfrac{r}{sin74degree}&=16.984\
end{aligned}$$
$$begin{aligned}
dfrac{r}{sin74degree}cdot(sin74degree)&=16.984cdot(sin74degree)\
r&=16.326medspacetext{mm}
end{aligned}$$
$$begin{aligned}
length_{overset{largefrown}{AB}}&=dfrac{overset{largefrown}{AB}}{360degree}cdot2pi r
end{aligned}$$
$$begin{aligned}
length_{overset{largefrown}{AB}}&=dfrac{32degree}{360degree}cdot2(3.1416)(16.326)\
length_{overset{largefrown}{AB}}&=0.089cdot102.579\
length_{overset{largefrown}{AB}}&=9.129medspacetext{mm}
end{aligned}$$
First, recognize that the first equation represents a vertical parabola and that the second equation represents a line. Therefore, this system can have no solutions if the line and parabola do not intersect each other, one solution if the line and parabola touch each other, and two solutions if the line intersects the parabola. Graph both to determine which of these possibilities is the case.
For the parabola:
$$begin{aligned}
f(-2)&=-2(-2-1)^2-3\
&=-2cdot(-3)^2-3\
&=-2cdot9-3\
&=-18-3\
&=-21
end{aligned}$$
The table of values for the parabola is:
$$begin{array}{|c|c|}
hline
x & y \
hline
-2 & -21\
hline
-1 & -11\
hline
0 & -5\
hline
1 & -3\
hline
2 & -5\
hline
3 & -11\
hline
4 & -21\
hline
end{array}$$
For the line:
$$begin{aligned}
f(0)&=-frac{5}{2}cdot0-5\
&=-5
end{aligned}$$
The table of values for the line is:
$$begin{array}{|c|c|}
hline
x & y \
hline
-3 & 2.5\
hline
-2 & 0\
hline
-1 & -2.5\
hline
0 & -5\
hline
1 & -7.5\
hline
2 & -10\
hline
3 & -12.5\
hline
end{array}$$


Conclude that the line intersects the parabola twice, meaning there are $2$ solutions to this system of equations.
Where
$a$ – leading coefficient,
$(h, k)$ – vertex point of parabola
In approximating the value of $x$, $sin(theta)$ will be used since the size computing is the opposite side, and the given one is the hypotenuse.
$$begin{aligned}
sin(theta) &= frac{opp}{hyp}\\
sin(60^circ) &= frac{x}{10}\\
10 cdot 0.469 &= x \
boxed{4.69} &= x
end{aligned}$$
To compute the length of the hypotenuse, use Pythagorean Theorem.
[](https://postimg.cc/mc35F6Y1)
$$begin{aligned}
z^2 &= x^2 +y^2\
sqrt{z^2} &= sqrt{x^2 +y^2}\
& boxed{z = sqrt{x^2 +y^2}}
end{aligned}$$
Compute for the number of pizzas the pizza parlor can create with five or fewer toppings.
For the five toppings:
$$begin{aligned}
_{12}C_5 &= frac{12!}{7! cdot 5!} \\
&= 792
end{aligned}$$
$$begin{aligned}
_{12}C_4 &= frac{12!}{8! cdot 4!} \\
&= 495
end{aligned}$$
$$begin{aligned}
_{12}C_3 &= frac{12!}{9! cdot 3!} \\
&= 220
end{aligned}$$
$$begin{aligned}
_{12}C_2 &= frac{12!}{10! cdot 2!} \\
&= 66
end{aligned}$$
$$begin{aligned}
_{12}C_1 &= frac{12!}{11! cdot 1!} \\
&= 12
end{aligned}$$
$$begin{aligned}
_{12}C_0 &= frac{12!}{12! cdot 0!} \\
&= 1
end{aligned}$$
$$begin{aligned}
&= _{12}C_5 + _{12}C_4 +_{12}C_3+_{12}C_2+_{12}C_1+_{12}C_0 \
&= 792 + 495+220 +66+12+1 \
&= boxed{1586}\
end{aligned}$$
a. By plotting the points, we can see that the quadrilateral $GHIJ$ is a rhombus. It is a quadrilateral with equal opposite angles, and sides that are are congruent.
[](https://postimg.cc/Lqw8nDpP)
[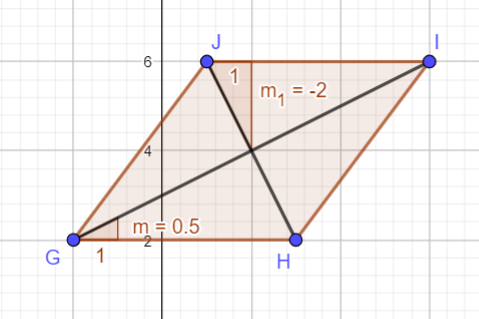](https://postimg.cc/kVWsD1r6)
$$begin{aligned}
frac{y-y_1}{x-x_1} &= frac{y_2-y_1}{x_2-x_1} \\
frac{y-2}{x+2} &= frac{6-2}{6+2} \\
frac{y-2}{x+2} &= frac{4}{8} \\
x+2 cdot frac{y-2}{x+2} &= frac{4}{8} cdot x+2\\
y-2 &= frac{4(x+2)}{8}\\
y-2 &= frac{4x+8}{8} \\
y &= frac{1}{2}x + 2\\
end{aligned}$$
$$begin{aligned}
frac{y-y_1}{x-x_1} &= frac{y_2-y_1}{x_2-x_1} \\
frac{y-2}{x-3} &= frac{6-2}{1-3} \\
frac{y-2}{x-3} &= frac{4}{-2} \\
x-3 cdot frac{y-2}{x-3} &= -2 cdot x-3\\
y-2 &= -2x+6\\
y &= -2x+8\\
end{aligned}$$
[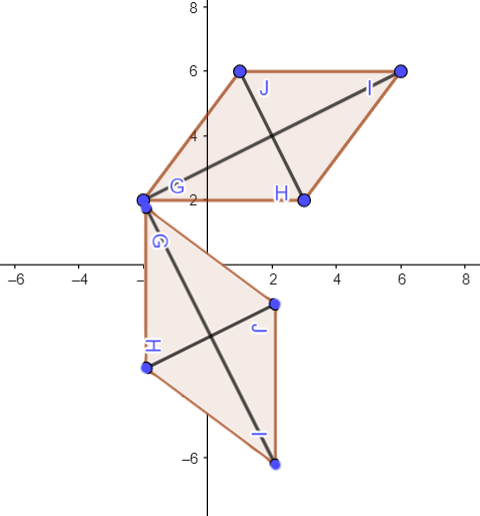](https://postimg.cc/zLg7VT2Q)
$$begin{aligned}
d_1 &= sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \
&= sqrt{(6+2)^2+(6-2)^2} \
&= sqrt{(8)^2+(4)^2} \
&= sqrt{64+16} \
&= sqrt{80} \
&= 8.94
end{aligned}$$
$$begin{aligned}
d_2 &= sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \
&= sqrt{(1-3)^2+(6-2)^2} \
&= sqrt{(-2)^2+(4)^2} \
&= sqrt{4+16} \
&= sqrt{20} \
&= 4.47
end{aligned}$$
$$begin{aligned}
A &= frac{p cdot q}{2} \
&= frac{8.94 cdot 4.47}{2} \
&=19.98 text{ units}^2 \
end{aligned}$$
Use the formulas for the perimeter and diagonal of a rectangle to set up a system of equations.
Label the sides of the rectangle with the variables $a$ and $b$.
The perimeter of the rectangle is determined by the formula $P=2a+2b$.
Label the diagonal of the rectangle with the variable $d$. The diagonal of a rectangle bisects it into two right triangles. The diagonal of the rectangle represents the hypotenuse of the right triangles. Use the Pythagorean Principle to determine the formula for the diagonal.
$$begin{aligned}
d^2&=a^2+b^2\
d&=sqrt{a^2+b^2}
end{aligned}$$
$$
left{
begin{array}{cc}
2a+2b=100 &&text{Equation 1}\
sqrt{a^2+b^2}=40 &&text{Equation 2}
end{array}
right.$$
Transform the system of equations by dividing the entire Equation $1$ by $2$ and squaring the entire Equation $2$.
$$begin{aligned}
a+b&=50 &&text{Equation 3}\
a^2+b^2&=1600&&text{Equation 4}
end{aligned}$$
Isolate the variable $b$ from Equation $3$.
$$begin{aligned}
a+b=50 rightarrow b= 50-a
end{aligned}$$
$$begin{aligned}
a^2+b^2&=1600\
a^2+(50-a)^2&=1600\
a^2+50^2-2cdot50a+a^2&=1600\
2a^2-100a+2500&=1600\
2a^2-100a+900&=0\
a^2-50a+450&=0
end{aligned}$$
Solve the quadratic equation using the Quadratic Formula.
$$begin{aligned}
a=1, b=-50, c=450
end{aligned}$$
$$begin{aligned}
a_{1,2}&= frac{-bpmsqrt{b^2-4ac}}{2a}\
&= frac{-(-50)pmsqrt{(-50)^2-4cdot1cdot450}}{2cdot1}\
&= frac{50pmsqrt{2500-1800}}{2}\
&= frac{50pmsqrt{700}}{2}\
&= frac{50pm10sqrt7}{2}\
a_1&=25+5sqrt7\
&approxboxed{38.23}\
a_2&=25-5sqrt7\
&approxboxed{11.77}
end{aligned}$$
$$begin{aligned}
b_1&=50-a_1\
&=50-38.23\
&approxboxed{11.77}\
\
b_2&=50-a_2\
&=50-11.77\
&approxboxed{38.23}\
end{aligned}$$
Conclude that the dimensions of the garden are $38.23times 11.77$ meters.
$$begin{aligned}
P&=2a+2b\
&=2cdot38.23+2cdot11.77\
&=76.46+23.54\
&=100
end{aligned}$$
Let,
$P$ – perimeter of the rectangle garden = $100$ meters
$d$ – diagonal of the rectangular garden = $40$ meters
$l$ – length of the rectangular garden
$w$ – width of the rectangular garden
$$begin{aligned}
P&=2l+2w\
d&=sqrt{l^2+w^2}
end{aligned}$$
$$begin{aligned}
P&=2l+2w\
100&=2l+2w
end{aligned}$$
$$begin{aligned}
100-2w&=2l+2w-(2w)\
100-2w&=2l\
end{aligned}$$
$$begin{aligned}
dfrac{100-2w}{2}&=dfrac{2l}{2}\
dfrac{100}{2}-dfrac{2w}{2}&=l\
50-w&=l
end{aligned}$$
$$begin{aligned}
d&=sqrt{l^2+w^2}\
40&=sqrt{(50-w)^2+w^2}\
(40)^2&=(50-w)^2+w^2\
1600&=w^2-100w+2500+w^2\
1600&=2w^2-100w+2500
end{aligned}$$
$$begin{aligned}
1600-(1600)&=2w^2-100w+2500-(1600)\
0&=2w^2-100w+900enspacetext{(standard form of quadratic equation)}
end{aligned}$$
$$begin{aligned}
w&=dfrac{-bpmsqrt{b^2-4ac}}{2a}
end{aligned}$$
where,
$a=2$
$b=-100$
$c=900$
$$begin{aligned}
w&=dfrac{-(-100)pmsqrt{(-100)^2-4(2)(900)}}{2(2)}\
w&=dfrac{100pmsqrt{10000-7200}}{4}\
w&=dfrac{100pmsqrt{2800}}{4}\
w&=dfrac{100pm52.915}{4}
end{aligned}$$
$$begin{aligned}
w&=dfrac{100+52.915}{4}\
w&=dfrac{152.915}{4}\
w&=38.229medspacetext{meters}
end{aligned}$$
$$begin{aligned}
w&=dfrac{100-52.915}{4}\
w&=dfrac{47.085}{4}\
w&=11.771medspacetext{meters}
end{aligned}$$
For $w=38.229$ meters.
$$begin{aligned}
50-w&=l\
50-38.229&=l\
11.771&=l
end{aligned}$$
$$begin{aligned}
50-w&=l\
50-11.771&=l\
38.229&=l
end{aligned}$$
$$begin{aligned}
l&=11.771medspacetext{meters}, w=38.229medspacetext{meters}\
l&=38.229medspacetext{meters}, w= 11.771medspacetext{meters}
end{aligned}$$
Solve for the volume of the bigger cone.
$$begin{aligned}
V_1 &= frac{pi r^2 h}{3}\
&= frac{pi (6)^2 5}{3} \
&= 188.50 text{ inches}^3
end{aligned}$$
where height became $3$ inches because Matt cut $2$ inches.
$$begin{aligned}
V_2 &= frac{pi r^2 h}{3}\
&= frac{pi (4)^2 2}{3} \
&= 33.51 text{ inches}^3
end{aligned}$$
V &= V_1 – V_2 \
&= 188.50 – 33.51\
&= boxed{154.99 text{ inches}^3} \
end{aligned}$$
Solve the perimeter of the sector.
$$begin{aligned}
P &= 6 text{ ft} + 6 text{ ft} + frac{30^circ}{360^circ} cdot(2pi cdot 6 text{ ft}) \\
&= 12 text{ ft} + frac{30^circ}{360^circ} cdot(12pi text{ ft}) \\
&= 12 text{ ft} + frac{360^circpi}{360^circ}text{ ft}\\
&= 12 + pi text{ ft}\
end{aligned}$$
a. The triangles are similar because their angles are congruent.
For $triangle ABC$:
$$begin{aligned}
180^circ &= 43^circ + 20^circ +x \
180 ^circ &= 63^circ +x \
180 ^circ -63^circ &= x \
117 ^circ &= x \
end{aligned}$$
$$begin{aligned}
180^circ &= 43^circ + 117^circ +x \
180 ^circ &= 160^circ +x \
180 ^circ -160^circ &= x \
20 ^circ &= x \
end{aligned}$$
Therefore, $triangle ABC$ ~ $triangle EDF$.
$$begin{aligned}
overline{AB} &= 13 times 1.8 = 23.4 = overline{KM}\
overline{BC} &= 10 times 1.8 =18= overline{KL} \
overline{AC} &= 5 times 1.8 =9 = overline{LM}\
end{aligned}$$
Therefore, $triangle ABC$ ~ $triangle KLM$.
Therefore, $triangle ABC$ is not similar to $triangle XYZ$.
a. Since the length is $9$ square units and the width is $8$ square units, the actual dimensions are:
$$begin{aligned}
l &= 9cdot 32 \
&= 288 text{ ft} \
\
w &= 8cdot 32 \
&= 256text{ ft} \
end{aligned}$$
$$begin{aligned}
A&= l cdot w \
&= 288text{ ft} cdot 256text{ ft}\
&= 73,728 text{ ft}^2
end{aligned}$$
$$begin{aligned}
A&= frac{bcdot h}{2} \
&= frac{74 text{ ft} cdot 74text{ ft}}{2} \
&= 2,738 text{ ft}^2
end{aligned}$$
$$begin{aligned}
A&= lcdot w\
&= 74 text{ ft} cdot 96text{ ft} \
&= 7,104 text{ ft}^2
end{aligned}$$
$$begin{aligned}
A&= lcdot w\
&= 128 text{ ft} cdot 32 text{ ft} \
&= 4,096 text{ ft}^2
end{aligned}$$
$$begin{aligned}
A&= frac{bcdot h}{2} \
&= frac{32 text{ ft} cdot 32text{ ft}}{2} \
&= 512 text{ ft}^2
end{aligned}$$
$$begin{aligned}
&= 73,728 – (2,738+7,104+4,096+512) \
&= 73,728 – 14450 \
&= 59,278 text{ ft}^2\
end{aligned}$$
a. Move the given graph $4$ units to the left.
[](https://postimg.cc/5YLhDbjk)
[](https://postimg.cc/rR9vFj11)

