All Solutions
Page 64: Closure Activity
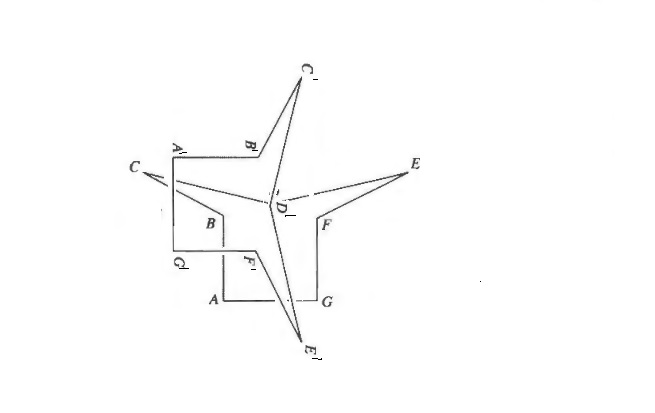
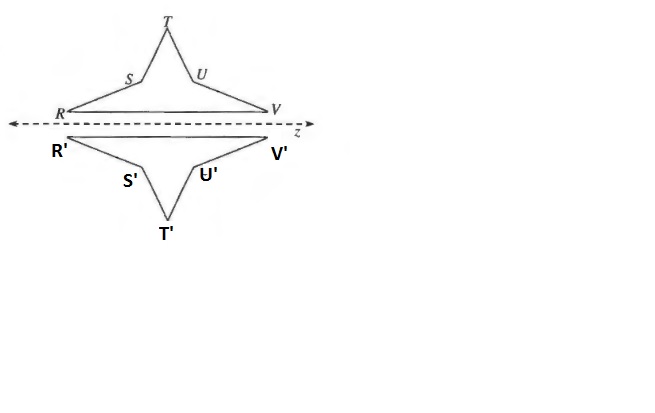
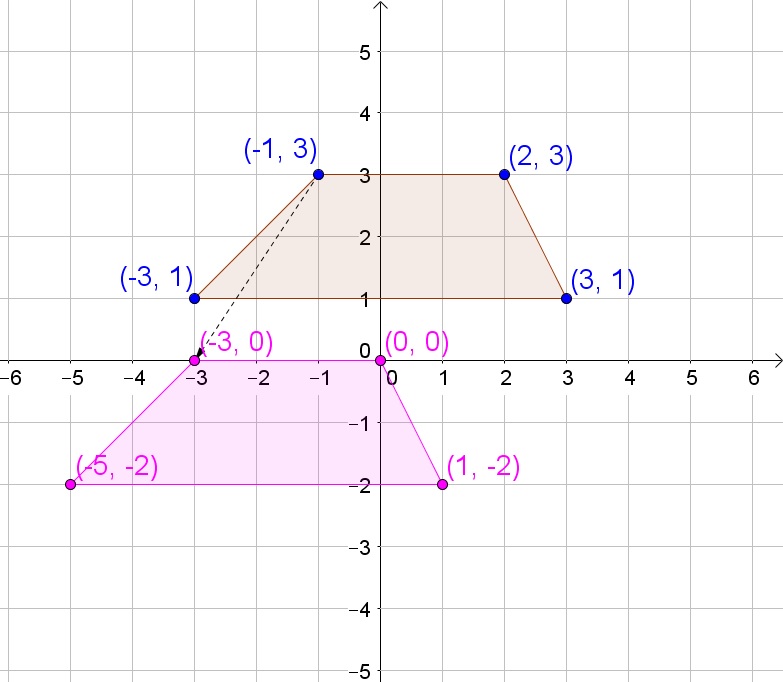
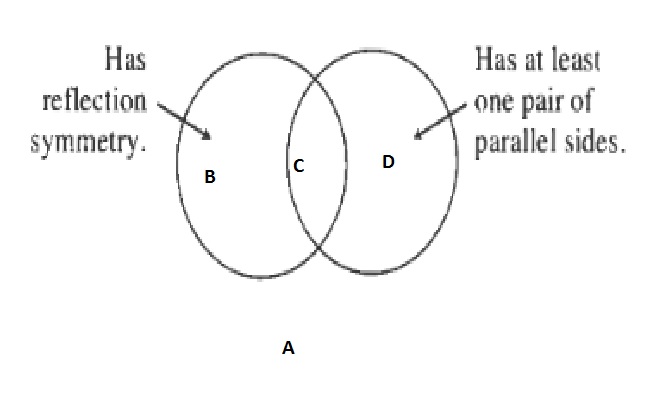
(B) The quadrilateral has two pairs of equal sides and thus is a kite.
(C) The quadrilateral has four right angles and two pairs of equal sides, thus the quadrilateral is a rectangle.
(D) The quadrailateral has one pair of parallel sides and thus is a trapezium.
$$
4x-3=2x+11
$$
Group like terms:
$$
4x-2x=11+3
$$
Simplify:
$$
2x=14
$$
Divide both sides of the equation by 2:
$$
x=7
$$
$$
3(4x-3)=3(4(7)-3)=3(28-3)=3(25)=75
$$
x=7
$$
Perimeter: 75
$$
x+15=102
$$
Subtract 15 from both sides of the equation:
$$
x=87
$$
b. Vertical angles:
$$
x+21=7x-3
$$
Group like terms:
$$
x-7x=-3-21
$$
Simplify:
$$
-6x=-24
$$
Diivde both sides of the equation by $-6$:
$$
x=4
$$
$$
3x+8+2x+2=180
$$
Combine like terms:
$$
5x+10=180
$$
Subtract 10 from both sides of the equation:
$$
5x=170
$$
Divide both sides of the equation by 5:
$$
x=34
$$
b. $x=4$
c. $x=34$
$$
sqrt[3]{dfrac{75 }{250}}=sqrt[3]{dfrac{3}{10}}approx 0.7
$$
An equation for this situation is then:
$$
f(x)=250(0.7)^x
$$
b. The monthly multiplier was about 0.7. The percent of decrease is then 100% decreased by the monthly multiplier:
$$
100%-0.7=100%-70%=30%
$$
b. 0.7; 30%
$$
(x+6)(3x-2)=3x^2+18x-2x-12=3x^2+16x-12
$$
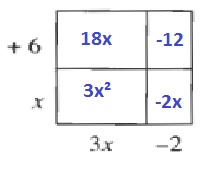
$$
(2y-7)(6y-4)=12y^2-42y-8y+28=12y^2-50y+28
$$
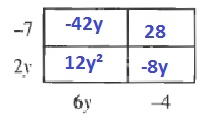
b. $(2y-7)(6y-4)=12y^2-50y+28$
c. See explanation
$$
3x+5+x+x-20=180text{textdegree}
$$
Combine like terms:
$$
5x-15=180text{textdegree}
$$
Add 15 to both sides of the equation:
$$
5x=195text{textdegree}
$$
Divide both sides of the equation by 15:
$$
x=39text{textdegree}
$$
Determine the measures of the other angles:
$$
mangle A=3x+5=3(39)+5=122text{textdegree}
$$
$$
mangle C=x-20=39-20=19text{textdegree}
$$
mangle A=122text{textdegree}
$$
$$
mangle B=39text{textdegree}
$$
$$
mangle C=19text{textdegree}
$$

