a. The exterior angle of a regular polygon is 360$text{textdegree}$ divided by the number of sides:

$$
x=dfrac{360text{textdegree}}{6}=60text{textdegree}
$$

b. The interior angle of a regular polygon with $n$ sides is $dfrac{n-2}{n}180text{textdegree}$:

$$
x=dfrac{n-2}{n}180text{textdegree}=dfrac{8-2}{8}180text{textdegree}=135text{textdegree}
$$

c. Note that the pentagon can contain exactly 10 congruent triangles (such as the given triangle):

$$
x=dfrac{360text{textdegree}}{10}=36text{textdegree}
$$

a. 60$text{textdegree}$

b. 135$text{textdegree}$

c. 36$text{textdegree}$

Determine the area of the base:

$$
B=2(1+sqrt{2})a^2=2(1+sqrt{2})0.8^2approx 3.09m^2
$$

The volume of the prism is the product of the area of the base and the height:

$$
V=3.09cdot 2=6.18m^3
$$

The surface area consists of 8 rectangles and the octagon base if the fish tank doesn’t contain a top, while the surface area contains two octagons instead of 1 if the fish tank does contain a top. The area of a rectangle is the product of the length and the width.

$$
begin{align*}
SA(text{no top})&=B+8lw=3.09+8cdot 0.8cdot 2=15.89text{ m}^2
\ SA(text{top})&=2B+8lw=2cdot 3.09+8cdot 0.8cdot 2=18.98text{ m}^2
end{align*}
$$

Volume: 6.18 m$^3$

Surface area (no top): 15.89 m$^2$

Surface area (top): 18.98 m$^2$

Since the diameter is 14, the radius is $frac{14}{2}=7$.

The area of a circle is the product of $pi$ and the squared radius. Determine the area of the base:

$$
B=dfrac{38text{textdegree}}{360text{textdegree}}pi r^2=dfrac{38text{textdegree}}{360text{textdegree}}pi 7^2=dfrac{931}{180}pi approx 16.25 in^3
$$

The volume of the prism is the product of the area of the base and the height:

$$
V=16.25cdot 6=97.50 in^3
$$

About 97.50 in$^3$

The base is a square, while the area of a square is the square of the side length of the square.

$$
B=s^2=6^2=36
$$

The height of a triangle is the hypotenuse of a right triangle with side lengths $frac{6}{2}=3$ (half the side length of a square) and 10 (height pyramid). Use the Pythagorean theorem:

$$
begin{align*}
text{Height triangle}&=sqrt{3^2+10^2}=sqrt{9+100}=sqrt{109}
end{align*}
$$

The surface area contains a square and four triangles. The area of a triangle is the length of the base (side length square) multiplied with the height, divided by 2.

$$
D=B+4cdot dfrac{6cdot sqrt{109}}{2}=36+12sqrt{109}approx 161units^2
$$

Determine the volume:

$$
V=dfrac{Bcdot h}{3}=dfrac{36cdot 10}{3}=120units^3
$$

Surface area 161 units$^2$

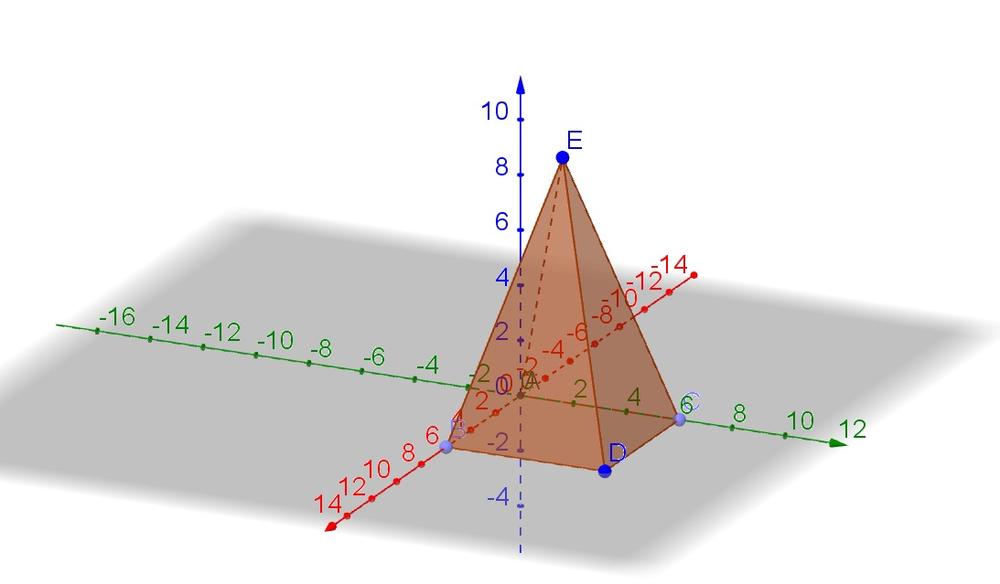
Volume 120 units

Determine the volume of the cone:

$$
V=dfrac{pi r^2 h}{3}=dfrac{pi 1.5^2 (6)}{3}=4.5pi
$$

Determine the volume of the cylinder with height $h$:

$$
V=pi r^2 h=pi 1.5^2h=2.25pi h
$$

The volumes should be equal:

$$
2.25pi h=4.5pi
$$

Divide both sides of the equation by $2.25pi$ :

$$
h=2 in
$$

a. Determine the diameter using the Pythagorean theorem:

$$
BD=sqrt{15^2-9^2}=sqrt{144}=12cm
$$

The radius is thus 6 cm and the area of the circle is then:

$$
A=pi r^2=pi 6^2=36pi approx 113cm^2
$$

b. The inscribed angle is half the measure of the arc it stands on:

$$
angle B=dfrac{1}{2}(30text{textdegree})=15text{textdegree}
$$

The sum of all angles in a triangle is 180$text{textdegree}$:

$$
mangle BDE=180text{textdegree}-15text{textdegree}-90text{textdegree}=75text{textdegree}
$$

The measure of the arc is twice the inscribed angle on the arc:

$$
moverarc{EB}=150text{textdegree}
$$

The tangent ratio is the opposite side divided by the adjacent rectangular side:

$$
AD=20tan{15text{textdegree}}approx 5.36cm
$$

c. The inscribed angle is half the measure of the arc it stands on:

$$
angle EDB=dfrac{1}{2}(86text{textdegree})=43text{textdegree}
$$

The sine ratio is the opposite side divided by the hypotenuse:

$$
EB=14sin{43text{textdegree}}approx 9.55
$$

a. $36pi approx 113$ cm$^2$

b. $moverarc{EB}=150text{textdegree}$, $AD=5.36$ cm

c. 9.55 cm

**Concept**
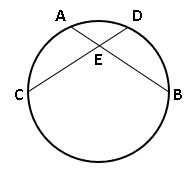
When there are two intersecting chords inside a circle, as shown in the figure:

[](https://postimg.cc/QVJQR05H)

The measures of the segment of each chord can be described by the equation:
$$begin{gather}
AE cdot EB = CE cdot ED
end{gather}$$

**Given**
We are given with the figure:
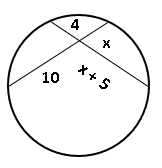[](https://postimg.cc/752fyZcm)

Determine the value of $x$

**Solution**
Using the concept for two intersecting chords, we obtain the relationship between the segments using Eq (1) as follows:
$$begin{aligned}
AE cdot EB &= CE cdot ED \
4 cdot (x+5) &= 10 cdot x \
4x + 20 &= 10x
end{aligned}$$

Using the expression from the relationship of the segments we obtain the value of $x$ as follows:
$$begin{aligned}
4x + 20 &= 10x \
20 &= 10x – 4x \
20 &= 6x \
x &= frac{20}{6} \
&= boxed{3.33}
end{aligned}$$

The value of $x$ in the circle with two intersecting chords is $3.33$

$x=3.33$

a. Substitute $y$ with $-3x+5$:

$$
(x-1)^2+(-3x+5)^2=4
$$

Rewrite:

$$
x^2-2x+1+9x^2-30x+25=4
$$

Subtract 4 from both sides of the equation:

$$
10x^2-32x+22=0
$$

Factorize:

$$
2(x-1)(5x-11)=0
$$

Zero product property:

$$
x-1=0text{ or }5x-11=0
$$

Solve each equation to $x$:

$$
x=1text{ or }5x=11
$$

$$
x=1text{ or }x=dfrac{11}{5}
$$

Next, determine the corresponding $y$-value to each $x$-value:

$$
begin{align*}
y&=-3x+5=-3(1)+5=
\ y&=-3x+5=-3cdot frac{11}{5}+5=-frac{33}{5}+frac{25}{5}=-frac{8}{5}
end{align*}
$$

Thus the graphs intersect at $(1,2)$ and $left(frac{11}{5}, -frac{8}{5}right)$.

b. Subtract the two equations:

$$
0=x^2-3x-10
$$

Factorize:

$$
(x-5)(x+2)=0
$$

Zero product property:

$$
x-5=0text{ or }x+2=0
$$

Solve each equation to $x$:

$$
x=5text{ or }x=-2
$$

Since we also have the equation $y=2$, the graphs intersect at $(5,2)$ and $(-2,2)$.

a. $(1,2)$ and $left(frac{11}{5}, -frac{8}{5}right)$

b. $(5,2)$ and $(-2,2)$

a. The ratio of the sides is:

$$
dfrac{8}{6}=dfrac{4}{3}
$$

b. The area is the product of the area of the similar figure and the ratio squared:

$$
A=27cdot left( dfrac{4}{3}right)^2=27cdot dfrac{16}{9}=48units^2
$$

c. The volume is the product of the volume of the similar figure and the ratio cubed:

$$
V=135cdot left( dfrac{4}{3}right)^3=135cdot dfrac{64}{27}=320units^3
$$

a. $frac{4}{3}$

b. 48 units$^2$

c. 320 units$^3$

b. An appropriate domain is for only non-negative heights and thus for $0leq xleq 7.2$.

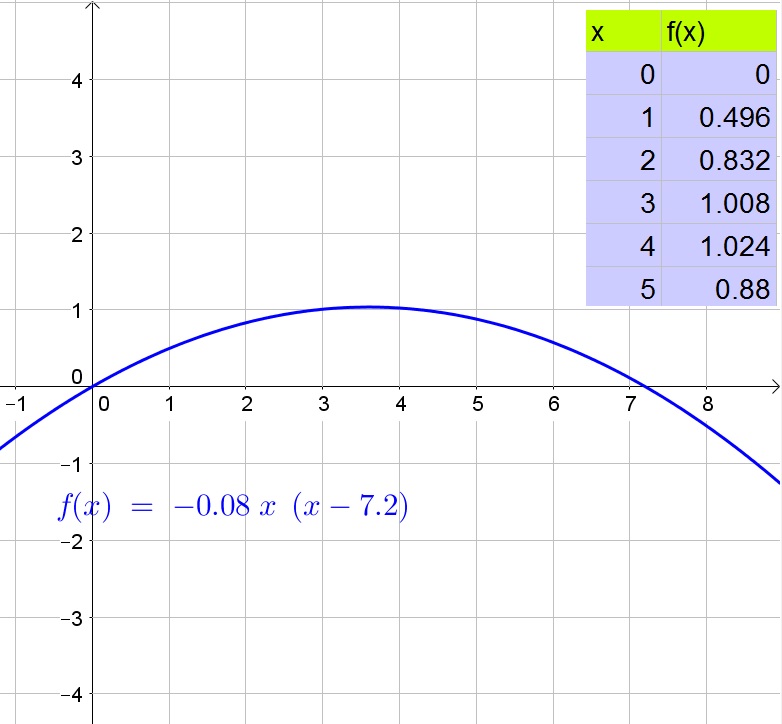
c. The $x$-intercepts are $x=0$ and $x=7.2$, while the $y$-intercepts is $y=0$. The vertex is $(3.6, f(3.6))=(3.6,1.0368)$.

Domain $0leq xleq 7.2$

$x$-intercepts: 0 and 7.2

$y$-intercept: $y=0$

Vertex $(3.6, 1.0368)$

a. The domain of a quadratic function contains all real values $mathbb{R}$. The line of symmetry is:

$$
x=-dfrac{b}{2a}=-dfrac{-2}{2(1)}=1
$$

Its image is then:

$$
f(1)=1^2-2(1)-8=1-2-8=-9
$$

The vertex is then $(1,-9)$ and since $a=1>0$ the vertex is then the minimum. The range is then also $[-9,+infty)$.

Determine the $x$-intercepts:

$$
0=x^2-2x-8
$$

Factorize:

$$
0=(x-4)(x+2)
$$

Zero product property:

$$
x-4=0text{ or }x+2=0
$$

Solve each equation to $x$:

$$
x=4text{ or }x=-2
$$

thus the $x$-intercepts are $x=4$ and $x=-2$.

Finally the $y$-intercept is $y=-8$.

Domain: $mathbb{R}$

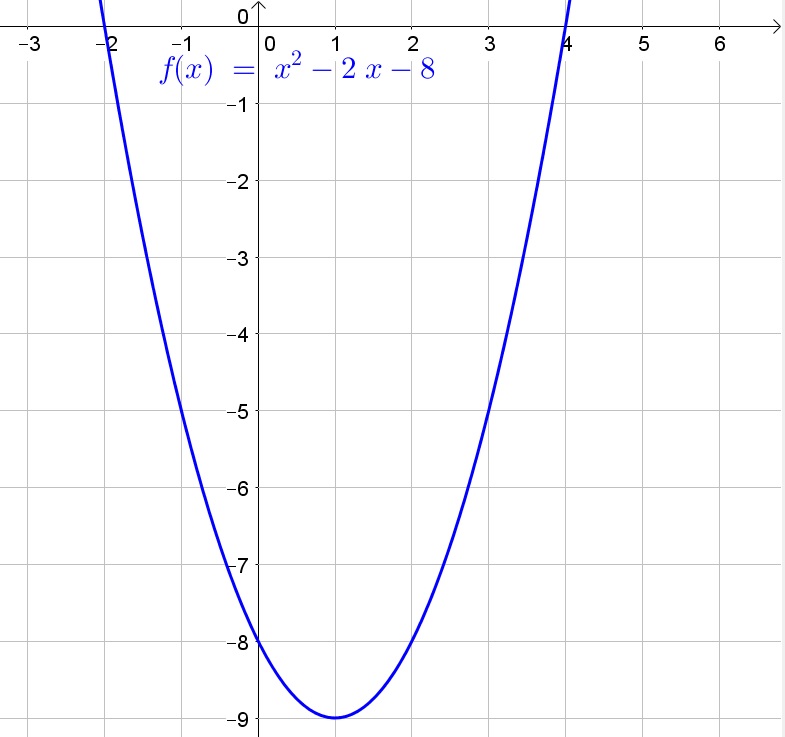
Range: $[9,+infty)$

$x$-intercepts: $-2$ and 4

$y$-intercepts: $-8$

Vertex $(1,-9)$