The surface area of the front surface is 6, the right surface is 8 and the upper surface is 12. Since there are 2 surfaces of each size:

$$
S=2(6)+2(8)+2(12)=52
$$

The volume is equal to the number of blocks in the figure and since each layer contains 12 blocks:

$$
V=2(12)=24
$$

a. Copy the prism from the textbook.

b. The surface area is the sum of the area of each surface:

$$
S=2cdot dfrac{3cdot 4}{2}+9cdot 4+9cdot 3+9cdot 5=120cm^2
$$

c. The volume of the triangular prism is the area of the base surface multiplied by the height:

$$
V=dfrac{3cdot 4}{2}cdot 9=54cm^3
$$

a. Copy the prism from the textbook.

b. 120 cm$^2$

c. 54 cm$^3$

Yes, we can use the same method.

Determine the area of the regular hexagon that is the base:

$$
A=dfrac{3sqrt{3}}{2}a^2=dfrac{3sqrt{3}}{2}(4)^2=6sqrt{3}in
$$

The surface area is the sum of the areas of each surface:

$$
S=2(6sqrt{3})+6(4cdot 7)=12sqrt{3}+168in^2
$$

The volume is the product of the area of the base and the height:

$$
V=6sqrt{3}cdot 7=42sqrt{3}in^3
$$

Surface area $12sqrt{3}+168$ in$^2$

Volume $42sqrt{3}$ in$^3$

Note that the mantel of the cylinder is a rectangle with length the circumference of the circle and width 8:

$$
A=2pi (5)cdot 8=80pi units^2
$$

The surface area is the sum of the areas of each surface:

$$
S=2(pi 5^2)+80pi=130pi units^2
$$

The volume is the product of the area of the base and the height:

$$
V=pi 5^2 cdot 8=200pi units^3
$$

Volume $200pi$ units$^3$

Surface area $130pi$ units$^2$

a. No, the volume will remain the same because the tower contains the same amount of pennies.

b. No, the volume would remain the same.

c. The volume of the cylinder is then the product of the area of the base and the height:

$$
V=pi 5^2cdot 8=200pi units^3
$$

a. No

b. No

c. 200$pi$ units$^3$

The volume of the cylinder is the product of the area of the base and the height:

$$
V=pi 1^2cdot 3=3pi ft^3approx 9.42ft^3
$$

Determine the number of gallons:

$$
dfrac{9.42}{0.1337}approx 70 gallons
$$

Thus we note that the tank can only contain 70 gallons and thus the tank will not provide enough water.

Determine the area of the regular hexagon that is the base:

$$
A=dfrac{3sqrt{3}}{2}a^2=dfrac{3sqrt{3}}{2}(14)^2=294sqrt{3}cm^2
$$

The volume is the product of the area of the base and the height:

$$
h=dfrac{V}{A}=dfrac{2546.13}{294sqrt{3}}approx 5cm
$$

The surface area is the sum of the areas of each surface:

$$
S=2(294sqrt{3})+6(14cdot 5)=588sqrt{3}+420cm^2
$$

Height 5 cm

Surface area $588sqrt{3}+420$cm$^2$

Since $overline{DE}$ is the midsegment:
$$
triangle ADEsim triangle ABC
$$

and the linear scale factor is $dfrac{1}{2}$.

The area of the smaller triangle is then the area of the larger triangle multiplied by the linear scale factor squared:

$$
A=96cdot dfrac{1}{2^2}=24units^2
$$

$$
24units^2
$$

The proportions of two intersecting chords are equal:

$$
dfrac{DE}{4}=dfrac{10}{16-10}
$$

Multiply both sides of the equation by $4$:

$$
DE=dfrac{10(4)}{6}=6dfrac{2}{3}
$$

The diameter is then:

$$
DC=DE+EC=6dfrac{2}{3}+4=10dfrac{2}{3}
$$

Since the radius is half the diameter:

$$
r=5dfrac{1}{3}
$$

$$
5dfrac{1}{3}
$$

a. Both have the same central angle $angle P$.

b. By dilating the circle(s) about $P$.

c. The arc length is
$$
dfrac{theta}{360text{textdegree}}(2pi r)=dfrac{60text{textdegree}}{360text{textdegree}}(2pi 14)=dfrac{14}{3}pi
$$

a. Both have the same central angle $angle P$.

b. By dilating the circle(s) about $P$.

c. $=dfrac{14}{3}pi$

$x^2+y^2=25$ is a circle with center $(0,0)$ and radius $5$.

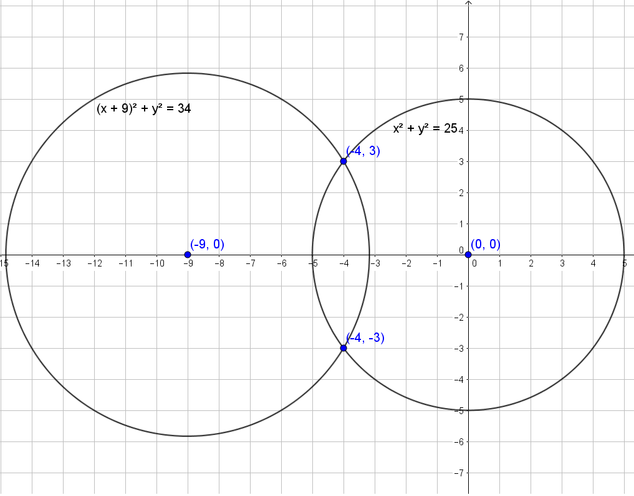
$(x+9)^2+y^2=34$ is a circle with center $(-9,0)$ and radius $sqrt{34}approx 5.831$

On the graph, we note that the intersection of the two graphs is
$$
(-4,pm 3)
$$

Subtract the two equations:

$$
(x+9)^2-x^2=34-25
$$

Simplify:

$$
18x+81=9
$$

Subtract 81 from both sides of the equation:

$$
18x=-72
$$

Divide both sides of the equation by 18:

$$
x=-4
$$

Determine $y$:

$$
y^2=25-x^2=25-(-4)^2=25-16=9
$$

Take the square root of both sides of the equation:

$$
y=pm 3
$$

Thus the solutions are $(-4, pm 3)$.

$$
(-4, pm 3)
$$

We note that the three dashed lines are the bisectors of the angles of the triangle and thus is $X$ lies in the center of the triangle. Thus $X$ is then the centroid of the triangle.

a. Rewrite 25 and 125 as a power of 5:

$$
5^4=(5^2)^2=25^2=125^{x+1}=(5^3)^{x+1}=5^{3(x+1)}
$$

The powers have to be equal:

$$
4=3(x+1)
$$

Divide both sides of the equation by 3:

$$
dfrac{4}{3}=x+1
$$

Subtract 1 from both sides of the equation:

$$
dfrac{1}{3}=x
$$

b. Given equation:
$$
dfrac{x}{5}+dfrac{x-1}{3}=2
$$

Multiply both sides of the equation by 15:

$$
3x+5(x-1)=30
$$

Use distributive property:

$$
3x+5x-5=30
$$

Add 5 to both sides of the equation:

$$
8x=35
$$

Divide both sides of the equation by 8:

$$
x=dfrac{35}{8}=4.375
$$

c. Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):

$$
(x-2)^2=25
$$

Take the square root of both sides of the equation:

$$
x-2=pm 5
$$

Add 2 to both sides of the equation:

$$
x=2pm 5=7text{ or }-3
$$

d. Rewrite 9 and $dfrac{1}{3}$ as a power of 3:

$$
3^{2x}=(3^2)^x=9^x=left( dfrac{1}{3}right)^{x+3}=(3^{-1})^{x+3}=3^{-(x+3)}
$$

The powers have to be equal:

$$
2x=-(x+3)
$$

Add $x$ to both sides of the equation:

$$
3x=-3
$$

Divide both sides of the equation by 3:

$$
x=-1
$$

a. $x=frac{1}{3}$

b. $x=frac{35}{8}$

c. $x=7$ and $x=-3$

d. $x=-1$

The isosceles triangle is made up of two right triangles, when you draw a line from the top of the ladder to the middle point of the bottom line. This triangle (colored in light blue in the figure) has then one rectangular side with length 2 (orange line in figure) and the hypotenuse with length 8.

The sine ratio is the opposite side of the angle divided by the hypotenuse:

$$
sin theta =dfrac{2}{8}=dfrac{1}{4}
$$

Solve to $theta$ using the $sin^{-1}$ command on your calculator:

$$
theta = sin^{-1}dfrac{1}{4}approx 14.48text{textdegree}
$$

The angle of the ladder is then double as big (see figure):

$$
2theta approx 28.96text{textdegree}approx 29text{textdegree}
$$

Or in radians: $0.5054$.

Degrees: 28.96$text{textdegree}$ or 29$text{textdegree}$

Radian: 0.0504

d. The volume is multiplied by the linear scale factor cubed. Thus if the linear scale factor is 10, the volume is increased by $10^3=1000$. If the linear scale factor is $r$, then the linear scale factor is $r^3$.

a. $4times 3times 2$

b. Graph

c. Ratio $1/R^3$

d. 1000, $r^3$

**A**

Build the solid using wooden boxes with the dimensions $1times1times1$.

**B**
If each of the dimensions of the solid is enlarged by the linear scale factor of $2$, then each dimension of the solid is doubled, resulting in a solid with the dimensions of $2times2times6$.

**C**
If you would build the solid from the part **B**, you would need $7$ more solids of the dimensions $1times1times3$. You need to add one solid on top of the existing solid, add two more solids laterally to the first two solids, and then add four more solids in front of the first two solids to make a solid with the dimensions of $2times2times6$.

**D**
If the solid of the dimensions $1times1times3$ would be enlarged by the linear scale factor of $3$, then the resulting solid would have a dimension of $3times3times9$. Its volume can be calculated using the formula $V=abc$.
$$begin{aligned}
V&=3cdot3cdot9\
V&=81
end{aligned}$$

If the volume of the initial solid is $3$, then the volume of the resulting solid is $27$ times larger.

The volume should be multiplied by the linear scale factor cubed:

$$
320cdot 1.5^3=1080
$$

Thus the medium tub should hold 1,080 kernels of popcorn.

Volumes of similar solids.

If the linear scale factor is 2, then the volume increases by $2^3=8$ times.

If the linear scale factor is $r$, then the volume increases by $r^3$ times.

If the linear scale factor is $r$, then the volume increases by $r^3$ times.

The linear scale factor is 2 (since the width needs to double) and thus the volume needs to increase $2^3=8$ times:

$$
2^3cdot 3=8cdot 3=24text{breaths}
$$

We thus require 24 breaths in total.

However, she already made 3 breaths and thus $24-3=21$ additional breaths are required.

a. Determine the area of the base:

$$
B=pi r^2=pi 6^2=36pi in^2
$$

The surface area is then the sum of all areas of the surfaces:

$$
S=2(36pi)+(2pi (6))(9)=72pi +108pi = 180pi in^2
$$

b. The volume of the cylinder is the product of the area of the base and the height:

$$
V=pi 6^2cdot 9=324pi in^3
$$

c. If the linear scale factor is 3, then the volume is multiplied by the scale factor cubed:

$$
V=3^3cdot 324pi = 8,748pi in^3
$$

The volume of the cylinder is the product of the area of the base and the height:

$$
V=pi 6^2cdot 9=324pi in^3
$$

We know that 12 in = 1 ft:

$$
V=dfrac{324pi}{12^3}=dfrac{3pi}{16}ft^3
$$

$$
dfrac{3pi}{16}ft^3
$$

a. The exterior angle and the interior angle are supplementary and thus the exterior angle is:

$$
180text{textdegree}-135text{textdegree}=45text{textdegree}
$$

The exterior angle is 360$text{textdegree}$ divided by the number of sides $n$ and thus:

$$
n=dfrac{360text{textdegree}}{45text{textdegree}}=8
$$

Thus the number of sides is 8.

b. The area of the base is:

$$
B=2(1+sqrt{2})a^2=2(1+sqrt{2})25^2=1250+1250sqrt{2}in^2
$$

The volume is then the area of the base multiplied by the height:

$$
V=(1250+1250sqrt{2})10=12500+12500sqrt{2}ft^3approx 30,178ft^3
$$

a. 8

b. 30,178 ft$^3$

a. Use the Pythagorean theorem:

$$
OX=sqrt{20^2-15^2}=sqrt{175}=5sqrt{7}
$$

The area of the circle is the product of $pi$ and the radius squared:

$$
A=pi (sqrt{175})^2=175pi cm^2
$$

b. The sine ratio is the opposite side divided by the hypotenuse:

$$
theta = sin^{-1}dfrac{15}{20}approx 49text{textdegree}
$$

The area of the circle sector is then:

$$
A=dfrac{theta}{360text{textdegree}}pi r^2=dfrac{49text{textdegree}}{360text{textdegree}}175pi approx 75cm^2
$$

c. The area of the region is the area of the rectangle decreased by the area of the circle sector:

$$
A=dfrac{5sqrt{7}cdot 15}{2}-75approx 24 cm^2
$$

a. 175$pi$ cm$^2$

b. 75 cm$^2$

d. 24 cm$^2$

Add and subtract 2.25:

$$
y=(x^2+3x+2.25)+4-2.25
$$

Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):

$$
y=(x+1.5)^2+1.75
$$

Let $y$ be zero:

$$
0=(x+1.5)^2+1.75
$$

Subtract 1.75 from both sides of the equation:

$$
-1.75=(x+1.5)^2
$$

Take the square root of both sides of the equation:

$$
pm 0.5sqrt{7}i=pm sqrt{-1.75}=x+1.5
$$

Subtract 1.5 from both sides of the equation:

$$
-1.5pm 0.5sqrt{7}i=x
$$

Thus we note that the solutions are complex, because the graph does not intersect the $x$-axis.

$$
x=-1.5pm 0.5sqrt{7}i
$$

Graph doesn’t intersect $x$-axis

a. A right triangle with a 45$text{textdegree}$ angle is an isosceles triangle and the hypotenuse is the length of the other two sides multiplied by $sqrt{2}$:

$$
P=7+7+7sqrt{2}=14+7sqrt{2}mmapprox 24mm
$$

b. Determine the missing sides using the Pythagorean theorem:

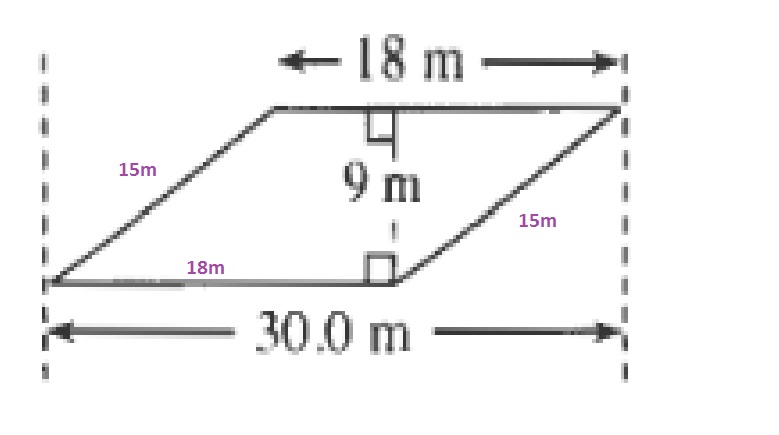
$$
P=18+15+18+15=66m
$$

c. Determine the missing lengths using the sine and cosine ratio in the rectangular triangle.

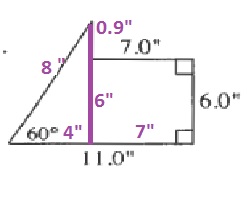
$$
P=8+11+6+7+0.9=32.9ft
$$

a. The vertex lies in the middle between the focus and the directrix and thus is
$$
(1,-3)
$$

b. Use the Pythagorean theorem:

$$
sqrt{(x-1)^2+(y+2)^2}
$$

c. The distance is the difference in $y$-values:

$$
y-4
$$

d.
$$
sqrt{(x-1)^2+(y+2)^2}=y+4
$$

Square both sides of the equation:

$$
(x-1)^2+(y+2)^2=y^2+8y+16
$$

Subtract $y^2$ from both sides of the equation:

$$
(x-1)^2+4y+4=8y+16
$$

Subtract $4y$ from both sides of the equation:

$$
(x-1)^2+4=4y+16
$$

Subtract 16 from both sides of the equation:

$$
(x-1)^2-12=4y
$$

Divide both sides of the equation by $4$:

$$
dfrac{1}{4}(x-1)^2-3=y
$$

Thus the equation of the parabola $y=dfrac{1}{4}(x-1)^2-3$.

a. $(1,-3)$

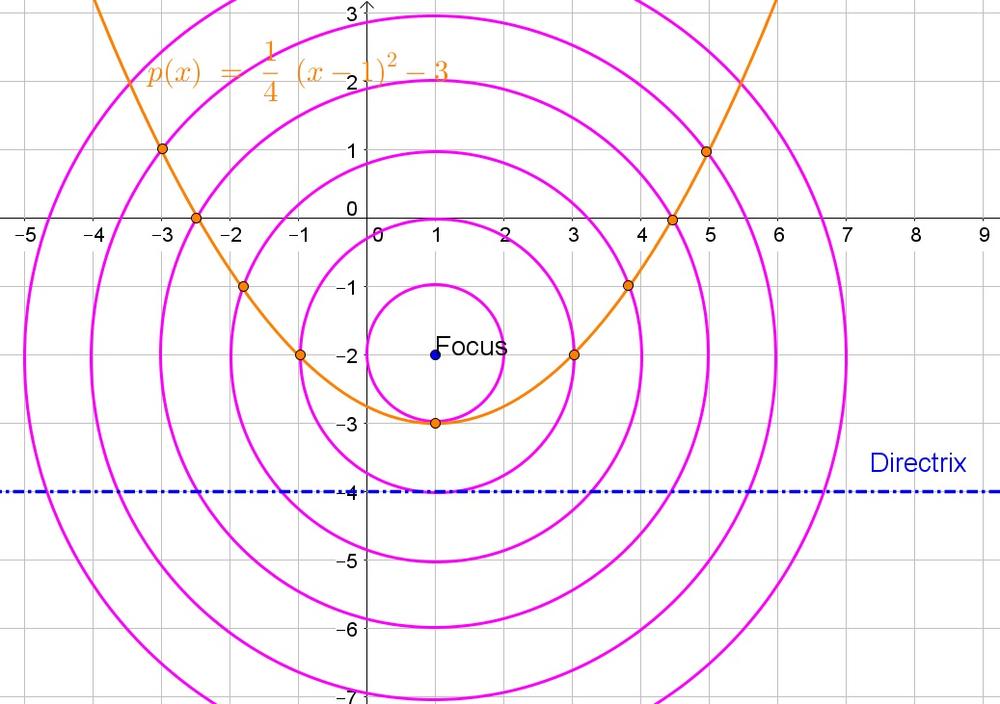
b. $sqrt{(x-1)^2+(y-2)^2}$

c. $y-4$

d. $y=frac{1}{4}(x-1)^2-3$

a. Since the surface area needs to be painted, the surface area of the life-sized statue is the surface area of the small statue multiplied by the scale factor (4) squared:

$$
1.5pintscdot 4^2=24pints=3gallons
$$

b. The weight is the volume and thus the weight is multiplied by the scale factor cubed:

$$
14pounds cdot 4^3=896pounds
$$

a. The storage capacity is the volume and thus the storage capacity is multiplied by the linear scale factor $dfrac{5}{4}$ cubed:

$$
V=20cdot 12,000cdot dfrac{5^3}{4^3}=468,750gallons
$$

Determine the difference in volume:

$$
Delta V=468,750-20cdot 12,000=228,750gallons
$$

b. We note that the jumbo tanks store less than 50% more and thus the standard tanks are better.

c.
$$
V=dfrac{12,000}{7.48}approx 1,604 ft^3
$$

d.
$$
V=dfrac{1,604}{3.28^3}approx 45m^3
$$

e. In (d) you needed to divide by the cubed factor and in (c) not, this is because the factor was given in feet and the units were given in cubic feet.

a. 228,750 gallons

b. Standard tanks

c. 1,604 ft$^3$

d. 45 m$^3$

e. Cubed factor

The volume is the product of the length, width and height (use that 1in=12ft):

$$
V=9.5cdot 12cdot dfrac{1}{3}=38ft^3
$$

Since 1 ft = 3 yards:

$$
V=dfrac{38}{3^3}=dfrac{38}{27}approx 1.4 text{yards}^3
$$

Her error was thus that she did not write the inches in feet to determine the volume.

a. We note that the width, depth and height have been multiplied by 2 and thus the linear scale factor is 2.

b. The surface area is the sum of the areas of the surfaces:

$$
S=3+1+4+2+2+4+4+4=24
$$

The surface area of the bigger solid is then the product of the surface area and the linear scale factor squared:

$$
S=24cdot 2^2=96
$$

The ratio of the surface areas is then the linear scale factor squared: 4.

c. The volume is the number of blocks in the solid:

$$
V=6
$$

The volume of the bigger solid is then the product of the volume and the linear scale factor cubed:

$$
S=6cdot 2^3=48
$$

The ratio of the volumes is then the linear scale factor cubed: 8.

a. 2

b. 24, 4, $2^2$

c. 6

The sum of the interior angles of a $n$-gon is
$$
(n-2)180text{textdegree}
$$

Thus if $n=1002$:

$$
(1002-2)180text{textdegree}=(1000)180text{textdegree}=180,000text{textdegree}
$$

180,000$text{textdegree}$

Determine the area of the base:

$$
B=dfrac{45text{textdegree}}{360text{textdegree}}(pi 2^2)=dfrac{pi}{2}ft^2
$$

The volume of the solid is then the product of the area of the base and the height:

$$
V=dfrac{pi}{2}cdot 4=2pi ft^3
$$

$$
2pi ft^3
$$

The proportions of intersecting chords are equal (Note: values in one fraction should corresponds with the values of the same chord!):

$$
dfrac{IG}{6}=dfrac{9}{8}
$$

Multiply both sides of the equation by 6:

$$
IG=dfrac{9cdot 6}{8}=6.75
$$

$$
6.75
$$

The equation of a circle with center $(x_1,y_1)$ and radius $r$ is of the form:

$$
(x-x_1)^2+(y-y_1)^2=r^2
$$

The given circle has center $(0,0)$ and radius $3$, thus the equation is:

$$
x^2+y^2=3^2
$$

a. Replace $x$ with 1 and $y$ with $sqrt{5}$:

$$
1^2+(sqrt{5})^2=1+5=6neq 9=3^2
$$

Thus the point does NOT lie on the circle.

b. Replace $y$ with $sqrt{5}$:

$$
x^2+5=x^2+(sqrt{5})^2=3^2=9
$$

Subtract 5 from both sides of the equation:

$$
x^2=4
$$

Take the square root of both sides of the equation:

$$
x=pm 2
$$

c. Given that the radius is 3, we know that $(3,0)$, $(-3,0)$ and $(0,-3)$ are also on the circle.

a. Disproven

b. $x=pm 2$

c. $(3,0)$, $(-3,0)$, $(0,-3)$

Since the volume of a cube is the length of its side cubed, the length of the side is the cubic root of the volume:

$$
s=sqrt[3]{27}=sqrt[3]{3^3}=3
$$

b. On the graph we note that the maximum height is 2 yd (since the vertex is $(1,2)$).

a. Let $x$ be the number of parcipants:

$$
f(x)=45x
$$

Since there cannot be a nonnegative number of participants, the domain contains only the nonnegative integers:
$$
mathbb{N}
$$

b. The profit is the revenue decreased by the cost:

$$
p(x)=45x-1200
$$

Let $p(x)$ be zero:

$$
0=45x-1200
$$

Add 1200 to both sides of the equation:

$$
1200=45x
$$

Divide both sides of the equation by 45:

$$
27approx x
$$

Thus Jamie makes a profit if she has at least 27 participants per month.

a. $f(x)=45x$, $mathbb{N}$

b. 27 participants

Determine the volumes:

$$
V_A=dfrac{5cdot 6}{2}cdot 6=90in^3
$$

$$
V_B=dfrac{1}{3}dfrac{3sqrt{3}}{2}cdot 4^2cdot 6=48sqrt{3}approx 83in^3
$$

Determine the base areas:

$$
B_A=6cdot 6=36in^2
$$

$$
B_B=dfrac{3sqrt{3}}{2}cdot 4^2=24sqrt{3}approx 42in^2
$$

Determine the surface area:

$$
S_A=36+2cdot dfrac{5cdot 6}{2}+2cdot sqrt{34}cdot 6=66+12sqrt{34}approx 136in^2
$$

$$
S_B=24sqrt{3}+6cdot dfrac{4sqrt{52}}{2}approx 128in^2
$$

The volume of the first tent is bigger, thus you should buy this tent.

Determine the slant height:

$$
sqrt{96^2+220^2}=sqrt{57,616}approx 240
$$

The area of one of its upstanding surface is then:

$$
S=dfrac{240cdot 96}{2}=11,520 m^2
$$

The total surface area (without the base) is then:

$$
4S=4(11,520 )=46,080 m^2
$$

The number of gallons needed is then:

$$
dfrac{46,080 }{250}=184.32approx 184
$$

Thus about 184 gallons are needed.

a. The volume of the prism is the product of the width, length and height:

$$
V=7cdot 13cdot 12=1,092in^3approx 0.632 ft^3
$$

b. Determine the number of gallons:

$$
0.632cdot 7.48=4.727gallons
$$

a. 1,092 in$^3$

b. 4.727 gallons

Determine the ratio of the volumes:

$$
dfrac{500pi}{4pi}=125
$$

The ratio of the heights is the cubic root of the ratio of the volumes:

$$
sqrt[3]{125}=sqrt[3]{5^3}=5
$$

a. The central angle is equal to the measure of the arc and the total circle is 360$text{textdegree}$:

$$
mangle C=moverarc{PQ}=360text{textdegree}-314text{textdegree}=46text{textdegree}
$$

The tangent ratio is the opposite side divided by the adjacent rectangular side:

$$
CP=dfrac{5}{tan{46text{textdegree}}}=4.83
$$

The sine ratio is the opposite side divided by the hypotenuse:

$$
CR=dfrac{5}{sin{46text{textdegree}}}approx 6.95
$$

Then we obtain:

$$
x=CR-CQ=CR-CP=6.95-4.83=2.12
$$

b. The sine ratio is the opposite side divided by the hypotenuse:

$$
dfrac{x}{2}=7sin{102text{textdegree}}approx 6.85
$$

Multiply both sides of the equation by 2:

$$
xapprox 13.7
$$

a. $x=2.12$

b. $x=13.7$

a. On the graph we note that $(1,-3)$ is a point and thus $f(1)=-3$.

b. On the graph we note that $(0,-4)$ is a point and thus $f(0)=-4$.

c. On the graph we note that $(-3.8,4)$ and $(2.8,4)$ are points and thus $x=-3.8$ and $x=2.8$.

d. On the graph we note that $(-2,0)$ and $(2,0)$ are points and thus $x=-2$ and $x=2$.

a. $-3$

b. $-4$

c. $x=-3.8$ and $x=2.8$

d. $x=-2$ and $x=2$

b. The equation of a line through two points $(x_1,y_1)$ and $(x_2, y_2)$ is
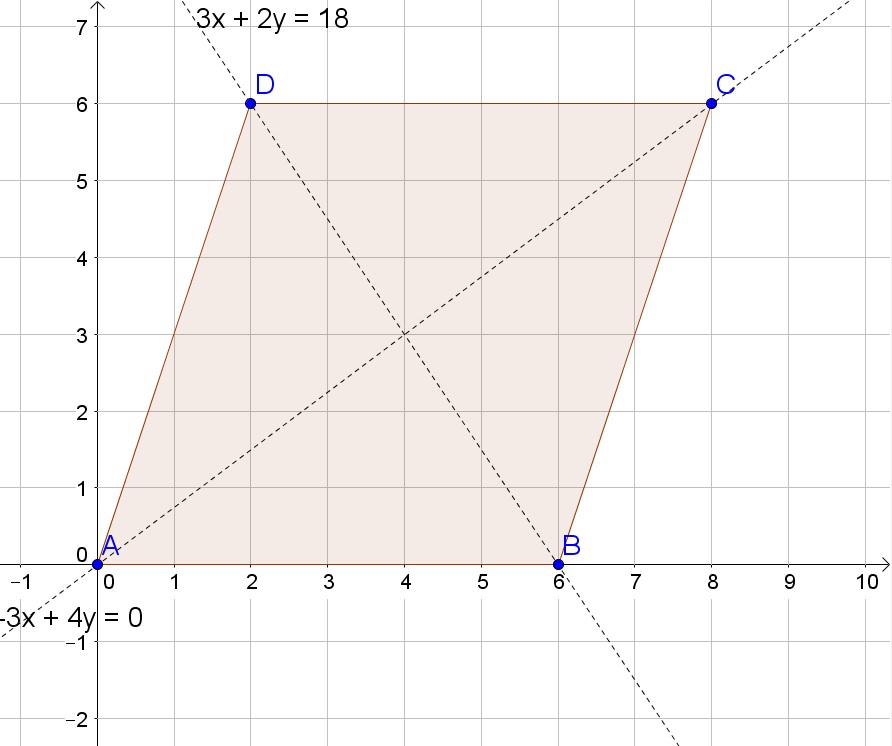
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$

Thus we then obtain for the line $overline{AC}$:

$$
y=dfrac{4}{3}x
$$

and for line $overline{BD}$:

$$
y=-dfrac{3}{2}(x-6)
$$

a. Parallelogram

b. $y=frac{4}{3}x$, $y=-frac{3}{2}(x-6)$.

a. Add 1500 to both sides of the equation:

$$
300x=3900
$$

Divide both sides of the equation by 300:

$$
x=13
$$

b. Multiply both sides of the equation by 12:

$$
18x=10x+24
$$

Subtract $10x$ from both sides of the equation:

$$
8x=24
$$

Divide both sides of the equation by 8:

$$
x=3
$$

c. Factorize:

$$
(x-5)(x+5)leq 0
$$

Since the function $y=(x-5)(x+5)$ opens upwards:

$$
-5leq x leq 5
$$

d. Rewrite as two inequalities:

$$
3x-24
$$

Add 2 to both sides of the equation:

$$
3×6
$$

Divide both sides of the equation by 3:

$$
x2
$$

a. $x=13$

b. $x=3$

c. $-5leq xleq 5$

d. $x2$

a. Multiply both sides of the equation by 3:

$$
3V=pi r^2 h
$$

Divide both sides of the equation by $pi r^2$:

$$
dfrac{3V}{pi r^2}=h
$$

Interchange left and right sides of the equation:

$$
h=dfrac{3V}{pi r^2}
$$

Multiply both sides of the equation by 2:

$$
2K=mv^2
$$

Divide both sides of the equation by $m$:

$$
dfrac{2K}{m}=v^2
$$

Take the square root of both sides of the equation (and note that a negative velocity is impossible):

$$
sqrt{dfrac{2K}{m}}=v
$$

Interchange left and right sides of the equation:

$$
v=sqrt{dfrac{2K}{m}}
$$

a. $h=frac{3V}{pi r^2}$

b. $v=sqrt{frac{2K}{m}}$

Determine the area of the base:

$$
B=6^2=36units^2
$$

The volume of the pyramid is the product of the area of the base and the height divided by 3:

$$
V=dfrac{36cdot 4}{3}=48units^3
$$

Determine the slant height using the Pythagorean theorem:

$$
s=sqrt{3^2+4^2}=sqrt{25}=5units
$$

Determine the area of the triangle:

$$
A=dfrac{6cdot 5}{2}=15units^2
$$

Determine the surface area:

$$
S=B+4A=36+4(15)=96units^2
$$

Volume 48 units$^3$

Surface area 96 units$^2$

Since the perimeter is the sum of the lengths of all sides, we then know that each side is 1 unit long. Divide the polygon into 100 congruent triangles. Determine the height of these triangles using the tangent ratio:

$$
h=0.5sin{88.2text{textdegree}}approx 0.5
$$

The area of a triangles is the product of the base and the height divided by 2:

$$
dfrac{1cdot 0.5}{2}=0.25
$$

Since the polygon is made up out of 100 triangles, the area of the polygon is:

$$
100cdot 0.25=25units^2
$$

$$
25units^2
$$

The volume of the enlarged solid is the product of the volume of the original solid and the factor cubed:

$$
Vcdot 9^3=729V
$$

Determine the area of the base:

$$
B=pi 3^2=9pi ft^2
$$

The volume of the cylinder is the product of the area of the base and the height:

$$
V=9pi cdot 4=36pi ft^3approx 113ft^3
$$

$$
36pi ft^3
$$

a. The inscribed angle on an arc is half the measure of the arc:

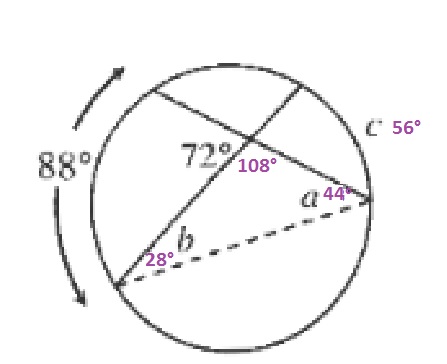
$$
a=dfrac{88text{textdegree}}{2}=44text{textdegree}
$$

The exterior angle is equal to the sum of the angles of the triangle with the exception of the corresponding interior angle:

$$
b=72text{textdegree}-44text{textdegree}=28text{textdegree}
$$

The meausre of the arc is twice the measure ofthe inscribed angle:

$$
c=2(28text{textdegree})=56text{textdegree}
$$

a. $a=44text{textdegree}$, $b=28text{textdegree}$, $c=56text{textdegree}$

b. No

d.
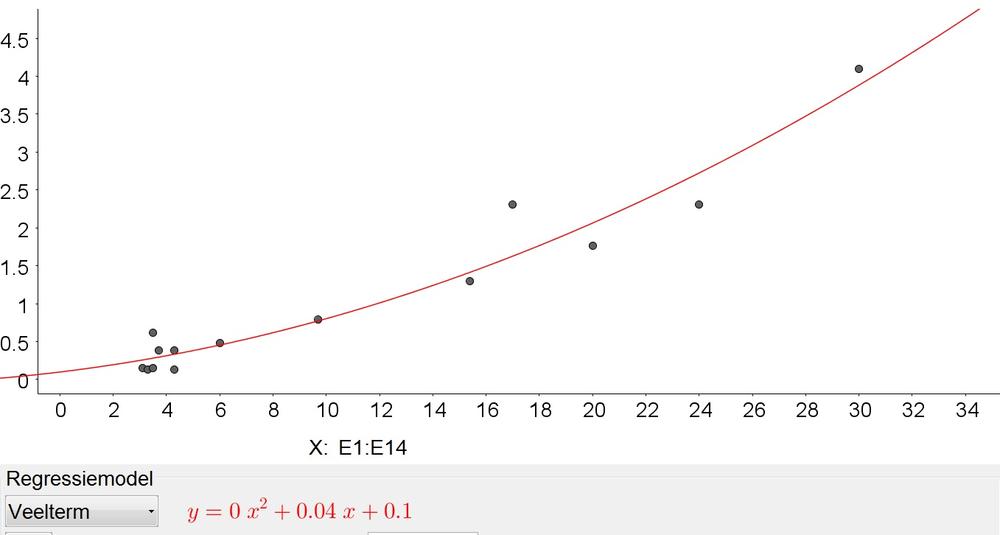
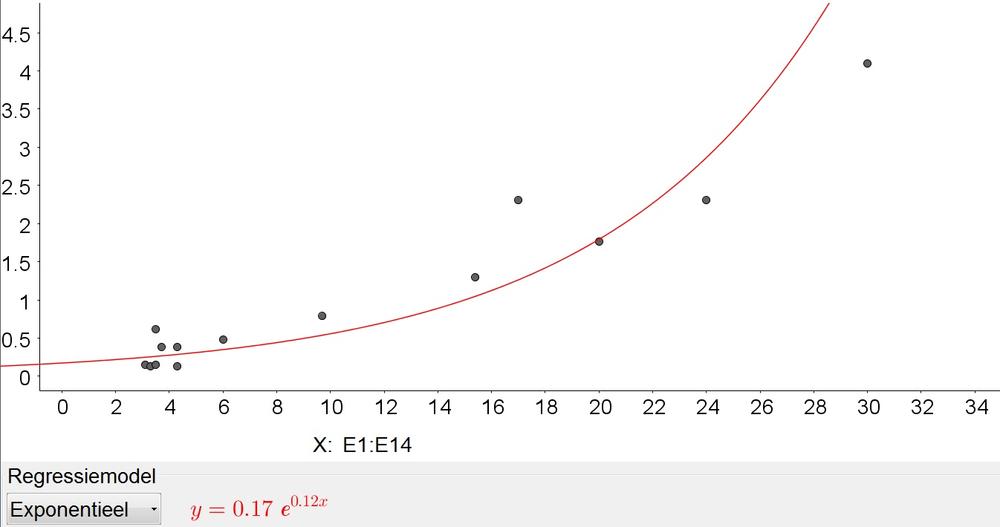
$$
2,100,000=0.00279x^2+0.04x+0.1Rightarrow xapprox 27,428in
$$

$$
2,100,000=0.17e^{0.12x}Rightarrow xapprox 136in
$$

We note that the exponential model gives a more reaqonable diagonal.

e. The area of the screen, because it will represent the pixels better than the diagonal.

a. Scatterplot

b. Quadratic

c. $y=0.00729x^2+0.04x+0.1$, $y=0.17e^{0.12x}$

d. 2,428 in, 136 in

e. Area of the screen

Subtract the two equations:

$$
0=(x+2)^2-1-dfrac{1}{2}x-2
$$

Simplify:

$$
0=x^2+dfrac{7}{2}x+1
$$

Multiply both sides of the equation by 2:

$$
0=2x^2+7x+2
$$

Determine the roots using the quadratic formula:

$$
x=dfrac{-7pm sqrt{7^2-4(2)(2)}}{2(2)}=-dfrac{7}{4}pm dfrac{sqrt{33}}{4}
$$

Determine $y$:

$$
y=dfrac{1}{2}x+2=-dfrac{7}{8}pm dfrac{sqrt{33}}{8}+2=dfrac{9}{8}pm dfrac{sqrt{33}}{8}
$$

Thus the solutions are $left( -dfrac{7}{4}pm dfrac{sqrt{33}}{4}, dfrac{9}{8}pm dfrac{sqrt{33}}{8}right)$

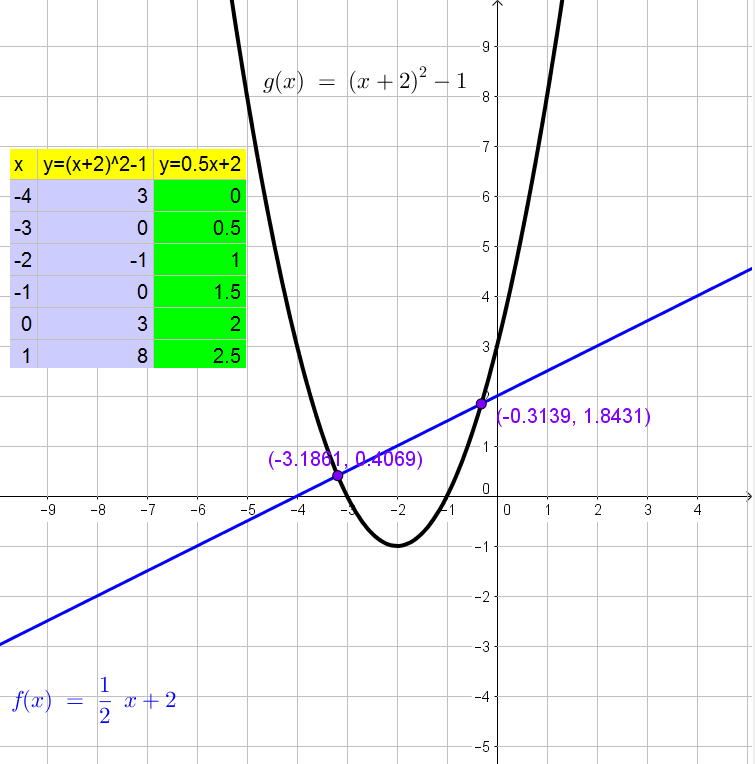
$$
left( -dfrac{7}{4}pm dfrac{sqrt{33}}{4}, dfrac{9}{8}pm dfrac{sqrt{33}}{8}right)
$$

b. The domain only makes sense if the height is nonnegative:

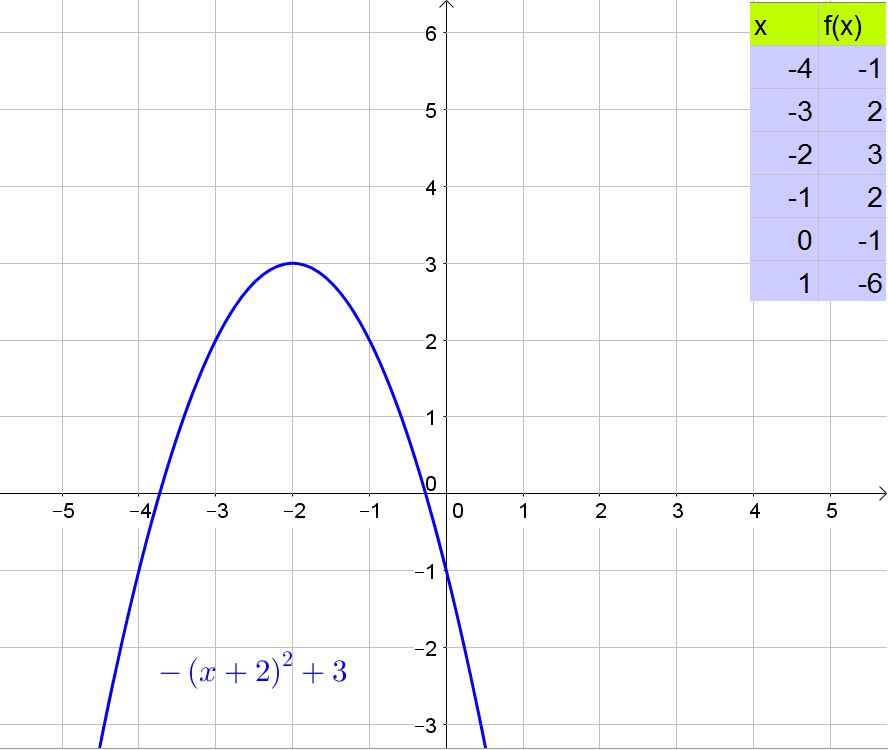
$$
0=-(x+2)^2+3
$$

Add $(x+2)^2$ to both sides of the equation:

$$
(x+2)^2=3
$$

Take the square root of both sides of the equation:

$$
x+2=pm sqrt{3}
$$

Subtract 2 from both sides of the equation:

$$
x=-2pm sqrt{3}
$$

Thus the domain should be $[-2-sqrt{3},-2+ sqrt{3}]$.

d. The balloon is launched at $x=-2+sqrt{3}$, lands at $x=-2-sqrt{3}$ and reaches its maximum height of 3 at $x=-2$.

a. Graph

b. $[-2-sqrt{3}, -2+sqrt{3}]$

c. 3

d. Balloon is launched at $x=-2+sqrt{3}$, lands at $-2-sqrt{3}$, and reaches its maximum height of 3 at $x=-2$.

The volume of a pyramid is the product of the area of the base and the height divided by 3:

a.
$$
V=dfrac{14cdot 6 cdot 19}{3}=532
$$

b.
$$
V=dfrac{dfrac{3sqrt{3}}{2} 10^2cdot 36}{3}=1800sqrt{3}approx 3,118
$$

c.
$$
V=dfrac{dfrac{9cdot 4}{2} cdot 13}{3}=78
$$

a. The volume of the cone is one third of the volume of a cylinder.

b.
$$
V=dfrac{Bcdot h}{3}=dfrac{pi r^2 h}{3}
$$

c. Replace $r$ with 8 (radius is half the diameter of 16) and $h$ with 12:

$$
V=dfrac{pi 8^2 (12)}{3}=256pi approx 804mm^3
$$

a. The volume of the cone is one third of the volume of a cylinder.

b. $dfrac{pi r^2 h}{3}$

c. $804mm^3$

We thus need to determine the lateral surface area of a cone, which is a circle sector with radius the slant height $l$ of the pyramid. The area is then:

$$
A_L=dfrac{2pi r}{2pi l}pi l^2=pi r l = pi rsqrt{r^2+h^2}
$$

$$
A_l=pi rsqrt{r^2+h^2}
$$

The volume of the cone is one third of the volume of a cylinder.

$$
V=dfrac{pi 2^2 sqrt{6^2-2^2}}{3}=dfrac{16pi sqrt{2}}{3} approx 7.5in^3
$$

The lateral surface area of a cone is:

$$
A_L=pi r l=pi (2)(6)=12pi approx 38in^2
$$

Volume 7.5 in$^3$

Lateral surface area 38 in$^2$

The volume of a cone is
$$
V=dfrac{Bcdot h}{3}=dfrac{pi r^2h}{3}
$$

The lateral surface area of a cone is:

$$
A_L=pi rl = pi rsqrt{r^2+h^2}
$$

and the surface area of the cone is then the sum of the lateral surface area increased by the area of the base.

Volume $frac{pi r^2h}{3}$, lateral surface area $pi rsqrt{r^2+h^2}$

a. The volume is hte product of the area of the base and the height:

$$
V=dfrac{7cdot 24}{2}cdot 12=1008in^3
$$

Note that the 24 is the length of the missing side (height of the triangle and 7,24,25 is a Pythagorean triple).

Determine the surface area:

$$
S=2cdot dfrac{7cdot 24}{2}+7cdot 12+24cdot 12+25cdot 12=840in^2
$$

b. The volume is the product of the area of the base and the height, divided by 3:

$$
V=dfrac{pi 5^2cdot 12}{3}=100piapprox 314m^3
$$

Determine the surface area:

$$
S=pi r sqrt{r^2+h^2}+pi r^2
$$

$$
=pi (5)sqrt{12^2+5^2}+pi 5^2=65pi+25pi=90piapprox 283 m^2
$$

a. Volume 1008 in$^3$, Surface area 840 in$^2$

b. Volume 314 m$^3$, Surface area 283 m$^2$

a. Determine the volume of the cylinder:

$$
V=pi r^2 h=pi 1.5^2 (7)=15.75pi approx 49cm^3
$$

Determine the volume of the missing cylinder:

$$
V=pi r^2 h=pi 0.5^2 (7)=1.75pi approx 5.8cm^3
$$

Determine the difference in volumes that obtain the volume of the cylinder with the hole:

$$
V=15.75pi-1.75pi=14piapprox 44cm^3
$$

b. Determine the area of the base:

$$
B=2(1+sqrt{2})a^2=2(1+sqrt{2})2^2approx 19ft^2
$$

Determine the volume of the prism:

$$
V=Bcdot h=19cdot 7=133ft^3
$$

a. 44 cm$^3$

b. 133 ft$^3$

a. The volume of a cube is the length of its side cubed:

$$
V=12^3=1728in^3
$$

The surface area contains 6 squares:

$$
S=6A=6(12^2)=864in^2
$$

b. Since 12 inches = 1 foot. The volume of a cube is the length of its side cubed:

$$
V=1^3=1ft^3
$$

The surface area contains 6 squares:

$$
S=6A=6(1^2)=6ft^2
$$

a. Volume 1728 in$^3$, Surface area 864 in$^2$

b. Volume 1 ft$^3$, Surface area 6ft$^2$

The volume of a pyramid is the product of the area of the base and the height divided by 3:

$$
108=dfrac{27h}{3}
$$

Simplify:

$$
108=9h
$$

Divide both sides of the equation by 9:

$$
12=h
$$

Thus the height is 12 inches.

The inscribed angle on an arc is half the measure of the arc:

$$
b=dfrac{21text{textdegree}}{2}=10.5text{textdegree}
$$

The exterior angle is equal to the sum of the angles of the triangle with the exception of the corresponding interior angle:

$$
a=62text{textdegree}-10.5text{textdegree}=51.5text{textdegree}
$$

The measure of the arc is twice the measure of the inscribed angle:

$$
x=c=2(51.5text{textdegree})=103text{textdegree}
$$

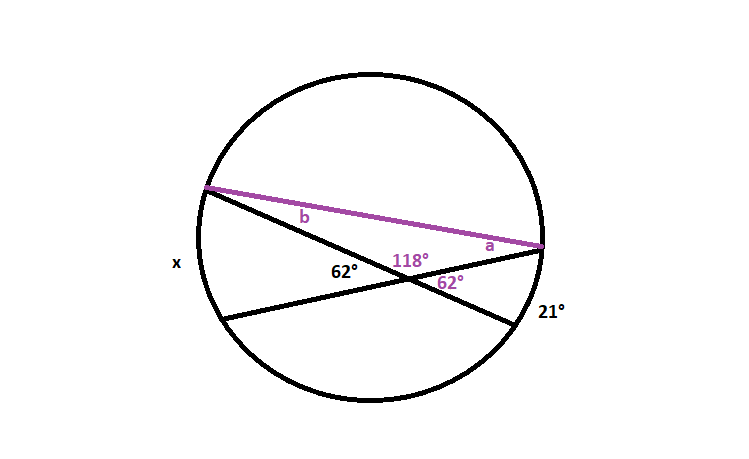
$$
x=103text{textdegree}
$$

a. Substitute $y$ with $-x$ in the second equation:

$$
x^2+(-x)^2=8
$$

Simplify:

$$
2x^2=8
$$

Divide both sides of the equation by 2:

$$
x^2=4
$$

Take the square root of both sides of the equation:

$$
x=pm 2
$$

Determine $y$:

$$
y=-x=-(pm 2)=mp 2
$$

Thus the solutions are $(pm 2, mp 2)$.

b. The intersections of the graphs are indeed $(pm 2, mp 2)$.

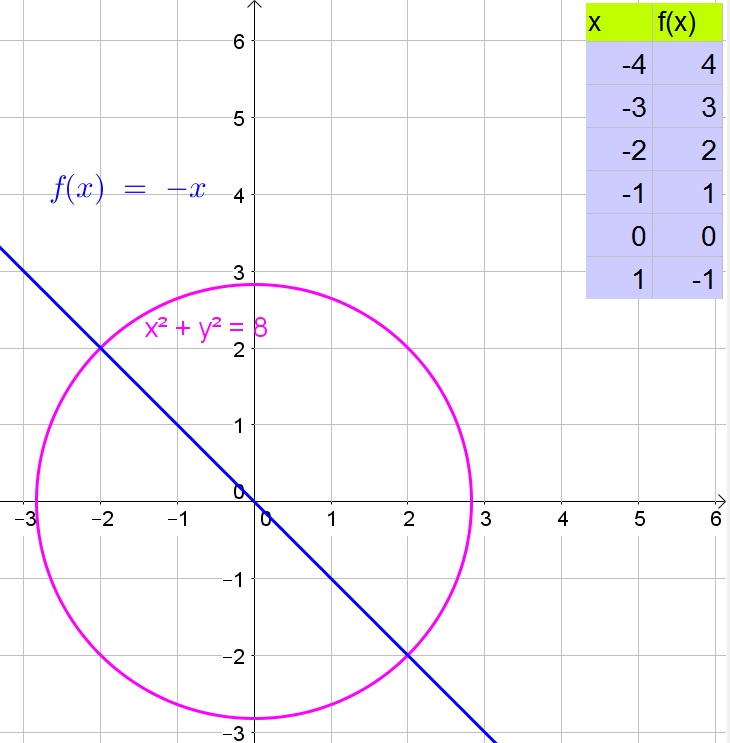
$$
(pm 2, mp 2)
$$

$$
angle Dcong angle F (text{both are 90text{textdegree} because of tangent lines})
$$

$$
DE=EF(text{ both are the radius of the circle})
$$

$$
EA=EA(text{Shared side})
$$

$$
Downarrow text{Pythagorean theorem}
$$

$$
AD=sqrt{EA^2+DE^2}=sqrt{EA^2+EF^2}=AF
$$

a. The multiplier you need to use is 100% increased by 5% and thus is:

$$
100%+5%=105%=1.05
$$

b. Thus we need to value of the house 6 years ago:

$$
175,000(1.05)^{-6}approx $130,588
$$

c. $a$ is the initial value and thus is $130,588$ and $b$ is the multiplier:

$$
f(t)=130,588(1.05)^t
$$

a. 1.05

b. $$130,588$

c. $133,588(1.05)^t$

b. If the radius is $r$, then the height is $2r$.

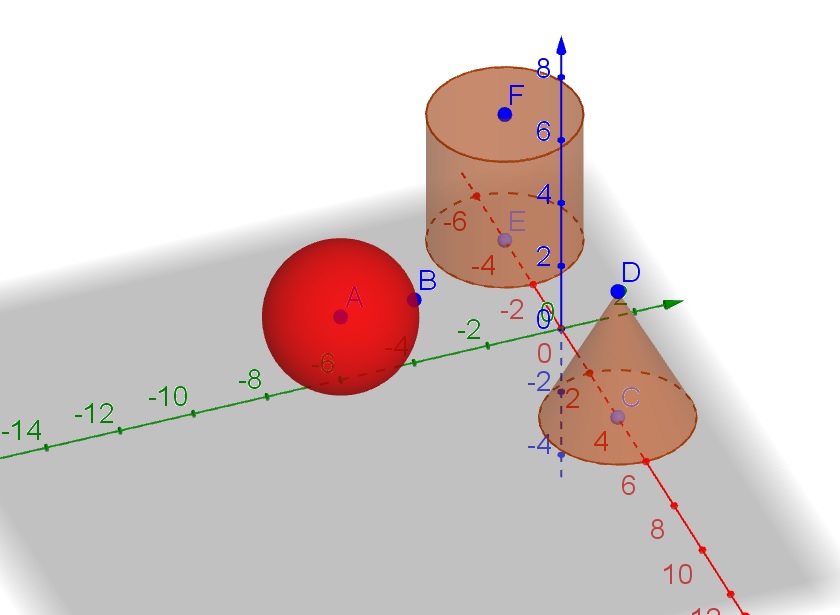
c. Let $V$ be the volume of the sphere:

$$
V=V_{cilinder}-V_{cone}=pi r^2 (2r)-dfrac{pi r^2 (2r)}{3}=dfrac{2pi r^2(2r)}{3}=dfrac{4pi r^3}{3}
$$

Height $2r$

$$
V=frac{4pi r^3}{3}
$$

The surface area of the sphere is equal to the surface area of the cylinder (with $h=2r$):

$$
S=S_L :_{cilinder}=2pi r h=2pi r (2r)=4pi r^2
$$

$$
4pi r^2
$$

Determine the surface area of Earth:

$$
S=4pi r^2=4pi (4000)^2=64,000,000pi mi^2
$$

70% of earth is covered in water:

$$
70% cdot 64,000,000pi=44,800,000pi approx 140,743,350mi^2
$$

The percent of Earth’s surface that lies in the US:

$$
dfrac{3,537,438}{64,000,000pi}approx 0.0176=1.76%
$$

Determine the volume of the earth:

$$
V=dfrac{4pi r^3}{3}=dfrac{4pi 4000^3}{3}approx 26,808,527,310 mi^3
$$

140,743,350 mi$^2$

1.76%

26,808,527,310 mi$^3$

The volume of a sphere with radius $r$ is:

$$
V=dfrac{4pi r^3}{3}
$$

and its surface area is:

$$
S=4pi r^2
$$

$V=frac{4pi r^3}{3}$, $S=4pi r^2$

Determine the surface area:

$$
S=4pi r^2=4pi 4^2=64pi approx 201cm^2
$$

Determine the volume:

$$
V=dfrac{4pi r^3}{3}=dfrac{4pi 4^3}{3}=dfrac{256pi}{3}approx 268cm^3
$$

Surface area 201 cm$^2$

Volume 268 cm$^3$

a. The measure of the interior angle of a $n$-gon is $dfrac{n-2}{n}180text{textdegree}$ and thus is $n=20$:

$$
dfrac{n-2}{n}180text{textdegree}=dfrac{20-2}{20}180text{textdegree}=162text{textdegree}
$$

b. The interior and exterior angle are supplementary and thus the exterior angle is:

$$
180text{textdegree}-157.5text{textdegree}=22.5text{textdegree}
$$

The number of sides is then 360$text{textdegree}$ divided by the exterior angle:

$$
dfrac{360text{textdegree}}{22.5text{textdegree}}=16
$$

Thus the polygon has 16 sides.

c. A octagon has 8 vertices. Divide the octagon into 8 congruent triangles. Determine the height of these triangles using the tangent ratio:

$$
h=2.5tan{67.5text{textdegree}}approx 6
$$

The area of a triangles is the product of the base and the height divided by 2:

$$
dfrac{5cdot 6}{2}=15
$$

Since the octagon is made up out of 8 triangles, the area of the octagon is:

$$
8cdot 15=120cm^2
$$

a. 162$text{textdegree}$

b. 16 sides

c. 120 cm$^2$

The radius is half the diameter:

$$
r=frac{text{Diameter}}{2}=frac{12}{2}:6
$$

Determine the volume of the cylinder:

$$
V=pi r^2 h=pi 6^2 (14.5)=522pi approx 1640 in^3
$$

Determine the volume in gallons:

$$
dfrac{1640 }{231}approx 7gallons
$$

a. Use distributive property and $i^2=-1$:

$$
(x-i)(x-i)=x^2-ix-ix+i^2=x^2-2ix-1
$$

b. Use distributive property and $i^2=-1$:

$$
(x-2i)(x-2i)=x^2-2ix-2ix+4i^2=x^2-4ix-4
$$

c. Factorize and use $i^2=-1$:

$$
x^2-6ix-9=x^2-6ix+9i^2=(x-3i)(x-3i)=(x-3i)^2
$$

a. $x^2-2ix-1$

b. $x^2-4ix-4$

c. $(x-3i)^2$

a. The surface area contains a circle, a rectangle (side of cylinder) and a circle sector (side pyramid):

$$
S=pi 6^2+2pi (6)cdot 11+pi (6)sqrt{6^2+7^2}=36pi +132pi +6sqrt{85}pi=(168+6sqrt{85})piapprox 702m^2
$$

b. The volume is made up of a cylinder and a cone:

$$
V=pi 6^2 (11)+dfrac{pi 6^2 (7)}{3}=396pi+84pi=480piapprox 1,508m^3
$$

a. 702 m$^2$

b. 1,508 m$^3$

Add and subtract 16:

$$
y=(x^2+8x+16)+10-16
$$

Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):

$$
y=(x+4)^2-6
$$

Thus the vertex is $(-4,-6)$ and from the original equation we note that $y=10$ is the $y$-intercept.

Vertex $(-4,-6)$

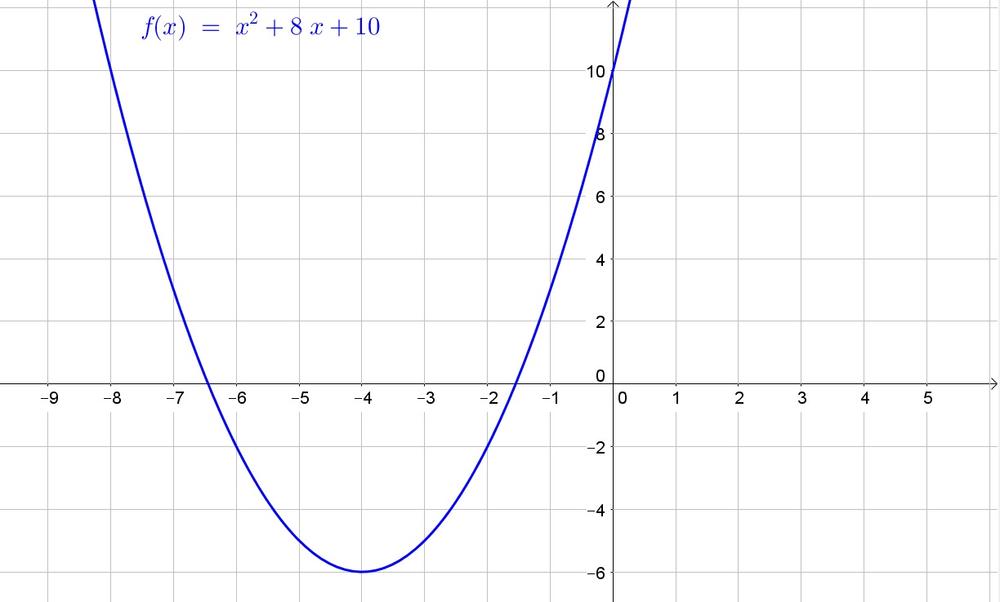
$y$-intercept: $y=10$

Using that the measure of the arc is equal to the central angle on the arc:

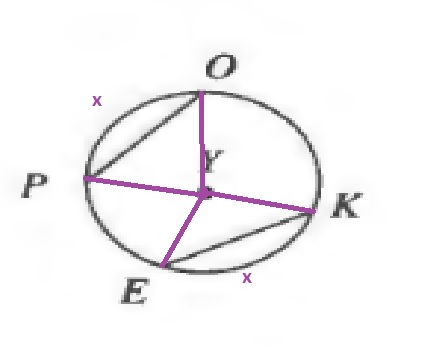
$$
angle OYPcong angle KYE(text{Equal arcs})
$$

$$
OY=YK (text{Both are the radius of the circle})
$$

$$
PY=YE (text{Both are the radius of the circle})
$$

$$
Downarrow SAS
$$

$$
triangle OYP cong triangle KYE
$$

$$
Downarrow
$$

$$
overline{PO}cong overline{EK}
$$