a. $(2,9)$ is the vertex and it has to be a minimum because $a=1>0$.

b. Because if you subtract 9 from both sides of the equation, then you obtain that the square is equal to a negative number. Since only complex numbers have a negative square, the function can have no real roots.

c. Let $f(x)$ be 0:

$$
0=(x-2)^2+9
$$

Subtract 9 from both sides of the equation:

$$
-9=(x-2)^2
$$

Take the square root of both sides of the equation:

$$
pm 3i=pm sqrt{-9}=x-2
$$

Add 2 to both sides of the equation to obtain the roots of the function:

$$
2pm 3i=x
$$

b. No real roots

c. $x=2pm 3i$

$$
g(x)=f(x)+2=2x^2+2
$$

b. The graph is the graph of $f$ stretched vertically by factor 2:

$$
g(x)=2f(x)=2(2x^2)=4x^2
$$

c. The graph is the graph of $f$ translated left by 2 units:

$$
g(x)=f(x+2)=2(x+2)^2
$$

d. The graph is the graph of $f$ stretched horizontally by factor $dfrac{1}{2}$:

$$
g(x)=f(2x)=2(2x)^2=8x^2
$$

b. $g(x)=4x^2$

c. $g(x)=2(x+2)^2$

d. $g(x)=8x^2$

$$
y=(x^2-10x+25)+22-25
$$

Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):

$$
y=(x-5)^2-3
$$

The vertex is then $(5,-3)$ and the $y$-intercept is $y=22$. Determine the $x$-intercepts using the quadratic formula:

$$
x=dfrac{10pm sqrt{(-10)^2-4(1)(22)}}{2(1)}=5pm sqrt{3}
$$

$$
y=(x^2+11x+30.25)+73-30.25
$$

Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):

$$
y=(x+5.5)^2+42.75
$$

The vertex is then $(-5.5,42.75)$ and the $y$-intercepts is $y=73$. Determine the $x$-intercepts using the quadratic formula:

$$
x=dfrac{-11pm sqrt{11^2-4(1)(73)}}{2(1)}=dfrac{-11pm 3sqrt{19}i}{2}
$$

Thus this function has no $x$-intercepts.

Vertex $(5,-3)$

$x$-intercepts: $(5pm sqrt{3},0$

$y$-intercept: $(0,22)$

b.

Vertex $(-5.5,42.75)$

$x$-intercepts: None

$y$-intercepts: $(0,73)$

b. Subtract the two equations:

$$
0=(x+2)^2+2x+4=x^2+6x+8
$$

Factorize:

$$
0=(x+4)(x+2)
$$

Zero product property:

$$
x+4=0text{ or }x+2=0
$$

Solve each equation to $x$:

$$
x=-4text{ or }x=-2
$$

Determine $y$:

$$
y=-2x-4=-2(-4)-4=8-4=4
$$

$$
y=-2x-4=-2(-2)-4=4-4=0
$$

Thus the solutions are $(-4,4)$ and $(-2,0)$.

b. $(-4,4)$ and $(-2,0)$

$$
x-2geq 2
$$

Add 2 to both sides of the inequality;

$$
xgeq 4
$$

$$
3x+7=pm 12
$$

Subtract 7 from both isdes of the equation:

$$
3x=-7pm 12
$$

Divide both sides of the equation by 3:

$$
x=-dfrac{7}{3}pm 4=dfrac{5}{3}text{ or }-dfrac{19}{3}
$$

$$
(x-4)(x+1)<0
$$

Since the function opens upwards:

$$
-1<x<4
$$

b. $x=frac{5}{3}$ or $x=-frac{19}{3}$

c. $-1<x<4$

b. The axis of symmetry is

$$
x=-dfrac{b}{2a}=-dfrac{-12}{2(2)}=3
$$

Determine the image at $x=3$:

$$
y=2(3)^2-12(3)+6=18-36+6=-12
$$

Thus the vertex is $(3,-12)$.

c.

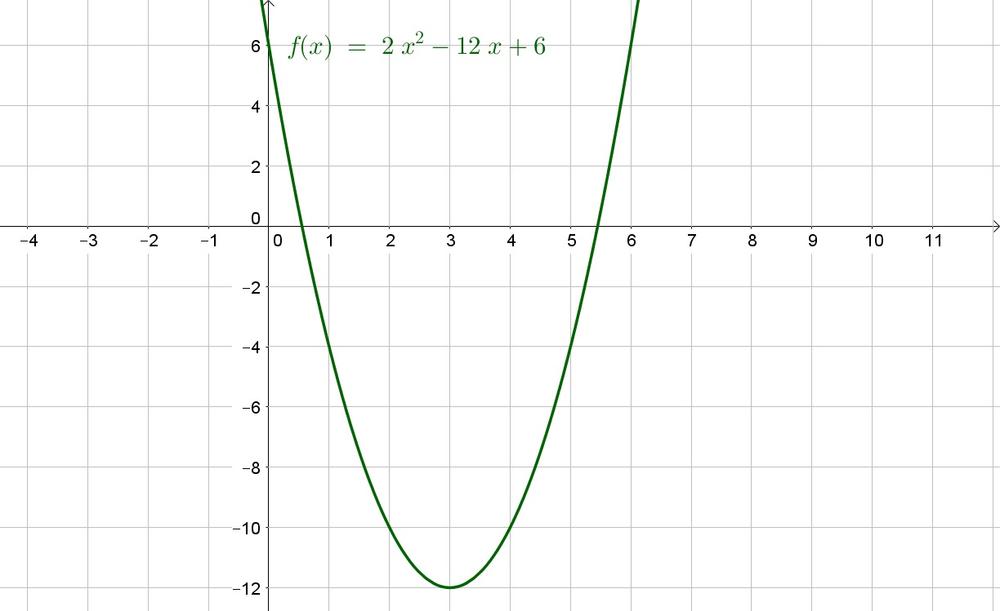
b. $(3,-12)$

c. Graph

$$
P(6)=dfrac{2}{3}cdot dfrac{1}{4}+dfrac{1}{3}cdot dfrac{1}{4}=dfrac{2}{12}+dfrac{1}{12}=dfrac{1}{4}=0.25=25%
$$

Then we obtain:

$$
P(4or6)=P(4)+P(6)=30%+25%=55%
$$

c. The probability of an event happening is 100% decreased by the probability of the event not happening:

$$
P(not 0)=100%-P(0)=100%-16.7%=83.3%
$$

d. Use the multiplication rule:

$$
P(S2given2)=dfrac{P(S2and2)}{P(2)}=dfrac{dfrac{2}{3}cdot dfrac{1}{4}}{dfrac{2}{3}cdot dfrac{1}{4}+dfrac{1}{3}cdot dfrac{7}{20}}=dfrac{1/6}{17/60}=dfrac{10}{17}approx 0.588=58.8%
$$

e. The multiplication rule states that the probability of an event A happening given that event B has happened is the probability of both events happening (at the same time) divided by the probability of event B happening.

b. $frac{1}{6}approx 0.167=16.7%$

c. $frac{5}{6}approx 0.833=83.3%$

d. $frac{10}{17}approx0.588=58.8%$

e. Answers wil lvary

$$
dfrac{NE}{AK}=dfrac{96′}{24′}=frac{4}{1}color{#4257b2}=4:1
$$

b. The perimeter ratio is equal to the side length ratio and thus the perimeter of $triangle ENC$ is four times as large as the perimeter of $triangle KAR$.

c. Multiply the corresponding side length with the ratio:

$$
EC=7’cdot 4=28′
$$

b. $4:1$

c. 28′

$$
(28-2)180text{textdegree}=4,680text{textdegree}
$$

$$
n=dfrac{360text{textdegree}}{42text{textdegree}}approx 8.5
$$

Since the result is not an integer, this regular polygon does not exist.

$$
text{color{#4257b2}Note: If the pentagon is regular, then:\

The sum of all interior angles is $(n-2)180text{textdegree}$ with $n$ the number of sides:

$$(5-2)180text{textdegree}=540text{textdegree}$$

The measure of the interior angle is then the sum of all interior angles divided by the number of angles:

$$dfrac{540text{textdegree}}{5}=108text{textdegree}$$}
$$

$$
(10-2)180text{textdegree}=1,440text{textdegree}
$$

The measure of the interior angle is then the sum of all interior angles divided by the number of angles:

$$
dfrac{1,440text{textdegree}}{10}=144text{textdegree}
$$

b. Not possible

c. Not possible

d. 144$text{textdegree}$

a.
$$
$1000cdot dfrac{1}{4} +$0cdot dfrac{3}{4}=$250
$$

b.
$$
$1000cdot dfrac{1}{360} +$0cdot dfrac{359}{360}approx $2.78
$$

c. Since the expected value is one fifth of the winning price:

$$
P(winning$1000)=dfrac{1}{5}=0.2=20%
$$

Thus for the angle we then obtain:

$$
mangle ACB = dfrac{360text{textdegree}}{5}=72text{textdegree}
$$

b. $$2.78$

c. $frac{1}{5}$, 72$text{textdegree}$

$$
overline{AC}cong overline{CD}(text{Radius circle})
$$

$$
overline{BC}cong overline{CE}(text{Radius circle})
$$

$$
Downarrow SSS
$$

$$
triangle ABC cong triangle DEC
$$

$$
Downarrow
$$

$$
angle ACB cong angle DCE
$$