All Solutions
Page 483: Questions
b.
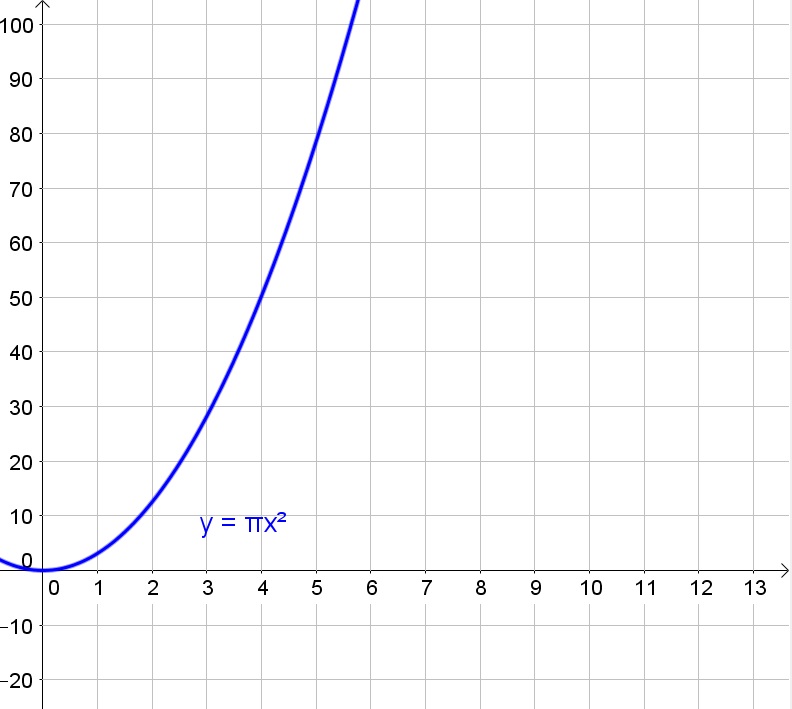
d. Replace $A$ with the mass in the equation of the area of the disk:
$$
m=pi r^2
$$
e. The mass would be four times as largest mass measured.
b. Graph
c. Positive half quadratic function
d. $m=pi r^2$
e. Four times
b. The function is a good model when $r>0$ (since the radius has to be nonnegative and nonzero).
b. $r>0$
This means that only the part of the graph on the right side of the $y$-axis was used (because the radius is nonnegative).
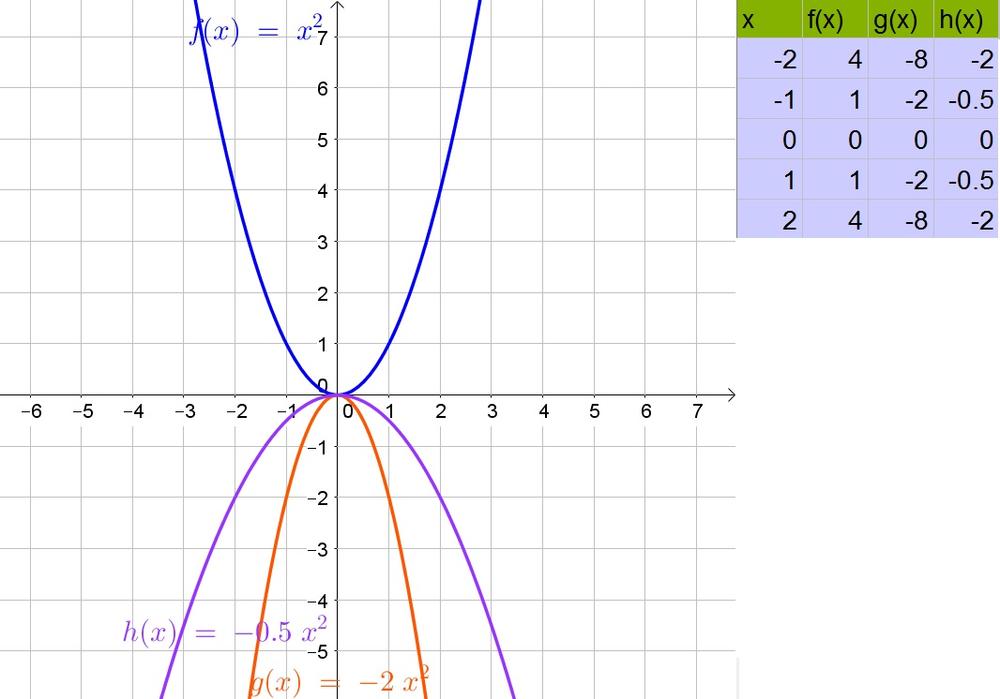
a. Minimum at $x=-dfrac{-2}{2(1)}=1$ (since $f(x)=(x-1)^2=x^2-2x+1$).
b. Minimum at $x=-dfrac{0}{2(1)}=0$
c. Minimum at $x=-dfrac{4}{2(1)}=-2$ (since $f(x)=(x+2)^2=x^2+4x+4$).
d. Maximum at $x=-dfrac{0}{2(-1)}=0$
e. See part (a) to (d)
b. $x=0$
c. $x=-2$
d. $x=0$
e. Minima at (a) to (c), Maximum at (d)
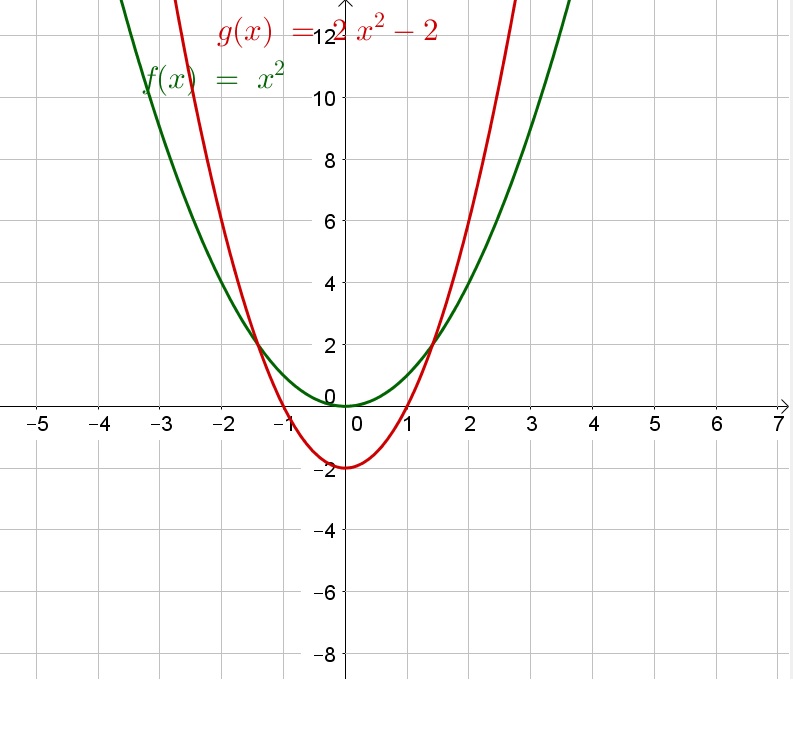
Thus the negative coefficient of $x^2$ reflects the graph of $x^2$ about the $x$-axis.
Moreover if the coefficient is smaller than $-1$ then the graph becomes narrower and if the coefficient is greater than $-1$ (and negative), then the graph becomes wider.

$$
6x<12
$$
Divide both sides of the inequality by 6:
$$
x<2
$$

$$
xgeq 6
$$

$$
x-2>2
$$
Add 2 to both sides of the inequality:
$$
x>4
$$

$$
20-xleq 2
$$
Add $x$ to both sides of the inequality:
$$
20leq 2+x
$$
Subtract 2 from both sides of the inequality:
$$
18leq x
$$

d. $xgeq 18$
$$
dfrac{(n-2)180text{textdegree}}{n}
$$
Thus we then obtain:
$$
dfrac{(n-2)180}{n}=60
$$
Multiply both sides of the equation by $n$:
$$
180n-360=60n
$$
Subtract $60n$ from both sides of the equation:
$$
120n-360=0
$$
Add 360 to both sides of the equation:
$$
120n=360
$$
Divide both sides of the equation by 120:
$$
n=3
$$
$$
dfrac{(n-2)180text{textdegree}}{n}
$$
Thus we then obtain:
$$
dfrac{(n-2)180}{n}=156
$$
Multiply both sides of the equation by $n$:
$$
180n-360=156n
$$
Subtract $156n$ from both sides of the equation:
$$
24n-360=0
$$
Add 360 to both sides of the equation:
$$
24n=360
$$
Divide both sides of the equation by 24:
$$
n=15
$$
$$
dfrac{(n-2)180text{textdegree}}{n}
$$
Thus we then obtain:
$$
dfrac{(n-2)180}{n}=90
$$
Multiply both sides of the equation by $n$:
$$
180n-360=90n
$$
Subtract $90n$ from both sides of the equation:
$$
90n-360=0
$$
Add 360 to both sides of the equation:
$$
90n=360
$$
Divide both sides of the equation by 90:
$$
n=4
$$
$$
dfrac{(n-2)180text{textdegree}}{n}
$$
Thus we then obtain:
$$
dfrac{(n-2)180}{n}=140
$$
Multiply both sides of the equation by $n$:
$$
180n-360=140n
$$
Subtract $140n$ from both sides of the equation:
$$
40n-360=0
$$
Add 360 to both sides of the equation:
$$
40n=360
$$
Divide both sides of the equation by 90:
$$
n=9
$$
b. 15
c. 4
d. 9
Subtract the two equations:
$$
0=-dfrac{5}{2}x+15
$$
Subtract 15 from both sides of the equation:
$$
-15=-dfrac{5}{2}x
$$
Multiply both sides of the equation by $-dfrac{2}{5}$:
$$
6=x
$$
Determine $y$:
$$
y=-2x+6=-2(6)+6=-6
$$
Thus the solution is $(6,-6)$.
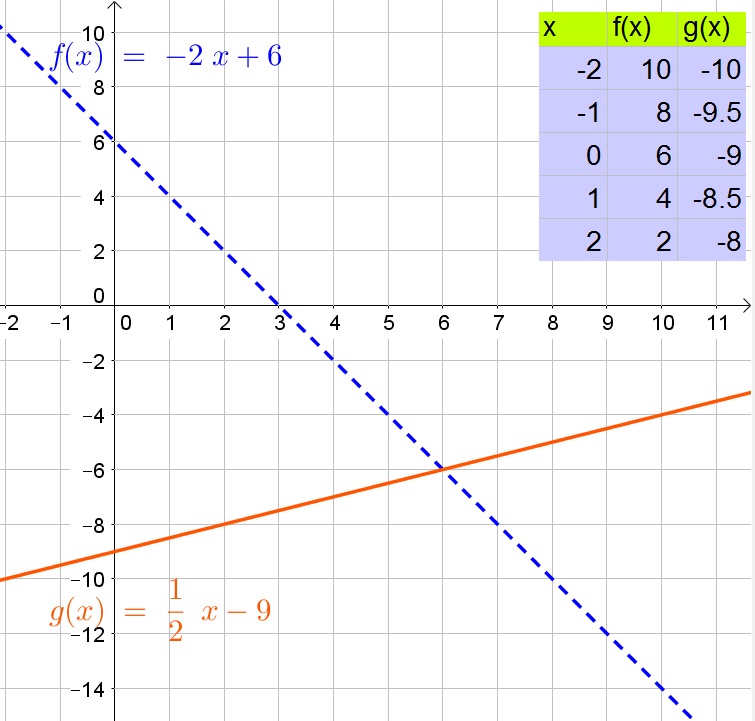
b. Perpendicular
$$
dfrac{10}{15}=dfrac{12}{18}=1.5neq dfrac{11}{17}
$$
$$
dfrac{8}{4}=dfrac{6}{3}=dfrac{10}{5}=2
$$
b. SAS
c. SSS
d. SSS
If the equation of the parabola is $f(x)=(bx)^2$, then the graph is the graph of $f(x)=x^2$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=(x-c)^2$, then the graph is the graph of $f(x)=x^2$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=x^2+d$, then the graph is the graph of $f(x)=x^2$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
b. If you multiply the equation by a factor $a$ (with $a<1$ and $a$ positive), then the equation becomes $f(x)=ax^2$ and this graph will then be wider than the graph of $f(x)=x^2$.
c. If you multiply the equation by a factor $a$ (with $a1$.
If the equation of the parabola is $f(x)=(bx)^2$, then the graph is the graph of $f(x)=x^2$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=(x-c)^2$, then the graph is the graph of $f(x)=x^2$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=x^2+d$, then the graph is the graph of $f(x)=x^2$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
Thus an equation of the form $f(x)=-a(x+2)^2+6$ with $a<1$ then is the graph of $y=x^2$ vertically compressed, open downward, sifted six units up and shifted two units to the left.
If the equation of the parabola is $f(x)=(bx)^2$, then the graph is the graph of $f(x)=x^2$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=(x-c)^2$, then the graph is the graph of $f(x)=x^2$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=x^2+d$, then the graph is the graph of $f(x)=x^2$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
If the equation of the parabola is $f(x)=(bx)^2$, then the graph is the graph of $f(x)=x^2$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=(x-c)^2$, then the graph is the graph of $f(x)=x^2$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=x^2+d$, then the graph is the graph of $f(x)=x^2$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
$$
y=(x-7)^2-4
$$
The parabola was also stretched vertically by a factor of 2.
$$
y=2(x+3)^2
$$
The vertex is at $(-5,2)$, which means that the parabola was shifted left by 5 units and shifted up by 2 units.
$$
y=-0.5(x+5)^2+2
$$
b. $y=2(x+3)^2$
c. $y=-0.5(x+5)^2+2$
$$
(2-1)^2+2=1+2=3
$$
b. Replace $x$ with $-4$:
$$
(-4-1)^2+2=25+2=27
$$
c. Replace $x$ with $-11.3$:
$$
(-11.3-1)^2+2=151.29+2=153.29
$$
b. 27
c. 153.29
$$
4xgeq 12
$$
Divide both sides of the inequality by 4:
$$
xgeq 3
$$

$$
x+4<dfrac{5}{3}
$$
Subtract 4 from both sides of the inequality:
$$
x<-dfrac{7}{4}
$$

$$
2x<56
$$
Divide both sides of the inequality by 2:
$$
x<28
$$

$$
5x+4>-3x+24
$$
Add $3x$ to both sides of the inequality:
$$
8x+4>24
$$
Subtract 4 from both sides of the inequality:
$$
8x>20
$$
Divide both sides of the inequality by 8:
$$
x>dfrac{5}{2}
$$

b. $x<-frac{7}{4}$
c. $xfrac{5}{2}$
$$
y=a(x+2)(x-5)
$$
We know that if $x=0$, then $y=-10$:
$$
-10=a(2)(-5)=-10a
$$
Divide both sides of the equation by $-10$:
$$
1=a
$$
Replace $a$ with 1 in the function equation:
$$
y=(x-5)(x+2)
$$
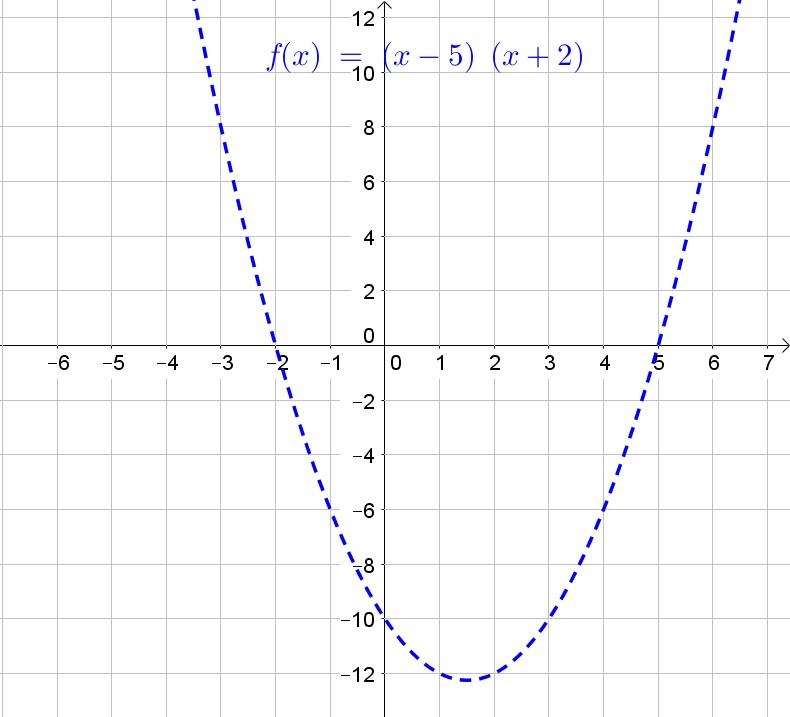
y=(x-5)(x+2)
$$
$$
y=3-3y+5
$$
Add $3y$ to both sides of the equation:
$$
4y=8
$$
Divide both sides of the equation by 4:
$$
y=2
$$
Determine $x$:
$$
x=3y-5=3(2)-5=1
$$
Thus the solution is $(1,2)$.
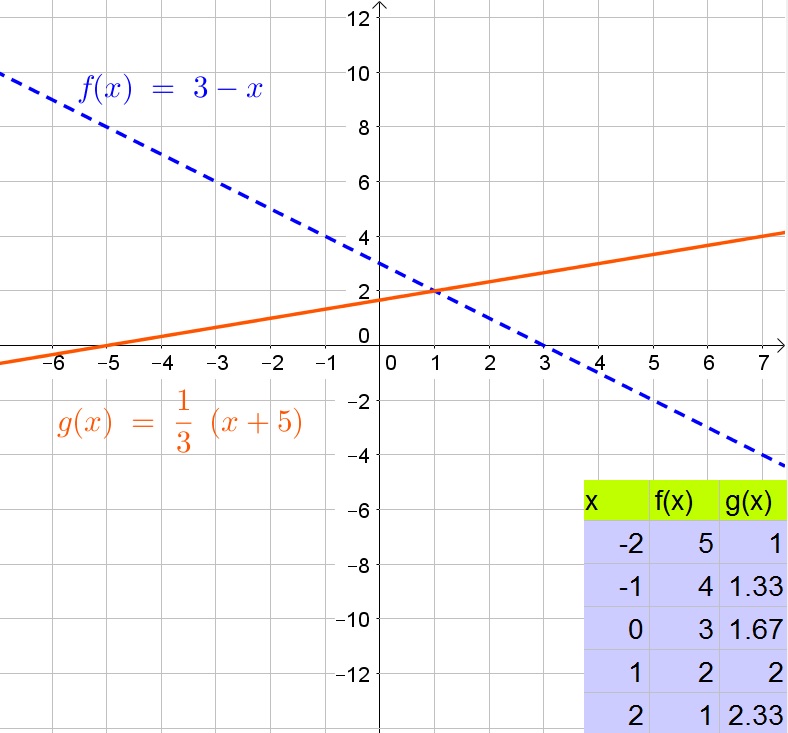
$$
x=-5-2x-4
$$
Add $2x$ to both sides of the equation:
$$
3x=-9
$$
Divide both sides of the equation by 3:
$$
x=-3
$$
Determine $y$:
$$
y=-2x-4=-2(-3)-4=6-4=2
$$
Thus the solutions is $(-3,2)$.
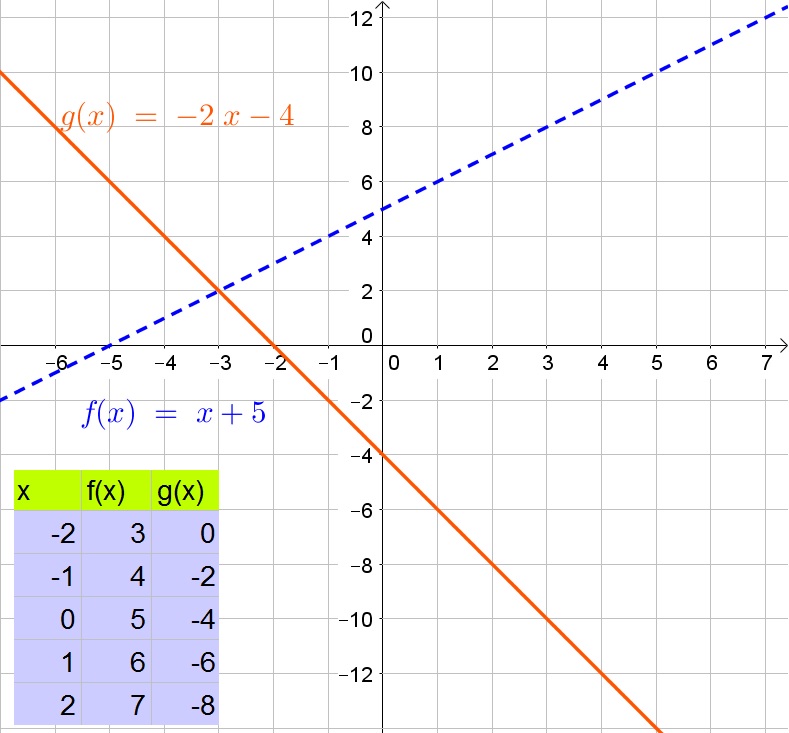
b. $(-3,2)$
$$
102.6=2pi r
$$
Divide both sides of the equation by $2pi$:
$$
16.33approx dfrac{102.6}{2pi}=r
$$
The diameter is twice the radius:
$$
2r=2(16.33)=32.66
$$
Thus the diameter is 32.66ft.
$$
x=180text{textdegree}-23text{textdegree}-48text{textdegree}=109text{textdegree}
$$
Same-side interior angles of parallel lines and vertical angles are congruent:
$$
y=180text{textdegree}-x=180text{textdegree}-109text{textdegree}=71text{textdegree}
$$
The sum of all angles in a quadrilaterial is 360$text{textdegree}$:
$$
z=360text{textdegree}-81text{textdegree}-x-y=360text{textdegree}-81text{textdegree}-109text{textdegree}-71text{textdegree}=99text{textdegree}
$$
x=109text{textdegree}
$$
$$
y=71text{textdegree}
$$
$$
z=99text{textdegree}
$$
The vertex of $f$ is $(0,0)$, while the vertex of $g$ is $(3,-4)$.
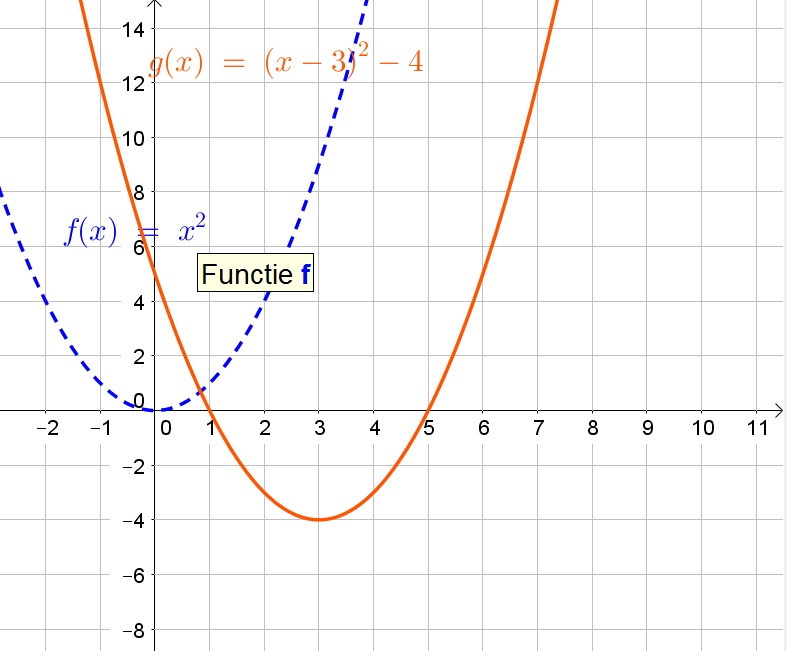
c. The equation is standard form is:
$$
g(x)=x^2-6x+9-4=x^2-6x+5
$$
The equation in factored form is then:
$$
g(x)=(x-1)(x-5)
$$
d. The graphing form (the given form) is easier because it immediately tells you the vertex and the roots can be easily determine from it.
e. Because we can read the vertex from the function equation, namely the vertex is $(h,k)$.
b.
$x$-intercepts: $(1,0)$, $(5,0)$
$y$-intercepts: $(0,5)$
c. $g(x)=(x-1)(x-5)$
d. Graphing form
e. Vertex is $(h,k)$
Add and subtract 9 from the given equation:
$$
f(x)=(x^2-6x+9)+5-9
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x-3)^2-4
$$
Thus the equation is now in graphing form.
$$
f(x)=(x+3)^2
$$
Thus the equation is now in graphing form and the vertex is $(-3,0)$.
$$
g(x)=(x^2+6x+9)+1-9
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
g(x)=(x+3)^2-8
$$
Thus the equation is now in graphing form and the vertex is $(-3,-8)$.
b. $g(x)=(x+3)^2-8$, $(-3,-8)$
$$
f(x)=(x^2-4x+4)+3-4
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x-2)^2-1
$$
Thus the equation is now in graphing form and the vertex is $(-3,0)$.
$$
g(x)=(x^2-3x+2.25)-5+2.25
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
g(x)=(x-1.5)^2-2.75
$$
Thus the equation is now in graphing form and the vertex is $(1.5,-2.75)$.
$$
j(x)=2(x^2+8x+16)+29-32
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
j(x)=2(x+4)^2-3
$$
Thus the equation is now in graphing form and the vertex is $(-4,3)$.
$$
k(x)=-(x+4)^2
$$
Thus the equation is now in graphing form and the vertex is $(-4,0)$.
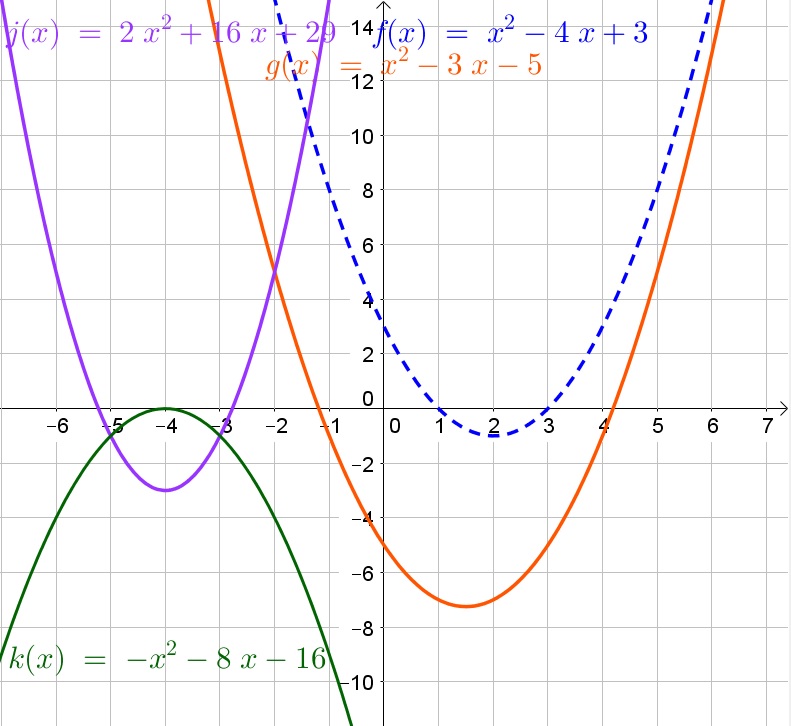
b. $g(x)=(x-1.5)^2-2.75$
c. $j(x)=2(x+4)^2-3$
d. $k(x)=-(x+4)^2$
$$
4. g(x)+23-18=-2(x^2+6x+9)
$$
Factorize:
$$
5.g(x)+5=-2(x+3)^2
$$
Subtract 5 from both sides of the equation:
$$
6. g(x)=-2(x+3)^2-5
$$
g(x)=-2(x+3)^2-5
$$
Rewrite the equation using the complete the square method, by adding/subtracting a number such that you get a term of the form $x^2pm 2xb+b^2$, then factorize this into $(xpm b)^2$ to obtain the graphing form.
$$
f(x)=x^2-1
$$
f(x)=x^2-1
$$
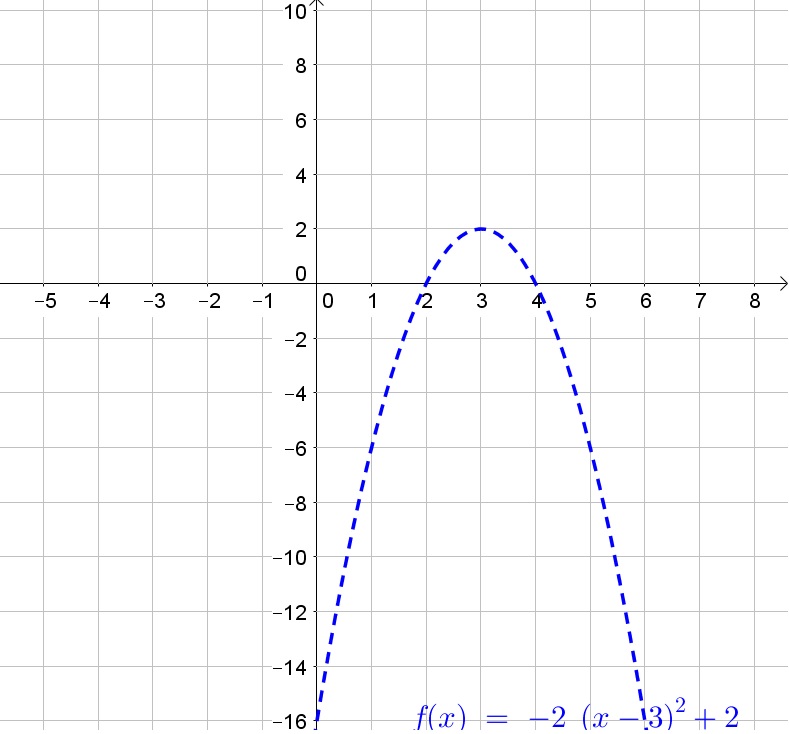
$$
0=-2(x-3)^2+2
$$
Subtract 2 from both sides of the equation:
$$
-2=-2(x-3)^2
$$
Divide both sides of the equation by $-2$:
$$
1=(x-3)^2
$$
Take the square root of both sides of the equation:
$$
pm 1 =x-3
$$
Add 3 to both sides of the equation:
$$
4text{ or }2=3pm 1=x
$$
Thus the $x$-intercepts are $x=2$ and $x=4$.
Let $x$ be zero:
$$
f(x)=-2(-3)^2+2=-16
$$
Thus the $y$-intercept is $y=-16$.
b. $x$-intercepts $(2,0)$ and $(4,0)$, $y$-intercepts $(0,-16)$
a. Replace $h$ with 0 and $k$ with $-5$:
$$
f(x)=ax^2-5
$$
Replace $x$ with $-1$ and $f(x)$ with 2:
$$
2=a(-1)^2-5=a-5
$$
Add 5 to both sides of the equation:
$$
7=a
$$
Replace $a$ in the equation with 7:
$$
f(x)=7x^2-5
$$
$$
text{color{white} jmlirjtet mjretm lijretm lrejtj erjtl jrljtlr jlktjrl jtrlj ljr litelrj tlretm ermthmre hmtlrel thmrleht hlirht lhr}
$$
$$
f(x)=a(x-1)^2+4
$$
Replace $x$ with $5$ and $f(x)$ with $-4$:
$$
-4=a(5-1)^2+4=16a+4
$$
Subtract 4 from both sides of the equation:
$$
-8=16a
$$
Divide both sides of the equation by $16$:
$$
-dfrac{1}{2}=a
$$
Replace $a$ in the equation with 7:
$$
f(x)=-dfrac{1}{2}(x-1)^2+4
$$
$$
text{color{white} jmlirjtet mjretm lijretm lrejtj erjtl jrljtlr jlktjrl jtrlj ljr litelrj tlretm ermthmre hmtlrel thmrleht hlirht lhr}
$$
b. $f(x)=-dfrac{1}{2}(x-1)^2+4$
$$
x^2+1<65
$$
Subtract 1 from both sides of the inequality:
$$
x^2<64
$$
Since the graph of $f(x)=x^2$ opens upwards:
$$
-8<x<8
$$
-8<x<8
$$
a. Since $n=6$, we exterior angle is:
$$
dfrac{360text{textdegree}}{6}=60text{textdegree}
$$
Since the interior and exterior angle are supplementary, we know that the interior angle is then 120$text{textdegree}$, thus (3).
b. Since $n=6$, we central angle is:
$$
dfrac{360text{textdegree}}{10}=36text{textdegree}
$$
c. Since $n=3$, we exterior angle is:
$$
dfrac{360text{textdegree}}{3}=120text{textdegree}
$$
d. Since $n=4$, we exterior angle is:
$$
dfrac{360text{textdegree}}{4}=90text{textdegree}
$$
b. (1)
c. (4)
d. (2)
a.
$$
left( dfrac{1}{16}right)^{-1/4}=16^{1/4}=sqrt[4]{16}=sqrt[4]{2^4}=2
$$
b.
$$
x^{-1}y^{-3}=dfrac{1}{x}cdot dfrac{1}{y^3}=dfrac{1}{xy^3}
$$
c.
$$
(25x^4)^{1/2}=sqrt{25x^4}=sqrt{25}cdot sqrt{x^4}=5x^2
$$
b. $frac{1}{xy^3}$
c. $5x^2$
$$
4y=2x-16
$$
$$
x-4y=12
$$
Add the two equations:
$$
x=2x-16+12
$$
Subtract $2x$ from both sides of the equation:
$$
-x=-4
$$
Multiply both sides of the equation by $-1$:
$$
x=4
$$
Determine $y$:
$$
y=dfrac{1}{2}x-4=dfrac{1}{2}(4)-4=2-4=-2
$$
Thus the solution is $(4,-2)$.
b. Input is the same number or the opposite number
The domain of the function is $mathbb{R}$ and the range contains only nonnegative values $[0,+infty)$.
If the equation of the parabola is $f(x)=|bx|$, then the graph is the graph of $f(x)=|x|$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=|x-c|$, then the graph is the graph of $f(x)=|x|$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=|x|+d$, then the graph is the graph of $f(x)=|x|$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
If the equation of the parabola is $f(x)=|bx|$, then the graph is the graph of $f(x)=|x|$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=|x-c|$, then the graph is the graph of $f(x)=|x|$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=|x|+d$, then the graph is the graph of $f(x)=|x|$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
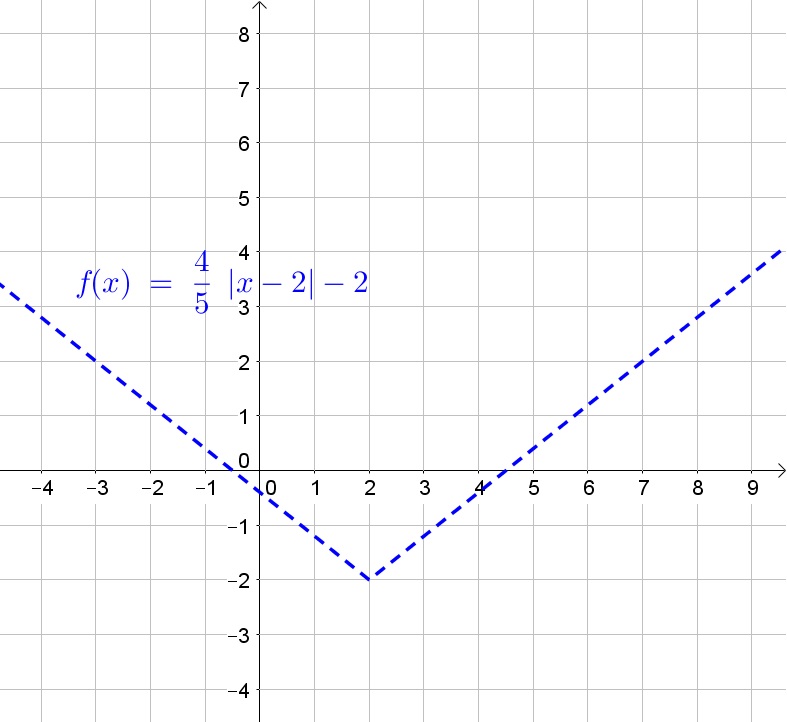
We note that the given graph is the graph of the absolute function reflected about the $x$-axis, stretched verticaly by factor 2, translated up by 2 untis and translated right by 1 unit. The equation of the graph is then:
$$
f(x)=-2|x-1|+2
$$
f(x)=-2|x-1|+2
$$
If the equation of the parabola is $f(x)=|bx|$, then the graph is the graph of $f(x)=|x|$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=|x-c|$, then the graph is the graph of $f(x)=|x|$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=|x|+d$, then the graph is the graph of $f(x)=|x|$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
We note that the given graph is the graph of the absolute function stretched verticaly by factor $dfrac{4}{5}$, translated down by 2 units and translated right by 2 units.
f(x)=-2|x-1|+2
$$
If the equation of the parabola is $f(x)=a|x|$, then the graph is the graph of $f(x)=|x|$ stretched vertically by factor $a$. If $a$ is negative, then the graph is also reflected about the $x$-axis.
If the equation of the parabola is $f(x)=|bx|$, then the graph is the graph of $f(x)=|x|$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=|x-c|$, then the graph is the graph of $f(x)=|x|$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=|x|+d$, then the graph is the graph of $f(x)=|x|$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
If the equation of the parabola is $f(x)=|bx|$, then the graph is the graph of $f(x)=|x|$ stretched horizontally by factor $b$.
If the equation of the parabola is $f(x)=|x-c|$, then the graph is the graph of $f(x)=|x|$ translated right by $c$ units (if $c$ is negative, then the translation is to the left by $|c|$ units).
If the equation of the parabola is $f(x)=|x|+d$, then the graph is the graph of $f(x)=|x|$ translated up by $d$ units (if $d$ is negative, then the translation is down by $|d|$ units).
Thus the given equation is the graph of the absolute value function translated right by 3 units and down by 1 unit.
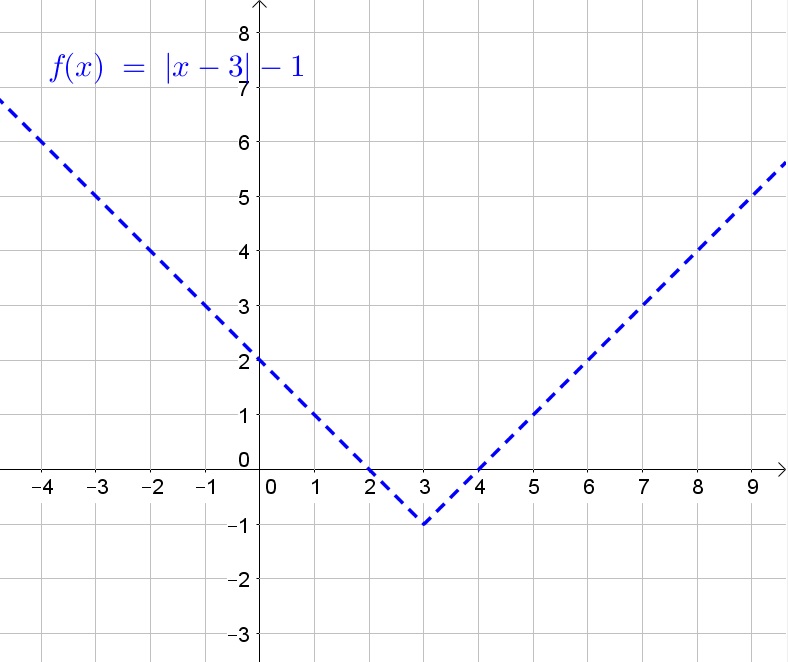
The range of the function contains all possible $y$-values and thus is $[0,+infty)$.
b. We note that the vertex of $g$ is $(6,3)$ and seems to have stretched by factor 2, thus the equation is then:
$$
g(x)=2(x-6)^2+3
$$
We note that the vertex of $h$ is $(6,3)$ and seems to have stretched by factor $-dfrac{1}{2}$, thus the equation is then:
$$
h(x)=-dfrac{1}{2}(x-6)^2+3
$$
c. The domain contains all possible $x$-values that the function can take on and thus is $mathbb{R}$.
The range of the function contains all possible $y$-values and thus is $[3,+infty)$.
b. $g(x)=2(x-6)^2+3$, $h(x)=-frac{1}{2}(x-6)^2+3$
c. $mathbb{R}$, $[3,+infty)$
Let $f(x)$ be 0:
$$
0=x^2-2x-48
$$
Factorize:
$$
0=(x-8)(x+6)
$$
Zero product property:
$$
x-8=0text{ or }x+6=0
$$
Solve each equation to $x$:
$$
x=8text{ or }x=-6
$$
Let $x$ be 0:
$$
y=f(x)=0^2-2(0)-48=-48
$$
$$
f(x)=x^2-2x-48
$$
Add and subtract 1 from the equation:
$$
f(x)=(x^2-2x+1)-48-1
$$
Factorize:
$$
f(x)=(x-1)^2-49
$$
Thus the vertex is $(1,-49)$.

$y$-intercepts: $(0,-48)$
Vertex $(1,-49)$
b. The speed is the distance covered divided by the time needed (in hours):
$$
dfrac{2}{1/3}=6mph
$$
c. 0 mph, because the slope of the graph is then zero.
d. The speed is the distance covered divided by the time needed (in hours):
$$
dfrac{2}{18/60}=6dfrac{2}{3}mph
$$
b. 6 mph
c. 0 mph
d. $6frac{2}{3}$ mph
A hexagon has 6 vertices. Divide the hexagon into 6 congruent triangles. Determine the the height of these triangles using the sine and cosine ratio:
$$
h=dfrac{3}{sin{60text{textdegree}}}approx 3.46
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{6cdot 3.46}{2}=10.38
$$
Since the hexagon is made up out of 6 triangles, the area of the hexagon is:
$$
6cdot 10.38=62.28in^2
$$
$$
A=pi r^2=pi (3.46)^2approx 37.61in^2
$$
The area of the shaded region is the difference in areas:
$$
62.28in^2-37.61in^2=24.67in^2
$$
24.67in^2
$$
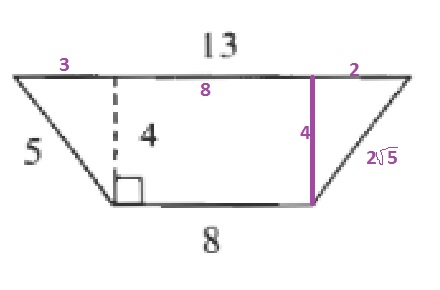
$$
A=dfrac{(13+8)4}{2}=42
$$
The perimeter is the sum of the lengths of all sides:
$$
P=13+5+8+2sqrt{5}=26+2sqrt{5}
$$
b. The new area is the previous area are multiplied by the linear scale factor squared:
$$
A=dfrac{1}{3^2}cdot 42=dfrac{14}{3}
$$
The new perimeter is the previous perimeter are multiplied by the linear scale factor:
$$
P=dfrac{1}{3}(26+2sqrt{5})
$$
b. Area $frac{14}{3}$ and perimeter $frac{1}{3}(26+2sqrt{5})$
A hexagon has 6 vertices. Divide the hexagon into 6 congruent triangles. Determine the the height and base of these triangles using the sine and cosine ratio:
$$
dfrac{b}{2}=3cos{60text{textdegree}}=1.5Rightarrow b=3
$$
$$
h=3sin{60text{textdegree}}approx 2.6
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{3cdot 2.6}{2}=3.9
$$
Since the hexagon is made up out of 6 triangles, the area of the hexagon is:
$$
6cdot 3.9=23.4ft^2
$$
$$
A=1cdot 3=3ft^2
$$
The total area is then:
$$
23.4ft^2+6cdot 3ft^2=41.4ft^2
$$
41.4ft^2
$$
$$
y=a(x-50)(x-150)
$$
At $x=0$ we need $y=300$:
$$
300=a(-50)(-150)=7500a
$$
Divide both sides of the equation by 7500:
$$
dfrac{1}{25}=a
$$
Replace $a$ with its value in the equation:
$$
y=dfrac{1}{25}(x-50)(x-150)
$$
Thus if
$$
dfrac{1}{25}(x-50)(x-150)<0
$$
we then know that
$$
50<x0
$$
we then know that
$$
x150
$$
$$
dfrac{1}{25}(x-50)(x-150)>0
$$
Multiply both sides of the inequality by 25:
$$
(x-50)(x-150)>0
$$
Since the graph of $y=(x-50)(x-150)$ opens upwards:
$$
x150
$$
b. $50<x<150$
c. $x150$
d. $x150$
$$
P(x)=100x(0.05x+5)-300,000=5x^2+500x-300,000
$$
b.
$$
5x^2+500x-300,000<0
$$
Factorize
$$
5(x+300)(x-200)<0
$$
Since the function $y=5(x+300)(x-200)$ opens upwards:
$$
-300<x<200
$$
Thus the park loses money if there are less than 200 visitors.
c.
$$
5x^2+500x-300,000<0
$$
Factorize
$$
5(x+300)(x-200)<0
$$
Since the function $y=5(x+300)(x-200)$ opens upwards:
$$
-300<x<200
$$
d. They are the same because they are solutions of the same inequality. They are different because in (b) you are only interested in $xgeq 0$.
b. Less than 200 visisotrs
c. $-300<x<200$
d. Solutions of same inequality, we are only interested in $xgeq 0$
$$
-16t^2+64t>40
$$
Subtract 40 from both sides of the inequality:
$$
-16t^2+64t-40>0
$$
Determine the roots using the quadratic formula:
$$
t=dfrac{-64pm sqrt{64^2-4(-16)(-40)}}{2(-16)}=2pm dfrac{1}{2}sqrt{6}
$$
Since the function opens downwards, we then know
$$
0.78approx 2- dfrac{1}{2}sqrt{6}<t<2+dfrac{1}{2}sqrt{6}approx 3.22
$$

$$
x=-dfrac{b}{2a}=-dfrac{64}{2(-16)}=2
$$
The maximum height is then the image:
$$
h(2)=-16(2)^2+64(2)=64
$$
Thus the football reaches the maximum height of 64 ft at 2 s.
b. Maximum height of 64 ft at 2 s.
$$
x^2+2x-3<0
$$
Factorize:
$$
(x+3)(x-1)<0
$$
Thus the boundary points are $x=-3$ and $x=1$.


b. 3 regions
c. Region between boundary points
$$
(x+4)(x-3)<0
$$
Thus the roots are $x=-4$ and $x=3$. Since the function opens upwards:
$$
-4<x<3
$$
$$
-2x^2+10x-7geq 0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-10pm sqrt{10^2-4(-2)(-7)}}{2(-2)}=dfrac{5}{2}pm dfrac{1}{2}sqrt{11}
$$
Since the function opens downwards:
$$
dfrac{5}{2}- dfrac{1}{2}sqrt{11}leq xleq dfrac{5}{2}+ dfrac{1}{2}sqrt{11}
$$
$$
x-27
$$
Add 2 to both sides of the inequality:
$$
x9
$$
b. $frac{5}{2}-frac{1}{2}sqrt{11}leq xleq frac{5}{2}+frac{1}{2}sqrt{11}$
c. $x9$
$$
5x-7geq 2x+5
$$
Subtract $2x$ from both sides of the inequality:
$$
3x-7geq 5
$$
Add 7 to both sides of the inequality:
$$
3xgeq 12
$$
Divide both sides of the inequality by 3:
$$
xgeq 4
$$
$$
6x-29>4x+12
$$
Subtract $4x$ from both sides of the inequality:
$$
2x-29>12
$$
Add 29 to both sides of the inequality:
$$
2x>41
$$
Divide both sides of the inequality by 41:
$$
x>dfrac{41}{2}
$$
$$
x^2leq -4x+5
$$
Add $4x-5$ to both sides of the inequality:
$$
x^2+4x-5leq 0
$$
Factorize:
$$
(x+5)(x-1)leq 0
$$
Thus the roots are $x=-5$ and $x=1$. Since $y=x^2+4x-5$ opens upwards:
$$
-5leq xleq 1
$$
(b) $x>frac{41}{2}$
(c) $-5leq xleq 1$
b. Since the increase is constant, the best type of function is linear.
c. The apple will travel an arc in the shape of a parabola and thus a quadratic function is best.
b. Linear
c. Quadratic
$$
y=(x^2+6x+9)+15-9
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x+3)^2+6
$$
Thus the equation is now in graphing form with vertex $(-3,6)$ and from the original equation we note that $y=15$ is the $y$-intercept.
$$
y=(x^2-3x+2.25)+9-2.25
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x-1.5)^2+6.75
$$
Thus the equation is now in graphing form with vertex $(1.5,6.75)$ and from the original equation we note that $y=9$ is the $y$-intercept.
b. $(1.5,6.75)$, $y=9$
We take note that the properties of a triangle’s circumcenter are as follows:
1. The circumcenter is the center of the circumcircle
2. All the vertices of a triangle are equidistance from the circumcenter
3. In an obtuse-angled triangle, the circumcenter lies outside of the triangle
4. In an acute-angle triangle, the circumcenter is inside of the triangle
5. In a right-angle triangle, the circumcenter is at the midpoint of the hypotenuse side of the triangle
The diagram of the $bigtriangleup$ XYZ is as follows:

We are to determine which point is the circumcenter of the triangle
We first determine what kind of triangle $bigtriangleup$ XYZ is. We can observe that $bigtriangleup$ XYZ is an obtuse-angled triangle, hence, from the property of the triangle’s circumcenter, we note that we can locate the circumcenter of this triangle outside of the triangle. Hence, point A cannot be a circumcenter.
$$
3x-y=14
$$
$$
3x=6y+24
$$
Subtract the two equations:
$$
-y=-6y-10
$$
Add $6y$ to both sides of the equation:
$$
5y=-10
$$
Divide both sides of the equation by 5:
$$
y=-2
$$
Determine $x$:
$$
x=2(-2)+8=-4+8=4
$$
Thus the solution is $(4,-2)$.
$$
0=3y+12
$$
Subtract 12 from both sides of the equation:
$$
-12=3y
$$
Divide both sides of the equation by 3:
$$
-4=y
$$
Determine $x$:
$$
x=2y+2=2(-4)+2=-8+2=-6
$$
Thus the solution is $(-6,-4)$.
$$
18x=9
$$
Divide both sides of the equation by 18:
$$
x=dfrac{1}{2}
$$
Determine $y$:
$$
y=13-2x=13-1=12
$$
Thus the solution is $left(dfrac{1}{2},12right)$
b. $(-6,-4)$
c. $left(frac{1}{2},12right)$
$$
left( dfrac{x_1+y_1}{2}, dfrac{x_2+y_2}{2}right)
$$
Thus we then obtain:
$$
D=left( dfrac{1-1}{2}, dfrac{9-1}{2}right)=(0,4)
$$
$$
E=left( dfrac{7+1}{2}, dfrac{5+9}{2}right)=(4,7)
$$
b. Determine the length using the distance formula $sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$:
$$
DE=sqrt{(4-0)^2+(7-4)^2}=sqrt{25}=5
$$
$AC$ will be twice $DE$ and thus will be 10 (since $overline{DE}$ is the median).
c.
$$
AC=sqrt{(7+1)^2+(5+1)^2}=sqrt{100}=10
$$
d. $F$ is the middle of $overline{BD}$:
$$
F=left( dfrac{0+1}{2}, dfrac{4+9}{2}right)=(0.5,6.5)
$$
$G$ is the middle of $overline{BE}$:
$$
G=left( dfrac{1+4}{2}, dfrac{9+7}{2}right)=(2.5,8)
$$
$overline{FG}$ is then twice as long as $overline{DE}$ and thus is four times as long as $overline{AC}$.
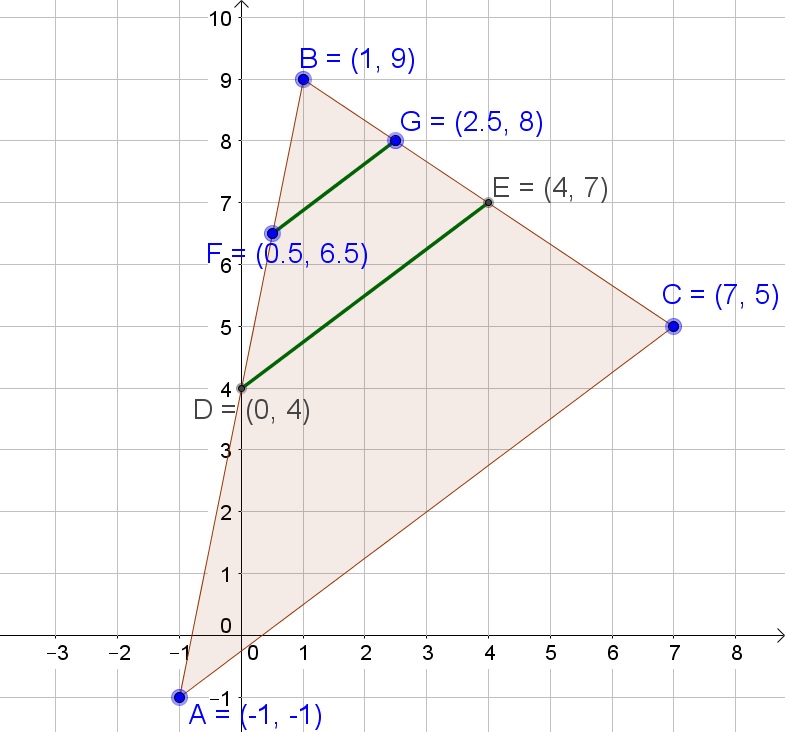
b. 5, 10
c. 10
d. $(0.5,6.5)$, $(2.5,8)$
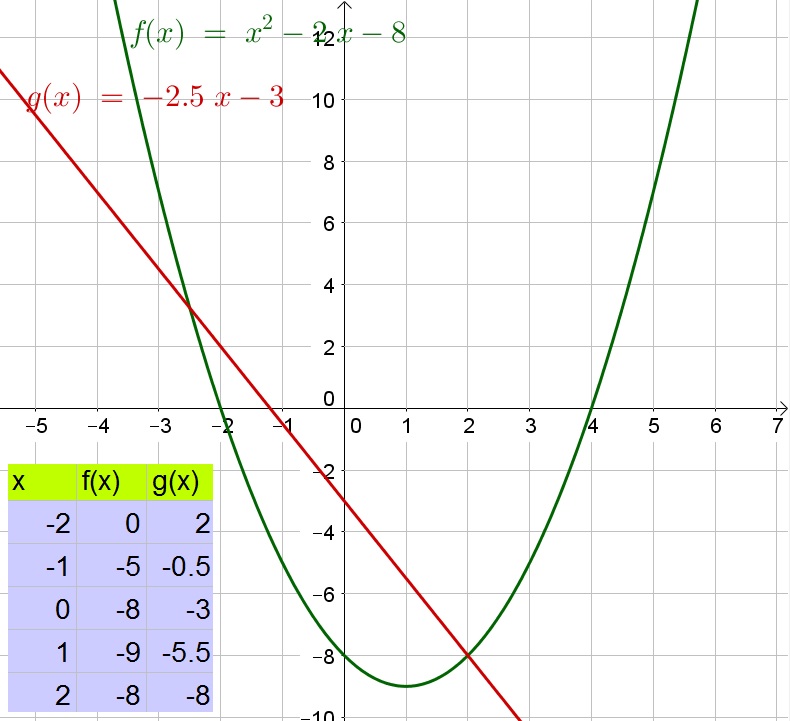
c. The points of intersection are about $(-2.5,3)$ and $(2,-8)$.
b. Twice
c. $(-2.5,3)$ and $(2,-8)$
b. Subtract the two equations:
$$
0=x^2+0.5x-5
$$
Factorize:
$$
0=0.5(x-2)(2x+5)
$$
Zero product property:
$$
x-2=0text{ or }2x+5=0
$$
Solve each equation to $x$:
$$
x=2text{ or }2x=-5
$$
$$
x=2text{ or }x=-dfrac{5}{2}=-2.5
$$
Determine $y$:
$$
y=-2.5(2)-3=-5-3=-8
$$
$$
y=-2.5left( -dfrac{5}{2}right)-3=6.25-3=3.25
$$
Thus the solutions are $(2,-8)$ and $(-2.5,3.25)$.
b. $(2,-8)$ and $(-2.5,3.25)$
$$
0=x^2-2x+5
$$
Determine the solution using the quadratic formula:
$$
x=dfrac{2pm sqrt{(-2)^2-4(1)(5)}}{2(1)}=dfrac{2pm sqrt{-16}}{2}=dfrac{2pm 4i}{2}=1pm 2i
$$
Determine $y$:
$$
y=2x-5=2(1pm 2i)-5=2pm 4i-5=-3pm 4i
$$
Thus the note that the solutions are complex. This relates to (a) because complex solutions are not shown on a set of real axis.
b. $(1pm 2i, -3pm 4i)$
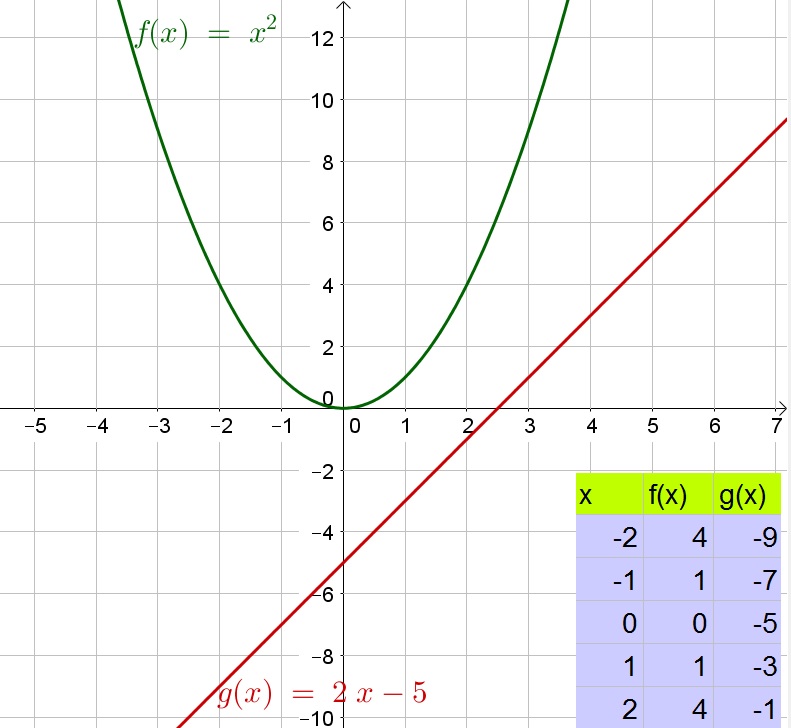
$$
y=x^2
$$
$$
y=2x-1
$$
Subtract the two equations:
$$
0=x^2-2x+1
$$
Factorize:
$$
0=(x-1)^2
$$
Zero product property:
$$
0=x-1
$$
Add 1 to both sides of the equation:
$$
1=x
$$
Determine $y$:
$$
y=x^2=(1)^2=1
$$
Thus the note that the system has one real solution $(1,1)$. This relates to the graph because the graphs will have one intersection.
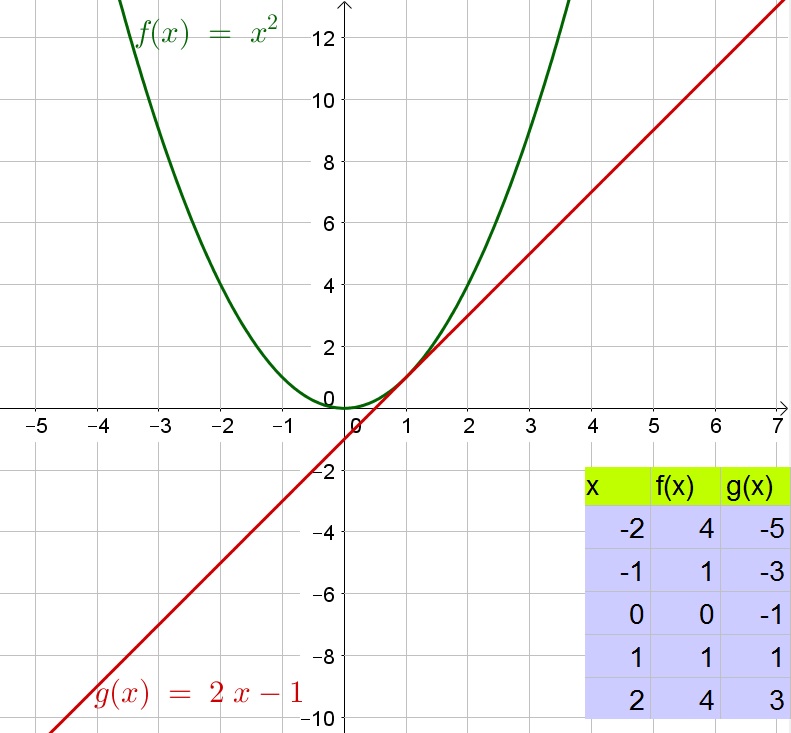
$$
begin{align*}
y&=x^2-5x+6
\ y&=-x^2
end{align*}
$$
The left-side of the two equations is the same expression and thus the right-sides of the equations need to be equal.
$$
x^2-5x+6=-x^2
$$
Add $x^2$ to each side:
$$
2x^2-5x+6=0
$$
Determine roots of quadratic equation $ax^2+bx+c=0$ using the quadratic formula $x=frac{-bpm sqrt{b^2-4ac}}{2a}$
$$
begin{align*}
x&=frac{-(-5)pm sqrt{(-5)^2-4(2)(6)}}{2(2)}=frac{5pm sqrt{-23}}{4}
end{align*}
$$
However, we now note that we take the square root of a negative integer, which is not possible and thus there are no real solutions. This then indicates that there are no intersections between the two graphs.
This relates to the graph because the graphs will have no intersections.
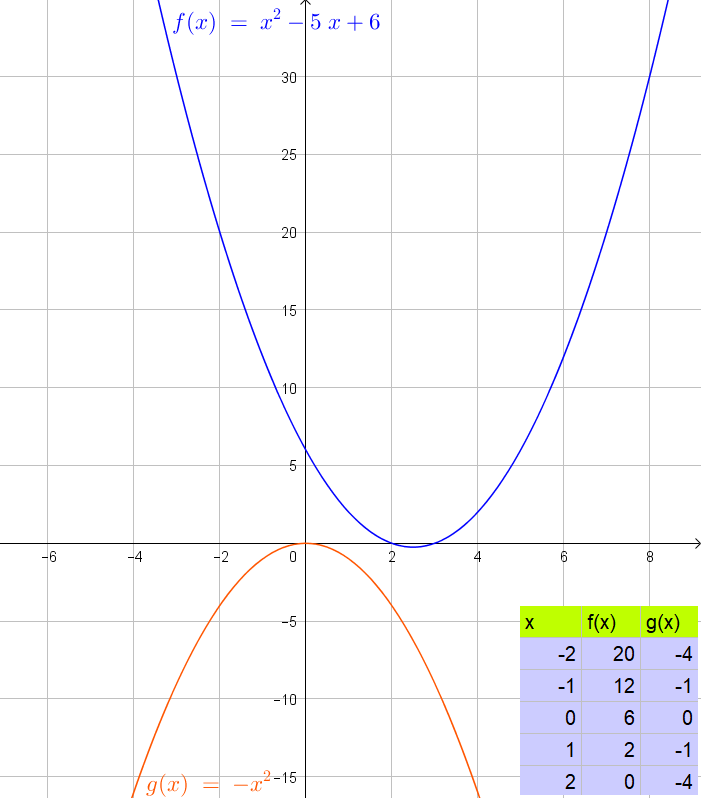
$$
begin{align*}
y&=x^2-4x+5
\ y&=-x^2+4x-1
end{align*}
$$
Subtract the two equations:
$$
0=2x^2-8x+6
$$
Use distributive property:
$$
0=2(x^2-4x+3)
$$
Factorize:
$$
0=2(x-3)(x-1)
$$
Zero product property:
$$
0=x-3text{ or }0=x-1
$$
Solve each equation to $x$:
$$
x=3text{ or }x=1
$$
Determine corresponding $y$-values:
$$
begin{align*}
y&=x^2-4x+5=3^2-4(3)+5=2
\ y&=x^2-4x+5=1^2-4(1)+5=2
end{align*}
$$
Thus the note that the system has two real solutions $(3,2)$ and $(1,2)$. This relates to the graph because the graphs will have two intersections.
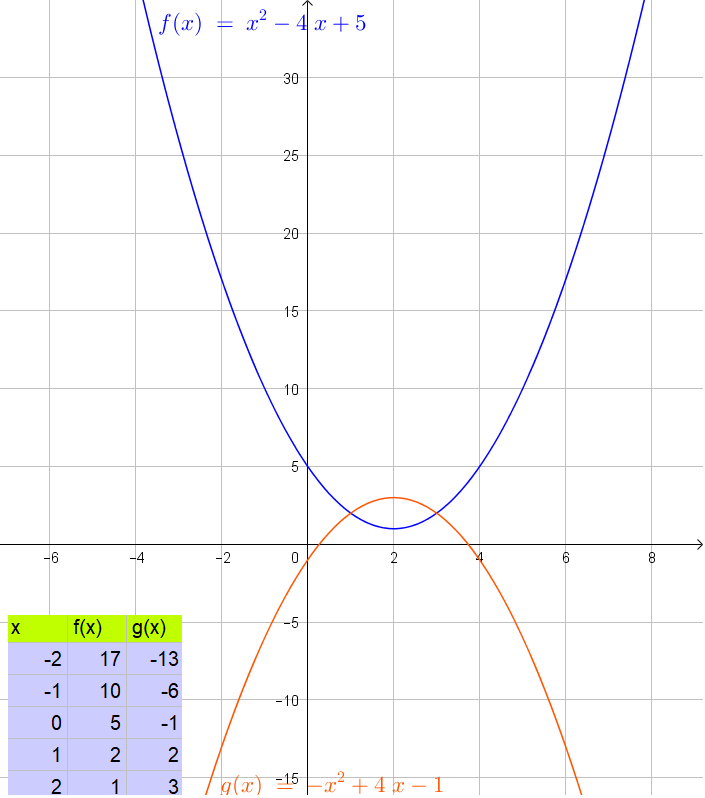
$$
begin{align*}
y&=x^2-x-2
\ y&=x^2+2x+1
end{align*}
$$
Subtract the two equations:
$$
0=-3x-3
$$
Factorize:
$$
0=-3(x+1)
$$
Zero product property:
$$
0=x+1
$$
Subtract 1 from both sides of the equation:
$$
-1=x
$$
Determine $y$:
$$
y=x^2-x-2=(-1)^2-(-1)-2=1+1-2=0
$$
Thus the note that the system has one real solution $(-1,0)$. This relates to the graph because the graphs will have one intersection.
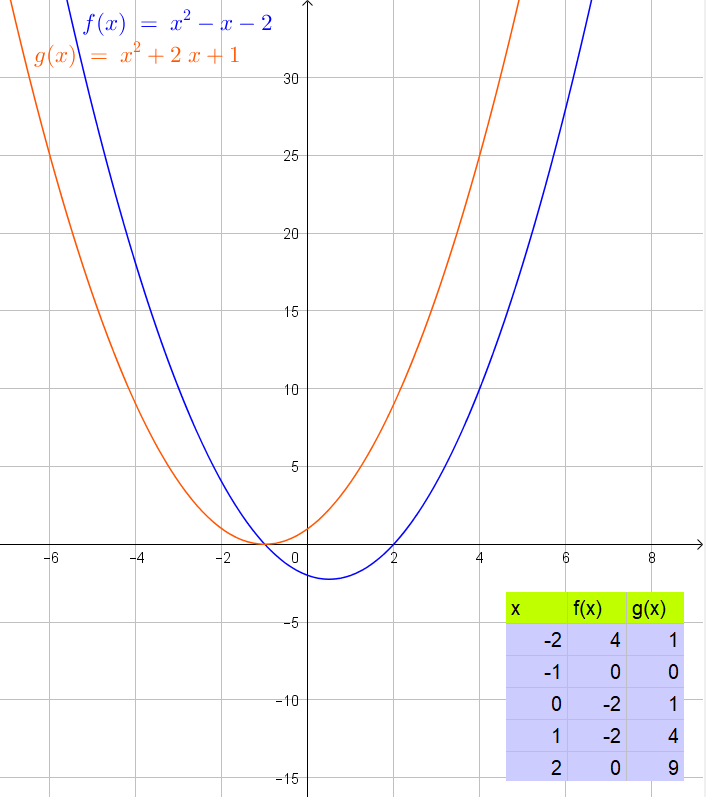
$$
begin{align*}
y&=x^2-x-2
\ y&=x-6
end{align*}
$$
The left-side of the two equations is the same expression and thus the right-sides of the equations need to be equal.
$$
x^2-x-2=x-6
$$
Subtract $x$ from each side:
$$
x^2-2x-2=-6
$$
Add $6$ to each side:
$$
x^2-2x+4=0
$$
Determine roots of quadratic equation $ax^2+bx+c=0$ using the quadratic formula $x=frac{-bpm sqrt{b^2-4ac}}{2a}$
$$
begin{align*}
x&=frac{-(-2)pm sqrt{(-2)^2-4(1)(4)}}{2(1)}=frac{2pm sqrt{-12}}{2}
end{align*}
$$
However, we now note that we take the square root of a negative integer, which is not possible and thus there are no real solutions. This then indicates that there are no intersections between the two graphs.
This relates to the graph because the graphs will have no intersections.

$$
begin{align*}
y&=2x^2+3x-9
\ y&=x-5
end{align*}
$$
Subtract the two equations:
$$
0=2x^2+2x-4
$$
Use distributive property:
$$
0=2(x^2+x-2)
$$
Factorize:
$$
0=2(x-1)(x+2)
$$
Zero product property:
$$
0=x-1text{ or }0=x+2
$$
Solve each equation to $x$:
$$
x=1text{ or }x=-2
$$
Determine corresponding $y$-values:
$$
begin{align*}
y&=x-5=1-5=-4
\ y&=x-5=-2-5=-7
end{align*}
$$
Thus the note that the system has two real solutions $(1,-4)$ and $(-2,-7)$. This relates to the graph because the graphs will have two intersections.
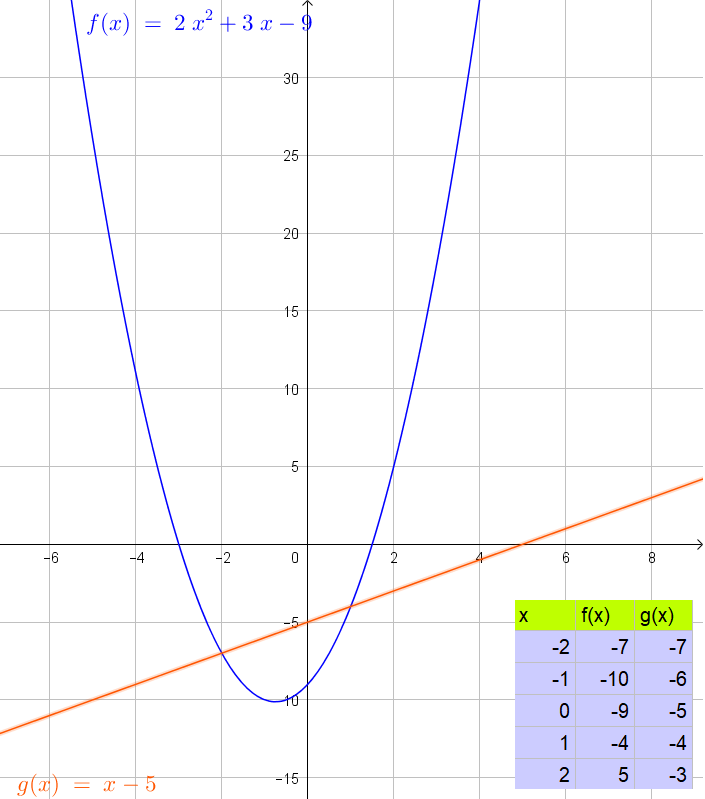
(a) One intersection $(1,1)$
(b) No intersection
(c) Two intersections $(3,2)$ and $(1,2)$
(d) One intersection $(-1,0)$
(e) No intersections
(f) Two intersections $(1,-4)$ and $(-2,-7)$
b. Subtract the two equations:
$$
0=2x^2-dfrac{17}{3}x+4
$$
Multiply both sides of the equation by 3:
$$
0=6x^2-17x+18
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{17pm sqrt{(-17)^2-4(6)(18)}}{2(6)}=dfrac{17pm sqrt{-143}}{12}=dfrac{17pm sqrt{143}i}{12}
$$
Thus the note that the solutions are complex and thus the graphs do not intersect.
b. No intersection

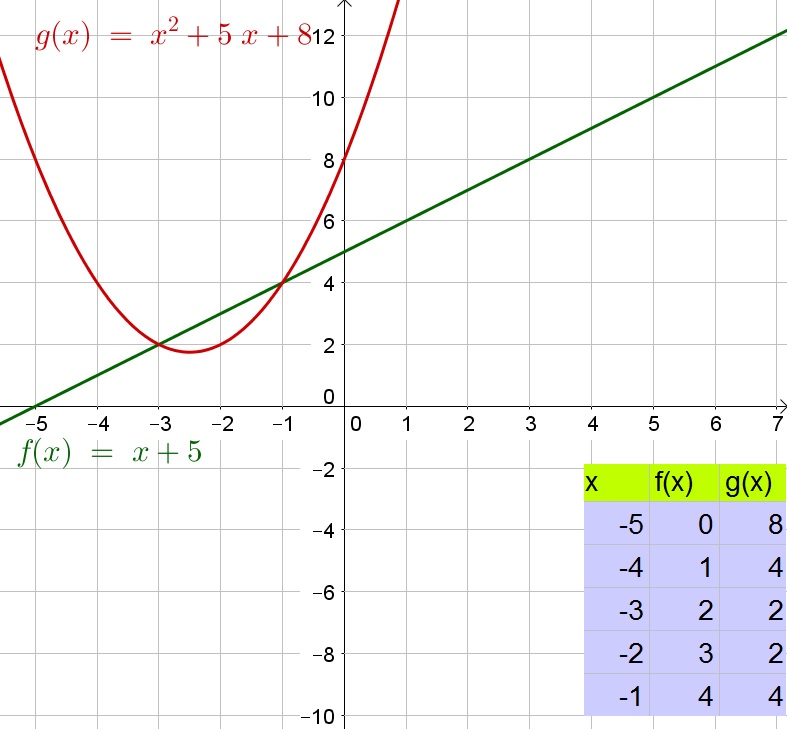
$$
0=x^2+4x+3
$$
Factorize:
$$
0=(x+3)(x+1)
$$
Zero product property:
$$
x+3=0text{ or }x+1=0
$$
Solve each equation to $x$:
$$
x=-3text{ or }x=-1
$$
Determine $y$:
$$
y=x+5=-3+5=2
$$
$$
y=x+5=-1+5=4
$$
Thus the solutions are $(-3,2)$ and $(-1,4)$.
b. The average speed is the difference in distance divided by the distance in time (in hours):
$$
dfrac{4.8-3.7}{5/6-4/6}=dfrac{1.1}{1/6}=6.6mph
$$
b. 6.6 mph
a. $(-3.5,10.25)$
b. $(-1,1)$
c. $(2.5,0.75)$
b. $(-1,1)$
c. $(2.5,0.75)$
mangle ECB=mangle EAD (text{Given})
$$
$$
overline{AE}cong overline{EC} (Etext{ is the midpoint of} overline{AC})
$$
$$
mangle AED=mangle BEC (text{Vertical angles})
$$
$$
Downarrow SAS
$$
$$
triangle AEDcong triangle CEB
$$
$$
Downarrow
$$
$$
overline{AD}cong overline{CB}
$$
$$
h=12sin{60text{textdegree}}approx 10.39
$$
The area of a parallelogram is the product of the length and the height:
$$
A_p=15cdot 10.39=155.85in^2
$$
The area of a circle sector with center angle $theta$ is $dfrac{theta}{360text{textdegree}}pi r^2$:
$$
A_c=dfrac{60text{textdegree}}{360text{textdegree}}pi 12^2=24piapprox 75.40in^2
$$
Thus the total area is then:
$$
A=A_p+A_c=155.85in^2+75.40in^2=231.25in^2
$$
$$
C=dfrac{60text{textdegree}}{360text{textdegree}}2pi 12=4pi
$$
The perimeter is then the sum of all lengths of the sides:
$$
15+12+15+12+4pi=54+4pi approx 66.57 in
$$
Perimeter 66.57 in
$$
P(AorUnder 20)=P(A)+P(Under20)-P(AandUnder20)
$$
$$
=dfrac{152+107+78+34}{1000}+dfrac{152+40+44}{1000}-dfrac{152}{1000}=dfrac{455}{1000}=0.455=45.5%
$$
b. The probability of an event not happening is 100% decreased by the probability of the event happening:
$$
P(notAandNotUnder 20)=100%-P(AorUnder 20)=100%-45.5%=54.5%
$$
c. The probability of an event not happening is 100% decreased by the probability of the event happening:
$$
begin{align*}
P(20orOlder)&=100%-P(Under20)
\ &=100%-dfrac{152+40+44}{1000}
\ &=100%-dfrac{236}{1000}
\ &=100%-23.6%
\ &=76.4%
end{align*}
$$
d. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(AGivenUnder 20)=dfrac{152}{250}=0.608=60.8%
$$
b. 54.5%
c. 76.4%
d. 60.8%
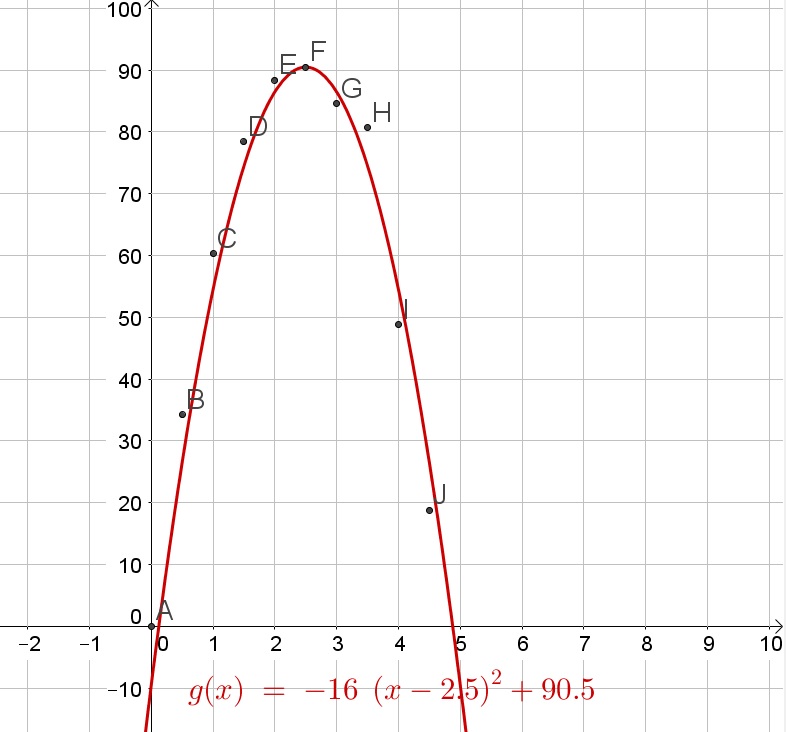
$$
dfrac{Delta y}{Delta x}=dfrac{60.3-34.2}{1-0.5}=52.2
$$
Thus the average rate of change is 52.2 ft per second.
c. The velocity is the distance traveled divided by the time:
$$
dfrac{88.4-78.4}{2-1}=10ft/s
$$
d. The maximum height is about 90.5ft. The velocity is the distance traveled divided by the time:
$$
dfrac{84.6-88.4}{3-2}approx -3.8 ft/s
$$
e. At about 2.5 seconds, yes because this is about half the time it takes for the balloon to land on the ground again.
f. The velocity is the distance traveled divided by the time:
$$
dfrac{0-18.8}{4.8-4.5}approx -63ft/s
$$
b. 52.2 ft per second
c. 10 ft/s
d. $-3.8$ ft/s
e. At about 2.5 seconds
f. $-63$ ft/s
a.
$$
dfrac{96-90}{2.5-1.875}=9.6ft/s
$$
b.
$$
dfrac{90-90}{3.125-1.875}=0ft/s
$$
c.
$$
dfrac{42-72}{4.375-3.75}=-48ft/s
$$
d.
$$
dfrac{42-0}{0.625-0}=67.2ft/s
$$
e. The height is increasing before the maximum and thus at less than 2.5s. The height is decreasing after the maximum and thus at more than 2.5s.
b. 0 ft/s
c. $-48$ ft/s
d. 67.2 ft/s
c. Increasing at less than 2.5 s, Decreasing at more than 2.5 s.
Replace $h$ with 2.25 and $k$ with $81$:
$$
f(x)=a(x-2.25)^2+81
$$
Replace $x$ with $4.5$ and $f(x)$ with $0$:
$$
0=a(4.5-2.25)^2+81=5.0625a+81
$$
Subtract 81 from both sides of the equation:
$$
-81=5.0625a
$$
Divide both sides of the equation by $5.0625$:
$$
-16=-dfrac{81}{5.0625}=a
$$
Replace $a$ in the equation with $-16$:
$$
f(x)=-16(x-2.25)^2+81
$$
$$
f(0.5)=-16(0.5-2.25)^2+81=32
$$
The average rate of change is the change in distance divided by the change:
$$
dfrac{32-0}{0.5-0}=64ft/s
$$
f(x)=-16(x-2.25)^2+81
$$
64 ft/s
The equation of motion of the projectile can be described by the following:
$$begin{gather}
f(x) = a(x-h)^2 + k
end{gather}$$
Since Char used Al’s slingshot, the equation of Char’s launch will be similar to Al’s. From Problem 9-75, we observe that the equation of motion of Al’s launch is described by the equation: $f(x) = -16(x-2.25)^2 + 81$.
However, in Char’s launch, he launched the balloon at a height $15 text{ ft}$. Hence, the maximum height of the balloon will change.
Since Char used Al’s slingshot, we use the equation of motion of Al’s launch. However, we increase the maximum height of the launch since Char initially launched the balloon from the top of the bleachers. We obtain the maximum height of the launch as follows:
$$begin{aligned}
k &= k_i + Delta k \
&= 81 + 15 \
&= boxed{96 text{ ft}}
end{aligned}$$
$$begin{aligned}
-16(x-h)^2 + k &=15 \
-16(0-h)^2 + (81 + 15) &= 15 \
-16(0-h)^2 + 96 &= 15 \
-16 h^2 + &= -81 \
h^2 &= frac{-81}{-16} \
h^2 &= 5.0625 \
h &= sqrt{5.0625} \
& boxed{h = 2.25}
end{aligned}$$
Hence, the time will not change for Char’s launch.
$$begin{aligned}
f(x) &= a(x-h)^2 + k \
& h = 2.25 \
& k = 96 \
f(x) &= -16(x-h)^2 + k \
f(x) &= -16(x-2.25)^2 + 96
end{aligned}$$
Hence, the equation of Char’s launch will be described by the function: $boxed{f(x) = -16(x-2.25)^2 +96}$
We obtain the time period where the height of Char’s balloon to be increasing using the equation of motion of Char’s launch. Since we know that the maximum height of the launch is $96 text{ ft}$, we know that the height is increasing at a time wherein the height of the launch is less than the maximum height and when the time is less than the value of $h$.
$$begin{aligned}
f(x) &= -16(x-2.25)^2 +96 \
x &= 2.25 \
f(x) &= -16(2.25-2.25)^2 +96 \
f(x) &= 96
end{aligned}$$
We observe that at time $t=2.25 text{ s}$, the maximum height is reached by the balloon. After this point, the balloon will then travel downwards. Hence, at time $t=0 text{ s}$ to $t=2.25 text{ s}$, the height of Char’s balloon is increasing. The height of Char’s balloon increases at $boxed{0 text{ s} < x le 2.25 text{ s}}$
We then determine the time period of when the height of Char’s balloon is decreasing. Since we know that the the maximum height is reached when the balloon is at a time $t=2.25 text{ s}$, after this height is reached the balloon will then travel downward, hence, the balloon height will be decreasing after this time. Therefore, the height of Char’s balloon decreases at $boxed{2.25 text{ s} < x le 4.5 text{ s}}$
b. $text{increasing at } 0 le x le 2.25 text{ s}$
c. $text{decreasing at } 2.25 text{ s} < x le 4.5 text{ s}$
The general equation for projectile motion is given by the equation:
$$begin{gather}
f(t) = frac{1}{2}at^2 + v_o t + h_o
end{gather}$$
Al’s balloon equation of motion: $f(x) = -16(t-2.25)^2 + 81$
Char’s balloon equation of motion: $f(x) = -16(t-2.25)^2 + 96$
$a = g$
Obtain (a) Al’s equation in standard form, (b) Char’s equation in standard form, and (c) determine what the coefficients represent
We know that the general equation for the projectile motion is described by Eq (1). Using Al’s equation we determine its standard form as follows:
$$begin{aligned}
f(t) &= -16(t-2.25)^2 +81 \
&= -16(t^2 -4.5t+5.0625) + 81 \
&= -16t^2 +(-16 cdot -4.5t) + (-16 cdot 5.0625) + 81 \
&= -16t^2 +72t -81 + 81 \
&= boxed{-16t^2 + 72t}
end{aligned}$$
$$begin{aligned}
v(t) &= frac{d}{dt}f(t) \
v(t) &= frac{d}{dt}(-16(t-2.25)^2 + 81) \
v(t) &= -32(t-2.25) \
v(0) &= -32(0-2.25) \
&= boxed{72 frac{text{ft}}{text{s}}}
end{aligned}$$
$$begin{aligned}
f(t) &= -16(t-2.25)^2 + 81 \
h(t) &= -16(t-2.25)^2 + 81 \
h(0) &= -16(0-2.25)^2 + 81 \
&= boxed{0 text{ ft}}
end{aligned}$$
$$begin{aligned}
f(t) &= frac{1}{2}at^2 + v_o t + h_o \
&= frac{1}{2}gt^2 + 72t + 0 \
&= frac{1}{2}gt^2 + 72t
end{aligned}$$
We verify that Al’s equation in standard form is: $boxed{-16t^2 + 72t}$
We know that the general equation for the projectile motion is described by Eq (1). Using Char’s equation we determine its standard form as follows:
$$begin{aligned}
f(t) &= -16(t-2.25)^2 +96 \
&= -16(t^2 -4.5t+5.0625) + 96 \
&= -16t^2 +(-16 cdot -4.5t) + (-16 cdot 5.0625) + 96 \
&= -16t^2 +72t -81 + 96 \
&= boxed{-16t^2 + 72t+15}
end{aligned}$$
$$begin{aligned}
v(t) &= frac{d}{dt}f(t) \
v(t) &= frac{d}{dt}(-16(t-2.25)^2 + 96) \
v(t) &= -32(t-2.25) \
v(0) &= -32(0-2.25) \
&= boxed{72 frac{text{ft}}{text{s}}}
end{aligned}$$
$$begin{aligned}
f(t) &= -16(t-2.25)^2 + 96 \
h(t) &= -16(t-2.25)^2 + 96 \
h(0) &= -16(0-2.25)^2 + 96 \
&= boxed{15 text{ ft}}
end{aligned}$$
$$begin{aligned}
f(t) &= frac{1}{2}at^2 + v_o t + h_o \
&= frac{1}{2}gt^2 + 72t + 15 \
&= frac{1}{2}gt^2 + 72t +15
end{aligned}$$
We verify that Char’s equation in standard form is: $boxed{-16t^2 + 72t+15}$
Based on the the general equation for the projectile motion, the coefficients of the equations of motion of Al’s and Char’s balloons, represents the value of $frac{1}{2}g$, the initial velocity, and the initial height of the projectile.
a.
$$
dfrac{12-7}{0.5-0.25}=20ft/s
$$
b.
$$
dfrac{16-12}{1-0.5}=8ft/s
$$
c. The velocity appears to become zero, this makes sense because the velocity changes sign after the top of her jump (after the top the velocity will be negative, while before it was positive, this is because the velocity changes direction).
b. 8 ft/s
c. Become zero
a. Function
b. Not a function
c. Function
d. Not a function
e. Yes, (a) is a constant function, because the function always takes on the value 2 no matter the input.
b. Not a function
c. Function
d. Not a function
e. Yes, (a)
$$
A’=(-1,-2)
$$
b. Reflecting a point about the $x$-axis, changes the sign of the $y$-coordinate and thus we obtain:
$$
C’=(4,-4)
$$
c. Apply the same transformation to the coordinates of $B$:
$$
B’=(4-1,1+3)=(3,4)
$$
b. $(4,-4)$
c. $(3,4)$
$$
a(x)=f(x)-2=x^2-2
$$
b. The given transformation reflects the function about the $x$-axis and stretches the function vertically by factor 2:
$$
b(x)=-2f(x)=-2x^2
$$
c. The given transformation translates the function to the right by 2 units:
$$
c(x)=f(x-2)=(x-2)^2
$$
d. The given transformation stretches the function horizontally by factor $dfrac{1}{2}$.
$$
d(x)=f(2x)=(2x)^2=4x^2
$$
b. $b(x)=-2x^2$
c. $c(x)=(x-2)^2$
d. $d(x)=4x^2$
a. The vertex is $(2,6)$ and this vertex represents the maximum value, because $a=-2$ is negative and thus the function opens downwards.
b.

$$
180text{textdegree}-29text{textdegree}=151text{textdegree}
$$
b. The interior angle of a polygon with $n$ sides is $dfrac{n-2}{n}180text{textdegree}$ and thus let:
$$
dfrac{n-2}{n}180text{textdegree}=170text{textdegree}
$$
Multiply both sides of the equation by $n$:
$$
(n-2)180=170n
$$
Divide both sides of the equation by 180:
$$
n-2=dfrac{17}{18}
$$
Add 2 to both sides of the equation:
$$
n=dfrac{53}{18}
$$
Since $n$ is not an integer, the regular polygon does not exist.
c. The sum of the interior angles of a regular $n$-gon is $(n-2)180text{textdegree}$ and thus we obtain for the 29-gon:
$$
(29-2)180text{textdegree}=27cdot 180text{textdegree}=4,860text{textdegree}
$$
b. No
c. 4,860$text{textdegree}$
$$
A: 80cdot dfrac{1}{4}=20
$$
$$
B: 80cdot dfrac{3}{8}=30
$$
$$
C: 80cdot dfrac{3}{8}=30
$$
Thus we expect to land on A 20 times and on B and C 30 times each.
B: 30 times
C: 30 times
$$
0=-16t^2+80t
$$
Factorize:
$$
0=-16t(t-5)
$$
Zero product property:
$$
t=0text{ or }t-5=0
$$
Solve each equation to $t$:
$$
t=0text{ or }t=5
$$
Since at $t=0s$ we hit the ball, the ball lands on the ground at $t=5s$.
$$
h=-16(2.5)^2+80(2.5)=100
$$
Thus the maximum height is 100ft.
c. The domain only makes sense on $[0,5]$, because outside of this domain the function will be negative and thus this would mean that the ball is under the ground, which is impossible.
b. 100 ft
c. $[0,5]$
$$
0=x^2-6x+9
$$
Factorize:
$$
0=(x-3)^2
$$
Zero product property:
$$
0=x-3
$$
Add 3 to both sides of the equation:
$$
3=x
$$
Determine $y$:
$$
y=4x-7=4(3)-7=12-7=5
$$
Thus the graphs intersect once at $(3,5)$.
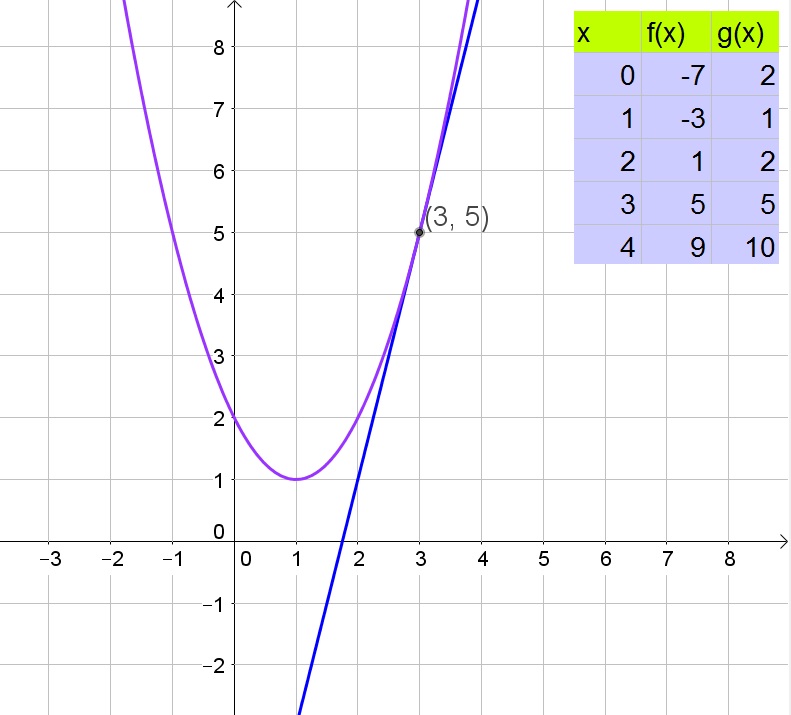
$$
-sqrt{12}<b-4<sqrt{12}
$$
Add 4 to all sides of the inequality:
$$
4-sqrt{12}<b<4+sqrt{12}
$$
Evaluate:
$$
0.5359<b<7.4641
$$

$$
x+3sqrt{4}
$$
Subtract 3 from all sides of the inequality:
$$
x-3+sqrt{4}
$$
Evaluate square root:
$$
x-3+2
$$
Evaluate sum/difference:
$$
x-1
$$

$$
2(x-3)>4
$$
Divide both sides of the inequality by 2:
$$
x-3>2
$$
Add 3 to both sides of the inequality:
$$
x>5
$$

b. $x1$
c. $x>5$
$$
f(x)=(x^2+4x+4)+5-4
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x+2)^2+1
$$
Thus the vertex is then $(-2,1)$.
$$
f(x)=(x^2-7x+12.25)-12.25
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
f(x)=(x-3.5)^2-12.25
$$
Thus the vertex is then $(3.5,-12.25)$.
b. $(3.5,-12.25)$
c. Minima
A pentagon has 5 vertices. Divide the pentagon into 5 congruent triangles. Determine the the height of these triangles using the tangent ratio:
$$
h=460.5tan{54text{textdegree}}approx 633.8
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{921cdot 633.8}{2}approx 291,864.9
$$
Since the pentagon is made up out of 5 triangles, the area of the pentagon is:
$$
5cdot 291,864.9=1,459,324.5 ft^2
$$
$$
dfrac{1,459,324.5 }{5280^2}approx 0.0524 mi^2
$$
$$
text{color{white} jmlirjtet mjretm lijretm lrejtj erjtl jrljtlr jlktjrl jtrlj ljr litelrj tlretm ermthmre hmtlrel thmrleht hlirht lhr}
$$
b. 0.0524 mi$^2$
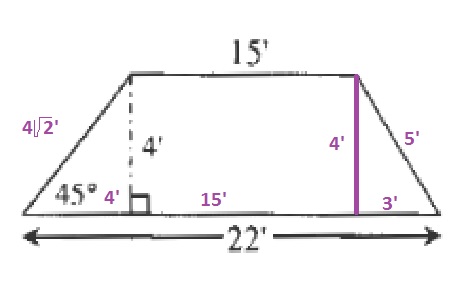
$$
dfrac{(15+22)4}{2}=74in^2
$$
The perimeter is the sum of all side lengths:
$$
4sqrt{2}’+15’+5’+22’=(4sqrt{2}+42)’
$$
Perimeter $(4sqrt{2}+42)’$
$$
r^2=x^2+y^2
$$
b. The sine ratio is the opposite side divided by the hypotenuse:
$$
sin{theta}=dfrac{y}{r}
$$
If $r=1$, we then obtain:
$$
sin{theta}=dfrac{y}{1}=y
$$
c. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
cos{theta}=dfrac{x}{r}
$$
If $r=1$, we then obtain:
$$
cos{theta}=dfrac{x}{1}=x
$$
b. $sin{theta}=dfrac{y}{r}$, $y$
c. $cos{theta}=dfrac{x}{r}$, $x$
b. $e$ is largest and $c$ is smallest
c. $f$ is largest and $d$ is smallest
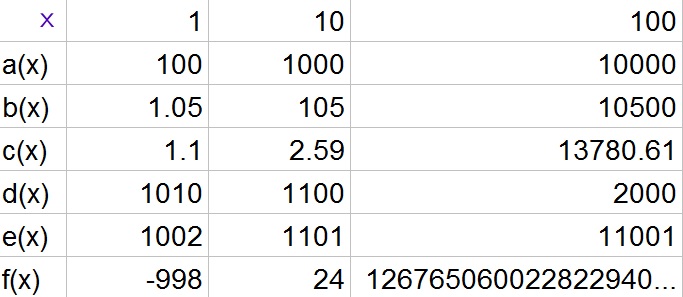
e. The value $x$ at which the order of finish no longer changes is the largest $x$-value of all the intersections between the functions. At this point in the race the order will no longer change.
b. $e$ is largest and $c$ is smallest
c. $f$ is largest and $d$ is smallest
d. $f$
e. Largest $x$-value of all the intersections between the functions.
If you have more than one type of the function, then the largest coefficient of $x$ (for linear), the largest coefficient of $x^2$ (for quadratic) and the largest base (for exponential) will win over the other functions of the same kind.
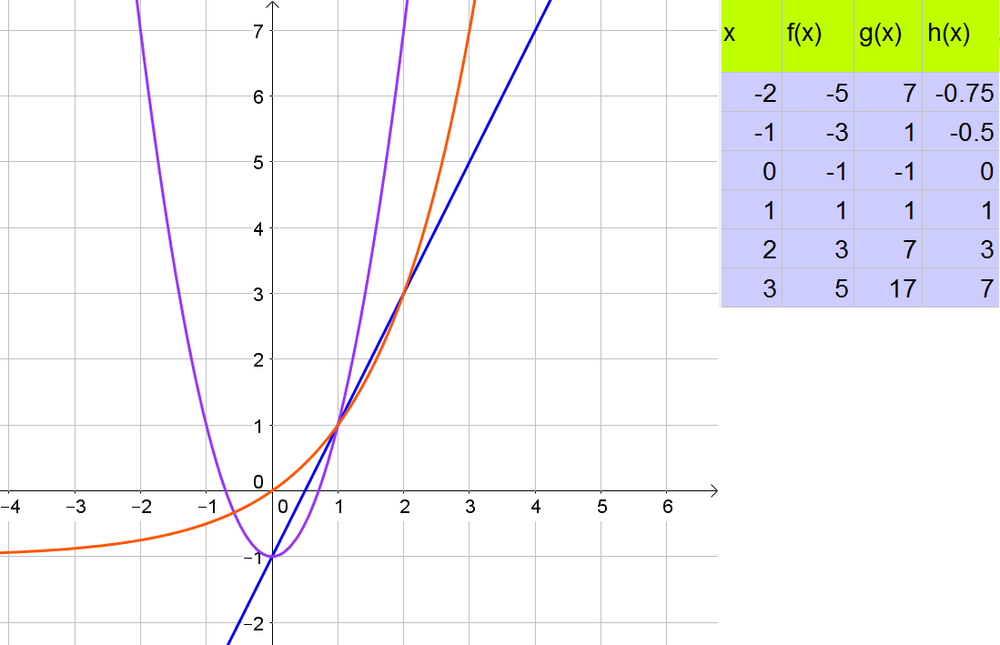
c. The average rate of change is the difference in $y$-values divided by the difference in $x$-values. Let us first determine it for the interval $1leq xleq 2$:
$$
f:dfrac{3-1}{2-1}=2
$$
$$
g:dfrac{7-1}{2-1}=4
$$
$$
h:dfrac{3-1}{2-1}=2
$$
Next for the interval $2leq xleq 3$:
$$
f:dfrac{5-3}{3-2}=2
$$
$$
g:dfrac{17-7}{3-2}=10
$$
$$
h:dfrac{7-3}{3-2}=4
$$
d. We note that $f$ will keep increasing at a constant factor and thus this function will be last. The average rate of change of the other two functions are not really representative, because $h$ will increase faster than $g$, but this is not noticable yet at low $x$-values.
b. $f$ and $h$ are always increasing, $g$ is decreasing on $(-infty, 0)$ while increasing on $(0,+infty)$
c.
$1leq xleq 2$: 2, 4, 2
$2leq xleq 3$: 2, 10, 4
d. $h$ first and $f$ last

$$
Mateo: dfrac{1400-1000}{2-0}=200
$$
$$
Marcy: dfrac{1251.4-1085}{2-0}=83.2
$$
c. The average rate of change is the difference in $y$-values divided by the difference in $x$-values:
$$
Mateo: dfrac{2000-1600}{5-3}=200
$$
$$
Marcy: dfrac{1554.33-1344.71}{5-3}=108.81
$$
d. Marcy’s account will have more money in the long run because the average rate of change will keep increasing, while Mateo’s rate of change will remain constant.
b. 200, 83.2
c. 200, 108.81
d. Marcy’s account
$$
0=x^2+0.6x-0.55
$$
Factorize:
$$
0=0.05(2x-1)(10x+11)
$$
Zero product property:
$$
2x-1=0text{ or }10x+11=0
$$
Solve each equation to $x$:
$$
2x=1text{ or }10x=-11
$$
$$
x=dfrac{1}{2}text{ or }x=-dfrac{11}{10}
$$

x=dfrac{1}{2}text{ and }x=-dfrac{11}{10}
$$
$$
h=11
$$
Thus the height of the platform is 11 meters.
b. The firwork hits the ground at $h=0$:
$$
0=-4.9t^2+50t+11
$$
Determine the roots using the quadratic formula:
$$
t=dfrac{-50pmsqrt{50^2-4(-4.9)(11)}}{2(-4.9)}=dfrac{-50pm sqrt{2715.6}}{-9.8}approx -0.2text{ or }10.4
$$
Thus the firework hits the ground after about 10.4 seconds.
c. The maximum height is attained at the line of symmetry:
$$
t=-dfrac{50}{2(-4.9)}approx 5.1
$$
The corresponding height is then the maximum height:
$$
h=-4.9(5.1)^2+50(5.1)+11approx 139
$$
Thus the maximum height is about 11 meters.
b. 10.4 seconds
c. 11 meters
b. The graph of $y=f(x)$ is stretched vertically by factor 3.
c. The graph of $y=f(x)$ is translated left by 3 units.
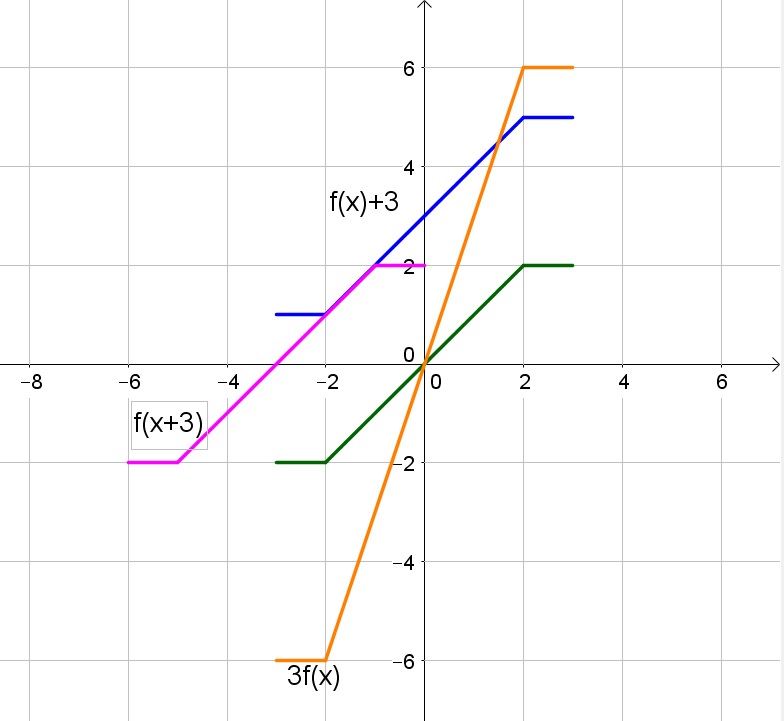
b. Stretch vertically by factor 3
c. Translate to the left by 3 units
$$
2x+4x-3+7x-6+3x+12+x+10=540
$$
Combine like terms:
$$
17x+13=540
$$
Subtract 13 from both sides of the equation:
$$
17x=527
$$
Divide both sides of the equation by 17:
$$
x=31
$$
$$
4x+20+5x-2=180
$$
Combine like terms:
$$
9x+18=180
$$
Subtract 18 from both sides of the equation:
$$
9x=162
$$
Divide both sides of the equation by 9:
$$
x=18
$$
b. $x=18$
$$
360A=theta pi r^2
$$
Divide both sides of the equation by $pi r^2$:
$$
dfrac{360A}{pi r^2}=theta
$$
Interchange the left and right side of the equation:
$$
theta=dfrac{360A}{pi r^2}
$$
$$
360A=theta pi r^2
$$
Divide both sides of the equation by $theta pi$:
$$
dfrac{360A}{theta pi}=r^2
$$
Take the square root of both sides of the equation:
$$
sqrt{dfrac{360A}{theta pi}}=r
$$
Interchange the left and right side of the equation:
$$
r=sqrt{dfrac{360A}{theta pi}}
$$
b. $r=sqrt{frac{360A}{thetapi}}$
$$
left( dfrac{2}{5}right)^2=dfrac{4}{25}
$$
b. The ratio of the areas is the ratio of the perimeters squares:
$$
14^2:1^2=196:1
$$
c. The ratio of the perimeters is the square root of the ratio of the areas:
$$
sqrt{81}=9
$$
b. 196:1
c. 9
b. The domain contains only nonnegative integer values (since the time cannot be negative):
$$
f(t)=450
$$
c. The second piece is $f(t)=450.50$ while the third piece is $f(t)=451$.
d. Yes, because for every $x$-value, there is exactly one corresponding $y$-value.
e. Because the graph takes on the shape of steps (of a staircase). Other situations are for example the greatest integer of real numbers.
b. $f(t)=450$
c. $f(t)=450.50$, $f(t)=451$
d. Yes
c. Shape of steps of a staircase, greatest integer of real numbers.
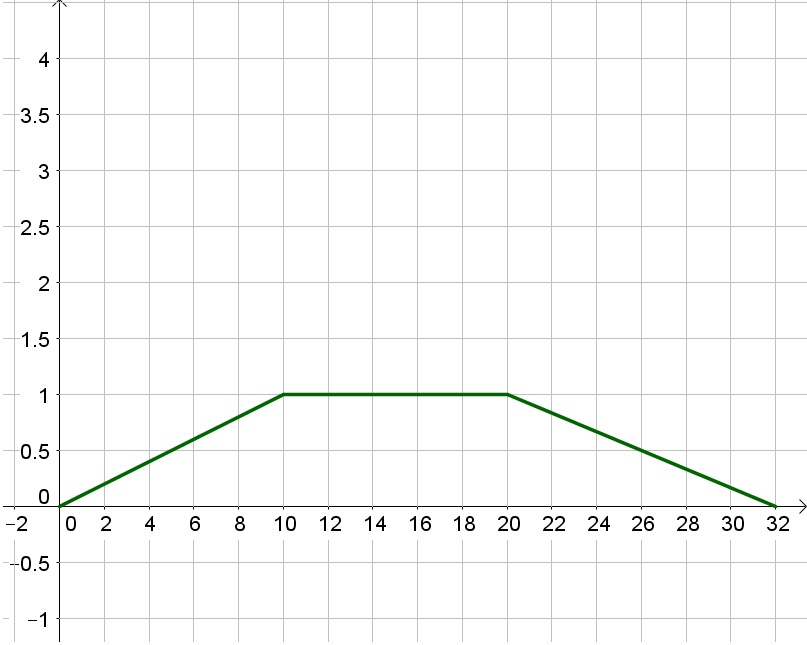
c.
$$
f(x)=left{ begin{matrix} dfrac{1}{10}x & 0leq x leq 10 \ 1 & 10<xleq 20\ -dfrac{1}{12}(x-32) & 20<xleq 32end{matrix}right.
$$
$$
f(x)=left{ begin{matrix} dfrac{1}{10}x & 0leq x leq 10 \ 1 & 10<xleq 20\ -dfrac{1}{12}(x-32) & 20<xleq 32end{matrix}right.
$$
$$
$37.78+10cdot $3.64=$74.18
$$
b. He has to pay the basic fee increase by the product of the billin rate and the HCF:
$$
$37.78+dfrac{30,000}{748.05}cdot $8.19=$366.23
$$
c.
$$
dfrac{$200-$37.78}{$5.82}=27.87HCF=20,850gallons
$$
Thus the water usage needs to be reduced by about 10,000 gallons for the bill to be than $200.
$$
dfrac{$150-$37.78}{$4.08}=27.5HCF>24HCF=17,953gallons
$$
Thus the water usage needs to be reduced by about 12,000 gallons for the bill to be than $150.
\
\
d.$
$$
f(x)=left{ begin{matrix}3.64x & 0leq xleq 8 \ 4.08x & 8<xleq 24 \ 5.82x & 24<xleq 36\ 8.19x & 36<xend{matrix}right.
$$
$
b. $$366.23$
c. 10,000 gallons, 12,000 gallons
d.
$$
f(x)=left{ begin{matrix}3.64x & 0leq xleq 8 \ 4.08x & 8<xleq 24 \ 5.82x & 24<xleq 36\ 8.19x & 36<xend{matrix}right.
$$
Piecewise-Defined functions contain multiply expression for the function definition, where each expression is defined on a different interval.
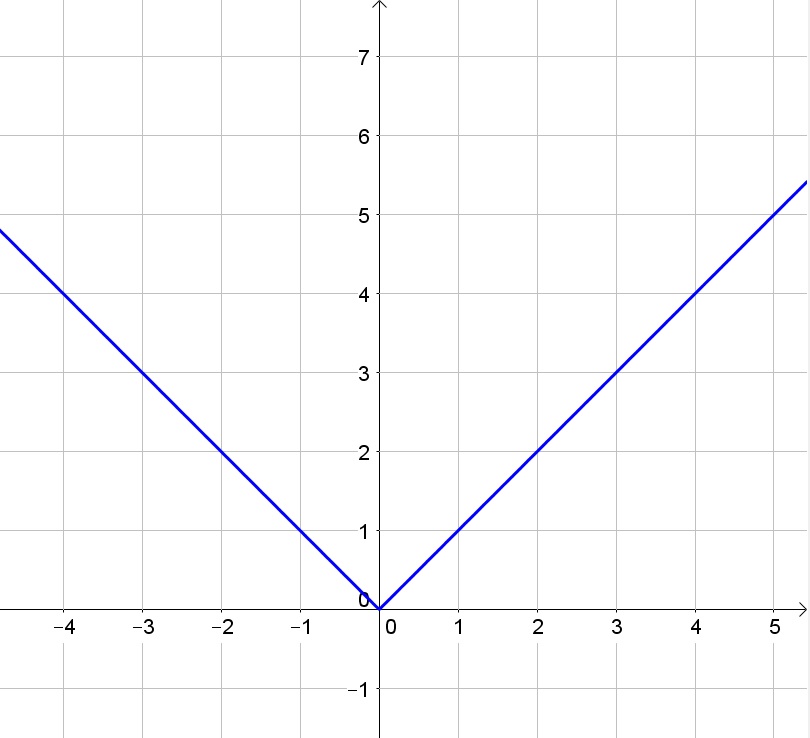
$$
f(x)=left{ begin{matrix}x & xgeq 0 \ -x & x<0end{matrix}right.
$$
f(x)=left{ begin{matrix}x & xgeq 0 \ -x & x<0end{matrix}right.
$$
$$
(x-1)^2+2=6
$$
Subtract 2 from both sides of the equation:
$$
(x-1)^2=4
$$
Take the square root of both sides of the equation:
$$
x-1=pm 2
$$
Add 1 to both sides of the equation:
$$
x=1pm 2=3text{ or }-1
$$
Thus 3 or $-1$ has been dropped in.
a. The vertex is $(-1,-5)$ and since $a=2$ is positive, the function opens upwards and thus the vertex is a minimum.
b. The value of the function at the minimum is the $y$-coordinate of the vertex (see part (a)) and thus is $y=-5$.
b. $y=-5$
A pentagon has 5 vertices. Divide the pentagon into 5 congruent triangles. Determine the the height these triangles using the tangent ratio:
$$
h=5tan{54text{textdegree}}approx 6.8819
$$
The area of a triangles is the product of the base and the height divided by 2:
$$
dfrac{10cdot 6.8819}{2}=34.4095
$$
Since the shaded region of the pentagon is made up out of 3 triangles, the area of the shaded region is:
$$
3cdot 34.4095=103.2285units^2approx 103 units^2
$$
103 units^2
$$
$$
P(green)=sqrt{16%}=sqrt{0.16}=0.4=40%
$$
The probability of purple is then the complement:
$$
P(purple)=1-0.4=0.6=60%
$$
The probability of landing on purple twice is then the product of each probability:
$$
P(PurpleTwice)=0.6cdot 0.6=0.36=36%
$$
$$
dfrac{11}{33}=dfrac{1}{3}
$$
b. The ratio of the areas is the linear scale factor squared:
$$
left( dfrac{1}{3}right)^2=dfrac{1}{9}
$$
b. $frac{1}{9}$
$$
g(10)=10(10)^2=1000
$$
$$
h(10)=1.01^{10}=1.104622125
$$
$$
m(10)=0.01(2)^{10}=10.24
$$
Thus we note that $g$ is ahead.
b. The average rate of change is the difference in $y$-values divided by the difference in $x$-values:
$$
g: dfrac{40-0}{2-0}=20
$$
$$
h: dfrac{1.0201-1}{2-0}=0.01005
$$
$$
m: dfrac{0.04-0.01}{2-0}=0.015
$$
c. From the table we note that the equation of $m$ is
$$
m(x)=0.01cdot 2^x
$$
d. The function $m$ will win, because it is the exponential function with the largest base. Then determine when it will take the lead:
$$
1.01^x=0.01(2)^x
$$
Divide both sides of the equation by $1.01^x$:
$$
1=0.01left( dfrac{2}{1.01}right)^x
$$
Multiply both sides of the equation by 100:
$$
100=left( dfrac{2}{1.01}right)^x
$$
Then we note that if $x=7$ the function $m$ will take the lead.
b.20, 0.01005, 0.015
c. $m(x)=0.01cdot 2^x$
d. $m$, $x=7$
a. The function $a$ is quadratic:
$$
a(x)=f(x)+c(x)=x^2+3
$$
b. The function $b$ is quadratic:
$$
b(x)=c(x)cdot g(x)=3x^2
$$
c. The function $d$ is linear:
$$
d(x)=g(x)-c(x)=2x+1-3=2x-2
$$
d. The function $e$ is linear:
$$
e(x)=c(x)cdot g(x)=3cdot (2x+1)=6x+3
$$
b. $b(x)=3x^2$
c. $d(x)=2x-2$
d. $e(x)=6x+3$
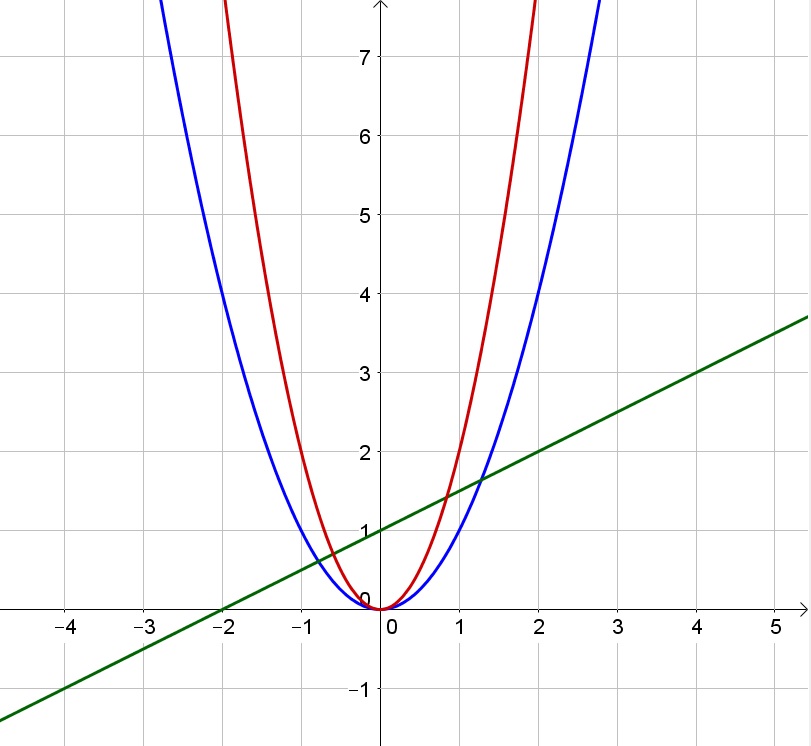
e. No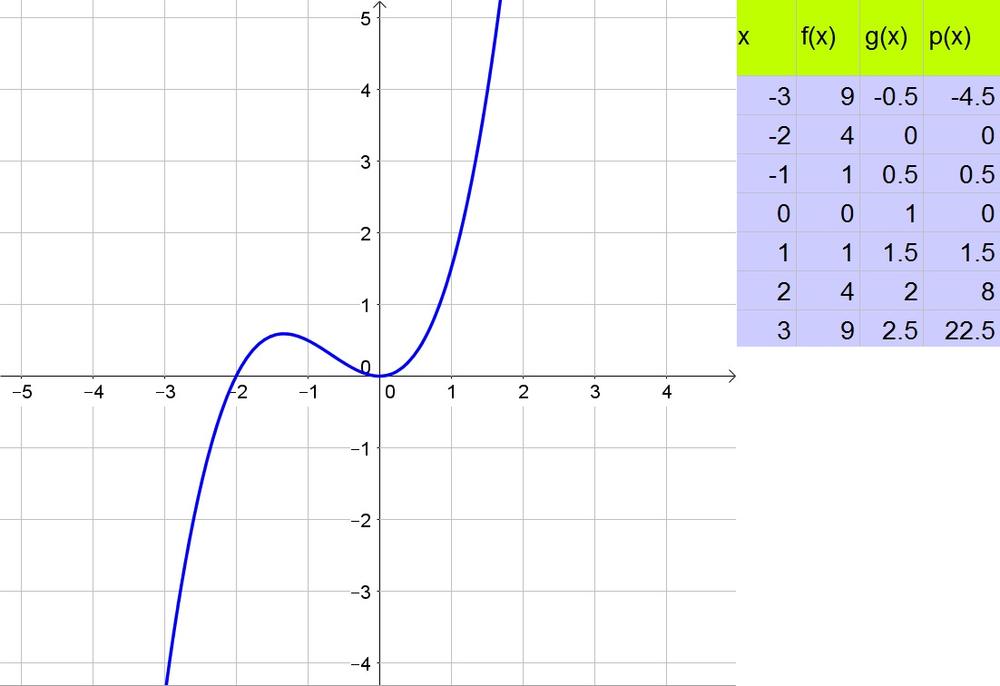
b. Table
c. parabolas
c. Cubic Curve
e. No
a. Replace $h$ with 22 and $k$ with 43:
$$
h(x)=a(x-22)^2+43
$$
Replace $x$ with 100 and $h(x)$ with 0:
$$
0=a(100-22)^2+43=6084a+43
$$
Subtract 43 from both sides of the equation:
$$
-43=6084a
$$
Divide both sides of the equation by 6084:
$$
-dfrac{43}{6084}=a
$$
Replace $a$ with its value:
$$
h(x)=-dfrac{43}{6084}(x-22)^2+43
$$
$$
j(x)=a(x-24)^2+45
$$
Replace $x$ with 0 and $j(x)$ with 40:
$$
40=a(0-24)^2+45=576a+45
$$
Subtract 45from both sides of the equation:
$$
-5=576
$$
Divide both sides of the equation by 2025:
$$
-dfrac{5}{576}=a
$$
Replace $a$ with its value:
$$
j(x)=-dfrac{5}{576}(x-24)^2+45
$$
$$
h(24)=-dfrac{43}{6084}(24-22)^2+43approx 42.97
$$
Determine the difference in heights:
$$
45-42.97=2.03
$$
Thus the skier is about 2.03 ft about the landing hill at her peak.
b. $j(x)=-frac{5}{576}(x-24)^2+45$
c. 2.03 ft
$$
f(x)=j(x)-h(x)
$$
b. We note on the graph that the skier lands at about $x=70$ ft.
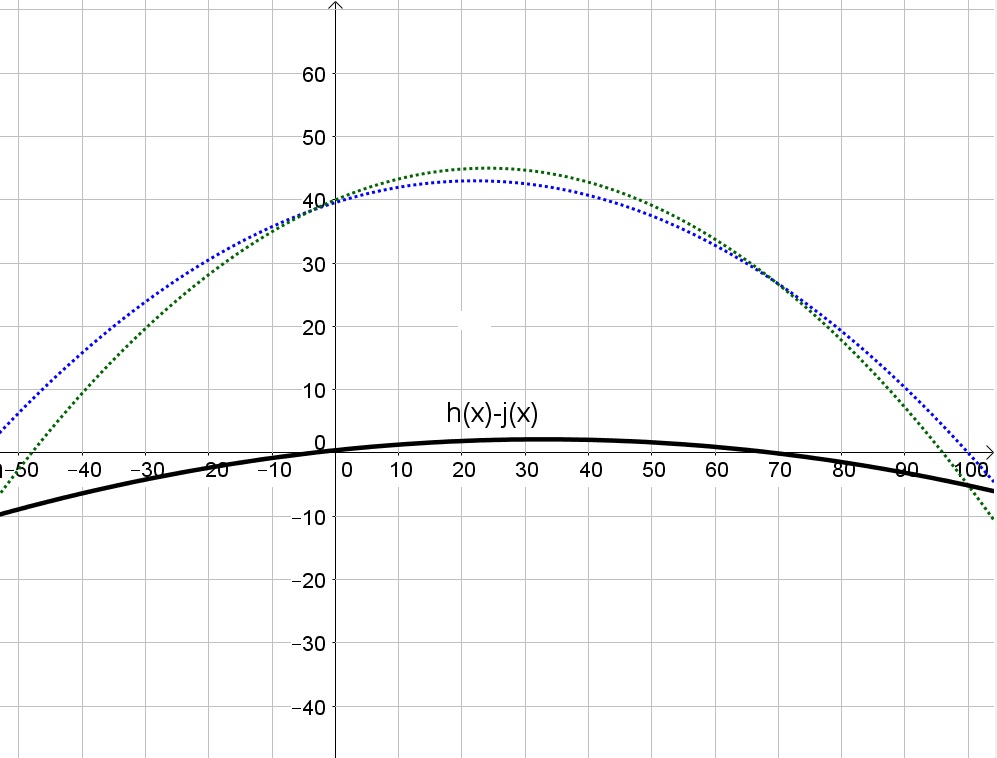
$$
f(x)=left{ begin{matrix} j(x) & 0leq x leq 70\ h(x) & x>70end{matrix}right.
$$
b. $x=70$ ft
c.
$$
f(x)=left{ begin{matrix} j(x) & 0leq x leq 70\ h(x) & x>70end{matrix}right.
$$
$$
y=f(0)=0^2+0-6=-6
$$
b. Replace $f(x)$ with 0:
$$
0=x^2+x-6
$$
Factorize:
$$
0=(x+3)(x-2)
$$
Zero product property:
$$
x+3=0text{ or }x-2=0
$$
Solve each equation to $x$:
$$
x=-3text{ or }x=2
$$
Thus the $x$-intercepts are $x=-3$ and $x=2$.
$$
g(x)=f(x)+c(x)=x^2+x-6+6=x^2+x
$$
d. Since the function $g$ is the function $f$ translated up by 6 units, we know that the $y$-intercept is $y=0$ and the $x$-intercepts is $x=0$ and $x=-1$:
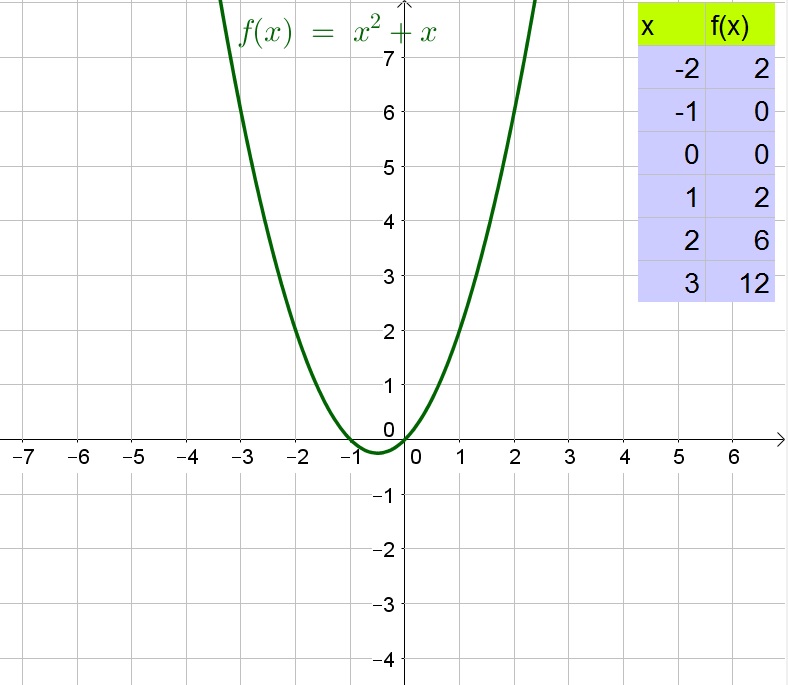
b. $(-3,0)$ and $(2,0)$
c. $g(x)=x^2+x$
d.
$x$-intercepts: $(0,0)$ and $(1,0)$
$y$-intercepts: $(0,0)$
The left part of the function has $y$-intercept $b=-3$ and the slope is
$$
a=dfrac{y_2-y_1}{x_2-x_1}=dfrac{1+3}{2-0}=2
$$
Thus the equation of the left part of the equation is then $y=2x-3$.
The right part of the function has $y$-intercept $b=1$ (if you draw the line further) and the slope is
$$
a=dfrac{y_2-y_1}{x_2-x_1}=dfrac{5-3}{4-2}=1
$$
Thus the equation of the left part of the equation is then $y=1x+1=x+1$.
Then the equation of the piecewise function:
$$
f(x)=left{ begin{matrix} 2x-3 & x<2\ x+1 & xgeq 2end{matrix} right.
$$
f(x)=left{ begin{matrix} 2x-3 & x<2\ x+1 & xgeq 2end{matrix} right.
$$
$$
EV=$3cdot dfrac{3}{12}-$1 cdot dfrac{7}{12}+$ 10cdot dfrac{2}{12}approx $1.83
$$
The game is not fair, because the expected value is not zero. Since the expected value is positive, the person that selects the beads will have the advantage in this game.
$$
0=-16t^2+92t
$$
Factorize:
$$
0=-4t(4t-23)
$$
Zero product property:
$$
t=0text{ or }4t-23=0
$$
Solve each equation to $t$:
$$
t=0text{ or }4t=23
$$
$$
t=0text{ or }t=dfrac{23}{4}=5.75
$$
Thus at 5.75 seconds the rocket reaches the ground (again).
$$
-16t^2+92t>76
$$
Subtract 76 from both sides of the inequality:
$$
-16t^2+92t-76>0
$$
Factorize
$$
-4(t-1)(4t-19)>0
$$
Since the function $y=-4(t-1)(4t-19)$ opens downwards:
$$
1leq t leq 4.75
$$
$$
Domain=[0,5.75]
$$
b. $-16t^2+92t>76$, $1leq tleq 4.75$
c. No
d. $[0,5.75]$
$$
y=a(x+9)(x-5)
$$
If $x=0$, then $y=11.25$:
$$
11.25=a(9)(-5)=-45a
$$
Divide both sides of the equation by $-45$:
$$
-0.25=a
$$
Replace $a$ with its value:
$$
y=-0.25(x+9)(x-5)
$$
$$
y=a(x+7)(x+4)
$$
If $x=-5.5$, then $y=-4.5$:
$$
-4.5=a(1.5)(-1.5)=-2.25a
$$
Divide both sides of the equation by $-2.25$:
$$
2=a
$$
Replace $a$ with its value:
$$
y=2(x+7)(x+4)
$$
$$
y=a(x+6)^2
$$
If $x=0$, then $y=12$:
$$
12=a(6)^2=36a
$$
Divide both sides of the equation by $36$:
$$
dfrac{1}{3}=a
$$
Replace $a$ with its value:
$$
y=dfrac{1}{3}(x+6)^2
$$
b. $y=2(x+7)(x+4)$
c. $y=frac{1}{3}(x+6)^2$
$$
C=2pi 14=28pi in.
$$
Then the distance is the product of the time, the numner of revolutions per time and the circumference of the tire:
$$
5cdot 120cdot 28pi in.=16,800 pi in.
$$
$$
P_s=7+3+5=15
$$
Since $triangle ABC$ and $triangle ACD$ are similar with scale factor 2, the perimeter is then also multiplied by the scale factor 2:
$$
P_l=2cdot 15=30units
$$
b. The area of the larger triangle is the product of the area of the smaller triangle with the scale factor squared:
$$
A_l=2^2cdot 6.5=26 units^2
$$
b. 26 units$^2$
$$
f(x)=3x+4
$$
b. If 16 is put in, then 4 should come out and if $-5$ is put in, then $-3$ should come out.
c. The function would first need to subtract 4 and then divided the number by 3.
d. Thus the function equation then becomes:
$$
f^{-1}(x)=dfrac{1}{3}(x-4)
$$
b. $-3$
c. Subtract 4, Divide by 3
d. $f^{-1}(x)=frac{1}{3}(x-4)$
$$
5x
$$
Then subtract 8:
$$
5x-8
$$
Finally divide by 2:
$$
dfrac{1}{2}(5x-8)
$$
Thus the equation is then:
$$
g(x)=dfrac{1}{2}(5x-8)
$$
Let $x$ be 3:
$$
g(3)=dfrac{1}{2}(5(3)-8)=dfrac{7}{2}=3.5
$$
$$
2x
$$
Then add 8 8:
$$
2x+8
$$
Finally divide by 5:
$$
dfrac{1}{5}(2x+8)
$$
Thus the equation is then:
$$
g^{-1}(x)=dfrac{1}{5}(2x+8)
$$
b. $g^{-1}(x)=frac{1}{5}(2x+8)$
$$
y=4x-12
$$
Interchange $x$ and $y$:
$$
x=4y-12
$$
Solve the equation to $y$ by first adding 12 to both sides of the equation:
$$
x+12=4y
$$
Divide both sides of the equation by 4:
$$
dfrac{1}{4}(x+12)=y
$$
Interchange left and right side of the equation and replace $y$ with $n^{-1}(x)$:
$$
n^{-1}(x)=dfrac{1}{4}(x+12)
$$
$$
y=dfrac{x-7}{10}
$$
Interchange $x$ and $y$:
$$
x=dfrac{y-7}{10}
$$
Solve the equation to $y$ by first multiplying both sides of the equation by 10:
$$
10x=y-7
$$
Add 7 to both sides of the equation:
$$
10x+7=y
$$
Interchange left and right side of the equation and replace $y$ with $j^{-1}(x)$:
$$
j^{-1}(x)=10x+7
$$
b. $j^{-1}(x)=10x+7$
$$
F=aC+32
$$
When $C=100$, then $F=212$:
$$
212=100a+32
$$
Subtract 32 from both sides of the equation:
$$
180=100a
$$
Divide both sides of the equation by 100:
$$
dfrac{9}{5}=a
$$
Replace $a$ with its value:
$$
F=dfrac{9}{5}C+32
$$
$$
F=dfrac{9}{5}(30)+32=86
$$
$$
F=dfrac{9}{5}(25)+32=77
$$
Thus it will be 86$text{textdegree}$ F warm and 77$text{textdegree}$ F cold.
$$
C=a(x-32)
$$
When $F=212$, then $C=100$:
$$
100=a(212-32)=180a
$$
Divide both sides of the equation by 180:
$$
dfrac{5}{9}=a
$$
Replace $a$ with its value:
$$
y=dfrac{5}{9}(x-32)
$$
b. 86$text{textdegree}$ F warm and 77$text{textdegree}$ F cold
c. $y=frac{5}{9}(x-32)$
d. Inverses
$$
y=2x-1
$$
Interchange $x$ and $y$:
$$
x=2y-1
$$
Solve the equation to $y$ by first adding 1 to both sides of the equation:
$$
x+1=2y
$$
Divide both sides of the equation by 2:
$$
dfrac{1}{2}(x+1)=y
$$
Interchange left and right side of the equation and replace $y$ with $h^{-1}(x)$:
$$
h^{-1}(x)=dfrac{1}{2}(x+1)
$$
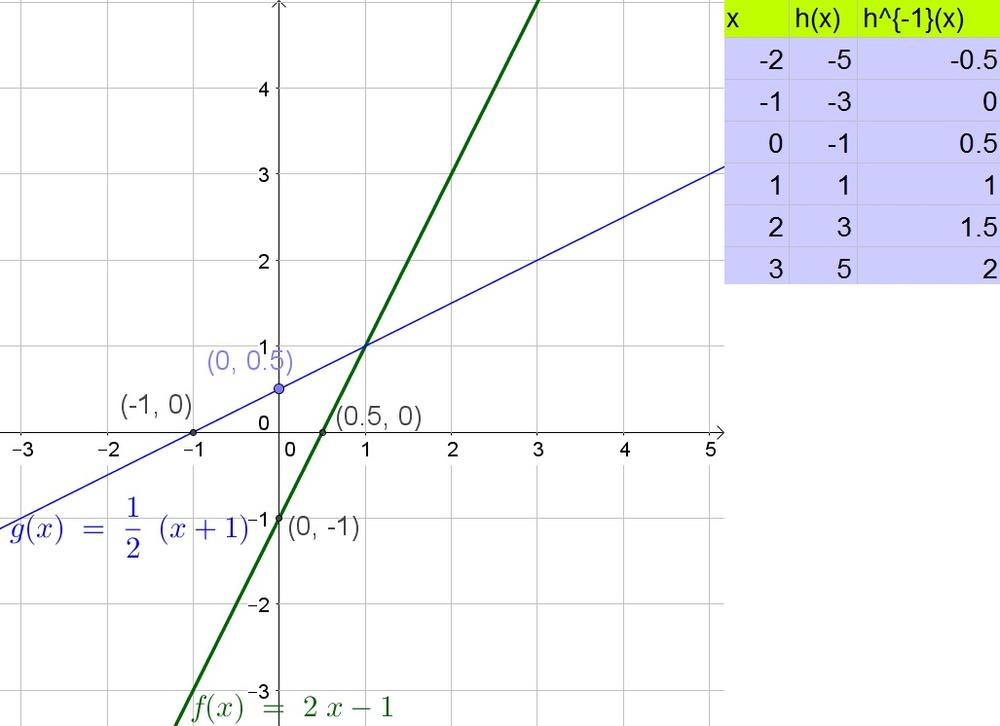

b. Intercepts interchange
c. Values two columns interchange.
$$
f^{-1}(x)=sqrt{x}
$$
If $x$ of the original function is nonpositive:
$$
f^{-1}(x)=-sqrt{x}
$$
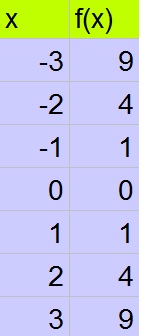
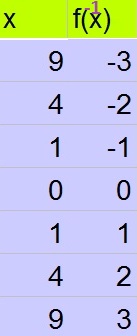
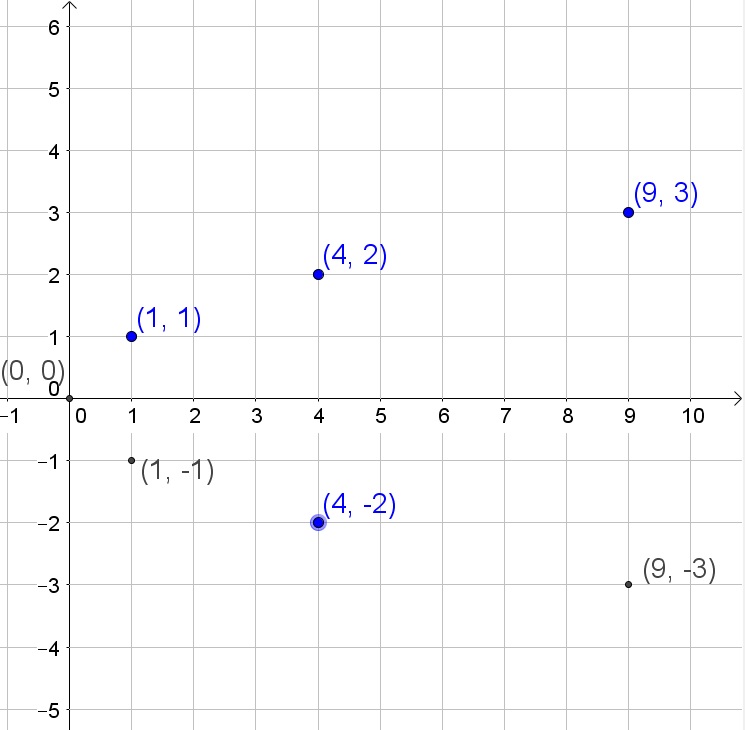
b. Swith columns of table of part (a)
c. No
d. $f^{-1}(x)=pm sqrt{x}$
$$
y=x^2+2
$$
Interchange $x$ and $y$:
$$
x=y^2+2
$$
Solve the equation to $y$ by first subtracting 2 from both sides of the equation:
$$
x-2=y^2
$$
Assume that $x$ is positive in the original function. Take the square root of both sides of the equation:
$$
sqrt{x-2}=y
$$
Interchange left and right side of the equation and replace $y$ with $p^{-1}(x)$:
$$
p^{-1}(x)=sqrt{x-2}
$$
$$
y=2(x-3)
$$
Interchange $x$ and $y$:
$$
x=2(y-3)
$$
Solve the equation to $y$ by first dividing both sides of the equation by 2:
$$
dfrac{1}{2}x=y-3
$$
Add 3 to both sides of the equation:
$$
dfrac{1}{2}x+3=y
$$
Interchange left and right side of the equation and replace $y$ with $q^{-1}(x)$:
$$
q^{-1}(x)=dfrac{1}{2}x+3
$$
b. $q^{-1}(x)=frac{1}{2}x+3$
$$
y=2x+3
$$
Interchange $x$ and $y$:
$$
x=2y+3
$$
Solve the equation to $y$ by first subtracting 3 from both sides of the equation:
$$
x-3=2y
$$
Divide both sides of the equation by 2:
$$
dfrac{1}{2}(x-3)=y
$$
Interchange left and right side of the equation and replace $y$ with $f^{-1}(x)$:
$$
f^{-1}(x)=dfrac{1}{2}(x-3)
$$
$$
y=dfrac{x-5}{4}
$$
Interchange $x$ and $y$:
$$
x=dfrac{y-5}{4}
$$
Solve the equation to $y$ by first multiplying both sides of the equation by 4:
$$
4x=y-5
$$
Add 5 to both sides of the equation:
$$
4x+5=y
$$
Interchange left and right side of the equation and replace $y$ with $g^{-1}(x)$:
$$
g^{-1}(x)=4x+5
$$
b. $g^{-1}(x)=4x+5$
(ii) The function is quadratic with a vertex at $(-2,4)$ and $y$-intercept at $y=24$.
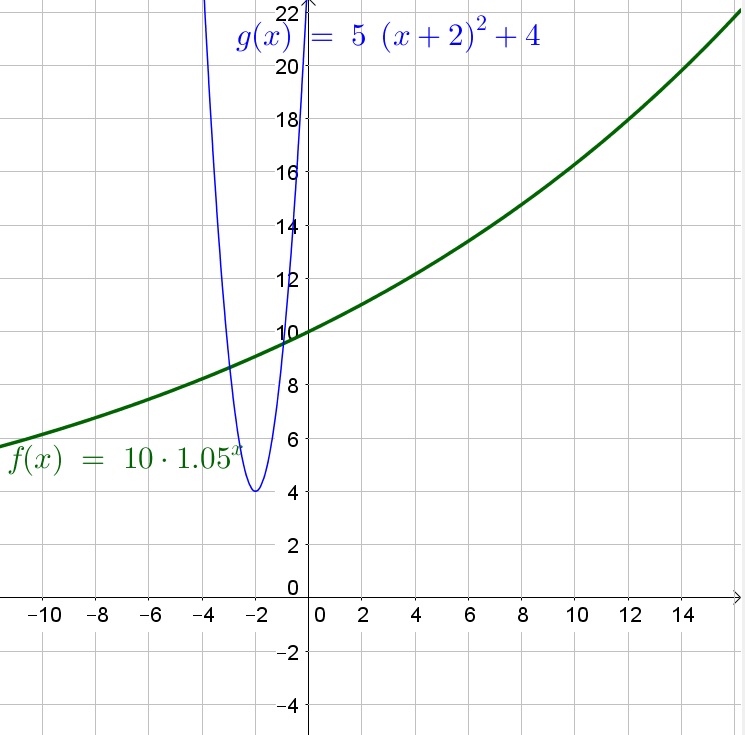
b. Exponential grows faster than quadratic
$$
y=(x-2)(x-5)
$$
is a possible equation of the given graph.
c. We can factorize the equation:
$$
y=(x+7)(x+1)
$$
Then we know that $x=-7$ and $x=-1$ are the $x$-intercepts. The vertex lies in the middle of the two intercepts and thus at $x=-4$:
$$
y=(-4+7)(-4+1)=-9
$$
Thus the vertex is $(-4,-9)$.
$$
y=16x(8-x)
$$
Thus the $x$-intercepts are $x=0$ and $x=8$. The vertex then lies in the middle of the intercepts and thus at $x=4$:
$$
y=128(4)-16(4)^2=256
$$
Thus the maximal height is 256ft after 4 seconds.
b. $y=(x-2)(x-5)$
c. $(-4,-9)$
d. 256 ft
a.
$$
s(x)=f(x)+g(x)=x^2+2x+1+x-3=x^2+3x-2
$$
b.
$$
m(x)=f(x)-g(x)=x^2+2x+1-(x-3)=x^2+x+4
$$
c.
$$
v(x)=2f(x)=2(x^2+2x+1)=2x^2+4x+2
$$
d.
$$
d(x)=g(x)-f(x)=x-3-(x^2+2x+1)=-x^2-x-4
$$
b. $x^2+x+4$
c. $2x^2+4x+2$
d. $-x^2-x-4$
a. $x-2$
b. $5-x$
b. $5-x$
$$
A_s=6^2=36
$$
The area of the circle is the product of $pi$ and the radius squared (note: The radius is half the width of the square):
$$
A_c=pi 3^2=9pi
$$
The area of the part of the square outside the circle is then:
$$
A=A_s-A_c=36-9pi
$$
Only half of this area is shaded:
$$
dfrac{36-9pi}{2}=18-dfrac{9}{2}pi units^2approx 3.8628units^2
$$
$$
A=dfrac{(13+9)3}{2}+dfrac{4cdot 8}{2}+9cdot 5=33+16+45=94
$$
The perimeter is the sum of all lengths of the sides:
$$
P=17+5+5+9+4sqrt{5}=36+4sqrt{5}
$$

Perimater $36+4sqrt{5}$
$$
y=2x-3
$$
Interchange $x$ and $y$:
$$
x=2y-3
$$
Solve the equation to $y$ by first adding 3 to both sides of the equation:
$$
x+3=2y
$$
Divide both sides of the equation by 2:
$$
dfrac{1}{2}(x+3)=y
$$
Interchange left and right side of the equation and replace $y$ with $f^{-1}(x)$:
$$
f^{-1}(x)=dfrac{1}{2}(x+3)
$$
$$
y=(x-3)^2+2
$$
Interchange $x$ and $y$:
$$
x=(y-3)^2+2
$$
Solve the equation to $y$ by first subtract 2 from both sides of the equation:
$$
x-2=(y-3)^2
$$
Take the square root of both sides of the equation:
$$
sqrt{x-2}=y-3
$$
Add 3 to both sides of the equation:
$$
sqrt{x-2}+3=y
$$
Interchange left and right side of the equation and replace $y$ with $h^{-1}(x)$:
$$
h^{-1}(x)=sqrt{x-2}+3
$$
b. $h^{-1}(x)=sqrt{x-2}+3$
c. $[0,+infty)$
$$
0=2x^2-8x+6
$$
Factorize:
$$
0=2(x-3)(x-1)
$$
Zero product property:
$$
x-3=0text{ or }x-1=0
$$
Solve each equation to $x$:
$$
x=3text{ or }x=1
$$
Determine $y$:
$$
y=x^2-4x+5=3^2-4(3)+5=2
$$
$$
y=x^2-4x+5=1^2-4(1)+5=2
$$
Thus the solutions are: $(3,2)$ and $(1,2)$.
$$
0=-3x-3
$$
Add 3 to both sides of the equation:
$$
3=-3x
$$
Divide both sides of the equation by 3:
$$
-1=x
$$
Determine $y$:
$$
y=x^2-x-2=(-1)^2-(-1)-2=0
$$
Thus the solutions is: $(-1,0)$.
b. $(-1,0)$
b. The BLUE graph is the given graph reflected about the $x$-axis.
c. The PINK graph is the graph translated to the right by 1 unit.
b. Reflect about $x$-axis
c. Translate right by 1 unit
Solving for the function $M$ which represents the income of Jill with $x$ number of children.
$$begin{aligned}
M(x)&= begin{cases}
50 &text{$xleq6$}\
50+5(x-6) &text{$x>6$}\
end{cases}
end{aligned}$$
$$begin{aligned}
M(x)&= begin{cases}
50 &text{$xleq6$}\
50+5x-30 &text{$x>6$}\
end{cases}\
M(x)&= begin{cases}
50 &text{$xleq6$}\
20+5x &text{$x>6$}\
end{cases}
end{aligned}$$
$$begin{aligned}
M(x)&=20+5x\
M(x)&=20+5(20)\
M(x)&=120\
end{aligned}$$
$$begin{aligned}
E(x)&=3x
end{aligned}$$
$$begin{aligned}
N(x)&=M(x)-E(x)\
end{aligned}$$
$$begin{aligned}
N(x)&= begin{cases}
M(x)-E(x) &text{$xleq6$}\
M(x)-E(x) &text{$x>6$}\
end{cases}\
end{aligned}$$
$$begin{aligned}
N(x)&= begin{cases}
50-3x &text{$xleq6$}\
20+5x-3x &text{$x>6$}\
end{cases}\
N(x)&= begin{cases}
50-3x &text{$xleq6$}\
20+2x &text{$x>6$}\
end{cases}\
end{aligned}$$
$$begin{aligned}
N(x)&=50-3x\
N(x)&=50-3(6)\
N(x)&=32
end{aligned}$$
$$begin{aligned}
N(x)&=20+2x\
N(x)&=20+2(20)\
N(x)&=60
end{aligned}$$
$$
y=(x^2+8+16)-16
$$
Factorize the perfect square trinomial ($a^2pm 2ab+b^2=(apm b)^2$):
$$
y=(x+4)^2-16
$$
Thus the vertex is then $(-4,-16)$.
$$
0=x^2+8x
$$
Factorize:
$$
0=x(x+8)
$$
Zero product property:
$$
x=0text{ or }x+8=0
$$
Solve each equation to $x$:
$$
x=0text{ or }x=-8
$$
Thus the $x$-intercepts are $x=0$ and $x=-8$.
$x$-intercepts: $x=0$ and $x=-8$
b. Square (or regular quadrilateral)
c. The interior angle sum is given by $(n-2)180text{textdegree}$ with $n$ the number of sides of the polygon:
$$
(n-2)180=1260
$$
Divide both sides of the equation by 180:
$$
n-2=7
$$
Add 2 to both sides of the equation:
$$
n=9
$$
Thus the polygon is a nonagon.
d. A rhombus is a quadrilateral with perpendicular diagonals that bisect each other.
b. Square
c. Nonagon
d. Rhombus
The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
begin{align*}
P(text{Coffee})&=dfrac{text{# of favorable outcomes}}{text{# of possible outcomes}}=frac{42}{63}=frac{2}{3}
\ P(text{Dairy})&=dfrac{text{# of favorable outcomes}}{text{# of possible outcomes}}=frac{21}{63}=frac{1}{3}
end{align*}
$$
We need to assume that choosing a coffee drink is independent of choosing a dairy product drink. Use the $textbf{Multiplication rule}$ for independent events: $P(Acap B)=P(Atext{ and }B)=P(A)times P(B)$
$$
begin{align*}
P(text{Coffee and Dairy})&=P(text{Coffee})times P(text{Dairy})
\ &=frac{2}{3}times frac{1}{3}
\ &=frac{2}{9}
\ &approx 0.2222
\ &=22.22%
end{align*}
$$
$$
begin{align*}
P(text{Coffee or Dairy})&=P(text{Coffee})+P(text{Dairy})-P(text{Coffee and Dairy})
\ &=frac{2}{3}+frac{1}{3}-frac{2}{9}
\ &=1-frac{2}{9}
\ &=frac{7}{9}
end{align*}
$$
Use the $textbf{Complement rule}$: $P(A^C)=P(text{not }A)=1-P(A)$
$$
begin{align*}
P(text{Not Coffee nor Dairy})&=1-P(text{Coffee or Dairy})
\ &=1-frac{7}{9}
\ &=frac{2}{9}
\ &approx 0.2222
\ &=22.22%
end{align*}
$$
Neither: $frac{2}{9}approx 0.2222=22.22%$

