a. Given

b. Given

c. $mangle CTA=mangle MTA$

d. Same size

5. SAS

6. $overline{CA}cong overline{MA}$

a. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:

$$
cos{42text{textdegree}}=dfrac{x}{10}
$$

Multiply both sides of the equation by 10:

$$
7.4approx 10cos{42text{textdegree}}=x
$$

b. We know that two of the sides of the triangle are equal, thus the bottom two angles are then also of equal size and thus measure both 45$text{textdegree}$.

Since the sum of all angles in a triangle is 180$text{textdegree}$, we can then determine the top angle in the triangle:

$$
180text{textdegree}-45text{textdegree}-45text{textdegree}=90text{textdegree}
$$

Since the top angle is 90$text{textdegree}$, we then know that the triangle is a right triangle.

The sine ratio is the opposite side divided by the hypotenuse:

$$
sin{45text{textdegree}}=dfrac{x}{15}
$$

The sine of 45$text{textdegree}$ is $dfrac{sqrt{2}}{2}$:

$$
dfrac{sqrt{2}}{2}=dfrac{x}{15}
$$

Multiply both sides of the equation by 15:

$$
10.6066approx dfrac{15sqrt{2}}{2}=x
$$

c. The sine ratio is the opposite side divided by the hypotenuse:

$$
theta=sin^{-1}dfrac{10}{18}approx 34text{textdegree}
$$

a. $x=7.4$

b. $x=frac{15sqrt{2}}{2}approx 10.6066$

c. $theta approx 34text{textdegree}$

a. Rewrite the rational exponents as roots and add powers of corresponding variables:

$$
sqrt{9}sqrt[3]{27}x^2y^{1-1}
$$

Simplify:

$$
3cdot 3x^2y^0
$$

Simplify:

$$
9x^2
$$

b. Power of power property:

$$
(x^{1/2})^{-2}=x^{1/2(-2)}=x^{-1}=dfrac{1}{x}
$$

c. Power of quotient property:

$$
dfrac{1^{2/3}}{125^{2/3}}
$$

Rewrite rational exponent as root:

$$
dfrac{1}{(sqrt[3]{125})^2}
$$

Evaluate root:

$$
dfrac{1}{5^2}
$$

Simplify:

$$
dfrac{1}{25}
$$

d. Subtract powers of corresponding variables:

$$
dfrac{8}{-2}x^{3+2}
$$

Simplify:

$$
-4x^5
$$

a. $9x^2$

b. $frac{1}{x}$

c. $frac{1}{25}$

d. $-4x^5$

a. The probability is the number of favorable outcomes divided by the number of possible outcomes:

$$
18% cdot dfrac{27000-7776-6750-6750}{27000}=18%cdot dfrac{5724}{27000}=0.18cdot 0.212=0.03816=3.816%
$$

b. Yes, because 18% of every class is in the performing arts.

c. Because of independency:

$$
begin{align*}
P(SENIOR given PERFORMANCE)&=P(senior)
\ &=dfrac{27000-7776-6750-6750}{27000}
\ &=dfrac{5724}{27000}
\ &=0.212
\ &=21.2%
end{align*}
$$

a. Factorize:

$$
x^2-x-56=(x-8)(x+7)
$$

b. Factorize:

$$
3x^2-4x+1=(3x-1)(x-1)
$$

c. Factor out the greatest common factor:

$$
2x^3+x^2+x=x(2x^2+x+1)
$$

d. Factor out the greatest common factor:

$$
2x^2-50=2(x^2-25)
$$

Factorize the difference of squares ($a^2-b^2=(a-b)(a+b)$):

$$
2x^2-50=2(x-5)(x+5)
$$

a. $(x-8)(x+7)$

b. $(3x-1)(x-1)$

c. $x(2x^2+x+1)$

d. $2(x-5)(x+5)$

a. Use the quadratic formula:

$$
x=dfrac{1pm sqrt{(-1)^2-4(2)(-5)}}{2(2)}=dfrac{1pm sqrt{41}}{4}
$$

Thus we note that the answers are irrational.

b. Subtract $4x^2$ from both sides of the equation:

$$
0=-4x^2+4x-1
$$

Factorize:

$$
0=(2x-1)^2
$$

Take the square root of both sides of the equation:

$$
0=2x-1
$$

Add 1 to both sides of the equation:

$$
1=2x
$$

Divide both sides of the equation by 2:

$$
dfrac{1}{2}=x
$$

Thus the answers are rational.

a. $s=frac{1pm sqrt{41}}{4}$, Irrational

b. $x=frac{1}{2}$, Rational

Given equation:
$$
0=x^2+9x+16.25
$$
Add 4 to both sides of the equation:

$$
4=x^2+9x+20.25
$$

Factorize:

$$
4=(x+4.5)^2
$$

Take the square root of both sides of the equation:

$$
pm 2 = x+4.5
$$

Subtract 4.5 from both sides of the equation:

$$
-2.5text{ or }-6.5=-4.5pm 2=x
$$

Thus the $x$-intercepts are $x=-2.5$ and $x=-6.5$, the $y$-intercepts is the constant term of the equation thus $y=16.25$. The vertex finally is $(-4.5,-4)$.

$x$-intercepts: $(-6.5,0)$ and $(-2.5,0)$

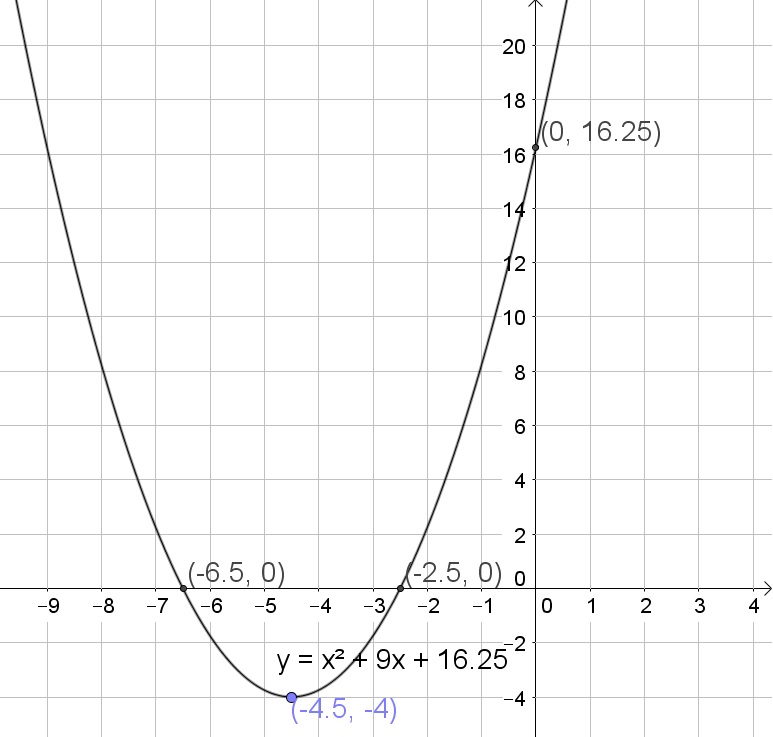
$y$-intercept: $(0,16.25)$

Vertex $(-4.5,-4)$

a. Opposite angles of a parallelogram are congruent:

$$
2x+50=3x+25
$$

Subtract $2x$ from both sides of the equation:

$$
50=x+25
$$

Subtract 25 from both sides of the equation:

$$
25=x
$$

b. The perimeter is the sum of the lengths of all sides:

$$
5t+1+2t+5+t+3t-2=202
$$

Combine like terms:

$$
11t+4=202
$$

Subtract 4 from both sides of the equation:

$$
11t=198
$$

Divide both sides of the equation by 11:

$$
t=18
$$

c. The diagonals of a rhombus intersect at a right angle:

$$
4x-2=90
$$

Add 2 to both sides of the equation:

$$
4x=92
$$

Divide both sides of the equation by 4:

$$
x=23
$$

d. Base angles of a trapezoid with equally long non-parallel sides are congruent:

$$
13m-9=7m+15
$$

Subtract $7m$ from both sides of the equation:

$$
6m-9=15
$$

Add 9 to both sides of the equation:

$$
6m=24
$$

Divide both sides of the equation by 6:

$$
m=4
$$

a. $x=25text{textdegree}$

b. $t=18$

c. $x=23text{textdegree}$

d. $m=4$