a. Factorize:

$$
x^2+x-30=(x+6)(x-5)
$$

b. Factor out the greatest common factor:

$$
-3x^3+23x^2-14x=-x(3x^2-23x+14)
$$

Factorize further:

$$
-3x^3+23x^2-14x=-x(x-7)(3x-2)
$$

d. Factor out the greatest common factor:

$$
6x^3+10x^2-24x=2x(3x^2+5x-12)
$$

Factorize further:

$$
6x^3+10x^2-24x=2x(x+3)(3x-4)
$$

a. $(x+6)(x-5)$

b. $-x(x-7)(3x-2)$

c. Not possible to factorize

d. $2x(x+3)(3x-4)$

b. The area is the product of the length and the width:

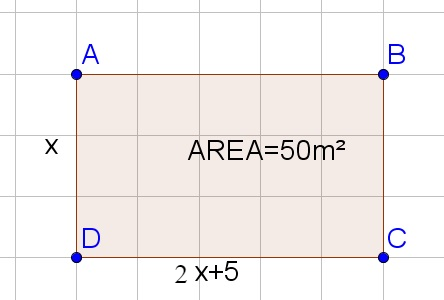
$$
x(2x+5)=50
$$

c. Subtract 50 from both sides of the equation:

$$
2x^2+5x-50=0
$$

Determine the roots using the quadratic formula $x=frac{-bpm sqrt{b^2-4ac}}{2a}$ for a quadratic equation of the form $ax^2+bx+c=0$.

$$
begin{align*}
x&=frac{-5pm sqrt{5^2-4(2)(-50)}}{2(2)}
\ &=frac{-5pm sqrt{425} }{4}
\ &=frac{-5pm 5sqrt{17} }{4}
\ &approx -6.4039text{ or }3.9039
end{align*}
$$

Since the width has to be positive, the width is approximately 3.9039m and the length is $2cdot 3.9039+5=$12.8078m.

a. Width $x$ and length $2x+5$

b. $x2(x+5)=50$

c. Width $3.9039$ m and length 12.8078 m.

The shorter leg of a 30$text{textdegree}$-60$text{textdegree}$-90$text{textdegree}$ is half of the hypotenuse and the longer leg is $sqrt{3}$ the shorter leg.

The legs of a 45$text{textdegree}$-45$text{textdegree}$-90$text{textdegree}$ are equal and the hypotenuse can be determined using the Pythagorean theorem, moreover the legs are half the hypotenuse multiplied by $sqrt{2}$.

If two lengths of the right triangle are given, determine the third using the Pythagorean theorem.

$$
a^2+b^2=c^2
$$

The sum of all angles is in a triangle should be a 180$text{textdegree}$.

a. 2 cm, $2sqrt{2}$ cm

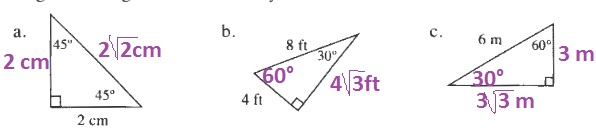
b. 60$text{textdegree}$, $4sqrt{3}$ ft

c. 30$text{textdegree}$, 3m, $3sqrt{3}$ m

If two lengths of the right triangle are given, determine the third using the Pythagorean theorem.

$$
a^2+b^2=c^2
$$

a.
$$
x=sqrt{15^2-12^2}=sqrt{81}=9
$$

b.
$$
x=sqrt{24^2+10^2}=sqrt{676}=26
$$

Rewrite the rational exponent as a root:

a.
$$
8^{1/3}=sqrt[3]{8}=sqrt[3]{2^3}=2
$$

b.
$$
32^{2/5}=(sqrt[5]{32})^2=(sqrt[5]{2^5})^2=2^2=4
$$

c.
$$
125^{4/3}=(sqrt[3]{125})^4=(sqrt[3]{5^3})^4=5^4=625
$$

a. Determine the solution using the quadratic formula:

$$
x=dfrac{-4pm sqrt{4^2-4(3)(-7)}}{2(3)}=dfrac{-4pm 10}{6}=1text{ or }-dfrac{7}{3}
$$

b. Factorize:

$$
(x-6)(x+3)=0
$$

Zero product property:

$$
x-6=0text{ or }x+3=0
$$

Solve each equation to $x$:

$$
x=6text{ or }x=-3
$$

c. Add 3 to both sides of the equation:

$$
x^2+4x+4=3
$$

Factorize:

$$
(x+2)^2=3
$$

Take the square root of both sides of the equation:

$$
x+2=pm sqrt{3}
$$

Subtract 2 from both sides of the equation:

$$
x=-2pm sqrt{3}
$$

d. The solutions of the equation are the intersections of the graph with the $x$-axis and thus are $x=-4$ and $x=1.5$

a. $x=1$ or $x=-frac{7}{3}$

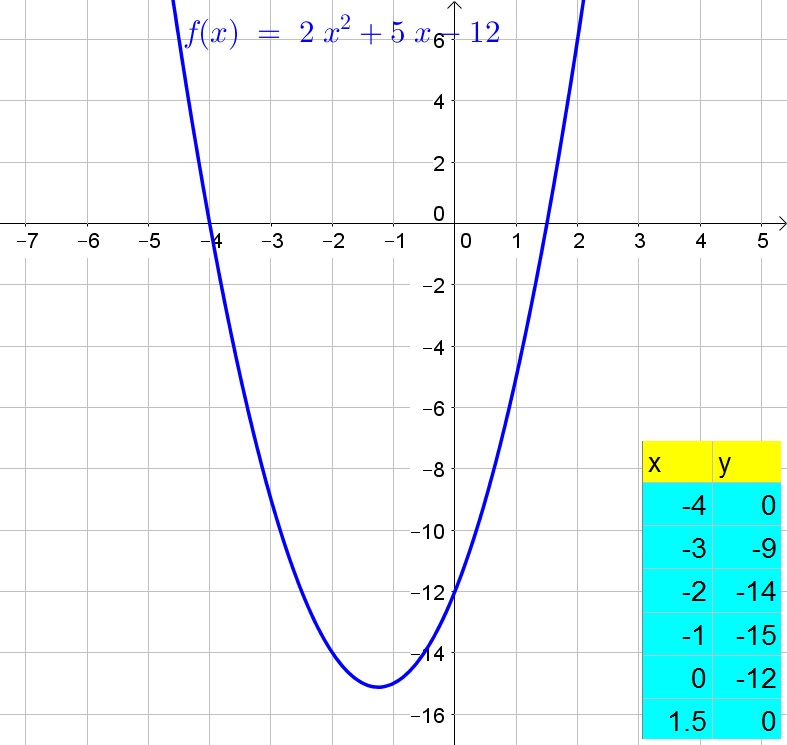
b. $x=6$ or $x=-3$

c. $x=-2pm sqrt{3}$

d. $x=-4$ or $x=1.5$

Use $i^2=-1$ and combine like terms:

a.
$$
(3+4i)+(7-2i)=(3+7)+(4i-2i)=10+2i
$$

b.
$$
(3+5i)^2=9+30i+25i^2=9+30i-25=-16+30i
$$

c.
$$
(7+i)(7-i)=49-i^2=49+1=50
$$

d.
$$
(3i)(2i)^2=(3i)(4i^2)=(3i)(-4)=-12i
$$

a. $10+2i$

b. $-16+30i$

c. 50

d. $-12i$

Determine the length of the missing sides using the pythagorean theorem:

$$
sqrt{8^2-5^2}=sqrt{39}
$$

The perimeter of the polygon is the sum of the lengths of all sides:

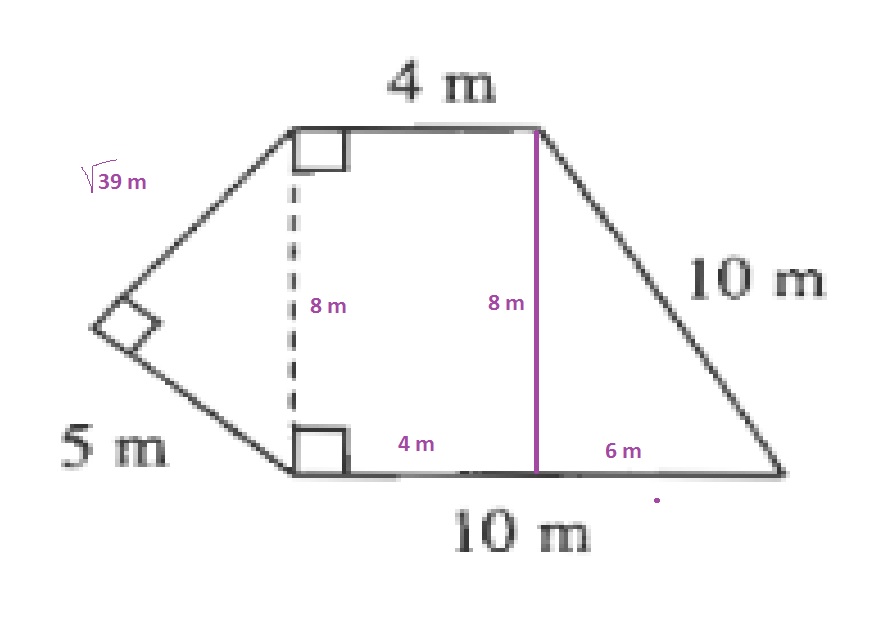
$$
PERIMETER=4+10+10+5+sqrt{39}=29+sqrt{39}mapprox 35.24m
$$

The area of a trapezium is the sum of the bases, multiplied by the height divided by 2. The area of a rectangle is the product of the base and the height divided by 2.

$$
AREA=dfrac{(4+10)8}{2}+dfrac{5sqrt{39}}{2}=56+dfrac{5sqrt{39}}{2}m^2approx 71.61m^2
$$

Perimeter 35.24 m

Area $71.61$ m$^2$

a. The probability of the event is the sum of the probabilities of the possibilities that are part of the event. The probability of each spin is equal. Multiply the probability for each spinner.

$$
P(pool)=P(1,5)+P(3,5)+P(1,7)=dfrac{3}{4}cdot dfrac{1}{3}+ dfrac{1}{4}cdot dfrac{1}{3}+ dfrac{3}{4}cdot dfrac{1}{3}=dfrac{7}{12}approx 0.5833=58.33%
$$

b. The probability of the event is the sum of the probabilities of the possibilities that are part of the event. The probability of each spin is equal.
$$
P(pool)=P(2,4)+P(2,5)+P(2,6)+P(3,4)+P(3,5)+P(3,6)+P(4,4)+P(4,5)+P(5,4)
$$

$$
=9P(2,4)=9cdot dfrac{1}{4}cdot dfrac{1}{3}=dfrac{3}{4}=0.75=75%
$$