All Solutions
Page 259: Questions
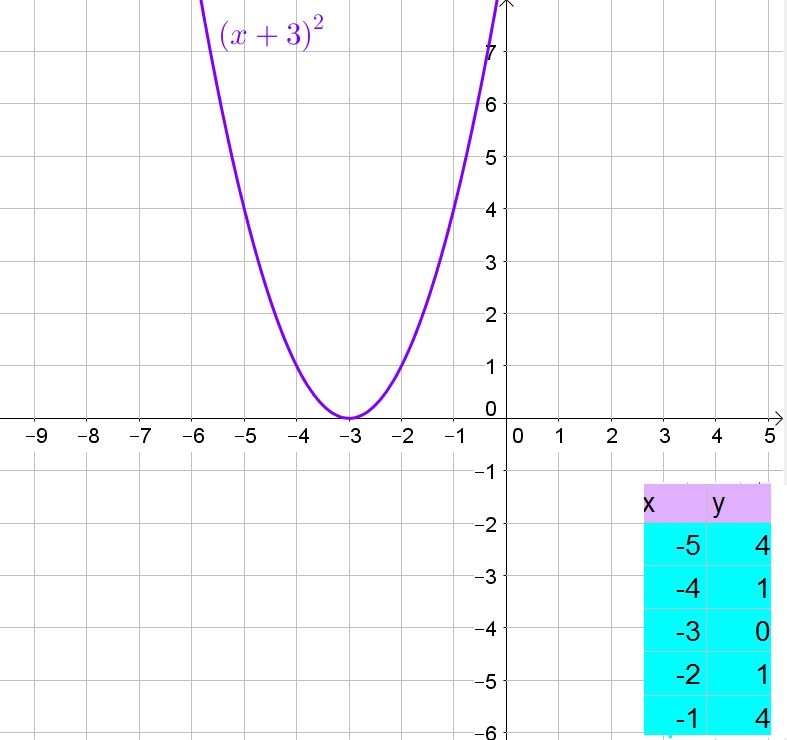
The function has $x$-intercepts at $x=-2$ and $x=4$, while it has an $y$-intercept at $y=-8$.
The function is negative on $-2<x<4$ and positive on $x4$.
The function is decreasing for $x1$.
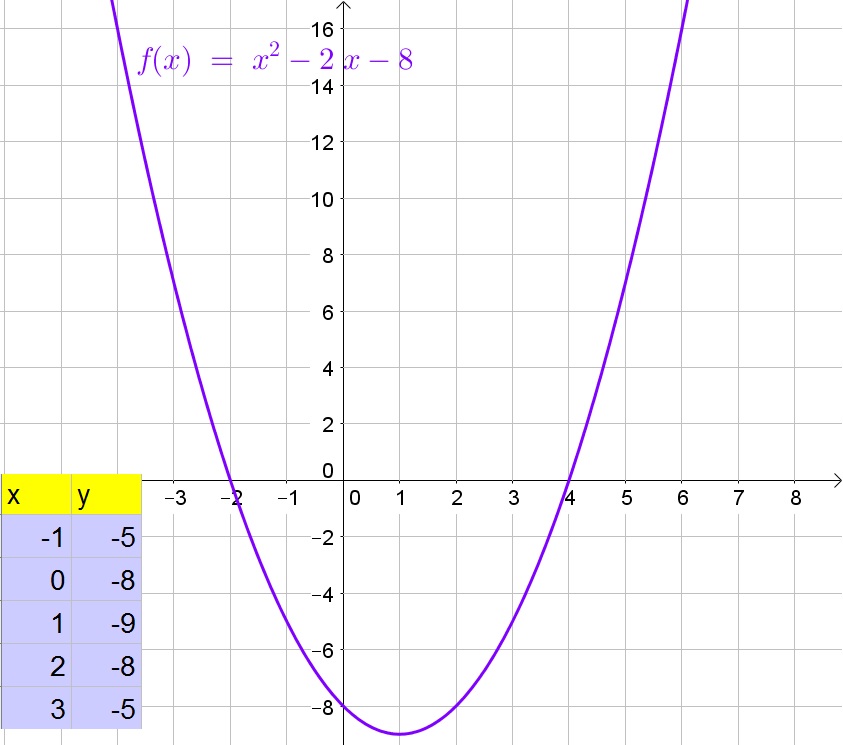
The function opens upwards.
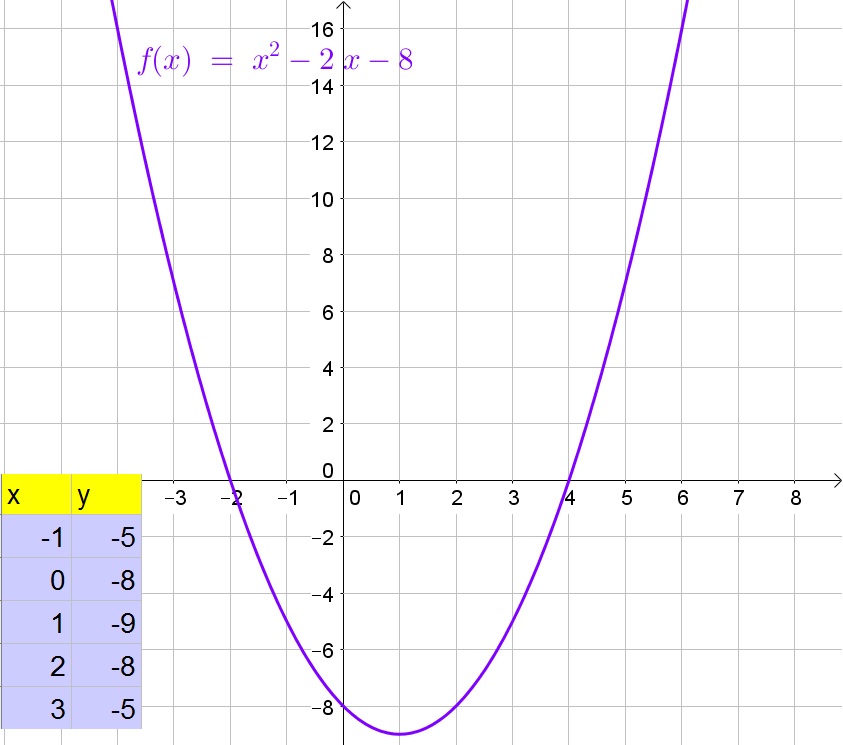
The function has $x$-intercepts at $x=-2$ and $x=4$, while it has an $y$-intercept at $y=-8$.
The function is negative on $-2<x<4$ and positive on $x4$.
The function is decreasing for $x1$.
$$
2x=10
$$
Divide both sides of the equation by 2:
$$
x=5
$$
$$
x=-6
$$
$$
2x-10=0text{ or } x+6=0
$$
Use the result from (a) and (b):
$$
x=5text{ or }x=-6
$$
$$
4x=-1
$$
Divide both sides of the equation by 4:
$$
x=-dfrac{1}{4}
$$
$$
x=8
$$
$$
4x+1=0text{ or } x-8=0
$$
Use the result from (d) and (e):
$$
x=-dfrac{1}{4}text{ or }x=8
$$
b. $x=-6$
c. $x=5$ and $x=-6$
d. $x=-dfrac{1}{4}$
e. $x=8$
f. $x=-frac{1}{4}$ and $x=8$

Let
$$begin{aligned}
x&=text{figure number}\
y&=text{number of tiles}
end{aligned}$$

$$begin{aligned}
y&=(x^2)+(2x-1)\
y&=x^2+2x-1enspacetext{(equation representing the number of tiles)}
end{aligned}$$
$$begin{aligned}
y&=x^2+2x-1
end{aligned}$$
$$begin{aligned}
y&=(5)^2+2(5)-1\
y&=25+10-1\
y&=34enspacetext{tiles}
end{aligned}$$
The figure can be illustrated as follows:

$$begin{aligned}
P &= 76 \
P &= x + 2x + (x-1) + 2x + (2x-3) \
76 &= x + 2x + (x-1) + 2x + (2x-3) \
76 &= (x+2x +x+ 2x +2x) + (-1-3)\
76 &= 8x -4 \
76 + 4 &= 8x \
80 &= 8x \
x &= frac{80}{8} \
& boxed{x=10 text{ units}}
end{aligned}$$
The figure can be illustrated as follows:

$$begin{aligned}
L_1 &= L_2 \
3x-2 &= 5x – 14 \
3x-5x &= -14 + 2 \
-2x &= -12 \
x &= frac{-12}{-2} \
& boxed{x = 6}
end{aligned}$$
The figure can be illustrated as follows:

$$begin{aligned}
theta_1 + theta_2 &= 180^circ \
3x + 20^circ + 5x &= 180^circ \
8x + 20^circ &= 180^circ \
8x &= 180^circ – 20^circ \
8x &= 160^circ \
x &= frac{160^circ}{8} \
& boxed{x = 20^circ}
end{aligned}$$
The figure can be illustrated as follows:

$$begin{aligned}
3x + 20^circ &= 5x \
3x -5x &= -20^circ \
-2x &= -20^circ \
x &= frac{-20^circ}{-2} \
& boxed{x=10^circ}
end{aligned}$$
b. $x = 6$
c. $x=20^circ$
d. $x=10^circ$
$$
(x+4)^2-2x-5=(x-1)^2
$$
Use $(apm b)^2=a^2pm 2ab +b^2$:
$$
x^2+8x+16-2x-5=x^2-2x+1
$$
Subtract $x^2$ from both sides of the equation:
$$
6x+11=-2x+1
$$
Add $2x$ to both sides of the equation:
$$
8x+11=1
$$
Subtract 11 from both sides of the equation:
$$
8x=-10
$$
Divide both sides of the equation by 8:
$$
x=-dfrac{5}{4}
$$
x=-dfrac{5}{4}
$$
$$
180text{textdegree}-47text{textdegree}-27text{textdegree}=106text{textdegree}
$$
The two triangles are then similar because of AA (two congruent angles).
$$
dfrac{98}{18}approx 5.44
$$
$$
dfrac{64}{12}approx 5.33
$$
Since the ratios are not the same, the rectangles are not similar.
b. Not similar
c. Impossible to determine
$$
SE=LI=MI=sqrt{3^2+1^2}=sqrt{10}
$$
$$
MS=LE=sqrt{3^2+2^2}=sqrt{13}
$$
$$
x=pm 4
$$
$$
x=sqrt{16}=4
$$
$$
x=pm 4
$$
$$
x=sqrt{16}-3=4-3=1
$$
$$
x^2=-4
$$
The square root of a number cannot be negative and thus no $x$ value will make this equation true.
b. $x=4$
c. $x=pm 4$
d. $x=1$
e. No solution
f. No solution
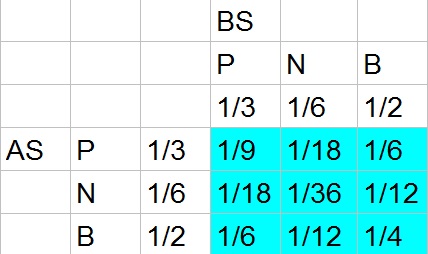
$$
dfrac{1}{4}=0.25=25%
$$
c. The probability is the sum of all probabilities that neither photo is of the niece:
$$
dfrac{1}{9}+dfrac{1}{6}+dfrac{1}{6}+dfrac{1}{4}=dfrac{4}{36}+dfrac{6}{36}+dfrac{6}{36}+dfrac{9}{36}=dfrac{25}{36}approx 0.694=69.4%
$$
b. $frac{1}{4}=0.25=25%$
c. $frac{25}{36}approx 0.694=69.4%$
$$
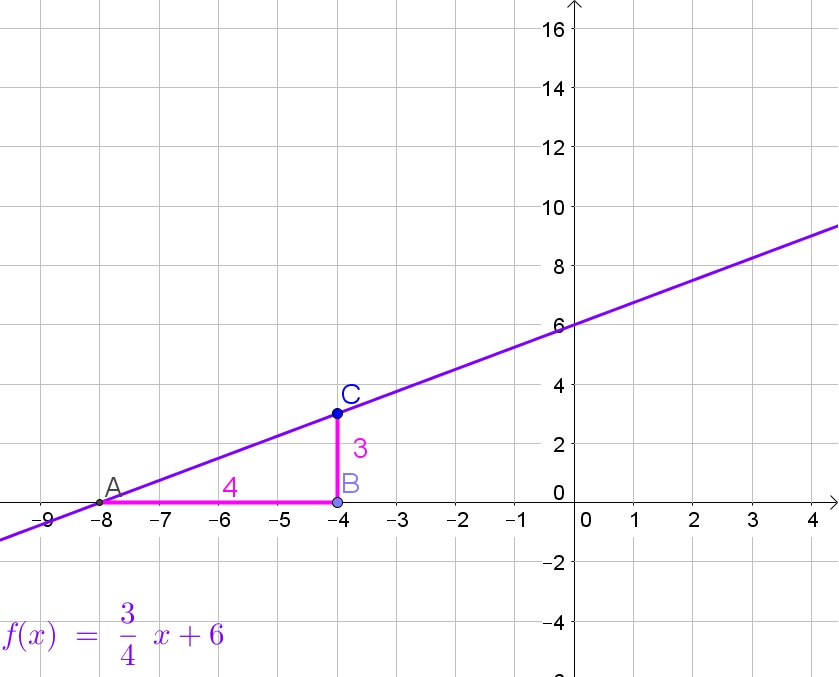
theta=tan^{-1}{dfrac{3}{4}}approx 37text{textdegree}
$$
$$
dfrac{y}{3}=dfrac{15}{6}
$$
Multiply both sides of the equation by 3:
$$
y=dfrac{15cdot 3}{6}=7.5
$$
Determine $z$:
$$
dfrac{z}{24}=dfrac{6}{15}
$$
Multiply both sides of the equation by 24:
$$
z=dfrac{6cdot 24}{15}=9.6
$$
$$
90+6x+8+2x+2=180
$$
Combine like terms:
$$
8x+100=180
$$
Subtract 100 from both sides of the equation:
$$
8x=80
$$
Divide both sides of the equation by 8:
$$
x=10
$$
Replace $x$ with 10 in the expression of the measure of the angles:
$$
mangle A=6x+8=6(10)+8=68text{textdegree}
$$
$$
mangle B=2x+2=2(10)+2=22text{textdegree}
$$
The angles are acute, since they are both less than 90$text{textdegree}$.
The angles are also complementary because their sum is 90$text{textdegree}$.
$$
y-y_1=a(x-x_1)
$$
a. Perpendicular lines have slopes whose product is $-1$, thus the perpendicular line then has slope $dfrac{5}{2}$:
$$
y+3=dfrac{5}{2}(x-2)
$$
b. Determine the slope of the given line:
$$
-3x+2y=10
$$
Add $3x$ to both sides of the equation:
$$
2y=10+3x
$$
Divide both sides of the equation by 2:
$$
y=5+dfrac{3}{2}x
$$
Thus the line has slope $dfrac{3}{2}$. Since parallel lines have the same slopes, the parallel line will have slope $dfrac{3}{2}$:
$$
y-7=dfrac{3}{2}(x-4)
$$
b. $y-7=dfrac{3}{2}(x-4)$
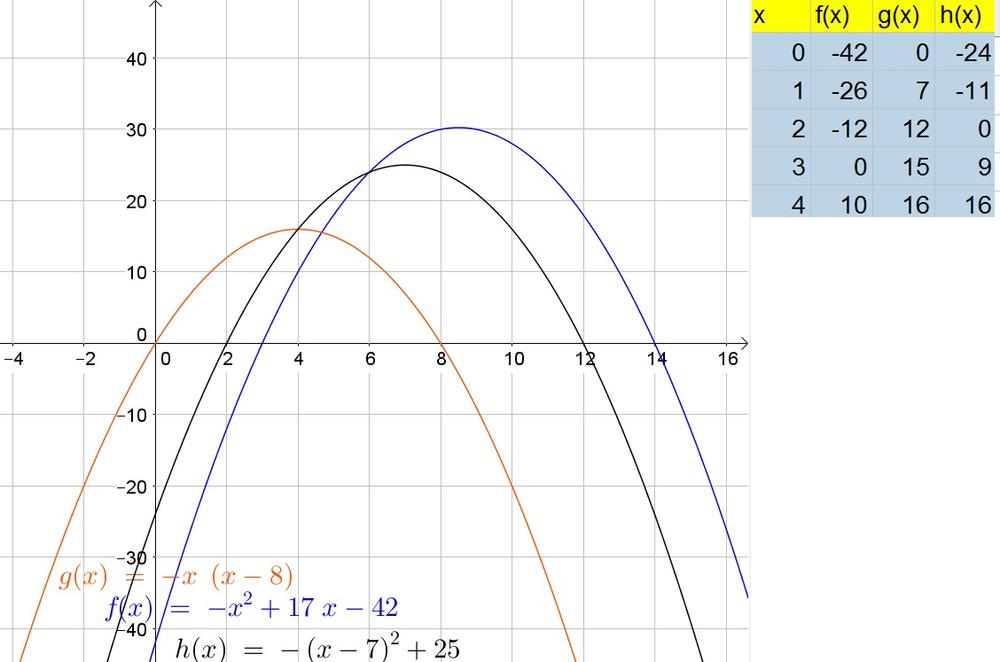
Maggie: $x=3$ and $x=14$
Jen: $x=0$ and $x=8$
Imp: $x=2$ and $x=12$
The difference between the $x$-intercepts is the distance that the balloon traveled.
c. The vertex is the maximum of each parabola:
Maggie: $(8.5,30.25)$
Jen: $(4,16)$
Imp: $(7,25)$
b.
Maggie: $x=3$ and $x=14$
Jen: $x=0$ and $x=8$
Imp: $x=2$ and $x=12$
c.
Maggie: $(8.5,30.25)$
Jen: $(4,16)$
Imp: $(7,25)$
$$
y=-(2)^2+17(2)-42=-4+34-42=-12
$$
This tells you that the height would have been 12 yards under the ground. This is impossible and is caused by the fact that the balloon is launched further away at 3 yards.
b. An appropriate domain would then contain all $x$-values between the launch and the landing: $(3,14)$.
The range contains only non-negative distances: $[0, +infty)$.
c. Domain $(3,14)$ and range $[0,+infty)$
b. We note that the blocks form a rectangle with length $n+2$ and width $n+1$ that are increased by 2 blocks:
$$
f(n)=(n+2)(n+1)+2=n^2+3n+2+2=n^2+3n+4
$$
c. The equation is quadratic, because if simplified you obtain a term $n^2$ that is quadratic (and their are no terms with a greater power).
b. $f(x)=n^2+3n+4$
c. Yes
The graph opens upward.
The graph is negative on $(1,7)$ and positive on $(-infty, 1)$ and $(1,+infty)$.
The function is decreasing on $(-infty,4)$ and increasing on $(4,+infty)$.

We calculate the sum of the following expressions:
$$begin{aligned}
text{i. }& 0+3 = boxed{3} \
text{ii. }& -7 + 0 = boxed{-7} \
text{iii. }& 0 + 6 = boxed{6} \
text{iv. }& 0 + (-2) = boxed{-2} \
end{aligned}$$
The special thing about adding zero is that “when you add zero to a number, the sum is the number itself”
When Julia added number $a$ and $b$ she was able to to get a sum of $b$, this means that either $a$ is equal to zero or $a$ and $b$ are both zero.
We calculate the product of the following expressions:
$$begin{aligned}
text{i. }& 3cdot 0 = boxed{0} \
text{ii. }& (-7) cdot 0 = boxed{0} \
text{iii. }& 0 cdot 6 = boxed{0} \
text{iv. }& 0 cdot (-2) = boxed{0} \
end{aligned}$$
The special thing about multiplying by zero is that “when you multiply a number by zero, the product is zero”
When Julia multiplied the number $a$ and $b$, she was able to to get a product of $0$. This means that either one number is equal to zero or both are zero.
$$
sin{75text{textdegree}}=dfrac{26}{x}
$$
Multiply both sides of the equation by $x$:
$$
xsin{75text{textdegree}}=26
$$
Divide both sides of the equation by $sin{75text{textdegree}}$:
$$
x=dfrac{26}{sin{75text{textdegree}}}approx 27
$$
Thus the ladder needs to be about 27 ft.
b. The time increases as the distance increases and the time increases in an almost linear more, thus the group should be almost a line, this means that the graph is Graph 2.
b. Graph 2
b. The purple triangle is the rotated triangle and its coordinates are $A”(-3,3), B”(-3,-9)$ and $C”(-6,3)$. The $y$-coordinates have changed sign.
c. Since the $x$-coordinates of $A$ increased by 6 and the $y$ coordinates increased by 4, the same happens to the coordinates of $B$: $(3+6,-1+4)=(9,3)$
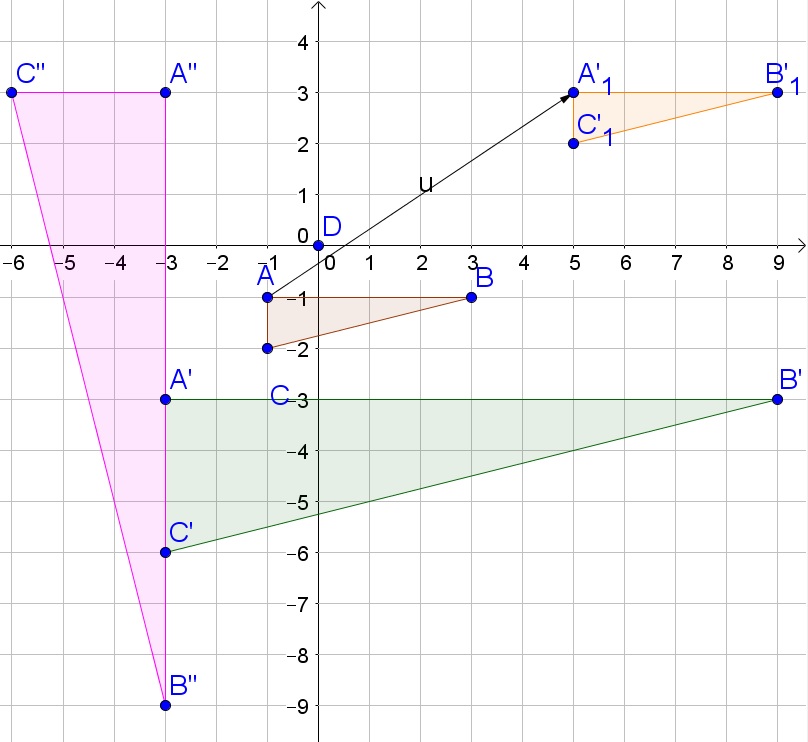
b. $A”(-3,3)$, $B”(-3,-9)$, $C”(-6,3)$
c. $(9,3)$
$$
dfrac{x}{41}=dfrac{324}{128}
$$
Multiply both sides of the equation by 41:
$$
x=dfrac{324cdot 41}{128}=dfrac{13284}{128}=dfrac{3321}{32}approx 103.78m
$$
b. No, because for example you cannot know where the graph will intersect the $y$-axis.
c. Yes, in this case we can only draw exactly one parabola.
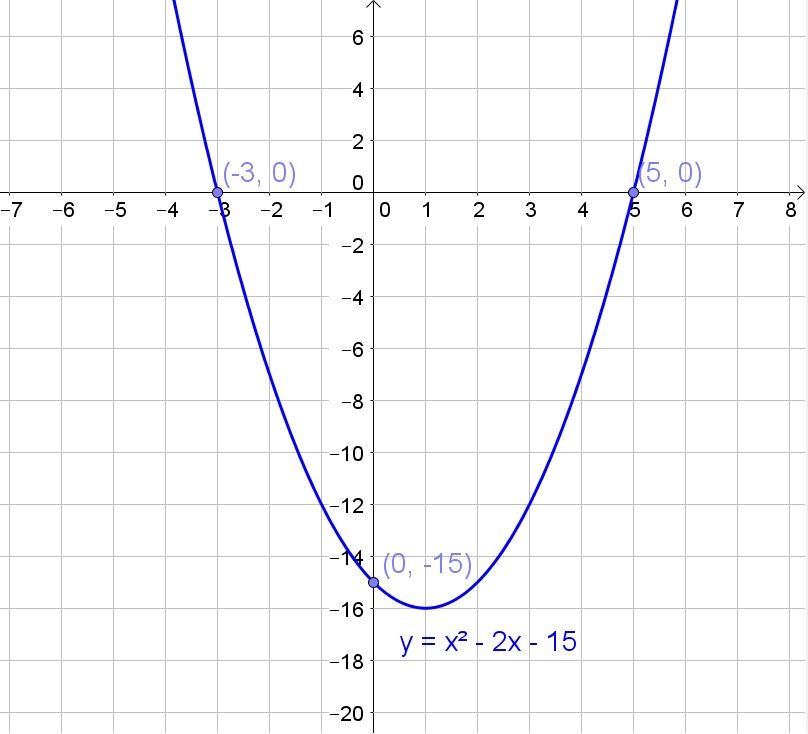
b. No
c. Yes
b. Replace $x$ with 0 in the equation:
$$
y=2(0)^2+5(0)-12=-12
$$
c. Replace $y$ with 0:
$$
0=2x^2+5x-12
$$
Thus this would be the equation that would need to be solved.
d. Yes, Factorize:
$$
0=(2x-3)(x+4)
$$
Zero product property:
$$
2x-3=0text{ or }x+4=0
$$
Solve each equation to $x$:
$$
x=dfrac{3}{2}text{ or }x=-4
$$
b. $(0,-12)$
c. $0=2x^2+5x-12$
d. $x=frac{3}{2}$ or $x=-4$
b. Nathan’s number is zero, Nancy’s number is zero, or Gaston’s number is zero. However, if Gaston’s number is zero, then we will of course know it.
c. No, if the product is zero, then at least one term in the product has to be zero.
b. Nathan’s number is zero, Nancy’s number is zero, or Gaston’s number is zero.
c. No
$$
0=(2x-3)(x+4)
$$
b. Zero product property:
$$
2x-3=0text{ or }x+4=0
$$
Solve each equation to $x$:
$$
x=dfrac{3}{2}text{ or }x=-4
$$
c. You need to determine the $y$-intercept, which is the constant term of the equation of the parabola: $y=-12$.
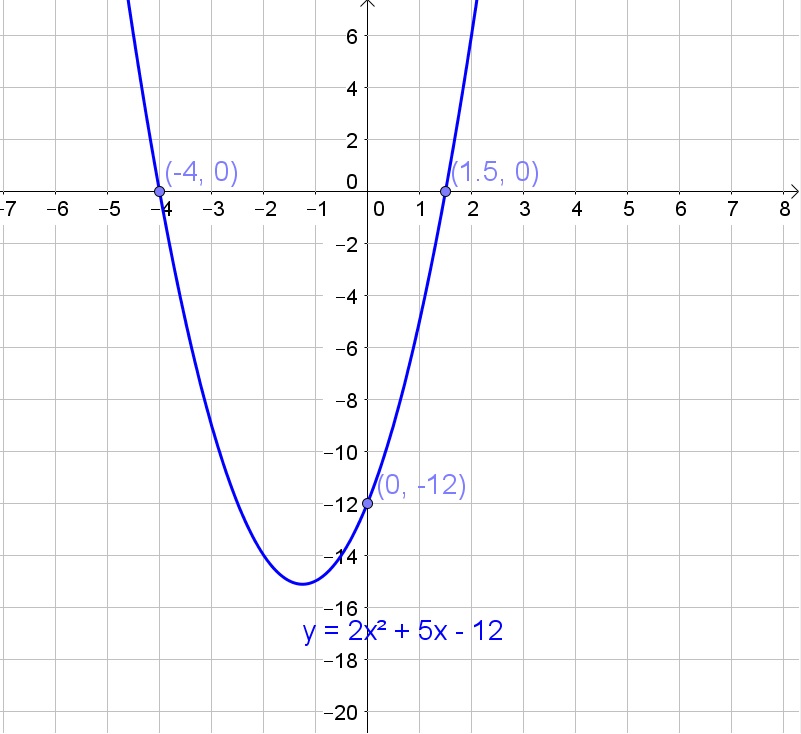
b. $x=frac{3}{2}$ or $x=-4$
c. $y$-intercept $(0,-12)$
The zero product property states that if the product of $a$ and $b$ is zero, then $a=0$, $b=0$, or both numbers are equal to zero.
We determine the x-intercepts of the parabola $y=x^2+4x-5$ by setting the value of $y$ to zero. We calculate for the value of $x$ using the zero product property as follows:
$$begin{aligned}
y&=x^2+4x-5 \
0 &= x^2 +4x-5 \
0 &= (x+5)(x-1) \
x + 5 &= 0 \
& boxed{x = -5} \
x – 1 &= 0 \
& boxed{x = 1} \
end{aligned}$$
Therefore, the x-intercepts of the parabola are the points $boxed{(1,0)}$ and $boxed{(-5,0)}$
The vertex of a parabola is the point where the line of symmetry and the parabola intersects. The axis of symmetry of the parabola is between the x-intercepts, it is a line that passes through the midpoint of these intercepts. We determine the axis of symmetry as follows:
$$begin{aligned}
text{axis of symmetry} &= frac{x_1 + x_2}{2} \
text{axis of symmetry} &= frac{-5+1}{2} \
text{axis of symmetry} &= -2
end{aligned}$$
Therefore, the axis of symmetry is $x=-2$

From the graph, we observe that the vertex of the parabola is the point $boxed{(-2,9)}$
The sketch of the parabola $y=x^2 + 4x -5$ along with its intercepts and vertex is as follows:

Determine the $x$-intercepts. Replace $y$ with 0:
$$
0=x^2+x-6
$$
Factorize:
$$
0=(x+3)(x-2)
$$
Zero product property:
$$
x+3=0text{ or }x-2=0
$$
Solve each equation to $x$:
$$
x=-3text{ or }x=2
$$
Thus the $x$-intercepts are $x=-3$ and $x=2$.
The axis of symmetry then lies in the middle between the two $x$-intercepts and thus at $x=-0.5$. Determine the corresponding $y$-value:
$$
y=(-0.5)^2+(-0.5)-6=-6.25
$$
The vertex is then $(-0.5,-6.25)$.
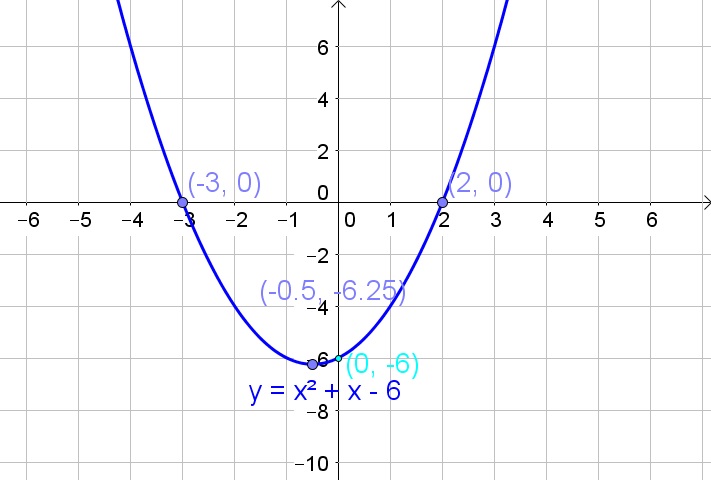
$y$-intercept $(0,-6)$
$x$-intercepts $(-3,0)$ and $(2,0)$
The zero product property states that if the product of $a$ and $b$ is zero, then $a=0$, $b=0$, or both numbers are equal to zero.
The equations have similar factors, which are:
$$begin{equation}
(x+2)
end{equation}$$
$$begin{equation}
(x-1)
end{equation}$$
But they are using different operations. The first one is a multiplication operation, while the other one is an addition.
For the first equation:
Since the operation is multiplication, use Zero Product Property.
$$begin{aligned}
(x+2)(x-1) &=0 \
end{aligned}$$
becomes
$$begin{aligned}
(x+2) &=0 \
end{aligned}$$
and
$$begin{aligned}
(x-1) &=0 \
end{aligned}$$
$$begin{aligned}
x+2-2 &= 0-2 \
&boxed{x = -2} \
end{aligned}$$
and
$$begin{aligned}
x-1+1 &=0+1 \
&boxed{x =1} \
end{aligned}$$
Simply add the factors
$$begin{aligned}
(x+2)+(x-1) &=0 \
x+2+x-1 &=0 \
2x+1 &= 0\
2x+1-1 &= 0-1\
2x &= -1\
frac{2x}{2} &= frac{-1}{2}\
&boxed{x = frac{-1}{2}}\
end{aligned}$$
b. The value of $x$ for:
Equation 1 are $x = -2$ and $x =1$
Equation 2 is $x = -frac{1}{2}$
The zero product property states that if the product of $a$ and $b$ is zero, then $a=0$, $b=0$, or both numbers are equal to zero.
Use Zero Product Property.
$$begin{aligned}
(x-2)(x+8) &=0 \
end{aligned}$$
becomes
$$begin{aligned}
(x-2) &=0 \
end{aligned}$$
and
$$begin{aligned}
(x+8) &=0 \
end{aligned}$$
$$begin{aligned}
x-2+2 &= 0+2 \
&boxed{x = 2} \
end{aligned}$$
and
$$begin{aligned}
x+8-8 &=0-8 \
&boxed{x = -8} \
end{aligned}$$
Use Zero Product Property.
$$begin{aligned}
(3x-9)(x-1) &=0 \
end{aligned}$$
becomes
$$begin{aligned}
(3x-9) &=0 \
end{aligned}$$
and
$$begin{aligned}
(x-1) &=0 \
end{aligned}$$
$$begin{aligned}
3x-9+9 &= 0+9 \
3x &= 9 \
frac{3x}{3} &= frac{9}{3} \
&boxed{x = 3} \
end{aligned}$$
and
$$begin{aligned}
x-1+1 &=0+1 \
&boxed{x = 1} \
end{aligned}$$
Use Zero Product Property.
$$begin{aligned}
(x+10)(2x-5) &=0 \
end{aligned}$$
becomes
$$begin{aligned}
(x+10) &=0 \
end{aligned}$$
and
$$begin{aligned}
(2x-5) &=0 \
end{aligned}$$
$$begin{aligned}
x+10-10 &=0-10\
&boxed{x = -10}
end{aligned}$$
and
$$begin{aligned}
2x-5 &=0 \
2x-5+5 &= 0+5 \
2x &= 5 \
frac{2x}{2} &= frac{5}{2} \
&boxed{x = frac{5}{2}} \
end{aligned}$$
Use Zero Product Property.
$$begin{aligned}
(x-7)^2 &=0 \
end{aligned}$$
becomes
$$begin{aligned}
(x-7) &=0 \
end{aligned}$$
and
$$begin{aligned}
(x-7) &=0 \
end{aligned}$$
$$begin{aligned}
x-7+7 &=0+7\
&boxed{x = 7}
end{aligned}$$
and
$$begin{aligned}
x-7+7 &=0+7\
&boxed{x = 7}
end{aligned}$$
b. $x = 3$ and $x = 1$
c. $x = -10$ and $x = frac{5}{2}$
d. $x = 7$
The vertex formula can be computed as:
$$begin{aligned}
y=ax^2+bx+c
end{aligned}$$
Vertex $(h,k) = left(frac{-b}{2a}, frac{b^2-4ac}{4a} right)$
Compute for the x-coordinate of the vertex:
$$begin{aligned}
h &= frac{-b}{2a} \\
h &= frac{-(-16)}{2(2)} \\
&= frac{16}{4} \\
&boxed{= 4}
end{aligned}$$
To compute for the y-coordinate, substitute the obtained x-coordinate to the equation.
$$begin{aligned}
y &= 2x^2-16x+30 \
&= 2(4)^2-16(4)+30 \
&boxed{= -2}
end{aligned}$$
b. y-coordinate $=-2$
The vertex is $(4,-2)$.
$$
P(red)=dfrac{3}{8}=0.375=37.5%
$$
b. The probability is the height of the yellow bar:
$$
P(yellow)=dfrac{1}{8}=0.125=12.5%
$$
c. The probability is the height of the blue bar:
$$
P(blue)=dfrac{3}{8}=0.375=37.5%
$$
d. The total probability should be 1(=100%) and thus the remaining probability will be for the color green:
$$
P(green)=1-dfrac{3}{8}-dfrac{1}{8}-dfrac{3}{8}=dfrac{1}{8}=0.125=12.5%
$$
b. 12.5%
c. 37.5%
d. 12.5%
$$
dfrac{30%}{12}=2.5%=0.025
$$
b. The interest (which is what you will need to pay) is the product of the principal and the monthly interest rate (increased by 1) to the power of the number of months:
$$
f(x)=500(1.025)^x
$$
c. Replace $x$ with 6:
$$
f(6)=500(1.025)^6approx $579.85
$$
d. Replace $x$ with 12:
$$
f(12)=500(1.025)^{12}approx $672.44
$$
The interest is the new principal decreased by the previous principal:
$$
$672.44-$500=$172.44
$$
The effective annual rate of interest is then the interest divided by the original principal:
$$
dfrac{$172.44}{$500}=0.34488=34.488%
$$
b. $f(x)=500(1.025)^x$
c. $579.85
d. 34.488%
$$
10x+5=15x-30
$$
Subtract $10x$ from both sides of the equation:
$$
5=5x-30
$$
Add 30 to both sides of the equation:
$$
35=5x
$$
Divide both sides of the equation by 5:
$$
7=x
$$
x=7text{textdegree}
$$
Solve the equation by completing the square method.
$$begin{aligned}
x^2+6x+8 &= 0 \
x^2+6x+8-8 &= 0-8 \
x^2+6x &= -8 \
end{aligned}$$
Get the coefficient of the $x$-term, divide it by $2$, and add its square to both sides of the equation.
$$begin{aligned}
x^2+6x+ left(frac{6}{2} right)^2 &= -8+left(frac{6}{2} right)^2 \
x^2+6x+ 9 &= 1 \
end{aligned}$$
$$begin{aligned}
x^2+6x+ 9 &= 1 \
(x+3)^2 &= 1 \
sqrt{(x+3)^2} &= sqrt{1} \
x+3 &= pm1 \
end{aligned}$$
$$begin{aligned}
x+3 &= 1 \
x+3-3 &= 1-3 \
&boxed{x = -2} \
end{aligned}$$
and
$$begin{aligned}
x+3 &= -1 \
x+3-3 &= -1-3 \
&boxed{x = -4} \
end{aligned}$$
Solve the equation by factoring out $x$.
$$begin{aligned}
x^2+6x =0 \
x(x+6)=0
end{aligned}$$
$$begin{aligned}
x(x+6)=0 \
end{aligned}$$
becomes
$$begin{aligned}
boxed{x=0} \
end{aligned}$$
and
$$begin{aligned}
x+6&=0 \
x+6-6&=0-6 \
&boxed{x=-6}
end{aligned}$$
Solve the equation by Zero Product Property.
$$begin{aligned}
0=3(x-5)(2x+3)\
end{aligned}$$
becomes
$$begin{aligned}
0&=x-5\
-x&=-5\
frac{-x}{-1} &= frac{-5}{-1}\
&boxed{x=5}\
end{aligned}$$
and
$$begin{aligned}
0&=2x+3\
-2x&=3\
frac{-2x}{-2} &= frac{3}{-2}\
&boxed{x=-frac{3}{2}}
end{aligned}$$
Solve the equation by completing the square method.
$$begin{aligned}
x^2 +4x-9 &= 3 \
x^2 +4x-9+9 &= 3+9 \
x^2 +4x &= 12 \
end{aligned}$$
Get the coefficient of the $x$-term, divide it by $2$, and add its square to both sides of the equation.
$$begin{aligned}
x^2+4x+ left(frac{4}{2} right)^2 &= 12+left(frac{4}{2} right)^2 \
x^2+4x+ 4 &= 16 \
end{aligned}$$
$$begin{aligned}
x^2+4x+ 4 &= 16 \
(x+2)^2 &= 16 \
sqrt{(x+2)^2} &= sqrt{16} \
x+2 &= pm 4 \
end{aligned}$$
$$begin{aligned}
x+2 &= 4 \
x+2-2 &= 4-2 \
&boxed{x = 2} \
end{aligned}$$
and
$$begin{aligned}
x+2 &= -4 \
x+2-2 &= -4-2 \
&boxed{x = -6} \
end{aligned}$$
b. $x=0$ and $x=-6$
c. $x=5$ and $x=-frac{3}{2}$
d. $x=2$ and $x=-6$
Given Table.

$$begin{aligned}
y=ax^2+bx+c
end{aligned}$$
$$begin{aligned}
y&=a(0)^2+b(0)+c\
y&=c
end{aligned}$$
$$begin{aligned}
y&=c\
-6&=c
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=a(1)^2+b(1)+c\
y&=a+b+c
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=a(2)^2+b(2)+c\
y&=4a+2b+c
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=a(3)^2+b(3)+c\
y&=9a+3b+c
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=a(4)^2+b(4)+c\
y&=16a+4b+c
end{aligned}$$
|x |0 |1 |2 | 3|4 |
|–|–|–|–|–|–|
|y |c |a+b+c |4a+2b+c |9a+3b+c |16a+4b+c |
$$begin{aligned}
2a&=2\
a&=dfrac{2}{2}\
a&=1
end{aligned}$$
a+b&=2\
1+b&=2\
b&=2-1\
b&=1
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=(1)x^2+(1)x-6\
y&=x^2+x-6
end{aligned}$$
Based on the table shown in **Step 12**, when $x$ = -4, the value of $y$ should be $6$,
$$begin{aligned}
y&=x^2+x-6\
y&=(-4)^2+(-4)-6\
y&=16-4-6\
y&=6
end{aligned}$$
Given table.

$$begin{aligned}
y=ax^2+bx+c
end{aligned}$$
$$begin{aligned}
y=c
end{aligned}$$
$$begin{aligned}
y&=c\
-5&=c
end{aligned}$$
|x |0 |1 |2 | 3|4 |
|–|–|–|–|–|–|
|y |c |a+b+c |4a+2b+c |9a+3b+c |16a+4b+c |
$$begin{aligned}
2a&=2\
a&=dfrac{2}{2}\
a&=1
end{aligned}$$
a+b&=5\
1+b&=5\
b&=5-1\
b&=4
end{aligned}$$
$$begin{aligned}
y&=ax^2+bx+c\
y&=(1)x^2+(4)x-5\
y&=x^2+4x-5
end{aligned}$$
Based on the table shown in **Step 23**, when $x$ = -5, the value of $y$ should be $0$,
$$begin{aligned}
y&=x^2+4x-5\
y&=(-5)^2+4(-5)-5\
y&=25-20-5\
y&=0
end{aligned}$$
$$
y=a(x+3)(x-2)
$$
Evaluate the function at one of the given points:
$$
-12=a(3)(-2)=-6a
$$
Divide both sides of the equation by $-6$:
$$
2=a
$$
Replace $a$ in the equation with 2:
$$
y=2(x+3)(x-2)
$$
y=2(x+3)(x-2)
$$
We note that the vertex is $(7,25)$ (since in the table we note that ti is the maximum and $x=7$ is also obviously the axis of symmetry). The equation of the parabola is then of the form:
$$
y=a(x-7)^2+25
$$
Next evaluate the function at one point:
$$
0=a(2-7)^2+25=25a+25
$$
Subtract 25 from both sides of the equation:
$$
-25=25a
$$
Divide both sides of the equation by 25:
$$
-1=a
$$
Replace $y$ in the equation with $-1$:
$$
y=-(x-7)^2+25
$$
y=-(x-7)^2+25
$$
If you are able to determine the $x$-intercepts from the table $x=a$ and $x=b$, then the equation is of the form $f(x)=c(x-a)(x-b)$.
Determine the remaining constant by evaluating the function at another point (than those you’ve used).
a. In the table we note that $x=3$ and $x=-5$ is a root, thus the equation is then of the form:
$$
y=a(x-3)(x+5)
$$
Evaluate the function at one of the given points:
$$
16=a(-3)(5)=-15a
$$
Divide both sides of the equation by $-15$:
$$
-dfrac{16}{15}=a
$$
Replace $a$ in the equation with $-dfrac{16}{15}$:
$$
y=-dfrac{16}{15}(x-3)(x+5)
$$
$$
y=a(x-1)(x-2.5)
$$
Evaluate the function at one of the given points:
$$
-2.5=a(1)(2.5)=2.5a
$$
Divide both sides of the equation by $2.5$:
$$
-1=a
$$
Replace $a$ in the equation with $-1$:
$$
y=-(x-1)(x-2.5)
$$
$$
y=a(x-8)(x-b)
$$
Evaluate the function at two of the given points:
$$
-16=a(-8)(-b)=8abRightarrow a=dfrac{-16}{8b}=dfrac{-2}{b}
$$
$$
-2=a(-5)(3-b)=-5a(3-b)
$$
Replace $a$ in the second equation with $-dfrac{2}{b}$:
$$
-2=-dfrac{10}{b}(3-b)
$$
Use distributive property:
$$
-2=-dfrac{30}{b}+10
$$
Subtract 10 from both sides of the equation:
$$
-12=-dfrac{30}{b}
$$
Multiply both sides of the equation by $b$:
$$
-12b=-30
$$
Divide both sides of the equation by $-12$:
$$
b=2.5
$$
Determine $a$:
$$
a=dfrac{-2}{b}=dfrac{-2}{2.5}=-0.8
$$
Thus the equation then becomes:
$$
y=-0.8(x-8)(x-2.5)
$$
b. $y=-(x-1)(x-2.5)$
c. $y=-0.8(x-8)(x-2.5)$
$$
6x-18=0text{ or }3x+2=0
$$
Solve each equation to $x$:
$$
6x=18text{ or }3x=-2
$$
$$
x=3text{ or }x=-dfrac{2}{3}
$$
$$
(x-5)(x-2)=0
$$
Zero product property:
$$
x-5=0text{ or }x-2=0
$$
Solve each equation to $x$:
$$
x=5text{ or }x=2
$$
$$
(x+4)(x-3)=0
$$
Zero product property:
$$
x+4=0text{ or }x-3=0
$$
Solve each equation to $x$:
$$
x=-4text{ or }x=3
$$
$$
(2x-1)(2x+1)=0
$$
Zero product property:
$$
2x-1=0text{ or }2x+1=0
$$
Solve each equation to $x$:
$$
2x=1text{ or }2x=-1
$$
$$
x=dfrac{1}{2}text{ or }x=-dfrac{1}{2}
$$
$$
x^2-9=0
$$
Factorize:
$$
(x-3)(x+3)=0
$$
Zero product property:
$$
x-3=0text{ or }x+3=0
$$
Solve each equation to $x$:
$$
x=3text{ or }x=-3
$$
$$
(x-1)(x-1)=0
$$
Zero product property:
$$
x-1=0
$$
Add 1 to both sides of the equation:
$$
x=1
$$
b. $x=5$ or $x=2$
c. $x=-4$ or $x=3$
d. $x=frac{1}{2}$ or $x=-frac{1}{2}$
e. $x=3$ or $x=-3$
f. $x=1$
$$
x=pm 8
$$
$$
x+1=pm 8
$$
Subtract 1 from both sides of the equation:
$$
x=-1pm 8=7text{ or }-9
$$
$$
(x-1)^2=64
$$
Take the square root of both sides of the equation:
$$
x+1=pm 8
$$
Subtract 1 from both sides of the equation:
$$
x=-1pm 8=7text{ or }-9
$$
b. $x=7$ or $x=-9$
c. $x=7$ or $x=-9$
$$
theta = sin^{-1}{dfrac{14}{16}}approx 61text{textdegree}
$$
The sum of all angles in a triangle is 180$text{textdegree}$ and the base angles in a triangle are congruent:
$$
28+2x=180
$$
Subtract 28 from both sides of the equation:
$$
2x=152
$$
Divide both sides of the equation by 2:
$$
x=76
$$
Corresponding angles are equivalent since the lines are parallel:
$$
y=76(=x)
$$
Supplementary angles sum up to 180$text{textdegree}$:
$$
x+z=180
$$
Replace $x$ with its known value:
$$
76+z=180
$$
Subtract 76 from both sides of the equation:
$$
z=104
$$
x=y=76text{textdegree}
$$
$$
z=104text{textdegree}
$$
$$
P(preparationtext{ or }lost)=P(preparation)+P(lost)-P(preparationtext{ and }lost)
$$
The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
P(preparation)=dfrac{18}{200}=dfrac{9}{100}=0.09=9%
$$
$$
P(lost)=dfrac{12}{200}=dfrac{3}{50}=0.06=6%
$$
Fill in the known values in the equation:
$$
11%=9%+6%-P(preparationtext{ and }lost)
$$
Add $P(preparationtext{ and }lost)$ to both sides of the equation:
$$
11%+P(preparationtext{ and }lost)=9%+6%
$$
Subtract 11% from both sides of the equation:
$$
P(preparationtext{ and }lost)=9%+6%-11%=4%
$$
$$
(x+7)(x-4)=x^2+7x-4x-28=x^2+3x-28
$$
Thus the equation is (b).
$$
(x+6)(x+4)=x^2+6x+4x+24=x^2+10x+24
$$
Thus the equation is (e).
Thus the equation is (a).
$$
(x)(x-4)=x^2-4x
$$
Thus the equation is (g).
$$
(x+2)(x-2)=x^2+2x-2x-4=x^2-4
$$
Note that the function also opens downwards, then we need to multiply the product of the factors with $-1$:
$$
(-1)(x^2-4)=-x^2+4
$$
Thus the equation is (d).
$$
(x+0.5)(x-1.5)=x^2+0.5x-1.5x-0.75=x^2-x-0.75
$$
The factors can still be multiplied by a constant, then we note that equation (i) is the only multiple of these factors and thus this is the equation of the graph.
(2) e
(3) a
(4) g
(5) d
(6) i
B. The $x$-intercepts are $x=-3$ and $x=2$. Then the equation is of the form:
$$
y=a(x+3)(x-2)
$$
Evaluate the function at one of the given points (note that $(0,6)$ is a point):
$$
6=a(3)(-2)=-6a
$$
Divide both sides of the equation by $-6$:
$$
-1=a
$$
Replace $a$ in the equation with $-1$:
$$
y=-(x+3)(x-2)
$$
$$
y=a(x-5)^2
$$
However if we want to determine the exact graph that she wants, we would need one more point, but we could try the graph with $a=1$ and see if this is what she wants (if she wants a more precise graph, she will need to supply an extra point).
$$
y=(x-5)^2
$$
B. $y=-(x+3)(x-2)$
C. $y=(x-5)^2$
a. The $x$-intercepts are $x=0$ and $x=8$. Then the equation is of the form:
$$
y=a(x)(x-8)
$$
Evaluate the function at one of the given points (note that $(4,32)$ is a point):
$$
32=a(4)(-4)=-16a
$$
Divide both sides of the equation by $-16$:
$$
-2=a
$$
Replace $a$ in the equation with $-2$:
$$
y=-2x(x-8)
$$
$$
y=a(x-10)(x-16)
$$
Evaluate the function at one of the given points (note that $(13,27)$ is a point, because of the symmetry of a parabola):
$$
27=a(3)(-3)=-9a
$$
Divide both sides of the equation by $-9$:
$$
-3=a
$$
Replace $a$ in the equation with $-3$:
$$
y=-3(x-10)(x-16)
$$
b. $y=-3(x-10)(x-16)$
c. See explanation
b. We know that if $x=a$ is a root, then $(x-a)$ is a factor of the function equation. Since $x=5$ is a double root, we know that $(x-5)^2$ will need to be a factor of the equation.
c. Rewriting the equation we obtain:
$$
y=x^2-8x+16=(x-4)^2
$$
We note that in this equation $x=4$ is a double root, however we needed a double root at $x=5$ and thus this function does not meet Vera’s needs.
b. $(x-5)^2$ needs to be a factor of the equation
c. $x$-intercept and vertex is both $(4,0)$
Solve for $x$.
$$begin{aligned}
|x-4|=3
end{aligned}$$
becomes
$$begin{aligned}
x-4&=3\
x-4+4&=3+4\
&boxed{x=7}
end{aligned}$$
and
$$begin{aligned}
x-4+4&=-3+4 \
&boxed{x=1}
end{aligned}$$
For $x=7$:
$$begin{aligned}
|x-4| &stackrel{?}{=} 3\
|7-4| &stackrel{?}{=} 3\
3 &stackrel{checkmark}{=} 3\
end{aligned}$$
For $x=1$:
$$begin{aligned}
|1-4| &stackrel{?}{=} 3\
|-3| &stackrel{?}{=} 3\
3 &stackrel{checkmark}{=} 3\
end{aligned}$$
Solve for $x$.
$$begin{aligned}
|x-4|-3 &= 0\
|x-4|-3+3 &= 0+3\
|x-4| &= 3\
end{aligned}$$
becomes
$$begin{aligned}
x-4&=3\
x-4+4&=3+4\
&boxed{x=7}
end{aligned}$$
and
$$begin{aligned}
x-4+4&=-3+4 \
&boxed{x=1}
end{aligned}$$
For $x=7$:
$$begin{aligned}
|x-4|-3 &stackrel{?}{=} 0\
|7-4|-3 &stackrel{?}{=} 0\
|3|-3&stackrel{?}{=} 0\
0 &stackrel{checkmark}{=} 0\
end{aligned}$$
For $x=1$:
$$begin{aligned}
|x-4|-3 &stackrel{?}{=} 0\
|1-4|-3 &stackrel{?}{=} 0\
|-3|-3 &stackrel{?}{=} 0\
0 &stackrel{checkmark}{=} 0\
end{aligned}$$
Solve for $x$.
$$begin{aligned}
|x-4|=-3
end{aligned}$$
Since absolute value can never be negative, so there are **no solutions.**
$$begin{aligned}
boxed{x = empty}
end{aligned}$$
Solve for $x$.
$$begin{aligned}
(x-4)^2 &= 9\
sqrt{(x-4)^2} &= sqrt{9}\
x-4 &= pm 3\
end{aligned}$$
becomes
$$begin{aligned}
x-4 &= 3\
x-4+4&=3+4\
&boxed{x=7}
end{aligned}$$
and
$$begin{aligned}
x-4 &= -3\
x-4+4&=-3+4 \
&boxed{x=1}
end{aligned}$$
For $x=7$:
$$begin{aligned}
(x-4)^2 &stackrel{?}{=} 9\
(7-4)^2 &stackrel{?}{=} 9\
3^2 &stackrel{?}{=} 9\
9 &stackrel{checkmark}{=} 9\
end{aligned}$$
For $x=1$:
$$begin{aligned}
(x-4)^2 &stackrel{?}{=} 9\
(1-4)^2 &stackrel{?}{=} 9\
-3^2 &stackrel{?}{=} 9\
9 &stackrel{checkmark}{=} 9\
end{aligned}$$
Solve for $x$.
$$begin{aligned}
(x-4)^2-9 &= 0\
(x-4)^2-9+9 &= 0+9\
(x-4)^2 &= 9\
sqrt{(x-4)^2} &= sqrt{9}\
x-4 &= pm 3\
end{aligned}$$
becomes
$$begin{aligned}
x-4 &= 3\
x-4+4&=3+4\
&boxed{x=7}
end{aligned}$$
and
$$begin{aligned}
x-4 &= -3\
x-4+4&=-3+4 \
&boxed{x=1}
end{aligned}$$
For $x=7$:
$$begin{aligned}
(x-4)^2-9 &stackrel{?}{=} 0\
(7-4)^2-9 &stackrel{?}{=} 0\
3^2-9 &stackrel{?}{=} 0\
0 &stackrel{checkmark}{=} 0\
end{aligned}$$
For $x=1$:
$$begin{aligned}
(x-4)^2-9 &stackrel{?}{=} 0\
(1-4)^2-9 &stackrel{?}{=} 0\
-3^2-9 &stackrel{?}{=} 0\
0 &stackrel{checkmark}{=} 0\
end{aligned}$$
Solve for $x$.
$$begin{aligned}
(x-4)^2 &= -9\
end{aligned}$$
Since the equation is squared, the result can never be negative, so there are **no solutions.**
$$begin{aligned}
boxed{x = empty}
end{aligned}$$
b. $x=7$ and $x=1$
c. $x = empty$
d. $x=7$ and $x=1$
e. $x=7$ and $x=1$
f. $x = empty$
**Part a**
$$begin{aligned}
&= 5-sqrt{36} \
&= 5-6 \
&boxed{= -1}
end{aligned}$$
$$begin{aligned}
&= 1+sqrt{39} \
&boxed{= 7.245}
end{aligned}$$
$$begin{aligned}
&= -2-sqrt{5} \
&boxed{= -4.236}
end{aligned}$$
b. $7.245$
c. $-4.236$
$$
y=a(x+4)(x-2)
$$
$$
y=a(x-3)^2
$$
$$
y=a(x)(x-7)
$$
$$
y=a(x+5)(x-1)
$$
b. $y=a(x-3)^2$
c. $y=ax(x-7)$
d. $y=a(x+5)(x-1)$
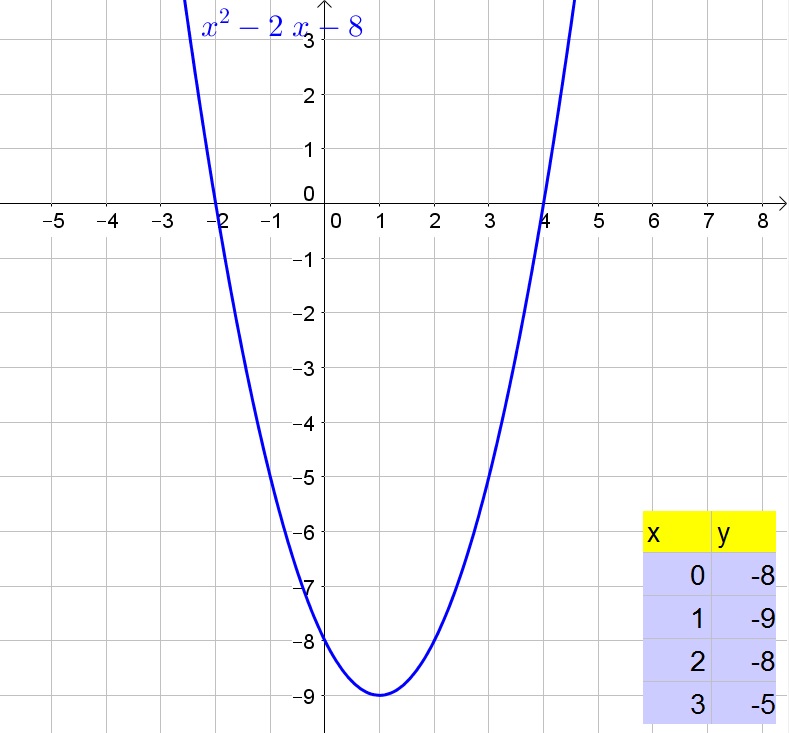
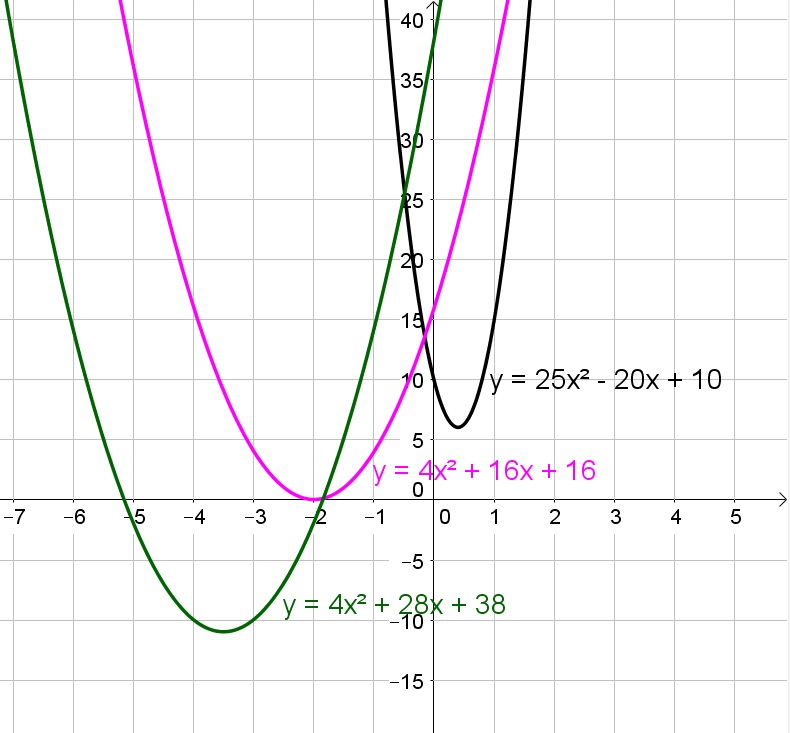
The graph opens upward.
The $x$-intercepts are $x=-2$ and $x=4$, while the $y$-intercept is $x=-8$.
The graph is negative on $(-2,4)$ and positive on $(-infty, -2)$ and $(4,+infty)$.
The function is decreasing on $(-infty,-2)$ and increasing on $(4,+infty)$.
$$
theta=tan^{-1}dfrac{9}{3}approx 72text{textdegree}
$$
b. The equation of a line in slope-intercept form is $y=ax+b$ with $a$ the slope and $b$ the $y$-intercept.
The slope angle is 45$text{textdegree}$ if the slope is equal to:
$$
tan{45text{textdegree}}=1
$$
We have also given that $y=3$ is the $y$ intercept. Thus the equation is then:
$$
y=1x+3=x+3
$$
c. The given system of equations:
$$
y=3x+1
$$
$$
y=x+3
$$
Subtract the two equations:
$$
0=2x-2
$$
Add 2 to both sides of the equation:
$$
2=2x
$$
Divide both sides of the equation by 2:
$$
1=x
$$
Determine $y$:
$$
y=3x+1=3(1)+1=4
$$
Thus the solution is $(1,4)$.
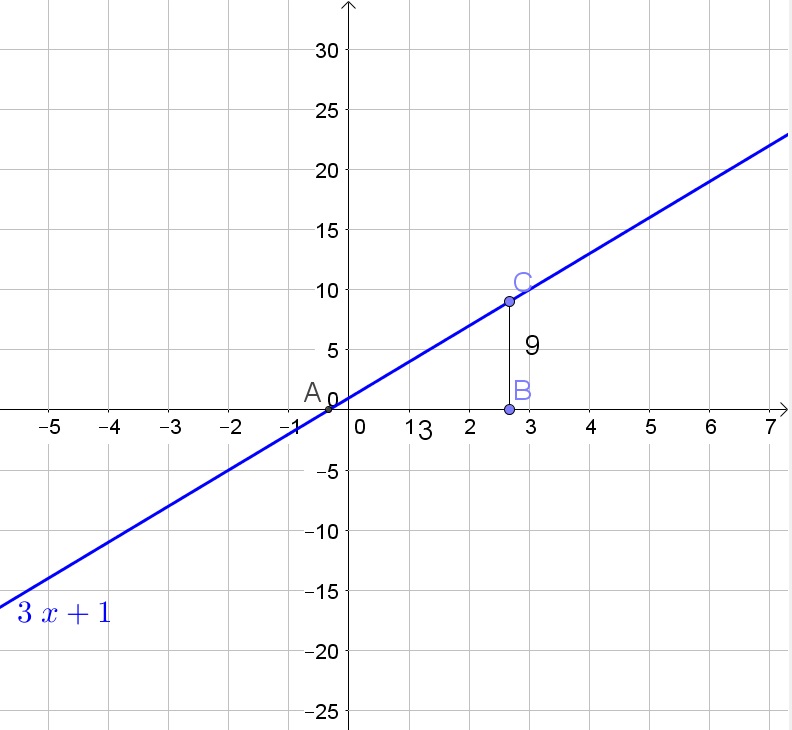
b. $y=x+3$
c. $(1,4)$
$$
triangle SQPcong triangle SQR
$$
$$
triangle EDGcong triangle GFE
$$
$$
triangle ABC cong triangle DEF
$$
b. GFE
c. DEF
$$
(x+3)^2=169
$$
Take the square root of both sides of the equation:
$$
x+3=pm 13
$$
Subtract 3 from both sides of the equation:
$$
x=-3pm 13=10text{ or } -16
$$
Only a positive length will make sense:
$$
x=10
$$

$$
sqrt{12}=2sqrt{3}ft
$$
The length of a side of the large square is then:
$$
2sqrt{3}ft+12’=2sqrt{3}ft+1ft=(2sqrt{3}+1)ft
$$
The area of the larger square is then the length of one side squared:
$$
(2sqrt{3}+1)^2=12+4sqrt{3}+1=13+4sqrt{3}text{ square ft }
$$
Determine the difference in area:
$$
13+4sqrt{3}-12=1+4sqrt{3}approx 8text{ square feet}
$$
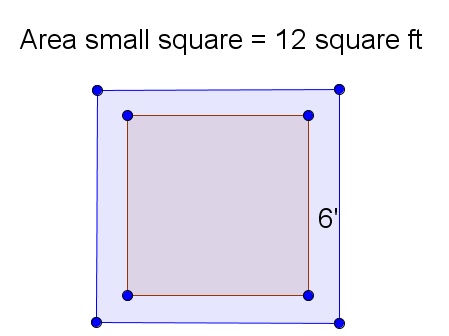
b. about 8 square feet
b. If $x=1$, then $x-1=0$ and thus $(x-1)^2=0$
c. The equation cannot have any $x$-values that make the equation true, because the square can never take on negative values.
d. You first determine the square root of both sides of the equation and then solve this equation to $x$.
b. $x=1$
c. No solution
d. You first determine the square root of both sides of the equation and then solve this equation to $x$.
$$
x-3=pm sqrt{12}=pm 2sqrt{3}
$$
Add 3 to both sides of the equation:
$$
x=3pm 2sqrt{3}
$$
b. We note that there are two solutions.
c.
$$
2+sqrt{3}approx 3.732….
$$
$$
2-sqrt{3}approx 0.2679….
$$
b. 2
c. $2+sqrt{3}approx 3.732…$ and $2-sqrt{3}approx 0.2679….$
$$
2x-3=pm 7
$$
Add 3 to both sides of the equation:
$$
2x=3pm 7
$$
Divide both sides of the equation by 2:
$$
x=dfrac{3pm 7}{2}=5text{ or }-2
$$
Thus there are two solutions.
$$
x+4=pm sqrt{20}=pm2sqrt{5}
$$
Subtract 4 from both sides of the equation:
$$
x=-4pm 2sqrt{5}
$$
Thus there are 2 solutions
$$
5-10x=0
$$
Subtract 5 from both sides of the equation:
$$
-10x=-5
$$
Divide both sides of the equation by $-10$:
$$
x=dfrac{1}{2}
$$
Thus there is 1 solution.
$$
(x+11)^2=0
$$
Take the square root of both sides of the equation:
$$
x+11=0
$$
Subtract 11 from both sides of the equation:
$$
x=-11
$$
Thus there is 1 solution.
b. 0 solutions
c. 2 solutions
d. 1 solution
e. 0 solutions
f. 1 solution
b. The square equals zero and thus the equation will have 1 solution.
c. The square equals a positive number, thus the equation will have two solutions.
b. 1
c. 2
b. Add7 to both sides of the equation:
$$
7=(x+4)^2
$$
Take the square root of both sides of the equation:
$$
pm sqrt{7}= x+4
$$
Subtract 4 from both sides of the equation:
$$
-4pm sqrt{7}=x
$$
Thus we note that the solutions are irrational numbers (because the root can only be approximated by a decimal).
c. On the graph we note that the vertex is $(-4,7)$, this answer is exact because if an equation is of the form $y=(x-a)^2+b$ then $(a,b)$ is the vertex of the parabola.
b. Irrational
c. $(-4,7)$

Triangle Inequality Theorem states that the length of a side of a triangle is less than the sum of the lengths of the two sides and is greater than the absolute value of their difference.
$$begin{aligned}
|overline{ MS} -overline{SL}|<overline{ML}<overline{ MS} +overline{SL}
end{aligned}$$
Solve for the possible lengths of side $overline{ML}$.
$$begin{aligned}
\
|overline{ MS} -overline{SL}|&<overline{ML}<overline{ MS} +overline{SL} \
|10-4|&<overline{ML}<10+4 \
6&<overline{ML}<14\
end{aligned}$$
**Part a**
$$begin{aligned}
&= sqrt{3} cdot sqrt{6} \
&= sqrt{3 cdot 6}\
&= sqrt{18}\
&= sqrt{9 cdot 2}\
&= sqrt{9} cdot sqrt{2} \
&boxed{= 3 sqrt{2}} \
end{aligned}$$
$$begin{aligned}
&= 2sqrt{27} cdot 5sqrt{3} \
&= 10sqrt{81} \
&= 10 cdot 9 \
&boxed{= 90} \
end{aligned}$$
$$begin{aligned}
&= sqrt{5 cdot 16} \
&= sqrt{5} cdot sqrt{16} \
&boxed{= 4sqrt{5}} \
end{aligned}$$
b. $90$
c. $4sqrt{5}$
$$
theta = sin^{-1}{dfrac{6}{9}}approx 42text{textdegree}
$$
b. The cosine ratio is the adjacent rectangular side divided by the hypotenuse:
$$
theta = cos^{-1}{dfrac{5}{7}}approx 44text{textdegree}
$$
c. The tangent ratio is the opposite side divided by the adjacent rectangular side:
$$
theta = tan^{-1}{dfrac{7}{9}}approx 38text{textdegree}
$$
b. 44$text{textdegree}$
c. 38$text{textdegree}$
c. Determine the lengths of the sides using the distance formula:
$$
WZ=sqrt{(6-7)^2+(5-3)^2}=sqrt{5}
$$
$$
WX=sqrt{(6-3)^2+(5-4)^2}=sqrt{10}
$$
$$
XY=sqrt{(9-3)^2+(1-4)^2}=sqrt{45}=3sqrt{5}
$$
$$
YZ=sqrt{(9-5)^2+(1-6)^2}=sqrt{41}
$$
The perimeter is then the sum of all lengths:
$$
4sqrt{5}+sqrt{10}+sqrt{41}
$$
c. The given transformation is the reflection about the $y$-axis, which changes the sign of the $x$-coordinates.
d. The rotation interchanges the $x$-and $y$-coordinates, and then changes the sign $y$-coordinates.
$$
begin{align*}
&W”(7,-3)
\ &Z”(6,-5)
end{align*}
$$
Determine the slope of the line $W”Z”$
$$
begin{align*}
text{Slope}&=frac{y_2-y_1}{x_2-x_1}=frac{-5-(-3)}{6-7}=frac{-5+3}{6-7}=frac{-2}{-1}=2
end{align*}
$$
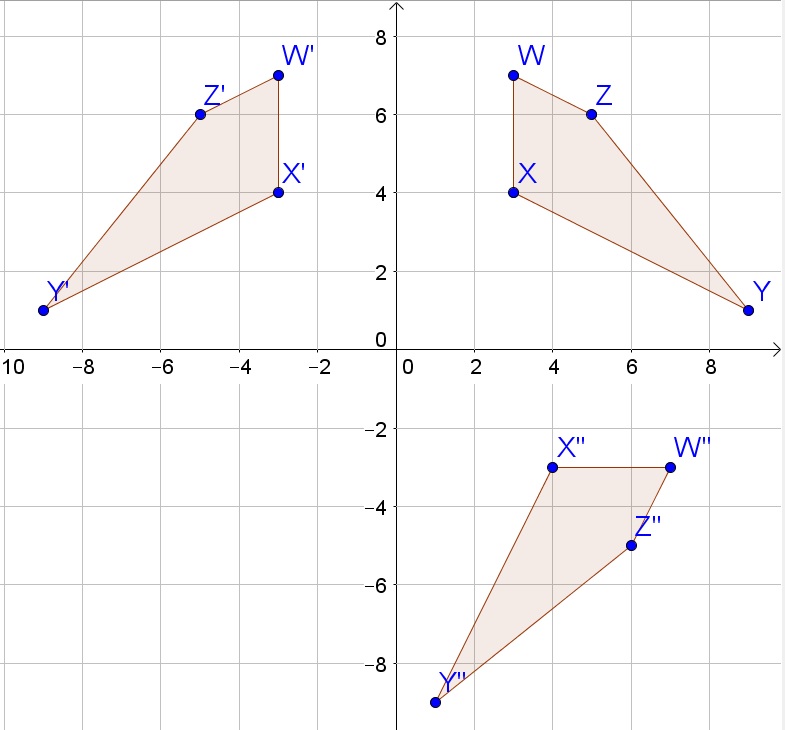
b. $4sqrt{5}+sqrt{10}+sqrt{41}$
c. $Y'(-9,1)$
d. 2
$$
x^2+4x=-1
$$
Complete the square:
$$
x^2+4x+4=-1+4
$$
Factorize:
$$
(x+2)^2=3
$$
Take the square root of both sides of the equation:
$$
x+2=pm sqrt{3}
$$
Subtract 2 from both sides of the equation:
$$
x=-2pm sqrt{3}
$$
$$
x+2=pm sqrt{3}
$$
Subtract 2 from both sides of the equation:
$$
x=-2pm sqrt{3}
$$
b. $x=-2pm sqrt{3}$
b. The complete the square method requires more steps than the other solution method.
b. Because afterwards you obtain a term on one side that can be rewritten as a square.
$$
x^2+6x+9=4
$$
Factorize:
$$
(x+3)^2=4
$$
Take the square root of both sides of the equation:
$$
x+3=pm 2
$$
Subtract 3 from both sides of the equation:
$$
x=-3pm 2=-1text{ or }-5
$$
$$
x^2+2x+1=6
$$
Factorize:
$$
(x+1)^2=6
$$
Take the square root of both sides of the equation:
$$
x+1=pm sqrt{6}
$$
Subtract 1 from both sides of the equation:
$$
x=-1pmsqrt{6}
$$
b. $x=-1pmsqrt{6}$
$$
x^2+4x+4=9
$$
Factorize:
$$
(x+2)^2=9
$$
Take the square root of both sides of the equation:
$$
x+2=pm 3
$$
Subtract 2 from both sides of the equation:
$$
x=-2pm 3=1text{ or }-5
$$
$$
x^2-6x+9=10
$$
Factorize:
$$
(x-3)^2=10
$$
Take the square root of both sides of the equation:
$$
x-3=pm sqrt{10}
$$
Add 3 to both sides of the equation:
$$
x=3pm sqrt{10}
$$
$$
x^2-2x+1=5
$$
Factorize:
$$
(x-1)^2=5
$$
Take the square root of both sides of the equation:
$$
x-1=pm sqrt{5}
$$
Add 1 to both sides of the equation:
$$
x=1pm sqrt{5}
$$
b. $x=3pm sqrt{10}$
c. $x=1pm sqrt{5}$
$$begin{aligned}
2x^2+12x+3=11
end{aligned}$$
$$begin{aligned}
2x^2+12x+3-textcolor{#4257b2}{3}&=11-textcolor{#4257b2}{3}\
2x^2+12x&=8
end{aligned}$$
$$begin{aligned}
2(x^2+6x)=8
end{aligned}$$
$$begin{aligned}
dfrac{2(x^2+6x)}{2}&=dfrac{8}{2}\
x^2+6x&=4
end{aligned}$$

$$begin{aligned}
(x+3)^2=13
end{aligned}$$
$$begin{aligned}
sqrt{(x+3)^2}&=pmsqrt{13}\
x+3&=pmsqrt{13}\
end{aligned}$$
$$begin{aligned}
x+3-textcolor{#4257b2}{3}&=pmsqrt{13}-textcolor{#4257b2}{3}\
x&=pmsqrt{13}-3\
end{aligned}$$
$$begin{aligned}
x&=sqrt{13}-3\
x&=0.605
end{aligned}$$
x&=-sqrt{13}-3\
x&=-6.605
end{aligned}$$
a. Note that $a=5$ and thus $a^2=25$ is the number of unit tiles.
b. Note that $a=3$ and thus $a^2=9$ is the number of unit tiles.
c. Note that $a=11$ and thus $a^2=11^2=121$ is the number of unit tiles.
b. 9
c. 121
We can calculate the value of the expression: $frac{2+sqrt{16}}{3}$ by getting the value of the radical as follows:
$$begin{aligned}
&= frac{2+sqrt{16}}{3} \
&= frac{2+4}{3} \
&= frac{6}{3} \
&= boxed{2}
end{aligned}$$
We can calculate the value of the expression: $frac{-1+sqrt{49}}{-2}$ by getting the value of the radical as follows:
$$begin{aligned}
&= frac{-1+sqrt{49}}{-2} \
&= frac{-1+7}{-2} \
&= frac{6}{-2} \
&= boxed{-3}
end{aligned}$$
We can calculate the value of the expression: $frac{-10 – sqrt{5}}{2}$ as by separating the expression as follows:
$$begin{aligned}
&= frac{-10 – sqrt{5}}{2} \
&= frac{-10}{2} – frac{sqrt{5}}{2} \
&= -5 – frac{sqrt{5}}{2} \
&approx boxed{-6.12}
end{aligned}$$
b. $-3$
c. $-6.12$
b. You cannot use the zero product property, because you cannot factorize the given equation, you will first need to complete the square.
b. Not possible to factorize equation
The standard form of a parabola can be described by the following equation:
$$begin{gather}
(x-h)^2 = 4p(y-k)
end{gather}$$
where the vertex at the point $(h,k)$, focus at $(h,k+p)$, and the directrix at $y=k-p$
We want to verify whether a parabola always has two solutions. We are to draw an example in which (a) the parabola only intersects the x-axis once and (b) what does it mean if the quadratic equation has no solution
A parabola can intersect the x-axis twice, once, or not at all. If a parabola has two solutions, then it intersects the x-axis twice. One example in which the parabola intersects the x-axis once is when the vertex of the parabola is located on the origin.

When a quadratic equation has no solution, this means that the solution of the equation is imaginary, hence, it has no real solution. In a parabola, it means that the parabola does not intersect the x-axis. One example of this scenario is when the parabola only intersects the y-axis.

overline{PQ}cong overline{SR}
$$
$$
overline{PR}cong overline{SQ}
$$
$$
overline{QR}cong overline{QR}
$$
$$
Downarrow SSS
$$
$$
triangle PQRsim triangle SRQ
$$
$$
Downarrow
$$
$$
angle P cong angle S
$$
$$
EV=5cdot dfrac{1}{2}+3cdot dfrac{1}{4}+2cdot dfrac{1}{4}=dfrac{10}{4}+dfrac{3}{4}+dfrac{2}{4}=dfrac{15}{4}=3.75
$$
The number of tickets she is expected the win is then the product of the number of games and the expected value:
$$
3cdot 3.75=11.25
$$
Thus it is expected that she wins more than 10 tickets and thus we can predict that she will win enough tickets.
$$
x^2-6x+9=2
$$
Factorize:
$$
(x-3)^2=2
$$
Take the square root of both sides of the equation:
$$
x-3=pm sqrt{2}
$$
Add 3 to both sides of the equation:
$$
x=3pm sqrt{2}
$$
$$
(p+1)^2=0
$$
Take the square root of both sides of the equation:
$$
p+1=0
$$
Subtract 1 from both sides of the equation:
$$
p=-1
$$
$$
x^2-4x+4=-5
$$
Factorize:
$$
(x-2)^2=-5
$$
The equation has no solutions because the square is never negative.
b. $p=-1$
c. No solutions
$$begin{aligned}
x^2-6x+7&=0\
x^2-6x&=-7\
end{aligned}$$
$$begin{aligned}
x^2-6x+9&=-7+9\
x^2-6x+9&=2
end{aligned}$$

$$begin{aligned}
(x-3)^2&=2
end{aligned}$$
$$begin{aligned}
p^2+2p+1
end{aligned}$$

$$begin{aligned}
(p+1)^2
end{aligned}$$
$$begin{aligned}
k^2-4k+9&=0\
k^2-4k&=-9\
end{aligned}$$
$$begin{aligned}
k^2-4k+4&=-9+4\
k^2-4k+4&=-5
end{aligned}$$

$$begin{aligned}
(k-2)^2&=-5
end{aligned}$$
$$
(2.5)^2=6.25
$$
b. Thus we need to add 6.25 to both sides of the equation:
$$
x^2+5x+6.25=-2+6.25=4.25
$$
b. $x^2+5x+6.25=4.25$
b. Since the coefficient of $x$ is 10, the constant in the parentheses is half of 10 (which is 5) and thus the expression in the parentheses is $x+5$. The dimensions of the square is then $x+5$ by $x+5$.
b. $x+5$, $x+5$ by $x+5$
$$
w^2+28w+196=144
$$
Factorize:
$$
(x+14)^2=144
$$
Take the square root of both sides of the equation:
$$
x+14=pm 12
$$
Subtract 14 from both sides of the equation:
$$
x=-14pm 12=-2text{ or }-26
$$
$$
x^2+5x+6.25=2.25
$$
Factorize:
$$
(x+2.5)^2=2.25
$$
Take the square root of both sides of the equation:
$$
x+2.5=pm 1.5
$$
Subtract 2.5 from both sides of the equation:
$$
x=-2.5pm 1.5=-1text{ or }-4
$$
$$
k^2-16k+64=81
$$
Factorize:
$$
(k-8)^2=9
$$
Take the square root of both sides of the equation:
$$
k-8=pm 3
$$
Add 8 to both sides of the equation:
$$
k=8pm 3=11text{ or }5
$$
$$
x^2-24x+144=15
$$
Factorize:
$$
(x-12)^2=15
$$
Take the square root of both sides of the equation:
$$
x-12=pm sqrt{15}
$$
Add 12 to both sides of the equation:
$$
x=12pm sqrt{15}
$$
b. $x=-1$ and $x=-4$
c. $k=5$ and $k=11$
d. $x=12pm sqrt{15}$
Make sure that the constant term (on the side with the $x$’s) is the square of half the coefficient of $x$ (by adding or subtracting the same number of both sides of the equation).
Then factorize (rewrite the expression with the $x$-terms as a square).
Next take the square root of both sides of the equation and solve to the unknown variable.
Then factorize (rewrite the expression with the $x$-terms as a square).
Next take the square root of both sides of the equation and solve to the unknown variable.
$$
x^2+4x+4=1
$$
Factorize:
$$
(x+2)^2=1
$$
Take the square root of both sides of the equation:
$$
x+2=pm 1
$$
Subtract 2 from both sides of the equation:
$$
x=-2pm 1=-1text{ or }-3
$$
$$
x^2-8x+16=9
$$
Factorize:
$$
(x-4)^2=9
$$
Take the square root of both sides of the equation:
$$
x-4=pm 3
$$
Add 4 to both sides of the equation:
$$
x=4pm 3=7text{ or }1
$$
$$
x^2+5x+6.25=8.25
$$
Factorize:
$$
(x+2.5)^2=8.25
$$
Take the square root of both sides of the equation:
$$
x+2.5=pm sqrt{8.25}=pm dfrac{sqrt{33}}{2}
$$
Subtract 2.5 from both sides of the equation:
$$
x=-2.5pm dfrac{sqrt{33}}{2}=dfrac{-5pmsqrt{33}}{2}
$$
b. $x=1$ and $x=7$
c. $x=dfrac{-5pmsqrt{33}}{2}$
$$
x^2+6x+9=49
$$
Factorize:
$$
(x+3)^2=49
$$
Take the square root of both sides of the equation:
$$
x+3=pm 7
$$
Subtract 3 from both sides of the equation:
$$
x=-3pm 7=4text{ or }-10
$$
$$
(2x-3)(x+8)=0
$$
Zero product property
$$
2x-3=0text{ or }x+8=0
$$
Solve each equation to $x$:
$$
2x=3text{ or }x=-8
$$
$$
x=dfrac{3}{2}text{ or }x=-8
$$
b. $x=dfrac{3}{2}$ and $x=-8$
$$
dfrac{-6+sqrt{196}}{2}=dfrac{-6+14}{2}=dfrac{8}{2}=4
$$
b.
$$
dfrac{-6-sqrt{196}}{2}=dfrac{-6-14}{2}=dfrac{-20}{2}=-10
$$
c.
$$
dfrac{-13-sqrt{361}}{4}=dfrac{-13-19}{4}=dfrac{-32}{4}=-8
$$
d.
$$
dfrac{-13+sqrt{361}}{4}=dfrac{-13+19}{4}=dfrac{6}{4}=dfrac{3}{2}
$$
We note that the solutions to the equations in the previous exercise are equal to the expressions evaluated here.
b. $-10$
c. $-8$
d. $frac{3}{2}$
$$
9+3x=pm 39
$$
Subtract 9 from both sides of the equation:
$$
3x=-9pm 39
$$
Divide both sides of the equation by 3:
$$
x=-3pm 13=10text{ or }-16
$$
$$
2x+1=pm 10
$$
Subtract 1 from both sides of the equation:
$$
2x=-1pm 10
$$
Divide both sides of the equation by 2:
$$
x=-dfrac{1}{2}pm 5=dfrac{9}{2}text{ or }-dfrac{11}{2}
$$
$$
-3x+9=pm 10
$$
Subtract 9 from both sides of the equation:
$$
-3x=-9pm 10
$$
Divide both sides of the equation by $-3$:
$$
x=3pm dfrac{10}{3}=dfrac{19}{3}text{ or }-dfrac{1}{3}
$$
b. $x=frac{9}{2}$ or $x=-frac{11}{2}$
c. $x=frac{19}{3}$ or $x=-frac{1}{3}$
d. No solution
$$
dfrac{Delta y}{Delta x}=dfrac{-5}{6}
$$
b. The distance we can determine using the Pythagorean theorem:
$$
LD=sqrt{5^2+6^2}=sqrt{61}approx 7.81
$$
c. The coordinates of $M$ are:
$$
M=left( -2+dfrac{2}{3}cdot 6, 1-dfrac{2}{3}cdot 5right)=left( 2, -dfrac{7}{3}right)
$$
d. You can determine the lengths using the distance formula:
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
$$
while you can determine the slope using the ratio:
$$
dfrac{y_2-y_1}{x_2-x_1}
$$

b. $7.81$
c. $left(2,-frac{7}{3}right)$
d. Use distance formula
a. We note that there is 1 scalene triangle out of 4:
$$
P(scalene)=dfrac{1}{4}=0.25=25%
$$
b. We note that there are 3 isosceles triangles out of 4:
$$
P(isosceles)=dfrac{3}{4}=0.75=75%
$$
c. We note that 2 triangles out of 4 have a side with length 6 cm:
$$
P(6cm)=dfrac{2}{4}=dfrac{1}{2}=0.5=50%
$$
b. 75%
c. 50%
$$
x^2-3x+2.25=9.25
$$
Factorize:
$$
(x-1.5)^2=9.25
$$
Take the square root of both sides of the equation:
$$
x-1.5=pm sqrt{9.25}=pm dfrac{sqrt{37}}{2}
$$
Add 1.5 to both sides of the equation
$$
x=1.5pm dfrac{sqrt{37}}{2}=dfrac{3}{2}pm dfrac{sqrt{37}}{2}approx 4.54text{ or }-1.54
$$
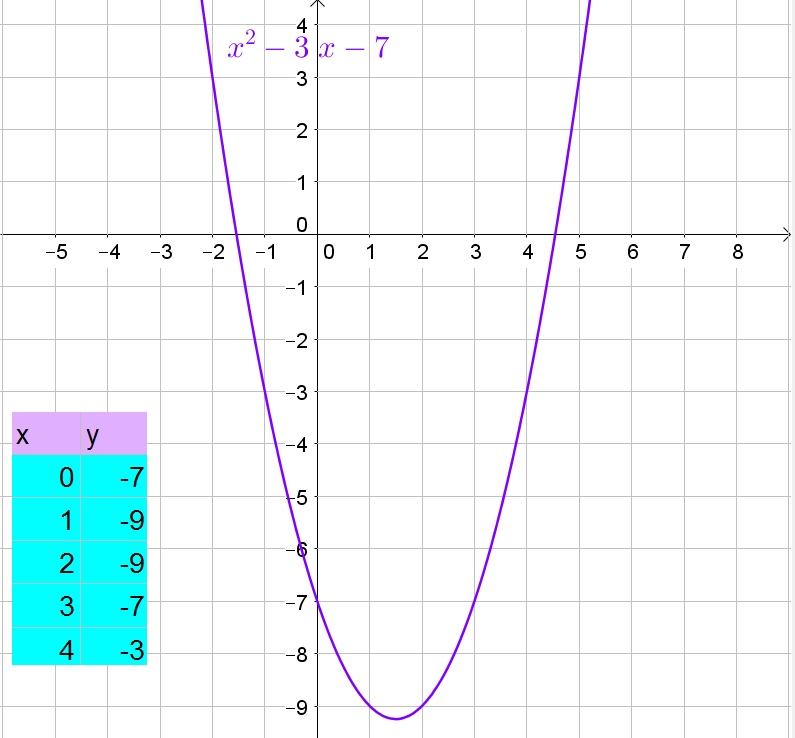
b. $dfrac{3}{2}pm dfrac{sqrt{37}}{2}$
c. Yes
$$
x=dfrac{3pm sqrt{(-3)^2-4(1)(-7)}}{2(1)}=dfrac{3pm sqrt{37}}{2}=dfrac{3}{2}pm dfrac{sqrt{37}}{2}
$$
We note that the solution is the same as that in the previous exercise.
b. $x=dfrac{3}{2}pm dfrac{sqrt{37}}{2}$
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
a.
$$
x=dfrac{-7pm sqrt{7^2-4(3)(2)}}{2(3)}=dfrac{-7pm 5}{6}=-dfrac{1}{3}text{ or } -2
$$
b.
$$
x=dfrac{9pm sqrt{(-9)^2-4(2)(-35)}}{2(2)}=dfrac{9pm 19}{4}=7text{ or } -dfrac{5}{2}
$$
c.
$$
x=dfrac{-10pm sqrt{10^2-4(8)(3)}}{2(8)}=dfrac{-10pm 2}{16}=-dfrac{1}{2}text{ or } -dfrac{3}{4}
$$
d.
$$
x=dfrac{5pm sqrt{(-5)^2-4(1)(9)}}{2(1)}=dfrac{5pm sqrt{-11}}{2}=text{ does not exist}
$$
b. $x=7$ or $x=-frac{5}{2}$
c. $x=-frac{1}{2}$ or $x=-frac{3}{4}$
d. No solution
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
QUADRATIC FORMULA METHOD
$$
x=dfrac{-bpm sqrt{b^2-4(1)(c)}}{2(1)}=dfrac{-bpm sqrt{b^2-4c}}{2}
$$
COMPLETE THE SQUARE METHOD
Subtract $c$ from both sides of the equation:
$$
x^2+bx=-c
$$
Add $left( dfrac{b}{2}right)^2$ to both sides of the equation:
$$
x^2+bx+left( dfrac{b}{2}right)^2=-c+left( dfrac{b}{2}right)^2
$$
Factorize:
$$
left( x+dfrac{b}{2}right)^2=dfrac{b^2}{4}-c=dfrac{b^2-4c}{4}
$$
Take the square root of both sides of the equation:
$$
x+dfrac{b}{2}=pm dfrac{sqrt{b^2-4c}}{2}
$$
Subtract $dfrac{b}{2}$ from both sides of the equation:
$$
x=-dfrac{b}{2}pm dfrac{sqrt{b^2-4c}}{2}=dfrac{-bpm sqrt{b^2-4c}}{2}
$$
Thus we note that both methods give the same solution.
The quadratic formula is
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
where $a$ is the coefficient of $x^2$, $b$ is the coefficient of $x$ and $c$ is the constant term.
Solve the equation by replacing $a$, $b$ and $c$ by their values and then simplify to obtain the solution.
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
where $a$ is the coefficient of $x^2$, $b$ is the coefficient of $x$ and $c$ is the constant term.
Solve the equation by replacing $a$, $b$ and $c$ by their values and then simplify to obtain the solution.
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
with $a$ the coefficient of $x^2$, $b$ the coefficient of $x$ and $c$ the constant term.
a.
$$
x=dfrac{13pm sqrt{(-13)^2-4(1)(42)}}{2(1)}=dfrac{13pm 1}{2}=7text{ or } 6
$$
b.
$$
x=dfrac{-10pm sqrt{(10)^2-4(3)(-8)}}{2(3)}=dfrac{-10pm 14}{6}=dfrac{2}{3}text{ or } -4
$$
c.
$$
x=dfrac{10pm sqrt{(-10)^2-4(2)(0)}}{2(2)}=dfrac{10pm 10}{4}=5text{ or } 0
$$
d.
$$
x=dfrac{-8pm sqrt{8^2-4(4)(-60)}}{2(4)}=dfrac{-8pm 32}{8}=3text{ or }-5
$$
b. $x=frac{2}{3}$ or $x=-4$
c. $x=5$ or $x=0$
d. $x=3$ or $x=-5$
b. Use distributive property:
$$
x^2-5x+2x-10=-6
$$
Add 6 to both sides of the equation:
$$
x^2-3x-4=0
$$
Factorize:
$$
(x-4)(x+1)=0
$$
c. Zero product property:
$$
x-4=0text{ or }x+1=0
$$
Solve each equation to $x$:
$$
x=4text{ or }x=-1
$$
b. $(x-4)(x+1)=0$
c. $x=4$ or $x=-1$
$$
y=a(x+3)(x-1)
$$
Another point on the graph is $(0,-3)$:
$$
-3=a(3)(-1)=-3a
$$
Divide both sides of the equation by $-3$:
$$
1=a
$$
Replace $a$ with 1 in the equation:
$$
y=(x+3)(x-1)
$$
$$
y=a(x+2)(x-2)
$$
Another point on the graph is $(0,-4)$:
$$
-4=a(2)(-2)=-4a
$$
Divide both sides of the equation by $-4$:
$$
1=a
$$
Replace $a$ with 1 in the equation:
$$
y=(x+2)(x-2)
$$
b. $y=(x+2)(x-2)$
c. Neither
$$
P(oak )=dfrac{35}{45}=dfrac{7}{9}
$$
The probability of the two events is then the product of the probability of both events (because they have been randomly assigned:
$$
dfrac{7}{9}cdot 20%=dfrac{7}{9}cdot dfrac{1}{5}=dfrac{7}{45}approx 0.156=15.6%
$$
$$
sqrt{4^2+3^2}=sqrt{25}=5
$$
$$
x=sqrt{5^2+12^2}=sqrt{169}=13
$$
$$
x=180text{textdegree}-35text{textdegree}-65text{textdegree}=80text{textdegree}
$$
b. $x=80text{textdegree}$
$$
L:sqrt{6^2-3^2}=sqrt{27}=3sqrt{3}
$$
$$
R: sqrt{9^2-3^2}=sqrt{72}=6sqrt{2}
$$
The length is then the sum of the left and the right part:
$$
3sqrt{3}+6sqrt{2}
$$
$$
AREA =dfrac{(3sqrt{3}+6sqrt{2})3}{2}=dfrac{9}{2}sqrt{3}+9sqrt{2}
$$
c. The perimeter is the sum of the lengths of all sides:
$$
PERIMETER=3sqrt{3}+6sqrt{2}+6+9=15+3sqrt{3}+6sqrt{2}
$$
b. $frac{9}{2}sqrt{3}+9sqrt{2}$
c. $15+3sqrt{3}+6sqrt{2}$
$$
(x+3)(x+9)=0
$$
Zero product property:
$$
x+3=0text{ or }x+9=0
$$
Solve each equation to $x$:
$$
x=-3text{ or }x=-9
$$
$$
(2x-11)^2=0
$$
Zero product property:
$$
2x-11=0
$$
Add 11 to both sides of the equation:
$$
2x=11
$$
Divide both sides of the equation by 2:
$$
x=dfrac{11}{2}
$$
$$
3x+4=0text{ or }2x-1=0
$$
Solve each equation to $x$:
$$
3x=-4text{ or }2x=1
$$
$$
x=-dfrac{4}{3}text{ or }x=dfrac{1}{2}
$$
$$
x^2-8x+16=0
$$
Factorize:
$$
(x-4)^2=0
$$
Zero product property:
$$
x-4=0
$$
Add 4 to both sides of the equation:
$$
x=4
$$
$$
36x^2-60x+25=0
$$
Factorize:
$$
(6x-5)^2=0
$$
Zero product property:
$$
6x-5=0
$$
Add 5 to both sides of the equation:
$$
6x=5
$$
Divide both sides of the equation by 6:
$$
x=dfrac{5}{6}
$$
$$
20x^2-32x-45=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{32pm sqrt{(-32)^2-4(20)(-45)}}{2(20)}=dfrac{32pm 68}{40}=dfrac{5}{2}text{ or }-dfrac{9}{10}
$$
b. $x=frac{11}{2}$
c. $x=-frac{4}{3}$ or $x=frac{1}{2}$
d. $x=4$
e. $x=frac{5}{6}$
f. $x=frac{5}{2}$ or $x=-frac{9}{10}$
If the equation is easy to factorize or has been given in factorized form, then use the zero product property.
If the coefficient of $x^2$ is 1 and the coefficient of $x$ is even, then use the completing the square method.
Else use the quadratic formula.
If the coefficient of $x^2$ is 1 and the coefficient of $x$ is even, then use the completing the square method.
Else use the quadratic formula.
$$
x(100-2x)=600
$$
Subtract 600 from both sides of the equation:
$$
-2x^2+100x-600=0
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-100pm sqrt{100^2-4(-2)(-600)}}{2(-2)}=dfrac{-100pm sqrt{5200}}{-4}approx 6.97text{ or } 43.03
$$
Determine the length:
$$
100-2(6.97)approx 86.06
$$
$$
100-2(43.03)approx 13.94
$$
Since the length should be longer than the width, the length is then 86.06 ft and the width is 6.97 ft.
$$
x+10+x=108
$$
Subtract 10 from both sides of the equation:
$$
2x=98
$$
Divide both sides of the equation by 2:
$$
x=49
$$
Detemrine the speed of Melinda:
$$
x+10=49+10=59
$$
Thus Karen drives 49 mph and Melinda drives 59 mph.
In the table we note that $x=-315$ and $x=315$ is a root, thus the equation is then of the form:
$$
y=a(x-315)(x+315)
$$
Evaluate the function at one of the given points ($(0,630)$ is a point of the parabola):
$$
630=a(-315)(315)=-99225a
$$
Divide both sides of the equation by $-99225$:
$$
-dfrac{2}{315}=a
$$
Replace $a$ in the equation with $-dfrac{2}{315}$:
$$
y=-dfrac{2}{315}(x-315)(x+315)
$$
$$
y=-dfrac{2}{315}(-300-315)(-300+315)=dfrac{410}{7}approx 58.6ft
$$
b. 58.6 ft
c. $[-315,315]$
$$
0=2x^2-4.8x
$$
Factorize:
$$
0=2x(x-2.4)
$$
Zero product property:
$$
x=0text{ or }x-2.4=0
$$
Solve each equation to $x$:
$$
x=0text{ or }x=2.4
$$
Thus the yo-yo was 2.4 s out of his hand.
$$
dfrac{2.4}{2}=1.2s
$$
c. Replace $x$ in the equation with 1.2:
$$
y=2(1.2)^2-4.8(1.2)=-2.88
$$
Thus the string is 2.88ft.
d.
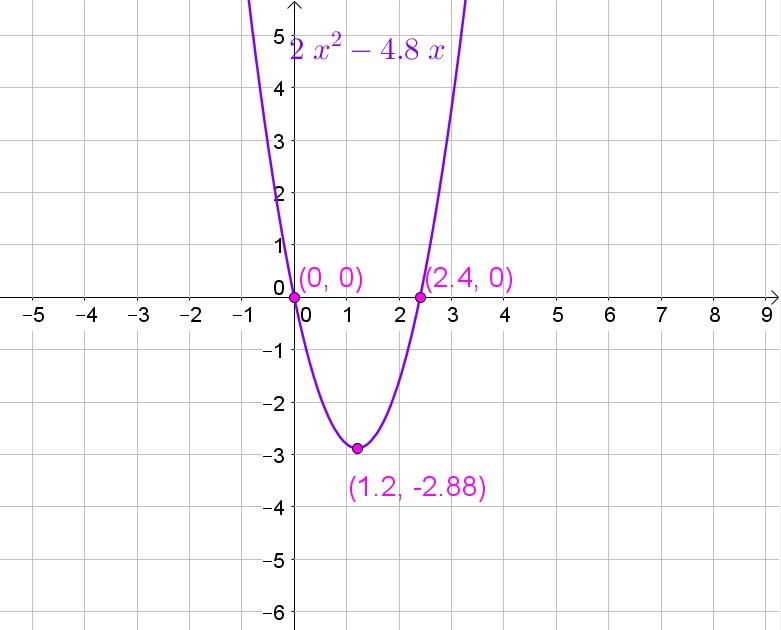
b. 1.2 s
c. 2.88 ft
d. Graph
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
QUADRATIC FORMULA METHOD
$$
x=dfrac{-6pm sqrt{6^2-4(1)(11)}}{2(1)}=dfrac{-6pm sqrt{-8}}{2}=text{ does not exist }
$$
COMPLETE THE SQUARE METHOD
Subtract 2 from both sides of the equation:
$$
x^2+6x+9=-2
$$
Factorize:
$$
left( x+3right)^2=-2
$$
The equation has no solutions since the square is never negative.
$$
x=pm 12
$$
$$
x=12
$$
$$
x^2=144
$$
Take the square root of both sides of the equation:
$$
x=pm 12
$$
$$
x-1=12
$$
Add 1 to both sides of the equation:
$$
x=13
$$
$$
x^2=-5
$$
The equation has no solutions, because the square is never negative.
b. $x=12$
c. $x=pm 12$
d. $x=13$
e. No solutions
f. No solutions
$$
dfrac{x}{12}=dfrac{9}{6}
$$
Multiply both sides of the equation by 12:
$$
x=dfrac{9cdot 12}{6}=18
$$
b. Corresponding sides of similar figures have the same proportions:
$$
dfrac{w}{5}=dfrac{12}{3}
$$
Multiply both sides of the equation by 5:
$$
w=dfrac{12cdot 5}{3}=20
$$
c. Corresponding sides of similar figures have the same proportions:
$$
dfrac{n}{3}=dfrac{16}{7}
$$
Multiply both sides of the equation by 3:
$$
n=dfrac{16cdot 3}{7}=dfrac{48}{7}approx 6.86
$$
d. Corresponding sides of similar figures have the same proportions:
$$
dfrac{m}{7}=dfrac{11}{10}
$$
Multiply both sides of the equation by 7:
$$
m=dfrac{7cdot 11}{10}=dfrac{77}{10}=7.7
$$
b. $w=20$
c. $n=6.86$
d. $m=7.7$
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$
a. The line goes through the points $(0,3)$ and $(5,0)$:
$$
y-3=dfrac{0-3}{5-0}(x-0)
$$
Thus the equation is then:
$$
y=-dfrac{3}{5}x+3
$$
b. The $x$-intercept is the intersection of the graph with the $x$-axis and thus is $x=5$. The $y$-intercept is the intersection of the graph with the $y$-axis and thus is $y=3$.
c. The area of a triangle is the product of the base and the height divided by 2:
$$
dfrac{5cdot 3}{2}=7.5
$$
The perimeter is the sum of the lengths of all sides:
$$
3+5+sqrt{3^2+5^2}=8+sqrt{34}
$$
d. Perpendicular lines have slopes whose product is $-1$ and thus the slope of the perpendicular line is $dfrac{5}{3}$:
$$
y-3=dfrac{5}{3}(x-0)
$$
Thus the equation becomes:
$$
y=dfrac{5}{3}x+3
$$
b. $x$-intercept $(5,0)$ and $y$-intercept $(0,3)$
c. Area 7.5 and Perimeter $8+sqrt{34}$
d. $y=frac{5}{3}x+3$
$$
tan 15.5text{textdegree}=dfrac{x}{5280}
$$
Multiply both sides of the equation by 5280:
$$
1,464approx 5280tan 15.5text{textdegree}=x
$$
Add the height of the eyes to the result:
$$
1464+5=1469
$$
Thus the heigh of the building is about 1,469 feet.
$$
sqrt[3]{-64}=-sqrt[3]{64}=-sqrt[3]{4^3}=-4
$$
b.
$$
sqrt[5]{32}=sqrt[5]{2^5}=2
$$
c.
$$
sqrt[3]{-8}=-sqrt[3]{8}=-sqrt[3]{2^3}=-2
$$
d.
$$
sqrt[4]{10000}=sqrt[4]{10^4}=10
$$
b. 2
c. $-2$
d. 10
$$
(100x-8)(100x+8)=0
$$
Zero product property:
$$
100x-8=0text{ or }100x+8=0
$$
Solve each equation to $x$:
$$
100x=8text{ or }100x=-8
$$
$$
x=dfrac{2}{25}text{ or }x=-dfrac{2}{25}
$$
$$
9x^2+34x-8=0
$$
Factorize:
$$
(9x-2)(x+4)=0
$$
Zero product property:
$$
9x-2=0text{ or }x+4=0
$$
Solve each equation to $x$:
$$
9x=2text{ or }x=-4
$$
$$
x=dfrac{2}{9}text{ or }x=-4
$$
$$
x=dfrac{4pm sqrt{(-4)^2-4(2)(7)}}{2(2)}=dfrac{4pm sqrt{-40}}{4}=text{ does not exist }
$$
$$
x=dfrac{-0.2pm sqrt{(0.2)^2-4(3.2)(-5)}}{2(3.2)}=dfrac{-0.2pm sqrt{64.04}}{6.4}
$$
b. $x=frac{2}{9}$ or $x=-4$
c. No solution
d. $x=frac{-0.2pm sqrt{64.04}}{6.4}$
$$
alpha = 85text{textdegree}
$$
Supplementary angles have sum 180$text{textdegree}$ and alternate interior angles of parallel lines are congruent:
$$
theta=180text{textdegree}-112text{textdegree}=68text{textdegree}
$$
alpha = 85text{textdegree}
$$
$$
theta=68text{textdegree}
$$
$$
4x+20=pm 8
$$
Subtract 20 from both sides of the equation:
$$
4x=-20pm 8
$$
Divide both sides of the equatino by 4:
$$
x=-5pm 2=-3text{ or }-7
$$
$$
x-13=2
$$
Add 13 to both sides of the equation:
$$
x=15
$$
$$
sqrt{x-4}=7
$$
Square both sides of the equation:
$$
x-4=49
$$
Add 4 to both sides of the equation:
$$
x=53
$$
$$
6|x-8|=18
$$
Divide both sides of the equation by 6:
$$
|x-8|=3
$$
Property absolute value:
$$
x-8=pm 3
$$
Add 8 to both sides of the equation:
$$
x=8pm 3=11text{ or } 5
$$
$$
(x+12)^2=9
$$
Take the square root of both sides of the equation:
$$
x+12=pm 3
$$
Subtract 12 from both sides of the equation:
$$
x=-12pm 3=-9text{ or }-15
$$
$$
6^4=(6^2)^x=6^{2x}
$$
The powers have to be equal:
$$
4=2x
$$
Divide both sides of the equation by 2:
$$
2=x
$$
b. $x=15$
c. $x=53$
d. $x=11$ or $x=5$
e. $x=-9$ or $x=-15$
f. $x=2$
$$
(x+2)60=300
$$
Divide both sides of the equation by 60:
$$
x+2=5
$$
Subtract 2 from both sides of the equation:
$$
x=3
$$
Thus he needs to was 3 feet per second.
$$
(2-1)18=18
$$
Thus he travels for 18ft.
b. 18 feet
$$
0=3x^2-7x+4
$$
Factorize:
$$
0=(x-1)(3x-4)
$$
Zero product property:
$$
x-1=0text{ or }3x-4=0
$$
Solve each equation to $x$:
$$
x=1text{ or }3x=4
$$
$$
x=1text{ or }x=dfrac{4}{3}
$$
$$
(x+5)(-2x+3)=0
$$
Zero product property:
$$
x+5=0text{ or }-2x+3=0
$$
Solve each equation to $x$:
$$
x=-5text{ or }-2x=-3
$$
$$
x=-5text{ or }x=dfrac{3}{2}
$$
$$
x^2+6x=0
$$
Factorize:
$$
0=x(x+6)
$$
Zero product property:
$$
x=0text{ or }x+6=0
$$
Solve each equation to $x$:
$$
x=0text{ or }x=-6
$$
$$
0=3(x-5)(2x+3)
$$
Zero product property:
$$
x-5=0text{ or }2x+3=0
$$
Solve each equation to $x$:
$$
x=5text{ or }2x=-3
$$
$$
x=5text{ or }x=-dfrac{3}{2}
$$
b. $x=-5$ or $x=frac{3}{2}$
c. $x=0$ or $x=-6$
d. $x=5$ or $x=-frac{3}{2}$
c. True, because a 360$text{textdegree}$ rotation will rotate the figure onto itself.
b. False
c. True
b. The graph will then have two $x$-intercepts, because you obtain the equation from (a) by letting $f(x)=0$ and add 2 to both sides of the equation.
c. Take the square root of both sides of the equation:
$$
x=pm sqrt{2}=pm 1.4142
$$
b. 2
c. $x=pm sqrt{2}approx pm 1.4142$
$$
x^2=-1
$$
If you then take the square root of both sides of the equation, you obtain:
$$
x=pm sqrt{-1}
$$
But the square root of a negative number does not exist.
a.
$$
sqrt{-4}=sqrt{4(-1)}=sqrt{4i^2}=2i
$$
b.
$$
(2i)(3i)=6i^2=6(-1)=-6
$$
c.
$$
-5(2i)^2=-5(4i^2)=-20i^2=-20(-1)=20
$$
d.
$$
sqrt{-25}=sqrt{25(-1)}=sqrt{25i^2}=5i
$$
b. $-6$
c. 20
d. $5i$
b. No, because the corresponding graph does not cross the $x$-axis.
c.
$$
x=dfrac{4pm sqrt{(-4)^2-4(1)(5)}}{2(1)}=dfrac{4pm sqrt{-4}}{2}=dfrac{4pm 2i}{2}=2pm i
$$
d. See (c)
e. Replace $x$ with $2+i$:
$$
y=(2+i)^2-4(2+i)+5=4+4i+i^2-8-4i+5=1+i^2=1-1=0
$$
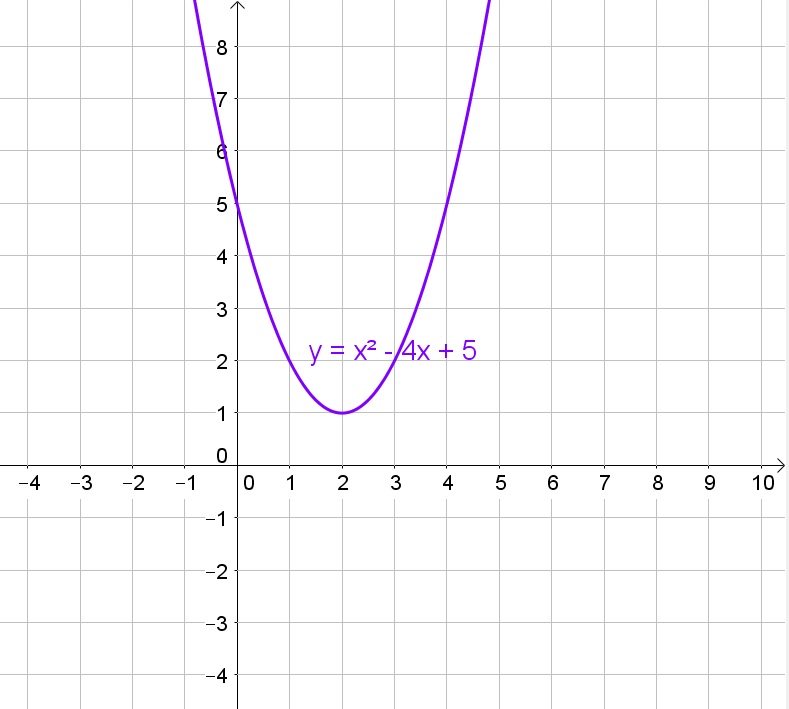
b. No
c. $x=2pm i$
d. $x=2pm i$
e. $y=0$
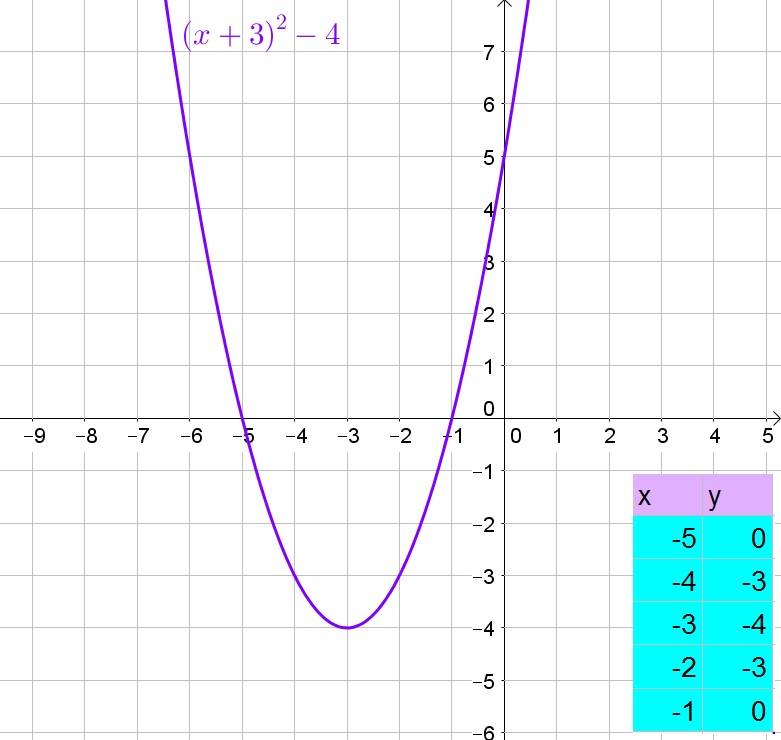

$$
0=(x+3)^2+4
$$
Subtract 4 from both sides of the equation:
$$
-4=(x+3)^2
$$
Take the square root of both sides of the equation:
$$
pm 2i=pm sqrt{-4}=x+3
$$
Subtract 3 from both sides of the equation:
$$
-3pm 2i=x
$$
b. $x=-3$
c. No
d. $x=-3pm 2i$
e. If the graph intersects the $x$-axis twice, then the function has two real roots. If the graph intersects the $x$-axis once, then the function has one real root. If the graph does not intersect the $x$-axis, then the function has two complex roots.
$$
2(3+i)=(2)(3)+(2)(i)=6+2i
$$
$$
10-9i-i=10+(-9-1)i=10-10i
$$
$$
(-2-7i)+(-1+4i)=(-2-1)+(-7i+4i)=-3-3i
$$
$$
(-8+2i)-(1-6i)=(-8-1)+(2i-6i)=-9-4i
$$
$$
(1-i)(8-6i)=8-8i-6i+6i^2=8-6-14i=2-14i
$$
b. $10-10i$
c. $-3-3i$
d. $-9-4i$
e. $2-14i$
b.
$$
16x^2div 4x=dfrac{16x^2}{4x}=dfrac{16}{4}x^{2-1}=4x
$$
$$
4xdiv 16x^2=dfrac{4x}{16x^2}=dfrac{1}{4x}
$$
Thus we note that the polynomials are not closed under division, because if you divide $4x$ by $16x^2$ you do not obtain a polynomial.
c. Polynomials are closed under addition, subtraction and multiplication, but are not closed under division. Note that this is the same as for integers.
b. Yes, No
c. Closed under addition, subtraction, and multiplication. Not closed under division.
Same for integers
a.
$$
sqrt{-49}=sqrt{49(-1)}=sqrt{49i^2}=7i
$$
b.
$$
sqrt{-2}=sqrt{2(-1)}=sqrt{2i^2}=sqrt{2}i
$$
c.
$$
(4i)^2=16i^2=16(-1)=-16
$$
d.
$$
3i+2i-5=(3+2)i-5=5i-5
$$
b. $sqrt{2}i$
c. $-16$
d. $5i-5$
$$
49=x^2+18x+81
$$
Factorize:
$$
49=(x+9)^2
$$
Take the square root of both sides of the equation:
$$
pm 7=x+9
$$
Subtract 9 from both sides of the equation (and interchange les and right sides of the equation):
$$
x=-9pm 7=-2text{ or }-16
$$
$$
0=x^2+12x+36
$$
Factorize:
$$
0=(x+6)^2
$$
Take the square root of both sides of the equation:
$$
0=x+6
$$
Subtract 6 from both sides of the equation (and interchange les and right sides of the equation):
$$
x=-6
$$
b. $x=-6$

$$
P(salami text{ or }mayo)=P(salami)+P(mayo)+P(salami text{ and }mayo)
$$
$$
=dfrac{1}{2}+dfrac{2}{3}-dfrac{1}{2}cdot dfrac{2}{3}=dfrac{3}{6}+dfrac{4}{6}-dfrac{2}{6}=dfrac{5}{6}
$$
c. The sum of an event and its complement is 1(=100%)
$$
P(text{not salami and not mayo})=1-P(text{salami or mayo})=1-dfrac{5}{6}=dfrac{1}{6}
$$
d. See (c)
e. There are two outcomes that have both salami and mayonnaise (white and whole grain).
b. $frac{5}{6}$
c. $frac{1}{6}$
d. $frac{1}{6}$
e. white and whole grain
$$
x=dfrac{-bpm sqrt{b^2-4ac}}{2a}
$$
with $a$ the coefficient of $x^2$, $b$ the coefficient of $x$ and $c$ the constant term.
a. The $x$-intercepts seem to be about $x=0.8$ and $x=4.2$:
$$
x=dfrac{5pm sqrt{(-5)^2-4(1)(3)}}{2(1)}=dfrac{5pm sqrt{13}}{2}approx 4.3text{ or } 0.7
$$
b. The $x$-intercepts seem to be about $x=-3.8$ and $x=1.8$:
$$
x=dfrac{-2pm sqrt{(2)^2-4(1)(-6)}}{2(1)}=dfrac{-2pm 2sqrt{7}}{2}=-1pm sqrt{7}approx 1.6text{ or }-3.6
$$
b. $x=-1pmsqrt{7}$
$$
(x^2)(x^2y^3)=x^{2+2}y^3=x^4y^3
$$
b. Subtract powers of the same variables:
$$
dfrac{x^3y^4}{x^2y^3}=x^{3-2}y^{4-3}=x^1y^1=xy
$$
c. Add the powers of the same variables:
$$
(2x^2)(-3x^4)=(2)(-3)x^{2+4}=-6x^6
$$
d.
$$
(2x)^3=2^3x^3=8x^3
$$
b. $xy$
c. $-6x^6$
d. $8x^3$

