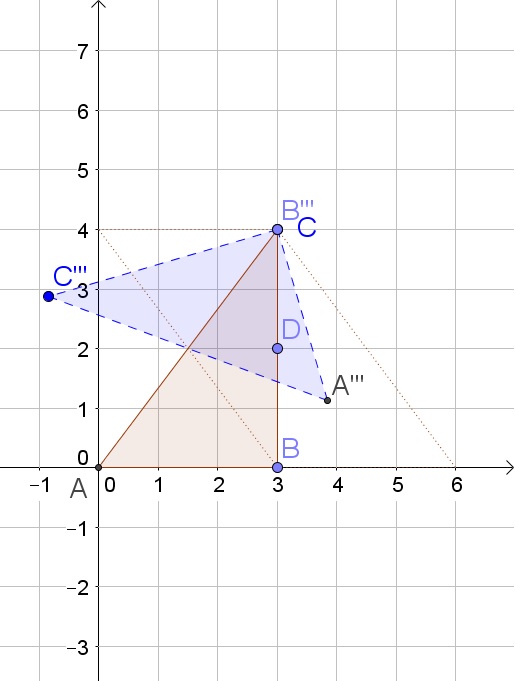
All Solutions
Page 202: Closure Activity
$$
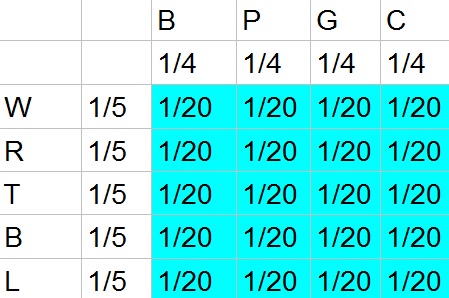
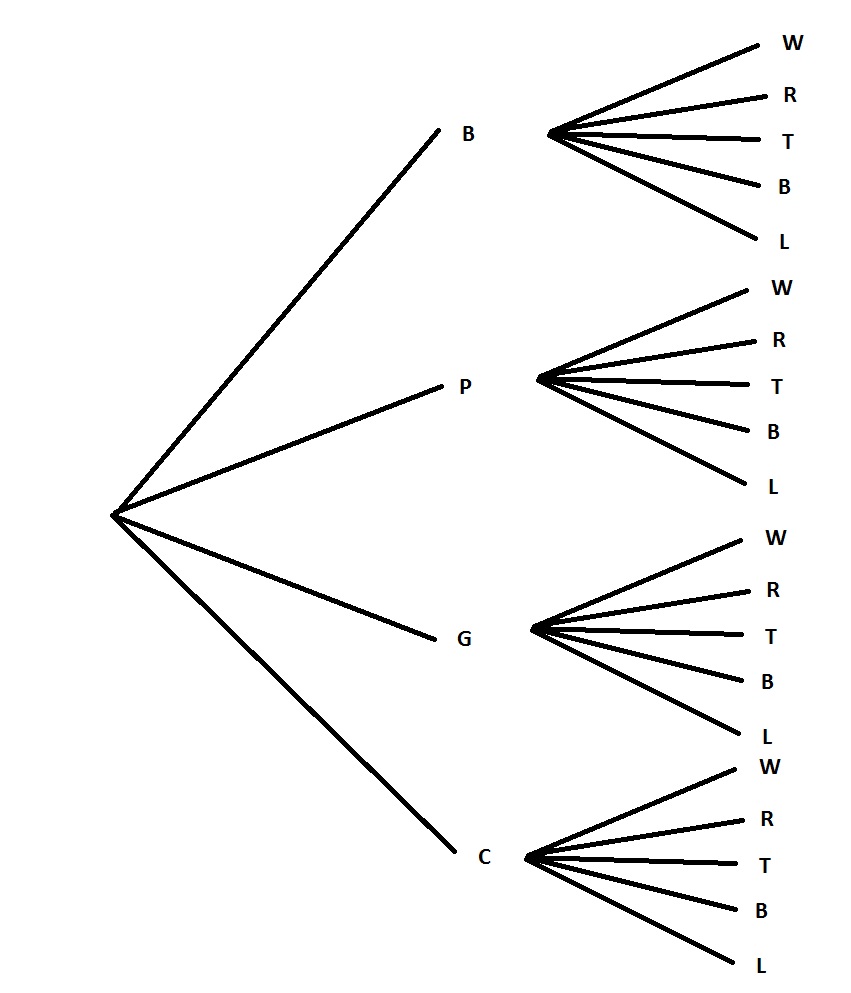
9cdot dfrac{1}{20}=dfrac{9}{20}=0.45=45%
$$
b. $frac{9}{20}=0.45=45%$
$$
45% cdot 70%=0.45cdot 0.7=0.315=31.5%
$$
The probability of not having a trait is 100% decreased by the probability of having the trait. The probability of having neither traits is then the product of each probability:
$$
(100%-45%)cdot (100%-70%)=55%cdot 30%=0.55cdot 0.3=0.165=16.5%
$$
$$
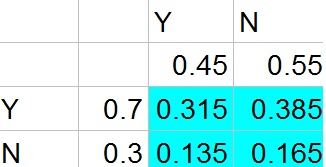
angle Acong angle Etext{(alternate interior angles)}
$$
$$
angle ACBcong angle ECDtext{(vertical angles)}
$$
$$
Downarrow AA
$$
$$
triangle ABCsim triangle EDC
$$
b. Corresponding sides of similar triangles have the same proportions:
$$
dfrac{CE}{AC}=dfrac{DE}{AB}
$$
Enter the known values:
$$
dfrac{CE}{20}=dfrac{12}{14}
$$
Multiply both sides of the equation by 20:
$$
CE=dfrac{12cdot 20}{14}=dfrac{240}{14}=dfrac{120}{7}approx 17.1
$$
b. 17.1
$$
EV=10cdot dfrac{2}{6}+(-5)cdot dfrac{4}{6}=dfrac{20}{6}-dfrac{20}{6}=0
$$
Since the expected value is zero, the game is fair.
$$
sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=sqrt{(7-3)^2+(2+4)^2}=sqrt{16+36}=sqrt{52}=2sqrt{13}
$$
b. The slope is
$$
dfrac{y_2-y_1}{x_2-x_1}=dfrac{2+4}{7-3}=dfrac{6}{4}=dfrac{3}{2}=1.5
$$
c. The area of a triangle is the product of the base and the height divided by 2:
$$
dfrac{4cdot 6}{2}=12
$$
d. The equation of a line through two points is in general: $y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$ and thus for this line is:
$$
y+4=dfrac{2+4}{7-3}(x-3)
$$
Simplify:
$$
y+4=dfrac{3}{2}(x-3)
$$
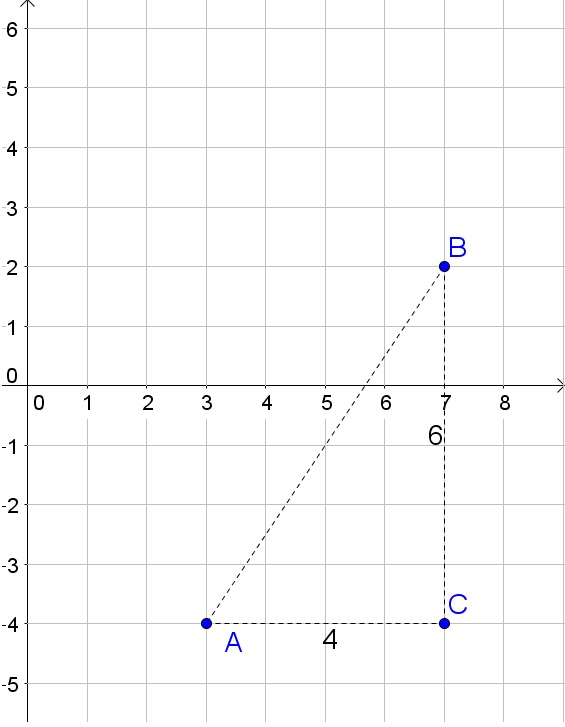
b. 1.5
c. 12
d. $y+4=frac{3}{2}(x-3)$
a. $y$ is between $17-10=7$ and $10+17=27$.
b. $z$ is between $17-15=2$ and $17+15=32$.
b. Between 2 and 32
a.
$$
tan{40text{textdegree}}=dfrac{x}{11}
$$
Multiply both sides of the equation by 11:
$$
9.23approx 11tan{40text{textdegree}}=x
$$
b.
$$
tan{52text{textdegree}}=dfrac{7}{x}
$$
Multiply both sides of the equation by $x$:
$$
tan{52text{textdegree}}cdot x=7
$$
Divide both sides of the equation by $tan{52text{textdegree}}$:
$$
x=dfrac{7}{tan{52text{textdegree}}}approx 5.47
$$
c.
$$
tan{45text{textdegree}}=tan{theta}=dfrac{5}{5}=1
$$
Thus we then know:
$$
theta=45text{textdegree}
$$
b. $x=5.47$
c. $theta=45text{textdegree}$
a.
$$
dfrac{16}{52}approx 0.308=30.8%
$$
b. Drawing a card that is NOT less then 5 is the smae as drawing a card that is 5 or more:
$$
1-dfrac{16}{52}=dfrac{36}{52}approx 0.692=69.2%
$$
c. Addition rule: $P(Acup B)=P(A) +P(B)-P(Acap B)$
$$
P(red cup face)=P(red)+P(face)-P(redcap face)
$$
$$
=dfrac{26}{52}+dfrac{12}{52}-dfrac{6}{52}=dfrac{32}{52}=dfrac{8}{13}approx 0.615=61.5%
$$
b. $frac{36}{52}approx 0.692=69.2%$
c. $frac{8}{13} approx 0.615=61.5%$
$$
4x+9=5x+5
$$
Group like terms:
$$
9-5=5x-4x
$$
Simplify:
$$
4=x
$$
$$
40+z=117
$$
Subtract 40 from both sides of the equation:
$$
z=77
$$
b. Not possible to determine
c. $z=77text{textdegree}$
$$
a=180text{textdegree}-b=180text{textdegree}-101text{textdegree}=79text{textdegree}
$$
(2) $a$ and $f$ are vertical angles:
$$
f=a=79text{textdegree}
$$
(3) $m$ cannot be determined because the line in not parallel to the line with the known angle.
(4) Vertical angles:
$$
g=101text{textdegree}
$$
(5) $h$ anf $f$ are corresponding angles:
$$
h=f=79text{textdegree}
$$
(6) $i$ cannot be determined because the line in not parallel to the line with the known angle.
$$
m=180text{textdegree}-130text{textdegree}=50text{textdegree}
$$
(6) The sum of all angles in a triangle is 180$text{textdegree}$:
$$
i=180text{textdegree}-79text{textdegree}-50text{textdegree}=51text{textdegree}
$$
b. (3) $50text{textdegree}$ (i) $51text{textdegree}$
$$
(2x)(x)+(5)(x)+(2x)(6)+(5)(6)
$$
Simplify:
$$
2x^2+5x+12x+30
$$
Combine like terms
$$
2x^2+17x+30
$$
$$
(m)(3m)+(-3)(3m)+(m)(5)+(-3)(5)
$$
Simplify:
$$
3m^2-9m+5m-15
$$
Combine like terms
$$
3m^2-4m-15
$$
$$
(12x)(x)+(1)(x)+(12x)(-5)+(1)(-5)
$$
Simplify:
$$
12x^2+x-60x-5
$$
Combine like terms
$$
12x^2-59x-5
$$
$$
(3)(2)+(-5y)(2)+(3)(y)+(-5y)(y)
$$
Simplify:
$$
6-10y+3y-5y^2
$$
Combine like terms
$$
6-7y-5y^2
$$
b. $3m^2-4m-15$
c. $12x^2-59x-5$
d. $6-7y-5y^2$
The perimeter is the sum of all sides:
$$
PERIMETER=3+4+5=12
$$
The area is the product of the base and the height divided by 2.
$$
AREA=dfrac{3cdot 4}{2}=6
$$