All Solutions
Page 145: Questions
$$
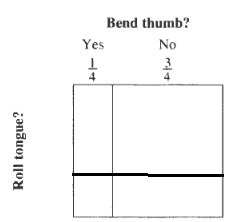
dfrac{1}{4}=0.25=25%
$$
b. We note that the combination, Yes/No or No/Yes agrees with two of the four squares and thus the probability is
$$
dfrac{2}{4}=dfrac{1}{2}=0.5=50%
$$
c. By assigning a probability for each square that is the product of the probability of the column and the probability of the row (and these fractions have been replaced by the actual fractions).
b. $frac{1}{2}=0.5=50%$
c. By assigning a probability for each square that is the product of the probability of the column and the probability of the row.
$$
dfrac{1}{4}cdot dfrac{7}{10}=dfrac{7}{40}
$$
This means that the probability that somebody has both traits is $dfrac{7}{40}$.
c. Multiply the corresponding probabilities:
$$
dfrac{3}{4}cdot dfrac{7}{10}=dfrac{21}{40}=0.525=52.5%
$$
b. $frac{7}{40}$
c. $frac{21}{40}=0.525=52.5%$
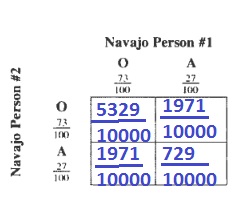
$$
dfrac{729}{10000}=0.0729=7.29%
$$
The probability of having the same blood type is then the combination O/O and A/A:
$$
dfrac{729}{10000}+dfrac{5329}{10000}=dfrac{6058}{10000}=0.6058=60.58%
$$
b. 7.29%, 60.58%
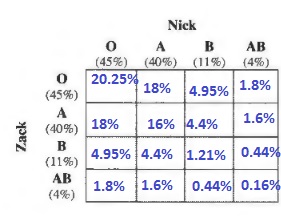
$$
20.25%+16%+1.21%+0.16%=37.62%
$$
c.
$$
20.25%+18%+16%+4.95%+4.4%+1.21%+1.8%+1.6%+0.44%+0.16%=68.81%
$$
b. 37.62%
c. 68.81%
b. Independence between the variables (for example Zack and Nick cannot be related in (a)).
b. Independence
$$
{2,3,4,5,6,7,8,9,10,11,12}
$$
b.
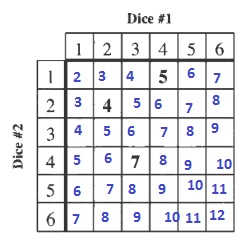
$$
P(even)=dfrac{18}{36}=dfrac{1}{2}=0.5=50%
$$
$$
P(10)=dfrac{3}{36}=dfrac{1}{12}approx 0.083=8.3%
$$
$$
P(15)=dfrac{0}{36}=0=0%
$$
d. 7 is the most likely because 7 appears the most in the table3.
$$
P(7)=dfrac{6}{36}=dfrac{1}{6}approx 0.1667=16.67%
$$
b. Yes
c. $frac{1}{2}=0.5=50%$, $frac{1}{12}approx 0.083=8.3%$, $0=0%$
d. 7, $frac{1}{6}approx 0.1667=16.67%$
$$
110=5x-20
$$
Add 20 to both sides of the equation:
$$
130=5x
$$
Divide both sides of the equation by 5:
$$
26=x
$$
$$
4x-11+x+26=180
$$
Combine like terms:
$$
5x+15=180
$$
Subtract 15 from both sides of the equation:
$$
5x=165
$$
Divide both sides of the equation by 5:
$$
x=33
$$
Determine $n$:
$$
n=x+26=33+26=59text{textdegree}
$$
b. $x=33$ and $n=59text{textdegree}$
a. Upper: $9cdot (-9)=-81$ and Lower: $9-9=0$
b. We thus need to find two numbers whose product is $-36$ and whose sum is 0, these numbers are then $-6$ and 6 and need to be filled in the left and right cell (order does not matter).
c. Right: $dfrac{-20}{4}=-5$ and Lower: $4-5=-1$
d. Left: $dfrac{1}{2}-dfrac{4}{5}=dfrac{5}{10}-dfrac{8}{10}=-dfrac{3}{10}$ and Upper: $-dfrac{3}{10}cdot dfrac{4}{5}=-dfrac{6}{25}$
b. $-6$ and 6
c. $-5$ and $-1$
d. $-frac{3}{10}$ and $-frac{6}{25}$
a.
$$
dfrac{x}{6}=dfrac{4}{2}
$$
Multiply both sides of the equation by 6:
$$
x=dfrac{4cdot 6}{2}=12
$$
b.
$$
dfrac{x-5}{6}=dfrac{4}{3}
$$
Multiply both sides of the equation by 6:
$$
x-5=8
$$
Add 5 to both sides of the equation:
$$
x=13
$$
$$
dfrac{x}{21}=dfrac{3}{w}
$$
The perimeter is the sum of all sides and thus the width is:
$$
w=dfrac{60-21-21}{2}=9
$$
Replace $w$ with 9 in the equation:
$$
dfrac{x}{21}=dfrac{3}{9}
$$
Multiply both sides of the equation by 21:
$$
x=dfrac{3cdot 21}{9}=7
$$
b. $x=13$
c. $x=7$
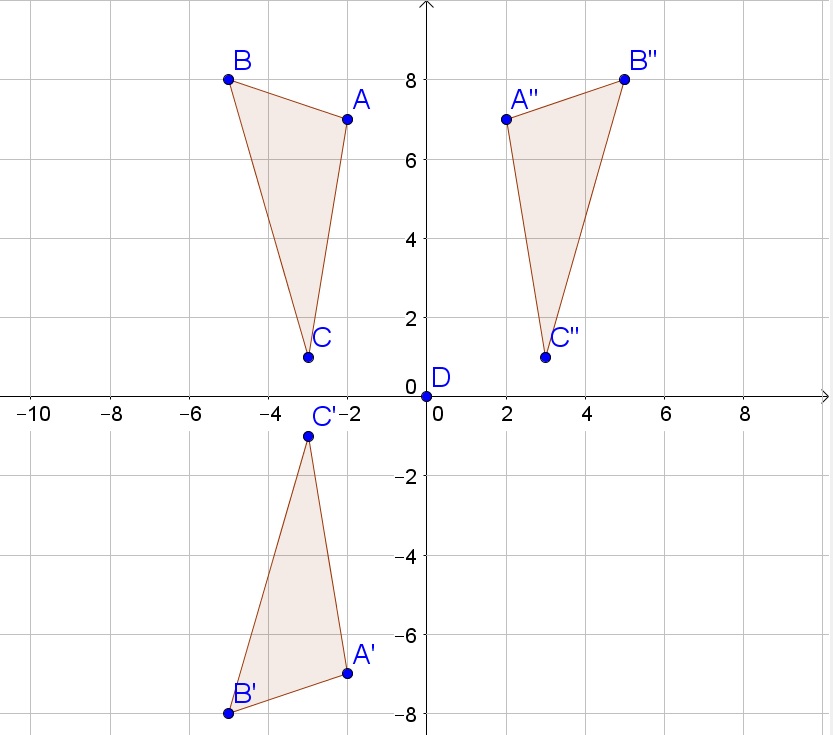
b. $A”(2,7)$, $B”(5,8)$, and $C”(3,1)$
c. Reflect triangle about $y$-axis
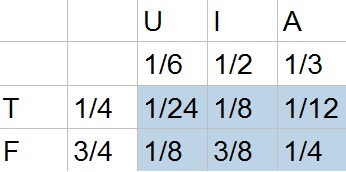
b. Since IT, AT and IF are the only two-letter English words possible, the probability to win is:
$$
dfrac{1}{8}+dfrac{1}{12}+dfrac{3}{8}=dfrac{7}{12}approx 0.467= 46.7%
$$
However you cannot be sure this will happen, you could also wins more in total in 100 games, but as you keep playing more games you will loose more than you win.
b. $frac{7}{12}approx 0.467= 46.7%$
c. No
b.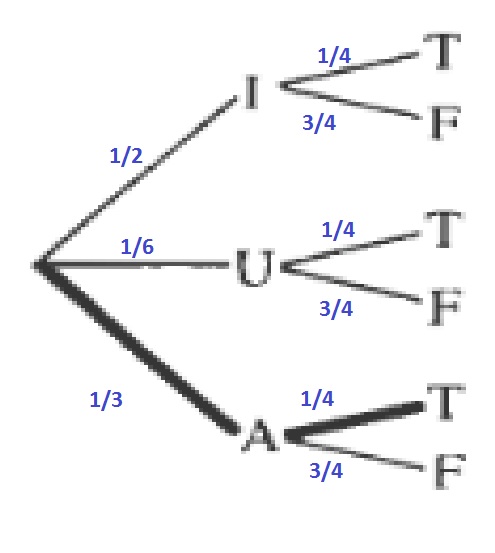
$$
dfrac{1}{12}approx 0.083=8.3%
$$
You can also determine this probability, by multiplying the probabilities of the branches to form the word AT.
d. Yes, it is possible and the answer will match those of the table.
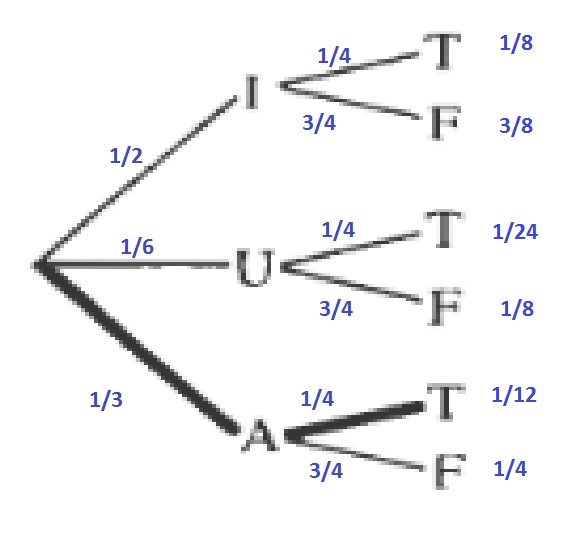
$$
dfrac{1}{8}+dfrac{3}{8}+dfrac{1}{12}=dfrac{7}{12}approx 0.467=46.7%
$$
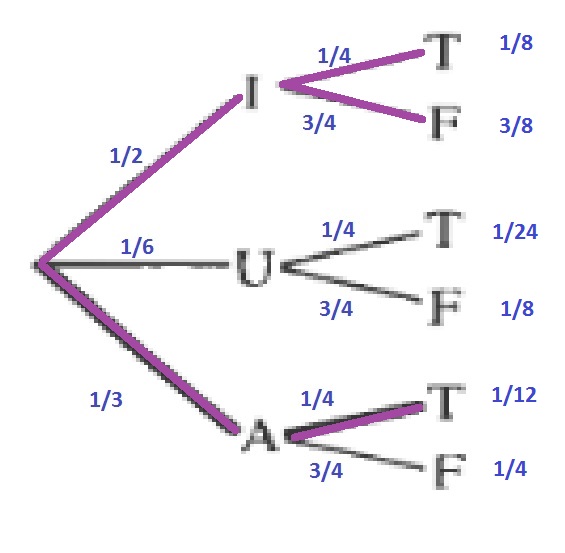
b. Add probabilities to trees
c. $frac{1}{12}approx 0.083=8.3%$
d. Yes
e. $frac{7}{12}approx 0.467=46.7%$
$$
dfrac{1}{3}cdot dfrac{1}{2}=dfrac{1}{6}
$$
$$
dfrac{1}{3}
$$
$$
dfrac{1}{3}cdot dfrac{1}{3}=dfrac{1}{9}
$$
Thus their sum is then:
$$
dfrac{1}{3}+dfrac{1}{6}+dfrac{1}{9}=dfrac{11}{18}=61.1%
$$
This method was used because the branches have been given.
b. Multiply the number of tries with the probability:
$$
dfrac{11}{18}cdot 100approx 61
$$
Thus about 61 times.
c. It is possible that he learned something since the number of succesfull attempts is larger than the number of expected succesfull attempts.
But it is also possible that it has happened randomly and not because of the learning ability, because 66 is still relatively close to 61.
b. About 61 times
c. See explanation
$$
dfrac{1}{2}cdot dfrac{1}{3}=dfrac{1}{6}
$$
$$
dfrac{1}{2}cdot dfrac{1}{3}=dfrac{1}{6}
$$
$$
dfrac{1}{2}cdot dfrac{1}{3}=dfrac{1}{6}
$$
$$
dfrac{1}{2}cdot dfrac{1}{2}cdot dfrac{1}{2}=dfrac{1}{8}
$$
$$
dfrac{1}{2}cdot dfrac{1}{2}cdot dfrac{1}{2}=dfrac{1}{8}
$$
$$
dfrac{1}{2}cdot dfrac{1}{2}=dfrac{1}{4}
$$
Thus their sum is then:
$$
A:dfrac{1}{6}+dfrac{1}{6}=dfrac{1}{3}=33.3%
$$
$$
B:dfrac{1}{6}+dfrac{1}{8}=dfrac{7}{24}=29.2%
$$
$$
C:dfrac{1}{4}+dfrac{1}{6}=dfrac{5}{12}=41.7%
$$
Thus it is best to use room C since it has the highest probability.
b. Yes, because you would expect for Romeo to find the cheese $41.7% cdot 10approx 4$ times and he finds it more times.
b. Yes
a. There are 10 girls out of 20 contestants.
$$
dfrac{10}{20}=dfrac{1}{2}=0.5=50%
$$
b. Since 1 girl was already chosen, there are 9 girls out of 19 contestants left.
$$
dfrac{9}{20}=0.45=45%
$$
c. No, because the probability of part (a) differs from the probability of part (b). If they would have been independent, then the probability would have remained the same in (a) and (b).
b. $dfrac{9}{20}=0.45=45%$
c. No
There is 1 locker (nummer 831) out of 535 lockers:
$$
dfrac{1}{535}approx 0.002=0.2%
$$
He should not be worried because the probability of the event is almost zero.
No
b. Let $H$ represent heads and $T$ tails:
$$
{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
$$
Thus we note that there are 8 possible outcomes.
c. The probability is the number of favorible outcomes divided by the total number of possible outcomes:
(i)
$$
dfrac{1}{8}=0.125=12.5%
$$
(ii)
$$
dfrac{3}{8}=0.375=37.5%
$$
(iii)
$$
dfrac{7}{8}=0.875=87.5%
$$
(iv)
$$
dfrac{3}{8}=0.375=37.5%
$$
d. Both are equally likely, since both probabilities will be 3 out of 8.
b. 8 outcomes
c.
(i) $frac{1}{8}=0.125=12.5%$
(ii) $frac{3}{8}=0.375=37.5%$
(iii) $frac{7}{8}=0.875=87.5%$
(iv) $frac{3}{8}=0.375=37.5%$
d. Both are equally likely
b. This triangle is also not possible, because the sum of all angles should be 180$text{textdegree}$:
$$
119text{textdegree}+26text{textdegree}+42text{textdegree}=187text{textdegree}
$$
b. Not possible
$$
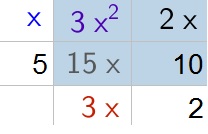
(x+5)(3x+2)=3x^2+2x+15x+10=3x^2+17x+10
$$
$$
(y-6)(2x+3y-4)=2xy+3y^2-4y-12x-18y+24
$$
$$
=2xy+3y^2-22y-12x+24
$$
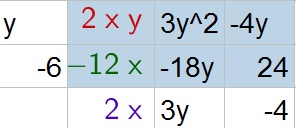
b. $2xy+3y^2-22y-12x+24$
$$
angle X=180text{textdegree}-65text{textdegree}-75text{textdegree}=40text{textdegree}
$$
Then we know that the two triangles are similar because of $AA$ and not congruent (because $overline{AB}$ and $overline{YZ}$ are not corresponding sides but are equal).
b. Neither, because the triangle has two different angle measure than the original triangle.
c. The sum of all angles in a triangle is 180$text{textdegree}$:
$$
angle R=180text{textdegree}-40text{textdegree}-75text{textdegree}=65text{textdegree}
$$
Then we know that the two triangles are similar because of $AA$ and not congruent because of $ASA$.
b. Neither
c. Congruent
b. Player B should get the most points because the smallest probability is for 3 and not matches.
c. No, because player B gets a lot more points than the other players.
d. Note that B is the probability that not A and not C wins:
$$
A: dfrac{3}{27}=dfrac{1}{9}approx 0.11=11%
$$
$$
B:1-dfrac{1}{9}-dfrac{2}{9}=dfrac{6}{9}=dfrac{2}{3}approx 0.67=67%
$$
$$
C: dfrac{6}{27}=dfrac{2}{9}approx 0.22=22%
$$
e. If $A$ has Rocks, then $A$ gets the point. If $A$ has Paper, then $B$ gets the point. If $A$ has Scissors, then $C$ gets the points.
b. Player B should get the most points
c. No
d. 11%, 67%, 22%
e. If $A$ has Rocks, then $A$ gets the point. If $A$ has Paper, then $B$ gets the point. If $A$ has Scissors, then $C$ gets the points.
b.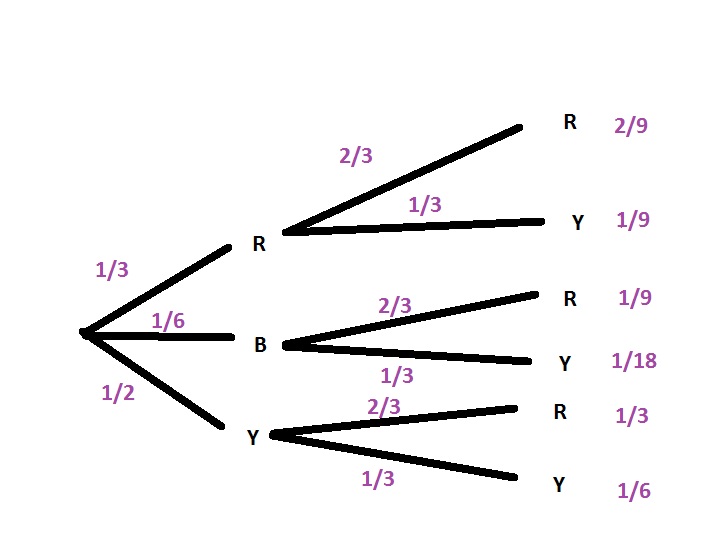
$$
dfrac{1}{9}approx 0.111=11.1%
$$
d. No, because you only have a chance of 11.1% to win.
b. Tree diagram
c. $frac{1}{9}approx 0.111=11.1%$
d. No
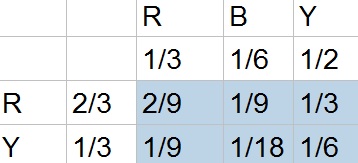
c. I prefer the tree model, because it is easier to see each possibility.
d. No, because you didn’t need to know all possible outcomes, but only how many matches there were and these you needed to calculate anyway.
b. Multiply length and width
c. Tree model
d. No
b.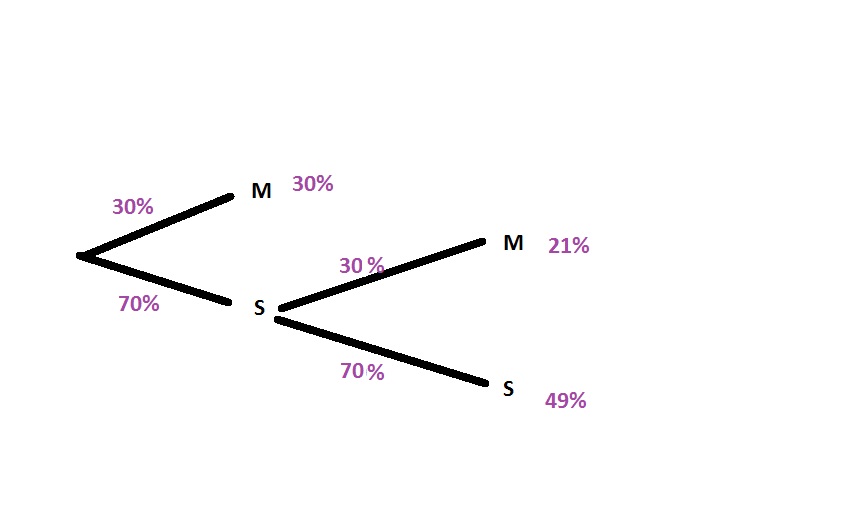
$$
0.7cdot 0.3=0.21=21%
$$
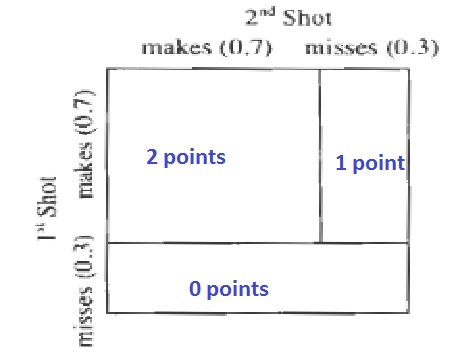
$$
0.7cdot 0.7=0.49=49%
$$
0 points:
$$
0.3cdot 1=0.3=30%
$$
b. Tree diagram
c. 0.21=21%
d. 2 points is the most likely
Note: If you use the (large) rectangle at the bottom in the area model, then you have dimensions of 0.3 by 1.
b. The total area is the product of the length and the width:
$$
(0.7+0.3)cdot (0.7+0.3)=1cdot 1=1
$$
c. The event of scoring 0 points, 1 point and 2 points and their corresponding probabilities.
b. 1
c. 0 points, 1 point, and 2 points
Use the sample space if there are a small limited number of possibilities that are all equally likely.
Use a probability area model if there are 2 actions (such as first and second shot).
Use a tree model if there are more than 2 actions.
Use a probability area model if there are 2 actions (such as first and second shot).
Use a tree model if there are more than 2 actions.
3 flips:
$$
{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
$$
4 flips:
$$
{HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH,
$$
$$
HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
$$
The probability is then the number of favorable outcomes divided by the number of possible outcomes:
3 flips: $dfrac{3}{8}=0.375=37.5%$
4 flips: $dfrac{6}{16}=dfrac{3}{8}=0.375=37.5%$
We note that both evens are equally likely.
$$
dfrac{6+2}{36}=dfrac{8}{36}=dfrac{2}{9}approx 0.22=22%
$$
b. The probability is the number of favorable outcomes divided by the number of possible outcomes:
$$
dfrac{1+2+1}{36}=dfrac{4}{36}=dfrac{1}{9}approx 0.11=11%
$$
c. The total probability of all events should be 1:
$$
1-dfrac{1}{9}-dfrac{1}{4}=dfrac{23}{36}approx 64%
$$
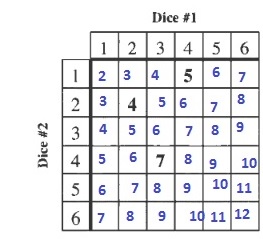
b. 11%
c. 64%
$$
y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)
$$
Use the two points $C(-2,1)$ and $M(2,3)$:
$$
y-1=dfrac{3-1}{2+2}(x+2)=dfrac{1}{2}(x+2)
$$
b. The $x$-intercept is the intersection of the graph with the $x$-axis, thus $x=4$.
The $y$-intercept is the intersection fo the graph with the $y$-axis and thus is $y=2$.
c. The area of a triangle is the product of the base and the height divided by 2:
$$
AREA=dfrac{4cdot 2}{2}=4
$$
Determine $CM$ using the Pythagorean theorem:
$$
CM=sqrt{4^2+2^2}=sqrt{20}=2sqrt{5}
$$
The perimeter is the sum of all sides of the triangle:
$$
PERIMETER=4+2+2sqrt{5}=6+2sqrt{5}
$$
d. Perpendicular lines have slopes whose product equal $-1$, thus the slope of this line is $-2$ and the equation then becomes:
$$
y-3=-2(x-2)
$$
b. $x$-intercept $(4,0)$ and $y$-intercept $(0,2)$
c. Area 4 and Perimeter $6+2sqrt{5}$
d. $y-3=-2(x-2)$
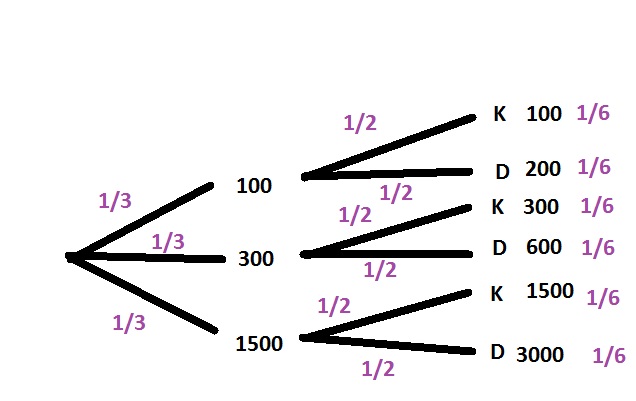
c. Look in the tree diagram to determine the probability
$$
P(200)=dfrac{1}{6}approx 0.167=16.7%
$$
$$
P(>500)=dfrac{1}{6}+dfrac{1}{6}+dfrac{1}{6}=dfrac{1}{2}=0.5=50%
$$
d. No, only on the result of the second spinner.
$$
P(D)=dfrac{1}{6}+dfrac{1}{6}+dfrac{1}{6}=dfrac{1}{2}=0.5=50%
$$
e. The 300 in the tree diagram would become 200, and then we obtain:
$$
P(200)=dfrac{1}{6}+dfrac{1}{6}=dfrac{1}{3}approx 0.333=33.3%
$$
b. Yes
c. $frac{1}{6}approx 0.167=16.7$, $frac{1}{2}=0.5=50%$
d. No
e. $frac{1}{3}approx 0.333=33.3%$
$$
4x-12text{textdegree}=60text{textdegree}
$$
Add 12$text{textdegree}$ to both sides of the equation:
$$
4x=72text{textdegree}
$$
Divide both sides of the equation by 4:
$$
x=18text{textdegree}
$$
$$
3.1^2+x^2=4.9^2
$$
Subtract $4.9^2$ from both sides of the equation:
$$
x^2=4.9^2-3.1^2=14.4
$$
Take the square root of both sides of the equation:
$$
x=pm sqrt{14.4}approx 3.8
$$
$$
180text{textdegree}-103text{textdegree}-51text{textdegree}=26text{textdegree}
$$
Since alternative interior angles are congruent and the sum of all angles in a triangle is 180$text{textdegree}$:
$$
x=180text{textdegree}-82text{textdegree}-26text{textdegree}=72text{textdegree}
$$
$$
3x-2=2x+9
$$
Group like terms:
$$
3x-2x=9+2
$$
Simplify
$$
x=11
$$
b. $x=pm sqrt{14.4}approx 3.8$
c. $x=72text{textdegree}$
d. $x=11$
$$
53%cdot 37%=0.53cdot 0.37=0.1961=19.61%
$$
b. Let D represent democrat and R Republican and the first letter represents the Governor while the second represents the Attorney General:
$$
{RR, RD, DR, DD}
$$
c. Democratic Governor: DR and DD
Democratic Attorney general: RD and DD
d. Only DD is in this possibility and this event has probability 0.1961 in the model.
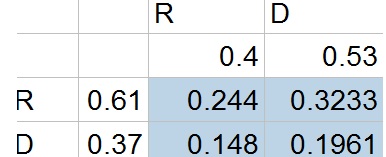
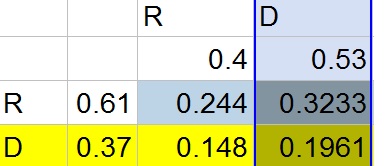
b. ${RR,RD, DR, DD}$
c. Dr and DD; RD and DD
d. DD
e. The intersection of the events is the cell that lies in the respective column and row.
b. DR, DD, RD
These are all possibilities that contain a D and thus are contained in the second column and second row.
c. Add the probabilities of the events
$$
0.148+0.3233+0.1961=0.6674=66.74%
$$
d. This possibility only contains RD:
$$
0.148=14.8%
$$
e. Add the probabilities of the events
$$
0.244+0.148+0.1961=0.5881=58.81%
$$
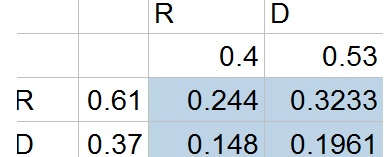
b. DR, DD, RD
c. 0.6674=66.74%
d. 0.148=14.8%
e. 0.5881=58.81%
b. No, because the columns do not contain the sum of the probabilities and thus you cannot use this method.
b. No
$$
(8%+6%+5%)cdot 60%=19%cdot 60%=0.19cdot 0.6=0.114=11.4%
$$
b. In part (a) we analyzed an intersection. The intersection contains only one possibility (55 or older AND BBQ), while the union contains more possibilities (such as 55 or older AND Fet Cheese).
c. Addition Rule: $P(Atext{ or }B)=P(A)+P(B)-P(Atext{ and }B)$
$$
P(55text{ or older OR BBQ})=P(55text{ or older})+P(BBQ)+P(55text{ or older AND BBQ})
$$
$$
=(8%+6%+5%)+60%-8% cdot 60%
$$
$$
=0.19+0.6-0.048=0.742=74.2%
$$
d. 75 or under contains all percentages expect for the last column:
$$
P(Under 75)=36%+14%+17%+14%+8%+6%=95%
$$
e. You could also obtain this result by using that in total we have 100% and 5% of those people are 75 and over, their difference is then the percentage of people that are under 75.
$$
P(Under 75)=100%-5%=95%
$$
b. Intersection, One possibility vs. more possibilities
c. $0.742=74.2%$
d. 95%
e. 95%
$$
10%+10%+20%=40%
$$
$$
100%-60%=40%
$$
b. The sum of the probability of an event and not the even is always 100% (which is also equal to 1):
$$
P(A)=100%-P(text{ not } A)=1-P(text{ not } A)
$$
b. $P(A)=100%-P(text{ not } A)=1-P(text{ not } A)$
a. There are 4 kings out of 52 cards:
$$
P(king)=dfrac{4}{52}=dfrac{1}{13}approx 0.077=7.7%
$$
There are 4 queens out of 52 cards:
$$
P(queen)=dfrac{4}{52}=dfrac{1}{13}approx 0.077=7.7%
$$
There are 13 clubs out of 52 cards:
$$
dfrac{13}{52}=dfrac{1}{4}=0.25=25%
$$
b. Addition rule: $P(Atext{ or }B)=P(A)+P(B)-P(Atext{ and }B)$
$$
P(kingtext{ or }club)=P(king)+P(club)-P(kingtext{ and }club)=dfrac{4}{52}+ dfrac{13}{52}-dfrac{1}{52}=dfrac{16}{52}=dfrac{4}{13}approx 0.308=30.8%
$$
The answer relates because we have used the probability of king and club.
c. Addition rule: $P(Atext{ or }B)=P(A)+P(B)-P(Atext{ and }B)$
$$
P(kingtext{ or }queen)=P(king)+P(queen)-P(kingtext{ and }queen)=dfrac{4}{52}+ dfrac{4}{52}-dfrac{0}{52}=dfrac{8}{52}=dfrac{2}{13}approx 0.154=15.4%
$$
The answer relates because we have used the probability of king and queen.
d. The probability event of something not happening is 1 decreased by the probability of the event happening (complement).
$$
P(not face)=1-P(face)=1-dfrac{12}{52}=dfrac{40}{52}=dfrac{10}{13}approx 0.769=76.9%
$$
b. $frac{4}{13}approx 0.308=30.8%$
c. $frac{2}{13}approx 0.154=15.4%$
d. $frac{10}{13}approx 0.769=76.9%$
a. The sum can only be 4 if the first spinner lands on 2 and the second spinner also lands on 2:
$$
P(text{ sum is 4})=dfrac{1}{4}cdot dfrac{1}{3}=dfrac{1}{12}approx 0.083=8.3%
$$
b. The sum is 8 if the first spinner lands on 2 and the second on 6 OR the first spinner lands on 4 and the second on 4.
$$
P(text{ sum is 8})=P(2,6)+P(4,4)=dfrac{1}{4}cdot dfrac{1}{3}+dfrac{3}{4}cdot dfrac{1}{3}=dfrac{1}{12}+dfrac{3}{12}=dfrac{4}{12}=dfrac{1}{3}approx 0.333=33.3%
$$
b. $frac{1}{3}approx 0.333=33.3%$
a.
$$
(2x+5)(x+6)=2x^2+12x+5x+30=2x^2+17x+30
$$
b.
$$
(m-3)(3m+5)=3m^2+5m-9m-15=3m^2-4m-15
$$
c.
$$
(12x+1)(x^2-5)=12x^3+x^2-60x-5
$$
d.
$$
(3-5y)(2+y)=6+3y-10y-5y^2=6-7y-5y^2
$$
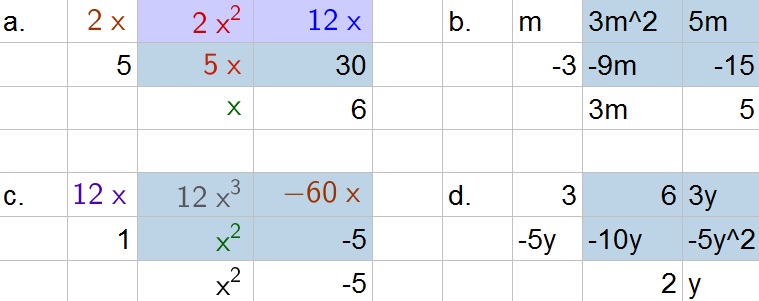
b. $3m^2-4m-15$
c. $12x^3+x^2-60x-5$
d. $6-7y-5y^2$
$$
18^2+x^2=30^2
$$
Subtract $18^2$ from both sides of the equation:
$$
x^2=900-324=576
$$
Take the square root of both sides of the equation (and remember that only a positive length makes sense):
$$
x=24
$$
$$
2x+x+3x+20+2x+20=360
$$
Combine like terms:
$$
8x+40=360
$$
Subtract 40 from both sides of the equation:
$$
8x=320
$$
Divide both sides of the equation by 8:
$$
x=40
$$
$$
dfrac{x}{12}=dfrac{3}{5}
$$
Multiply both sides of the equation by 12:
$$
x=dfrac{3cdot 12}{5}=dfrac{36}{5}=7.2
$$
b. $x=40$
c. $x=7.2$
b. The total number of tickets sold is increasing (it cannot decrease) and thus only graph 1 is possible.
c. The time for the 400-meter run will decrease over a season, but it cannot go to zero and thus graph 4 is the only possibility.
b. Graph 1
c. Graph 4
$$
5cdot $4=$20
$$
If we play the games 30 times, we expect to win 15 times:
$$
15cdot $4=$60
$$
If we play the game 100 times, we expect to win the game 50 times:
$$
50cdot $4=$200
$$
$$
dfrac{1}{2}cdot $4=$2
$$
However, it is not actually possible to win that amount, because you win either nothing or $$4$.
b. $$2$, No
c. Yes, the answers match
b. $$26$
c. Yes
b. The expected value is the sum of the product of every possibility and the probability of that possibility happening:
$$
EV=6cdot dfrac{1}{4}+2cdot dfrac{1}{4}+(-5)cdot dfrac{3}{8}+(-2)cdot dfrac{1}{8}=dfrac{12}{8}+dfrac{4}{8}-dfrac{15}{8}-dfrac{2}{8}=-dfrac{1}{8}=-0.125
$$
This agrees with what we had determined in (a).
c. 0, because then you don’t expect to win or lose anything from the game after many spins. A spinner is thus fair if you have an equal chance of winning the game and losing the game after many spins.
d. Make every piece of the spinner equally large, and change $-5$ to $-6$ (or 6 to 5), such that the negative and positive numbers are equal.
b. $-frac{1}{8}=-0.125$
c. 0, Equally likely to win or lose money
d. Make every piece of the spinner equally large and change $-5$ to $-6$.
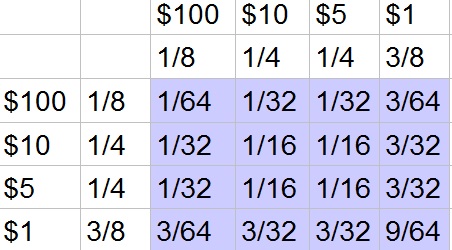
$$
EV=100cdot dfrac{1}{64}+10cdot dfrac{1}{16}+5cdot dfrac{1}{16}+1cdot dfrac{9}{64}=dfrac{100}{64}+dfrac{40}{64}+dfrac{20}{64}+dfrac{9}{64}=dfrac{169}{64}approx $2.64
$$
c. No, because the game costs more every run, than what you expect to win ($$3>$2.64$).
d. No, because you expect to lose many in the long run, it would be fair if you would win equally much as loose in the long run.
b. $$2.64$
c. No
d. No
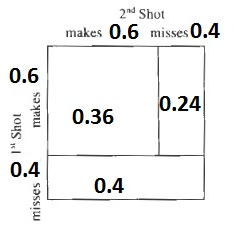
c. The expected value is the sum of the product of every possibility and the probability of that possibility happening:
$$
EV=0.4cdot 0+0.24cdot 1+0.36cdot 2=0+0.24+0.72=0.96
$$
d. If $p$ is the probability of making a throw, then the expected value is:
$$
EV=(1-p)cdot 0+p(1-p)cdot 1+p^2cdot 2=p(1-p)+2p^2=p-p^2+2p^2=p^2+p
$$
b. Some points
c. 0.96 points
d. $p^2+p$
b. The expected value is the sum of the product of every possibility and the probability of that possibility happening:
$$
EV=dfrac{3}{6}cdot 2 +dfrac{1}{6}cdot 1 +dfrac{2}{6}cdot (-4)=dfrac{6}{6}+dfrac{1}{6}-dfrac{8}{6}=-dfrac{1}{6}
$$
Since the expected value is negative, the game is not fair.
c. Turn one of the $-4$ into a $-3$.
d. That the game is fair and that you have an equal chance of winning and losing.
b. $-frac{1}{6}$, No
c. Turn one $-4$ into $-3$
d. Game is fair
The expected value is the sum of the product of every possibility and the probability of that possibility happening and calculate the probability as the measure of the angle to the total angle of 360$text{textdegree}$:
$$
EV=dfrac{7}{360}cdot 100 +dfrac{353}{360}cdot 2=dfrac{700}{360}+dfrac{706}{360}=dfrac{1406}{360}approx 3.9
$$
METHOD 2
Determine the probability as the area of the region to the area of the circle (assume the radius is 1):
$$
EV=dfrac{7pi /360}{pi}cdot 100 +dfrac{353pi /360}{pi}cdot 2=dfrac{700}{360}+dfrac{706}{360}=dfrac{1406}{360}approx 3.9
$$
3.9
$$
a.
$$
EV=dfrac{1}{4}cdot x +dfrac{3}{4}cdot 2=dfrac{x}{4}+dfrac{6}{4}=dfrac{x+6}{4}
$$
Since the expected value should be 3:
$$
dfrac{x+6}{4}=3
$$
Multiply both sides of the equation by 4:
$$
x+6=12
$$
Subtract 6 from both sides of the equation:
$$
x=6
$$
b.
$$
EV=dfrac{4}{6}cdot x +dfrac{1}{6}cdot (-3)+ dfrac{1}{6}cdot 1=dfrac{4x}{6}-dfrac{3}{6}+dfrac{1}{6}=dfrac{4x-2}{6}
$$
Since the expected value should be 3:
$$
dfrac{4x-2}{6}=3
$$
Multiply both sides of the equation by 6:
$$
4x-2=18
$$
Add 2 to both sides of the equation:
$$
4x=20
$$
Divide both sides of the equation by 4:
$$
x=5
$$
$$
EV=dfrac{1}{4}cdot x +dfrac{1}{4}cdot (-3)+ dfrac{1}{9}cdot 18+dfrac{7}{18}cdot 9=dfrac{9x}{36}-dfrac{27}{36}+dfrac{72}{36}+dfrac{126}{36}=dfrac{9x+171}{36}
$$
Since the expected value should be 3:
$$
dfrac{9x+171}{36}=3
$$
Multiply both sides of the equation by 36:
$$
9x+171=108
$$
Subtract 171 from both sides of the equation:
$$
9x=-63
$$
Divide both sides of the equation by 9:
$$
x=dfrac{-63}{9}=-7
$$
b. $x=5$
c. $x=-7$
$$
dfrac{1}{4}cdot dfrac{1}{3}=dfrac{1}{12}approx 0.083=8.3%
$$
b. Intersection, because an event on the first spinner has to occur AND an event on the second spinner has to occur (AND is represented by the intersection).
c. No, yellow would be a better choice, because the probability of yellow is greatest on the first spinner and the probability of each color is equal on the second spinner.
d. All possibilities that make the two colors not the same:
$$
dfrac{1}{2}cdot dfrac{2}{3}+dfrac{1}{4}cdot dfrac{2}{3}+dfrac{1}{4}cdot dfrac{2}{3}=dfrac{8}{12}=dfrac{2}{3}approx 0.667=66.7%
$$
e. Another manner is using the complement. The probability of the complement of an event is 1 decrease by the probability of the event not happening:
$$
1-left(dfrac{1}{2}cdot dfrac{1}{3}+dfrac{1}{4}cdot dfrac{1}{3}+dfrac{1}{4}cdot dfrac{1}{3}right)=1-dfrac{4}{12}=dfrac{8}{12}=dfrac{2}{3}approx 0.667=66.7%
$$
b. Intersection
c. No
d. 66.7%
e. 66.7%
$$
12x^2+8x-15x-10
$$
Combine like terms:
$$
12x^2-7x-10
$$
$$
16x^2-8x+1
$$
$$
2x^2+6x=2x^2+2x-5x-5
$$
Combne like terms:
$$
2x^2+6x=2x^2-3x-5
$$
Subtract $2x^2$ from both sides of the equation:
$$
6x=-3x-5
$$
Add $3x$ to both sides of the equation:
$$
9x=-5
$$
Divide both sides of the equation by 9:
$$
x=-dfrac{5}{9}
$$
$$
9+x^2+2x+1=x^2+4x+4
$$
Subtract $x^2$ from both sides of the equation:
$$
10+2x=4x+4
$$
Subtract $2x$ fropm both sides of the equation:
$$
10=2x+4
$$
Subtract 4 from both sides of the equation:
$$
6=2x
$$
Divide both sides of the equation by 2:
$$
3=x
$$
b. $16x^2-8x+1$
c. $x=-dfrac{5}{9}$
d. $x=3$
$$
AB=sqrt{(-1-3)^2+(4-2)^2}=sqrt{16+4}=sqrt{20}=2sqrt{5}
$$
$$
AC=sqrt{(0-3)^2+(-2-2)^2}=sqrt{9+16}=sqrt{25}=5
$$
$$
BC=sqrt{(0+1)^2+(-2-4)^2}=sqrt{1+36}=sqrt{37}
$$
The perimeter is the sum of all sides:
$$
2sqrt{5}+5+sqrt{37}
$$
b. The blue triangle is the original triangle and the green triangle is the dilated triangle.
Since all sides are doubled in length, the perimeter is also multiplied by 2.
$$
text{Perimeter}=2(2sqrt{5}+5+sqrt{37})=4sqrt{5}+10+2sqrt{37}
$$
c. The blue triangle is the original triangle and the purple triangle is the rotated triangle.
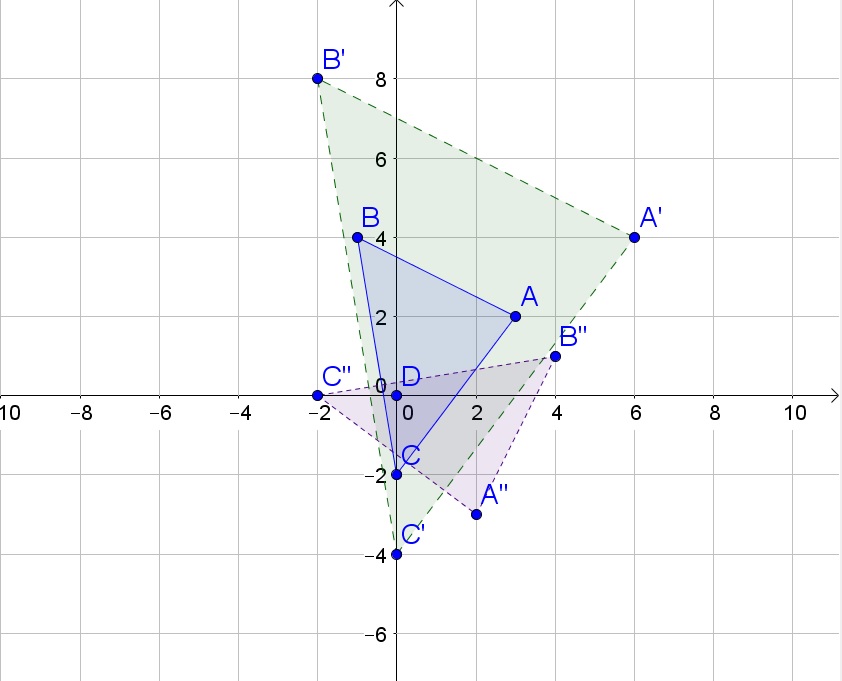
b. $4sqrt{5}+10+2sqrt{37}$
c. $C”(-2,0)$
$$
mangle A=mangle E
$$
$$
mangle B=mangle B=90text{textdegree}
$$
$$
Downarrow AA
$$
$$
triangle ABDsim triangle EBC
$$
b. Using the pythagorean theorem:
$$
BD=sqrt{15^2-12^2}=sqrt{81}=9
$$
Thus we then know that the triangles are congruent because of ASA since all angles in a triangle sum up to 180$text{textdegree}$.
b. Yes
b. (i)
$$
left( dfrac{4}{5}right)^3=dfrac{64}{125}
$$
(ii)
$$
3cdot dfrac{4}{5}cdot dfrac{1}{5}cdot dfrac{1}{5}=dfrac{12}{125}
$$
(iii) The probability of having at least one tail is 100%(=1) decreased by the probability of having no tails (you have no tails, which means that we obtained 3 heads and thus we can use the probability of part (i)),
$$
1-dfrac{64}{125}=dfrac{61}{125}
$$
(iv)
$$
3cdot dfrac{4}{5}cdot dfrac{1}{5}cdot dfrac{1}{5}=dfrac{12}{125}
$$
b. (i) $frac{64}{125}$ (ii) $frac{12}{125}$, (iii) $frac{61}{125}$ (iv) $frac{12}{125}$


$$
EV=0cdot dfrac{3}{8}+5cdot dfrac{1}{4}+20cdot dfrac{3}{8}=dfrac{10}{8}+dfrac{60}{8}=dfrac{70}{8}=8.75
$$
b. No, because you are expected to win less than you pay.
b. No
a. Right: $dfrac{1}{3/4}=dfrac{4}{3}$ and Lower: $dfrac{3}{4}+dfrac{4}{3}=dfrac{9}{12}+dfrac{16}{12}=dfrac{25}{12}$
b. We thus need to find two numbers whose product is $6$ and whose sum is $5$, these numbers are then $2$ and 3 and need to be filled in the left and right cell (order does not matter).
c. Left: $dfrac{5}{-1}=-5$ and Lower: $-5-1=-6$
d. Right: $4-6=-2$ and Upper: $6cdot (-2)=-12$
b. 2, 3
c. $-5$, $-6$
d. $-2$, $-12$
$$
82text{textdegree}+2x=180text{textdegree}
$$
Subtract 82$text{textdegree}$ from both sides of the equation:
$$
2x=98text{textdegree}
$$
Divide both sides of the equation by 2:
$$
x=49text{textdegree}
$$
$$
71text{textdegree}+ 71text{textdegree}+x=180text{textdegree}
$$
Subtract 142$text{textdegree}$ from both sides of the equation:
$$
x=38text{textdegree}
$$
b. $x=38text{textdegree}$
$$
48=acdot b^2
$$
$$
750=acdot b^5
$$
Solve the first equation to $a$:
$$
a=dfrac{48}{b^2}
$$
$$
750=acdot b^5
$$
Replace $a$ with $dfrac{48}{b^2}$ in the second equation:
$$
750=dfrac{48}{b^2}cdot b^5
$$
Divide both sides of the equation by 48:
$$
15.625=b^3
$$
Take the cubic root of both sides of the equation:
$$
2.5=b
$$
Determine $a$:
$$
a=dfrac{48}{2.5^2}=7.68
$$
The equation then becomes:
$$
f(x)=7.68(2.5)^x
$$
f(x)=7.68(2.5)^x
$$
b. Corresponding sides in similar figures have the same proportions:
$$
dfrac{x}{11}=dfrac{24}{8}
$$
Multiply both sides of the equation by 11:
$$
x=dfrac{24cdot 11}{8}=33
$$
Determine $y$:
$$
dfrac{y-4}{18}=dfrac{8}{24}
$$
Multiply both sides of the equation by 18:
$$
y-4=dfrac{8cdot 18}{24}=6
$$
Add 4 to both sides of the equation:
$$
y=10
$$
c. You will need a dilation, rotation and translation.
b. $x=33$ and $y=10$
c. Dilation, rotation and translation
b. We note in the table that there are 6 ways to obtain a sum of seven.
c. 11 possible outcomes (sum of the ways in (a) and (b))
d. The probability is the number of favorable outcomes divided by the total number of possible outcomes:
$$
dfrac{5}{11}approx 0.455=45.5%
$$
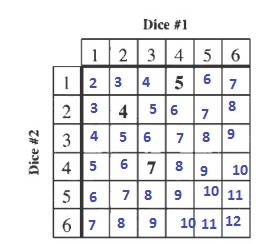
b. 6 ways
c. 11 possible outcomes
d. $frac{5}{11}approx 0.455=45.5%$
b. No, you can determine it using the tangent of the triangle as we will learn later.
c. You could describe is with the slope of the side of the tower.
b. No
c. Slope
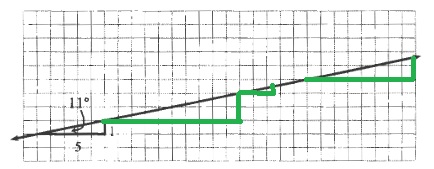
c. This means that the slope ratios are also all the same.
d.
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}=0.2
$$
b. Sides are parallel and angles are the same
c. Slope ratios are the same
d. $frac{1}{5}=0.2$
$$
dfrac{6}{Delta x}=0.2
$$
Multiply both sides of the equation by $Delta x$:
$$
6=0.2Delta x
$$
Multiply both sides of the equation by 5:
$$
30=Delta x
$$
b. In the previous problem we found that the slope is $0.2$:
$$
dfrac{Delta y}{40}=0.2
$$
Multiply both sides of the equation by $40$:
$$
Delta y=0.2cdot 40=8
$$
c. No, because a different line could have a different slope, however if the lines are parallel then it is possible, because parallel lines have the same slope.
b. $Delta y=8$
c. No
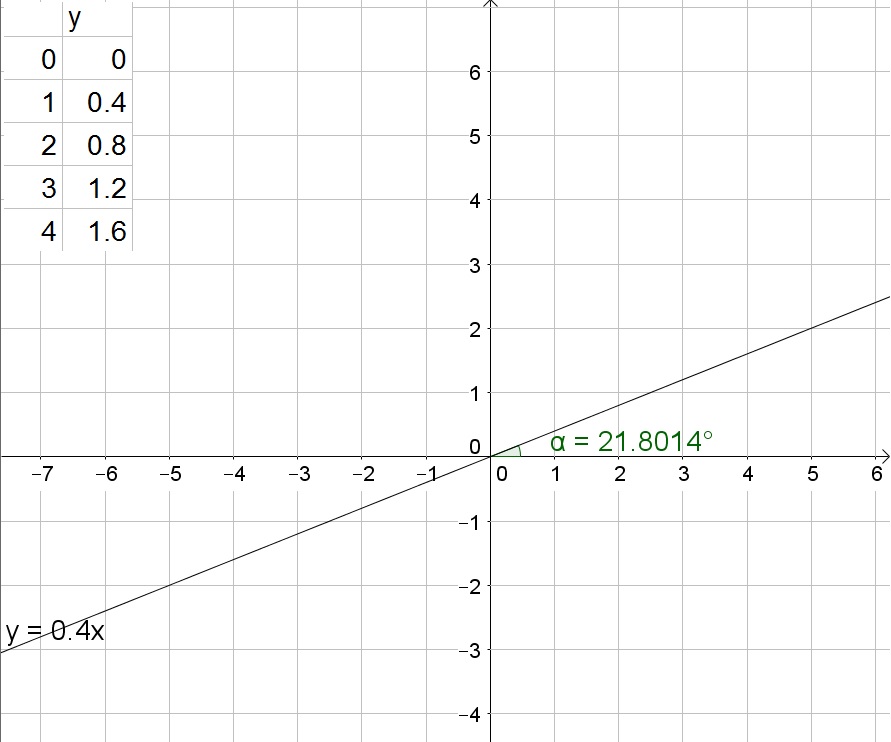
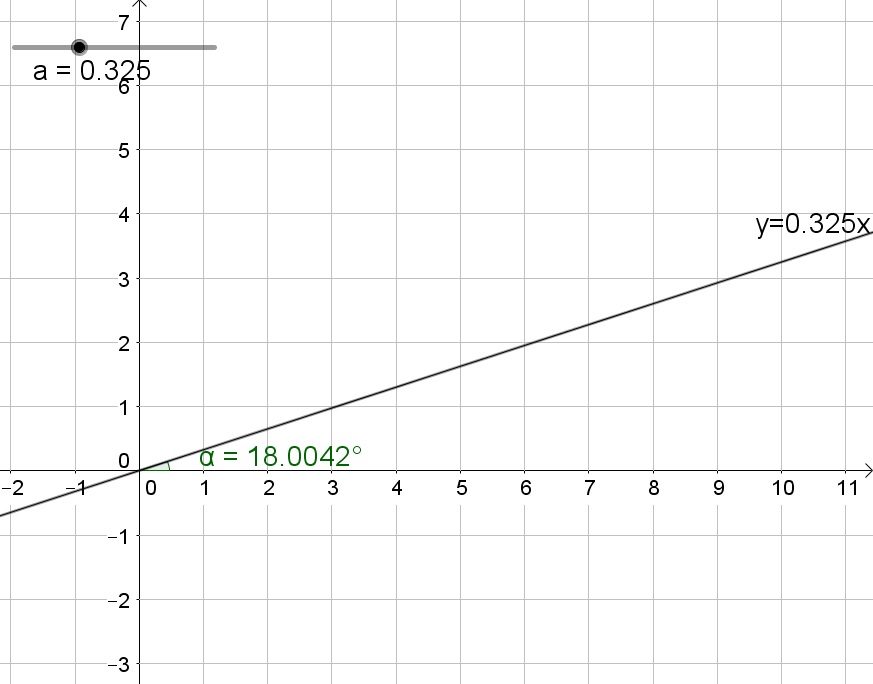
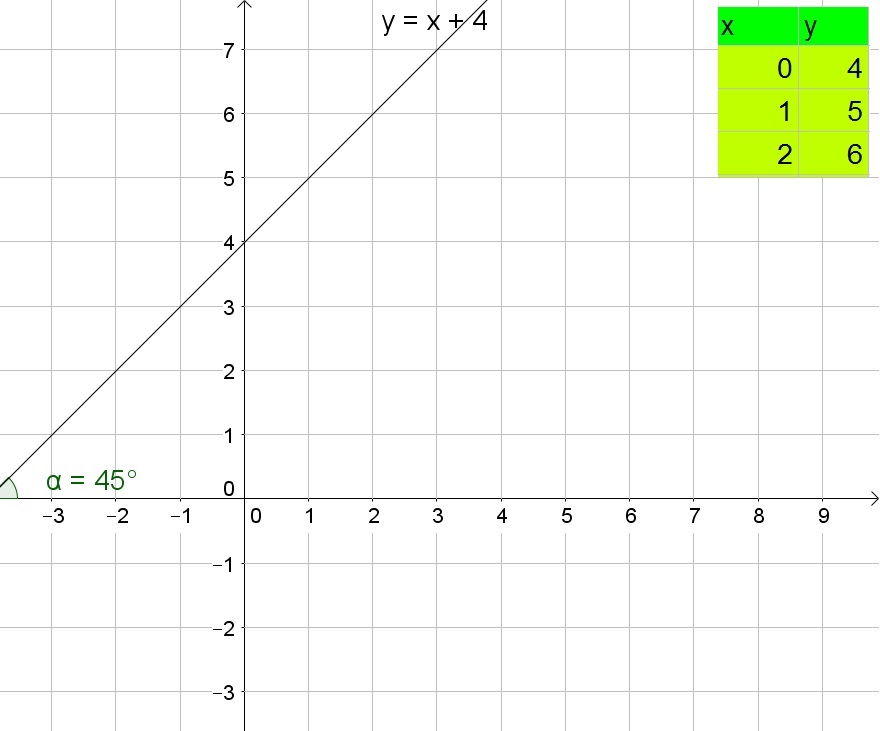
b. 0.325
c. 1, 45$text{textdegree}$
True, we saw this in problem 3-68.
True, we saw this in problem 3-68.
False, if the different lines are parallel then they have the same slope angles and the same slope ratios.
True
True
False
We consider that one interior angle in a right triangle is $90^circ$, the sum of all the interior angles of a right triangle is equal to $180^circ$.
Given the following illustration in triangle a, we are to determine the value of $x$ in the triangle as follows:
$$begin{aligned}
text{sum of all interior angles} &= 180^circ \
79^circ + 90^circ + x &= 180^circ \
x &= 180^circ – 79^circ – 90^circ \
x &= boxed{11^circ}
end{aligned}$$
Given the following illustration in triangle b, we are to determine the value of $x$ in the triangle as follows:
$$begin{aligned}
text{sum of all interior angles} &= 180^circ \
x + x + 90^circ &= 180^circ \
2x &= 180^circ – 90^circ \
x &= frac{90^circ}{2} \
&= boxed{45^circ}
end{aligned}$$
Given the following illustration in triangle c, we are to determine the value of $x$ in the triangle as follows:
$$begin{aligned}
text{sum of all interior angles} &= 180^circ \
2x + x + 90^circ &= 180^circ \
3x &= 180^circ – 90^circ \
x &= frac{90^circ}{3} \
&= boxed{30^circ}
end{aligned}$$
Given the following illustration in triangle d, we are to determine the value of $x$ in the triangle as follows:
$$begin{aligned}
text{sum of all interior angles} &= 180^circ \
x + 22^circ + 90^circ &= 180^circ \
x &= 180^circ – 90^circ – 22^circ\
&= boxed{68^circ}
end{aligned}$$
b. $45^circ$
c. $30^circ$
d. $68^circ$
a. Since OR is used, the event is a union. Addition rule: $P(Atext{ or }B)=P(A)+P(B)-P(Atext{ and }B)$:
$$
P(text{ club or face})=P(club)+P(face)-P(text{ club and face})=dfrac{13}{52}+dfrac{12}{52}-dfrac{3}{52}=dfrac{22}{52}=dfrac{11}{26}approx 0.423=42.3%
$$
b. Since AND is used, the event is a intersection.
$$
P(text{ club and face})=dfrac{3}{52}approx 0.058=5.8%
$$
The answer relates because we have used the probability of king and club.
c. The probability event of something not happening is 1 decreased by the probability of the event happening (complement).
$$
P(text{not a club and not a face})=1-P(text{ club or face})=1-dfrac{11}{26}=dfrac{15}{26}approx 0.577=57.7%
$$
b. $frac{3}{52}approx 0.058=5.8%$, Intersection
c. $frac{15}{26}approx 0.577=57.7%$
a.
$$
dfrac{f}{6}=dfrac{6}{4}
$$
Multiply both sides of the equation by 6:
$$
f=dfrac{6cdot 6}{4}=9
$$
b.
$$
dfrac{g}{15}=dfrac{24}{20}
$$
Multiply both sides of the equation by 15:
$$
g=dfrac{24cdot 15}{20}=18
$$
$$
dfrac{h}{7}=dfrac{10}{3}
$$
Multiply both sides of the equation by 7
$$
h=dfrac{10cdot 7}{3}=dfrac{70}{3}
$$
d. You will need a rotation of 90 $text{textdegree}$ and a translation.
b. $g=18$
c. $h=frac{70}{3}$
d. Rotation of 90$text{textdegree}$ and translation
a) $(2x+1)(3x-2)=6x^2-4x+3x-2=6x^2-x-2$
b) $(2x+1)(3x^2-2x-5)=6x^3-4x^2-10x+3x^2-2x-5=6x^3-x^2-12x-5$
c) $(3y-8)(-x+y)=-3xy+3y^2+8x-8y$
d) $(x-3y)(x+3y)=x^2+3xy-3xy-9y^2=x^2-9y^2$
b. We do not know if $overleftrightarrow{BD}$ and $overleftrightarrow{EG}$ are parallel.
b. Unknown whether $overleftrightarrow{BD}$ and $overleftrightarrow{EG}$ are parallel.
b. The angles take on the shape of a Z.
b. The angles take on the shape of a Z.
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}
$$
Since we now know that $Delta x=20$:
$$
dfrac{y}{20}=dfrac{1}{5}
$$
Multiply both sides of the equation by 20:
$$
y=dfrac{20}{5}=4
$$
y=4
$$
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}
$$
If the angle is $22text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=dfrac{2}{5}
$$
If the angle is $45text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=1
$$
a.
$$
dfrac{y}{25}=dfrac{2}{5}
$$
Multiply both sides of the equation by 25:
$$
y=dfrac{50}{5}=10
$$
b.
$$
dfrac{100}{x}=dfrac{1}{5}
$$
Use cross multiplication
$$
500=100(5)=1(x)=x
$$
c.
$$
dfrac{13}{a}=1
$$
Multiply both sides of the equation by $a$:
$$
13=a
$$
e. Since the ratio is $dfrac{2}{5}$, we then know that the angle is $theta=22text{textdegree}.$
f. Since the sum of all angles in a triangle is 180$text{textdegree}$:
$$
180text{textdegree}-90text{textdegree}-79text{textdegree}=11text{textdegree}
$$
We then know:
$$
dfrac{7}{b}=dfrac{1}{5}
$$
Use cross multiplication
$$
35=7(5)=1(b)=b
$$
b. $x=500$
c. $a=13$
d. $theta=45text{textdegree}$
e. $theta=22text{textdegree}$
f. $b=35$
b. Since the slope ratio is $dfrac{1}{5}$ if the angle is 11$text{textdegree}$. We know that the slope ratio will be $dfrac{5}{1}=5$ if the angle is 79$text{textdegree}$ (because the $x$ and $y$ values of the slope will be switched in the triangle).
c. We note that the relationship between 11$text{textdegree}$ and 79$text{textdegree}$ is complementary and their slope ratios are each others reciprocals.
b. Ratio is 5
c. Complementary angles, Slope ratios are reciprocals
$$
90text{textdegree}-22text{textdegree}=68text{textdegree}
$$
Since the slope ratio for 22$text{textdegree}$ was $dfrac{2}{5}$, the slope ratio for 68$text{textdegree}$ is then $dfrac{5}{2}$.
b. We know what the ratio is because of (a):
$$
dfrac{30}{x}=dfrac{5}{2}
$$
Use cross multiplication:
$$
60=30(2)=5x
$$
Divide both sides of the equation by 5:
$$
12=x
$$
c. If one angle of a right trangle has slope ratio $dfrac{a}{b}$, then the complementary angle of the triangle has slope ratio $dfrac{b}{a}$.
b. $x=12$
c. The complementary angle of the triangle has slope ratio $frac{b}{a}$
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}
$$
If the angle is $22text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=dfrac{2}{5}
$$
If the angle is $45text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=1
$$
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}
$$
If the angle is $22text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=dfrac{2}{5}
$$
If the angle is $45text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=1
$$
a.
$$
dfrac{95}{x}=dfrac{5}{1}
$$
Use cross multiplication
$$
95=5x
$$
Divide both sides of the equation by 5:
$$
19=x
$$
Finally we also know that the sum of all angles is 180$text{textdegree}$:
$$
theta=180text{textdegree}-90text{textdegree}-79text{textdegree}=11text{textdegree}
$$
b. Since the ratio is $dfrac{40}{40}=1$, we then know that the angle is $a=b=45text{textdegree}.$
c.
$$
dfrac{70}{y}=dfrac{2}{5}
$$
Use cross multiplication:
$$
350=2y
$$
Divide both sides of the equation by $2$:
$$
175=y
$$
b. $a=b=45text{textdegree}$
c. $y=175$
$$
EV=-6cdot dfrac{1}{4}+3cdot dfrac{3}{8}+5cdot dfrac{3}{8}=-dfrac{12}{8}+dfrac{9}{8}+dfrac{15}{8}=dfrac{12}{8}=frac{3}{2}=1.5
$$
The game is not fair, because the expected value is not zero.
a. Left: $-dfrac{4}{3}cdot (-1)=dfrac{4}{3}$ and Lower: $dfrac{4}{3}-1=dfrac{1}{3}$
b. Lower: $-frac{3}{5}+left(-frac{4}{5}right)=-frac{7}{5}$ and Upper: $-dfrac{3}{5}cdot left(-dfrac{4}{5}right)=dfrac{12}{25}$
c. Left: $1dfrac{5}{6}+dfrac{1}{6}=2$ and Upper: $2cdot left(-dfrac{1}{6}right)=-dfrac{1}{3}$
d. We thus need to find two numbers whose product is $dfrac{1}{16}$ and whose sum is $dfrac{1}{2}$, these numbers are then $dfrac{1}{4}$ and $dfrac{1}{4}$ and need to be filled in the left and right cell (order does not matter).
b. $-frac{7}{5}$, $dfrac{12}{25}$
c. $2$, $-dfrac{1}{3}$
d. $dfrac{1}{4}$, $dfrac{1}{4}$
Equation B is NOT correct, because we know that the sum of $2x-1text{textdegree}$ and $4text{textdegree}-x$ is 180$text{textdegree}$, but we don’t know that they are necessarily equal (because then we obtain two right angles and the two angles do not appear to be right angles).
Since alternate interior angles are equal, we know that equation (C) is correct.
Equation D is correct, because the sum of consecutive interior angles is 180$text{textdegree}$.
$$
0=3x-12
$$
Add 12 to both sides of the equation:
$$
12=3x
$$
Divide both sides of the equation by 3:
$$
4=x
$$
Determine $y$:
$$
y=5(4)-2=20-2=18
$$
Thus the solution is $(4,18)$.
$$
2x=-4y-2
$$
$$
2x+y=-20
$$
Subtract the two equations:
$$
-y=-4y+18
$$
Add $4y$ to both sides of the equation:
$$
3y=18
$$
Divide both sides of the equation by 3:
$$
y=6
$$
Determine $x$:
$$
x=-2(6)-1=-12-1=-13
$$
Thus the solution is $(-13,6)$.
b. $(-13,6)$
$$
dfrac{13.5}{9}=dfrac{12}{8}=dfrac{9}{6}=1.5
$$
b. Similar because of AA, since corresponding angles are equivalent if the lines are parallel.
c. Not similar, because not enough information is given and the triangle could thus be similar and could also be not similar.
d. Similar (even congruent) because of AA, since the sum of all angles in a triangles are 180$text{textdegree}$ and the base angles of a isosceles triangle are equal.
b. Similar
c. Not similar
d. Similar
b. We note that the slope is about 1.425:
$$
dfrac{8}{x}=1.425
$$
Multiply both sides of the equation by $x$:
$$
8=1.425x
$$
Divide both sides of the equation by 1.425:
$$
5.6approx x
$$
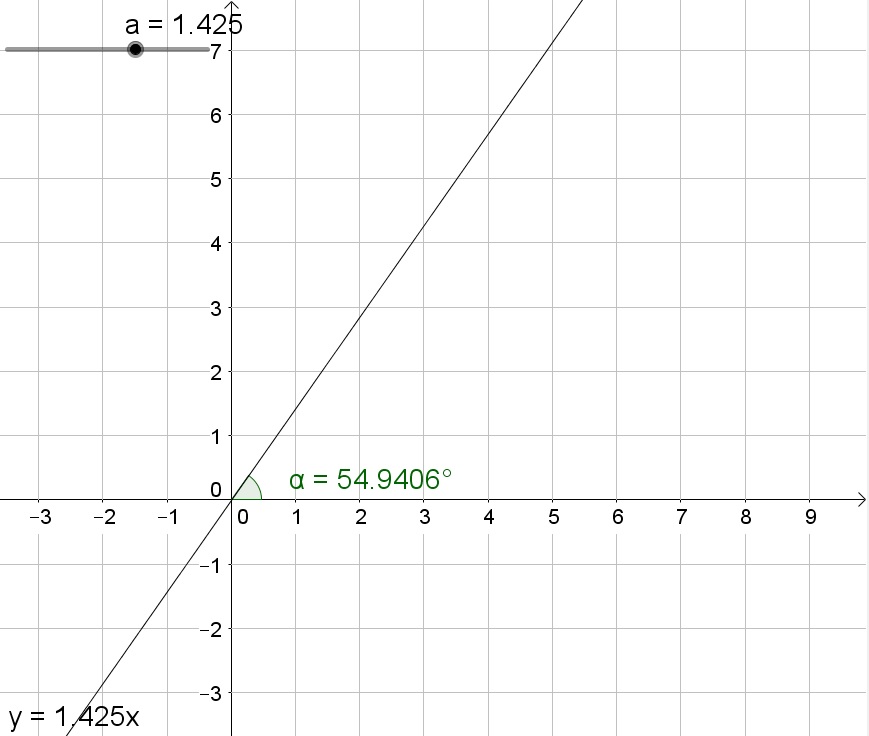
b. $x=5.6$
$$
yapprox 28
$$
ALTERNATIVE SOLUTION
The tangent of an angle is the opposite side divided by the adjacent side:
$$
tan 70text{textdegree}=dfrac{y}{10}
$$
Multiply each side by 10 and evaluate:
$$
y=10tan 70text{textdegree}approx 27.4748
$$
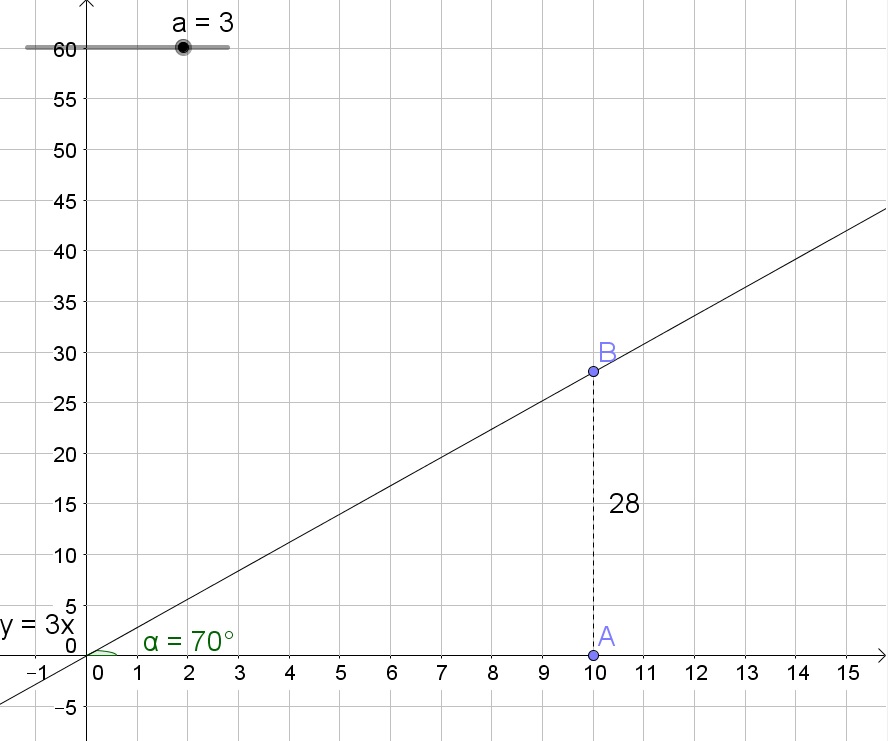
$$
thetaapprox 83text{textdegree}
$$
ALTERNATIVE SOLUTION
The tangent of an angle is the opposite side divided by the adjacent side:
$$
tan theta=dfrac{50}{6}=dfrac{25}{3}
$$
Solve to $theta$:
$$
theta=tan^{-1} dfrac{25}{3}=arctan dfrac{25}{3}approx 83text{textdegree}
$$
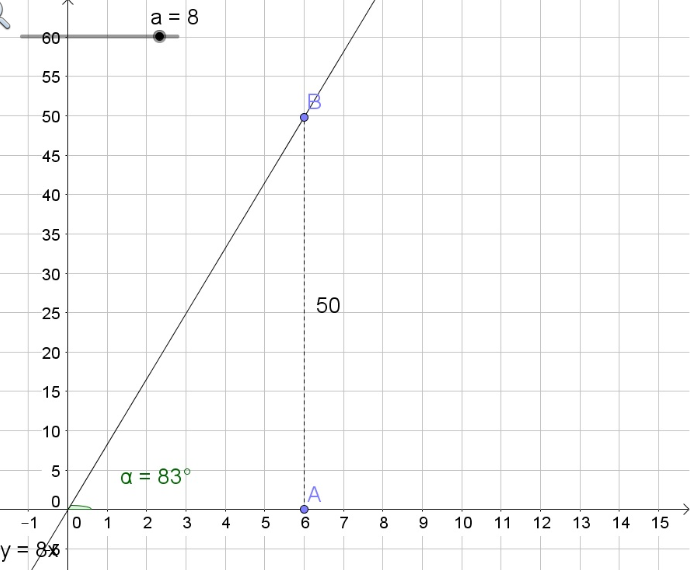
$$
thetaapprox 84text{textdegree}
$$
ALTERNATIVE SOLUTION
The tangent of an angle is the opposite side divided by the adjacent side:
$$
tan theta=dfrac{10}{1}=10
$$
Solve to $theta$:
$$
theta=tan^{-1} 10=arctan 10approx 84text{textdegree}
$$
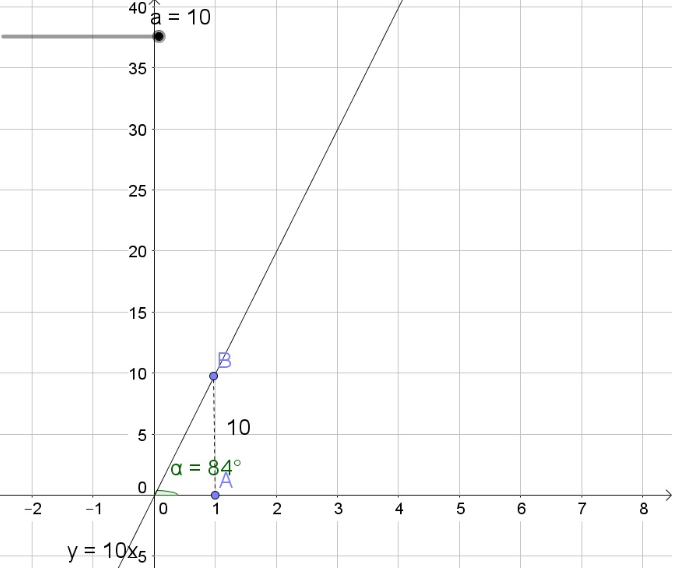
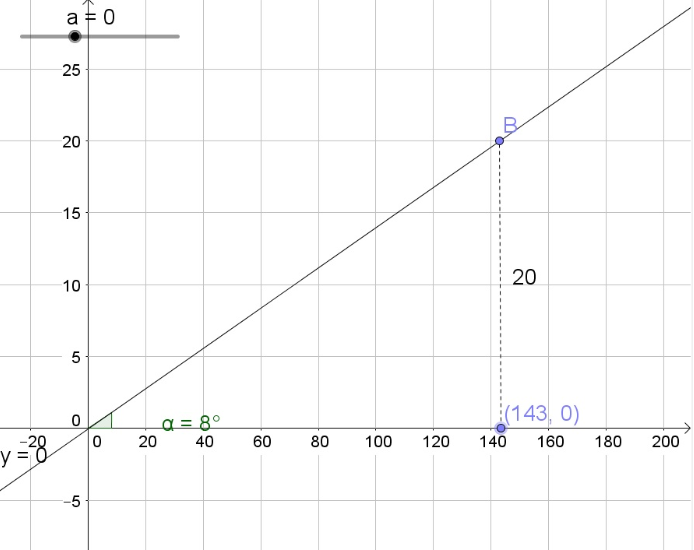
$$
xapprox 143
$$
ALTERNATIVE SOLUTION
The tangent of an angle is the opposite side divided by the adjacent side:
$$
tan 8text{textdegree}=dfrac{20}{x}
$$
Multiply each side by $x$:
$$
xtan 8text{textdegree}=20
$$
Divide each side by $tan 8text{textdegree}$:
$$
x=dfrac{20}{tan 8text{textdegree}}approx 143
$$
$$
yapprox 115
$$
ALTERNATIVE SOLUTION
The tangent of an angle is the opposite side divided by the adjacent side:
$$
tan 89text{textdegree}=dfrac{y}{2}
$$
Multiply each side by 10 and evaluate:
$$
y=2tan 89text{textdegree}approx 114.5799
$$
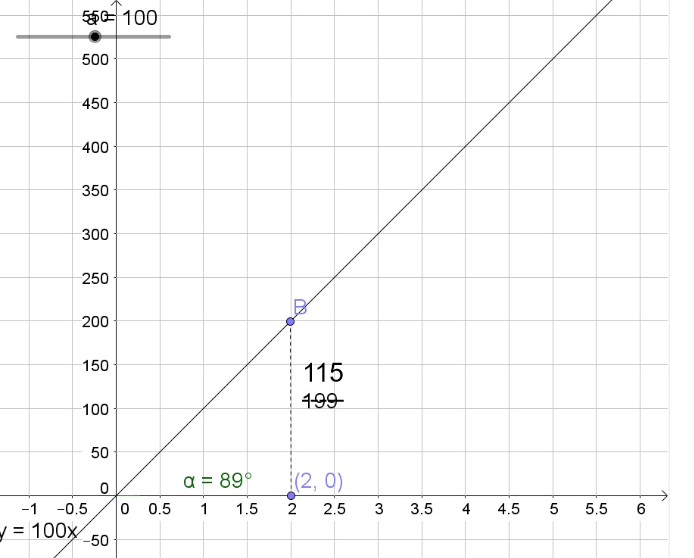
(b) $thetaapprox 83text{textdegree}$
c. $thetaapprox 84text{textdegree}$
d. $xapprox 143$
e. Not possible
f. $yapprox 115$
g. Not possible
$$
dfrac{Delta y}{Delta x}=dfrac{1}{5}
$$
If the angle is $22text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=dfrac{2}{5}
$$
If the angle is $45text{textdegree}$, then the ratio of the triangle is
$$
dfrac{Delta y}{Delta x}=1
$$
If $Delta y$ is zero (and thus angle 0$text{textdegree}$) and if the angle is 90$text{textdegree}$ (and thus a vertical line), then the slope triangles will not work.
The slope becomes zero if the angle is 0$text{textdegree}$ and the slope is undefined if the angle is 90$text{textdegree}$.
The slope ratio is more than 1 if the angle is more than 45$text{textdegree}$ and the slope ratio is less than 1 if the angle is less than 45$text{textdegree}$.
The slope becomes zero if the angle is 0$text{textdegree}$ and the slope is undefined if the angle is 90$text{textdegree}$.
The slope ratio is more than 1 if the angle is more than 45$text{textdegree}$ and the slope ratio is less than 1 if the angle is less than 45$text{textdegree}$.
a. Since the ratio is $dfrac{6}{4}=1.5>1$, we know that the angle is more than 45$text{textdegree}$.
b. Isiah, because the slope ratio cannot be correct. The slope ratio has to be less than 1 because the angle is less than 45$text{textdegree}$.
c. Since the angle is more than 76$text{textdegree}$, we know that the slope ratio is more than 1 and thus $x$ is less than 9 (and nonzero and nonnegative).
b. Isiah
c. Less than 9
b. Congruent:
$$
angle Ocong angle Q
$$
$$
angle Mcong angle P
$$
$$
NO=QR
$$
$$
Downarrow AAS
$$
$$
triangle MNOcong triangle PQR
$$
c. Cannot be determined because we have only one pair of corresponding angles and one pair of corresponding sides.
b. AAS
c. Cannot be determined
$$
(2x)(3x)+(2x)(-4)
$$
Simplify:
$$
6x^2-8x
$$
$$
(x)(2x)+(x)(-5)+(3)(2x)+(3)(-5)
$$
Simplify:
$$
2x^2-5x+6x-15
$$
Combine like terms:
$$
2x^2+x-15
$$
$$
(2x)(2x)+(2x)(-5)+(5)(2x)+(5)(-5)
$$
Simplify:
$$
4x^2-10x+10x-25
$$
Combine like terms:
$$
4x^2-25
$$
$$
(x)(2x)(x)+(x)(2x)(-3)+(x)(1)(x)+(x)(1)(-3)
$$
Simplify:
$$
2x^3-6x^2+x^2-3x
$$
Combine like terms:
$$
2x^3-5x^2-3x
$$
b. $2x^2+x-15$
c. $4x^2-25$
d. $2x^3-5x^2-3x$
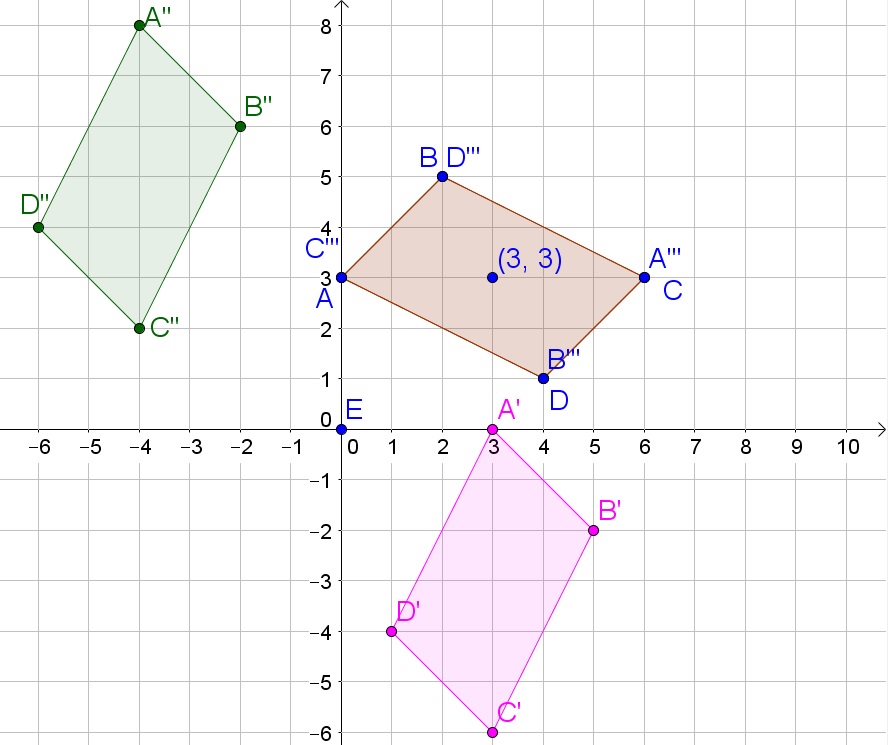
b. $C”(-4,2)$
c. $(3,3)$
$$
Original: 3+4+6+5=18
$$
$$
Enlarged: 6+8+12+10=36
$$
Thus we note that the perimeter has been doubled.
The area is the sum of the bases, multiplied by the height and divided by 2.
$$
Original: dfrac{(3+6)4}{2}=18
$$
$$
Enlarged: dfrac{(6+12)8}{2}=72
$$
We note that the area has been quadrupled.
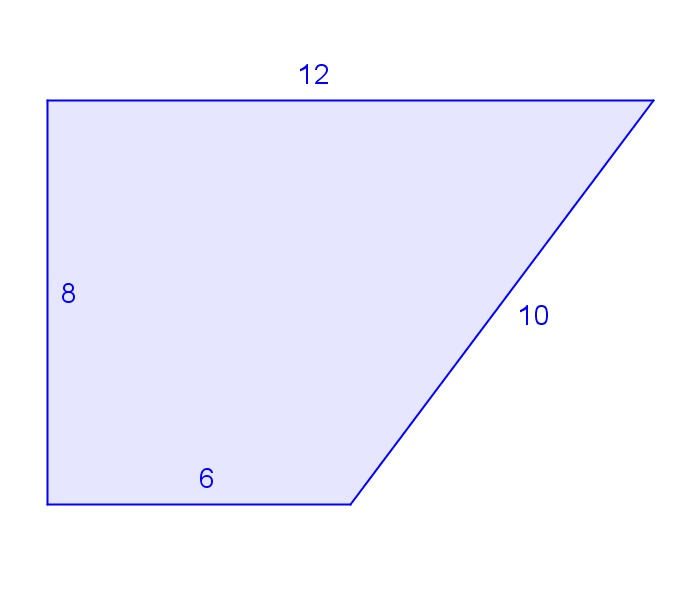
Enlarged figure: Perimeter 36 and Area 72
b. No, because the angle is about 84$text{textdegree}$.
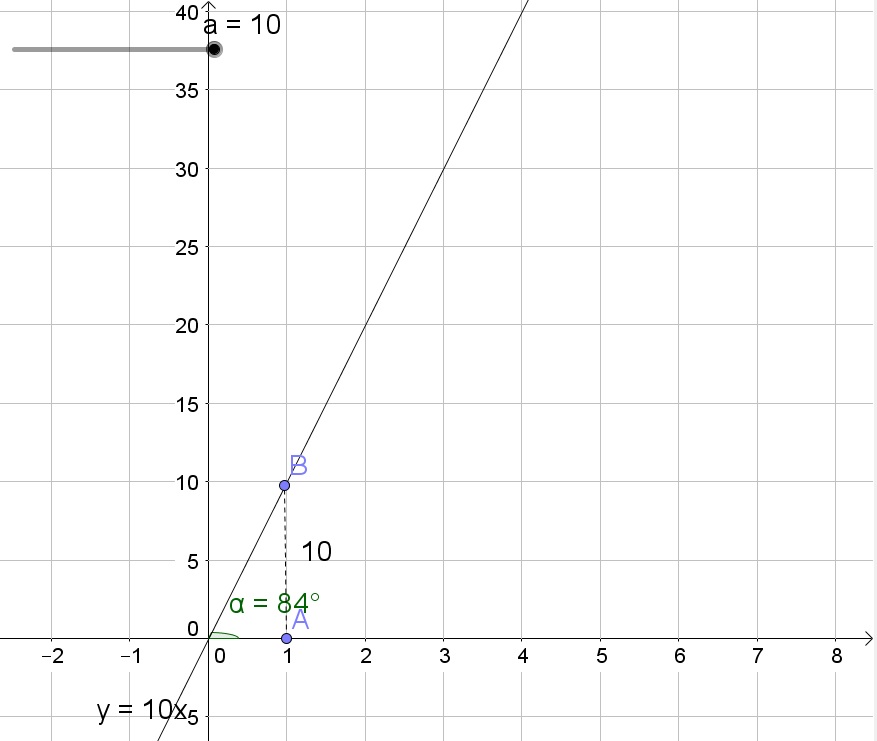
b. No
$$
theta=180text{textdegree}-79text{textdegree}-90text{textdegree}=11text{textdegree}
$$
We know that the slope ratio is then $dfrac{1}{5}$
$$
dfrac{w}{12}=dfrac{1}{5}
$$
Multiply both sides of the equation by 12:
$$
w=dfrac{12}{5}=2.4
$$
$$
theta=180text{textdegree}-22text{textdegree}-90text{textdegree}=68text{textdegree}
$$
We know that the slope ratio of 22$text{textdegree}$ is $dfrac{2}{5}$
$$
dfrac{z}{8}=dfrac{2}{5}
$$
Multiply both sides of the equation by 8:
$$
z=dfrac{2cdot 8}{5}=dfrac{16}{5}=3.2
$$
$$
theta=180text{textdegree}-18text{textdegree}-90text{textdegree}=72text{textdegree}
$$
We know that the slope ratio of 18$text{textdegree}$ is about $0.325$
$$
dfrac{x}{15}=0.325
$$
Multiply both sides of the equation by 15:
$$
x=0.325cdot 15=4.875
$$
b. $z=3.2$
c. $x=4.875$
$$
dfrac{4}{a}=0.325
$$
Multiply both sides of the equation by $a$:
$$
4=0.325a
$$
Divide both sides of the equation by 0.325:
$$
12.3approx a
$$
b. Because $Delta y$ is always opposite the angle.
c. Eddie uses the other angle (whose measure is not gven) and then $Delta x$ and $Delta y$ are interchanged.
d.
$$
dfrac{a}{4}=dfrac{1}{0.325}
$$
Multiply both sides of the equation by $4$:
$$
a=dfrac{4}{0.325}approx 12.3
$$
We note that we obtain the same answer
b. $Delta y$ is always opposite the angle
c. Eddie uses the other angle.
d. $a=12.3$
$$
dfrac{5}{8}=0.625
$$
b. The slope ratio is the side opposite the angle divided by the rectangular side adjacent to the angle:
$$
dfrac{8}{5}=1.6
$$
c. $tan{32text{textdegree}}approx 0.625$ and $tan{58text{textdegree}} approx 1.600$
d.
$$
tan{58text{textdegree}}=dfrac{8}{5}
$$
b. $frac{8}{5}=1.6$
c. Yes
d. $tan 58text{textdegree} =frac{8}{5}$
a.
$$
tan{38text{textdegree}} = dfrac{x}{8}
$$
Multiply both sides of the equation by 8:
$$
6.25approx 8cdot tan{38text{textdegree}}=x
$$
b.
$$
tan{73text{textdegree}} = dfrac{9}{x}
$$
Multiply both sides of the equation by $x$:
$$
xcdot tan{73text{textdegree}}=9
$$
Divide both sides of the equation by $tan{73text{textdegree}}$:
$$
x=dfrac{9}{tan{73text{textdegree}}}approx 2.75
$$
c.
$$
tan{45text{textdegree}} = dfrac{x}{14}
$$
Multiply both sides of the equation by 14:
$$
14= 14cdot tan{45text{textdegree}}=x
$$
b. $x=2.75$
c. $x=14$
a.
$$
tan{8text{textdegree}} = dfrac{t}{82}
$$
Multiply both sides of the equation by 82:
$$
11.5approx 82cdot tan{8text{textdegree}}=t
$$
b.
$$
tan{75text{textdegree}} = dfrac{12}{p}
$$
Multiply both sides of the equation by $p$:
$$
pcdot tan{75text{textdegree}}=12
$$
Divide both sides of the equation by $tan{75text{textdegree}}$:
$$
p=dfrac{12}{tan{75text{textdegree}}}approx 3.22
$$
c.
$$
tan{68text{textdegree}} = dfrac{b}{60}
$$
Multiply both sides of the equation by 60:
$$
148.5= 60cdot tan{68text{textdegree}}=b
$$
b. $p=3.22$
c. $b=148.5$
$$
tan{25text{textdegree}} approx 0.467
$$
The equation of a line is then $y=ax+b$ with $a$ the slope and $b$ the $y$-intercept. Thus the equation of the line becomes then:
$$
y=0.467x+4
$$
y=0.467x+4
$$
a. Left: $dfrac{-25}{5}=-5$ and Lower: $-5+5=0$
b. Upper: $8cdot (-2)=-16$ and Lower: $8-2=6$
c. Left: $9-6=3$ and Upper: $3cdot 6=18$
d. We thus need to find two numbers whose product is $-20$ and whose sum is 19, these numbers are then $20$ and $-1$ and need to be filled in the left and right cell (order does not matter).
b. $-16$, 6
c. 3, 18
d. 20, $-1$
$$
EV=-3cdot dfrac{1}{4}+10cdot dfrac{1}{4}+6cdot dfrac{1}{2}=-dfrac{3}{4}+dfrac{10}{4}+dfrac{12}{4}=dfrac{19}{4}=4.75
$$
4.75
$$
$$
4x-3+3x+1=180
$$
Combine like terms:
$$
7x-2=180
$$
Add 2 to both sides of the equation:
$$
7x=182
$$
Divide both sides of the equation by 7:
$$
x=26
$$
$$
5x+6=2x+21
$$
Subtract $2w$ from both sides of the equation:
$$
3x+6=21
$$
Subtract 6 from both sides of the equation:
$$
3x=15
$$
Divide both sides of the equation by 3:
$$
x=5
$$
$$
4x+28+x+19+3x+13=180
$$
Combine like terms:
$$
8x+60=180
$$
Subtract 60 from both sides of the equation:
$$
8x=120
$$
Divide both sides of the equation by 8:
$$
x=15
$$
$$
4x-10=40+90
$$
Add 10 to both sides of the equation:
$$
4x=140
$$
Divide both sides of the equation by 4:
$$
x=35
$$
b. $x=5text{textdegree}$
c. $x=15text{textdegree}$
d. $x=35text{textdegree}$
b. Congruent shapes will have a ratio of 1 between any pair of corresponding sides, because the sides will be equally long.
c. No, for example the rectangle with measure 16 and 11 units will also be a parallelogram but can not be congruent with the given parallelogram since their angles are not congruent.
b. 1
c. No
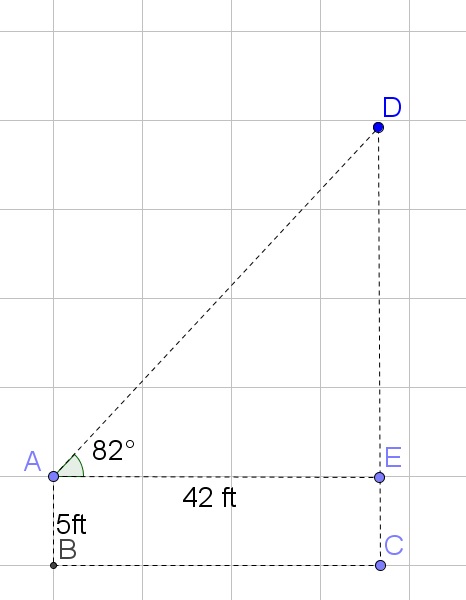
$$
tan{82text{textdegree}} = dfrac{x}{42}
$$
Multiply both sides of the equation by 42:
$$
299approx 42cdot tan{82text{textdegree}}=x
$$
Add the 5ft (of the eye level) to the height:
$$
299ft+5ft=304ft
$$
Thus the height is more than 300 ft and thus she will get a nose leed and shouldn’t climb to the top.
Take into account your eye level and thus know how high your eyes are from the ground.
You would need to measure the angle (parallel with the ground) to the top of what you want to measure.
You also need to know the distance betweeen you and the object of which you want to know the height.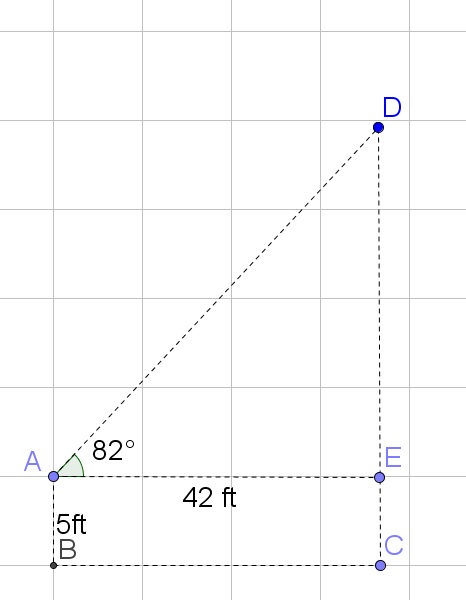
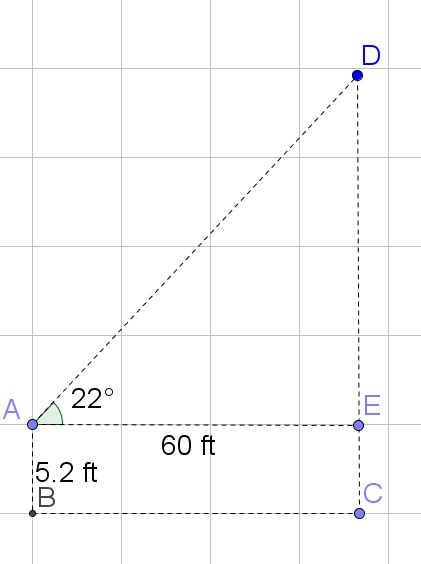
$$
tan{22text{textdegree}} = dfrac{x}{60}
$$
Multiply both sides of the equation by 60:
$$
24.24approx 60cdot tan{22text{textdegree}}=x
$$
Add your eye level:
$$
5.2 ft+24.24ft=29.44ft
$$
Thus the height of the telephone pole is about 29.44ft
$$
tan{33.7text{textdegree}} approx 0.667
$$
The equation of a line is then $y=ax+b$ with $a$ the slope and $b$ the $y$-intercept. Thus the equation of the line becomes then:
$$
y=0.667x+7
$$
y=0.667x+7
$$
dfrac{DE}{BC}=dfrac{6}{4}=1.5
$$
$$
dfrac{DF}{AC}=dfrac{7.5}{5}=1.5
$$
$$
mangle C=mangle Dtext{ (vertical angles and alternate interior angles are equivalent) }
$$
$$
Downarrow SAS
$$
$$
triangle ABC sim triangle EDF
$$
We determine the value of $y$ when $x=-3$ as follows:
$$begin{aligned}
y &= -frac{1}{3}x -5 \
& x = -3 \
y &= -frac{1}{3}(-3) -5 \
&= 1-5 \
&= boxed{-4}
end{aligned}$$
We determine the value of $y$ when $x=-3$ as follows:
$$begin{aligned}
y &= 2x^2-3x-2 \
& x = -3 \
y &= 2(-3)^2-3(-3)-2 \
&= 18+9-2 \
&= boxed{25}
end{aligned}$$
We determine the value of $y$ when $x=-3$ as follows:
$$begin{aligned}
2x -5y &= 4 \
-5y &= 4 -2x \
y &= frac{2}{5}x – frac{4}{5} \
& x = -3 \
y &= frac{2}{5}(-3) – frac{4}{5} \
&= -frac{6}{5} – frac{4}{5} \
&= – frac{10}{5}\
&= boxed{-2}
end{aligned}$$
b. $y=25$
c $y = -2$
$$
dfrac{28}{x}=dfrac{2}{5}
$$
Use cross multiplication:
$$
28(5)=2x
$$
Divide both sides of the equation by 2:
$$
70=dfrac{28(5)}{2}=x
$$
$$
dfrac{13+17}{22+8+13+15+17}=dfrac{30}{75}approx 0.4=40%
$$
c. Let $x$ be the total number of stuffed animals. The probability is then the number of stuffed alligators divided by the number of stuffed animals:
$$
dfrac{3}{x}=5%
$$
Multiply both sides of the equation by $x$:
$$
3=0.05x
$$
Divide both sides of the equation by 0.05:
$$
60=x
$$
b. 40%
c. 60
$$
9+14=23
$$
$$
14-9=5
$$
Thus the length of the third side is between 5 and 23 units.

