$$
angle ZYWcong angle XWY text{(alternate interior angles)}
$$

$$
overleftrightarrow{WY}cong overleftrightarrow{YW}
$$

$$
Downarrow ASA
$$

$$
triangle ZWY cong triangle XYW
$$

a.
$$
dfrac{y}{7}=dfrac{3}{4}Rightarrow y=dfrac{3cdot 7}{4}=dfrac{21}{4}
$$

$$
dfrac{w}{6}=dfrac{4}{3}Rightarrow w=dfrac{4cdot 6}{3}=8
$$

b.
$$
dfrac{x}{6}=dfrac{15}{9}Rightarrow x=dfrac{15cdot 6}{9}=10
$$

$$
dfrac{z}{12}=dfrac{9}{15}Rightarrow z=dfrac{9cdot 12}{15}=dfrac{36}{5}
$$

c.
$$
dfrac{u}{8}=dfrac{10}{4.2}Rightarrow u=dfrac{8cdot 10}{4.2}=dfrac{400}{21}
$$

$$
dfrac{v}{32}=dfrac{4.2}{10}Rightarrow v=dfrac{32cdot 4.2}{10}=dfrac{134.4}{10}=13.44
$$

d. You will need a dilation, reflection, translation and rotation.

b. $x=10$, $z=frac{36}{5}$

c. $u=frac{400}{21}$, $v=frac{134.4}{10}=13.44$

d. Dilation, Reflection, Translation, and rotation

$$
triangle DEF simtriangle ABC
$$

Corresponding sides of similar figures are proportional.

$$
dfrac{6}{4}=dfrac{x}{2.4}
$$

Multiply both sides of the equation by 2.4

$$
3.6=dfrac{6cdot 2.4}{4}=x
$$

b. ASA and since the common ratio is 1.5:

$$
triangle HGMsimtriangle JGK
$$

Corresponding sides of similar figures are proportional.

$$
dfrac{4+2}{4}=dfrac{x}{3}
$$

Multiply both sides of the equation by 3:

$$
4.5=dfrac{6cdot 3}{4}=x
$$

b. $x=4.5$

a. Possible and a right triangle (since the Pythagorean theorem is not ):

$$
8^2+15^2=289=17^2
$$

b. Not possible, because the largest side is equal to the sum of the other two sides and thus all sides will fall together creating a line.

$$
180text{textdegree}-110text{textdegree}-30text{textdegree}=40text{textdegree}
$$

However we also know that the shortest side should be opposite the shortest angle, which is not the case in this triangle. Thus this design is not possible to be build.

a.
$$
x(3x-2)=3x^2-2x
$$

b.
$$
(x+1)(x+2)=x^2+2x+x+2=x^2+3x+2
$$

c.
$$
(3x+1)(x-2)=3x^2-6x+x-2=3x^2-5x-2
$$

d.
$$
(x+3)(x-1)=x^2-x+3x-3=x^2+2x-3
$$

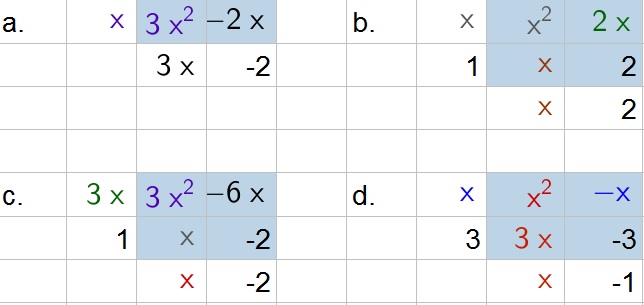
b. $x^2+3x+2$

c. $3x^2-5x-2$

d. $x^2+2x-3$

a. If a pair of corresponding angles are congruent, then the two lines are parallel. TRUE

b. If $mangle C=70text{textdegree}$ in $triangle ABC$, then the sum of of $mangle A$ and $mangle B$ is 110$text{textdegree}$. TRUE (sum of the measure of all angles is 180$text{textdegree}$).

c. If the two lines cut by a transversal are not parallel, then the alternate interior angles are not congruent. TRUE

d. If Johan loses his money, then he throws coins in the fountain. FALSE ( You cannot throw coins in the fountain after you’ve lost your money).

b. 45$text{textdegree}$ and 90$text{textdegree}$, because the sum of all angles in a triangle is 180$text{textdegree}$ and the base angle in a isosceles triangle are equal and a right angle is 90$text{textdegree}$.

c. 73$text{textdegree}$, because the sum of all angles in a triangle is 180$text{textdegree}$ and the base angle in a isosceles triangle are equal.

The shortest side of the triangle is opposite the shortest angle: $overline{BC}$.

The longest side of the triangle is opposite the largest angle: $overline{AC}=overline{AB}$.

b. 90$text{textdegree}$, 45$text{textdegree}$, and 45$text{textdegree}$

c. 73$text{textdegree}$

$$
dfrac{3cdot 3}{2}=4.5
$$

$$
dfrac{3cdot 5}{2}=7.5
$$

$$
dfrac{3cdot 4}{2}=6
$$

The arae of a trapezium is the sum of the bases multiplied by the height, divided by 2:

$$
dfrac{(5+2)4}{2}=14
$$

Thus the total area is then:

$$
A=4.5+7.5+6+14=32
$$

Using the Pythagorean theorem $a^2+b^2=c^2$, you can find the length of the sides:

$$
begin{align*}
&sqrt{3^2+3^2}=sqrt{9+9}=sqrt{18}
\ &sqrt{3^2+5^2}=sqrt{9+25}=sqrt{34}
\ &sqrt{3^2+4^2}=sqrt{9+16}=sqrt{25}=5
\ &sqrt{4^2+3^2}=sqrt{16+9}=sqrt{25}=5
end{align*}
$$

The perimeter is the sum of the length of all sides:

$$
P=sqrt{18}+sqrt{34}+5+2+5=12+sqrt{18}+sqrt{34}
$$

$$
4cdot 5=20
$$

$$
3cdot 4=12
$$

$$
2cdot 1=2
$$

$$
2cdot 1=2
$$

Thus the total area is then:

$$
A=20+12+2+2=36
$$

The perimeter is the sum of the length of all sides:

$$
P=4+3+1+2+2+2+1+1+4+3+2+5=30
$$

b. Area 36 and Perimeter 30