$$begin{aligned}
cos(x) &= dfrac{3}{4} \\
cos^{-1} (cos(x)) &= cos^{-1}dfrac{3}{4} \\
x& = 41.41degree
end{aligned}$$

Now we know cosine is positive in the first and fourth quadrant. This implies
$$cos (360degree – theta) = cos theta$$

Therefore,
$$begin{aligned}
cos(360 degree – x) &= cos (41.41degree) \
cos(360degree – 41.41degree ) &= (cos 41.41degree) \
cos(318.59degree)& = cos (41.41degree)
end{aligned}$$

This implies $x = 318.59degree$

The period of $costheta$ is $2pi$. Therefore the value will repeat if we add $360degree$, n number of times to the values of x where n is a positive integer.

Therefore for $cos x = dfrac{3}{4}$

$x=41.41degree + 360degree(n)$ and
$x=318.59degree + 360degree(n)$

Thus for these values of x $cos x = dfrac{3}{4}$ will always be true.

$$begin{aligned}
2tan(x) &= 0 \
tan(x) &= 0 \
tan^{-1} (tan(x)) &= tan^{-1} (0) \
x& = 0
end{aligned}$$

Now we know tan is positive in the first and third quadrant. This implies
$$tan (pi + theta) = tan theta$$

Therefore,
$$begin{aligned}
tan(pi + x) &= tan x \
tan(pi + 0) &= tan 0 \
tan(pi)& = tan 0
end{aligned}$$

This implies $x = pi$

The period of $tantheta$ is $2pi$. Therefore the value will repeat if we add $2pi$, n number of times to the values of x where n is a positive integer.

Therefore for $2tan x =0$

$x=0 + 2pi n$ or $2npi$ and
$x=pi + 2pi n$ or $x= pi(1+2n)$

As we can see the values are (2n) $pi$ and (2n+1)$pi$. We know (2n) implies an even integer and (2n+1) is an odd integer. So we can further simplify and state

For the values of x = n$pi$ we have $2tan x = 0$ and that will always be true.

Now we know $sintheta = dfrac{text{Prependicular}}{text{Hypotenuse}}$

and Hypotenuse is the longest side of the triangle. The value of $sintheta$ can, thus, never be greater than one.

Thus, $sin x = dfrac{5}{2}$ can never be true.

$sintheta = dfrac{text{Prependicular}}{text{Hypotenuse}}$

$costheta = dfrac{text{Base}}{text{Hypotenuse}}$

We can see that sine and cosine are complementary to each other.
So $sin (x) = cos left(dfrac{pi}{2} – xright )$ is always true.

Now we know cosine is positive in the first and fourth quadrant. This implies
$$cos (360degree – theta) = cos theta$$

Therefore,
$$begin{aligned}
cos(360 degree – x) &= cos (60degree) \
cos(360degree – 60degree ) &= (cos 60degree) \
cos(300degree)& = cos (60degree)
end{aligned}$$

This implies $x = 300degree$

Therefore for $2cos x = 1$

$x=60degree$ or $dfrac{pi}{3}$ and

$x=300degree$ or $dfrac{5pi}{3}$

where $0<xle2pi$

$$begin{aligned}
4tan(x)+4 &= 0 \
4tan(x)&= -4 \\
tan (x) &= -dfrac{4}{4} \\
tan (x) &= -1 \
tan^{-1} (tan(x)) &= tan^{-1}(-1) \
x&=tan^{-1}(-1)
end{aligned}$$

We know $tan(45degree) = 1$
Also $tan$ is negative in second quadrant.
So, $tan(180degree-theta) = -tantheta$
Therefore,
$$begin{aligned}
tan(180degree-45) &= -tan(45degree) \
tan(135degree)&= -1
tan^{-1}(tan(135degree))&=tan^{-1}(-1) \
135degree&=tan^{-1}(-1)
end{aligned}$$

Therefore we have x = $135 degree$

Now we know tangent is positive in the first and third quadrant. This implies
$$tan (180degree + theta) = tan theta$$

Therefore,
$$begin{aligned}
tan(180 degree + x) &= tan (x) \
tan(180 degree + 135degree) &= tan (135degree) \
tan(315degree)& = tan (135degree)
end{aligned}$$

This implies $x = 315degree$

Therefore for $4tan(x)+4 = 0$.

$x=135degree$ or $dfrac{3pi}{4}$ and

$x=315degree$ or $dfrac{7pi}{4}$

where $0<xle2pi$

$$begin{aligned}
2sin^2(x)-sin(x)-1 &= 0 \
2sin^2(x)-2sin(x)+sin(x)-1 &= 0 \
2sin(x)[sin(x)-1]+1[sin(x)-1] &= 0 \
[sin(x)-1][2sin(x)+1] &=0 \
end{aligned}$$

We have $sin(x)-1 = 0$ and $2sin(x)+1 = 0$

Therefore, we have $x = 90degree$ or $x = dfrac{pi}{2}$

$$begin{aligned}
2sin(x)+1 &= 0 \
2sin(x)&= -1 \\
sin (x) &= -dfrac{1}{2} \\
sin^{-1} (sin(x)) &= sin^{-1}left(-dfrac{1}{2}right) \\
x&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

We know $sin(30degree) = dfrac{1}{2}$

Also, $sin$ is negative in the third quadrant.
So, $sin(180degree+theta) = -sintheta$
Therefore,
$$begin{aligned}
sin(180degree+30) &= -sin(30degree) \\
sin(210degree)&= -dfrac{1}{2} \\
sin^{-1}(sin(210degree))&=sin^{-1}left(-dfrac{1}{2}right) \\
210degree&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

Therefore we have x = $210 degree$ or $x = dfrac{7pi}{6}$

Also, $sin$ is negative in the fourth quadrant.
So, $sin(360degree-theta) = -sintheta$
Therefore,
$$begin{aligned}
sin(360degree-30) &= -sin(30degree) \\
sin(330degree)&= -dfrac{1}{2} \\
sin^{-1}(sin(330degree))&=sin^{-1}left(-dfrac{1}{2}right) \\
330degree&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

This implies $x = 330degree$ or $x = dfrac{11pi}{6}$

Therefore for $2sin^2(x)-sin(x)-1 = 0$

$x=90degree$ or $dfrac{pi}{2}$ and

$x=210degree$ or $dfrac{7pi}{6}$ and

$x=330degree$ or $dfrac{11pi}{6}$ and

where $0<xle2pi$

We know, $csctheta = dfrac{1}{sintheta}$

Thus, $dfrac{1}{sin (x)} = -2$ or $sin(x) = -dfrac{1}{2}$

Simplifying it,

$$begin{aligned}
sin (x) &= -dfrac{1}{2} \\
sin^{-1} (sin(x)) &= sin^{-1}left(-dfrac{1}{2}right) \\
x&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

We know $sin(30degree) = dfrac{1}{2}$

Also, $sin$ is negative in the third quadrant.
So, $sin(180degree+theta) = -sintheta$
Therefore,
$$begin{aligned}
sin(180degree+30) &= -sin(30degree) \\
sin(210degree)&= -dfrac{1}{2} \\
sin^{-1}(sin(210degree))&=sin^{-1}left(-dfrac{1}{2}right) \\
210degree&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

Therefore we have x = $210 degree$ or $x = dfrac{7pi}{6}$

Also, $sin$ is negative in the fourth quadrant.
So, $sin(360degree-theta) = -sintheta$
Therefore,
$$begin{aligned}
sin(360degree-30) &= -sin(30degree) \\
sin(330degree)&= -dfrac{1}{2} \\
sin^{-1}(sin(330degree))&=sin^{-1}left(-dfrac{1}{2}right) \\
330degree&=sin^{-1}left(-dfrac{1}{2}right)
end{aligned}$$

This implies $x = 330degree$ or $x = dfrac{11pi}{6}$

Therefore for $csc (x) = -2$

$x=210degree$ or $dfrac{7pi}{6}$ and

$x=330degree$ or $dfrac{11pi}{6}$

where $0<xle2pi$

$$
frac {-2}{x-4} + frac {x^2}{x^2 – 16} = frac {12}{x+4}
$$

Using the formula

$$
color{#c34632}{a^2 – b^2 = (a-b)(a+b)}
$$

then

$$
begin{align*}
frac {-2}{x-4} + frac {x^2}{(x-4)(x+4)} &= frac {12}{x+4}\
frac {-2 (x+4) + x^2}{(x-4)(x+4)} &= frac {12}{x+4}\
frac {-2x – 8 +x^2}{(x-4)(x+4)} &= frac {12}{x+4}\
(x+4) frac {x^2 -2x -8}{(x-4)(x+4)} &= 12\
frac {x^2 -2x-8}{x-4} &= 12\
x^2 -2x-8 &= 12(x-4)\
x^2 -2x-8 &= 12x – 48\
x^2 – 14x + 40 &= 0
end{align*}
$$

The solution of a square equation $ax^2 + bx+c=0$ are shape

$$
x + frac {-b pm sqrt {b^2 – 4ac}}{2a}
$$

Now, we have

$$
begin{align*}
x &= frac {14 pm sqrt {196-160}}{2}\
x &= frac {14 pm sqrt {36}}{2}\
x &= frac {14 pm 6}{2}\
x &= 10 qquad x=4
end{align*}
$$

The solutions are

$$
x = 10 qquad x=4
$$

$$
begin{align*}
-8 log_3 ( 7+x) +1 &= -7\
-8 log_3 (7+x) &= -8\
log_3 (7+x) &= 1
end{align*}
$$

Using the formula

$$
begin{align*}
color{#c34632}{log_b a = x}\
color{#c34632}{a=b^x}
end{align*}
$$

we obtain

$$
begin{align*}
7+x &= 3^1\
7+x &=3\
x &= -4
end{align*}
$$

The solution is

$$
x=-4
$$

$$
begin{align*}
-10 &= 10 |-3x + 4| – 4\
-6 &= 10 | -3x +4|\
|-3x &+4| = – frac {6}{10}
end{align*}
$$

The equation has no solution, because the left side of equation can never be negative.

$$
begin{align*}
5+2 (9^{x+8}) &= 10\
2 ( 9^{x+8}) &= 5\
9^{x+8} &= frac 52
end{align*}
$$

Using the $ln$ function

$$
ln 9^{x+8} = ln frac 52
$$

According to the formula

$$
color{#c34632}{ ln a^b = b ln a}
$$

we obtain

$$
begin{align*}
(x+8) ln 9 &= ln frac 52\
x+8 &= frac {ln frac 52}{ln 9}
end{align*}
$$

Since

$$
color{#c34632}{ ln frac ab = ln a – ln b}
$$

we have

$$
begin{align*}
x+8 &= frac {ln 5 – ln 2}{ln 9}\
x+8 &= frac {ln 5}{ln 9}- frac {ln 2}{ln 9}
end{align*}
$$

According to the formula

$$
color{#c34632}{ frac {ln a}{ln b} = log_b a}
$$

we get

$$
begin{align*}
x+8 &= log_95 – log_92\
x &= log_95 – log_92 -8\
x &= log_{9}{frac 52} -8\
x &= 0.42 – 8\
x &= – 7.58
end{align*}
$$

The solution is

$$
x = – 7.58
$$

b) $x=-4$

c) no solution

d) $x = – 7.58$

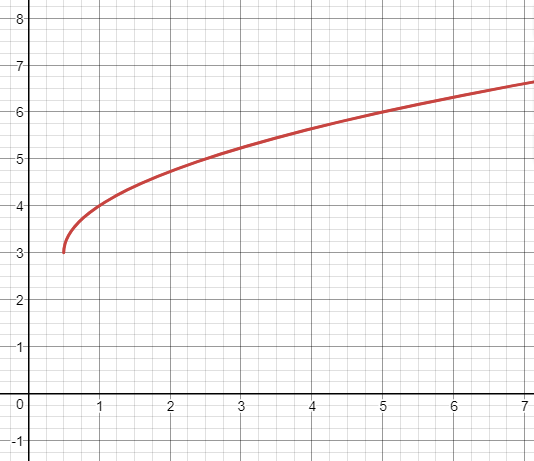
$2xgeq 1$

$xgeq 0.5$

The domain: $[0.5,infty)$

$x=3+sqrt{2y-1}$

$x-3=sqrt{2y-1}$

$(x-3)^2=2y-1$

$2y=(x-3)^2+1$

$y=0.5(x-3)^2+0.5$

$f^{-1}(x)=0.5(x-3)^2+0.5$

$$begin{aligned}
y &= 3 sin 2 ( x – dfrac{pi}{4})+ 1\
end{aligned}$$

$$
begin{align*}
7 + (-2) + (-11) + (-20) + dots =\
= 7+[7-9] + [7- 2 cdot 9] + [7-3 cdot 9] +dots
end{align*}
$$

where

$$
a=7 qquad text{and} qquad d=-9
$$

Using the formula

$$
color{#c34632}{a_{n}=a+(n-1)d}
$$

The $40^{th}$ term is

$$
a_{40} = 7-39 cdot 9 = 7 – 351 = – 344
$$

According to the formula

$$
color{#c34632}{ S = frac n2 [ 2a +(n-1) d]}
$$

we obtain

$$
begin{align*}
S &= frac {40}{2} [ 2 cdot 7 + (40-1)(-9)]\
S &= 20 [14 – 39 cdot 9]\
S &= 20 [ 14 – 351]\
S &= 20 cdot (-337)\
S &= -6740
end{align*}
$$

The sum is

$$
S=-6740
$$

$$
begin{align*}
150 &+ 100 + frac {200}{3} + frac {400}{9} + dots =\
= 150 &+ 150 cdot frac 23 + 150 cdot left( frac 23 right)^2 + 150 cdot left( frac 23 right)^3 + dots
end{align*}
$$

where

$$
a=150 qquad text{and} qquad r=frac 23
$$

The $10^{th}$ term is

$$
begin{align*}
a_{10} = 150 cdot left( frac 23 right)^9 &= 150 cdot frac {512}{19683} \
&= frac {76800}{19683}\
&= frac {25600}{6561}\
&= 3.9
end{align*}
$$

According to the formula

$$
color{#c34632}{S= a left( frac {1-r^{n+1}}{1-r} right)}
$$

we obtain

$$
begin{align*}
S &= 150 left( frac {1- left( frac 23 right)^{9+1}}{1 – frac 23} right)\
S &= 150 left( frac {1- left( frac 23 right)^{10}}{frac {3-2}{3}} right)\
S &= 150 left( frac {frac {3^{10} – 2^{10}}{3^{10}}}{frac 13} right)\
S &= 150 frac {left( 3^{10} – 2^{10} right)}{3^9}\
S &= 150 frac {( 59049 – 1024)}{19683}\
S &= 150 cdot frac {58025}{19683}\
S &= 150 cdot 2.95\
S &= 442.5
end{align*}
$$

$$
S = 442.5
$$

The sum for infinite terms is

$$
color{#c34632}{S= frac a{1-r}}
$$

Then

$$
begin{align*}
S&= frac {150}{1- frac 23}\
S&= frac {150}{frac13}\
S&= 150 cdot 3\
S&=450
end{align*}
$$

b) $S = 442.5 text{ and } S = 450$

$$
begin{align*}
P(x) &= x^5 – 9x^4 + 17x^3 – 153x^2 -200x + 1800\
&= x^4(x-9) + 17x^2(x-9) – 200(x-9)\
&= (x-9)(x^4 + 17x^2 -200)
end{align*}
$$

Now we have

$$
begin{align*}
x-9 &= 0\
x &= 9
end{align*}
$$

and

$$
x^4 + 17x^2 -200 =0
$$

Let $x^2 = y$ then

$$
y^2 + 17y -200 =0
$$

The solutions of a square equation $ax^2 + bx +c = 0$ are shape

$$
x = frac {-b pm sqrt {b^2 -4ac}}{2a}
$$

Now, we have

$$
begin{align*}
y &= frac {-17 pm sqrt {17^2 – 4 cdot 200}}{2}\
y &= frac {-17 pm sqrt {289+800}}{2}\
y &= frac {-17 pm sqrt {1089}}{2}\
y &= frac {-17 pm 33}{2}\
y &= -25 qquad y = 8
end{align*}
$$

Substitute $y=x^2$ we obtain

$$
x^2 = -25 qquad x^2 = 8
$$

Now, we have

$$
begin{align*}
x &= pm sqrt {-25}\
x &= pm 5i
end{align*}
$$

$$
begin{align*}
x &= pm sqrt 8\
x &= pm 2 sqrt 2
end{align*}
$$

The solutions are

$$
begin{align*}
x &=9\
x &= 5_i qquad x = – 5_i\
x &= 2 sqrt 2 qquad x = – 2 sqrt 2
end{align*}
$$

$$
begin{align*}
5x – 4y – 6z &= – 19 tag{$1$}\
-2x + 2y + z &= 5 tag{$2$}\
3x – 6y – 5z &= 16 tag{$3$}
end{align*}
$$

From $(2)$ we obtain

$$
z=5+2x-2y
$$

Substitution in $(1)$ and $(3)$

$$
begin{align*}
5x -4y – 6(5+2x -2y) &= -19\
3x -6y -5(5+2x -2y) &= -16
end{align*}
$$

Simplify

$$
begin{align*}
5x – 4y -30 – 12x + 12y &= -19\
3x -6y -25 -10x +10y &= -16
end{align*}
$$

and

$$
begin{align*}
-7x +8y -30 &= -19\
-7x + 4y -25 &= -16
end{align*}
$$

We have the system of two equations

$$
begin{align*}
-7x + 8y &= 11\
-7x +4y &= 9 tag{$star$}
end{align*}
$$

We can subtract these two equations

$$
begin{align*}
-7x + 8y – ( -7x +4y) &= 11-9\
-7x +8y + 7x -4y &= 2\
4y &= 2\
y &= frac 24\
y &= frac 12
end{align*}
$$

Substitution $y= frac 12$ in $(*)$

$$
begin{align*}
-7x + 4 cdot frac 12 &= 9\
-7x + 2 &= 9\
– 7x &= 7\
x &= -1
end{align*}
$$

$$
begin{align*}
-2 cdot (-1) + 2 cdot frac 12 + z &= 5\
2 + 1 + z &= 5\
3 + z &= 5\
z &= 2
end{align*}
$$

The solution of the system of equations is

$$
(x,y,z) = left( -1, frac 12, 2 right)
$$

$$
y= ax^2 + bx + c
$$

It is necessary to calculate $a$, $b$ and $c$.

We have three points

$$
begin{align*}
(2,11) – 11 &= 2^2a + 2b +c\
11 &= 4a + 2b + c tag{$*$}\
(-1, -4) – -4 &= (-1)^2 a + (-1) b + c\
-4 &= a-b+c tag{$**$}\
(0, -5) – -5 &= 0 cdot a + 0 cdot b + c\
-5 &= c
end{align*}
$$

Substitution $c=-5$ in $(*)$ and $(**)$

$$
begin{align*}
11 &= 4a + 2b -5\
-4 &= a-b-5
end{align*}
$$

Then we have

$$
begin{align*}
16 &= 4a +2b\
1 &= a-b
end{align*}
$$

The first equation divide by 2

$$
begin{align*}
8 &= 2a + b\
a &= 1 + b
end{align*}
$$

Substitution $a=1+b$ in the first equation

$$
begin{align*}
8 &= 2 ( 1+b) +b\
8 &= 2 + 2b + b\
6 &= 3b\
b &= 2
end{align*}
$$

Now, we can calculate

$$
a=1+b = 1+2=3
$$

The equation of the parabola is

$$
y= 3x^2 + 2b -5
$$

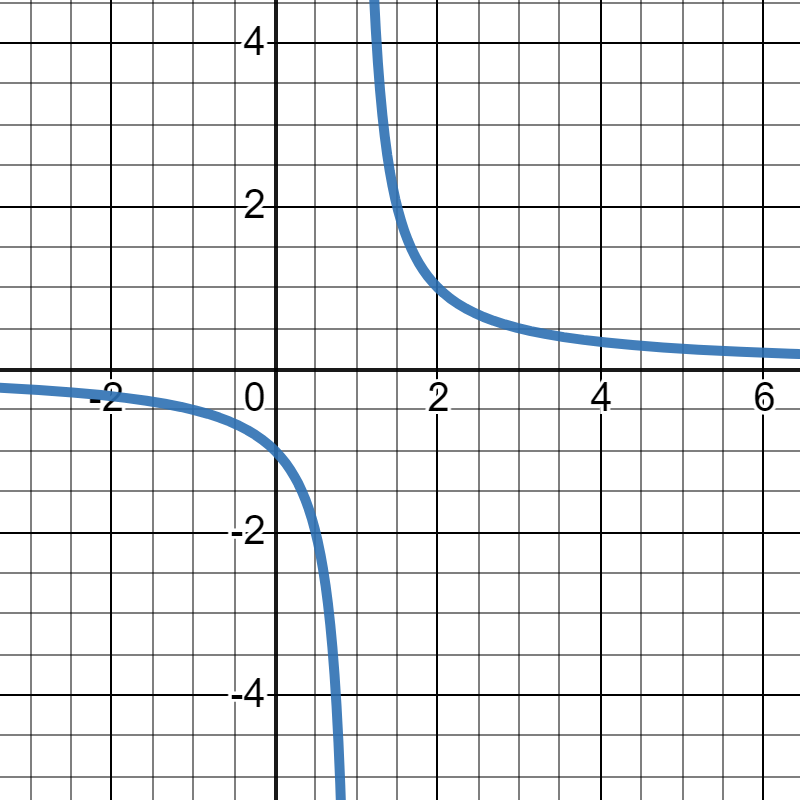
$$
dfrac{5x}{x+3} + dfrac{3+x}{x^2-9}
$$

Now we will simplify the equation,

$$
begin{align*}
dfrac{5x}{x+3} + dfrac{3+x}{x^2-9} &= dfrac{5x}{x+3} + dfrac{3+x}{x^2-(3)^2} \\
&=dfrac{5x}{x+3} + dfrac{3+x}{(x-3)(x+3)} tag{text{using} $a^2-b^2=(a-b)(a+b)$}\\
&=dfrac{5x(x+3) + (3+x)}{(x-3) (x+3)} &tag{text{Taking L.C.M}} \\
&=dfrac{5x(x+3) + 1(x+3)}{(x-3) (x+3)}\\
&=dfrac{(x+3)(5x+1)}{(x+3)(x-3)} &tag{text{Taking (x+3) common}}\\
&=dfrac{5x+1}{x-3} &tag{(x+3) text{are canceled}} \\
end{align*}
$$

Therefore we get,

$dfrac{5x}{x+3} + dfrac{3+x}{x^2-9} = dfrac{5x+1}{x-3}$

As we know (x-3) is in the denominator, therefore the value of x cannot be 3, for if x=3 is punched into the equation, the denominator becomes 0 and the result is thus not defined. This implies x $ne$ 3

Therefore, the domain of the equation is $left(-infty, 3right)cup left(3, inftyright)$

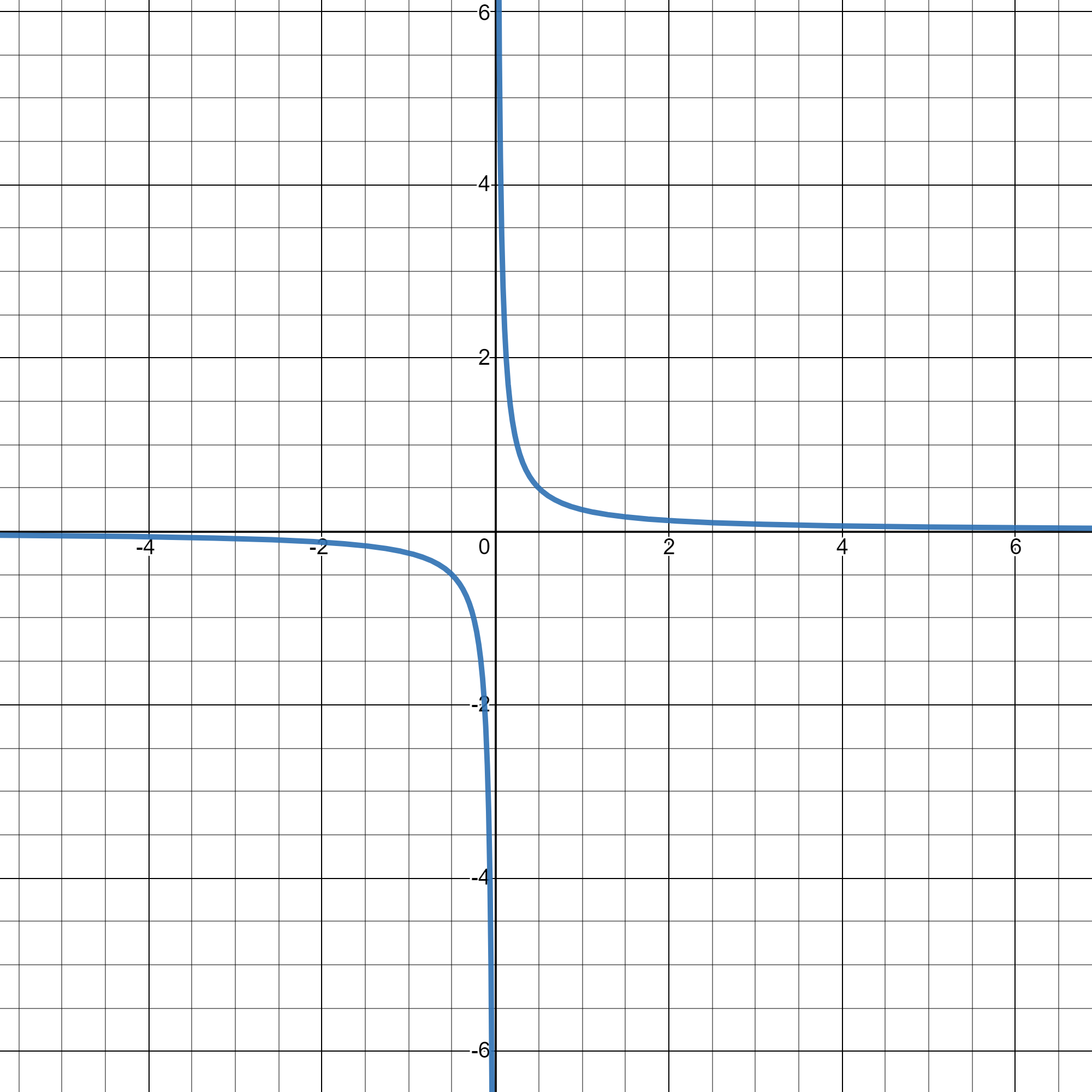
$$
dfrac{x}{x-1}-1
$$

$$
begin{align*}
dfrac{x}{x-1}-1 & = dfrac{x – 1(x-1)}{x-1} tag{text{Taking L.C.M}} \\
&= dfrac{x-x+1}{x-1} \\
&=dfrac{1}{x-1} \\
end{align*}
$$

We get,

$dfrac{x}{x-1}-1= dfrac{1}{x-1}$

As we know (x-1) is in the denominator, therefore the value of x cannot be 1, for if x=1 is punched into the equation, the denominator becomes 0 and the result is thus not defined. This implies x $ne$ 1

Therefore, the domain of the equation is $left(-infty, 1right)cup left(1, inftyright)$

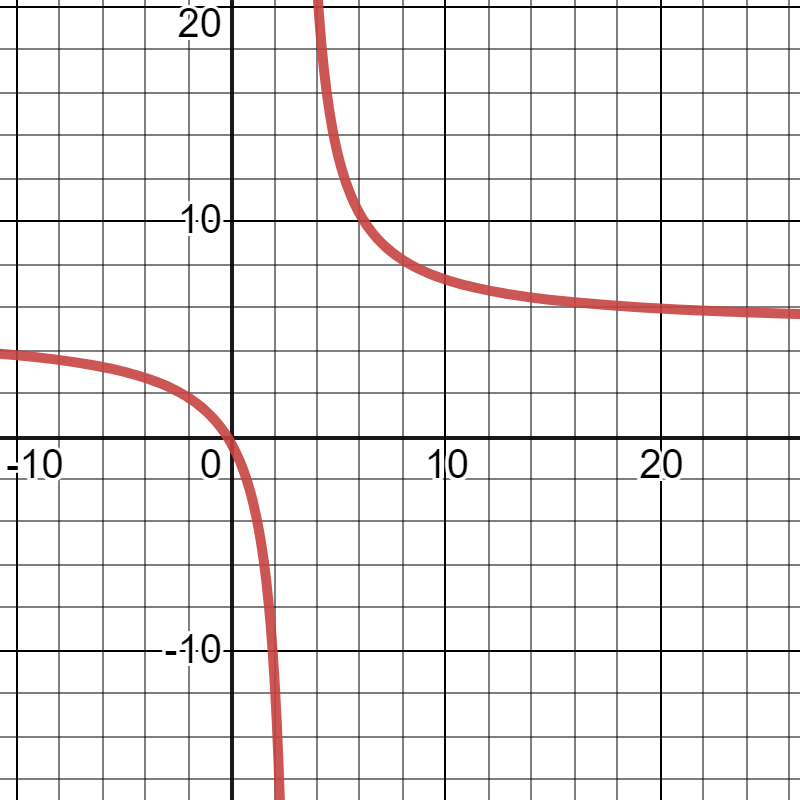
$$
dfrac{x^2+5x+6}{x^2-4x} . dfrac{4x}{x+2}
$$

Now we will simplify the equation,

$$
begin{align*}
dfrac{x^2+5x+6}{x^2-4x} . dfrac{4x}{x+2} &= dfrac{x^2+3x+2x+6}{x^2-4x} times dfrac{4x}{x+2} \\
&=dfrac{x(x+3)+2(x+3)}{x^2-4x} times dfrac{4x}{x+2} \\
&=dfrac{(x+3) (x+2)}{x^2-4x} times dfrac{4x}{x+2} tag{text{Taking (x+3) common}}\\
&=dfrac{x+3}{x(x-4)} times dfrac{4x}{x+2} \\
&=dfrac{(x+3)4x}{x(x-4)(x+2)} \\
&=dfrac{4x^2+12x}{x(x-4)(x+2)} \
end{align*}
$$

Therefore we get,

$dfrac{x^2+5x+6}{x^2-4x} . dfrac{4x}{x+2} = dfrac{4x^2+12x}{x(x-4)(x+2)}$

As we know x, (x-$4$), (x+2) is in the denominator, therefore the value of x cannot be 0, 4, or -2 for if x=0, or x=4, or x=$-2$ is punched into the equation, the denominator becomes 0 and the result is thus not defined. This implies x $ne 0, -2, 4$

Therefore, the domain of the equation is $left(-infty, -2right)cup left(-2, 0right)cup left(0, 4right)cup left(4, infty right)$

$$
dfrac{x^2-2x}{x^2-4x+4} div dfrac{4x^2}{x-2}
$$

Now we will simplify the equation,

$$
begin{align*}
dfrac{x^2-2x}{x^2-4x+4} div dfrac{4x^2}{x-2} &= dfrac{x^2-2x}{x^2-2x-2x+4} div dfrac{4x^2}{x-2}\\
&=dfrac{x(x-2)}{x(x-2)-2(x-2)} times dfrac{(x-2)}{4x^2}\\
&=dfrac{x(x-2)}{(x-2) (x-2)} times dfrac{(x-2)}{4x^2} \\
&=dfrac{x}{4x^2} \\
&=dfrac{1}{4x} \
end{align*}
$$

Therefore we get,

$dfrac{x^2-2x}{x^2-4x+4} div dfrac{4x^2}{x-2} =dfrac{1}{4x}$

As we know 4x is in the denominator, therefore the value of x cannot be 0 for if x=0 is punched into the equation, the denominator becomes 0 and the result is thus not defined. This implies x $ne 0$

Therefore, the domain of the equation is $left(-infty, 0right)cup left(0, infty right)$