All Solutions
Page 483: Closure Activity
$$
y=cos (x)
$$
$dfrac{pi}{180text{textdegree}}cdot xtext{textdegree}=y$ radians.
theta=225text{textdegree}=dfrac{pi}{180text{textdegree}}cdot 225text{textdegree}=dfrac{5pi}{4}
$$
theta=75text{textdegree}=dfrac{pi}{180text{textdegree}}cdot 75text{textdegree}=dfrac{5pi}{12}
$$
theta=-15text{textdegree}=-dfrac{pi}{180text{textdegree}}cdot 15text{textdegree}=-dfrac{pi}{12}
$$
theta=330text{textdegree}=dfrac{pi}{180text{textdegree}}cdot 330text{textdegree}=dfrac{11pi}{6}
$$
$$
M(x,y) = M( cos theta , sin theta )
$$
For $theta = 110^{text{textdegree}}$ we have
$$
M( cos 110^{text{textdegree}} , sin 110^{text{textdegree}})
$$
$$
M( cos 110^{text{textdegree}}, sin 110^{text{textdegree}}) = ( -0.34, 0.94)
$$
$$
begin{align*}
sin^2 theta + cos^2 theta &= 1\
sin^2 110^{text{textdegree}} + cos 110^{text{textdegree}} &= 1\
(0.94)^2 + 0-0.34)^2 &= 1\
0.8836 + 0.1156 &= 1\
0.99 &approx 1
end{align*}
$$
The Pythagorean identity is valid.
b) $( -0.34, 0.94)$
c) The Pythagorean identity is valid.
sin (60text{textdegree})
$$
sin (60text{textdegree})=dfrac{sqrt 3}{2}
$$
cos (180text{textdegree})
$$
cos(180text{textdegree})=-1
$$
tan (225text{textdegree})
$$
tan (225text{textdegree})=tan(225text{textdegree}-180text{textdegree})=tan (45text{textdegree})=1
$$
sinleft(dfrac{pi}{4}right)
$$
tan (225text{textdegree})=dfrac{sqrt 2}{2}
$$
cosleft(dfrac{2pi}{3}right)
$$
cosleft(dfrac{2pi}{3}right)=-cos left(pi-dfrac{2pi}{3}right)=-cosleft(dfrac{pi}{3}right)=-dfrac{1}{2}
$$
tanleft(dfrac{3pi}{2}right)
$$
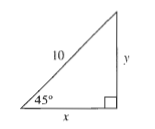
x=y
$$
$2x^2=2y^2=100$
$x^2=y^2=dfrac{100}{2}=50$
$$
x=y=sqrt{50}=5sqrt 2
$$
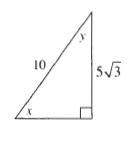
$sin x=dfrac{sqrt 3}{2}$
$$
x=60text{textdegree}
$$
$$
y=90text{textdegree}-60text{textdegree}=30text{textdegree}
$$
b) $x=60text{textdegree}; y=30text{textdegree}$
$$
5^x = 72
$$
We can use the $ln$ function
$$
ln 5^x = ln 72
$$
Using the formula
$$
begin{align*}
color{#c34632}{ln a^b = b ln a} tag {$*$}
end{align*}
$$
We have
$$
begin{align*}
x ln 5 &= ln 72\
x &= frac {ln 72}{ln 5}\
x &= frac {4.27}{1.61}\
x &= 2.65
end{align*}
$$
The solution of equation is
$$
x = 2.65
$$
$$
2^{3x} =7
$$
We can use the $ln$ function
$$
ln 2^{3x} = ln 7
$$
Using the formula $(*)$
$$
begin{align*}
3x cdot ln 2 &= ln 7\
3x &= frac {ln 7}{ln 2}\
3x &= frac {1.94}{0.69}\
3x &= 2.81\
x &= 0.93
end{align*}
$$
The solution of equation is
$$
x = 0.93
$$
$$
3^{(2x+4)} = 17
$$
We can use the $ln$ formula
$$
ln 3^{(2x+4)} = ln 17
$$
According to $(*)$
$$
begin{align*}
(2x+4) ln 3 &= ln 17\
2x + 4 &= frac {ln 17}{ln 3}\
2x + 4 &= frac {2.83}{1.09}\
2x + 4 &= 2.59\
2x &= -1.4\
x &= -0.7
end{align*}
$$
The solution of equation is
$$
x=-0.7
$$
$$
begin{align*}
3x^4 &= 150\
x^4 &= 50\
x &= sqrt[4]{50}\
x &=pm 2.66
end{align*}
$$
The solution of equation is
$$
x=pm 2.66
$$
b) $x = 0.93$
c) $x=-0.7$
d) $x=pm 2.66$
5^x=72
$$
$xlog (5)=log (72)$
$x=dfrac{log (72)}{log (5)}$
$$
xapprox 2.657
$$
2^{3x}=7
$$
$3xlog (2)=log (7)$
$x=dfrac{log (7)}{3log (2)}$
$$
xapprox 0.936
$$
3^{2x+4}=17
$$
$(2x+4)log (3)=log (17)$
$2x+4=dfrac{log (17)}{log (3)}$
$2x=dfrac{log (17)}{log (3)}-4$
$x=dfrac{dfrac{log (17)}{log (3)}-4}{2}$
$$
xapprox -0.711
$$
3x^4=150
$$
$x^4=50$
$x=pmsqrt[4]{50}$
$$
x=pm 2.659
$$
$$
color{#c34632}{ log_ca – log_cb = log_c {ab}}
$$
Therefore
$$
begin{align*}
log_8 {(9)} + log_8 {(x)} &= 1\
log_8 {(9x)} &= 1
end{align*}
$$
We can use the formula
$$
begin{align*}
color{#c34632}{log_ca =b} tag{$*$}\
color{#c34632}{a = c^b}
end{align*}
$$
Then
$$
begin{align*}
9x &= 8^1\
x &= frac 89\
x &= 0.88
end{align*}
$$
$$
begin{align*}
color{#c34632}{ log_ca – log_cb = log_c {frac ab}} tag{**}\
end{align*}
$$
Therefore
$$
begin{align*}
log_x {(8)} – log_x {(19)} &= -1\
log_x {left( frac {8}{19} right) } &= -1
end{align*}
$$
Using the $(*)$
$$
begin{align*}
frac {8}{19} &= x^{-1}\
frac 1x &= frac {8}{19}\
x &= frac {19}{8}\
x &= 2.37
end{align*}
$$
$$
begin{align*}
log_5 {(17+6x)} &= log_5 {(35)}\
17 + 6x &= 35\
6x &= 18\
x &= 3
end{align*}
$$
$$
begin{align*}
log {(18x)} – log {(9)} &= log {(3)}\
log { left( frac {18x}{9} right) } &= log {(3)}\
log {(2x)} &= log {(3)}\
2x &= 3\
x &= frac 32\
x &= 1.5
end{align*}
$$
b) $x = 2.37$
c) $x = 3$
d) $x = 1.5$
log_8 (9)+log_8 (x)=1
$$
$9x=8^1$
$9x=8$
$$
x=dfrac{8}{9}
$$
log_x (8)-log_x (19)=-1
$$
$x^{-1}=dfrac{8}{19}$
$dfrac{1}{x}=dfrac{8}{19}$
$8x=19$
$$
x=dfrac{19}{8}
$$
log_5 (17+6x)=log_5 (35)
$$
$6x=35-17$
$6x=18$
$x=dfrac{18}{6}$
$$
x=3
$$
log (18x)-log (9)=log (3)
$$
$log (2x)=log (3)$
$2x=3$
$$
x=dfrac{3}{2}
$$
$$
begin{align*}
(2x^3 + x^2 – 19x + 36) div (x+4) &= frac {2x^3 + x^2 – 19x + 36}{x+4}\
&= frac{2x^3 + 8x^2 +7x^2 -28x +9x + 36}{x+4} && text{ ($x^2=8x^2 +7x^2$)}\
&text{} && text{ ($- 19x=-28x +9x$)}\
&= frac{(2x^3 + 8x^2) +(7x^2 -28x) + (9x + 36)}{x+4}\
&= frac{ 2x^2 (x+4) -7x (x +4) + 9(x+4)}{x+4}\
&= frac{(x+4)(2x^2 -7x +9)}{x+4}\
&= 2x^2 -7x+9
end{align*}
$$
$$
(2x^3 + x^2 – 19x + 36) div (x+4) = 2x^2 -7x+9
$$
(2x^3 + x^2 – 19x + 36) div (x+4) = 2x^2 -7x+9
$$
Solution to this example is given below\
begin{align*}
&frac{2x^3+x^2-19x+36}{x+4}&&boxed{text{Given proportion}}\
&2x^2+frac{-7x^2-19x+36}{x+4}&&boxed{text{Simplify}}\
&2x^2-7x+frac{9x+36}{x+4}&&boxed{text{Simplify}}\
&2x^2-7x+9&&boxed{text{Simplify}}\\
&boxed{{color{Maroon}2x^2-7x+9} }&&boxed{text{Final solution}}\
end{align*}
color{#4257b2} text{ } 2x^2-7x+9
$$
polylongdiv{2x^3+x^2-19x+36}{x+4}
$$
2x^2-7x+9
$$
$$
begin{align*}
P(x) &=x^3+8\
P(x) &= x^3 + 2^3
end{align*}
$$
$$
color{#c34632}{ a^3 + b^3 = (a+b)(a^2 -ab + b^2)}
$$
$$
P(x) = (x + 2)(x^2 -2x +4)
$$
$$
x = frac {-b pm sqrt {b^2 -4ac}}{2a}
$$
$$
begin{align*}
x &= frac {2 pm sqrt {4-16}}{2}\
x &= frac {2 pm sqrt {-12}}{2}\
x &= frac {2 pm i 2 sqrt 3}{2}\
x &= 1 pm i sqrt 3
end{align*}
$$
$$
begin{align*}
P(x) &= (x+2)(x -( 1 + i sqrt 3)) (x- ( 1 – i sqrt 3))\
&= (x+2) (x-1 – i sqrt 3)(x-1+ i sqrt 3)
end{align*}
$$
$$
P(x) = (x+2)(x^2 -2x+4)
$$
we can see that the factor of this polynomial is
$$
(x+2)
$$
b) $(x+2)$
$$
begin{align*}
P(x) &= x^4 – x^3 -2x -4\
&= x^4 -2x^3 + x^3 +2x^2 -2x^2 -4x + 2x -4\
&= x^4 + x^3 -2x^3 -2x^2 +2x^3 + 2x -4x -4\
&= x^3(x+1) – 2x^2 (x+1) + 2x (x+1) -4 (x+1)\
&= (x+1) (x^3 – 2x^2 +2x-4)
end{align*}
$$
$$
begin{align*}
P_1 (x) &= x^3 -2x^2 + 2x -4\
&= x^2 (x-2) + 2 (x-2)\
&= (x-2)(x^2 +2)
end{align*}
$$
$$
P(x) = (x+1)(x-2)(x^2 +2)
$$
$$
begin{align*}
x+1 &= 0\
x -2 &=0\
x^2 + 2 &= 0
end{align*}
$$
$$
begin{align*}
x &= -1\
x &= 2\
x^2 &= -2
end{align*}
$$
$$
begin{align*}
x &= -1\
x &= 2\
x &=pm sqrt { -2} =pm i sqrt 2
end{align*}
$$
begin{align*}
x &= -1\
x &= 2\
x & =pm i sqrt 2
end{align*}
$$

