All Solutions
Page 151: Closure Activity
Parent graph is shifted up by 2 units, then shifted right by 8 units. and then it is horizontally compressed by factor 4.
$textbf{(b)}$ $x^2+y^2=5^2$ i.e. circle with radius of 5 units and centre at (0,0) is the parent graph for $(x+3)^2+y^2=25$.
Parent graph is shifted left by 3 units.
$textbf{(c)}$ $y=|x|$ is the parent graph for $y=|x-5|+3$.
Parent graph is shifted right by 5 units and shifted up 3 units
$y=dfrac {1}{3}x^2+1$ (1)
$y=2x-2$ (2)
$dfrac {1}{3}x^2+1=2x-2$ (Equating both equations)
$x^2+3=6x-6$ (Multiply each side by 3)
$x^2-6x+9=0$
$(x-3)^2=0$
$$
x=3
$$
Substituting for $x=3$ in equation (1)
$y=dfrac {1}{3} (9)+1$
$$
y=4
$$
This solution tells us that the line of the equation $y=2x-2$ intersects the parabola of the quadratic equation $y=dfrac {1}{3}x^2+1$ at only one point $(3, 4)$
$y=sqrt {x-3}$ (1)
$y=x-5$ (2)
$sqrt {x-3}=x-5$ (Equating both equations)
$x-3=(x-5)^2$ (Square of each side)
$x-3=x^2-10x+25$
$x^2-11x+28=0$
$(x-7)(x-4)=0$
$x=7$ or $x=4$
Checking solution with the original equations:
For $x=7$
$y=sqrt {7-3}=sqrt {4}=2$ (Equation (1))
$y=7-5=2$ (Equation (2))
$x=7$ is a valid solution.
For $x=4$
$y=sqrt {4-3}=sqrt {1}=1$ (Equation (1))
$y=4-5=-1$ (Equation (2))
$x=4$ is an extraneous solution.
This solution tells us that this system has only one valid solution $(7, 2)$
$6x-2y=-4$ (Given)
$2y=6x+4$ (Solving for $y$)
$y=3x+2$ (1)
This equation is the equivalent to equation (2)
b- Both equations intersect at only one point $(7, 2)$
c- Both equations are equivalent.
Now we can write two equations. The first one is:
$$
begin{equation}
2x=4y-3
end{equation}
$$
And the second is:
$$
begin{equation}
3x=3y+9
end{equation}
$$
We can start solving the equations by expressing $x$ from equation (1) and we can do that by dividing the whole equation (1) by $2$.
$$
begin{equation}
x=2y- frac{3}{2}
end{equation}
$$
Now we can take that $x$ and implement it in the equation (2).
$$
begin{equation}
3(2y- frac{3}{2})=3y+9
end{equation}
$$
We can divide the whole equation (4) by $3$.
$$
begin{equation}
2y- frac{3}{2}=y+3
end{equation}
$$
To find $y$ from equation (5) we must put all the parts of the equation with $y$ on the left hand side and all the others on the right hand side.
$$
begin{equation}
2y-y=3+ frac{3}{2}
end{equation}
$$
From that we can see that:
$$
begin{equation}
y= frac{9}{2}
end{equation}
$$
Now we can take that $y$ and return it to the equation (1) to find $x$.
$$
begin{equation}
2x=4 frac{9}{2}-3
end{equation}
$$
We just have to divide equation (8) by $2$ and we get the solution to the $x$.
$$
begin{equation}
x=9- frac {3}{2}
end{equation}
$$
$$
begin{equation}
x=frac{15}{2}
end{equation}
$$
y=4.5
$$
begin{align*}
g(x)&=(x+1)^{2} \
end{align*}
$$
$$
begin{align*}
g(x)&=(x+1)^{2}\
g(5)&=(5+1)^{2}\
g(5)&=(6)^{2}\
g(5)&=36 \
end{align*}
$$
Therefore the value of g$(5)$ is $36$.
$$
begin{align*}
g(x)&=(x+1)^{2}\
g(2m+4)&=(2m+4+1)^{2}\
g(2m+4)&=(2m+5)^{2} \
g(2m+4)&=4m^{2}+20m+25\
end{align*}
$$
Therefore the value of g$(2m+4)$ is $4m^{2}+20m+25$.
$$
begin{align*}
g(x)&=(x+1)^{2}\
9&=x^{2}+2x+1 \
9&=x^{2}+x+x+1\
9&=x(x+1)+1(x+1)\
x&=-1,-1\
end{align*}
$$
Therefore the value of g$(x) = 9$ is $x = -1,-1$.
$$
begin{align*}
& y=x^{2}+4x+6\
& x^{2}+6x+y^{2}-8y=0\
end{align*}
$$
$$
begin{align*}
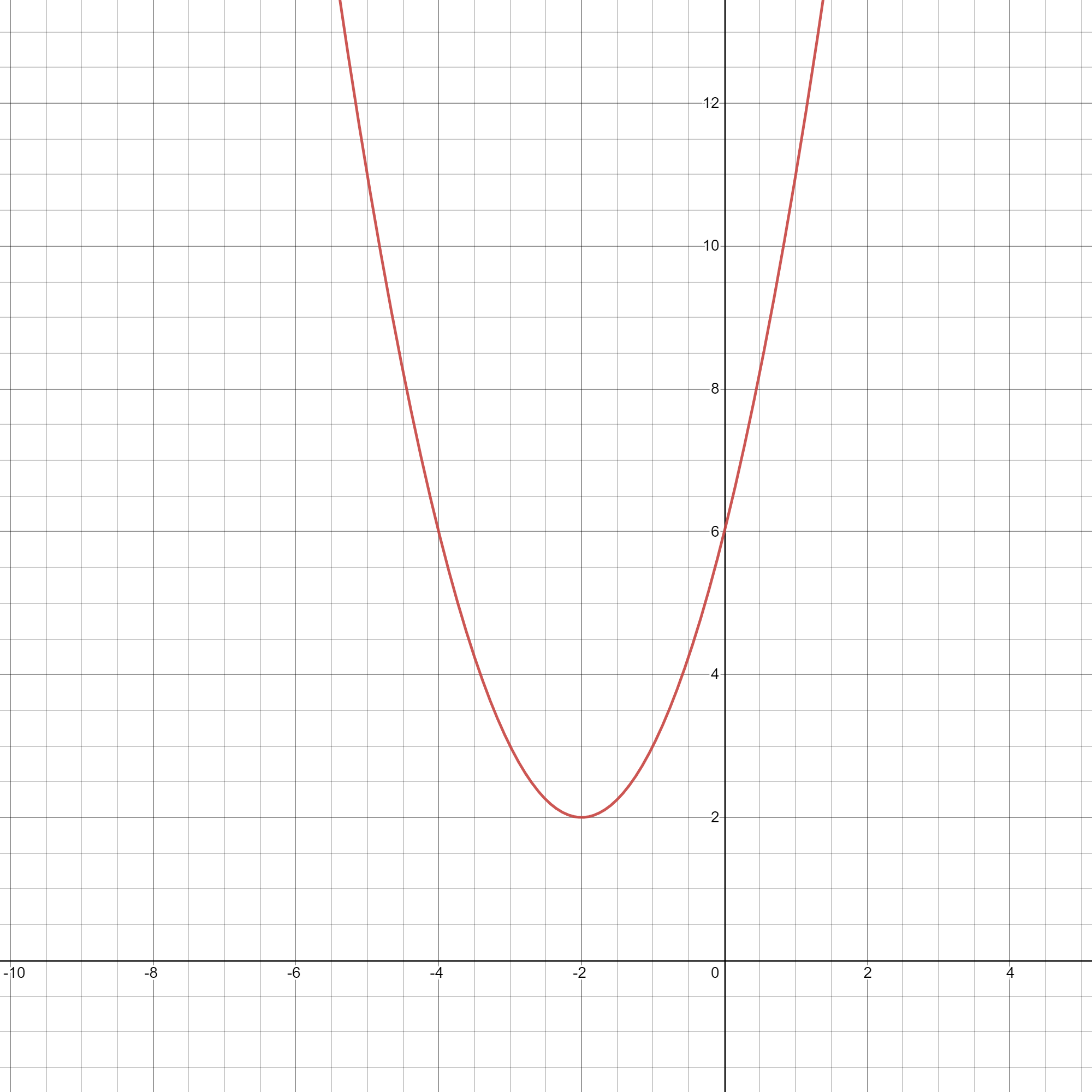
y&=x^{2}+4x+6\
y&=(x^{2}+4)+2 \
end{align*}
$$
Therefore the equation describes a parabola with vertex $(-2,2)$.
$$
begin{align*}
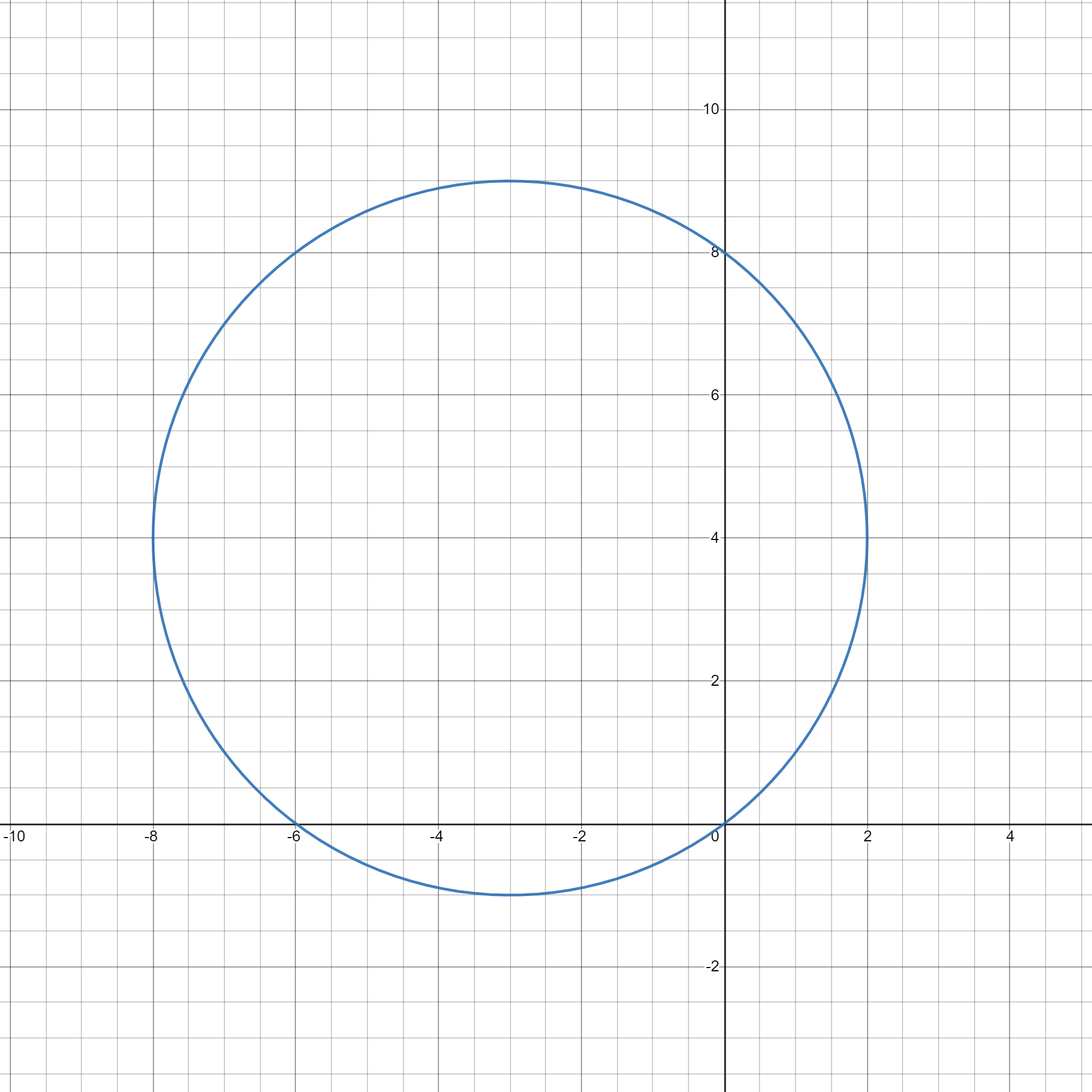
x^{2}+6x+y^{2}-8y&=0\
(x^{2}+6x+9)+(y^{2}-8y+16)&=0+9+16\
(x+3)^{2}+(y-4)^{2}&=25\
& text{Center}:(-3,4)\
& text{Radius}= sqrt{25}\
& text{Radius}= 5\end{align*}
$$
Therefore the equation describes a circle with center $(-3,4)$ and radius $5$.


$$begin{aligned}
y leq 4x+16tag1\
end{aligned}$$
$$begin{aligned}
y > dfrac{-4}{3} x – 4tag2\
end{aligned}$$
$$begin{aligned}
y &=4x+16\ \
y &= dfrac{-4}{3} x – 4\\
end{aligned}$$

For equation (1).
$$begin{aligned}
y leq 4x+16\\
0 leq 16\
end{aligned}$$
For equation (2).
$$begin{aligned}
y > dfrac{-4}{3} x – 4\\
0 > – 4\
end{aligned}$$
Both equations hold true for the given inequality.
So, shade the half-plane in the linear inequality graph, which includes the point (0,0).

$$begin{aligned}
y < x^{2} -2x – 3tag1\
end{aligned}$$
$$begin{aligned}
y leq dfrac{3}{4} x + 2tag2\
end{aligned}$$
$$begin{aligned}
y &= x^{2} – 2x – 3\\
y &= dfrac{3}{4} x + 2\\
end{aligned}$$

For equation (1).
$$begin{aligned}
y < x^{2} -2x – 3\\
0 < -3\
end{aligned}$$
For equation (2).
$$begin{aligned}
y leq dfrac{3}{4} x + 2\\
0 leq 2\
end{aligned}$$
Equation (1) doesn't hold true for the given inequality but equation (2) holds true for the given inequality.
So, doesn't shade the half-plane in the linear inequality graph, which doesn't include the point (0,0) $but$ shade the half-plane in the linear inequality graph, which includes the point (0,0)

$$
begin{align*}
&a. 3(2x-1)^{2}+12=4x-3\
&b. sqrt{3x+1}-x=-3\
&c. dfrac{3}{4}x^{2}=dfrac{5}{4}x+dfrac{1}{2} \
&d. 4x(x-2)=(2x+1)(2x-3) \
end{align*}
$$
$$
begin{align*}
3(2x-1)^{2}+12&=4x-3\
3(2x-1)^{2}+12-4x+3&=0\
3(4x^{2}-4x+1)+15-4x&=0\
12x^{2}-12x+3+15-4x&=0\
12x^{2}-16x+18&=0\
2(6x^{2}-8x+9)&=0\
6x^{2}-8x+9&=dfrac{0}{2}\
6x^{2}-8x+9&=0\
end{align*}
$$
$$
begin{align*}
x&=dfrac{8pm sqrt{(-8)^{2}-(6)(9)}}{2(6)} \
x&=dfrac{8pm sqrt{-152}}{12}\
x&=dfrac{8pm 2sqrt{-38}}{12}\
x&=dfrac{8pm 2sqrt{38i}}{12}\
x&=dfrac{2(4pm sqrt{38i})}{12}\
x&=dfrac{4pm sqrt{38i}}{6}\
x&=dfrac{4+ 2sqrt{-38}}{12},dfrac{4- 2sqrt{-38}}{12}\
end{align*}
$$
Therfore the value of $x$ is $dfrac{4+ 2sqrt{38i}}{12},dfrac{4- 2sqrt{38i}}{12}$.
$$
begin{align*}
sqrt{3x+1}-x&=-3\
sqrt{3x+1}&=x-3\
end{align*}
$$
Thus, the domain of the function is,
$$
begin{align*}
&3x+1 geq 0 = x geq -dfrac{1}{3}\
&x-3 geq 0 = x geq 3 \
end{align*}
$$
So, the domain of the function is $x = [3,infty)$.
$$
begin{align*}
(sqrt{3x+1})^{2}&=(x-3)^{2}\
3x+1&=x^{2}-6x+9\
x^{2}-6x+9-3x-1&=0\
x^{2}-9x+8&=0\
x^{2}-x-8x+8&=0\
x(x-1)-8(x-1)&=0\
(x-1)(x-8)&=0\
x&=1,8\
end{align*}
$$
Thus the value of $x$ is $8$ as $8$ belongs to the equation’s domain.
$$
begin{align*}
dfrac{3}{4}x^{2}&=dfrac{5}{4}x+dfrac{1}{2} \
dfrac{3}{4}x^{2}&=dfrac{5x+2}{4}\
3x^{2}&=5x+2\
end{align*}
$$
$$
begin{align*}
3x^{2}&=5x+2\
3x^{2}-5x-2&=0\
3x^{2}-6x+x-2&=0\
3x(x-2)+1(x-2)&=0\
(3x+1)(x-2)&=0 \
x&=-dfrac{1}{3},2\
end{align*}
$$
Therefore the value of $x$ is $-dfrac{1}{3},2$.
$$
begin{align*}
4x(x-2)&=(2x+1)(2x-3)\
4x^{2}-8x&=4x^{2}-6x+2x-3 \
4x^{2}-8x&=4x^{2}-4x-3\
end{align*}
$$
$$
begin{align*}
4x^{2}-8x-4x^{2}+8x&=4x^{2}-4x-3-4x^{2}+8x \
0&=4x-3\
4x&=3\
x&=dfrac{3}{4}\
end{align*}
$$
Therefore the value of $x$ is $dfrac{3}{4}$.
In order to show the relationship between the number of students in a school and the average number of classrooms required graphically, we will conclude the data.
$textbf{ Case 1}$:
” If the number of students is under 36 i.e. 1,2,3,4,…. 36″
$$begin{aligned}
&boxed{f(x)= 1, 0<xleq 36}rightarrow(1)\
end{aligned}$$
where $x$ is an integer.
” If the number of students is more than 36 i.e. 37,38,39…..72″
$$begin{aligned}
&boxed{f(x)= 2, 36<xleq 72}rightarrow(2)\
end{aligned}$$
where $x$ is an integer.
” If the number of students is more than 72 i.e. 72,73,74…….108″
$$begin{aligned}
&boxed{f(x)= 3, 72<xleq 108}rightarrow(3)\
end{aligned}$$
where $x$ is an integer.

$$
begin{align*}
&a. y=x^{3}+x\
&b. y=6x^{2}-x\
&c. y=x^{4}+3x^{2}\
end{align*}
$$
$$
begin{align*}
y&=x^{3}+x\
f(x)&=x^{3}+x\
f(-x)&=(-x)^{3}-x\
f(-x)&=-x^{3}-x\
f(-x)&=-(x^{3}+x)\
-f(x)&=-(x^{3}+x)\
end{align*}
$$
Thus, the given function is an even function.
$$
begin{align*}
y&=6x^{2}-x\
f(x)&=6x^{2}-x\
f(-x)&=6(-x)^{2}-(-x)\
f(-x)&=6x^{2}+x\
f(x)&ne6x^{2}+x\
-f(x)&ne6x^{2}+x\
end{align*}
$$
Thus, the given function is neither odd nor even.
$$
begin{align*}
y&=x^{4}+3x^{2}\
f(x)&=x^{4}+3x^{2}\
f(-x)&=(-x)^{4}+3(-x)^{2}\
f(-x)&=x^{4}+3x^{2}\
f(x)&=x^{4}+3x^{2}\
end{align*}
$$
Thus, the given function is odd.
1. Check your answers using the table at the end of this section.
2. Construct a table in your Learning Log.
3. Write a list of topics you need help on.
4. Write a list of topics you need to practice more.

