Given,

$a$.

$$
begin{align*}
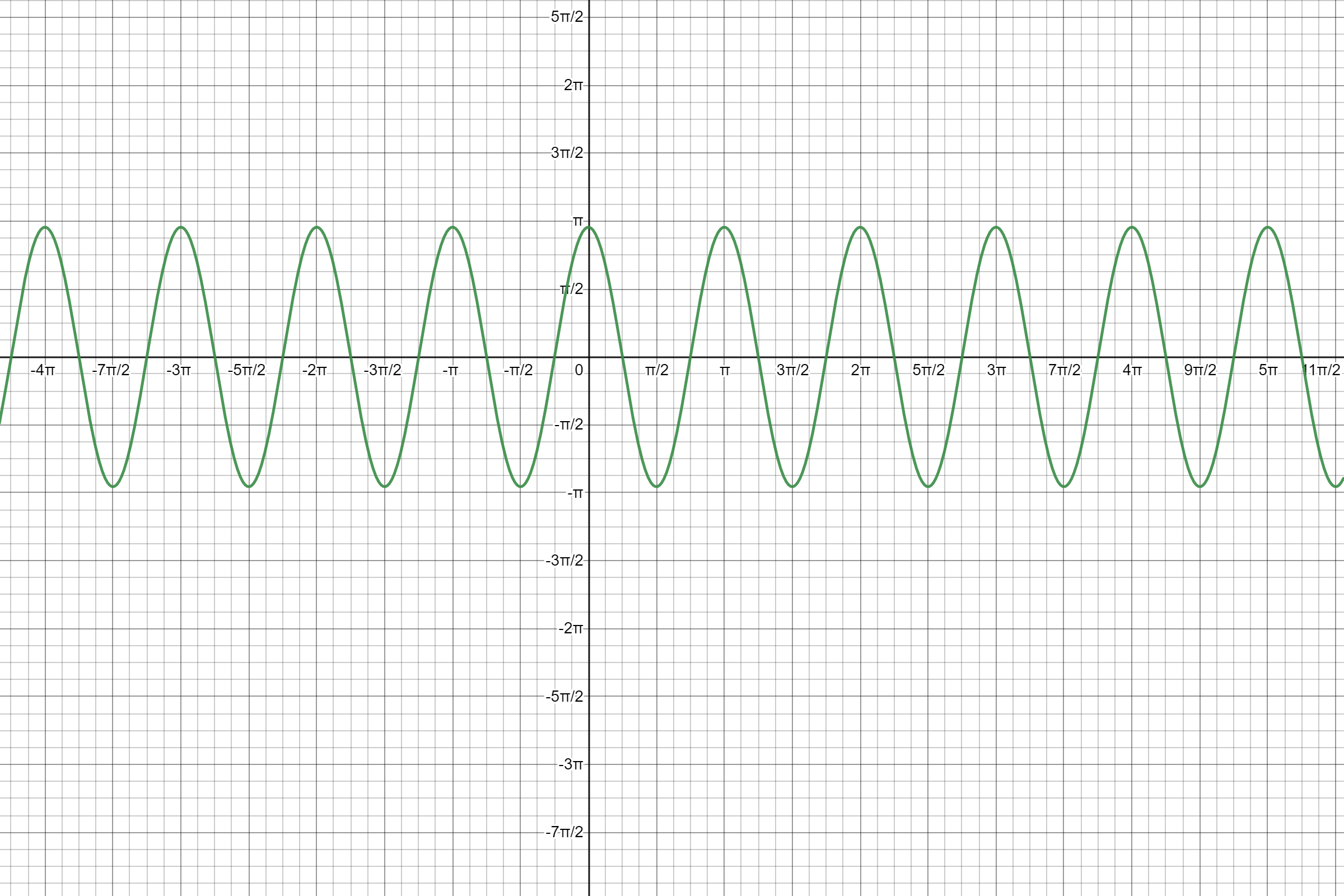
y = 3cdot cos(2x) tag{1} \
end{align*}
$$

Since we know that the amplitude and period of a function $y = A cdot cos(Bx)$ is given by,

$$
begin{align*}
text{Amplitude} & = A \
text{ Period} & = dfrac{2pi}{B}\
end{align*}
$$

Comparing $(1)$ with the general form, $A = 3$ and $B = 2$. Thus, the amplitude and the period of the given function are given as follows.

$$
begin{align*}
text{Amplitude} & = 3 \
text{ Period} & = dfrac{2pi}{2}\
& = pi\
end{align*}
$$

Sketching the graph of $(1)$.

Given,

$b$.

$$
begin{align*}
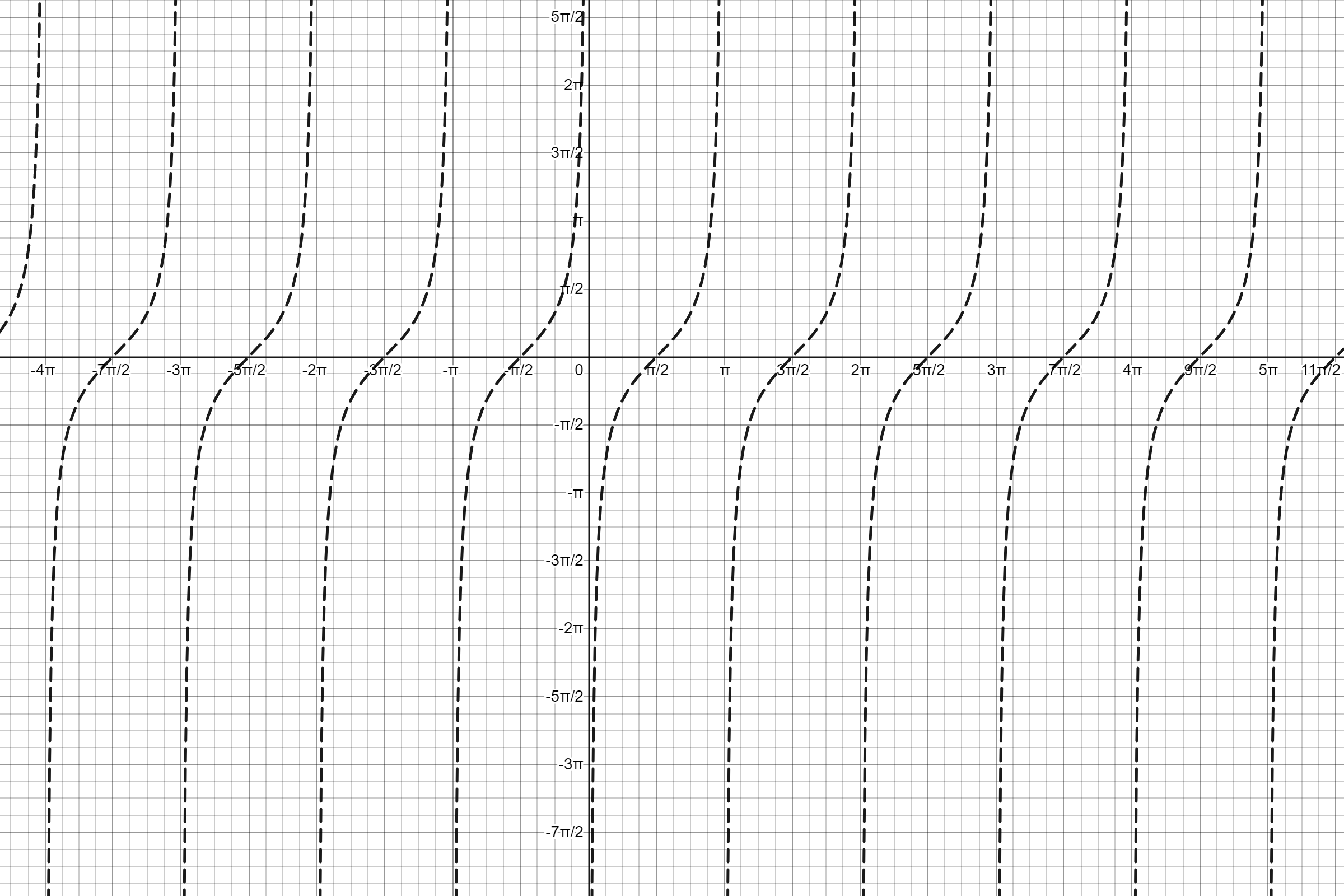
y = 3cdot tan(x- dfrac{pi}{2}) tag{2}\
end{align*}
$$

Since we know that the tangent function does not have any amplitude. So, the period of a function $y = A cdot tan(Bx)$ is given by,

$$
begin{align*}
text{ Period} & = dfrac{pi}{left|Bright|} \
end{align*}
$$

Comparing $(1)$ with the general form,$B = 1$. Thus, the period of the given function is given as follows.

$$
begin{align*}
text{ Period} & = dfrac{pi}{left|1right|}\
& = pi\
end{align*}
$$

Sketching the graph of $(2)$.

The equation of a goniometric function is $y=asin{b(x-c)}+d$ where $a$ is the amplitude (difference between maximum and minimum, divided by 2), $b$ is $dfrac{2pi}{p}$ with $p$ the period of the function and $(c,d)$ is the locator point (starting point of a cycle).

a. $f(x)=sin{x+dfrac{pi}{2}}$ (period $2pi$)

b. $f(x)=sin{x-pi}-3$ (period $2pi$)

c. $f(x)=5sin{4x}$ (period $dfrac{pi}{2}$)

d. $f(x)=sin{dfrac{1}{3}left( x-dfrac{pi}{2}right)}$ (period $6pi$)

a. $f(x)=sin{x+dfrac{pi}{2}}$

b. $f(x)=sin{x-pi}-3$

c. $f(x)=5sin{4x}$

d. $f(x)=sin{dfrac{1}{3}left( x-dfrac{pi}{2}right)}$

Given ,

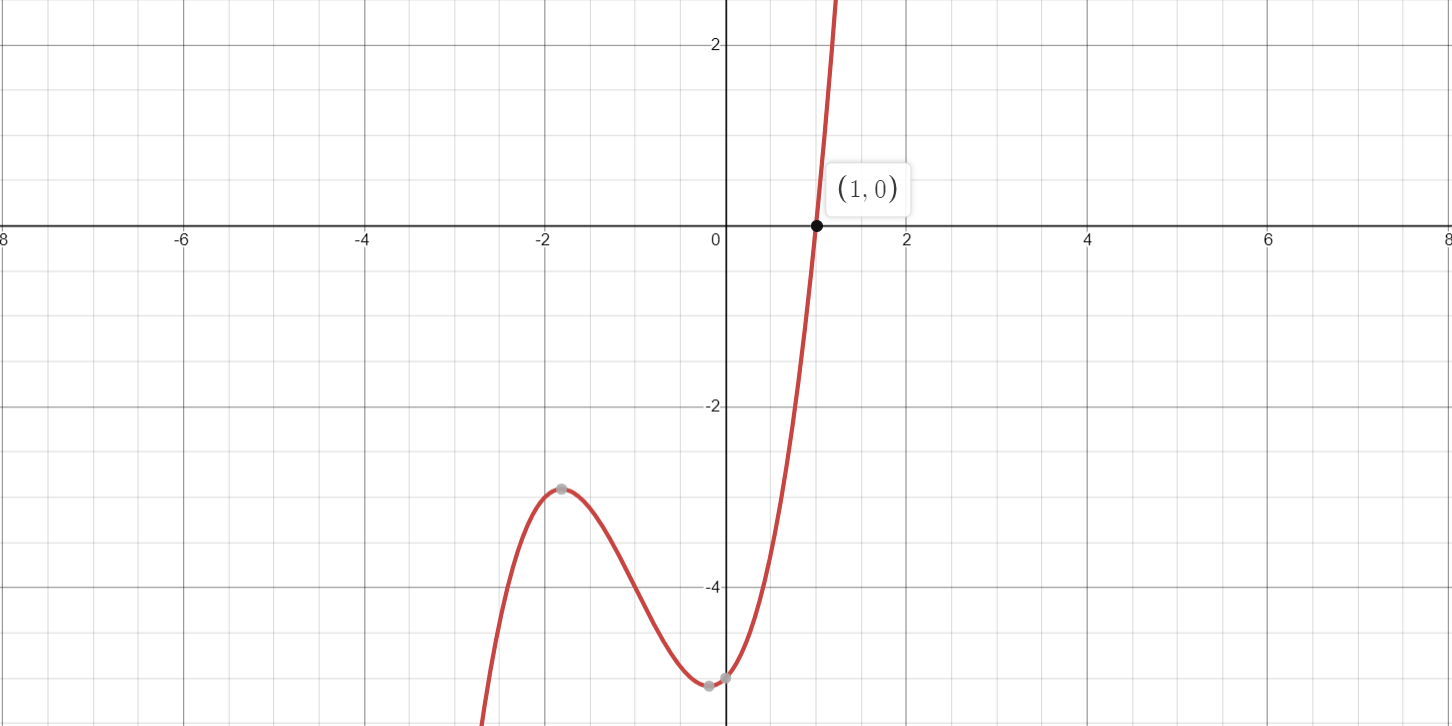
$f( x) = x^{3} + 3x^{2} + x – 5$
Graph of $f(x)$ we can have a point that will satisfy the given function.

From the given graph, we can have a zero of $f( x)$ i.e. $x = 1$ and it will satisfy the given function. Mathematically which can be justified as follows,

$$
begin{align*}
f(x) &= x^{3} + 3x^{2} + x – 5\
f(1) & = (1)^{3} + 3 (1)^{2} + 1 – 5 \
&= 1 + 3 + 1 -5 \
&= 0 \
end{align*}
$$

According to the remainder theorem, we can say that $(x – 1)$ is the factor of the polynomial.

Dividing $f( x)$ by the linear factor $(x – 1)$ in order to have other two zeroes.\

$
begin{array}{ccccccccccccccccccccc}
&&&&&&x^2 &+4x&+5&\
cline{3-10}
multicolumn{2}{r}{x – 1surd}
&x^3 & &+3x^2&+x&- 5& \
& &x^3& &+x^2& & & & \
cline{3-7}
&&&&4x^2&+x&-5& \
&&&&4x^2&+4x&& \
cline{4-8}
&&&&&5x&-5& \
&&&&&5x&+5& \
cline{5-9}
cline{6-10}
end{array}
$

Thus, we can describe $f(x)$ as,

$$
begin{align*}
f(x) &= (x-1) (x^{2} + 4x + 5)\
end{align*}
$$

Solving $x^{2} + 4x + 5$ separately,

$$
begin{align*}
&= (x^{2}+ 4x + (2)^{2} – (2)^{2} + 5) left[text{ Using Completing the square method}right]\
&= (x+2)^{2} + (1)^{2}\
-1&= (x + 2)^{2}\
-1&= (x + 2)^{2} \
i^{2}&= (x+2)^{2} left[-1 = i^{2}right]\
end{align*}
$$

Taking square root both sides, we get

$$
begin{align*}
i &= +(x+ 2)\
x&= -2 + i \
text{ or}\
i&= – (x + 2)\
x&= -2 – i\
end{align*}
$$

$1$ ; $-2 + i$ ; $-2 – i$

a. Since the first term is 3 and the consecutive terms increase by 3:

$$
sum_{n=1}^{10} (3+3(n-1))=sum_{n=1}^{10}(3n)
$$

b. Since the first term is $-7$ and the consecutive terms increase by 3:

$$
sum_{n=1}^{7} (-7+3(n-1))=sum_{n=1}^{7}(-10+3n)
$$

a. $sum_{n=1}^{10}(3n)$

b. $sum_{n=1}^{7}(-10+3n)$

a. Geometric, because it has a common ratio of $r=-dfrac{2}{3}$.

b. No, because the upper boundary of the sum is $infty$.

c. Since $r<1$, the sum will exist. The infinite sum of a geometric sequence is

$$
dfrac{a}{1-r}
$$

with $a$ the first term and $r$ the common ratio.

Thus we then obtain:

$$
S=dfrac{4}{1+dfrac{2}{3}}=dfrac{12}{5}=2.4
$$

a. Geometric

b. No

c. $dfrac{12}{5}$

a. The number of terms is the difference between the first and last term divided by the common difference and increased by 1:

$$
dfrac{63-3}{0.3}+1=200+1=201
$$

b. The sum of an arithmetic sequence is the sum of the first and last term, multiplied by the number of terms, divided by 2:

$$
dfrac{(3+63)201}{2}=6,633
$$

The sum of a geometric sequence is given by
$$
adfrac{1-r^n}{1-r}
$$

with $a$ the first term and $r$ the common ratio and $n$ the number of terms:

$$
20dfrac{1-(0.7)^5}{1-0.7}=55.462
$$

a-

$dfrac {27}{sin {40}}=dfrac {x}{sin {30}}$          (The law of sins)

$dfrac {27}{0.6428}=dfrac {x}{0.5}$

$x=0.5 cdot dfrac {27}{0.6428}$

$$
x approx 21
$$

b-

The missing angle of the triangle is: $180-(27+39)=114 text{textdegree}$

$dfrac {81}{sin {39}}=dfrac {x}{sin {114}}$          (The law of sins)

$dfrac {81}{0.6293}=dfrac {x}{0.9135}$

$x=0.9135 cdot dfrac {81}{0.6293}$

$$
x approx 117.58
$$

a-          $x approx 21$

b-          $x approx 117.58$

Given ,

$$
begin{align*}
cos(alpha) & = dfrac{5}{13}\
end{align*}
$$

Also, the range is $dfrac{3pi}{2}$ $leq$ $alpha$ $leq$ $2pi$. The range explains fourth quadrant.

The values of other trigonometric ratio is given as follows,

Using Identity $sin^{2}(x) + cos^{2}(x) = 1$. Thus, value of $sin$ $alpha$ is given as follows,

$$
begin{align*}
sin (alpha) &= sqrt{left[1-left(dfrac{5}{13}right)^{2}right]}\\
&=sqrt{1- dfrac{25}{169}} \\
&= sqrt{dfrac{169-25}{169}} \\
&= sqrt{dfrac{144}{169}} \\
&= +dfrac{12}{13} (text{ ignoring because of IV quadrant})\\
&= – dfrac{12}{13}\\
end{align*}
$$

Thus, $sin(alpha) = -dfrac{12}{13}$.

Since , we know that $cosec(x) = dfrac{1}{sin( x)}$ and $sec(x) = dfrac{1}{cos(x)}$.

Thus,

$$
begin{align*}
cosec (alpha) &= -dfrac{13}{12} \
end{align*}
$$

And,

$$
begin{align*}
sec (alpha) &= dfrac{13}{5} \
end{align*}
$$

And , $tan(x) = dfrac{sin( x)}{cos(x)}$ and $cot (x) = dfrac{1}{tan(x)}$.

$$
begin{align*}
tan (alpha) & = dfrac{-dfrac{12}{13}}{dfrac{5}{13}}\\
tan ( alpha) & = -dfrac{12}{5} \
end{align*}
$$

Also,

$$
begin{align*}
cot (alpha) & = – dfrac{5}{12}\
end{align*}
$$