All Solutions
Page 259: Closure Activity


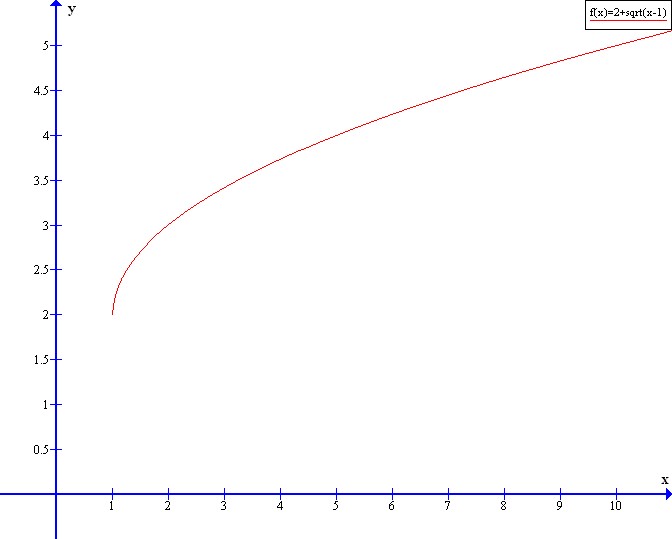
x=2+sqrt{f^{-1}(x)-1}
$$
(x-2)^{2}+1=f^{-1}(x)
$$
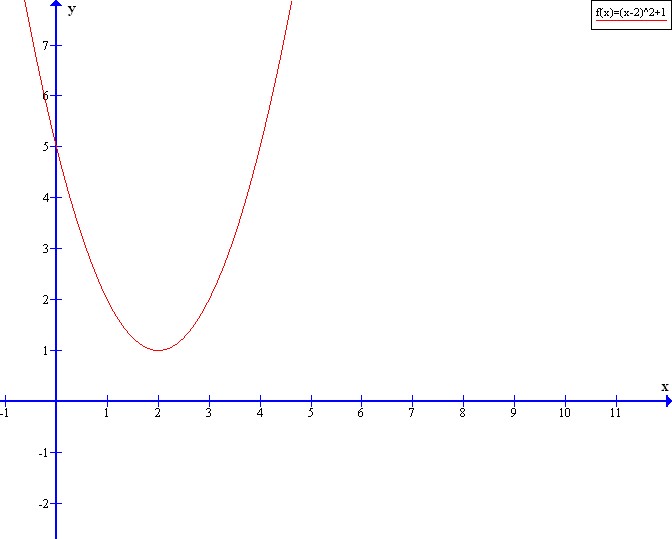
f^{-1}(f(5))=f^{-1}(4)=(4-2)^{2}+1=5
$$
(c)
$$
f(f^{-1}(5))=f(10)=2+sqrt{10-1}=5
$$
(d)
$$
So, if
$$
begin{equation}
y=b^x
end{equation}
$$
And
$$
begin{equation}
x=log_b(y)
end{equation}
$$
Then
$$
begin{equation}
64=8^x
end{equation}
$$
Now the question is which exponent we have to use to get $64$ from $8$ and the answer is clearly $2$ because $8^2=64$.
If we go by the same principle from equations (1) and (2) from problem a) just with reversed $x$ and $y$ we get:
$$
begin{equation}
9^frac{1}{2}=x
end{equation}
$$
We can also write equation (1) like this:
$$
begin{equation}
sqrt{9}=x
end{equation}
$$
Now we can easily see that $x=3$, because square root of $9$ is $3$.
Again by the same principle from a):
$$
begin{equation}
3^4=3^x
end{equation}
$$
From equation (1) we can conclude that $x=4$, because for to left hand side of the equation and the right hand one to be equal exponents must be equal.
$$
begin{equation}
log_{10}4=log_{10}x
end{equation}
$$
$$
begin{equation}
x=4
end{equation}
$$
From problem c) we can conclude that if the base of the logarithm and the number (without the exponent) on which we are performing the function are equal than the solution to the equation is equal to the exponent.
$$
begin{equation}
log_a(b^c)=x
end{equation}
$$
So if $a=b$ than $x=c$.
From problem d) we can conclude that if the base of the logarithm in the exponent of a number and that number are equal, than the solution to the equation is equal to the number on which we are performing the log function.
$$
begin{equation}
a^{log_b(c)}=x
end{equation}
$$
So again if $a=b$ than $x=c$.
b) $x=3$
c) $x=4$
d) $x=4$
$$
color{#c34632}{Z = frac {X-M}{s}}
$$
where
$X$ – the values after upgrade
$M$ – the average
$s$ – the standard deviation
$star$ Model $760$:
$$
begin{align*}
X &= 90\
M &= 76\
s &= 11
end{align*}
$$
we have
$$
begin{align*}
Z &= frac {90-76}{11}\
Z &= frac {14}{11}\
Z &= 1.27
end{align*}
$$
$star$ Model $S22$:
$$
begin{align*}
X &= 57\
M &= 50\
s &= 5
end{align*}
$$
we have
$$
begin{align*}
Z &= frac {57-50}{5}\
Z &= frac 75\
Z &= 1.4
end{align*}
$$
Since $1.27<1.4$ we can conclude that for the Model $S22$ the upgrade had a grater impact.
y=dfrac{2x}{3}-5
$$
y=(x+dfrac{1}{2})^{2}-6
$$
(x-1)^{2}+(y-4)^{2}=16
$$
1. Check your answers using the table at the end of this section.
2. Construct a table in your Learning Log.
3. Write a list of topics you need help on.
4. Write a list of topics you need to practice more.

