Home Page Textbooks Core Connections Integrated 3 Page 605: Closure Activity

Core Connections Integrated 3

1st Edition

Brian Hoey, Judy Kysh, Leslie Dietiker, Tom Sallee

ISBN: 9781603283939

Textbook solutions

All Solutions

Page 605: Closure Activity

Exercise 114

Step 1

1 of 2

#### (a)

If we solve quadratic equations which are in this fraction, we will get the following:

$$
dfrac{2x^2-5x-3}{3x^2-11x+6}=dfrac{2left(x+tfrac{1}{2} right)(x-3)}{3left(x-tfrac{2}{3} right)(x-3)}=dfrac{(2x+1)}{(3x-2)}cdotdfrac{x-3}{x-3}=dfrac{2x+1}{3x-2}cdot1=dfrac{2x+1}{3x-2}
$$

#### (b)

We will simplify this expression in the following way:

$$
dfrac{x^3-8}{4x^3-3x^2-10x}=dfrac{(x-2)(x^2+2x+4)}{x(4x^2-3x-10)}=dfrac{(x-2)(x^2+2x+4)}{x(4x+5)(x-2)}=dfrac{x^2+2x+4}{x(4x+5)}
$$

Result

2 of 2

a) $dfrac{2x+1}{3x-2}$; b) $dfrac{x^2+2x+4}{x(4x+5)}$

Exercise 115

Step 1

1 of 2

#### (a)

We will simplify the given expression in the following way:

$$
dfrac{x^2-x-6}{x^2-9}cdotdfrac{x^2+5x+6}{x^2+4x+4}=dfrac{(x-3)(x+2)}{(x-3)(x+3)}cdotdfrac{(x+3)(x+2)}{(x+2)^2}=1, x=pm 3, xne -2
$$

#### (b)

We will simplify this expression in the following way:

$$
dfrac{x^2-1}{x}cdotdfrac{2x^2+x}{x^2-2x+1}=dfrac{(x-1)(x+1)}{x}cdotdfrac{x(2x+1)}{(x-1)^2}=dfrac{(x+1)(2x+1)}{x-1}, xne 0, xne 1
$$

Result

2 of 2

a) $1, x=pm 3, xne -2$; b) $dfrac{(x+1)(2x+1)}{x-1}, xne 0, xne 1$

Exercise 116

Step 1

1 of 7

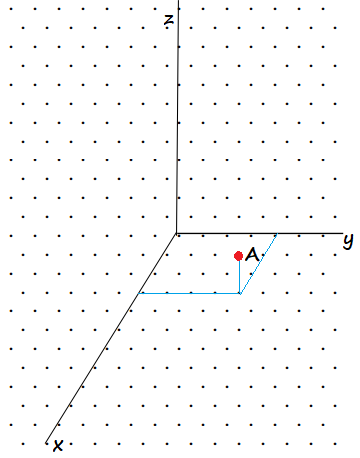
$$
A(3,4,2)
$$

a) We are given the point:

Step 2

2 of 7

We graph the point:

Step 3

3 of 7

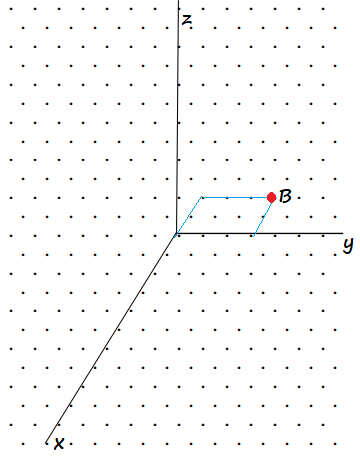
$$
B(-2,3,0)
$$

b) We are given the point:

Step 4

4 of 7

We graph the point:

Step 5

5 of 7

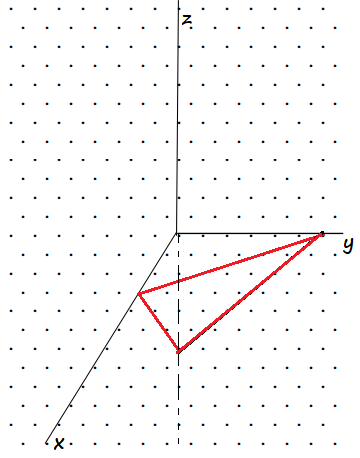
$$
2x+y-z=6
$$

c) We are given the plane:

Step 6

6 of 7

$y=0,z=0Rightarrow 2x=6Rightarrow x=3$

$z=0,x=0Rightarrow y=6$

$x=0,y=0Rightarrow -z=6Rightarrow z=-6$

We determine its intercepts with the axis:

Step 7

7 of 7

We graph the plane:

Exercise 117

Step 1

1 of 3

$$
left(2m+dfrac{1}{m}right)^4
$$

We are given the expansion:

Step 2

2 of 3

$n=4$

$a=2m$

$b=dfrac{1}{m}=m^{-1}$

$(2m+m^{-1})^4$

$=_4C_0(2m)^4+_4C_1(2m)^3(m^{-1})^1+_4C_2(2m)^2(m^{-1})^2+_4C_3(2m)^1(m^{-1})^3+_4C_4(m^{-1})^4$

$=16m^4+dfrac{4!}{3!1!}(8m^3)(m^{-1})+dfrac{4!}{2!2!}(4m^2)(m^{-2})+dfrac{4!}{1!3!}(2m)(m^{-3})+m^{-4}$

$=16m^4+dfrac{3!cdot 4}{3!cdot 1}(8m^2)+dfrac{2!cdot 3cdot 4}{2!cdot 1cdot 2}(4)+dfrac{3!cdot 4}{1cdot 3!}(2m^{-2})+m^{-4}$

$=16m^4+32m^2+24+8m^{-2}+m^{-4}$

$=16m^4+32m^2+24+dfrac{8}{m^2}+dfrac{1}{m^4}$

We expand using the Binomial Theorem:

$(a+b)^n=_nC_0a^n+_nC_qa^{n-1}b^1+_nC_2a^{n-2}b^2+…+_nC_{n-1}a^1b^{n-1}+_nC_nb^n$.

Result

3 of 3

$$
16m^4+32m^2+24+dfrac{8}{m^2}+dfrac{1}{m^4}
$$

Exercise 118

Step 1

1 of 7

We are given:

Step 2

2 of 7

$x_1=-2$

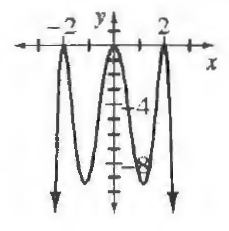
$x_2=0$

$$
x_3=2
$$

The graph touches the $x$-axis 3 times, therefore it has 3 double real roots:

Step 3

3 of 7

$$
f(x)=a(x+2)^2x^2(x-2)^2
$$

The function has the form:

Step 4

4 of 7

As both ends go down, the function has a negative leading coefficient.

Step 5

5 of 7

$a(1+2)^2(1^2)(1-2)^2=-9$

$9a=-9$

$$
a=-1
$$

In order to determine $a$we use the fact that $f(1)approx-9$:

Step 6

6 of 7

$$
f(x)=-x^2(x-2)^2(x+2)^2
$$

The equation of the function can be:

Result

7 of 7

$$
f(x)=-x^2(x-2)^2(x+2)^2
$$

Exercise 119

Step 1

1 of 5

$P=3000$

$A=4000$

$$
t=10
$$

a) We are given:

Step 2

2 of 5

$A=Pe^{rt}$

$4000=3000e^{10r}$

$e^{10r}=dfrac{4000}{3000}$

$e^{10r}=dfrac{4}{3}$

$ln (e^{10r})=ln (dfrac{4}{3})$

$10r=ln (dfrac{4}{3})$

$r=dfrac{ln (dfrac{4}{3})}{10}$

$rapprox 0.0287=2.87%$

We determine the rate $r$:

Step 3

3 of 5

$P=3000$

$A=4000$

$r=0.0275$

$$
n=4
$$

b) We are given:

Step 4

4 of 5

$A=Pleft(1+dfrac{r}{n}right)^{nt}$

$4000=3000left(1+dfrac{0.0275}{4}right)^{4t}$

$dfrac{4000}{3000}=(1.006875)^{4t}$

$dfrac{4}{3}=(1.006875)^{4t}$

$ln (dfrac{4}{3})=ln (1.006875)^{4t}$

$ln (dfrac{4}{3})=4tln (1.006875)$

$t=dfrac{ln (dfrac{4}{3})}{4ln (1.006875)}$

$tapprox 10.5$ years

We determine the number of years $t$ until $A=4000$:

Result

5 of 5

a) $0.0287=2.87%$

b) $10.5$ years

Exercise 120

Step 1

1 of 8

a) We are given the triangle:

Step 2

2 of 8

$x^2+20^2=29^2$

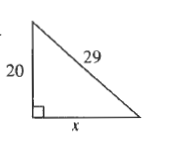
$x^2=841-400$

$x^2=441$

$x=sqrt{441}$

$$
x=21
$$

As the triangle is a right triangle, we use the Pythagorean Theorem:

Step 3

3 of 8

b) We are given the triangle:

Step 4

4 of 8

$dfrac{sin 45text{textdegree}}{x}=dfrac{sin 30text{textdegree}}{25sqrt 2}$

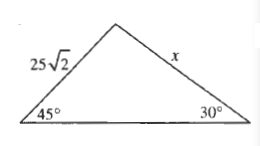
$25sqrt 2sin 45text{textdegree}=xsin 30text{textdegree}$

$x=dfrac{25sqrt 2cdot dfrac{sqrt 2}{2}}{dfrac{1}{2}}$

$x=dfrac{25}{dfrac{1}{2}}$

$x=25cdot 2$

$$
x=50
$$

We use the Law of Sines:

Step 5

5 of 8

c) We are given the triangle:

Step 6

6 of 8

$37^2=20^2+x^2-2cdot 20cdot xcdotcos 120text{textdegree}$

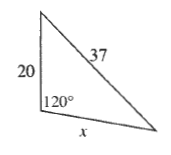
$1369=400+x^2-40xcdot left(-dfrac{1}{2}right)$

$x^2+20x+400-1369=0$

$(x^2+20x+100)-1069=0$

$(x+10)^2=1069$

$x+10pmsqrt{1069}$

$x+10=pm 32.7$

$x+10=-32.7Rightarrow x_1=-42.7$

$x+10=32.7Rightarrow x_2=22.7$

We use the Law of Cosines:

Step 7

7 of 8

Only the positive value fits.

Result

8 of 8

a) $21$;

b) $50$

c) $22.7$

Exercise 121

Step 1

1 of 2

a. The graph is the graph of $y=sin{x}$ stretched vertically by factor 3, stretched horizontally by factor $dfrac{1}{2}$, translated to the right over $dfrac{pi}{4}$ units and translated up by 1 units.

Exercise scan

Step 2

2 of 2

b. The graph is the graph of $y=cos{x}$ stretched vertically by factor $dfrac{1}{2}$, stretched horizontally by factor $4$ and translated to the left by $pi$ units.

Exercise scan

Exercise 122

Step 1

1 of 6

$V(3,3)$

$$
A(7,5)
$$

The curve can represent a parabola, passing through the points:

Step 2

2 of 6

$h=3$

$$
k=3
$$

From the vertex coordinates we determine $h, k$ from the function’s equation:

$y=a(x-h)^2+k$.

Step 3

3 of 6

$$
y=a(x-3)^2+3
$$

The function’s equation has the form:

Step 4

4 of 6

$a(7-3)^2+3=5$

$16a+3=5$

$16a=2$

$a=dfrac{2}{16}$

$$
a=dfrac{1}{8}
$$

We determine $a$ using the point $A$::

Step 5

5 of 6

$$
y=dfrac{1}{8}(x-3)^2+3
$$

The function’s equation is:

Result

6 of 6

$$
y=dfrac{1}{8}(x-3)^2+3
$$

Exercise 123

Step 1

1 of 2

Graphing the periodic functions seems to be the easiest because the equations give us all the information we need for the graph.

Step 2

2 of 2

Expanding binomials by using the Binomial Theorem and simplifying fractions with polynomials seems to be the hardest since there is a lot of work and we need to keep the track of a lot of variables with different degrees.

unlock

All Solutions

Page 605: Closure Activity

Haven't found what you were looking for?

Search for samples, answers to your questions and flashcards