All Solutions
Page 489: Questions
$50, $53, $56, $59, $62, $65, $68, $71, $74, $77, $80, $83
Thus we note that in the 12th month $83 is added to the college fund.
\
\
b. Since the amount starts at 50 at$n=1$and every month the amount increases by 3:$ $a(n)=50+3(n-1)=50+3n-3=47+3n$$
b.$a(n)=47+3n$
The deposits for the first few months are:
50, 53, 56, 59, 62, 65, 68, 71, 74, 77, 80, 83, 86,…..
The deposit added in the 12th month is: $83
The amount deposited in the nth month is:
= 50 + 3(n – 1)
In the first month when n is 1:
Deposit = 50 + 3$times$ (1 – 1) = $50\\
Deposit in the last month after 18 years:\
= 50 + 3$times$(12$times$ 18 – 1) = $695
b) $695
$$
50+3(n-1)=50+3n-3=47+3n
$$
The first form is easier to use for calculations, while the second form is easier to use to determine what had been originally given.
b. Replace $n$ with 12:
$$
t(12)=47+3(12)=47+36=83
$$
c.The fifth bithday is then $5cdot 12=60$ deposits:
$$
t(60)=47+3(60)=47+180=227
$$
b. 83
c. 227
t(n) = 50 + 3(n – 1) = 47 + 3n
Both equations are correct and will give the same result
Angla’s form is abstracted and easily gives the value of a term
Uncle Zakhary’s form is general and gives more details like the first term and the increasing base
The value of the 12th deposit:
= 50 + 3(12 – 1) = $83\
The sum of 12 deposits is:\
S = (50 + 83)$times $dfrac{12}{2}$ = $798$
Think of a series of 5 terms:\
50, 53, 56, 59, 62\
First term is: 50, and last term is: 62\
Inverse the sequence:\
62, 59, 56, 53, 50\
Add each term to its opponent:\
begin{tabular}{ccccc}
50&53&56&59&62\
62&59&56&53&50\
hline
textcolor{red}{112}&textcolor{red}{112}&textcolor{red}{112}&textcolor{red}{112}&textcolor{red}{112}\
end{tabular}\
The result is the same for each two terms:\
So, the sum can be calculated from the following formula:\
S = ($text{a}_{1} + text{a}_{text{n}}) times dfrac{text{n}}{2}$\
Where:\
$text{a}_{1}$ is the first term\
$text{a}_{text{n}}$ is the last term\
n is the number of terms\
So, by Angla’s 5th birthday:\
n = 5 $times$ 12 = 60 terms\
$text{a}_{60} = 50 + 3 times 59 = $227$\
The total fund will be:\
S = (50 + 227) $times$ 30 = $8310
b) $798
c) $8310
The first term of the sequence is: 5
And it increases by 1
So the sequence is:
5, 6, 7, 8, 9, 10, 11, ……..
When the manufacturer wants to calculate
the raw material amount required to make
this toy, in this situation he should
find the sum of its diameters
If it consists of 12 dolls, the series will be:
5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
The sum is:
S = (5 + 16) $times$ 6 = 126 cm
t(n) = 8 + 3(n – 1)
The smallest doll diameter is 8,
And it increases by 3
So, the series is:
8, 11, 14, 17, 20, 23, 26, 29, 32, 35,
38, 41, 44, 47, 50, 53, 56, 59, 62, 65
The line length is the sum of the series:
S = (8 + 65) $times$ 10 = 730 mm
b) 126 cm
c) 730 mm
$$
a(n)=5+1(n-1)=5+n-1=4+n
$$
b. If you place all 5 dolls next to each other what is the combined length of all dolls.
$$
5+6+7+8+9+10=45
$$
c.
$$
8+11+14+17+20+23+26+29+32+35+38+41+44+47+50+53+56+59+62+65=730
$$
Thus the line is 730 mm.
b. See explanation
c. 730 mm
$$
t(n)=1+2(n-1)=1+2n-2=-1+2n
$$
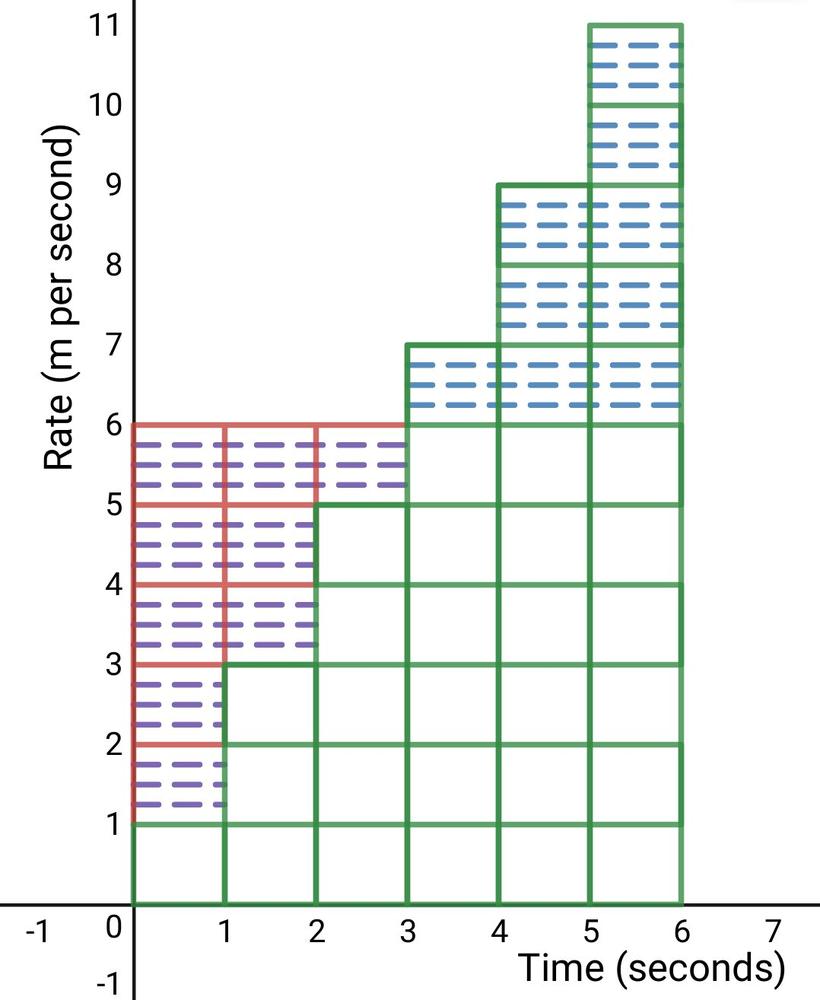
The first term means that during the first second Flo travels 1 m and every second the distance traveled increases by 2 m.
b. The series represents then the total distance traveled during the 6 seconds.
c. The terms are shown by a number of squares equal to the value of the term. The total distance is then represented by all the squares next to each other.
d. You can approximate the area of the squares by approximated it by a trapezium and calculating the area of this trapezium.
b. Total distance traveled during the 6 seconds.
c. The total distance is then represented by all the squares next to each other.
d. Approximate area by trapezium
The first term is the distance traveled in the first second,
In this case it is 1 meter
The common difference is the distance increased every second,
In this case it is 2 meters
And the equation is:
t(n) = 1 + 2(n – 1)
Since, the increasing amount is constant,
So, This is an arithmetic series represents
the distance traveled in meters during
the first six seconds of Flo’s race
The series is represented in a progressive sequence,
For each second on the horizontal axis a rectangle
represents the distance traveled during this second
Rearrange the columns by rotating the up right area
and move it down to the left to form one rectangle
as shown below, the area of the new rectangle is
the sum of the series:
S = 6 $times$ 6 = 36 meters
a.
$$
5cdot 7 = 35
$$
b.
$$
dfrac{(4+10)cdot 16}{2}=320
$$
c.
$$
dfrac{(228+48)cdot 6}{2}=828
$$
d.
$$
dfrac{(14+20)cdot 32}{2}=544
$$
b. 320
c. 828
d. 544
Sum of the series is the rectangle area:
S = 5 $times$ 7 = 35
Sum of the series is the trapezium area:
S = $dfrac{4 + 10}{2} times 16 = 112$
Sum of the series is the trapezium area:
S = $dfrac{48 + 228}{2} times 6 = 828$
Sum of the series is the trapezium area:
S = $dfrac{14 + 20}{2} times 31 = 527$
b) 112
c) 828
d) 527
a. The number of terms is $dfrac{72-18}{4.5}=12$ and the series is $18,22.5,27,31.5,…,72$.
$$
SUM=dfrac{(18+72)cdot 12}{2}=540
$$
b. The common difference is the sum multiplied by 2 divided by the difference last/first term:
$$
dfrac{336cdot 2}{21-6}=44.8
$$
c. It is not possible to determine the series because you need either the first term or the common difference.
d. The first term is than 9 and the last 179: 9,19,29,…,179.
$$
SUM=dfrac{(9+179)cdot 18}{2}=1692
$$
First term is: 18, last term is: 72
and common difference is 4.5
So, the series is:
18, 22.5, 27, 31.5, 36, 40.5, 45, 49.5, 54, 58.5, 63, 67.5, 72
The sum is:
S = (18 + 72) $times dfrac{13}{2} = 585$
Since,
S = (first term + last term) $times dfrac{text{number of terms}}{2}$
So,
336 = (first term + 21) $times dfrac{6}{2}$
First term = 91
Since,
6th term = first term + common difference $times$ (6 – 1)
So,
21 = 91 + common difference $times$ 5
Common difference = – 14
So, the series is:
91, 77, 63, 49, 35, 21
Since,
18 = first term + common difference $times$ (9 – 1)
In this equation there are two unknown values,
So, it is impossible to find such values
Since
S = (first term + 18) $times dfrac{9}{2}$
Again there are two unknown values
So, we need to know at least one more information:
first term, or common difference, to find the sum and the series
29 = first term + 10 $times$ (3 – 1)
First term = 9
So, the series is:
9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 109,
119, 129, 139, 149, 159, 169, 179
And the sum is:
S = (9 + 179) $times dfrac{18}{2} = 1692$
Sum is: 585
b) 91, 77, 63, 49, 35, 21
c) impossible requirements
d) series is: 9, 19, …… , 169, 179
Sum is: 1692
$$
300,550,800,1050,1300,1550,1800,2050,2300,2550,
$$
$$
2800,3050,3300,3550,3800,4050
$$
Thus we note that the last quarter before noon 4050 people have entered.
b. The number of people start at 300 with $n=1$ and increase by 250 every quarter:
$$
t(n)=300+250(n-1)=300+250n-250=50+250n
$$
b. $t(n)=50+250n$
On Angla’s second birthday, n = 24
So,
t(24) = 50 + 5 $times$ (24 -1) = $165
The formula of $text{n}^{text{th}}$ term of this sequence is:
t(n) = 50 + 5(n – 1)
Deposit on the $text{12}^{text{th}}$ is:
t(12) = 50 + 5 $times$ (12 – 1) = $105\
The fund after 12 months is:\
S = (50 + 105)$times $dfrac{12}{2}$ = $930$
b) t(n) = 50 + 5(n – 1)
c) $930
$$
t(n)=50+5(n-1)=50+5n-5=45+5n
$$
The second birthday is then at $n=24$:
$$
t(24)=45+5(24)=45+120=165
$$
b. As found in (a):
$$
t(n)=50+5(n-1)=50+5n-5=45+5n
$$
c. The second birthday is then at $n=12$:
$$
t(12)=45+5(12)=45+60=105
$$
We then need to determine the sum of the first twelve terms:
$$
SUM=dfrac{(50+105)cdot 12}{2}=930
$$
b.$t(n)=45+5n$
c. $930
On a six-person bowling team, only four players bowl in any game. So, as per the statement.\
begin{align*}
intertext {Total number of items in the sample, n = 6} \
intertext {The number of items to be selected from the sample, r = 4}\
end{align*}
We determine the number of ways in which different four-person teams can be made by using combination because it is given that the order in which they bowl does not matter.\
Then, the number of combinations of $n$ object taken $r$ at times is determined by the following formula as stated:\
begin{align*}
^{n}C_{r} &= dfrac {n!}{(n-r)! r !}\
intertext {Put the values in the formula, we get}\
^{6}C_{4} &= dfrac {6!}{(6 – 4)! 4!} \
&= dfrac {6cdot5cdot4!}{2! cdot 4!}\
&= dfrac{6cdot5}{2cdot1}\
^{6}C_{4} &= 15\
intertext {Thus, there are 15 different four-person teams can be made.}\
end{align*}
We determine the number of bowling lineups of four player by using permutations, because it is given that the order of bowling lineups does matter.\
Then, the number of permutation of $n$ object taken $r$ at times is determined by the following formula as stated:\
begin{align*}
^{n}P_{r} &= dfrac {n!}{(n-r)!}\
intertext {Put the values in the formula, we get}\
^{6}P_{4} &= dfrac {6!}{(6 – 4)!}\
&= dfrac {6cdot5cdot4cdot3cdot2!}{2!}\
&= dfrac{6cdot5cdot4cdot3}{1}\
^{6}P_{4} &= 360\
intertext {Thus, there are 360 different bowling lineups of four players can be made.}\
end{align*}
$b.) 360$
First term: 3, common difference: 7
So,
t(n) = 3 + 7(n – 1)
First term: 20, common difference: – 9
So,
t(n) = 20 – 9(n – 1)
b) t(n) = 20 – 9(n – 1)
$$
t(n)=3+7(n-1)=3+7n-7=-4+7n
$$
b. The terms start at 20 ($n=1$)and decreases by 9 every next term:
$$
t(n)=20-9(n-1)=20-9n+9=29-9n
$$
b. $t(n)=29-9n$
$$
dfrac{-29-13}{17-3}=dfrac{-42}{14}=-3
$$
We can then continue from the third term to obtain the eigth term:
$$
13,10,7,4,1,-2
$$
Thus the eigth term is $-2$.
-2
$$
From the diagram, we get the values.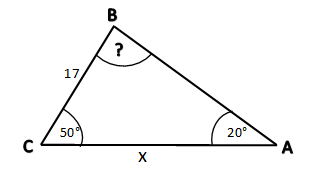
begin{align*}
intertext {Angle: A = 20textdegree, C = 50textdegree and B is desired.}\
intertext {Therefore,}\
20textdegree + 50textdegree + B &= 180textdegree \
text {B} &= 180textdegree – 70textdegree\
text {B} &= 110textdegree\
end{align*}
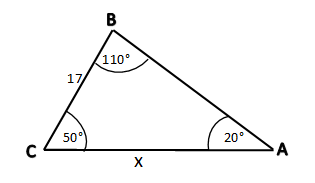
intertext {Side: a = 17, b = x}\
intertext {By using the Law of Sines, we conclude that}\
text {Formula}: dfrac {text{a}}{text {SinA}} &= dfrac {text{b}}{text{SinB}}\
dfrac {17}{text {Sin (20textdegree)}} &= dfrac {text{x}}{text {Sin (110textdegree)}}\
dfrac {17}{0.3420} &= dfrac {text{x}}{0.9396}\
text {x} &= dfrac{17times 0.9396}{0.3420} \
text {x} &= 46.70\
end{align*}
From the diagram, we get the values.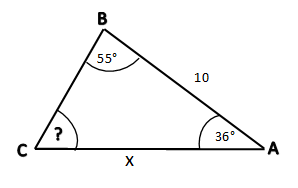
begin{align*}
intertext {Angle: A = 36textdegree, B = 55textdegree and C is desired.}\
intertext {Therefore,}\
36textdegree + 55textdegree + C &= 180textdegree\
text {C} &= 180textdegree – 91textdegree\
text {C} &= 89textdegree\
end{align*}
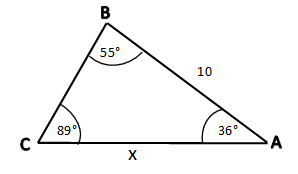
intertext {Side: c = 10, b = x}\
intertext {By using the Law of Sines, we conclude that}\
text {Formula}: dfrac {text{b}}{text {SinB}} &= dfrac {text{c}}{text{SinC}}\
dfrac {text {x}}{text {Sin (55textdegree)}} &= dfrac {10}{text {Sin (89textdegree)}}\
dfrac {text{x}}{0.8191} &= dfrac {10}{0.9998}\
text {x} &= dfrac{10times 0.8191}{0.9998} \
text {x} &= 8.19\
end{align*}
$(b.) 8.19$
As per the given graph.\
We can say that the graph represents a sine function.\
The equation of sine is stated below:\
begin{align*}
text {Y} &= text {A Sin(B (x – C)) + D}tag{1}\
intertext {Where, A = Amplitude}\
intertext {B = Period (The number of cycles the graph complete in an interval 0 to 2pi)} \
intertext {C = Phase Shift}\
intertext {D = Vertical Shift}
end{align*}
As shown in the graph,\
begin{align*}
intertext {Vertically stretched by a factor of 1, i.e A = 1 and cycle completes in graph, i.e B = 1}\
intertext {The graph is shifted up by two units, i.e, D = 2}\
intertext {The graph is shifted to the right side by} dfrac{pi}{4} text{i.e, C} = dfrac{pi}{4}\
end{align*}
$$
begin{align*}
text {Y}&= 1 times text {Sin} (1 (text x – dfrac{pi}{4})) + 2\
text {Y} &= text {Sin} (text x – dfrac {pi}{4}) + 2\
end{align*}
$$
As per the given graph.
We can say that the graph represents a Cosine function.
The equation of sine is stated below:
$$
begin{align*}
text {Y} &= text{A Cos(B (x – C)) + D}tag{1}\
end{align*}
$$
As shown in the graph,\
begin{align*}
intertext {Vertically stretched by a factor of 1.5, i.e A = 1.5 and cycle completes in graph, i.e B = 1}\
intertext {The graph is shifted up by one and half units, i.e, D = 0.5 and C = 0}\
end{align*}
$$
begin{align*}
text {Y}&= 1.5 times text {Cos} (1 (text x)) + 0.5\
text {Y} &= 1.5 text {Cos x} + 0.5\
end{align*}
$$
As per the given graph.
We can say that the graph represents a Cosine function.
The equation of sine is stated below:
$$
begin{align*}
text {Y} &= text{A Cos(B (x – C)) + D}tag{1}\
end{align*}
$$
As shown in the graph,\
begin{align*}
intertext {Vertically stretched by a factor of 1, i.e A = 1 and cycle completes in graph, i.e B = 1}\
intertext {The graph is shifted up by two units, i.e, D = 2}\
intertext {The graph is shifted to the left side by} – dfrac{pi}{3} text{i.e, C} = – dfrac{pi}{3}\
end{align*}
$$
begin{align*}
text {Y} &= 1 times text {Cos} (1 (text x + dfrac{pi}{3})) + 2\
text {Y} &= text {Cos} (text x + dfrac{pi}{3}) + 2\
end{align*}
$$
As per the given graph.
We can say that the graph represents a sine function.
The equation of sine is stated below:
$$
begin{align*}
text {Y} &= text{A Sin(B (x – C)) + D}tag{1}\
end{align*}
$$
As shown in the graph,\
begin{align*}
intertext {Vertically stretched by a factor of 3, i.e A = 3, and cycle completes in graph, i.e B = 1}\
intertext {The graph is shifted down by one unit, i.e, D = -1}\
intertext {The graph is shifted to the right side by} dfrac{2pi}{3} text{i.e, C} = dfrac{2pi}{3}\
end{align*}
$$
begin{align*}
text {Y}&= 3 times text {Sin} (1 (text x – dfrac{2pi}{3})) – 1\
text {Y} &= 3text {Sin} (text x – dfrac {2pi}{3}) – 1\
end{align*}
$$
(c.) Y = Cos ( x + $dfrac{pi}{3}$) + 2
(d.) Y = 3Sin ( x – $dfrac {2pi}{3}$) – 1
$
$$
dfrac{(350+4050)16}{2}=35,200
$$
$$
t(1)=13+3(1-1)=13+0=13
$$
Determine the diameter of the 20th doll:
$$
t(20)=13+3(20-1)=13+57=70
$$
The sum of a arithmetic series is the product of the sum of the first and last term and the number of terms divided by 2:
$$
dfrac{(70+13)20}{2}=830mm=83cm
$$
Thus we note that the dolls will fit on the windowsill.
t(n) = 13 + 3(n – 1)
So, the first doll’s diameter is:
t(1) = 13 + 3(1 – 1) = 13 mm = 1.3 cm
And the last doll’s diameter is:
t(20) = 13 + 3(20 – 1) = 70 mm = 7 cm
Placing all dolls in a raw, the raw length is the sum of its diameters
Since, diameters are represented in an arithmetic series,
So, the sum of series is:
S = (1.3 + 7) $times dfrac{20}{2}$ = 83 cm
So, the entire set of 20 dolls will fit in the windowsill of 92 cm long
$$
1
$$
Determine the 10th term:
$$
46
$$
The sum of a arithmetic series is the product of the sum of the first and last term and the number of terms divided by 2:
$$
dfrac{(1+46)10}{2}=235
$$
235
$$
Common difference is: 5
Find the $10^{text{th}}$ term:
t(10) = 1 + 5(10 – 1) = 46
The sum of series is:
S = (1 + 46) $times dfrac{10}{2}$ = 235
So,
18 = first term + common difference(9 – 1)
First term = 18 – 8 $times$ common difference
And the $5^{text{th}}$ term is 6
6 = first term + common difference (5 – 1)
So,
6 = 18 – 8 $times$ common difference + 4 $times$ common difference
So,
Common difference = 3
First term = 18 – 8 $times$ 3 = – 6
So, the series is:
-6, -3, 0, 3, 6, 9, 12, 15, 18
$$
d=dfrac{18-6}{9-5}=dfrac{12}{4}=3
$$
Thus every term is the previous term increased by 3:
$$
-6,-3,0,3,6,9,12,15,18
$$
-6,-3,0,3,6,9,12,15,18
$$
Common difference is: 8
Check the term 435,
if n is integer it will be a term of the series
435 = 3 + 8 $times$ (n – 1)
n = 55
So,
435 is the $55^{text{th}}$ term of this series
$$
t(n)=3+8(n-1)=3+8n-8=-5+8n
$$
Replace $t(n)$ with 435:
$$
435=-5+8n
$$
Add 5 to both sides of the equation:
$$
440=8n
$$
Divide both sides of the equation by 8:
$$
55=n
$$
Thus 435 is the 55th term of the sequence.
hline
$xtext{(angle)}$ & $-90^circ$ & $-45^circ$ & $0^circ$ & $45^circ$ & $90^circ$ & $135^circ$ & $180^circ$ & $cdots$ & $270^circ$ \
hline
$xtext{(height)}$ & $-30$ & $-15 sqrt{2}$ & $0$ & $15 sqrt{2}$ & $30$ & $15 sqrt{2}$ & $0$ & $cdots$ & $-30$ \
hline
end{tabular}
$$
y=30 sin x
$$
The maximum distance above the center that the top of the seat attains during the ride occurs when $x=90^circ$ and it is equal to $y=30 sin 90^circ=30$
The maximum distance below the center that the top of the seat attains during the ride occurs when $x=-90^circ$ and it is equal to $left|30 sin -90^circright|=30$
The equation that fits the County Fair Ferris wheel ride is
$$
y=30 cos x
$$
Graph
b)
The maximum distance above the center that the top of the seat attains during the is $30$
The maximum distance below the center that the top of the seat attains during the ride is $30$
c)
$$
y=30 cos x
$$
b. The sum is the area of the rectangle which is the product of the length and the width of the rectangle:
$$
8cdot 13=104
$$
c. The first column contains the first and the 16th term. The height of this column is 13 which is the sum of the first and the 16th term.
d. The first element of the series is 2 and every consective element is increased by $dfrac{11-2}{16}=dfrac{9}{16}$:
$$
t(n)=2+dfrac{9}{16}(n-1)=2+dfrac{9}{16}n-dfrac{9}{16}=dfrac{23}{16}+dfrac{9}{16}n
$$
The sum of the series is the sum of the first and last term multiplied by the number of terms divided by 2:
$$
dfrac{(2+11)16}{2}=104
$$
b. 104
c. The first column contains the first and the 16th term. The height of this column is 13 which is the sum of the first and the 16th term
d. 104
Only when the number of terms is even,
rearranging it like this will be a rectangle
The sum of a series is the result of adding up all of its terms,
this can be found easily if we rearranged the rectangles
represent each term to form one rectangle,
the sum is area of the new rectangle:
S = 8 $times$ 13 = 104
The first column is formed by the first and last terms of the series
and its hight is the sum of both terms,
In this case its is: 2 + 11 = 13
Since last term is: 11 and it is term number: 16
So,
11 = 2 + common difference $times$ (16 – 1)
Common difference = $dfrac{9}{15}$ = 0.6
So, the series is:
2, 2.6, 3.2, 3.8, 4.4, 5, 5.6, 6.2, 6.8, 7.4, 8, 8.6, 9.2, 9.8, 10.4, 11
And the sum is:
S = (2 + 11) $times dfrac{16}{2}$ = 104
b) 104
c) 13
d) 104
You can then use Antonio’s method by dividing the middle block into two even pieces and placing the second piece on the first.
Then the area of the rectangle would be
$$
4cdot 1.5=6=1+2+3
$$
1, 3, 5, 7, 9
Antonio’s method apply here by rotating all columns as shown below instead of its half and calculate the area and divide the area by two,
Area = 5 $times$ 10 = 50
Sum = $dfrac{50}{2}$ = 25
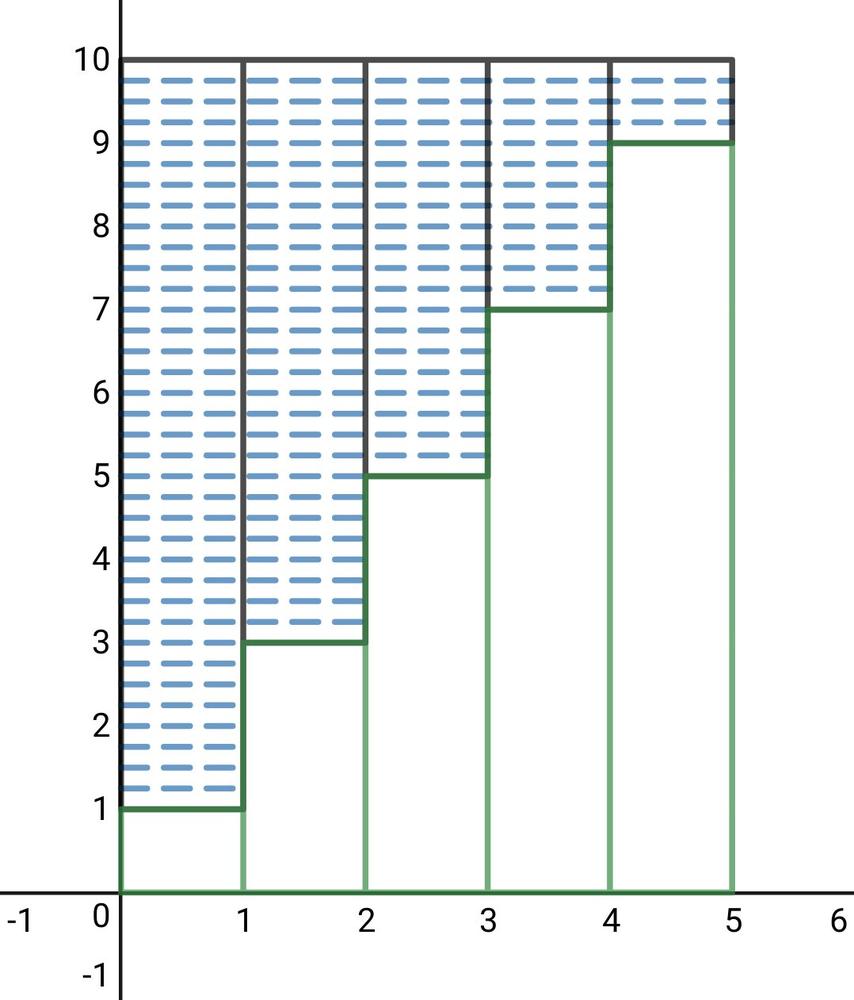
But, a simple modification of the method will make it work for all arithmetic series;
Rotate all columns instead of its half, calculate the area, and divide the area by two
For example:
The series: 1, 3, 5, 7, 9
As shown in the graph below,
Area = 5 $times$ 10 = 50
Sum = $dfrac{50}{2}$ = 25
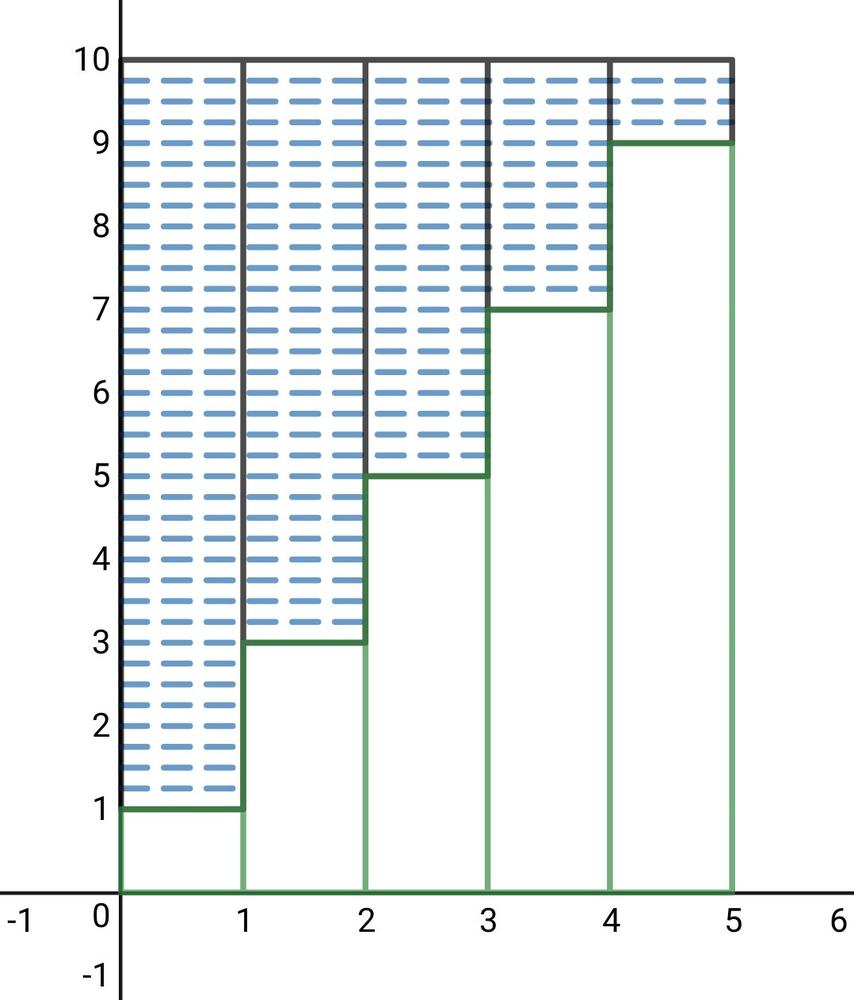
a. The number of terms is the difference between the last and first term divided by the common difference increased by 1:
$$
dfrac{74-11}{7}+1=dfrac{63}{7}+1=9+1=10
$$
The sum is then:
$$
dfrac{(74+11)10}{2}=425
$$
b.
$$
dfrac{(8+151)14}{2}=1113
$$
c. The first term is 4 and the 25th term is $t(25)=4+6(24)=148$
$$
dfrac{(4+148)25}{2}=1900
$$
b. 1113
c. 1900
Yes, by rotating all columns,
The dimensions of the new rectangle will be:
Find number of terms n as follows:
74 = 11 + 7(n – 1)
n = 10
So,
Horizontal dimension is 10.
Vertical dimension is 85,
this the sum of the first and last terms
Sum of the series is the half of the new rectangle area:
S = $dfrac{85 times 10}{2}$ = 425
Since, number of terms is 14,
So,
Horizontal dimension is: 14
Vertical dimension is the sum of t(1) and t(14) =159
So, sum of the series is:
S = $dfrac{159 times 14}{2}$ = 1113
Number of terms is 25,
So,
Horizontal dimension is 25
Last term is:
t(25) = 4 + 6 $times$ (25 – 1) = 148
So, vertical dimension = 148 + 4 = 152
Sum of the series is:
S = $dfrac{152 times 25}{2}$ = 1900
b) 1113
c) 1900
Value of the last term is:
t(216) = 50 + 3 $times$ (216 – 1) = 695
Vertical dimension = 50 + 695 = 745
Total money for Angla on her $18^{text{th}}$ birthday is the sum of series:
S = $dfrac{745 times 216}{2}$ = $80460
$$
a(n)=50+3(n-1)=50+3n-3=47+3n
$$
Determine the amount of the payment on her 18th birthday ($12cdot 18=216$):
$$
a(216)=50+3(215)=695
$$
The total amount is then the sum of the first and last payment multiplied by the number of payments divided by 2:
$$
dfrac{(50+695)216}{2}=80,460
$$
$$
6+12+18+24+30+36+42+48+54+60
$$
The total amount is then the sum of the first and last payment multiplied by the number of payments divided by 2:
$$
dfrac{(6+60)10}{2}=330
$$
b. Sequence, every term is the previous term increased by 55:
$$
190,245,300,355,410,465,520,575
$$
c. Series, determine the allowance after one year:
$$
t(52)=1.5+0.25(52-51)=14.25
$$
The total amount is then the sum of the first and last payment multiplied by the number of payments divided by 2:
$$
dfrac{(1.5+14.25)52}{2}=409.5
$$
Thus he has enough money.
b. $575
c. Yes
The terms are: 6, 12, 18, …..
Since it is constantly increasing by 6,
And each term is added to its next term to form the sum,
So, this is an arithmetic series,
The last term is:
t(10) = 6 + 6 $times$ (10 – 1) = 60
The sum of cells is:
S = $dfrac{(60 + 6) times 10}{2}$ = 330 cells
The balance is increasing constantly by $55,\
But each term is not added to its next term to form the sum\
So, this is a sequence\
The balance after the$8^${text{th}} month will be:\
= 190 + 55$times$ 7 = $575
Since it is constantly increasing by 0.25,
And each term is added to its next term to form the sum,
So, this is an arithmetic series,
The last term is after 1 year = 52 weeks:
t(52) = 1.5 + 0.25 $times$ (52 – 1) = $14.25\
Total savings is the sum of series:\
S = (1.5 + 14.25)$times $$dfrac{52}{2}$ = $409.5
So, Evan can buy the device for $180
b) $575
c) Yes
And every sales is added to the sum,
So, this is an arithmetic series,
Last term = 1800000 + 20000 $times$ (14 – 1) = $2060000\
The sum of series is:\
S = (1800000 + 2060000)$times $$dfrac{14}{2}$ = $27020000
Since, the jackpot started with $29000000,
So, the jackpot when the tickets are drown is expected to be:
29000000 + 27020000 = $56020000
So, the other state will have larger jackpot
$$
t(14)=1,800,000+20,000(14-1)=2,060,000
$$
The total amount is then the sum of the first and last payment multiplied by the number of payments divided by 2:
$$
dfrac{(1,800,000+2,060,000)14}{2}=27,020,000
$$
This amount still needs to be added to the starting amount: $27,020,000+$29,000,000=$56,020,000 and thus we note that the jackpot in this tate is higher than in her own state.
$$
dfrac{(t(1)+t(n))n}{2}
$$
dfrac{(t(1)+t(n))n}{2}
$$
S = (t(1) + t(n)) $times dfrac{text{n}}{2}$
Where:
S is the sum
t(1) is the first term
t(n) is the last term
n is the number of terms
$$
dfrac{(t(1)+t(n))n}{2}
$$
dfrac{(t(1)+t(n))n}{2}
$$
2-Dec-2018\
Finding the sum of an arithmetic series:\
Consider the series: 1, 3, 5, 7, 9\
Write the series and its inverse\
and add each term to its opponent in the inverse\
begin{tabular}{ccccc}
1&3&5&7&9\
9&7&5&3&1\
hline
10&10&10&10&10
end{tabular}\
The result is the same value for each pair of terms\
So, the sum of the series is:\
S = (t(1) + t(n)) $times dfrac{text{n}}{2}$\
Where:\
S is the sum\
t(1) is the first term\
t(n) is the last term\
n is the number of terms\
S = (1 + 9) $times dfrac{5}{2}$ = 25
Represent the series in a graph as shown below,
Rotate the columns to form one rectangle,
Find the area of the rectangle,
The sum is the half of the rectangle area
Area = 5 $times$ 10 = 50
S = $dfrac{50}{2}$ = 25
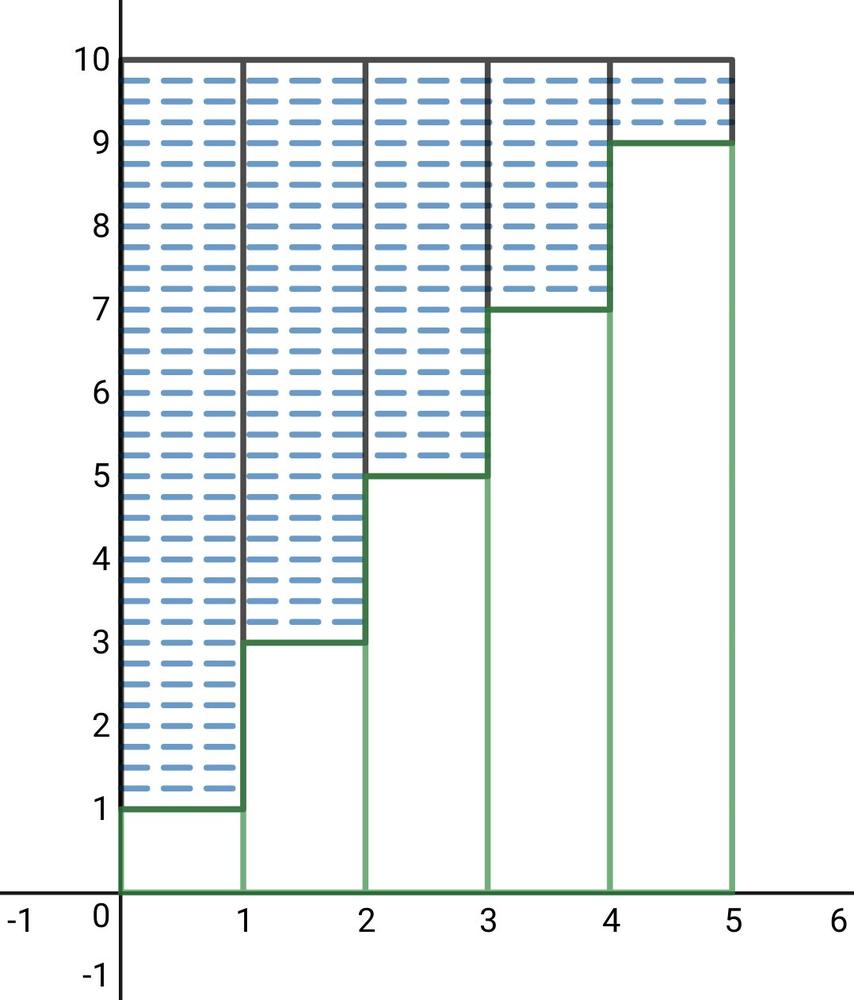
For odd numbers:
t(n) = 1 + 2(n – 1)
For even numbers:
t(n) = 2 + 2(n – 1)
For odd numbers:
149 = 1 + 2 $times$ (n – 1)
n = 75
S = (1 + 149) $times dfrac{75}{2}$ = 5625
For even numbers:
150 = 2 + 2 $times$ (n – 1)
n = 75
S = (2 + 150) $times dfrac{75}{2}$ = 5700
For odd numbers: t(n) = 1 + 2(n – 1)
For even numbers: t(n) = 2 + 2(n – 1)
b)
Odd numbers sum = 5625
Even numbers sum = 5700
$$
o(n)=1+2(n-1)=1+2n-2=-1+2n
$$
$$
e(n)=2+2(n-1)=2+2n-2=0+2n=2n
$$
b. The sum of an arithmetic series is then the sum of the first and last payment multiplied by the number of terms divided by 2:
$$
text{odd: }dfrac{(1+149)75}{2}=5625
$$
$$
text{even: }dfrac{(2+150)75}{2}=5700
$$
b. 5625, 5700
$$
t(n)=21-4(n-1)=21-4n+4=25-4n
$$
b. The number of terms is the difference between the last and the first term divided by the common difference increased by 1 (we increase by 1, because else we only count the number of increments and thus forgot one term):
$$
dfrac{-99-21}{-4}+1=31
$$
c. The sum of an arithmetic series is then the sum of the first and last payment multiplied by the number of terms divided by 2:
$$
dfrac{(21+(-99))31}{2}=-1,209
$$
b. 31 terms
c. $-1,209$
t(n) = 21 – 4(n – 1)
Where terms are decreased by 4,
So, common difference is negative
Last term is: – 99
So,
– 99 = 21 – 4 $times$ (n – 1)
n = 31
So, number of terms is 31
The sum of series is:
S = (21 – 99) $times dfrac{31}{2}$ = – 1209
b) 31 terms
c) – 1209
Using one of the Laws of Cosine
$$
c^2=a^2+b^2-2ab cos C
$$
8^2=10^2+12^2-2(10)(12) cos C
$$
64=100+144-240 cos C
$$
64=244-240 cos C
$$
64textcolor{#c34632}{-244}=244textcolor{#c34632}{-244}-240 cos C
$$
-180=-240 cos C
$$
dfrac{-180}{textcolor{#c34632}{-240}}=dfrac{-240}{textcolor{#c34632}{-240}} cos C
$$
0.75=cos C
$$
cos^{-1}(0.75)=C
$$
boxed{41.41text{textdegree} approx C}
$$
Using Trig Ratios
$$
tan theta = dfrac{opposite}{adjascent}
$$
tan C= dfrac{7}{13}
$$
C=tan^{-1}left( dfrac{7}{13}right)
$$
boxed{Capprox 28.30text{textdegree}}
$$
$n$ represents the number of murals
$r$ represents the number of times
_{4}P_{4}=dfrac{4!}{(4-4)!}= dfrac{4!}{0!}=dfrac{4cdot3cdot2cdot1}{1} = dfrac{24}{1} =boxed{24}
$$

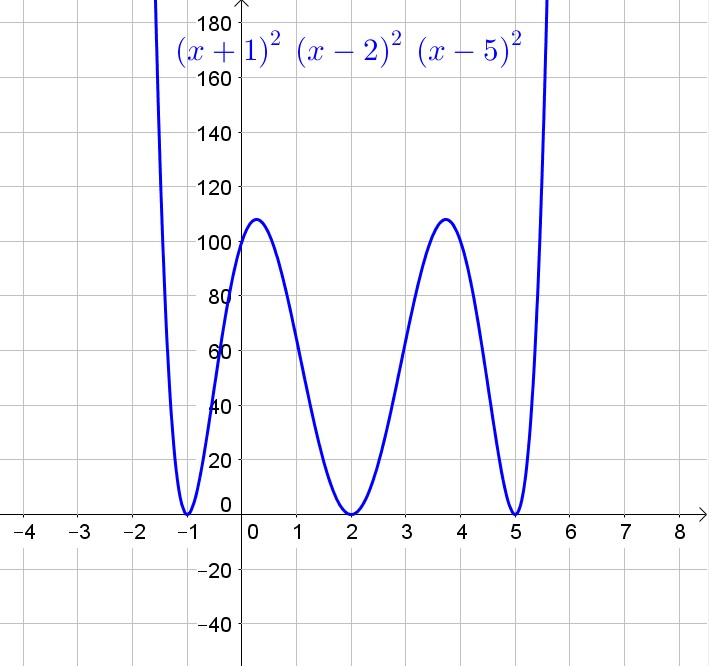
$x=-2+sqrt3$,
$x=-2-sqrt3$
factored polynomial for
$x=-2+sqrt3$ is $x+2-sqrt3$ , and
$x=-2-sqrt3$ is $x+2+sqrt3$
$boxed{(x+2-sqrt3)(x+2+sqrt3)}$
standard polynomial
$(x+2-sqrt3)(x+2+sqrt3)$
$(x+2)^2-sqrt3^2$
$(x+2)^2-3$
$x^2+2x+2x+4-3$
$$
boxed{x^2+4x+1}
$$
$x=-2+i$
$x=-2-i$
factored polynomial for
$x=-2+i$ is $x+2-i$ , and
$x=-2-i$ is $x+2+i$
$boxed{(x+2-i)(x+2+i)}$
standard polynomial
$(x+2-i)(x+2+i)$
$(x+2)^2-i^2$
$left[Rule: i^2=-1right]$
$(x+2)^2-(-1)$
$(x+2)^2+1$
$x^2+2x+2x+4+1$
$$
boxed{x^2+4x+5}
$$
{color{#4257b2}text{a)}}
$$
To solve the problem, we use this formula
$$
boldsymbol{x^{circ}=frac{pi}{180}}textbf{ radians}
$$
$$
begin{align*}
&60^{circ}cdot frac{pi}{180}text{ radians}&&boxed{text{Given proportion}}\
&frac{60cdot pi}{180}text{ radians}&&boxed{text{Multiply fractions}}\
&frac{pi}{3}text{ radians}&&boxed{text{Cancel the common factor: }60}\\
&boxed{{color{#c34632}frac{pi}{3}text{ radians}} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Multiply:fractions}:quad :acdot frac{b}{c}=frac{a:cdot :b}{c} }
$$
{color{#4257b2}text{b)}}
$$
To solve the problem, we use this formula
$$
boldsymbol{x^{circ}=frac{pi}{180}}textbf{ radians}
$$
$$
begin{align*}
&75^{circ}cdot frac{pi}{180}text{ radians}&&boxed{text{Given proportion}}\
&frac{75cdot pi}{180}text{ radians}&&boxed{text{Multiply fractions}}\
&frac{5pi}{12}text{ radians}&&boxed{text{Cancel the common factor: }15}\\
&boxed{{color{#c34632}frac{5pi}{12}text{ radians}} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Multiply:fractions}:quad :acdot frac{b}{c}=frac{a:cdot :b}{c}}
$$
{color{#4257b2}text{c)}}
$$
To solve the problem, we use this formula
$$
boldsymbol{x^{circ}=frac{pi}{180}}textbf{ radians}
$$
$$
begin{align*}
&210^{circ}cdot frac{pi}{180}text{ radians}&&boxed{text{Given proportion}}\
&frac{210cdot pi}{180}text{ radians}&&boxed{text{Multiply fractions}}\
&frac{7pi}{6}text{ radians}&&boxed{text{Cancel the common factor: }30}\\
&boxed{{color{#c34632}frac{7pi}{6}text{ radians}} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Multiply:fractions}:quad :acdot frac{b}{c}=frac{a:cdot :b}{c}}
$$
{color{#4257b2}text{d)}}
$$
To solve the problem, we use this formula
$$
boldsymbol{x^{circ}=frac{pi}{180}}textbf{ radians}
$$
$$
begin{align*}
&225^{circ}cdot frac{pi}{180}text{ radians}&&boxed{text{Given proportion}}\
&frac{225cdot pi}{180}text{ radians}&&boxed{text{Multiply fractions}}\
&frac{5pi}{4}text{ radians}&&boxed{text{Cancel the common factor: }45}\\
&boxed{{color{#c34632}frac{5pi}{4}text{ radians}} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Multiply:fractions}:quad :acdot frac{b}{c}=frac{a:cdot :b}{c}}
$$
color{#4257b2} text{ a) } frac{pi}{3}text{ radians}
$$
$$
color{#4257b2} text{ b) }frac{5pi}{12}text{ radians}
$$
$$
color{#4257b2} text{ c) }frac{7pi}{6}text{ radians}
$$
$$
color{#4257b2} text{ d) } frac{5pi}{4}text{ radians}
$$
a. $60text{textdegree}=dfrac{60pi}{180text{textdegree}}$ radians $=dfrac{pi}{3}$ radians
b. $75text{textdegree}=dfrac{75pi}{180text{textdegree}}$ radians $=dfrac{5pi}{12}$ radians
c. $210text{textdegree}=dfrac{210pi}{180text{textdegree}}$ radians $=dfrac{7pi}{6}$ radians
d. $225text{textdegree}=dfrac{225pi}{180text{textdegree}}$ radians $=dfrac{5pi}{4}$ radians
b. $dfrac{5pi}{12}$
c. $dfrac{7pi}{6}$
d. $dfrac{5pi}{4}$
a. 3 terms:
$$
dfrac{(1+3)3}{2}=6
$$
10 terms:
$$
dfrac{(1+10)10}{2}=55
$$
b.
$$
dfrac{(1+n)n}{2}
$$
c.
$$
dfrac{(1+100)100}{2}=5050
$$
b. $dfrac{(1+n)n}{2}$
c. 5,050
a.
$$
dfrac{(2+2n)n}{2}=(1+n)n
$$
b.
$$
dfrac{(1+2n-1)n}{2}=dfrac{n^2}{2}=n^2
$$
c.
$$
Even: (1+100)100=10,100
$$
$$
Odd: 100^2=10,000
$$
b. $n^2$
c. 10,100 and 10,000
For even numbers,
n is the number of terms,
2n is the value of the last term
We will use the same formula to find the sum:
S = (2 + 2n) $times dfrac{text{n}}{2} = text{n} + text{n}^{2}$
For odd numbers,
n is the number of terms,
(2n – 1) is the value of the last term
We will use the same formula to find the sum:
S = (1 + 2n – 1) $times dfrac{text{n}}{2} = dfrac{2text{n} times text{n}}{2} = text{n}^{2}$
Sum of the first 100 even numbers:
S = 100 + (100)$^{2}$ = 10100
Sum of the first 100 odd numbers is:
S = (100)$^{2}$ = 10000
b) S = n$^{2}$
c) even S = 10100, odd S = 10000
a. The new series is arithmetic since the common difference is 3 and the series contains $n$ terms.
b.
$$
text{First series}:dfrac{(1+n)n}{2}
$$
$$
text{Second series}:dfrac{(2+2n)n}{2}
$$
Add the two expression to obtain the sum of the new series:
$$
dfrac{(1+n)n+(2+2n)n}{2}=dfrac{(1+n+2+2n)n}{2}=dfrac{(3+3n)n}{3}
$$
c. You could also determine the sum of the new series directly:
$$
dfrac{(3+3n)n}{2}
$$
d. We note that the equations obtained in (b) and (c) are identical.
b. $dfrac{(3+3n)n}{3}$
c. $dfrac{(3+3n)n}{3}$
d. Identical
The new series is constantly increasing by 3,
And every term is added to form the sum,
So, it is an arithmetic series
The number of terms is n,
And the value of the last term is 3n
Sum of the new series = sum of the two original series:
S = (1 + n) $times dfrac{text{n}}{2}$ + (2 + 2n) $times dfrac{text{n}}{2}$
= (3 + 3n) $dfrac{text{n}}{2} = dfrac{3text{n} + 3text{n}^{2}}{2}$
We can apply the formula directly on the new series:
S = (3 + 3n) $times dfrac{text{n}}{2}$
Consider 4 terms in each series:
Sum of the first series is:
S = (1 + 4) $times dfrac{4}{2}$ = 10
Sum of the second series is:
S = (2 + 8) $times dfrac{4}{2}$ = 20
Sum of both series = 10 + 20 = 30
Sum of the new series is:
S = (3 + 12) $times dfrac{4}{2}$ = 30
b) (3 + 3n) $dfrac{text{n}}{2}$
c) (3 + 3n) $dfrac{text{n}}{2}$
d) see verification above
a. Since every term in the sum is multiplied by 2, the sum itself will also be multiplied by 2 as we note is obvious in the formulas as well:
$$
text{First series}:dfrac{(1+n)n}{2}
$$
$$
text{Second series}:dfrac{(2+2n)n}{2}=(1+n)n
$$
b. We note that ever term is decreased by 1 and thus in total the sum is decreased by $n$; as we note in the formulas as well:
$$
text{First series}:dfrac{(2+2n)n}{2}=(1+n)n=n^2+n
$$
$$
text{Second series}:dfrac{(1+2n-1)n}{2}=dfrac{2n^2}{2}=n^2
$$
b. Sum is decreased by $n$
Every term of the second series is double every term of the first series,
So, Sum of the second series is double the sum of the first series
S = 2 $times$ (1 + n) $times dfrac{text{n}}{2}$ = n + n$^{2}$
To test the result consider 4 terms of each series:
Sum of the first series is:
S = (1 + 4) $times dfrac{4}{2}$ = 10
Sum of the second series is:
S = (2 + 8) $times dfrac{4}{2}$ = 20 = 2 $times$ 10
Every term of the second series is lower than every term of the first series by 1,
So, the sum of the second series is lower than the sum of the first series by n
S = (2 + 2n) $times dfrac{text{n}}{2}$ – n = n + n$^{2}$ -n = n$^{2}$
To test the result, consider 4 terms of each series:
Sum of the first series is:
S = (2 + 8) $times dfrac{4}{2}$ = 20
Sum of the second series is:
S = (1 + 7) $times dfrac{4}{2}$ = 16 = 20 – 4
b) sum is decreased by n
a. We note that the terms contain: 1, 3, 5, 7, 9, etc. terms and thus the nth terms is $2n-1$. (See previous exercise).
b.
$$
text{3 terms}:dfrac{(1+5)3}{2}=9
$$
$$
text{5 terms}:dfrac{(1+9)5}{2}=25
$$
The sum could be representated by adding the blocks together and wethen note that they form a square with length $n$ (when $n$ terms were added)
c.
$$
n text{terms}:dfrac{(1+2n-1)n}{2}=dfrac{2n^2}{2}=n^2
$$
Thus the sum is a square with length $n$.
d. The sum of the first $(n+1)$ odd numbers is then: $(n+1)^2$.
b. 9, 25
c. $n^2$, square with length $n$
d. $(n+1)^2$
Let us add the second and third series: $3+7+11+15+…+(4n-1)$
$$
text{Second series}:dfrac{(2+2n)n}{2}=(1+n)n=n^2+n
$$
$$
text{Third series}:dfrac{(1+2n-1)n}{2}=dfrac{2n^2}{2}=n^2
$$
Add the two expression to obtain the sum of the new series:
$$
n^2+n+n^2=2n^2+n
$$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
The first term is $5$,
and the difference between the terms is $boldsymbol{5}$
Because $5+5$ = $10$.
The number of terms is the
difference between the last and first term
divided by the common difference
and incerased by 1.
$$
begin{align*}
t&=frac{400-5}{5}+1&&boxed{text{Use the formula}}\
t&=frac{395}{5}+1&&boxed{text{Subtract the numbers: }400-5=395}\
t&=79+1&&boxed{text{Divide the numbers: } frac{395}{5}=79}\\
t&=color{#c34632}{80}&&boxed{text{Simplify}}\\
end{align*}
$$
the sum of the first and last term,
multiplied by the number of terms
and divided by 2
$$
begin{align*}
S(n)&=frac{(5+400)n}{2}&&boxed{text{Use the formula}}\
S(80)&=frac{5+400)color{#c34632}{80}}{2}&&boxed{text{Substitute }80 text{ for }n}\
S(80)&=frac{405cdot80}{2}&&boxed{text{Calculate within parentheses: }5+400=405}\
S(80)&=frac{32,400}{2}&&boxed{text{Multiply the numbers }}\
S(80)&=16,200&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}S(80)=16,200} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
The first term is $3$,
and the difference between the terms is $boldsymbol{5}$
Because $3+5$ = $8$.
The number of terms is the
difference between the last and first term
divided by the common difference
and incerased by 1.
$$
begin{align*}
t&=frac{398-3}{5}+1&&boxed{text{Use the formula}}\
t&=frac{395}{5}+1&&boxed{text{Subtract the numbers: }398-3=395}\
t&=79+1&&boxed{text{Divide the numbers: } frac{395}{5}=79}\\
t&=color{#c34632}{80}&&boxed{text{Simplify}}\\
end{align*}
$$
the sum of the first and last term,
multiplied by the number of terms
and divided by 2
$$
begin{align*}
S(n)&=frac{(3+398)n}{2}&&boxed{text{Use the formula}}\
S(80)&=frac{3+398)color{#c34632}{80}}{2}&&boxed{text{Substitute }80 text{ for }n}\
S(80)&=frac{401cdot80}{2}&&boxed{text{Calculate within parentheses: }3+398=401}\
S(80)&=frac{32,080}{2}&&boxed{text{Multiply the numbers }}\
S(80)&=16,040&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}S(80)=16,040} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{c)}}
$$
Solution to this example is given below
The first term is $80$,
and the difference between the terms is $boldsymbol{-6}$
Because $80-6$ = $74$.
The number of terms is the
difference between the last and first term
divided by the common difference
and incerased by 1.
$$
begin{align*}
t&=frac{14-80}{-6}+1&&boxed{text{Use the formula}}\
t&=frac{-66}{-6}+1&&boxed{text{Subtract the numbers: }14-80=-66}\
t&=11+1&&boxed{text{Divide the numbers: } frac{-66}{-6}=11}\\
t&=color{#c34632}{12}&&boxed{text{Simplify}}\\
end{align*}
$$
the sum of the first and last term,
multiplied by the number of terms
and divided by 2
$$
begin{align*}
S(n)&=frac{(80+14)n}{2}&&boxed{text{Use the formula}}\
S(12)&=frac{80+14)color{#c34632}{12}}{2}&&boxed{text{Substitute }12 text{ for }n}\
S(12)&=frac{94cdot12}{2}&&boxed{text{Calculate within parentheses: }80+14=94}\
S(12)&=frac{1,128}{2}&&boxed{text{Multiply the numbers }}\
S(12)&=564&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}S(12)=564} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ a) }S(80)=16,200
$$
$$
color{#4257b2} text{ b) }S(80)=16,040
$$
$$
color{#4257b2} text{ c) }S(12)=564
$$
a.
$$
dfrac{(5+400)80}{2}=16,200
$$
b.
$$
dfrac{(3+398)80}{2}=16,040
$$
c.
$$
dfrac{(80+14)12}{2}=564
$$
b. 16,040
c. 564
The series is:
$$
11+22+33+44+55+66+77+88+99
$$
The sum is then:
$$
dfrac{(11+99)9}{2}=495
$$
11+22+33+44+55+66+77+88+99
$$
Sum: 495
a. We note that the second term is the first term decreased by 2 and the next term is then increased by 7, then decreased by 2 again and then increased by 7 again and so on.
b. Yes, since the sequence does not have a common difference, the sequence is not arithmetic, however we do note that this sum is the sum of two arithmetic sequences and thus we can determine the sum.
c.
$$
text{First series}:dfrac{(5+400)80}{2}=16,200
$$
$$
text{Second series}:dfrac{(3+398)80}{2}=16,040
$$
Add the two sums to obtain the sum of the original series:
$$
16,200+16,040=32,240
$$
32,240
$$
$$
C_{10}^{12}=dfrac{12!}{(12-10)!10!}=dfrac{12cdot 11}{2cdot 1}=66
$$
b. Since the order does not matters, we need to use a combination:
$$
C_{7}^{9}=dfrac{9!}{(9-7)!7!}=dfrac{9cdot 8}{2cdot 1}=36
$$
b. 36
$x^2=(35)^2+(43)^2-2 cdot 35 cdot 43 cos 50$ (The law of cosins)
$x^2=1225+1849-2 cdot 35 cdot 43 cdot 0.6428$
$x^2=1225+1849-1934.83$
$x^2=1139.17$
$$
x approx 33.75 mathrm { ~ft}
$$
$dfrac {sin 25text{textdegree}}{x}=dfrac {sin 41text{textdegree}}{15}$ (The law of sins)
$dfrac {0.4226}{x}=dfrac {0.6561}{15}$
$x=0.4226 times dfrac {15}{0.6561}$
$$
x approx 9.66 mathrm { ~ft}
$$
b- $x approx 9.66 mathrm { ~ft}$
$$
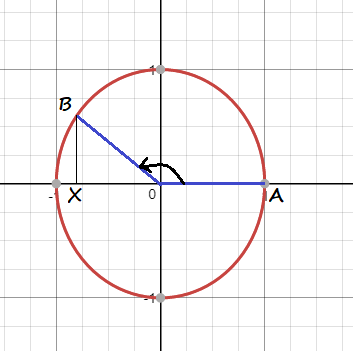
y=cosleft(theta-dfrac{pi}{2}right)
$$
$y=sintheta=BX$
$$
angle COB=90text{textdegree}
$$
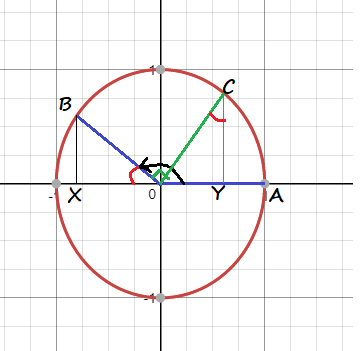
angle BOXcongangle OCY
$$
triangle BOXcongtriangle YCO
$$
OY=BX
$$
cosleft(theta-dfrac{pi}{2}right)=cos AOC=OY=BX=sintheta
$$
The average cost of a movie ticket is 9.50 dollars, i.e,
$$begin{aligned}
a_{1} &= 9.50\
end{aligned}$$
As per the statement, the cost is increasing 4% per annum, which means:
$$begin{aligned}
q &= 1+ dfrac{4}{100}\\
q &= 1.04\
end{aligned}$$
$$begin{aligned}
a_{n} &= a_{0}.r^{n-1} tag 1\\
end{aligned}$$
Now to determine the value of $n$ ,so that
$$begin{aligned}
a_{n} &= 2 . a_{0}\\
a_{n} &= 2 times 9.50\\
a_{n} &= 19\
end{aligned}$$
$$begin{aligned}
19 &= 9.50 (1.04)^{n-1}\\
dfrac {19}{9.50} &= (1.04)^{n-1}\\
2 &= (1.04)^{n}\\
log {2} &= (n-1) log (1.04)\\
n-1 &= dfrac {log(2)}{log(1.04)}\\
n-1 &= 17.67\\
n &= 18.67\\
n &approx 19\
end{aligned}$$
$$begin{aligned}
&=dfrac {a_{11}-a_{1}}{11-1}\\
&=dfrac {9.50 (1.04)^{10}-9.50}{10}\\
&= dfrac{14.062 – 9.50}{10}\\
&approx 0.46\
end{aligned}$$
Thus, during the next 10 years, the ticket’s cost will be increased by $ $0.46$ per year.
(b.) $0.46 per year.
b. The sum of the series is then 100 times 101 divided by 2:
$$
dfrac{100cdot 101}{2}=5,050
$$
c. The sum of the series is also the sum of the first and last term, multiplied by the number of terms divided by 2; we note that this is the same as has been done in (a) and (b).
d. The sum is the sum of the first and last term, multiplied by the number of terms divided by 2:
$$
dfrac{(2+59)20}{2}=610
$$
$$
sum_{n=1}^{5}(15+4(n-1))=sum_{n=1}^{5}(15+4n-4)=sum_{n=1}^{5}(11+4n)
$$
$$
1^2+2^2+3^3+4^2+5^2+6^2=1+4+9+16+25+36=91
$$
b. $1^2+2^2+3^3+4^2+5^2+6^2=91$
$$
sum_{n=1}^{80}(5n)
$$
Note that the sum contains 80 terms and the common difference is 5:
$$
sum_{n=1}^{80}(3+5(n-1))=sum_{n=1}^{80}(3+5n-5)=sum_{n=1}^{80}(-2+5n)
$$
$$
sum_{n=1}^{80}(5n-2+5n)=sum_{n=1}^{80}(-2+10n)
$$
b. $sum_{n=1}^{80}(-2+10n)$
$$begin{aligned}
sum ^{10} _{t=1} (13t-5)\
end{aligned}$$
$$begin{aligned}
a_{1} &= 13times1-5\\
a_{1} &= 8\\
a_{10} &= 13times10-5\\
a_{10} &= 125\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{n(a_{1}+a_{n})}{2}\\
S_{10} &= dfrac{10(8+125)}{2}\\
S_{10} &= dfrac {10(133)}{2}\\
S_{10} &= 665
end{aligned}$$
$$begin{aligned}
a_{1} &= 105.5\\
a_{23} &= 6.5\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{n(a_{1}+a_{n})}{2}\\
S_{23} &= dfrac{23(105.5+6.5)}{2}\\
S_{23} &= dfrac {23 (112)}{2}\\
S_{23} &= 1288
end{aligned}$$
4+10+16+22+……..+(6n-2)
$$begin{aligned}
a_{1} &=4\\
d &= 10-4\\
d &= 6\
end{aligned}$$
$$begin{aligned}
a_{N} &= a_{1}+(N-1)d\\
6n-2 &= 4+(N-1) (6)\\
6n-2 &= 4+6N-6\\
6n-2+2 &= 6N\\
6n &= 6N\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{n(a_{1}+a_{n})}{2}\\
S_{n} &= dfrac{n(4+6n-2)}{2}\\
S_{n} &= dfrac {n (6n+2)}{2}\\
S_{n} &= dfrac {2n (3n+1)}{2}\\
S_{n} &= n (3n+1)\
end{aligned}$$
$$begin{aligned}
sum ^{30} _{t=1} (-5t+10)\
end{aligned}$$
$$begin{aligned}
a_{1} &= -5times1+10\\
a_{1} &= 5\\
a_{30} &= -5times30+10\\
a_{30} &= -140\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{n(a_{1}+a_{n})}{2}\\
S_{30} &= dfrac{30 (5 – 140)} {2}\\
S_{30} &= dfrac {30 (-135)} {2}\\
S_{30} &= -2025
end{aligned}$$
$(b.)$ $1288$
$(c.)$ $n(3n+1)$
$(d.)$ $-2025$
a.
$$
Sigma_{n=1}^{11}(47-13(n-1))=dfrac{(47-83)11}{2}=-198
$$
b.
$$
Sigma_{n=1}^{n}(3+7(n-1))=dfrac{(3+3+7(n-1))n}{2}=dfrac{(6+7n-7)n}{2}=dfrac{(-1+7n)n}{2}
$$
b. $Sigma_{n=1}^{n}(3+7(n-1))=dfrac{(-1+7n)n}{2}$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
The first term is $100$,
and the difference between the terms is $boldsymbol{1}$
Because $100+1$ = $101$.
The number of terms is the
difference between the last and first term
divided by the common difference
and incerased by 1.
$$
begin{align*}
t&=frac{1,000-100}{1}+1&&boxed{text{Use the formula}}\
t&=frac{900}{1}+1&&boxed{text{Subtract the numbers: }1,000-100=900}\
t&=900+1&&boxed{text{Divide the numbers: } frac{900}{1}=900}\\
t&=color{#c34632}{901}&&boxed{text{Simplify}}\\
end{align*}
$$
the sum of the first and last term,
multiplied by the number of terms
and divided by 2
$$
begin{align*}
S(n)&=frac{(100+1,000)n}{2}&&boxed{text{Use the formula}}\
S(901)&=frac{100+1,000)color{#c34632}{901}}{2}&&boxed{text{Substitute }901 text{ for }n}\
S(901)&=frac{1100cdot901}{2}&&boxed{text{Calculate within parentheses: }100+1,000=1,100}\
S(901)&=frac{991,100}{2}&&boxed{text{Multiply the numbers }}\
S(901)&=495,550&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}S(901)=495,550} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ }S(901)=495,550
$$
$$
dfrac{(100+1000)901}{2}=495,550
$$
495,550
$$
(a.) The total number of ways the five students from the 12 members can be lined up will be calculated by using the Permutation formula is stated below.
$$begin{aligned}
^{n}P_{r}&= dfrac{n!}{(n-r)}
end{aligned}$$
where,
$n$ represents the number of members.
$r$ represents the number of students.
^{12}P_{5}&= dfrac{12!}{(12 – 5)}\\
^{12}P_{5}&= dfrac{12!}{7!}\\
^{12}P_{5}&= dfrac{12.11.10.9.8.7!}{7!}\\
^{12}P_{5}&= 12.11.10.9.8\\
^{12}P_{5}&= 95040\\
end{aligned}$$
Hence, the total number of ways 5 students can be lined for a picture will be 95040.
$$begin{aligned}
^{n}C_{r} &= dfrac{^{n}P_{r}}{(r!)}\\
^{n}C_{r} &= dfrac{n!}{(n-r)! r!}\
end{aligned}$$
where,
$n$ represents the number of members.
$r$ represents the number of students.
^{12}C_{5} &= dfrac{^{12}P_{5}}{5!}\\
^{12}C_{5} &= dfrac{95040}{5!}\\
^{12}C_{5} &= dfrac{95040}{5.4.3.2.1}\\
^{12}C_{5} &= dfrac{95040}{120}\\
^{12}C_{5} &= 792\\
end{aligned}$$
Hence, 792 students are chosen to visit the rival school before the big game.
$(b.)$ $792$

As per the figure, we get,
tantheta &= dfrac{opp}{adj}\\
tan (24degree) &= dfrac {36}{x}\\
x &= dfrac {36}{tan 24degree}\\
x &= 80.85
end{aligned}$$

As per the figure, we get
$$begin{aligned}
dfrac{Sin A}{a} &= dfrac{Sin B}{b}\\
end{aligned}$$
Put the given values in the equation.
$$begin{aligned}
dfrac{Sin 23degree}{10} &= dfrac{Sin 70degree}{x}\\
end{aligned}$$
Cross multiply the equation to get the value of $x$.
$$begin{aligned}
Sin (23degree).x &= 10. Sin(70degree)\\
x &= dfrac{10.Sin 70degree}{sin 23degree}\\
x &= dfrac{9.3969}{0.390}\\
x &approx 24.05\
end{aligned}$$

As per the figure, we get
$$begin{aligned}
a^{2} &= b^{2} + c^{2} – 2.b.c.CosA
end{aligned}$$
Put the given values in the equation.
$$begin{aligned}
(3)^{2} &= (10)^{2} + (11)^{2}+2.10.11.Cos(x)\\
9 &= 100+121+220.Cos(x)\\
220.Cos(x) &= 221-9\\
Cosx &= dfrac {212}{220}\\
Cosx &= 0.9636\\
x &= Cos^{-1}(0.9636)\\
x &approx 15.50
end{aligned}$$
$(b.)$ $24.05$
$(c.)$ $15.50$
Find the amplitude |a|. So,
$$begin{aligned}
text{ Amplitude} &= 4\
end{aligned}$$
Now, find the period (b).
The period of the function can be calculated using
$$begin{aligned}
dfrac{2pi}{|b|}\
end{aligned}$$
Replace $b$ with 1 in the formula for the period.
$$begin{aligned}
dfrac{2pi}{|1|}\
end{aligned}$$
The absolute value is the distance between a number and zero. The distance between 0 and 1 is 1.
Divide 2 pi by 1.
$$begin{aligned}
text{ Period} &= 2pi\
end{aligned}$$
Phase Shift = 0
As per the values.
So, the given graph is that of a Sine function, having the same period 2 pi, vertically stretched by a factor of 4 and shifted up by 2 units.
The equation is given below:
$$begin{aligned}
y &= 4cdot sin x + 2\
end{aligned}$$
$$begin{aligned}
cx – a &= b\\
end{aligned}$$
Adding $a$ on both sides, to solve the equation,
$$begin{aligned}
cx – a+a &= b+a\\
cx &= a+b\\
end{aligned}$$
Divide L.H.S and R.H.S by $c$, to get the value of $x$.
$$begin{aligned}
dfrac{cx}{c} &= dfrac{a+b}{c}\\
x &= dfrac {a+b}{c}\
end{aligned}$$
$$begin{aligned}
dfrac{x}{a} – b^{2}&= c\\
end{aligned}$$
Adding $b^{2}$ on both sides, to solve the equation,
$$begin{aligned}
dfrac{x}{a} – b^{2} + b^{2} &= c + b^{2}\\
dfrac{x}{a} &= c + b^{2}\\
end{aligned}$$
Multiply L.H.S and R.H.S by $a$, to get the value of $x$.
$$begin{aligned}
(a)dfrac{x}{a} &= a(b^{2} + c)\\
x &=ab^{2} + ac\
end{aligned}$$
$$begin{aligned}
(x-a)(x-b) &= 0\\
x-a &= 0, x-b = 0\\
x-a+a &= 0+a, x-b+b =0+b\\
x &= a, x = b
end{aligned}$$
$$begin{aligned}
ax^{3} – acx^{2} &= 0\\
ax^{2} (x-c) &=0\\
ax^{2} &=0 and x-c=0\\
x^{2} &= dfrac{0}{a} and x = c\\
sqrt {x^{2}} &= 0 and x = c\\
x &=0 and x = c
end{aligned}$$
$$begin{aligned}
dfrac {x}{a+b} &= dfrac {1}{c}\\
end{aligned}$$
Multiplying $(a+b)$ on both side i.e L.H.S and R.H.S
$$begin{aligned}
(a+b)dfrac {x}{a+b} &= (a+b) dfrac {1}{c}\\
x &= dfrac {a+b}{c}\\
end{aligned}$$
$$begin{aligned}
dfrac {1}{x^{3}} + a&= b\\
end{aligned}$$
Subtracting $(a)$ on both side i.e L.H.S and R.H.S
$$begin{aligned}
dfrac {1}{x^{3}} + a – a &= b-a\\
dfrac {1}{x^{3}} &= b-a\\
end{aligned}$$
Multiplying $(x^{3})$ on both side i.e L.H.S and R.H.S
$$begin{aligned}
(x^{3})dfrac {1}{x^{3}} &= (x^{3}) (b-a)\\
1 &= (x^{3}) (b-a)\\
end{aligned}$$
Divide $(b-a)$ on both side i.e L.H.S and R.H.S
$$begin{aligned}
dfrac {1}{(b-a)} &= (x^{3})dfrac {(b-a)} {(b-a)}\\
dfrac {1}{(b-a)} &= x^{3}\\
sqrt[3]{dfrac {1}{(b-a)}} &= x\\
end{aligned}$$
$(b.)$ $ab^{2} + ac$
$(c.)$ $x = a, x = b$
$(d.)$ $x = 0 , x = c$
$(e.)$ $dfrac{a+b}{c}$
$(f.)$ $sqrt[3]{dfrac{1}{b-a}}$
Identify the elements of the arithmetic series:
$$begin{aligned}
a_{1} &=1\
d &= 3 – 1\
d &= 2\
end{aligned}$$
$$S_{2} = 2^{2}$$
$$S_{2} = 4$$
In the same way, to get $S_{3}$ add the square of side 2 which we got by adding $a_{1}$ and $a_{2}$ to $a_{2}$ and we get a square of side 3 which means
$$S_{3} = 3^{2}$$
$$S_{3} = 9$$
Therefore,
$$S_{n} = n^{2}$$
$$begin{aligned}
a_{1} &= 1^{2}\
1 &= 1\
end{aligned}$$
$$begin{aligned}
a_{1} +a_{2}+a_{3}+a_{4}+a_{5} &= 5^{2}\
1+3+5+7+9 &= 25\
25 &= 25\
end{aligned}$$
$$begin{aligned}
a_{1} +a_{2}+a_{3}+a_{4}+a_{5}+a_{6} +a_{7} +a_{8} &= 8^{2}\
1+3+5+7+9+11+13+15 &= 64\
64 &= 64\
25 &= 25\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac {n(a_{1}+a_{n})}{2}\\
&= dfrac {n(1+(2n-1))}{2}\\
&= dfrac {n(1+2n-1)}{2}\\
&= dfrac {2n^{2}}{2}\\
&boxed {S_{n} = n^{2}}\
end{aligned}$$
It is not reasonable to try to test all $n$ because there is an infinity of numbers and we cannot do this an infinite number of times.
We need to prove that for the starting point the property is also true. If we want to prove the property is true. for all the positive integers we must prove that $p(1)$ is true, which means that the property is true for $n=1$.
$$= k (k+1)+1(k+1)$$
$$=(k+1) (k+1)$$
$$1 + 3 + 5 + …. + (2n-1)= n^2$$
for all $n geq 1$
$$(2(1)- 1)^2= (1)^2$$
$$(2-1)^2= 1$$
$$1=1rightarrow(text{True for n = 1})$$
$$begin{aligned}
1 + 3 + 5 + …. + (2(k)-1)&= k^2\
1 + 3 + 5 + …. +(2k-1)&=k^2rightarrow(1)
end{aligned}$$
$$begin{aligned}
1 + 3 + 5 + …. +(2k – 1)+ (2(k+1)-1)&= (k+1)^2rightarrow(2)\
end{aligned}$$
Solving left-hand side of equation (2):
$$begin{aligned}
&= 1 + 3 + 5 + …. +(2k – 1)+ (2(k+1)-1)\
&= 1 + 3 + 5 + …. +(2k – 1)+ (2k+2-1)\
&= 1 + 3 + 5 + …. +(2k – 1)+ (2k+1)\
&= k^2 + 2k + 1\
text{Factorizing,}\
&= k^2+ k+k+1\
&= k (k+1)+1(k+1)\
&= (k+1) (k+1) text{or} k^2
end{aligned}$$
Hence, the above series is true for every value of $n geq 1$.

Conclusion: We conclude that the series is true for every value of $n geq 1$.
We will use the value $n =1$ in order to demonstrate the relationship is true at the first step.
Mathematical explanation is shown below:
$$n = dfrac{n(n+1)}{2}$$
for , $n = 1$
$$1 = dfrac{1(1+1)}{2}$$
$$1= dfrac{1(2)}{2}$$
$$1= dfrac{2}{2}$$
$$1=1rightarrow(TRUE, text{for} n = 1)$$
For $n = k+1$.
$$begin{aligned}
1 + 2 + 3 + ………. n&= dfrac{n(n+1)}{2}\
text{Put , n = k+1.}\
1 + 2 + 3 + ………. k+1&= dfrac{k+1(k+1+1)}{2}\\
&boxed{1 + 2 + 3 + ………. k+1=dfrac{(k+1)(k+2)}{2}}\\
end{aligned}$$
Since,
$$begin{aligned}
1 + 2 + 3 + ………. k&= dfrac{k(k+1)}{2}rightarrow(1)\
text{Also,}\
1 + 2 + 3 + ………. k + k+1&= dfrac{k(k+1)}{2}\\
1 + 2 + 3 + ……….k+k+1&=dfrac{(k+1)(k+2)}{2} rightarrow(2)\\
end{aligned}$$
Solving the left hand side of the above equation and from(1), we can say that
$$begin{aligned}
&= dfrac{k(k+1)}{2} +k + 1\\
&= dfrac{k^2+k+2k+2}{2}\\
&=dfrac{k^2+3k + 2}{2}\\
&= dfrac{k^2+2k + 1k + 2}{2}\\
&= dfrac{k(k+2)+1(k+2))}{2}\\
&= dfrac{(k+1)(k+2)}{2}rightarrow(text{True})\\
end{aligned}$$
Therefore by mathematical induction we concluded that the result is true for every $n$ natural number greater than one.
$$begin{aligned}
p(n): 2+4+6+……+ 2n = n(n+1)
end{aligned}$$
Prove $p(1)$ is true.
$$begin{aligned}
2 cdot 1 &= 1(1+1)\
2 &= 2\
end{aligned}$$
Thus, $p(1)$ is true.
For $p(k)$
$$begin{aligned}
p(k): 2+4+6+…….2k &= k(k+1)\
end{aligned}$$
For $p(k+1)$
$$begin{aligned}
p(k+1): 2+4+6+…….2k+ 2(k+1) &= (k+1)(k+2)\
end{aligned}$$
$$begin{aligned}
2+4+6+…….2k &= k(k+1)\
2+4+6+…….2k + 2(k+1) &= k(k+1)+ 2(k+1)\
2+4+6+…….2k + 2(k+1) &= (k+1)+(k+2)\
end{aligned}$$
Thus, $p(k)$ is true and $p(k+1)$ is also true, which means that now both steps are accomplished and the property is proved.
$p(n): 5+8+11+…….+ (3n+2) = dfrac{n(3n+7)}{2}$
Prove $p(1)$ is true.
$$begin{aligned}
3 cdot 1 + 2 &= dfrac{1(3 cdot 1+7)}{2}\\
3+2 &= dfrac{1(10)}{2}\\
5 &= 5\\
end{aligned}$$
Thus, $p(1)$ is true.
For $p(k)$
$$begin{aligned}
p(k): 5+8+11+…….+ (3k+2) &= dfrac{k(3k+7)}{2}\
end{aligned}$$
For $p(k+1)$
$$begin{aligned}
p(k+1): 5+8+11+…….+ (3k+2) + (3(k+1)+2) &= dfrac{(k+1)(3(k+1)+7)}{2}\\
p(k+1): 5+8+11+…….+ (3k+2) + (3(k+1)+2) &= dfrac{(k+1)(3k+10)}{2}\\
end{aligned}$$
$$begin{aligned}
p(k): 5+8+11+…….+ (3k+2) &= dfrac{k(3k+7)}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{k(3k+7k)}{2} + (3k+5)\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k^{2} + 7k + 2(3k+5)}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k^{2} + 7k + 6k+10}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k^{2} + 13k +10}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k^{2} + 3k + 10k +10}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k(k + 1) + 10(k +1)}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{3k(k + 1) + 10(k +1)}{2}\\
5+8+11+…….+ (3k+2)+(3k+5) &= dfrac{(k + 1)(3k+10)}{2}\\
end{aligned}$$
Thus, $p(k)$ is true and $p(k+1)$ is also true, which means that now both steps are accomplished and the property is proved.
$$begin{aligned}
p(n): 1^{2}+2^{2}+3^{2}+…….+ n^{2} = dfrac{n(n+1)(2n+1)}{6}
end{aligned}$$
Prove $p(1)$ is true.
$$begin{aligned}
1^{2} &= dfrac{1(1+1)(2 cdot 1+1)}{6}\
1 &= dfrac{6}{6}\
1 &= 1\
end{aligned}$$
Thus, $p(1)$ is true.
For $p(k)$
$$begin{aligned}
p(k): 1^{2}+2^{2}+3^{2}+…….+ k^{2} &= dfrac{k(k+1)(2k+1)}{6}\\
end{aligned}$$
For $p(k+1)$
$$begin{aligned}
p(k+1): 1^{2}+2^{2}+3^{2}+…….+ k^{2}+ (k+1)^{2} &= dfrac{(k+1)(k+2)(2(k+1)+1)}{6}\\
p(k+1): 1^{2}+2^{2}+3^{2}+…….+ k^{2}+ (k+1)^{2} &= dfrac{(k+1)(k+2)(2k+3)}{6}\\
end{aligned}$$
$$begin{aligned}
p(k): 1^{2}+2^{2}+3^{2}+…….+ k^{2} &= dfrac{k(k+1)(2k+1)}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{k(k+1)(2k+1)}{6} + (k+1)^{2}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{k(k+1)(2k+1) + 6(k+1)^{2}}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{(k+1)(2k^{2}+k + 6k+6)}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{(k+1)(2k^{2}+7k+6)}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{(k+1)(2k^{2}+4k+3k+6)}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{(k+1)(2k(k+2)+3(k+2)}{6}\\
1^{2}+2^{2}+3^{2}+…….+ k^{2} + (k+1)^{2} &= dfrac{(k+1)(k+2)(2k+3)}{6}\\
end{aligned}$$
Thus, $p(k)$ is true and $p(k+1)$ is also true, which means that now both steps are accomplished and the property is proved.
$$begin{aligned}
p(n):1 + 2+ 3+……+ n = dfrac {n(n+1)}{2}
end{aligned}$$
Prove $p(1)$ is true.
$$begin{aligned}
1 &= dfrac {1(1+1)}{2}\\
1 &= dfrac {2}{2}\\
1 &= 1
end{aligned}$$
Thus, $p(1)$ is true.
For $p(k)$
$$begin{aligned}
p(k):1 + 2+ 3+……+ k = dfrac {k(k+1)}{2}\\
end{aligned}$$
For $p(k+1)$
$$begin{aligned}
p(k+1): 1 + 2+ 3+……+ k+ (k+1)= dfrac {(k+1)(k+2)}{2}\\
end{aligned}$$
$$begin{aligned}
1 + 2+ 3+……+ k = dfrac {k(k+1)}{2}\\
1 + 2+ 3+……+ k+ (k+1)= dfrac {k(k+1)}{2}+(k+1)\\
1 + 2+ 3+……+ k+ (k+1)= dfrac {k(k+1)+2(k+1)}{2}\\
1 + 2+ 3+……+ k+ (k+1)= dfrac {(k+1)(k+2)}{2}\\
end{aligned}$$
Thus, $p(k)$ is true and $p(k+1)$ is also true, which means that now both steps are accomplished and the property is proved.
$$dfrac{3k^2 + 7k}{2}+ 3k + 5 = dfrac{3k^2+13k+10}{2}rightarrow(1)$$
$$begin{aligned}
&=dfrac{3k^2+7k + 2(3k + 5)}{2}\\
&= dfrac{3k^2+7k+ 6k + 10}{2}\\
&= dfrac{3k^2+13k+10}{2}rightarrow(text{Equivalent to right-hand side})\\
end{aligned}$$
$$21, 26,31, 36, 41,………..$$
Since, the difference between first term and second term $(i.e. 26-21 = 5)$ and the difference between the second term and third term $(i.e. 31-26 = 5)$ is equal. Thus, the given series is an Arithmetic Progression.
$$begin{aligned}
text{First term}, a&= 21\
text{Common Difference}, d&= 5\
end{aligned}$$
$$begin{aligned}
a_n&= a + (n-1)d\
a_{11}&= 21+ (11-1)5\
a_{11}&= 21+ 10(5)\
a_{11}&=21+ 50\
&boxed{a{11}=71}
end{aligned}$$
$$begin{aligned}
S_n&= dfrac{n}{2}[a + a_{n}]\
text{Substituting the values,}\
S_{11}&= dfrac{11}{2}[21+ 71]\\
S_{11}&= 5.5 (92)\\
&boxed{S_{11}=506}
end{aligned}$$
$$2 + 4 + 6+ ……$$
$$begin{aligned}
text{First term}, a &= 2\
text{Common difference}, d&= 2\
end{aligned}$$
$sum 2n, n= 1 text{to} 10$.
On putting $n = 10$. The sum calculates as follows:
$$2(10)= 20$$
Multiples of 7 between 0 and 500 =
$$begin{aligned}
7,14,21,……….,497 text { i.e,}\\
S_{n} &= 0+ 7cdot1 + 7cdot 2 + 7 cdot 3 + 7 cdot 4+…………+7 cdot n\
end{aligned}$$
This forms an Arithmetic progression.
Common difference, $d = 14 – 7 = 7$
$a_{n} = 497$
Now, The formula of $n^{th}$ term,
$$begin{aligned}
a_{n} &= a + (n – 1) cdot d\\
497 &= 7 + (n – 1) cdot 7\\
497 – 7 &= (n-1) cdot 7\\
(n-1) &= dfrac{490}{7}\\
n &= 70+1\\
&boxed {text {n} =71}\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{n}{2}(a+a_{n})\\
S_{71} &= dfrac{71}{2}(7 + 497)\\
S_{71} &= dfrac{71}{2}(504)\\
S_{71} &= 252cdot 71\\
&boxed {S_{71} = 17892}\\
end{aligned}$$
Hence the sum of all multiples of 7 between 0 and 500 is 17892
b. At $x=0$ we obtain $y=sin{0}=0$ and thus $(0,0)$ has to lie on the graph. At $x=pi$ we note that $y=sin{2pi}=0$ and thus $(pi,0)$ also has to lie on the graph. Then only graph 4 is possible.
c. At $x=0$ we obtain $y=sin{0}=0$ and thus $(0,0)$ has to lie on the graph. At $x=pi$ we note that $y=2sin{dfrac{pi}{2}}=2(1)=2$ and thus $(pi,2)$ also has to lie on the graph.Then only graph 5 is possible.
d. At $x=0$ we note that $y=sin{0}-3=-3$ and thus $(0,-3)$ also has to lie on the graph. Then only graph 3 is possible.
e. At $x=0$ we note that $y=-sin{left(-dfrac{pi}{4}right)}=dfrac{sqrt{2}}{2}approx 0.7$ and thus $(0,0.7)$ also has to lie on the graph. Then only graph 1 is possible.
b. 4
c. 5
d. 3
e. 1
The graph of $y=sinleft(x+dfrac{pi}{2}right)$ is the same as the graph of $y=sinleft(xright)$ translated $dfrac{pi}{2}$ units to the left which is figure (2)
b)
The graph of $y=sinleft(2xright)$ is the same as the graph of $y=sinleft(xright)$ horizontally shrinked with a scale factor of $dfrac{1}{2}$ which is figure (4)
c)
The graph of $y=2sinleft(dfrac{x}{2}right)$ is the same as the graph of $y=sinleft(xright)$ horizontally stretched with a scale factor of $2$ and vertically stretched with a scale factor of $2$ which is figure (5)
d)
The graph of $y=sinleft(xright)-3$ is the same as the graph of $y=sinleft(xright)$ translated vertically downwards $3$ units which is figure (3)
e)
The graph of $y=-sinleft[2 left(x-dfrac{pi}{8}right)right]$ is the same as the graph of $y=sinleft(xright)$ translated horizontally to the right $dfrac{pi}{8}$ units, horizontally shrinked with a scale factor of $dfrac{1}{2}$ and reflected through the $x-$axis which is figure (1)
figure (2)
b)
figure (4)
c)
figure (5)
d)
figure (3)
e)
figure (1)
$$
begin{align*}
logleft(8^{2/3}right)&=left(2/3right)log 8 tag{Using log property $log_{a}b^c=clog_{a}b$}\ \
&=dfrac{2}{3} log 8 tag{Simplifying}
end{align*}
$$
$textbf{b.)}$
$$
begin{align*}
-2log(5)&=log 5^{(-2)} tag{Using log property $clog_{a}b=log_{a}b^c$}\ \
&=log_{}left(frac{1}{25}right) tag{Simplifying}
end{align*}
$$
$textbf{c.)}$
$$
begin{align*}
log(na)^{ba}&=left(abright)log (na) tag{Using log property $log_{a}b^c=clog_{a}b$}\ \
&=(ab)[log n+log a] tag{Using log property $log ab=log a+log b$}\ \
&=ablog n+ablog a tag{Simplifying}\
end{align*}
$$
logleft(8^{2/3}right)=dfrac{2}{3} log 8
$$
$$begin{aligned}
h &= -4.9 t^{2} + 49t +11.27\\
end{aligned}$$
The height of the platform is the height at $t = 0$.
$$begin{aligned}
h &= -4.9 (0)^{2} + 49 (0) +11.27\\
&boxed {h = 11.27 text {m}}\
end{aligned}$$
$$begin{aligned}
h &= -4.9 t^{2} + 49t +11.27\
end{aligned}$$
On comparing the given equation form to the standard parabolic form,
$$begin{aligned}
y &=ax^{2} + bx +c\
end{aligned}$$
$$begin{aligned}
x &= -dfrac {b}{2a}\\
x &= -dfrac {49}{2 (-4.9)}\\
&boxed {x =5}\
end{aligned}$$
The maximum height is then obtained at $t = 5$.
$$begin{aligned}
h &= -4.9 (5)^{2} + 49 (5) +11.27\\
h &= -4.9 cdot 25 + 245 + 11.27\
&boxed {h = 133.77 text { m}}\
end{aligned}$$
$$begin{aligned}
t &= dfrac{- b pmsqrt{ b^{2} – 4 cdot a cdot c}}{2a}\\
t &=dfrac{- 49 pmsqrt{ (49)^{2} – 4 cdot (-4.9) cdot (11.27)}}{2cdot (-4.9)}\\
t &= dfrac{- 49 pmsqrt{2621.892}}{-9.8}\\
t &= dfrac{- 49 pm 51.20}{-9.8}\\
&boxed {t = -0.22 text{ or } 10.22}\
end{aligned}$$
Since only the positive times make sense, we know that it took $10.22$ s to hit the ground.
$(b.)$ 133.77 m
$(c.)$ 10.22 s
$$9 + 14 + 19 + ….. + (4n + 5)= n (2n + 7)$$
Checking whether the series is true for $n geq 1$.
$$boxed{4 (1) + 5 = 1(2(1) + 7)}$$
Solving further,
$$begin{aligned}
4 + 5& = 2 + 7\
9 &= 9rightarrow(text{TRUE})\
end{aligned}$$
$$9 + 14 + 19 + ….. + (4k + 5)=k (2k + 7)rightarrow(1)$$
$$9 + 14 + 19 + ….. +(4k + 5)+(4(k+1) + 5)=k+1 (2(k+1) + 7)$$
$$9 + 14 + 19 + ….. +(4k + 5)+(4(k+1) + 5)=k+1 (2k+2 + 7)$$
$$9 + 14 + 19 + ….. +(4k + 5)+(4(k+1) + 5)=k+1 (2k+9)$$
Solving further,
$$begin{aligned}
&=9 + 14 + 19 + …..+(4k+5) + (4k+4 + 5)\
text{From (1),}\
&=k (2k+7)+ (4k+ 9)\
&= 2k^2 + 7k + 4k + 9\
&= 2k^2 + 11k+9\
text{Factorizing,}\
&= 2k^2+ 2k + 9k+9\
&= 2k(k + 1)+ 9 (k + 1)\
&= (2k+9) (k+1)rightarrow(text{TRUE})\
end{aligned}$$
Kari proved that
$$3+6+9+…. + 3n = dfrac{3}{2}n(n +1)$$
It is true for all integer $n geq 2$.
She verified the following result:
$3 + 6 + 9 + …….+3n = dfrac{3}{2}n (n +1)$
It is true for $n = 1$.
5,-2,-9 ,- 16, …
The arithmetic sequence is stated as follows.
$$begin{aligned}
a_{n} &= a_{1} + (n-1)d\
end{aligned}$$
where,
n is the $n^{th}$ term : 50
$a_{1}$ is the first term: 5
d is the common difference between the terms i.e (-2 – 5) = – 7
$$begin{aligned}
a_{n} &= a_{1} + (n-1)d\
a_{50} &= 5 + (50-1)cdot (-7)\
a_{50} &= 5+49 cdot (-7)\
a_{50} &= 5 – 343\
&boxed {a_{50} = -338}\
end{aligned}$$
$$begin{aligned}
S_{n} &= n left(a_{1}+ dfrac {(n-1)d}{2}right)\\
end{aligned}$$
Put the value in the above formula.
$$begin{aligned}
S_{50} &= 50 left(5 + dfrac {(50-1) cdot (-7)}{2}right)\\
S_{50} &= 50 left(5 + dfrac {(49) cdot (-7)}{2}right)\\
S_{50} &= 50 left(5 + dfrac {-343}{2}right)\\
S_{50} &= 50 (-166.5)\\
&boxed {S_{50} = -8325}\\
end{aligned}$$
$$(b.) -8325$$
1 + 4 + 7 + 10 + 13 + 16
The above-given series is an arithmetic sequence.
The arithmetic sequence is stated as follows.
$$begin{aligned}
a_{n} &= a_{1} + (n-1)d\
end{aligned}$$
where,
$a_{1}$ is the first term : 1
d is the common difference between the terms i.e (4 – 1) = 3
$$begin{aligned}
a_{n} &= a_{1} + (n-1)d\
a_{n} &= 1 + (n-1)cdot (3)\
a_{n} &= 1 + (n-1) cdot (3)\
a_{n} &= 1 + 3 text {n} -3\
&boxed {a_{n} = 3 text{n}-2}\
end{aligned}$$
$$begin{aligned}
displaystylesum_{k=1}^n a_{n}\
end{aligned}$$
Where,
k = 1 $rightarrow$ begin at smallest value
n $rightarrow$ end at greatest value
$a_{n}$ $rightarrow$ sequence formula
$$begin{aligned}
boxed {displaystylesum_{k=1}^6 (3 text{n}-2)}\
end{aligned}$$
$$begin{aligned}
tan(theta) &= dfrac{1}{2}\\
end{aligned}$$
$tan(theta)$ is positive in the third quadrant.
and
$$begin{aligned}
pi < theta <dfrac{3pi}{2}\
end{aligned}$$
means, $theta$ will be in the third quadrant.
$$begin{aligned}
tan(theta) &= dfrac{y}{x} = dfrac{text{opp}}{text {adj}} = dfrac{1}{2}\\
end{aligned}$$
Determine the value of $sin(theta)$,
$$begin{aligned}
sin(theta) &= dfrac{text{opp}}{text {hyp}}\
end{aligned}$$
$$begin{aligned}
a^{2} + b^{2} &= c^{2}
end{aligned}$$
Put the values in above formula,
$$begin{aligned}
1^{2} + 2^{2} &= c^{2}\
1+ 4 &= c^{2}\
5 &= c^{2}\
&boxed {c = sqrt{5}} rightarrowtext{hyp.}\
end{aligned}$$
$$begin{aligned}
sin(theta) &= dfrac{text{opp}}{text {hyp}}\\
&boxed {sin(theta) = dfrac{-1}{sqrt{5}}}\\
end{aligned}$$
$$tan theta = dfrac{1}{2}$$
Range $rightarrow pi leq theta leq dfrac{3pi}{2}$
Since we know that,
$tan theta = dfrac{text{Perperdicular}}{text{Base}}$
Thus, we conclude that
$$boxed{text{Perpendicular} rightarrow 1}$$
$$boxed{text{Base} rightarrow 2}$$
$$begin{aligned}
text{Hypotenuse}&= sqrt{(text{Base})^2+ (text{Perpendicular})^2}\
text{Substituting the values,}\
text{Hypotenuse}&=sqrt{(2)^2+(1)^2}\
text{Hypotenuse}&=sqrt{4+1}\
&boxed{text{Hypotenuse}=sqrt{5}}\
end{aligned}$$
$$sin theta = dfrac{text{perpendicular}}{text{Hypotenuse}}$$
Thus,
$$boxed{sintheta= dfrac{1}{sqrt{5}}}$$
$$begin{aligned}
text {h} &= 2.5 text {ft}\
text {h} &= 2.5 cdot 12\
text {h} &= 30 text { inches}\
text {Circumference} &= 2pi text {r}\
14 &= 2pi text {r}\
dfrac {14}{2 pi} &= text {r}\
dfrac {14}{2cdot 3.14} &= text {r}\
text {r} &approx 2.23 text { inches}\
end{aligned}$$
$$begin{aligned}
text {V} &= pi r^{2} cdot h\
text {V} &= 3.14 cdot (2.23)^{2} cdot 30\
&boxed {text {V} = 468.68 text { cubic meter}}\
end{aligned}$$
Now determine the quantity of dirt.
$$begin{aligned}
75 text { Percent of volume} &= dfrac {75}{100} cdot (text {V})\\
&= 0.75 cdot (text {V})\
&= 0.75 cdot 468.68\
&boxed {355.51 text { cubic inches}}\
end{aligned}$$
$(b.)$ 355.51 Cubic inches.
$$
y=10cdot 5^{n-1}=2cdot 5 cdot 5^{n-1}=2cdot 5^{n-1+1}=2cdot 5^n
$$
b. The advange of the equation of Katelyn is that it is easier to determine the graph, while the equation of Janelle makes it easier to determine the first and consecutive terms.
c.
$$
t(n)=18cdot 3^n=18cdot 3 cdot 3^{n-1}=54cdot 3^{n-1}
$$
b. See explanation
c. $t(n)=54cdot 3^{n-1}$
$$
t(n)=1,500,000(1.05)^{n-1}
$$
b. Replace $n$ with 20:
$$
t(20)=1,500,000(1.05)^{19}=$3,790,425.29
$$
c.
$$
Sigma_{n=1}^{20} (1,500,000(1.05)^{n-1})
$$
d. The sum of a geometric serie with $n$ terms is:
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
b. $3,790,425.29
c.$Sigma_{n=1}^{20} (1,500,000(1.05)^{n-1})$d.$a$dfrac{1-r^n}{1-r} with$a$the first term and$r$ the ratio.
begin{tabular}{lllllllll}
& $s(6)$ & = & 2 & +10 & +50 & +250 & +1250 & +6250 \
+ & $s(6)$ & = & 6250 & +1250 & +250 & +50 & +10 & +2 \ hline
& $2s(6)$ & = & 6252 & +1260 &+ 300 & +300 & +1260 &+ 6252
end{tabular}
begin{align*}
2s(6)&= 2(6252 +1260 + 300 ) \
2s(6)&= 2(7812)\
s(6)&=7812
end{align*}
It can be observed that it doesn’t simplify the process instead makes it more complex than before\
textbf{(b)} Using Luann’s method we have below result:\\
begin{align*}
s(6)&=2+10+50+250+1250+6250\
rcdot s(6)&=5(s(6))\
&=5(2+10+50+250+1250+6250)\
&=10+50+250+1250+6250+31250
intertext{Evaluating $5(s(6))-s(6)$:}
5(s(6))-s(6)&=(10+50+250+1250+6250+31250)-(2+10+50+250+1250+6250)\
4(s(6))&=10+50+250+1250+6250+31250-2-10-50-250-1250-6250\
4s(6)&=31250-2\
4s(6)&=31248\
s(6)&=textcolor{blue}{7812}
end{align*}
begin{align*}
s(n)&=2+10+50+dots+2cdot5^{n-1}\
rcdot s(n)&=5(s(n))\
&=5(2+10+50+dots+2cdot5^{n-1})\
&=10+50+250+dots+2cdot5^{n}
intertext{Evaluating $5(s(6))-s(6)$:}
5(s(n))-s(n)&=(10+50+250+dots+2cdot5^{n})-(2+10+50+dots+2cdot5^{n-1})\
4s(n)&=2cdot5^{n}-2\
4s(n)&=2(5^{n}-1)\
s(n)&=textcolor{blue}{dfrac{(5^{n}-1)}{2}}
end{align*}
s(n)=dfrac{(5^{n}-1)}{2}
$$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
b. Sum of the first 37 terms:
$$
30dfrac{1-1.2^{37}}{1-1.2}=-150(1-1.2^{37})approx 127,434
$$
Sum of the first 99 terms:
$$
30dfrac{1-1.2^{99}}{1-1.2}=-150(1-1.2^{99})approx 1,035,224,667
$$
The sum of the 38th through the 99th term is then:
$$
1,035,224,667-127,434=1,035,097,233
$$
b. $1,035,097,233$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
Option 1:
$$
51% times $50,000,000(1.04)^{20}=$ 55,873,640.15
$$
Option 2:
$$
$1,500,000dfrac{1-1.05^{20}}{1-1.05}approx $49,598,931
$$
Thus option 1 is better.
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a.
$$
51% times $50,000,000=$25,500,000
$$
b.
$$
$25,500,000(1.04)^{20}=$ 55,873,640.15
$$
c. No, it is a sequence.
b. $ 55,873,640.15
c. No
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a.
$$
$1,500,000(1.05)^{2}=$ 1,653,750
$$
$$
$1,500,000(1.05)^{5}=$ 1,914,422
$$
b.
$$
$1,500,000dfrac{1-1.05^{n}}{1-1.05}
$$
c.
$$
$1,500,000dfrac{1-1.05^{20}}{1-1.05}approx $49,598,931
$$
b.$$1,500,000dfrac{1-1.05^{n}}{1-1.05}$
c. $49,598,931
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
Option 1:
$$
51% times $50,000,000(1.04)^{20}=$ 55,873,640.15
$$
Option 2:
$$
$1,500,000dfrac{1-1.05^{20}}{1-1.05}approx $49,598,931
$$
Thus option 1 is better.
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a.
$$
t(n)=0.1(1+0.02)^{n-1}=0.1(1.02)^{n-1}
$$
b. Replace $n$ with 100:
$$
t(100)=0.1(1.02)^{99}=$0.71
$$
Replace $n$ with 200:
$$
t(200)=0.1(1.02)^{199}=$5.15
$$
c. 150 pieces:
$$
0.1dfrac{1-1.02^{150}}{1-1.02}=$92.50
$$
200 pieces:
$$
0.1dfrac{1-1.02^{200}}{1-1.02}=$257.42
$$
d.
$$
t(n)=0.1+0.01(n-1)=0.1n
$$
Replace $n$ with 100:
$$
t(100)=0.01(100)=$1
$$
Replace $n$ with 200:
$$
t(200)=0.1(200)=$2
$$
$$
t(150)=0.1(150)=$1.50
$$
The sum is then:
$$
dfrac{(0.1+1.5)150}{2}=$120
$$
Thus we note that Greg’s payment scheme results in more money.
f. Greg’s method gives:
$$
dfrac{(0.1+2)200}{2}=$210
$$
Thus we note that Scott’s payment scheme gives more money.
b. $$0.71$, $$5.15$
c. $$92.50$, $$257.42$
d. Greg’s payment scheme results in more money.
e. Scott’s payment scheme results in more money.
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a.
$$
t(n)=15-0.35n
$$
Replace $n$ with 2:
$$
t(2)=15-0.35(2)=14.3
$$
Replace $n$ with 7:
$$
t(7)=15-0.35(7)=12.55
$$
The last bucket was used in week 12:
$$
t(12)=15-0.35(12)=10.8
$$
b. We note that this series is arithmetic, because the common difference is 0.35 gallons.
c.
$$
dfrac{(14.65+10.8)12}{2}=152.70
$$
b. Arithmetic
c. $152.70
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. Since every child has two parents: $1,2,4$
b. The sequence is geometric since the common ratio is 2.
c.
$$
t(n)=2^{n-1}
$$
Evaluate at $n=12$:
$$
t(12)=2^{11}=2,048
$$
Then the total number of ancestors in the first 12 generations are:
$$
1dfrac{1-2^{12}}{1-2}=4,095
$$
b. Geometric
c. 4,095
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. Geometric since the common ratio is 2:
$$
5dfrac{1-2^{16}}{1-2}=327,675
$$
b. Arithmetic, since the common difference is 4:
$$
dfrac{(16-696)179}{2}=-60,860
$$
c. Arithmetic, since the common difference is 4:
$$
dfrac{(4+392)98}{2}=19,404
$$
d. Arithmetic, since the common difference is 11:
$$
dfrac{(11+3,432)312}{2}=537,108
$$
e. Geometric since the common ratio is $dfrac{1}{2}$:
$$
5dfrac{1-0.5^{12}}{1-0.5}=9.99755859375
$$
b. Arithmetic: $-60,860$
c. Arithmetic, 19,404
d. Arithmetic, 537,108
e. Geometric, $9.99755859375$
$$S(n)=dfrac{(a+l)n}{2}$$
where $n$ is number of terms in series, $a$ is first term and $l$ is last term\\
According to given data:
begin{align*}
dfrac{(12+(-9+21n))n}{2}&=3429\
dfrac{(3+21n)n}{2}&=3429\
3n+21n^2&=6858\
3(7n^2+n-2286)&=0\
7n^2+n-2286&=0
intertext{Evaluating determinant:}
D&=(1)^2-4(7)(-2286)\
&=1+64008\
&=64009\
&=253^2
intertext{Finding $n$ using determinant method:}
n&=dfrac{-1pm sqrt{253^2}}{2(7)}\
&=dfrac{-1pm 253}{14}\
&=dfrac{252}{14} textrm{ or } dfrac{-254}{14}\
&=18 textrm{ or } -18.1428
end{align*}
As number of terms in a series is always non negative therefore textcolor{blue}{$n=18$}
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
A series is arithmetic if the terms have a common difference and geometric if the terms have a common ratio.
adfrac{1-r^n}{1-r}
$$
$$
a,ar,ar^2,ar^3,ar^4,dots,ar^{n-1}
$$
Where is as a geometric series is sum of terms of a geometric sequence as shown below:
$$
a+ar+ar^2+ar^3+ar^4+dots+ar^{n-1}
$$
To find sum of a geometric series we multiply $r$ with the series itself and then subtract the ordinal series from it as shown below:
$$
begin{align*}
rS(n)-S(n)&= r(a+ar+ar^2+ar^3+ar^4+dots+ar^{n-1})-(a+ar+ar^2+ar^3+ar^4+dots+ar^{n-1})\
(r-1)S(n)&= ar+ar^2+ar^3+ar^4+dots+ar^n-a-ar-ar^2-ar^3-ar^4-dots-ar^{n-1})\
(r-1)S(n)&= ar^n-a\
S(n)&= dfrac{ar^n-a}{r-1}\
S(n)&= adfrac{r^n-1}{r-1}\
textcolor{#4257b2}{S(n)}&textcolor{#4257b2}{= adfrac{1-r^n}{1-r}}\
end{align*}
$$
S(n)= adfrac{1-r^n}{1-r}
$$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. $3, 33, 333, 3333, 33333, 333333$
b.The sum of $n$ terms is the number with $n$ digits and each digit is a 3.
c.$Sigma_{k=1}^n(3cdot 10^{k-1})=333333333($n digits)
b.The sum of $n$ terms is the number with $n$ digits and each digit is a 3.
c.$Sigma_{k=1}^n(3cdot 10^{k-1})=333333333($n digits)
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. The sequence represents the number of graduates in each year while the series represents the total number of graduates of the school up to that year.
b.
$$
dfrac{(42+42+12(9))10}{2}=960
$$
c.
$$
dfrac{(42+42+12(n-1))n}{2}=(42+6(n-1))n=(36+6n)n=6n^2+36n
$$
b. 960 students
c. $6n^2+36n$ invitations
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. The series is arithmetic since the common difference is $-7$. The number of terms is then the difference between the last and first term divided by the common difference, increased by 1:
$$
dfrac{-90-8}{-7}+1=14+1=15
$$
b.
$$
dfrac{(8-90)15}{2}=-615
$$
b. $-615$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
The first term is $8$,
and the difference between the terms is $boldsymbol{-7}$
Because $8-7$ = $1$.
The number of terms is the
difference between the last and first term
divided by the common difference
and incerased by 1.
$$
begin{align*}
t&=frac{-90-8}{-7}+1&&boxed{text{Use the formula}}\
t&=frac{-98}{-7}+1&&boxed{text{Subtract the numbers: }-90-8=-98}\
t&=14+1&&boxed{text{Divide the numbers: } frac{-98}{-7}=14}\\
t&=15&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}t=15} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
The sum of an arithmetic series is
the sum of the first and last term,
multiplied by the number of terms
and divided by 2
$$
begin{align*}
S(n)&=frac{(8-90)n}{2}&&boxed{text{Use the formula}}\
S(15)&=frac{8-90)15}{2}&&boxed{text{Substitute }15 text{ for }n}\
S(15)&=frac{-82cdot15}{2}&&boxed{text{Calculate within parentheses: }8-90=-82}\
S(15)&=frac{-1230}{2}&&boxed{text{Multiply the numbers: }-82cdot15=-1230}\
S(15)&=-615&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}S(15)=-615} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ a) }t=15
$$
$$
color{#4257b2} text{ b) }S(15)=-615
$$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
The series is arithmetic since the common difference is $5$. The sum is then:
$$
dfrac{(15+45)7}{2}=210
$$
Cold Scoop has 18 flavors, $n = 18$.
and
Amelia wants three scoops, $r = 3$.
$$begin{aligned}
^{n}P_{r} &=dfrac{n!}{(n- r)} = n(n-1)(n-2)…….(n-r+1)\
end{aligned}$$
for $n$ items chosen $r$ at a time.
^{18}P_{3} &=dfrac{18!}{(18-3)}\\
^{18}P_{3} &=dfrac{18!}{15!}\\
^{18}P_{3} &= dfrac{18 cdot 17 cdot 16 cdot 15…..cdot1}{15 cdot 14 cdot 13 cdot 12…..cdot1}\\
^{18}P_{3} &= 18 cdot 17 cdot 16 \\
&boxed {^{18}P_{3} = 4896}\
end{aligned}$$
$4896$ different cones can Amelia get if all other scoops are different.
$$begin{aligned}
^{n}C_{r} &=dfrac{^{n}P_{r}}{(r)} \
end{aligned}$$
^{18}C_{3} &=dfrac{4896}{3!}\\
^{18}C_{3} &=dfrac{4896}{3 cdot 2 cdot 1}\\
^{18}C_{3} &=dfrac{4896}{6}\\
&boxed {^{18}C_{3} = 816}\
end{aligned}$$
$816$ ways can she order.
$$(b.) 816$$
$$begin{aligned}
theta &= 34degree\
text{Hyp} &= 124
end{aligned}$$

text{ sin}(theta) &= dfrac{text{opp}}{text{hyp}}\\
text{ sin}(34degree) &= dfrac {text{x}}{124}\\
text {x} &= text{ sin}(34degree) cdot 124\\
text {x} &= text{ sin}(0.559) cdot 124\\
text {x} &= 69.33\\
&boxed {text {x}approx 69.3}\\
end{aligned}$$
$$begin{aligned}
text{A} &= 42degree\
text{a} &= text{x}\
text{b} &= 6\
text{c} &= 8\
end{aligned}$$

This is side-angle-side (SAS)
$$begin{aligned}
text {a}^{2} &= text{b}^{2} + c^{2} -2 cdottext {b} cdot text {c} cdotcos text {A}\
text {x}^{2} &= 6^{2} + 8^{2} -2 cdot 6 cdot 8cdotcos text {42degree}\
text {x}^{2} &= 100 – 96(0.743)\
text {x}^{2} &= 100-71.432\
text {x} &= sqrt{}28.658\
&boxed {text {x}approx 5.35}\\
end{aligned}$$
$$(b.) 5.35$$
b. The graph is the graph of $y=sin(x)$ stretched horizontally by factor $dfrac{1}{4}$ units and stretched vertically by factor $-2$.
$$begin{aligned}
text{ The amount Joe will get at the age of 55}, A&= $30,000\
text{ Rate of interest}, r&= 3%\
&=0.03\
end{aligned}$$
Also, the amount he will get next year can be expressed using the formula stated below.
$$begin{aligned}
A&=P (1 + r)\
end{aligned}$$
Thus, next year amount is given as follows.
$$begin{aligned}
&boxed{A= 30,000(1+0.03)}
end{aligned}$$
The series can be defines as follows.
$30,000 + 30,000(1 + 0.03) + 30,000(1 + 0.03)^{2}+………. 30,000(1 + 0.03)^{n}$
$$begin{aligned}
text{First term}, a&= 30,000\
text{ Common ratio}, r&= 1.03\
text{Number of terms or years}, n&= 80-55 text{ years}\
&= 25\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{a(r^{n-1})}{r-1}\
end{aligned}$$
Since, $r > 1$.
$$begin{aligned}
S_{25}&= dfrac{30,000left[(1.03)^{25}-1
right]}{1.03-1}\\
&=dfrac{30,000(2.09-1)}{0.03}\\
&= dfrac{30,000(1.09)}{0.03}\\
&= dfrac{32,700}{0.03}\\
&=1,090,000\
end{aligned}$$
The amount Joe will get at the age of $80$ is $$1,090,000$ at the rate of $3%$ with the starting pension at $%30,000$ at the age of $55$.
$$begin{aligned}
text{ The amount Joe will get at the age of 65}, A&= $60,000\
text{ Rate of interest}, r&= 3%\
&=0.03\
end{aligned}$$
Also, the amount he will get next year can be expressed using the formula stated below.
$$begin{aligned}
A&=P (1 + r)\
end{aligned}$$
Thus, next year amount is given as follows.
$$begin{aligned}
&boxed{A= 60,000(1+0.03)}
end{aligned}$$
The series can be defines as follows.
$60,000 + 60,000(1 + 0.03) + 60,000(1 + 0.03)^{2}+………. 60,000(1 + 0.03)^{n}$
$$begin{aligned}
text{First term}, a&= 60,000\
text{ Common ratio}, r&= 1.03\
text{Number of terms or years}, n&= 80-65 text{ years}\
&= 15\
end{aligned}$$
$$begin{aligned}
S_{n} &= dfrac{a(r^{n-1})}{r-1}\
end{aligned}$$
Since, $r > 1$.
$$begin{aligned}
S_{15}&= dfrac{60,000left[(1.03)^{25}-1
right]}{1.03-1}\\
&=dfrac{60,000(2.09-1)}{0.03}\\
&= dfrac{60,000(1.09)}{0.03}\\
&= dfrac{65,400}{0.03}\\
&=2,180,000\
end{aligned}$$
The amount Joe will get at the age of $80$ is $$2,180,000$ at the rate of $3%$ with the starting pension at $%60,000$ at the age of $65$.
$y$ be the amount invested at $6%$.
$$begin{aligned}
x+y&= 50,000\
&boxed{x= 50,000 – y}\
end{aligned}$$
Let us assume, if $$1$ invested today.
So, after one year at the rate of the interest of $8%$ the amount of $$1$ will become,
$$begin{aligned}
text{ Amount}, A&= 1 times (1 + 0.08)\
&=$1.08\
end{aligned}$$
Similarly, the amount after one year at the rate of $6.5%$ is given as follows.
$$begin{aligned}
text{ Amount}, A&= 1 times (1 + 0.065)\
&=$1.065\
end{aligned} $$
$$begin{aligned}
&boxed{1.08x + 1.065y = 53,550}\
end{aligned}$$
$$begin{aligned}
1.08(50,000-y) + 1.065y&= 53,550\
54,000- 1.08y + 1.065y &= 53,550\
-0.015y&= 53,550-54,000\
-0.015y&= -450\
y&= dfrac{-450}{-0.015}\
y&=30,000\
end{aligned}$$
$$begin{aligned}
x&= 50,000-30,000\
x&= 20,000\
end{aligned}$$

Concluding the given things,
$$begin{aligned}
QR&= 7 text{cm}\
PQ&= 8 text{cm}\
angle PQR&= 70^o\
angle RSP&= 110^o\
angle SRP &= 35^o\
angle SPR&= 35^o\
end{aligned}$$
$$begin{aligned}
PR^2&= PQ^2 + QR^2 – 2cdot PQ cdot QR cdot cosQ\
text{Substituting the values,}\
PR^2&=8^2 + 7^2 – 2 cdot 8 cdot 7 cdot cos 70^o\
PR^2&= 64 + 49 – 112 cdot 0.34202014\
PR^2&=74. 693744\
text{Taking square root.}
PR&= pm sqrt{74. 693744}\
&boxed{PRapprox 8.64}\
end{aligned}$$
In $triangle PRS$,
$$angle SRP = angle SPR$$
We know that sides opposite to equal angles are also equal.
Thus,
$$SR = PSrightarrow(1)$$
From condition (1), $triangle PRS$ is an isosceles triangle.
$$dfrac{SR}{ sin 35^o}= dfrac{PR}{ sin 110^o}$$
Substituting the values,
$$begin{aligned}
SR&= dfrac{PR sin 35^o}{ sin 110^o}\\
SR&= dfrac{8.64 cdot 0.57357644}{0.93969262}\\
&boxed{SRapprox 5.27}\\
end{aligned}$$
$$begin{aligned}
text{Perimeter}&=PQ + QR + 2SR\
text{Substituting the values,}\
&= 8 + 7 + 2(5.27)\
&= 25.54 text{units}\
end{aligned}$$
$$begin{aligned}
cosleft(dfrac{pi}{3}right)= dfrac{1}{2}
end{aligned}$$
In order to find the three other true statements using the given function an the angles that will be multiple of $dfrac{pi}{3}$, we will set some values for eg. $dfrac{2pi}{3}$, $dfrac{4pi}{3}$, and $dfrac{5pi}{3}$ which are the multiple of $dfrac{pi}{3}$.
$$begin{aligned}
cosleft(dfrac{2pi}{3}right) &= -cosleft(pi-dfrac{2pi}{3}right)\
end{aligned}$$
Since, $cos(x)$ is negative in second quadrant.
Thus,
$$begin{aligned}
cosleft(dfrac{2pi}{3}right) &= -cosleft(dfrac{3pi-2pi}{3}right)\\
&=-cosleft(dfrac{pi}{3}right)\\
&= -dfrac{1}{2}\\
end{aligned}$$
$$begin{aligned}
cosleft(dfrac{4pi}{3}right) &= -cosleft(dfrac{4pi}{3}-piright)\
end{aligned}$$
Since, $cos(x)$ is negative in third quadrant.
Thus,
$$begin{aligned}
cosleft(dfrac{4pi}{3}right) &= -cosleft(dfrac{4pi-3pi}{3}right)\\
&=-cosleft(dfrac{pi}{3}right)\\
&= -dfrac{1}{2}\\
end{aligned}$$
$$begin{aligned}
cosleft(dfrac{5pi}{3}right) &= cosleft(2pi-dfrac{5pi}{3}right)\
end{aligned}$$
Since, $cos(x)$ is positive in fourth quadrant.
Thus,
$$begin{aligned}
cosleft(dfrac{5pi}{3}right) &= cosleft(dfrac{6pi-5pi}{3}right)\\
&=cosleft(dfrac{pi}{3}right)\\
&= dfrac{1}{2}\\
end{aligned}$$
In order to simplify further we will take $x$ common.
$$begin{aligned}
&=x(a+b)\
end{aligned}$$
In order to simplify further we will take $x$ common.
$$begin{aligned}
&=x(a+b)\
end{aligned}$$
using $(a+b)^{2}$ = $a^{2} + 2ab + b^{2}$
$$begin{aligned}
&=dfrac{a(x+1)}{(x+1)^{2}}\\
&= dfrac{a}{x+1}\\
end{aligned}$$
using , $a^{2} – b^{2}$ = $(a+b) (a-b)$
$$begin{aligned}
&=dfrac{(x+b)(x-b)}{a(x+b)}\\
&= dfrac{x-b}{a}\\
end{aligned}$$
$$begin{aligned}
1 + 3& = 4 &= 2^2\
4 + 5&= 9&= 3^2\
9 + 7&= 25&= 5^2\
end{aligned}$$
$$25 + 11 = 36 = 6^2$$
$$1 + 3 + 5 + 7 + ……+ (2n-1)= n^2$$
where , n is a real number.
Given ,
$$begin{aligned}
x^{tfrac{-4}{3}} + 1 &= 17rightarrow(1)
end{aligned}$$
$$begin{aligned}
x^{tfrac{-4}{3}} + 1 -1&= 17-1\
x^{tfrac{-4}{3}}&= 16rightarrow(2)\
end{aligned}$$
$$begin{aligned}
(x^{tfrac{-4}{3}})^{tfrac{1}{4}}&= (16)^{tfrac{1}{4}}\
x^{tfrac{-1}{3}}&= 2^{4(tfrac{1}{4})}\
&boxed{x^{tfrac{-1}{3}}= 2}
end{aligned}$$
Given,
$$log A = a$$
$$begin{aligned}
log (dfrac{m}{n})&= log m – log n\
end{aligned}$$
Thus,
$$begin{aligned}
log (dfrac{A}{100})&= log A – log 100\
&= log A – log 10^{2}\
&= log A – 2\
&boxed{log (dfrac{A}{100})= a – 2}\
end{aligned}$$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. 20 meters, because it travels 10 meters up and 10 meters down.
b.
$$
60% times 10 = 6
$$
Thus the ball will have traveled $20m+6m+6m=32m$
c.
$$
t(n)=20cdot 0.6^{n-1}
$$
d. The sum of the first 15 terms is then:
$$
20dfrac{1-0.6^{15}}{1-0.6}approx 50
$$
b. 32m
c. $t(n)=20cdot 0.6^{n-1}$
d. $50$
The sum of an arithmetic series is the sum of the first and last term multiplied by the number of terms divided by 2. The sum of a geometric series with $n$ terms is:
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
The sum of the first $n$ terms is then:
$$
20dfrac{1-0.6^{n}}{1-0.6}
$$
As $nrightarrow infty$, $0.6^nrightarrow 0$ and thus as $n$ becomes larger and larger, we then obtain that:
$$
20dfrac{1-0.6^{n}}{1-0.6}rightarrow 20dfrac{1}{1-0.6}=50
$$
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
The sum of the first $n$ terms is then:
$$
20dfrac{1-0.6^{25}}{1-0.6}approx 50
$$
$$
20dfrac{1-0.6^{35}}{1-0.6}approx 50
$$
$$
20dfrac{1-0.6^{50}}{1-0.6}approx 50
$$
$$
20dfrac{1-0.6^{100}}{1-0.6}approx 50
$$
As $nrightarrow infty$, $0.6^nrightarrow 0$ and thus as $n$ becomes larger and larger, we then obtain that:
$$
20dfrac{1-0.6^{n}}{1-0.6}rightarrow 20dfrac{1}{1-0.6}=50
$$
50
$$
$$
S_n = A_1cdotfrac{r^n-1}{r-1}
$$
$S_n$ – the sum of first $n$ numbers in the sequence
$A_1$ – first number in the sequence
$r$ – change rate
$n$ – index of numbers in sequence
begin{tabular}{ >{centeringarraybackslash}m{2in} |>{centeringarraybackslash}m{2in} }
$A_1 = 200$ & $A_1 = 200$\
$r = frac{1}{2} = 0.5$ & $r = frac{1}{2} = 0.5$\
$n = 10$ & $n = 30$\
end{tabular}\\
Now we input the known variables into the formula.\\
begin{tabular}{ >{centeringarraybackslash}m{2in} |>{centeringarraybackslash}m{2in} }
$S_{10} = 200 cdot frac{0.5^{10}-1}{0.5-1}$ & $S_{30} = 200 cdot frac{0.5^{30}-1}{0.5-1}$\\
$S_{10} = 399frac{39}{64}$ & $S_{30} approx 400$\
end{tabular}
begin{tabular}{ >{centeringarraybackslash}m{2in} |>{centeringarraybackslash}m{2in} }
$A_1 = 16$ & $A_1 = 16$\
$r = frac{3}{2} = 1.5$ & $r = frac{3}{2} = 1.5$\
$n = 10$ & $n = 30$\
end{tabular}\\
Now we input the known variables into the formula.\\
begin{tabular}{ >{centeringarraybackslash}m{2in} |>{centeringarraybackslash}m{2in} }
$S_{10} = 16 cdot frac{1.5^{10}-1}{1.5-1}$ & $S_{30} = 16 cdot frac{1.5^{30}-1}{1.5-1}$\\
$S_{10} = 1,813frac{9}{32}$ & $S_{30} approx 6,136,001$\
end{tabular}
center$1 1 – $ the sequence is increasing\
$-1 1 -$ the sequence is decreasing\
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
a. $n=10$:
$$
200dfrac{1-0.5^{10}}{1-0.5}approx 399.6
$$
$n=30$:
$$
200dfrac{1-0.5^{30}}{1-0.5}approx 400
$$
b. $n=10$:
$$
16dfrac{1-1.5^{10}}{1-1.5}approx 1,813
$$
$n=30$:
$$
16dfrac{1-1.5^{30}}{1-1.5}approx 6,136,002
$$
c. The common ratio in (a) is smaller than 1 (sequence is decreasing), while the common ratio in (b) is larger than 1 (sequence is increasing).
b. 1813, 6136002
c. Common ratio in (a) is smaller than 1, while common ratio in (b) is larger than 1.
$$
adfrac{1-r^n}{1-r}
$$
with $a$ the first term and $r$ the ratio.
If $r>1$, then the sequence will be increasing and the sum will keep getting larger and larger. If $r<1$, then as $n$ becomes very large: $r^napprox 0$ and thus
$$
adfrac{1-r^n}{1-r}approx adfrac{1}{1-r}
$$
Thus the sum will be approximately $adfrac{1}{1-r}$.
As $nrightarrow infty$, $0.6^nrightarrow 0$ and thus as $n$ becomes larger and larger, we then obtain that:
$$
20dfrac{1-0.6^{n}}{1-0.6}rightarrow 20dfrac{1}{1-0.6}=50
$$
$$
adfrac{1-r^n}{1-r}approx adfrac{1}{1-r}
$$
Thus the sum will be approximately $adfrac{1}{1-r}$.
adfrac{1}{1-r}
$$
$$
S(n)=dfrac{rar^{n-1}-ar^{1-1}}{r-1}=dfrac{ar^n-a}{r-1}
$$
b. Multiply numerator and denominator by $-1$:
$$
S(n)=dfrac{a-ar^n}{1-r}
$$
Factor out $a$ in the numerator:
$$
S(n)=dfrac{a(1-r^n)}{1-r}
$$
c. As $n$ becomes larger and larger: $r^n$ will become closer to zero since $0.6<1$.
d. Since $r^napprox 0$ for very large values of $n$ (if $r<1$), then:
$$
S(n)approxdfrac{a(1-0)}{1-r}=dfrac{a}{1-r}=S
$$
e.
$$
S=dfrac{20}{1-0.6}=dfrac{20}{0.4}=50
$$
$$
Sigma_{n=1}^{infty} left(dfrac{1}{2}right)^n
$$
b. The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{0.5}{1-0.5}=1
$$
c. Zeno is correct, because you obtain 1 (which means that you crossed the whole way) only in the limit.
b. 1
c. Zeno is correct
$$
Sigma_{n=1}^{infty} 0.63left(0.01right)^{n-1}
$$
b. The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{0.63}{1-0.01}=dfrac{0.63}{0.99}=dfrac{63}{99}=dfrac{7}{9}
$$
b. $dfrac{7}{9}$
$$
Sigma_{n=1}^{infty} 0.143left(0.001right)^{n-1}
$$
The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{0.143}{1-0.01}=dfrac{0.143}{0.999}=dfrac{143}{999}
$$
dfrac{143}{999}
$$
$$
Sigma_{n=1}^{infty} 0.9left(0.1right)^{n-1}
$$
The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{0.9}{1-0.1}=dfrac{0.9}{0.9}=1
$$
1
$$
$$
S=dfrac{a}{1-r}
$$
with $a$ the first term of the sequence and $r$ the common ratio.
S=dfrac{a}{1-r}
$$
$$begin{aligned}
text{ Favorable cases of choosing six balls} & = {}^{49}C_6\
text{ Total number of cases} & = {}^{49}C_{49} \
end{aligned}$$
$$begin{aligned}
P(E_{1}) & = dfrac{text{ Favorable Cases}}{text{ Total number of cases}}\\
&= dfrac{{}^{49}C_6}{{}^{49}C_{49}}\\
&= dfrac{dfrac{49!}{(43!)(6!)}}{dfrac{49!}{(49!)(0!)(49!)}} \\
&= dfrac{49times 48 times times 47times 46times 45 times 44 times 43!}{(43!)(6times 5 times 4 times 3 times 2 times 1)}\\
&= 13, 983, 816\
end{aligned}$$
b. The graph is the graph of $y=sin(x)$ stretched horizontally by factor $dfrac{1}{3}$ and stretched vertically by factor $10$ and translated down by 2 units.
d. The graph is the graph of $y=cos(x)$ stretched horizontally by factor $dfrac{1}{2}$ and translated right by $dfrac{pi}{4}$ units.
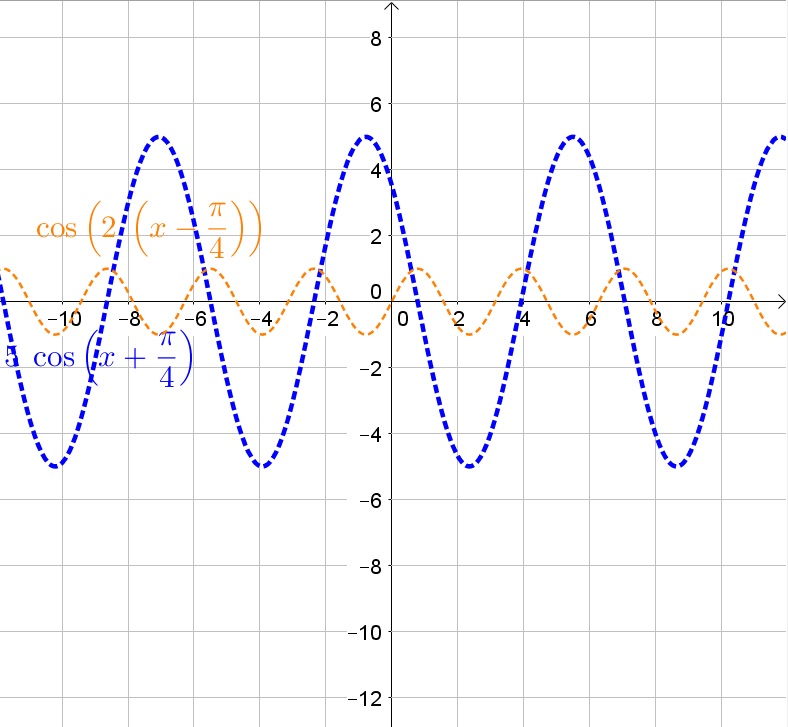
Pattern $1rightarrow$ $dfrac{x-1}{x-1}= 1$.
Pattern $2rightarrow$ $dfrac{x^2-1}{x-1}= x+1$.
Pattern $3rightarrow$ $dfrac{x^3-1}{x-1}= x^2 + x+ 1$.
Pattern $4rightarrow$ $dfrac{x^4-1}{x-1}= x^3 + x^2 + x+ 1$.
$$begin{aligned}
x-1&= 1(x-1)\
x-1&= x-1rightarrow(text{Correct})
end{aligned}$$
$$begin{aligned}
x^2-1&= (x-1)(x+1)\
x^2-1&= x(x+1)-1(x+1)\
x^2-1&=x^2+x-x-1\
x^2-1&= x^2-1 rightarrow(text{Correct})
end{aligned}$$
$$begin{aligned}
x^3-1&= (x-1)(x^2+x+1)\
x^3-1&= x(x^2+x+1)-1(x^2+x+1)\
x^3-1&= x^3 + x^2+ x – x^2-x-1\
x^3-1&=x^3 – 1rightarrow{text{(Correct)}}\
end{aligned}$$
$$begin{aligned}
x^4-1&= (x-1)(x^3+x^2+x+1)\
x^4-1&= x(x^3+x^2+x+1)- 1(x^3+x^2+x+1)\
x^4-1&= x^4 + x^3 +x^2 + x-x^3-x^2-x-1\
x^4-1&=x^4 – 1rightarrow{text{(Correct)}}\
end{aligned}$$
$$begin{aligned}
&boxed{dfrac{x^5-1}{x-1}= x-1(x^4 + x^3 +x^2+x+1)}\
end{aligned}$$
$$begin{aligned}
&boxed{dfrac{x^n-1}{x-1}=(x^{n-1}+x^{n-2}+………+x^3+x^2+x+1)}
end{aligned}$$
Thus, the above equation is the conjecture.
$$y = x^3(x-2)(x+2)^2$$
$$begin{aligned}
x^3&=0\
&boxed{x=0}rightarrow(1)\
x-2&=0\
&boxed{x=2}rightarrow(2)\
x+2&=0\
&boxed{x=-2}rightarrow(3)\
end{aligned}$$
$$begin{aligned}
y&= (0)^3 (0-2)(0+2)^2\
&boxed{y= 0}\
end{aligned}$$
Because the leading term is positive, both ends go upwards.
$f(x)$ $rightarrow$ $infty$ $text{as}$ $x$ $rightarrow -infty$.
$f(x)$ $rightarrow$ $infty$ $text{as}$ $x$ $rightarrow infty$.

$MN=48$
$$
YN=ZM=24
$$
$$
x^2+y^2=676
$$
The circle has the equation:
$y^2=676-121$
$y^2=555$
$y=sqrt{555}$
$$
y=PNapprox 23.56
$$
$$
begin{align*}
15% x+22%($2700-x)&=$513.01&&boxed{text{Given proportion}}\
end{align*}
$$
When $x=$ the amount earned during lunch
and $boldsymbol{(2700-x)}$ the amount earned during dinner.
$$
begin{align*}
0.15x+0.22($2700-x)&=$513.01&&boxed{text{Convert the percent to a decimal form}}\
0.15x+594-0.22x&=513.01&&boxed{text{Distributive property}}\
-0.07x+594&=513.01&&boxed{text{Combine like terms}}\
-7x+59400&=51301&&boxed{text{Multiply both sides by 100}}\
-7x+59400-59400&=51301-59400&&boxed{text{Subtract }59400 text{ from both sides}}\
-7x&=-8099&&boxed{text{Simplify}}\
frac{-7x}{-7}&=frac{-8099}{-7}&&boxed{text{Divide both sides by }-7}\
x&=$1157&&boxed{text{Simplify}}\
end{align*}
$$
Betty made $boldsymbol{$1157}$ during lunch.
$$
begin{align*}
&boxed{{color{#c34632}x=$1157} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ }x=$1157
$$
$$
0.15x+0.22(2700-x)=513.01
$$
Use distributive property:
$$
0.15x+594-0.22x=513.01
$$
Add $0.22x$ to both sides of the equation:
$$
-0.07x=-80.99
$$
Divide both sides of the equation by $-0.07$:
$$
x=1,157
$$
Thus Betty made $1,157 during lunch.
$$begin{aligned}
y &= x^{2} – x + 12tag{1} \
end{aligned}$$
In order to determine the intersecting points of the functions given in the table , we will sketch the graph of the quadratic function and we will plot the values given in the table.
$$
Sigma_{n=1}^{infty} 25left(1-0.05right)^{n-1}=Sigma_{n=1}^{infty} 25left(0.95right)^{n-1}
$$
The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{25}{1-0.95}=dfrac{25}{0.05}=500
$$
$$
Sigma_{n=1}^{infty} 0.27left(0.01right)^{n-1}
$$
The sum of an infinite geometric series is:
$$
S=dfrac{a}{1-r}=dfrac{0.27}{1-0.01}=dfrac{0.27}{0.99}=dfrac{27}{99}=dfrac{3}{11}
$$
dfrac{3}{11}
$$
$a, ar , ar^2, ar^3, ar^4 ………. ar^{n-1}$.
where,
$a rightarrow$ First term of the geometric progression.
$ar rightarrow$ Second term of the geometric progression, and so.
Using,
$$begin{aligned}
a_n&= acdot r^{n-1}
end{aligned}$$
where, $n= 1,2,3,4,……..$
$$begin{aligned}
S_n&= dfrac{a(1- r^n)}{1 – r}\\
text{According to the given series,}\
S_n&= dfrac{a+ ar +ar^2+ ar^3+ar^4 ……….+ ar^{n-1}}{1-r}\\
&= dfrac{a(1 + r + r^2 + r^3 + r^4+ ………… r^{n-1})}{1-r}\\
&=a cdot dfrac{1- r^n}{1-r}rightarrow(2)\
&end{aligned}$$
conditions ,
$$0 < |r| < 1$$
$$
Sigma_{n=1}^{5} 3left(dfrac{1}{3}right)^{n-1}
$$
The sum of an finite geometric series is:
$$
S(n)=dfrac{a(1-r^n)}{1-r}=dfrac{3left( 1-left( dfrac{1}{3}right)^5right)}{1-dfrac{1}{3}}=dfrac{121}{27}
$$
dfrac{121}{27}
$$
$$begin{aligned}
a^{2} &= b^{2} + c^{2} – 2bccdot cos A\
end{aligned}
$$begin{aligned}
x^{2}&= (6)^{2} + (4)^{2} – 2times 6 times 4 cos 130^{o} \
x^{2}&= 36 + 16 – 48 times -0.64\
x&= sqrt{82.72}\
x&= 9.10 text{ units} \
end{aligned}$$
$$begin{aligned}
text{ Area}&= dfrac{1}{2}times btimes c times sin A\
end{aligned}$$
$$begin{aligned}
text{ Area}&= dfrac{1}{2}times (6)times (4 ) sin (130^{o} \
&= 0.5 times 24 times 0.76\
&= 9.12 text{ square units}\
end{aligned}$$
$b.$ $9.12 text{ square units}$

$x^2=36+16-48(-0.64278761)$
$x^2=82.853805$
$x=sqrt{82.853805}$
$$
approx 9.1
$$
$=dfrac{24cdot 0.76604444}{2}$
$$
approx 9.19
$$
$S_{triangle ABC}=dfrac{ABcdot ACsin A}{2}$.
b) Area: $9.19$
begin{align*}
sinbeta&= -dfrac{4}{5}tag{1} \
intertext{ $pi$ $leq$ $beta$$leq$ $dfrac{3pi}{2}$} \\
end{align*}
begin{align*}
sin^{2}(x) + cos^{2}(x) &= 1 \
intertext{ The above formula can be used to determine the value of the $cos$ as well.}\
intertext{ Mathematically it is stated as follows.} \
cos^{2}(x)&= 1 – sin^{2}(x)\
cos(x)&=pm sqrt{1- sin^{2}(x)}\
end{align*}
$$
begin{align*}
cos(beta)&= pm sqrt{1- left(-dfrac{4}{5}right)^{2}} \\
&= pm sqrt{1- dfrac{16}{25}}\\
&= pm sqrt{dfrac{25 – 16}{25}}\\
&= pm sqrt{dfrac{9}{25}}\\
&= pm dfrac{3}{5}\\
end{align*}
$$
But , $cos(x)$ in third quadrant is only negative. Thus, the value of $cos(x)$ will be given as follows.
$$
begin{align*}
cos(beta)&= -dfrac{3}{5}tag{2}\
end{align*}
$$
begin{align*}
sec(x)&= dfrac{1}{cos(x)}\
intertext{So,}\
sec(beta)&= dfrac{1}{dfrac{-3}{5}} \\
sec(beta)&= dfrac{-5}{3}tag{3}\
end{align*}
begin{align*}
cosec(x)&= dfrac{1}{sin(x)}\
intertext{So,}\
cosec(beta)&= dfrac{1}{dfrac{-4}{5}} \\
cosec(beta)&= dfrac{-5}{4}tag{4} \
end{align*}
$$
begin{align*}
tan(x)&=dfrac{sin(x)}{cos(x)}\\
end{align*}
$$
Thus,
$$
begin{align*}
tan(beta)&= dfrac{dfrac{-4}{5}}{dfrac{-3}{5}} \\
tan(beta)&= dfrac{4}{3}\\
end{align*}
$$
$$
begin{align*}
cot(x)&= dfrac{1}{tan(x)}\
end{align*}
$$
So,
$$
begin{align*}
cot(beta)&= dfrac{1}{dfrac{4}{3}}\\
cot(beta)&= dfrac{3}{4}\\
end{align*}
$$
$left(-dfrac{4}{5}right)^2+cos^2beta=1$
$dfrac{16}{25}+cos^2beta=1$
$cos^2beta=1-dfrac{16}{25}$
$cos^2beta=dfrac{9}{25}$
$$
cosbeta=pmdfrac{3}{5}
$$
cosbeta=-dfrac{3}{5}
$$
tanbeta=dfrac{sinbeta}{cosbeta}=dfrac{-dfrac{4}{5}}{-dfrac{3}{5}}=dfrac{4}{3}
$$
cotbeta=dfrac{cosbeta}{sinbeta}=dfrac{-dfrac{3}{5}}{-dfrac{4}{5}}=dfrac{3}{4}
$$
secbeta=dfrac{1}{cosbeta}=dfrac{1}{-dfrac{3}{5}}=-dfrac{5}{3}
$$
cscbeta=dfrac{1}{sinbeta}=dfrac{1}{-dfrac{4}{5}}=-dfrac{5}{4}
$$
In order to determine which region appear the disease is spreading faster, we will find the range of the two regions.
$$begin{aligned}
text{ Range}, r_1&= dfrac{text{Highest frequency – Lowest frequency}}{text{Highest frequency – Lowest frequency}}\\
&= dfrac{170-120}{21-7}\\
&=dfrac{50}{14}\\
&approx 3.57\
end{aligned}$$
$$begin{aligned}
text{ Range}, r_2&= dfrac{text{Highest frequency – Lowest frequency}}{text{Highest frequency – Lowest frequency}}\\
&= dfrac{62-22}{19-7}\\
&=dfrac{40}{12}\\
&approx 3.33\
end{aligned}$$
A linear model can be a good choice to represent the outbreak data.
Since the average rate of change is higher in the first region and after June 19th there are already more infected people in Region A, it is more useful to set up the hospital in Region A.
Determining the regression model for each region:
$$begin{aligned}
text{region A}, y&= 3.62x + 92.98\
text{region B}, y&= 3.33x – 3.93\
end{aligned}$$
For, $x = 20$.
$$begin{aligned}
text{region A}, y&= 3.62(20) + 92.98\
&boxed{yapprox135}rightarrow(text{Region A})\
text{region B}, y&= 3.33x – 3.93\
&boxed{yapprox63}rightarrow(text{Region B})\
end{aligned}$$
Very confident.
$$P(x)=_nC_xs^xf^{n-x},$$
where $_nC_x=dfrac{n!}{x!(n-x)!}$ and $n!=1cdot2cdotdots n$.
$$begin{align*}
P(3)&=_5C_30.65^3cdot0.35^{5-3}\
&=dfrac{5!}{3!(5-3)!}cdot0.275cdot0.1225\
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5}{1cdot2cdot3cdot1cdot2}cdot0.034\
&=10cdot0.034\
&=0.34
end{align*}
$$begin{align*}
P(4)&=_5C_40.65^4cdot0.35^{5-4}\
&=dfrac{5!}{4!(5-4)!}cdot0.18cdot0.35\
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5}{1cdot2cdot3cdot4cdot1}cdot0.06\
&=5cdot0.063\
&=0.315
end{align*}
$$begin{align*}
P(5)&=_5C_50.65^5cdot0.35^{5-5}\
&=dfrac{5!}{5!(5-5)!}cdot0.12cdot1\
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5}{1cdot2cdot3cdot4cdot5cdot1}cdot0.12\
&=0.12\
end{align*}

$$6.25%cdot16text{ outcomes}=100%.$$
$$P(x)=_nC_xs^xf^{n-x}.$$
P(2)&=_5C_2cdot0.5^2cdot0.5^{5-2}\
&=dfrac{5!}{2!(5-2)!}cdot0.03125
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5}{1cdot2cdot1cdot2cdot3}cdot0.03125\
&=10cdot0.03125\
&=0.3125
end{align*}$$
We have $n=6$ because there are $6$ engines $s=f=0.5$ because the engine can either fail or work.
$$begin{align*}
P(0)&=_6C_0cdot0.5^0cdot0.5^{6-0}\
&=dfrac{6!}{0!(6-0)!}cdot1cdot0.02
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5cdot6}{1cdot1cdot2cdot3cdot4cdot5cdot6}cdot0.02\
&=0.02
end{align*}$$
$$begin{align*}
P(1)&=_6C_1cdot0.5^1cdot0.5^{6-1}\
&=dfrac{6!}{1!(6-1)!}cdot0.5cdot0.5^5
end{align*}$$
$$begin{align*}
&=dfrac{1cdot2cdot3cdot4cdot5cdot6}{1cdot1cdot2cdot3cdot4cdot5}cdot0.02\
&=6cdot0.02\
&=0.12
end{align*}$$
$$P(x)=_nC_xs^xf^{n-x}.$$
P(0)&=_{20}C_0cdot0.36^0cdot0.64^{20}\
&=dfrac{20!}{0!(20-0)!}cdot1cdot0.64^{20}\
&=0.00013
end{align*}
P(1)&=_{20}C_1cdot0.36^1cdot0.64^{19}\
&=dfrac{20!}{1!(20-1)!}cdot0.36cdot0.00021\
&=0.0015
end{align*}
P(2)&=_{20}C_2cdot0.36^2cdot0.64^{18}\
&=dfrac{20!}{2!(20-2)!}cdot0.1296cdot0.00032\
&=190cdot0.1296cdot0.00032\
&=0.0079
end{align*}$$
In how many ways can a committee of 10 be selected from a group of 45 people?
How many different selections of $3$ shifts are possible if we need to select $3$ out of $9$?
P(2)&=_{21}C_2cdotdfrac{1}{365^2}cdotleft(dfrac{364}{365}right)^{19}\
&=210cdot0.00000712485\
&=0.0015\
&=0.15%
end{align*}$$
$8 + 4 + 2+………..$
From the series, we concluded that,
$$
begin{align*}
text{ First term}, a_{1}&= 8 \
text{ Common ratio}, r&= dfrac{a_{2}}{a_{1}}\\
&= dfrac{4}{8}\\
&= dfrac{1}{2} \\
end{align*}
$$
$$
begin{align*}
S_{n}&= dfrac{a(1-r^{n})}{1-r} \
end{align*}
$$
$$
begin{align*}
S_{n}&= dfrac{8left[1-(tfrac{1}{2})^{n}right]}{1-(tfrac{1}{2})}\\
&= dfrac{8left[1-(tfrac{1}{2})^{n}right]}{tfrac{1}{2}}\\
&= 16left[1-(tfrac{1}{2})^{n}right]\\
end{align*}
$$
$3 + 9 + 27+. 81……….$
From the series, we concluded that,
$$
begin{align*}
text{ First term}, a_{1}&= 3 \
text{ Common ratio}, r&= dfrac{a_{2}}{a_{1}}\\
&= dfrac{9}{3}\\
&= 3\
end{align*}
$$
$$
begin{align*}
S_{n}&= dfrac{a(r^{n}-1)}{r-1} \
end{align*}
$$
$$
begin{align*}
S_{n}&=dfrac{3left[(3)^{n}-1right]}{3-1} \\
&=dfrac{3left[(3)^{n}-1right]}{2}\\
&= 1.5 left[(3)^{n}-1right] \\
end{align*}
$$
$b$. $1.5 left[(3)^{n}-1right]$
$$
begin{align*}
text{ George made four copies of the letter and sent it to four friends}, a_{1}&=1\
text{ Friends made the copy and sent it to four more friends}, a_{2}&= 4\
end{align*}
$$
The above conditions can be perfectly expressed using Geometric Progression in which we ca say that,
$$
begin{align*}
text{ First Term}, a_{1}&= 1 \
text{ Second term}, a_{2}&= 4 \
text{ Common ratio}, r&= dfrac{4}{1}\
&= 4\
end{align*}
$$
The formula is stated as follows.
$$
begin{align*}
a_{n}&= atimes r^{n-1} \
end{align*}
$$
Where, $n = 6$
$$
begin{align*}
a_{6}&= 1 times 4^{6-1} \
&= 1times (4)^{5}\
&=1024\
end{align*}
$$
Thus, there will $1024$ people who will receive the letter during round six.
$$
begin{align*}
y&= -2 cos(x+tfrac{pi}{2})tag{1}\
end{align*}
$$
$$
begin{align*}
cos theta&=sin(tfrac{pi}{2}-theta) \
end{align*}
$$
Thus, expression $(1)$ can be re-written as.
$$
begin{align*}
y&=- 2 sinleft[(tfrac{pi}{2}-(x+tfrac{pi}{2})right] \\
y&= -2 sinleft[tfrac{pi}{2}-x-tfrac{pi}{2}right]\\
y&= -2 sin(-x)\\
y&= 2 sin(x)\\
end{align*}
$$
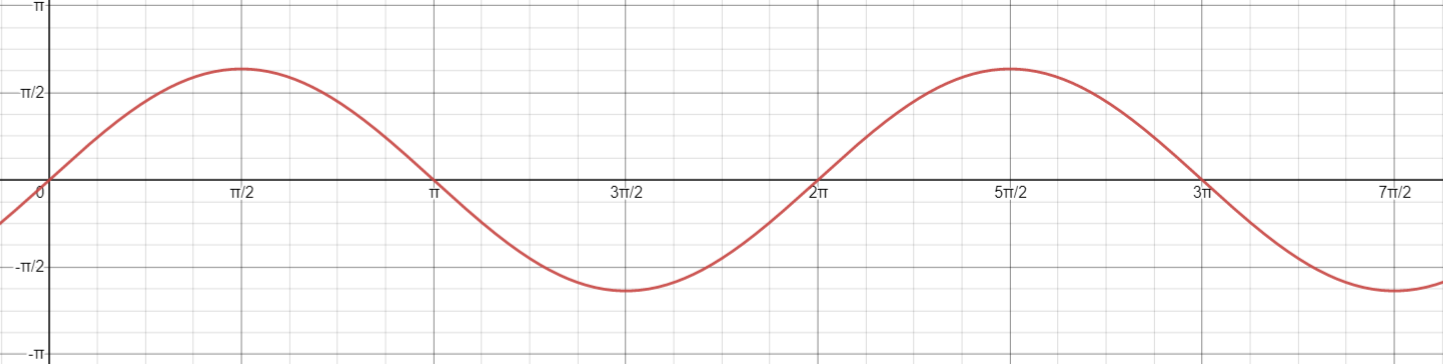
$$
begin{align*}
y = sin (x-tfrac{pi}{2})\
end{align*}
$$
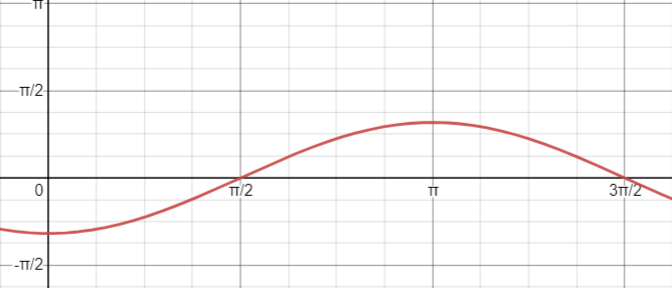
$$
begin{align*}
p(x)&= x^{4}-11x^{2}+11x-15\
g(x)&= x-3\
end{align*}
$$
begin{array}{ccccccccccc}
& & & x^3 & +3x^2& -2x &+5 &\
cline{3-10}
multicolumn{2}{r}{x-3 surd}
& x^4&-11x^2& +11x&-15& \
& &-x^4&&&&+3x^3& & & & \
cline{3-7}
& & &3x^3&-11x^2&+11x&-15 & \
& & &-3x^3&+9x^2&\
cline{4-8}
& & & & -2x^2&+11x &-15& \
& & & &+2x^2 &-6x& \
cline{5-9}
& & & & &+5x&-15& \
& & & & &-5x &+15& \
cline{6-10}
& & & && &0 \
end{array}
$

It is given that,
VO = 25
AB = 32
BC = 60
AM = BM
BN = CN
As it is given that the wires connect the top of the antenna to each corner of the roof and to the midpoint of each edge,
So,
AB = BM = ON =
$$begin{aligned}
&= dfrac {32}{2}\
&= 16\
end{aligned}$$
BN = CN = OM =
$$begin{aligned}
&= dfrac {60}{2}\
&= 30\
end{aligned}$$
$$begin{aligned}
VM^{2} &= VO^{2} + OM^{2}\
VM^{2} &= (25)^{2} + (30)^{2}\
VM^{2} &= 625 + 900\
VM^{2} &= 1525\
end{aligned}$$
Squaring on both sides
$$begin{aligned}
VM &=sqrt {1525}\
VM &= 39.05\
end{aligned}$$
$$begin{aligned}
VN^{2} &= VO^{2} + ON^{2}\
VN^{2} &= (25)^{2} + (16)^{2}\
VN^{2} &= 625 + 256\
VN^{2} &= 881\
end{aligned}$$
Squaring on both sides
$$begin{aligned}
VN &=sqrt {881}\
VN &= 29.68\
end{aligned}$$
$$begin{aligned}
VB^{2} &= VM^{2} + BM^{2}\
VB^{2} &= 1525 + 256\
VB^{2} &= 625 + 256\
VB^{2} &= 1781\
end{aligned}$$
Squaring on both sides
$$begin{aligned}
VB &=sqrt {1781}\
VB &= 42.20\
end{aligned}$$
$$begin{aligned}
4VB + 2VM + 2VN\
&=4 (42.20) + 2 (39.05) + 2(29.68)\
&=168.8 + 78.10 + 59.36\
&= 306.26\
end{aligned}$$
The total length of the wire used to connect the antenna to the roof is 306.26 ft.
$$begin{aligned}
sin (text{VBO}) &= dfrac{VO}{VB}\\
sin (text{VBO}) &= dfrac {25}{42.2}\\
sin (text{VBO}) &= 0.592\
text{VBO} &= sin^{-1}(0.592)\
text{VBO} &= 36.3degree
end{aligned}$$
Then $VO = x$.
$$begin{aligned}
text{VM} &= sqrt{x^{2}+900}\
text{VN} &= sqrt{x^{2}+256}\
text{VB} &= sqrt{x^{2}+900+256}\
text{VB} &= sqrt{x^{2}+1156}\
end{aligned}$$
And if $VO = x$ then the total length of the wire used to connect the antenna to the roof is;
$$begin{aligned}
text{4VB + 2VM + 2VN}\
&= 4sqrt{x^{2}+1156} +2sqrt{x^{2}+900}+2sqrt{x^{2}+256}\
end{aligned}$$
$(b.)$ 36.3$degree$
$(c.)$ $4sqrt{x^{2}+1156} +2sqrt{x^{2}+900}+2sqrt{x^{2}+256}$
$0.70x$ with $r_2=0.09$
0.07(0.30x)=0.021x
$$
0.09(0.70x)=0.063x
$$
$0.084x=5,000$
$x=dfrac{5,000}{0.084}$
$$
xapprox 59,523.81
$$
begin{tabular}{|c|c|c|c|c|c|c|c|c|c|}
hline
$_nC_r$ & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ hline
0 & 1 & & & & & & & & \ hline
1 & 1 & 1 & & & & & & & \ hline
2 & 1 & 2 & 1 & & & & & & \ hline
3 & 1 & 3 & 3 & 1 & & & & & \ hline
4 & textcolor{blue}{1} & textcolor{blue}{4} & textcolor{blue}{6} & textcolor{blue}{4} & textcolor{blue}{1} & & & & \ hline
5 & textcolor{blue}{1} & textcolor{blue}{5} & textcolor{blue}{10} & textcolor{blue}{10} & textcolor{blue}{5} & textcolor{blue}{1} & & & \ hline
6 & textcolor{blue}{1} & textcolor{blue}{6} & textcolor{blue}{15} & textcolor{blue}{20} & textcolor{blue}{15} & textcolor{blue}{6} & textcolor{blue}{1} & & \ hline
7 & textcolor{blue}{1} & textcolor{blue}{7} & textcolor{blue}{21} & textcolor{blue}{35} & textcolor{blue}{35} & textcolor{blue}{21} & textcolor{blue}{7} & textcolor{blue}{1} & \ hline
8 & textcolor{blue}{1} & textcolor{blue}{8} & textcolor{blue}{28} & textcolor{blue}{56} & textcolor{blue}{70} & textcolor{blue}{56} & 28 & 8 & 1 \ hline
end{tabular}\\\
It can be observed table is symmetrical about $r=dfrac{n}{2}$
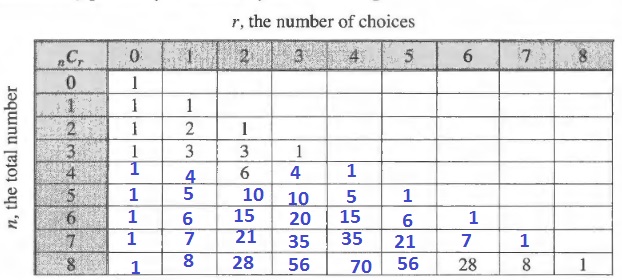
$textbf{(b)}$ It can be observed that sum of numbers of row is equal to $2^n$
It can also be observed that each row is symmetrical
$textbf{(c)}$ Below is triangle till row 10 using the rule described in (a)
$textbf{n}$ & & & & & & & & & & & & & & & & & & & & & & \
0 & & & & & & & & & & & & 1 & & & & & & & & & & \
1 & & & & & & & & & & & 1 & & 1 & & & & & & & & & \
2 & & & & & & & & & & 1 & & 2 & & 1 & & & & & & & & \
3 & & & & & & & & & 1 & & 3 & & 3 & & 1 & & & & & & & \
4 & & & & & & & & 1 & & 4 & & 6 & & 4 & & 1 & & & & & & \
5 & & & & & & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & & & & \
6 & & & & & & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & & & & \
7 & & & & & 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 & & & \
8 & & & & 1 & & 8 & & 28 & & 56 & & 70 & & 56 & & 28 & & 8 & & 1 & & \
9 & & & 1 & & 9 & & 36 & & 84 & & 126 & & 126 & & 84 & & 36 & & 9 & & 1 & \
10 & & 1 & & 10 & & 45 & & 120 & & 210 & & 252 & & 210 & & 120 & & 45 & & 10 & & 1
end{tabular}
Every row is symmetric.
Every number is the sum of the two above it (if there are two above it).
The left and right side of the triangles contains only ones.
c. The next row starts and ends with a 1, the other numbers are the sum of the two numbers above it.
Every row is symmetric.
Every number is the sum of the two above it (if there are two above it).
The left and right side of the triangles contains only ones.
$$
(a+b)^2=a^2+2ab+b^2
$$
We note that the polynomial has three terms and the coefficients are 1,2,1. We note that the coefficients are given in the secondrow of Pascal’s triangle.
b.
$$
(a+b)^3=(a+b)(a^2+2ab+b^2)=a^3+3a^2b+3ab^2+b^2
$$
We note that the polynomial has four terms and the coefficients are 1,3,3,1. We note that the coefficients are given in the third row of Pascal’s triangle.
c. Four terms and the coefficients will be given in the forth row of Pascal’s triangle:
$$
(a+b)^4=(a+b)(a^3+3a^2b+3ab^2+b^3)=a^4+4a^3b+6a^2b^2+4ab^3+b^4
$$
d. The coefficients of the expension are given in the sixth row of Pascal’s triangle:
$$
(a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6
$$
b. Since order is not important, we use a combination:
$$
_5C_3=dfrac{5!}{(5-3)!3!}=dfrac{5cdot 4}{2cdot 1}=10
$$
Thus the coefficient will be 10.
b. $_5C_3=10$
$$
_9C_3=dfrac{9!}{(9-3)!3!}=dfrac{9cdot 8cdot 7}{3cdot 2cdot 1}=84
$$
Thus the coefficient will be 84. He could however also use the combination $_9C_6$ which will result in the same coefficient.
_9C_3=84
$$
b. Since order is not important, we use a combination:
$$
_{11}C_7=dfrac{11!}{(11-7)!7!}=dfrac{11cdot 10 cdot 9cdot 8}{4cdot 3cdot 2cdot 1}=330
$$
Thus the coefficient will be 330. He could however also use the combination $_{11}C_4$ which will result in the same coefficient.
c. We know from (b) that the 5th term is
$$
330a^7b^4
$$
Replace $a$ with $x$ and $b$ with $-2$:
$$
330x^7(-2)^4=330x^7(16)=5,280x^7
$$
b. 330
c. $5,280x^7$
$$
(2x+3)^3=(U+V)^3
$$
With help of Pascal’s triangle we have:
$$
(U+V)^3=(1)U^3+(3)U^2V+(3)UV^2+(1)V^3
$$
Putting $U=2x$ and $V=3$ we have:
$$
begin{align*}
(2x+3)^3&=(2x)^3+3(2x)^2(3)+3(2x)(3)^2+3^3\
&=textcolor{#4257b2}{8x^3+36x^2+54x+27}
end{align*}
$$
$textbf{(b)}$To solve $(x-1)^5$, $text{textcolor{#4257b2}{substitute $x$ by U and $-1$ by V}}$
With help of Pascal’s triangle we have:
$$
(U+V)^5=(1)U^5+(5)U^4V+(10)U^3V^2+(10)U^2V^3+(5)UV^4+(1)V^5
$$
Putting $U=x$ and $V=-1$ we have:
$$
begin{align*}
(x-1)^5&=x^5+(5)x^4(-1)+(10)x^3(-1)^2+(10)x^2(-1)^3+(5)x(-1)^4+(-1)^5\
&=textcolor{#4257b2}{x^5-5x^4+10x^3-10x^2+5x-1}\
end{align*}
$$
$textbf{(c)}$ It can be observed from previous exercise that:
For $n=3$, terms =4
For $n=5$, terms =6
Therefore for $n^{textrm{th}}$ power number of terms is $color{#4257b2}{n+1}$
$$
(2x+3)^3=(2x)^3+3(2x)^2(3)+3(2x)(3)^2+3^3=8x^3+36x^2+54x+27
$$
b.
$$
(x-1)^5=x^5+5x^4(-1)+10x^3(-1)^2+10x^2(-1)^3+5x(-1)^4+(-1)^5=x^5-5x^4+10x^3-10x^2+5x-1
$$
c. (a) contains 4 terms and (b) contains 6 terms. the $n$th power of a binomial then contains $n+1$ terms.
b. $x^5-5x^4+10x^3-10x^2+5x-1$
c. $4,6 , n+1$
$$
_3C_0+_3C_1+_3C_2+_3C_3=1+3+3+1=8=2^3
$$
b.
$$
_4C_0+_4C_1+_4C_2+_4C_3+_4C_4=1+4+6+4+1=16=2^4
$$
c. Because you are looking for all possibilities of the two factors $a$ and $b$ and the total number of possibilities in $(a+b)^n$ will then be $2^n$.
$nC_{n} + nC_{n-1} +nC_{n-2} +…………..+nC_{2} +nC_{1} +nC_{0} = 2^{n}$
$$
begin{align*}
(a+b)^{n} &= nC_{0}a^{n}++nC_{1}a^{n-1}b+nC_{2}a^{n-2}b^{2}+………..nC_{n-1}ab^{n-1}+nC_{n}b^{n}\
end{align*}
$$
$$
begin{align*}
(1+1)^{n}&= nC_{0}1^{n}++nC_{1}1^{n-1}(1)+nC_{2}1^{n-2}1^{2}+………..nC_{n-1}(1)(1)^{n-1}+nC_{n}1^{n} \
(2)^{n}&= nC_{0} + nC_{1} + nC_{2} + ……. + nC_{n-1} + nC_{n}\
end{align*}
$$
$$
begin{align*}
(2)^{n}&= nC_{n} + nC_{n-1} + nC_{n-2} + ……………+ nC_{2} + nC_{1}+ nC_{0}\
end{align*}
$$
$(a+b)^1$ would use row 1.
$(a+b)^0$ would use row 0.
$$
(x+y)^7=x^7+7x^6y+21x^5y^2+35x^4y^3+35x^3y^4+21x^2y^5+7xy^6+y^7
$$

x^7+7x^6y+21x^5y^2+35x^4y^3+35x^3y^4+21x^2y^5+7xy^6+y^7
$$
$$
(a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5
$$
Replace $a$ with $w$ and $b$ with $-4z$:
$$
(w-4z)^5=w^5+5w^4(-4z)+10w^3(-4z)^2+10w^2(-4z)^3+5w(-4z)^4+(-4z)^5
$$
$$
=w^5-20w^4z+160w^3z^2-640w^2z^3+1280wz^4+1024z^5
$$
Thus the fourth term is $-640w^2z^3$.
-640w^2z^3
$$
b. Thus she needs to choose 4 bracelets from six bracelets, the number of possible combination is then the fifth number in row 6: $15$ possibilities.
b. 15 possibilities
b. If we then let the tenth volunteer on the next teams, their are two spaces:
$$
_9C_2=dfrac{9!}{(9-2)!2!}=dfrac{9cdot 8}{2cdot 1}=dfrac{72}{2}=36
$$
c. Thus in total there are then $84+36=120$ possible teams.
d. 84 and 36 are the two numbers above 120 in the Pascal’s triangle.
Solving for $x$.
From the given figure we can say that ,
$$
begin{align*}
text{ Perpendicular}&= x\
text{ Base}&= 5\
text{ Angle}&= 35text{textdegree} \
end{align*}
$$
$$
begin{align*}
tantheta&= dfrac{text{ Perpendicular}}{text{ Base}} \\
tan(35text{textdegree})&=dfrac{x}{5}\
0.7&approx dfrac{x}{5} \
0.7 times 5 &approx x\
3.5&approx x\
end{align*}
$$
Solving for $theta$.
From the given figure we can say that ,
$$
begin{align*}
text{ Hypotenuse}&= x \
text{ Base}&= 5 \
end{align*}
$$
$$
begin{align*}
costheta&= dfrac{text{ Base}}{text{ Hypotenuse}}\\
costheta&=dfrac{5}{6}\\
theta &=cos^{-1}left(dfrac{5}{6}right) \\
&approx 33.55text{textdegree} + 360 k
end{align*}
$$
Sketching the figure using given information.
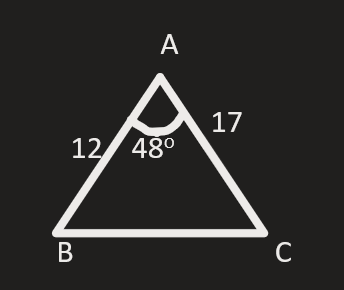
$$
begin{align*}
AB&= 12 \
AC &= 17\
angle CAB &= 48 text{textdegree}\
end{align*}
$$
Thus,
$$
begin{align*}
text{ Area} A&= dfrac{1}{2} AB times AC times sin (CAB) \
&= 0.5 times 17 times 12 sin(48text{textdegree})\
&=0.5 times 17 times 12 times 0.74\
&= 75.48 text{square units}\
end{align*}
$$
Sketching the figure from the given information ,
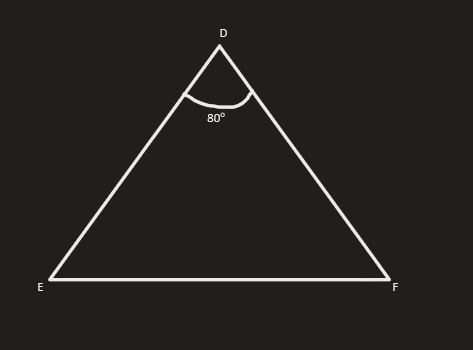
$$
begin{align*}
DE &= 5 text{ feet}\
DF &= 7 text{ feet}\
angle EDF&= 80 text{textdegree} \
end{align*}
$$
In order to find the value of the third side, we will apply LAW OF COSINES which is stated below.
$$
begin{align*}
EF^{2}&= DE^{2} + DF^{2} – 2times DEtimes DF times cos\
end{align*}
$$
begin{align*}
EF&= sqrt{DE^{2} + DF^{2} – 2times DE times DF} \
EF&= sqrt{25+49-2(5)(7)times cos(80text{textdegree})}\
&= sqrt{74 – 70 times 0.17} \
&= sqrt{62.1}\
&=7.88 text{ feet}\
end{align*}
$$
$$
begin{align*}
y=&x^{3}-5x^{2}+8x -6 \
end{align*}
$$
Also, one real root is $x=3$
In order to find another root, we will first convert the given real root into a linear polynomial.
$$
begin{align*}
x-3&=0tag{1}\
end{align*}
$$
$
begin{array}{ccccccccccc}
& & & x^{2} &-2x &+2& \
cline{3-10}
multicolumn{2}{r}{x-3 surd}
&+x^3&-5x^2 &+8x & -6& \
&&+x^3&+3x^2& & & & \
cline{3-7}
&&&-2x^2&+8x &-6 & & & & \
&&&2x^2&-6x \
cline{4-8}
& & && 2x&-6& \
& & & &-2x&+6& \
cline{5-9}
&&&&&0\
end{array}
$
$$
begin{align*}
y&= (x-3) (x^{2}-2x+2) \
end{align*}
$$
$$
begin{align*}
d&= b^{2}-4ac \
&= 4-4(1)(2)\
&= 4-8\
&=-4\
end{align*}
$$
where,
$$
begin{align*}
a&=1\
b&=-2\
c&=2\
end{align*}
$$
begin{align*}
alpha&= dfrac{-b+sqrt{d}}{2a} \
&= dfrac{2+sqrt{-4}}{2times1}\
&= dfrac{2+2i}{2}\
intertext{Using $i^{2}=-1$}\
&= dfrac{2(1+i)}{2}\
&= 1+i\
end{align*}
begin{align*}
beta&= dfrac{-b-sqrt{d}}{2a}\
&= dfrac{2-sqrt{-4}}{2times1}\
&= dfrac{2-2i}{2}\
intertext{Using $i^{2}=-1$}\
&= dfrac{2(1-i)}{2}\
&= 1-i\
end{align*}
Thus, the other roots are as follows,
$$
begin{align*}
x&= 1+i\
x&= 1-i\
end{align*}
$$
b. $theta = 180text{textdegree}-45text{textdegree}=135text{textdegree}$ and $theta = 360text{textdegree}-45text{textdegree}=315text{textdegree}$
c. $theta = 60text{textdegree}$ and $theta = 180text{textdegree}-60text{textdegree}=120text{textdegree}$
d. $theta = 180text{textdegree}-30text{textdegree}=150text{textdegree}$ and $theta = 180text{textdegree}+30text{textdegree}=210text{textdegree}$
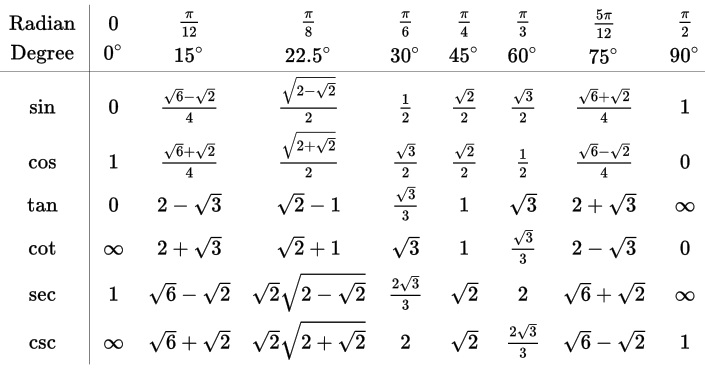
b. $135text{textdegree}, 315text{textdegree}$
c. $60text{textdegree}, 120text{textdegree}$
d. $150text{textdegree}, 210text{textdegree}$
The general solution for
$$
cos theta=frac{1}{2}
$$
is
$$
theta=60^circ+360^circ n,quad theta=300^circ+360^circ n
$$
For $n=0$
$$
theta=60^circ,quad theta=300^circ
$$
The general solution for
$$
tan theta=-1
$$
is
$$
theta =135^circ n+180^circ n
$$
For $n=0$
$$
theta=135^circ
$$
For $n=1$
$$
theta=135^circ +180^circ=315^circ
$$
Then
$$
theta=135^circ,quad theta=315^circ
$$
The general solution for
$$
sin theta=frac{sqrt{3}}{2}
$$
is
$$
theta=60^circ+360^circ n,quad theta=120^circ+360^circ n
$$
For $n=0$
$$
theta=60^circ,quad theta=120^circ
$$
The general solution for
$$
cos theta=-frac{sqrt{3}}{2}
$$
is
$$
theta=150^circ+360^circ n,quad theta=210^circ+360^circ n
$$
For $n=0$
$$
theta=150^circ,quad theta=210^circ
$$
$$
theta=60^circ,quad theta=300^circ
$$
b)
$$
theta=135^circ,quad theta=315^circ
$$
c)
$$
theta=60^circ,quad theta=120^circ
$$
d)
$$
theta=150^circ,quad theta=210^circ
$$
$$
(a+b)^7=a^7+7a^6b+21a^5b^2+35a^4b^3+35a^3b^4+21a^2b^5+7ab^6+b^7
$$
Replace $a$ with $2x$ and $b$ with $dfrac{1}{4x}$ in the third term:
$$
21(2x)^5left( dfrac{1}{4x}right)^2=21(32x^5)left( dfrac{1}{16x^2}right)=42x^3
$$
Thus the third term is $42x^3$.
42x^3
$$
$$
Sigma_{n=1}^{6} 2left(3right)^{n-1}
$$
The sum of an finite geometric series is:
$$
S(n)=dfrac{a(1-r^n)}{1-r}=dfrac{2left( 1-left( 3right)^6right)}{1-3}=728
$$
728
$$
$$
(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4
$$
Replace $a$ with $3x$ and $b$ with $1$:
$$
(3x)^4+4(3x)^3(1)+6(3x)^2(1)^2+4(3x)(1)^3+(1)^4=81x^4+108x^3+54x^2+12x+1
$$

81x^4+108x^3+54x^2+12x+1
$$
As shown by the graph, the highest point of a piece of gum got is 26 inches, which means the
The diameter of the wheel is;
$$begin{aligned}
text{The diameter of the wheel is} &= 26 text{ inches}\
end{aligned}$$
The piece of gum started its journey at $t=0$ and reached the ground again at $t=0.5$, which means the wheel made a revolution in 0.5 seconds.
So, the speed $v$ of the bicycle =
$$begin{aligned}
text{v} &= 2 text { revolutions per second}\
end{aligned}$$
as the wheel completes 2 revolutions in 1 second.
The general equation of Sine is stated below:
$$begin{aligned}
y &= Acdot sin (B(x-C)+D\
end{aligned}$$
Put the values of A, B, C and D in the general equation.
A = 13, as it is amplitude
B = 4 pi, as it is Period
C = 0.25, as it Phase shift (shifts right side with 0.25 units)
D = 13, as it is vertical shift (vertically stretched by 13 units)
So, the equation is:
$$begin{aligned}
boxed {y = 13cdot sin (4pi (x – 0.25) + 13}\
end{aligned}$$
$(b.)$ 2 revolutions per second
$(c.)$ $y = 13cdotsin (4pi (x – 0.25) + 13$
$$
begin{align*}
x&=2\
x&= -5\
x&= 4+i\
x&= 4-i\
end{align*}
$$
In order to find the polynomial function of degree four with these roots we will first evaluate the linear factor from the given roots.
Thus, the linear factors are given as follows.
$$
begin{align*}
x -2&=0tag{1}\
x+5&=0 tag{2}\
x-(4+i)&=0tag{3}\
x-(4-i)&=0tag{4}\
end{align*}
$$
Mathematically it stated as follows,
$$
begin{align*}
f(x)&= (x-x_{1})times (x-x_{2})times (x-x_{3})times (x-x_{4})tag{A}\
end{align*}
$$
$$
begin{align*}
f(x)&= (x-2)times (x+5) times(x-4-i) times(x-4+i)tag{5}\
end{align*}
$$
$$
begin{align*}
f(x)&= x^{2} + 5x -2x -10 times (x-4-i) times (x-4+i)\
f(x)&= x^{2}+3x -10 times left[(x-4)-iright] times left[(x-4)+iright]\
end{align*}
$$
begin{align*}
f(x)&= x^{2} + 3x -10 times (x-4)^{2} – i^{2}\
intertext{ $(a+b) (a-b)$= $a^{2}$ – $b^{2}$}\
&= x^{2} + 3x -10 times left[ (x^{2}-8x+16)+1right]\
intertext{ Using $i^{2}=-1$}\
&= (x^{2} + 3x -10) times (x^{2}-8x+17)\
end{align*}
$$
begin{align*}
f(x)&= x^{4} – 8x^{3} + 17x + 3x^{3} -24x^{2} + 51x -10x^{2} + 80x -170\
&= x^{4} -5x^{3}-34x^{2} + 131x -170\
end{align*}
$$
The standard form is given as follows $f(x)=x^{4} -5x^{3}-34x^{2} + 131x -170$
$$
begin{align*}
2x + y &= 12 tag{1}\
xy&= 16 tag{2} \
end{align*}
$$
In order to solve equation $(1)$ and $(2)$, we will first substitute $y$’s value from condition $(2)$ in condition $(1)$.
$$
begin{align*}
y &= dfrac{16}{x}tag{3}\
end{align*}
$$
Also, condition $(1)$ becomes.
$$
begin{align*}
2x + dfrac{16}{x}&=12 \\
dfrac{2x^{2}+16}{x}&=12 \\
2x^{2} + 16&= 12x \\
2x^{2} – 12x + 16&= 0 tag{4}\\
end{align*}
$$
Mathematically it can be expressed as follows.
$$
begin{align*}
d&= b^{2}- 4ac\
&= (12^{2}) – 4 times 2 times 16\
&= 144 – 128\
&= 16 \
end{align*}
$$
where,
$$
begin{align*}
text{Co-efficient of $x^{2}$} , a&= 2\
text{ Co-efficient of $x$} , b &= -12\
text{ Constant term} ,c &= 16\
end{align*}
$$
$$
begin{align*}
alpha &= dfrac{-b + sqrt{d}}{2a} \\
&= dfrac{12 + sqrt{16}}{2times2}\\
&= dfrac{(12+4)}{4}\\
&= dfrac{16}{4}\\
&= 4tag{5}\\
end{align*}
$$
$$
begin{align*}
beta &= dfrac{-b – sqrt{d}}{2a}\\
&= dfrac{12 – sqrt{16}}{2times2}\\
&= dfrac{(12-4)}{4}\\
&= dfrac{8}{4}\\
&= 2tag{6}\\
end{align*}
$$
From $(5)$ and $(6)$, we can say that the possible values of $x$ are $4$ and $2$.
$$
begin{align*}
y&= dfrac{16}{4}\\
y&= 4tag{7} \\
end{align*}
$$
$$
begin{align*}
y&= dfrac{16}{2}\\
y&= 8tag{8}\\
end{align*}
$$
Thus the values are stated below.
$$
begin{align*}
(x, y) & = (4, 4) ; (2,8)\
end{align*}
$$
Given systems are,
$$
begin{align*}
2x + y &= 12 tag{1} \
xy&= 20 tag{2}\
end{align*}
$$
In order to solve equation $(1)$ and $(2)$, we will first substitute $y$’s value from condition $(2)$ in condition $(1)$.
$$
begin{align*}
y &= dfrac{20}{x}tag{3}\
end{align*}
$$
Also, condition $(1)$ becomes.
$$
begin{align*}
2x + dfrac{20}{x}&=12\\
dfrac{2x^{2}+20}{x}&=12\\
2x^{2} + 20&= 12x\\
2x^{2} – 12x + 20&= 0 tag{4}\\
end{align*}
$$
Mathematically it can be expressed as follows.
$$
begin{align*}
d&= b^{2}- 4ac\
&= (12^{2}) – 4 times 2 times 20 \
&= 144 – 160\
&= -16\
end{align*}
$$
where,
$$
begin{align*}
text{Co-efficient of $x^{2}$} , a&= 2\
text{ Co-efficient of $x$} , b &= -12\
text{ Constant term} ,c &= 20\
end{align*}
$$
$$
begin{align*}
alpha &= dfrac{-b + sqrt{d}}{2a}\\
&= dfrac{12 + sqrt{-16}}{2times2} \\
end{align*}
$$
$$
begin{align*}
text{ Since, }i^{2}&= -1\
end{align*}
$$
$$
begin{align*}
alpha&= dfrac{(12+ 4i)}{4}\\
&= dfrac{4(3+i)}{4} \\
&= 3+itag{5} \\
end{align*}
$$
begin{align*}
beta &= dfrac{-b – sqrt{d}}{2a}\\
&= dfrac{12 – sqrt{-16}}{2times2}\\
&= dfrac{(12-4i)}{4}\\
&= dfrac{4(3-i)}{4}\\
&= 3-itag{6} \\
end{align*}
$$
From $(5)$ and $(6)$, we can say that the possible values of $x$ are $3+i$ and $3-i$.
begin{align*}
y&= dfrac{20}{3+i}\\
intertext{Rationalising the complex denominator} \\
&=dfrac{20times(3-i)}{(3+i) times(3-i)}\\
&= dfrac{20(3-i)}{9- i^{2}}\\
&= dfrac{20(3-i)}{10}\\
&= 6 – 2i tag{7}\\
end{align*}
y&= dfrac{20}{3-i}\\
intertext{Rationalising the complex denominator} \\
y&=dfrac{20times(3+i)}{(3-i) times(3+i)} \\
&= dfrac{20(3+i)}{9- i^{2}}\\
&= dfrac{20(3+i)}{10}\\
&= 6 + 2i tag{8}\\
end{align*}
Thus, the values of $x$ and $y$ are stated below. \
begin{align*}
(x, y)& = (3+i , 6-2i);(3-i, 6+2i)\
end{align*}
Sketching the graph of $a$.

Then, using the sine function with period $T = 52$.
As there are 52 weeks in a year.
$(b.)$ See the graph.
$(c.)$ sine function.
$$A_q=$10,000 left(1+dfrac{0.03}{4}right)^4$$
$$textcolor{blue}{A_q= $10,303.39}$$
If amount is compounded monthly then amount is given by:
$$A_m=$10,000 left(1+dfrac{0.03}{12}right)^{12}$$
$$textcolor{blue}{A_m= $10,304.16}$$
If amount is compounded daily then amount is given by:
$$A_d=$10,000 left(1+dfrac{0.03}{365}right)^{365}$$
$$textcolor{blue}{A_m= $10,304.53}$$
If amount is compounded hourly then amount is given by:
$$A_h=$10,000 left(1+dfrac{0.03}{365cdot 24}right)^{365cdot 24}$$
$$A_h=$10,000 left(1+dfrac{0.03}{8760}right)^{8760}$$
$$textcolor{blue}{A_h= $10,304.54}$$
Below is the table:\\
begin{tabular}{|c|c|}
hline
Compounding Period & Received Amount after an year \ hline
Annually & $$10300$ \ hline
Semiannually & $$10302.25$ \ hline
Quaterly & $$10303.39$ \ hline
Monthly & $$10304.16$ \ hline
Daily & $$10304.53$ \ hline
Hourly & $$10304.54$ \ hline
end{tabular}
It can also be observed that as compounding period became more smaller, increment in amount is reduced
$$
$10,000left( 1+dfrac{0.03}{n}right)^n
$$
Then we obtain:
Quarterly: $n=4$
Monthly: $n=12$
Daily: $n=365$
Hourly: $n=365cdot 24=8760$
$$
$1left( 1+dfrac{1}{n}right)^n=left( 1+dfrac{1}{n}right)^n
$$
b.
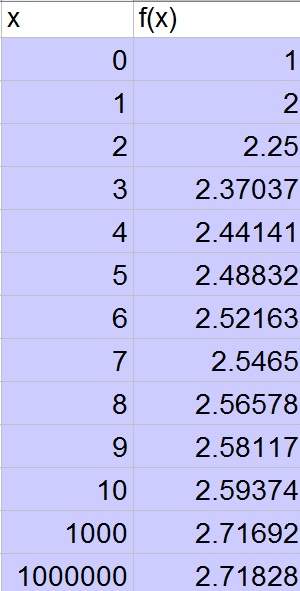
$$
begin{align*}
A&= Pe^{rt}
end{align*}
$$
where,
$$
begin{align*}
A&= text{Amount}\
P&= text{ Principle} \
r&= text{ Rate of interest} \
t&= text{ Time}\
end{align*}
$$
Given,
$$
begin{align*}
text{ Principle}&= $ 10,000 \
text{ Rate of interest}&= 3%\
text{ Time}&= 1 text{ year}\
end{align*}
$$
Using the given formula stated above to find the amount Tabitha will have after investing her $$10,000$.
A&= 10,000 e^{0.03times1}\
intertext{ Using , $e^{0.03} = 1.030$} \
A&= 10,000 times 1.030\
A&= $ 10,300\
end{align*}
Thus, we can say that the amount after investing $$10,000$ for one year at the rate of interest of $3%$ is near equals to her expectations of having $$10,304$ \
In order to find the results for compounding daily, we will use the formula stated below.
$$
begin{align*}
A(t)&= Pleft[1+ dfrac{r}{n}right]^{n times t} \
end{align*}
$$
where,
$$
begin{align*}
A&= text{Amount}\
P&= text{ Principle}\
r&= text{ Rate of interest}\
t&= text{ Time}\
n&= text{ Number of days}\
end{align*}
$$
$$
begin{align*}
text{Principal}&= $10,000 \
text{ Rate of interest}&=3% \
text{ Time}&= 10 text{ years}\
text{ Number of days in a year}&= 365\
end{align*}
$$
Using the formula stated above,
$$
begin{align*}
A(10) &= 10,000 left[1+dfrac{0.03}{365}right]^{365times10}\\
&= 10,000 left[dfrac{365+0.03}{365}right]^{3650}\\
&=10,000left[1.00008219right]^{3650}\
&=10,000 times 1.35\
&= $ 13,498.82 \
end{align*}
$$
$$
begin{align*}
text{Principal}&= $10,000\
text{ Rate of interest}&=3% \
text{ Time}&= 20 text{ years}\
text{ Number of days in a year}&= 365\
end{align*}
$$
Using the formula stated above,
$$
begin{align*}
A(20) &= 10,000 left[1+dfrac{0.03}{365}right]^{365times20}\\
&= 10,000 left[dfrac{365+0.03}{365}right]^{7300}\\
&=10,000left[1.00008219right]^{7300}\
&=10,000 times 1.82 \
&= $ 18,220.74 \
end{align*}
$$
$$
begin{align*}
text{Principal}&= $10,000\
text{ Rate of interest}&=3% \
text{ Time}&= 50 text{ years}\
text{ Number of days in a year}&= 365\
end{align*}
$$
Using the formula stated above,
$$
begin{align*}
A(50) &= 10,000 left[1+dfrac{0.03}{365}right]^{365times50}\\
&= 10,000 left[dfrac{365+0.03}{365}right]^{18250}\\
&=10,000left[1.00008219right]^{18250}\
&=10,000 times 4.48\
&= $ 44,814.13 \
end{align*}
$$
$$
begin{align*}
A&= Pe^{rt}
end{align*}
$$
where,
$$
begin{align*}
A&= text{Amount} \
P&= text{ Principle}\
r&= text{ Rate of interest} \
t&= text{ Time}\
end{align*}
$$
begin{align*}
text{ Principle}&= $ 10,000\
text{ Rate of interest}&= 3%\
text{ Time}&= 10 text{ year}\
end{align*}
Using the given formula stated above to find the amount Tabitha will have after investing her $$10,000$.\
begin{align*}
A&= 10,000 e^{0.03times10}\
intertext{ Using , $e^{0.3} = 1.349$} \
A&= 10,000 times 1.349\
A&= $ 13,498.59 \
end{align*}
begin{align*}
text{ Principle}&= $ 10,000\
text{ Rate of interest}&= 3% \
text{ Time}&= 20 text{ year}\
end{align*}
Using the given formula stated above to find the amount Tabitha will have after investing her $$10,000$.\
begin{align*}
A&= 10,000 e^{0.03times20}\
intertext{ Using , $e^{0.6} = 1.822$}\
A&= 10,000 times 1.822\
A&= $ 18,221.19\
end{align*}
begin{align*}
text{ Principle}&= $ 10,000 \
text{ Rate of interest}&= 3%\
text{ Time}&= 50 text{ year}\
end{align*}
Using the given formula stated above to find the amount Tabitha will have after investing her $$10,000$.\
begin{align*}
A&= 10,000 e^{0.03times50}\
intertext{ Using , $e^{1.5} =4.482 $}\
A&= 10,000 times 4.482\
A&= $ 44,816.89\
end{align*}
setlength{tabcolsep}{10 pt}
renewcommand{arraystretch}{1.5}
begin{center}
begin{tabular}{|c | c | c |}
hline
text{ Time}& text{Compounding Amount (daily)} & text{Compounding Amount (continuously) }\
hline
10 text{ years}& $$$13,498.82 & $$$13,498.59 \
hline
20 text{ years} & $$$ 18,220.74 & $$$18,221.19\
hline
50 text{ years}& $$$ 44,814.13& $$$44,816.89 \
hline
end{tabular}
end{center}
$$
begin{align*}
text{Principal}&= $10,000,000,000 \
text{ Rate of interest}&=8% \
text{ Time}&= 1 text{ years}\
text{ Number of days in a year}&= 365\
end{align*}
$$
Using the formula stated above,
$$
begin{align*}
A(1) &= 10,000,000,000 left[1+dfrac{0.08}{365}right]^{365times1} \\
&= 10,000,000,000 left[dfrac{365+0.08}{365}right]^{365} \\
&=10,000,000,000 left[1.000219right]^{365}\
&=10,000,000,000 times 1.08\
&= 10,832,781,000\
end{align*}
$$
begin{align*}
A(10) &= 10,000,000,000 left[1+dfrac{0.08}{365}right]^{365times10}\\
&= 10,000,000,000 left[dfrac{365+0.08}{365}right]^{3650}\\
&=10,000,000,000 left[1.000219right]^{3650} \
&=10,000,000,000 times 2935.87\
&= $ 22,253,000,000 \
end{align*}
$$
begin{align*}
text{ Principle}&= $ 10,000,000,000 \
text{ Rate of interest}&= 8%\
text{ Time}&= 1 text{ year}\
end{align*}
begin{align*}
A&= 10,000,000,000 e^{0.08times1}\
intertext{ Using , $e^{0.08} = 1.349$}\
A&= 10,000,000,000 times 1.083\
A&= $ 10,800,000,000\
end{align*}
begin{align*}
text{ Principle}&= $ 10,000,000,000 \
text{ Rate of interest}&= 8%\
text{ Time}&= 10 text{ year}\
end{align*}
begin{align*}
A&= 10,000,000,000 e^{0.08times10}\
intertext{ Using , $e^{0.8} = 2.226$}\
A&= 10,000,000,000 times 2.226\
A&= $ 22,300,000,000 \
end{align*}
setlength{tabcolsep}{10 pt}
renewcommand{arraystretch}{1.5}
begin{center}
begin{tabular}{|c | c | c |}
hline
text{ Time}& text{Compounding Amount (daily)} & text{Compounding Amount (continuously) }\
hline
1 text{ years}& $$$10,832,781,000 & $$$10,800,000,000\
hline
10 text{ years} & $$$ 22,253,000,000 & $$$22,300,000,000\
hline
end{tabular}
end{center}
The investors who invests small amount compounded daily method is useful , and the investors who invests big amount compound continuously is better.
$$begin{aligned}
f(x) &= e^{x}\
f^{-1} &= ln x\
end{aligned}$$

$$begin{aligned}
y &= log_{n}(x) < y=ln (x)< y = log_{n+1}(x)\\
end{aligned}$$
As 2 < e < 3, Now sketch the graph of
$$begin{aligned}
y &= log_{2}(x)\
y &= log_{3}(x)\\
end{aligned}$$
Thus, the value of integer , $n = 2$.

The graph of $y = ln(x)$ is above the graph $y=log_{2}(x)$ for $x in (0,1)$ and below the same graph for $x in (1, infty)$.
In case of $y=log_{3}x$,
The graph of $y = ln(x)$ is above the graph $y=log_{3}(x)$ for $x in (1, infty)$ and below the same graph for $x in (0, 1)$.
b. The series becomes then
$$
1+1+dfrac{1}{2!}+dfrac{1}{3!}+dfrac{1}{4!}+….=Sigma_{n=0}^{infty} dfrac{1}{n!}
$$
as $n$ becomes infinitely large.
b. $Sigma_{n=0}^{infty} dfrac{1}{n!}$
b. First 5 terms:
$$
1+1+dfrac{1}{2!}+dfrac{1}{3!}+dfrac{1}{4!}=1+1+dfrac{1}{2}+dfrac{1}{6}+dfrac{1}{24}=dfrac{65}{24}approx 2.708
$$
First 7 terms:
$$
1+1+dfrac{1}{2!}+dfrac{1}{3!}+dfrac{1}{4!}+dfrac{1}{5!}+dfrac{1}{6!}=1+1+dfrac{1}{2}+dfrac{1}{6}+dfrac{1}{24}+dfrac{1}{120}+dfrac{1}{720}=dfrac{1957}{720}approx 2.718
$$
The sum of the first $n$ terms has denominator $n!$ and both lie close to the value of $e$.
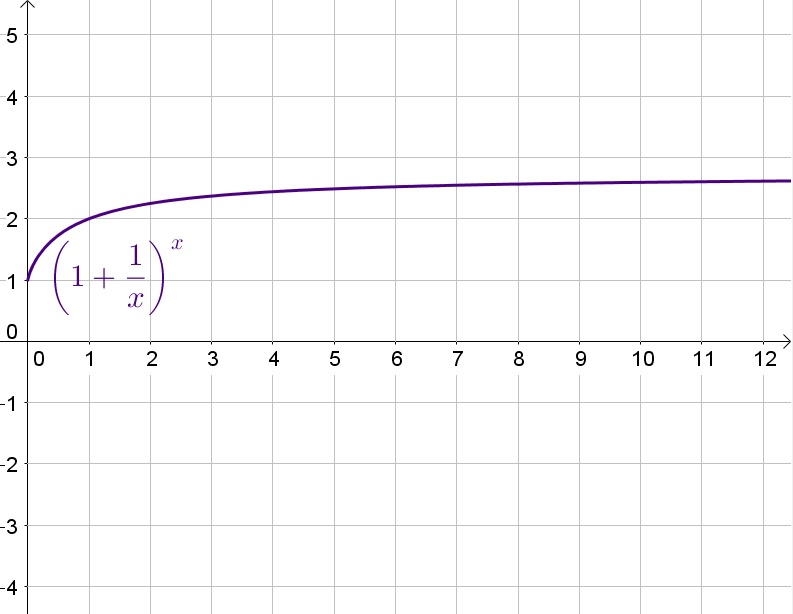
$$
K=kleft(1+dfrac{r}{t}right)^{nt}
$$
with $k$ the starting kapital, $r$ the interest rate, $t$ the number of periods per year and $n$ the number of years:
Monthly:
$$
K=8,000left(1+dfrac{0.039}{12}right)^{10cdot 12}approx $11,808.38
$$
Semi-annually:
$$
K=8,000left(1+dfrac{0.04}{2}right)^{10cdot 2}approx $11,887.58
$$
Thus we note that the semi-annual plan will reward more.
It is given that,
$$
begin{align*}
10,000(1.08)^{x} &= 20,000 \\
(1.08)^{x} &=dfrac{20,000}{10,000} \\
(1.08)^{x} &= 2\\
end{align*}
$$
$$
begin{align*}
log(1.08)^{x} &= log (2)tag{1} \
end{align*}
$$
The above value in $(1)$ can be further re-calculated using the logarithm formula stated below.
$$
begin{align*}
log(m)^{n} &= n times log(m)\
end{align*}
$$
Thus, $(1)$ becomes.
$$
begin{align*}
x times log(1.08)&= log(2)\
x &= dfrac{log(2)}{log(1.08)} \
x & approx 9.006\
end{align*}
$$
where , $base = 1.08$.
$$
begin{align*}
ln(1.08)^{x} &= ln (2)tag{2}\
end{align*}
$$
The above value in $(1)$ can be further re-calculated using the logarithm formula stated below.
$$
begin{align*}
ln(m)^{n} &= n times ln(m) \
end{align*}
$$
Thus, $(2)$ becomes.
$$
begin{align*}
x times ln(1.08)&= ln(2)\
x &= dfrac{ln(2)}{ln(1.08)}\
x & approx 9.006\
end{align*}
$$
where, $base , e = 1.08$.
It is given that,
$$
begin{align*}
30,000(0.8)^{x} &=15,000 \\
(0.8)^{x} &= dfrac{15,000}{30,000}\\
(0.8)^{x} &= dfrac{1}{2}\\
(0.8)^{x} &= 0.5 \\
end{align*}
$$
$$
begin{align*}
log(0.8)^{x} &= log (0.5)tag{1} \
end{align*}
$$
The above value in $(1)$ can be further re-calculated using the logarithm formula stated below.
$$
begin{align*}
log(m)^{n} &= n times log(m)\
end{align*}
$$
Thus, $(1)$ becomes.
$$
begin{align*}
x times log(0.8)&= log(0.5)\
x &= dfrac{log(0.5)}{log(0.8)}\
x & approx3.106\
end{align*}
$$
where, $base = 0.8$.
$$
begin{align*}
ln(0.8)^{x} &= ln (0.5)tag{2} \
end{align*}
$$
The above value in $(1)$ can be further re-calculated using the logarithm formula stated below.
$$
begin{align*}
ln(m)^{n} &= n times ln(m)\
end{align*}
$$
Thus, $(2)$ becomes.
$$
begin{align*}
x times ln(0.8)&= ln(0.5)\
x &= dfrac{ln(0.5)}{ln(0.8)}\
x & approx 3.106\
end{align*}
$$
where, $base , e = 0.8$.
Using the expression $A= P e^{rt}$
we can interpret from $a$ i.e. $10,000 (1.08)^{x} = 20,000$ that the value are interpreted as follows.
$$
begin{align*}
text{ Amount}&= 20,000\
text{ Principle}&=10,100\
e = 1.08\
text{ Given rate of interest}, x&= 8 %\
end{align*}
$$
To find ,
$$
begin{align*}
text{time},t &= ?\
end{align*}
$$
$$
begin{align*}
20,000 & = 10,000 (1.08)^{0.08times t} \\
dfrac{20,000}{10,00}&=(1.08)^{0.08times t} \\
2&= (1.08)^{0.08times t}tag{3}\
end{align*}
$$
$$
begin{align*}
log(2) & = 0.08 times t times log(1.08) \\
dfrac{log(2)}{log(1.08)}& = 0.08 times t \\
9.006 &= 0.08 times t\\
dfrac{9.006}{0.08}&= t\\
112.57&= t\\
112 approx t\\
end{align*}
$$
Thus, we can say that time will $112$ years.
Using the expression $A= P e^{rt}$
we can interpret from $a$ i.e. $30,000 (0.8)^{x} = 50,000$ that the value are interpreted as follows.
$$
begin{align*}
text{ Amount}&= 15,000 \
text{ Principle}&=30,100 \
e = 0.8\
text{ Given rate of interest}, x&= 20 %\
end{align*}
$$
To find ,
$$
begin{align*}
text{time},t &= ?\
end{align*}
$$
$$
begin{align*}
15,000 & = 30,000 (0.8)^{0.2times t} \\
dfrac{15,000}{30,000}&= (0.8)^{0.2times t} \\
dfrac{1}{2}&= (0.8)^{0.2times t}\\
0.5 & =(0.8)^{0.2times t} tag{3}\\
end{align*}
$$
$$
begin{align*}
log(0.5) & = 0.2 times t times log(0.8) \\
dfrac{log(0.5)}{log(0.8)}& = 0.08 times t \\
3.106 &= 0.08 times t \\
dfrac{3.106}{0.08}&= t\\
38.825&= t\\
38 approx t\\
end{align*}
$$
Thus, we can say that time will $38$ years.
$$
begin{align*}
ln(2) approx 0.69315\
ln(3) approx 1.0986\
end{align*}
$$
Let a function $f(x)= 1$.
It’s brings that $f(x) = ln(x)$ is an ascending function. As $f(x) = 1$ for $x = e approx 2.71$ , so for $x e$ the function is greater than $1$.
Thus, from above explanation the conditions written below explains the possible values of $x$.
$$
begin{align*}
x > e\
end{align*}
$$
$i$.
Evaluating $ln(6)$
Since,
$$
begin{align*}
ln(6) &= ln(2.3)tag{1}\
end{align*}
$$
The above value can be further expand by using the property of logarithm function which is explained as follows.
$$
begin{align*}
ln(m) cdot ln(m) & = ln (n) + ln(m)\
end{align*}
$$
So, $1$ can be now re-evaluated as below.
$$
begin{align*}
&=ln (2) + ln (3)\
&= 0.69315 + 1.0986\
&= 1.79175\
end{align*}
$$
Evaluating $ln(12)$
Since,
$$
begin{align*}
ln(12) &= ln(2)^{2} + ln(3)tag{2}\
end{align*}
$$
The above value can be further expand by using the property of logarithm function which is explained as follows.
$$
begin{align*}
ln(m) cdot ln(m) & = ln (n) + ln(m)\
ln(m)^{n}&= n times ln(m)\
end{align*}
$$
So, $(2)$ can be now re-evaluated as below.
$$
begin{align*}
&=2 ln (2) + ln (3)\
&= 2 times 0.69315 + 1.0986 \
&= 2.4849\
end{align*}
$$
Evaluating $ln(12)$
Since,
$$
begin{align*}
ln(16) &= ln(2)^{4}tag{3}\
end{align*}
$$
The above value can be further expand by using the property of logarithm function which is explained as follows.
$$
begin{align*}
ln(m)^{n}&= n times ln(m)\
end{align*}
$$
So, $(3)$ can be now re-evaluated as below.
$$
begin{align*}
&=4 ln (2)\
&= 4 times 0.69315 \
&= 2.7726\
end{align*}
$$
Evaluating $lnleft[dfrac{1}{3}right]$
The above value can be further expand by using the property of logarithm function which is explained as follows.
$$
begin{align*}
lnleft[dfrac{m}{n}right] & = ln left[mright] – lnleft[nright]\
end{align*}
$$
So, the given value can be now re-evaluated as below.
$$
begin{align*}
&= ln (1) – ln (3)\
&= 0 – 1.0986 \
&= -1.0986\
end{align*}
$$
$$begin{aligned}
(3x – 2)^{3}\\
text {Expand the equation in form of } (a + b)^{3}\
end{aligned}$$
$$begin{aligned}
(a + b)^{3} &= a^{3} + 3a^{2}b + 3ab^{2} + b^{2}\\
&= (3x)^{3} + 3cdot(3x)^{2}cdot(-2) + 3cdot(3x)cdot(-2)^{2} + (-2)^{3}\\
&= 27x^{3} + (-6)(9x) + 12(3x) – 8\\
&boxed {27x^{3} – 54x^{2} + 36x – 8}\\
end{aligned}$$
Given series,
$11 + 12 + 13 +. . . . . . . 40$
From the series, we can conclude that
$$
begin{align*}
text{ First term}, a &= 11\
text{ Common Difference}&= 12-11 \
&= 1\
end{align*}
$$
$$
begin{align*}
a_{n}&= a + (n-1)d\
end{align*}
$$
where $a_{n}$ is the last term i.e. $40$ from the given series.
Thus, putting the given value.
$$
begin{align*}
40&= 11+ (n-1) 1 \
40 – 11& = n – 1 \
29 + 1 &= n\
&boxed{30 = n}\
end{align*}
$$
Thus, number of terms are $30$.
$$
begin{align*}
S_{n} &= dfrac{n}{2} left[ a + a_{n}right]\\
&= dfrac{30}{2} left[11+40right] \\
&= 15 (51)\\
&= 765\\
end{align*}
$$
Given series,
$90 + 84 + 78 +. . . . . . . 24$
From the series, we can conclude that
$$
begin{align*}
text{ First term}, a &= 90\
text{ Common Difference}&= 84-90\
&= -6\
end{align*}
$$
$$
begin{align*}
a_{n}&= a + (n-1)d\
end{align*}
$$
where $a_{n}$ is the last term i.e. $24$ from the given series.
Thus, putting the given value.
$$
begin{align*}
24&= 90+ (n-1) -6\\
24 – 90& = -6n + 6\\
-66 &= -6n + 6\\
-66-6&= -6n\\
-72&= -6n\\
dfrac{72}{6}&=n\\
&boxed{12 = n}\\
end{align*}
$$
Thus, number of terms are $12$.
$$
begin{align*}
S_{n} &= dfrac{n}{2} left[ a + a_{n}right]\\
&= dfrac{12}{2} left[90+24right]\\
&= 6 (114)\\
&= 684\\
end{align*}
$$
$b$. $684$
$$
theta=sin^{-1}{0.5}=30text{textdegree}text{ or } 180text{textdegree}-30text{textdegree}=150text{textdegree}
$$
b.
$$
theta=cos^{-1}{-0.5}=180text{textdegree}-60text{textdegree}=120text{textdegree}text{ or } 180text{textdegree}+60text{textdegree}=240text{textdegree}
$$
c. Add 4 to both sides of the equation:
$$
4tan{theta}=4
$$
Divide both sides of the equation by 4:
$$
tan{theta}=1
$$
$$
theta=tan^{-1}{1}=45text{textdegree}text{ or } 180text{textdegree}+45text{textdegree}=225text{textdegree}
$$
d. Divide both sides of the equation by 3:
$$
sin^2{theta}=dfrac{1}{3}
$$
Take the square root of both sides of the equation:
$$
sin{theta}=pm dfrac{sqrt{3}}{3}
$$
$$
theta=sin^{-1}{pm dfrac{sqrt{3}}{3}}approx 35text{textdegree}text{ or } 180text{textdegree}-35text{textdegree}=145text{textdegree}text{ or }180text{textdegree}+35text{textdegree}=215text{textdegree}text{ or }360text{textdegree}-35text{textdegree}=325text{textdegree}
$$
b. $theta=120text{textdegree}, 240text{textdegree}$
c. $theta=45text{textdegree}, 225text{textdegree}$
d. $thetaapprox 35text{textdegree}, 145text{textdegree}, 215text{textdegree}, 325text{textdegree}$
In order to find the equation of a circle centered at point $O$ and passing through the point $R$, we will first find the length of $OR$ i.e. the radius of the circle. Mathematically it can be calculated using the distance formula which is stated below.
$$
begin{align*}
text{ Distance}&= sqrt{(x_{2} – x_{1})^{2} + (y_{2}-y_{1})^{2}}\
end{align*}
$$
Thus, $OR$ is given as follows.
$$
begin{align*}
OR &= sqrt{(-5 -0)^{2} + (-12-0)^{2}}\
OR&= sqrt{25 + 144}\
OR&= sqrt{169}\
OR&= 13 \
end{align*}
$$
$$
begin{align*}
(x-h)^{2} + (y-k)^{2} &= r^{2} \
end{align*}
$$
where $’h’$ and $’k’$ are the coordinate of the centre of the circle.
So,
$$
begin{align*}
(x-0)^{2} + (y-0)^{2} &= 13^{2}\
x^{2} + y^{2} & = 169\
end{align*}
$$
The angle formed by $overline{OR}$ and the positive x- axis, we will use the formula stated below.
$$
begin{align*}
tan theta &= dfrac{y_{2} – y_{1}}{x_{2}-x_{1}} \\
theta&= tan^{-1} dfrac{-12-0}{-5-0} \\
theta&= tan^{-1} dfrac{-12}{-5} \\
theta&= tan^{-1} dfrac{12}{5}\\
theta&= 67.38^{o} + k (180^{o})\\
text{ or in radian}&= 1.16 + pi\\
&approx 4.32\
end{align*}
$$
Sketching the graph of the equation of circle formed in $a$.
Since, the favourable case of the shooting area is zero. So, the probability of hitting is zero.
$$
begin{align*}
text{ Principle}, P&= $800 \
text{Rate of interest}, r&= 3%\
text{ Time}, t&= 2 text{ years}\
end{align*}
$$
$$
begin{align*}
text{ Amount}&= Pe^{rt}\
&= 800 e^{0.03 times2} \
&= 800 e^{0.06}\
&= 800 times 1.06\
&approx $848
end{align*}
$$
$$
(a+b)^3=a^3+3a^2b+3ab^2+b^3
$$
Replace $a$ with $1$ and $b$ with $dfrac{1}{n}$:
$$
left(1+dfrac{1}{n}right)^3=1^3+3(1)^2left(dfrac{1}{n}right)+3(1)left(dfrac{1}{n}right)^2+left(dfrac{1}{n}right)^3=1+dfrac{3}{n}+dfrac{3}{n^2}+dfrac{1}{n^3}
$$
$$
(a+b)^5=a^5+5a^4b+10a^3b^2+5b^4a+b^5
$$
Replace $a$ with $1$ and $b$ with $dfrac{1}{n}$:
$$
left(1+dfrac{1}{n}right)^5=1^5+5(1)^4left(dfrac{1}{n}right)+10(1)^3left(dfrac{1}{n}right)^2+10(1)^2left(dfrac{1}{n}right)^3+5(1)left(dfrac{1}{n}right)^4+left(dfrac{1}{n}right)^5=1+dfrac{5}{n}+dfrac{10}{n^2}+dfrac{10}{n^3}+dfrac{5}{n^4}+dfrac{1}{n^5}
$$
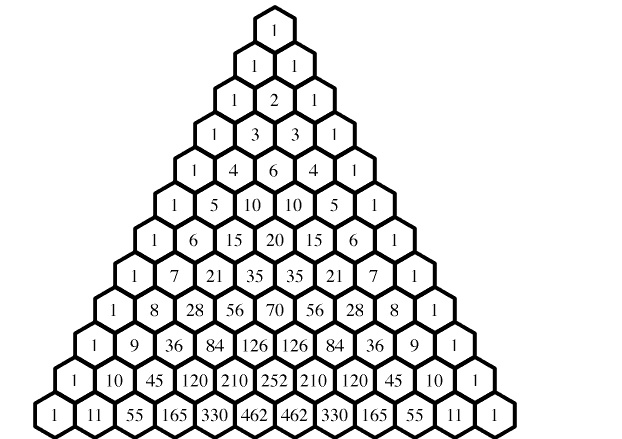
b. $1+dfrac{5}{n}+dfrac{10}{n^2}+dfrac{10}{n^3}+dfrac{5}{n^4}+dfrac{1}{n^5}$
$$
P=14.7e^{-0.00003(0)}=14.7
$$
b. Since 1 mile = 5280 ft:
$$
P=14.7e^{-0.00003(5280)}=12.55
$$
c. Replace $h$ with 285:
$$
P=14.7e^{-0.00003(285)}=14.57
$$
b. 12.55 lbs. per square inch
c. 14.57 lbs. per square inch
$324 + 54 + 9 + 1.5 +……$ \
From the above series, we can say the following things. \
begin{align*}
text{ First term}, a_{1}&= 324\
text{ Second term},a_{2}&= 54\
text{ Common Ratio}, r&= dfrac{a_{1}}{a_{2}}\
&= dfrac{54}{324}\
&= dfrac{1}{6}\
intertext{ $r < 1$.}\
end{align*}
$$
begin{align*}
&= dfrac{text{ Second term}}{text{ First term}}\\
&=dfrac{54}{324}\\
&=dfrac{1}{6}tag{1} \\
end{align*}
$$
Also,
$$
begin{align*}
&= dfrac{text{Third term}}{text{ Second term}}\\
&=dfrac{9}{54}\\
&=dfrac{1}{6}tag{2}\\
end{align*}
$$
From $1$ and $2$, we can say that the series is having the same ratio throughout. Thus, the above series is G.P.
$$
begin{align*}
text{ Sum} &= dfrac{a(1-r^{n})}{1-r}\
end{align*}
$$
$$
begin{align*}
&= dfrac{324left[1- dfrac{1}{6}^{n}right]}{1-dfrac{1}{6}}\\
&= dfrac{324left[1-dfrac{1}{6}^{n}right]}{dfrac{6-1}{6}} \\
&=dfrac{324left[1-dfrac{1}{6}^{n}right]}{dfrac{5}{6}}\\
&= dfrac{1944left[1-dfrac{1}{6}^{n}right]}{5}\\
&= 388.8left[1-dfrac{1}{6}^{n}right] \
end{align*}
$$
388.8left[1-dfrac{1}{6}^{n}right]
$$
$$
begin{align*}
text{ Radius of the circle}&= 1 \
y -text{ coordinate}&= dfrac{3}{7} \
end{align*}
$$
$$
begin{align*}
(x-h)^{2} + (y-k)^{2} = r^{2}\
x^{2} + y^{2} & = r^{2}\
end{align*}
$$
Thus,
$$
begin{align*}
x^{2}&= r^{2} – y^{2}\
x^{2}&= (1)^{2} – left(dfrac{3}{7}right)^{2} \\
x^{2}&= 1 – dfrac{9}{49}\\
x^{2}&= dfrac{49 – 9 }{49}\\
x^{2}&= dfrac{40}{49}\\
x &= sqrt{left(dfrac{40}{49}right)}\\
x &= dfrac{sqrt{40}}{7}\\
x & = + dfrac{2sqrt{10}}{7} ; – dfrac{2sqrt{10}}{7}\\
end{align*}
$$
x^2+y^2-4x-16=0
$$
$$
(x-2)^2+y^2=4
$$
We graph the circle:
$$
begin{align*}
dfrac{x}{x+1}&= dfrac{5}{7} \
end{align*}
$$
$$
begin{align*}
7 times x & = 5 times (x + 1) \
7x &= 5x + 5\
7x – 5x &= 5\
2x & = 5 \
x&= dfrac{5}{2}\\
x&= 2.5\
end{align*}
$$
$$
begin{align*}
dfrac{2}{y} &= dfrac{3}{y + 5} \
end{align*}
$$
$$
begin{align*}
2(y + 5)&= 3y\
2y + 10 &= 3y\
2y – 3y &= -10\
-y &= -10\
y &= 10\
end{align*}
$$
$b$. $10$

