All Solutions
Page 47: Closure Activity
$g(x)=x^2-x$ (Given)
b- $g(-1)=(-1)^2-(-1)=1+1=2$
c- $f(x)=10$
$10=sqrt {x+4}$
$100=x+4$
$$
x=96
$$
d- $g(x)=6$
$6=x^2-x$
$x^2-x-6=0$
$(x-3)(x+2)=0$
$x-3=0$ or $x+2=0$
$$
x=3 textrm { ~or ~} x=-2
$$
b- $g(-1)=2$
c- $x=96$
d- $x=3$ or $x=-2$
$\\$The x-values are less than 6 therefore the domain is$$text{color{#4257b2}(-infty, 6)$.
$\\$The y-values are less than 6 therefore the range is $color{#4257b2}(-infty, 6)$.}$
$\\$All x-values are part of the domain therefore the domain is$$text{color{#4257b2}(-infty, +infty)$.
$\\$The y-values are from -3 to 3 therefore the range is $color{#4257b2}[-3, 3]$.}$
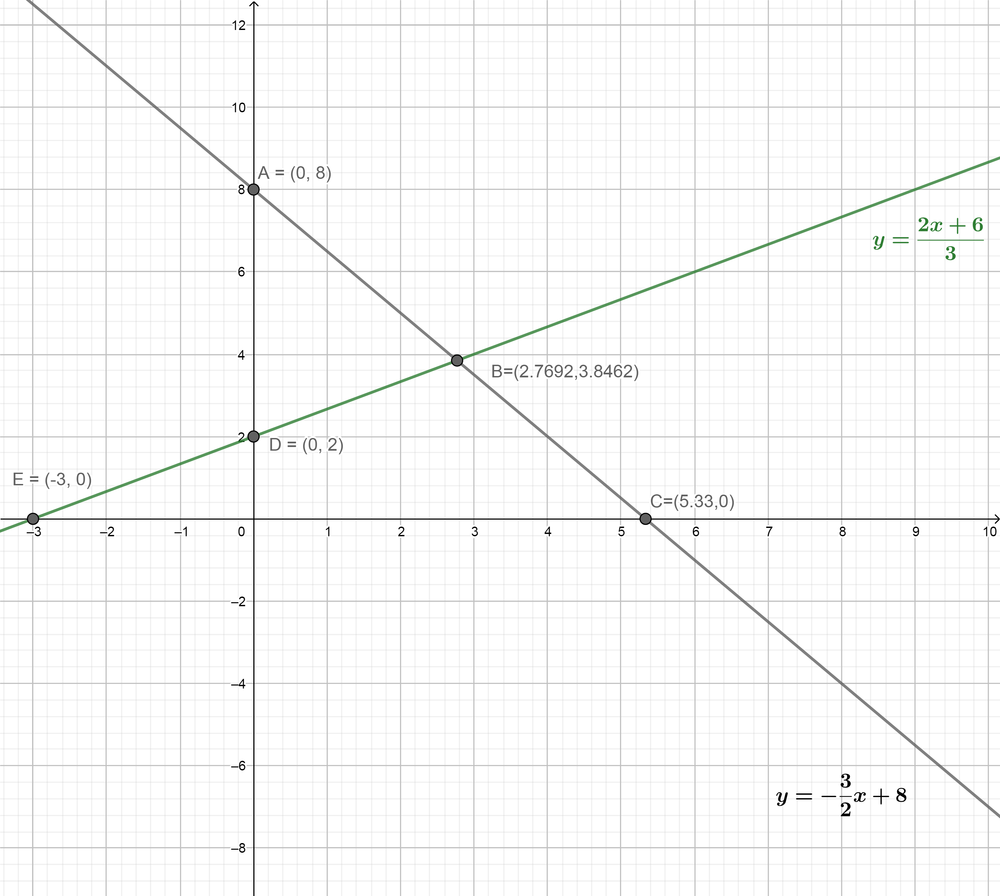
x-intercept is $(5.33,0)$
y-intercept is $(0.8)$
b- $2x-3y=-6$
x-intercept is $(-3, 0)$
y-intercept is $(0.2)$
x-intercept is $(5.33,0)$
y-intercept is $(0.8)$
b- $2x-3y=-6$
x-intercept is $(-3, 0)$
y-intercept is $(0.2)$
$$
begin{equation}
frac{x+2}{5}=frac{10-2x}{3}
end{equation}
$$
We can multiply the whole equation by $15$ to get rid of the fractions.
$$
begin{equation}
frac{15(x+2)}{5}=frac{15(10-2x)}{3}
end{equation}
$$
Now we can divide $15$ by $5$ on the left hand side and $15$ by $3$ on the right hand side of the equation.
$$
begin{equation}
3(x+2)=5(10-2x)
end{equation}
$$
If we multiply each side of the equation (3) we get:
$$
begin{equation}
3x+6=50-10x
end{equation}
$$
Now we can separate parts of the equation (4) with $x$s and those without.
$$
begin{equation}
3x+10x=50-6
end{equation}
$$
If we sum that we get:
$$
begin{equation}
13x=44
end{equation}
$$
Now if we divide equation (6) by $13$ we get the value of $x$.
$$
begin{equation}
x=frac{44}{13}
end{equation}
$$
$$
begin{equation}
frac{3}{x}-1=8
end{equation}
$$
We can start by moving $-1$ to the right hand side of the equation.
$$
begin{equation}
frac{3}{x}=8+1
end{equation}
$$
$$
begin{equation}
frac{3}{x}=9
end{equation}
$$
We can also divide the whole equation (3) by $3$.
$$
begin{equation}
frac{1}{x}=3
end{equation}
$$
If we now use the reciprocal equation of equation (4) we have the value of $x$.
$$
begin{equation}
x=frac{1}{3}
end{equation}
$$
$$
begin{equation}
x^2+3x=18
end{equation}
$$
We can start solving the equation by moving $18$ to the left hand side of the equation (1). That way we can solve equation (1) using the quadratic formula.
$$
begin{equation}
x^2+3x-18=0
end{equation}
$$
Quadratic formula:
$$
begin{equation}
x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}
end{equation}
$$
For this equation $a=1$, $b=3$ and $c=-18$.
So now we can write:
$$
begin{equation}
x_{1,2}=frac{-3pmsqrt{3^2-4cdot1cdot(-18)}}{2cdot1}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-3pmsqrt{9+72}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-3pmsqrt{81}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-3pm9}{2}
end{equation}
$$
If we separate the two equations:
$$
begin{equation}
x_1=frac{-3+9}{2}
end{equation}
$$
$$
begin{equation}
x_2=frac{-3-9}{2}
end{equation}
$$
From equation (8) $x_1=3$ and from equation (9) $x_2=-6$.
b) $x=frac{1}{3}$
c) $x_1=3$, $x_2=-6$
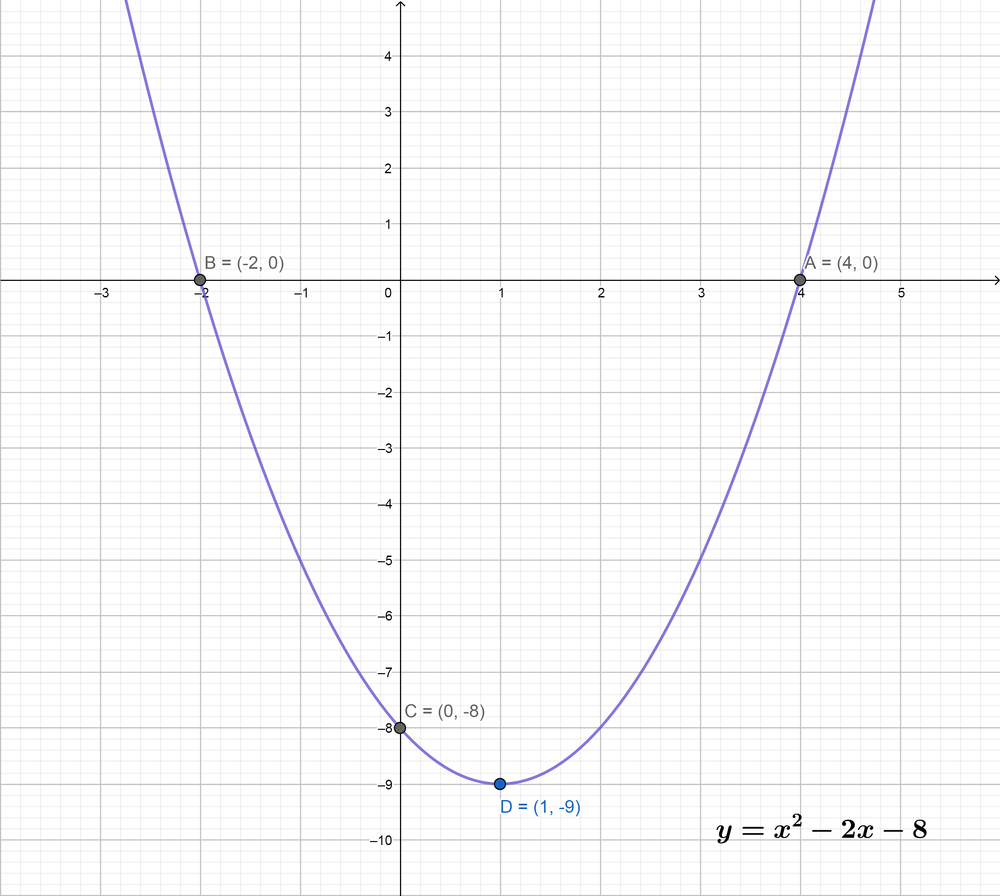
The domain of the function is: $(-infty<x<infty)$
The range of the function is: $(-9<y<infty)$
x-intercepts are: $(-2, 0)$ and $(4, 0)$
y-intercepts is: $(0, -8)$
The vertex of the parabola is: $(1, -9)$
x-intercepts are: $(-2, 0)$ and $(4, 0)$ y-intercepts is: $(0, -8)$
The vertex of the parabola is: $(1, -9)$
$\\$The graphs will intersect at the point where the two equations have the same y-values.$
$To find this point, equate the two equations to each other to have:$
3x+15 = 3-3x
$Solve for$x$to have:$
3x+3x=3-15
6x=-12
x = $frac{-12}{6}$
x=-2
$Find the value of$y$when$x = -2$to have:$
y=3x+15
y=3(-2)+15
y=-6+15
y=9
$Thus, the graphs will intersect at the point$(-2, 9)$.
$\\$The graphs will intersect at the point/s where the y-value of$y=x^2-3x-8$is equal to 2.$
$To find this point, substitute 2 to the$y$of the first equation to obtain:$
y= x^2-6x-8
2 = x^2-3x-8
0 = x^2-3x-8-2
0=x^2-3x-10
$Factor the trinomial to obtain:$
0=(x-5)(x+2)
$Equate each factor to 0 then solve each equation to have:$
x-5=0 or x + 2 =0
x=5 or x = -2
$Thus, the graph will intersect in the points$(-2, 2)$and$(5, 2)$.
Let us solve the following equation
$$
color{#4257b2} x^2-x-6=0.
$$
Since the expression of the left is a quadratic function we can use the quadratic formula
$$
x = frac{-b pm sqrt{b^2-4ac}}{2a}.
$$
We have
$$
a=1 hspace{12mm} b=-1 hspace{12mm} c=-6.
$$
Hence, we have
$$
begin{align*}
x &= frac{-(-1) pm sqrt{(-1)^2-4 cdot 1 cdot (-6)}}{2 cdot 1} \
x &= frac{1 pm sqrt{1+24}}{2} \
x &= frac{1 pm sqrt{25}}{2} \
x &= frac{1 + sqrt{25}}{2} hspace{3mm} text{or} hspace{3mm} frac{1 – sqrt{25}}{2} \
x &= frac{1 + 5}{2} hspace{3mm} text{or} hspace{3mm} frac{1 – 5}{2} \
x &= frac{6}{2} hspace{3mm} text{or} hspace{3mm} frac{-4}{2} \
x &=3 hspace{3mm} text{or} hspace{3mm} -2
end{align*}
$$
Therefore, the solutions are
$$
color{#c34632} x=3 hspace{3mm} text{color{default}or} hspace{3mm} x=-2.
$$
Let us solve the following equation
$$
color{#4257b2} 5x^2-8=12x.
$$
First we transform the equation a little bit and get
$$
5x^2-12x-8=0.
$$
Since the expression of the left is a quadratic function we can use the quadratic formula
$$
x = frac{-b pm sqrt{b^2-4ac}}{2a}.
$$
We have
$$
a=5 hspace{12mm} b=-12 hspace{12mm} c=-8.
$$
Hence, we have
$$
begin{align*}
x &= frac{-(-12) pm sqrt{(-12)^2-4 cdot 5 cdot (-8)}}{2 cdot 5} \
x &= frac{12 pm sqrt{144+160}}{10} \
x &= frac{12 pm sqrt{304}}{10} \
x &= frac{12 + sqrt{304}}{10} approx 2,94 hspace{3mm} text{or} hspace{3mm} frac{12 – sqrt{304}}{10} approx -0,54.
end{align*}
$$
Therefore, the solutions are
$$
color{#c34632} x=frac{12 + sqrt{304}}{10} approx 2,94 hspace{3mm} text{color{default}or} hspace{3mm} x=frac{12 – sqrt{304}}{10} approx -0,54.
$$
Let us solve the following equation
$$
color{#4257b2} x^2-8x-20=0.
$$
Since the expression of the left is a quadratic function we can use the quadratic formula
$$
x = frac{-b pm sqrt{b^2-4ac}}{2a}.
$$
We have
$$
a=1 hspace{12mm} b=-8 hspace{12mm} c=-20.
$$
Hence, we have
$$
begin{align*}
x &= frac{-(-8) pm sqrt{(-8)^2-4 cdot 1 cdot (-20)}}{2 cdot 1} \
x &= frac{8 pm sqrt{64+80}}{2} \
x &= frac{8 pm sqrt{144}}{2} \
x &= frac{8 + sqrt{144}}{2} hspace{3mm} text{or} hspace{3mm} frac{8 – sqrt{144}}{2} \
x &= frac{8 + 12}{2} hspace{3mm} text{or} hspace{3mm} frac{8 – 12}{2} \
x &= frac{20}{2} hspace{3mm} text{or} hspace{3mm} frac{-4}{2} \
x &=10 hspace{3mm} text{or} hspace{3mm} -2
end{align*}
$$
Therefore, the solutions are
$$
color{#c34632} x=10 hspace{3mm} text{color{default}or} hspace{3mm} x=-2.
$$
Let us solve the following equation
$$
color{#4257b2} 2y^2-5y=12.
$$
First we transform the equation a little bit and get
$$
2y^2-5y-12=0.
$$
Since the expression of the left is a quadratic function we can use the quadratic formula
$$
y = frac{-b pm sqrt{b^2-4ac}}{2a}.
$$
We have
$$
a=2 hspace{12mm} b=-5 hspace{12mm} c=-12.
$$
Hence, we have
$$
begin{align*}
y &= frac{-(-5) pm sqrt{(-5)^2-4 cdot 2 cdot (-12)}}{2 cdot 2} \
y &= frac{5 pm sqrt{25+96}}{4} \
y &= frac{5 pm sqrt{121}}{4} \
y &= frac{5 + 11}{4} hspace{3mm} text{or} hspace{3mm} frac{5 – 11}{4} \
y &= frac{16}{4} hspace{3mm} text{or} hspace{3mm} frac{-6}{4} \
y &= 4 hspace{3mm} text{or} hspace{3mm} -1,5.
end{align*}
$$
Therefore, the solutions are
$$
color{#c34632} y=4 hspace{3mm} text{color{default}or} hspace{3mm} y=-1,5.
$$
begin{align*}
&text{a.} hspace{3mm} x=3 hspace{3mm} text{color{default}or} hspace{3mm} x=-2 \
&text{b.} hspace{3mm} x=frac{12 + sqrt{304}}{10} approx 2,94 hspace{3mm} text{color{default}or} hspace{3mm} x=frac{12 – sqrt{304}}{10} approx -0,54 \
&text{c.} hspace{3mm} x=10 hspace{3mm} text{color{default}or} hspace{3mm} x=-2 \
&text{d.} hspace{3mm} y=4 hspace{3mm} text{color{default}or} hspace{3mm} y=-1,5 \
end{align*}
$$
begin{center}
renewcommand{arraystretch}{1.5}
begin{tabular}{|r|r|}
hline
Weeks $x$ & Remaining $y$ \
hline
1 & 185 \
hline
2 & 170 \
hline
3 & 155 \
hline
4 & 140 \
hline
5 & 125 \
hline
6 & 110 \
hline
7 & 95 \
hline
8 & 80 \
hline
9 & 65 \
hline
10 & 50 \
hline
11 & 35 \
hline
12 & 20 \
hline
13 & 5 \
hline
end{tabular}
end{center}
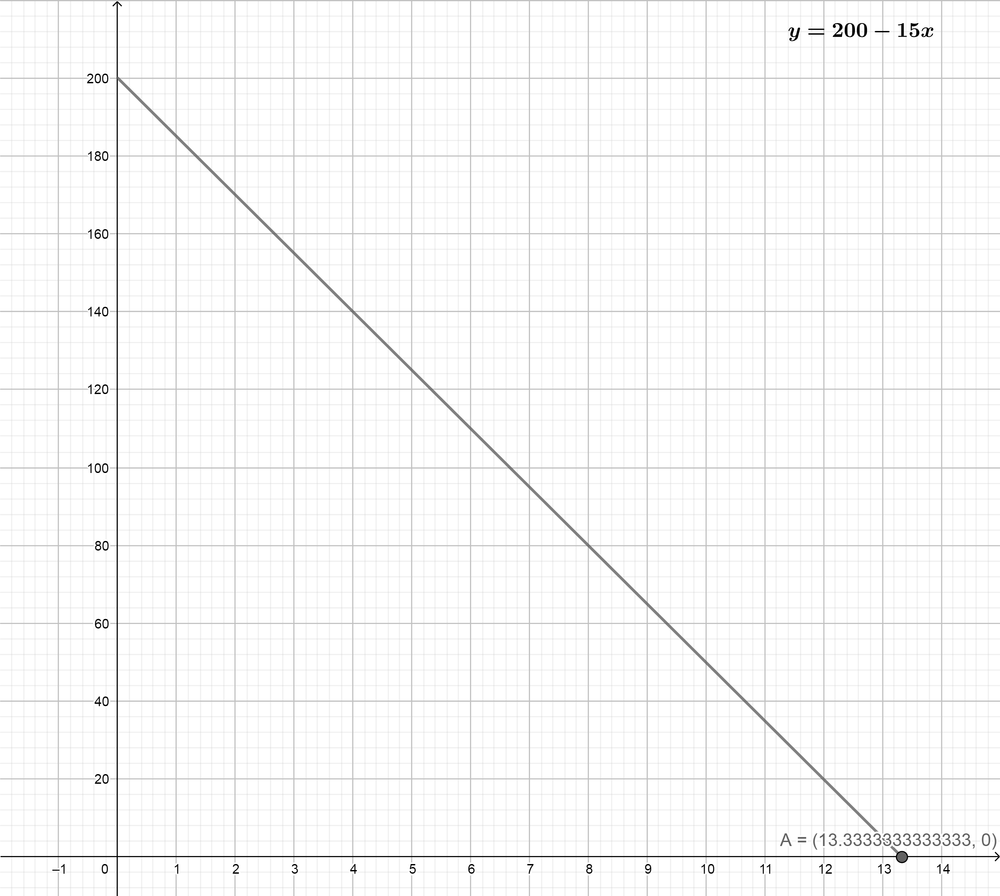
The initial value is $200\
The rate of change is $15 per week.\
The equation that represents this relation is:\
$$y=200-15x$$
\
When the money is gone $y=0$\
$0=200-15x$\
$x=dfrac {200}{15}$\
$x=13.3333$\
The money is gone after 13.3333 weeks.
The money is gone after 13.3333 weeks.
1. Check your answers using the table at the end of this section.
2. Construct a table in your Learning Log.
3. Write a list of topics you need help on.
4. Write a list of topics you need to practice more.

