All Solutions
Page 431: Questions
Since $overline {AC}=1$ (Given)
Then:
$overline {BC}=dfrac {1}{2}$
$overline {AB}=dfrac {sqrt {3}}{2}$
Since $overline {AC}=1$ (Given)
Then:
$overline {BC}=dfrac {1}{sqrt {2}}$
$overline {AB}=dfrac {1}{sqrt {2}}$
The missing side lengths of the $(45 – 45 -90)$ triangle are: $dfrac {1}{sqrt {2}}$ and $dfrac {1}{sqrt {2}}$
a. $log_3{5m}$
b. $log_6{dfrac{p}{m}}$
c. $log_2{r}+3log_6{z}=log_2{r}+3dfrac{log_2{z}}{log_2{6}}=log_2{r}+dfrac{log_2{z}}{dfrac{1}{3}log_2{6}}=log_2{r}+dfrac{log_2{z}}{log_2{6^{1/3}}}=log_2{r}+dfrac{log_2{z}}{log_2{sqrt[3]{6}}}=log_2{r}+log_2{z^{1/log_2{sqrt[3]{6}}}}=log_2{rz^{1/log_2{sqrt[3]{6}}}}$
d. $log{dfrac{90cdot 4}{36}}=log{10}=1$
b. $log_6{dfrac{p}{m}}$
c. $log_2{rz^{log_2{1/sqrt[3]{6}}}}$
d. $1$
$$
color{#c34632}{(a+b)^2 = a^2 + 2ab + b^2}
$$
Now, we have
$$
begin{align*}
f(x) &= (x+4)(x+1)^2 (x-2)\
&= (x+4)(x^2 + 2x +1)(x-2)\
&= (x^3 + 2x^2 +x+4x^2 +8x +4) (x-2)\
&= (x^3 + 6x^2 +9x +4) (x-2)\
&= x^4 + 6x^3 +9x^2 +4x – 2x^3 – 12x^2 -18x-8\
&= x^4 + 4x^3 – 3x^2 – 14x-8
end{align*}
$$
This function is a fourth-degree.
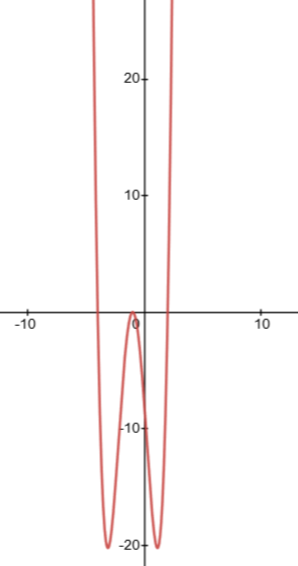
f(x) = x^4 + 4x^3 – 3x^2 – 14x-8
$$
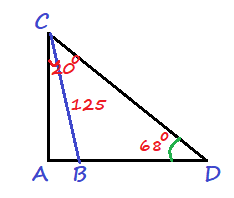
CBD=A+ACB=90text{textdegree}+20text{textdegree}=110text{textdegree}
$$
$=180text{textdegree}-110text{textdegree}-68text{textdegree}$
$$
=1text{textdegree}
$$
$sin BCDcdot BC=BDsin D$
$BC=dfrac{125cdot sin 1text{textdegree}}{sin 68text{textdegree}}$
$=dfrac{125cdot 0.01745241}{0.92718385}$
$$
approx 2.35
$$
n^3=49
$$
n=sqrt[3]{49}approx 3.66
$$
3^n=49
$$
$nlog (3)=log (49)$
$$
n=dfrac{log (49)}{log (3)}approx 3.54
$$
3^{n+1}=49
$$
$(n+1)log (3)=log (49)$
$n+1=dfrac{log (49)}{log (3)}$
$$
n=dfrac{log (49)}{log (3)}-1approx 2.54
$$
b) $dfrac{log (49)}{log (3)}approx 3.54$
c) $dfrac{log (49)}{log (3)}-1approx 2.54$
a)
$$
begin{align*}
n^3 &= 49\
n &= sqrt[3]{49}\
n &= 3.6593\
n &approx 3.66
end{align*}
$$
The solution of equation is
$$
n approx 3.66
$$
$$
3^n =49
$$
We can use the $ln$ function
$$
ln 3^n = ln 49
$$
According to the formula
$$
begin{align*}
color{#c34632}{ln a^b = b ln a} tag{$star$}
end{align*}
$$
we obtain
$$
begin{align*}
n cdot ln 3 &= ln 49\
n &= frac {ln 49}{ln 3}\
n &= frac {3.8918}{1.0986}\
n &= 3.5425\
n &approx 3.54
end{align*}
$$
The solution of equation is
$$
n approx 3.54
$$
$$
3^{n+1} = 49
$$
We can use the $ln$ function
$$
ln 3^{n+1} = ln 49
$$
According to the formula $(*)$ we obtain
$$
begin{align*}
(n+1) ln 3 &= ln 49\
n+1 &= frac {ln 49}{ln 3}\
n+1 &= 3.5425\
n &= 2.5425\
n &approx 2.54
end{align*}
$$
The solution of equation is
$$
n approx 2.54
$$
b) $n approx 3.54$
c) $n approx 2.54$
begin{tabular}{|| c|c| c||}
hline
Degree of rotation & Height & Actual height \ [0.5ex]
hline
0&0&0\
hline
30& 0.5 & 50\
hline
45& 0.7 & 71\
hline
60& 0.9 & 87\
hline
90& 1 & 100\
hline
120& 0.9 & 87\
hline
135& 0.7 & 71\
hline
150& 0.5 & 50\
hline
180& 0 & 0\
hline
210& -0.5 & -50\
hline
225& -0.7 & -71\
hline
240& -0.9 & -87\
hline
270& -1 & -100\
hline
300& -0.9 & -87\
hline
315& -0.7 & -71\
hline
330& -0.5 & -50\
hline
360& 0 & 0\[1ex]
hline
end{tabular}
end{center}


$$
h=sin 40text{textdegree}
$$
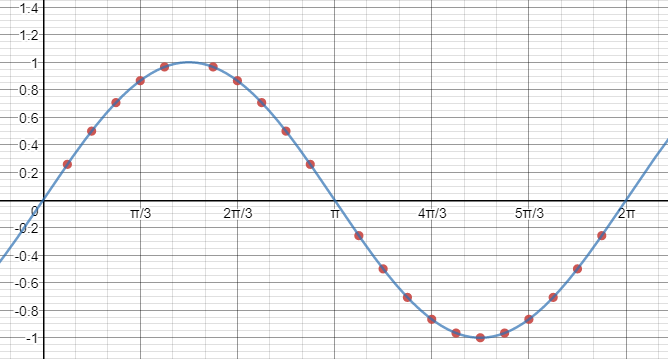
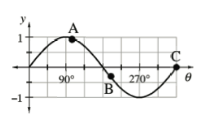
y=sintheta
$$
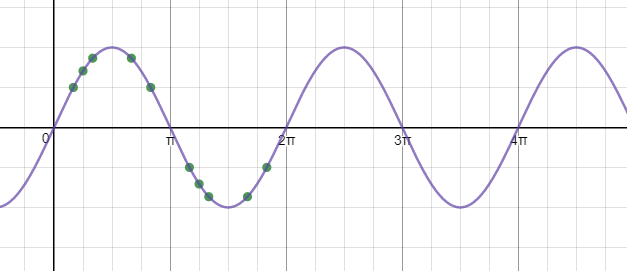
begin{tabular}{|| c|c|c| c||}
hline
Degree of rotation,$x$ & Height & Actual height & $y=sin x$ \ [0.5ex]
hline
0&0&0 & 0\
hline
30& 0.5 & 50 & 0.50\
hline
45& 0.7 & 71 & 0.71\
hline
60& 0.9 & 87 & 0.87\
hline
90& 1 & 100 & 1\
hline
120& 0.9 & 87 & 0.87\
hline
135& 0.7 & 71 & 0.71\
hline
150& 0.5 & 50& 0.50\
hline
180& 0 & 0 & 0\
hline
210& -0.5 & -50 & -0.50\
hline
225& -0.7 & -71 & -0.71\
hline
240& -0.9 & -87 & -0.87\
hline
270& -1 & -100 & -1\
hline
300& -0.9 & -87 & -0.87\
hline
315& -0.7 & -71 & -0.71\
hline
330& -0.5 & -50 & -0.50\
hline
360& 0 & 0 & 0\[1ex]
hline
end{tabular}
end{center}

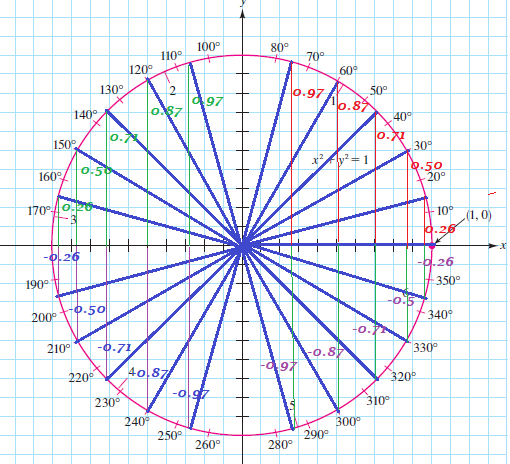
$30text{textdegree} – 60text{textdegree} – 90text{textdegree}$ triangle sides are with the ratio $1: sqrt {3}:2$
A $30text{textdegree} – 60text{textdegree} – 90text{textdegree}$ triangle is called a half-equilateral because when reflecting it around the long leg we obtain an equilateral.
. $45text{textdegree} – 45text{textdegree} – 90text{textdegree}$ triangle sides are with the ratio $1: 1: sqrt {2}$
b- A $30text{textdegree} – 60text{textdegree} – 90text{textdegree}$ triangle is called a half-equilateral because when reflecting it around the long leg we obtain an equilateral.
$mangle A=17.46$$text{textdegree}$
y=a(x-h)^2+k
$$
$h=dfrac{250}{2}=125$
$$
Rightarrow y=a(x-125)^2+15
$$
$0=15,625a+15$
$$
a=-dfrac{15}{15,625}=-0.00096
$$
y=-0.00096(x-125)^2+15
$$
$$
y=a(x-120)^2+k
$$
begin{cases}
a(0-120)^2+k=0\
a(20-120)^2+k=5.5
end{cases}
$$
$$
begin{cases}
14,400a+k=0\
10,000a+k=5.5
end{cases}
$$
$14,400a+k-10,000a-k=0-5.5$
$4400a=-5.5$
$a=-dfrac{5.5}{4400}=-0.00125$
$$
k=-14,400(-0.00125)=18
$$
y=-0.00125(x-120)^2+18
$$
$$
x^3 – 2x^2 + 25x -50
$$
we can write
$$
begin{align*}
x^3 – 2x^2 + 25x – 50 &= x^2 (x-2)+25 (x-2)\
&= (x-2)(x^2 + 25)
end{align*}
$$
Now, we have
$$
begin{align*}
frac {x^3 – 2x^2 + 25x – 50}{x-2} &= frac {(x-2)(x^2 +25)}{x-2}\
&= x^2 + 25
end{align*}
$$
Therefore
$$
frac {x^3 – 2x^2 + 25x – 50}{x-2} = x^2 + 25
$$
frac {x^3 – 2x^2 + 25x – 50}{x-2} = x^2 + 25
$$
$$
x^3 – 2x^2 + 25x – 50 = (x-2)(x^2 + 25)
$$
we have
$$
begin{align*}
x^3 – 2x^2 + 25x – 50 &= 0\
(x-2)(x^2 + 25) &= 0\
x-2 = 0 qquad x^2 + 25 &= 0\
x=2 qquad x^2 &= -25\
x &= pm sqrt {-25}\
x &= pm 5_i
end{align*}
$$
The solutions of equation are
$$
x=2 qquad x=5_i qquad x=-5_i
$$
x=2 qquad x=5_i qquad x=-5_i
$$
m_{2-6}=dfrac{160-700}{6-2}=-dfrac{540}{4}=-135
$$
m_{10-13}=dfrac{80-50}{13-10}=dfrac{30}{3}=10
$$
$$
=2304pi r^3
$$
b) $V=2304pi r^3$
$$
y = sin theta
$$
is
$$
( – infty , + infty )
$$
( – infty , + infty )
$$
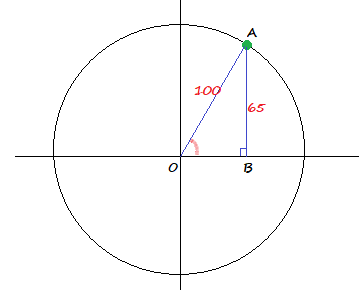
$sin^{-1} 0,65approx 40.5text{textdegree}$
$AOB=40.5text{textdegree}$ or $AOB=180text{textdegree}-40.5text{textdegree}=139.5text{textdegree}$
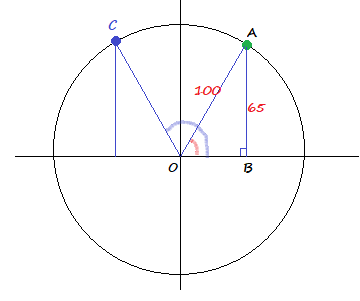
40.5text{textdegree}; 139.5text{textdegree}
$$
$h(n)=4cdot 3^n$
$$
q(n)=n^2-6n+17
$$
$=50-7n-7-50+7n$
$$
-7
$$
$$
d=-7
$$
dfrac{h(n+1)}{h(n)}=dfrac{4cdot 3^{n+1}}{4cdot 3^n}=3
$$
$$
q=3
$$
$=n^2+2n+1-6n-6+17-n^2+6n-17$
$=2n+1$
$dfrac{q(n+1)}{q(n)}=dfrac{(n+1)^2-6(n+1)+17}{n^2-6n+17}$
$q(n)=(n^2+6n+9)+8=(n+3)^2+8$
$$
q(1)=(1+3)^2+9=16+9=25
$$
43, 36, 29, 22, 15, 8….
$$
$h(1)=12; h(2)=36; h(3)=108$
$q(1)=12$
$q(2)=9$
$q(3)=8$
$q(4)=9$
$$
q(5)=72
$$
h(1)=t(1)=12
$$
2^{x-1}=64
$$
$x-1=6$
$x=1+6$
$$
x=7
$$
9^3=17^{2x-1}
$$
$3^{2cdot 3}=3^{3(2x-1)}$
$3^6=3^{6x-3}$
$6=6x-3$
$6x=6+3$
$6x=9$
$x=dfrac{9}{6}$
$$
x=dfrac{3}{2}
$$
$ln 6^x=ln 29$
$xln 6=ln 29$
$x=dfrac{ln 29}{ln 6}$
$$
xapprox 1.88
$$
b) $x=dfrac{3}{2}$
c) $xapprox 1.75$
d) $xapprox 1.88$
a)
$$
2^{(x-1)} = 64
$$
We can use the $ln$ function
$$
ln 2^{(x-1)} = ln 64
$$
According to the formula
$$
color{#c34632}{ln a^b = b ln a}
$$
we obtain
$$
begin{align*}
(x-1) ln 2 &= ln 64\
x-1 &= frac {ln 64}{ln 2}\
x-1 &= frac {4.158}{0.693}\
x-1 &= 6\
x &= 7
end{align*}
$$
The solution of equation is
$$
x=7
$$
$$
9^3 = 27^{2x-1}
$$
Since
$$
9=3^2
$$
and
$$
27=3^3
$$
we obtain
$$
begin{align*}
3^{2 cdot 3} &= 3^{3(2x-1)}\
3^6 &= 3^{6x-3}
end{align*}
$$
According to the formula
$$
color{#c34632}{a^b=a^c}
$$
$$
color{#c34632}{b=c}
$$
we obtain
$$
begin{align*}
6 &= 6x-3\
6x &= 9\
x &= frac 96\
x &= frac 32
end{align*}
$$
The solution of equation is
$$
x = frac 32
$$
$$
begin{align*}
x^6 &= 29\
x &= sqrt[6]{29}\
x &= 1.75
end{align*}
$$
The solution of equation is
$$
x = 1.75
$$
$$
6^x = 29
$$
We can use the $ln$ function
$$
ln 6^x = ln 29
$$
According to the formula
$$
color{#c34632}{ ln a^b = b ln a}
$$
we obtain
$$
begin{align*}
x ln 6 &= ln 29\
x &= frac {ln 29}{ln 6}\
x &= frac {3.367}{1.791}\
x &= 1.88
end{align*}
$$
The solution of equation is
$$
x= 1.88
$$
b) $x = frac 32$
c) $x = 1.75$
d) $x= 1.88$
$$
sin theta = frac ax
$$
where $a= frac 12$ and $theta = 30^{text{textdegree}}$. Then
$$
begin{align*}
sin 30^{text{textdegree}} &= frac {frac 12}{x}\
frac 12 &= frac {1}{2x}\
x cdot frac 12 &= frac 12\
x &= 1
end{align*}
$$
$$
cos theta = frac xa
$$
where $a=1$ and $theta = 45^{text{textdegree}}$. Then
$$
begin{align*}
cos 45^{text{textdegree}} &= frac x1\
frac {sqrt 2}{2} &= x
end{align*}
$$
b) $frac {sqrt 2}{2} = x$
dfrac{A_{rugs}}{A_{floor}}=dfrac{392.7}{500}=0.7854=78.54%
$$
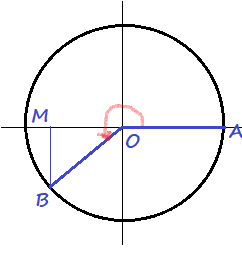
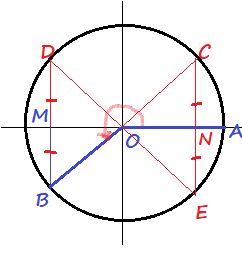
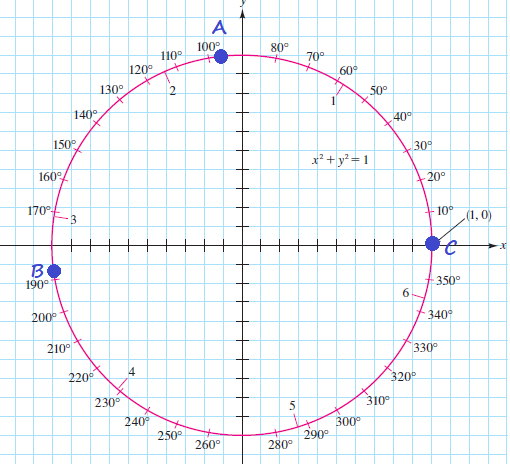
$AOB=180text{textdegree}+theta$
$AOE=360text{textdegree}-theta$.
Let’s suppose we are given
$theta=AOC$.
We express the angles $AOD, AOB, AOE$ in terms of $theta$:
sin 130text{textdegree}approx 0.77
$$
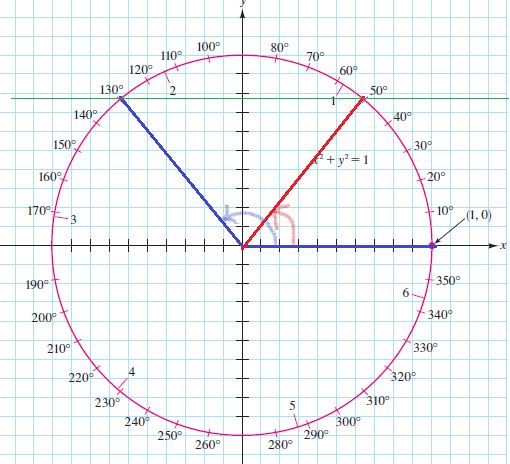
$$
180text{textdegree}-130text{textdegree}=50text{textdegree}
$$
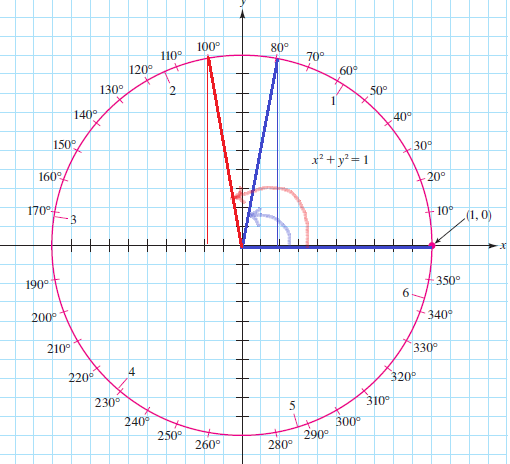
theta=80text{textdegree}
$$
theta=200text{textdegree}
$$
sintheta=sin 200text{textdegree}approx -0.34=sin 340text{textdegree}
$$
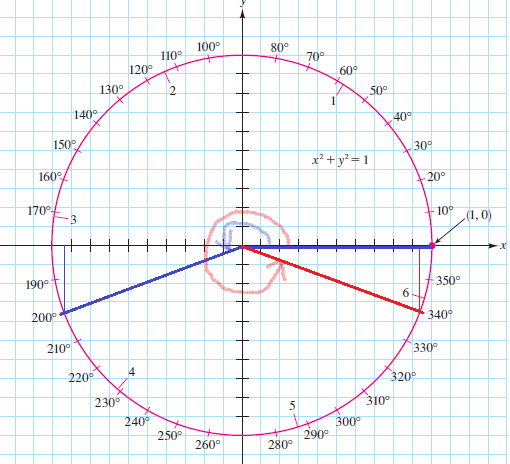
theta=310text{textdegree}
$$
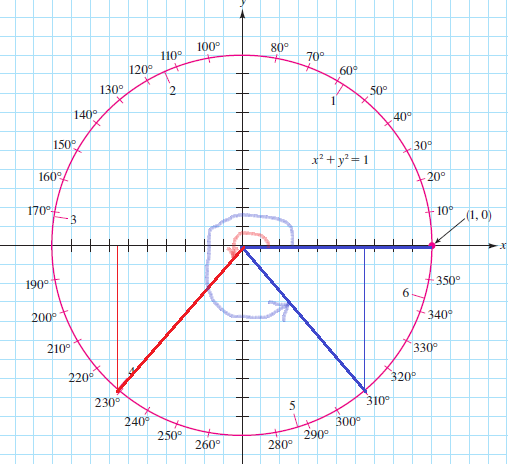
sintheta=sin 310text{textdegree}approx -0.77=sin 230text{textdegree}
$$


$$y = log_2(x-1)rightarrow(1)$$
$$y = x^3 – 4xrightarrow(2)$$
Intersecting point : $(2, 0)$ and $(1.1187, -3.075)$.
$$begin{aligned}
log_2(2-1)&= (2)^3 – 4(2)\
log_2(1)&= 8 – 8\
log_2(1)&= 0 \
0 = 0\
end{aligned}$$
$$
begin{align*}
x^5 + 8x^2 y^3 &= x^2 ( x^3 + 8y^3)\
&= x^2 [ x^3 + (2y)^3]
end{align*}
$$
According to the formula
$$
begin{align*}
color{#c34632}{a^3 + b^3 = (a+b)(a^2 – 2ab + b^2)} tag {*}
end{align*}
$$
we obtain
$$
x^5 + 8x^2 y^3 = x^2 (x+2y)(x^2 – 2xy +4y^2)
$$
$$
8y^6 – 125x^3 = (2y^2)^3 – (5x)^3
$$
According to the $(*)$ we have
$$
8y^6 – 125^3 = (2y^2 + 5x)(4y^4 – 10xy^2 + 25x^2)
$$
b) $8y^6 – 125^3 = (2y^2 + 5x)(4y^4 – 10xy^2 + 25x^2)$
$$
color{#c34632}{c^2 = a^2 + b^2 – 2ab cos theta}
$$
where
$$
begin{align*}
a &= 620 text{ m }\
b &= 455 text{ m }\
theta &= 150^{text{textdegree}}
end{align*}
$$
Then we have
$$
begin{align*}
c^2 &= 620^2 + 455^2 – 2 cdot 620 cdot 450 cos 150^{text{textdegree}}\
c^2 &= 384400 + 207025 – 564200 cdot (-0.86)\
c^2 &= 591425 + 485 212\
c^2 &= 1076637\
c &= sqrt {1076637}\
c &= 1037.61
end{align*}
$$
The lake is $1037.61$ meters long.
Yee Ping can’t swim the lake.
c = 1037.61
$$
$$
begin{align*}
a &= 2 +3 i\
b &= 1- i
end{align*}
$$
a) We will add $a$ and $b$
$$
begin{align*}
a+b &= (2+ 3 i) + (1- i)\
&= 2 + 3 i + 1 – i\
&= 3 + i (3 -1)\
&= 3 + 2 i
end{align*}
$$
$$
begin{align*}
a-b &= (2+ 3 i) – (1- i)\
&= 2 +3 i – 1 + i\
&= 1 + i (3+1)\
&= 1 + 4 i
end{align*}
$$
$$
begin{align*}
a cdot b &= (2+3 i) (1- i)\
&= 2 – 2 i + 3 i – 3 i^2\
&= 2 + i – 3 i^2
end{align*}
$$
Since
$$
i^2 = -1
$$
we obtain
$$
begin{align*}
a cdot b &= 2 + i – 3 cdot (-1)\
&= 2 + i + 3\
&= 5 + i
end{align*}
$$
b) $a-b = 1 + 4_i$
c) $a cdot b = 5 + i$
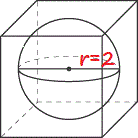
$13=8r^3$
$r^3=dfrac{13}{8}$
$r=sqrt[3]{dfrac{13}{8}}approx 1.176$ feet
$v=8r^3$
$$
r=dfrac{sqrt[3]{v}}{2}
$$
b) 1.176 ft
c) $r=dfrac{sqrt[3]{v}}{2}$
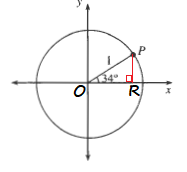
$$
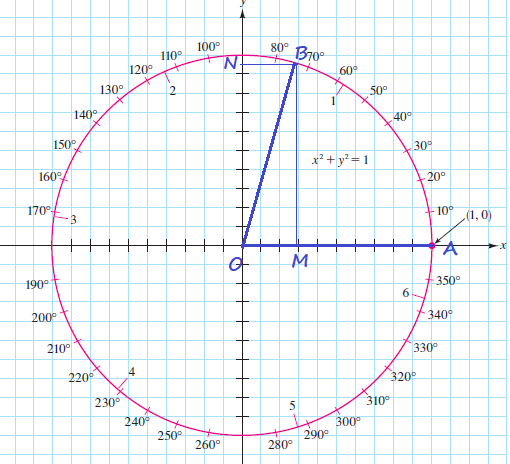
y=PR
$$
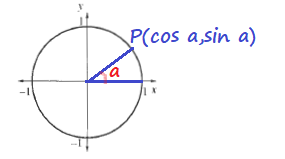
The coordinates $(x,y)$ of the point $P$ are:
$OR=OPcos 34text{textdegree}$
$OR=1cdot cos 34text{textdegree}$
$$
textcolor{#4257b2}{OR=cos 34text{textdegree}}
$$
$PR=OPsin 34text{textdegree}$
$PR=1cdot sin 34text{textdegree}$
$$
textcolor{#4257b2}{PR=sin 34text{textdegree}}
$$
P(cos 34text{textdegree},sin 34text{textdegree})
$$
P(cos 34text{textdegree},sin 34text{textdegree})
$$
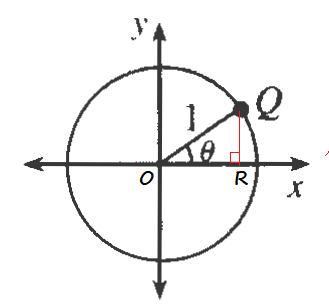
$$
y=QR
$$
The coordinates $(x,y)$ of the point $Q$ are:
$OR=OQcos theta$
$OR=1cdot cos theta$
$$
textcolor{#4257b2}{OR=cos theta}
$$
$QR=OPsin theta$
$QR=1cdot sin theta$
$$
textcolor{#4257b2}{QR=sin theta}
$$
Q(cos theta,sin theta)
$$
Q(cos theta,sin theta)
$$
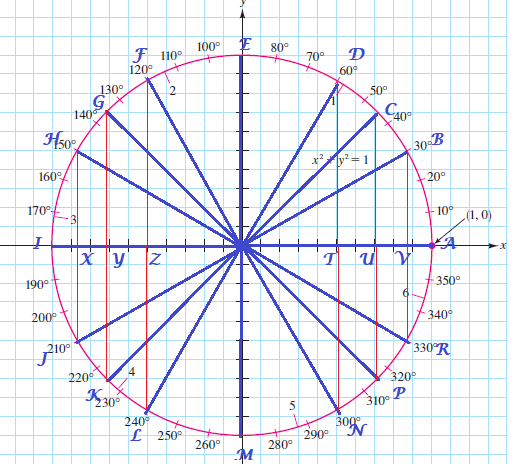
Then $sin theta$ tells us the ratio between y-coordinate of $B$ and the radios of the circle.
$cos theta$ tells us the ratio between x-coordinate of $B$ and the radios of the circle
$cos theta$ tells us the ratio between x-coordinate of $B$ and the radios of the circle
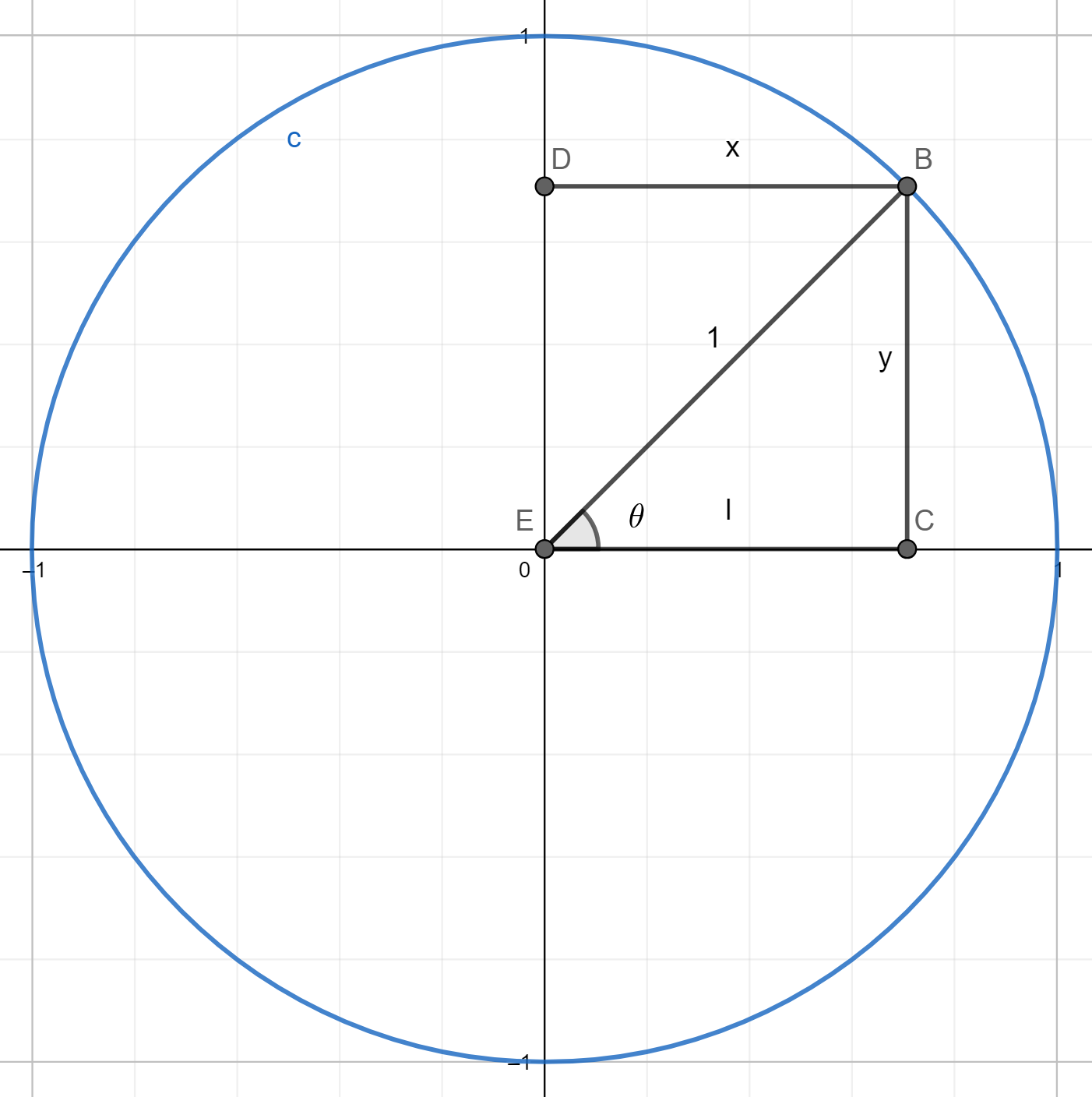
The opposite graph is a unit circle with the point $B$ on the circle.
Since $sin theta$ is the y-coordinate of $B$
$cos theta$ is the x-coordinate of $B$
$1^2=x^2+y^2$ (Pythagorean theorem)
$x=sqrt {1^2-y^2}$
$cos theta=sqrt {1^2-y^2}$
$cos theta=sqrt {1^2-(sin theta)^2}$
Since, $cos theta=$ x-coordinate
Then x-coordinate of the point on the unit circle is $dfrac {3}{4}$
$1^2=x^2+y^2$ (Pythagorean theorem)
$y=sqrt {1-x^2}$
$y=sqrt {1-dfrac {9}{16}}=sqrt {dfrac {7}{16}}$
$y=dfrac {sqrt 7}{4}$
The exact coordinates of point $Q$ are $(dfrac {3}{4}, qquad dfrac {sqrt 7}{4})$
$sin theta=$ y-coordinate of the point $Q$
$$
sin theta=dfrac {sqrt 7}{4}
$$
Since $(x, y)$ are the coordinates of the point $Q$ on the unit circle, then:
$1^2=x^2+y^2$ (Pythagorean theorem)
$sin theta=y$
$cos theta=x$
So,
$$
1^2=(sin theta)^2+(cos theta)^2
$$
b- $sin theta=dfrac {sqrt 7}{4}$
c- $1^2=(sin theta)^2+(cos theta)^2$
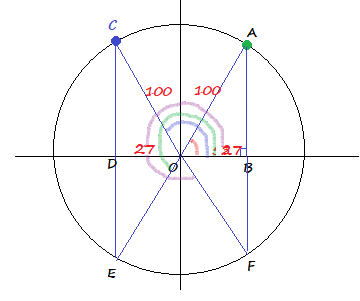
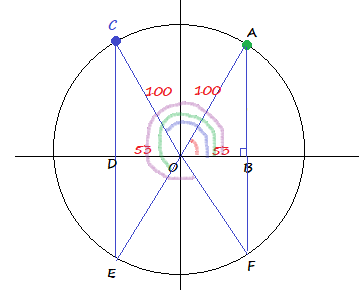
$cos^{-1} 0.27approx 74.3text{textdegree}$
$$
AOB=74.3text{textdegree}
$$
$EOB=180text{textdegree}+74.3text{textdegree}=254.3text{textdegree}$
$$
FOB=360text{textdegree}-74.3text{textdegree}=285.7text{textdegree}
$$
74.3text{textdegree}; 105.7text{textdegree}; 254.3text{textdegree}; 285.7text{textdegree}
$$
The following is the graph of the function $y=cos(theta)$
From the graph:
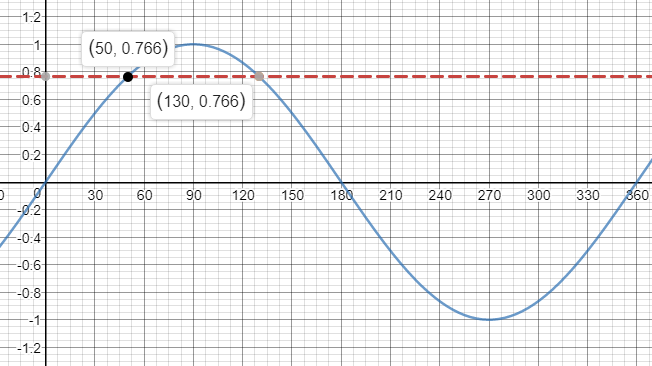
$cos (130text{textdegree})=-0.6428$
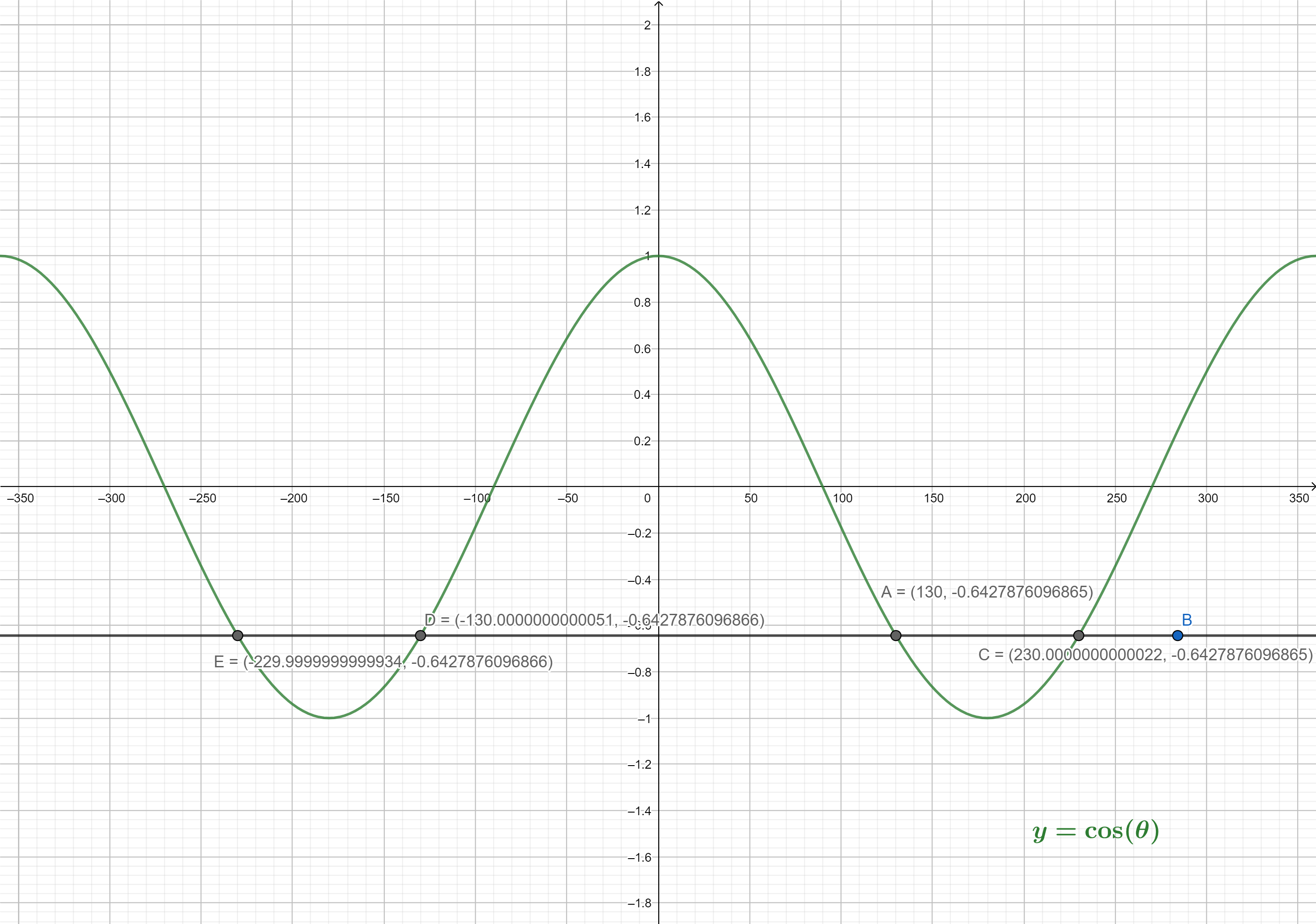
From the graph, the other angel that has the same base is $230$$text{textdegree}$
We can use the symmetry of the cosine-calculator graph to calculate the angle location by drawing the line $x=180$ and reflect the point $(130, -0.6428)$ about it to get the corresponding point as in the graph below.
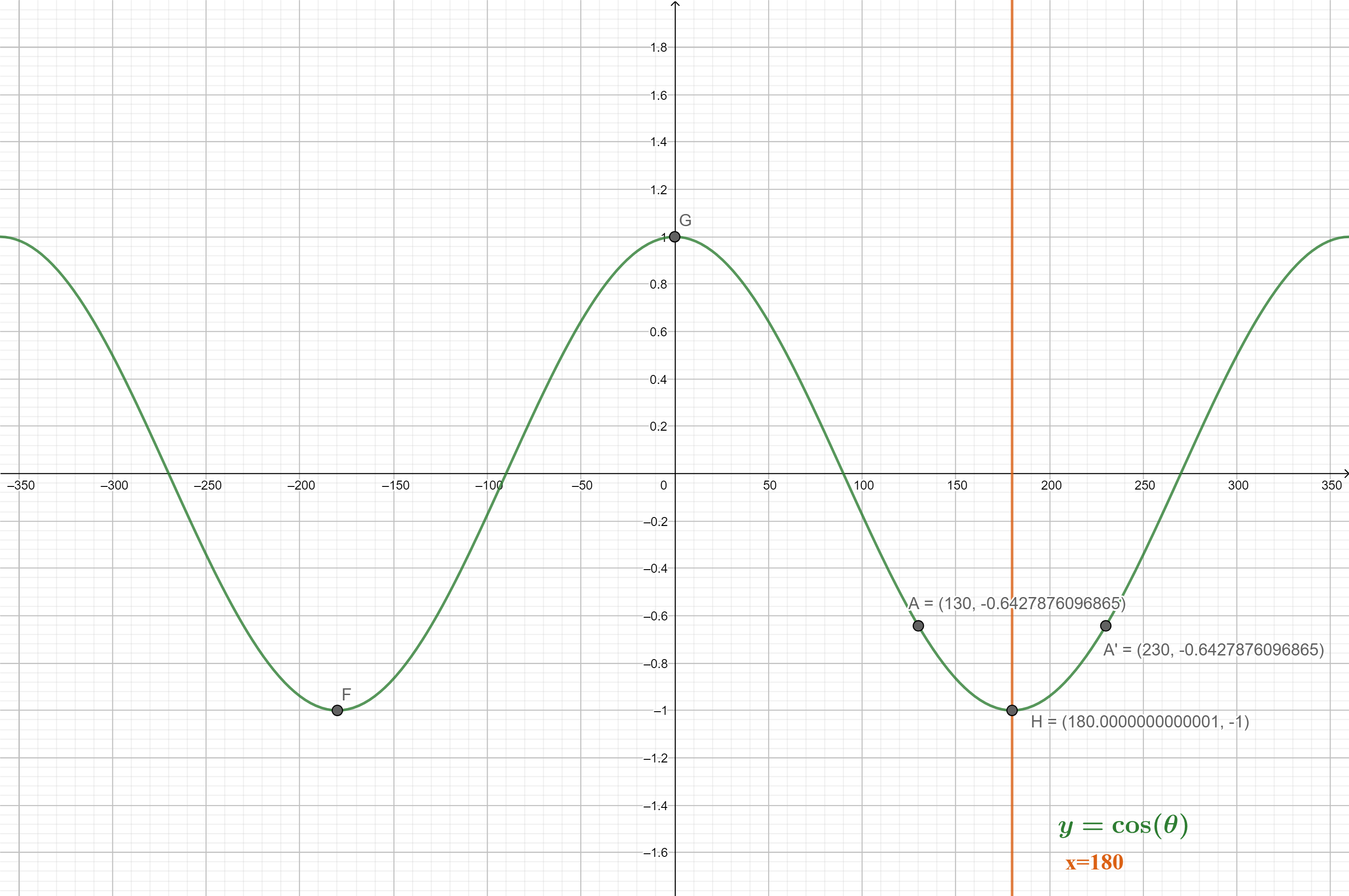
b- The other angel that has the same base is $230$$text{textdegree}$
$sin 50=0.766$
$cos 50=0.6428$
The coordinates of $P$ are: $(0.6428, qquad 0.766)$
$sin 110=0.9397$
$cos 110=-0.342$
The coordinates of $Q$ are: $(-0.342, qquad 0.9397)$
The coordinates of $Q$ are: $(-0.342, qquad 0.9397)$
$mangle ROS=60$$text{textdegree}$ (Given)
$overline {OR}$ rotation angle $=360-60=300$$text{textdegree}$
$cos {SOR}=dfrac {overline {OS}}{overline {OR}}=dfrac {overline {OS}}{1}=overline {OS}$
$cos 60=0.5$
$overline {OS}=0.5$ units
$sin {SOR}=dfrac {overline {SR}}{overline {OR}}=dfrac {overline {SR}}{1}=overline {SR}$
$sin 60=0.866$
$overline {SR}=0.866$ units
The exact coordinates of point $R$ are: $(0.5, qquad -0.866)$
b- $overline {OS}=0.5$ units $overline {SR}=0.866$ units
c- The exact coordinates of point $R$ are: $(0.5, qquad -0.866)$
$(sin theta)^2+(cos theta)^2=1$ (Pythagorean Identity)
$(cos theta)^2=1-left(dfrac {1}{4} right)^2$
$(cos theta)^2=dfrac {16}{16}-dfrac {1}{16}$
$(cos theta)^2=dfrac {15}{16}$
$cos theta=pm dfrac {sqrt {15}}{4}$
The exact coordinates of a point on the unit circle than has $sin theta=dfrac {1}{4}$ are:
$left(dfrac {sqrt {15}}{4}, qquad dfrac {1}{4} right)$
left(dfrac {sqrt {15}}{4}, qquad dfrac {1}{4} right)
$$
$r=0.06$
$A=4000$
$$
n=12
$$
$A=Pleft(1+dfrac{r}{n}right)^{nt}$.
$4=left(1+dfrac{0.06}{12}right)^{12t}$
$$
4=(1.005)^{12t}
$$
$ln 4=12tln 1.005$
$$
tapprox 23.16
$$
$$
color{#c34632}{FV = P left( 1 + frac rn right)^{nt}}
$$
where
$$
begin{align*}
FV &= text{ future value of the deposit} = 4000\
P &= text{amount of money deposited} = 1000\
r &= text{annual interest rate} = 6 % = 0.06\
n &= text{number of times compounded per year} = 12\
t &= text{time in years}
end{align*}
$$
we obtain
$$
begin{align*}
4000 &= 1000 left( 1 + frac {0.06}{12} right)^{12 cdot t}\
4 &= (1 + 0.005 )^{12 cdot t}\
4 &= 1.005^{12t}
end{align*}
$$
We can use the $ln$ function
$$
color{#c34632}{ ln a^b = b ln a}
$$
we have
$$
begin{align*}
ln 4 &= 12t cdot ln 1.005\
12t &= frac {ln 4}{ln 1.005}\
12t &= frac {1.386}{0.005}\
12t &= 277.25\
t &= 23.1
end{align*}
$$
It takes $23.1$ years to account worth $$ 4000$.
$$
(x-1),(x+1),(x-7),(x+7)
$$
b.
$$
polylongdiv{x^4-6x^3-6x^2+6x-7}{x+1}
$$
Since the remainder is nonzero, $(x+1)$ is not a factor.
$$
polylongdiv{x^4-6x^3-6x^2+6x-7}{x-1}
$$
Since the remainder is nonzero, $(x-1)$ is not a factor.
b. Neither are factors
$$
begin{align*}
f(x) &= 2x^2 + 5x -3\
g(x) &= x^2 + 4x +3
end{align*}
$$
a) Therefore
$$
begin{align*}
f(x) &= g(x)\
2x^2 + 5x – 3 &= x^2 + 4x +3\
2x^2 + 5x -3 -x^2 -4x -3 &= 0\
x^2 + x -6 &=0
end{align*}
$$
The solutions of a square equation $ax^2 + bx + c =0$ are shape
$$
x= frac {-b pm sqrt {b^2 – 4ac}}{2a}
$$
Now we have
$$
begin{align*}
x &= frac {-1 pm sqrt {1+24}}{2}\
x &= frac {-1 pm sqrt {25}}{2}\
x &= frac {-1 pm 5}{2}\
x &= – 3 qquad x=2
end{align*}
$$
If $x=-3$ we get
$$
y=0
$$
Then
$$
(x,y) = (-3,0)
$$
If $x=2$ we get
$$
y=15
$$
Then
$$
(x,y)=(2,15)
$$
begin{align*}
f(x) &= 2x^2 + 5x -3- text{ blue}\
g(x) &= x^2 + 4x +3-text{ green}\
h(x) &=x^2+x-6-text{ red}
end{align*}
$$

$$
begin{align*}
f(x) &> g(x)\
2x^2 + 5x – 3 &> x^2 + 4x + 3\
2x^2 + 5x – 3 &- x^2 – 4x – 3 > 0\
x^2 + x – 6 &> 0\
x2
end{align*}
$$
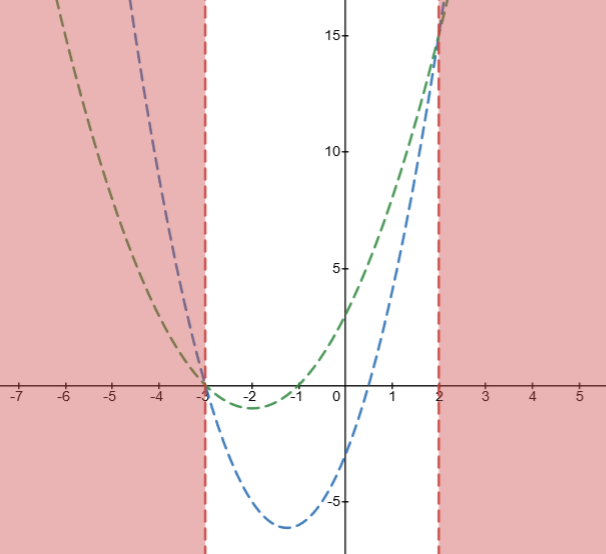
$(x,y) = (-3,0)$
b) $x2$
$g(x)=x^2+4x+3$
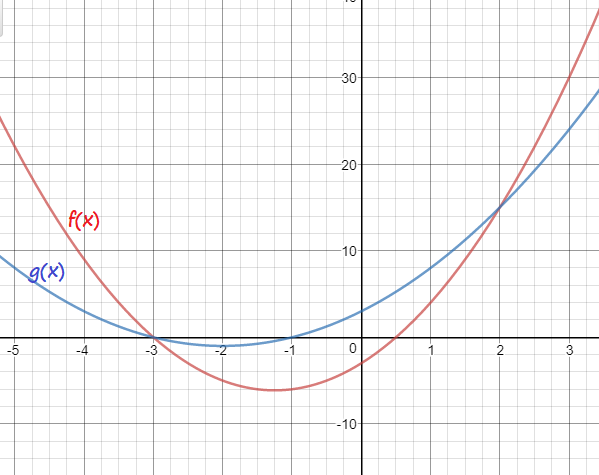
$$
(2,15)
$$
$2(-3)^2+5(-3)-3stackrel{?}{=}(-3)^2+4(-3)+3$
$18-15-3stackrel{?}{=}9-12+3$
$0=0checkmark$
$x=2$
$2(2)^2+5(2)-3stackrel{?}{=}(2)^2+4(2)+3$
$8+10-3stackrel{?}{=}4+8+3$
$15=15checkmark$
(-infty,-3)cup(2,infty)
$$
b) $(-infty,-3)cup(2,infty)$
7=4.2^x
$$
$$
ln 7=xln 4.2
$$
$$
xapprox 1.356
$$
$7stackrel{?}{=}7.0004513$
$$
7approx7checkmark
$$
3x^5=126
$$
$x^5=42$
$$
xapprox 2.112
$$
$3(42.0213)stackrel{?}{=}126$
$$
126approx 126checkmark
$$
14=2cdot 4^x-10
$$
$24=2cdot 4^x$
12=4^x
$$
$$
ln 12=xln 4
$$
$$
xapprox 1.792
$$
$14stackrel{?}{=}2cdot 12-10$
$$
14=14checkmark
$$
b) $xapprox 2.112$
c) $xapprox 1.792$
$$
7= 4,2^x
$$
We can use the $ln$ function
$$
ln 7 = ln 4,2^x
$$
Using the formula
$$
begin{align*}
color{#c34632}{ ln a^b = b ln a} tag{$*$}
end{align*}
$$
Now we have
$$
begin{align*}
ln 7 &= x ln 4,2\
x &= frac {ln 7}{ln 4,2}\
x &= frac {1.945}{1.435}\
x &= 1.355
end{align*}
$$
The solution of equation is:
$$
x = 1.355
$$
$$
begin{align*}
3x^5 &= 126\
x^5 &= 42\
x &= sqrt[5]{42}\
x &= 2.112
end{align*}
$$
The solution of equation is
$$
x = 2.112
$$
$$
begin{align*}
14 &= 2 cdot 4^x – 10\
2 cdot 4^x &= 24\
4^x &= 12
end{align*}
$$
We can use the $ln$ function
$$
ln 4^x = ln 12
$$
Using the formula $(*)$ we have
$$
begin{align*}
x ln 4 &= ln 12\
x &= frac {ln 12}{ ln 4}\
x &= frac {2.485}{1.386}\
x &= 1.793
end{align*}
$$
The solution of equation is
$$
x = 1.793
$$
b) $x = 2.112$
c) $x = 1.793$
$cos^{-1} 0.53approx 58text{textdegree}$
$$
AOB=58text{textdegree}
$$
$EOB=180text{textdegree}+58text{textdegree}=238text{textdegree}$
$$
FOB=360text{textdegree}-58text{textdegree}=302text{textdegree}
$$
58text{textdegree}; 122text{textdegree}; 238text{textdegree}; 302text{textdegree}
$$

$sin^2theta+cos^2thetastackrel{?}{=}1$
$0.9^2+0.8^2stackrel{?}{=}1$
$$
1.45not=1
$$
$sintheta=0.9$
$costheta=0.8$.

$sin theta=dfrac{y}{OR}$
$y=ORsintheta=1cdotsin 70text{textdegree}approx 0.9397$
$cos theta=dfrac{x}{OR}$
$x=ORcostheta=1cdotcos 70text{textdegree}approx 0.3420$
$$
R(0.3420,0.9397)
$$
R(cos 70text{textdegree},sin 70text{textdegree})
$$
sin^2theta+cos^2theta=0.9397^2+0.3420^2approx 1checkmark
$$
$y=costheta$
$$
cos 0text{textdegree}=1
$$
We know:
Function B: $y=cos theta$
So we have:
B: $y=cos theta$
begin{cases}
y=cos x\
y=-1
end{cases}
$$
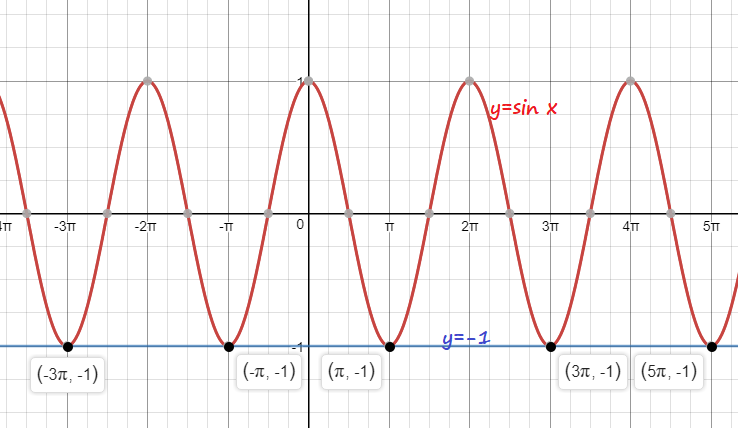
$x=-pi$
$x=pi$
$x=3pi$
$$
x=5pi
$$
$$
y=a(x+2)^2(x-2)
$$
We also note that if $x=0$, then we need $y=2$:
$$
2=y=a(2)^2(-2)=-8a
$$
Divide both sides of the equation by $-8$:
$$
-dfrac{1}{4}=a
$$
Thus we then obtain the equation:
$$
y=-dfrac{1}{4}(x+2)^2(x-2)
$$
y=-dfrac{1}{4}(x+2)^2(x-2)
$$
f(x)=dfrac{sqrt{x+4}}{2}-1
$$

$x=dfrac{sqrt{y+4}}{2}-1$
$x+1=dfrac{sqrt{y+4}}{2}$
$2(x+1)=sqrt{y+4}$
$[2(x+1)]^2=(sqrt{y+4})^2$
$4(x+1)^2=y+4$
$4x^2+8x+4-4=y$
$y=4x^2+8x$
$f^{-1}(x)=4x^2+8x$
[-1,infty)
$$
[-4,infty)
$$
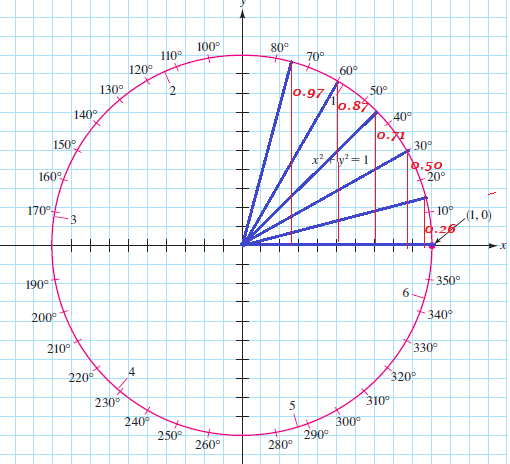
A radian equals to $dfrac{360text{textdegree}}{2pi}approx 57.2958text{textdegree}$.
r=1
$$
A=pi r^2=pi(1^2)=pi
$$
L=2pi r=2pi(1)=2pi
$$
dfrac{L}{r}=dfrac{2pi}{1}=2piapprox 6.28
$$
dfrac{L}{r}=dfrac{2pi r}{r}=2piapprox 6.28
$$
2pi
$$
dfrac{2pi}{4}=dfrac{pi}{2}
$$
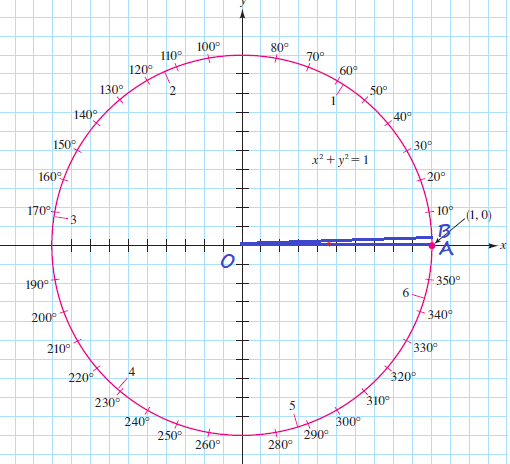
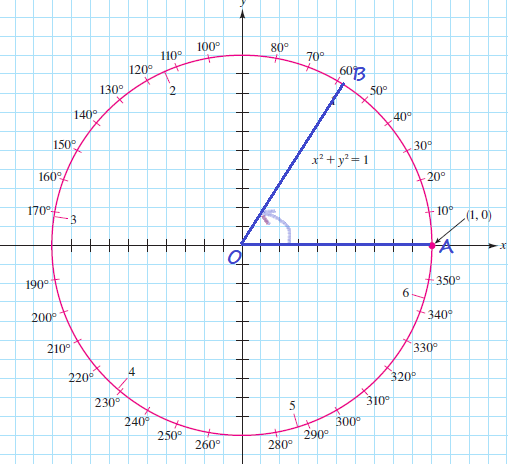
theta=1text{textdegree}
$$
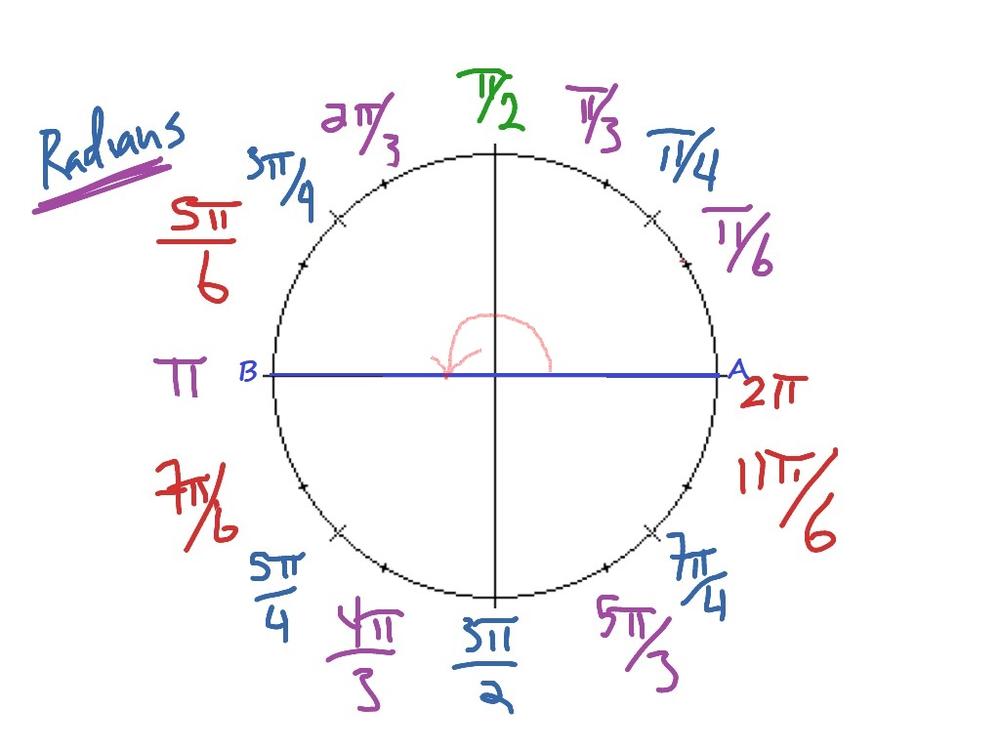
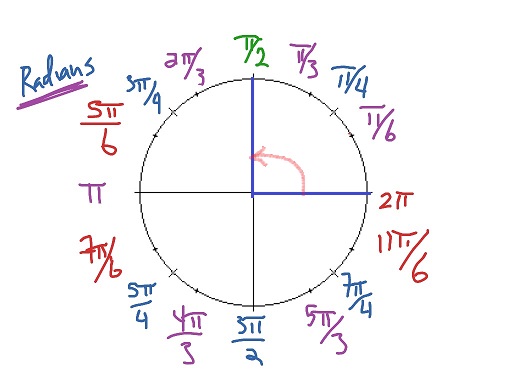


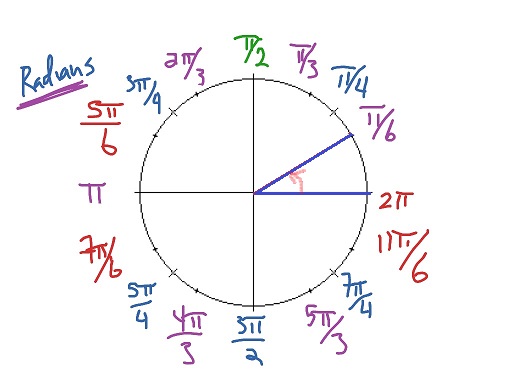
$$begin{align*}
30^{circ}&=0.523text{ rad}\
60^{circ}&=1.047text{ rad}\
90^{circ}&=1.57text{ rad}\
end{align*}$$
120^{circ}&=2.09text{ rad}\
180^{circ}&=pitext{ rad}\
270^{circ}&=4.712text{ rad}\
360^{circ}&=2pitext{ rad}
end{align*}$$
sin 60text{textdegree}=0.8660254
$$
sin dfrac{pi}{3}=0.8660254
$$
60text{textdegree}=dfrac{pi}{3}
$$
sin dfrac{pi}{4}=0.70710678
$$
sin 45text{textdegree}=0.70710678
$$
sin 135text{textdegree}=0.70710678
$$
$sin (dfrac {pi}{4})=sin 45$
$sin (dfrac {pi}{4})=dfrac {1}{sqrt {2}}=0.7071$
$sin(dfrac {2pi}{3})=sin (120)$
$sin(dfrac {2pi}{3})=sin 60$ (sin (180-60)=sin 60)
$sin(dfrac {2pi}{3})=dfrac {sqrt 3}{2}=0.8660$
b- $sin(dfrac {2pi}{3})=dfrac {sqrt 3}{2}=0.8660$
$$
sin ( 30 text{radians}) = – 0.9880316241
$$
Jolleen is calculate
$$
sin ( 30^{text{textdegree}}) = 0.5
$$
Both calculators are correct.
$sin 30text{textdegree}=0.5$,
while Colleen set hers in radians and she got:
$sin 30$ radians $=-0.9880316241$.
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
log _2left(xleft(x-2right)right)&=3&&boxed{text{Apply log rule}}\
log _2left(xleft(x-2right)right)&=log _2left(8right)&&boxed{text{Apply log rule}}\
xleft(x-2right)&=8&&boxed{text{Simplify}}\
x^2-2x&=8&&boxed{text{Distributive property}}\
x^2-2x-8&=8-8&&boxed{text{Subtract 8 from both sides}}\
x^2-2x-8&=0&&boxed{text{Simplify}}\
end{align*}
$$
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-2right)pm sqrt{left(-2right)^2-4cdot :1left(-8right)}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -2 text{ for } b, text{ and } -8 text{ for } c.} \
end{align*}
$$
$$
begin{align*}
x_1&=frac{-left(-2right)+sqrt{left(-2right)^2-4cdot :1left(-8right)}}{2cdot :1}&&boxed{text{Simplify}}\
x_1&=frac{2+sqrt{left(-2right)^2+4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Remove parentheses: }-(-a)=a}\
x_1&=frac{2+sqrt{4+4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Evaluate: }(-2)^2=4}\
x_1&=frac{2+sqrt{4+32}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot8=32}\
x_1&=frac{2+sqrt{4+32}}{2}&&boxed{text{Multiply the numbers: } 2cdot1=2}\
x_1&=frac{2+sqrt{36}}{2}&&boxed{text{Add the numbers: }4+32=36 }\
x_1&=frac{2+6}{2}&&boxed{text{Simplify}}\
x_1&=frac{8}{2}&&boxed{text{Add the numbers: } 2+6=8}\
x_1&=color{#c34632}{4} text{ True }&&boxed{text{Divide the numbers: } frac{8}{2}=4}\
end{align*}
$$
$$
begin{align*}
x_2&=frac{-left(-2right)-sqrt{left(-2right)^2-4cdot :1left(-8right)}}{2cdot :1}&&boxed{text{Simplify}}\
x_2&=frac{2-sqrt{left(-2right)^2+4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Remove parentheses: }-(-a)=a}\
x_2&=frac{2-sqrt{4+4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Evaluate: }(-2)^2=4}\
x_2&=frac{2-sqrt{4+32}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot8=32}\
x_2&=frac{2-sqrt{4+32}}{2}&&boxed{text{Multiply the numbers: } 2cdot1=2}\
x_2&=frac{2-sqrt{36}}{2}&&boxed{text{Add the numbers: }4+32=36 }\
x_2&=frac{2-6}{2}&&boxed{text{Simplify}}\
x_2&=frac{-4}{2}&&boxed{text{Subtract the numbers: } 2-6=-4}\
x_2&=color{#c34632}{-2} text{ False }&&boxed{text{Divide the numbers: } frac{-4}{2}=-2}\
&boxed{{color{#c34632}x=4} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:log:rule}:quad log _cleft(aright)+log _cleft(bright)=log _cleft(abright) }
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:log:rule}:quad :a=log _bleft(b^aright) }
$$
$$
boxed{ color{#c34632} text{ } mathrm{When:the:logs:have:the:same:base:::}log _bleft(fleft(xright)right)=log _bleft(gleft(xright)right)quad Rightarrow quad fleft(xright)=gleft(xright)}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
log _{10}left(2right)+log _{10}left(xright)-2log _{10}left(xright)&=-2&&boxed{text{Apply log rule}}\
log _{10}left(2right)-log _{10}left(xright)&=-2&&boxed{text{Simplify}}\
log _{10}left(2right)-log _{10}left(xright)-log _{10}left(2right)&=-2-log _{10}left(2right)&&boxed{text{Subtract }log_{10}(2) text{ from both sides}}\
-log _{10}left(xright)&=-2-log _{10}left(2right)&&boxed{text{Simplify}}\
frac{-log _{10}left(xright)}{-1}&=-frac{2}{-1}-frac{log _{10}left(2right)}{-1}&&boxed{text{Divide both sides by }-1}\
log _{10}left(xright)&=2+log _{10}left(2right)&&boxed{text{Simplify}}\
log _{10}left(xright)&=log _{10}left(200right)&&boxed{text{Apply log rule}}\
x&=200text{ True}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=200} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:log:rule}:quad log _aleft(cx^bright)=log _aleft(cright)+bcdot log _aleft(xright) }
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:log:rule}:quad :a=log _bleft(b^aright) }
$$
$$
boxed{ color{#c34632} text{ } mathrm{When:the:logs:have:the:same:base:::}log _bleft(fleft(xright)right)=log _bleft(gleft(xright)right)quad Rightarrow quad fleft(xright)=gleft(xright)}
$$
color{#4257b2} text{ a) }x=4
$$
$$
color{#4257b2} text{ b) }x=200
$$
$$
log_2{(x(x-2))}=3
$$
Take the exponential with base 2 of both sides of the equation:
$$
x(x-2)=2^3
$$
Rewrite the equation:
$$
x^2-2x-8=0
$$
Factorize:
$$
(x-4)(x+2)=0
$$
Zero product property:
$$
x-4=0text{ or } x+2=0
$$
Solve each equation to $x$:
$$
x=4text{ or } x=-2
$$
It is only possible to take the logarithm of a positive number and thus $x=-2$ cannot be a solution.
$$
log{dfrac{2x}{x^2}}=-2
$$
Take the exponential with base 10 of both sides of the equation:
$$
dfrac{2}{x}=10^{-2}
$$
Multiply both sides of the equation by 10
$$
2=0.01x
$$
Multiply both sides of the equation by 100:
$$
200=x
$$
b. $x=200$
$4x^2-9y^2$ (Write the equation)
$(2x)^2-(3y)^2$
$=(2x+3y)(2x-3y)$ (Difference of two squares)
$8x^3-2x^7$ (Write the equation)
$=2x^3(4-x^4)$ (Factor out $2x^3$)
$=2x^3(2+x^2)(2-x^2)$ (Difference of two squares)
$x^4-81y^4$ (Write the equation)
$(x^2)^2-(9y^2)^2$
$=(x^2+9y^2)(x^2-9y^2)$ (Difference of two squares)
$=(x^2+9y^2)(x+3y)(x-3y)$ (Difference of two squares)
$8x^3+2x^7$ (Write the equation)
$=2x^3(4+x^4)$ (Factor out $2x^3$)
b- $8x^3-2x^7=2x^3(2+x^2)(2-x^2)$
c- $x^4-81y^4=(x^2+9y^2)(x+3y)(x-3y)$
d- $8x^3+2x^7=2x^3(4+x^4)$
$$
begin{align*}
frac 3x &= frac {5}{x-7}\
3(x-7) &= 5x\
3x – 21 &= 5x\
2x &= -21\
x&= – frac {21}{2}\
x &= 10.5
end{align*}
$$
The solution of equation is
$$
x = 10.5
$$
$$
begin{align*}
frac {2x+3}{4} – frac {x-7}{6} &= frac {2x-3}{12}\
frac {6(2x+3)-4(x-7)}{24} &= frac {2x-3}{12}\
frac {12x+18-4x+28}{24} &= frac {2x-3}{12}\
frac {8x+46}{24} &= frac {2x-3}{12}
end{align*}
$$
Multiply both sides by $24$
$$
begin{align*}
24 cdot frac {8x+46}{24} &= 24 cdot frac {2x-3}{12}\
8x+46 &= 2 cdot (2x-3)\
8x+46 &= 4x-6\
4x &= -52\
x &= -13
end{align*}
$$
The solution of equation is
$$
x=-13
$$
b) $x=-13$
dfrac{3}{x}=dfrac{5}{x-7}
$$
(-infty,0)cup(0,7)cup(7,infty)
$$
$3x-21=5x$
$3x-21-3x=5x-3x$
$2x=-21$
$$
x=-dfrac{21}{2}
$$
$3(2x+3)-2(x-7)=2x-3$
$6x+9-2x+14=2x-3$
$$
4x+23=2x-3
$$
$$
2x+23=-3
$$
$$
2x=-26
$$
b) $x=-13$
$h=12$ cm
$d=3$ cm
$V<80$g
$=picdot 1.5^2cdot 12=27piapprox 84.82$ $cm^3$
$sin 0=0$
$cos 0=1$
$textcolor{#4257b2}{theta=dfrac{pi}{2}}$
$sin dfrac{pi}{2}=1$
$cos dfrac{pi}{2}=0$
$textcolor{#4257b2}{theta=pi}$
$sin pi=0$
$cos pi=-1$
$textcolor{#4257b2}{theta=dfrac{3pi}{2}}$
$sin dfrac{3pi}{2}=-1$
$cos dfrac{3pi}{2}=0$
left{0, dfrac{pi}{2},pi,dfrac{3pi}{2}right}
$$
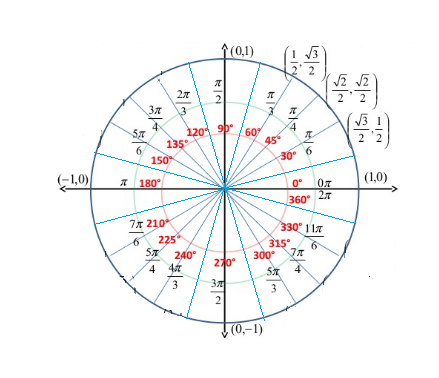
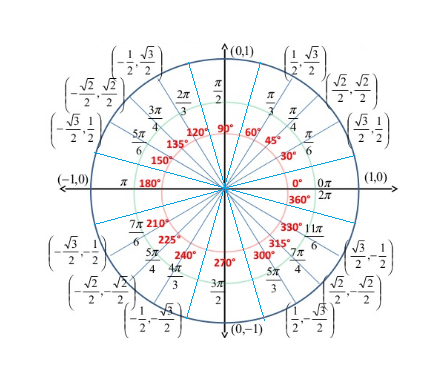
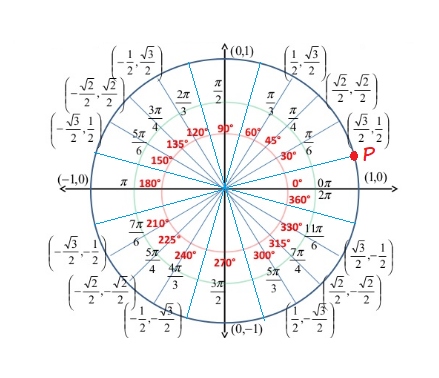
$$
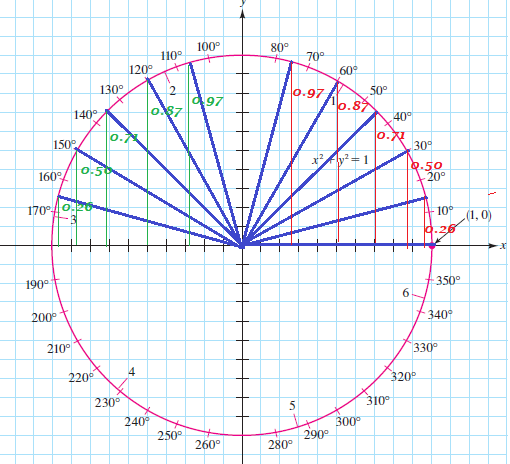
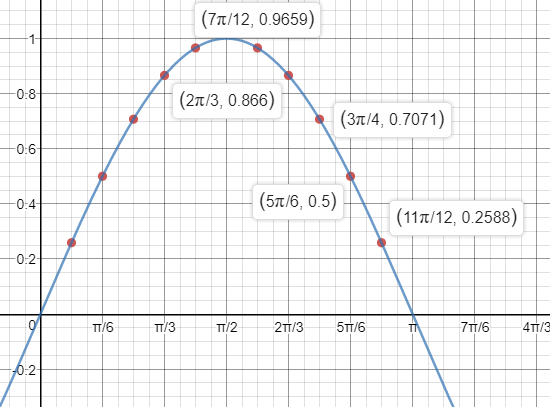
cosdfrac{pi}{12}approx 0.96592583
$$
P(0.96592583,0.25881905)approx (0.97,0.26)
$$

$Q$ – corresponding to $dfrac{11pi}{12}$
$R$ – corresponding to $dfrac{13pi}{12}$
$S$ – corresponding to $dfrac{7pi}{12}$
Q(-0.97,0.26)
$$
R(-0.97,-0.26)
$$
S(-0.26,0.97)
$$
$(sin alpha)^2+(cos alpha)^2=1$
$(sin alpha)^2=1-left(dfrac {8}{17} right)^2$
$(sin alpha)^2=dfrac {289}{289}-dfrac {64}{289}$
$(sin alpha)^2=dfrac {225}{289}$
$$
sin alpha=dfrac {15}{17}
$$
$angle (pi+alpha)$ lies in the third quadrant. So:
$sin (pi+alpha)=-sin alpha$
$sin (pi+alpha)=-dfrac {15}{17}$
$angle (2 pi -alpha)$ lies in the fourth quadrant. So:
$cos (2 pi -alpha)=cos alpha$
$cos (2 pi -alpha)=dfrac {8}{17}$
b- $sin (pi+alpha)=-dfrac {15}{17}$
c- $cos (2 pi -alpha)=dfrac {8}{17}$
theta=330text{textdegree}
$$
360text{textdegree}-theta=360text{textdegree}-330text{textdegree}=30text{textdegree}
$$
theta=120text{textdegree}
$$
180text{textdegree}-theta=text{textdegree}-120text{textdegree}=60text{textdegree}
$$
theta=113text{textdegree}
$$
180text{textdegree}-theta=180text{textdegree}-113text{textdegree}=67text{textdegree}
$$
theta=203text{textdegree}
$$
theta-180text{textdegree}=203text{textdegree}-180text{textdegree}=23text{textdegree}
$$
b) $60text{textdegree}$
c) $67text{textdegree}$
d) $23text{textdegree}$
$sin (4)=sin left(4 times dfrac {180}{pi} right)$
$sin (4)=sin (229.18)$
$$
sin (4) approx -0.7568
$$
$sin (dfrac {4 pi}{3})=sin (dfrac {4 times 180}{3})$
$sin (dfrac {4 pi}{3})=sin (240)$
$angle 240=angle (180+60)$ ($angle 240$$text{textdegree}$ $textrm { ~lies in the third quadrant}$)
$sin (dfrac {4 pi}{3}) =-sin (60)$
$$
sin (dfrac {4 pi}{3})=-dfrac {sqrt {3}}{2}
$$
$$
sin (dfrac {4 pi}{3}) approx -0.866
$$
b- $sin (dfrac {4 pi}{3})=-dfrac {sqrt {3}}{2} approx -0.866$
sin theta=0.5
$$
$theta_2=dfrac{5pi}{6}$
$theta_2=dfrac{5pi}{6}+2kpi, k$ integer
$theta_2=dfrac{5pi}{6}+2kpi, k$ integer
|Degrees |Radians |
|–|–|
|0$degree$ |0 |
|30$degree$ | $dfrac{pi}{6}$|
|45$degree$ |$dfrac{pi}{4}$ |
| 60$degree$|$dfrac{pi}{3}$ |
|90$degree$ |$dfrac{pi}{2}$ |
|120$degree$ |$dfrac{2pi}{3}$ |
|135$degree$ | $dfrac{3pi}{4}$|
|150$degree$ | $dfrac{5pi}{6}$|
| 180$degree$|$pi$ |
| 210$degree$|$dfrac{7pi}{6}$ |
|225$degree$ | $dfrac{5pi}{4}$|
|240 $degree$|$dfrac{4pi}{3}$ |
|270 $degree$| $dfrac{3pi}{2}$|
|300 $degree$| $dfrac{5pi}{3}$|
|315$degree$ | $dfrac{7pi}{4}$|
|330 $degree$| $dfrac{11pi}{12}$|
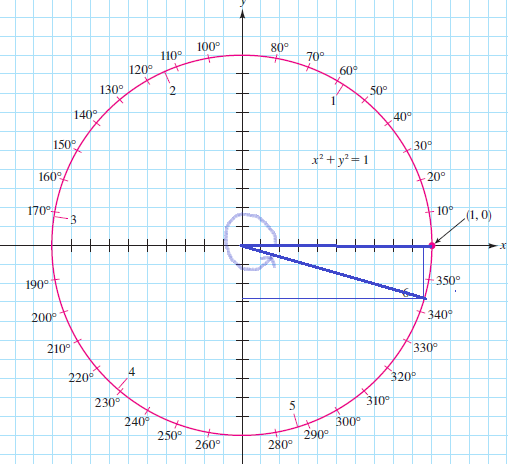
6cdotdfrac{180text{textdegree}}{pi}approx 344text{textdegree}
$$
sin 6approx -0.27
$$
$$
f(2)=2,400,000
$$
f(t)=ab^t+k
$$
$f(5)=ab^5+k=79979(5.47792)^5+21$
$$
approx 394,000,000
$$
$(5.47792)^t=dfrac{2}{79,979}$
$ln (5.47792)^t=ln dfrac{2}{79,979}$
$tln 5.47792=(5.47792)^t=ln dfrac{2}{79,979}$
$t=dfrac{ln dfrac{2}{79,979}}{ln 5.47792}$
$$
tapprox -6
$$
The model shows a very fast grow, which is not real for a great value of $t$.
$$
begin{align*}
frac {2x^5-6x^4-2x^2+7x-4}{x-3} &= frac {2x^4(x-3)-2x^2+6x+x-4}{x-3}\
&= frac {2x^4(x-3)-2x(x-3)+x-3-1}{x-3}\
&= frac {2x^4(x-3)-2x(x-3) + (x-3) -1}{x-3}\
&= frac {2x^4(x-3)}{x-3} – frac {2x(x-3)}{x-3} + frac {x-3}{x-3} – frac {1}{x-3}\
&= 2x^4 – 2x + 1 – frac {1}{x-3}
end{align*}
$$
The expression is
$$
frac {2x^5-6x^4-2x^2+7x-4}{x-3} = 2x^4 – 2x + 1 – frac {1}{x-3}
$$
frac {2x^5-6x^4-2x^2+7x-4}{x-3} = 2x^4 – 2x + 1 – frac {1}{x-3}
$$
(2x^5-6x^4-2x^2+7x-4)div(x-3)
$$
polyhornerscheme[x=3]{2x^5-6x^4-2x^2+7x-4}
$$
dfrac{2x^5-6x^4-2x^2+7x-4}{x-3}=2x^4-2x+1-dfrac{1}{x-3}
$$
dfrac{2x^5-6x^4-2x^2+7x-4}{x-3}=2x^4-2x+1-dfrac{1}{x-3}
$$
$$
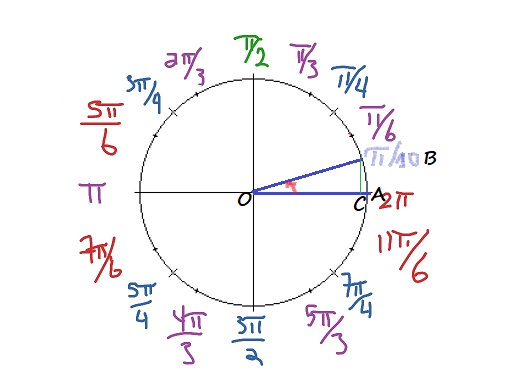
=dfrac{sin AOB}{cos AOB}=dfrac{sin dfrac{pi}{10}}{cos dfrac{pi}{10}}
$$
$=tan dfrac{pi}{10}$
$$
=tandfrac{pi}{10}
$$
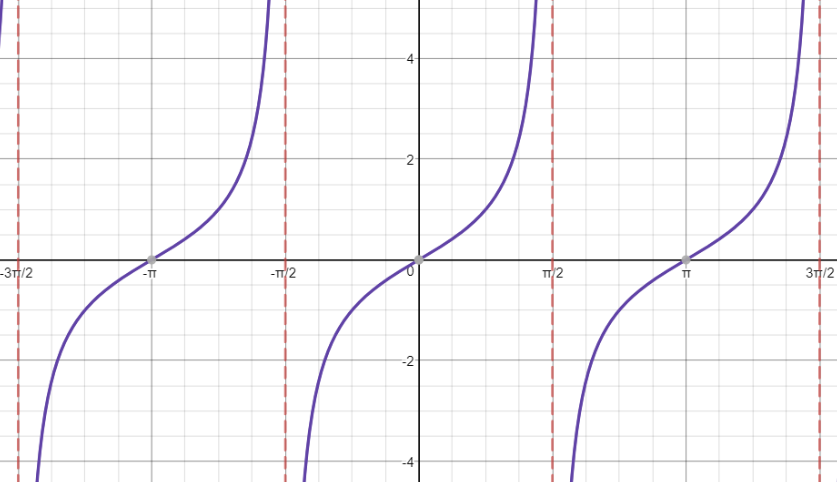
The domain: $mathbb{R}-left{dfrac{(2k+1)pi}{2}, k text{ integer}right}$
T=pi
$$
The $sine$ and $cosine$ functions increase and decrease, while the $tangent$ is only increasing.
The $sine$ and $cosine$ functions do not have asymptotes, while the $tangent$ function has vertical asymptotes:
begin{tabular}{|| c|c|c|c| c||}
hline
$theta$ & $cos (theta)$ & $sin(theta)$ & $tan(theta)$ & $tan(theta)$ \
& & & & (approximate to nearest 0.01)\[0.5ex]
hline
$0textdegree$ & 0& 1& 0& 0 \
hline
$30textdegree$ &$dfrac{sqrt 3}{2}$ & 0.5 & $dfrac{sqrt 3}{3}$ & 0.58 \
hline
$45textdegree$ & $dfrac{sqrt 2}{2}$ &$dfrac{sqrt 2}{2}$ &1 &1 \
hline
$60textdegree$ & 0.5 &$dfrac{sqrt 3}{2}$ & $sqrt 3$ & 1.73 \
hline
$90textdegree$ & 0& 1& undefined& undefined\
hline
$120textdegree$ &-0.5 &$dfrac{sqrt 3}{2}$ &$-sqrt 3$ &-1.73 \
hline
$135textdegree$ & $-dfrac{sqrt 2}{2}$ & $dfrac{sqrt 2}{2}$&-1 &-1 \
hline
$150textdegree$ &$-dfrac{sqrt 3}{2}$ &0.5 & $-dfrac{sqrt 3}{3}$ & -0.58 \
hline
$180textdegree$ &-1 &0 &0 &0 \
hline
$210textdegree$ &$-dfrac{sqrt 3}{2}$ &-0.5 &$dfrac{sqrt 3}{3}$ & 0.58 \
hline
$225textdegree$ & $-dfrac{sqrt 2}{2}$ &$-dfrac{sqrt 3}{2}$ &1 &1 \
hline
$240textdegree$ & -0.5& $-dfrac{sqrt 3}{2}$& $sqrt 3$& 1.73 \
hline
$270textdegree$ & 0&-1 &undefined &undefined \
hline
$300textdegree$ &0.5 &$-dfrac{sqrt 3}{2}$ & $-sqrt 3$& -1.73 \
hline
$330textdegree$ &$dfrac{sqrt 3}{2}$ &-0.5 & $-dfrac{sqrt 3}{3}$ & -0.58 \
hline
$315textdegree$ & $dfrac{sqrt 2}{2}$ &$-dfrac{sqrt 2}{2}$ &-1 &-1 \
hline
$360textdegree$ & 1& 0&0 & 0\[1ex]
hline
end{tabular}
end{center}
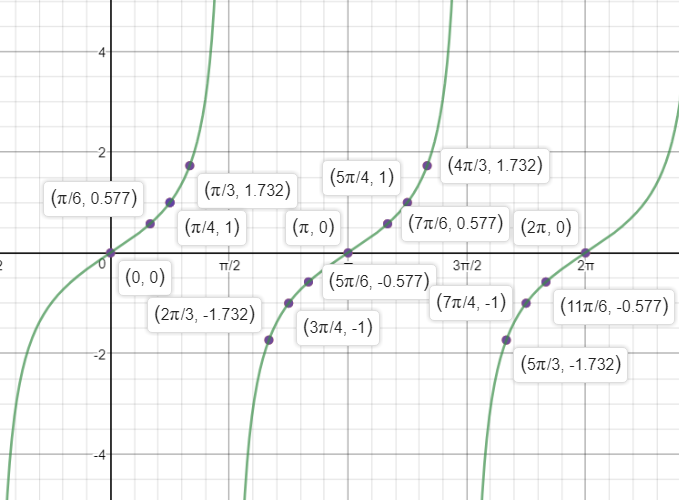
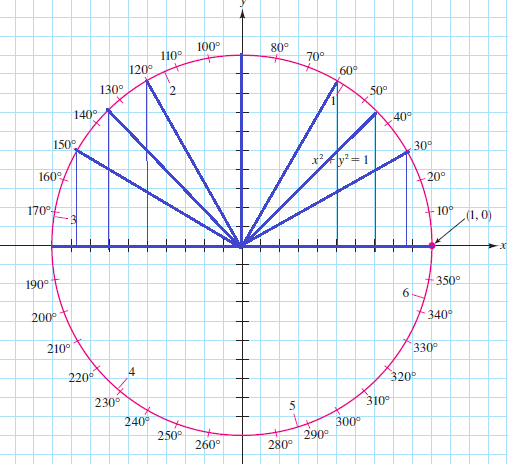
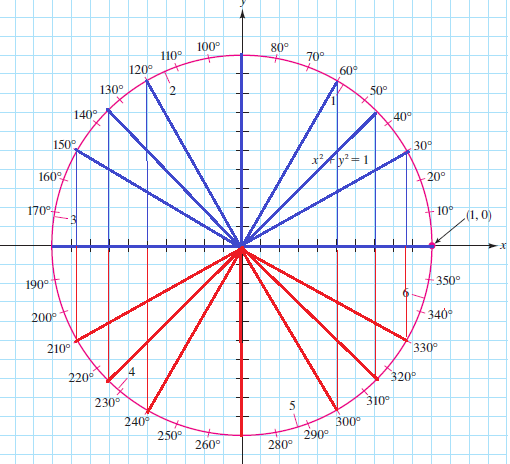
y=tan(theta)
$$
mathbb{R}-left{dfrac{(2k+1)pi}{2}| k text { integer}right}
$$
mathbb{R}
$$
x=dfrac{(2k+1)pi}{2}, k text { integer}
$$
tan(-x)=dfrac{sin(-x)}{cos(-x)}=dfrac{-sin x}{cos x}=-tan x
$$
The graph of $tangent$ has vertical asymptotes, while the graphs of $sine$ and $cosine$ do not.
The graph of $tangent$ increases, while the $sine$ and $cosine$ increase and decrease.
$$
mathbb{R}-left{dfrac{(2k+1)pi}{2}| k text { integer}right}
$$
Please see solution for parts b-d.
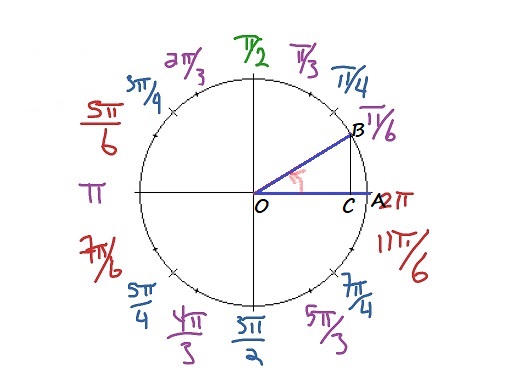
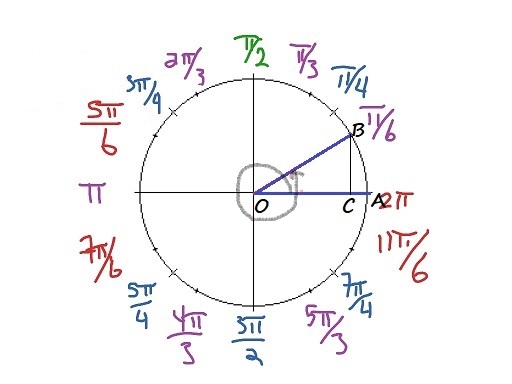
$x_B=OC=OBcos dfrac{pi}{6}=1cdot dfrac{sqrt 3}{2}=dfrac{sqrt 3}{2}$
$sin BOC=dfrac{BC}{OB}$
$y_B=BC=OBsin dfrac{pi}{6}=1cdot dfrac{1}{2}=dfrac{1}{2}$
$$
Rightarrow Bleft(dfrac{sqrt 3}{2},dfrac{1}{2}right)
$$
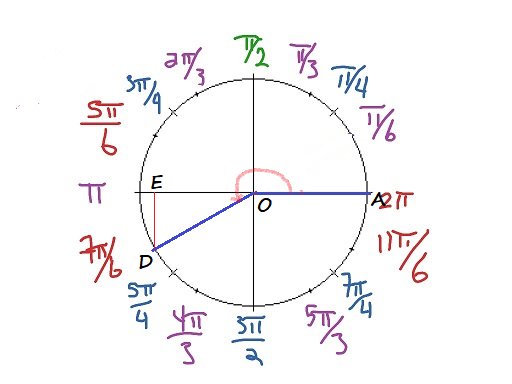
$OE=ODcos dfrac{pi}{6}=1cdot left(dfrac{sqrt 3}{2}right)=dfrac{sqrt 3}{2}$
$x_D=cos AOD=-dfrac{sqrt 3}{2}$
$sin DOE=dfrac{DE}{OD}$
$DE=ODsin dfrac{pi}{6}=1cdot dfrac{1}{2}=dfrac{1}{2}$
$y_D=sin AOD=-dfrac{1}{2}$
$$
tandfrac{7pi}{6}=dfrac{sin AOD}{cos AOD}=dfrac{y_D}{x_D}=dfrac{-dfrac{1}{2}}{-dfrac{sqrt 3}{2}}=dfrac{1}{sqrt 3}=dfrac{sqrt 3}{3}
$$
cos dfrac{13pi}{6}=cosdfrac{pi}{6}=dfrac{sqrt 3}{2}
$$
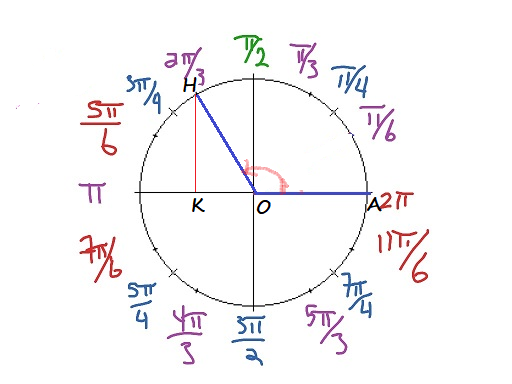
$OK=OHcos dfrac{pi}{3}=1cdot left(dfrac{1}{2}right)=dfrac{1}{2}$
$x_H=cos AOH=-dfrac{1}{2}$
$sin HOK=dfrac{HK}{OH}$
$HK=OHsin dfrac{pi}{3}=1cdot dfrac{sqrt 3}{2}=dfrac{sqrt 3}{2}$
$y_H=sin AOH=dfrac{sqrt 3}{2}$
$$
tandfrac{2pi}{3}=dfrac{sin AOH}{cos AOH}=dfrac{y_H}{x_H}=dfrac{dfrac{sqrt 3}{2}}{-dfrac{1}{2}}=-sqrt 3
$$
theta=dfrac{7pi}{3}
$$
theta=dfrac{7pi}{3}cdot dfrac{180text{textdegree}}{pi}=420text{textdegree}
$$
$alpha=theta+kcdot 360text{textdegree}=420text{textdegree}+kcdot 360text{textdegree}$ integer
corresponds to the same point on the circle.
k=-1Rightarrowalpha=420text{textdegree}+(-1)360text{textdegree}=60text{textdegree}
$$
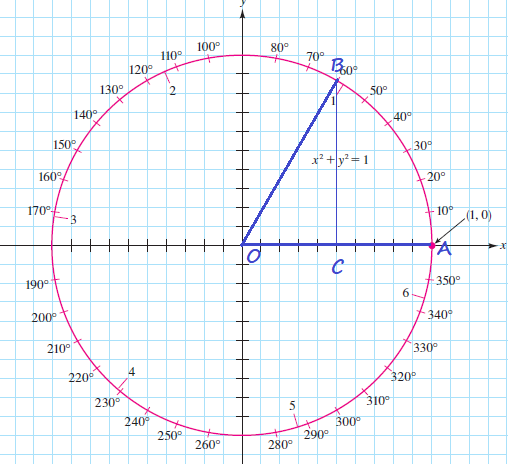
$BC=OBsin 60text{textdegree}=1cdot dfrac{sqrt 3}{2}=dfrac{sqrt 3}{2}$
$cos AOB=dfrac{OC}{OB}$
$OC=OBcos 60text{textdegree}=1cdot dfrac{1}{2}=dfrac{1}{2}$
$cos dfrac{7pi}{3}=cos dfrac{pi}{3}=dfrac{1}{2}$
$tan dfrac{7pi}{3}=tan dfrac{pi}{3}=dfrac{sin dfrac{pi}{3}}{cos dfrac{pi}{3}}$
$$
=dfrac{dfrac{sqrt 3}{2}}{dfrac{1}{2}}=sqrt 3
$$
b) $sin360text{textdegree}=sin (360text{textdegree}-360text{textdegree})=sin 0text{textdegree}=0$
c) $sin(-90text{textdegree})=sin (-90text{textdegree}+360text{textdegree})=sin 270text{textdegree}=-1$
d) $sin510text{textdegree}=sin (510text{textdegree}-360text{textdegree})$
$=sin 150text{textdegree}=sin (180text{textdegree}-150text{textdegree})$
$=sin 30text{textdegree}=0.5$
e) $cos 90text{textdegree}=0$
f) $tan (-90text{textdegree})$ (undefined!)
$x$ radians………. $ytext{textdegree}$
$$
y=dfrac{360text{textdegree}}{2pi}cdot x=dfrac{180text{textdegree}}{pi}cdot x
$$
$xtext{textdegree}$………. $y$ radians
$$
y=dfrac{2pi}{360text{textdegree}}cdot x=dfrac{pi}{180text{textdegree}}cdot x
$$
dfrac{7pi}{6}=dfrac{7pi}{6}cdot dfrac{180text{textdegree}}{pi}=210text{textdegree}
$$
dfrac{5pi}{3}=dfrac{5pi}{3}cdot dfrac{180text{textdegree}}{pi}=300text{textdegree}
$$
45text{textdegree}=45text{textdegree}cdotdfrac{pi}{180text{textdegree}}=dfrac{pi}{4}
$$
100text{textdegree}=100text{textdegree}cdotdfrac{pi}{180text{textdegree}}=dfrac{5pi}{9}
$$
810text{textdegree}=810text{textdegree}cdotdfrac{pi}{180text{textdegree}}=dfrac{9pi}{2}
$$
dfrac{7pi}{2}=dfrac{7pi}{2}cdot dfrac{180text{textdegree}}{pi}=630text{textdegree}
$$
$sin^2theta+dfrac{144}{169}=1$
$sin^2theta=1-dfrac{144}{169}$
$sin^2theta=dfrac{25}{169}$
$sintheta=pmdfrac{5}{13}$
$sin^2theta+cos^2theta=1$.
tantheta=dfrac{sintheta}{costheta}=dfrac{-dfrac{5}{13}}{-dfrac{12}{13}}=dfrac{5}{12}
$$
b) $tantheta=dfrac{5}{12}$
$$
log_2(x) = 2^x
$$
Let
$$
begin{align*}
y &= log_2(x)-text{blue}\
y &= 2^x-text{red}
end{align*}
$$
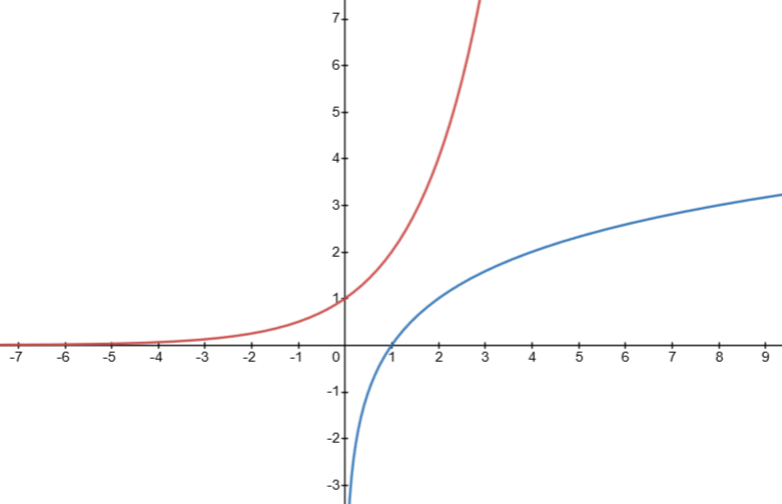
log_2 x=2^x
$$
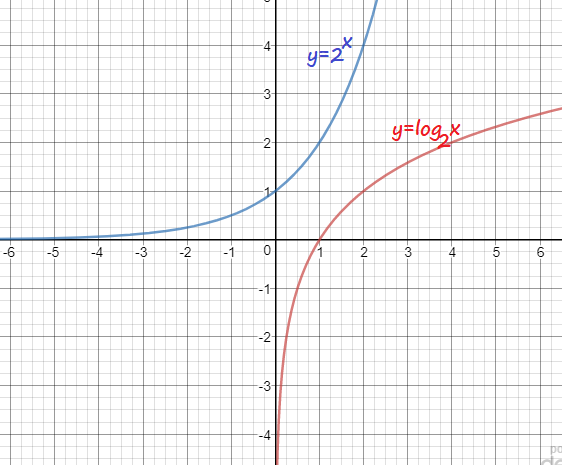
$$
color{#c34632}{ (x-a)(x-b)(x-c) =0}
$$
Since
$$
begin{align*}
a&=3\
b&=2\
c&=-1
end{align*}
$$
We obtain
$$
begin{align*}
(x-3)(x-2)(x+1) &= 0\
(x^2 -2x-3x+6)(x+1) &= 0\
(x^2 – 5x + 6)(x+1) &= 0\
x^3 – 5x^2 + 6x + x^2 -5x +6 &= 0\
x^3 – 4x^2 + x +6 &= 0
end{align*}
$$
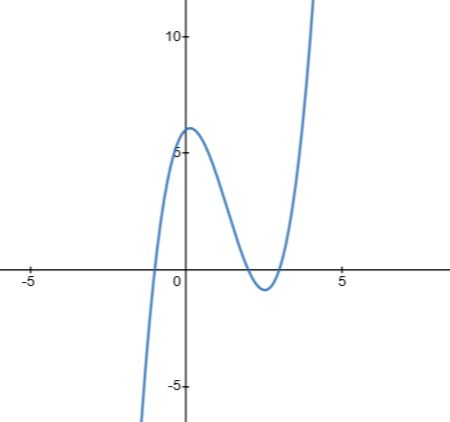
$$
k (x^3 -4x^2 + x +6) = 0
$$
Since $(1,1)$ we obitan
$$
y(1) =1
$$
Then
$$
begin{align*}
k ( 1^3 – 4 cdot 1^2 + 1 +6) &= 1\
k (1-4+1+6) &= 1\
4k &= 1\
k &= frac 14
end{align*}
$$
The function passing through point $(1,1)$ is
$$
y = frac 14 ( x^3 – 4x^2 + x +6)
$$
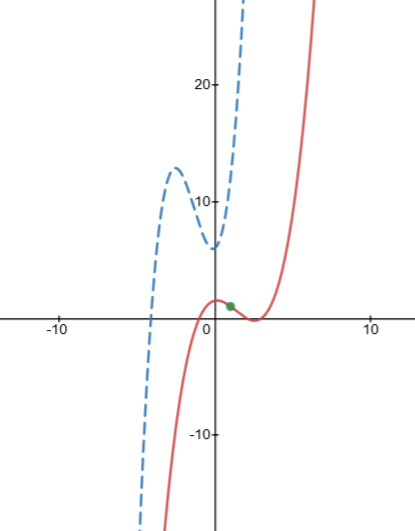
y = frac 14 ( x^3 – 4x^2 + x +6)
$$

$$y=Asin(B(x-k))+c,$$
where $k$ represents horizontal shift, $c$ represents the vertical shift, $B$ represents the horizontal stretching and $|A|$ is an amplitude.
$$y=Acos(B(x-k))+c.$$
y=sin (x)
$$
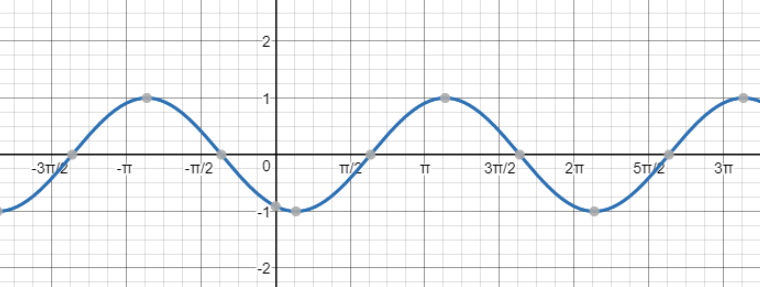
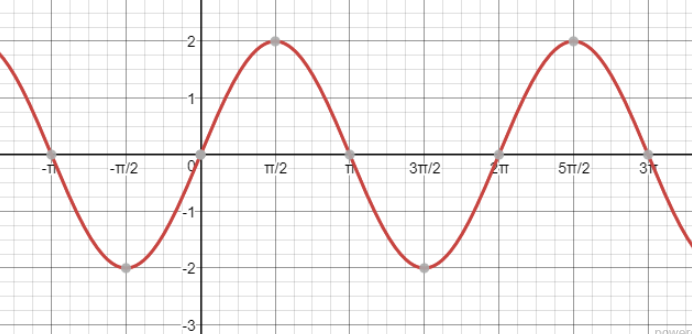
y=asin (bx+c)+d
$$
y=sin (x)
$$
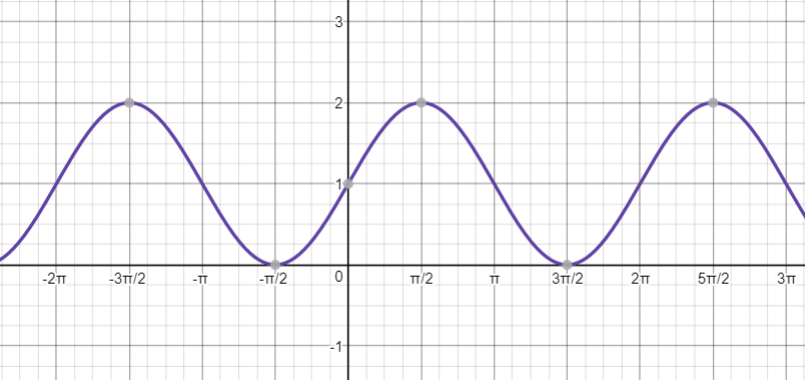
y=sin (x)+1
$$
y=1
$$
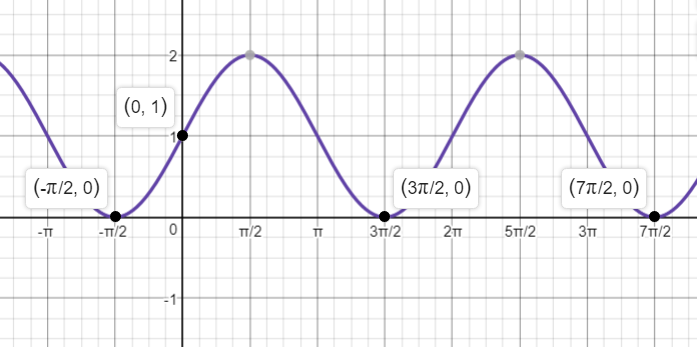
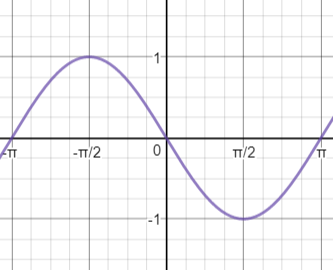
y=sin (x-pi)
$$
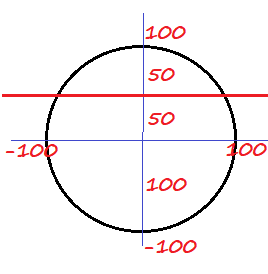
begin{tabular}{|| c|c|c|c|c|c| c||}
hline
x (degrees) & y feet) \ [0.5ex]
hline
0 & 50 \
hline
90 &-50 \
hline
180 & -150 \
hline
270 & -50 \
hline
360 & 50 \[1ex]
hline
end{tabular}
end{center}
y = acos(x-h) + k
$$
Vertical shift: $k=-50$
Amplitude: $a=100$
y=100cos x-50
$$
y=100cos x-50
$$
$$
y=cos (x)
$$
$y=cos (x)=sinleft(x-dfrac{pi}{2}right)$
y=12x^3+55x^2-27x-10
$$
polyhornerscheme[x=-5]{12x^3+55x^2-27x-10}
$$
y=(x+5)(12x^2-5x-2)
$$
$=(x+5)[4x(3x-2)+(3x-2)]$
$$
(x+5)(3x-2)(4x+1)
$$
$4x+1=0Rightarrow 4x=-1Rightarrow x=-dfrac{1}{4}$
left{-dfrac{1}{4},dfrac{2}{3}right}
$$
$$
y = 12x^3 + 55x^2 -27x-10
$$
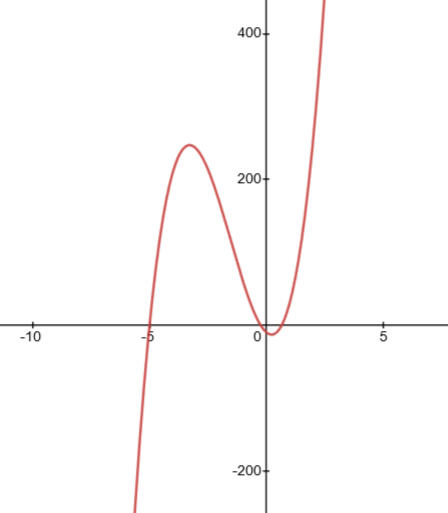
$$
(12x^3 + 55x^2 -27x-10) div (x+5) = 12x^2 – 5x-2
$$
Now, we calculate
$$
12x^2 -5x-2 =0
$$
The solutions of a square equation $ax^2 + bx +c=0$ are shape
$$
x = frac {-b pm sqrt {b^2 – 4ac}}{2a}
$$
Now we have
$$
begin{align*}
x &= frac {5 pm sqrt {25+96}}{24}\
x &= frac {5 pm sqrt {121}}{24}\
x &= frac {5 pm 11}{24}\
x &= frac 23 qquad x =-frac 14
end{align*}
$$
The $x$ – intercepts are
$$
x=-5 qquad x=frac 23 qquad x=- frac 14
$$
x=-5 qquad x=frac 23 qquad x=- frac 14
$$
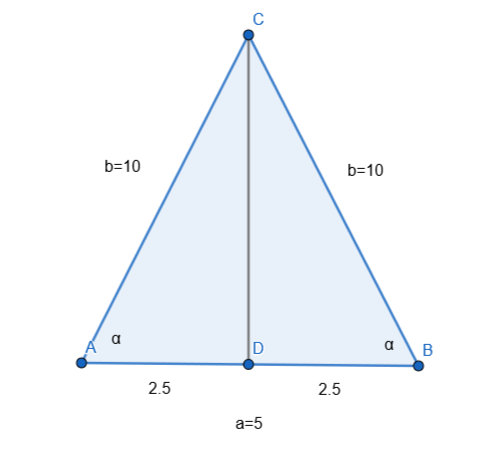
$$
cos alpha = frac {frac a2}{b}
$$
Then
$$
begin{align*}
cos alpha &= frac {2.5}{10}\
cos alpha &= 0.25
end{align*}
$$
We can use the inverse function
$$
begin{align*}
alpha &= arccos 0.25\
alpha &= 75.5^{text{textdegree}}
end{align*}
$$
The sum of the interior angles of a triangle is $180^{text{textdegree}}$
$$
begin{align*}
alpha + alpha + beta &= 180^{text{textdegree}}\
75.5^{text{textdegree}} + 75.5^{text{textdegree}} + beta &= 180^{text{textdegree}}\
151^{text{textdegree}} + beta &= 180^{text{textdegree}}\
beta &= 29^{text{textdegree}}
end{align*}
$$
The angles in the triangle are
$$
75.5^{text{textdegree}} , qquad 75.5^{text{textdegree}} qquad text{and} qquad 29^{text{textdegree}}
$$
75.5^{text{textdegree}} , qquad 75.5^{text{textdegree}} qquad text{and} qquad 29^{text{textdegree}}
$$
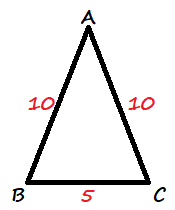
$10^2=10^2+5^2-2cdot 10cdot 5cdot cos B$
$100cos B=25$
$cos B=dfrac{25}{100}$
$cos B=0.25$
$B=cos^{-1} 0.25$
$$
Bapprox 75.5text{textdegree}
$$
B=C=75.5text{textdegree}
$$
$$
=29text{textdegree}
$$
29text{textdegree};75.5text{textdegree}; 75.5text{textdegree};
$$
y=asin(x-h)+k
$$
y=asin (bx-h)+k
$$
For example:
begin {center}
renewcommand{arraystretch}{2.5}
begin{tabular}{ | m{2cm} | m{2cm} || m{2cm} | m{2cm} | }
hline
t (seconds) & d(t) & t (seconds) & d(t) \
hline
1 & $dfrac { pi}{12}$ & 13 & $dfrac {13 pi}{12}$ \
hline
2 & $dfrac { pi}{6}$ & 14 & $dfrac {7 pi}{6}$ \
hline
3 & $dfrac { pi}{4}$ & 15 & $dfrac {5 pi}{4}$ \
hline
4 & $dfrac { pi}{3}$ & 16 & $dfrac {4 pi}{3}$ \
hline
5 & $dfrac {5 pi}{12}$ & 17 & $dfrac {17 pi}{12}$ \
hline
6 & $dfrac { pi}{2}$ & 18 & $dfrac {3 pi}{2}$ \
hline
7 & $dfrac {7 pi}{12}$ & 19 & $dfrac {19 pi}{12}$ \
hline
8 & $dfrac {2 pi}{3}$ & 20 & $dfrac {5 pi}{3}$ \
hline
9 & $dfrac {3 pi}{4}$ & 21 & $dfrac {7 pi}{4}$ \
hline
10 & $dfrac {5 pi}{6}$ & 22 & $dfrac {11 pi}{6}$ \
hline
11 & $dfrac {11 pi}{12}$ & 23 & $dfrac {23 pi}{12}$ \
hline
12 & $pi$ & 24 & $2 pi$ \
hline
end {tabular}
end{center}
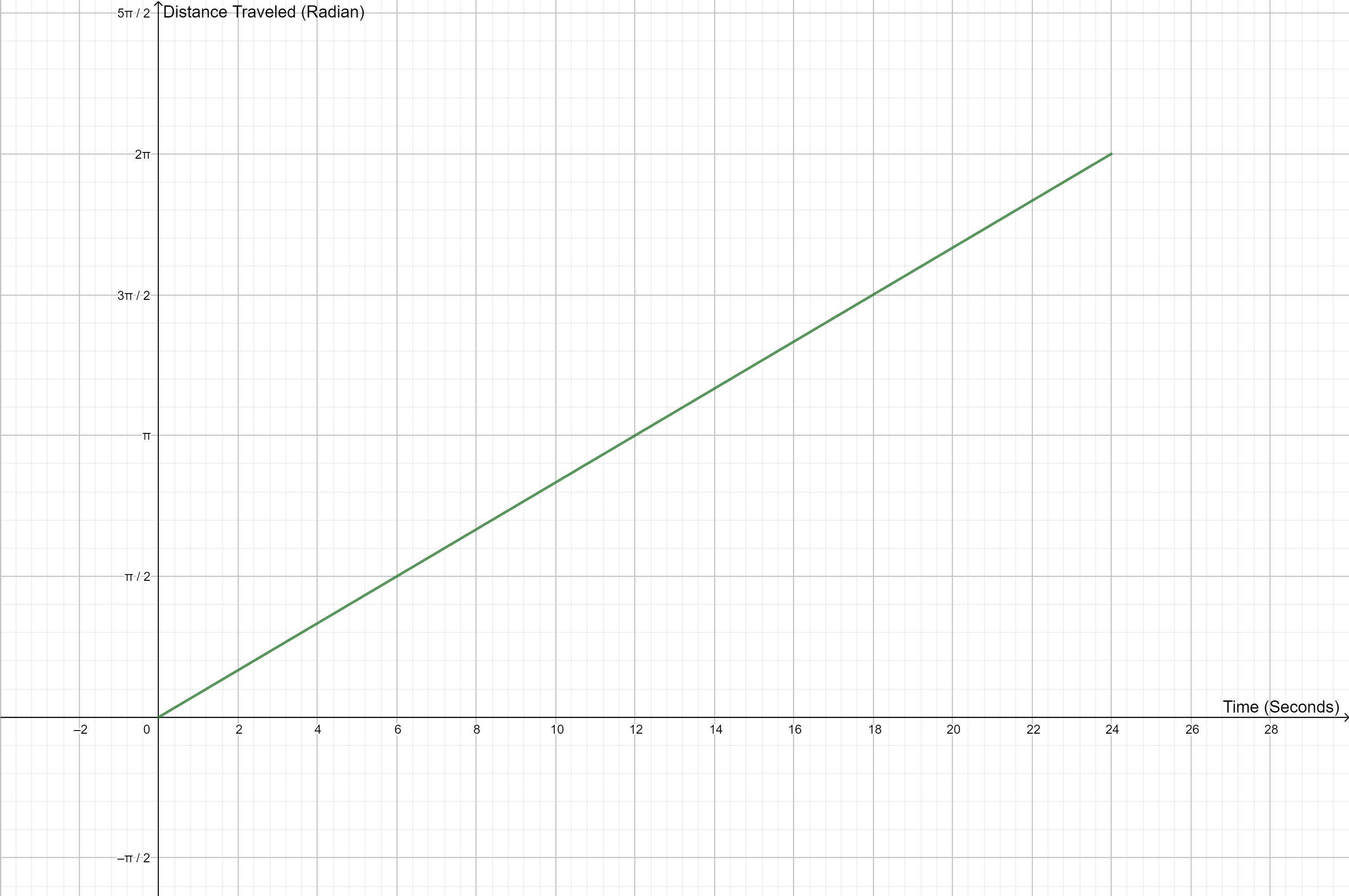
Then, we can calculate the output with the equation:
$d(t)=dfrac {t}{2}times dfrac { pi}{6}$
It takes 24 seconds to complete on full cycle on the radar screen
From the graph, the line reaches $2 pi$ on y-axis at 24 seconds on x-axes
It takes 24 seconds to complete on full cycle on the radar screen
y=asin(x-h)+k
$$

$y=sin (2x-1)+1$
$y=sin (3x-1)+1$
$y=sin (4x-1)+1$
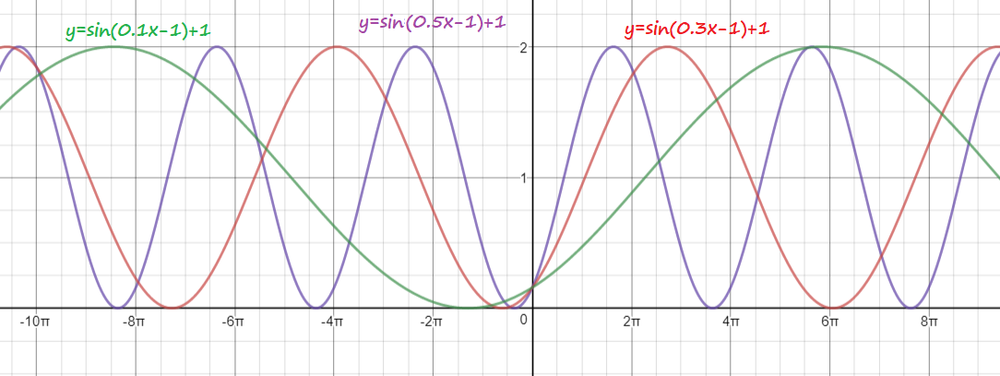
$y=sin (0.5x-1)+1$
$y=sin (0.3x-1)+1$
$y=sin (0.1x-1)+1$
y=asin (bx-h)+k
$$
y=asin(bx-h)+k
$$
T_1=pi
$$
T_2=2pisqrt{dfrac{L}{g}}=3
$$
T_3=2pi
$$
y=sin (x-pi)
$$
$y=cosleft(dfrac{3pi}{2}-xright)$
y=-sin (x)
$$
y=-sin x
$$
So the value of $y=cos theta=cos (theta+360text{textdegree})=cos (theta+720text{textdegree})=cos (theta+n2pi)$ will be same.
$$
begin{align*}
color{#c34632}{tan theta = frac {sin theta}{cos theta}} tag{$*$}
end{align*}
$$
we obtain
$$
tan left( frac {2 pi}{3} right) = frac {sin left( frac {2 pi}{3} right)}{cos left( frac {2 pi}{3} right)}
$$
Since
$$
begin{align*}
sin left( frac {2 pi}{3} right) &= frac {sqrt 3}{2}\
cos left( frac {2 pi}{3} right) &= – frac 12
end{align*}
$$
we have
$$
tan left( frac {2 pi}{3} right) = frac {frac {sqrt 3}{2}}{- frac 12} = – sqrt 3
$$
$$
tan left( frac {7 pi}{6} right) = frac {sin left( frac {7 pi}{6} right)}{cos left( frac {7 pi}{6} right)}
$$
Since
$$
begin{align*}
sin left( frac {7 pi}{6} right) &= – frac 12\
cos left( frac {7 pi}{6} right) &= – frac {sqrt 3}{2}
end{align*}
$$
we have
$$
tan left( frac {7 pi}{6} right) = frac {- frac 12}{ – frac {sqrt 3}{2}} = frac {1}{sqrt 3} = frac {sqrt 3}{3}
$$
b) $tan left( frac {7 pi}{6} right) = frac {sqrt 3}{3}$
tanleft(dfrac{2pi}{3}right)
$$
$$
=-tanleft(dfrac{pi}{3}right)=-sqrt 3
$$
tanleft(dfrac{7pi}{6}right)
$$
$$
=tanleft(dfrac{pi}{6}right)=dfrac{sqrt 3}{3}
$$
b) $dfrac{sqrt 3}{3}$
$b=0.5$
$$
c=dfrac{sqrt 3}{2}
$$
$$
b<c<a
$$
$0.5^2+left(dfrac{sqrt 3}{2}right)^2stackrel{?}{=}1^2$
$0.25+dfrac{3}{4}stackrel{?}{=}1$
$0.25+0.75stackrel{?}{=}1$
$$
1=1checkmark
$$
$$
color{#c34632}{c^2=a^2 + b^2}
$$
Let
$$
begin{align*}
a &= 0.5\
b &= frac {sqrt 3}{2}\
c &= 1
end{align*}
$$
we get
$$
begin{align*}
1^2 &= 0.5^2 + left( frac {sqrt 3}{2} right)^2\
1 &= 0.25 + frac 34\
1 &= frac 14 + frac 34\
1 &= 1
end{align*}
$$
This triangle is a right triangle.
$$
K=k(1+r)^n
$$
Replace $K$ with 25,000, $k$ with $15,000$ and $r$ with $8%=0.08$:
$$
25,000=15,000(1.08)^n
$$
Divide both sides of the equation by 15,000:
$$
dfrac{5}{3}=(1.08)^n
$$
Take the logarithm with base 1.08 from both sides of the equation:
$$
log_{1.08}{dfrac{5}{3}}=n
$$
Determine $n$:
$$
n=log_{1.08}{dfrac{5}{3}}=dfrac{log{dfrac{5}{3}}}{log{1.08}}approx 7
$$
Thus it will take approximately 7 years.
$$
begin{align*}
f(x) &= x^3 – 5x^2 + 11x – 15\
&= x^3 – 3x^2 -2x^2 + 6x + 5x -15\
&= x^2 (x-3) – 2x (x-3) + 5 (x-3)\
&= (x-3)( x^2 – 2x + 5)
end{align*}
$$
The possible factor is
$$
d) (x-3)
$$
$$
begin{align*}
f(x) &= x^3 – 5x^2 + 11x -15\
&= (x-3)(x^2 – 2x +5)
end{align*}
$$
$$
begin{align*}
x-3 &= 0\
x &= 0
end{align*}
$$
and
$$
x^2 -2x + 5 =0
$$
The solution of a square equation $a^2 + bx + c =0$ are shape
$$
x = frac {-b pm sqrt {b^2 – 4ac}}{2a}
$$
Now we have
$$
begin{align*}
x &= frac {2 pm sqrt {4-20}}{2}\
x &= frac {2 pm sqrt {-16}}{2}\
x &= frac {2 pm 4 i}{2}\
x &= 1+ 2 i qquad x= 1- 2 i
end{align*}
$$
The roots of the polynomial
$$
x=3 qquad x=1+2 i qquad x=1-2 i
$$
b) $x=3 qquad x=1+2 i qquad x=1-2 i$
f(x)=x^3-5x^2+11x-15
$$
f(x)=(x-3)Q(x)
$$
polyhornerscheme[x=3]{x^3-5x^2+11x-15}
$$
f(x)=(x-3)(x^2-2x+5)
$$
$=(x-3)[(x-1)^2-(21)^2]$
$$
=(x-3)(x-1-2i)(x-1+2i)
$$
$x-1+2i=0Rightarrow x_3=1-2i$
{3, 1+2i,1-2i}
$$
y=costheta
$$
T=2pi
$$
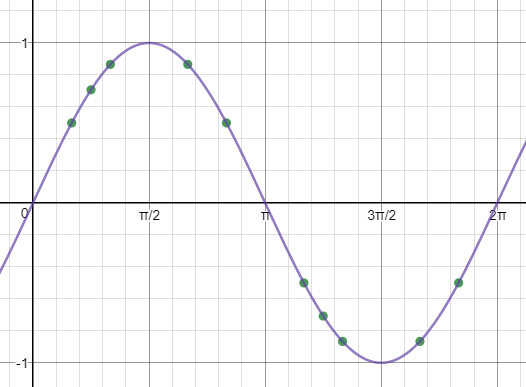
The domain of one cycle of the function $y=sin(x)$ is: $0 leq x leq 2 pi$
The range of one cycle of the function $y=sin(x)$ is: $-1 leq y leq 1$
The table below represents the cycles number, midline, amplitude and cycle length of each graph.\
begin {center}
renewcommand{arraystretch}{2.5}
begin{tabular}{|l|c|c|c|c|c|}
hline
Function & Cycles # & Midline Equation & Amplitude & Period & Function? (Yes/No) \
hline
$y=sin(x)$ & 1 & $y=0$ & 1 & $2 pi$ & Yes \
hline
$y=sin(0.5 x)$ & $dfrac {1}{2}$ & $y=0$ & 1 & $4 pi$ & Yes \
hline
$y=sin(2 x)$ & 2 & $y=0$ & 1 & $dfrac {1}{2} pi$ & Yes \
hline
$y=sin(3 x)$ & 3 & $y=0$ & 1 & $dfrac {2}{3} pi$ & Yes \
hline
$y=sin(5 x)$ & 5 & $y=0$ & 1 & $dfrac {2}{5} pi$ & Yes \
hline
end{tabular}
end {center}
All the graph are equations because they pass the vertical line test.\
For the graph of $y=sin(bx)$
i. The cycles number $=b$
ii. The midline equation is: $y=0$
iii. The amplitude: $=1$
iv. The period (Cycle length) is: $dfrac {2 pi}{b}$
v. The equation is a function.
The graph of the equation $y=sin(6x)$
i. The cycles number $=6$
ii. The midline equation is: $y=0$
iii. The amplitude: $=1$
iv. The period (Cycle length) is: $dfrac {2 pi}{6}$
v. The equation is a function.

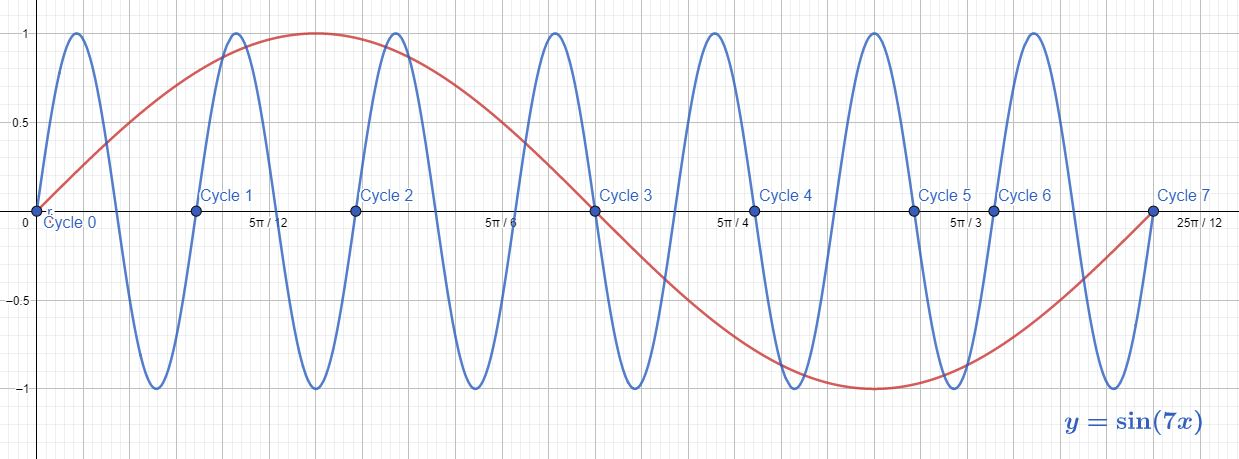
i. The cycles number $=7$
ii. The midline equation is: $y=0$
iii. The amplitude: $=1$
iv. The period (Cycle length) is: $dfrac {2 pi}{7}$
v. The equation is a function.
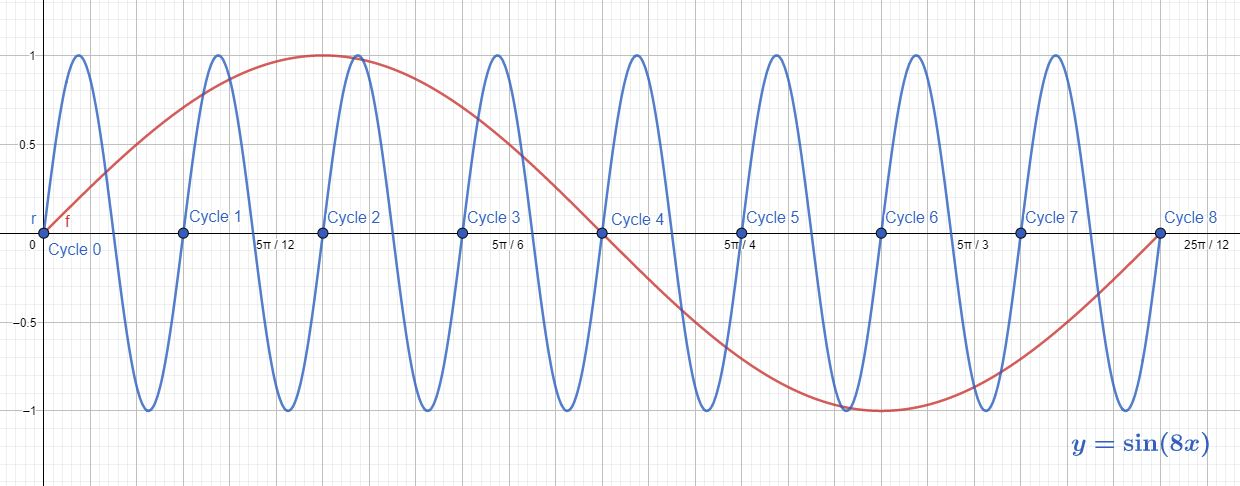
i. The cycles number $=8$
ii. The midline equation is: $y=0$
iii. The amplitude: $=1$
iv. The period (Cycle length) is: $dfrac {2 pi}{8}$
v. The equation is a function.
For the graph of $y=sin(bx)$, the relation between the period of the sing graph and $b$ is:
The period (Cycle length) is: $dfrac {2 pi}{b}$
i. The cycles number $=b$
ii. The midline equation is: $y=0$
iii. The amplitude: $=1$
iv. The period (Cycle length) is: $dfrac {2 pi}{b}$
v. The equation is a function.
We should draw x-axis exactly below the meter stick and parallel to it and the y-axis at the start point of releasing the pendulum and perpendicular to x-axis.
There are more than one possible equation, it varies according the speed of the pendulum and the speed of moving the butcher paper.
y=sin 2left(x-dfrac{pi}{6}right)
$$
Period: $T=dfrac{2pi}{2}=pi$
Horizontal shift: $-dfrac{-dfrac{pi}{6}}{1}=dfrac{pi}{6}$
Vertical shift: $0$
y=3+sin left(dfrac{1}{3}xright)
$$
Period: $T=dfrac{2pi}{dfrac{1}{3}}=6pi$
Horizontal shift: $-dfrac{0}{dfrac{1}{3}}=0$
Vertical shift: $3$

y=3sin (4x)
$$
Period: $T=dfrac{2pi}{4}=dfrac{pi}{2}$
Horizontal shift: $-dfrac{0}{4}=0$
Vertical shift: $0$
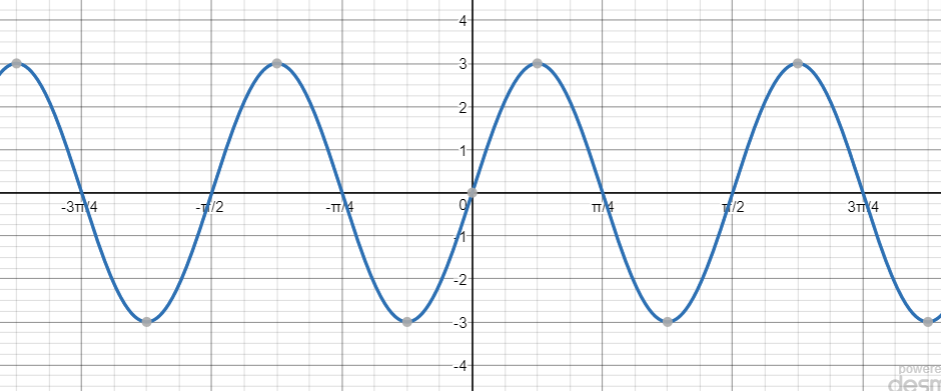
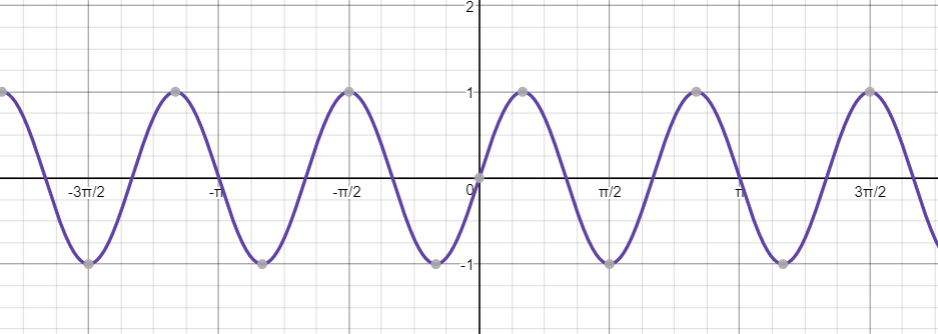
y=sin dfrac{1}{2}left(x+1right)
$$
Period: $T=dfrac{2pi}{dfrac{1}{2}}=4pi$
Horizontal shift: $-dfrac{dfrac{1}{2}}{dfrac{1}{2}}=-1$
Vertical shift: $0$
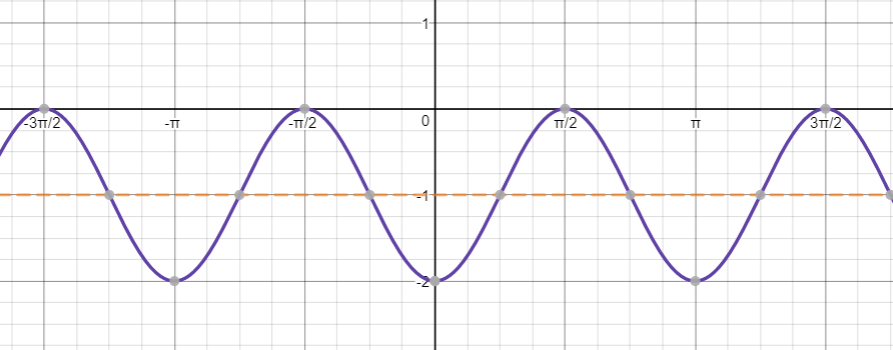
y=-sin 3left(x-dfrac{pi}{3}right)
$$
Period: $T=dfrac{2pi}{3}$
Horizontal shift: $-dfrac{-pi}{3}=dfrac{pi}{3}$
Vertical shift: $0$
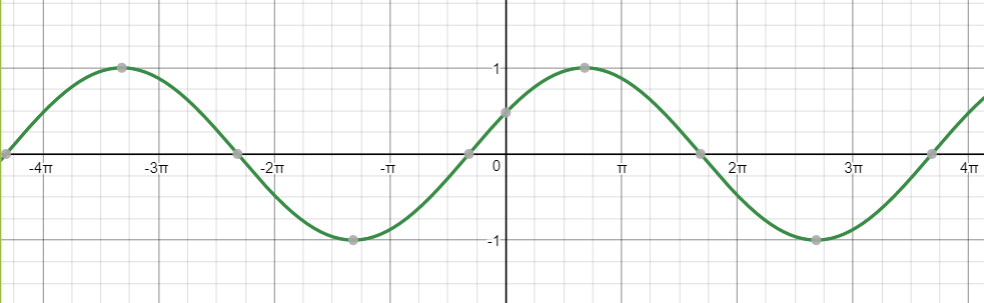
y=-1+sin left(2x-dfrac{pi}{2}right)
$$
Period: $T=dfrac{2pi}{2}=pi$
Horizontal shift: $-dfrac{-dfrac{pi}{2}}{2}=dfrac{pi}{4}$
Vertical shift: $-1$
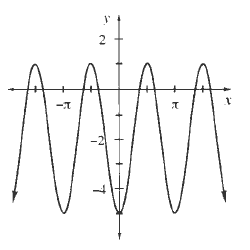
Horizontal shift: $dfrac{pi}{4}$
Midline: $y=-2$
y=Asin(Bx+C)+D
$$
$D=-2$
$$
-dfrac{C}{B}=dfrac{pi}{4}
$$
C=-dfrac{pi}{4}cdot B=-dfrac{pi}{4}cdot 2=-dfrac{pi}{2}
$$
$$
y=3sin 2left(x-dfrac{pi}{4}right)-2
$$
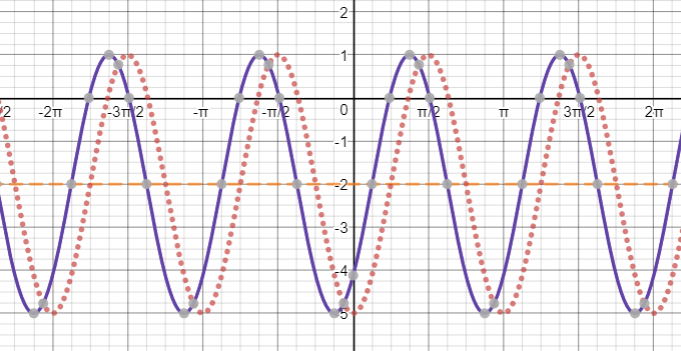
$y=3sin left(2x-dfrac{pi}{4}right)-2$
in continuous line, and the correct function:
$y=3sin left(2x-dfrac{pi}{2}right)-2$
in dotted line:
$A$=the amplitude
$dfrac{2pi}{B}$=the period
$-dfrac{C}{B}$=the horizontal shift
$D$=the vertical shift (midline)
$$
g(x)=3sinleft(dfrac{1}{2} xright)
$$
The similarities in both the graph is that there is no horizontal or vertical shift.
y=sin (2pi x)
$$
T=dfrac{2pi}{2pi}=1
$$
T=1
$$
y=sin [2(x-1)]=sin (2x-2)
$$
$$
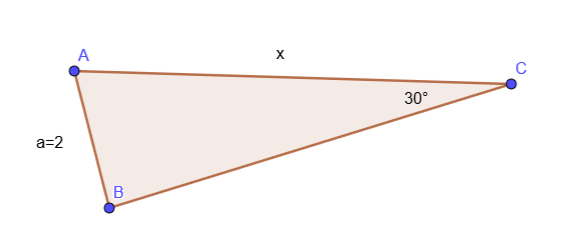
sin theta = frac ax
$$
$$
begin{align*}
sin 30^{text{textdegree}} &= frac 2x\
frac {1}{2} &= frac 2x\
x &= 2 cdot 2\
x &= 4
end{align*}
$$
$$
cos theta = frac ax
$$
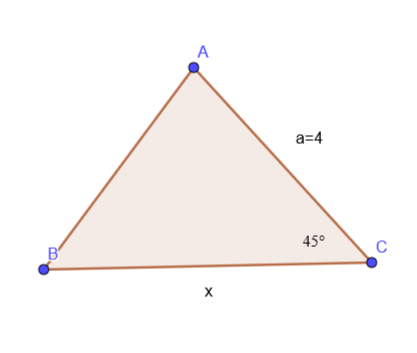
$$
begin{align*}
cos 45^{text{textdegree}} &= frac 4x\
frac {sqrt 2}{2} &= frac 4x\
x sqrt 2 &= 4 cdot 2\
x sqrt 2 &= 8\
x &= frac {8}{sqrt 2}\
x &= frac {8 sqrt 2}{2}\
x &= 4 sqrt 2
end{align*}
$$
b) $x = 4 sqrt 2$
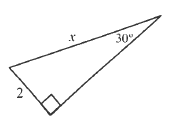
$dfrac{1}{2}=dfrac{2}{x}$
$x=2cdot 2$
$$
x=4
$$
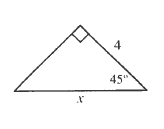
$dfrac{sqrt 2}{2}=dfrac{4}{x}$
$xsqrt 2=2cdot 4$
$x=dfrac{8}{sqrt 2}$
$$
x=4sqrt 2
$$
b) $x=4sqrt 2$
29=3^x
$$
$log (29)=xlog(3)$
$x=dfrac{log (29)}{log (3)}$
$$
xapprox 3.0650
$$
$$
3^x=29^{-1}
$$
$xlog (3)=-log (29)$
$x=dfrac{-log (29)}{log (3)}$
$$
xapprox -3.0650
$$
29=x^3
$$
$$
xapprox 3.0723
$$
-29=x^3
$$
$$
xapprox -3.0723
$$
$A=10(1+0.07)^t$
$$
A=10(1.07)^t
$$
$(1.07)^t=dfrac{15}{10}$
$(1.07)^t=1.5$
$log ((1.07)^t)=log (1.5)$
$tlog (1.07)=log (1.5)$
$t=dfrac{log (1.5)}{log (1.07)}$
$$
tapprox 6
$$
b) $xapprox -3.0650$
c) $xapprox 3.0723$
d) $xapprox -3.0723$
e) 6 years
$$
begin{align*}
29 &= 3^x\
ln 29 &= ln 3^x
end{align*}
$$
Using the formula
$$
begin{align*}
color{#c34632}{ ln a^b = b ln a} tag {$*$}
end{align*}
$$
we obtain
$$
begin{align*}
ln 29 &= x ln 3\
x &= frac {ln 29}{ln 3}\
x &= frac {3.3673}{1.0986}\
x &= 3.0651
end{align*}
$$
The solution of equation is
$$
x = 3.0651
$$
$$
begin{align*}
3^x &= frac {1}{29}\
ln 3^x &= ln frac {1}{29}
end{align*}
$$
Using the $(*)$
$$
begin{align*}
x ln 3 &= ln frac {1}{29}\
x &= frac {ln frac {1}{29}}{ln 3}\
x &= frac {-3.3673}{1.0986}\
x &= – 3.0651
end{align*}
$$
The solution of equation is
$$
x = – 3.0651
$$
$$
begin{align*}
29 &= x^3\
x &= sqrt[3]{29}\
x &= 3.0723
end{align*}
$$
The solution of equation is
$$
x = 3.0723
$$
$$
begin{align*}
-29 &= x^3\
x &= sqrt[3]{-29}\
x &= – 3.0723
end{align*}
$$
The solution of equation is
$$
x = – 3.0723
$$
$$
A=P ( 1+r )^t
$$
where
$$
A=$15, qquad P=$10, qquad r=7%=0.07
$$
Therefore
$$
begin{align*}
15 &= 10 (1+ 0.07)^t\
15 &= 10 cdot 1.007^t\
1.007^t &= 1.5
end{align*}
$$
We can use $ln$ function
$$
ln 1.007^t = ln 1.5
$$
According to $(*)$ we obtain
$$
begin{align*}
t ln 1.007 &= ln 1.5\
t &= frac {ln 1.5}{ln 1.007}\
t &= frac {0.4054}{0.0069}\
t &approx 6
end{align*}
$$
Ticket will cost $$15$ for $6$ years.
b) $x = – 3.0651$
c) $x = 3.0723$
d) $x = – 3.0723$
e) $6$ years
begin{cases}
y=x^2-5\
y=x+1
end{cases}
$$
$x+1-x-1=x^2-5-x-1$
$x^2-x-6=0$
$x^2+2x-3x-6=0$
$x(x+2)-3(x+2)=0$
$(x+2)(x-3)=0$
$x+2=0Rightarrow x_1=-2$
$x-3=0Rightarrow x_2=3$
$x_2=3Rightarrow y_2=3+1=4$
{(-2,-1),(3,4)}
$$
{(-2,-1),(3,4)}
$$
y=x^2+4x+c
$$
$16-4c+4c<0+4c$
$16<4c$
$4<c$
5,6,7,8,9,10,11,12
$$
P(c>4)=dfrac{8}{12}=dfrac{2}{3}approx 66.66%
$$
dfrac{2}{3}approx 66.66%
$$
$y=Acos (Bx+C)+D$
$sin x=cosleft(dfrac{pi}{2}-xright)$
$B$ which gives us the period $T=dfrac{2pi}{B}$
$C$ which gives us the horizontal shift $-dfrac{C}{B}$
$D$=the vertical shift (midline)
A=2
$$
D=-3
$$
$$
Rightarrow -dfrac{C}{2}=dfrac{pi}{6}Rightarrow C=-dfrac{pi}{3}
$$
y=2sin left(2x-dfrac{pi}{3}right)-3
$$
y=2sin left(2x-dfrac{pi}{3}right)-3
$$
y=3cos(2x-pi)+1
$$
Period: $T=dfrac{2pi}{2}=pi$
Vertical shift: $D=1$
Horizontal shift: $-dfrac{C}{B}=-dfrac{-pi}{2}=dfrac{pi}{2}$

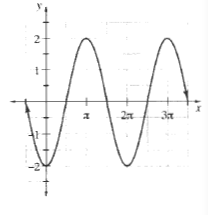
$y=-2sinleft(dfrac{pi}{2}-xright)$
$y=-2sinleft(dfrac{pi}{2}-x+2npiright)$
where $n$ in any integer
$y=-2sinleft(dfrac{pi}{2}-x+2piright)=-2sinleft(dfrac{5pi}{2}-xright)$
$y=-2cos (x+4pi)$
$y=-2sinleft(dfrac{pi}{2}-x-2piright)=-2sinleft(dfrac{9pi}{2}-xright)$
$$y=Acos(B(x-c))+D.$$
$$dfrac{26+12}{2}=dfrac{38}{2}=19.$$
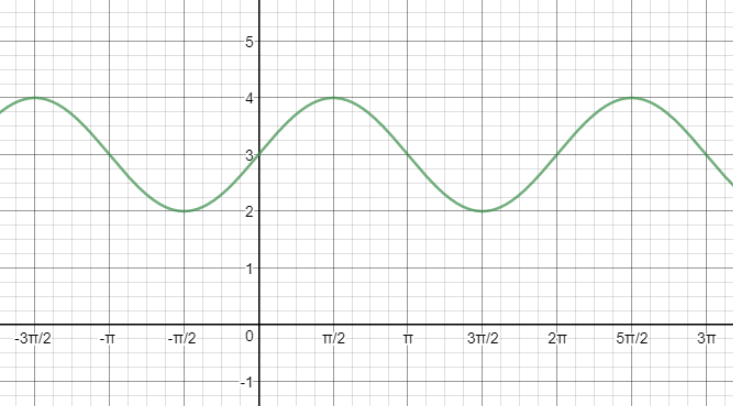
$$y=7cos(B(x-0.5))+19.$$
$$y=7cos(0.85(x-0.5))+19.$$
y=cos(2pi(x-1))-3
$$
Period: $T=dfrac{2pi}{2pi}=1$
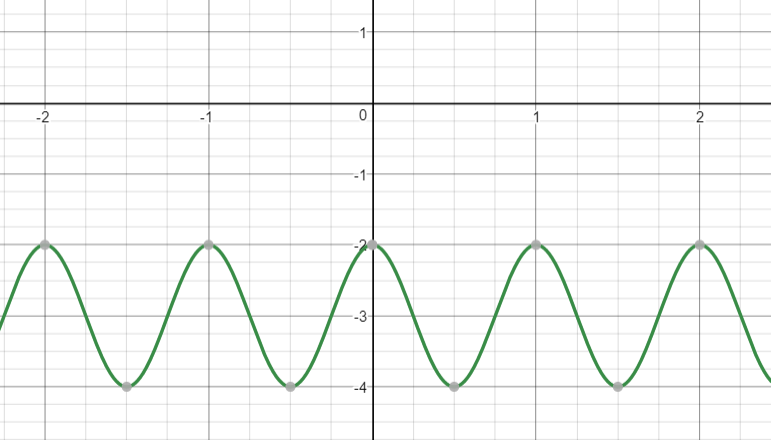
y=3sinleft(dfrac{pi}{2}(x-2)right)+1
$$
Period: $T=dfrac{2pi}{dfrac{pi}{2}}=4$
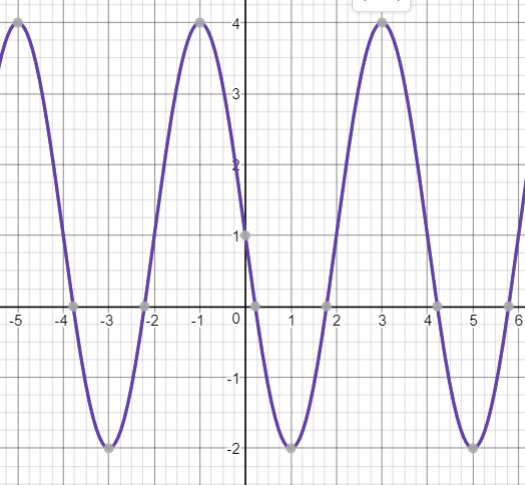
Period: $T=8pi$
y=asin[b(x-h)]+k
$$
$8pi=dfrac{2pi}{b}$
$8pi b=2pi$
$b=dfrac{2pi}{8pi}$
$$
b=dfrac{1}{4}
$$
y=7sin left[dfrac{1}{4}(x-h)right]+k
$$
$k=2$
$$
y=7sin left[dfrac{1}{4}(x-1)right]+2
$$
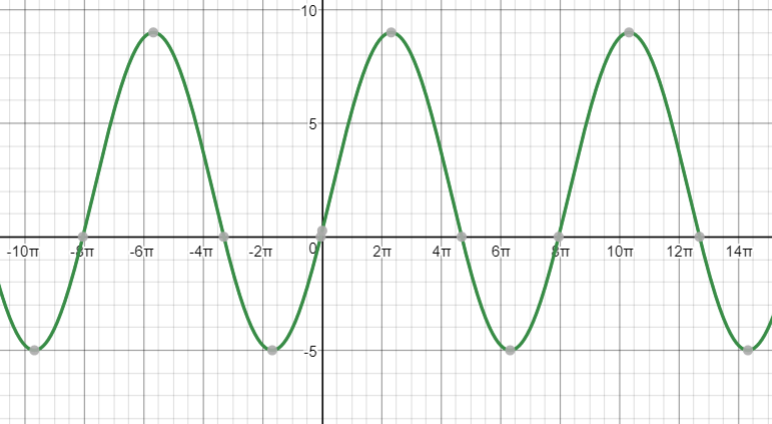
y=7sinleft[frac{1}{2}(x-1)right]+2
$$
theta=dfrac{180text{textdegree}}{pi}cdot pi=180text{textdegree}
$$
theta=3pi
$$
theta=dfrac{180text{textdegree}}{pi}cdot 3pi=540text{textdegree}
$$
theta=30text{textdegree}
$$
theta=dfrac{pi}{4}
$$
theta=dfrac{180text{textdegree}}{pi}cdot dfrac{pi}{4}=45text{textdegree}
$$
theta=225text{textdegree}
$$
theta=dfrac{3pi}{2}
$$
theta=dfrac{180text{textdegree}}{pi}cdot dfrac{3pi}{2}=270text{textdegree}
$$
cosleft(dfrac{3pi}{4}right)
$$
cosleft(dfrac{3pi}{4}right)=-cosleft(pi-dfrac{3pi}{4}right)=-cosleft(dfrac{pi}{4}right)=-dfrac{sqrt 2}{2}
$$
tanleft(dfrac{4pi}{3}right)
$$
tanleft(dfrac{4pi}{3}right)=tanleft(dfrac{4pi}{3}-piright)=tanleft(dfrac{pi}{3}right)=sqrt 3
$$
sinleft(dfrac{11pi}{6}right)
$$
sinleft(dfrac{11pi}{6}right)=-sinleft(2pi-dfrac{11pi}{6}right)=-sin dfrac{pi}{6}=-dfrac{1}{2}
$$
sinleft(dfrac{3pi}{4}right)
$$
sinleft(dfrac{3pi}{4}right)=sinleft(pi-dfrac{3pi}{4}right)=sin dfrac{pi}{4}=dfrac{sqrt 2}{2}
$$
tanleft(dfrac{5pi}{4}right)
$$
tanleft(dfrac{5pi}{4}right)=tanleft(dfrac{5pi}{4}-piright)=tan dfrac{pi}{4}=1
$$
tanleft(dfrac{17pi}{6}right)
$$
$$
=-tanleft(pi-dfrac{5pi}{6}right)=-tanleft(dfrac{pi}{6}right)=-dfrac{sqrt 3}{3}
$$
tan^{-1}(1), thetain[0,2pi)
$$
tan^{-1}(1)=dfrac{pi}{4}
$$
tan^{-1}(-1), thetain[0,2pi)
$$
tan^{-1}(-1)=-dfrac{pi}{4}
$$
$$
color{#c34632}{ log_ca – log_cb = log_c {frac ab}}
$$
Therefore
$$
begin{align*}
log_2{(30x)} – log_2{(6)} &= log_2{left( frac {30x}{6} right)}\
&= log_2 {(5x)}
end{align*}
$$
$$
begin{align*}
color{#c34632}{log_ca + log_cb = log_c {a cdot b}} tag{**}\
color{#c34632}{log_c {a^b} = b log_ca}
end{align*}
$$
Therefore
$$
begin{align*}
2 log_3 {(x)} + log_3 {(5)} &= log_3 {(x^2)} + log_3 {(5)}\
&= log_3 {(x^2 cdot 5)}
end{align*}
$$
$$
begin{align*}
color{#c34632}{log_ca = b} tag{*}\
color{#c34632}{a = c^b}
end{align*}
$$
Then
$$
begin{align*}
log_7 {(3x-2)} &= 2\
3x -2 &= 7^2\
3x-2 &= 49\
3x &= 47\
x &= frac {47}{3}\
x &= 15.66
end{align*}
$$
$$
begin{align*}
log {(2x+1)} &= -1\
log_{10}{(2x+1)} &= -1\
2x+1 &= 10^{-1}\
2x+1 &= 0.1\
2x &= -0.9\
x &= -0.45
end{align*}
$$
$$
begin{align*}
log_5 {(3y)} + log_5 {(9)} &= log_5 {(405)}\
log_5 {(3y cdot 9)} &= log_5 {(405)}\
log_5 {(27y)} &= log_5 {(405)}\
27y &= 405\
y &= frac {405}{27}\
y &= 15
end{align*}
$$
$$
begin{align*}
log {(x)} + log {(x+21)} &= 2\
log_{10}{(x)} + log_{10}{(x+21)} &= 2\
log_{10}{(x cdot (x+21))} &= 2\
log_{10}{(x^2 + 21x)} &= 2
end{align*}
$$
Using the $(*)$
$$
begin{align*}
x^2 + 21x &= 10^2\
x^2 + 21x &= 100\
x^2 + 21x – 100 &= 0
end{align*}
$$
The solution of a square equation $ax^2 + bx + c = 0$ are shape
$$
x = frac {-b pm sqrt {b^2 -4ac}}{2a}
$$
Now we can
$$
begin{align*}
x &= frac {-21 pm sqrt {441 + 400}}{2}\
x &= frac {-21 pm sqrt {841}}{2}\
x &= frac {-21 pm 29}{2}\
x &= -25 qquad x=4
end{align*}
$$
b) $log_3 {(x^2 cdot 5)}$
c) $x = 15.66$
d) $x = -0.45$
e) $y = 15$
f) $x = -25 qquad x=4$
log_2 (30x)-log_2(6)
$$
log_2 (30x)-log_2(6)=log_2left(dfrac{30x}{6}right)=log_2 (5x)
$$
$log_a (x)-log_a (y)=log_a left(dfrac{x}{y}right)$.
$log_a (x^m)=mlog_2 (x)$,
then we use the Product Property of Logarithms:
$log_a x+log_a y=log_a (xy)$.
log_7 (3x-2)=2
$$
$3x-2=49$
$3x=49+2$
$3x=51$
$x=dfrac{51}{3}$
$$
x=17
$$
log (2x+1)=-1
$$
$2x+1=0.1$
$2x=0.1-1$
$2x=-0.9$
$x=dfrac{-0.9}{2}$
$$
x=-0.45
$$
log_5 (3y)+log_5 (9)=log_5 (405)
$$
$log_5 (27y)=log_5 (405)$
$27y=405$
$y=dfrac{405}{27}$
$$
y=15
$$
$log_a x+log_a y=log_a (xy)$.
log (x)+log (x+21)=2
$$
$x^2+21x=10^2$
$x^2+21x=100$
$x^2-4x+25x-100=0$
$x(x-4)+25(x-4)=0$
$(x-4)(x+25)=0$
$x-4=0Rightarrow x_1=4$
$x+25=0Rightarrow x_2=-25$
$log_a x+log_a y=log_a (xy)$.
x=4
$$
P(x)=x^2+kx+18
$$
$Deltageq 0$
$k^2-72geq 0$
$k^2geq 72$
$|k|geq sqrt{72}$
$|k|geq 6sqrt 2$
$$
kin (-infty,-6sqrt 2]cup[6sqrt 2,infty)
$$
kin (-infty,-6sqrt 2]cup[6sqrt 2,infty)
$$
-23,-19,-15,…
$$
$$
d=-19-(-23)=4
$$
$a_1+(n-1)d>10,000$
$-23+(n-1)cdot 4>10,000$
$-23+4n-4>10,000$
$4n-27>10,000$
$4n>10,000+27$
$4n>10,027$
$n>dfrac{10,027}{4}$
$$
n>2506
$$
a_{2507}=-23+(2507-1)cdot 4=10,001
$$
$$
color{#c34632}{ a_n = a_1 + (n-1) d}
$$
where
$$
a_1 = -23
$$
and
$$
begin{align*}
a_2 &= a_1 + (2-1) d\
-19 &= -23 + (2-1) d\
-19 &= -23 + d\
d &= 4
end{align*}
$$
$$
begin{align*}
a_n &> 10000\
a_1 + ( n-1 ) d &> 10000\
-23 + ( n-1 ) 4 &>10000\
4 (n-1) &> 10000 +23\
4 (n-1) &> 10023\
n-1 &> 2505.75\
n &> 2506.75
end{align*}
$$
Check
$$
begin{align*}
a_{2507} &= a_1 + (2507-1)d\
a_{2507} &= -23 + 2506 cdot 4\
a_{2507} &= -23 + 10024\
a_{2507} &= 10001
end{align*}
$$
The first number that is higher than 10000 is 2507.
b) $2507$
$x$=the number of miles traveled with the car
$y$=the number of days the car is rented
C_1(x)=25y+0.50x
$$
C_2(x)=0.03(2^{x-1})
$$
$C_1(10)=2cdot 25+0.50cdot 10=55$
$x=20$
$C_1(10)=2cdot 25+0.50cdot 20=60$
$x=100$
$C_1(10)=2cdot 25+0.50cdot 100=100$
$C_2(10)=0.03(2^9)=15.36$
$x=20$
$C_2(20)=0.03(2^{19})=15,728.64$
$x=100$
$C_2(100)=0.03(2^{199})=2.41cdot 10^{58}$

