All Solutions
Page 373: Questions
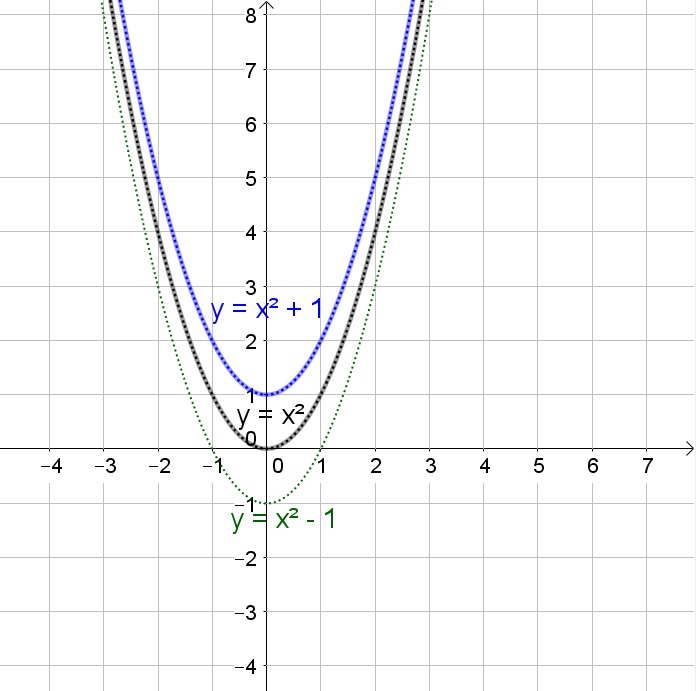
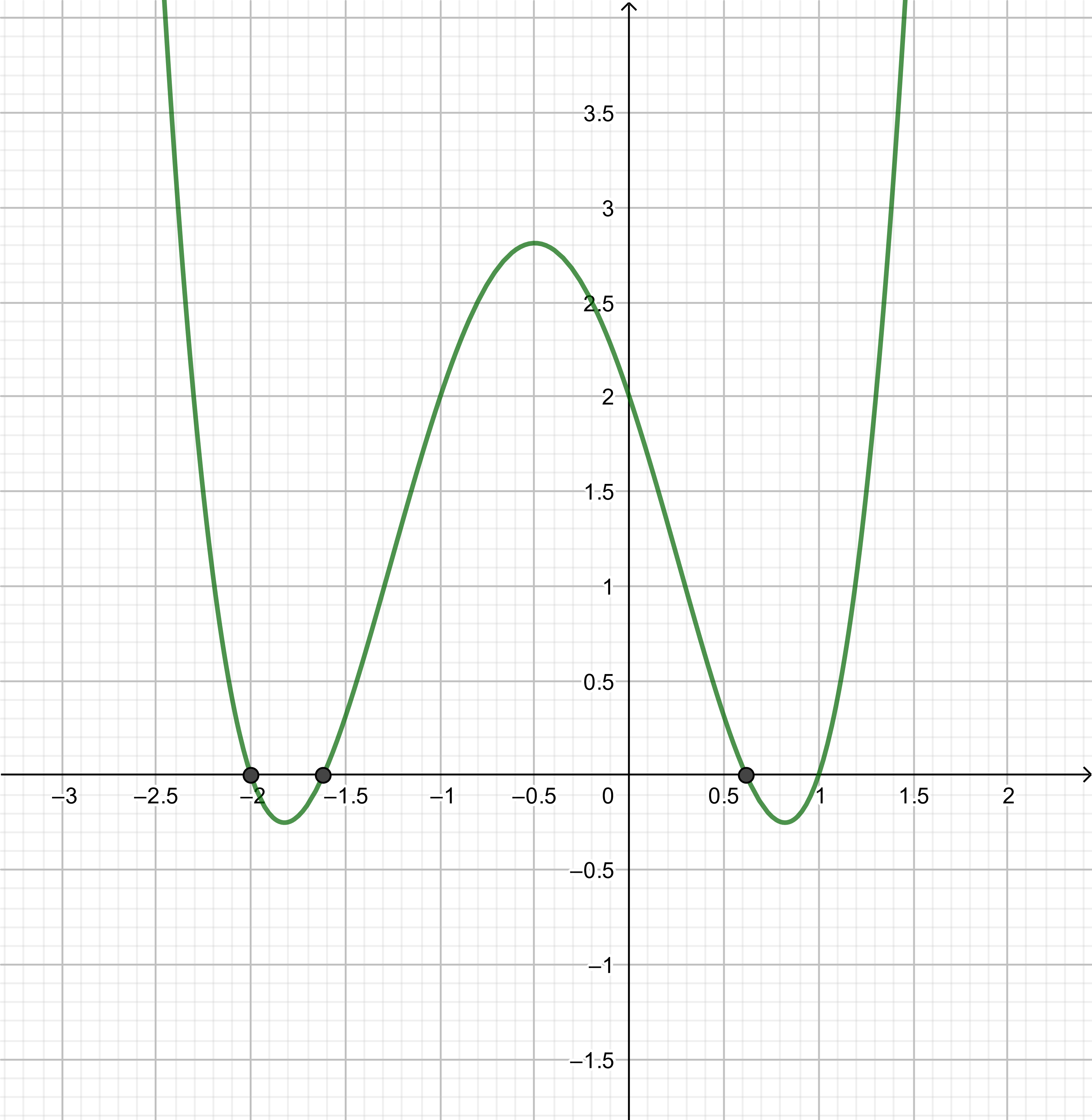
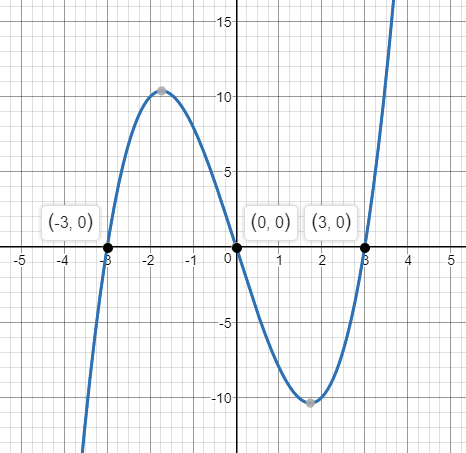
The given graph has a root at $x=0$ and $x=3$ and a double root at $x=2$, thus the equation of this function is then $y=x(x-2)^2(x-3)$ (as we note on this graph, this function matches the given graph).
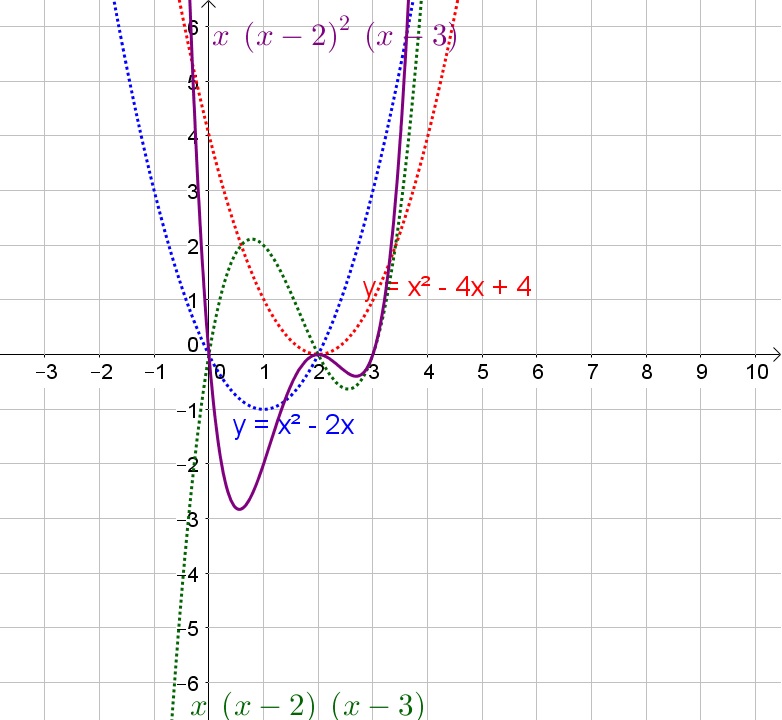
y=x(x-2)^2(x-3)
$$
If a factor of the function is of the form $(x-a)^2$ then $x=a$ is a double root (function will touch the $x$-axis in this point but not go to the other side of the axis) and if it is of the form $(x-a)^3$ then it is a triple root (function becomes almost zero at an interval close to the point $x=a$).
We note that if the function is negative before a single root, then it will become positive after the single root.
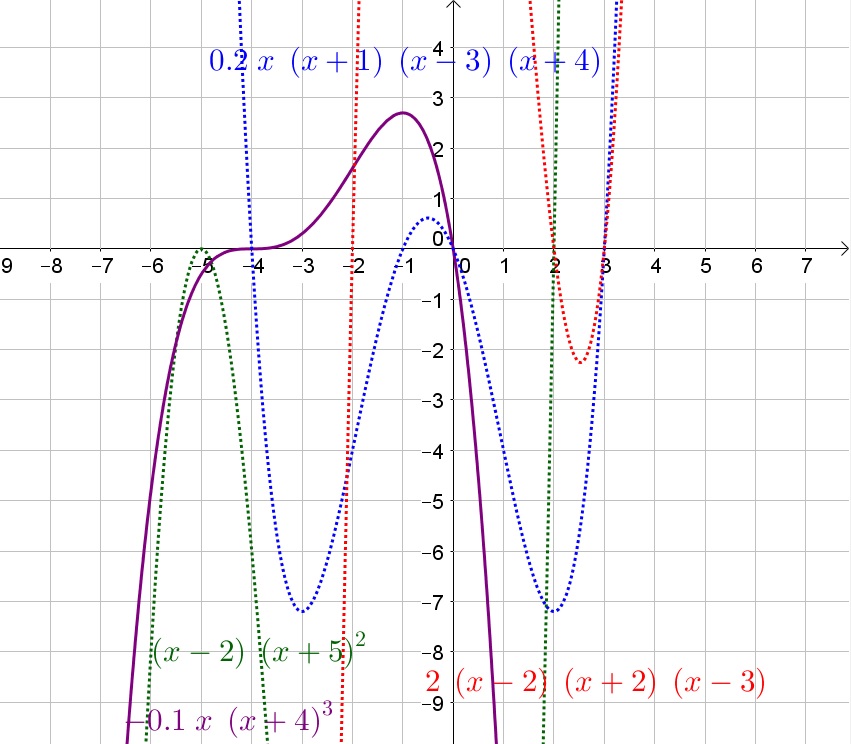
Before the first $x$-intercept the function is negative and increasing, between the $x$-intercepts the function is negative (partly increasing and partly decreasing) and after the last $x$-intercepts the function is positive and increasing.
b. $x=2$ and $x=-5$
The graph of the function will have 3 $x$-intercepts because the function contains three factors of the form $(x-a)$.
We note that this graph differs at the $x$-intercepts, because before and after each $x$-intercept the function changes from negative to positive or from positive to negative.
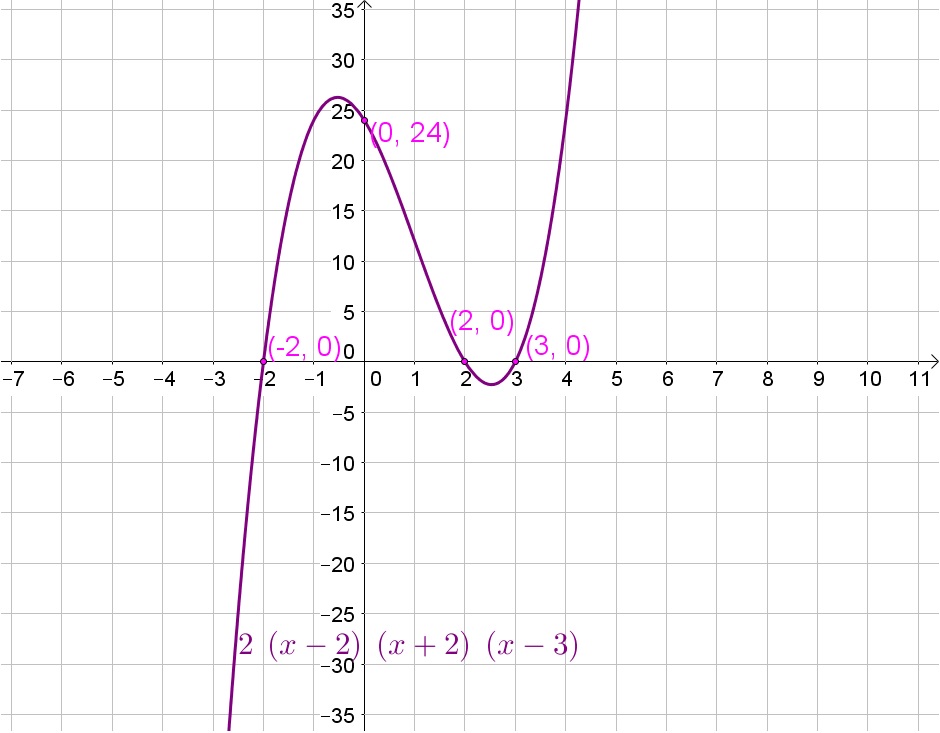
The shape of the graph is affected by the factor 2 because it stretches the function $P(x)=(x-2)(x+2)(x-3)$ vertically be a factor 2.
The $y$-intercepts are also influenced because the $y$-intercept of $P(x)=(x-2)(x+2)(x-3)$ is $y=12$ and of this function is $y=24$.
If the factor 2 is changed to $-2$ than the graph of the function will be reflected about the $x$-axis.
b. No, yes, yes, reflection about the $x$-axis
From the equation of the function we know that $x=0$ will be an $x$-intercept, because every term contains a factor $x$ and thus this factor could be factored out as $P_3=x(x^3-21x+20)$.
On the graph of the function we then note that $x=-5$, $x=0$, $x=1$ and $x=4$ are the $x$-intercepts.

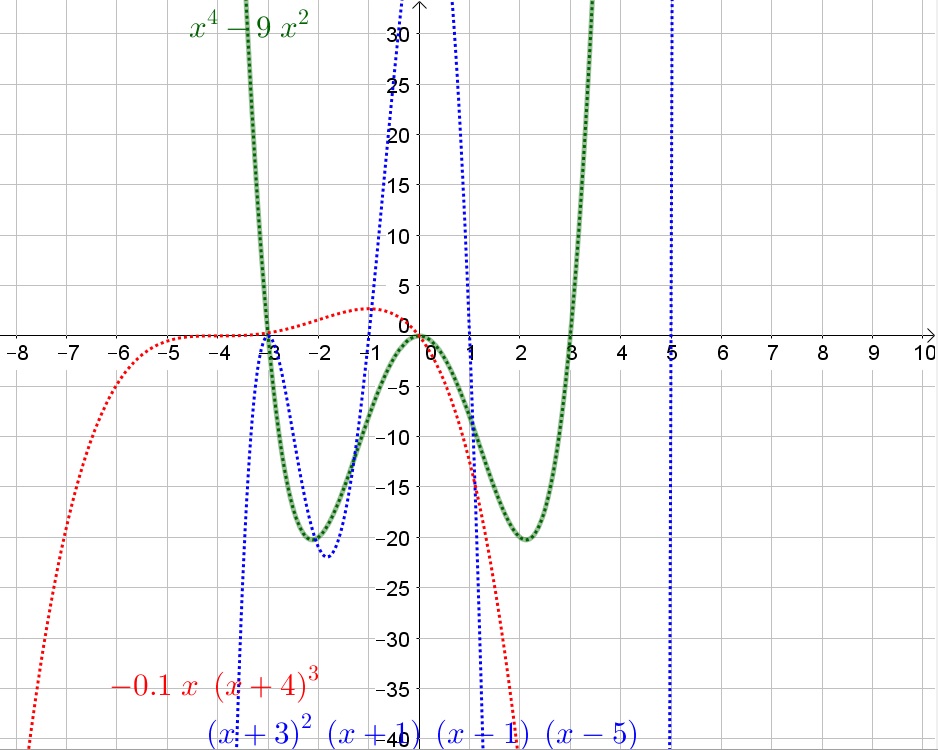
We note that $P_5(x)$ has roots at $x=0$ and $x=-4$ (triple).
We note that $P_6(x)$ has roots at $x=0$ (double), $x=-3$, $x=3$.
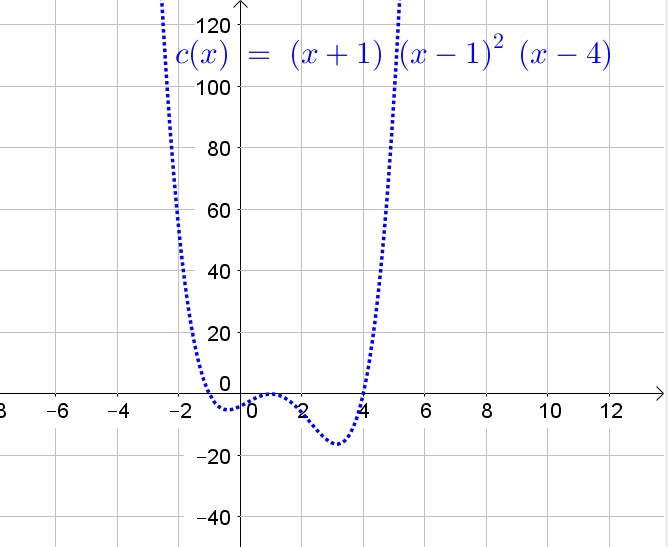
We note that $P_8(x)$ has roots at $x=-1$ (double), $x=2$ and $x=4$.
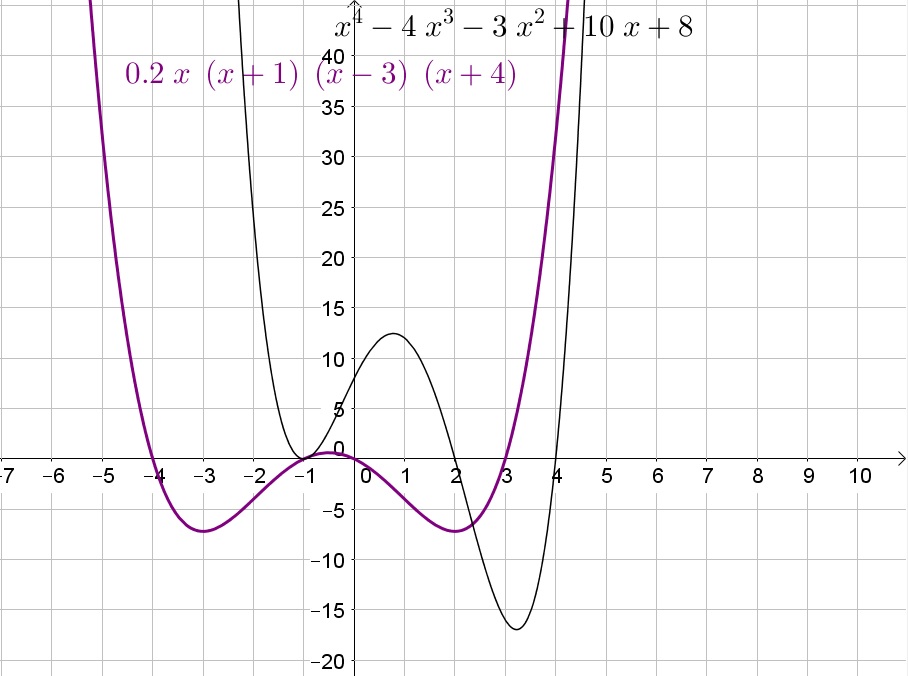
Determine if the function is positive or negative before, between and after all $x$-intercepts.
The function will change sign (positive/negative) after a single root and a triple root, however it will not change sign after a double root.
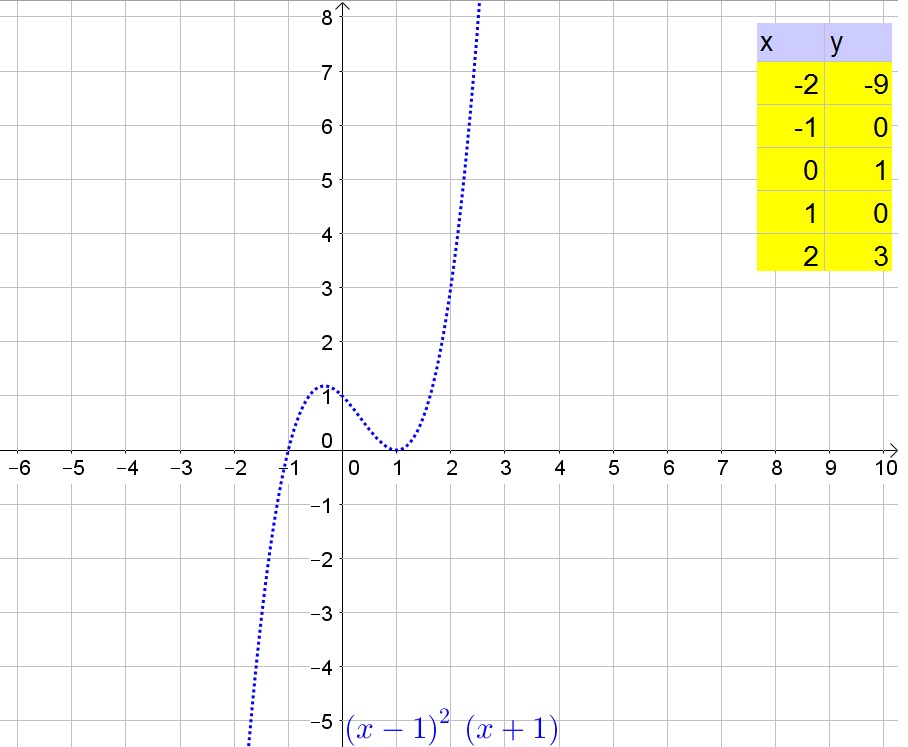
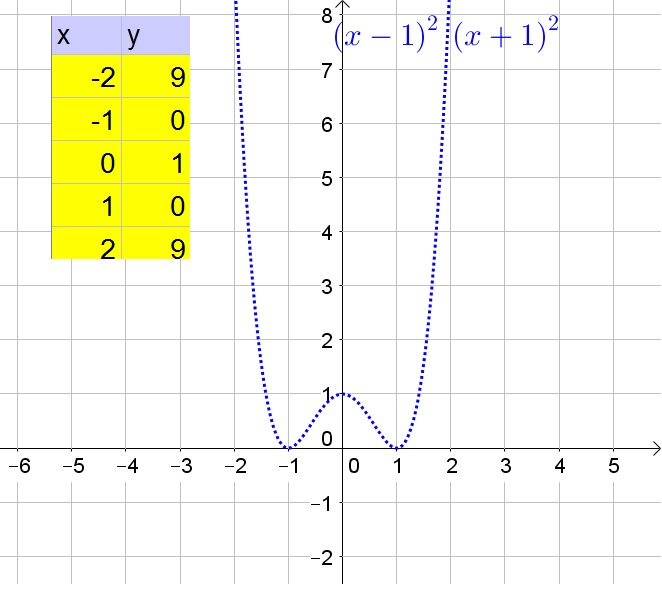

The second function has four $x$-intercepts and is thus of degree 4, which has as parent function $y=x^4$.
text{The polynomial which has degree $n$ and coefficients $a_n, a_{n-1} ,…, a_1, a_0$ is the following,}
$$
$$
Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0
$$
#### a.
$text{The function is a polynomial because it is of shape $Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0$.}$
$$
text{The given polynomial has degree $5$ and coefficients $a_5=8, a_4=6.5, a_2=1$ and $a_0=6$.}
$$
#### b.
$text{The function is a polynomial because it is of shape $Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0$.}$
$$
text{The given polynomial has degree $6$ and coefficients $a_6=dfrac{3}{5}$ and $a_2=19$.}
$$
#### c.
$$
text{The function in graph textbf{c.} is not a polynomial because it has a horizontal asymptote $rightarrow y=8$.}
$$
#### d.
$$
text{The function in graph textbf{d.} is not a polynomial because its left end doesn’t go to $-infty$ or $infty$.}
$$
#### e.
$$
text{The function in graph textbf{e.} is a polynomial.}
$$
#### f.
The function is not a polynomial because it contains the variable in the denominator of a fraction.
#### g.
For example:
$$
pleft(xright)=6x^4+3x^3-2x^2+7x-1
$$
$text{The function is a polynomial because it is of shape $Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0$.}$
$text{The given polynomial has degree $4$ and coefficients $a_4=6, a_3=3, a_2=-2, a_1=7$ and $a_0=-1$.}$
For example:
$$
pleft(xright)=5x^2+frac{1}{x+6}
$$
The function is not a polynomial because it contains the variable in the denominator of a fraction.
text{The polynomial functions are: textbf{a., b., e.}}
$$
begin{tabular}{ p{4cm}| |p{2cm} |p{2.5cm}| p{2cm}| p{2cm}}
& 1st & 2nd & 3rd & 4th \
hline
What does $g$ to $x$ & adds $1$ & $left(quad right)^2$ & divides by $3$ & subtracts $2$\
hline
What does $g^{-1}$ to $x$ & adds $2$ & multiplies by $3$ & $sqrt{ } $ & subtracts $1$\
end{tabular}
$$
fleft(xright)=2sqrt{x-1}+3
$$
$$
f^{-1}left(xright)=left(frac{x-3}{2}right)^2+1
$$
$$
gleft(xright)=frac{1}{3}left(x+1right)^2-2
$$
$$
g^{-1}left(xright)=sqrt{3left(x+2right)}-1
$$
f^{-1}left(xright)=left(frac{x-3}{2}right)^2+1
$$
$$
g^{-1}left(xright)=sqrt{3left(x+2right)}-1
$$

$$
f^{-1}(x)=left(dfrac{x-3}{2}right)^2+1
$$
$$
g^{-1}(x)=sqrt{3left(x+3right)}-1
$$
b. $f^{-1}(x)=left(dfrac{x-3}{2}right)^2+1$ and $g^{-1}(x)=sqrt{3left(x+3right)}-1$
$text{In order to find the $x$-intercept we should set $fleft(xright)$ to zero and thus find the $x$ coordinate.}$
$$
begin{align*}
0&=left(x+3right)^2-5 && text{Substitute} fleft(xright)
=0. \
left(x+3right)^2&=5 && text{Add} 5 text{to both sides.} \
x+3&=pmsqrt{5} && text{Square root of both sides.} \
x&=pmsqrt{5}-3 && text{Subtract} 3 text{from both sides.} \
end{align*}
$$
$$
text{The $x$-intercepts of the graph of $f$ are $left(-sqrt{5}-3, 0right)$ and $left(sqrt{5}-3, 0right)$.}
$$
#### b.
$text{In order to find the $x$-intercept we should set $fleft(xright)$ to zero and thus find the $x$ coordinate.}$
$$
begin{align*}
0&=left(x-74right)^2left(x+29right) && text{Substitute} fleft(xright)=0. \
x-74&=0 text{or} x+29=0 && acdot b=0Rightarrow a=0 text{or} b=0. \
x&=74 text{or} x=-29 && text{Solve for} x. \
end{align*}
$$
$$
text{The $x$-intercepts of the graph of $f$ are $left(74, 0right)$ and $left(-29, 0right)$.}
$$
$textbf{b.}$ $text{The $x$-intercepts of the graph of $f$ are $left(74, 0right)$ and $left(-29, 0right)$.}$
$$
begin{align*}
log left(1right)&=0 && text{Basic properties of logarithms:} log_a1=0.
end{align*}
$$
#### b.
$$
begin{align*}
log left(10^3right)&=3log left(10right) && text{Power rule:} log_ax^p=plog_ax. \
&=3 cdot 1 && text{Basic properties of logarithms:} log_aa=1. \
&=3
end{align*}
$$
#### c.
$$
begin{align*}
10^{log left(4right)}&=4 && text{Basic properties of logarithms:} a^{log_ax}=x. \
end{align*}
$$
#### d.
$$
begin{align*}
10^{3log left(4right)}&=10^{log left(4^3right)} && text{Power rule:} log_ax^p=plog_ax. \
&=10^{log left(64right)} && text{Simplify.} \
&=64 && text{Basic properties of logarithms:} a^{log_ax}=x. \
end{align*}
$$
$$
(3+7)+(4i-2i)
$$
Simplify:
$$
10+2i
$$
b. Use $(a+b)^2=a^2+2ab+b^2$:
$$
(3+5i)^2=9+30i+25i^2=9+30i-25=-16+30i
$$
c. Use $(a+b)(a-b)=a^2-b^2$:
$$
(7+i)(7-i)=49-i^2=49+1=50
$$
d.
$$
(3i)(2i)^2=(3i)(4i^2)=(3i)(-4)=-12i
$$
e.
$$
i^3=i^2cdot i=-1cdot i=-i
$$
f.
$$
i^{32}=(i^4)^8=1^8=1
$$
b. $-16+30i$
c. $50$
d. $-12i$
e. $-i$
f. $1$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
&left(3+7right)+left(4-2right)i&&boxed{text{Group }}\
&10+(4-2)i&&boxed{text{Calculate within parentheses}}\
&10+2i&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}10+2i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }text{Group:the:real:part:and:the:imaginary:part:of:the:complex:number }}
$$
$$
boxed{ color{#c34632} text{ } left(a+biright)pm left(c+diright)=left(a:pm :cright)+left(b:pm :dright)i}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
&3^2+2cdot :3cdot :5i+left(5iright)^2&&boxed{text{Perfect square formula }}\
&9+2cdot :3cdot :5i+left(5iright)^2&&boxed{text{Evaluate }3^2=9}\
&9+30i+left(5iright)^2&&boxed{text{Multiply the numbers: }2cdot3cdot5i=30i}\
&9+30i+5^2i^2&&boxed{text{Raise to the second power}}\
&9+30i+25i^2&&boxed{text{Evaluate: }5^2=25}\
&9+30i+25(-1)&&boxed{text{Apply imaginary number rule }i^2=-1}\
&9+30i-25&&boxed{text{Multiply the numbers: } 25(-1)=-25}\
&-16+30i&&boxed{text{Subtract the numbers: } 9+25=-16}\
&boxed{{color{#c34632}-16+30i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:Perfect:Square:Formula}:quad left(a+bright)^2=a^2+2ab+b^2}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad left(acdot :bright)^n=a^nb^n}
$$
{color{#4257b2}text{c)}}
$$
Solution to this example is given below
$$
begin{align*}
&7^2+1^2&&boxed{text{Apply complex arithmetic rule}}\
&49+1^2&&boxed{text{Evaluate }7^2=49}\
&49+1&&boxed{text{Evaluate }1^2=1}\
&50&&boxed{text{Add the numbers: } 49+1=50}\\
&boxed{{color{#c34632}50} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:complex:arithmetic:rule}:quad left(a+biright)left(a-biright)=a^2+b^2}
$$
{color{#4257b2}text{d)}}
$$
Solution to this example is given below
$$
begin{align*}
&3ileft(2iright)^2&&boxed{text{Remove parentheses }}\
&3i2^2i^2&&boxed{text{Raise to the second power}}\
&2^23ii^2&&boxed{text{Simplify}}\
&2^23i^{1+2}&&boxed{text{Add exponents when multiplying powers}}\
&2^23i^3&&boxed{text{Simplify exponents}}\
&4cdot3i^3&&boxed{text{Evaluate: } 2^2=4}\
&4cdot3(-i)&&boxed{text{Apply imaginary number rule: } i^3=-i}\
&4cdot(-3i)&&boxed{text{Simplify}}\
&-12i&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}-12i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad left(acdot :bright)^n=a^nb^n}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad :a^bcdot :a^c=a^{b+c}}
$$
{color{#4257b2}text{e)}}
$$
Solution to this example is given below
$$
begin{align*}
&i^2i&&boxed{text{Apply exponent rule }}\
&-1i&&boxed{text{Apply imaginary number rule: }i^2=-1}\
&-i&&boxed{text{Multiply: }-1cdot i=-i}\\
&boxed{{color{#c34632}-i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad :a^{b+c}=a^ba^c}
$$
{color{#4257b2}text{f)}}
$$
Solution to this example is given below
$$
begin{align*}
&left(i^2right)^{16}&&boxed{text{Apply exponent rule }}\
&left(-1right)^{16}&&boxed{text{Apply imaginary number rule: }i^2=-1}\
&1^{16}&&boxed{text{Remove parenthseses: }(-1)^{16}=1^{16}}\
&1&&boxed{text{Evaluate: } 1^{16}=1}\\
&boxed{{color{#c34632}1} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:exponent:rule}:quad :a^{b+c}=a^ba^c}
$$
color{#4257b2} text{ a) }10+2i
$$
$$
color{#4257b2} text{ b) } -16+30i
$$
$$
color{#4257b2} text{ c) }50
$$
$$
color{#4257b2} text{ d) }-12i
$$
$$
color{#4257b2} text{ e) }-1
$$
$$
color{#4257b2} text{ f) }1
$$
$overline {AC}$ is a transversal of both parallel lines.
So,
$mangle {BAC}=mangle {ACP}$ (A pair of alternate interior angles)
$4x-3y=65$ (1)
$mangle {AMB}=mangle {CMP}$ (A pair of vertical angles)
$3x-y=2x+3y$
$3x-2x=3y+y$
$x=4y$ (2)
Substituting for $x$ in equation (1)
$4(4y)-3y=65$
$13y=65$
$$
y=5
$$
$4x-3(5)=65$ (Substituting 5 for $y$ in equation (1))
$4x-15=65$
$4x=80$
$$
x=20
$$
$mangle CMP=2(20)+3(5)=40+15=55$ $text{textdegree}$
$mangle PCM=4(20)-3(5)=80+15=65$ $text{textdegree}$
$mangle {CPM}=180-(65+55)=180-120=60$ $text{textdegree}$
$$
0=(x-4)(x-2)
$$
Zero product property:
$$
x-4=0 text{ or } x-2=0
$$
Solve each equation to $x$:
$$
x=4 text{ or } x=2
$$
b. Let $y=0$ and factorize:
$$
0=(x-3)^2
$$
Zero product property:
$$
x-3=0
$$
Solve each equation to $x$:
$$
x=3
$$
c. Let $y=0$ and factorize:
$$
0=x(x-2)(x+2)
$$
Zero product property:
$$
x=0text{ or }x-2=0 text{ or } x+2=0
$$
Solve each equation to $x$:
$$
x=0text{ or }x=2 text{ or } x=-2
$$
b. $x=3$
c. $x=0$ and $x=2$ and $x=-2$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
0&=x^2-6x+8&&boxed{text{Substitute 0 for }y}\
x^2-6x+8&=0&&boxed{text{Switch sides}}\
end{align*}
$$
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-6right)pm sqrt{left(-6right)^2-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -6 text{ for } b, text{ and } 8 text{ for } c.} \
end{align*}
$$
First we solve $x_1$
$$
begin{align*}
x_1&=frac{-left(-6right)+sqrt{left(-6right)^2-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Simplify}}\
x_1&=frac{6-sqrt{left(-6right)^2-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_1&=frac{6+sqrt{36-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Evaluate: }(-6)^2=36}\
x_1&=frac{6+sqrt{36-32}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot8=32}\
x_1&=frac{6+sqrt{36-32}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_1&=frac{6+sqrt{4}}{2}&&boxed{text{Subtract the numbers: }36-32=4}\
x_1&=frac{6+2}{2}&&boxed{text{Simplify}}\
x_1&=frac{8}{2}&&boxed{text{Add the numbers: } 6+2=8}\
x_1&=color{#c34632}{4}&&boxed{text{Simplify}}\
end{align*}
$$
Second we solve $x_2$
begin{align*}
x_2&=frac{-left(-6right)-sqrt{left(-6right)^2-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Simplify}}\
x_2&=frac{6-sqrt{left(-6right)^2-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_2&=frac{6-sqrt{36-4cdot :1cdot :8}}{2cdot :1}&&boxed{text{Evaluate: }(-6)^2=36}\
x_2&=frac{6-sqrt{36-32}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot8=32}\
x_2&=frac{6-sqrt{36-32}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_2&=frac{6-sqrt{4}}{2}&&boxed{text{Subtract the numbers: }36-32=4}\
x_2&=frac{6-2}{2}&&boxed{text{Simplify}}\
x_2&=frac{4}{2}&&boxed{text{Subtract the numbers: } 6-2=4}\
x_2&=color{red}{2}&&boxed{text{Simplify}}\\
&boxed{{color{Maroon}x_1=4, x_2=2} }&&boxed{text{Final solution}}\
end{align*}
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
0&=x^2-6x+9&&boxed{text{Substitute 0 for }f(x)}\
x^2-6x+9&=0&&boxed{text{Switch sides}}\
end{align*}
$$
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-6right)pm sqrt{left(-6right)^2-4cdot :1cdot :9}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -6 text{ for } b, text{ and } 9 text{ for } c.} \
x_{1,:2}&=frac{6pm sqrt{left(-6right)^2-4cdot :1cdot :9}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_{1,:2}&=frac{6pm sqrt{36-4cdot :1cdot :9}}{2cdot :1}&&boxed{text{Evaluate: }(-6)^2=36}\
x_{1,:2}&=frac{6pm sqrt{36-36}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot9=36}\
x_{1,:2}&=frac{6pm sqrt{36-36}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_{1,:2}&=frac{6pm sqrt{0}}{2}&&boxed{text{Subtract the numbers: }36-36=0}\
x&=frac{6}{2}&&boxed{text{Simplify}}\
x&=color{#c34632}{3}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=3} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{c)}}
$$
Solution to this example is given below
$$
begin{align*}
0&=x^3-4x&&boxed{text{Substitute 0 for }y}\
x^3-4x&=0&&boxed{text{Switch sides}}\
end{align*}
$$
Solve by factoring
$$
begin{align*}
x^2x-4x&=0&&boxed{text{Apply exponent rule}}\
xleft(x^2-4right)&=0&&boxed{text{Factor out common term }x}\
x(x^2-2^2)&=0&&boxed{text{Rewrite 4 as }2^2}\
xleft(x+2right)left(x-2right)&=0&&boxed{text{Squares formula}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
x&=color{#c34632}{0} &&boxed{text{Simplify}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
x+2&=0 &&boxed{text{Simplify}}\
x+2-2&=0-2&&boxed{text{Subtract 2 from both sides}}\
x&=color{#c34632}{-2}&&boxed{text{Simplify}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
x-2&=0 &&boxed{text{Simplify}}\
x-2+2&=0+2&&boxed{text{Add 2 from both sides}}\
x&=color{#c34632}{2}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=0, x=-2, x=2} }
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Apply:exponent:rule}:quad :a^{b+c}=a^ba^c}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:Difference:of:Two:Squares:Formula::}x^2-y^2=left(x+yright)left(x-yright) }
$$
color{#4257b2} text{ a) }x_1=4, x_2=2
$$
$$
color{#4257b2} text{ b) } x=3
$$
$$
color{#4257b2} text{ c) }x=0, x=-2, x=2
$$
$$
begin{align*}
y&=2x-3 && text{Substitute} y text{for} fleft(xright). \
y+3&=2x && text{Add} 3 text{to both sides.} \
frac{y+3}{2}&=x && text{Divide both sides by} 2. \
frac{y+3}{2}&=f^{-1}left(yright) && text{Substitute} f^{-1}left(yright) text{for} x. \
end{align*}
$$
#### b.
$$
begin{align*}
y&=left(x-3right)^2+2 && text{Substitute} y text{for} hleft(xright). \
y-2&=left(x-3right)^2 && text{Subtract} 2 text{from both sides.} \
sqrt{y-2}&=x-3 && text{Square root of both sides.} xgeq 0 \
sqrt{y-2}+3&=x && text{Add} 3 text{ro both sides.} \
sqrt{y-2}+3&=h^{-1}left(yright) && text{Substitute} h^{-1}left(yright) text{for} x. \
end{align*}
$$
$$
begin{align*}
log left(6right)&=log left(2 cdot 3right) \
&=log left(2right)+log left(3right) && text{Product Rule:} log_a left(mnright)=log_a left(mright)+log_a left(nright). \
&=0.3010+0.4771 && text{Substitute the given data.} \
&=0.7781
end{align*}
$$
#### b.
$$
begin{align*}
log left(15right)&=log left(3 cdot 5right) \
&=log left(3right)+log left(5right) && text{Product Rule:} log_a left(mnright)=log_a left(mright)+log_a left(nright). \
&=0.4771+0.6990 && text{Substitute the given data.} \
&=1.1761
end{align*}
$$
#### c.
$$
begin{align*}
log left(9right)&=log left(3 cdot 3right) \
&=log left(3right)+log left(3right) && text{Product Rule:} log_a left(mnright)=log_a left(mright)+log_a left(nright). \
&=0.4771+0.4771 && text{Substitute the given data.} \
&=0.9542
end{align*}
$$
#### d.
$$
begin{align*}
log left(50right)&=log left(2 cdot 5 cdot 5right) \
&=log left(2right)+log left(5right)+log left(5right) && text{Product Rule:} log_a left(mnright)=log_a left(mright)+log_a left(nright). \
&=0.3010+0.6990+0.6990 && text{Substitute the given data.} \
&=1.699
end{align*}
$$
$textbf{b.}rightarrow 5.$
$textbf{c.}rightarrow 3.$
$textbf{d.}rightarrow 1.$
$textbf{e.}rightarrow 2.$

$bullet,,$a) Since we have the slope of the line and a point on it we can find one more point on this line by using the definition of the slope:
$color{#c34632} text{$m=dfrac{text{change in $,y,$}}{text{change in $,x,$}}$}$
$Rightarrow dfrac{text{change in $,y,$}}{text{change in $,x,$}}=dfrac{3}{1}$
$bullet,,$Given the point $color{#c34632} text{$,,(0,2),,$}$ we can find one more point the:
$,,(0+1 ,,, 2+3)=color{#4257b2}text{$(1,5)$}$
$bullet,,$For the graph of the indicated line plot the points $color{#c34632} text{$,,(0,2),,$}$ , $color{#c34632} text{$,,(1,5),,$}$ and connect them as shown in the picture below:
$y-y_{0}=m(x-x_{0})qquadqquadqquadqquadqquad$ $color{#c34632} text{[set $m=3$ , $(x_{0} , y_{0})=(0,2)$]}$
$Rightarrow y-2=3(x-0)$
$Rightarrow color{#4257b2} text{$y=3x+2$}$
The equation of the indicated line is: $color{#4257b2} text{$,,,y=3x+2$}$
$bullet,,$c) For the first term of this sequence set $color{#c34632} text{$,,n=1,,$}$ and estimate $color{#c34632} text{$,,t(1)$}$:
$t(n)=3n-1qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $n=1$]}$
$Rightarrow t(1)=3(1)-1$
$Rightarrow color{#4257b2} text{$t(1)=2$}$
For the 2nd, 3rd, 4th terms:
$$
t(2)=3(2)-1Rightarrow color{#4257b2}text{$t(2)=5$}
$$
$$
t(3)=3(3)-1Rightarrow color{#4257b2} text{$t(3)=8$}
$$
$t(4)=3(4)-1Rightarrow color{#4257b2} text{$t(4)=11$}$
Plot the points on the form $color{#c34632}text{$,,big(n , t(n)big),,$}$ for the graph of this sequence as shown in the picture below:
The main difference is that while the graph of the line in part a) is a continuous line, the graph of the sequence in part c) consists of discrete points.
obtained by dividing the number of people who consume chicken soup with total
number of respondents.
$$
frac{580}{1024}approx 0.566=56.6%
$$
Adding and subtracting the margin of error, we can be reasonably sure the population
$$
text{proportion is between $53.6%$ and $59.6%$, which is greater than $50%$.}
$$
text{Yes, because more than $50\%$ of people believe that chicken soup helps relieve cold and flu symptoms.}
$$
$$
begin{align*}
log_6 left(5xright)&=3 && text{Product Rule:} log_a left(mnright)=log_a left(mright)+log_a left(nright). \
5x&=6^3 && log_ax=bLeftrightarrow x=a^b. \
5x&=216 && text{Simplify.} \
x&=frac{216}{5} && text{Divide bith sides by} 5.
end{align*}
$$
#### b.
$$
begin{align*}
1-log_7 left(xright)&=5 && text{Basic properties of logarithms:} log_aa=1. \
-log_7 left(xright)&=4 && text{Subtract} 1 text{from both sides.} \
log_7 left(xright)&=-4 && text{Multiply both sides by} -1. \
x&=7^{-4} && log_ax=bLeftrightarrow x=a^b. \
x&=frac{1}{7^4} && text{Use} a^{-n}=frac{1}{a^n}. \
x&=frac{1}{2401}
end{align*}
$$
#### c.
$$
begin{align*}
8-x&=6 && text{Equality rule:} log_ax=log_ayrightarrow x=y. \
-x&=-2 && text{Subtract} 8 text{from both sides.} \
x&=2 && text{Multiply both sides by} -1. \
end{align*}
$$
#### d.
$$
begin{align*}
log_5left(frac{x}{10}right)&=log_5left(2right) && text{Quotient Rule:} log_a left(frac{m}{n}right)=log_a left(mright)-log_a left(nright). \
frac{x}{10}&=2 && text{Equality rule:} log_ax=log_ayrightarrow x=y. \
x&=20 && text{Multiply both sides by} 10. \
end{align*}
$$
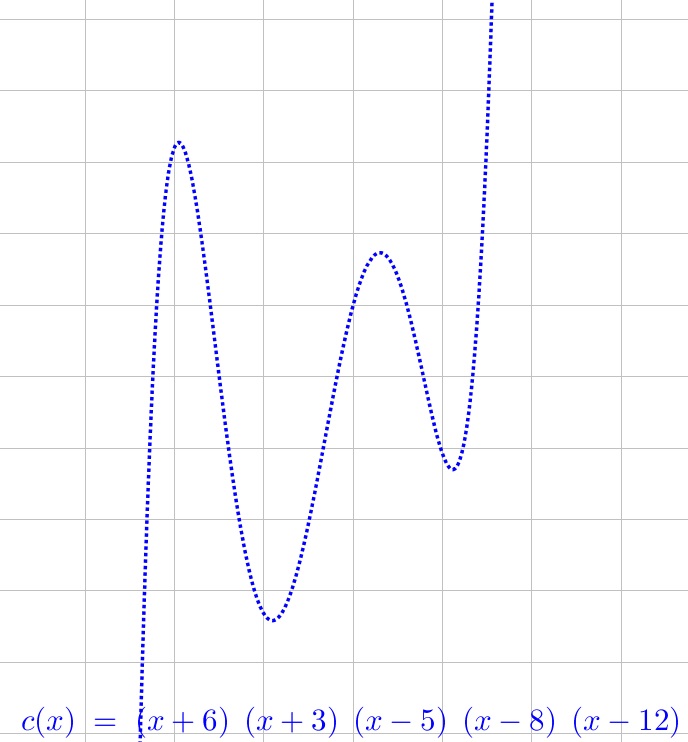
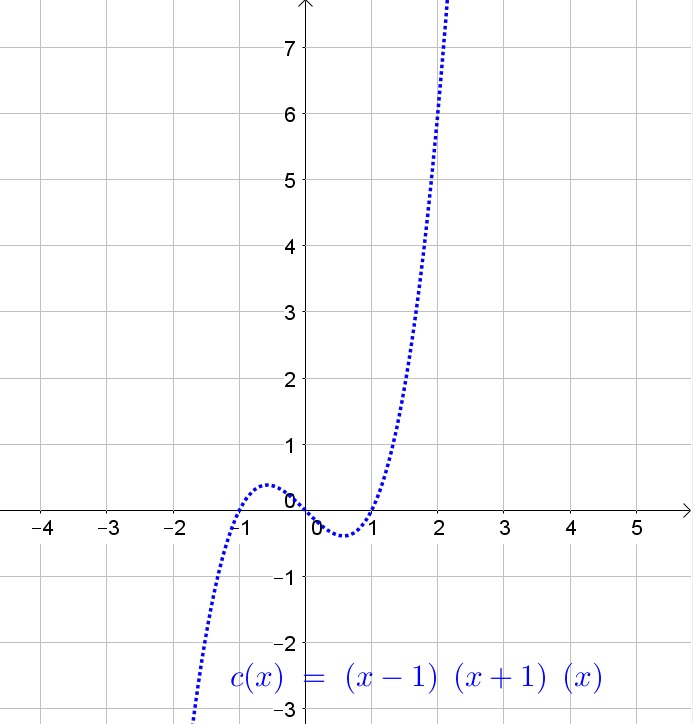
c. Yes, if it contain a factor such as (for example) $x^2+1$ which has no real roots.
b. $n$
c. Yes
b. The other graphs will be decreasing and thus the $y$ values will become smaller and smaller as the $x$ values get very large.
c. Graph i. and iii. have a positive orientation and graph ii. and iv. have a negative orientation.
b. $y$-values become smaller and smaller
c. i. and iii. have positive orientation, graph ii. and iv. have negative orientation
b. No, because it does not contain a part at the top that seems constantly zero.
c. No, because a polynomial of odd degree will be increasing to the left and decreasing to the right (or the other way around).
d. The two graphs have the same roots $x=0$, however the graph $y=x^5$ will be closer to zero about the root than the graph of $y=x^3$.
e. Repeated factors will only represent one root on the graph, however multiple different factors will represent multiple roots.
b. Np
c. No
d. Same roots
e. Repeated factors will only represent one root on the graph.
b. A triple root behaves the same as a single root, however the function will be very close to zero on an interval about the root.
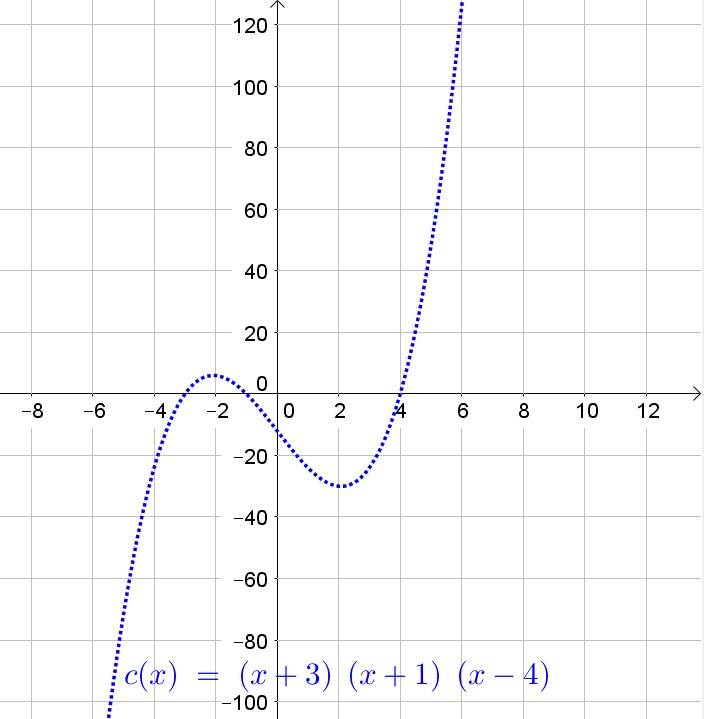
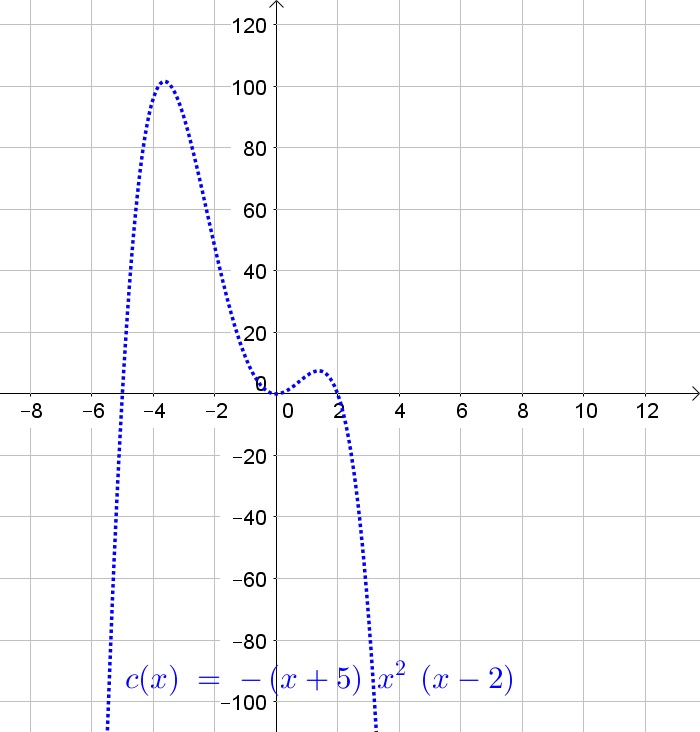

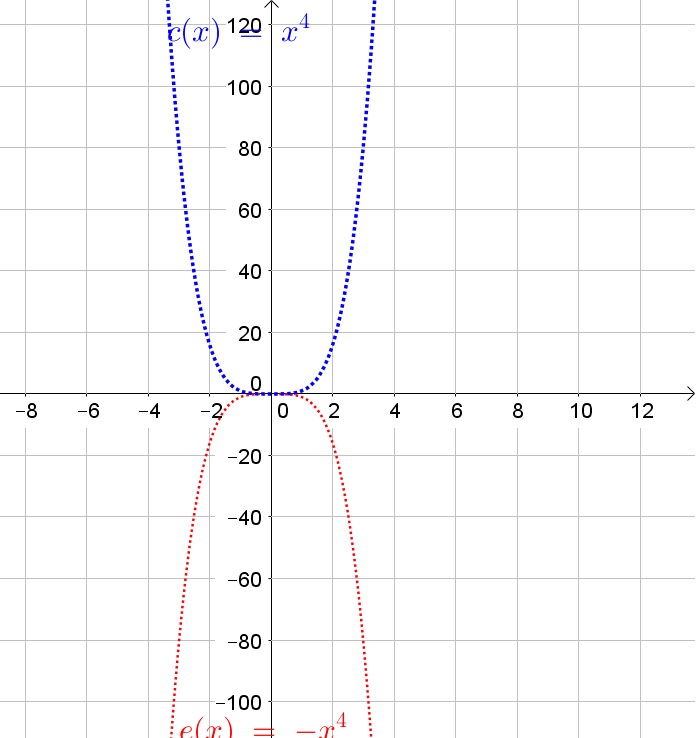
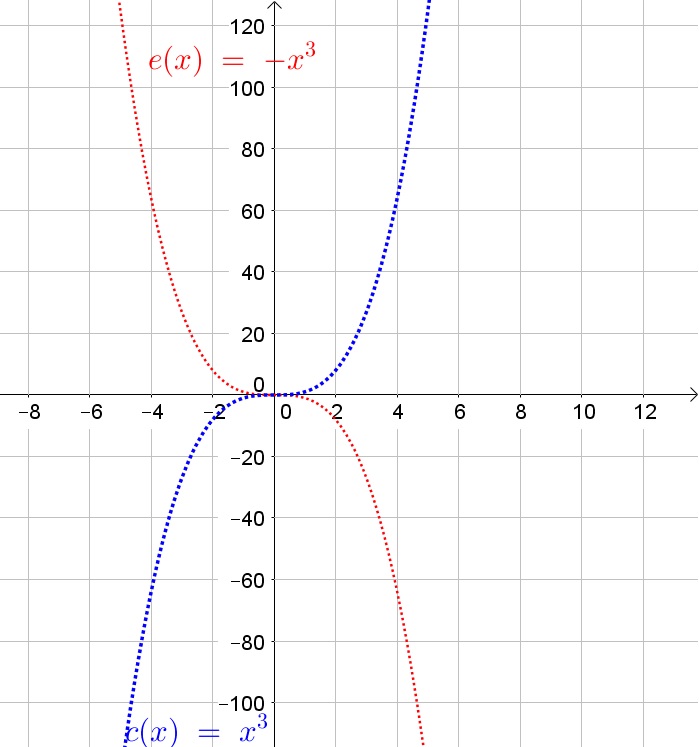
A polynomial of odd degree will be positive for very large $x$-values and negative for very small $x$-values, or the other way around.
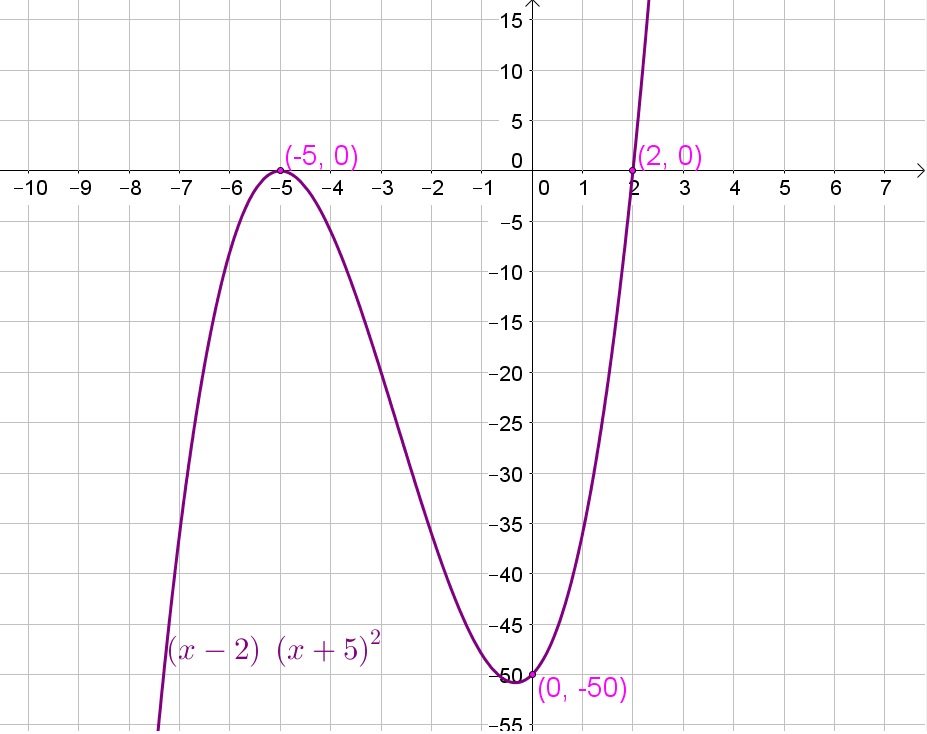
P_1 left(xright)=left(x-2right)left(x+5right)^2
$$
The bold part of the line shows where the output values of a polynomial function are positive.

P_3 left(xright)=x^4-21x^2+20x=xleft(x-1right)left(x-4right)left(x+5right)
$$
The bold part of the line shows where the output values of a polynomial function are positive.

P_7 left(xright)=0.2xleft(x+1right)left(x-3right)left(x+4right)
$$
The bold part of the line shows where the output values of a polynomial function are positive.

P_1 left(xright)=left(x-2right)left(x+5right)^2
$$
$$
P_3 left(xright)=xleft(x-1right)left(x-4right)left(x+5right)
$$
$$
P_7 left(xright)=0.2xleft(x+1right)left(x-3right)left(x+4right)
$$
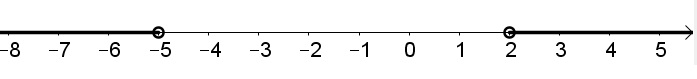
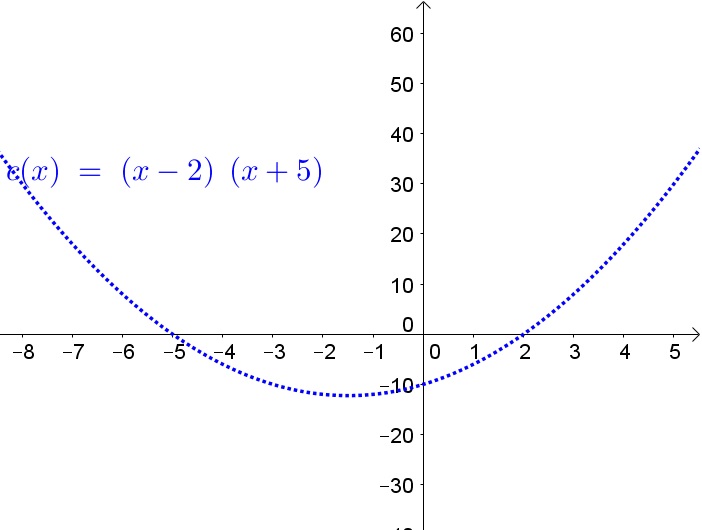
Determine every root of the function and then determine if the function is positive or negative before, between and after every root.
a.
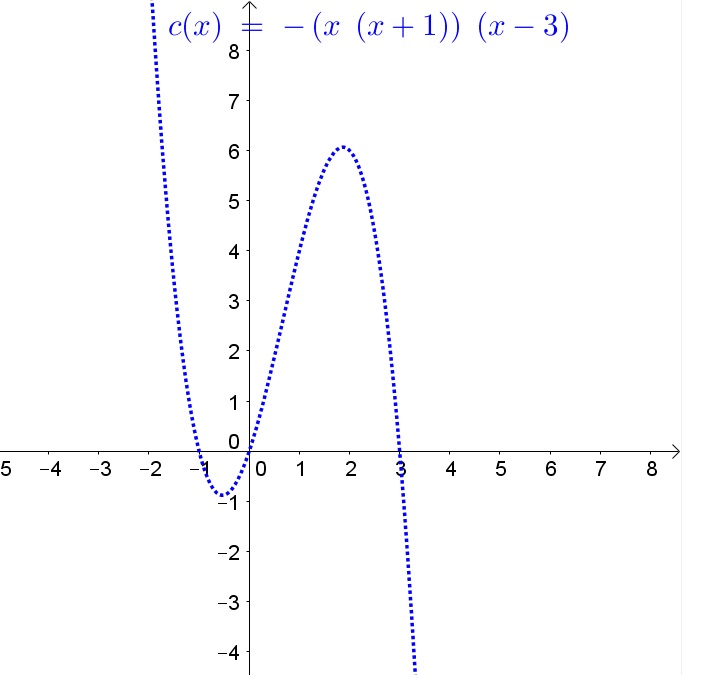
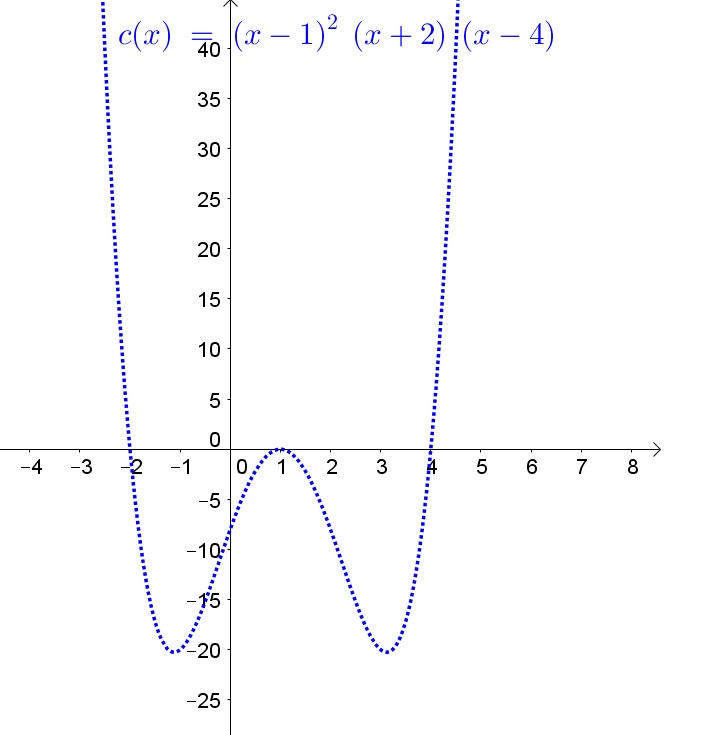

$$
begin{align*}
0&=x^2+6x+14 && text{Substitute} fleft(xright)
=0. \
Delta&=6^2-4 cdot1 cdot 14 && text{We compute the discriminant:} Delta=b^2-4ac \
&text{} && a=1, b=6, c=14. \
Delta&=36-56 \
Delta&=-20<0
end{align*}
$$
As the discriminant is negative, the equation has no real solution.
$text{This means the function's graph has no intersection with the $x$-axis.}$
$$
text{The graph does not cross the $x$-axis.}
$$
text{The function’s graph has no intersection with the $x$-axis }
$$
f(x)=x^2+6x+14
$$
$$
x^2+6x+14=0
$$
Delta=6^2-4(1)(14)=36-56=-20<0
$$
$$
fleft(xright)=ax^2+bx+c
$$
$text{where $a, b$ and $c$ are real numbers and $aneq0$.}$
Quadratic function in the intercept form is:
$$
fleft(xright)=aleft(x-pright)left(x-qright)
$$
$$
text{The $x$-intercepts are the points $left(p, 0right)$ and $left(q, 0right)$.}
$$
#### a.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-left(-3right)right)left(x-frac{1}{2}right) && text{Substitute} a=1, p=-3, text{and} q=frac{1}{2}. \
fleft(xright)&=left(x+3right)left(x-frac{1}{2}right) && text{Simplify.} \
fleft(xright)&=x^2-frac{1}{2}x+3x-frac{3}{2} \
fleft(xright)&=x^2+frac{5}{2}x-frac{3}{2} && text{Standard form.}
end{align*}
$$
#### b.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=aleft(x-left(-3right)right)left(x-2right) && text{Substitute} p=-3, text{and} q=2. \
fleft(xright)&=aleft(x+3right)left(x-2right) && text{Simplify.} \
-12&=aleft(3+3right)left(3-2right) && text{Substitute} left(x, fleft(xright)right)=left(3, -12right). \
-12&=a cdot 6 cdot 1 && text{Simplify.} \
a&=-2 \\
fleft(xright)&=aleft(x+3right)left(x-2right) && text{Intercept form.} \
fleft(xright)&=-2left(x+3right)left(x-2right) && text{Substitute} a=2. \
fleft(xright)&=-2left(x^2-2x+3x-6right) \
fleft(xright)&=-2x^2-2x+12 && text{Standard form.}
end{align*}
$$
$textbf{b.}$ $fleft(xright)=-2x^2-2x+12$
text{The polynomial which has degree $n$ and coefficients $a_n, a_{n-1} ,…, a_1, a_0$ is the following,}
$$
$$
Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0
$$
#### a.
$$
text{The given polynomial has degree $2$.}
$$
#### b.
$$
text{The given polynomial has degree $5$.}
$$
#### c.
$$
text{The function’s graph has $3$ intersections with the $x$-axis, therefore its minimum degree is $3$.}
$$
#### d.
$$
text{The function’s graph touches the $x$-axis twice, therefore its minimum degree is $2 cdot 2=4$.}
$$
P(x)=0.08x^2+28x
$$
y=8x^2-dfrac{1}{7}x^5+9
$$
b. Exponential functions are of the form $y=a^x$ with $a$ a constant and since the $x$ is in the power, the function is not a polynomial function.
c. Cubics are graphs of three degree functions and thus of a polynomial function.
d. Lines are graphs of one degree functions and thus of a polynomial function.
e. Circles have equations of the form $(x-a)^2+(y-b)^2=c^2$ with $a,b,c$ constants and thus is not a polynomial function (because of equations contains a term $y^2$).
b. No
c. Yes
d. Yes
e. No
$(3,7.5)$
$$
(4,6.25)
$$
k=5
$$
begin{cases}
ab^3+5=7.5\
ab^4+5=6.25
end{cases}
$$
begin{cases}
ab^3=7.5-5\
ab^4=6.25-5
end{cases}
$$
$$
begin{cases}
ab^3=2.5\
ab^4=1.25
end{cases}
$$
$dfrac{ab^4}{ab^3}=dfrac{1.25}{2.5}$
$b=dfrac{1}{2}$
$aleft(dfrac{1}{2}right)^3=2.5$
$acdot dfrac{1}{8}=dfrac{5}{2}$
$a=dfrac{5}{2}cdot 8$
$$
a=20
$$
f(x)=20(0.5)^x+5
$$
w=f(8)=20(0.5)^8+5approx5.078
$$
b) $5.078$
$dfrac {50}{320}=dfrac {60}{60+x}$
$320 cdot 60=50(60+x)$
$32 cdot 60=5(60+x)$
$1920=300+5x$
$5x=1620$
$$
x=324
$$
The distance to the hotel $=x+60=324+60=384$ ft.
text{Solve the second equation for $x^2$:}
$$
$$
left{
begin{aligned}
x^2+y^2&=16 \
x^2=y+4 \
end{aligned}
right.
$$
$$
text{We take $x^2=y+4$ from the second equation and substitute it in the first:}
$$
$$
left{
begin{aligned}
y+4+y^2&=16 \
x^2=y+4 \
end{aligned}
right.
$$
$$
text{Solve the first equation for $y$:}
$$
$$
left{
begin{aligned}
y^2+y-12&=0 \
x^2=y+4 \
end{aligned}
right.
$$
$$
left{
begin{aligned}
y^2-3y+4y+12&=0 \
x^2=y+4 \
end{aligned}
right.
$$
$$
left{
begin{aligned}
yleft(y-3right)+4left(y-3right)&=0 \
x^2=y+4 \
end{aligned}
right.
$$
$$
left{
begin{aligned}
left(y-3right)left(y+4right)&=0 \
x^2=y+4 \
end{aligned}
right.
$$
$$
left{
begin{aligned}
y&=3 text{or} y=-4 \
x^2&=y+4 \
end{aligned}
right.
$$
$$
text{Substitute $y=3$ and $y=4$ in the second equation:}
$$
$$
left{
begin{aligned}
y&=3 text{or} y=-4 \
x^2&=3+4 text{or} x^2=-4+4 \
end{aligned}
right.
$$
$$
text{Solve the second equation for $x$:}
$$
$$
left{
begin{aligned}
y&=3 text{or} y=-4 \
x^2&=7 text{or} x^2=0 \
end{aligned}
right.
$$
$$
left{
begin{aligned}
y&=3 text{or} y=-4 \
x&=pm sqrt{7} text{or} x=0 \
end{aligned}
right.
$$
The system’s solutions are:
$$
boxed{leftlbraceleft(-sqrt{7}, 3right), left(sqrt{7}, 3right), left(0, -4right)rightrbrace}
$$
leftlbraceleft(-sqrt{7}, 3right), left(sqrt{7}, 3right), left(0, -4right)rightrbrace
$$
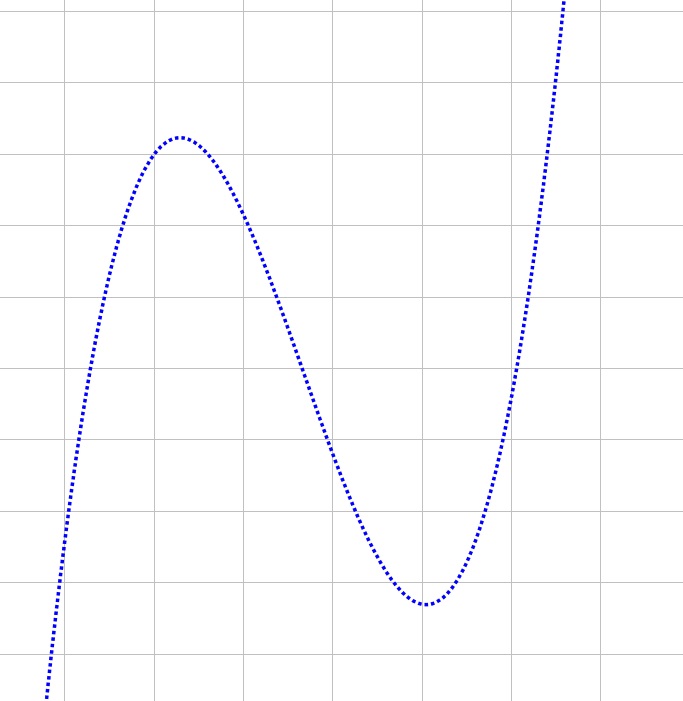
The graph shows that the curve of the function intersects the $x-$axis at the points $left(-3,0right)$, $left(0,0right)$ and $left(2,0right)$
Then $x$, $x+3$ and $x-2$ are factors of the function
A reasonable equation is
$$
y=xleft(x+3right)left(x-2right)
$$
Since the curve passes through the point $left(-2,8right)$ , then
$$
fleft(-2right)=-2left(-2+3right)left(-2-2right)=8
$$
Since the curve passes through the point $left(1,-4right)$ , then
$$
fleft(1right)=1left(1+3right)left(1-2right)=-4
$$
The equation fits all the curve criteria, then it is accurate
The graph shows that the curve of the function intersects the $x-$axis at the points $left(-3,0right)$, $left(0,0right)$ and $left(2,0right)$
Then $x$, $x+3$ and $x-2$ are factors of the function
A reasonable equation is
$$
y=x^3left(x+3right)left(x-2right)
$$
Since the curve passes through the point $left(-2,-30right)$ , then
$$
fleft(-2right)=left(-2right)^3left(-2+3right)left(-2-2right)=32
$$
Since the curve passes through the point $left(1,1right)$ , then
$$
fleft(-1right)=left(-1right)^3left(-1+3right)left(-1-2right)=6
$$
The equation does not fit all the curve criteria, then it is accurate
We need to multiply the function by $-1$, and the equation will become
$$
y=-x^3left(x+3right)left(x-2right)
$$
The graph shows that the curve of the function intersects the $x-$axis at the points $left(1,0right)$ and bounces of the pont $left(-2,0right)$
Then $x-1$ is a factor of the function and $x+2$ is a quadratic factor
A reasonable equation is
$$
y=left(x+2right)^2left(x-1right)
$$
Since the curve passes through the point $left(0,8right)$ , then
$$
fleft(0right)=left(0+2right)^2left(0-1right)=-4
$$
The equation does not fit all the curve criteria, then it is accurate
We need to multiply the function by $-2$, and the equation will become
$$
y=-2left(x+2right)^2left(x-1right)
$$
$$
y=xleft(x+3right)left(x-2right)
$$
b)
$$
y=-x^3left(x+3right)left(x-2right)
$$
c)
$$
y=-2left(x+2right)^2left(x-1right)
$$
a. $f(x)=(x+3)x(x-2)$ and let us evaluate this as $x=-2$:
$$
f(-2)=(1)(-2)(-4)=8
$$
this is correct, thus the function equation is correct.
b. $f(x)=(x+3)x^3(x-2)$ and let us evaluate this as $x=-2$:
$$
f(-2)=(1)(-2)^3(-4)=32
$$
We note that the function value at $x=-2$ should be $-32$, thus we still need to multiply the function equation by $-1$: $f(x)=-(x+3)x^3(x-2)$.
a. $f(x)=(x+2)^2(x-1)$ and let us evaluate this as $x=0$:
$$
f(0)=2^2(-1)=-4
$$
We note that the function value at $x=0$ should be $8$, thus we still need to multiply the function equation by $-2$: $f(x)=-2(x+2)^2(x-1)$.
b. $f(x)=-(x+3)x^3(x-2)$
c. $f(x)=-2(x+2)^2(x-1)$

$$
f(0)=(3)(1)(-2)^2=12
$$
We note that the function value at $x=0$ should be 24 instead of 21, thus we need to multiply te function equation by 2:
$$
y=2(x+3)(x+1)(x-2)^2
$$
b. You evaluate the function at $x=1$, which should equal 16:
$$
16=a(4)(2)(-1)^2=8a
$$
Divide both sides of the equation by 8 to obtain a:
$$
2=a
$$
b. $a=2$
The given equation is
$$
y=left(x+3right)left(x+1right)left(x-2right)^2
$$
For the $x-$intercepts, let $y=0$
$$
x=-3 , quad x=-1 , quad x=2
$$
For the $y-$intercepts, let $x=0$
$$
y=left(0+3right)left(0+1right)left(0-2right)^2=12
$$
The $x-$intercepts of the given function are the same as the $x-$intercepts of the given graph while the $y-$intercept of the given function is half the $y-$intercept of the given graph
Then we need to multiply the expression for $y$ by a factor of $2$
$$
y=2left(x+3right)left(x+1right)left(x-2right)^2
$$
b)
Given that
$$
y=aleft(x+3right)left(x+1right)left(x-2right)^2
$$
and the point $left(1,16right)$ lies on the curve of the function, then
$$
16=aleft(1+3right)left(1+1right)left(1-2right)^2=8a
$$
$$
a=frac{16}{8}=2
$$
$$
y=2left(x+3right)left(x+1right)left(x-2right)^2
$$
b
$$
a=2
$$
b. The roots are the intersections of the graph with the $x$-axis: $x=0$, $x=2$ (double) and $x=3$
c. Because of the roots we know that the equation is of the form:
$$
y=ax(x-2)^2(x-3)
$$
Evaluate at $x=2.5$ (which should be -0.2):
$$
-0.2=a(2.5)(0.5)^2(-0.5)=-0.3125a
$$
Divide both sides of the equation by $-0.3125$:
$$
0.64=a
$$
Thus the equation then becomes:
$$
y=0.64x(x-2)^2(x-3)
$$
d. The deepest point is obtained at about $x=0.5$:
$$
y=0.64(0.5)(-1.5)^2(-2.5)=-1.8
$$
This corresponds with 180 feet.
b. $x=0$, $x=2$ (double) and $x=3$
c. $y=0.64x(x-2)^2(x-3)$
d. 180 ft
$$
y=a(x+2)^2(x-2)
$$
Evaluate at $x=0$ (which should be 16):
$$
16=a(2)^2(-2)=-8a
$$
Divide both sides of the equation by $-8$:
$$
-2=a
$$
Thus the equation then becomes:
$$
y=-2(x+2)^2(x-2)
$$
$$
y=a(x+2)^2(x-1)^2
$$
Evaluate at $x=0$ (which should be $-3$):
$$
-3=a(2)^2(-1)^2=4a
$$
Divide both sides of the equation by $4$:
$$
-dfrac{3}{4}=a
$$
Thus the equation then becomes:
$$
y=-dfrac{3}{4}(x+2)^2(x-1)^2
$$
b. $y=-dfrac{3}{4}(x+2)^2(x-1)^2$
$$
y=a(x+1)^2(x-4)
$$
Evaluate at $x=-2$ (which should be -18):
$$
-18=a(-1)^2(-6)=-6a
$$
Divide both sides of the equation by $-6$:
$$
3=a
$$
Thus the equation then becomes:
$$
y=3(x+1)^2(x-4)
$$
y=3(x+1)^2(x-4)
$$
$$
y=3(x+1)^2(x-4)
$$
Now let us use what Armando did: The roots are the intersections of the graph with the $x$-axis: $x=-1$(quadruple), $x=4$. Then we know that the equation is of the form:
$$
y=a(x+1)^4(x-4)
$$
Evaluate at $x=-2$ (which should be -18):
$$
-18=a(-1)^2(-6)=-6a
$$
Divide both sides of the equation by $-6$:
$$
3=a
$$
Thus the equation then becomes:
$$
y=3(x+1)^4(x-4)
$$
Thus we note that Armando’s solution is also correct, because we do not know if the bounce of is a double or quadruple root (could be an even higher root).
$x-$axis at $(-1 , 0)$ , crosses it at $( 4, 0)$ , and goes through the point $(-2, -18)$ , then the equation fits all of the given criteria.
The two equations fit all of the given criteria but have different graphs.
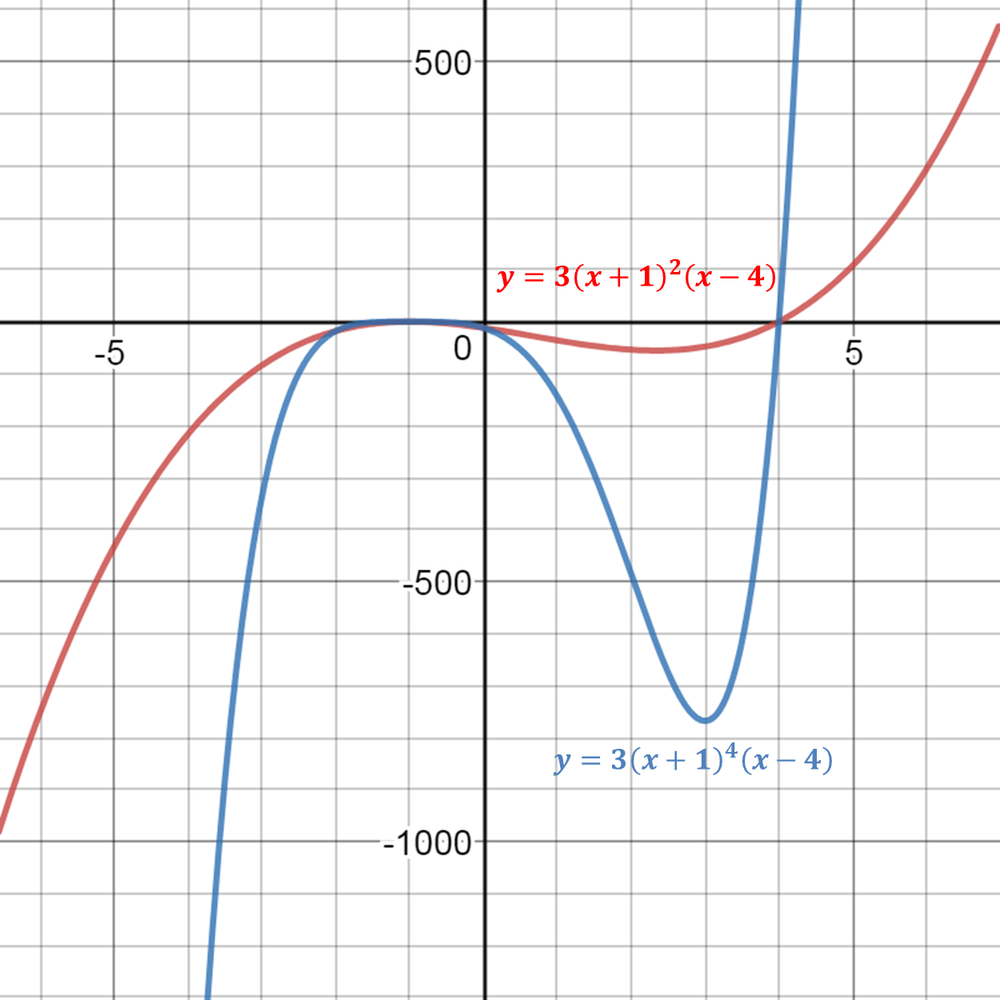
The two equations fit all of the given criteria but have different graphs.
$$
y=3(x+1)^2(x-4)
$$
$$
y=3(x+1)^4(x-4)
$$
Evaluate at $x=1$ (which should be -36):
$$
y=6=3(2)^2(-3)=-36
$$
$$
y=6=3(2)^4(-3)=-144
$$
Thus the first equation is correct and the second equation is not correct.
For the first equation $y=3left(x+1right)^2left(x-4right)$
$$
-36=3left(1+1right)^2left(1-4right)
$$
$$
-36=3times 4 times left(-3right)
$$
$$
-36=-36
$$
Then the first equation $y=3left(x+1right)^2left(x-4right)$ satisfies the new condition.
For the second equation $y=3left(x+1right)^4left(x-4right)$
$$
-36=3left(1+1right)^4left(1-4right)
$$
$$
-36=3times 16 times left(-3right)
$$
$$
-36=-144
$$
which is a contradiction, then the second equation $y=3left(x+1right)^4left(x-4right)$ does not satisfy the new condition.
Then there is only one possible equation.
$$
y=a(x+4)(x-1)(x-3)
$$
Evaluate at $x=-1$ (which should be 60):
$$
60=a(3)(-2)(-4)=24a
$$
Divide both sides of the equation by $24$:
$$
dfrac{5}{2}=a
$$
Thus the equation then becomes:
$$
y=dfrac{5}{2}(x+4)(x-1)(x-3)
$$
y=dfrac{5}{2}(x+4)(x-1)(x-3)
$$
Then $x+4$ , $x-1$ and $x-3$ are factors of the equation.
A reasonable equation is
$$
y=aleft(x+4right)left(x-1right)left(x-3right)
$$
Since the curve passes through the point $left(-1,60right)$ , then
$$
fleft(-1right)=left(-1+4right)left(-1-1right)left(-1-3right)a=24a
$$
Then
$$
24a=60 quad rightarrow quad a=frac{60}{24}=frac{5}{2}
$$
The equation will become
$$
y=frac{5}{2}left(x+4right)left(x-1right)left(x-3right)
$$
y=frac{5}{2}left(x+4right)left(x-1right)left(x-3right)
$$
$$
text{Without solving, we will check the solution $x=5+2i$ by substituting it in the equation.}
$$
$$
begin{align*}
left(5+2iright)^2-10left(5+2iright)&=-29 && text{Substitute} x=5+2i. \
25+20i-4-50-20i&=-29 && text{Use:} left(a+bright)^2=a^2+2ab+b^2, i^2=-1. \
-29&=-29
end{align*}
$$
#### b.
$text{The quadratic equation has $2$ complex solutions. Another solution to the equation is $x=5-2i$.}$
$$
text{We will check the solution $x=5-2i$ by substituting it in the equation.}
$$
$$
begin{align*}
left(5-2iright)^2-10left(5-2iright)&=-29 && text{Substitute} x=5+2i. \
25-20i-4-50+20i&=-29 && text{Use:} left(a-bright)^2=a^2-2ab+b^2, i^2=-1. \
-29&=-29
end{align*}
$$
#### c.
The equation has no real solution.
$text{The parabola does not intersect the $x$-axis.}$
$text{The graph does not cross the $x$-axis.}$
$textbf{b.}$ $5-2i$
$textbf{c.}$ $text{The parabola does not intersect the $x$-axis.}$
text{The polynomial which has degree $n$ and coefficients $a_n, a_{n-1} ,…, a_1, a_0$ is the following,}
$$
$$
Pleft(xright)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0
$$
#### a.
$$
text{The given polynomial has degree $4$ and coefficients $a_4=6, a_3=-3, a_2=5, a_1=1$ and $a_0=8$.}
$$
#### b.
$$
text{The given polynomial has degree $3$ and coefficients $a_3=-5, a_2=10, a_1=0$ and $a_0=8$.}
$$
#### c.
$$
text{The given polynomial has degree $2$ and coefficients $a_2=-1, a_1=1$ and $a_0=0$.}
$$
#### d.
$$
begin{align*}
Pleft(xright)&=xleft(x^2-5x-3x+15right) \
Pleft(xright)&=x^3-8x^2+15x
end{align*}
$$
$$
text{The given polynomial has degree $3$ and coefficients $a_3=1, a_2=-8, a_1=15$ and $a_0=0$.}
$$
#### e.
$$
text{The given polynomial has degree $1$ and coefficients $a_1=1$ and $a_0=0$.}
$$
#### f.
$$
text{The given polynomial has degree $0$ and coefficient $a_0=10$.}
$$
$textbf{b.}$ $text{degree}=3, a_3=-5, a_2=10, a_1=0$ and $a_0=8$,
$textbf{c.}$ $text{degree}=2, a_2=-1, a_1=1,$ and $a_0=0$
$textbf{d.}$ $text{degree}=3, a_3=1, a_2=-8, a_1=15$ and $a_0=0$,
$textbf{e.}$ $text{degree}=1, a_1=1$ and $a_0=0$,
$textbf{f.}$ $text{degree}=0, a_0=0$,
2(x-1)^2=18
$$
$(x-1)^2=9$
$x-1=pm sqrt 9$
$x-1=pm 3$
$x=1pm 3$
$x_1=1-3=-2$
$$
x_2=1+3=4
$$
$2^x=7$
$log (2^x)=log (7)$
$xlog (2)=log (7)$
$$
x=dfrac{log (7)}{log (2)}approx 2.81
$$
b) $x=dfrac{log (7)}{log (2)}approx 2.81$
f(t)=5,000,000left(dfrac{1}{2}right)^t
$$
f(0)=5,000,000left(dfrac{1}{2}right)^0=5,000,000
$$
$5,000,000left(dfrac{1}{2}right)^t=1000$
$left(dfrac{1}{2}right)^t=dfrac{1000}{5,000,000}$
$left(dfrac{1}{2}right)^t=dfrac{1}{5000}$
$2^t=5000$
$log (2^t)=log (5000)$
$tlog (2)=log (5000)$
$t=dfrac{log (5000)}{log (2)}$
$tapprox 12.29$ minutes
$5,000,000left(dfrac{1}{2}right)^t<1$
$left(dfrac{1}{2}right)^t5,000,000$
$log (2^t)>log (5,000,000)$
$tlog (2)>log (5,000,000)$
$t>dfrac{log (5,000,000)}{log (2)}$
$$
t>22.25
$$
b) $12.29$ minutes
c) $22.25$ minutes
Pythagorean Theorem is valid in a right-angled triangle:
$$
begin{align*}
c^2&=a^2+b^2 \
a^2&=c^2-b^2 \
b^2&=c^2-a^2 \
end{align*}
$$
$$
text{where $c$ is the hypotenuse, $a$ and $b$ are legs.}
$$
#### a.
We use the Pythagorean Theorem to calculate the missing leg:
$$
begin{align*}
a^2&=c^2-b^2 \
a^2&=1^2-left(frac{1}{2}right)^2 \
a^2&=1-frac{1}{4} \
a^2&=frac{3}{4} \
a&=frac{sqrt{3}}{2} \
end{align*}
$$
#### b.
We use the Pythagorean Theorem to calculate the missing leg:
$$
begin{align*}
a^2&=c^2-b^2 \
a^2&=8^2-left(4sqrt{3}right)^2 \
a^2&=64-48 \
a^2&=16 \
a&=4 \
end{align*}
$$
We use the Pythagorean Theorem to calculate the missing hypotenuse:
$$
begin{align*}
c^2&=a^2+b^2 \
c^2&=6^2+6^2 \
c^2&=36+36 \
c^2&=72 \
c&=sqrt{72} \
c&=6sqrt{2}
end{align*}
$$
#### d.
We use the Pythagorean Theorem to calculate the missing leg:
$$
begin{align*}
a^2&=c^2-b^2 \
a^2&=left(sqrt{2}right)^2-1^2 \
a^2&=2-1 \
a^2&=1 \
a&=1 \
end{align*}
$$

$dfrac{1}{4}+x^2=1$
$x^2=1-dfrac{1}{4}$
$x^2=dfrac{3}{4}$
$$
x=dfrac{sqrt 3}{2}
$$
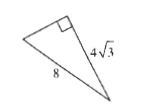
$x^2+48=64$
$x^2=64-48$
$x^2=16$
$$
x=4
$$
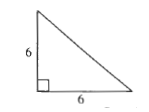
$x^2=36+36$
$x^2=72$
$x=sqrt{72}$
$$
x=6sqrt 2
$$
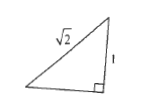
$x^2+1=2$
$x^2=2-1$
$x^2=1$
$$
x=1
$$
b) $4$
c) $6sqrt 2$
d) $1$
|7-y|leq 3
$$
$-3-7leq 7-y-7leq 3-7$
$-10leq -yleq -4$
$10geq ygeq 4$
$$
yin [4,10]
$$
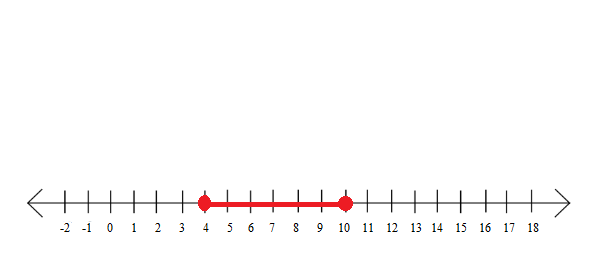
3|2m+1|-1>8
$$
$3|2m+1|>9$
$|2m+1|>3$
$2m+13$
$2m+1-13-1$
$2m2$
$m1$

b) $(-infty,-2)cup(1,infty)$
We determine the roots:
$$
begin{align*}
left(x-2right)^2-4&=0 && text{Substitute} y=0. \
left(x-2right)^2-4+4&=0+4 && text{Add} 4 text{to both sides.}\
left(x-2right)^2&=4 && text{Simplify.} \
x-2&=pm sqrt{4} && text{Square root of both sides.} \
x-2&=pm 2 \
x&=-2+2 text{or} x=2+2 && text{Add} 2 text{to both sides.}\
x&=0 text{or} x=4
end{align*}
$$
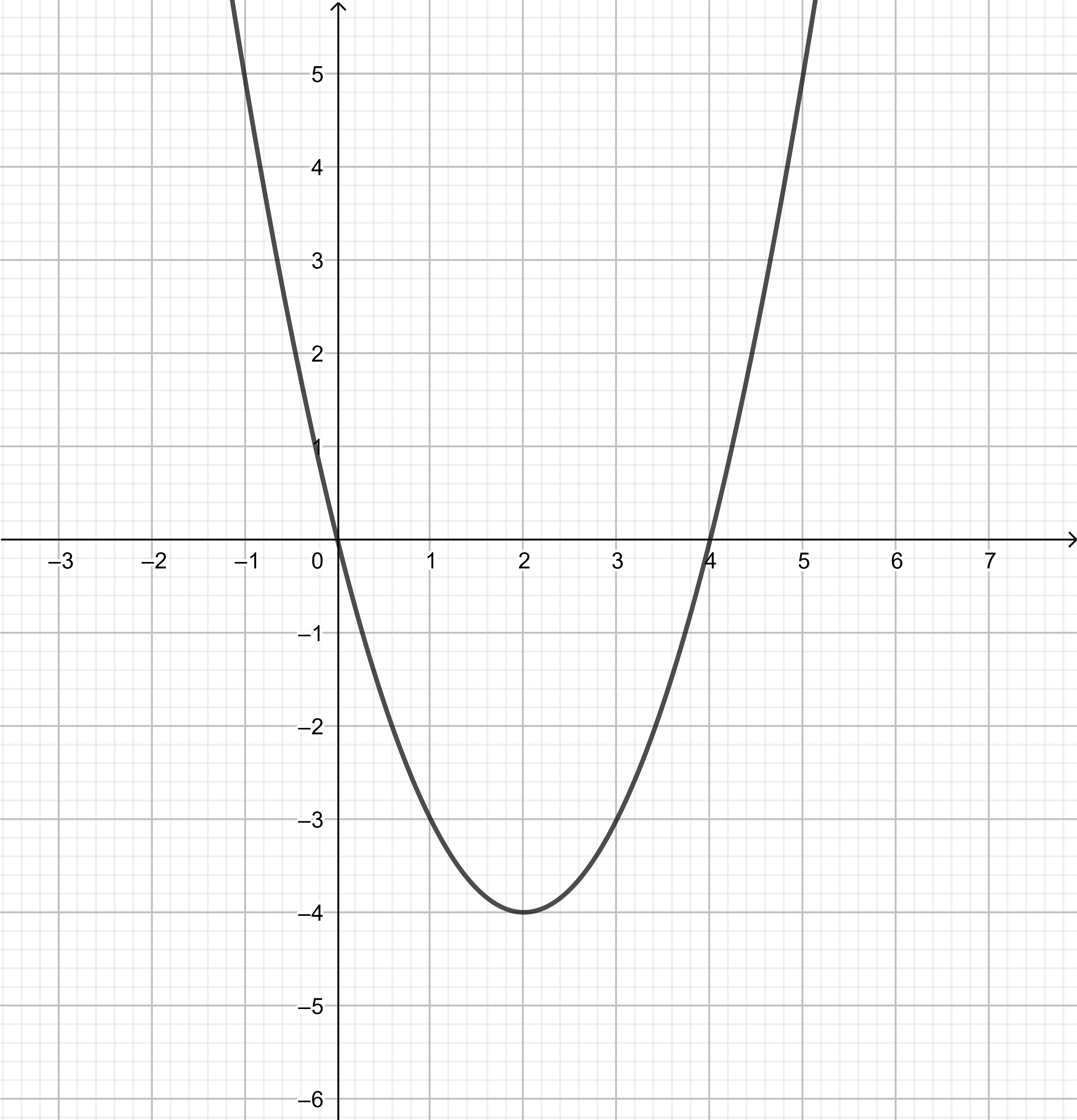
We determine the roots:
$$
begin{align*}
left(x-2right)^2&=0 && text{Substitute} y=0. \
x-2&=0 && text{Square root of both sides.} \
x&=0+2 && text{Add} 2 text{to both sides.}\
x&=2
end{align*}
$$
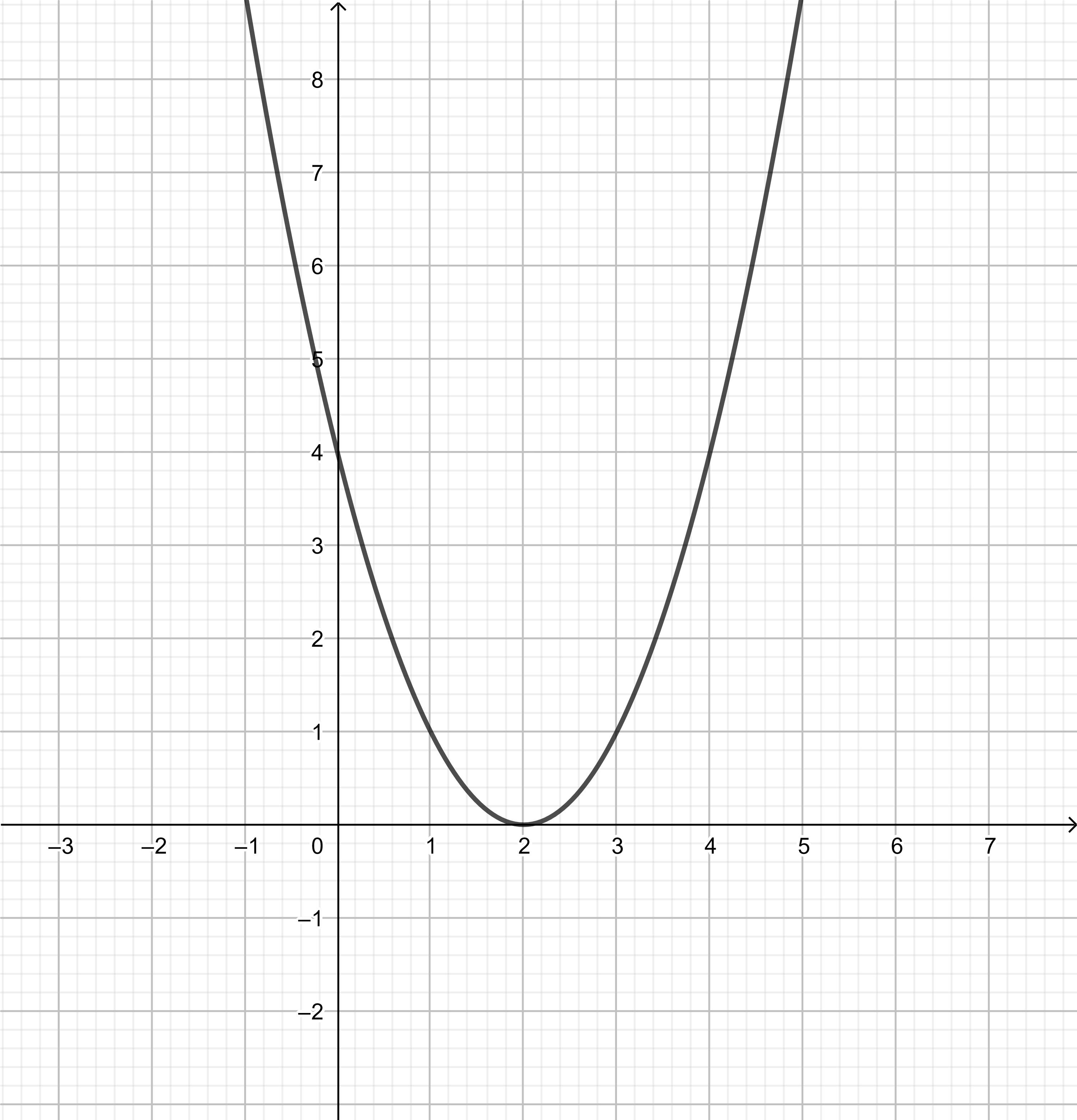
We determine the roots:
$$
begin{align*}
left(x-2right)^2+3&=0 && text{Substitute} y=0. \
left(x-2right)^2+3-3&=0-3 && text{Subtract} 3 text{from both sides.}\
left(x-2right)^2&=-3 && text{Simplify.} \
x-2&=pm sqrt{3}i && text{Square root of both sides.} i^2=-1. \
x&=2-sqrt{3}i text{or} x=2+sqrt{3}i && text{Add} 2 text{to both sides.}\
end{align*}
$$
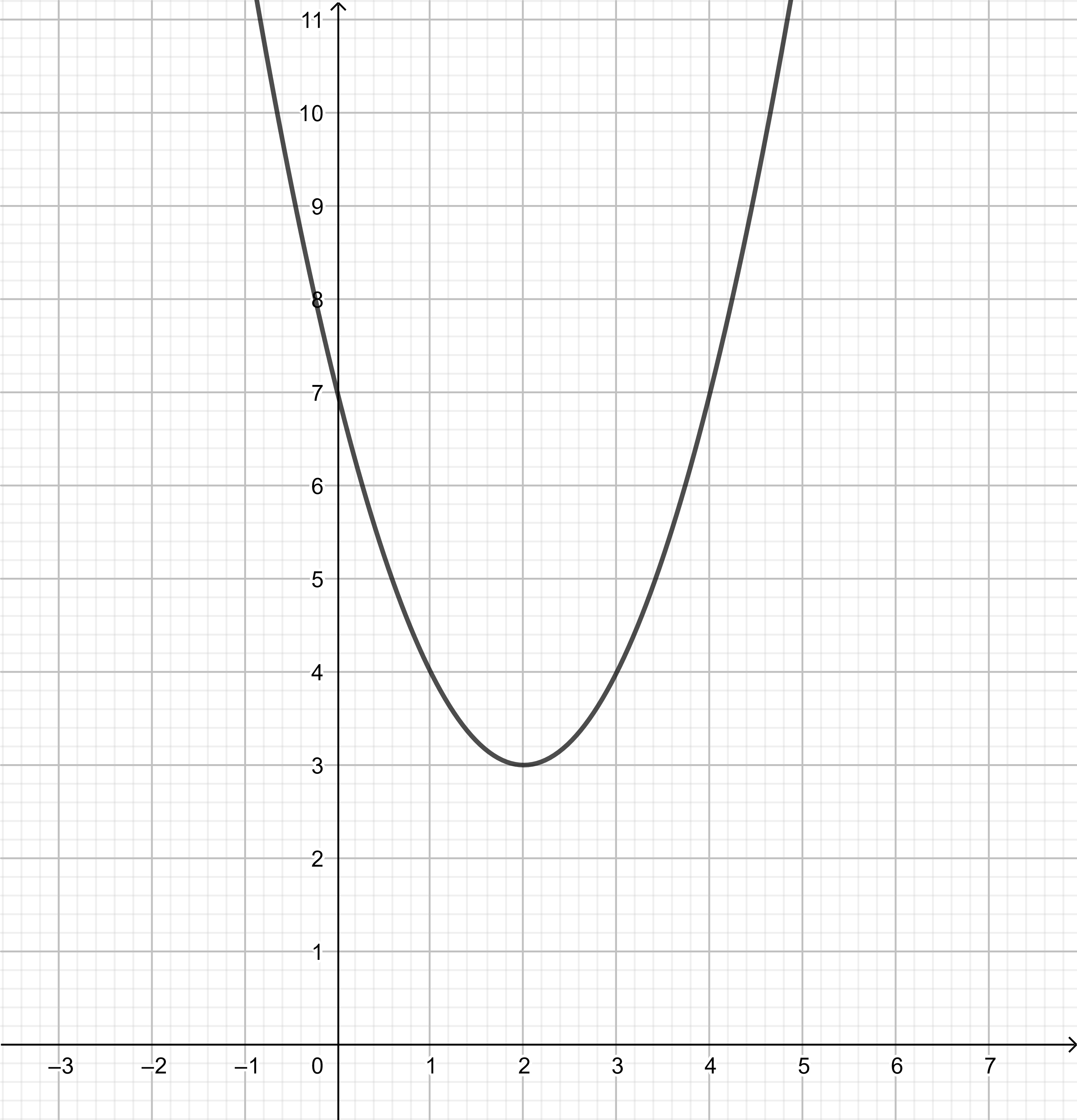
$text{$1$.The parabola has two real roots when it crosses the $x$-axis twice.}$
$text{$2$.The parabola has one real double root when it touches the $x$-axis.}$
$text{$3$.The parabola has two conjugate imaginary roots when it doesn’t cross the $x$-axis.}$
$textbf{d.}$ $text{$1$.The parabola has two real roots when it crosses the $x$-axis twice.}$
$text{$2$.The parabola has one real double root when it touches the $x$-axis.}$
$text{$3$.The parabola has two conjugate imaginary roots when it doesn’t cross the $x$-axis.}$
The given equation is
$$
y=left(x+5right)^2+9
$$
Replace $y$ with $0$
$$
left(x+5right)^2+9=0
$$
Subtract $9$ from both sides
$$
left(x+5right)^2=-9
$$
Apply the square root to both sides
$$
x+5=pmsqrt{-9}=pm 3i
$$
$$
x=-5+3i quad text{or}quad x=-5-3i
$$
Since the roots of the equation are complex numbers, then the graph does not intersect the $x-$axis.
b)
The given equation is
$$
y=x^2-4x+9
$$
Replace $y$ with $0$
$$
x^2-4x+9=0
$$
The discriminant is
$$
D=b^2-4ac=16-36=-20
$$
Apply the quadratic formula
$$
x=frac{4pm sqrt{-20}}{2}=2pmsqrt{5}i
$$
Since the roots of the equation are complex numbers, then the graph does not intersect the $x-$axis.
$$
x=-5+3i quad text{or}quad x=-5-3i
$$
Since the roots of the equation are complex numbers, then the graph does not intersect the $x-$axis.
b)
$$
x=frac{4pm sqrt{-20}}{2}=2pmsqrt{5}i
$$
Since the roots of the equation are complex numbers, then the graph does not intersect the $x-$axis.
$$
0=(x+5)^2+9
$$
Subtract 9 from both sides of the equation:
$$
-9=(x+5)^2
$$
Take the square root of both sides of the equation:
$$
pm 3i=x+5
$$
Subtract 5 from both sides of the equation:
$$
-5pm 3i=x
$$
$$
0=x^2-4x+9
$$
Determine the discriminant of the given function $f(x)=x^2-4x+9$:
$$
D=b^2-4ac=(-4)^2-4(1)(9)=16-36=-20
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{4pm sqrt{-20}}{2(1)}=dfrac{4pm 2sqrt{5}i}{2}=2pm sqrt{5}i
$$
b. $x=2pm sqrt{5}i$
$$
2+i+2-i=4
$$
Multiply the two complex numbers:
$$
(2+i)(2-i)=4-i^2=4+1=5
$$
b. Add the two complex numbers:
$$
3-5i+3+5i=6
$$
Multiply the two complex numbers:
$$
(3-5i)(3+5i)=9-25i^2=9+25=34
$$
c. Add the two complex numbers:
$$
-4+i+-4-i=-8
$$
Multiply the two complex numbers:
$$
(-4+i)(-4-i)=16-i^2=16+1=17
$$
d. Add the two complex numbers:
$$
1+isqrt{3}+1-isqrt{3}=2
$$
Multiply the two complex numbers:
$$
(1+isqrt{3})(1-isqrt{3})=1-3i^2=1+3=4
$$
e. By its complex conjugate $3-2i$.
f. We obtain another complex number: $(-4+5i)(-4+3i)=16-20i-12i+15i^2=1-32i$
g. By its complex conjugate $a-bi$
b. 6, 34
c. $-8$, 17
d. 2, 4
e. $3-2i$
f. obtain a complex number
g. $a-bi$
a. $0=(x-(2+i))(x-(2-i))=x^2-4x+5$
b. $0=(x-(3-5i))(x-(3+5i))=x^2-6x+34$
c. $0=(x-(-4+i))(x-(-4-i))=x^2+8x+17$
d. $0=(x-(1+isqrt{3}))(x-(1-isqrt{3}))=x^2-2x+4$
Thus we note that if $a,b$ are solutions of an equation, that this equation is of the form $x^2-(a+b)x+(ab)$.
b. $x^2-6x+34$
c. $x^2+8x+17$
d. $x^2-2x+4$
$$
D=b^2-4ac=(-6)^2-4(1)(25)=36-100=-64
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{6pm sqrt{-64}}{2(1)}=dfrac{6pm 8i}{2}=3pm 4i
$$
Determine the sum of the solutions:
$$
3+4i+3-4i=6
$$
Determine the product of the solutions:
$$
(3+4i)(3-4i)=9-16i^2=9+16=25
$$
Thus we note that if $a, b$ are solutions of an equation, that this equation contains a factor of the form $(x^2-(a+b)x+(ab))$.
$$
(x-(2+i))(x-(2-i))=x^2-(2+i)x-(2-i)x+(2+i)(2-i)=x^2-4x+5
$$
Thus we can generalize the idea to complex pairs.
$$
x=-4pm i
$$
Add $4$ to both sides of the equation:
$$
x+4=pm i
$$
Square both sides of the equation
$$
(x+4)^2=(pm i)^2
$$
Simplify:
$$
x^2+8x+16=i^2
$$
Simplify:
$$
x^2+8x+16=-1
$$
Add 1 to both sides of the equation:
$$
x^2+8x+17=0
$$
Thus we note that this idea works and we can obtain the equation by working backwards.
$$
fleft(xright)=ax^2+bx+c
$$
$text{where $a, b$ and $c$ are real numbers and $aneq0$.}$
Quadratic function in the intercept form is:
$$
fleft(xright)=aleft(x-pright)left(x-qright)
$$
$$
text{The $x$-intercepts are the points $left(p, 0right)$ and $left(q, 0right)$.}
$$
#### a.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-frac{3}{4}right)left(x-left(-5right)right) && text{Substitute} a=1, p=frac{3}{4}, text{and} q=-5. \
fleft(xright)&=left(x-frac{3}{4}right)left(x+5right) && text{Simplify.} \
fleft(xright)&=x^2+5x-frac{3}{4}x-frac{15}{4} \
fleft(xright)&=x^2+frac{17}{4}x-frac{15}{4} && text{Standard form.}
end{align*}
$$
#### b.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-3iright)left(x-left(-3iright)right) && text{Substitute} a=1, p=3i, text{and} q=-3i. \
fleft(xright)&=left(x-3iright)left(x+3iright) && text{Simplify.} \
fleft(xright)&=x^2+3ix-3ix-9i^2 \
fleft(xright)&=x^2-9 cdot left(-1right) && i^2=-1. \
fleft(xright)&=x^2+9 && text{Standard form.}
end{align*}
$$
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-left(5+2iright)right)left(x-left(5-2iright)right) && text{Substitute} a=1, p=5+2i, \
&text{} && text{and} q=5-2i. \
fleft(xright)&=left(x-5-2iright)left(x-5+2iright) && text{Simplify.} \
fleft(xright)&=x^2-5x+2ix-5x+25-10i-2ix+10i-4i^2 \
fleft(xright)&=x^2-10x+25-4 cdot left(-1right) && i^2=-1. \
fleft(xright)&=x^2-10x+29 && text{Standard form.}
end{align*}
$$
#### d.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-left(-3+sqrt{2}right)right)left(x-left(-3-sqrt{2}right)right) && text{Substitute} a=1, p=-3+sqrt{2}, \
&text{} && text{and} q=-3-sqrt{2}. \
fleft(xright)&=left(x+3-sqrt{2}right)left(x+3+sqrt{2}right) && text{Simplify.} \
fleft(xright)&=x^2+3x+sqrt{2}x+3x+9+3sqrt{2}-sqrt{2}x-3sqrt{2}-2 \
fleft(xright)&=x^2+6x+7 && text{Standard form.}
end{align*}
$$
#### e.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-5right)left(x-5right) && text{Substitute} a=1, p=5, text{and} q=5. \
fleft(xright)&=x^2-5x-5x+25 && text{Simplify.} \
fleft(xright)&=x^2-10x+25 && text{Standard form.}
end{align*}
$$
#### f.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-sqrt{2}right)left(x-left(-sqrt{2}right)right) && text{Substitute} a=1, p=sqrt{2}, text{and} q=-sqrt{2}. \
fleft(xright)&=left(x-sqrt{2}right)left(x+sqrt{2}right) && text{Simplify.} \
fleft(xright)&=x^2+sqrt{2}x-sqrt{2}x-2 \
fleft(xright)&=x^2-2 && text{Standard form.}
end{align*}
$$
$textbf{c.}$ $fleft(xright)=x^2-10x+29$ $textbf{d.}$ $fleft(xright)=x^2+6x+7$
$textbf{e.}$ $fleft(xright)=x^2-10x+25$ $textbf{f.}$ $fleft(xright)=x^2-2$
Quadratic function in the standard form is:
$$
fleft(xright)=ax^2+bx+c
$$
$text{where $a, b$ and $c$ are real numbers and $aneq0$.}$
$text{$1$.The parabola has two real roots when it crosses the $x$-axis twice.}$
$text{$2$.The parabola has one real double root when it touches the $x$-axis.}$
$text{$3$.The parabola has two conjugate imaginary roots when it doesn’t cross the $x$-axis.}$
textbf{Example:}
$$
#### a.
$$
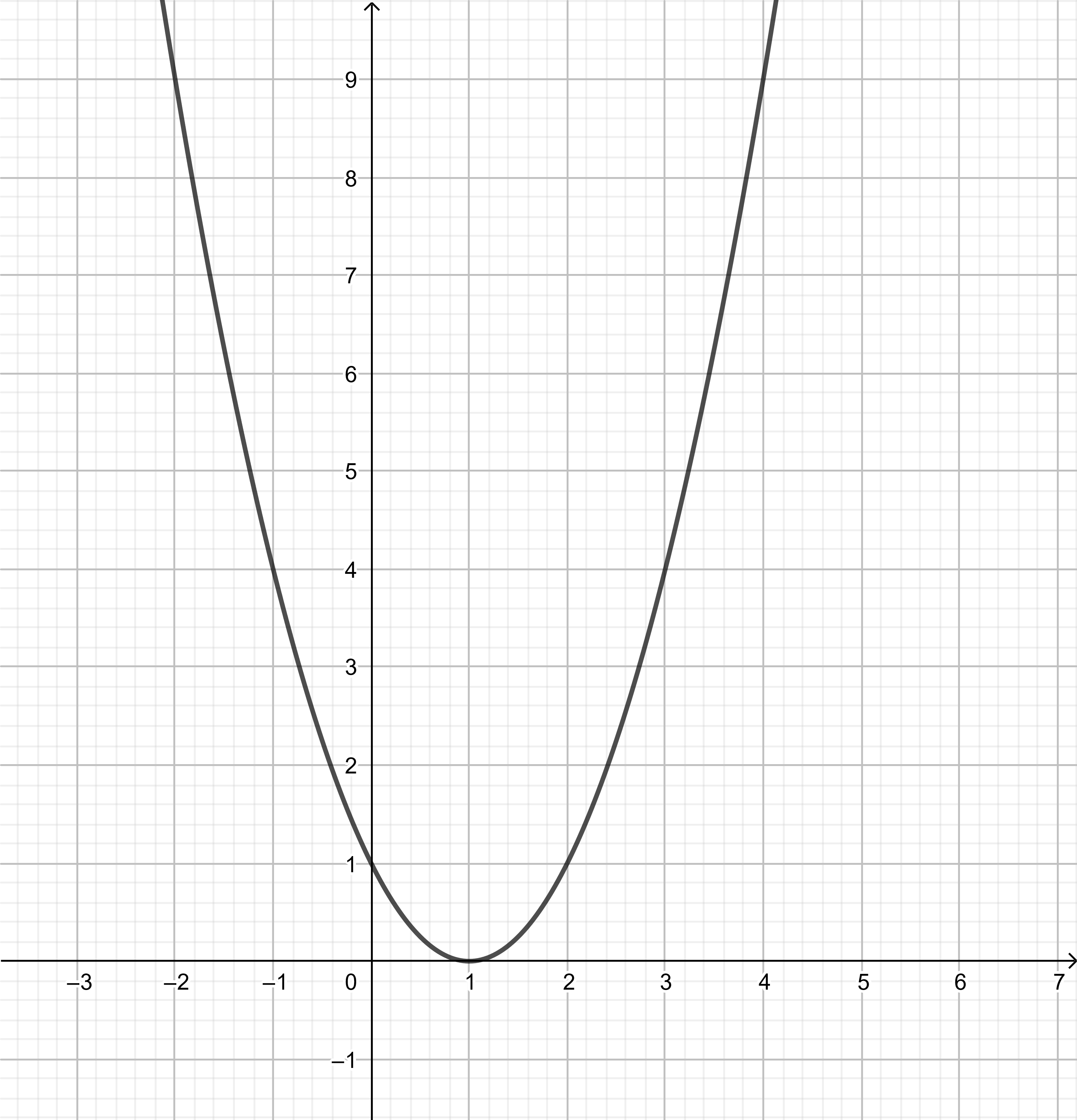
text{The parabola has two real roots: $y=left(x-1right)^2-9$}
$$
$$
begin{align*}
left(x-1right)^2-9&=0 && text{Substitute} y=0. \
left(x-1right)^2-9+9&=0+9 && text{Add} 9 text{to both sides.}\
left(x-1right)^2&=9 && text{Simplify.} \
x-1&=pm sqrt{9} && text{Square root of both sides.} \
x-1&=pm 3 \
x&=-3+1 text{or} x=3+1 && text{Add} 1 text{to both sides.}\
x&=-2 text{or} x=4
end{align*}
$$
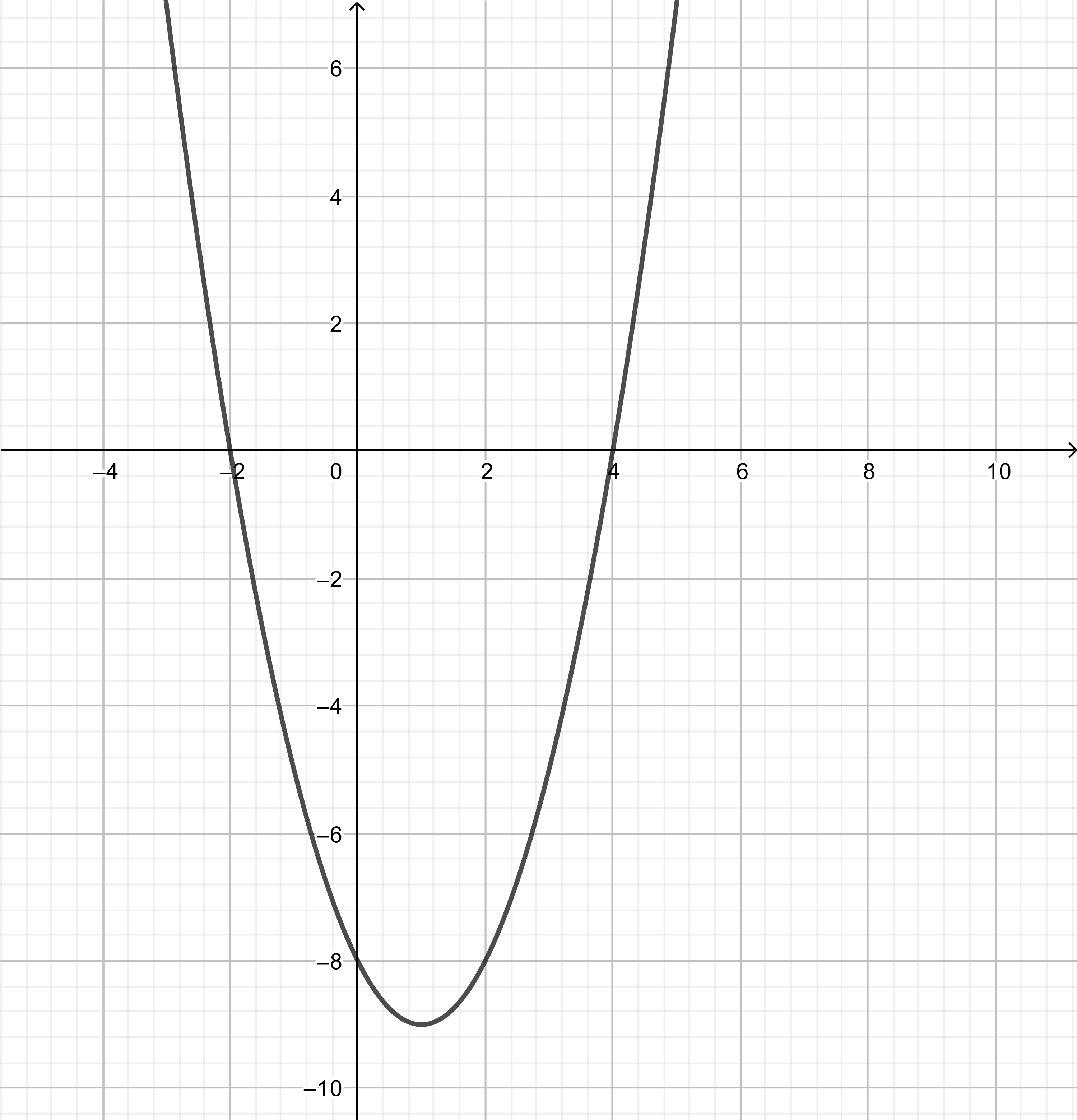
$$
text{The parabola has one real double root: $y=left(x-1right)^2$}
$$
$$
begin{align*}
left(x-1right)^2&=0 && text{Substitute} y=0. \
x-1&=0 && text{Square root of both sides.} \
x&=0+1 && text{Add} 1 text{to both sides.}\
x&=1
end{align*}
$$
$$
text{The parabola has two conjugate imaginary roots: $y=left(x-1right)^2+2$}
$$
$$
begin{align*}
left(x-1right)^2+2&=0 && text{Substitute} y=0. \
left(x-1right)^2+2-2&=0-2 && text{Subtract} 2 text{from both sides.}\
left(x-1right)^2&=-2 && text{Simplify.} \
x-1&=pm sqrt{2}i && text{Square root of both sides.} i^2=-1. \
x&=1-sqrt{2}i text{or} x=1+sqrt{2}i && text{Add} 1 text{to both sides.}\
end{align*}
$$
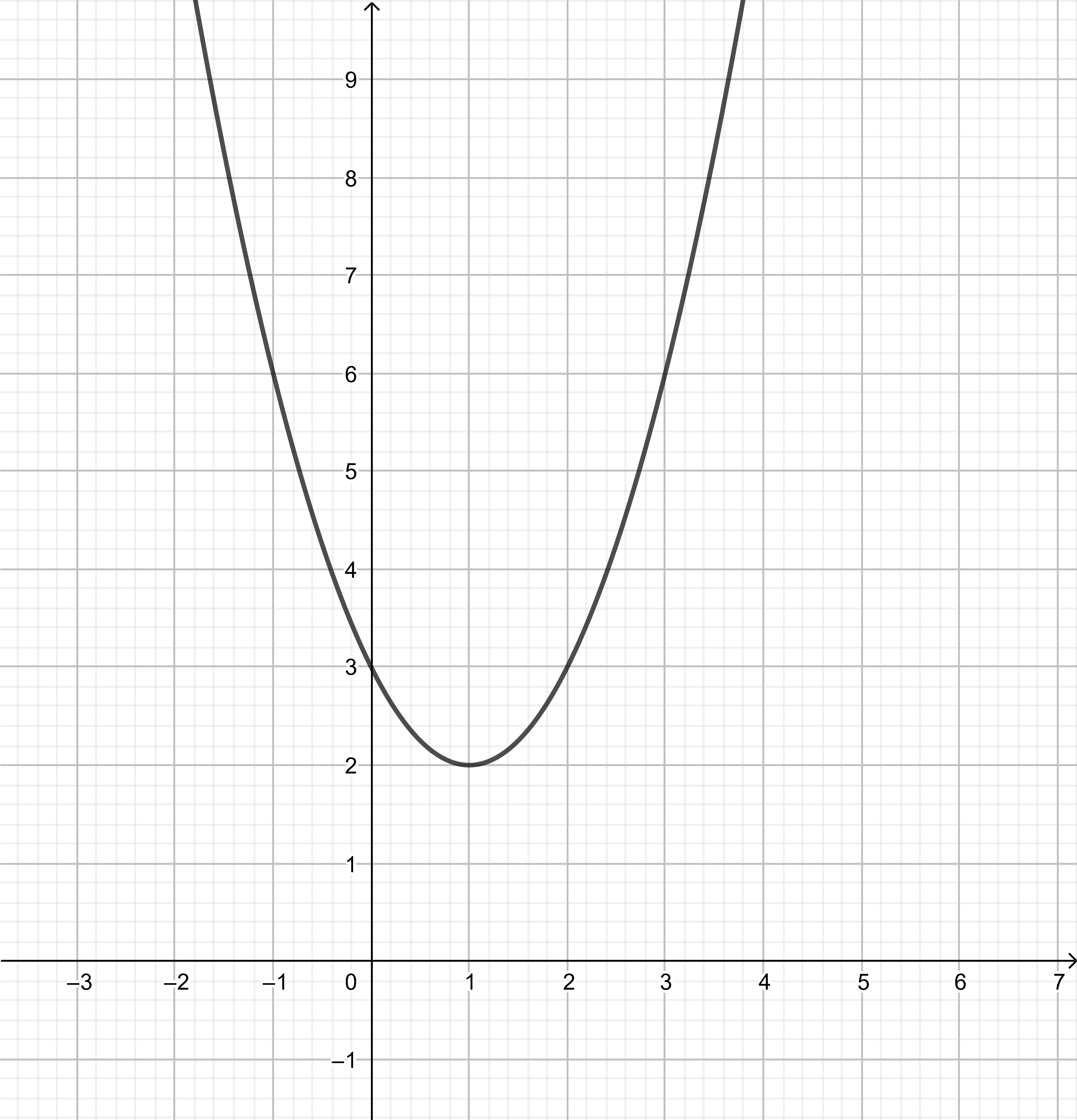
$text{$2$.The parabola has one real double root when it touches the $x$-axis.}$
$$
text{$3$.The parabola has two conjugate imaginary roots when it doesn’t cross the $x$-axis.}
$$
$$
(x-(3+4i))(x-(3-4i))=x^2-(3+4i)x-(3-4i)x+(3+4i)(3-4i)=x^2-6x+9-4i^2=x^2-6x+13
$$
$$
x=3+4i
$$
Subtract 3 from both sides of the equation:
$$
x-3=4i
$$
Square both sides of the equation:
$$
(x-3)^2=16i^2
$$
$i^2=-1$:
$$
(x-3)^2=-16
$$
Add 16 to both sides of the equation:
$$
(x-3)^2+16=0
$$
c. Alexia’s method is easier and requires less steps.
b. $(x-3)^2+16=0$
c. Alexia
a. Polynomial of degree 3
b. Polynomial of degree 7
c. Not a polynomial, because it contains $x$ in a power.
d. Not a polynomial, because it contains a square root.
e. Polynomial of degree 3
f. Not a polynomial, because it contains $x-2$ in a denominator.
b. Polynomial of degree 7
c. Not a polynomial
d. Not a polynomial
e. Polynomial of degree 3
f. Not a polynomial
$$
fleft(xright)=ax^2+bx+c
$$
$text{where $a, b$ and $c$ are real numbers and $aneq0$.}$
Quadratic function in the intercept form is:
$$
fleft(xright)=aleft(x-pright)left(x-qright)
$$
$$
text{The $x$-intercepts are the points $left(p, 0right)$ and $left(q, 0right)$.}
$$
#### a.
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=left(x-frac{3}{4}right)left(x-left(-2right)right) && text{Substitute} a=1, p=frac{3}{4}, text{and} q=-2. \
fleft(xright)&=left(x-frac{3}{4}right)left(x+2right) && text{Simplify.} \
fleft(xright)&=x^2+2x-frac{3}{4}x-frac{3}{2} \
fleft(xright)&=x^2+frac{5}{4}x-frac{3}{2} && text{Standard form.}
end{align*}
$$
$$
begin{align*}
fleft(xright)&=aleft(x-pright)left(x-qright) && text{Intercept form.} \
fleft(xright)&=aleft(x-left(-sqrt{5}right)right)left(x-sqrt{5}right) && text{Substitute} p=-sqrt{5}, text{and} q=sqrt{5}. \
fleft(xright)&=aleft(x+sqrt{5}right)left(x-sqrt{5}right) && text{Simplify.} \
fleft(xright)&=aleft(x^2-5right) && text{Use} left(a+bright)left(a-bright)=a^2-b^2. \
12&=aleft(left(-3right)^2-5right) && text{Substitute} left(x, fleft(xright)right)=left(-3, 12right). \
12&=aleft(9-5right) && text{Simplify.} \
12&=4a \
a&=3 && text{Divide both sides by} 4. \\
fleft(xright)&=aleft(x^2-5right) && text{Intercept form.} \
fleft(xright)&=3left(x^2-5right) && text{Substitute} a=3. \
fleft(xright)&=3x^2-15 && text{Standard form.}
end{align*}
$$
$textbf{b.}$ $fleft(xright)=3x^2-15$
$text{This function is called radical function. The domain of a radical function is any $x$ value}$
for which the radicand is positive or zero.
$$
2x-4geq 0Rightarrow 2xgeq 4Rightarrow xgeq 2
$$
$text{The domain: $left[2, inftyright)$}$
$$
text{As the square root is always positive or $0$, $sqrt{2x-4}geq0$.}
$$
$$
2+sqrt{2x-4}geq2+0=2
$$
$$
text{The range: $left[2, inftyright)$.}
$$
#### b.
$$
begin{align*}
y&=2+sqrt{2x-4} && text{Substitute} y text{for} fleft(xright). \
y-2&=sqrt{2x-4} && text{Subtract} 2 text{from both sides.} \
left(y-2right)^2&=2x-4 && text{Square each side}. \
y^2-4y+4&=2x-4 && text{Use} left(a-bright)^2=a^2-2ab+b^2. \
y^2-4y+8&=2x && text{Add} 4 text{to both sides.} \
x&=frac{y^2-4y+8}{2} && text{Divide both sides by} 2. \
f^{-1}left(yright)&=frac{y^2-4y+8}{2} && text{Substitute} f^{-1}left(yright) text{for} x. \
end{align*}
$$
#### c.
The domain of this function is limited to the range of the original function.
$text{The domain: $left[2, inftyright)$.}$
$$
text{The range: $left[2, inftyright)$.}
$$
$text{The range: $left[2, inftyright)$.}$
$textbf{b.}$ $f^{-1}left(yright)=dfrac{y^2-4y+8}{2}$
$textbf{c.}$ $text{The domain: $left[2, inftyright)$.}$
$text{The range: $left[2, inftyright)$.}$
$$
begin{align*}
left(3+2iright)left(4+iright)&=12+3i+8i+2i^2 && text{Distributive Property.} \
&=12+11i+2 cdot left(-1right) && i^2=-1. \
&=10+11i && text{Simplify.}
end{align*}
$$
#### b.
$$
begin{align*}
left(2+3iright)left(2-3iright)&=4-6i+6i-9i^2 && text{Distributive Property.} \
&=4-9 cdot left(-1right) && i^2=-1. \
&=13 && text{Simplify.}
end{align*}
$$
#### c.
$$
begin{align*}
left(5-2iright)left(5+2iright)&=25+10i-10i-4i^2 && text{Distributive Property.} \
&=25-4 cdot left(-1right) && i^2=-1. \
&=29 && text{Simplify.}
end{align*}
$$
#### d.
$$
begin{align*}
left(a+biright)left(a-biright)&=a^2-abi+abi-b^2i^2 && text{Distributive Property.} \
&=a^2-b^2 cdot left(-1right) && i^2=-1. \
&=a^2+b^2 && text{Simplify.}
end{align*}
$$
$textbf{c.}$ $29$ $textbf{d.}$ $a^2+b^2$
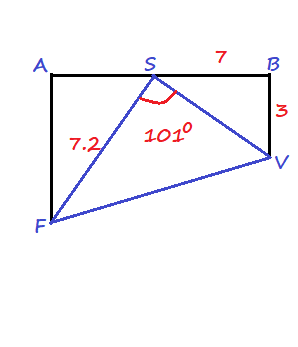
$SV^2=7^2+3^2$
$SV^2=58$
$$
SV=sqrt{58}approx 7.62
$$
First we determine $SV$ usisng the Pythagorean Theorem in the right triangle $BSV$:
$FV^2=7.2^2+7.62^2-2cdot 7.2cdot 7.62cdot (-0.190809)$
$FV^2=130.8415$
$FV=sqrt{130.8415}$
$$
FVapprox 11.44
$$
P_{triangle SVF}=SF+SV+FV=7.2+7.62+11.44=26.26
$$
begin{align*}
fleft(-2right)&=3 cdot left(5right)^{-2} \
&=frac{3}{25} \
&=0.12 \\
fleft(-1right)&=3 cdot left(5right)^{-1} \
&=frac{3}{5} \
&=0.6 \\
fleft(0right)&=3 cdot left(5right)^{0} \
&=3 cdot 1 \
&=3 \\
fleft(1right)&=3 cdot left(5right)^{1} \
&=3 cdot 5 \
&=15 \\
fleft(2right)&=3 cdot left(5right)^{2} \
&=3 cdot 25 \
&=75 \\
end{align*}
begin{table}[ht]
begin{center}
begin{tabular}{|c|c|}
hline
$x$&$fleft(xright)$\
hline
$-2$&$0.12$\
hline
$-1$&$0.6$\
hline
$0$&$3$\
hline
$1$&$15$\
hline
$2$&$75$\
hline
end{tabular}
end{center}
end{table}

text{The domain of function $fleft(xright)$ is $left(-infty, inftyright)$.}
subsection*{b.}
text{We build a table of values $ngeq 1$:}
begin{align*}
tleft(1right)&=3 cdot left(5right)^{1} \
&=3 cdot 5 \
&=15 \\
tleft(2right)&=3 cdot left(5right)^{2} \
&=3 cdot 25 \
&=75 \\
tleft(3right)&=3 cdot left(5right)^{3} \
&=3 cdot 125 \
&=375 \\
tleft(4right)&=3 cdot left(5right)^{4} \
&=3 cdot 625 \
&=1875 \\
end{align*}
begin{table}[ht]
begin{center}
begin{tabular}{|c|c|}
hline
$x$&$fleft(xright)$\
hline
$1$&$15$\
hline
$2$&$75$\
hline
$3$&$375$\
hline
$4$&$1875$\
hline
end{tabular}
end{center}
end{table}
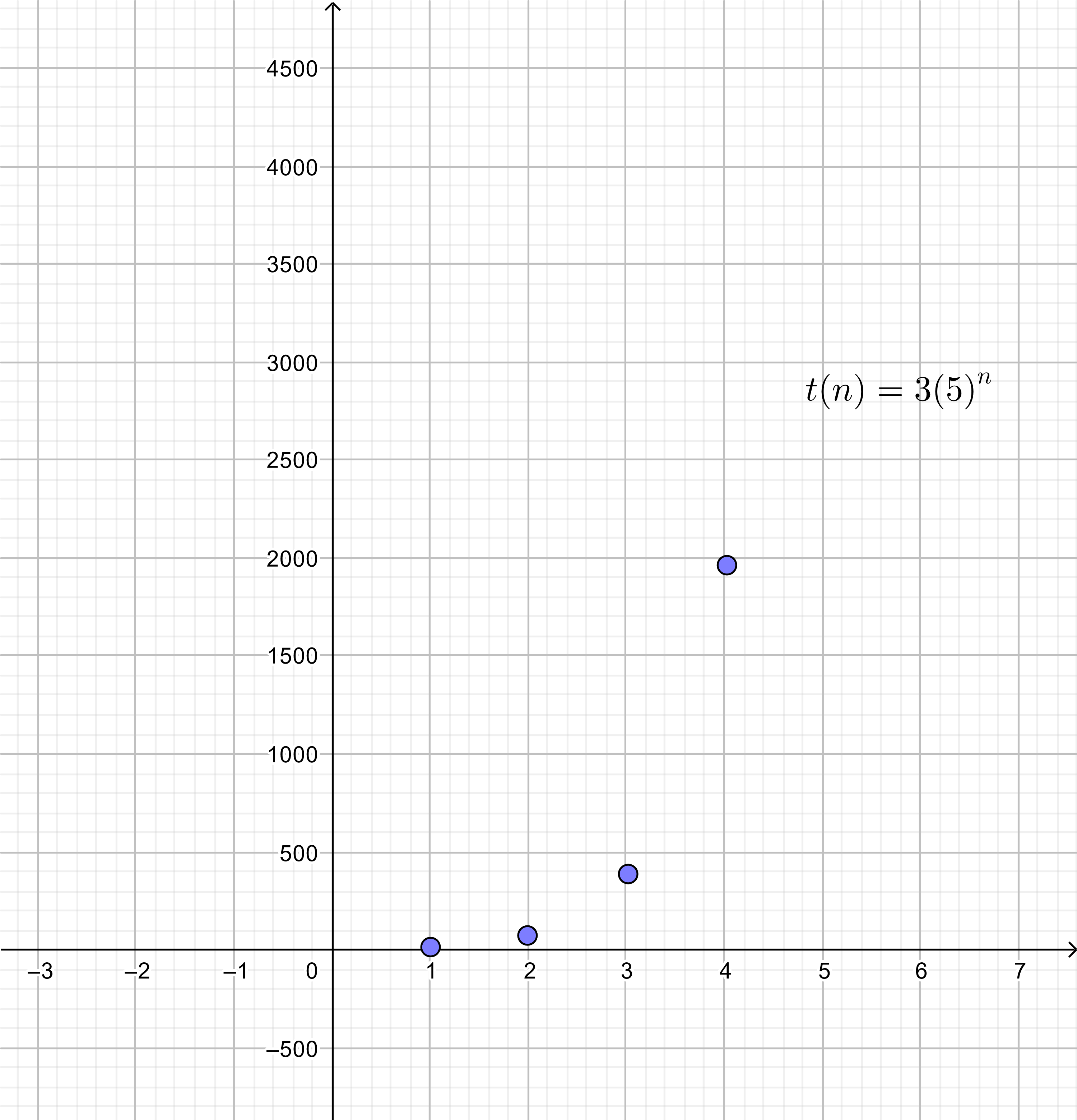
The domains of the two functions are different:
$$
begin{align*}
fleft(xright)&: left(-infty, inftyright) \
tleft(nright)&: leftlbrace1, 2, 3, 4, …rightrbrace
end{align*}
$$
The ranges of the two functions are different:
$$
begin{align*}
fleft(xright)&: left(0, inftyright) \
tleft(nright)&: leftlbrace15, 75, 375, 1875, …rightrbrace
end{align*}
$$
$$
text{$fleft(xright)$ is continuous function, while $tleft(nright)$ is discontinuous.}
$$
$textbf{b.}$ Sketch the graph by using the table.
$textbf{c.}$ $text{$fleft(xright)$ is continuous function, while $tleft(nright)$ is discontinuous.}$
a. 2
b. 3
c. 0
d. 1
b. 3
c. 0
d. 1
b. No
b. Use the distributive property:
$$
(x-2)(x^2-x+1)=x^3-x^2+x-2x^2+2x-2=x^2-3x^3+3x-2
$$
c. Use the zero product property:
$$
x-2=0text{ or } x^2-x+1=0
$$
Solve each equation to $x$:
$$
x=2text{ or } x=dfrac{-bpm sqrt{b^2-4ac}}{2a}=dfrac{1pm sqrt{-3}}{2(1)}=dfrac{1pm sqrt{3}i}{2}
$$
d. The function has one $x$-intercept (because the other roots are complex). The function also has one real root and 3 complex roots.
b. See explanation
c. $x=2$ and $x=dfrac{1pm sqrt{3}i}{2}$
d. 1, 1, 3
$$
fleft(xright)=ax^2+bx+c
$$
$text{where $a, b$ and $c$ are real numbers and $aneq0$.}$
The solutions of quadratic equation is:
$$
x_{1/2}=frac{-bpm sqrt{b^2-4ac}}{2a}
$$
#### a.
We determine the roots:
$$
begin{align*}
xleft(x^2+x-1right)&=0 && text{Substitute} p_1left(xright)=0. \
x&=0 text{or} x^2+x-1=0 && text{Use} a cdot b=0Rightarrow a=0 text{or} b=0. \
x&=0 text{or} x=frac{-1pm sqrt{1^2-4 cdot 1 cdot left(-1right)}}{2 cdot 1} && text{Quadratic equation.} \
x&=0 text{or} x=frac{-1pm sqrt{1+4}}{2} && text{Simplify.} \
x&=0 text{or} x=frac{-1pm sqrt{5}}{2} \
x&=0 text{or} x=frac{-1+sqrt{5}}{2} text{or} x=frac{-1-sqrt{5}}{2} \
end{align*}
$$
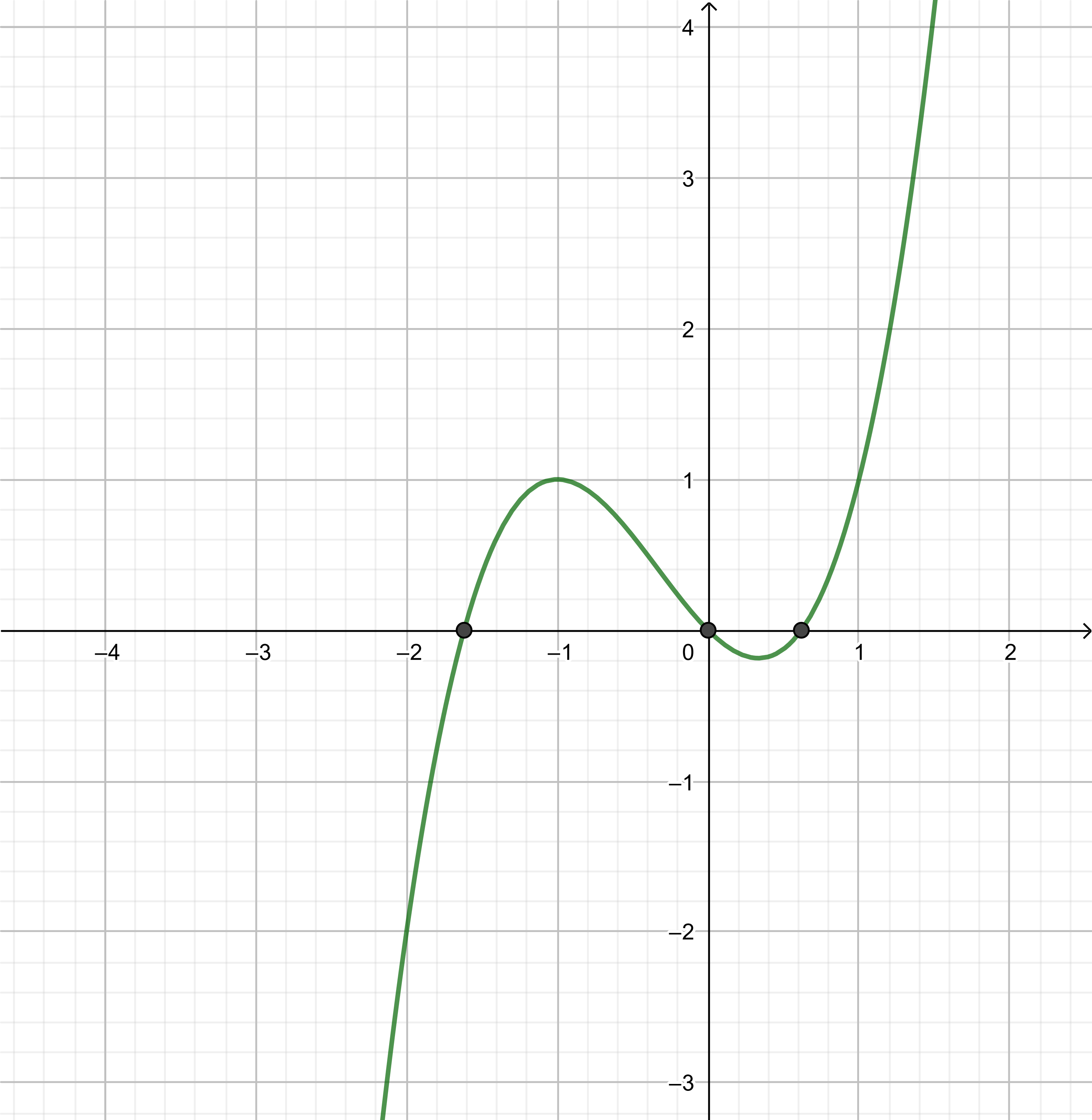
We determine the roots:
$$
begin{align*}
left(x+1right)left(5x^2+x+1right)&=0 && text{Substitute} p_2left(xright)=0. \
x+1&=0 text{or} 5x^2+x+1=0 && text{Use} a cdot b=0Rightarrow a=0 text{or} b=0. \
x&=-1 text{or} x=frac{-1pm sqrt{1^2-4 cdot 1 cdot 5}}{2 cdot 5} && text{Quadratic equation.} \
x&=-1 text{or} x=frac{-1pm sqrt{1-20}}{10} && text{Simplify.} \
x&=-1 text{or} x=frac{-1pm isqrt{19}}{10} \
x&=-1 text{or} x=frac{-1+isqrt{19}}{10} text{or} x=frac{-1-isqrt{19}}{10} \
end{align*}
$$
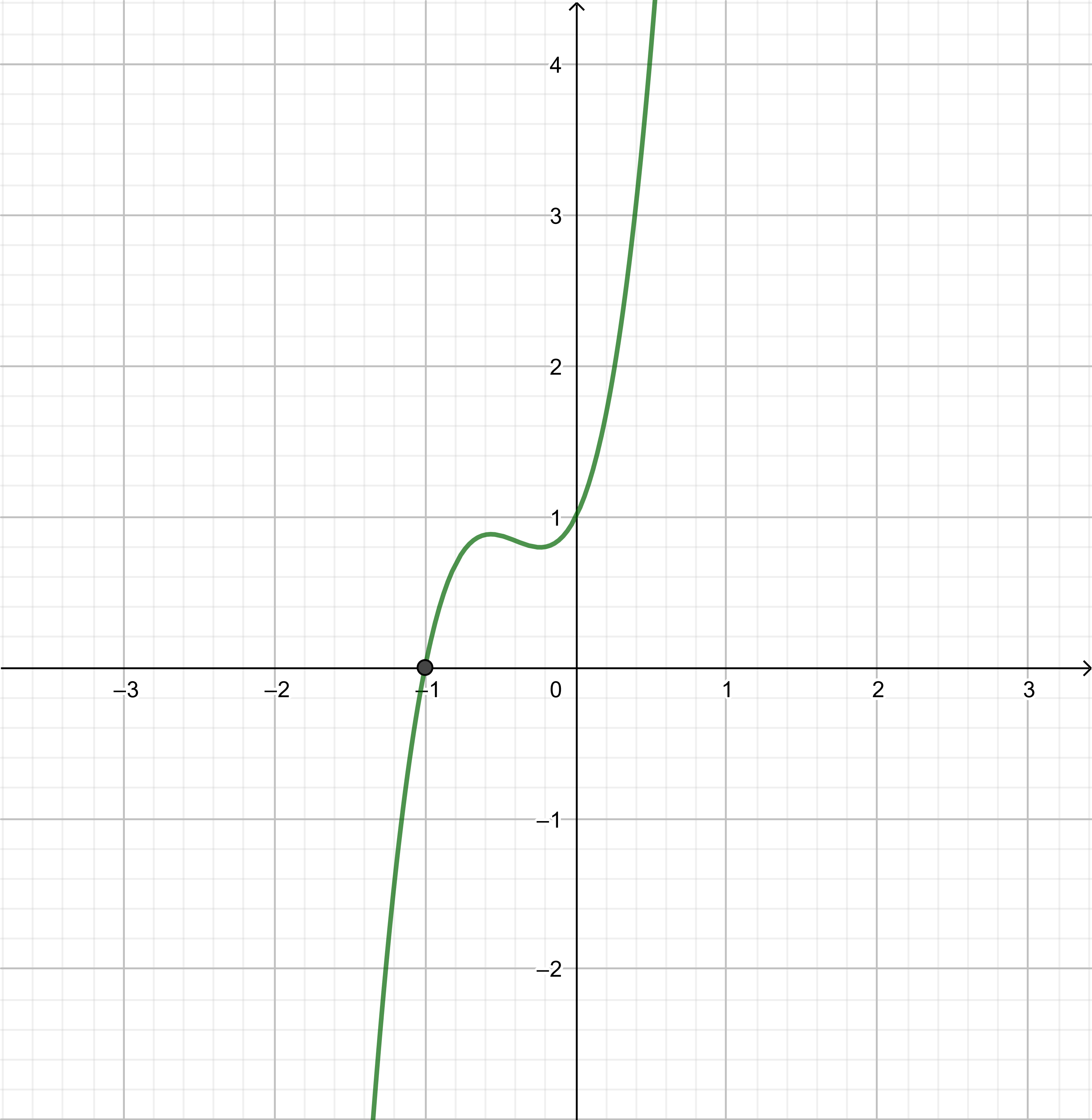
We determine the roots:
$$
begin{align*}
left(x^2+1right)left(x^2-4right)&=0 && text{Substitute} p_3left(xright)=0. \
x^2+1&=0 text{or} x^2-4=0 && text{Use} a cdot b=0Rightarrow a=0 text{or} b=0. \
x^2&=-1 text{or} x^2=4 && text{Solve for} x. \
x&=pm i text{or} x=pm 2 && text{Simplify.} \
x&=-i text{or} x=i text{or} x=-2 text{or} x=2 \
end{align*}
$$
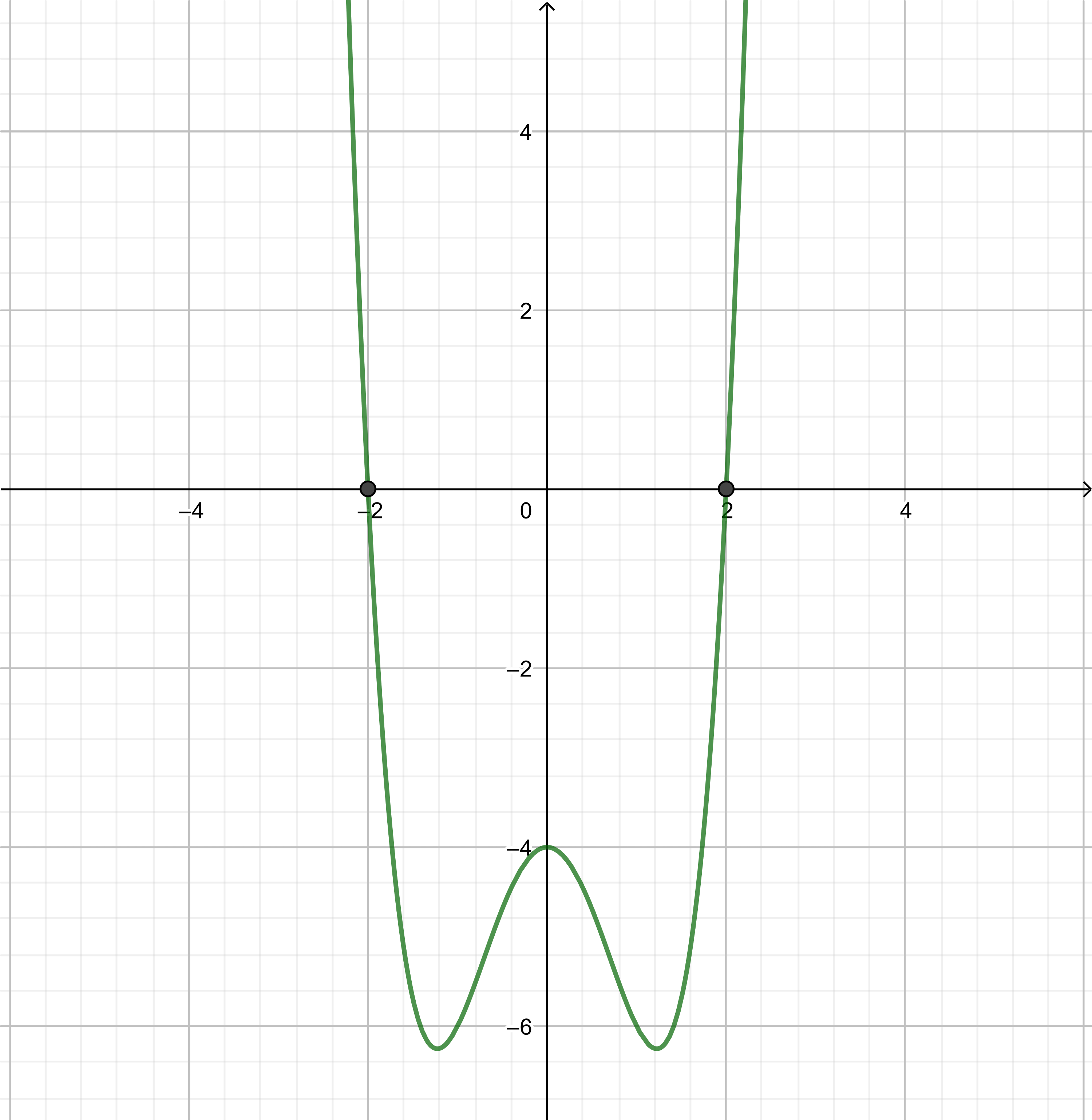
We determine the roots:
$$
begin{align*}
left(x^2+x-2right)left(x^2+x-1right)&=0 && text{Substitute} p_4left(xright)=0. \
x^2+x-2=0 text{or} x^2+x-1&=0 && text{Use} a cdot b=0Rightarrow a=0 text{or} b=0. \
x=frac{-1pmsqrt{1^2-4 cdot 1 cdot left(-2right)}}{2 cdot 1} text{or} x&=frac{-1pm sqrt{1^2-4 cdot 1 cdot left(-1right)}}{2 cdot 1} && text{Quadratic equation.} \
x=frac{-1pm sqrt{1+8}}{2} text{or} x&=frac{-1pm sqrt{1+4}}{2} && text{Simplify.} \
x=frac{-1pm3}{2} text{or} x&=frac{-1pm sqrt{5}}{2} \
x=-2 text{or} x=1 text{or} x&=frac{-1-sqrt{5}}{2} text{or} x=frac{-1+sqrt{5}}{2} \
end{align*}
$$
The equations can be factored completely and the solutions are easily found with the Zero Product Rule.
$textbf{b.}$ $x=-1 text{or} x=dfrac{-1+isqrt{19}}{10} text{or} x=dfrac{-1-isqrt{19}}{10}$
$textbf{c.}$ $x=-i text{or} x=i text{or} x=-2 text{or} x=2$
$textbf{d.}$ $x=-2 text{or} x=1 text{or} x=dfrac{-1-sqrt{5}}{2} text{or} x=dfrac{-1+sqrt{5}}{2}$
$$
text{In Problem $8$-$74$ we determined the roots of the polynomial:}
$$
$$
begin{align*}
x_1&=2 \
x_2&=frac{1-sqrt{3}i}{2} \
x_3&=frac{1+sqrt{3}i}{2}
end{align*}
$$
$$
text{We can write the polynomial as a product of $3$ linear factors:}
$$
$$
y=left(x-2right)left(x-frac{1-sqrt{3}i}{2}right)left(x-frac{1+sqrt{3}i}{2}right)
$$
#### b.
$$
text{In Problem $8$-$75$ we determined the roots of the polynomial:}
$$
$$
begin{align*}
x_1&=-i \
x_2&=i \
x_3&=-2 \
x_4&=2
end{align*}
$$
$$
text{We can write the polynomial as a product of $4$ linear factors:}
$$
$$
P_3left(xright)=left(x+iright)left(x-iright)left(x+2right)left(x-2right)
$$
#### c.
$$
text{In Problem $8$-$75$ we determined the roots of the polynomial:}
$$
$$
begin{align*}
x_1&=-2 \
x_2&=1 \
x_3&=frac{-1-sqrt{5}}{2} \
x_4&=frac{-1+sqrt{5}}{2}
end{align*}
$$
$$
text{We can write the polynomial as a product of $4$ linear factors:}
$$
$$
P_4left(xright)=left(x+2right)left(x-1right)left(x+dfrac{1+sqrt{5}}{2}right)left(x+dfrac{1-sqrt{5}}{2}right)
$$
$textbf{b.}$ $P_3left(xright)=left(x+iright)left(x-iright)left(x+2right)left(x-2right)$
$textbf{c.}$ $P_4left(xright)=left(x+2right)left(x-1right)left(x+dfrac{1+sqrt{5}}{2}right)left(x+dfrac{1-sqrt{5}}{2}right)$

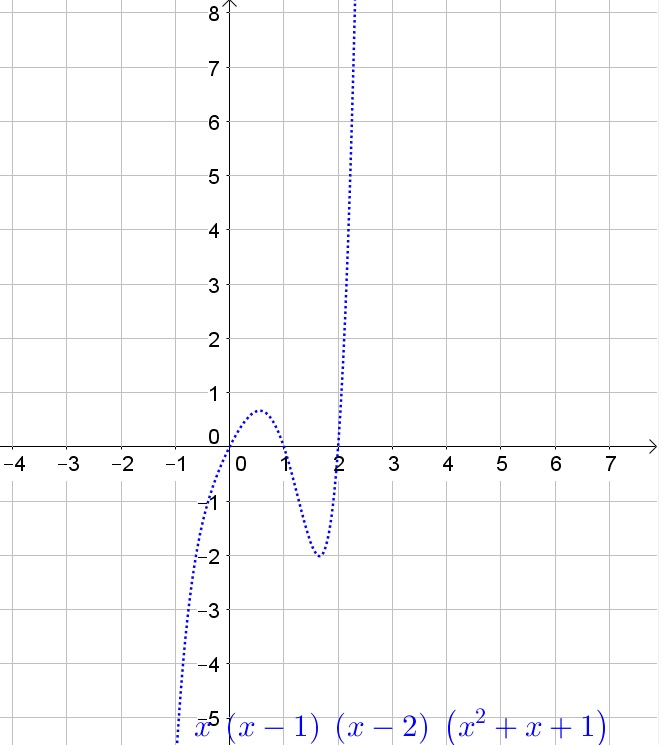
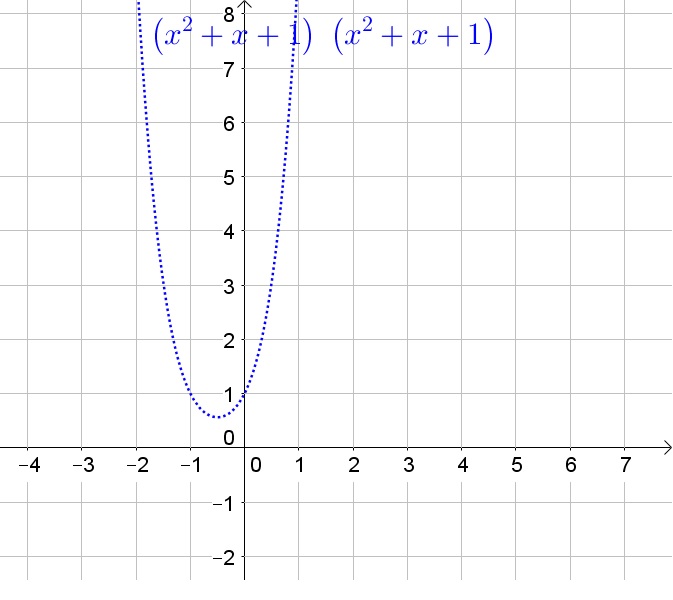
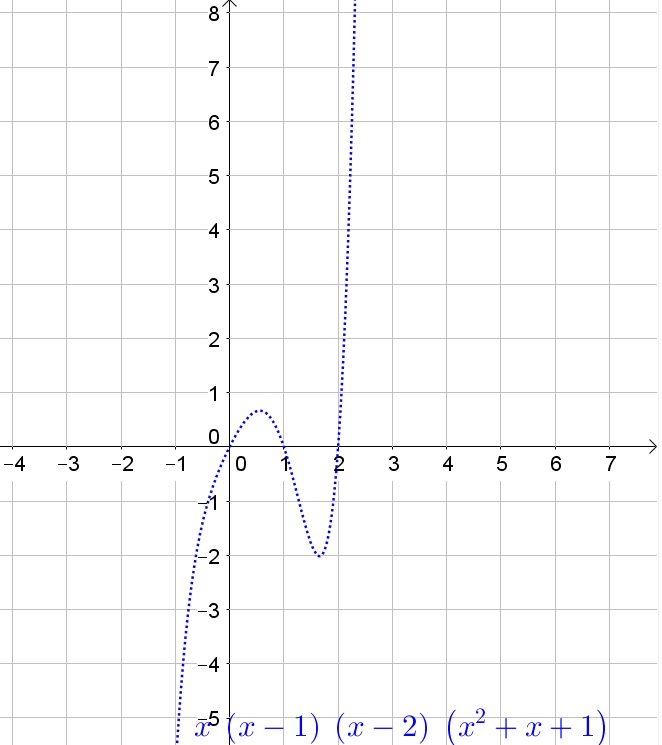
(a) 5
(b) 5
(c) 4
(d) 6
If $a,b$ are complex solutions of an equation, that this equation is of the form $x^2-2ax+(a^2+b^2)$.
a. $y=x^2-(-6)x+10=x^2+6x+10$
b. $y=(x-(5+sqrt{3}))(x-(5-sqrt{3}))=x^2-10x+12$
c. $y=(x+2)(x-sqrt{7})(x+sqrt{7})=(x+2)(x^2-7)$
d. $y=(x-4)(x^2+6x+10)$
b. $y=x^2-10x+12$
c. $y=(x+2)(x^2-7)$
d. $y=(x-4)(x^2+6x+10)$
y=x^3-9x
$$
y=x(x^2-9)=x(x-3)(x+3)
$$
$x-3=0Rightarrow x_2=3$
$x+3=0Rightarrow x_3=-3$
b) see graph
$$
begin{align*}
frac{171}{3}&=frac{3left(5right)^x}{3} && text{Divide both sides by} 3. \
57&=5^x && text{Simplify.} \
ln 57&=ln 5^x && text{Take the natural logarithmic of both sides.} \
ln 57&=xln 5 && text{Logarithmic properties:} log_ab^k=klog_ab \
x&=frac{ln 57}{ln 5} && text{Divide both sides by} ln 5. \
x&approx 2.512 && text{Use a calculator.}
end{align*}
$$
#### b.
$$
begin{align*}
frac{171y}{3}&=frac{3x^5}{3} && text{Divide both sides by} 3. \
57y&=x^5 && text{Simplify.} \
x&=sqrt[5]{57y} && text{Take the fifth root.} \
end{align*}
$$
$$
fleft(xright)=x^2+7x-9
$$
a)
Replace $x$ with $-3$
$$
fleft(-3right)=left(-3right)^2+7left(-3right)-9=-21
$$
b)
Replace $x$ with $i$
$$
fleft(iright)=left(iright)^2+7left(iright)-9
$$
$$
=-1+7i-9=-10+7i
$$
c)
Replace $x$ with $-3+i$
$$
fleft(-3+iright)=left(-3+iright)^2+7left(-3+iright)-9
$$
$$
=9-6i+i^2-21+7i-9=-6i-1-21+7i
$$
$$
fleft(-3+iright)=-22+i
$$
$$
fleft(-3right)=-21
$$
b)
$$
fleft(iright)=-10+7i
$$
c)
$$
fleft(-3+iright)=-22+i
$$
$$
f(-3)=(-3)^2+7(-3)-9=9-21-9=-21
$$
b. Replace $x$ with $i$:
$$
f(i)=(i)^2+7(i)-9=-1+7i-9=-10+7i
$$
c. Replace $x$ with $(-3+i)$:
$$
f(-3+i)=(-3+i)^2+7(-3+i)-9=9-6i+i^2-27+7i-9=-27+i+i^2=-28+i
$$
b. $-10+7i$
c. $-28+i$
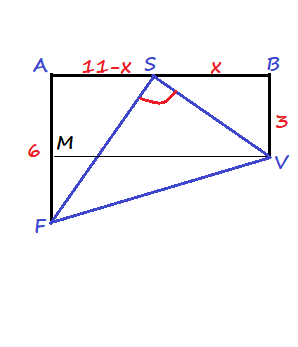
$SB=x$
$AS=11-x$.
We are given:
SV+SF=sqrt{x^2+3^2}+sqrt{6^2+(11-x)^2}
$$
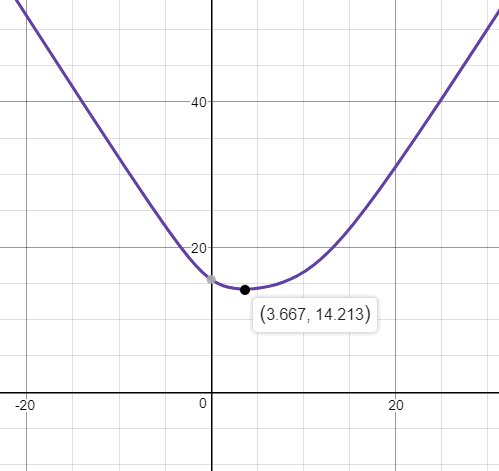
xapprox 3.67
$$
$FV^2=11^2+3^2$
$FV=sqrt{130}$
$$
FVapprox 11.40
$$
P_{triangle FSV}=SV+SF+FV=14.21+11.40=25.61
$$
text{Average rate of change}=frac{Delta y}{Delta x}=frac{y_2-y_1}{x_2-x_1}=m=text{slope}
$$
#### a.
$$
begin{align*}
text{Average rate of change}&=frac{y_2-y_1}{x_2-x_1} && text{Write the Formula.} \
&=frac{70^{circ}text{F}-85^{circ}text{F}}{3:00 text{p.m.}-2:04 text{p.m.}} && text{Substitute the given data.} \
&=frac{-15^{circ}text{F}}{56 text{minutes}} && text{Simplify.} \
&=-0.268^{circ}text{F}/text{minute}
end{align*}
$$
The point-slope form:
$$
y-y_1=mleft(x-x_1right)
$$
$$
begin{align*}
y-y_1&=mleft(x-x_1right) && text{The point-slope form.} \
y-85^{circ}text{F}&=-0.268^{circ}text{F}/text{minute}left(2:15 text{p.m.}-2:04 text{p.m.}right) && text{Substitute the given data.} \
y-85^{circ}text{F}&=-0.268^{circ}text{F}/text{minute}cdot 9 text{minutes} && text{Simplify} \
y-85^{circ}text{F}&=-2.41^{circ}text{F} \
y&=85^{circ}text{F}-2.41^{circ}text{F} && text{Add} 85^{circ}text{F} text{to both sides.} \
y&=82.59^{circ}text{F}
end{align*}
$$
#### b.
$$
begin{align*}
text{Average rate of change}&=frac{y_2-y_1}{x_2-x_1} && text{Write the Formula.} \
&=frac{70^{circ}text{F}-72^{circ}text{F}}{3:27 text{p.m.}-3:01 text{p.m.}} && text{Substitute the given data.} \
&=frac{-2^{circ}text{F}}{26 text{minutes}} && text{Simplify.} \
&=-0.077^{circ}text{F}/text{minute}
end{align*}
$$
$text{This means the temperature cooled by $0.077^{circ}text{F}/text{minute}$. The manager was wrong in his}$
$text{prediction because the average rate of change diminished as time went by from $3^{circ}text{F}$ in}$
$$
text{$11$ minutes to $1^{circ}text{F}$ in $9$ minutes.}
$$
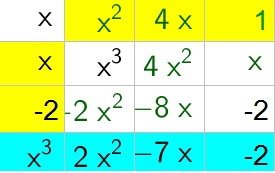
x^2+4x+1
$$
b. $-7x^3$ was obtained by adding the term in cell B3 to term C4.
c.

8x^4-22x^2-4x+15
$$
b. The third term in the answer is the sum of cell B5 and cell C4.
c. Cell B5 is 12x (part of the given solution) decreased by the value in cell C4.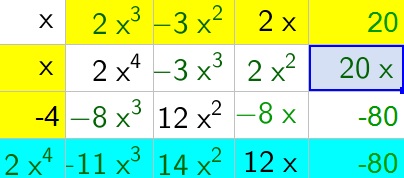
dfrac{6x^2+7x^2-16x+10}{2x+5}=3x^2-4x+2
$$
$$
(2x+5)cdot (3x^2-4x+2)=6x^3+7x^2-16x+10
$$
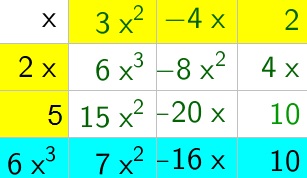
b. $dfrac{6x^3+7x^2-16x+18}{2x+5}=3x^2-4x+2+dfrac{8}{2x+5}$
c. $dfrac{6x^3+11x^2-12x-1}{3x+1}=2x^2+3x-5-dfrac{4}{3x+1}$
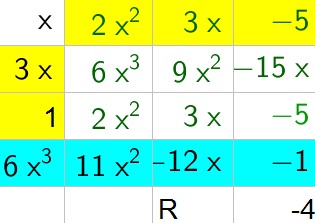
b. $3x^2-4x+2+dfrac{8}{2x+5}$
c. $2x^2+3x-5-dfrac{4}{3x+1}$
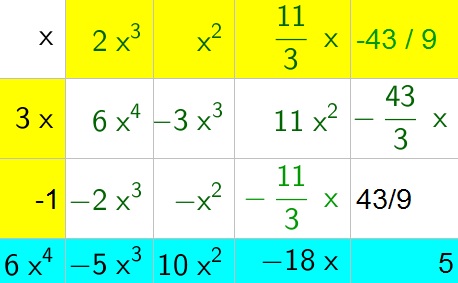
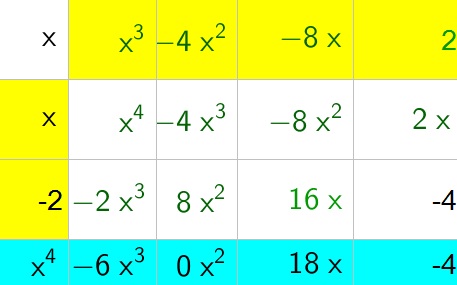
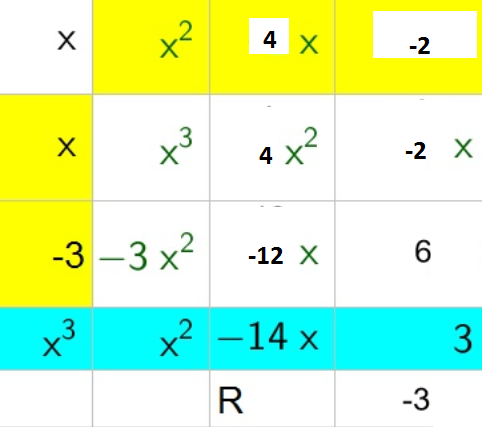
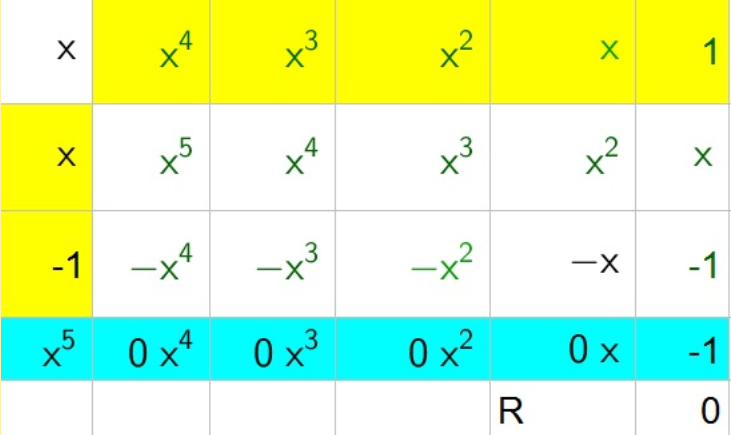
b. $x^3-4x^2-8x+2$
c. $x^2+4x-2-dfrac{3}{x-3}$
d. $x^4+x^3+x^2+x+1$
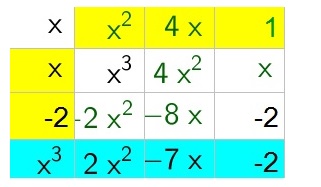
$$
begin{align*}
x^3+2x^3-7x-2&=(x-2)(x^2+4x+1)
end{align*}
$$
We then know that 2 is a root due to the term $(x-2)$.
Next, we determine the roots of $x^2+4x+1$ using the quadratic formula $x=frac{-bpm sqrt{b^2-4ac}}{2a}$ for a quadratic equation $ax^2+bx+c$.:
$$
begin{align*}
x&=frac{-4pm sqrt{(-4)^2-4(1)(1)}}{2(1)}
\ &=frac{-4pm sqrt{16-4}}{2}
\ &=frac{-4pm sqrt{12}}{2}
\ &=frac{-4pm sqrt{4cdot 3}}{2}
\ &=frac{-4pm 2sqrt{3}}{2}
\ &=-2pm sqrt{3}
end{align*}
$$
Thus the roots of the function are then $x=2$, $x=-2+sqrt{3}approx -0.2679$ and $x=-2-sqrt{3}approx -3.7321$.
$$
text{Divide $P_1left(xright)$ by $D_1left(xright)$:}
$$
$polylongdiv{2x^3-21x^2-9x-30}{x-11}$
$$
text{We rewrite $P_1left(xright)$ in the form: $P_1left(xright)=D_1left(xright)Qleft(xright)+R$.}
$$
$$
P_1left(xright)=left(x-11right)left(2x^2+x+2right)-8
$$
#### b.
$$
text{Divide $P_2left(xright)$ by $D_2left(xright)$:}
$$
$polylongdiv{3x^4+5x^3-4x+3}{x+2}$
$$
text{We rewrite $P_2left(xright)$ in the form: $P_2left(xright)=D_2left(xright)Qleft(xright)+R$.}
$$
$$
P_2left(xright)=left(x+2right)left(3x^3-x^2+2x-8right)+19
$$
#### c.
$$
begin{align*}
P_1left(11right)&=2 cdot 11^3-21 cdot 11^2-9 cdot 11-30 && text{Use the original polynomial.} \
&=2662-2541-99-30=-8 && text{Simplify.} \
P_1left(11right)&=left(11-11right)left(2 cdot 11^2+11+2right)-8 && text{Use the rewritten polynomial.} \
&=0-8=-8 && text{Simplify.}
end{align*}
$$
$$
text{We notice that the value of $P_1left(xright)$ in $x=11$ is the remainder of the division of $P_1left(xright)$ by $x-11$.}
$$
$$
begin{align*}
P_2left(-2right)&=3 cdot left(-2right)^4+5 cdot left(-2right)^3-4 cdot left(-2right)+3 && text{Use the original polynomial.} \
&=48-40+8+3=19 && text{Simplify.} \
P_2left(-2right)&=left(-2+2right)left(3 cdot left(-2right)^3-left(-2right)^2+2 cdot left(-2right)-8right)+19 && text{Use the rewritten polynomial.} \
&=0+19=19 && text{Simplify.}
end{align*}
$$
$$
text{We notice that the value of $P_2left(xright)$ in $x=-2$ is the remainder of the division of $P_2left(xright)$ by $x+2$.}
$$
#### e.
$$
text{We rewrite $Pleft(xright)$ in the form: $Pleft(xright)=Dleft(xright)Qleft(xright)+R$.}
$$
$$
Pleft(xright)=left(x-cright)left(2x^2+x+2right)-8
$$
$$
text{For $x=c$ we get:}
$$
$$
begin{align*}
Pleft(cright)&=left(c-cright)Qleft(cright)+R \
Pleft(cright)&=0 cdot Qleft(cright)+R \
Pleft(cright)&=0+R \
Pleft(cright)&=R
end{align*}
$$
#### f.
$$
text{If $Pleft(xright)$ is divided by $x-c$ and the remainder is $0$, it means that $c$ is the root of $Pleft(xright)$.}
$$
$textbf{b.}$ $P_2left(xright)=left(x+2right)left(3x^3-x^2+2x-8right)+19$
$textbf{c.}$ $P_1left(11right)=-8$, $textbf{d.}$ $P_2left(-2right)=19$,
$textbf{e.}$ True $textbf{f.}$ $text{$c$ is the root of $Pleft(xright)$.}$
b.
$$
(-7)^3+5(-7)^2-16(-7)-14=-343+245+112-14=0
$$
Thus $x=-7$ is a solution of the equation.
c. If $x=-7$ is a root, then the corresponding factor is $(x+7)$.
d.
$$
polylongdiv{x^3+5x^2-16x-14}{x+7}
$$
e.
$$
x^3+5x^2-16x-14=(x+7)(x^2-2x-2)=0
$$
f. Determine the discriminant of the given function $f(x)=x^2-2x-2$:
$$
D=b^2-4ac=(-2)^2-4(1)(-2)=4+8=12
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{2pm sqrt{12}}{2(1)}=dfrac{2pm 2sqrt{3}}{2}=1pm sqrt{3}
$$
b. $x=-7$ is a solution
c. $(x+7)$
d. $x^2-2x-2$
e. $x^2-2x-2$
f. $x=1pm sqrt{3}$
polylongdiv{2x^3+3x^2-8x+3}{x-1}
$$
$$
2x^3+3x^2-8x+3=(x-1)(2x^2+5x-3)=0
$$
Determine the discriminant of the given function $f(x)=2x^2+5x-3$:
$$
D=b^2-4ac=(5)^2-4(2)(-3)=25+24=49
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{-5pm sqrt{49}}{2(2)}=-3text{ or } dfrac{1}{2}
$$
x=-3,frac{1}{2},1
$$
If we multiply only the constants then we obtain 30 and thus the constant term of the polynomial should be 30.
Thus polynomial (c) is the correct polynomial.
$$
polylongdiv{5x^2-7x-6}{x-2}
$$
Thus the factors are $(x-2)$ and $(5x+3)$.
b. The solutions of the equation can then be obtained by setting every factor equal to zero:
$$
x-2=0 text{ or } 5x+3=0
$$
Solve each equation to $x$:
$$
x=2text{ and }x=-dfrac{3}{5}
$$
c. The roots of the factors are solutions of the equation.
d. The product of the numerators of the solutions are equal to the constant term, while the denominator of one of the solutions is equal to the lead coefficient.
b. $x=2text{ and }x=-dfrac{3}{5}$
c. See explanation
d. See explanation
begin{align*}
y&=left(x+1right)^2-3 && text{Substitute} y text{for} gleft(xright). \
y+3&=left(x+1right)^2 && text{Add} 3 text{to both sides.} \
sqrt{y+3}&=mid x+1mid && text{Square root each side}. \
sqrt{y+3}&=x+1 && text{Use} xgeq -1. \
sqrt{y+3}-1&=x && text{Subtract} 1 text{from both sides.} \
g^{-1}left(yright)&=sqrt{y+3}-1 && text{Substitute} g^{-1}left(yright) text{for} x. \
end{align*}
$$
$text{The domain of $g^{-1}left(xright)$ is: $left[-3, inftyright)$.}$
$$
text{The range of $g^{-1}left(xright)$ is: $left[-1, inftyright)$.}
$$
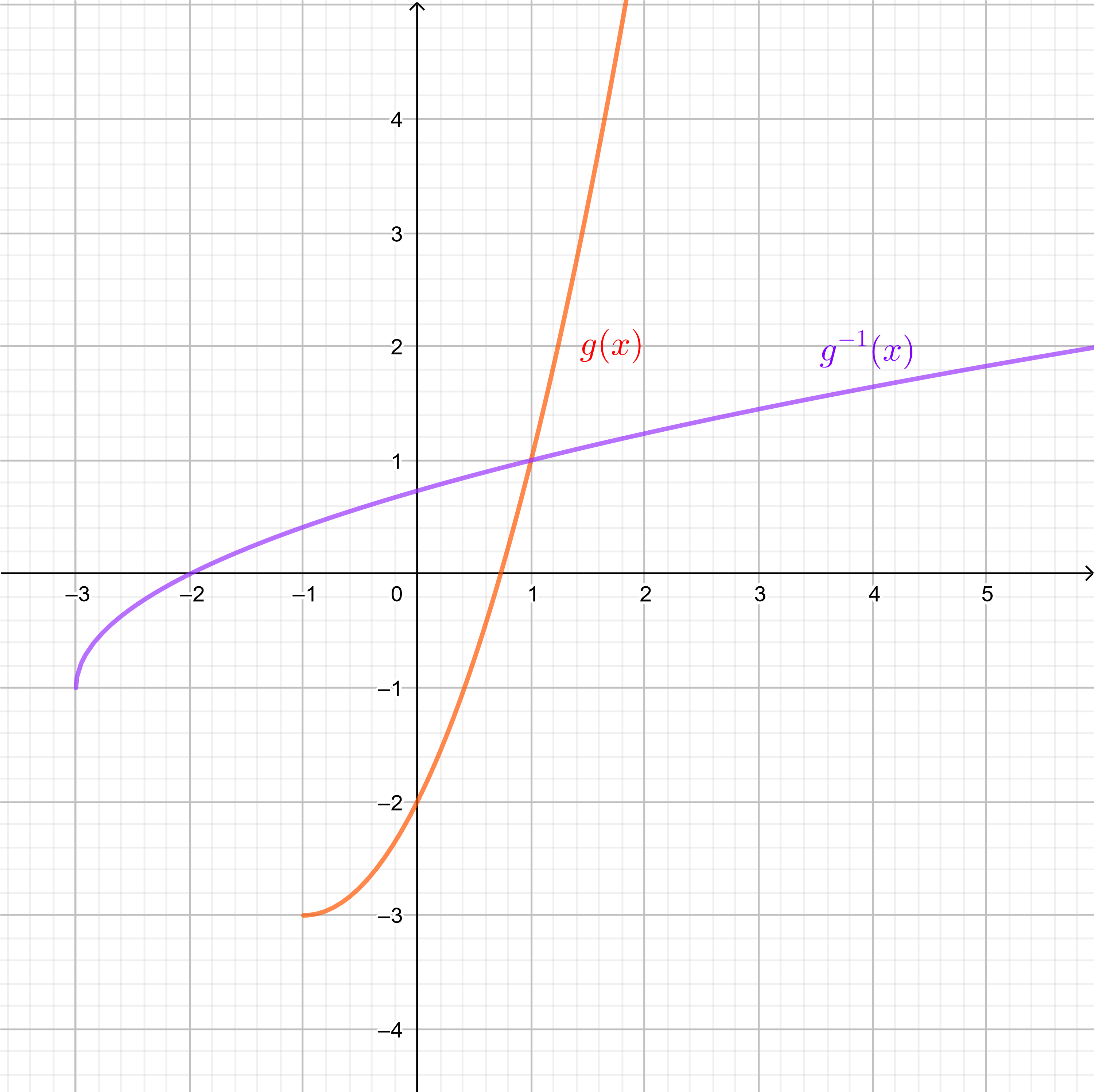
$text{The domain of $g^{-1}left(xright)$ is: $left[-3, inftyright)$.}$
$$
text{The range of $g^{-1}left(xright)$ is: $left[-1, inftyright)$.}
$$
$$
y=mx+b
$$
$text{where $m$ is slope.}$
$$
text{The slope of $y=-5x+2$ is $m_1=-5$.}
$$
$$
begin{align*}
m_1 cdot m_2&=-1 && text{The lines are perpendicular.} \
m_2&=-frac{1}{m_1} && text{Divide both sides by} m_1. \
m_2&=-frac{1}{-5} && text{Substitute} m_1=-5 \
m_2&=frac{1}{5} && text{Simplify.}
end{align*}
$$
The point-slope form:
$$
y-y_1=mleft(x-x_1right)
$$
$$
begin{align*}
y-y_1&=mleft(x-x_1right) && text{The point-slope form.} \
y-5&=frac{1}{5}left(x-left(-2right)right) && text{Substitute the given data.} \
y-5&=frac{1}{5}left(x+2right) && text{Simplify} \
y-5&=frac{1}{5}x+frac{2}{5} && text{Distibutive Property.} \
y&=frac{1}{5}x+frac{2}{5}+5 && text{Add} 5 text{to both sides.} \
y&=frac{1}{5}x+frac{27}{5}
end{align*}
$$
y=dfrac{1}{5}x+dfrac{27}{5}
$$
polylongdiv{x^3-9x^2+19x+5}{x-5}
$$
$$
x^3-9x^2+19x+5div (x-5)=x^2-4x-1
$$
x^2-4x-1
$$
$$
text{Divide $Pleft(xright)$ by $Dleft(xright)$:}
$$
$polylongdiv{2x^4-x^2+3x+5}{x-1}$
$$
text{We rewrite $Pleft(xright)$ in the form: $Pleft(xright)=Dleft(xright)Qleft(xright)+R$.}
$$
$$
Pleft(xright)=left(x-1right)left(2x^3+2x^2+x+4right)+9
$$
#### b.
$$
text{Divide $Pleft(xright)$ by $Dleft(xright)$:}
$$
$polylongdiv{x^5-2x^3+1}{x-3}$
$$
text{We rewrite $Pleft(xright)$ in the form: $Pleft(xright)=Dleft(xright)Qleft(xright)+R$.}
$$
$$
Pleft(xright)=left(x-3right)left(x^4+3x^3+7x^2+21x+63right)+190
$$
#### c.
$text{The rational solutions $dfrac{p}{q}$ to the equation $Pleft(xright)=0$ have $p$ dividing the constant term}$
$$
text{and $q$ dividing the leading coefficient.}
$$
$textbf{b.}$ $Pleft(xright)=left(x-3right)left(x^4+3x^3+7x^2+21x+63right)+190$
$textbf{c.}$ $text{$dfrac{p}{q}$ where $p$ divides the constant term and $q$ divides the leading coefficient.}$
$text{The graph of $y=fleft(xright)$ at right has degree $3$.}$
$text{It has $1$ real root with multiplicity $1$,}$
$$
text{$1$ real root with multiplicity $2$ and no complex roots.}
$$
#### b.
$text{The graph of $y=fleft(xright)$ at right has degree $3$.}$
$$
text{It has $1$ real root, and $2$ complex roots.}
$$
#### c.
$text{The graph of $y=fleft(xright)$ at right has degree $4$.}$
$$
text{It has $4$ real roots and no complex roots.}
$$
#### d.
$text{The graph of $y=fleft(xright)$ at right has degree $4$.}$
$$
text{It has $2$ real roots and $2$ complex roots.}
$$
$text{$1$ real root with multiplicity $2$ and no complex roots.}$
$textbf{b.}$ $text{Degree $=3$. It has $1$ real root, and $2$ complex roots.}$
$textbf{c.}$ $text{Degree $=4$. It has $4$ real roots and no complex roots.}$
$textbf{d.}$ $text{Degree $=4$. It has $2$ real roots and $2$ complex roots.}$
y=x(2x+5)(2x-7)
$$
$2x+5=0Rightarrow 2x=-5Rightarrow x_2=-dfrac{5}{2}$
$2x-7=0Rightarrow 2x=7Rightarrow x_3=dfrac{7}{2}$
$y=0$.
Because the leading coefficient is positive, the left end goes down,while the right end goes up.
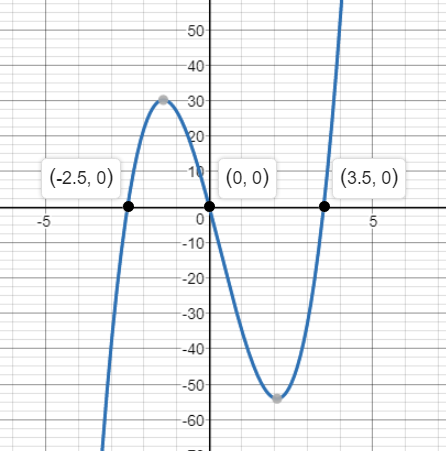
y=(15-2x)^2(x+3)
$$
$$
x+3=0Rightarrow x_2=-3
$$
$y=0$.
Because the leading coefficient is positive, the left end goes down,while the right end goes up.
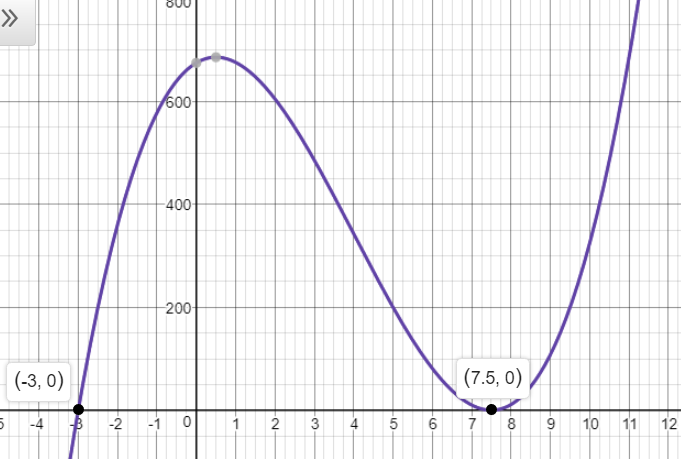
b- $log (sqrt {10})=dfrac {1}{2}$ ($10^{ left(frac {1}{2} right)}=sqrt {10}$)
c- $log (0)=-infty$ ($10^{-infty}=0)$
d- $10^{ left(frac {2}{3} times log (27) right)}=10^{ left(log (27)^{(frac {2}{3})} right)}=(27)^{(frac {2}{3})}$ ($10^{(log (x))}=x$)
$10^{ left(frac {2}{3} times log (27) right)}=(sqrt [3] {27})^2=9$
b- $log (sqrt {10})=dfrac {1}{2}$
c- $log (0)=-infty$
d- $10^{ left(frac {2}{3} times log (27) right)}=9$
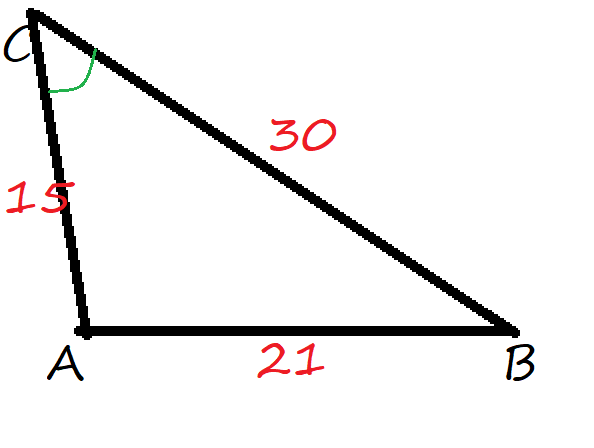
$cos C=dfrac{CA^2+BC^2-AB^2}{2cdot CAcdot BC}$
$=dfrac{15^2+30^2-21^2}{2cdot 15cdot 30}$
$=dfrac{684}{900}$
$=0.76$
$$
C=cos^{-1} 0.76approx 40.5text{textdegree}
$$
Capprox 40.5text{textdegree}
$$
polylongdiv{x^4-x^3-5x^2+3x+6}{x+1}
$$
$$
polylongdiv{x^3-2x^2-3x+6}{x-2}
$$
Thus we then obtain:
$$
x^4-x^3-5x^2+3x+6=(x+1)(x-2)(x^2-3)=(x+1)(x-2)(x-sqrt{3})(x+sqrt{3})
$$
Thus the zeros of the polynomial are then $x=-1, 2, pm sqrt{3}$.
x=-1, 2, pm sqrt{3}
$$
$$
(x+1)(x-2)(x-sqrt{3})(x+sqrt{3})
$$
P(x)=x^4-x^3-5x^2+3x+6
$$
(x-1), (x+1), (x-2), (x+2), (x-3), (x+3), (x-6), (x+6)
$$
{ pm 1, pm 2, pm 3, pm 6}
$$
$P(-1)=(-1)^4-(-1)^3-5(-1)^2+3(-1)+6=0checkmark$
$P(2)=2^4-2^3-5(2^2)+3(2)+6=0checkmark$
$P(-2)=(-2)^4-(-2)^3-5(-2)^2+3(-2)+6=4not =0$
$P(3)=3^4-3^3-5(3^2)+3(3)+6=24not =0$
$P(-3)=(-3)^4-(-3)^3-5(-3)^2+3(-3)+6=60not=0$
$P(6)=6^4-6^3-5(6^2)+3(6)+6=924not =0$
$P(-6)=(-6)^4-(-6)^3-5(-6)^2+3(-6)+6=1320not=0$
P(x)=(x+1)(x^3-2x^2-3x+6)
$$
$$
=(x+1)(x-2)(x-sqrt 3)(x+sqrt 3)
$$
$x-2=0Rightarrow x_2=2$
$x-sqrt 3=0Rightarrow x_3=sqrt 3$
$x+sqrt 3=0Rightarrow x_4=-sqrt 3$
$$
{-1, 2, -sqrt 3,sqrt 3}
$$
$text{of the constant term. Thus, the possible real roots of this polynomial are $pm 1$, or $pm 5$.}$
$text{In this case there are $4$ possible roots to check. In order to do this, we should substitute}$
each zero into the polynomial to see which of them, if any, make the polynomial equal to zero.
We will still have to divide by the corresponding expression until we have the root.
$text{Substituting values for $Q_1left(xright)$, we get:}$
$$
begin{align*}
Q_1left(1right)&=1^4-8 cdot 1^3+18 cdot 1^2-16 cdot 1+5 \
&=1-8+18-16+5 \
&=0 \\
Q_1left(-1right)&=left(-1right)^4-8 cdot left(-1right)^3+18 cdot left(-1right)^2-16 cdot left(-1right)+5 \
&=1+8+18+16+5 \
&=48 \\
Q_1left(5right)&=5^4-8 cdot 5^3+18 cdot 5^2-16 cdot 5+5 \
&=625-1000+450-80+5 \
&=0 \\
Q_1left(-5right)&=left(-5right)^4-8 cdot left(-5right)^3+18 cdot left(-5right)^2-16 cdot left(-5right)+5 \
&=625+1000+450+80+5 \
&=2160 \\
end{align*}
$$
Now we can divide the polynomial by this factor.
text{Divide $Q_1left(xright)$ by $x-1$:}
$$
$$
polylongdiv{x^4-8x^3+18x^2-16x+5}{x-1}
$$
text{Divide $x^3-7x^2+11x-5$ by $x-5$:}
$$
$$
polylongdiv{x^3-7x^2+11x-5}{x-5}
$$
$$
begin{align*}
Q_1left(xright)&=left(x-1right)left(x-5right)left(x^2-2x+1right) \
&=left(x-1right)left(x-5right)left(x-1right)^2 \
&=left(x-1right)^3left(x-5right)
end{align*}
$$
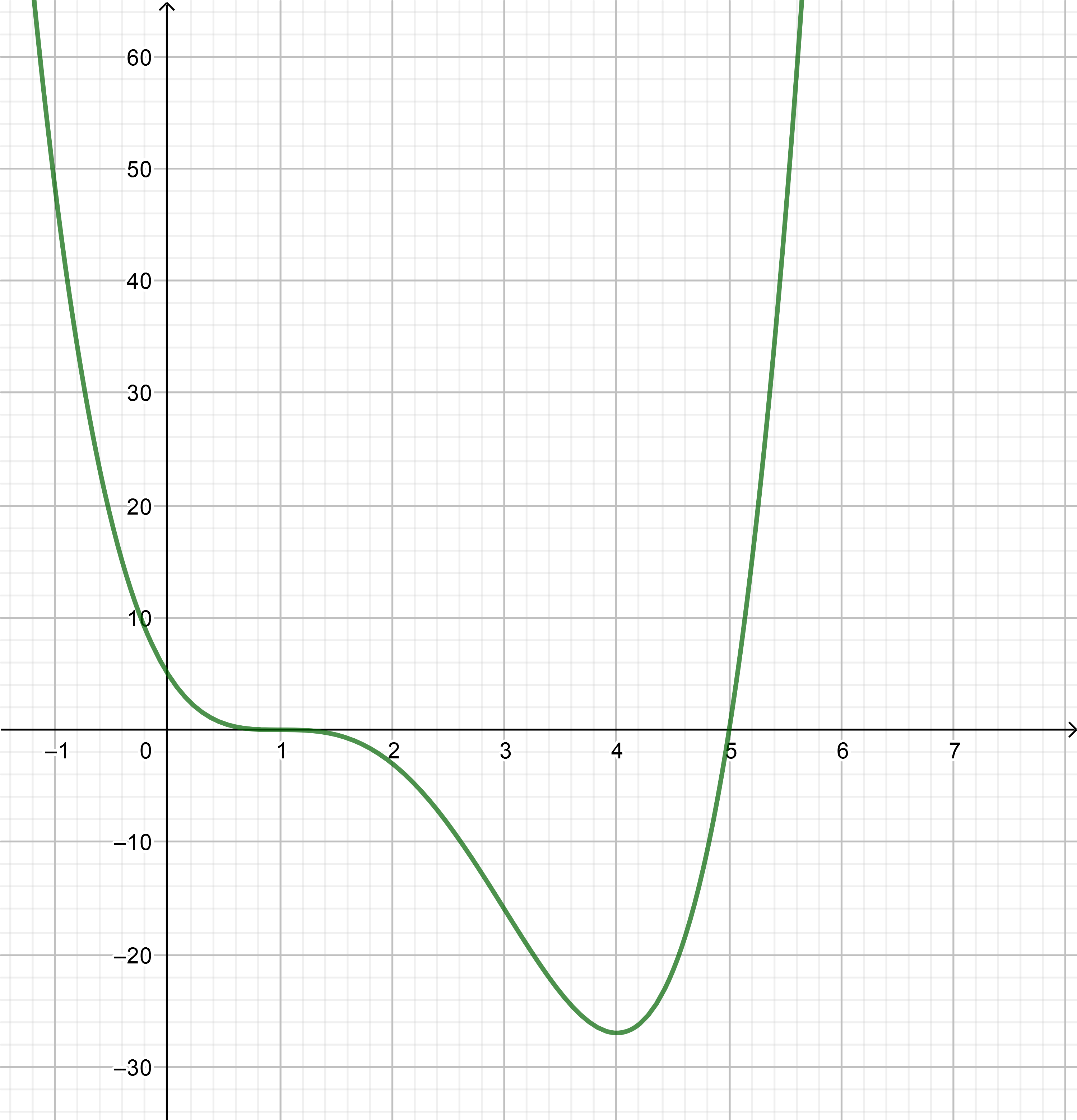
$text{The possible real roots of this polynomial are $pm 1$, or $pm 7$.}$
$text{Substituting values for $Q_2left(xright)$, we get:}$
$$
begin{align*}
Q_2left(1right)&=1^3+1^2-7 cdot 1-7 \
&=1+1-7-7 \
&=-12 \\
Q_2left(-1right)&=left(-1right)^3+left(-1right)^2-7 cdot left(-1right)-7 \
&=-1+1+7-7 \
&=0 \\
Q_2left(7right)&=7^3+7^2-7 cdot 1-7 \
&=343+49-7-7 \
&=378 \\
Q_2left(-7right)&=left(-7right)^3+left(-7right)^2-7 cdot left(-7right)-7 \
&=-343+49+49-7 \
&=-252 \\
end{align*}
$$
Now we can divide the polynomial by this factor.
text{Divide $Q_2left(xright)$ by $x+1$:}
$$
$polylongdiv{x^3+x^2-7x-7}{x+1}$
$$
begin{align*}
Q_2left(xright)&=left(x+1right)left(x^2-7right) \
&=left(x+1right)left(x-sqrt{7}right)left(x+sqrt{7}right) \
end{align*}
$$

$text{The possible real roots of this polynomial are $pm 1$, or $pm 5$.}$
$text{Substituting values for $Q_3left(xright)$, we get:}$
$$
begin{align*}
Q_3left(1right)&=1^3+3 cdot 1^2+1-5 \
&=1+3+1-5 \
&=0 \\
Q_3left(-1right)&=left(-1right)^3+3 cdot left(-1right)^2+left(-1right)-5 \
&=-1+3-1-5 \
&=-4 \\
Q_3left(5right)&=5^3+3 cdot 5^2+5-5 \
&=125+125+5-5 \
&=250 \\
Q_3left(-5right)&=left(-5right)^3+3 cdot left(-5right)^2+left(-5right)-5 \
&=-125+125-5-5 \
&=-10 \\
end{align*}
$$
Now we can divide the polynomial by this factor.
text{Divide $Q_3left(xright)$ by $x-1$:}
$$
$polylongdiv{x^3+3x^2+x-5}{x-1}$
$$
begin{align*}
Q_3left(xright)&=left(x-1right)left(x^2+4x+5right) \
end{align*}
$$
$$
begin{align*}
x^2+4x+5&=0 \
x&=frac{-4pm sqrt{4^2-4 cdot 1 cdot 5}}{2 cdot 1} \
&=frac{-4pm isqrt{4}}{2} \
&=frac{-4pm 2i}{2} \
&=-2pm i
end{align*}
$$
$$
Q_3left(xright)=left(x-1right)left(x^2+4x+5right)=left(x-1right)left(x+2+iright)left(x+2-iright)
$$
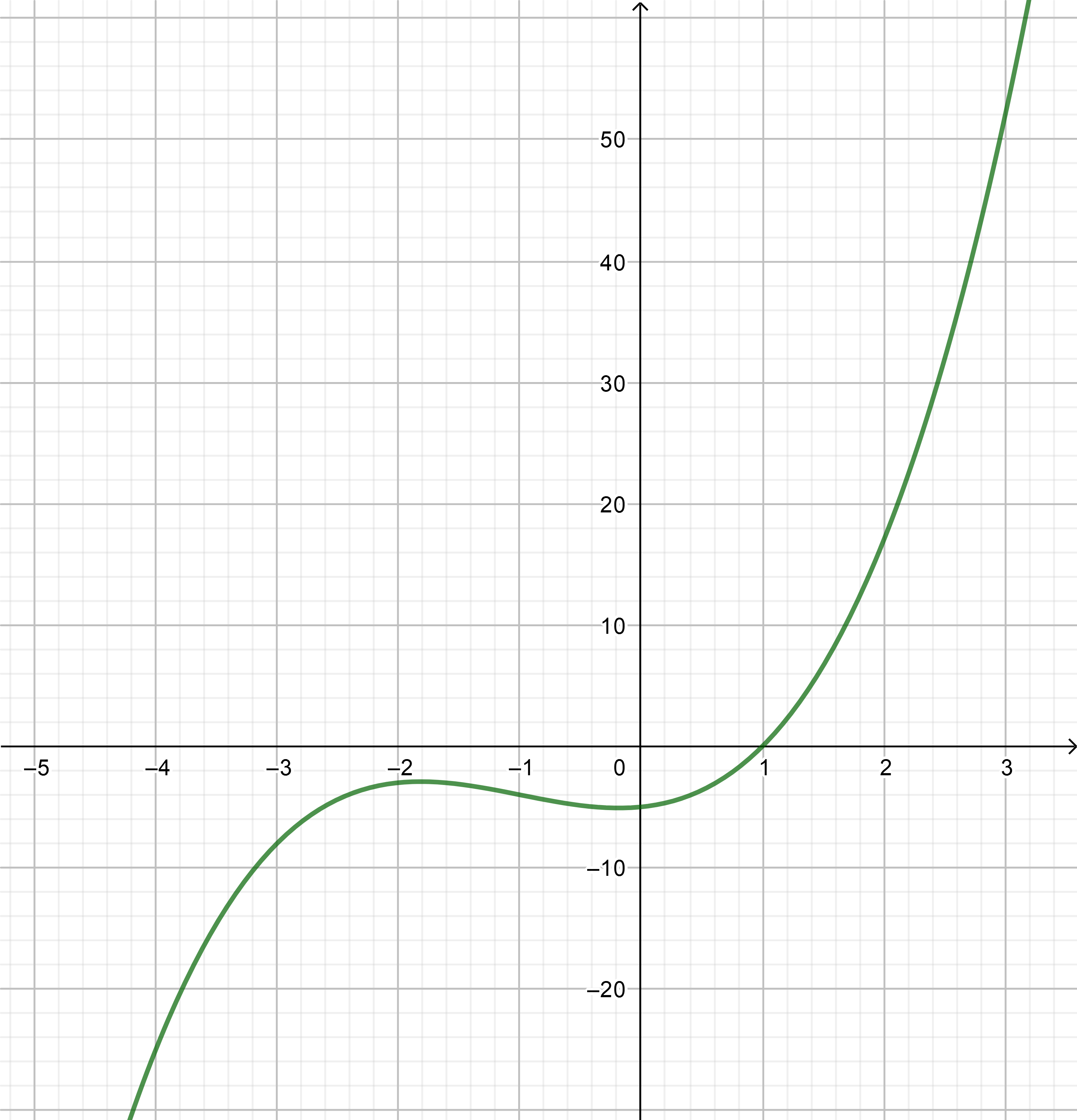
$text{textbf{a.} $Rightarrow$ It has $1$ real root with multiplicity $1$, $1$ real root with multiplicity $3$ and no complex roots.}$
$text{textbf{b.} $Rightarrow$ It has $3$ real root with multiplicity $1$, and no complex roots.}$
$$
text{textbf{c.} $Rightarrow$ It has $1$ real root with multiplicity $1$, and $2$ complex roots.}
$$
P(x)=6x^4+7x^3-36x^2-7x+6
$$
$left(x-dfrac{1}{2}right), left(x+dfrac{1}{2}right), left(x-dfrac{1}{3}right), left(x+dfrac{1}{3}right), left(x-dfrac{1}{6}right)., left(x+dfrac{1}{6}right)$
$left(x-dfrac{2}{3}right), left(x+dfrac{2}{3}right), left(x-dfrac{3}{2}right), left(x+dfrac{3}{2}right)$
pm 1, pm 2, pm 3, pm 6, pmdfrac{1}{2}, pmdfrac{1}{3}, pmdfrac{1}{6}, pmdfrac{2}{3}, pmdfrac{3}{2}
$$
$P(-1)=-24not=0$
$P(2)=0checkmark$
$P(-2)=-84not=0$
$P(3)=336not=0$
$P(-3)=0checkmark$
$P(x)=(x-2)(6x^3+19x^2+2x-3)$
$polyhornerscheme[x=-3]{6x^3+19x^2+2x-3}$
$$
P(x)=(x-2)(x+3)(6x^2+x-1)
$$
$=(x-2)(x+3)[3x(2x+1)-(2x+1)]$
$=(x-2)(x+3)(2x+1)(3x-1)$
$x_1=2$
$x_2=-3$
$2x+1=0Rightarrow x_3=-dfrac{1}{2}$
$3x-1=0Rightarrow x_4=dfrac{1}{3}$
For every quadratic term you can determine the roots using the quadratic formula to factor the equation as $(x-a)(x-b)$ with $a$ and $b$ the roots found using the quadratic formula.
ii. Then the function can have either 0 or 2 complex roots, because the total number of roots (real+complex) need to be equal to the degree of the function.
iii. For example $y=(x-1)(x-2)(x-3)$ has 3 real roots and $y=(x-1)(x^2+1)$ has one real root.
ii. Then the function can have either 0 or 2 or 4 complex roots, because the total number of roots (real+complex) need to be equal to the degree of the function.
iii. For example $y=(x-1)(x-2)(x-3)(x-4)$ has 4 real roots and $y=(x-1)(x-2)(x^2+1)$ has two real roots and $y=(x^2+2)(x^2+1)$ has no real roots.
ii. Then the function can have either 0 or 2 or 4 complex roots, because the total number of roots (real+complex) need to be equal to the degree of the function.
iii. For example $y=(x-1)(x-2)(x-3)(x-4)(x-5)$ has 5 real roots and $y=(x-1)(x-2)(x-3)(x^2+1)$ has 3 real roots and $y=(x-1)(x^2+2)(x^2+1)$ has one real root.
b.
$$
polylongdiv{x^3-x^2-7x+3}{x-3}
$$
Thus we then obtain:
$$
p(x)=(x-3)^2(x^2+2x-1)
$$
Determine the discriminant of the given function $f(x)=x^2+2x-1$:
$$
D=b^2-4ac=(2)^2-4(1)(-1)=4+4=8
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{-2pm sqrt{8}}{2(1)}=dfrac{-2pm 2sqrt{2}}{2}=-1pm sqrt{2}
$$
b. $x=-1pm sqrt{2}$
b.
$$
polylongdiv{x^3+4x^2+x-26}{x-2}
$$
Determine the discriminant of the given function $f(x)=x^2+6x+13$:
$$
D=b^2-4ac=(6)^2-4(1)(13)=36-52=-16
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{-6pm sqrt{-16}}{2(1)}=dfrac{-6pm 4i}{2}=-3pm 2i
$$
b. $x=2,-3pm 2i$
$$
text{Set $y=2sqrt{3left(x-1right)}+5$, and solve for $x$ in term of $y$.}
$$
begin{align*}
y&=2sqrt{3left(x-1right)}+5 && text{Substitute} y text{for} fleft(xright). \
y-5&=2sqrt{3left(x-1right)} && text{Subtract} 5 text{from both sides.} \
frac{y-5}{2}&=sqrt{3left(x-1right)} && text{Divide both sides by} 2. \
left(frac{y-5}{2}right)^2&=3left(x-1right) && text{Square each side}. xgeq 1 \
frac{y^2-10y+25}{4}&=3x-3 && text{Distributive Property.} \
frac{y^2-10y+25}{4}+3&=3x && text{Add} 3 text{to both sides.} \
frac{y^2-10y+25+12}{4}&=3x && text{Simplify.} \
frac{y^2-10y+37}{12}&=x && text{Divide both sides by} 3. \
f^{-1}left(yright)&=frac{y^2-10y+37}{12} && text{Substitute} f^{-1}left(yright) text{for} x. \
end{align*}
$$
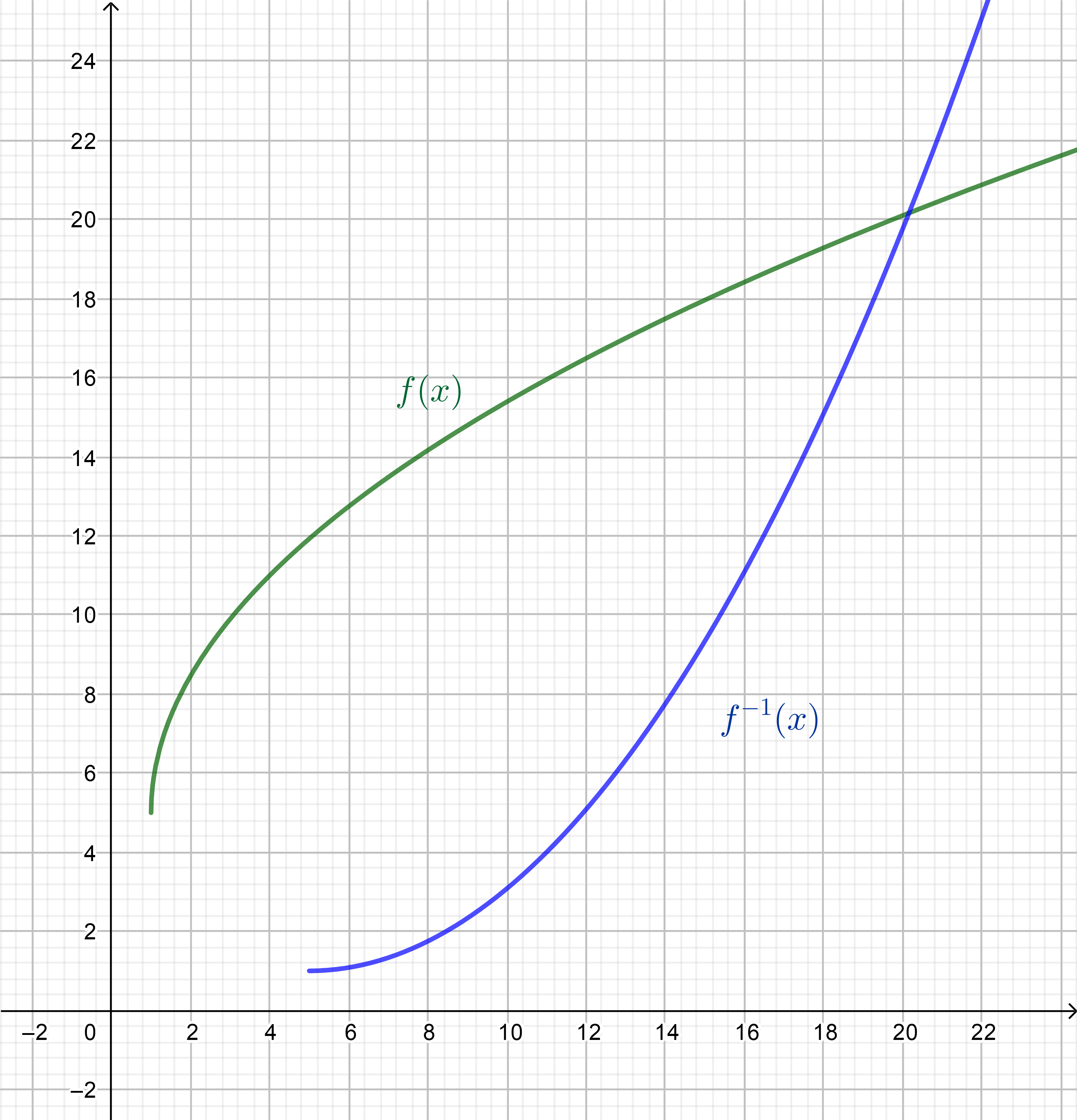
$$
y=ab^x+k
$$
text{Since asymptote is at $y=5$, therefore $k=5$. Thus, the final function is the following:}
$$
$$
y=ab^x+5
$$
$$
begin{align*}
5.64&=ab^2+5 \
15&=ab^{-1}+5 \\
0.64&=ab^2 && text{Subtract} 5 text{from both sides.} \
10&=ab^{-1} && text{Subtract} 5 text{from both sides.} \
end{align*}
$$
$$
begin{align*}
frac{0.64}{10}&=frac{ab^2}{ab^{-1}} \
0.064&=b^3 \
b&=0.4
end{align*}
$$
text{Substitute $b=0.4$ in the first equation in order to find the value of $a$.}
$$
$$
begin{align*}
0.64&=a cdot left(0.4right)^2 \
0.64&=0.16a \
a&=4
end{align*}
$$
$$
y=4left(0.4right)^x+5
$$
y=4left(0.4right)^x+5
$$
$$
(2^4)^{(x+2)}=(2^3)^x
$$
Power of power property:
$$
2^{4(x+2)}=2^{3x}
$$
The powers of the same base have to be equal:
$$
4(x+2)=3x
$$
Distributive property:
$$
4x+8=3x
$$
Subtract $3x$ of both sides of the equation:
$$
x+8=0
$$
Subtract 8 from both sides of the equation:
$$
x=-8
$$
x=-8
$$
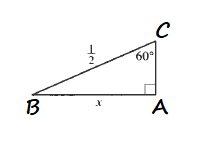
$sin 60text{textdegree}=dfrac{x}{dfrac{1}{2}}$
$dfrac{sqrt 3}{2}=2x$
$$
x=dfrac{sqrt 3}{4}
$$
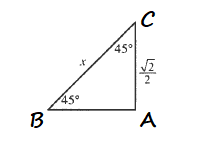
$sin 45text{textdegree}=dfrac{dfrac{sqrt 2}{2}}{x}$
$dfrac{sqrt 2}{2}=dfrac{dfrac{sqrt 2}{2}}{x}$
$dfrac{sqrt 2}{2}cdot x=dfrac{sqrt 2}{2}$
$$
x=1
$$
b) $x=1$
100 yards = 3600 inches
$53dfrac{1}{3}$ yards$=dfrac{160}{3}cdot 36=1920$ inches
$dfrac{3600}{3.5}approx1028$ cards
$dfrac{1920}{2.5}=768$ cards
1028cdot 768=789,504
$$
P(joker)=dfrac{1}{789,504}approx 0.000001
$$
$$
15,183cdot 0.99approx 15,031.17
$$
(789,504-1)cdot 5=3,947,515
$$
789,504cdot 5-1,000,000=2,947,520
$$
dfrac{176,000,000}{789,504}-1approx 223-1=222
$$
b) $$15,031.17$
c) $3,947,515$
d) $2,947,520$
e) $222$
$$
polylongdiv{x^3+1}{x+1}
$$
Determine the discriminant of the given function $f(x)=x^2-x+1$:
$$
D=b^2-4ac=(-1)^2-4(1)(1)=1-4=-3
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{1pm sqrt{-3}}{2(1)}=dfrac{1}{2}pm dfrac{sqrt{2}}{2}i
$$
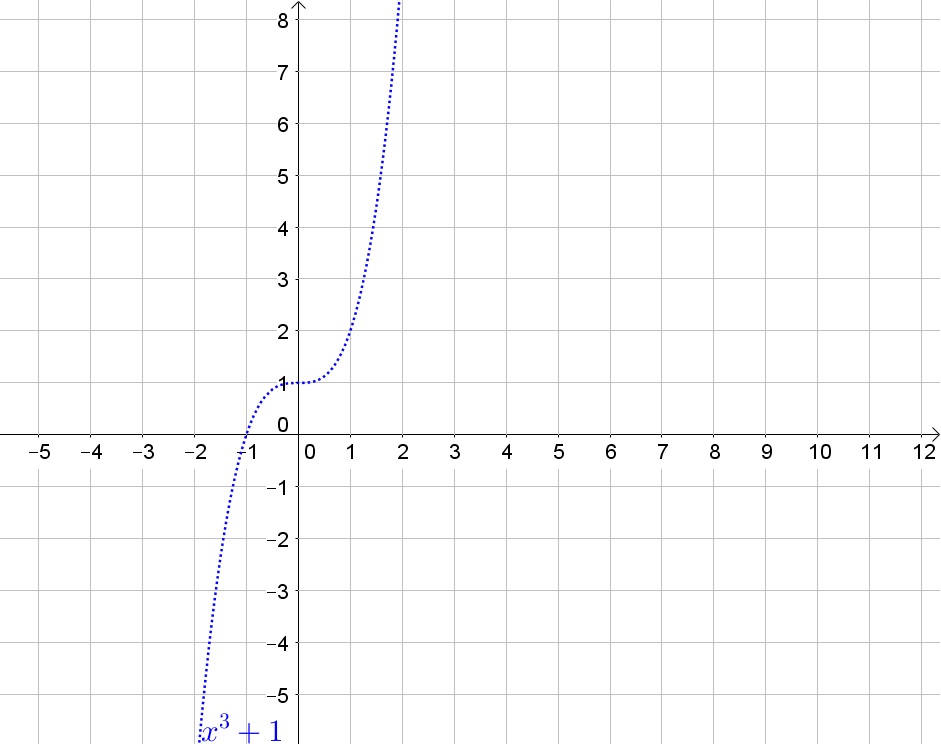
$$
polylongdiv{x^3-8}{x-2}
$$
Determine the discriminant of the given function $f(x)=x^2+2x+4$:
$$
D=b^2-4ac=(2)^2-4(1)(4)=4-16=-12
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{2pm sqrt{-12}}{2(1)}=dfrac{2pm 2sqrt{3}sqrt{-1}}{2}=1pm isqrt{3}
$$
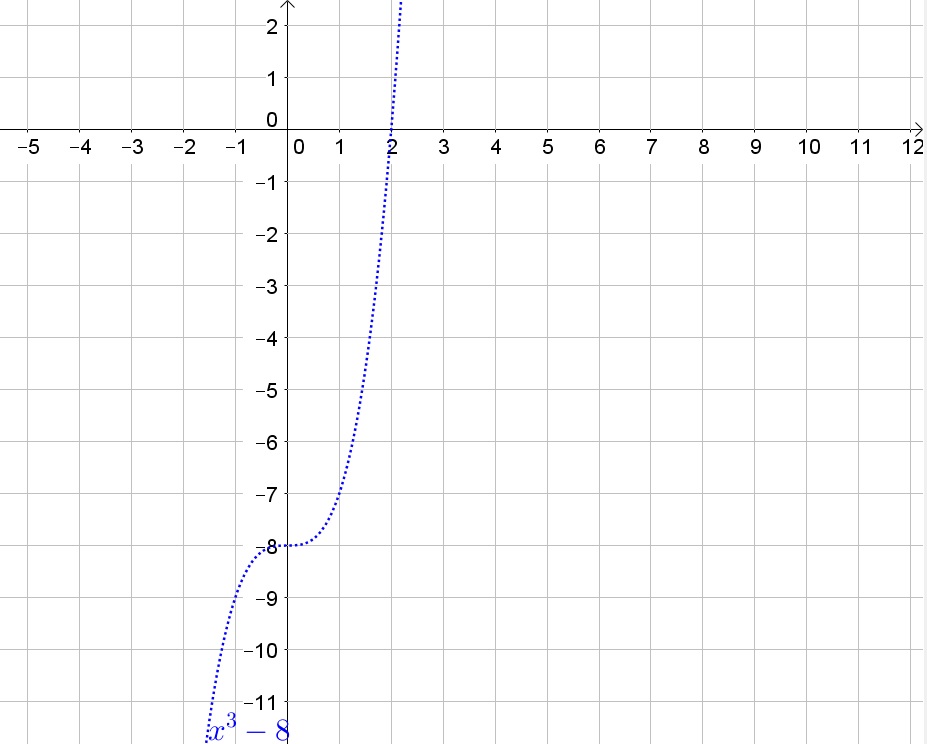
b. $x=2, 1pm isqrt{3}$
$$
y=(x+1)(x-(-2+5i))(x-(-2-5i))
$$
Use distributive property:
$$
y=(x+1)(x^2+4x+4-25i^2)
$$
Simplify and use $i^2=-1$.
$$
y=(x+1)(x^2+4x+29)
$$
y=(x+1)(x^2+4x+29)
$$
$$
p(2)=2^3-6(2)^2+7(2)+2=8-24+14+2=0
$$
b.
$$
polylongdiv{x^3-6x^2+7x+2}{(x-2)}
$$
c. $(x-2)$
d.
Determine the discriminant of the given function $f(x)=x^2-4x-1$:
$$
D=b^2-4ac=(-4)^2-4(1)(-1)=16+4=20
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{4pm sqrt{20}}{2(1)}=dfrac{4pm 2sqrt{5}}{2}=2pm sqrt{5}
$$
b. $(x-2)$
c. $(x-2)$
d. $x=2, 2pm sqrt{5}$
$$
Delta=b^2-4ac
$$
$$
text{The equation has real solutions when the discriminant $Delta$ is greater or equal to zero.}
$$
begin{align*}
Delta=b^2-4 cdot5 cdot 20&geq0 && text{We compute the discriminant:} Delta=b^2-4ac \
&text{} && a=5, c=20. \
b^2-400&geq0 && text{Simplify.} \
b^2&geq 400 && text{Add} 400 text{to both sides.} \
mid bmid &geq 20 && text{Square root of each side.} \
end{align*}
$$
$$
bin left(-infty, -20right]cupleft[20, inftyright)
$$
bin left(-infty, -20right]cupleft[20, inftyright)
$$
$$
380 cdot 75%=380 cdot 0.75=285
$$
text{The minimum score he needs to achieve in order to be considered for a scholarship is $285$.}
$$
285
$$
Q(t)=Q_{o}r^{t}=1e6times(0.87)^{t}
$$
Here $Q_{o}$ is the initial number of lightbulbs at t=0
Q(t)=1e5=1e6times(0.87)^{t}
$$
log_{0.87}left( dfrac{1e5}{1e6}right)=t=16.53months
$$
log_{0.87}left( dfrac{1}{1e6}right)=99.21months
$$
8log_3(y)+log_3 (2x)
$$
8log_3(y)+log_3 (2x)=log_3(y^8)+log_3 (2x)
$$
$log_a x^m=mlog_a x$.
$$
=log_3 (2xy^8)
$$
$log_a (xy)=log_a x+log_a y$.
log_4(5m)-9log_4 (n)
$$
log_4(5m)-9log_4 (n)=log_4 (5m)-log_4 (n^9)
$$
$log_a x^m=mlog_a x$.
log_4 (5m)-log_4 (n^9)=log_4 dfrac{5m}{n^9}
$$
$log_a left(dfrac{x}{y}right)=log_a x-log_a y$.
b) $log_4 dfrac{5m}{n^9}$
The length of the tank is then $11-2x$ (because on both sides of the length a square was cutout).
The length of the tank is then $8.5-2x$ (because on both sides of the width a square was cutout).
The volume of the tank is then the product of the length, width and the height:
$$
V(x)=x(11-2x)(8.5-2x)
$$
V(x)=x(11-2x)(8.5-2x)
$$
The length of the tank is then $11-2x$ (because on both sides of the length a square was cutout).
The length of the tank is then $8.5-2x$ (because on both sides of the width a square was cutout).
The volume of the tank is then the product of the length, width and the height:
$$
V(x)=x(11-2x)(8.5-2x)
$$
For example if the cutout is 1”, replace $x$ with 1:
$$
V(x)=1(11-2)(8.5-2)=1(9)(6.5)=58.5
$$
V(x)=x(11-2x)(8.5-2x)
$$
b. If $x$ is the length of the square that is cutout of each corner, then the height is equal to $x$.
The length of the tank is then $11-2x$ (because on both sides of the length a square was cutout).
The length of the tank is then $8.5-2x$ (because on both sides of the width a square was cutout).
c. The volume of the tank is then the product of the length, width and the height:
$$
V(x)=x(11-2x)(8.5-2x)
$$
d.
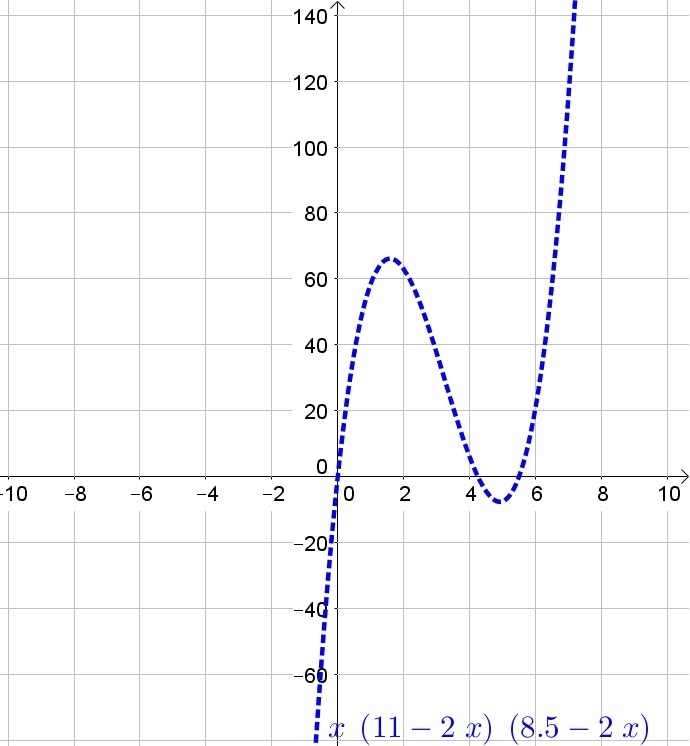
The range is then all the possible $y$-values and since the maximum on the domain seems to be less than 70: $(0,70)$.
f. The maximum volume is about 66in.$^3$ with height $x=1.6$”, length $11-2(1.6)=7.8$” and width $8.5-2(1.6)=5.3$”.
b. length: $11-2x$ and width: $8.5-2x$
c. $V(x)=x(11-2)(8.5-2x)$
d. See graph
e. Domain: $(0,4.25)$ and range: $(0,70)$
f. Maximum volume: 66in.$^3$ with height $1.6$”, length $7.8$” and width $5.3$”.
The range is then all the possible $y$-values and since the maximum on the domain seems to be less than 70: $(0,70)$.
b. As the height increases, the length and width will decrease. As the height decreases, the length and the width will increase.
c.
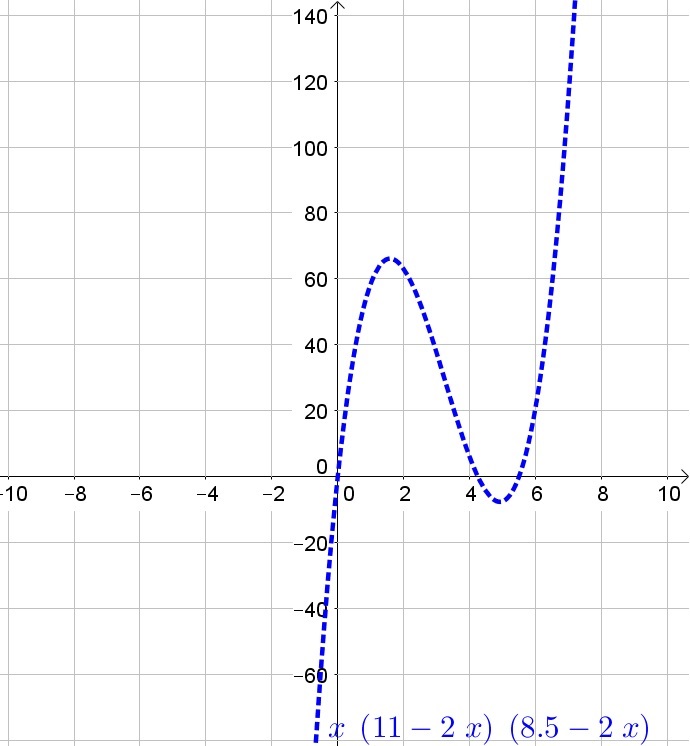
$$
begin{align*}
0&=x(x-3)^2(2x+1)&&boxed{text{Substitute }0 text{ for } P(x)}\
xleft(x-3right)^2left(2x+1right)&=0&&boxed{text{Switch sides}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
x&=color{#c34632}{0}&&boxed{text{Simplify}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
x-3&=0&&boxed{text{Simplify}}\
x-3+3&=0+3&&boxed{text{Add } 3 text{ to both sides}}\
x&=color{#c34632}{3}&&boxed{text{Simplify}}\
end{align*}
$$
Using the zero factor principle
$$
begin{align*}
2x+1&=0&&boxed{text{Simplify}}\
2x+1-1&=0-1&&boxed{text{Subtract } 1 text{ from both sides}}\
2x&=-1&&boxed{text{Simplify}}\
frac{2x}{2}&=frac{-1}{2}&&boxed{text{Divide both sides by }2}\
x&=color{#c34632}{-frac{1}{2}}&&boxed{text{Simplify}}\\
end{align*}
$$
The final solutions to the equations are:
$$
begin{align*}
&boxed{{color{#c34632}x=0, x=3, x=-frac{1}{2}} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ } x=0, x=3, x=-frac{1}{2}
$$
$$
0=x(x-3)^2(2x+1)
$$
Zero product property:
$$
x=0text{ or } x-3=0 text{ or } 2x+1=0
$$
Solve each equation to $x$:
$$
x=0text{ or } x=3 text{ or } x=-dfrac{1}{2}
$$
x=0text{ and } x=3 text{ and } x=-dfrac{1}{2}
$$

{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
x^2-10&=0&&boxed{text{Given proportion}}\
x^2-10+10&=0+10&&boxed{text{Add }10 text{ to both sides}}\
x^2&=10&&boxed{text{Simplify}}\
x=sqrt{10},:x&=-sqrt{10}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=sqrt{10},:x=-sqrt{10}} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{For:}x^2=fleft(aright)mathrm{:the:solutions:are:}x=sqrt{fleft(aright)},::-sqrt{fleft(aright)}}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$x^2-3x-7=0$ Given proportion.
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-3right)pm sqrt{left(-3right)^2-4cdot :1left(-7right)}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -3 text{ for } b, text{ and } -7 text{ for } c.} \
end{align*}
$$
First we solve $x_1$
$$
begin{align*}
x_1&=frac{-left(-3right)+sqrt{left(-3right)^2-4cdot :1left(-7right)}}{2cdot :1}&&boxed{text{Simplify}}\
x_1&=frac{3+sqrt{left(-3right)^2+4cdot :1cdot :7}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_1&=frac{3+sqrt{9+4cdot :1cdot :7}}{2cdot :1}&&boxed{text{Evaluate: }(-3)^2=9}\
x_1&=frac{3+sqrt{9+28}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot7=28}\
x_1&=frac{3+sqrt{9+28}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_1&=frac{3+sqrt{37}}{2}&&boxed{text{Add the numbers: }9+28=37}\
end{align*}
$$
$$
begin{align*}
x_2&=frac{-left(-3right)-sqrt{left(-3right)^2-4cdot :1left(-7right)}}{2cdot :1}&&boxed{text{Simplify}}\
x_2&=frac{3-sqrt{left(-3right)^2+4cdot :1cdot :7}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_2&=frac{3-sqrt{9+4cdot :1cdot :7}}{2cdot :1}&&boxed{text{Evaluate: }(-3)^2=9}\
x_2&=frac{3-sqrt{9+28}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot7=28}\
x_2&=frac{3-sqrt{9+28}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_2&=frac{3-sqrt{37}}{2}&&boxed{text{Add the numbers: }9+28=37}\\
&boxed{{color{#c34632}x_1=frac{3+sqrt{37}}{2}, x_2=frac{3-sqrt{37}}{2}} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{c)}}
$$
Solution to this example is given below
$$
begin{align*}
x^2+4&=0&&boxed{text{Given proportion}}\
x^2+4-4&=0-4&&boxed{text{Subtract }4 text{ from both sides}}\
x^2&=-4&&boxed{text{Simplify}}\
x=sqrt{-4},:x&=-sqrt{-4}&&boxed{text{Simplify}}\
end{align*}
$$
First we solve $boldsymbol{x=sqrt{-4}}$
$$
begin{align*}
x&=sqrt{-1}sqrt{4}&&boxed{text{Apply radical rule}}\
x&=sqrt{4}i&&boxed{text{Apply imaginary number rule: }sqrt{-1}=i}\
x&=sqrt{2^2}i&&boxed{text{Factor the number }4=2^2}\
x&=2i&&boxed{text{Simplify}}\
end{align*}
$$
Second we solve $boldsymbol{x=-sqrt{-4}}$
$$
begin{align*}
x&=-sqrt{-1}sqrt{4}&&boxed{text{Apply radical rule}}\
x&=-sqrt{4}i&&boxed{text{Apply imaginary number rule: }sqrt{-1}=i}\
x&=-sqrt{2^2}i&&boxed{text{Factor the number }4=2^2}\
x&=-2i&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=2i,:x=-2i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{For:}x^2=fleft(aright)mathrm{:the:solutions:are:}x=sqrt{fleft(aright)},::-sqrt{fleft(aright)}}
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:radical:rule}:quad sqrt{-a}=sqrt{-1}sqrt{a} }
$$
$$
boxed{ color{#c34632} text{ }mathrm{Apply:radical:rule}:quad sqrt[n]{a^n}=a }
$$
{color{#4257b2}text{d)}}
$$
Solution to this example is given below
$x^2-2x+2=0$ Given proportion.
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-2right)pm sqrt{left(-2right)^2-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -2 text{ for } b, text{ and } 2 text{ for } c.} \
end{align*}
$$
First we solve $x_1$
$$
begin{align*}
x_1&=frac{-left(-2right)+sqrt{left(-2right)^2-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Simplify}}\
x_1&=frac{2+sqrt{left(-2right)^2-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_1&=frac{2+sqrt{4-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Evaluate: }(-2)^2=4}\
x_1&=frac{2+sqrt{4-8}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot2=8}\
x_1&=frac{2+sqrt{4-8}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_1&=frac{2+sqrt{-4}}{2}&&boxed{text{Subtact the numbers: }4-8=-4}\
x_1&=frac{2+sqrt{-1}sqrt{4}}{2}&&boxed{text{Apply radical rule}}\
x_1&=frac{2+sqrt4 i}{2}&&boxed{text{Apply imaginary number rule: } -sqrt1=i}\
x_1&=frac{2+2i}{2}&&boxed{text{Simplify}}\
x_1&=frac{2left(1+iright)}{2}&&boxed{text{Factor}}\
x_1&=1+i&&boxed{text{Divide the numbers: } frac{2}{2}=1}\
end{align*}
$$
$$
begin{align*}
x_2&=frac{-left(-2right)-sqrt{left(-2right)^2-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Simplify}}\
x_2&=frac{2-sqrt{left(-2right)^2-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_2&=frac{2-sqrt{4-4cdot :1cdot :2}}{2cdot :1}&&boxed{text{Evaluate: }(-2)^2=4}\
x_2&=frac{2-sqrt{4-8}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot2=8}\
x_2&=frac{2-sqrt{4-8}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2}\
x_2&=frac{2-sqrt{-4}}{2}&&boxed{text{Subtact the numbers: }4-8=-4}\
x_2&=frac{2-sqrt{-1}sqrt{4}}{2}&&boxed{text{Apply radical rule}}\
x_2&=frac{2-sqrt4 i}{2}&&boxed{text{Apply imaginary number rule: } -sqrt1=i}\
x_2&=frac{2-2i}{2}&&boxed{text{Simplify}}\
x_2&=frac{2left(1-iright)}{2}&&boxed{text{Factor}}\
x_2&=1-i&&boxed{text{Divide the numbers: } frac{2}{2}=1}\\
&boxed{{color{#c34632}x_1=1+i, x_2=1-i} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Apply:radical:rule}:quad sqrt{-a}=sqrt{-1}sqrt{a}}
$$
color{#4257b2} text{ a) }x=sqrt{10}, x=-sqrt{10}
$$
$$
color{#4257b2} text{ b) }x_1=frac{3+sqrt{37}}{2}, x_2=frac{3-sqrt{37}}{2}
$$
$$
color{#4257b2} text{ c) } x=2i, x=-2i
$$
$$
color{#4257b2} text{ d) }x_1=1+i, x_2=1-i
$$
$$
x^2-10=0
$$
Add 10 to both sides of the equation:
$$
x^2=10
$$
Take the square root of both sides of the equation:
$$
x=pm sqrt{10}
$$
$$
x^2-3x-7=0
$$
Determine the discriminant:
$$
D=b^2-4ac=(-3)^2-4(1)(-7)=9+28=37
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{3pm sqrt{37}}{2}
$$
$$
x^2+4=0
$$
Subtract 4 from both sides of the equation:
$$
x^2=-4
$$
Take the square root of both sides of the equation:
$$
x=pm sqrt{-4}=pm 2i
$$
$$
x^2-2x+2=0
$$
Determine the discriminant:
$$
D=b^2-4ac=(-2)^2-4(1)(2)=4-8=-4
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{2pm sqrt{-4}}{2}=dfrac{2pm 2i}{2}=1pm i
$$
b. $x=dfrac{3pm sqrt{37}}{2}$
c. $x=pm 2i$
d. $x=1pm i$
$$
x=log_3{17}
$$
b. Take the cubic root of both sides of the equation:
$$
x=sqrt[3]{17}
$$
b. $x=sqrt[3]{17}$
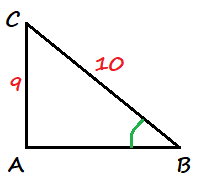
$$
B=sin^{-1} 0.9approx 64.2text{textdegree}
$$
(a+b)(a^2-ab+b^2)
$$
$$
=a^3+b^3
$$
(x-2)(x^2+2x+4)
$$
(x-2)(x^2+2x+4)=x^3+2x^2+4x-2x^2-4x-8=x^3-8
$$
(y+5)(y^2-5y+25)
$$
$$
=y^3+125
$$
(x-y)(x^2+xy+y^2)
$$
$$
=x^3-y^3
$$
$(a+b)(a^2-ab+b^2)=a^3+b^3$
(x-2y)(x^2+2xy+4y^2)=x^3-(2y)^3=x^3-8y^3
$$
$text{The probability that the paint pellet will hit the $50$ point ring can be obtained through}$
$$
text{the division of the area of $50$ point ring by the area of the complete target.}
$$
begin{align*}
Pleft(50 text{point ring}right)&=frac{text{The area of} 50 text{point ring }}{text{The area of the complete target}} \
&=frac{pi cdot 1^2}{pi cdot 4^2} \
&=frac{1}{16} \
&=0.0625
end{align*}
$$
$text{The probability that the paint pellet will hit the $20$ point ring can be obtained through}$
$$
text{the division of the area of $20$ point ring by the area of the complete target.}
$$
begin{align*}
Pleft(20 text{point ring}right)&=frac{text{The area of} 20 text{point ring }}{text{The area of the complete target}} \
&=frac{pi cdot 2^2-pi cdot 1^2}{pi cdot 4^2} \
&=frac{4pi-pi}{16pi} \
&=frac{3pi}{16pi} \
&=frac{3}{16} \
&=0.1875
end{align*}
$$
$textbf{b.}$ $0.1875$
$$
a^2-b^2=left(a-bright)left(a+bright)
$$
$$
begin{align*}
a^2-4b^2&=a^2-left(2bright)^2=left(a-2bright)left(a+2bright) && text{Use the difference of squares.}
end{align*}
$$
$$
begin{align*}
2x^2-16&=left(sqrt{2}xright)^2-4^2=left(sqrt{2}x-4right)left(sqrt{2}x+4right) && text{Use the difference of squares.}
end{align*}
$$
$$
begin{align*}
-x^2+y^4&=left(y^2right)^2-x^2=left(y^2-xright)left(y^2+xright) && text{Use the difference of squares.}
end{align*}
$$
The expression cannot be rewritten as a difference of squares.
$textbf{ii.}$ $left(sqrt{2}x-4right)left(sqrt{2}x+4right)$
$textbf{iii.}$ $left(y^2-xright)left(y^2+xright)$
$textbf{iv.}$ The expression cannot be rewritten as a difference of squares.
$$
polylongdiv{x^3-1}{x-1}
$$
b.
$$
polylongdiv{x^3+8}{x+2}
$$
c.
$$
polylongdiv{x^3-27}{x-3}
$$
d.
$$
polylongdiv{x^3+125}{x+5}
$$
b. $(x+2)(x^2-2x+4)$
c. $(x-3)(x^2+3x+9)$
d. $(x+5)(x^2-5x+25)$
$$
polylongdiv{x^3+a^3}{x+a}
$$
b.
$$
polylongdiv{x^3-b^3}{x-b}
$$
b. $(x-b)(x^2+bx+b^2)$
y=x^2+9
$$
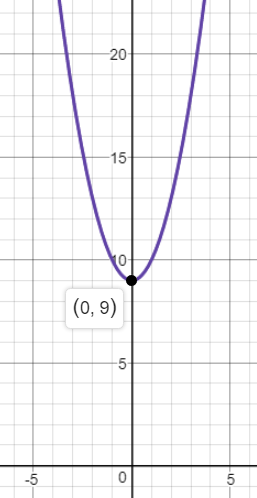
$x^2=-9$
$x^2=(3i)^2$
$$
x=pm 3i
$$
y=x^2+9=(x-3i)(x+3i)
$$
y=x^2-(ai)^2=(x-ai)(x+ai)
$$
$$
a^2-b^2=left(a-bright)left(a+bright)
$$
begin{align*}
x^4-b^4&=left(x^2right)^2-left(b^2right)^2 \
&=left(x^2-b^2right)left(x^2+b^2right) && text{Use the difference of squares.} \
&=left(x-bright)left(x+bright)left(x^2+b^2right) && text{Use the difference of squares again.} \
&=left(x-bright)left(x+bright)left(x-biright)left(x+biright) && text{Use} left(x-biright)left(x+biright)=x^2+b^2.
end{align*}
$$
left(x-bright)left(x+bright)left(x-biright)left(x+biright)
$$
$$
a^2-b^2=left(a-bright)left(a+bright)
$$
$$
begin{align*}
x^4-b^4&=left(x^2right)^2-left(b^2right)^2 \
&=left(x^2-b^2right)left(x^2+b^2right) && text{Use the difference of squares.} \
&=left(x-bright)left(x+bright)left(x^2+b^2right) && text{Use the difference of squares again.} \
end{align*}
$$
$$
text{We determine the root of $x^2+b^2$:}
$$
$$
begin{align*}
x^2+b^2&=0 \
x^2&=-b^2 && text{Subtract} -b^2 text{from both sides.} \
x^2&=left(biright)^2 && text{Use} i^2=-1. \
x&=pm bi && text{Square root of each side.}
end{align*}
$$
$$
text{The factor of the expression $x^2+b^2$ is $left(x-biright)left(x+biright)$.}
$$
$$
text{The final factored form of $x^4-b^4$ is}
$$
$$
left(x-bright)left(x+bright)left(x^2+b^2right)=left(x-bright)left(x+bright)left(x-biright)left(x+biright)
$$
$textbf{b.}$ $x^2+b^2=left(x-biright)left(x+biright)$
$textbf{c.}$ $left(x-bright)left(x+bright)left(x-biright)left(x+biright)$
a^2+2ab+b^2
$$
a^2+2ab+b^2=(a+b)^2
$$
$(A+B)^2=A^2+2AB+B^2$.
8x^3+27y^6
$$
$$
=(2x+3y^2)(4x^2-6xy^2+9y^4)
$$
$A^3+B^3=(A+B)(A^2-AB+B^2)$.
100x^2+169
$$
$$
=(10x-13i)(10x+13i)
$$
$A^2-B^2=(A-B)(A+B)$.
32x^3-500
$$
$=4[(2x)^3-5^3]$
$$
=4(2x-5)(4x^2+10x+25)
$$
$A^3-B^3=(A-B)(A^2+AB+B^2)$.
16x^4-81y^8
$$
$=(4x^2-9y^4)(4x^2+9y^4)$
$=(2x-3y^2)(2x+3y^2)[(2x)^2-(3y^2 i)^2]$
$$
=(2x-3y^2)(2x+3y^2)(2x-3y^2 i)(2x+3y^2 i)
$$
$A^2-B^2=(A-B)(A+B)$.
x^6-y^6
$$
$=(x^3-y^3)(x^3+y^3)$
$$
=(x-y)(x^2+xy+y^2)(x+y)(x^2-xy+y^2)
$$
$A^2-B^2=(A-B)(A+B)$,
then using the patterns:
$A^3-B^3=(A-B)(A^2+AB+B^2)$
$A^3+B^3=(A+B)(A^2-AB+B^2)$.
$$
a^2-b^2=left(a-bright)left(a+bright)
$$
Shinna ‘s expression is a difference of squares because
$$
begin{align*}
9x^2y^4-z^6&=left(3xy^2right)^2-left(z^3right)^2 \
end{align*}
$$
$$
text{The “squares” are $left(3xy^2right)^2$ and $left(z^3right)^2$.}
$$
$$
begin{align*}
left(3xy^2right)^2-left(z^3right)^2&=left(3xy^2-z^3right)left(3xy^2+z^3right) && text{Use the difference of squares.} \
end{align*}
$$
$textbf{b.}$ $left(3xy^2-z^3right)left(3xy^2+z^3right)$
$$
D=b^2-4ac=(0)^2-4(1)(-6)=0+24=24>0
$$
Since the discriminant is positive , the function has real roots.
b. Determine the discriminant:
$$
D=b^2-4ac=(0)^2-4(1)(6)=0-24=-24<0
$$
Since the discriminant is negative, the function has complex roots.
c. Determine the discriminant:
$$
D=b^2-4ac=(-2)^2-4(1)(10)=4-40=-360
$$
Since the discriminant is positive, the function has real roots.
e. Since the constant term is negative (it will become positive one it has been brought to the other side of the equation $(x-3)^2=4$), the function has real roots.
f. Since the constant term is positive (it will become negative one it has been brought to the other side of the equation $(x-3)^2=-4$), the function has complex roots.
b. Complex roots
c. Complex roots
d. Real roots
e. Real roots
f. Complex roots
$$
p(5)=5^3-3(5)^2-7(5)+9=125-75-35+9=24
$$
b. The remainder theorem states that if you divide the polynomial by $x-5$, then the remainder is $p(5)$:
$$
polylongdiv{x^3-3x^2-7x+9}{x-5}
$$
b. $24$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
&(x+i)(x-i)&&boxed{text{Given proportion}}\
&x^2+1^2&&boxed{text{Apply complex arithmetic rule}}\
&x^2+1&&boxed{text{Evaluate }1^2=1}\\
&boxed{{color{#c34632}x^2+1} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Apply:complex:arithmetic:rule}:quad left(a+biright)left(a-biright)=a^2+b^2}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
&(x-(1+sqrt2)(x-(1-sqrt2)&&boxed{text{Given proportion}}\
&(x-1-sqrt2)(x-1+sqrt2)&&boxed{text{Distribute parentheses}}\
&xcdot x-1cdot :x+sqrt{2}x-1cdot :x+1cdot :1-1cdot sqrt{2}-sqrt{2}x+1cdot sqrt{2}-sqrt{2}sqrt{2}&&boxed{text{Simplify}}\
&xcdot x-1cdot :x+sqrt{2}x-1cdot :x-sqrt{2}x+1cdot :1-sqrt{2}sqrt{2}&&boxed{text{Combine like terms}}\
&xcdot x-1cdot :x-1cdot :x+1cdot :1-sqrt{2}sqrt{2}&&boxed{text{Combine like terms}}\
&xcdot x-2x+1cdot :1-sqrt{2}sqrt{2}&&boxed{text{Combine like terms}}\
&x^{1+1}-2x+1cdot :1-sqrt{2}sqrt{2}&&boxed{text{Add exponents}}\
&x^2-2x+1cdot :1-sqrt{2}sqrt{2}&&boxed{text{Simplify exponents}}\
&x^2-2x+1-sqrt{2}sqrt{2}&&boxed{text{Multiply the numbers: } 1cdot1=1}\
&x^2-2x+1-2&&boxed{text{Apply radical rule}}\
&x^2-2x-1&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x^2-2x-1} }&&boxed{text{Final solution}}\
end{align*}
$$
$$
boxed{ color{#c34632} text{ } mathrm{Apply:radical:rule}:quad sqrt{a}sqrt{a}=a}
$$
color{#4257b2} text{ a) }x^2+1
$$
$$
color{#4257b2} text{ b) }x^2-2x-1
$$
a.
$$
y=(x+i)(x-i)=x^2-i^2=x^2+1
$$
b.
$$
y=(x-(1+sqrt{2}))(x-(1-sqrt{2}))=x^2-2x+1-2=x^2-2x-1
$$
b. $y=x^2-2x-1$
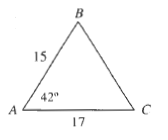
Then we can determine the angle $C$ or $B$ using the Law of Cosines again.
The last angle is obtained by subtracting the other two angles from $180text{textdegree}$.
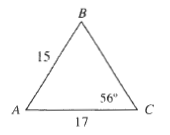
$15^2=17^2+x^2-2cdot 17cdot xcos 56text{textdegree}$
$x^2-34cdot 0.5591929x+289-225=0$
$x^2-19.01x+64=0$ and so on
On the other hand, if we want to use the Law of Cosines we can do this, but we get a quadratic equation. Let’s note:
$BC=x$.
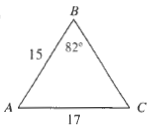
On the other hand, if we want to use the Law of Cosines we can do this, but we get a quadratic equation.
The ratio of a geometric sequence is always common.
$$
text{The formula for the $n$-th term is}
$$
$$
tleft(nright)=ab^{n-1}
$$
$text{where $tleft(nright)=n$-th term of the sequence, $a=$ first term of the sequence and $b$ common ratio.}$
$textbf{Arithmetic sequence}$
$text{An arithmetic sequence has the difference $d$ between each consecutive term, which is a constant.}$
$$
text{The formula for the $n$-th term is}
$$
$$
tleft(nright)=a+dleft(n-1right)
$$
$text{where $tleft(nright)=n$-th term of the sequence, $a=$ first term of the sequence and $b$ difference}$
between consecutive terms.
The sequence is a geometric because
$$
begin{align*}
frac{2.5}{10}&=0.25 \
frac{0.625}{2.5}&=0.25
end{align*}
$$
$text{On the basis of this, we conclude that the first term of the sequence is $a=10$ and}$
$$
text{the common ratio is $b=0.25$.}
$$
$$
tleft(nright)=10left(0.25right)^{n-1}
$$
The sequence is an arithmetic because
$$
begin{align*}
-8-left(-2right)&=-6 \
-14-left(-8right)&=-6
end{align*}
$$
$text{On the basis of this, we conclude that the first term of the sequence is $a=-2$ and}$
$$
text{the difference between consecutive terms is $d=-6$.}
$$
$$
begin{align*}
tleft(nright)&=a+dleft(n-1right) \
&=-2-6left(n-1right) \
&=-2-6n+6 \
&=-6n+4
end{align*}
$$
$textbf{b.}$ $tleft(nright)=-6n+4$

