All Solutions
Page 321: Questions
$$log_ax=b,quad a^b=x.$$
For example,
$$log_232=5,quad 2^5=32.$$
$$
a^y=x
$$
$$
2^y=x
$$
$log_a x=dfrac{ln x}{ln a}$
– the common logarithms key $textcolor{#4257b2}{log}$ which is used for logarithms on base 10;
– the natural logarithms key $textcolor{#4257b2}{ln}$ which is used for logarithms on base $e$.
For any other base we use the conversion formula to either base 10 or base $e$:

$$begin{align*}
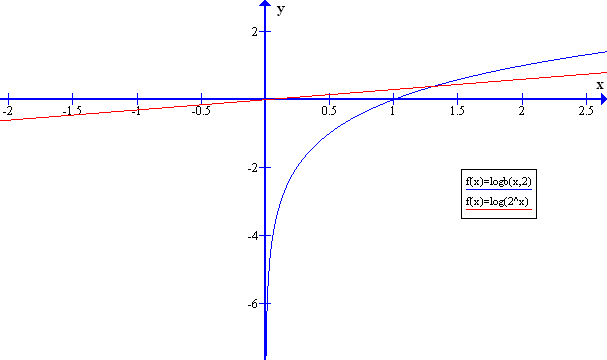
y&=log_2xquadtoquad 2^y=x\
y&=log 2^xquadtoquad 10^y=2^x
end{align*}$$
y&=log_525quadtoquad 5^y=25\
y&=log_{25}5quadtoquad 25^y=5
end{align*}$$
$$begin{align*}
log x^2&=(log x)^2\
2log x&=log xcdotlog x\
2&neqlog x
end{align*}
$$log 7^x=xlog7.$$
Therefore, the given logarithms are equal.
$$begin{align*}
y&=log2xquadtoquad 10^y=2x\
y&=log_2xquadtoquad 2^y=x
end{align*}$$
log (7^x)=xlog (7)
$$
$x=log (5^2)Rightarrow 10^x=25$
$y=2log (5)Rightarrow dfrac{y}{2}=log (5)Rightarrow 10^{y/2}=5Rightarrow 10^y=5^2=25$
$Rightarrow x=y$
$log (5^2)=2log (5)checkmark$
$log (7^3)stackrel{?}{=}3log (7)$
$x=log (7^3)Rightarrow 10^x=343$
$y=3log (7)Rightarrow dfrac{y}{3}=log (7)Rightarrow 10^{y/3}=7Rightarrow 10^y=7^3=343$
$Rightarrow x=y$
$log (7^3)=3log (7)checkmark$
$log (3^5)stackrel{?}{=}5log (3)$
$x=log (3^5)Rightarrow 10^x=243$
$y=5log (3)Rightarrow dfrac{y}{5}=log (3)Rightarrow 10^{y/5}=3Rightarrow 10^y=3^5=343$
$Rightarrow x=y$
$log (3^5)=5log (3)checkmark$
$log (2^8)stackrel{?}{=}8log (2)$
$x=log (2^8)Rightarrow 10^x=256$
$y=8log (2)Rightarrow dfrac{y}{8}=log (2)Rightarrow 10^{y/8}=2Rightarrow 10^y=2^8=256$
$Rightarrow x=y$
$log (2^8)=8log (2)checkmark$
log (m^n)=nlog (m)
$$
y&=log2^xquadtoquad 10^y=2^x\
y&=xlog2quadtoquad dfrac{y}{x}=log2quadtoquad 10^{tfrac{y}{x}}=2
end{align*}$$
$$10^{y}=2^x.$$
y&=log4^xquadtoquad 10^y=4^x\
y&=xlog4quadtoquad dfrac{y}{x}=log4quadtoquad 10^{tfrac{y}{x}}=4
end{align*}$$
y&=log a^bquadtoquad 10^y=a^b\
y&=blog aquadtoquad dfrac{y}{b}=log aquadtoquad 10^{tfrac{y}{b}}=a\
end{align*}$$
y&=log10^xquadtoquad 10^y=10^x\
y&=xlog10quadtoquad dfrac{y}{x}=log10quadtoquad 10^{tfrac{y}{x}}=10
end{align*}$$
$$log10^x=xlog10quad text{and}quad log a^b=blog a.$$
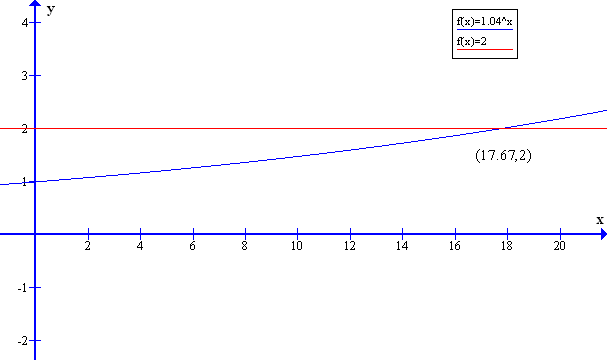
x=17.67…
$$
1.04^x=2
$$
$xlog (1.04)=log (2)$
$x=dfrac{log (2)}{log (1.04)}$
$$
xapprox 17.67
$$
xapprox 17.67
$$
log 1.04^x&=log2\
xlog1.04&=0.301\
end{align*}$$
$$begin{align*}
x&=dfrac{0.301}{log1.04}\
x&=17.673
end{align*}$$
Therefore, the solution to the equation is $x=17.673$.
$$begin{align*}
log5&=log2.25^x\
0.7&=xlog2.25
end{align*}$$
$$begin{align*}
dfrac{0.7}{log2.25}&=x\
1.99&=x
end{align*}$$
$$begin{align*}
log3.5^x&=log10\
xlog3.5&=1
end{align*}$$
$$begin{align*}
x&=dfrac{1}{log3.5}\
x&=1.84
end{align*}$$
8^x&=64\
log8^x&=log64\
xlog8&=1.81\
end{align*}$$
$$begin{align*}
x&=dfrac{1.81}{log8}\
x&=2
end{align*}$$
$$x^8=dfrac{128}{2}=64.$$
$$begin{align*}
sqrt[8]{x}&=sqrt[8]{64}\
x&=sqrt[8]{8^2}\
x&=sqrt[4]{8}
end{align*}$$
$$
3^x=12
$$
$$
x^3=12
$$
The first equation is exponential. The second equation is cubic.
We solve the first equation. Take the $log$ of both sides.
$$
ln left(3^xright)=ln left(12right)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
xln left(3right)=ln left(12right)
$$
Isolate $x$:
$$
x=frac{ln left(12right)}{ln left(3right)}
$$
Use the calculator:
$$
x approx 2.26
$$
Now, let’s solve the second equation.
$$
x^3 = 12 Rightarrow x=sqrt[3]{12}
$$
$$x=sqrt[3]{12}=2.29.$$
$$begin{align*}
log3^x&=log12\
xlog3&=1.08
end{align*}$$
$$begin{align*}
x&=dfrac{1.08}{log3}\
x&=2.26
end{align*}$$
log2&=log1.04^x\
log2&=xlog1.04\
dfrac{log2}{log1.04}&=x\
17.67&=x
end{align*}$$
x>100
$$
$$begin{align*}
99&=ab^2\
8,019&=ab^6
end{align*}$$
$$begin{align*}
dfrac{8,019}{99}&=dfrac{ab^6}{ab^2}\
81&=b^4
end{align*}$$
$$begin{align*}
99&=3^2a\
99&=9a\
11&=a
end{align*}$$
$$begin{align*}
50&=ab^{-1}\
25.6&=ab^2
end{align*}
$$25.6=50b^3.$$
$$begin{align*}
dfrac{25.6}{50}&=b^3\
0.512&=b^3\
0.8&=b
end{align*}$$
50&=acdot0.8^{-1}\
50&=acdotleft(dfrac{4}{5}right)^{-1}\
50&=adfrac{5}{4}
end{align*}$$
$$a=50cdotdfrac{4}{5}=40.$$
Assuming the exponential equation is: $y=ab^x$
Substituting for the given points $(2, 99)$ and $(6, 8019)$
$99=ab^2$ (1)
$8019=ab^6$ (2)
$dfrac {8019}{99}=dfrac {ab^6}{ab^2}$
$81=b^4$
$$
b=3
$$
$99=a(3)^2$
$99=9a$
$$
a=11
$$
The equation is:
$$
y=11(3)^x
$$
Assuming the exponential equation is: $y=ab^x$
Substituting for the given points $(-1, 50)$ and $(2, 25.6)$
$50=ab^{-1}$ (1)
$25.6=ab^2$ (2)
$dfrac {25.6}{50}=dfrac {ab^2}{ab^{-1}}$
$dfrac {64}{125}=b^3$
$$
b=dfrac {4}{5}
$$
$50=a times left(dfrac {4}{5}right)^{-1}$
$50=a times left(dfrac {5}{4}right)$
$a=50 times dfrac {4}{5}$
$$
a=40
$$
The equation is:
$$
y=40 times left(dfrac {4}{5}right)^x
$$
b- The equation is: $y=40 times left(dfrac {4}{5}right)^x$
Take the $log$ of both sides:
$$
ln left(1.04^xright) =ln left(2right)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
xln left(1.04right)=ln left(2right)
$$
$$
Rightarrow
$$
$$
x=frac{ln left(2right)}{ln left(1.04right)}
$$
$$
x approx 17.67
$$
b) We have $5^x=15$:
Take the $log$ of both sides:
$$
ln left(5^xright)=ln left(15right)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
xln left(5right)=ln left(15right)
$$
$$
Rightarrow
$$
$$
x=frac{ln left(15right)}{ln left(5right)}
$$
$$
x approx 1.68
$$
c) We have $3=8^x$:
Take the $log$ of both sides:
$$
ln left(3right)=ln left(8^xright)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
ln left(3right)=xln left(8right)
$$
$$
Rightarrow
$$
$$
x=frac{ln left(3right)}{3ln left(2right)}
$$
$$
xapprox0.528
$$
b) $x approx 1.68$
c) $x approx 0.528$
1.04^x=2
$$
$xlog (1.04)=log (2)$
$x=dfrac{log (2)}{log (1.04)}$
$$
xapprox 17.67
$$
5^x=15
$$
$xlog (5)=log (15)$
$x=dfrac{log (15)}{log (5)}$
$$
xapprox 1.68
$$
3=8^x
$$
$xlog (8)=log (3)$
$x=dfrac{log (3)}{log (8)}$
$$
xapprox 0.53
$$
b) $xapprox 1.68$
c) $xapprox 0.53$
|2x+1|<5
$$
$-5-1<2x+1-1<5-1$
$-6<2x<4$
$-3<x<2$
$$
xin(-3,2)
$$
2|3x-2|geq 10
$$
$3x-2leq -5$ or $3x-2geq 5$
$3x-2+2leq -5+2$ or $3x-2+2geq 5+2$
$3xleq -3$ or $3xgeq 7$
$xleq -1$ or $xgeq dfrac{7}{3}$
$$
xin(-infty,-1]cupleft[dfrac{7}{3},inftyright)
$$
b) $xin(-infty,-1]cupleft[dfrac{7}{3},inftyright)$
y^{-1}(x)=pmsqrt{dfrac{x+7}{3}}-2
$$
log_2 (30)
$$
$2^x=30$
$$
2^4<2^x<2^5
$$
4<x<5
$$
begin{tabular}{|| c| c||}
hline
x & $2^x$ \ [0.5ex]
hline
4 & 16 \
hline
4.1 & 17.1 \
hline
4.2 & 18.4 \
hline
4.3 & 19.7 \
hline
4.4 & 21.1 \
hline
4.5 & 22.6\
hline
4.6 &24.3 \
hline
4.7 &26 \
hline
4.8 &27.9 \
hline
4.9 &29.9 \
hline
5 & 32 \[1ex]
hline
end{tabular}
end{center}
$xlog_{10} (2)=log_{10} (30)$
$x=dfrac{log_{10} (30)}{log_{10} (2)}$
$$
xapprox 4.91
$$
log_5 (200)
$$
$5^x=200$
$log_{10} (5^x)=log_{10} (200)$
$xlog_{10} (5)=log_{10} (200)$
$x=dfrac{log_{10} (200)}{log_{10} (5)}$
$$
xapprox 3.29
$$
$b^x=y$
$log_{10} b^x=log_{10} y$
$xlog_{10} b=log_{10} y$
$$
x=dfrac{log_{10} y}{log_{10} b}
$$
b) $x=dfrac{log_{10} y}{log_{10} b}$
$$
dfrac{x^m}{x^n}=x^{m-n}
$$
$log (5cdot 6)=log (x)$
$log (30)=log (x)$
$$
x=30
$$
$log (5cdot 2)=log (x)$
$log (10)=log (x)$
$$
x=10
$$
$log (5cdot 5)=log (x)$
$log (25)=log (x)$
$$
x=25
$$
$log (10cdot 100)=log (x)$
$log (1000)=log (x)$
$$
x=1000
$$
$log (9cdot 11)=log (x)$
$log (99)=log (x)$
$$
x=99
$$
$log (mcdot n)=log (x)$
$log (mn)=log (x)$
$$
x=mn
$$
$log left(dfrac{20}{5}right)=log (x)$
$log (4)=log (x)$
$$
x=4
$$
$log left(dfrac{30}{3}right)=log (x)$
$log (10)=log (x)$
$$
x=10
$$
$log left(dfrac{5}{2}right)=log (x)$
$log (2.5)=log (x)$
$$
x=2.5
$$
$log left(dfrac{17}{9}right)=log (x)$
$$
x=dfrac{17}{9}
$$
$log left(dfrac{375}{17}right)=log (x)$
$$
x=dfrac{375}{17}
$$
$log left(dfrac{m}{n}right)=log (x)$
$$
x=dfrac{m}{n}
$$
Suppose you have some numbers $a, b, c$, where $a$ is neither 0 nor 1, and $a, b,$ and $c$ are strictly positive (not zero).
Then, for any values of $a, b,$ and $c$ in these conditions, it will be true that
$$
color[RGB]{150,0,0}log_a (b cdot c) = log_ab + log_ac
$$
$textbf{Example:}$
We wish to find the value of
$$
log_2{32}
$$
We know that $32 = 4 cdot 8$. So we can rewrite the expression as
$$
log_2(4 cdot 8)
$$
Now we have the logarithm of a product. We apply the property:
$$
log_2(4 cdot 8) = log_24 + log_28 = 2 + 3 = 5
$$
We can check that our result is correct, since $2^5 = 32$.
Suppose you have some numbers $a, b, c$, where $a$ is neither 0 nor 1, and $a, b,$ and $c$ are strictly positive (not zero).
Then, for any values of $a, b,$ and $c$ in these conditions, it will be true that
$$
color[RGB]{150,0,0}log_a left(frac{b}{c}right) = log_ab – log_ac
$$
$textbf{Example:}$
We wish to solve
$$
log_2{65536} – log_2{4096}
$$
Since we are subtracting two logarithms of the same base, we can turn the expression into the logarithm of a quotient.
$$
log_2{65536} – log_2{4096} = log_2 left(frac{65536}{4096}right)
$$
We can simplify the fraction and easily solve the logarithm:
$$
log_2 left(frac{65536}{4096}right) = log_216 = 4
$$
Suppose you have some numbers $a, b, c$, where $a$ and $b$ are neither 0 nor 1, and $a, b,$ and $c$ are strictly positive (not zero).
Then, for any values of $a, b,$ and $c$ in these conditions, it will be true that
$$
color[RGB]{150,0,0}log_ac = frac{log_bc}{log_ba}
$$
$textbf{Example:}$
We wish to solve the logarithm
$$
log_{27}243
$$
Note that both 27 and 243 are powers of 3. We can rewrite the logarithm in terms of base 3 using the Change of Base Property:
$$
log_{27}243 = frac{log_3{243}}{log_3{27}} = frac{5}{3}
$$
log_{3}60=log_{3}6+log_{3}10=log_{3}3+log_{3}20=log_{3}120-log_{3}2=log_{3}240-log_{3}4
$$
log_{7}36=log_{7}6+log_{7}6=log_{7}3+log_{7}12=log_{7}72-log_{7}2=log_{7}144-log_{7}4
$$
log_{6}18=log_{6}9+log_{6}2=log_{6}3+log_{6}6=log_{6}36-log_{6}2=log_{6}72-log_{6}4
$$
log_{25}50=log_{25}25+log_{25}2=log_{25}5+log_{25}5=log_{25}75-log_{25}1.5=log_{25}200-log_{25}4
$$
log40=log10+log4=log5+log8=log160-log4=log80-log2
$$
begin{align*}
log_{1/2} (4) +log_{1/2} (2) -log_{1/2} (5)&=log_{1/2} (4 cdot 2) -log_{1/2} (5) &textrm{Using Product property}\
&=log_{1/2} (8) -log_{1/2} (5)\
&=log_{1/2} left(dfrac{8}{5} right) &textrm{Using Quotient property}\
&=log_{1/2} left( 1.6 right)
intertext{textbf{(b)}}
log_2(M) +log_3 (N)&=log_2(M)+dfrac{log_2 (N)}{log_2 (3)} & textrm{Change of base property}\
&=log_2(M)+dfrac{log_2 (N)}{frac{log (2)}{log (3)}} & textrm{Change of base property}\
&=log_2(M)+dfrac{log_2 (N)}{frac{0.3010299957}{0.4771212547}} \
&=log_2(M)+dfrac{log_2 (N)}{0.631} \
&=log_2(M)+log_2 (N)^{1/0.631} & textrm{Using Power property}\
&=log_2 (M cdot N^{1/0.631}) &textrm{Using Product property}\
intertext{textbf{(c)}}
log(k) + x log(m) &= log(k) + log(m^x) & textrm{Using Power property}\
&= log (kcdot m^x)&textrm{Using Product property}\
intertext{textbf{(d)}}
dfrac{1}{2} log_5(x)+2log_5(x+1)&= log_5(sqrt{x})+log_5((x+1)^2)& textrm{Using Power property}\
&= log_5(sqrt{x} cdot (x+1)^2)\
&= log_5(sqrt{x} cdot (x^2+2x+1))\
&= log_5(x^{2.5}+2x^{1.5}+sqrt{x})\
end{align*}
intertext{textbf{(e)}}
log(4) -log(3) + log( pi) +3 log (r)&=log(4) -log(3) + log( pi) + log (r^3)& textrm{Using Power property}\
&=log (4 pi r^3)-log(3) &textrm{Using Product property} \
&=log left(dfrac{4 pi r^3}{3}right) &textrm{Using Quotient property}\
intertext{textbf{(f)}}
log (6) + 23&= log(6)+ log(10^{23})\
&= log(6 cdot 10^{23})&textrm{Using Product property}
end{align*}
(e) $log left( frac{4 pi r^3}{3} right)$ (f) $log (6 cdot 10^{23})$
$$
n=b^y
$$
mn=b^xcdot b^y=b^{x+y}
$$
$log_b (m)=xlog_b (b)$
$log_b (m)=x$
$n=b^yRightarrow log_b (n)=log_b (b^y)$
$log_b (n)=ylog_b (b)$
$log_b (n)=y$
$mn=b^{x+y}Rightarrow log_b (mn)=log_b (b^{x+y})$
$log_b (mn)=(x+y)log_b (b)$
$log_b (mn)=x+y$
$y=log_b (n)$
$$
x+y=log_b (mn)
$$
log_b (m)+log_b (n)=log_b (mn)
$$
$log_b left(dfrac{m}{n}right)=log_b (b^{x-y})$
$log_b left(dfrac{m}{n}right)=(x-y)log_b b$
$log_b left(dfrac{m}{n}right)=x-y$
log_b (m^n)=nlog_b (m)
$$
$U=log_b (m)$.
$m^n=(b^U)^n$
$m^n=b^{Un}$
$log_b (m^n)=log_b (b^{Un})$
$log_b (m^n)=Unlog_b b$
$log_b (m^n)=Un$
$$
log_b (m^n)=nlog_b (m)
$$
log_2 (3)=x
$$
dfrac{log_{10} (3)}{log_{10} (2)}=x
$$
log_5 (8)=x
$$
$3log_5 (2)=x$
$$
dfrac{3log_{10} (2)}{log_{10} (5)}=x
$$
log_7 (12)=x
$$
dfrac{log_{10} (12)}{log_{10} (7)}=x
$$
log_a (b)=x
$$
dfrac{log_{10} (b)}{log_{10} (a)}=x
$$
(x-3)log5.825=log120
$$
x=dfrac{log120}{log5.825}+3=5.717
$$
1.2^{(2x-1)}=50
$$
(b)
$$
(2x-1)log1.2=log50
$$
x=dfrac{1}{2}left[ dfrac{log50}{log1.2}+1right]=11.228
$$
dfrac{log_2 32}{log_2 4}
$$
$$
=dfrac{5log_2 (2)}{2log_2 (2)}=dfrac{5}{2}
$$
dfrac{log 32}{log 4}
$$
$$
=dfrac{5log (2)}{2log (2)}=dfrac{5}{2}
$$
We use the change of base formula:
log_2 (7)=dfrac{log_5 (7)}{log_5 (2)}
$$
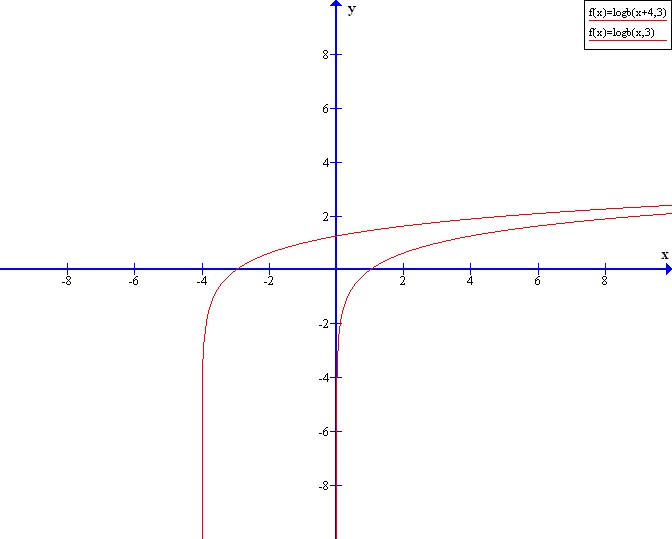
$$
y=log_{3}x
$$
shifted 4 units in the negative x direction.

y=3^{x}
$$
The vertex is $(2,3)$ (Given)
The parabola passes the point $(0, 0)$ Given
Substituting in the general form for the vertex and the given point.
$0=a(0-2)^2+3$
$4a=-3$
$a=-dfrac {3}{4}$
The equation of the parabola is:
$$
y=-dfrac {3}{4}(x-2)^2+3
$$

y=-dfrac {3}{4}(x-2)^2+3
$$
y=ab^x
$$
$$
x_1=2; y_2=392
$$
begin{cases}
ab^0=200\
ab^2=392
end{cases}
$$
$a=200$
$200b^2=392$
$b^2=dfrac{392}{200}$
$b^2=dfrac{49}{25}$
$$
b=dfrac{7}{5}=1.4
$$
y=200(1.4)^x
$$
$(1.4)^x=dfrac{5}{200}$
$(1.4)^x=0.25$
$log (1.4)^x=log 0.025$
$xlog 1.4=log 0.025$
$x=dfrac{log 0.025}{log 1.4}$
$$
xapprox-11
$$
Until April 1st: $31-10=21$ days
Until May 1st: $21+30=51$ days
Until June 1st: $51+31=82$ days
Until July 1st: $82+30=112$ days
Until August 1st: $112+31=143$ days
Until September 1st: $143+31=174$ days
Until October 1st: $174+30=204$ days
Until November 1st: $204+31=235$ days
Until December 1st: $235+30=265$ days
y=ab^x
$$
$$
(23,392)
$$
i) We are given:
begin{cases}
ab^{21}=200\
ab^{23}=392
end{cases}
$$
$b^2=1.96$
$b=sqrt{1.96}$
$$
b=1.4
$$
$a=dfrac{200}{(1.4)^{21}}$
$$
aapprox 0.1707
$$
y=0.1707(1.4)^x
$$
$$
(4,11.25)
$$
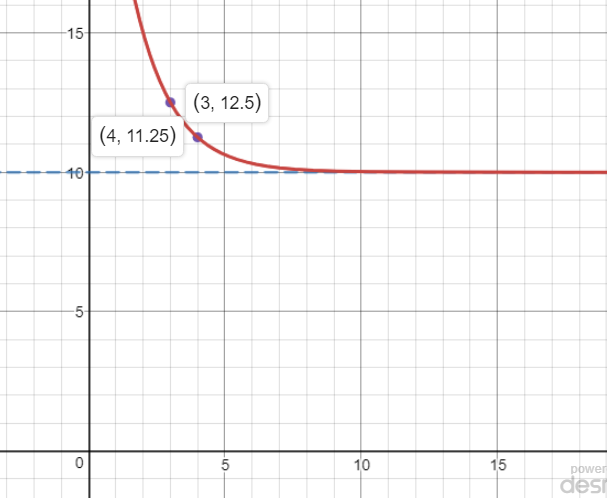
y=ab^x+k
$$
k=10
$$
begin{cases}
ab^3+10=12.5\
ab^4+10=11.25
end{cases}
$$
$$
begin{cases}
ab^3=12.5-10\
ab^4=11.25-10
end{cases}
$$
$$
begin{cases}
ab^3=2.5\
ab^4=1.25
end{cases}
$$
$dfrac{ab^4}{ab^3}=dfrac{1.25}{2.5}$
$b=0.5$
$a(0.5)^3=2.5$
$a=dfrac{2.5}{0.125}$
$a=20$
$$
y=20(0.5)^x+10
$$
x=0Rightarrow y=20(0.5)^0+10=30
$$
$A=40,000$
$n=1$
$$
t=8
$$
$$
A=P(1+r)^t
$$
$dfrac{40,000}{1000}=(1+r_1)^8$
$40=(1+r_1)^8$
$1+r_1=sqrt[8]{40}$
$r_1=1.5858-1$
$r_1=0.5868$
$$
r_1=58.58%
$$
$A=18,400$
$n=1$
$$
t=20
$$
$dfrac{18,400}{7800}=(1+r_2)^{20}$
$2.359=(1+r_2)^{20}$
$1+r_2=sqrt[20]{2.359}$
$r_2=1.0438-1$
$r_2=0.0438$
$$
r_2=4.38%
$$
dfrac{40,000-1000}{8-0}=dfrac{39,000}{8}=4875
$$
dfrac{18,400-7800}{20-0}=dfrac{10,600}{20}=530
$$
4875>>530
$$
$$
(3,135)
$$
$$
begin{cases}
ab^1=60\
ab^3=135
end{cases}
$$
$dfrac{ab^3}{ab^1}=dfrac{135}{60}$
$b^2=dfrac{9}{4}$
$b=dfrac{3}{2}$
$$
a=dfrac{60}{dfrac{3}{2}}=60cdot dfrac{2}{3}=40
$$
y=40(1.5)^x
$$
$(1.5)^x=dfrac{1}{40}$
$log_{10} (1.5)^x=log_{10} 0.025$
$xlog_{10} (1.5)=log_{10} 0.025$
$x=dfrac{log_{10} 0.025}{log_{10} (1.5)}$
$$
xapprox -9
$$
$t=20$
$t_1=6$
$$
A_1=132
$$
$$
A=P(1+r)^t
$$
$132=100(1+r)^6$
$dfrac{132}{100}=(1+r)^6$
$1.32=(1+r)^6$
$1+r=sqrt[6]{1.32}$
$r=1.0474-1$
$$
r=0.0474=4.74%
$$
$A=100(1+0.0474)^{20}$
$A=100(1.0474)^{20}$
$$
Aapprox 252.49
$$
$$
Aapprox $252.49
$$
where
$T$=the temperature of the cup at time $t$
$t$=time
$T_s$=the temperature of the room
$T_0$=the initial temperature of the cocoa
$k$=a cooling constant, specific to the cocoa
We usually consider Newton’s Law of Cooling:
$T_0=373.15$
$T(t)=293.15+(373.15-293.15)e^{-0.0015t}$
$$
T(t)=293.15+80e^{-0.0015t}
$$
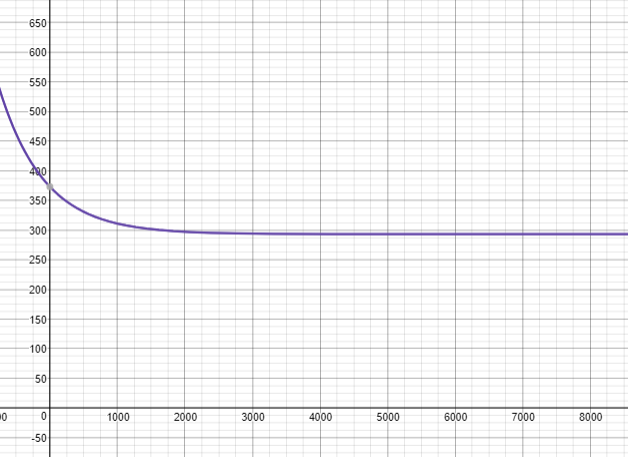
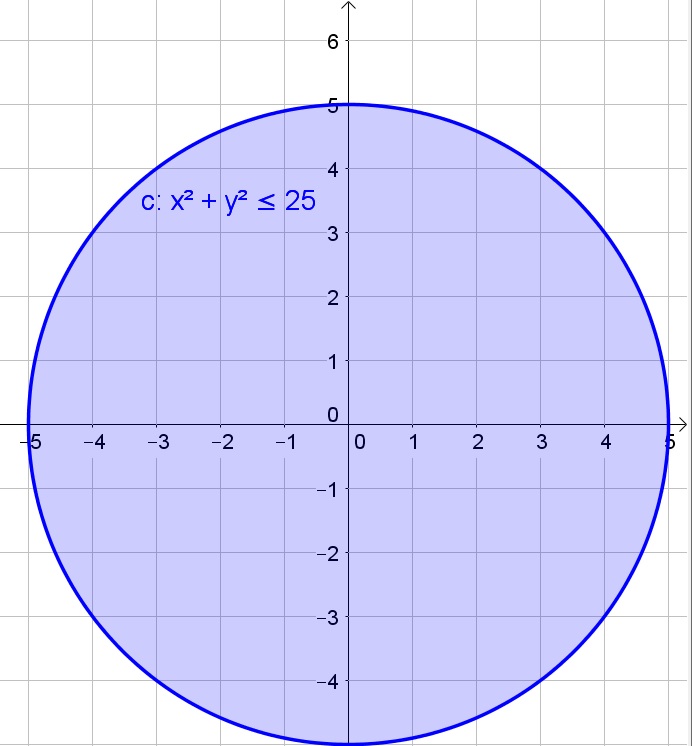
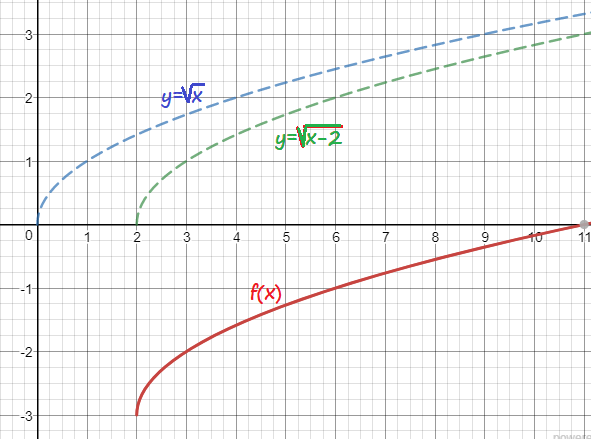
Sketch the graph in Desmos.
We graph both functions and shade the region above the first function and below the second and intersect them to get the solution region:
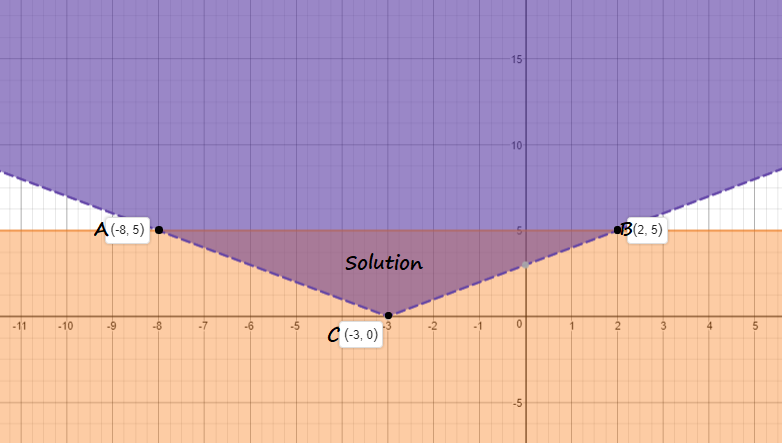
$$
AB = sqrt{(5-5)^2+(2-(-8))^2}
$$
$$
AB =sqrt{0+100}
$$
$$
AB= 10
$$
We know:
$$
P_{triangle ABC} = dfrac{AB cdot h}{2}
$$
From the graph we see $h=5$.
Substitute the values and we have:
$$
P_{triangle ABC} = dfrac{10 cdot 5 }{2}
$$
$$
P_{triangle ABC} = colorbox{yellow}{25}
$$
25
$$
$$
i^3=icdot i^2=icdot (-1)=-i
$$
$$
i^4=i^2cdot i^2=(-1)cdot (-1)=1
$$
1
$$
a) $(x+4)(2x-5)=0qquadqquadqquadqquadqquad$ $color{#c34632} text{[apply the zero product property]}$
Set each factor equal to zero and solve:
$bullet,,$ $x+4=0Rightarrow color{#4257b2} text{$x=-4$}$
$bullet,,$ $2x-5=0Rightarrow 2x=5Rightarrow color{#4257b2} text{$x=dfrac{5}{2}$}$
The solutions of the initial equation are: $color{#4257b2} text{$,,,x=-4$}$ and $color{#4257b2} text{$x=dfrac{5}{2}$}$
Set each factor equal to zero and solve:
$bullet,,$ $x+4=0Rightarrow color{#4257b2} text{$x=-4$}$
$bullet,,$ $x^2-5x+6=0qquadqquadqquadqquadqquad$ $color{#c34632} text{[$a=1$ , $b=-5$ , $c=6$]}$
$color{#c34632} text{Apply the quadratic formula:}$
$color{#c34632} text{$x_{1,2}=dfrac{-bpm sqrt{b^2-4ac}}{2a}$}$
$Rightarrow x_{1,2}=dfrac{5pm sqrt{(-5)^2-4(1)(6)}}{2(1)}$
$Rightarrow x_{1,2}=dfrac{5pm sqrt{25-24}}{2}$
$Rightarrow x_{1,2}=dfrac{5pm 1}{2}$
$Rightarrow color{#4257b2} text{$x=2,,$}$ or $color{#4257b2} text{$,,x=3$}$
The solutions of the initial equation are: $color{#4257b2} text{$,,,x=-4$}$ , $color{#4257b2} text{$x=2$}$ and $color{#4257b2} text{$x=3$}$
$color{#c34632} text{[apply the zero product property]}$
Set each factor equal to zero and solve the resulting equations as shown below:
$bullet,,$ $3x=0Rightarrow color{#4257b2} text{$x=0$}$
$bullet,,$ $x+1=0Rightarrow color{#4257b2} text{$x=-1$}$
$bullet,,$ $2x-7=0Rightarrow 2x=7Rightarrow color{#4257b2} text{$x=dfrac{7}{2}$}$
$bullet,,$ $3x+4=0Rightarrow 3x=-4Rightarrow color{#4257b2} text{$x=-dfrac{4}{3}quadquad$}$ $color{#4257b2} text{Multiplicity $2$}$
$bullet,,$ $x-13=0Rightarrow color{#4257b2} text{$x=13$}$
$bullet,,$ $x+7=0Rightarrow color{#4257b2} text{$x=-7$}$
The solutions of the initial equation are:
$color{#4257b2} text{$x=0$}$ , $color{#4257b2} text{$x=-1$}$ , $color{#4257b2} text{$x=dfrac{5}{2}$}$ , $color{#4257b2} text{$x=dfrac{7}{2}$ , $x=-dfrac{4}{3}$ , $x=13,,$}$ and $color{#4257b2} text{$,,x=-7$}$
That is, we set each factor equal to zero and solve the equations that occur one by one. The solutions we find for each equation are the solutions of the original equation.
y=17
$$
$$
y=ab^x+17
$$
begin{cases}
ab^{-1}+17=27\
ab^0+17=24
end{cases}
$$
$$
begin{cases}
dfrac{a}{b}=27-17=10\
a=24-17=7
end{cases}
$$
$dfrac{a}{b}=10$
$dfrac{7}{b}=10$
$$
b=dfrac{7}{10}=0.7
$$
We determine $a,b$ using the points $(-1,27), (0, 24)$:
y=7left(0.7right)^x+17
$$
$7left(0.7right)^x+17=37$
$7left(0.7right)^x=37-17$
$7left(0.7right)^x=20$
$(0.7)^x=dfrac{20}{7}$
$log (0.7)^x=log dfrac{20}{7}$
$xlog (0.7)=log dfrac{20}{7}$
$x=dfrac{log dfrac{20}{7}}{log (0.7)}$
$$
xapprox -2.94
$$
$$
6h12′-2h56.4’=5h72′-2h56.4’=3h 15.4′
$$
$$
A(t)=P(0.8)^t
$$
$P$=the initial value of the car.
After the first year its value will be $100%-20%=80%$ from the initial value, after the second year its value will be $80%$ from the value after the first year and so on. We can write the model:
P=23,500
$$
A(t)=23,500(0.8)^t
$$
A(4)=23,500(0.8)^4=9625.6
$$
dfrac{A(4)-P}{4-0}=dfrac{9625-23,500}{4}=3468.75
$$
$(0.8)^t=dfrac{6000}{23,500}$
$(0.8)^t=0.255319$
$log_{10} (0.8)^t=log_{10} 0.255319$
$tlog_{10} (0.8)=log_{10} 0.255319$
$t=dfrac{log_{10} 0.255319}{log_{10} (0.8)}$
$tapprox 6$ years
$P_0=dfrac{23,500}{(0.8)^{2.7}}$
$$
P_0=42,926.44
$$
$$
x=pm 2.236
$$
$x^{19}=796,262,400,000$
$x=sqrt[19]{796,262,400,000}$
$$
xapprox 4.230
$$
x^{-4}=100
$$
$1=100x^4$
$x^4=dfrac{1}{100}$
$x=pmdfrac{1}{sqrt[4]{100}}$
$$
x=pm 0.316
$$
(x+2)^3=65
$$
$x=4.021-2$
$$
x=2.021
$$
4(x-2)^{12.5}=2486
$$
$16(x-2)^{25}=6,180,196$
$(x-2)^{25}=dfrac{6,180,196}{16}$
$(x-2)^{25}=386,262.25$
$x-2=sqrt[25]{386,262.25}$
$x=2+1.673$
$$
x=3.673
$$
xlog(2)=log(3)
$$
x=dfrac{log(3)}{log(2)}=1.585
$$
b. The vertical equation has equation (about) $x=2$.
c. Since $ln{1}=0$, a possible function is $y=ln{(x-2)}$ (thus the parent function translates to the right by 2 units).
b. $x=2$
c. $y=ln{(x-2)}$
x=3left( p^{3}+6right)
$$
p^{-1}(x)=p=sqrt[3]{dfrac{x}{3}-6}
$$
x=3k^{3}+6
$$
k=sqrt[3]{dfrac{x-6}{3}}
$$
x=dfrac{h+1}{h-1}
$$
x=dfrac{h}{h-1}+dfrac{1}{h-1}
$$
x(h-1)=h+1
$$
xh-x-h-1=0
$$
h^{-1}(x)=h=dfrac{x+1}{x-1}
$$
x=dfrac{2}{3-j}
$$
j^{-1}(x)=j=3-dfrac{2}{x}
$$
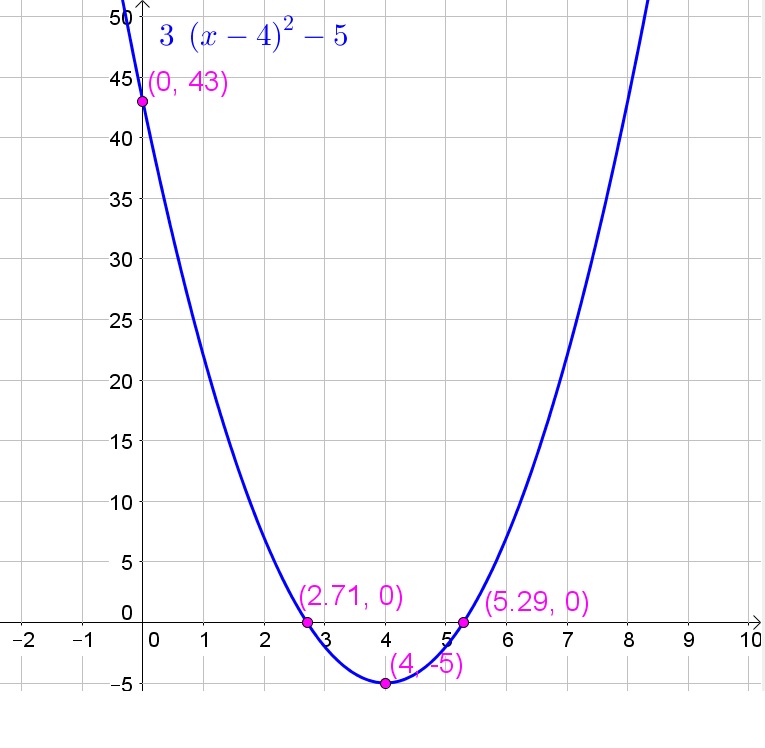
$f$(x) = 3(x – 4)$^{2}$ – 5
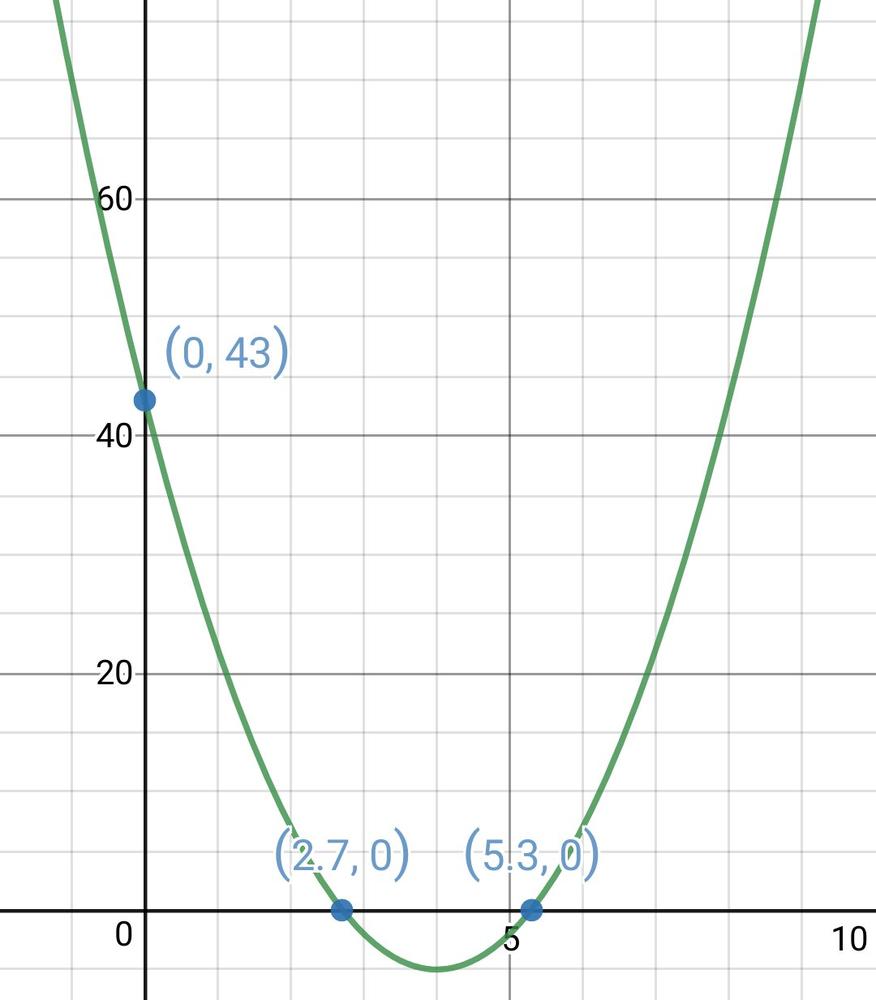
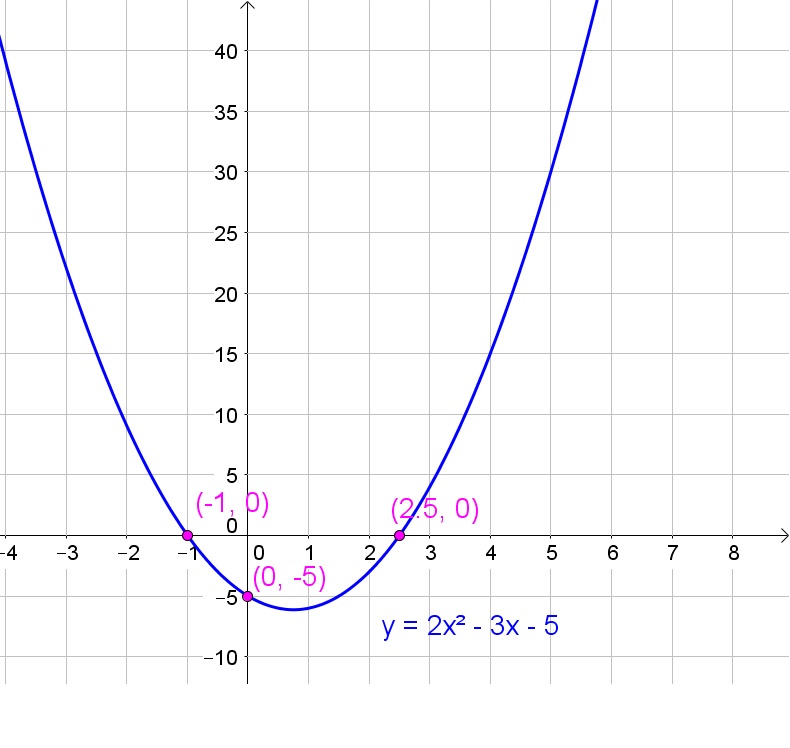
g(x) = 2x$^{2}$ – 3x – 5
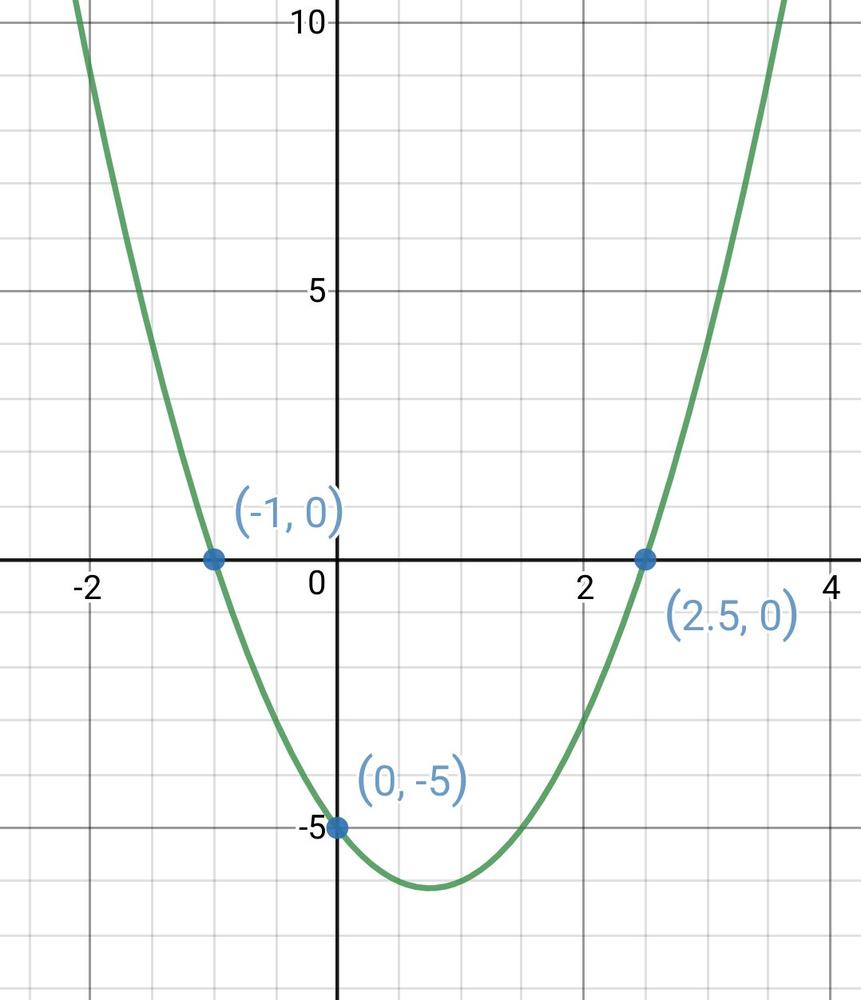
2) $2$ sides of a triangle and $1$ angle
3) $1$ side and $2$ angles of a triangle
4) all the $3$ angles of a triangle
2) $2$ sides of a triangle and $1$ angle
…
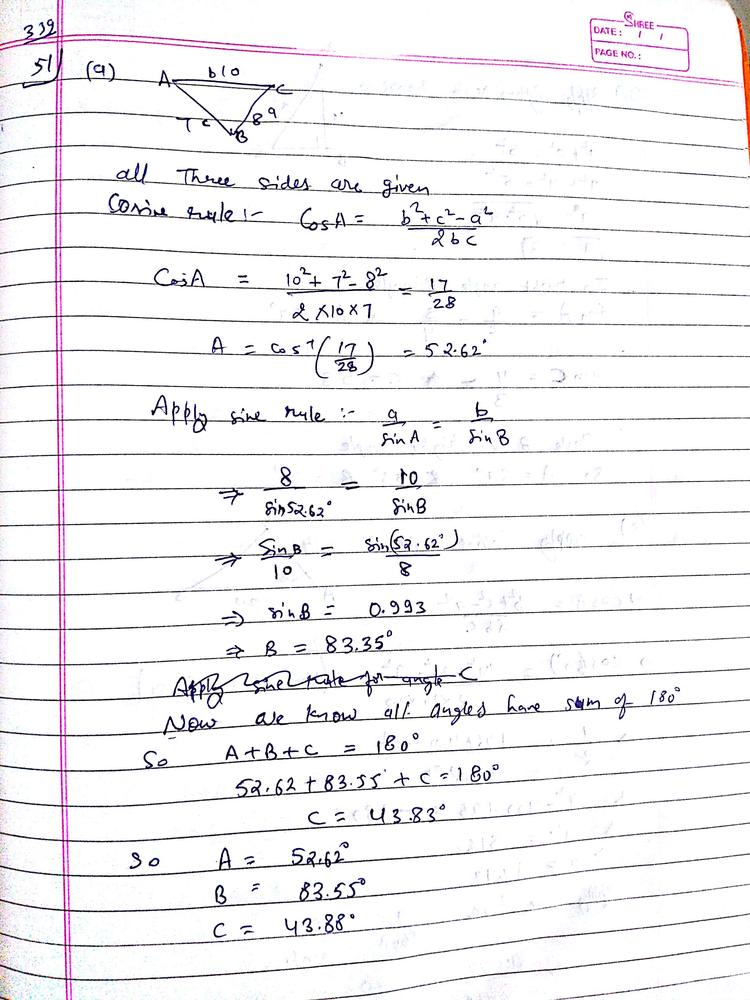




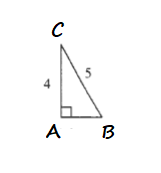
$AB^2+4^2=5^2$
$AB^2=25-16$
$AB^2=9$
$$
AB=3
$$
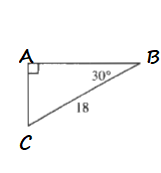
$AC=18sin 30text{textdegree}$
$AC=18cdot dfrac{1}{2}$
$AC=9$
$AB^2+AC^2=BC^2$
$AB^2=18^2-9^2$
$AB^2=243$
$AB=sqrt{243}$
$$
AB=9sqrt 3
$$
$a^2=14^2+20^2-2(14)(20)cdot dfrac{1}{2}$
$a^2=316$
$a=sqrt{316}$
$aapprox 17.78$
$14<17.78<20$
$14^2+17.78^2=512not=20^2Rightarrow$the triangle is not right
$5sin B=7sin 40text{textdegree}$
$sin B=dfrac{7cdot 0.64278761}{5}$
$sin B=0.8999$
$Bapprox 64.1text{textdegree}$
$C=180text{textdegree}-40text{textdegree}-64.1text{textdegree}=75.9text{textdegree}Rightarrow$the triangle is not right

$sin 30text{textdegree}=dfrac{BD}{14}$
$dfrac{1}{2}cdot 14=BD$
$$
BD=7
$$
$AD^2+7^2=14^2$
$AD^2=196-49$
$AD^2=147$
$$
AD=7sqrt 3
$$
$CD^2+AD^2=AC^2$
$13^2+147=AC^2$
$AC^2=316$
$AC=sqrt{316}$
$$
ACapprox 17.78
$$
$sin C=dfrac{7sqrt 3}{17.78}$
$sin Capprox 0.6819$
$$
Capprox 43text{textdegree}
$$
$=180text{textdegree}-60text{textdegree}-43text{textdegree}$
$$
=77text{textdegree}
$$
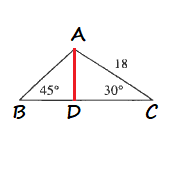
$AD=dfrac{1}{2}cdot 18$
$$
AD=9
$$
$CD^2=18^2-9^2$
$CD^2=275$
$CD=sqrt{243}$
$$
CD=9sqrt 3
$$
$BD^2+AD^2=AB^2$
$9^2+9^2=AB^2$
$162=AB^2$
$$
AB=9sqrt 2
$$
BC=CD+BD=9sqrt 3+9approx 24.59
$$
$$
=180text{textdegree}-45text{textdegree}-30text{textdegree}=105text{textdegree}
$$

$AD=sin 48text{textdegree}cdot 5$
$AD=0.74314483cdot 5$
$$
ADapprox 3.72
$$
$ACB=180text{textdegree}-48text{textdegree}-29text{textdegree}$
$$
=103text{textdegree}
$$
$AC=dfrac{3.72}{sin 77text{textdegree}}=dfrac{3.72}{0.97437006}$
$$
ACapprox 3.82
$$
$sin CAD=dfrac{CD}{AC}$
$CD=sin 13text{textdegree}cdot 3.82=0.22495105cdot 3.82$
$$
CDapprox 0.86
$$
$BD=cos 48text{textdegree}cdot 5=0.66913061cdot 5$
$$
BDapprox 3.35
$$
$$
BC=2.49
$$
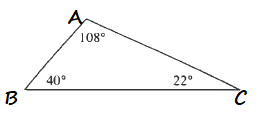
$$
=170text{textdegree}
$$
Apply the rule $log _cleft(aright)+log _cleft(bright)=log _cleft(abright)$ :
$$
log _{10}left(8right)+log _{10}left(125right)=log _{10}left(8cdot :125right)
$$
Multiply.
$$
log _{10}left(8cdot :125right)=log _{10}left(1000right)
$$
Rewrite.
$$
log _{10}left(1000right)=log _{10}left(10^3right)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
log _{10}left(10^3right)=3log _{10}left(10right)
$$
Apply the rule $log _aleft(aright)=1$:
$$
3log _{10}left(10right)=3cdot :1 = 3
$$
Rewrite.
$$
log _{25}left(125right)=log _{5^2}left(125right)
$$
Apply the rule $log _{a^b}left(xright)=frac{1}{b}log _aleft(xright)$:
$$
log _{5^2}left(125right)=frac{1}{2}log _5left(125right)
$$
Rewrite.
$$
frac{1}{2}log _5left(125right)=frac{1}{2}log _5left(5^3right)
$$
Apply the rule $log _aleft(a^xright)=x$:
$$
frac{1}{2}log _5left(5^3right)=frac{1}{2}cdot :3=frac{3}{2}
$$
Apply the rule $log _cleft(aright)+log _cleft(bright)=log _cleft(abright)$:
$$
log _{10}left(5right)+log _{10}left(20right) =log _{10}left(5cdot :20right)
$$
Multiply.
$$
log _{10}left(5cdot :20right)=log _{10}left(100right)
$$
Apply the rule $log _aleft(x^bright)=bcdot log _aleft(xright)$:
$$
log _{10}left(100right)=log _{10}left(10^2right)=2log _{10}left(10right)
$$
Apply the rule $log _aleft(aright)=1$:
$$
2log _{10}left(10right)=2cdot :1 = 2
$$
Apply the rule $a^{log _aleft(bright)}=b$:
$$
7^{log _7left(12right)}=12
$$
b) $1.5$
c) $2$
d) $12$
Mean score of French exam ($bar x_f$) = 81
Standard Deviation ($sigma_f$) = 5
Mean score of Spanish exam ($bar x_s$) = 72
Standard Deviation ($sigma_s$) = 12
In order to earn honors in language at graduation, a student must score in the 90th percentile on all their language finals.
Brynne has scored 88 in both French and Spanish finals. We have to see whether he has earned his honors or not.
In this case we are given the standard deviation and the mean. The sample scores are the scores of Brynne in his Spanish and French language final exams.
It is pertinent to note,
$$z=dfrac{x-bar{x}}{sigma}$$
$$begin{aligned}
x_f&=88 \
bar{x}_f& = 81 \
sigma_f &= 5\
end{aligned}$$
Calculating the $z$-score,
$$begin{aligned}
z_b&=dfrac{x_f-bar{x}_f}{sigma_f} \\
&=dfrac{88-81}{5} \\
&=-dfrac{7}{5}\\
&=1.4
end{aligned}$$
Now we will use the normal distribution table,
We get
$z<1.4 = 0.91924$
This implies Brynne falls in the $91.92^{text{th}}$ which is greater than the $90^{text{th}}$ percentile.Therefore, Brynne has qualified for honors in French.
$$begin{aligned}
x_s&=88 \
bar{x}_s& = 72 \
sigma_f &= 12\
end{aligned}$$
Calculating the $z$-score,
$$begin{aligned}
z_b&=dfrac{x_s-bar{x}_s}{sigma_s} \\
&=dfrac{88-72}{12} \\
&=-dfrac{16}{12}\\
&=1.333
end{aligned}$$
Now we will use the normal distribution table,
We get
$z<1.333 = 0.90879$
This implies Brynne falls in the $90.88^{text{th}}$ which is greater than the $90^{text{th}}$ percentile.Therefore, Brynne has qualified for honors in Spanish as well.
Since, Brynne's score for both the exams is 88 which is above the $90^{text{th}}$ percentile, he has earned the language honor at graduation.
$$
a)
$$
$color{#c34632} text{$y=7+2x^2+4x-5$}$
First write this quadratic equation in the standard form $color{#c34632} text{$,,y=ax^2+bx+c,,$}$ as shown:
$y=7+2x^2+4x-5$
$Rightarrow color{#4257b2} text{$y=2x^2+4x+2$}$
$y=0$
$Rightarrow 2x^2+4x+2=0qquadqquadqquadqquadqquad$ $color{#c34632} text{[factor out $2$]}$
$Rightarrow 2(x^2+2x+1)=0qquadqquadqquadqquad$ $color{#c34632} text{[factor the perfect square trinomial]}$
$Rightarrow 2(x+1)^2=0$
$Rightarrow (x+1)^2=0$
$Rightarrow x+1=0qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[subtract $1$ in both sides]}$
$Rightarrow color{#4257b2} text{$x=-1$}$
The $x$-intercept of the graph of this equation is the point $color{#4257b2} text{$,,(-1 , 0)$}$.
$bullet,,$For the $y$-intercept set $color{#c34632} text{$,,x=0,,$}$ and solve the resulting equation for $color{#c34632} text{$,,”y”$}$:
$y=2x^2+4x+2qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $x=0$]}$
$Rightarrow y=2(0)^2+4(0)+2qquadqquadqquadqquadqquad$
$Rightarrow color{#4257b2} text{$y=2qquadqquadqquadqquad$}$
The $y$-intercept of the graph of this equation is the point $color{#4257b2} text{$,,(0 , 2)$}$.
$color{#4257b2} text{$(h,k)=bigg(dfrac{-b}{2a} ,,, fbigg(dfrac{-b}{2a}bigg)bigg)$}$
In this case we have:
$color{#4257b2} text{$f(x)=2x^2+4x+2$}qquadqquadqquadqquadqquad$ $color{#c34632} text{[$a=2$ , $b=4$ , $c=2$]}$
$h=dfrac{-b}{2a}=dfrac{-4}{2(2)}=dfrac{-4}{4}=color{#4257b2} text{$-1$}$
$k=fbigg(dfrac{-b}{2a}bigg)=f(-1)=2(-1)^2+4(-1)+2=color{#4257b2} text{$0$}$
$bullet,,$The vertex of the graph of this function is the point $color{#4257b2} text{$,,(h,k)=(-1,0)$}$.
$bullet,,$Write this equation in the vertex form $color{#c34632} text{$,,y=a(x-h)^2+k,,$}$ as shown below:
$y=2x^2+4x+2qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[factor out $2$]}$
$Rightarrow y=2(x^2+2x+1)qquadqquadquadquadquad$ $color{#c34632} text{[factor the perfect square trinomial]}$
$$
Rightarrow color{#4257b2} text{$y=2(x+1)^2+0$}
$$
b)
$$
$color{#c34632} text{$x^2=2x+x(2x-4)+y$}$
First write this quadratic equation in the standard form $color{#c34632} text{$,,y=ax^2+bx+c,,$}$ as shown:
$x^2=2x+x(2x-4)+yqquadqquadqquadqquadqquad$ $color{#c34632} text{[solve for $y$]}$
$Rightarrow y=x^2-2x-x(2x-4)$
$Rightarrow y=x^2-2x-2x^2+4x$
$Rightarrow color{#4257b2} text{$y=-x^2+2x$}$
$y=0$
$Rightarrow -x^2+2x=0qquadqquadqquadqquadqquad$ $color{#c34632} text{[factor out $x$]}$
$Rightarrow x(2-x)=0qquadqquadqquadqquad$ $color{#c34632} text{[zero product property]}$
$Rightarrow x=0quad$ or $quad 2-x=0$
$Rightarrow color{#4257b2} text{$x=0quad$}$ or $color{#4257b2} text{$quad x=2$}$
The $x$-intercepts of the graph of this equation are the points $color{#4257b2} text{$,,(0 , 0),,$}$ and $color{#4257b2} text{$,,(2,0),,$}$.
$bullet,,$For the $y$-intercept set $color{#c34632} text{$,,x=0,,$}$ and solve the resulting equation for $color{#c34632} text{$,,”y”$}$:
$y=-x^2+2xqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $x=0$]}$
$Rightarrow y=-(0)^2+2(0)qquadqquadqquadqquadqquad$
$Rightarrow color{#4257b2} text{$y=0qquadqquadqquadqquad$}$
The $y$-intercept of the graph of this equation is the point $color{#4257b2} text{$,,(0 , 0)$}$.
$color{#4257b2} text{$(h,k)=bigg(dfrac{-b}{2a} ,,, fbigg(dfrac{-b}{2a}bigg)bigg)$}$
In this case we have:
$color{#4257b2} text{$f(x)=-x^2+2x$}qquadqquadqquadqquadqquad$ $color{#c34632} text{[$a=-1$ , $b=2$ , $c=0$]}$
$h=dfrac{-b}{2a}=dfrac{-2}{2(-1)}=dfrac{-2}{-2}=color{#4257b2} text{$1$}$
$k=fbigg(dfrac{-b}{2a}bigg)=f(1)=-1^2+2(1)=color{#4257b2} text{$1$}$
$bullet,,$The vertex of the graph of this function is the point $color{#4257b2} text{$,,(h,k)=(1,1)$}$.
$bullet,,$Write this equation in the vertex form $color{#c34632} text{$,,y=a(x-h)^2+k,,$}$ as shown below:
$y=-x^2+2xqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[factor out $-1$]}$
$Rightarrow y=-(x^2-2x)qquadqquadquadquadquad$ $color{#c34632} text{[add and subtract $1$ inside the parenthesses]}$
$Rightarrow y=-(x^2-2x+1-1)$
$Rightarrow y=-(x^2-2x+1)-(-1)$
$color{#c34632} text{[factor the perfect square trinomial]}$
$$
Rightarrow color{#4257b2} text{$y=-(x-1)^2+1$}
$$
construct a line that is parallel to AD to simply the figure.

As shown in the figure AM = 4, so we can say that
AM = AN = ND = 4
From this, we get the value of AD i.e,
AD = BE
2 . 4 = 8

$$begin{aligned}
tanB &= dfrac{BE}{CE}\\
CE &= dfrac{8}{tan 78degree}\\
CE &= dfrac{8}{4.7046}\\
CE &approx 1.70\
end{aligned}$$
$$begin{aligned}
DC &= DE + CE\\
DC &= 10 + 1.70\\
DC &= 11.70\
end{aligned}$$
$$begin{aligned}
Area &=A_{ABCD} – dfrac{1}{4} pi(r)^{2}\\
&= dfrac{1}{2} (h)(b_{1}+b_{2}) – dfrac{1}{4} pi(r)^{2}\\
&= (11.70)(8) – dfrac{1}{4} pi(4)^{2}\\
&= 86.802 – 12.566\
Area &approx 74.2 m^{2}\
end{aligned}$$
$$begin{aligned}
SinC &= dfrac{BE}{CE}\\
CE &= dfrac{8}{Sin78degree}\\
CE &= dfrac{8}{0.9781}\\
CE &approx8.18
end{aligned}$$
$$begin{aligned}
Perimeter &= DC+CB+BM+MN+ND\\
&= 11.7+8.18+6+ dfrac{1}{4}.2pi.4+4\\
&= 36.16\
end{aligned}$$
The total number of goats is 6. So,
Goats covered the frolic area is
$$begin{aligned}
6times1.1 &= 6.6\
end{aligned}$$
Since the area is 74.23 square meters.
Thus, yes this pen design meets animal rights advocate criteria.
$$(b.) 36.16 m^{2}$$
$$(c.) text{ Yes}$$
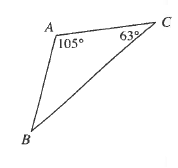
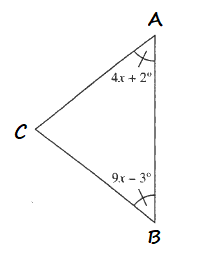
$B<C<A$
$$
AC<AB<BC
$$
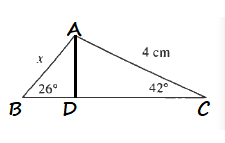
B<CRightarrow AC<x
$$
$AD=sin 42text{textdegree}cdot 4=0.66913061cdot 4$
$$
ADapprox 2.68
$$
$sin 26text{textdegree}=dfrac{2.68}{x}$
$x=dfrac{2.68}{0.43837115}$
$$
xapprox 6.11
$$
$CD=cos 42text{textdegree}cdot 4=0.74314483cdot 4$
$CDapprox 2.97$
$cos B=dfrac{BD}{AB}$
$BD=cos 26text{textdegree}cdot 6.11=0.89879405cdot 6.11$
$BDapprox 5.49$
$$
approx 11.34
$$
b) $x=6.11$
c) $11.34$
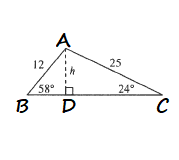
$$
sin 24text{textdegree}=dfrac{h}{25}
$$
$$
h=12sin 58text{textdegree}=12cdot 0.8480481approx 10.177
$$
$$
h=25sin 24text{textdegree}=25cdot 0.40673664approx 10.169
$$
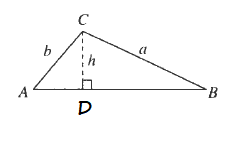
$$
sin B=dfrac{h}{a}
$$
$$
h=asin B
$$
$$
dfrac{sin B}{b}=dfrac{sin A}{a}
$$
$$
dfrac{sin B}{b}=dfrac{sin A}{a}=dfrac{sin C}{c}
$$

$xsin A=BCsin B$
$$
x=dfrac{BCsin B}{sin A}=dfrac{10cdot 0.8660254}{0.46947156}=18.45
$$
x=18.45
$$
Based on the image, we solve problems.
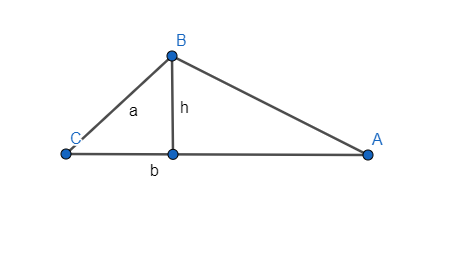
We know that the area of triangle is:
$$
P = dfrac{b cdot h_b}{2}
$$
So, in this case:
$$
P= dfrac{bcdot h}{2}
$$
From the definition of $sin x$ we have:
$$
sin C = dfrac{h}{a}
$$
$$
h = a sin C
$$
$$
P = dfrac{ba sin C}{2}
$$
$x= 18.45$.
We compute tha angle between $x$ and the side of $10$:
$$
180 text{textdegree} – 28 text{textdegree} -120 text{textdegree} = 32 text{textdegree}
$$
We determine the triangle’s area using the sinus formula in $c$:
$$
P = dfrac{18.45 cdot 10 cdot sin 32 text{textdegree} }{2} = dfrac{18.45 cdot 10 cdot 0.53}{2}
$$
Therefore,
$$
P approx 48.89
$$
$$dfrac{sin A}{a}=dfrac{sin B}{b}=dfrac{sin C}{c}.$$
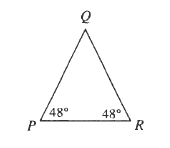
$Pcong RRightarrow sin P=sin R$
$$
dfrac{sin P}{QR}=dfrac{sin R}{QP}Rightarrow QR=QP
$$
Q=180text{textdegree}-48text{textdegree}-48text{textdegree}=84text{textdegree}
$$
$PRsin R=QPsin Q$
$PR=dfrac{QPsin Q}{sin R}$
$$
=dfrac{5cdot sin 84text{textdegree}}{sin 48text{textdegree}}=dfrac{5cdot 0.9945219}{0.74314483}approx 6.69
$$
b) $PR=6.69$ mm
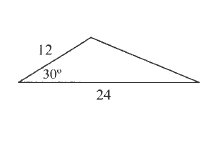
dfrac{12cdot 24sin 30text{textdegree}}{2}=dfrac{12cdot 24cdotdfrac{1}{2}}{2}=72
$$
72
$$
$B(4,2499)$
$$
y=-1
$$
$ab^{4}+k=2499$
k=-1
$$
$ab^{4}-1=2499$
$ab^{-1}=-0.2+1$
$ab^{4}=2499+1$
$ab^{-1}=0.8$
$ab^{4}=2500$
$b^5=3125$
$b=sqrt[5]{3125}$
$$
b=5
$$
$a=dfrac{2500}{625}$
$$
a=4
$$
y=4(5)^x-1
$$
$B(4,7.1536)$
$$
y=7
$$
k=7
$$
$ab^4+7=7.1536$
$ab^2=7.96-7$
$ab^4=7.1536-7$
$ab^2=0.96$
$ab^4=0.1536$
$dfrac{ab^4}{ab^2}=dfrac{0.1536}{0.96}$
$b^2=0.16$
$b=sqrt{0.16}$
$b=0.4$
$a=dfrac{0.96}{0.16}$
$$
a=6
$$
y=6(0.4)^x+7
$$
b) $y=6(0.4)^x+7$
$log_x (5)=b$
$log_x (7)=c$
log_x (10)=log_x (2cdot 5)=log_x (2)+log_x (5)=a+b
$$
log_x (49)=log_x (7^2)=2log_x (7)=2c
$$
$=log_x (2)+2log_x (5)$
$$
=a+2b
$$
$=3log_x (2)+log_x (7)$
$$
=3a+c
$$
b) $2c$
c) $a+2b$
d) $3a+c$
$$
g(x)=dfrac{1}{x+2}-3
$$
$$
y=-(x-1)^2+20
$$
$$
y=-3|x+71|
$$
$left(dfrac {1}{2} right)^{3(2x-3)}=left(dfrac {1}{2} right)^{(x+2)}$ (Unifying base)
$3(2x-3)=x+2$
$6x-9=x+2$
$6x-x=9+2$ (Grouping similar terms)
$5x=11$
$$
x=dfrac {11}{5}
$$
x=dfrac {11}{5}
$$
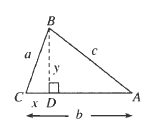
$$DA=b-x$$
$$a^2=x^2+y^2$$
Write an equation relating $c,y$ and $DA$:
$$c^2=y^2+(b-x)^2$$
Then, we isolate $y^2$ in both equations:
$$begin{aligned}
y^2&=a^2-x^2\
y^2&=c^2-(b-x)^2
end{aligned}$$
Expand the second equation:
$$begin{aligned}
a^2-x^2&=c^2-(b-x)^2\
a^2-x^2&=c^2-b^2+2bx-x^2
end{aligned}$$
Therefore, it follows that:
$$a^2+b^2-c^2=2bx$$
$$cos C=dfrac{x}{a} implies x=acos C$$
We replace $x$ in the equation:
$$a^2+b^2-c^2=2bacos C$$
Solve for $c^2$ and we get the Law of Cosines.
$$c^2=a^2+b^2-2abcos C$$
$$begin{aligned}
x^2&=6^2+7^2-2(6)(7)cos 120degree\
&=36+47-84cdot left(-dfrac{1}{2}right)\
&=125
end{aligned}$$
By taking the square root of both sides we obtain:
$$x=sqrt{125}=5sqrt 5$$
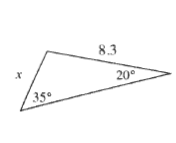
dfrac{sin 20text{textdegree}}{x}=dfrac{sin 35text{textdegree}}{8.3}
$$
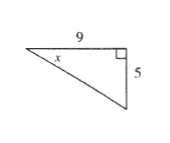
$$
x=tan^{-1}{dfrac{5}{9}}
$$
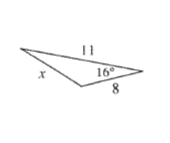
x^2=11^2+8^2-2(11)(8)cos 16text{textdegree}
$$
b) tangent
c) the Law of Cosines
We can use the $textbf{Law of cosines. }$
$$
c^2 = a^2+b^2 – 2abcos c
$$
$$
begin{align*}
10^2 &= 7^2 + 8^2 – 2cdot 7 cdot 8 cos alpha \
100 &= 49 + 64 – 112 cos alpha && text{Calculate} \
100 &= 113 – 112 cos alpha \
112 cos alpha &= 113 – 110 \
cos alpha &= dfrac{3}{112} &&text{Isolate $cos alpha$} \
cos alpha &approx 0.02679 \
alpha &approx 88.5text{textdegree}
end{align*}
$$
$$
begin{align*}
7^2 &= 10^2 + 8^2 – 2cdot 10 cdot 8 cos B \
49 &= 100+64 – 160 cos B && text{Calculate.} \
160 cos B &= 164 – 49 \
160 cos B&= 115 \
cos B &= dfrac{115}{160} &&text{We need to isolate $cos B$} \
cos B &= 0.7188 \
B &approx 44 text{textdegree}
end{align*}
$$
$$
A = 180 text{textdegree} – 88.5 text{textdegree} -44 text{textdegree} = 47.5 text{textdegree}
$$
b) $47.5$
The Law of Cosines gives a rule by which we can compute one side of a triangle when we are given the opposite angle and the sides near it.
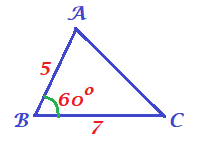
When given:
$AC^2=7^2+5^2-2(7)(5)cos 60text{textdegree}$
$AC^2=49+25-70cdotdfrac{1}{2}$
$AC^2=39$
$$
AC=sqrt{39}approx 6.24
$$
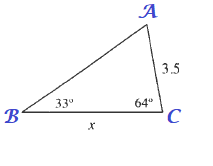
$A=180text{textdegree}-B-C$
$A=180text{textdegree}-33text{textdegree}-64text{textdegree}$
$$
A=83text{textdegree}
$$
$xsin B=ACsin A$
$x=dfrac{ACsin A}{sin B}$
$x=dfrac{3.5cdot sin 83text{textdegree}}{sin 33text{textdegree}}$
$x=dfrac{3.5cdot 0.99254615}{0.54463904}$
$$
xapprox 6.38
$$
$$
=dfrac{6.38cdot 3.5cdot 0.89879405}{2}approx 10.04
$$
b) $10.04$
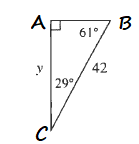
cos C=dfrac{y}{42}
$$
$$
approx 36.73
$$
b) $y=36.73$
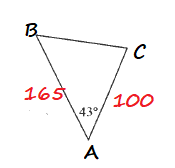
$=dfrac{165cdot 100cdot sin 43text{textdegree}}{2}=dfrac{165cdot 100cdot 0.68199836}{2}$
$approx 5626.49$ square miles
{x|x>1}
$$
f(t)=ab^t+k
$$
$$
f(50)=25.25
$$
k=0.20
$$
begin{cases}
ab+0.20=1.5\
ab^{50}+0.20=25.25
end{cases}
$$
$$
begin{cases}
ab=1.3\
ab^{50}=25.05
end{cases}
$$
$b^{49}=19.269231$
$B=sqrt[49]{19.269231}$
$bapprox 1.06$
$a=dfrac{1.3}{1.06}$
$$
aapprox 1.23
$$
f(t)=1.23(1.06)^t+0.20
$$
f(110)=1.23(1.06)^{110}+0.20approx 747.60
$$
b) $$747.60$
$$
g(x)=sqrt[3]{x+2}
$$
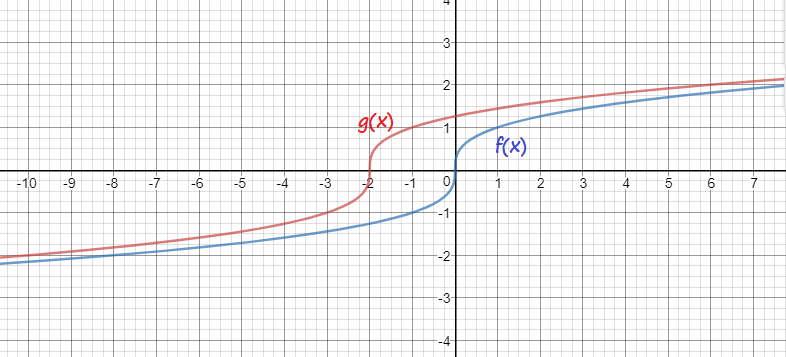
$sqrt[3] x=sqrt[3]{x+2}$
$(sqrt[3] x)^3=(sqrt[3]{x+2})^2$
$x=x+2$
$$
0=2
$$
f(x)=x^2+3
$$
$x=y^2+3$
$y^2=x-3$
$y=sqrt{x-3}$
$$
f^{-1}(x)=sqrt{x-3}
$$
We determine its inverse:
f(x)=left(dfrac{1}{4}x+6right)^3
$$
$x=left(dfrac{1}{4}y+6right)^3$
$sqrt[3] x=dfrac{1}{4}y+6$
$4sqrt[3] x=y+24$
$$
y=4sqrt[3] x-24
$$
We determine the inverse:
$x=sqrt{5y-6}$
$x^2=(sqrt{5y-6})^2$
$x^2=5y-6$
$5y=x^2+6$
$y=dfrac{x^2+6}{5}$
$$
f^{-1}(x)=dfrac{x^2+6}{5}
$$
We determine its inverse:
b) $f^{-1}(x)=4sqrt[3] x-24$
c) $f^{-1}(x)=dfrac{x^2+6}{5}$
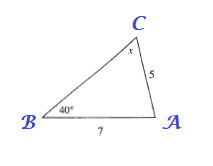
x>40text{textdegree}
$$
$5sin x=7sin 40text{textdegree}$
$sin x=dfrac{7sin 40text{textdegree}}{5}$
$sin x=dfrac{7cdot 0.64278761}{5}$
$sin xapprox 0.8999$
$sin^{-1} 0.8999approx 64.1text{textdegree}$
$$
x=64.1text{textdegree}
$$
x=115.9text{textdegree}
$$
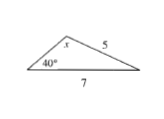
dfrac{sin 115.9text{textdegree}}{7}=0.8999=dfrac{sin 40text{textdegree}}{5}checkmark
$$
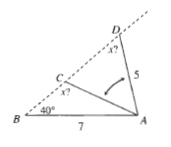
ADB=64.1text{textdegree}
$$
DAC=180text{textdegree}-2cdot 64.1text{textdegree}=51.8text{textdegree}
$$
ACB=ADB+DAC=64.1text{textdegree}+51.8text{textdegree}=115.9text{textdegree}
$$
64.1text{textdegree}+115.9text{textdegree}=180text{textdegree}
$$

$$begin{aligned}
a^{2} &= b^{2}+c^{2}-2cdot bcdot ccdot cos A\\
(10)^{2} &= (7)^{2} + (8)^{2} – 2cdot7cdot8cdotcos x\\
100 &= 49+64-112 cos x\\
cos x &= dfrac{49+64-100}{112} approx 0.1161\\
x &= cos^{-1}(0.1161)\\
end{aligned}$$
The equation has only one equation.

$$begin{aligned}
a^{2} &= b^{2}+c^{2}-2 cdot b cdot ccdot cos A\\
(x)^{2} &= (14)^{2} + (20)^{2} – 2.14.20.cos(60degree)\\
(x)^{2} &= 196 + 400 – 560 cos x\\
(x)^{2} &= 596 -560cdotleft(dfrac{1}{2}right)\\
x &= sqrt{316}\\
x &= 17.77
end{aligned}$$
The equation has only one equation.

$$begin{aligned}
A &= 180degree − 30degree − 45degree\\
A &= 105°\\
end{aligned}$$
$$begin{aligned}
dfrac {sin A}{a} &= dfrac {sin B}{b}\\
dfrac {sin (105degree)}{x} &= dfrac {sin (45degree)}{18}\\
x &= dfrac{18 times sin(105degree)}{sin (45degree)}\\
x &= dfrac{18 times 0.9659 }{0.7071}\\
x &= 24.58 approx 24.60
end{aligned}$$

$$begin{aligned}
180degree &= 60degree + 75degree + 45degree\\
180° &= 180degree \\
end{aligned}$$
The solution are all the similar triangles.
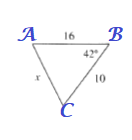
$x^2=356-320cdot 0.74314483$
$x^2=118.19365$
$xapprox sqrt{118.19365}$
$$
xapprox 10.87
$$
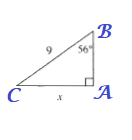
$x=9sin 56text{textdegree}$
$x=9cdot 0.82903757$
$$
xapprox 7.46
$$
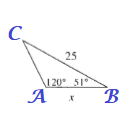
$dfrac{sin 9text{textdegree}}{x}=dfrac{sin 120text{textdegree}}{25}$
$xsin 120text{textdegree}=25sin 9text{textdegree}$
$x=dfrac{25cdot 0.15643447}{0.8660254}$
$$
xapprox 4.52
$$
b) $7.46$
c) $4.52$
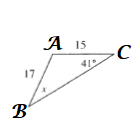
$17sin x=15sin 41text{textdegree}$
$sin x=dfrac{15cdot 0.65605903}{17}$
$sin xapprox 0.57887561$
$$
sin^{-1} 0.57887561approx 35.4text{textdegree}
$$
$x_2=180text{textdegree}-35.4text{textdegree}=144.6text{textdegree}$
$B+C=x+41text{textdegree}$
$x_1=35.4text{textdegree}$
$B+C=35.4text{textdegree}+41text{textdegree}=76.4text{textdegree}180text{textdegree}$
The lengths of the two sides that are still standing are116 feet and 224 feet and the angle between them 58°.

We can use the law of Cosine to find the length of the BC side fence that needs to be replaced.
$$begin{aligned}
BC^{2} &= AB^{2} + AC^{2} – 2 cdot AB cdot ACcdot cos A\\
BC^{2} &= (116)^{2} + (224)^{2} – 2 times 116 times224 times Cos(58degree)\\
BC^{2} &= 13456 + 50176 – 51968 times 0.5299\\
BC^{2}&= 63632 – 26589.229\\
BC^{2} &= 36093.156\\
end{aligned}$$
Squaring both sides, we get,
$$begin{aligned}
BC &= sqrt {36093.156}\\
BC &approx 189.98 text{ feet}
end{aligned}$$
The area of the triangle of (SAS) is stated below :
$$begin{aligned}
Area &= dfrac {1}{2} times AB times AC times sin A\\
&= dfrac {116 times 224 times sin (58degree)}{2}\\
&= dfrac {116 times 224 times 0.848048}{2}\\
Area &approx 11017.84\
end{aligned}$$
|x+1|geq 3
$$
$xleq -4$ or $xgeq 2$
(-infty,-4]cup[2,infty)
$$

x^2-9<0
$$
(x-3)(x+3)<0
$$
$x+3=0Rightarrow x_2=-3$
(-infty,-3), (-3,3), (3,infty)
$$
$f(0)=0^2-9=-00$
$$
(-3,3)
$$

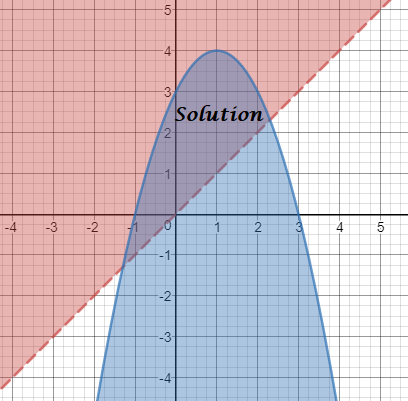
y+3>x^2
$$
y>x^2-3
$$

begin{cases}
y>x\
yleq -x^2+2x+3
end{cases}
$$
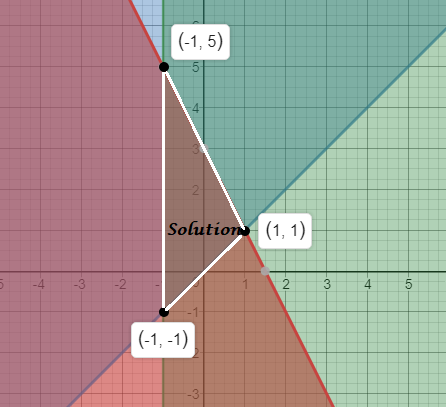
begin{cases}
yleq -2x+3\
ygeq x\
xgeq -1
end{cases}
$$
$$=dfrac{15}{100}$$
$$=0.15 %$$
She will have the profit at the rate of $0.15 % text{per hour}$.
New percentile as she is selling 48 cups of coffee now,
$$=dfrac{48}{100}$$
$$=0.48 %$$
From the above calculation we can see that the percentile is increasing. Thus, we can say that the advice by Duncan is right.
log_2 (x)=10
$$
x=2^{10}
$$
log_3 (x+1)=5
$$
$x+1=243$
$x=243-1$
$$
x=242
$$
log_3 (3^x)=4
$$
$$
x=4
$$
4^{log_4 (x)}=7
$$
x=7
$$
$a^{log_a (x)}=x$.
b) $x=242$
c) $x=4$
d) $x=7$
Sketch the graph in GeoGebra. From the graph we see:
The parabola is shifted $3$ units up.
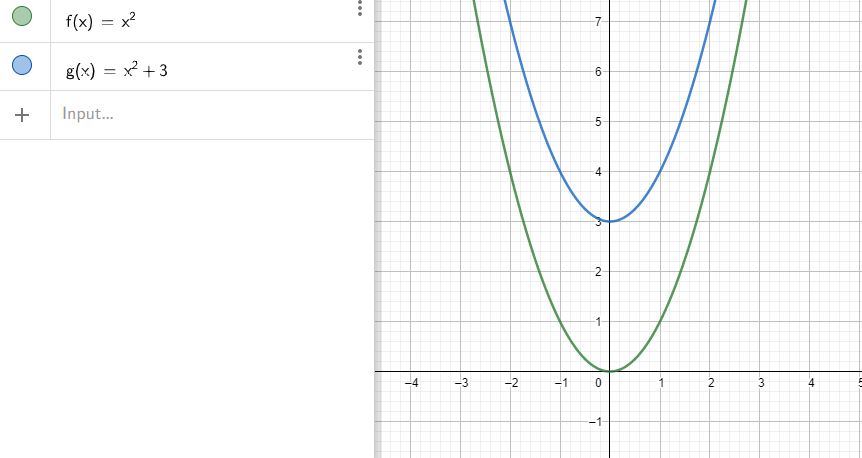
Sketch the graph in GeoGebra. From the graph we see:
The parabola is vertically narrowed by a factor of $3$ .
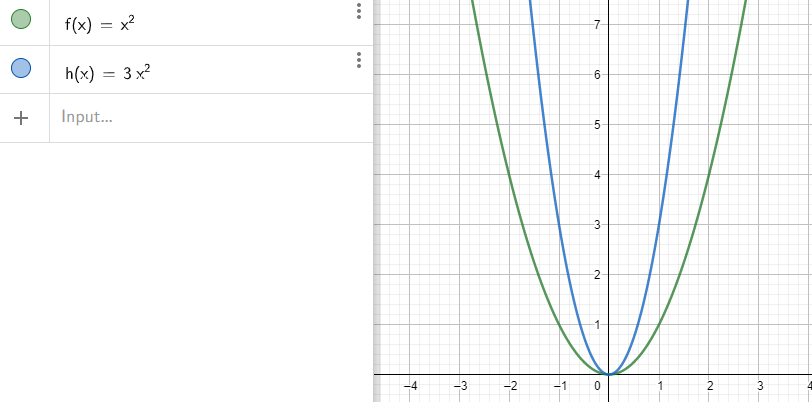
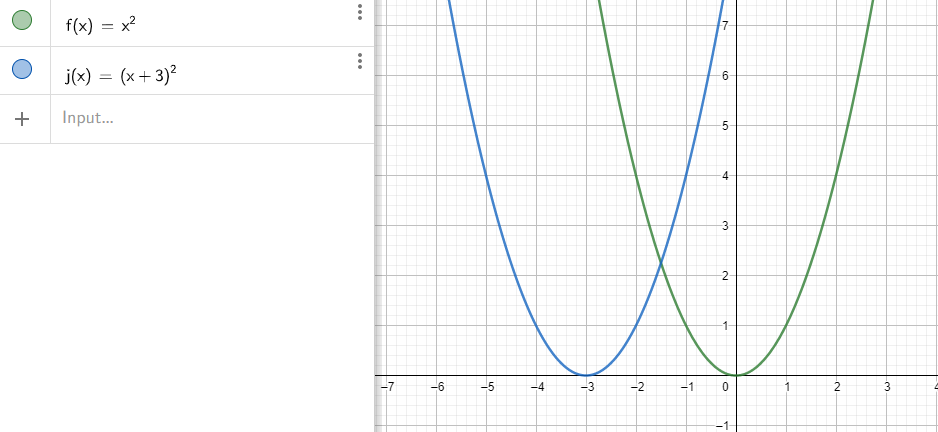
Sketch the graph in GeoGebra.
From the graph we see:
The parabola is shifted $3$ units to the left.
$$
sqrt{5-2x}+7=4
$$
Subtract $7$ from both sides
$$
sqrt{5-2x}=-3
$$
Squaring both sides
$$
left(sqrt{5-2x}right)^2=left(-3right)^2
$$
$$
5-2x=9
$$
$$
-2x=4
$$
$$
x=-2
$$
Replace $x$ with $-2$ in the original equation
$$
sqrt{5+4}+7=4
$$
$$
10=4
$$
which is a contradiction, then the equation has no real solution
$$
sqrt{5-2}=-3
$$
Since the square root can not take on negative values, the equation has no solutions.
f(x)=-2(x-3)^2+4
$$

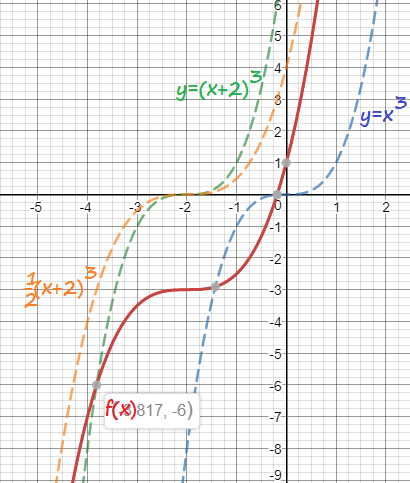
f(x)=dfrac{1}{2}(x+2)^3-3
$$
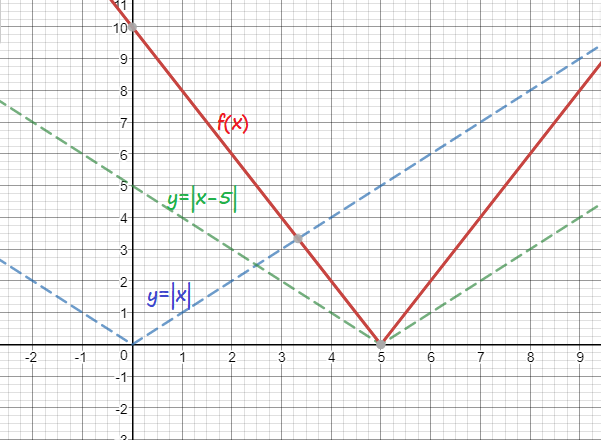
f(x)=2|x-5|
$$
f(x)=sqrt{x-2}-3
$$
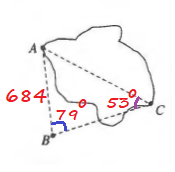
$ACsin C=ABsin B$
$AC=dfrac{ABsin B}{sin C}=dfrac{684cdot sin 79text{textdegree}}{sin 53text{textdegree}}$
$=dfrac{684cdot 0.98162718}{0.79863551}$
$$
approx 840.73
$$
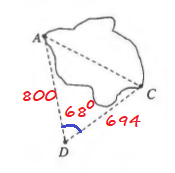
$=800^2+694^2-2cdot 800cdot 694cdot cos 68text{textdegree}$
$=1,121,636-1,110,400cdot 0.37460659$
$=705,672.84$
$$
AC=sqrt{705672.84}approx840.04
$$
Yes
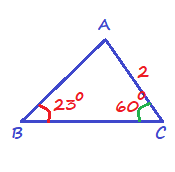
A=180text{textdegree}-23text{textdegree}-60text{textdegree}=97text{textdegree}
$$
$BCsin B=ACsin A$
$BC=dfrac{ACsin A}{sin B}=dfrac{2cdotsin 97text{textdegree}}{sin 23text{textdegree}}$
$=dfrac{2cdot 0.99254615}{0.39073113}$
$$
approx 5.08
$$
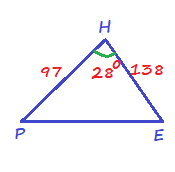
$=97^2+138^2-2cdot 97cdot 138cdot cos 28text{textdegree}$
$=28,453-26,772cdot 0.88294759$
$=4814.7271$
$$
PE=sqrt{4814.7271}approx 69.4
$$
HE+PE+HP=138+69.4+97=304.4
$$

$$
BC=sqrt{5467.54}approx 73.9
$$
First we determine $BC$ using the Pythagorean Theorem:
$=7099.7$
$$
AB=sqrt{7099.7}approx 84.3
$$
mangle Q=mangle R
$$
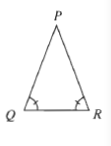
dfrac{sin Q}{PR}=dfrac{sin R}{PQ}
$$
sin Q=sin R
$$
PR=PQ
$$
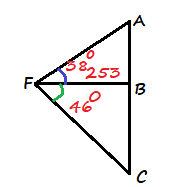
$AB=FBtan 38text{textdegree}=253cdot 0.78128563$
$$
=197.67
$$
First we determine $AB$ using the tangent function:
$BC=FBtan 46text{textdegree}=253cdot 1.03553031$
$$
=261.99
$$
AC=AB+BC=197.67+261.99=459.66
$$

$$begin{aligned}
BC^{2} &= AB^{2} + AC^{2} – 2cdot ABcdot ACcdot cos A\\
BC^{2} &= (5)^{2} + (7.4)^{2} – 2 times 5 times 7.4 times cos(38degree)\\
BC^{2} &= 25 + 54.76 – 58.312\\
BC^{2} &= 21.4472\\
BC &= sqrt{21.4472}\\
BC &approx 4.63 miles.\
end{aligned}$$
So, 4.63 miles far will Lisa have to hike from the lake to meet
Aaron at the campsite.
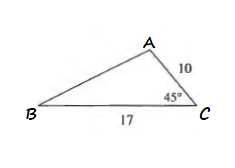
$=17^2+10^2-2cdot 17cdot 10cdot cos 45text{textdegree}$
$=389-340cdot 0.70710678$
$=148.5837$
$$
AB=sqrt{148.5837}approx 12.19
$$
$ABsin B=ACsin C$
$sin B=dfrac{ACsin C}{AB}=dfrac{10cdot 0.70710678}{12.19}$
$approx 0.5801$
$$
B=sin^{-1} 0.5801=35.5text{textdegree}
$$
A=180text{textdegree}-45text{textdegree}-35.5text{textdegree}=99.5text{textdegree}
$$
$$
=dfrac{10cdot 17cdot 0.70710678}{2}approx 60.1
$$
b. Area $approx 60.1$
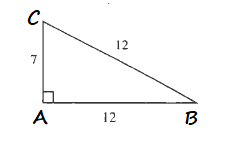
text{textcolor{#c34632}{textbf{Pythagorean theorem}}}
$$
$$
boxed{a^2+b^2=c^2}
$$
$$
textit{*where $a$ and $b$ are length of legs and $c$ is length of hypotenuse of the right triangle}
$$
From the picture we can see this is a right triangle with both legs with the same length $x$ and length of hypotenuse is $7$. Now we can set the equation as:
$$
x^2+x^2=7^2
$$
$$
2x^2=49
$$
$$
x^2=dfrac{49}{2}
$$
$$
boxed{xapprox4.95}
$$
text{textcolor{#c34632}{textbf{Sine function}}}
$$
$$
boxed{sin theta=dfrac{a}{c}}
$$
$$
textit{*where $theta$ is angle $theta$, $a$ is length of opposite side, $c$ is length of hypotenuse of the right triangle}
$$
Since this is right triangle with legs which are same length, both angles will be $45$ degrees.
Now we can apply sine function as:
$$
sin 45text{textdegree}=dfrac{x}{7}
$$
$$
x=sin 45 text{textdegree} cdot 7
$$
$$
boxed{xapprox 4.95}
$$
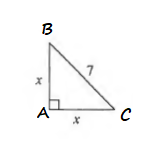
$2x^2=49$
$x^2=dfrac{49}{2}=24.5$
$$
x=sqrt{24.5}approx 4.95
$$
$sin C=dfrac{x}{7}$
$x=7sin C=7sin 45text{textdegree}=7cdot 0.70710678$
$$
approx 4.95
$$
x=4.95
$$

$$
AB=BDsqrt 2=5sqrt 2approx 7.07
$$
$CD^2+5^2=10^2$
$CD^2=100-25=75$
$$
CD=sqrt{75}=5sqrt 3approx 8.66
$$
AC=AD+CD=5+5sqrt 3=5+8.66=13.66
$$
$=5sqrt 2+10+5+5sqrt 3$
$$
=7.07+10+13.66=30.73
$$
$=dfrac{(5+5sqrt 3)cdot 5}{2}=dfrac{25(1+sqrt 3)}{2}$
$$
=dfrac{13.66cdot 5}{2}=34.15
$$
Area: $dfrac{25(1+sqrt 3)}{2}approx34.15$
$$
i^5=i
$$
$$
i^6=-1
$$
$$
i^7=-i
$$
$$
i^8=1
$$
$$
i^9=i
$$
$$
i^{10}=-1
$$
$$
i^{11}=-i
$$
$$
i^{12}=1
$$
$$
i^{13}=i
$$
$$
i^{14}=-1
$$
$$
i^{15}=-i
$$
Thus we know that if $n$ is a multiple of 4, then $i^n=1$; if $n$ is one more than a multiple of 4, then $i^n=i$; if $n$ is 2 more than a multiple of 4, then $i^n=-1$. if $n$ is 3 more than a multiple of 4, then $i^n=-i$.
$$
i^{16}=1
$$
$$
i^{25}=i
$$
$$
i^{39}=-i
$$
$$
i^{100}=1
$$
c.
$$
i^{4n}=(i^4)^n=1^n=1
$$
d.
$$
i^{4n+1}=i^{4n}i=i
$$
$$
i^{4n+2}=i^{4n}i^2=-1
$$
$$
i^{4n+3}=i^{4n}i^3=-i
$$
e.
$$
i^{396}=1
$$
$$
i^{397}=i
$$
$$
i^{398}=-1
$$
$$
i^{399}=-i
$$
$r=0.035$
$A(t)=400,000(1+0.035)^t$
$$
A(t)=400,000(1.035)^t
$$
A(10)=400,000(1.035)^{10}approx 564,240
$$
$400,000(1.035)^t=800,000$
$(1.035)^t=dfrac{800,000}{400,000}$
$(1.035)^t=2$
$log_{10} (1.035)^t=log_{10} 2$
$tlog_{10} 1.035=log_{10} 2$
$$
t=dfrac{log_{10} 2}{log_{10} 1.035}approx 20
$$
$$
P=200,000
$$
$A(t)=200,000(1-0.02)^t$
$$
A(t)=200,000(0.98)^t
$$
P-A(10)=200,000-200,000(0.98)^{10}=36,585
$$
$5x-3y=12$ (Given)
$3y=5x-12$
$$
y=dfrac {5x-12}{3}
$$
$F=dfrac {Gm_{1}m_{2}}{r^2}$ (Given)
$Fr^2=Gm_{1}m_{2}$
$$
m_{2}=dfrac {Fr^2}{Gm_{1}}
$$
$E=dfrac {1}{2}mv^2$ (Given)
$2E=mv^2$
$$
m=dfrac {2E}{v^2}
$$
$(x-4)^2+(y-1)^2=10$ (Given)
$(y-1)^2=10-(x-4)^2$
$y-1=pm sqrt {10-(x-4)^2}$
$$
y=1 pm sqrt {10-(x-4)^2}
$$
b- $F=dfrac {Gm_{1}m_{2}}{r^2} qquad rightarrow qquad m_{2}=dfrac {Fr^2}{Gm_{1}}$
c- $E=dfrac {1}{2}mv^2 qquad rightarrow qquad m=dfrac {2E}{v^2}$
d- $(x-4)^2+(y-1)^2=10 qquad rightarrow qquad y=1 pm sqrt {10-(x-4)^2}$
$$
begin{align*}
&dfrac{3}{x}+dfrac{2}{x+1}=5 tag{Given}\ \
&dfrac{3(x+1)+2x}{x(x+1)}=5 tag{Taking LCM}\ \
&3x+3+2x=5x(x+1) tag{Cross-multiplying}\ \
&5x+3=5x^2+5x tag{Adding and multiplying}\ \
&5x^2=3 tag{Simplifying}\ \
&x^2=dfrac{3}{5} tag{Dividing both side by 5}\ \
&x=pmsqrt{dfrac{3}{5}}tag{Solution}
end{align*}
$$
$$
begin{align*}
&x^2+6x+9=2x^2+3x+5 tag{Given}\ \
&6x+9=x^2+3x+5tag{Subtracting $x^2$ from both side}\ \
&x^2-3x-4=0 tag{Subtracting $6x$ $&$ 9 from both side}\ \
&x^2-4x+x-4=0 tag{$-3x$ as sum of $-4x+x$}\ \
&(x-4)(x+1)=0 tag{Factorising}\ \
&x=4 &x=-1 tag{Solution}\
end{align*}
$$
$$
begin{align*}
&8-sqrt{9-2x}=x+3 tag{Given}\ \
&-sqrt{9-2x}=x-5 tag{Simplifying}\ \
&9-2x=x^2-10x+25 tag{Squaring on both side}\ \
&x^2-8x+16=0 tag{Simplifying}\ \
&x^2-4x-4x+16=0 tag{$-8x$ as sum of $-4x & -4x$ }\ \
&(x-4)(x-4)=0 tag{Factorising}\ \
&x=4 tag{Solution}\
end{align*}
$$
a.) x=pmsqrt{dfrac{3}{5}}
$$
dfrac{3}{x}+dfrac{2}{x+1}=5
$$
$3(x+1)+2x=5x(x+1)$
$3x+3+2x=5x^2+5x$
$5x+3=5x^2+5x$
$5x^2+5x-5x-3=0$
$5x^2-3=0$
$x^2=dfrac{3}{5}$
$$
x=pmsqrt{dfrac{3}{5}}
$$
x^2+6x+9=2x^2+3x+5
$$
(-infty,infty)
$$
$x^2-3x-4=0$
$x^2+x-4x-4=0$
$x(x+1)-4(x+1)=0$
$(x+1)(x-4)=0$
$x+1=0Rightarrow x_1=-1$
$x-4=0Rightarrow x_2=4$
8-sqrt{9-2x}=x+3
$$
$$
-sqrt{9-2x}=x-5
$$
$(-sqrt{9-2x})^2=(x-5)^2$
$9-2x=x^2-10x+25$
$9-2x-9+2x=x^2-10x+25-9+2x$
$x^2-8x+16=0$
$(x-4)^2=0$
$$
x-4=0Rightarrow x=4
$$
$8-1stackrel{?}{=}4+3$
$$
7=7checkmark
$$
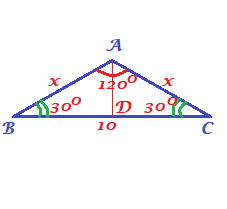
BD=CD=dfrac{BC}{2}=dfrac{10}{2}=5
$$
$cos 30text{textdegree}=dfrac{5}{x}$
$xcdot dfrac{sqrt 3}{2}=5$
$xsqrt 3=5(2)$
$$
x=dfrac{10}{sqrt 3}=dfrac{10sqrt 3}{3}approx 5.77
$$

$$
log_5 (2x) = 3
$$
Apply $log$ rules:
$$
begin{align*}
2x &= 5^3 \
2x &= 125 \
x &= dfrac{125}{2}
end{align*}
$$
Solve the equation. Apply log rules.
$$
begin{align*}
5^{-1} &= x+1 \
dfrac{1}{5} &= x+1 \
&text{Isolate $x$} \
x &= dfrac{1}{5} -1 \
x&= dfrac{-4}{5}
end{align*}
$$
Solve the equation. Apply log rules.
$$
begin{align*}
log dfrac{4}{x} &= 2 \
dfrac{4}{x} &= 10^2 \
dfrac{4}{x} &= 100 \
100 x &= 4 \
&text{Isolate $x$:} \
x&= dfrac{4}{100} = 0.04
end{align*}
$$
Solve the equation. Apply log rules.
$$
begin{align*}
log_3 6^2 + log_3 y &= 4 \
log_3 36y &= 4 \
3^4 &= 36 y \
81 &= 36y \
&text{Isolate $y$:} \
y&= dfrac{81}{36} \
y&= 2.25
end{align*}
$$
b) $-0.8$
c) $0.04$
d) $2.25$
$$
g(x)=x-3
$$
f(-5)=3(-5)^2-5=70
$$
7g(x)=7(x-3)=7x-21
$$
f(4)=3(4)^2-5=43
$$
g(3x)=3x-3
$$
$$
=3x^2+24x+43
$$
g(x)-f(x)=x-3-3x^2+5=-3x^2+x+2
$$
Substituting in the equation of the exponential function of form i.e,
$$begin{aligned}
y &= ab^{x} + k
end{aligned}$$
Now determine $k$ using the asymptotes, i.e
$$begin{aligned}
k &= -3\
end{aligned}$$
For the point $(1, 15)$,
$$begin{aligned}
15 &= tag{1} ab^{1} – 3\
end{aligned}$$
For the point $(4, 3885)$,
$$begin{aligned}
3885 &= tag{2} ab^{4} – 3\
end{aligned}$$
From equation (1), we get.
$$begin{aligned}
15 + 3 &= ab^{1}\\
18 &= tag{3} ab^{1}\\
end{aligned}$$
From equation (2), we get.
$$begin{aligned}
3885 + 3 &= ab^{4}\\
3888 &= tag{4} ab^{4}\\
end{aligned}$$
$$begin{aligned}
dfrac {ab^{4}}{ab} &= dfrac {3888}{18}\\
b^{3} &= 216\\
b &= sqrt [3]{216}\\
b &=6\
end{aligned}$$
Put this value of $b$ in equation (3),
$$begin{aligned}
18 &= ab\\
18 &= a times 6\\
a &= dfrac {18}{6}\\
a &= 3
end{aligned}$$
$$begin{aligned}
y &= 3 (6)^{x}-3\
end{aligned}$$
Substituting in the equation of the exponential function of form i.e,
$$begin{aligned}
y &= ab^{x} + k
end{aligned}$$
Now determine $k$ using the asymptotes, i.e
$$begin{aligned}
k &= 1\
end{aligned}$$
For the point $(-2, -7)$,
$$begin{aligned}
-7 &= tag{1} ab^{-2} +1\
end{aligned}$$
For the point $(3, 0.75)$,
$$begin{aligned}
0.75 &= tag{2} ab^{3} +1\
end{aligned}$$
From equation (1), we get.
$$begin{aligned}
-7 – 1 &= ab^{-2}\\
-8 &= tag{3} ab^{-2}\\
end{aligned}$$
From equation (2), we get.
$$begin{aligned}
0.75 – 1 &= ab^{3}\\
-0.25 &= tag{4} ab^{3}\\
end{aligned}$$
$$begin{aligned}
dfrac {ab^{3}}{ab^{-2}} &= dfrac {-0.25}{-8}\\
b^{5} &= dfrac{1}{32}\\
b &= sqrt [5]{dfrac{1}{32}}\\
b &= dfrac{1}{2}\\
end{aligned}$$
Put this value of $b$ in equation (4),
$$begin{aligned}
-0.25 &= ab^{3}\\
-0.25 &= a times (dfrac{1}{2})^{3}\\
dfrac {a}{8} &= -dfrac{1}{4}\\
-4a &= 8\\
a &= -2\
end{aligned}$$
$$begin{aligned}
y &= -2 (dfrac{1}{2})^{x} + 1\
end{aligned}$$
(a.) y &= 3 (6)^{x}-3\
(b.) y &= -2 (dfrac{1}{2})^{x} + 1\
end{aligned}$$
$$
2^x=2^3
$$
By dividing both sides by $2^3$ we get:
$$
dfrac{2^x}{2^3}=2^{x-3}=1
$$
$$
2^{x-3}=1=2^0
$$
This leads us to $x-3=0$, so $text{underline{x=3}}$.
$$
3^y=3^{x-2}
$$
Now by substituting $3$ for $x$ we get
$$
3^y=3^{3-2}=3^1
$$
This leads us to $text{underline{$y=1$}}$.
$$
5^z=5^{2x-3y}
$$
By substituting $3$ for $x$ and $1$ for $y$ we get:
$$
5^z=5^{6-3}=5^3
$$
By dividing both sides by $5^3$ we get:
$$
dfrac{5^z}{5^3}=1=5^0
$$
$$
5^{z-3}=5^0
$$
This leads us to $z-3=0$, so $text{underline{$z=3$}}$.
$$
boxed{(x,y,z)=(3,1,3)}
$$

