#### a.

$textbf{Statistic.}$

The difference between a statistic and a parameter is that statistics describe a sample.

A parameter describes an entire population.
#### b.

Selection bias and observer bias.
#### c.

Simple random sampling.

$textbf{a.}$ Statistic, $textbf{b.}$ Selection bias and observer bias, $textbf{c.}$ Simple random sampling.

#### b.

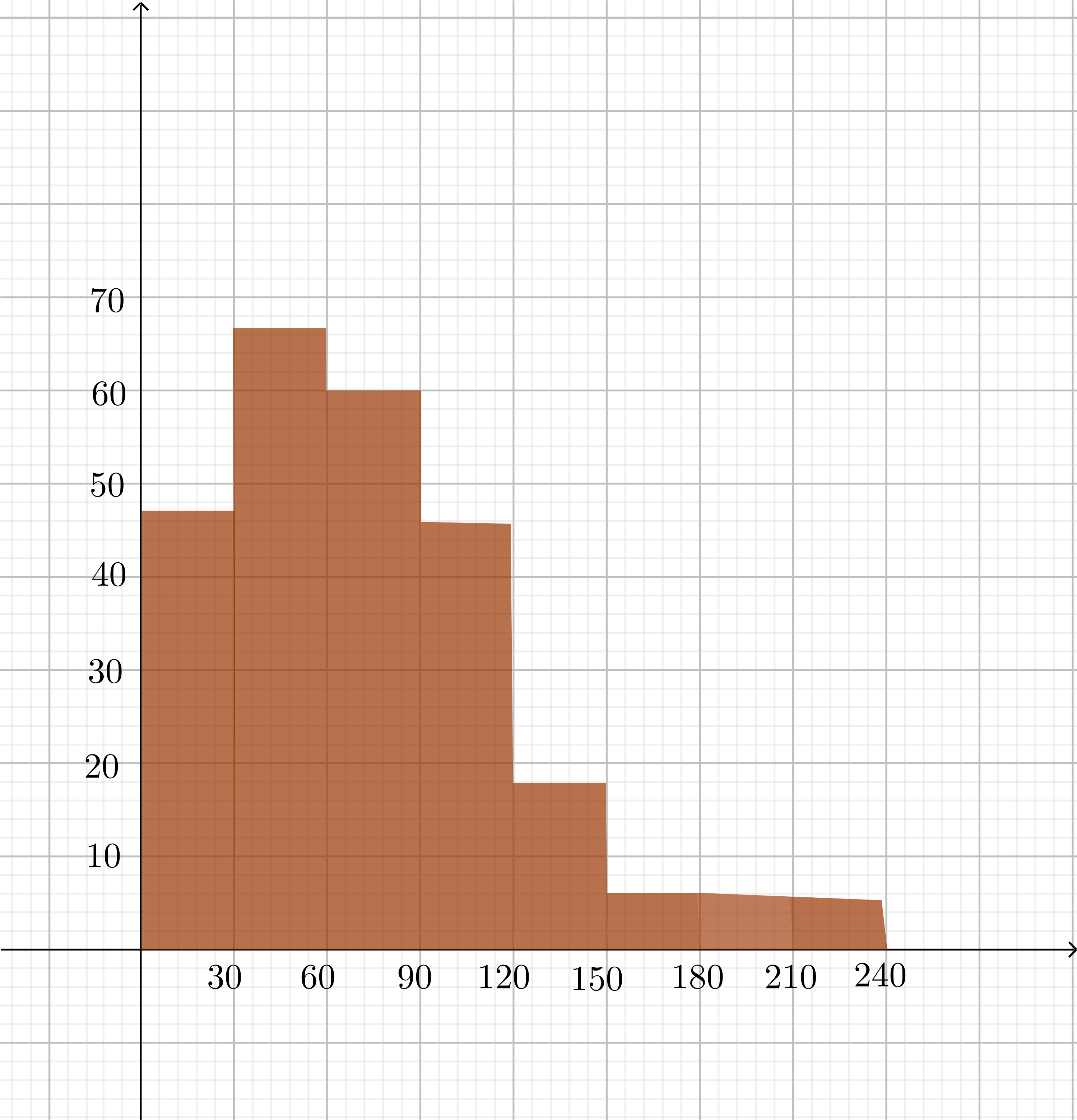
$text{The first quartile contains interval between $30$ and $60$.}$

$text{The first median contains interval between $60$ and $90$.}$

$text{The third quartile contains interval between $90$ and $120$.}$

#### c.

$$
text{The center of this graph is interval between $30$ and $60$.}
$$

The graph is symmetric.
#### d.

$$
boxed{text{Percent}=frac{12}{250} cdot 100%=4.8%}
$$

#### e.

$$
boxed{text{Percent}=frac{100}{250} cdot 100%=40%}
$$

#### f.

$$
text{These $250$ data points have the mean (average):}
$$

$$
begin{align*}
text{mean}&=frac{47 cdot 15+67 cdot 45+60 cdot 75+46 cdot 105+18 cdot 135+6 cdot 165+4 cdot 195+2 cdot 225}{250} \
&=frac{705+3015+4500+4830+2430+990+780+450}{250} \
&=frac{17700}{250} \
&=color{#c34632}{70.8}
end{align*}
$$

$textbf{b.}$ $text{first quartile}=left[30, 60right], text{median}=left[60, 90right], text{third quartile}=left[90, 120right]$,

$textbf{c.}$ $text{The center of this graph is interval between $30$ and $60$. The graph is symmetric.}$

$textbf{d.}$ $4.8%$, $textbf{e.}$ $40%$, $textbf{f.}$ $text{mean}=70.8$$

Given order:

$7.3, 12 .1, 4 .1, 11.9, 6 .3, 4 .9, 10.7, 6.3, 0 ,$ and $7 .0$ grams.

$n = 10$

Now determine the mean $(mu)$.

$$begin{aligned}
text {Mean} (mu) &= dfrac {7.3+12.1+ 4.1+11.9+6.3+ 4.9 + 10.7+ 6.3 +0 +7}{10}\\
mu &= dfrac {70.6}{10}\\
&boxed {mu = 7.06}\\
end{aligned}$$

Now determine the standard of deviation $(sigma)$,

$$begin{aligned}
sigma &= sqrt {dfrac{textstylesum_{i=1}^{n}(mu – x_{i})^{2}}{n}}\\
sigma &= sqrt {dfrac{textstylesum_{i=1}^{10}(mu – x_{i})^{2}}{10}}rightarrow (1)\
end{aligned}$$

$$begin{aligned}
&= textstylesum_{i=1}^{10}(mu – x_{i})^{2}\
&= (7.06 – 7.3)^{2} + (7.06 – 12.1)^{2} + (7.06 – 4.1)^{2} + (7.06 – 11.9)^{2} + (7.06 – 6.3)^{2} + (7.06 – 4.9)^{2} + (7.06 – 10.7)^{2} + (7.06 – 6.3)^{2} + (7.06 – 0)^{2} + (7.06 – 7.0)^{2}\
&= (-0.24)^{2} + (-5.04)^{2} + (2.96)^{2} + (-4.84)^{2} + (0.76)^{2} + (2.16)^{2} + (-3.64)^{2} + (0.76)^{2} + (7.06)^{2} + (0.06)^{2}\
&= 126.567
end{aligned}$$

Put the value $textstylesum_{i=1}^{10}(mu – x_{i})^{2}$ in equation in (1)

$$begin{aligned}
sigma &= sqrt {dfrac {126.567}{10}}\\
sigma &= sqrt {12.6567}\\
&boxed {sigma approx 3.6 }\
end{aligned}$$

Given equations,
$$begin{aligned}
x^2 – y &= 4rightarrow(1)\
y &= 2x- 1rightarrow(2)\
end{aligned}$$

Using the values of the table , sketching the graph of equation (1)(red graph) and equation (2)(green graph) :
|$x_3$ |$y_3$ |
|–|–|
| 3|5 |

|$x_1$ |$y_1$ |
|–|–|
| 0|-4 |
| -2| 0|
| 2|0 |

| $x_2$|$y_2$ |
|–|–|
| 0.5|0 |
| 0|-1 |
|1 |1 |


The intersecting point is where the graph intersects. Thus, the intersecting point is as follows:
$(x, y) rightarrow (3, 5)$.

$$(3, 5)$$

$a$.
Given systems of inequality,
$$begin{aligned}
ygeq |x+2| – 3\
end{aligned}$$

Sketching the graph of given inequality :
Initially we will graph using the function $y = |x|$, which we shift 2 units to the left, then 3 units down. The solution region is above the graph of the function which is being shaded.

$b$.
$$begin{aligned}
y leq dfrac{1}{2}x + 3rightarrow(1)\\
y geq (x+1)^2 -2rightarrow(2) \\
end{aligned}$$

$a$.
$$begin{aligned}
2^{(x-1)}&= 64rightarrow(1)\
end{aligned}$$

Re-writing equation (1):
$$begin{aligned}
2^{(x-1)}&= (2)^6rightarrow(2)\
end{aligned}$$
Comparing the base i.e $2$, we get
$$begin{aligned}
x-1&= 6\
x&= 6+1\
&boxed{x=7}\
end{aligned}$$

$b$.
$$begin{aligned}
4.7&= x^tfrac{1}{3}rightarrow(1)\
end{aligned}$$
Cubing both sides, we get
$$begin{aligned}
(4.7)^3&= (x^{tfrac{1}{3}})^3\\
&boxed{103.82= x}\
end{aligned}$$

$c$.
$$begin{aligned}
8^{(x+3)}&= 16^xrightarrow(1)\
end{aligned}$$

Re-writing equation (1):
$$begin{aligned}
(2^{3})^{(x+3)}&= (2^4)^x\
2^{(3x+9)}&= 2^{4x}
end{aligned}$$
comparing the base i.e. $2$.
$$begin{aligned}
3x+9&= 4x\
9&= 4x-3x\
&boxed{9= x}\
end{aligned}$$

$d$.
$$begin{aligned}
9^3&= 27^{(2x-1)}rightarrow(1)\
end{aligned}$$

Re-writing equation (1):
$$begin{aligned}
(3^2)^3&= (3^3)^{(2x-1)}\
3^6&= 3^{(6x-3)}
end{aligned}$$
comparing the base i.e. $3$.
$$begin{aligned}
6&=6x-3\
6+3&= 6x\\
dfrac{9}{6}&=x\\
&boxed{dfrac{3}{2}=x}\\
end{aligned}$$

$e$.
$$begin{aligned}
x^6&= 29rightarrow(1)\
end{aligned}$$

Taking sixth root both sides,
$$begin{aligned}
x&= pm sqrt[6]{29}\
&boxed{x=pm 1.75}\
end{aligned}$$

$f$.
$$begin{aligned}
25^x&= 125rightarrow(1)\
end{aligned}$$

Re-writing equation (1):
$$begin{aligned}
(5^2)^x&= 5^3\
5^{2x}&=5^3\
end{aligned}$$
Comparing base i.e. $5$,
$$begin{aligned}
2x&= 3\
&boxed{x=dfrac{3}{2}}\
end{aligned}$$

Given function,
$$begin{aligned}
f(x)&= 2 |x+1| – 3rightarrow(1)\
end{aligned}$$

From equation (1), determining $(h, k)$:
$h rightarrow -1$
$k rightarrow -3$
Thus, $(h, k)$ = $(-1, -3)$.
The function has no asymptotes.

Sketching the graph of $f(x)$ and $(f(-x)) = 2|x-1|-3$ by reflecting it across $y$-axis:


$b$.
$$begin{aligned}
f(x)&=dfrac{1}{x} – 2rightarrow(1)\
end{aligned}$$

From equation (1), determining $(h, k)$:
$h rightarrow 0$
$k rightarrow -2$
Thus, $(h, k)$ = $(0, -2)$.
The function has a vertical asymptotes and a horizontal one.

Sketching the graph of $f(x)$ and $f(-x)$ by reflecting it across the $y$-axis to get $f(-x) = – dfrac{1}{x}-2$:


$c$.
$$begin{aligned}
y&= (x-3)^2 + 4rightarrow(1)
end{aligned}$$

From equation (1), determining $(h, k)$:
$h rightarrow 3$
$k rightarrow 4$
Thus, $(h, k)$ = $(3, 4)$.
The function has no asymptotes.

Sketching the graph of $f(x)$ and $f(-x) = (x+3)^2+4$ by reflecting it across the $y$-axis:


Given function ,
$$begin{aligned}
y &= -x^3-3\
end{aligned}$$

From equation (1), determining $(h, k)$:
$h rightarrow 0$
$k rightarrow -3$
Thus, $(h, k)$ = $(0, -3)$.
The function has no asymptotes.

Sketching the graph of $f(x)$ and $f(-x) = -(x)^2-3$ by reflecting it across the $y$-axis:


a-          $3x^2+11x+10=(3x+5)(x+2)$

b-          $6x^3-31x^2+5x=x(6x-1)(x-5)$

c-          $6ab^2+15ab-21a=3a(2b^2+5b-7)=3a(2b+7)(b-1)$

d-          $y^2+5y-24=(y+8)(y-3)$