All Solutions
Page 157: Questions
How many students in our school participate have parents that are divorced?
How many people in out town own a car?
What percentage of people in our town eat meat?
c. We could ask each student in our school.
We could ask every tenth student that enters the school one morning.
We could ask two students of every class.
b. You might by influenced by who the plan is from. A better question would be do you support a plan that provides opportunities for students to be more succesfull in school?
c. It is not precise what is mend by a negative affect. A better question would be: Do students who frequently watch brutal violence in movies and games have more chance of going to prison?
d. If is not specified what is meant by effective. A better question would be: do you take into account the current movie rating before choosing a movie?
e. This question might be affected by which teacher you are thinking about (like or not liked teacher). A better question would be: Should teachers (in general) be paid more? or Do you think that teachers earn enough?
f. It is not specified what is meant by regularly. A better question would be: do you exercise every week?
b. This is used in (f). For example in (f) it is mentioned that moderate exercise is necessary to stay healthy which makes you more tempted to exaggerate the reality if you do not exercise regularly.
c. This is used in (b). For example in (b) it is first asked if you support the Government’s plan and that if you support that it ensures that students will be more succesful in school. However the question is asked as one question.
d. This is used in (a) and (c). For example the word “poor” will make you feel worse about the grades then if you would say “not good”.
e. This is used in (f). For example in (f) it is mentioned that moderate exercise is necessary to stay healthy which makes you more tempted to answer positively to the question if you exercise regularly.
c. (f)
c. (b)
d. (a) and (c)
e. (f)
Education is important. Do you think that students should go to school more? this question introduced bias through preface.
Do you think education is important enough to warrant for more school days in a year? This question introduces bias thourgh two questions in one.
a. Do you participate in a sport?
Do you participate in a sport outside of school?
Do you participate in a sport weekly?
Do you participate in a sport weekly outside of school?
c. No revisions need to be made.
b. Open questions will give more accurate information, because the responder is not limited to a certain answer. Closed questions are more conventient because the range of answers is limited and thus the information will be easier to process. It is best to choose an open question if accuracy is important and it is best to choose a closed question if you are genuinly interested in only the given categories (or one of the categories).
c. Do you participate in a sport? (OPEN)
Do you participate in a sport outside of school?
How often do you participate in sports? (CLOSED)
Daily Weekly Monthly Yearly
d. No question has been asked.
a. U.S. employees
b. Students in your math class
c. Carrots
d. All people in the state
e. Elevators
f. Your friends
b. Students in your math class
c. Carrots
d. All people in the state
e. Elevators
f. Your friends
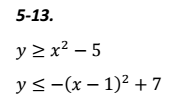
=x^{-12}y^{8}=dfrac{y^{8}}{x^{12}}
$$
=-18x^{3}y+6x^{5}y^{2}z=-6x^{3}yleft( 3-x^{2}yzright)
$$
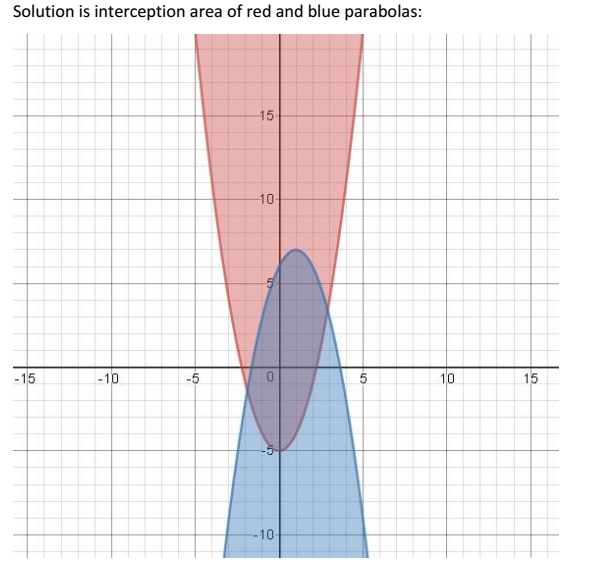
Los Angeles is about 400 moles away from Vacaville. Distance is represented on y-axis and graph demonstrates that the maximum point the graph reached is 400
The speed is calculated by the formula $s=dfrac {d}{t}$. where $s$ is the speed, $d$ is the distance and $t$ is the time.
According to the given graph, The trip was 5 stages:
The first stage: The distance was about 50 miles in 1 hour. so the speed $s_{1}=dfrac {50}{1}=50$ miles/hour.
The second stage: The distance was about $275-50=225$ miles in 3 hour. so the speed $s_{2}=dfrac {225}{3}=75$ miles/hour.
The third stage: They did not move for two hours. so the speed was 0 miles/hour.
The fourth stage: The distance was about $375-275=100$ miles in 2 hour. so the speed $s_{4}=dfrac {100}{2}=50$ miles/hour.
The fifth stage: The distance was about $400-375=25$ miles in 2 hour. so the speed $s_{5}=dfrac {25}{2}=12.5$ miles/hour.
This situation can be represented by the step function:
$$
s(t) = begin{cases}
50 & 0 leq x leq 1 \
75 & 1<x leq 4 \
0 & 4<x leq 6 \
50 & 6<x leq 8 \
12.5 & 8<x leq 10\
end{cases}
$$
b- Los Angeles is about 400 moles away from Vacaville.
a) $color{#c34632} text{$y=2x^2+3x-5$}$
$bullet,,$For the $x$-intercept(s), set $color{#c34632} text{$,,y=0,,$ }$ and solve the resulting equation for $color{#c34632} text{$,,”x”,$}$:
$y=0$
$Rightarrow 2x^2+3x-5=0qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[$a=2$ , $b=3$ , $c=-5$]}$
$color{#c34632} text{Apply the quadratic formula:}$
$color{#c34632} text{$x_{1,2}=dfrac{-bpm sqrt{b^2-4ac}}{2a}$}$
$Rightarrow x_{1,2}=dfrac{-3pm sqrt{3^2-4(2)(-5)}}{2(2)}$
$Rightarrow x_{1,2}=dfrac{-3pm sqrt{9+40}}{4}$
$Rightarrow x_{1,2}=dfrac{-3pm sqrt{49}}{4}$
$Rightarrow x_{1,2}=dfrac{-3pm 7}{4}$
$Rightarrow color{#4257b2} text{$x=-dfrac{5}{2},,,,$}$ or $color{#4257b2} text{$,,,, x=1$}$
The $x$-intercepts of the graph of this equation are the points:
$color{#4257b2} text{$bigg(-dfrac{5}{2} , 0bigg),,$}$ and $color{#4257b2} text{$,,big(1,0big)$}$.
$y=2x^2+3x-5qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $x=0$]}$
$Rightarrow y=2(0)^2+3(0)-5$
$Rightarrow y=0+0-5$
$Rightarrow color{#4257b2} text{$y=-5$}$
The $y$-intercept of the graph of this equation is the point $color{#4257b2} text{$,,big(0 , -5big)$}$.
$bullet,,$For the $x$-intercept(s), set $color{#c34632} text{$,,y=0,,$ }$ and solve the resulting equation for $color{#c34632} text{$,,”x”,$}$:
$y=0$
$Rightarrow sqrt{2x-4}=0qquadqquadqquadqquadqquadqquad$
$Rightarrow 2x-4=0qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[add $4$ in both sides]}$
$Rightarrow 2x=4qquadqquadqquadqquadqquadqquadquad$ $color{#c34632} text{[divide both sides by $2$]}$
$Rightarrow color{#4257b2} text{$x=2$}$
The $x$-intercept of the graph of this equation is the points $color{#4257b2} text{$,,,big(2,0big)$}$.
$y=sqrt{2x-4}qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $x=0$]}$
$Rightarrow y=sqrt{2(0)-4}$
$Rightarrow y=sqrt{0-4}$
$Rightarrow y=sqrt{-4}qquadqquadqquadqquadqquadquad$ $color{#4257b2} text{No solution in $mathbb{R}$}$
Since the equation above has no solutions in the set of real numbers, the graph of this equation has no $y$-intercepts.
$$
begin{align*}
y&=x^{2}+7x-8\
end{align*}
$$
$$
begin{align*}
y&=x^{2}+7x-8\
y&=(x^{2}+2cdotdfrac{7}{2}x+dfrac{49}{4})\
y&=(x+dfrac{7}{2})^{2}-dfrac{81}{4}\
end{align*}
$$
a. The most representative sample would be to include all students in our school in the survey. You could also randomly choose 50 students in the school, or randomly choose 2 students from each class.
b.The method of including all students of the school is better than randomly selecting because it includes the entire population and thus you are sure that everybody’s opinion is included.
b. The method of including all students of the school is better than randomly selecting.
To apply this exercise
1. look at your “video” picture for exactly five seconds.
2. Write down your estimate of a typical asteroid diameter in millimeters.
To apply this exercise
1. Collect the estimations of you and your collegues.
2. Sketch the histogram.
3. Describe the distribution, including the center, shape, spread, and any outliers.
To apply this exercise
1. Pick ten “typical” asteroids and measure the diameter of each in millimeters.
2. Record each of your measurements and then calculate the mean diameter.
3. This will be more accurate than that of your estimation.
To apply this exercise
1. Collect the estimations of you and your colleagues.
2. Sketch the histogram.
3. Describe the distribution, including the center, shape, spread, and any outliers
4. Describe how this histogram compares to the histogram of the class’s estimates from problem 4-15.
The second set of estimates is more accurate, because it depends on more stable equipment .
To apply this exercise
1. Prepare your calculator.
2. Pick ten asteroids that are randomly.
3. Calculate the mean diameter of your ten asteroids.
To apply this exercise
4. Sketch the histogram on your own paper
5. describe how this histogram compares to the histograms of the class’s estimates from problems 4-15 and 4-16.
b. The differences make sense because randomly chosen are not biased as intentionally chosen samples are biased.
c. The best results come from the randomly-chosen samples because they are not biased.
d. No, still because of the unbiasedness.
You might assign a number to each student and then have your calculator generate numbers and the students corresponding with these numbers will then be in the sample.
It is possible to survey a randomly-selected sample if you follow the steps mentioned earlier.
b. This question is unbiased because you are not influenced to choose one option over another.
c. This question makes the respondent say that they think that teacher salaries should be increased since the question says that it is important. Thus the question is biased.
b. What is the probability that the lights of a car still work after the cas has been crashed? The population contains all cars, but if you want to check this for every car then you will need to destroy every car in the world and thus the population will be destroyed.
c. How many of your school books have more than 100 pages?
d. How many books in the library have more than 100 pages?
$|5x+8| geq -4$
Thus, we can say that the inequality will be true for any real number i.e. (1,2,3,4,5……)
Hence the solution is $*R*$.
$x^2 + x – 20 < 0$
$$begin{aligned}
x^2 + 5x – 4x -20 < 20\
x(x+5) – 4 (x+5) < 20\
(x-4) (x+5) < 20\
end{aligned}$$
$$begin{aligned}
x-4&= 0 \
&boxed{x=4}\
end{aligned}$$
Also,
$$begin{aligned}
x+5&= 0 \
&boxed{x=-5}\
end{aligned}$$
$x$ $rightarrow$ $(-infty, -5)$, (-5, 4), $(4, infty)$.
But the solution is (-5, 4).
$$
begin{align*}
a. x^{2}&=x(2x-4)+y\
b. x&=3+(y-5)^{2}\
end{align*}
$$
$$
begin{align*}
x^{2}&=x(2x-4)+y\
x^{2}&=2x^{2}-4x+y\
y&=x^{2}-2x^{2}+4x\
y&=-x^{2}+4x\
end{align*}
$$
Thus, the value of $y$ is $y=-x^{2}+4x$.
$$
begin{align*}
x&=3+(y-5)^{2}\
x-3&=(y-5)^{2}\
pmsqrt{x-3}&=y-5\
y&=5pmsqrt{x-3}\
end{align*}
$$
Thus, the value of $y$ is $y=5pmsqrt{x-3}$.
From the figure ,
Domain $rightarrow$ $[-3, 3]$
Range : $rightarrow$ $[-3, 3]$
Since, the line test fails(non passing) . It is not a function.
From the figure ,
Domain $rightarrow$ $[-3, 4]$
Range : $rightarrow$ $[-2, 4]$
Since, the line test fails(non passing) . It is not a function.
From the figure ,
Domain $rightarrow$ $[-3, 3]$
Range : $rightarrow$ $[-3, 3]$
Since, it passes the line test. So, it is a function.
From the figure ,
Domain $rightarrow$ R
Range : $rightarrow$ $[-2, infty]$
Since, it passes the line test. So, it is a function.
One part of the cable is $x_{1}$ and the other is $x_{2}=x_{1}+18$
$y=x_{1}+x_{2}=x_{1}+x_{1}+18$
$84=2x_{1}+18$ (Substitute 84 for $y$)
$x_{1}=dfrac {66}{2}=33$ (Solve for $x_{1}$)
$x_{2}=x_{1}+18=33+18=51$
The first piece of the cable $x_{1}=33$ meters
The second piece of the cable $x_{2}=51$ meters
The second piece of the cable $x_{2}=51$ meters
As angle $a$ and angle $67$ are supplementary so their sum will be $180$ degrees,
$$
begin{align*}
a+67&=180 \
a&=180-67\
a&=113\
end{align*}
$$
Thus angle $a$ is equal to $120$ degrees.
As angles $a,b,c,d$ lie in a quadrilateral there sum will be equal to $360$ degrees,
$$
begin{align*}
a + b + c + d&=360\
113 + 67 + 54 +d &= 360 \
234 + d &= 360\
d&=360-234\
d&=126\
end{align*}
$$
Therefore angle $d$ is equal to $126$ degrees
b. The people in that town that go to that grocery store.
c. Do the same but in randomly choosen supermarkets in every state.
b. The actual population is everybody that volunteered to send the filled in questionnaires back. The bias is again a consequence of the voluntary response.
c. The actual population is the people who take this particular bus to school. The bias results from the fact that not everybody has been included, such as students that walk to school or take their bike.
Survey questions:
Do you participate in a sport?
Do you participate in a sport outside of school?
How often do you participate in sports?
Daily Weekly Monthly Yearly
We can assign a number to every student in the school and then let a calculator randomly pick numbers, the students corresponding to these numbers are then in the sample.
The sample will be representative because of its randomness.
b. No, because the sample is not representative for all men, since physicians in general live healthier than the general public.
c. No, because the sample is not representative for all men in the age category, since physicians in general live healthier than the general public.
d. Yes, because the sample contains male physicians in the given age category and thus the sample is representative.
e. No, because there are also negative side effects from taking aspirin.
b. No
c. No
d. Yes
e. No
Avoid them by asking closed questions that do not give too much information.
Sample by randomly selecting the sample elements.
b. A census would be needed and the results would be parameters.
c. A sample would be needed and the results would be statistics.
b. Census, parameters
d. Sample, statistics
a. Closed
b. Open
c. Open
d. Closed
b. Open
c. Open
d. Closed
b. The answers could range from a sport to lying on the couch or eating, which could thus contain answers that are not really methods of exercise.
c. The answers could range from a holiday to a concert to pranking a teachers, which you can not compare.
d. This information is always accurate because you always learn the country.
The graph demonstrates that only the point $b(-4, 5)$ is a solution for the equation.
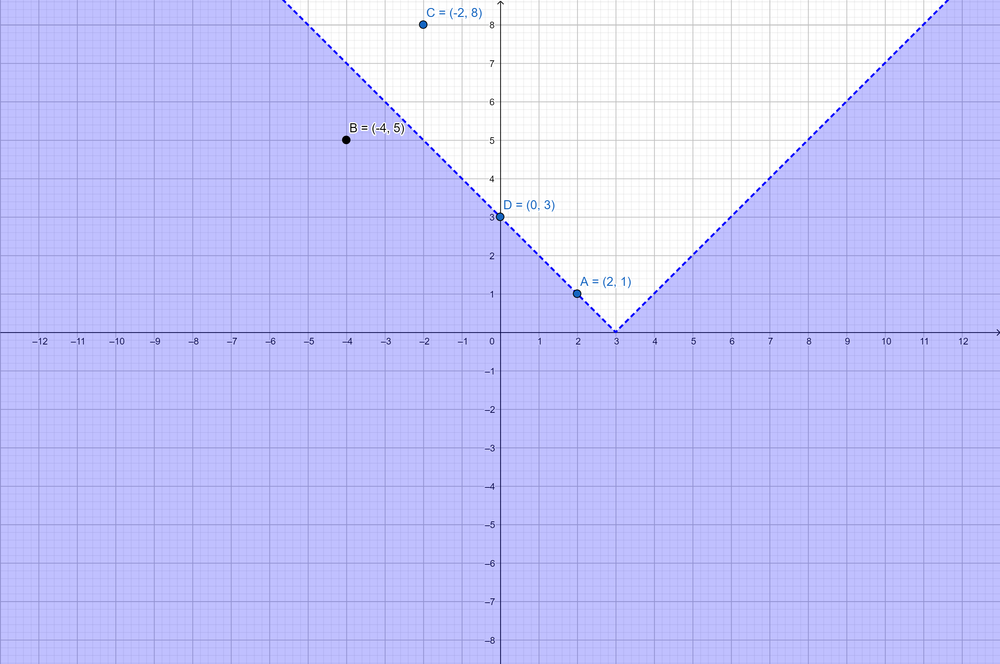
b qquad (-4, 5)
$$
$147=10m+b$ (2)
Substituting for $b$ in the second equation
$147=10m+342-23m$
$147-342=10m-23m$
$-13m=-195$
$$
m=15
$$
$147=10(15)+b$
$b=147-150$
$$
b=-3
$$
The number of the three sides painted cubes $=8$
The number of all cubes $=27$
The probability of choosing a cube with three painted sides $=dfrac {8}{27}$
The number of the two sides painted cubes $=12$
The number of all cubes $=27$
The probability of choosing a cube with two painted sides $=dfrac {12}{27}=dfrac {4}{9}$
The number of the one side painted cubes $=6$
The number of all cubes $=27$
The probability of choosing a cube with one painted side $=dfrac {6}{27}=dfrac {2}{9}$
The number of the cubes with no painted side$=1$
The number of all cubes $=27$
The probability of choosing a cube with no painted sides $=dfrac {1}{27}$
The first figure: All the three painted sides cubes are shaded. they are 8 cubes.
The second figure: All the tow painted sides cubes are shaded. they are 12 cubes.
The third figure: All the one painted side cubes are shaded. they are 6 cubes.
b- The probability of choosing a cube with two painted sides $=dfrac {4}{9}$
c- The probability of choosing a cube with one painted side $=dfrac {2}{9}$
d- The probability of choosing a cube with no painted sides $=dfrac {1}{27}$
Substituting for $mdfrac {1}{2}$ and the given point $(6, 1)$ in the equation $y=mx+b$
$1=dfrac {1}{2} cdot 6+b$
$1=3+b$
$b=-2$
The equation of the line is:
$$
y=dfrac {1}{2} x-2
$$
Substituting the given point $(1, 4)$ in the equation $y=2x+b$
$4=2 cdot 1+b$
$4=2+b$
$b=2$
The equation of the line is:
$$
y=2x+2
$$
b- $y=2x+2$
b. Use the old motor oil and drive until you have used 100 gallons of fuel. Then do the same for the new motor oil and compare the mileages.
c. We have done this in (b).
1. Prepare the sample of pennies
2. Apply the test procedures outlined by your teacher.
3. Collect and organize your data.
4. Make class histograms and box plots for the clean pennies and the regular pennies.
1. Invite your class team.
2. Collect your the histograms and boxplots.
3. Discuss your results.
4. Write a brief conclusion.
1. Invite your class team.
2. Discuss your brief conclusion .
3. Determine the lurking variable
4. Write a conclusion about the solution.
1. Prepare the sample of pennies
2. Apply the test procedures outlined by your teacher.
3. Collect and organize your data.
4. Make class histograms and box plots for the clean pennies and the regular pennies.
5. Write a conclusion to the question: “Does cleaning pennies cause them to hold a different amount of water than ordinary uncleaned pennies would hold?”.
1. Ask each of your respondents to make each of the following choices randomly. Make sure you read the choices exactly the same way to each respondent.
– Pick a number between 1 and 4.
– Pick a vowel (a, e, i, o, or u).
– Choose a color.
2. Make a bar graph for the responses to each of the three statements in your survey. Write the precise wording of the statement with each bar graph.
3. Determine if your results show that the people’s choices were truly random.
4. Explain any trends or interesting patterns that you observe.
5. Discuss why a mass email or a social networking site not be a good plan.
b. Because first it is mentioned that guns are used to protect our families and then there is talk about restrictions, it seems that the question implies if you want restrictions on being able to protect your family which causes bias.
c.Because first murders are mentioned and then there is talk about restrictions, it seems like owning a gun has murder as a direct consequence which causes bias.
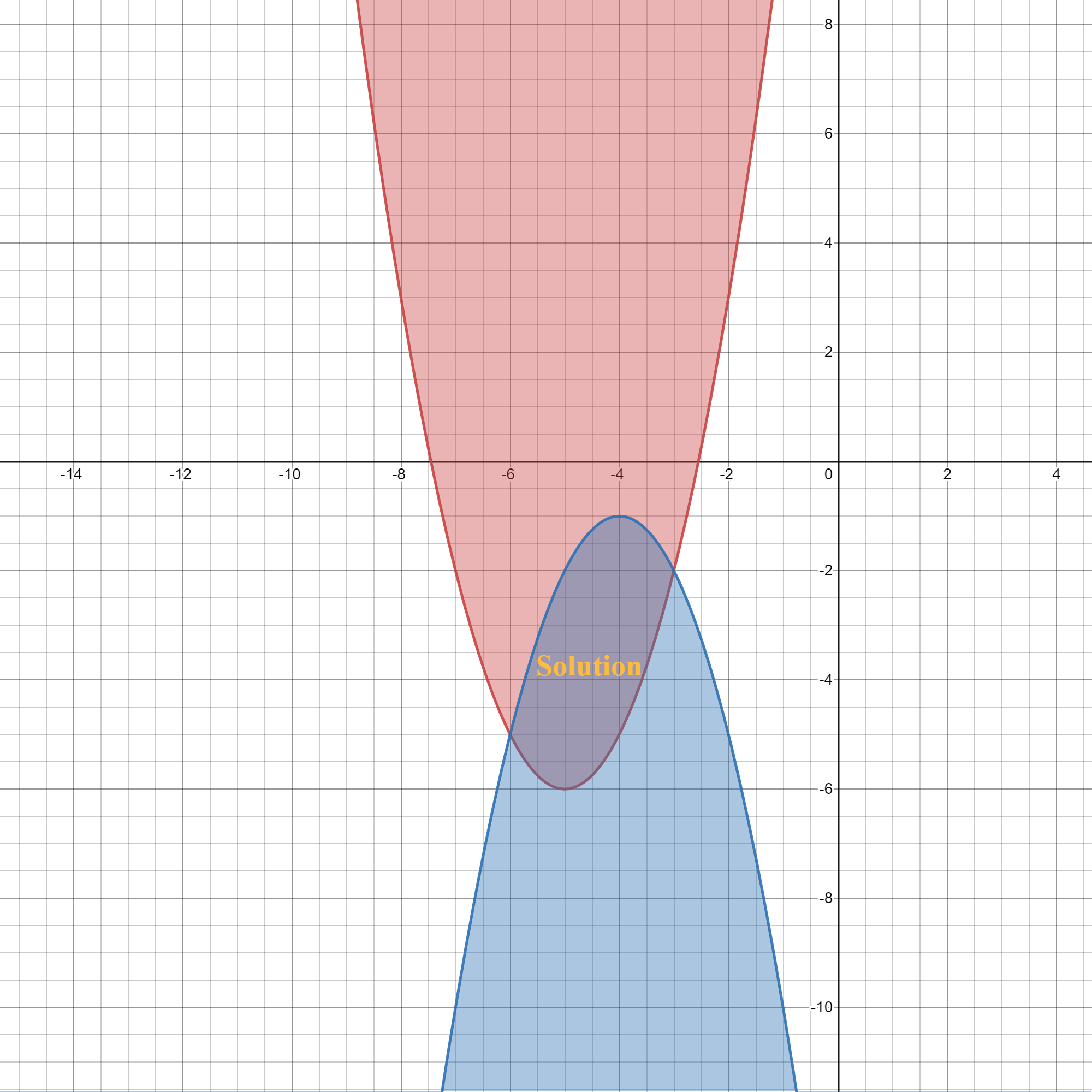
$$
begin{cases}
y & geq (x+5)^{2}-6 \
y & leq -(x+4)^{2}-1 \
end{cases}
$$
$25^{-dfrac {1}{2}}$
$=(5^2)^{-dfrac {1}{2}}$
$=5^{-1}$
$=dfrac {1}{5}$
$left(dfrac {1}{27} right)^{-dfrac {1}{3}}$
$=left(left(dfrac {1}{3} right)^3 right)^{-dfrac {1}{3}}$
$=left(dfrac {1}{3} right)^{-1}$
$dfrac {1}{left(dfrac {1}{3} right)}$
$=3$
`
$9^{left(dfrac {3}{2} right)}$
$=(3^2)^{left(dfrac {3}{2} right)}$
$=3^3$
$=27$
$(16)^{left(-dfrac {3}{4} right)}$
$=(2^4)^{left(-dfrac {3}{4} right)}$
$=2^{-3}`$
$=dfrac {1}{2^3}$
$=dfrac {1}{8}$
b- $left(dfrac {1}{27} right)^{-dfrac {1}{3}}=3$
c- $9^{left(dfrac {3}{2} right)}=27$
d- $(16)^{left(-dfrac {3}{4} right)}=dfrac {1}{8}$
The range of $y=2^x$ is the positive real numbers. $(y>0)$
The range of $y=-(2^x)$ is the negative real numbers. $(y<0)$
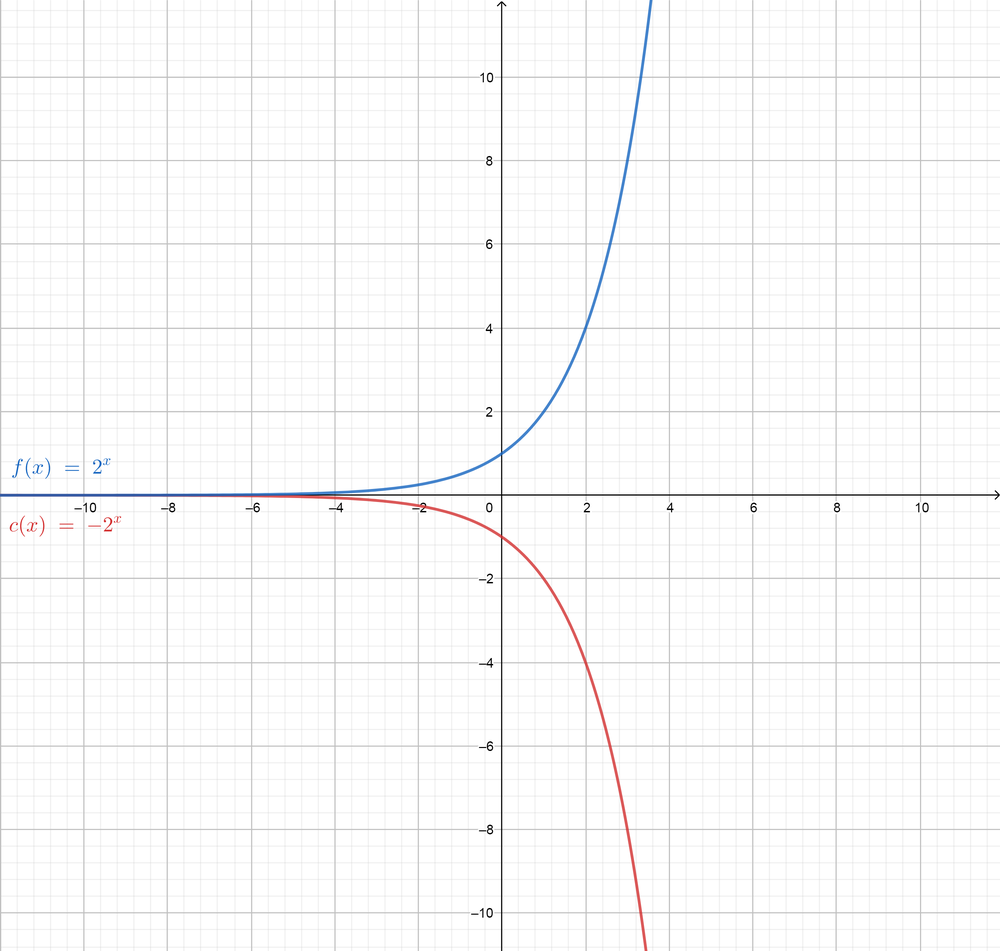
The range of $y=-(2^x)$ is the negative real numbers. $(y<0)$
The figure represents two right triangles sharing and angle. so they are similar by $AAA sim$ rule.
$dfrac {x}{47}=dfrac {18}{23}$ (Similar tirangles)
$x=47 cdot dfrac {18}{23}$ (Multiply each side by 47)
$x approx 36.78$ (Solve for $x$)
Two parallel lines and two transversals are composing two triangles with two pairs of corresponding angels a common angel.
Both triangles are similar by $AAA sim$ rule.
$dfrac {x}{20}=dfrac {55}{35}$ (Similar triangles)
$x=20 cdot dfrac {55}{35}$ (Multiply each side by 20)
$x=dfrac {220}{7}$ (Solve for $x$)
b- $x=dfrac {220}{7}$
$y=2(x^2+2 cdot dfrac {3}{4}x+dfrac {9}{16})-dfrac {7}{2}$
$y=2x^2+3x+dfrac {18}{16}-dfrac {7}{2}$
$y=2x^2+3x+dfrac {9}{8}-dfrac {28}{8}$
$y=2x^2+3x-dfrac {19}{8} neq 2x^2+3x+1$
So, Shuneel’s new equation is not correct.
b. Observational study, obtain the SAT scores for both states, calculate the mean and compare.
c. Sample
d. Sample
e. Experiment, let a group of both wear neckties and the others not and compare their SAT scores.
f. Sample
g. Census
h. Sample
i. Survey: time spent on homework, number of homework assignments, etc.
b. Observational study
c. Sample
d. Sample
e. Experiment
f. Sample
g. Census
h. Sample
i. Survey
In an observational study, the sample population being studied is measured, or surveyed, as it is.
Surveys are one form of an observational study, since the researchers do not influence the outcomes.
Statistical surveys collect information from a sample group to learn about the entire population.
Unlike an observational study, an experimental study has the researcher purposely attempting
to influence the results. The goal is to determine what effect a particular treatment has
on the outcome. Researchers take measurements or surveys of the sample population.
b. Not representative, because not everybody goes to the local grocery store.
c. Not representative, because not everybody goes to the local movie theater.
d. Representative, because of randomness
e. Not representative, because you cannot determine who they would vote for by just observing them.
b. Not representative
c. Not representative
d. Representative
e. Not representative
Solving.
$$begin{aligned}
sqrt{x+5} + sqrt{x} &= 5
end{aligned}$$
$$begin{aligned}
sqrt{x+5}&= 5- sqrt{x}\
end{aligned}$$
Squaring both sides.
$$begin{aligned}
(sqrt{x+5})^2 &= (5-sqrt{x})^2\
x+5&= 25-10sqrt{x} + x\
x+5-x-25&=-10sqrt{x}\
-20&= -10sqrt{x}\
20&= 10sqrt{x}\
2&= sqrt{x}\
end{aligned}$$
Squaring both sides.
$$begin{aligned}
&boxed{4= x}\
end{aligned}$$
$$begin{aligned}
sqrt{2x-2}-sqrt{x}&=1\
sqrt{2x-2}&= 1 +sqrt{x}rightarrow(1)\
end{aligned}$$
$$begin{aligned}
(sqrt{2x-2})^2&= (1 +sqrt{x})^2\
2x-2&= 1 + 2sqrt{x} + x\
2x-2-1-x&=2sqrt{x}\
x- 3&= 2sqrt{x}\
end{aligned}$$
Squaring both sides again.
$$begin{aligned}
(x- 3)^2&= (2sqrt{x})^2\
x^2-6x+9&= 4x\
x^2-6x-4x+9&=0\
x^2-10x+9&=0\
x^2-x-9x+9&=0\
x(x-1)-9(x-1)&=0\
&boxed{(x-1)(x-9)=0}rightarrow(2)\
end{aligned}$$
$$begin{aligned}
x-1&= 0\
&boxed{x=1}\
end{aligned}$$
Also,
$$begin{aligned}
x-9&= 0\
&boxed{x=9}\
end{aligned}$$
$b$. 1 ; 9
$$begin{aligned}
text{ Climbing angle}&= 5^o\
text{ Distance}&= 1000\
end{aligned}$$

$$begin{aligned}
sin B&= dfrac{text{ AC}}{text{ BC}}\
text{ AC}&= text{ BC}cdot sin 5^o\
&= 1000cdot 0.08715574\
&= 87.16 text{ yards}
end{aligned}$$
Given function,
$$begin{aligned}
f(x)&= 2|x-4| + 3\
end{aligned}$$

$$begin{aligned}
f(-x)&= 2|-x-4|+3\
&boxed{f(-x)= 2|x+4| + 3}rightarrow(1)\
end{aligned}$$
In order to sketch the graph of the function, $y = f(-x)$, we will first start with the parent function i.e. $f_{o}(x)= |x|$, then we shift it to 4 units to the left to get $f_{1}(x) = |x-4|$. After that we vertically stretch $f_{1}$ by a factor of 2 to get $f_{2}(x)=2|x+4|$ and finally we shift 3 units up to get $f(-x)$.

Given function,
$$begin{aligned}
f(x)&=dfrac{1}{x+4}\
end{aligned}$$

$$begin{aligned}
f(-x)&=dfrac{1}{-x+4}\
&boxed{f(-x)=-dfrac{1}{x-4}}rightarrow (2)
end{aligned}$$
in order to sketch the graph of $f(-x)$, we start with the parent function $f_o(x) = dfrac{1}{x}$, we shift it 4 units to the right to get $f_1(x)=dfrac{1}{x-4}$. After then we reflect $f_1$ across the $x$- axis to get f(-x):

Therefore it is not a function.
$textbf{(b)}$ Domain of function is $-3 le x le 3$
Range of function is $-2 le y le 2$
Given inequality,
$$begin{aligned}
y < (x-2)^3 + 5\
end{aligned}$$

$$begin{aligned}
0 <(0-2)^3 + 5\
0 < -8 + 5\
0 < -3\
end{aligned}$$
The condition is False. Thus, the strict linear inequality will have the region below the graph of the function.

Given inequality,
$$begin{aligned}
(x-2)^2 + (y+3)^2geq 9 \
end{aligned}$$

b.
d.
$$
dfrac{0+5+9+17}{40}=dfrac{31}{40}=0.775=77.5%
$$
b. See graph
c. 77.5%
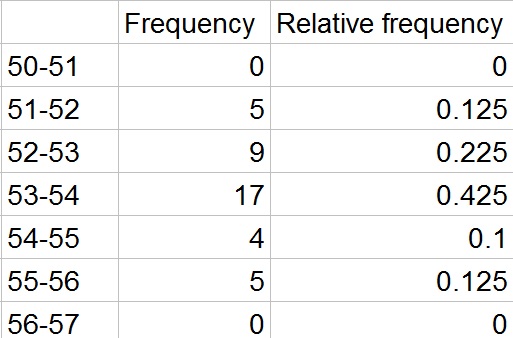
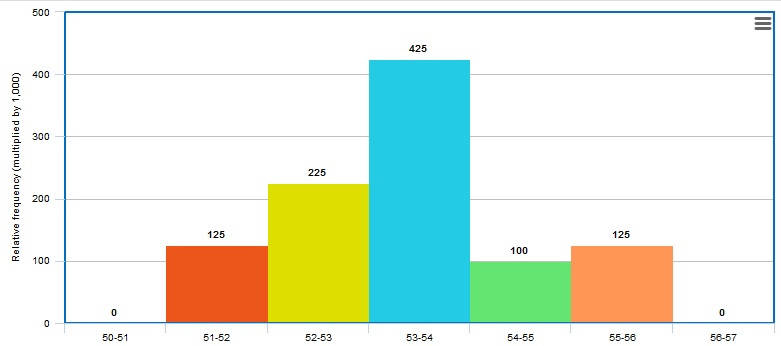
$$
0.225+0.425+0.1=0.75=75%
$$
d. We note that all hat sizes are below 56, thus $100%$
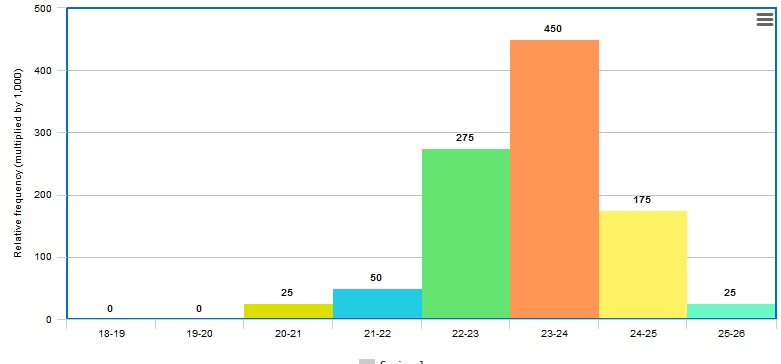
$$
0+0+0.025+0.05=0.075=7.5%
$$
d.
$$
0.275+0.45+0.175=0.9=90%
$$
The area of the bars on a relative frequency gives the percentage of data points that fall in the category.
Create a relative frequency histogram, by first determining the relative frequencies (number of items in category divided by the total number of items) and this is the height of each bar.
b. Students who go to the university gym will be more inclined to support a recreation hall than students who do not go to the gym.
c. No, more people drive during the day than during the night and thus the probability of an accident becomes much higher if there are more cars in that time period.
d. An active citizens’ group has unrealistic expectations of the safety because they only want to shut the plant down and nothing else.
b. Students who go to the university gym will be more inclined to support a recreation hall than students who do not go to the gym.
c. No
d. An active citizens’ group has unrealistic expectations of the safety
b. Randomly choose a group of people and randomly divide them in two groups, one group will test a car crash with the seat belt and the others without. Compare the results. This experiment would be unethical because people could die during the experiment.
c. Randomly choose a group of people and randomly divide them in two groups, one group will take extra vitamin C and the others won’t. Compare the results.
Let the points be $A(6, 1)$ and $(-10, -7)$.
$$begin{aligned}
m&= dfrac{y_2-y_1}{x_2-x_1}\
end{aligned}$$
Substituting the values,
$$begin{aligned}
m&= dfrac{-7-1}{-10-6}\
&= dfrac{-8}{-16}\
&= 0.5\
end{aligned}$$
$$begin{aligned}
y-y_1&= m (x-x_1)\
end{aligned}$$
Substituting the values, $A(6, 1)$ and slope, $m = 0.5$,
$$begin{aligned}
y- 1&= 0.5(x-6)\
y-1&= 0.5x – 3\
y&= 0.5x-3+1\
&boxed{y= 0.5x-2}rightarrow(1)\
end{aligned}$$
Given equation of line,
$$begin{aligned}
y&= dfrac{2}{3}x+1rightarrow(2)\
end{aligned}$$
Passing point $rightarrow (0, 5)$.
$$begin{aligned}
y&= mx+c\
end{aligned}$$
Thus, the slope of the equation of line given in (1) is, $m_1$ : $dfrac{2}{3}$
So, the slope of the perpendicular line (let say $m_2$) is,
$$begin{aligned}
m_2&= -dfrac{1}{m_1}\\
&= -dfrac{3}{2}rightarrow(3)\
end{aligned}$$
$$begin{aligned}
y-y_1&= m (x-x_1)\
end{aligned}$$
Substituting the values, $A(0, 5)$ and slope, $m_2 =-dfrac{3}{2}$,
$$begin{aligned}
y-5&= -dfrac{3}{2}(x-0)\
y-5&= -dfrac{3}{2}x\
&boxed{y= -dfrac{3}{2}x+5}rightarrow(4)\
end{aligned}$$
$b$. $y = -dfrac{3}{2}x+5$
$$begin{aligned}
3x^2+x+4&=0\
end{aligned}$$
$$begin{aligned}
x&= dfrac{-b pm sqrt{b^2- 4ac
}}{2a}
end{aligned}$$
Thus, equation (1) equivalent to,
$$begin{aligned}
x&= dfrac{-1pm sqrt{(1)^2-4times 3 times 4}}{2times 3}\\
&= dfrac{-1pmsqrt{1-48}}{6}\\
&= dfrac{-1pm sqrt{47 i}}{6}rightarrow(i^2= -1)\\
&boxed{x=dfrac{-1 + sqrt{47 i}}{6}}\\
&boxed{x=dfrac{-1 – sqrt{47 i}}{6}} \
end{aligned}$$
$$begin{aligned}
y^2 -12y +36+10-3y&=0\
y^2 -15y + 46&=0\
end{aligned}$$
$$begin{aligned}
y&= dfrac{-b pm sqrt{b^2- 4ac
}}{2a}
end{aligned}$$
The equation (2) equivalents to,
$$begin{aligned}
y&= dfrac{-(-15)pm sqrt{(-15)^2}-4times 1times 46}{2 times 1}\\
y&= dfrac{15 pm sqrt{225-184}}{2}\\
y&= dfrac{15pm sqrt{41}}{2}\\
&boxed{y=dfrac{15+sqrt{41}}{2}}\\
&boxed{y=dfrac{15-sqrt{41}}{2}}\\
end{aligned}$$
$b$. $y=dfrac{15 + sqrt{41}}{2}$ ; $dfrac{15 – sqrt{41}}{2}$
$$begin{aligned}
y &= -(x+1)^3+2rightarrow(1)\
end{aligned}$$
|$x_1$ |$y_1$ |
|–|–|
|-3 |10 |
| -2|3 |
|-1 |2 |
|0 |1 |
| 2|-25 |
|3 |-62 |

(x+1)^3 + 2$.
Taking $rightarrow$ $y = 3$

Thus, $x rightarrow 0.7$.
Given function,
$$begin{aligned}
f(x)&=|x-6| – 4\
end{aligned}$$

Given function,
$$begin{aligned}
g(x)&= ||x-6|-4|\
end{aligned}$$
$$begin{aligned}
g(x)&= |f(x)|rightarrow(1)
end{aligned}$$
In order to do that we will perform the same steps like we did in part $a$. We also reflect across the $x$-axis the part of the graph of $f(x)$ for which $f(x) < 0$.

Domain $(-5, infty)$
Range $(-infty, 6)$
$P (-2, 4)$ belongs to the graph
$$x = -5$$
$$ y = 6$$
$$y = dfrac {6x}{x+5}$$
|$x_1$ |$y_1$ |
|–|–|
| -2|-4 |

$$
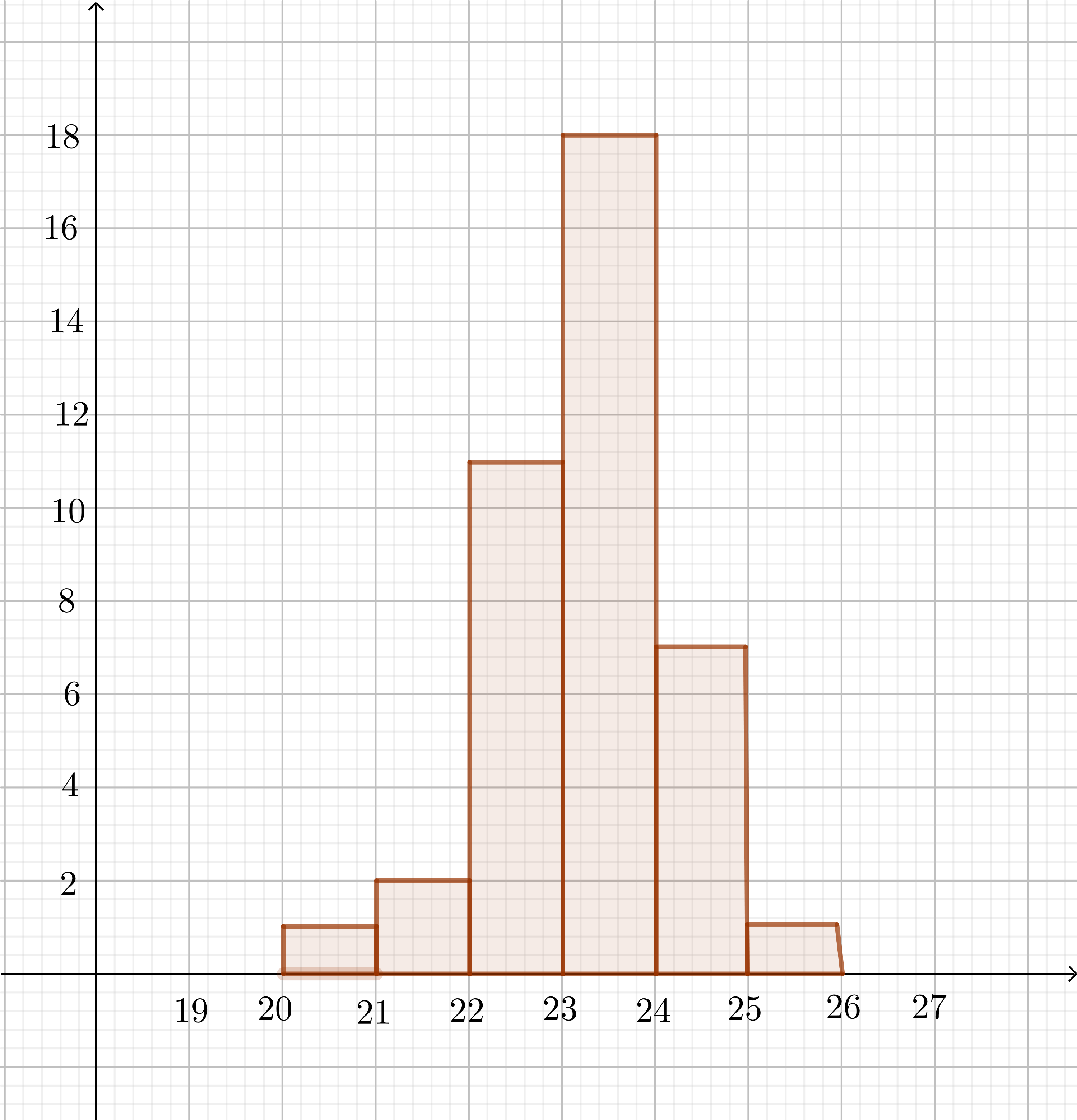
boxed{sigma=sqrt{frac{1}{N-1}sum_{i=1}^{N}left(x_i-x_0right)^2}}
$$
$text{where $x_1, x_2,…, x_N$ are the observed values of the sample items, $x_0$ is the mean value}$
$text{of these observations, and $N$ is the number of observations in the sample.}$
$$
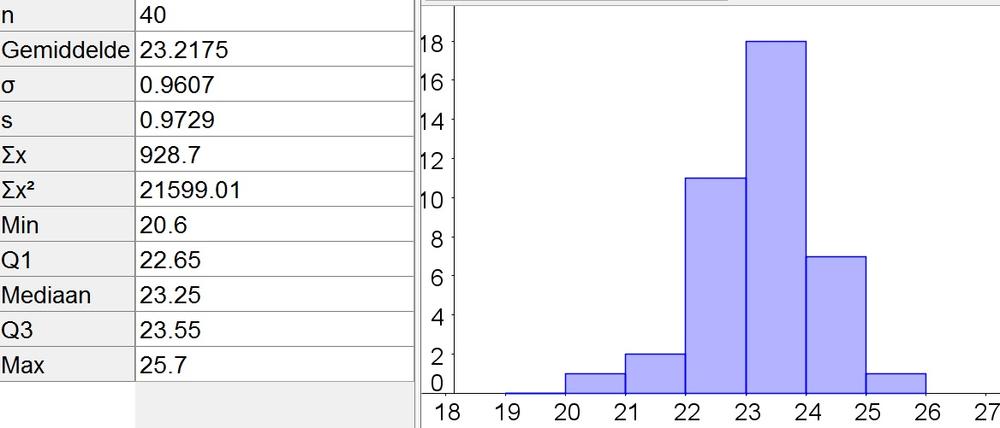
text{These $40$ data points have the mean (average):}
$$
$$
begin{align*}
x_0&=frac{22.2+22.6+24.9+23.5+22.8+23.3+23.1+21.6+21.3+22.9+25.7+}{40} \
&+frac{23.3+23.3+22.5+24.4+22.7+24.1+23+22.5+23.2+24.7+24.4+}{40} \
&+frac{23.3+23.5+23.1+22.5+22.3+22.6+23.6+23.3+23.3+23.4+23+}{40} \
&+frac{23.1+24.5+23.9+20.6+23.5+22.8+24.4}{40} \
&=color{#c34632}{23.2175}
end{align*}
$$
First, calculate the deviations of each data point from the mean, and square the result of each:
$$
begin{align*}
left(22.2-23.2175right)^2&=left(-1.0175right)^2=1.04 \
left(22.6-23.2175right)^2&=left(-0.6175right)^2=0.38 \
left(24.9-23.2175right)^2&=left(1.6825right)^2=2.83 \
left(23.5-23.2175right)^2&=left(0.2825right)^2=0.08 \
left(22.8-23.2175right)^2&=left(-0.4175right)^2=0.17 \
left(23.3-23.2175right)^2&=left(0.0825right)^2=0.006 \
left(23.3-23.2175right)^2&=left(0.0825right)^2=0.006 \
end{align*}
$$
$$
begin{align*}
sigma^2&=frac{1.04+0.38+2.83+0.08+0.17+0.006+0.06}{7} \
&=frac{4.62}{7} \
&=0.66
end{align*}
$$
and the population standard deviation is equal to the square root of the variance:
$$
begin{align*}
sigma&=sqrt{0.66} \
&=0.8124
end{align*}
$$
sigma=0.8124
$$
$text{Out of $40$ women that comprised this sample there are $32$ women whose running time}$
$text{amounts between $22.5$ and $24.5$ minutes.}$
$$
text{A percentage of women whose running time ranges from $22.5$ to $24.5$ is:}
$$
$$
boxed{text{Percent}=frac{32}{40} cdot 100%=80%}
$$
#### b.
$text{Out of $40$ women that comprised this sample there are $39$ women whose running time}$
$text{amounts between $20$ and $25$ minutes.}$
$$
text{A percentage of women whose running time ranges from $20$ to $25$ is:}
$$
$$
boxed{text{Percent}=frac{39}{40} cdot 100%=97.5%}
$$
#### c.
By using the model go normal probability density function, we arrive of a conclusion
$text{that the percentage of all women is the population who run faster than $26$ minutes}$
$$
text{approximates $99%$.}
$$
#### d.
$text{From the previous tasks we can see that mean$=23.2175$.}$
$text{Out of $40$ women that comprised this sample there are $32$ women whose running time}$
$text{is shorter than $23.2175$ minutes.}$
$$
text{A percentage of women whose running time is shorter than $23.2175$ is:}
$$
$$
boxed{text{Percent}=frac{20}{40} cdot 100%=50%}
$$
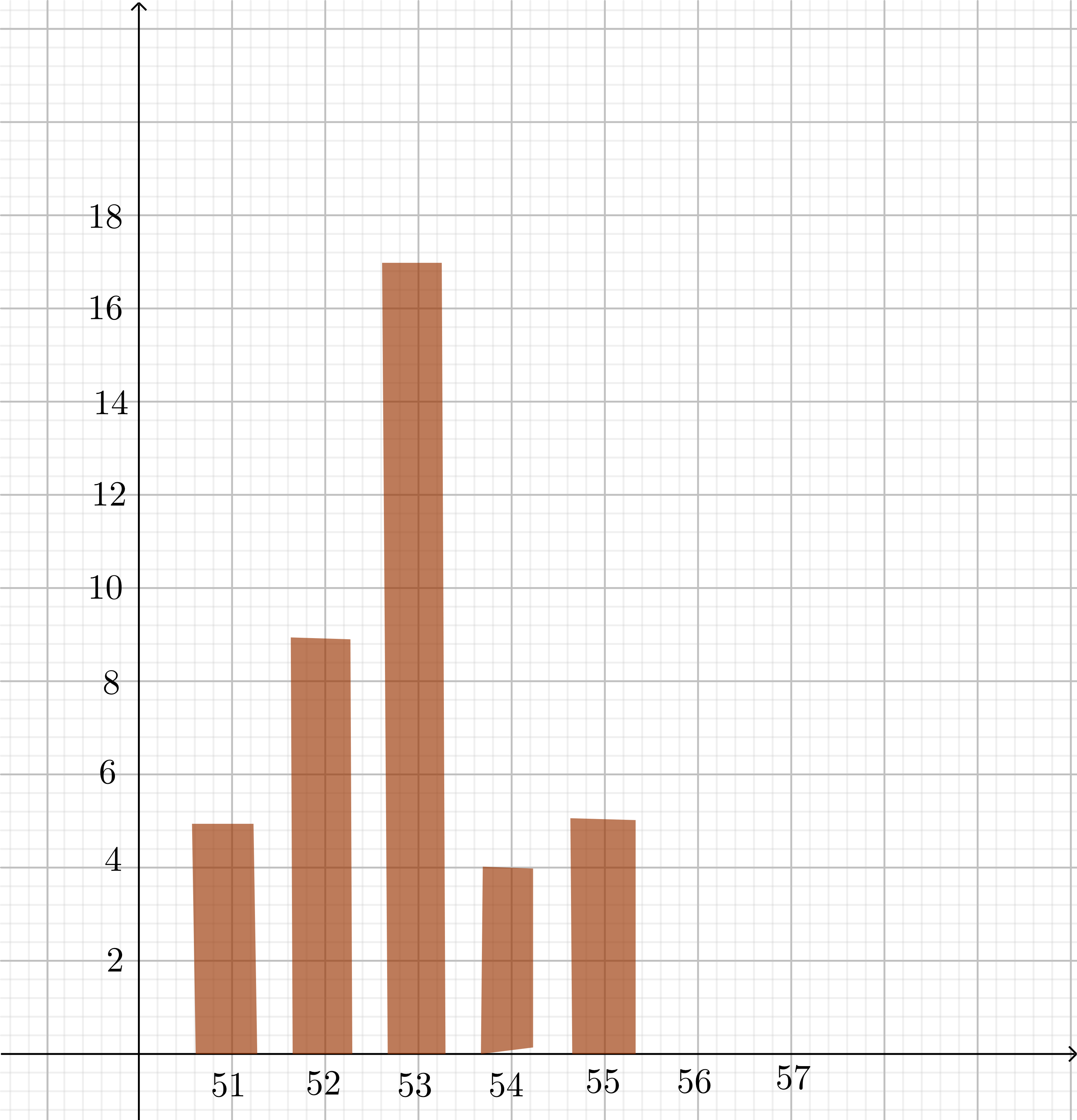
The formula for the sample standard deviation is
$$
boxed{sigma=sqrt{frac{1}{N}sum_{i=1}^{N}left(x_i-x_0right)^2}}
$$
$text{where $x_1, x_2,…, x_N$ are the observed values of the sample items, $x_0$ is the mean value}$
$text{of these observations, and $N$ is the number of observations in the sample.}$
$$
text{These $40$ data points have the mean (average):}
$$
$$
begin{align*}
x_0&=frac{55.5+53.7+53.7+53.4+53.1+55.2+53.9+53.8+53.1+52.2+}{40} \
&+frac{54.8+54.5+53.2+52.3+55.3+53.2+51.9+53.1+53.1+52.2+51.2+}{40} \
&+frac{55.4+53.3+51.4+52.6+53.7+52.7+52.8+51.9+54.3+55.4+53.7+}{40} \
&+frac{53.0+52.7+53.0+54.6+52.5+52.9+53.1+51.9}{40} \
&=color{#c34632}{53.3325}
end{align*}
$$
First, calculate the deviations of each data point from the mean, and square the result of each:
$$
begin{align*}
left(55.5-53.3325right)^2&=left(2.1675right)^2=4.7 \
left(53.7-53.3325right)^2&=left(0.3675right)^2=0.135 \
left(53.4-53.3325right)^2&=left(0.0675right)^2=0.004 \
left(55.2-53.3325right)^2&=left(1.8675right)^2=3.49 \
left(53.9-53.3325right)^2&=left(0.5675right)^2=0.32 \
left(53.8-53.3325right)^2&=left(0.4675right)^2=0.22 \
left(54.8-53.3325right)^2&=left(1.4675right)^2=2.15 \
end{align*}
$$
$$
begin{align*}
sigma^2&=frac{4.7+0.135+0.004+3.49+0.32+0.22+2.15}{7} \
&=frac{11.02}{7} \
&=1.57
end{align*}
$$
and the population standard deviation is equal to the square root of the variance:
$$
begin{align*}
sigma&=sqrt{1.57} \
&=1.25
end{align*}
$$
$$
boxed{text{Percent}=frac{5}{40} cdot 100%=12.5%}
$$
#### d.
$$
text{$12.5%$ of $775=0.125 cdot 775approx color{#c34632}{97}$}
$$
#### e.
$$
boxed{text{Percent}=3%}
$$
$$
boxed{text{Percent}=95.6%}
$$
$textbf{d.}$ $97$, $textbf{e.}$ $3%$, $textbf{f.}$ $95.6%$
Relative frequency is how often something happens divided by all the possible outcomes.
$text{A probability histogram is a graph that shows the probability of each outcome on the $y-$axis.}$
A relative frequency histogram is a minor modification of a typical frequency histogram.
$text{Since $100%=1$, all bars must have a height from $0$ to $1$. Furthermore, the heights}$
$text{of all of the bars in our relative frequency histogram must sum to $1$.}$
$textbf{Example:}$
$text{suppose that there are $30$ students in our class and six have scored more than $80$ points.}$
$$
text{Rather than constructing a bar of height five for this bin, we would have a bar of height $frac{6}{30}=0.2$.}
$$
b.
$$
30cdot(0.45+0.125+0.06)=30cdot 0.635approx 19
$$
Thus about 19 days
c.
$$
30cdot 0.035approx 1
$$
Thus about 1 day
b.Yes, because the groups were chosen randomly.
b.Yes
a = 20 ft
b = 15 ft
c = 10 ft
contains 625 butterflies.

$$begin{aligned}
text {The volume of prism’s} &= a cdot b cdot c\
&= 20 cdot 15 cdot 10\
&= 20 cdot 15 cdot 10\
&boxed {text {The volume of prism’s} = 3000 ft^{3}}\
end{aligned}$$
$$begin{aligned}
text { Volume of air} &= dfrac {text{Volume of prism}}{text{Total number of butterflies}}\\
V &= dfrac {3000}{625}\\
&boxed {text {The volume of air} = 4.8 ft^{3}}\
end{aligned}$$
$$begin{aligned}
text { Density} &= dfrac {text{Total number of butterflies}}{text{Volume of prism}}\\
V &= dfrac {625}{3000}\\
&boxed {text {Density} approx 0.208}\
end{aligned}$$
$(b.)$ $3000 ft^{3}$
$(c.)$ $4.8 ft^{3}$
$(d.)$ 0.208
b- $sqrt [3]{9}=(3^2)^{(dfrac {1}{3})}=3^{left(dfrac {2}{3} right)}$
c- $sqrt [8]{17^x}=(17^x)^{left(dfrac {1}{8} right)}=17^{left(dfrac {x}{8} right)}$
d- $7 sqrt [4]{x^3}=7 (x^3)^{left(dfrac {1}{4} right)}=7 x^{left(dfrac {3}{4} right)}$
$$
sqrt{x}=x-2
$$
Square both sides of the equation:
$$
x=x^2-4x+4
$$
Subtract $x$ from both sides of the equation:
$$
0=x^2-5x+4
$$
Factorize:
$$
0=(x-4)(x-1)
$$
Zero product property:
$$
x-4=0text{ or }x-1=0
$$
Solve each equation to $x$:
$$
x=4text{ or }x=1
$$
Since both solutions are positive, the square root exist.
$$
x+4sqrt{x}+4=x+6
$$
Subtract $x+4$ from both sides of the equation:
$$
4sqrt{x}=2
$$
Divide both sides of the equation by 4:
$$
x=dfrac{1}{2}
$$
Square both sides of the equation:
$$
x=dfrac{1}{4}
$$
Since the solution is positive, the square root exists.
b. $x=dfrac{1}{4}$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
sqrt{x}+2-2&=x-2&&boxed{text{Subtract 2 from both sides}}\
sqrt{x}&=x-2&&boxed{text{Simplify}}\
left(sqrt{x}right)^2&=left(x-2right)^2&&boxed{text{Square both sides}}\
x&=left(x-2right)^2&&boxed{text{Simplify}}\
x&=x^2-2xcdot :2+2^2&&boxed{text{Divide both sides by } 4}\
x&=x^2-4x+2^2&&boxed{text{Multiply the numbers: }2xcdot2=4x}\
x&=x^2-4x+4&&boxed{text{Evaluate: }2^2=4}\
x^2-4x+4&=x&&boxed{text{Switch sides}}\
x^2-4x+4-x&=x-x&&boxed{text{Subtract } x text{ from both sides}}\
x^2-5x+4&=0&&boxed{text{Combine like terms: }-4x-x=-5x}\
end{align*}
$$
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-5right)pm sqrt{left(-5right)^2-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Substitute }1 text{ for }a, -5 text{ for } b, text{ and } 4 text{ for } c.} \
end{align*}
$$
First we solve $x_1$
$$
begin{align*}
x_1&=frac{-left(-5right)+sqrt{left(-5right)^2-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Simplify}}\
x_1&=frac{5+sqrt{left(-5right)^2-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_1&=frac{5+sqrt{25-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Evaluate: }(-5)^2=25}\
x_1&=frac{5+sqrt{25-16}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot4=16}\
x_1&=frac{5+sqrt{25-16}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2 }\
x_1&=frac{5+sqrt{9}}{2}&&boxed{text{Subtract the numbers: }25+16=9}\
x_1&=frac{5+3}{2}&&boxed{text{Simplify}}\
x_1&=frac{8}{2}&&boxed{text{Add the numbers:} 5+3=8}\
x_1&=color{#c34632}{4}text{ True}&&boxed{text{Simplify}}\
end{align*}
$$
$$
begin{align*}
x_2&=frac{-left(-5right)-sqrt{left(-5right)^2-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Simplify}}\
x_2&=frac{5-sqrt{left(-5right)^2-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Remove parentheses}}\
x_2&=frac{5-sqrt{25-4cdot :1cdot :4}}{2cdot :1}&&boxed{text{Evaluate: }(-5)^2=25}\
x_2&=frac{5-sqrt{25-16}}{2cdot :1}&&boxed{text{Multiply the numbers: } 4cdot1cdot4=16}\
x_2&=frac{5-sqrt{25-16}}{2}&&boxed{text{Multiply the numbers: }2cdot1=2 }\
x_2&=frac{5-sqrt{9}}{2}&&boxed{text{Subtract the numbers: }25+16=9}\
x_2&=frac{5-3}{2}&&boxed{text{Simplify}}\
x_2&=frac{2}{2}&&boxed{text{Subtract the numbers:} 5-3=2}\
x_2&=color{#c34632}{1}text{ False}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=4} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
left(sqrt{x}+2right)^2&=left(sqrt{x+6}right)^2&&boxed{text{Square both sides}}\
left(sqrt{x}right)^2+2sqrt{x}cdot :2+2^2&=left(sqrt{x+6}right)^2&&boxed{text{Apply perfect square formula}}\
x+4sqrt{x}+4&=left(sqrt{x+6}right)^2&&boxed{text{Simplify}}\
x+4sqrt{x}+4&=x+6&&boxed{text{Remove parentheses}}\
x+4sqrt{x}+4-left(x+4right)&=x+6-left(x+4right)&&boxed{text{Subtract }x+6text{ from both sides}}\
4sqrt{x}&=2&&boxed{text{Simplify}}\
left(4sqrt{x}right)^2&=2^2&&boxed{text{Square both sides}}\
4^2left(sqrt{x}right)^2&=2^2&&boxed{text{Raise to the second power}}\
4^2x&=2^2&&boxed{text{Remove parentheses}}\
16x&=4&&boxed{text{Simplify}}\
frac{16x}{16}&=frac{4}{16}&&boxed{text{Divide both sides by 16}}\
x&=frac{4}{16}&&boxed{text{Simplify}}\
x&=frac{1}{4}&&boxed{text{Cross cancel common factor: }4}\\
&boxed{{color{#c34632}x=frac{1}{4}} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ a) } x_1=4
$$
$$
color{#4257b2} text{ b) }x=frac{1}{4}
$$
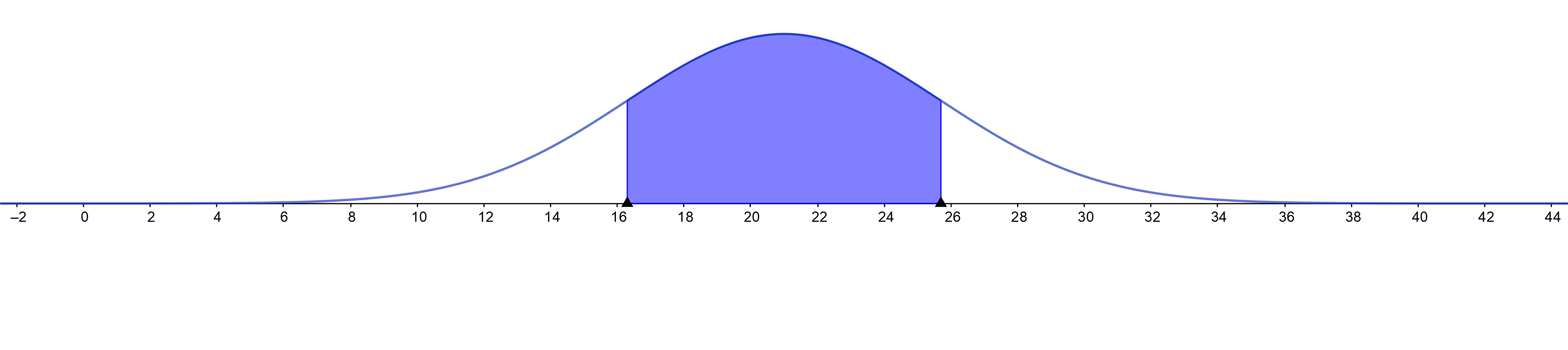
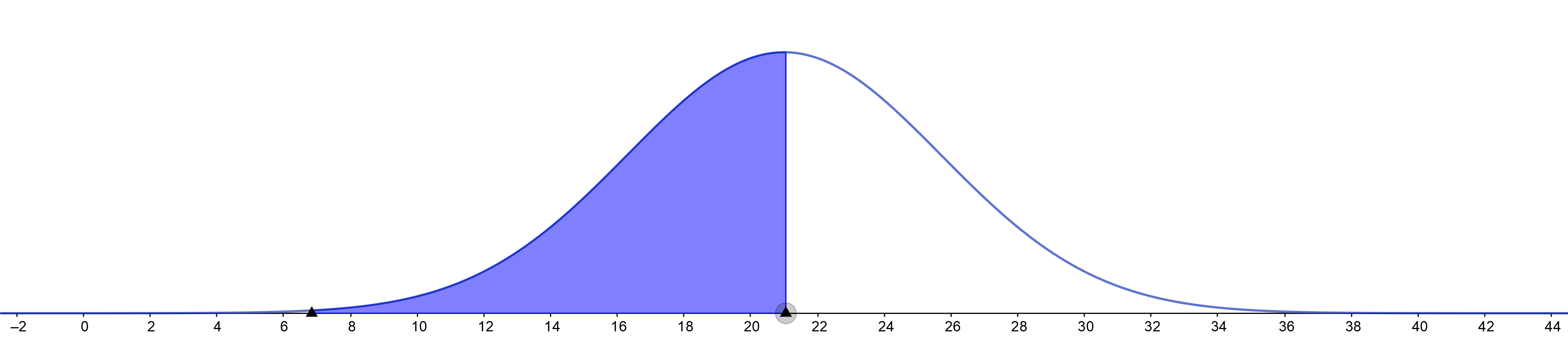
The shaded part of normal distribution shows that the percentage of results which
$$
text{are below Adele’s score is around $80\%$.}
$$

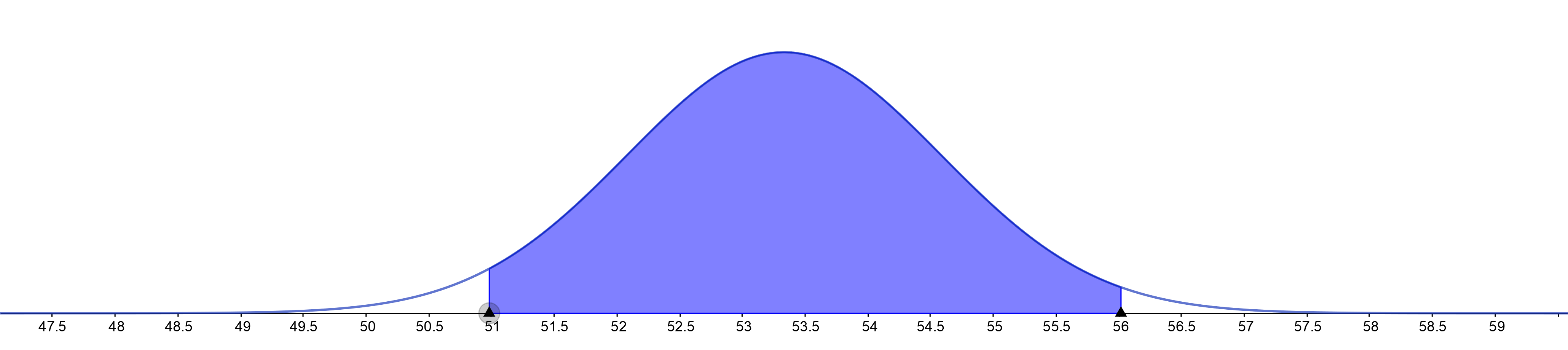
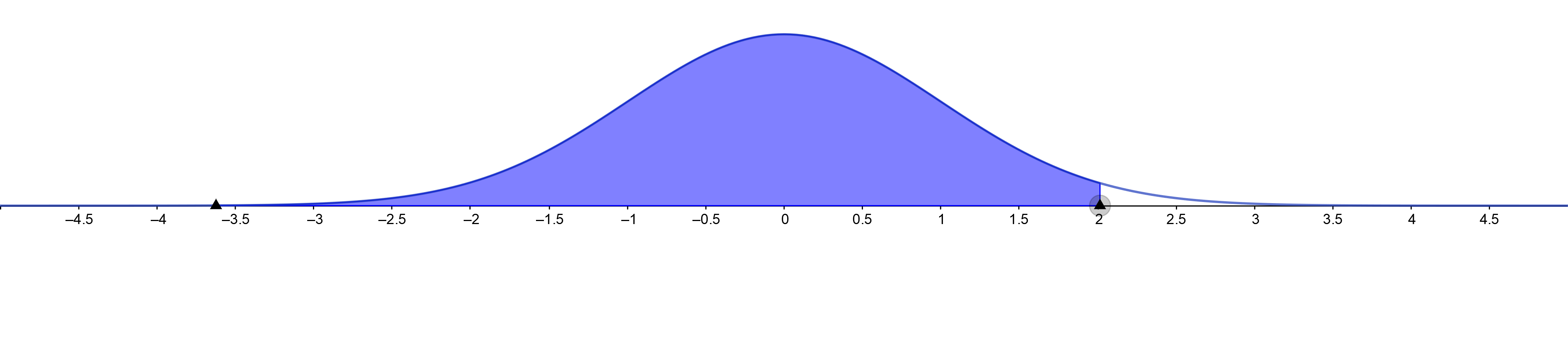
The shaded part of normal distribution shows that the percentage of results which
$text{are below Remy’s score is around $15%$.}$
$$
text{Since $15\%$ of test-takers scored below Remy, you can say that Remy scored in the $15$ percentile.}
$$
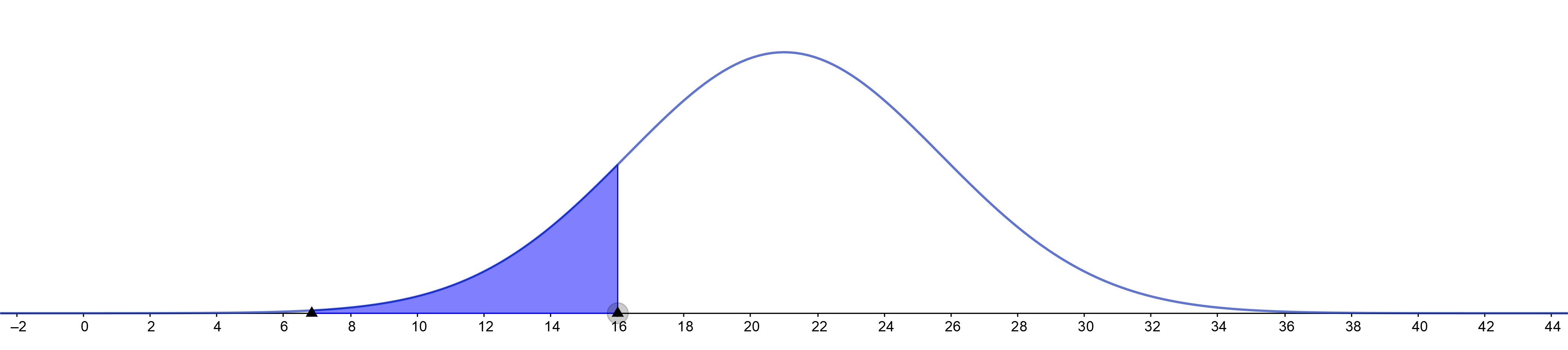
The shaded part of normal distribution shows that the percentage of results which
$text{are below Antoinette score is around $50%$.}$
$text{Since $50%$ of test-takers scored below Antoinette, you can say that Antoinette scored}$
$$
text{in the $50$ percentile.}
$$
The model using a normal distribution is not a good idea because the data is not symmetric,
single-peaked, and bell-shaped. A different model would represent the data better.
#### c.
$$
text{Lateefa scored higher than $20$ students.}
$$
$$
boxed{text{Percent}=frac{20}{35} cdot 100%=57%}
$$
$$
text{Farid scored higher than $29$ students.}
$$
$$
boxed{text{Percent}=frac{29}{35} cdot 100%=83%}
$$
#### d.
Put your numbers in ascending order (from smallest to largest).
For this particular data set, the order is:
$17,42,53,56,57,58,60,60,69,71,72,75,75,75,76,79,80,80,81,$
$83,86,86,86,89,89,89,90,91,92,93,93,93,94,94,94$
$text{The first quartile is the same as the $25^{text{th}}$ percentile and}$
$text{the third quartile is the same as the $75^{text{th}}$ percentile.}$
$$
25^{text{th}} text{percentile}=69 text{score}
$$
$$
75^{text{th}} text{percentile}=90 text{score}
$$
#### e.
$$
begin{align*}
text{minimum}&=17 \
text{first quartile}&=69 \
text{median}&=80 \
text{third quartile}&=90 \
text{maximum}&=94 \
end{align*}
$$
$textbf{c.}$ $57%, 83%$,
$textbf{d.}$ $69, 90$, $textbf{e.}$ $17, 69, 80, 90, 94$
$$
text{$10%$ of the sizes are above $7$ mm, so $90%$ are below 7 mm. The $90^{text{th}}$ percentile is 7 mm.}
$$
#### b.
The model using a normal distribution is not a good idea because the data is not symmetric,
single-peaked, and bell-shaped. A different model would represent the data better.
#### c.
$$
text{The $50^{text{th}}$ percentile is in other words called median.}
$$
$textbf{c.}$ median

$$
text{Using statistical computations, the boundaries are $30$ and $115$.}
$$
#### c.
$$
text{Using the normalcdf function on the TI$-84$.}
$$
#### d.
$text{$1.6449$ standard deviations is $42.7674$ feet, so the middle $90%$ is from}$
$$
text{$74 – 42.7674 = 31.23$ ft to $74 + 42.7674= 116.77$ ft.}
$$
$textbf{c.}$ $text{Using the normalcdf function on the TI$-84$.}$
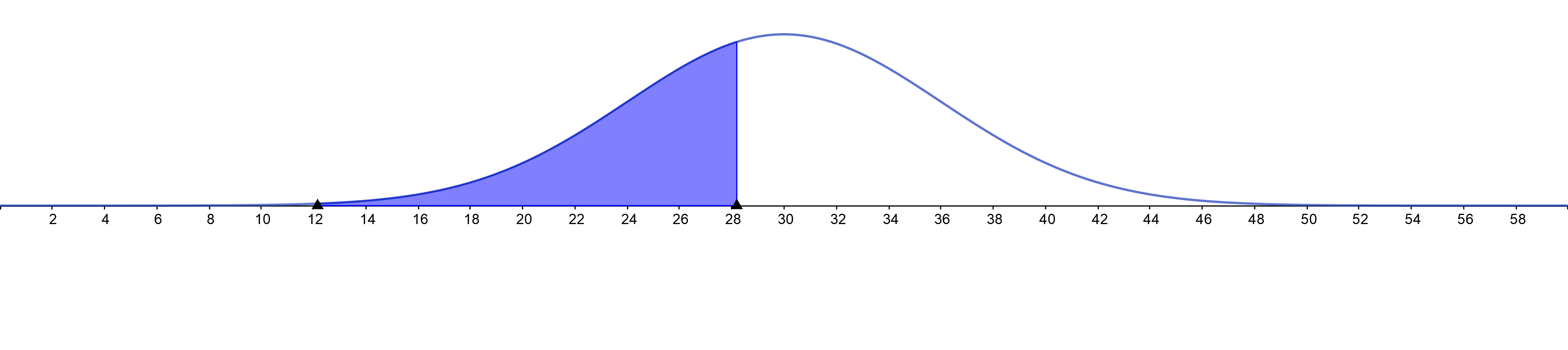
text{Rachna was in the $39^{text{th}}$ percentile.}
$$

text{Rakhi was in the $38^{text{th}}$ percentile.}
$$
text{$98^{text{th}}$ percentile. About $2%$ of dancers scored higher than Isabella and Tony.}
$$
2%
$$
The formula for the sample standard deviation is
$$
boxed{sigma=sqrt{frac{1}{N}sum_{i=1}^{N}left(x_i-x_0right)^2}}
$$
$text{where $x_1, x_2,…, x_N$ are the observed values of the sample items, $x_0$ is the mean value}$
$text{of these observations, and $N$ is the number of observations in the sample.}$
$$
text{These $37$ data points have the mean (average):}
$$
$$
begin{align*}
x_0&=frac{576+605+632+660+671+689+723+774584+606+636+661+671+}{37} \
&+frac{695+738+785+594+613+640+663+675+698+745+595+618+640+}{37} \
&+frac{665+677+703+755+603+630+652+666+678+721+774}{37} \
&=color{#c34632}{667.87}
end{align*}
$$
First, calculate the deviations of each data point from the mean, and square the result of each:
$$
begin{align*}
left(576-667.87right)^2&=left(-91.87right)^2=8440.1 \
left(660-667.87right)^2&=left(-7.87right)^2=61.94 \
left(689-667.87right)^2&=left(21.13right)^2=446.48 \
left(703-667.87right)^2&=left(35.13right)^2=1234.12 \
left(618-667.87right)^2&=left(-49.87right)^2=2487.02 \
left(630-667.87right)^2&=left(-37.87right)^2=1434.14 \
left(721-667.87right)^2&=left(53.13right)^2=2822.8 \
end{align*}
$$
$$
begin{align*}
sigma^2&=frac{8440.1+61.94+446.48+1234.48+2487.02+1434.14+2822.8}{7} \
&=frac{16926.5}{7} \
&=3155.06
end{align*}
$$
and the population standard deviation is equal to the square root of the variance:
$$
begin{align*}
sigma&=sqrt{3155.06} \
&=56.17
end{align*}
$$
#### b.
$$
boxed{576, 624, 665, 700.5, 785}
$$
#### c.
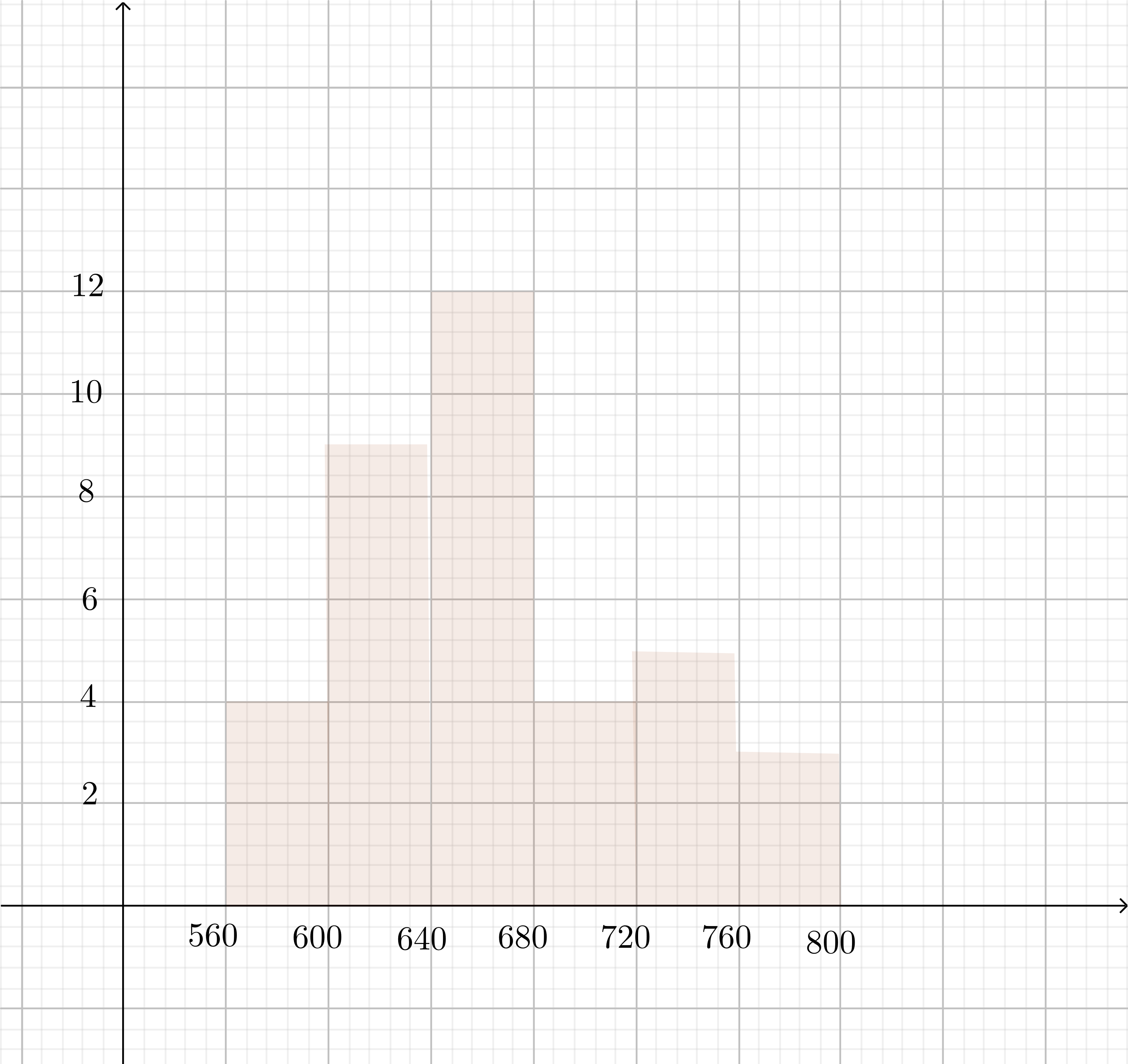
Since the shape is fairly symmetric, well use mean as the measure of center;
$text{the typical number of lunches served is $668$. The shape is single peaked and}$
$text{fairly symmetric with no gaps or clusters, the standard deviation is about $56$ lunches,}$
and there are no apparent outliers.
#### e.
$$
boxed{text{Percent}=frac{4}{37} cdot 100%=10.8%}
$$
#### f.
$$
boxed{text{Percent}=frac{24}{37} cdot 100%=61.5%}
$$
$textbf{e.}$ $10.8%$, $textbf{f.}$ $61.5%$
It is not ethical to use as an experiment because then you would have to spank kids for doing nothing wrong and risk causing lowering their IQs which is not benefitial for the child.
$rightarrow$ Determine the salary after 2 years at system incorporated:
$$begin{aligned}
&= 52,000 + 3,000+3,000\
&= 58,000\
end{aligned}$$
$$begin{aligned}
&= 52,000 + 10 cdot 3,000\
&= 52,000 + 30,000\
&= 82,000\
end{aligned}$$
with a rise of 11 % each year.
$P$ = 36,000 and Rate of intrest = 11%,
$rightarrow$ Determine the salary after 2 years at Functions Unlimited:
$$begin{aligned}
A &= P left(1 + dfrac{r}{100}right)^{n}\
&= 36,000 left(1 + dfrac{11}{100}right)^{2}\
&= 36,000 left(dfrac{100+11}{100}right)^{2}\
&= 36,000 left(dfrac{111}{100}right)^{2}\
&= 36,000 cdot (1.11)^{2}\
&boxed {44,355.6}\
end{aligned}$$
$$begin{aligned}
A &= P left(1 + dfrac{r}{100}right)^{n}\
&= 36,000 left(1 + dfrac{11}{100}right)^{10}\
&= 36,000 left(dfrac{100+11}{100}right)^{10}\
&= 36,000 left(dfrac{111}{100}right)^{10}\
&= 36,000 cdot (1.11)^{10}\
&boxed {102219.16}\
end{aligned}$$
$$begin{aligned}
text{Average rate of change} &=dfrac{text{Change of output}}{text {change of input}}\\
&= dfrac{58,000-52,000}{2-0}\\
&= dfrac{6,000}{2}\\
&boxed {3,000}\
end{aligned}$$
$$begin{aligned}
text{Average rate of change} &=dfrac{text{Change of output}}{text {change of input}}\\
&= dfrac{82,000-52,000}{10-0}\\
&= dfrac{30,000}{10}\\
&boxed {3,000}\
end{aligned}$$
$$begin{aligned}
text{Average rate of change} &=dfrac{text{Change of output}}{text {change of input}}\\
&= dfrac{44,355.6 – 36,000}{2-0}\\
&= dfrac{8,355.6}{2}\\
&boxed {4,177.8}\
end{aligned}$$
$$begin{aligned}
text{Average rate of change} &=dfrac{text{Change of output}}{text {change of input}}\\
&= dfrac{102219.16 – 36,000}{2-0}\\
&= dfrac{66,219.16}{2}\\
&boxed {6,621.92}\
end{aligned}$$
$$begin{aligned}
text {y}< left(dfrac{1}{3}right)^x+5\\
text {x + 2y} geq 6\\
end{aligned}$$
$$begin{aligned}
text {y} &= left(dfrac{1}{3}right)^x+5rightarrow(1)\\
&text {x + 2y} geq 6\\
text {2y} &= – text {x} + 6\
text {y} &= – dfrac{1}{2}text {x} + 3 rightarrow (2)\
end{aligned}$$

For equation (1),
$$begin{aligned}
text {y} &= left(dfrac{1}{3}right)^x+5\\
0 &= left(dfrac{1}{3}right)^0+5\\
text {So, 0 < 5}\
end{aligned}$$
This is true. So, the solution contains the point $(0,0)$. Shade lower half of the line.
$$begin{aligned}
text {y} &geq – dfrac{1}{2}text {x} + 3\\
0 &geq left(dfrac{1}{2}right)cdot (0)+3\\
text {So, } 0 geq 3\
end{aligned}$$
This is False. So, the solution does not contain the point $(0,0)$. Shade upper half of the line.
Since inequality is;
$<$ is a strict one, the borderline is dashed.
$geq$, not a strict one, the borderline is solid.

$$begin{aligned}
text {y}leq |x+3|-2\\
text {y} > -(x-1)^{2}+5\\
end{aligned}$$
$$begin{aligned}
text {y}&=|x+3|-2rightarrow(1)\\
text {y} &= -(x-1)^{2}+5rightarrow(2)\\
end{aligned}$$

For equation (1),
$$begin{aligned}
text {y} &leq |x+3|-2\\
text {0} &leq |0+3|-2\
text{So, } 0 leq 1
end{aligned}$$
This is true. So, the solution contains the point $(0,0)$. Shade lower half of the line.
$$begin{aligned}
text {y} > -(x-1)^{2}+5\\
text {0}> -(0-1)^{2}+5\\
text {0} > -((0)^{2} -2(0)+1) +5\\
text {0} > -1 +5\\
text {So, } 0 > 4\
end{aligned}$$
This is False. So, the solution does not contain the point $(0,0)$. Shade upper half of the line.
Since inequality is;
$<$ is a strict one, the borderline is dashed.
$geq$, not a strict one, the borderline is solid

.
Passing point $rightarrow (-5, -12)$.
equation of line , $y = -dfrac{5}{3}x + 8$
$$begin{aligned}
3y&= -5x + 24\
5x+3y-24&=0\
end{aligned}$$
$$begin{aligned}
d&= dfrac{|Ax+By+C|}{sqrt{A^2+B^2}}\
end{aligned}$$
Substituting the values,
$$begin{aligned}
d&=dfrac{5times (-5) + 3 times (-12) – 24}{sqrt{5^2 + 3^2}}\\
d&= dfrac{|-25-36-24|}{sqrt{25+9}}\\
d&= dfrac{|-85|}{sqrt{34}}\\
d&=dfrac{85}{sqrt{34}}\\
&boxed{d=14.57text{ units}}\
end{aligned}$$
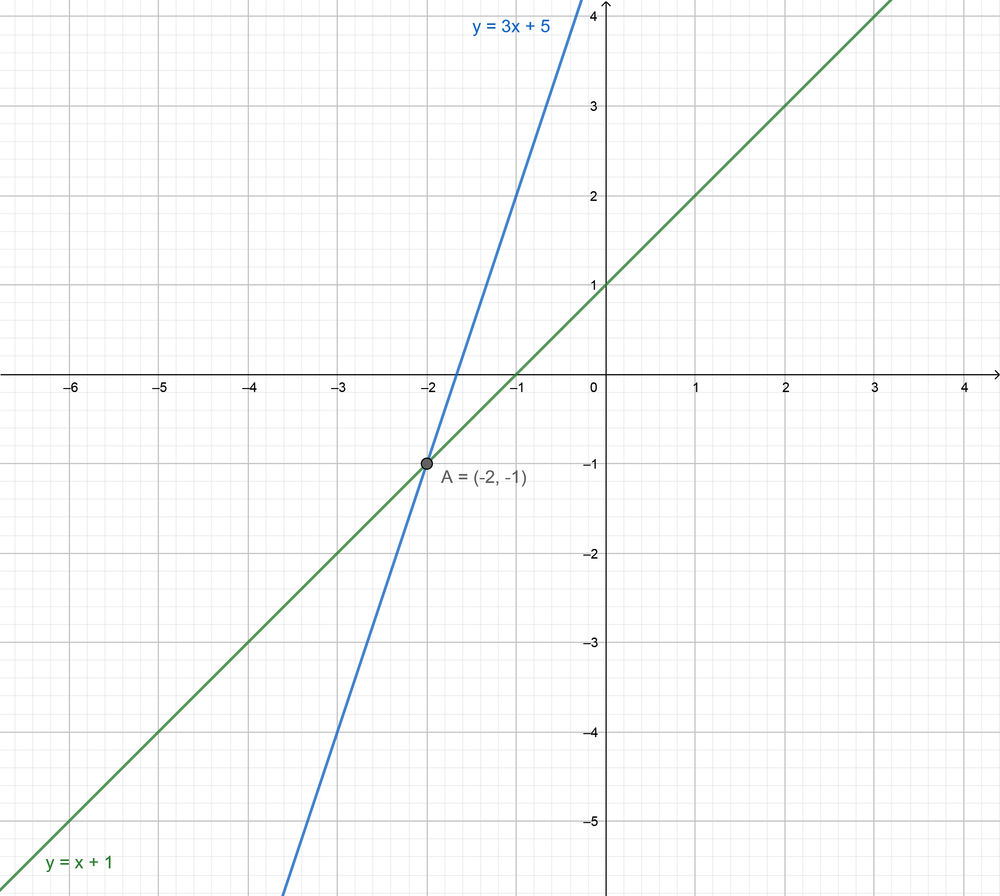
$f(x)=x+1$
$g(x)=3x+5$
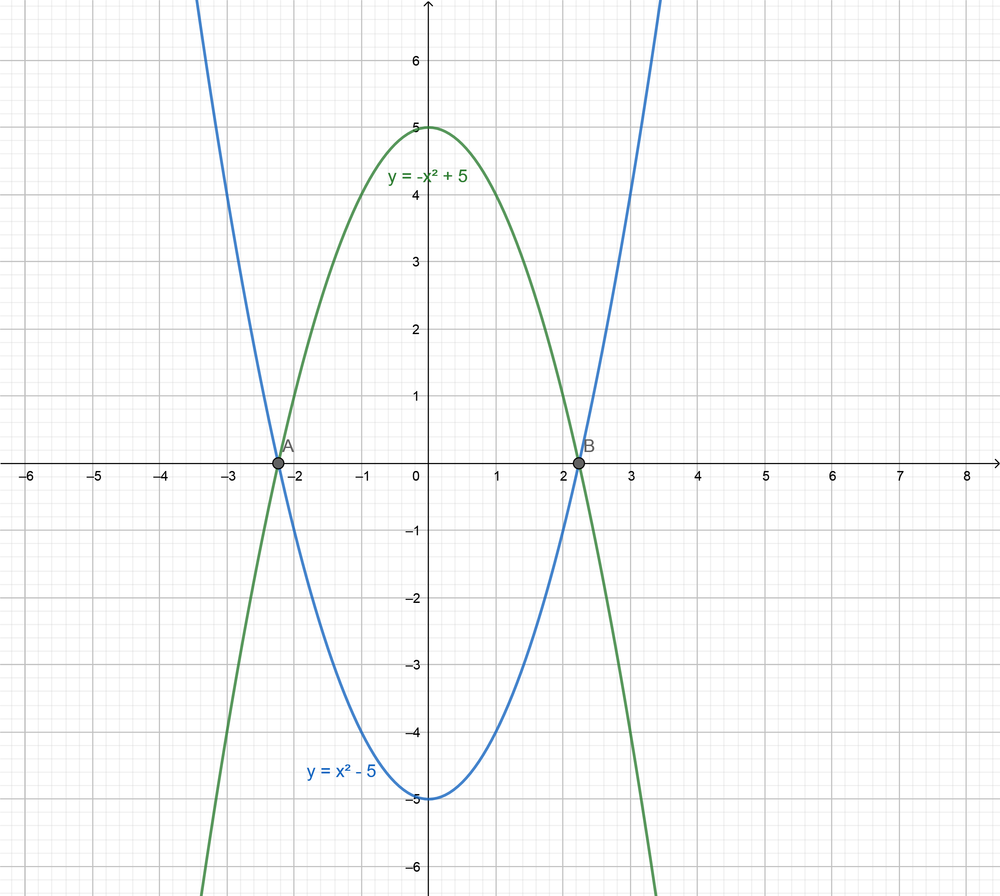
$f(x)=x^2-5$
$g(x)=-x^2+5$
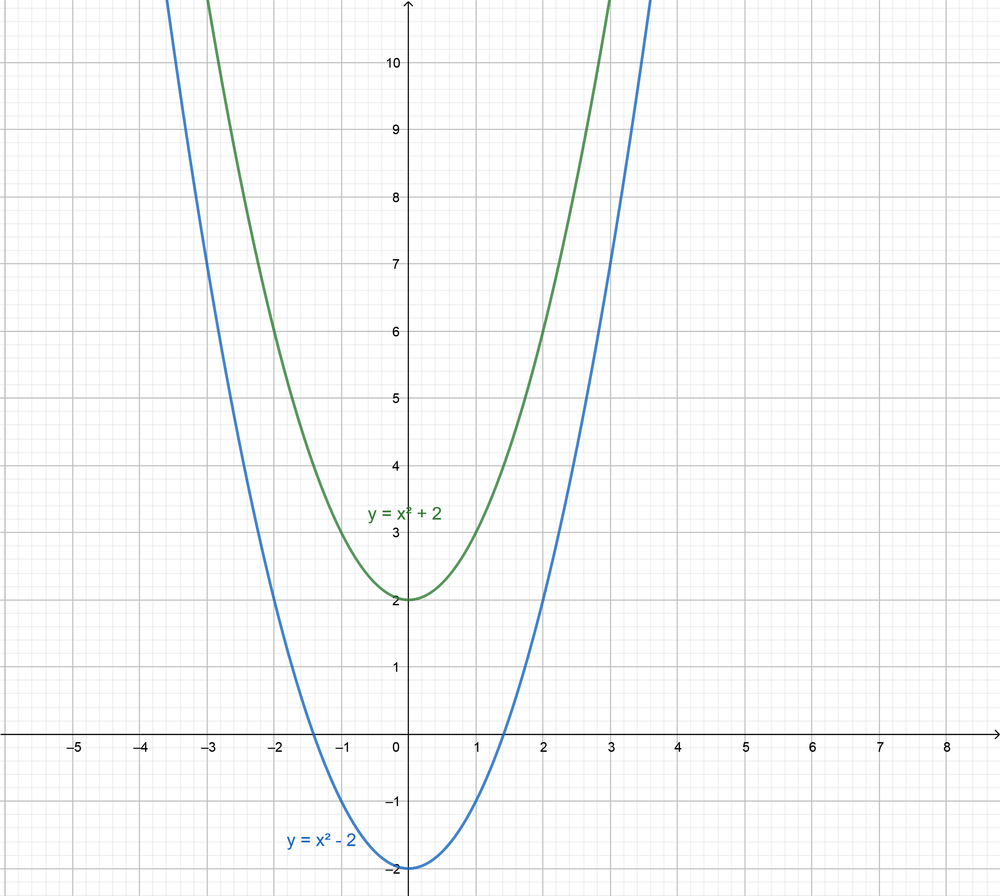
$f(x)=x^2+2$
$g(x)=x^2-2$
$f(x)=x+1$ $g(x)=3x+5$
b- Two equations intersect at two point
$f(x)=x^2-5$ $g(x)=-x^2+5$
c- Two equations with no intersection
$f(x)=x^2+2$ $g(x)=x^2-2$
5log(m)=log(50)
$$
log(m)=dfrac{log(50)}{5}
$$
m=10^{dfrac{log(50)}{5}}=2.187
$$
A tree brunch has the shape of along cone

The cross-section through the cone, perpendicular on its height, is a circle

The trunk has a cardioid as a cross-section. Its shape is

1. We make the 3 cross-sections.
2. The upper and the lower cross-sections are circle rings, while the middle cross-section is a circle.








The agenda book is rectangular but when he spins it, It doesn’t see anything rectangular anymore.
(a.) Let $x$ be the length of the long side and $y$ be the short side.
Rotating a rectangle around the long side leads to the cylinder of radius $y$ and height $x$.



Rotating a rectangle that is attached to the axis of evolution leads to the cylinder.

Rotating a rectangle separated to the axis of evolution leads to a cylinder from which a middle cylinder is taken out.


Rotating a rectangle attached to the axis of evolution leads to a cylinder.

Rotating a line segment leads to the exterior surface of a cylinder.
1. The artist started with the shape of a circle:
2. An ellipse would be another idea to start with.



1. Prepare your Learning Log.
2. Open a new page with title “Cross-Sections and Solids of Revolution” .
3. Explain how cross-sections, solids of revolution, and 3-D printers are related.
4. Explain how knowing about cross-sections help you understand how a 3-D printer works.
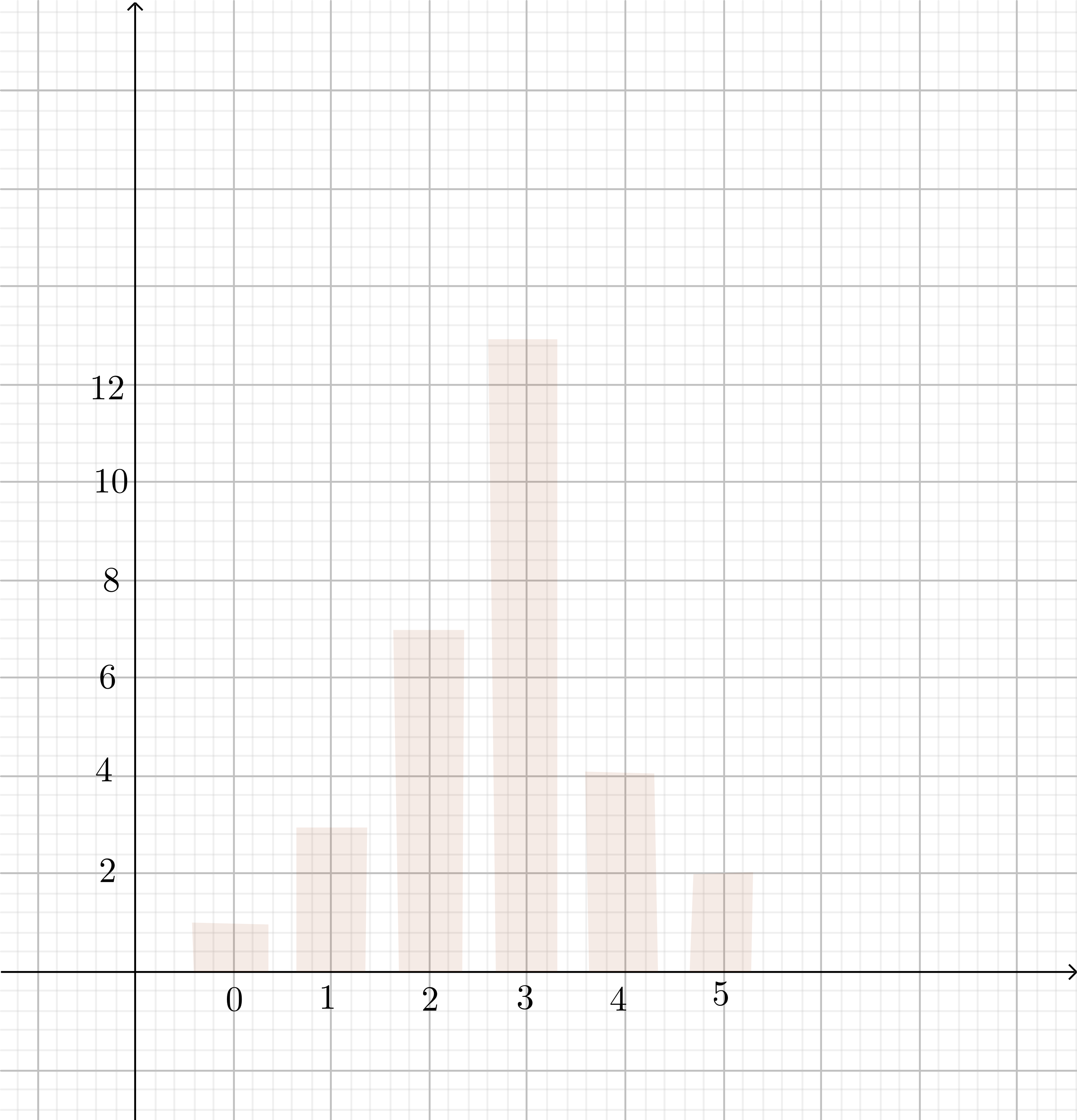
The formula for the sample standard deviation is
$$
boxed{sigma=sqrt{frac{1}{N}sum_{i=1}^{N}left(x_i-x_0right)^2}}
$$
$text{where $x_1, x_2,…, x_N$ are the observed values of the sample items, $x_0$ is the mean value}$
$text{of these observations, and $N$ is the number of observations in the sample.}$
$$
text{These $30$ data points have the mean (average):}
$$
$$
begin{align*}
x_0&=frac{2+4+3+3+4+2+1+3+3+4+3+2+2+3+1+2+3+3+3+0+2+}{30} \
&+frac{3+2+5+5+3+3+3+4+1}{30} \
&=color{#c34632}{2.7333}
end{align*}
$$
First, calculate the deviations of each data point from the mean, and square the result of each:
$$
begin{align*}
left(2-2.7333right)^2&=left(-0.7333right)^2=0.54 \
left(4-2.7333right)^2&=left(1.2667right)^2=1.6 \
left(3-2.7333right)^2&=left(0.2667right)^2=0.07 \
left(0-2.7333right)^2&=left(-2.7333right)^2=7.47 \
left(5-2.7333right)^2&=left(2.2667right)^2=5.14 \
left(1-2.7333right)^2&=left(-1.7333right)^2=3 \
end{align*}
$$
The variance is the mean of these values:
$$
begin{align*}
sigma^2&=frac{7.47+3 cdot 3+7 cdot 0.54+13 cdot 0.07+4 cdot 1.6+2 cdot 5.14}{30} \
&=frac{39.18}{30} \
&=1.306
end{align*}
$$
and the population standard deviation is equal to the square root of the variance:
$$
begin{align*}
sigma&=sqrt{1.306} \
&=1.1427
end{align*}
$$
$$
text{See graph. $color{#c34632}{11%}$}
$$
#### c.
Increase in saving per day $rightarrow$ $3.0
The above condition can be mathematically expressed in the form of series as:
100 + 103 + 106 + ………..
$100$ $rightarrow$ $a_{1}$
$103$ $rightarrow$ $a_{2}$
Moreover, we can say that the series concluded in Ella saving forming an arithmetic progression.
$$a_{2}-a_{1} = a_{3}-a_{2}$$
We know that in arithmetic progression series.
$$a_{n} = a_{1}+ (n-1)d$$
$a_{n}$ = Ella $n^{th}$ term savings on $n^{th}$ day.
$a_{1}$ = 100
$d$ = 103 – 100 = 3
Now, put all the values in the given formula.
$$begin{aligned}
a_{n} &= 100+ (n-1)3\
a_{n} &= 100+ 3n – 3\
&boxed {a_{n} = 3n + 97}\
end{aligned}$$
He plans to double his money each day $rightarrow$ $2.0
The above condition can be mathematically expressed in the form of series as:
2 + 4 + 6 + ………..
$1$ $rightarrow$ $a_{1}$
$2$ $rightarrow$ $r$
Moreover, we can say that the series concluded in Fitz’s saving forming a geometric progression.
$$dfrac {a_{2}}{a_{1}} = dfrac {a_{3}}{a_{2}}$$
We know that in geometric progression series.
$$a_{n} = a cdot r^{n-1}$$
$a_{n}$ = Fitz’s $n^{th}$ term savings on $n^{th}$ day.
$a_{1}$ = 1
$r$ = $dfrac {4}{2}$ = 2
Now, put all the values in the given formula.
$$begin{aligned}
a_{n} &= 1 cdot 2^{n-1}\\
&boxed {a_{n} = 2^{n-1}}\
end{aligned}$$

$$begin{aligned}
3n + 97 &= 2^{n-1}\
end{aligned}$$
Let put $n = 5$ in the above form.
$$begin{aligned}
3 cdot 5 + 97 &= 2 ^{5-1}\
15 + 97 &= 2 ^{4}\
112 &= 32
end{aligned}$$
$$text {Ella > Fitz’s}$$
Let put $n = 8$ in the above form.
$$begin{aligned}
3 cdot 8 + 97 &= 2 ^{8-1}\
24 + 97 &= 2 ^{7}\
121 &= 128
end{aligned}$$
$$text {Ella < Fitz's}$$
$text {Ella > Fitz’s}$ and
After the $8^{th}$ day, $text {Ella < Fitz's}$.
It means that they will never have the same amount of money.
$sqrt{-49}$
$$begin{aligned}
&= sqrt{49times (-1)}\
&= sqrt{49i^2} rightarrow(i^2 = -1)\
&boxed{= 0 + 7i}
end{aligned}$$
$sqrt{-2}$
$$begin{aligned}
&= sqrt{2times (-1)}\
&= sqrt{2i^2} rightarrow(i^2 = -1)\
&boxed{= 0 + sqrt{2}i}
end{aligned}$$
$(4i^2)$
$$begin{aligned}
&= 4^2cdot i^2\
&= -16 rightarrow(i^2= -1)\
&boxed{= -16 + 0i}\
end{aligned}$$
$(3i)^3$
$$begin{aligned}
&= 3^3cdot i^3\
&= 27 (i^2 cdot i )\
&= 27(-i) rightarrow(i^2= -1)\
&= -27i \
&boxed{= 0-27i}\
end{aligned}$$
Given,
$$begin{aligned}
6&= acdot b^orightarrow(1)\
24&= acdot b^2rightarrow(2)\
end{aligned}$$
Thus, equation (1) simplifies to,
$$begin{aligned}
6&= a(1)\
&boxed{6=a}rightarrow(3)\
end{aligned}$$
$$begin{aligned}
24&= (6)cdot b^2\
dfrac{24}{6}&= b^2\
4&= b^2\
end{aligned}$$
Taking square root both sides.
$$begin{aligned}
&boxed{pm 2= b}\
end{aligned}$$
Thus, $a = 6$ and $b = pm 2$.
Given equation,
$$begin{aligned}
32&= acdot b^2rightarrow(1)\
128 &= acdot b^3rightarrow(2)\
end{aligned}$$
$$begin{aligned}
dfrac{32}{128}&= dfrac{a cdot b^2}{acdot b^3}\\
dfrac{1}{4}&= dfrac{1}{b}\\
&boxed{b=4}rightarrow(3)\
end{aligned}$$
$$begin{aligned}
32&= a cdot (4)^2\\
32&= a cdot 16 \\
&boxed{dfrac{32}{16}= a}\\
end{aligned}$$
Thus, $a = 2$ and $b = 4$.
$$begin{aligned}
5^x&= 5^-3
end{aligned}$$
$$begin{aligned}
&boxed{x= -3}\
end{aligned}$$
$$begin{aligned}
6^x&= 216\
end{aligned}$$
$$begin{aligned}
6^x&= (6)^3\
end{aligned}$$
Comparing base on the both sides,
$$begin{aligned}
&boxed{x= 3}
end{aligned}$$
$y = mx + b$ for $m$
Subtracting $b$ on both sides
$$begin{aligned}
y-b &= mx + b -b\
y-b &= mx\\
text {Divide throughout by }x\\
dfrac {y – b}{x} &= dfrac {mx}{x}\\
&boxed {m =dfrac {y – b}{x}}\
end{aligned}$$
$C = 2pi r$ for $r$
Divide the equation by $2 pi$ on both sides
$$begin{aligned}
C &= 2pi r \
dfrac {C}{2 pi} &= dfrac{2pi r}{2 pi}\\
&boxed {r =dfrac {C}{2 pi}}\
end{aligned}$$
$V$ = $LHW$ for $L$
Divide the equation by $HW$ on both sides
$$begin{aligned}
dfrac {V}{HW} &= dfrac {LHW}{HW}\\
&boxed {L =dfrac {V}{HW}}\
end{aligned}$$
$dfrac {1}{y}-3x = 7$ for $y$
Adding $3x$ on both sides
$$begin{aligned}
dfrac {1}{y}-3x +3x &= 7 + 3x\\
dfrac {1}{y}&= 7 + 3x\\
text {Taking Reciprocals},\\
&boxed {y = dfrac {1}{7+3x}}\
end{aligned}$$
$(b.)$ $r = dfrac {C}{2 pi}$
$(c.)$ $L = dfrac {V}{HW}$
$(d.)$ $y = dfrac {1}{7+3x}$
**A rectangular prism** can be used to build a house, a TV-set, a fridge, a book, a computer, a train.
**A sphere** can be used to build a planet, a ball, a globe, a balloon.
**A square based pyramid** can be used to build a house’s roof, an Egyptian pyramid.
$$begin{aligned}
60 text{ feet} &= 60 times12\
&= 720 text { inches}\
40 text{ feet} &= 40 times12\
&= 480 text { inches}\
end{aligned}$$
Let’s assume that the base of the real prism in Mount Rushmore is 40 feet.
Now, determine the volume of concrete in cubic inches to create the model.
V &= L cdot H cdot W\
V &= 480 cdot 480 cdot 720\
V &= 165888000 text { cubic inches}\
end{aligned}$$
$$begin{aligned}
&=dfrac{0.8}{100}\\
&= 0.008\
end{aligned}$$
The amount of concrete in cubic inches to create the model.
$$begin{aligned}
&= 0.008 cdot V\
&= 0.008 cdot 165888000\
&boxed{= 13,27,104 text { cubic inches}}\
end{aligned}$$
$$begin{aligned}
1 text { yard} &= 36 text{ inches}\
&= dfrac {13,27,104 text{in}^{3}}{36^{3}}\\
&= dfrac {13,27,104 text{in}^{3}}{46656}\\
&approx 28.44 text { cubic yards}\
end{aligned}$$
$(b.)$ Lower bound
Let the exponential function $color{#c34632} text{$,,y=acdot b^x$}$.
$$
a)
$$
$-$If the graph of this function passes through the point $color{#c34632} text{$,,(2,9),,$}$ it’s coordinates satisfy this equation so we have:
$y=acdot b^xqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $(x,y)=(2,9)$]}$
$Rightarrow 9=acdot b^2qquadqquadqquadqquadqquad$ $color{#c34632} text{[solve for $a$]}$
$Rightarrow color{#4257b2} text{$a=dfrac{9}{b^2}quad$ [1]}$
$-$If the graph of this function passes through the point $color{#c34632} text{$,,(4,324),,$}$ it’s coordinates satisfy this equation so we have:
$y=acdot b^xqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $(x,y)=(4,324)$]}$
$Rightarrow 324=acdot b^4qquadqquadqquadqquadqquad$
$Rightarrow color{#4257b2} text{$ab^4=324quad$ [2]}$
$acdot b^4=324qquadqquadqquadqquadqquadqquad$ $color{#c34632} text{$bigg[$set $a=dfrac{9}{b^2}bigg]$}$
$Rightarrow dfrac{9}{b^2}cdot b^4=324$
$Rightarrow 9b^2=324qquadqquadqquadqquadqquad$ $color{#c34632} text{[divide both sides by $9$]}$
$Rightarrow b^2=36qquadqquadqquadqquadqquad$
$color{#c34632} text{[note that $,,btext{textgreater} 0,,$ by definition of exponential functions]}$
$Rightarrow color{#4257b2} text{$b=6$}$
$-$In the equation $color{#c34632} text{[1]}$ set $color{#c34632} text{$,,b=6,,$}$ and solve for $color{#c34632} text{$,,”a”,,$}$ as shown:
$a=dfrac{9}{b^2}qquadqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $b=6$]}$
$Rightarrow a=dfrac{9}{6^2}$
$Rightarrow a=dfrac{9}{36}$
$Rightarrow color{#4257b2} text{$a=dfrac{1}{4}$}$
$-$Finally for the values of the parameters $color{#c34632} text{$,,”a”,,$}$ and $color{#c34632} text{$,,”b”,,$}$ we found the indicated equation will be:
$y=acdot b^xqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{$bigg[$set $a=dfrac{1}{4}$ , $b=6bigg]$}$
$$
Rightarrow color{#4257b2} text{$y=dfrac{1}{4}cdot 6^x$}
$$
b)
$$
$-$If the graph of this function passes through the point $color{#c34632} text{$,,(-1,40),,$}$ it’s coordinates satisfy this equation so we have:
$y=acdot b^xqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $(x,y)=(-1,40)$]}$
$Rightarrow 40=acdot b^{-1}qquadqquadqquadqquadqquad$ $color{#c34632} text{[solve for $b$]}$
$Rightarrow color{#4257b2} text{$b=dfrac{a}{40}quad$ [1]}$
$-$If the graph of this function passes through the point $color{#c34632} text{$,,(0,12),,$}$ it’s coordinates satisfy this equation so we have:
$y=acdot b^xqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $(x,y)=(0,12)$]}$
$Rightarrow 12=acdot b^0qquadqquadqquadqquadqquad$
$Rightarrow color{#4257b2} text{$a=12quad$ [2]}$
$b=dfrac{a}{40}qquadqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $a=12$]}$
$Rightarrow b=dfrac{12}{40}$
$Rightarrow b=dfrac{3}{10}$
$Rightarrow color{#4257b2} text{$b=0.3$}$
$-$Finally for the values of the parameters $color{#c34632} text{$,,”a”,,$}$ and $color{#c34632} text{$,,”b”,,$}$ we found the indicated equation will be:
$y=acdot b^xqquadqquadqquadqquadqquadqquad$ $color{#c34632} text{[set $a=12$ , $b=0.3$]}$
$$
Rightarrow color{#4257b2} text{$y=12cdot 0.3^x$}
$$

$$begin{aligned}
AC cong GH\
AB cong HI\
BC cong GI\
end{aligned}$$
So, according to $SSS$ congurence, we have,
$$begin{aligned}
triangle {ABC} cong triangle {HIG}\
end{aligned}$$
$$begin{aligned}
AC cong JK\
angle{A} cong angle{K}\
AB cong KL\
end{aligned}$$
So, according to $SAS$ congurence, we have,
$$begin{aligned}
triangle {ABC} cong triangle {KLJ}\
end{aligned}$$
$$begin{aligned}
angle{E} cong angle{M}\
EF cong MN\
angle{F} cong angle{N}\
end{aligned}$$
So, according to $ASA$ congurence, we have,
$$begin{aligned}
triangle {DEF} cong triangle {OMN}\
end{aligned}$$
$$begin{aligned}
9m^2 – 4 \
end{aligned}$$
Re-writing the above equation,
$$begin{aligned}
&= (3m)^2 – (2)^2rightarrow(1)
end{aligned}$$
Using,
$$begin{aligned}
(a)^2 – (b)^2 &= (a+b)(a-b\
end{aligned}$$
The equation (1) equivalents to,
$$begin{aligned}
&= (3m+2)(3m-2)\
end{aligned}$$
$$begin{aligned}
5p^2+8p+3 rightarrow(1)\
end{aligned}$$
Factorizing equation (1),
$$begin{aligned}
&= 5p^2 + 5p + 3p+ 3\
&= 5p(p+1) + 3(p+1)\
&= (5p+3)(p+1)\
end{aligned}$$
$$begin{aligned}
2n^2-5n + 3rightarrow(1)\
end{aligned}$$
Factorizing equation (1),
$$begin{aligned}
&=2n^2 – 2n – 3n+ 3\
&= 2n(n-1)-3(n-1)\
&= (2n-3) (n-1)\
end{aligned}$$
$$begin{aligned}
2x^2+18x+28rightarrow(1)\
end{aligned}$$
Factorizing equation (1),
$$begin{aligned}
&=2x^2+ 14x + 4x+ 28\
&= 2x(x+7)+ 4(x+7)\
&= (2x+4) (x+7)\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
boxed {sqrt[5]{x} = (x)^dfrac{1}{5}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
boxed {dfrac {1}{x^{3}} = (x)^{-3}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
boxed {(x)^dfrac {2}{3} = sqrt[3]{x}^{2}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
boxed {dfrac {1}{sqrt{x}} = (x)^-{dfrac {1}{2}}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
boxed {x^{-1}y^{-8} = dfrac{1}{xy^{8}}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
(m^{2})^ – dfrac{3}{2} &=(m)^{2left(dfrac {-3}{2}right)}\\
&= m^{-3}\\
&boxed {(m^{2})^ – dfrac{3}{2} = dfrac{1}{m^{3}}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
(x^{3}y^{6})^dfrac{1}{2} &= x^{3left(dfrac{1}{2}right)}y^{6left(dfrac{1}{2}right)} \\
&= x^{dfrac{3}{2}} y^{3} \\
boxed {(x^{3}y^{6})^dfrac{1}{2} = sqrt[x]{x} y^{3}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
(9x^{3}y^{6})^{-2} &= dfrac{1}{(9x^{3}y^{6})^{2}}\\
boxed {(9x^{3}y^{6})^{-2} = dfrac{1}{81x^{6}y^{12}}}\
end{aligned}$$
Write an expression in an equivalent form:
$$begin{aligned}
&= dfrac{sqrt{4x^{2}}y}{z^{3}cdot sqrt[3]{z}}\\
&boxed { = dfrac{2sqrt{x}|y|y}{z^{3}cdot sqrt[3]{z}}}\
end{aligned}$$
$$begin{aligned}
2x^{2} &= 8 ^{2x-3}\
2x^{2} &= 2 ^{3(2x-3)}\
x^{2} &= 3 (2x-3)\
x ^{2} &= 6x-9\
x^{2}-6x+9 &=0\
(x-3)^{2} &=0\
x- 3 &=0 Rightarrow boxed {x = 3}\
end{aligned}$$
1. Invite your team
2. Study and discuss the Design.
3. Design a packaging system that can be printed on a 3-D printer.
4. Present your results in a report detailing what the packaging system will look like, how strong you expect it to be, the cost to produce the packaging system, and why the design is considered trendy.
5. Demonstrating your knowledge on all aspects of geometric modeling and design will help convince the company that you are the best team for the job.



There are $2$ of $218$ singers. Therefore the percentage is
$$p=dfrac{2}{218}times 100%=0.92%$$
$g(x)=dfrac{6x+8}{2}=3x+4$
$$
h(x)=dfrac{x+11}{3}
$$
$f(5)=5-5=0$
$g(0)=3(0)+4=4$
$h(4)=dfrac{4+11}{3}=dfrac{15}{3}=textcolor{#4257b2}{5}$
$x=textcolor{#c34632}{0}$
$f(0)=0-5=-5$
$g(-5)=3(-5)+4=-11$
$h(-11)=dfrac{-11+11}{3}=dfrac{0}{3}=textcolor{#c34632}{0}$
$x=textcolor{#19804f}{-2}$
$f(-2)=-2-5=-7$
$g(-7)=3(-7)+4=-17$
$h(-17)=dfrac{-17+11}{3}=dfrac{-6}{3}=textcolor{#19804f}{-2}$
h(g(f(x)))=x
$$
$f(c)=c-5$
$g(c-5)=3(c-5)+4=3c-15+4=3c-11$
$$
h(3c-11)=dfrac{3c-11+11}{3}=dfrac{3c}{3}=c
$$
h(g(f(c)))=c
$$
$$
1234x=964198
$$
Divide both sides of the equation by 1234:
$$
x=dfrac{964198}{1234}=dfrac{482,099}{617}
$$
$$
30=10+20=5x
$$
Divide both sides of the equation by 5:
$$
6=x
$$
Determine the discriminant of the given function $f(x)=5x^2-6x+1$:
$$
D=b^2-4ac=(-6)^2-4(5)(1)=36-20=16
$$
Determine the roots using the quadratic formula:
$$
x=dfrac{-bpm sqrt{D}}{2a}=dfrac{6pm sqrt{16}}{2(5)}=dfrac{6pm 4}{10}=1text{ or }-dfrac{1}{5}
$$
$$
x(x-2)(x-1)=x(x^3-3x+2)=0
$$
Zero product property:
$$
x=0text{ or } x-1= 0text{ or } x-2=0
$$
Solve each equation to $x$:
$$
x=0text{ or } x= 1text{ or } x=2
$$
b. $x=6$
c. $x=1,-dfrac{1}{5}$
d. $x=0, 1, 2$
{color{#4257b2}text{a)}}
$$
Solution to this example is given below
$$
begin{align*}
1234x+23456-23456&=987654-23456&&boxed{text{Subtract 23456 from both sides}}\
1234x&=964198&&boxed{text{Simplify}}\
frac{1234x}{1234}&=frac{964198}{1234}&&boxed{text{Divide both sides by } 4}\
x&=frac{482099}{617}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=frac{482099}{617}} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{b)}}
$$
Solution to this example is given below
$$
begin{align*}
frac{10}{x}x+frac{20}{x}x&=5x&&boxed{text{Multiply both sides by }x}\
30&=5x&&boxed{text{Simplify}}\
5x&=30&&boxed{text{Switch sides}}\
frac{5x}{5}&=frac{30}{5}&&boxed{text{Divide both sides by } 5}\
x&=6&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=6} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{c)}}
$$
Solve with the quadratic formula
$$
begin{align*}
x_{1,:2}&=frac{-bpm sqrt{b^2-4ac}}{2a}&&boxed{text{ Use quadratic formula}}\
x_{1,:2}&=frac{-left(-6right)pm sqrt{left(-6right)^2-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Substitute }5 text{ for }a, -6 text{ for } b, text{ and } 1 text{ for } c.} \
end{align*}
$$
First we solve $x_1$
$$
begin{align*}
x_1&=frac{-left(-6right)+sqrt{left(-6right)^2-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Simplify}}\
x_1&=frac{6+sqrt{left(-6right)^2-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Remove parentheses}}\
x_1&=frac{6+sqrt{36-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Evaluate: }(-6)^2=36}\
x_1&=frac{6+sqrt{36-20}}{2cdot :5}&&boxed{text{Multiply the numbers: } 4cdot5cdot1=20}\
x_1&=frac{6+sqrt{36-20}}{10}&&boxed{text{Multiply the numbers: }2cdot5=10}\
x_1&=frac{6+sqrt{16}}{10}&&boxed{text{Subtract the numbers: }36-20=16 }\
x_1&=frac{6+4}{10}&&boxed{text{Simplify}}\
x_1&=frac{10}{10}&&boxed{text{Add the numbers: } 6+4=10}\
x_1&=color{#c34632}{1}&&boxed{text{Simplify}}\
end{align*}
$$
$$
begin{align*}
x_2&=frac{-left(-6right)-sqrt{left(-6right)^2-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Simplify}}\
x_2&=frac{6-sqrt{left(-6right)^2-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Remove parentheses}}\
x_2&=frac{6-sqrt{36-4cdot :5cdot :1}}{2cdot :5}&&boxed{text{Evaluate: }(-6)^2=36}\
x_2&=frac{6-sqrt{36-20}}{2cdot :5}&&boxed{text{Multiply the numbers: } 4cdot5cdot1=20}\
x_2&=frac{6-sqrt{36-20}}{10}&&boxed{text{Multiply the numbers: }2cdot5=10}\
x_2&=frac{6-sqrt{16}}{10}&&boxed{text{Subtract the numbers: }36-20=16 }\
x_2&=frac{6-4}{10}&&boxed{text{Simplify}}\
x_2&=frac{2}{10}&&boxed{text{Add the numbers: } 6-4=2}\
x_2&=color{#c34632}{frac{1}{5}}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x_1=1, x_2=frac{1}{5}} }&&boxed{text{Final solution}}\
end{align*}
$$
{color{#4257b2}text{d)}}
$$
Solution to this example is given below
Solve by factoring
$$
begin{align*}
x^2x-3xx+2x&=0&&boxed{text{Apply exponent rule}}\
xleft(x^2-3x+2right)&=0&&boxed{text{Factor out common term }x}\
xleft(x-1right)left(x-2right)&=0&&boxed{text{Simplify}}\
end{align*}
$$
Using the Zero Factor Principle
$$
begin{align*}
x&=color{#c34632}{0}&&boxed{text{Simplify}}\
end{align*}
$$
Using the Zero Factor Principle
$$
begin{align*}
x-1&=0&&boxed{text{Simplify}}\
x-1+1&=0+1&&boxed{text{Add 1 to both sides}}\
x&=color{#c34632}{1}&&boxed{text{Simplify}}\
end{align*}
$$
Using the Zero Factor Principle
$$
begin{align*}
x-2&=0&&boxed{text{Simplify} }\
x-2+2&=0+2&&boxed{text{Add 2 to both sides}}\
x&=color{#c34632}{2}&&boxed{text{Simplify}}\\
&boxed{{color{#c34632}x=0, x=1, x=2} }&&boxed{text{Final solution}}\
end{align*}
$$
color{#4257b2} text{ a) }x=frac{482099}{617}
$$
$$
color{#4257b2} text{ b) } x=6
$$
$$
color{#4257b2} text{ c) }x_1=1, x_2=frac{1}{5}
$$
$$
color{#4257b2} text{ d) }x=0, x=1, x=2
$$
a) $color{#c34632} text{$g(x)=20$}$
$Rightarrow x^2-5=20qquadqquadqquadqquadqquad$ $color{#c34632} text{[add $5$ in both sides]}$
$Rightarrow x^2=25qquadqquadqquadqquadqquadquad$ $color{#c34632} text{[take square roots]}$
$Rightarrow sqrt{x^2}=sqrt{25}$
$Rightarrow |x|=5$
$Rightarrow color{#4257b2} text{$x=pm 5$}$
The values of $color{#c34632} text{$,,”x”,,$}$ for which $color{#c34632} text{$,,g(x)=0,,$}$ are the values $color{#4257b2} text{$,,x=-5,,$}$ and $color{#4257b2} text{$,,x=5$}$.
b) $color{#c34632} text{$g(x)=6$}$
$Rightarrow x^2-5=6qquadqquadqquadqquadqquad$ $color{#c34632} text{[add $5$ in both sides]}$
$Rightarrow x^2=11qquadqquadqquadqquadqquadquad$ $color{#c34632} text{[take square roots]}$
$Rightarrow sqrt{x^2}=sqrt{11}$
$Rightarrow |x|=sqrt{11}$
$Rightarrow color{#4257b2} text{$x=pm sqrt{11}$}$
The values of $color{#c34632} text{$,,”x”,,$}$ for which $color{#c34632} text{$,,g(x)=0,,$}$ are the values $color{#4257b2} text{$,x=-sqrt{11},$}$ and $color{#4257b2} text{$,x=sqrt{11}$}$.
$$y = f(x)$$

$$g(x)=-2f(x)rightarrow(1)$$

$$h(x)= f(x-1)-3rightarrow(1)$$

$$j(x)= f(-x)rightarrow(1)$$


