All Solutions
Page 100: Closure Activity
The vertex of the graph is the point $(14, 20)$
Substituting for the vertex and the point $(0, 0)$ in the general form of the equation $f(x)=a(x-h)^2+k$
$0=a(0-14)^2+20$
$0=196a+20$
$196a=-20$
$a=-dfrac {20}{196}=-dfrac {5}{49}$
The equation is:
$$
f(x)=-dfrac {5}{49}(x-14)^2+20
$$
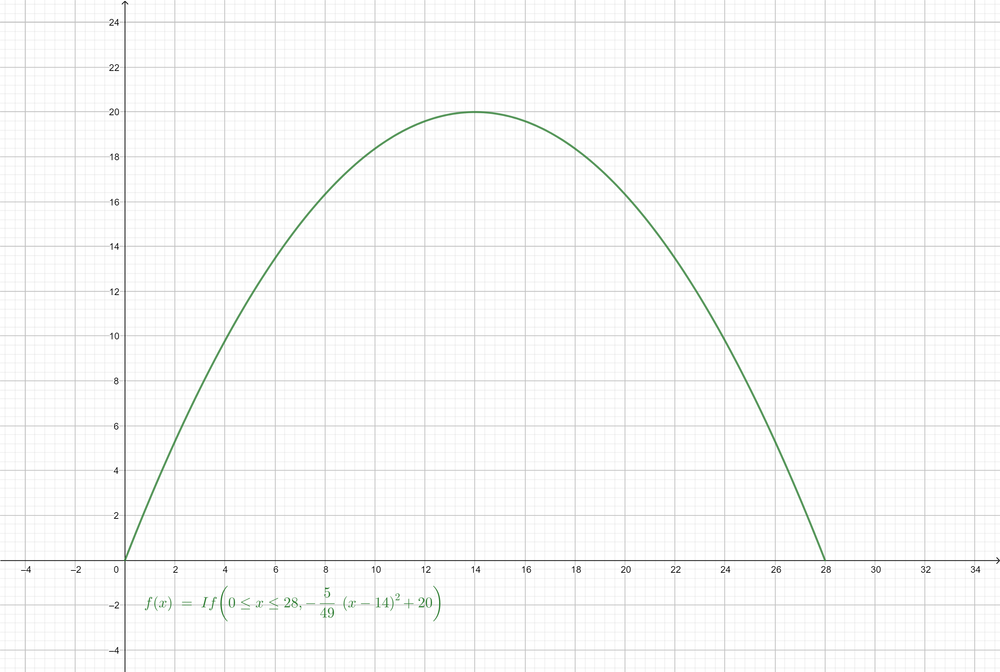
f(x)=-dfrac {5}{49}(x-14)^2+20
$$
The vertex $(h, k)$ is the point $(-4, 3)$ (Given)
The general form of the equation is: $y=(x-h)^2+k$
$$
y=(x+4)^2+3
$$
The equation of the line of symmetry is:
$$
x=-4
$$
To reflect the parabola to open downwards we multiply it by -1. and to compress it we multiply it by $a<1$
The equation that meets both desires:
$y=-a(x+4)^2+3$ (For $0<a<1$)
The line of symmetry does not change.
Moving the parabola 7 units to right: $h’=-4+7=3$
Moving the parabola 8 units down: $k’=3-8=-5$
The new vertex $(h’, k’)$ is $(3, -5)$
For stretching parabola, $a$ must be greater than 1.
The equation of the parabola is:
$$
y=-2(x-3)^2-5
$$
The equation of the line of symmetry is: $x=-4$
b- The equation that meets both desires: $y=-a(x+4)^2+3$ (For $0<a<1$)
c- The equation of the new parabola is: $y=-2(x-3)-5$
1) The $x$ and $y$ intercepts.
1.1) The $x$ intercept.
The $x$ intercept is a place where graph crosses $x$ axis so it is a dot on $x$ axis and therefore by default $y$ variable of that dot is $0$. So we can write an equation for finding the $x$ intercept.
$$
begin{equation}
0=x^2+8x+12
end{equation}
$$
By using the quadratic formula:
$$
x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}
$$
we can solve equation (1).
For equation (1) $a=1$, $b=8$ and $c=12$.
$$
begin{equation}
x_{1,2}=frac{-8pmsqrt{8^2-4cdot1cdot12}}{2cdot1}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-8pmsqrt{64-48}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-8pmsqrt{16}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-8pm4}{2}
end{equation}
$$
Now if we separate the two equations:
$$
begin{equation}
x_1=frac{-8+4}{2}=-2
end{equation}
$$
$$
begin{equation}
x_2=frac{-8-4}{2}=-6
end{equation}
$$
Now we know that the first $x$ intercept is $(-2,0)$ and the second is $(-6,0)$.
1.2) The $y$ intercept.
By same principle as the $x$ intercept, the $y$ intercept is a dot on $y$ axis where graph crosses it, so by default its $x$ variable equals $0$. The equation for finding this $y$ intercept is:
$$
begin{equation}
y=0^2+8cdot0+12
end{equation}
$$
$$
begin{equation}
y=12
end{equation}
$$
Now we know that the $y$ intercept is $(0,12)$.
2) The vertex.
To find the vertex of this parabola we must first derive its equation.
$$
begin{equation}
yprime=(x^2+8x+12)prime
end{equation}
$$
$$
begin{equation}
yprime=(x^2)prime+(8x)prime+12prime
end{equation}
$$
$$
begin{equation}
yprime=2x+8
end{equation}
$$
Vertex is a dot on the parabola where $yprime=0$, so we can write:
$$
begin{equation}
0=2x+8
end{equation}
$$
Therefore:
$$
begin{equation}
x=-4
end{equation}
$$
Now we can return that value of $x$ to our starting equation:
$$
begin{equation}
y=(-4)^2+8cdot(-4)+12
end{equation}
$$
$$
begin{equation}
y=16-32+12=-4
end{equation}
$$
Now that we know that $y=-4$ we can write that the vertex of this parabola is $(-4,-4)$.
3) Graphing form of the equation.
The graphing form of the equation looks like:
$$
begin{equation}
y=a(x-h)^2+k
end{equation}
$$
Where $h$ is $x$ variable of the vertex and $k$ is $y$ variable. $a$ is a number before $x^2$, in this case $1$. So graphing form of this parabola is:
$$
begin{equation}
y=1cdot(x+4)^2-4
end{equation}
$$
Before doing anything we are going to transform this equation in its standard form. We are going to do that by multiplying $(x-4)$ by $(x+2)$.
$$
begin{equation}
y=x^2-2x-8
end{equation}
$$
1) The $x$ and $y$ intercepts.
1.1) The $x$ intercepts.
$y=0$ so we have:
$$
begin{equation}
x^2-2x-8=0
end{equation}
$$
By using the quadratic formula we got:
$$
begin{equation}
x_{1,2}=frac{2pmsqrt{(-2)^2-4cdot1cdot(-8)}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{2pmsqrt{4+32}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{2pm6}{2}
end{equation}
$$
Now if we separate the equations we get $x_1=4$ and $x_2=-2$. Therefore the $x$ intercepts are $(4,0)$ and $(-2,0)$.
1.2) The $y$ intercept.
$x=0$ so we have:
$$
begin{equation}
y=0^2-2cdot0-8
end{equation}
$$
$y=-8$, so the $y$ intercept is $(0,-8)$.
2) The vertex.
$$
yprime=0
$$
$$
begin{equation}
yprime=2x-2
end{equation}
$$
$$
begin{equation}
2x-2=0
end{equation}
$$
$$
begin{equation}
x=1
end{equation}
$$
The $x$ variable of the vertex is $x=1$. Now we can return that in our starting equation to get the $y$.
$$
begin{equation}
y=(1-4)(1+2)=-9
end{equation}
$$
So the vertex of this parabola is $(1,-9)$.
3) The graphing for of the equation.
$a=1$, $h=1$ and $k=-9$.
$$
begin{equation}
y=1cdot(x-1)^2-9
end{equation}
$$
1.1) The $x$ intercepts.
$$
begin{equation}
x^2-6x-9=0
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{6pmsqrt{(-6)^2-4cdot1cdot(-9)}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{6pmsqrt{48}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{6pmsqrt{16}cdotsqrt{3}}{2}
end{equation}
$$
$$
begin{equation}
x_{1,2}=3pm2sqrt{3}
end{equation}
$$
$$
begin{equation}
x_1=3+2sqrt{3}
end{equation}
$$
$$
begin{equation}
x_2=3-2sqrt{3}
end{equation}
$$
So the $x$ intercepts are $(3+2sqrt{3},0)$ and $(3-2sqrt{3},0)$.
1.2) The $y$ intercept.
$$
begin{equation}
y=0^2-6cdot0-9=-9
end{equation}
$$
The $y$ intercept is $(0,-9)$.
2) The vertex.
$$
begin{equation}
yprime=0=2x-6
end{equation}
$$
$$
begin{equation}
x=3
end{equation}
$$
$$
begin{equation}
y=3^2-6cdot3-9
end{equation}
$$
$$
begin{equation}
y=-18
end{equation}
$$
The vertex of this parabola is $(3,-18)$.
3) The graphing form of the equation.
$$
begin{equation}
y=(x-3)^2-18
end{equation}
$$
1.1) The $x$ intercepts.
$$
begin{equation}
x_{1,2}=frac{-5pmsqrt{5^2-4cdot1cdot1}}{2cdot1}
end{equation}
$$
$$
begin{equation}
x_{1,2}=frac{-5pmsqrt{21}}{2}
end{equation}
$$
$$
begin{equation}
x_1=frac{-5+sqrt{21}}{2}
end{equation}
$$
$$
begin{equation}
x_2=frac{-5-sqrt{21}}{2}
end{equation}
$$
The $x$ intersects are $(frac{-5+sqrt{21}}{2},0)$ and $(frac{-5-sqrt{21}}{2},0)$.
1.2) The $y$ intercept.
$$
begin{equation}
y=0^2+5cdot0+1=1
end{equation}
$$
The $y$ intercept is $(0,1)$.
2) The vertex.
$$
begin{equation}
yprime=0=2x+5
end{equation}
$$
$$
begin{equation}
x=-frac{5}{2}
end{equation}
$$
$$
begin{equation}
y=frac{25}{4}-frac{25}{2}+1=-frac{21}{4}
end{equation}
$$
The vertex is $(-frac{5}{2},-frac{21}{4})$.
3) The graphing form of the equation.
$$
begin{equation}
y=(x+frac{5}{2})^2-frac{21}{4}
end{equation}
$$
b) $x$ intercepts: $(4,0)$ and $(-2,0)$, $y$ intercept: $(0,-8)$, vertex: $(1,-9)$, graphing form: $y=(x-1)^2-9$
c) $x$ intercepts: $(3+2sqrt{3},0)$ and $(3-2sqrt{3},0)$, $y$ intercept: $(0,-9)$, vertex: $(3,-18)$, graphing form: $y=(x-3)^2-18$
d) $x$ intercepts: $(frac{-5+sqrt{21}}{2},0)$ and $(frac{-5-sqrt{21}}{2},0)$, $y$ intercept: $(0,1)$, vertex: $(-frac{5}{2},-frac{21}{4})$, graphing form: $y=(x+frac{5}{2})^2-frac{21}{4}$
The general form of the quadratic equation is: $f(x)=a(x-h)^2+k$
Since the shift is 12 units downwards, then $k=-12$. and 3 units left, then $h=-3$
The vertex is: $(-3, -12)$
Since the parabola opens downwards, then $a=-0.25$
The equation is: $f(x)=-0.25(x+3)^2-12$
The general form of the cubic equation is: $y=a(x-h)^3+k$
$a=2$ (Given)
The locator $(h, k)$ is: $(-6, 1)$
The equation is:
$$
y=2(x+6)^3+1
$$
The general form of the hyperbola is: $y=dfrac {1}{x-h}+k$
At the asymptote $x=2 rightarrow h=2$
At the asymptote $y=-6 rightarrow k=-6$
The equation is:
$$
y=dfrac {1}{x-2}-6
$$
b- $y=2(x+6)^3+1$
c- $y=dfrac {1}{x-2}-6$
$$
begin{align*}
f(x)&= x^{2}-3x-10 \
g(x)&=-5x-7 \
end{align*}
$$
In order to find out the intersecting points, we will first $f(x)$ to the graphing form.
$$
begin{align*}
f(x)&= x^{2}-3x-10\
f(x)&= (x^{2}-3x+dfrac{9}{4})-dfrac{9}{4}-10 \
f(x)&=(x-dfrac{3}{2})^{2}-dfrac{49}{4} \
end{align*}
$$
Thus, the vertex of the given function is $left(dfrac{3}{2},-dfrac{49}{4}right)$
So, the graph is given below,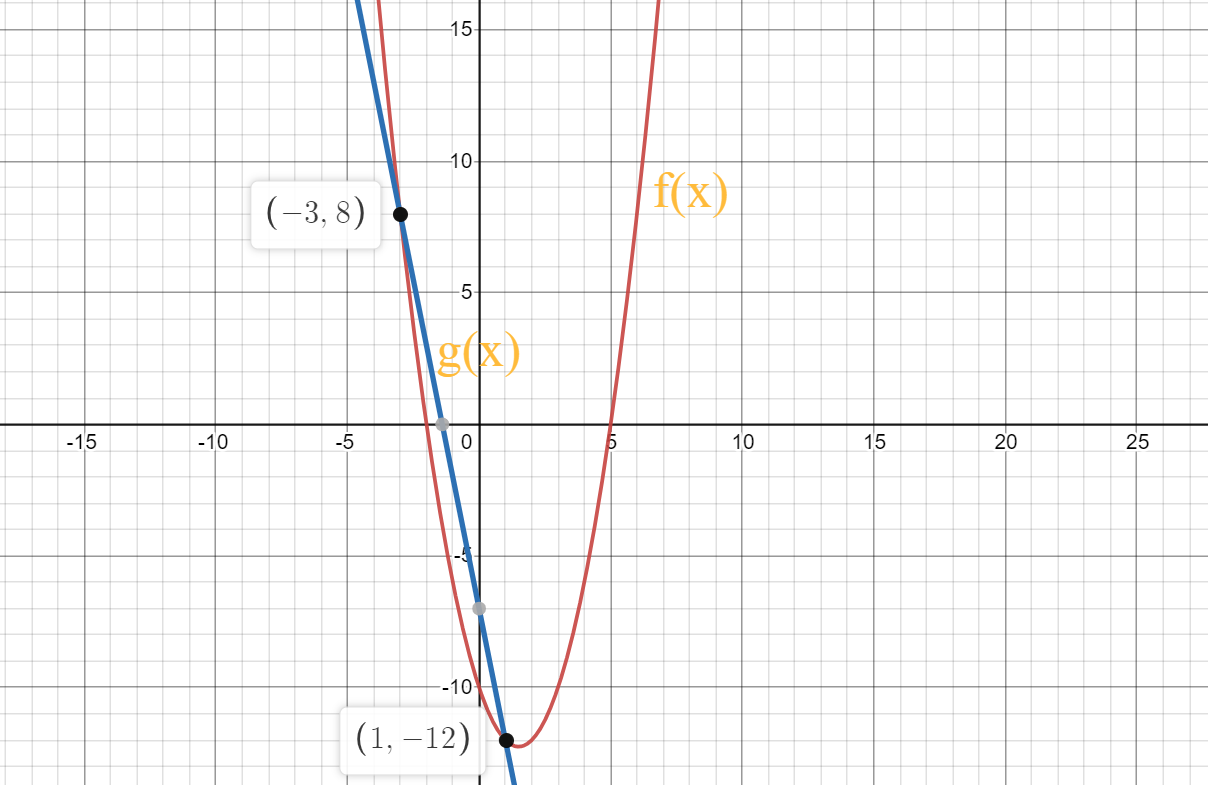
Now, we check the intersecting points,
$$
begin{align*}
(-3)^{2}-3(-3)-10&= -5(-3)-7\
8&=8\
end{align*}
$$
And,
$$
begin{align*}
1^{2}-3(1)-10&=-5(1)-7-12 \
-12&=-12\
end{align*}
$$
Therefore, the obtained intersecting points are correct.
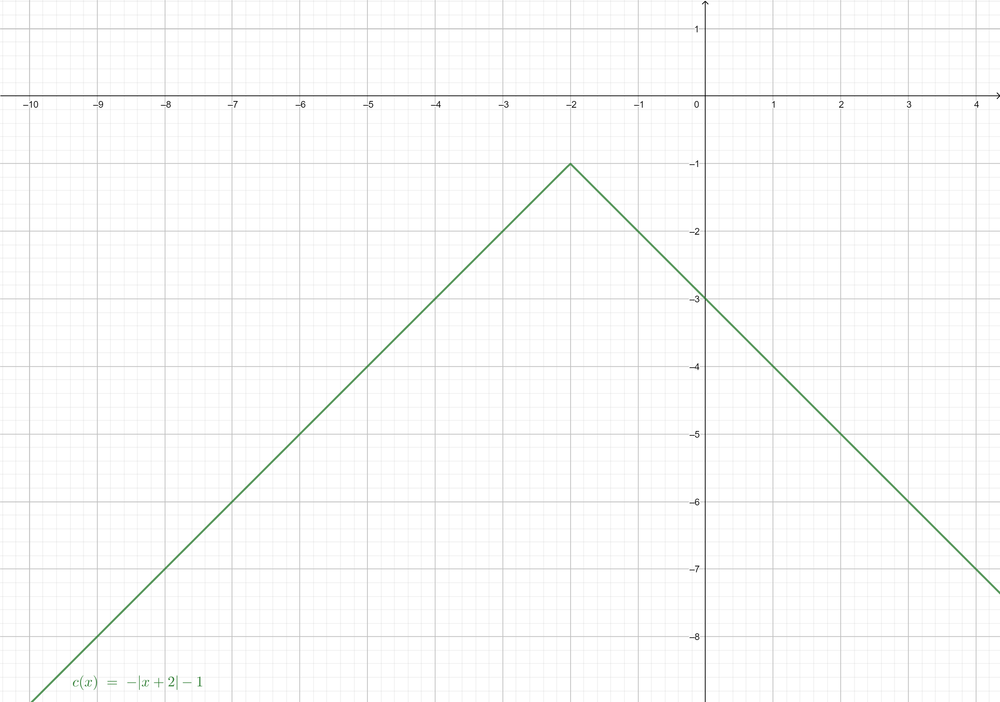
$f(x)=-|x+2|-1$ (Given)
The general of the equation is: $f(x)=a|x-h|+k$
The locator is: $(-2, -1)$
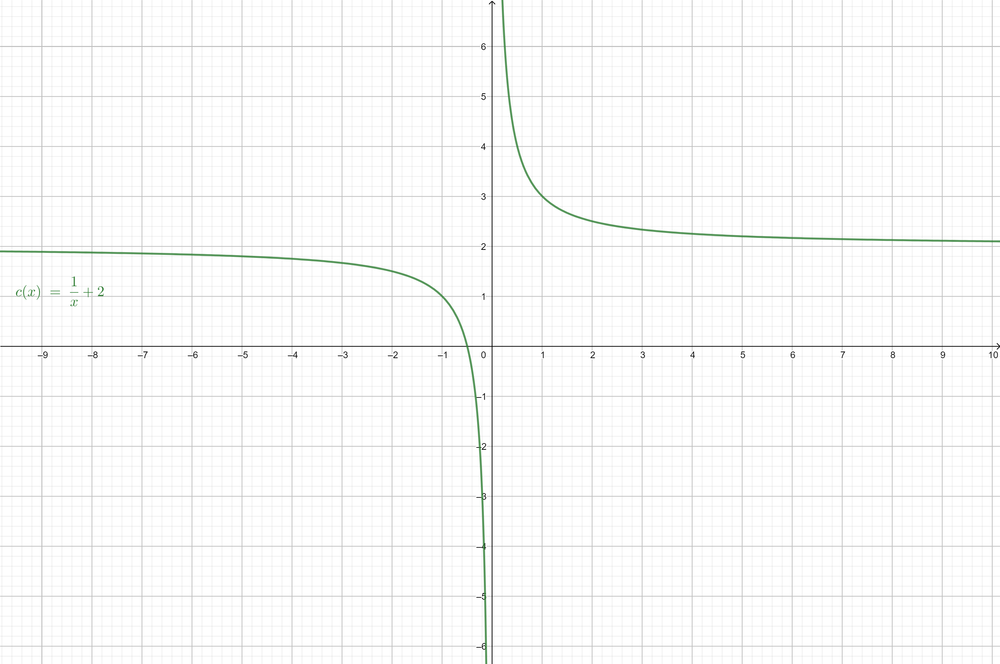
$y=dfrac {1}{x}+2$ (Given)
The general form of the equation is: $y=a left(dfrac {1}{x-h} right)+k$
The locator is the point $(0, 2)$
The asymptote is the y-axis.
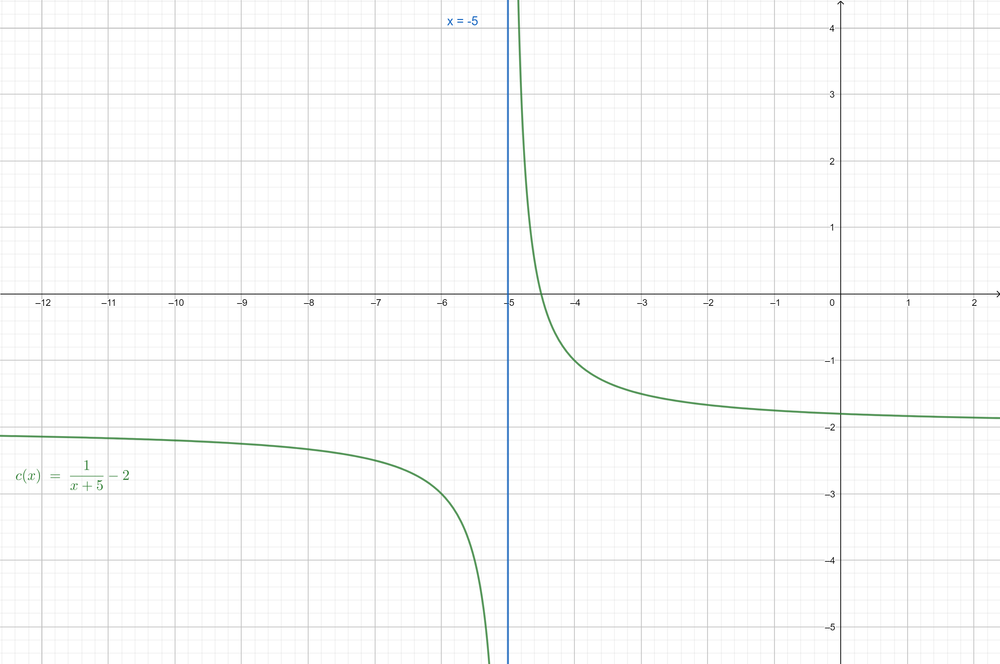
$y=dfrac {1}{x+5}-2$ (Given)
The locator is the point $(-5, -2)$
The equation of the asymptote is: $x=-5$
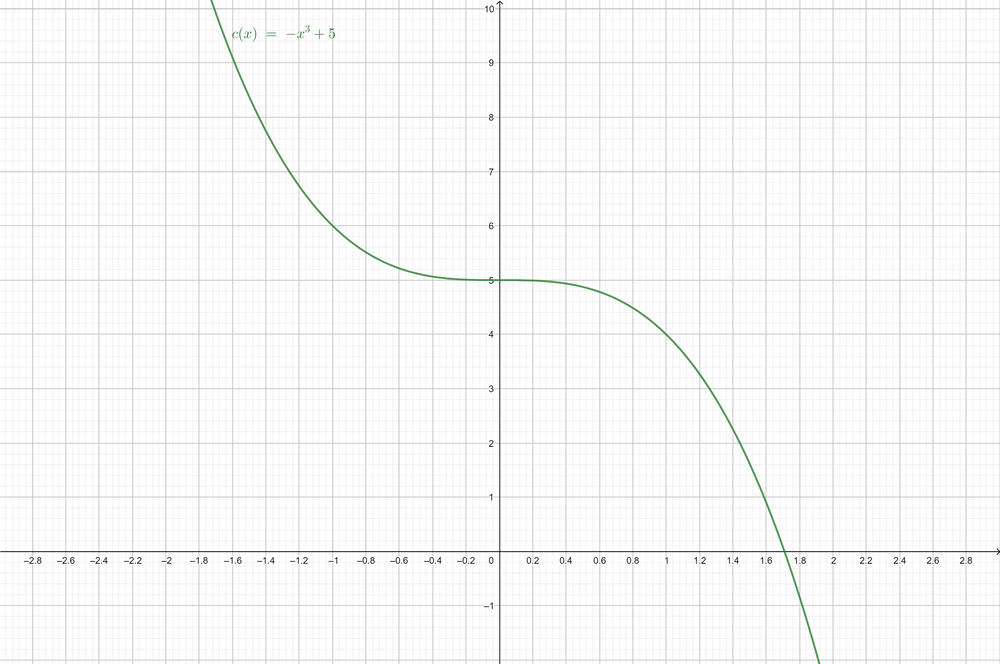
$y=-x^3+5$ (Given)
The locator of the equation is the point: $(0, 5)$
b- The locator is the point $(0, 2)$ The asymptote is the y-axis.
c- The locator: $(-5, -2)$ The asymptote is: $x=-5$
d- The locator of the equation is the point: $(0, 5)$
$$
begin{align*}
&a) 2(y-1)^{2}+8=80\
&b) (x-2)^{2}=0\
&c) x^{2}+25=0\
&d) 6x^{2}-36=6x\
end{align*}
$$
In order to solve these equations, we will simplify them.
$$
begin{align*}
& 2(y-1)^{2}+8=80\
& 2(y-1)^{2}=80-8\
& 2(y-1)^{2}=72\
& (y-1)^{2}= 36\
& y-1= sqrt{36}\
& y-1= pm 6\
& y= -6, +6
end{align*}
$$
Therefore the value of $y$ is $-6$ and $6$.
$$
begin{align*}
(x-2)^{2}&=0\
x-2&=0\
x&=2\
end{align*}
$$
Therefore the value of $x$ is $2$.
$$
begin{align*}
x^{2}+25&=0\
x^{2}&=-25\
x&=pm5\
end{align*}
$$
Therefore the value of $x$ is $pm5$.
$$
begin{align*}
6x^{2}-36&=6x\
6(x^{2}-x-6)&=0\
x^{2}-x-6&=0\
x^{2}+2x-3x-6&=0\
x(x+2)-3(x+2)&=0\
(x+2)(x-3)&=0\\
x&=-2,3\
end{align*}
$$
Therefore the value of $x$ is $-2$ and $3$.
$b)$ $x=2$
$c)$ $x=pm5$
$a)$ $y=-2,3$
Cost of a gallon of milk = $3.89$ dollars.
Price increase caused by inflation = $4$ percent per year.
Let $P$ be the price and $r$ be the inflation price.
$$
begin{align*}
A&=P(1+r)^{t}\
A&=3.89(1+0.04)^{t} \
A&=3.89(1.04)^{t} \
end{align*}
$$
$$
begin{align*}
A&=3.89(1.04)^{t}\
A(10)&=3.89(1.04)^{10} \
A(10)&=5.76\
end{align*}
$$
Thus the price of gallon milk after ten years will be $5.76$ dollars.
$b$. $A(10)=5.76$
$10^2=(1.5)^2+x^2$ (Pythagorean theorem)
$x^2=100-2.25=97.75$
$x=sqrt {97.75} approx 9.89$ feet
The distance from the top of the ladder to the roof:
$d=12-9.89=2.11$ feet
1. Check your answers using the table at the end of this section.
2. Construct a table in your Learning Log.
3. Write a list of topics you need help on.
4. Write a list of topics you need to practice more.

