All Solutions
Page 368: Closure Activity
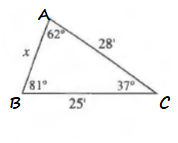
$=1409-1400cdot 0.79863551$
$=290.91019$
$$
x=sqrt{290.91019}approx 17.06
$$
$x=dfrac{sin 37text{textdegree}cdot 28}{sin 81text{textdegree}}$
$=dfrac{0.60181502cdot 28}{0.98768834}$
$$
approx 17.06
$$
x=17.06′
$$
We have to write this equation in exponential form.
This means for equation $text{underline{$log_{b}x=y$}}$, exponential form will be $text{underline{$b^y=x$}}$.
$$
begin{align*}
log_{3}(2x-1)&=-2 & text{logarithimic equation}\
3^{-2}&=2x-1 & text{exponential form}\
dfrac{1}{9}+1&=2x-1+1 & text{Add $1$ to both sides}\
dfrac{10}{9}&=2x\
x&=dfrac{10}{2cdot9} & text{Divide both sides by $2$}\
x&=boxed{dfrac{5}{9}} implies & text{textbf{solution}}\
end{align*}
$$
Apply logarithimic rule $underline{log_{b}b^k=k}$
$$
begin{align*}
5^{log_{5}x}&=3\
x&=boxed{3} implies & text{textbf{solution}}
end{align*}
$$
First we will apply rule $underline{log_{b}a-log_{b}c=log_{b}dfrac{a}{c}}$
$$
begin{align*}
log_{2}(x)-log_{3}(x)&=4\
log_{2}dfrac{x}{3}&=4 & text{apply logarithimic rule}\
2^4&=dfrac{x}{3} & text{write in exponential form}\
dfrac{x}{3}&=16\
x&=boxed{48} & text{textbf{solution}}
end{align*}
$$
$log_{3}{5}$ can be calculated right away, so $x=log_{3}5approx1.465$
b) $x=3$
c) $x=48$
d) $xapprox1.465$
begin{cases}
ygeq x^2\
ygeq (x-4)^2+2
end{cases}
$$
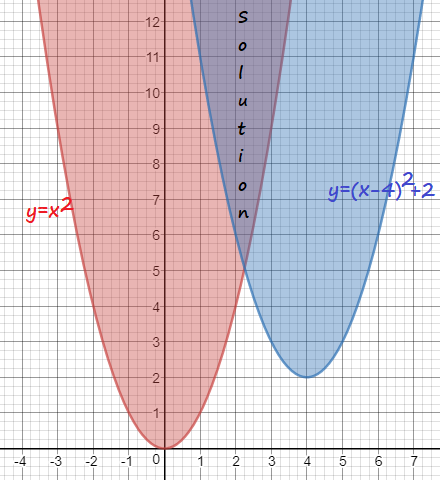
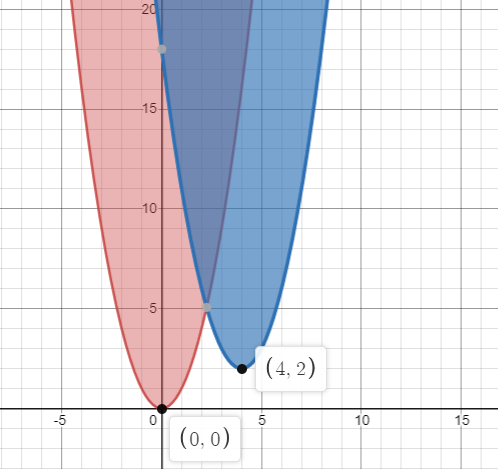
Both parabolas are opening upwards since $a>0$ in both expressions.
Parabola of $x^2$ has vertex at point $(0,0)$ and parabola of $(x-4)^2+2$ has vertex $(4,2)$.
The graph of $(x-4)^2+2$ is graph of $x^2$ positioned $4$ units to the right and $2$ units up.
x=2+sqrt{2y-4}
$$
y^{-1}(x)=dfrac{x^{2}}{2}-2x+4
$$
Solve the equation. Apply exponent rule. Apply $log$ on both sides.
$$
begin{align*}
ln left(27right)&=xln left(6right) \
x &= dfrac{ log 27}{log 6} \
x&approx 1.839
end{align*}
$$
Solve the equation. Apply exponent rules.
$$
begin{align*}
27 &= 6^{-x} \
log 27 &= log 6^{-x} \
x &= dfrac{log 27}{-log 6 } \
x &approx -1.839
end{align*}
$$
Solve the equation. Apply exponent rules.
$$
begin{align*}
27 &= dfrac{1}{6^{-x}} \
27 &= 6^x \
&text{We solved this. (a)} \
x &approx 1.839
end{align*}
$$
Solve the equation. Apply exponent rules.
$$
begin{align*}
dfrac{1}{left(dfrac{1}{6}right)^x} &= dfrac{1}{dfrac{1}{6^x}} \
&= 1 cdot dfrac{6^x}{1} \
&= 6^x
end{align*}
$$
All $x$.
b) $-1.839$
c) $1.839$
d) All $x$
By squaring both sides of the equation we get:
$$
begin{align*}
x+7&=(x+1)^2\
x+7&=x^2+2x+1 & text{ Use the fact $(x+1)^2=x^2+2x+1$}\
x+7-(x+7)&=x^2+2x+1-x-7 & text{Subtract $x+7$ from both sides}\
0&=x^2+x-6 & text{Combine like terms}\
x^2+3x-2x-6&=0 & text{Rewrite $x$ as $3x-2x$}\
x(x+3)-2x-6&=0 & text{ Factor out $x$ of first two terms}\
x(x+3)-2(x+3)&=0 & text{Factor out $2$ of second two terms}\
(x-2)(x+3)&= 0 & text{Factor out $x+3$}
end{align*}
$$
Now the solutions for equation $(x-2)(x+3)=0$ are $x=2$ or $x=-3$. We must check them.
$$
begin{align*}
sqrt{x+7}&=x+1\
sqrt{2+7}&=2+1 & text{Substitute $2$ for $x$}\
sqrt{9}&=3\
3&=3 implies & text{The solution $x=2$ is correct.}\
end{align*}
$$
CHECKING FOR SOLUTION $X=-3$
$$
begin{align*}
sqrt{x+7}&=x+1\
sqrt{-3+7}&=-3+1 & text{Substitute $-3$ for $x$}\
sqrt{4}&=-2\
2&ne-2 implies & text{The solution is extraneous.}
end{align*}
$$
By subtracting $4$ from both sides of the equation we get:
$$
begin{align*}
3x^4&=77\
x^4&=dfrac{77}{3} & text{Divide both sides by $3$}\
sqrt{x^4}&=sqrt{dfrac{77}{3}} & text{Take square root of both sides}\
x^2&=sqrt{dfrac{77}{3}} & text{Use the fact $x^2>0$}\
x&=boxed{pm sqrt[4]{dfrac{77}{3}}} & text{Take square root of both sides}\
end{align*}
$$
Now we must check both solutions.
$$
begin{align*}
3x^4+4&=81\
3left(sqrt[4]{dfrac{77}{3}}right)^4+4&=81\
3dfrac{77}{3}+4&=81\
77+4&=81\
81&=81 & text{The solution $x=sqrt[4]{dfrac{77}{3}}$ is correct}\
end{align*}
$$
CHECKING FOR SOLUTION $X=-sqrt[4]{dfrac{77}{3}}$
$$
begin{align*}
3x^4+4&=81\
3left(-sqrt[4]{dfrac{77}{3}}right)^4+4&=81\
3dfrac{77}{3}+4&=81\
77+4&=81\
81&=81 & text{The solution $x=-sqrt[4]{dfrac{77}{3}}$ is correct}\
end{align*}
$$
b)$x=pm sqrt[4]{dfrac{77}{3}}$
x(x-1)(2x+3)=0
$$
$x-1=0Rightarrow x_2=1$
$2x+3=0Rightarrow x_3=-dfrac{3}{2}$
2x^3+x^2-3x=0
$$
$x(2x^2-2x+3x-3)=0$
$x[2x(x-1)+3(x-1)]=0$
$$
x(x-1)(2x+3)
$$
left{-dfrac{3}{2}, 0, 1right}
$$
b) $left{-dfrac{3}{2}, 0, 1right}$
Assuming $n$ is the number of years, $a_1$ is the initial value, $r$ is the decreasing rate, and $a_n$ is the population after $n$ years.
$a_n=a_1 times (1-r)^n$
$70,379=72,000 times (1-r)^2$
$(1-r)^2=dfrac {70,379}{72,000}$
$(1-r)^2=0.9775$
$1-r=0.9887$
$r=0.0113=%1.13$
The equation that would model the changing population is:
$$
a_n=72,000 times (0.9887)^n
$$
For the population to level off eventually at 60,000:
$60,000=72,000 times (0.9887)^n$
$(0.9887)^n=dfrac {60}{72}$
$(0.9887)^n=dfrac {5}{6}$
$log (0.9887)^n=log (0.8333)$
$nlog (0.9887)=log (0.8333)$
$n cdot (-0.0049)=-0.0792$
$n=dfrac {-0.0792}{-0.0049}$
$$
n approx 16 mathrm { ~years}
$$
b- The equation that would model the changing population is:
$$
a_n=72,000 times (0.9887)^n
$$

