(a) $x=3y-2$ ; $y=dfrac{x+2}{3}$

Interchange x and y in the equation and solve for y to get inverse function. Check result for $(x,y)=(0,-2)$ gives inverse $(-2,0)rightarrow y=dfrac{(-2)+2}{3}=0$

(b) $x=dfrac{y+1}{4}$ ; $y=4x-1$

(c) $x=y^{3}+1$ ; $y=sqrt[3]{x-1}$

(d) $x=1+sqrt{y+5}$ ; $y=(x-1)^{2}-5$

(a) Plot shows $f(x)=2+sqrt{x-1}$ with domain $x=[1,infty)$ and range $f(x)=[2,infty)$

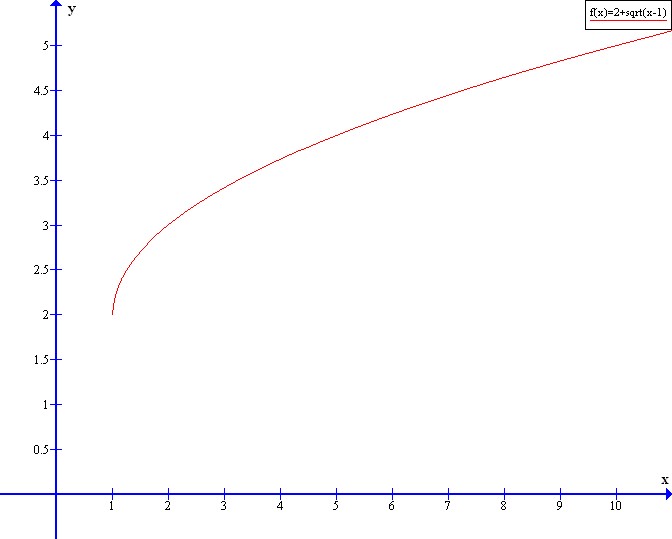
$$
x=2+sqrt{f^{-1}(x)-1}
$$

(b) Interchange x and the substituted inverse function $f^{-1}(x)$ for $f(x)$ then solve;

$$
(x-2)^{2}+1=f^{-1}(x)
$$

Plot shows $f^{-1}(x)$

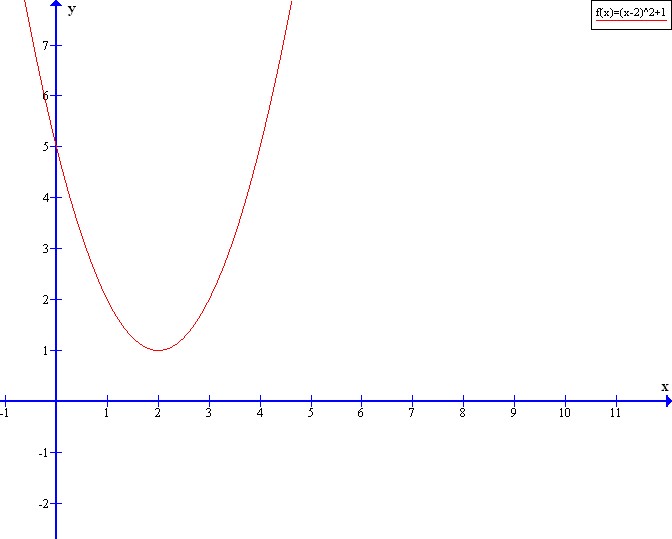
$$
f^{-1}(f(5))=f^{-1}(4)=(4-2)^{2}+1=5
$$

$$
(c)
$$

$$
f(f^{-1}(5))=f(10)=2+sqrt{10-1}=5
$$

$$
(d)
$$

(a) The domain is given by $x=[-4,3]$ and range $f(x)=[-5,5]$. f(x) is a function since there is a unique element of the domain for every element in the range, here we have a bijective function.

(b) Plot shows a series plot of $f^{-1}x$ where the inverse is obtained by interchanging x and f(x) coordinates. $f^{-1}x$ is not a function because there is more than one element of the range mapped to one element of the domain. The vertical line test confirms this. (d) The domain is given by interchanging the domain and range of f(x) such that $x=[-5,5]$ and $f^{-1}(x)=[-4,3]$

a) $log_8(64)=x$

So, if

$$
begin{equation}
y=b^x
end{equation}
$$

And

$$
begin{equation}
x=log_b(y)
end{equation}
$$

Then

$$
begin{equation}
64=8^x
end{equation}
$$

Now the question is which exponent we have to use to get $64$ from $8$ and the answer is clearly $2$ because $8^2=64$.

b) $log_9 (x)=frac{1}{2}$

If we go by the same principle from equations (1) and (2) from problem a) just with reversed $x$ and $y$ we get:

$$
begin{equation}
9^frac{1}{2}=x
end{equation}
$$

We can also write equation (1) like this:

$$
begin{equation}
sqrt{9}=x
end{equation}
$$

Now we can easily see that $x=3$, because square root of $9$ is $3$.

c) $log_3 (3^4)=x$

Again by the same principle from a):

$$
begin{equation}
3^4=3^x
end{equation}
$$

From equation (1) we can conclude that $x=4$, because for to left hand side of the equation and the right hand one to be equal exponents must be equal.

d) $10^{log_{10} 4}=x$

$$
begin{equation}
log_{10}4=log_{10}x
end{equation}
$$

$$
begin{equation}
x=4
end{equation}
$$

e)

From problem c) we can conclude that if the base of the logarithm and the number (without the exponent) on which we are performing the function are equal than the solution to the equation is equal to the exponent.

$$
begin{equation}
log_a(b^c)=x
end{equation}
$$

So if $a=b$ than $x=c$.

From problem d) we can conclude that if the base of the logarithm in the exponent of a number and that number are equal, than the solution to the equation is equal to the number on which we are performing the log function.

$$
begin{equation}
a^{log_b(c)}=x
end{equation}
$$

So again if $a=b$ than $x=c$.

a) $x=2$

b) $x=3$

c) $x=4$

d) $x=4$

In this exercise we can use the formula

$$
color{#c34632}{Z = frac {X-M}{s}}
$$

where

$X$ – the values after upgrade

$M$ – the average

$s$ – the standard deviation

$star$ Model $760$:

$$
begin{align*}
X &= 90\
M &= 76\
s &= 11
end{align*}
$$

we have

$$
begin{align*}
Z &= frac {90-76}{11}\
Z &= frac {14}{11}\
Z &= 1.27
end{align*}
$$

$star$ Model $S22$:

$$
begin{align*}
X &= 57\
M &= 50\
s &= 5
end{align*}
$$

we have

$$
begin{align*}
Z &= frac {57-50}{5}\
Z &= frac 75\
Z &= 1.4
end{align*}
$$

Since $1.27<1.4$ we can conclude that for the Model $S22$ the upgrade had a grater impact.

The Model $S22$ the upgrade had a grater impact.

$y=3a^{-x}$ where $atextgreater1$

(a) is hyperbolic with horizontal and vertical asymptotes so we need a decreasing function of the form shown that intercepts the y-axis at $y=3$

$$
y=dfrac{2x}{3}-5
$$

(b) is a linear increasing function with slope $dfrac{2}{3}$ and intercepts the y-axis at y=-5

$$
y=(x+dfrac{1}{2})^{2}-6
$$

(c) is a upward parabola with vertex $left( dfrac{1}{2},-6right)$

$$
(x-1)^{2}+(y-4)^{2}=16
$$

(d) is a circle with centre at $(1,4)$ and radius 4