$textbf{a.}$

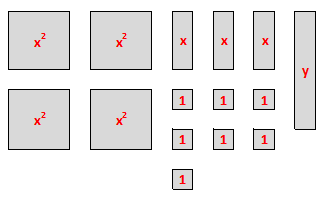
We will need a total of:

$$
text{4 $x^2$ tiles, 3 $x$ tiles, 1 $y$ tile, and 7 unit tiles}
$$

which can be simplified as:

$$
color{#c34632}4x^2+3x+y+7color{white}tag{1}
$$

$textbf{b.}$

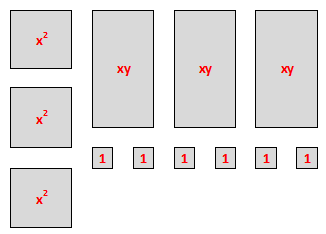
We will need a total of:

$$
text{3 $x^2$ tiles, 3 $xy$ tiles, and 6 unit tiles}
$$

which can be simplified as:

$$
color{#c34632}3x^2+3xy+6color{white}tag{1}
$$

$textbf{c.}$

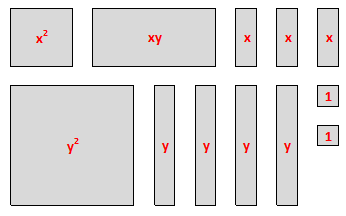
We will need a total of:

$$
text{1 $x^2$ tile, 1 $y^2$ tile, 1 $xy$ tile, 3 $x$ tiles, 4 $y$ tiles, and 2 unit tiles}
$$

which is not possible to simplify further since no tiles can be combined that will result to a new expression.

$textbf{d.}$

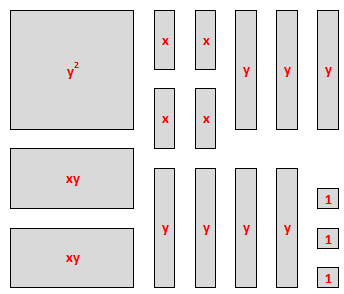
We will need a total of:

$$
text{1 $y^2$ tile, 2 $xy$ tiles, 4 $x$ tiles, $7$ $y$ tiles, and 3 unit tiles}
$$

which can be simplified as:

$$
color{#c34632}y^2+2xy+4x+7y+3color{white}tag{1}
$$

a. $4x^2+3x+y+7$

b. $3x^2+3xy+6$

c. not possible

d. $y^2+2xy+4x+7y+3$

Write algebraic expressions for each representation as follows:

$$
text{(a)} 2x-3 text{(b)} -3x-(xy+2)=-3x-xy-2
$$

$$
text{(c)} x^2-(y-4)=x^2-y+4 text{(d)} 2x+2-1-3
$$

$color{#4257b2}text{(a)} 2x-3 text{(b)} -3x-(xy+2)=-3x-xy-2$

$$
color{#4257b2}text{(c)} x^2-(y-4)=x^2-y+4 text{(d)} 2x+2-1-3
$$

We put the tiles as we did because we wanted to have

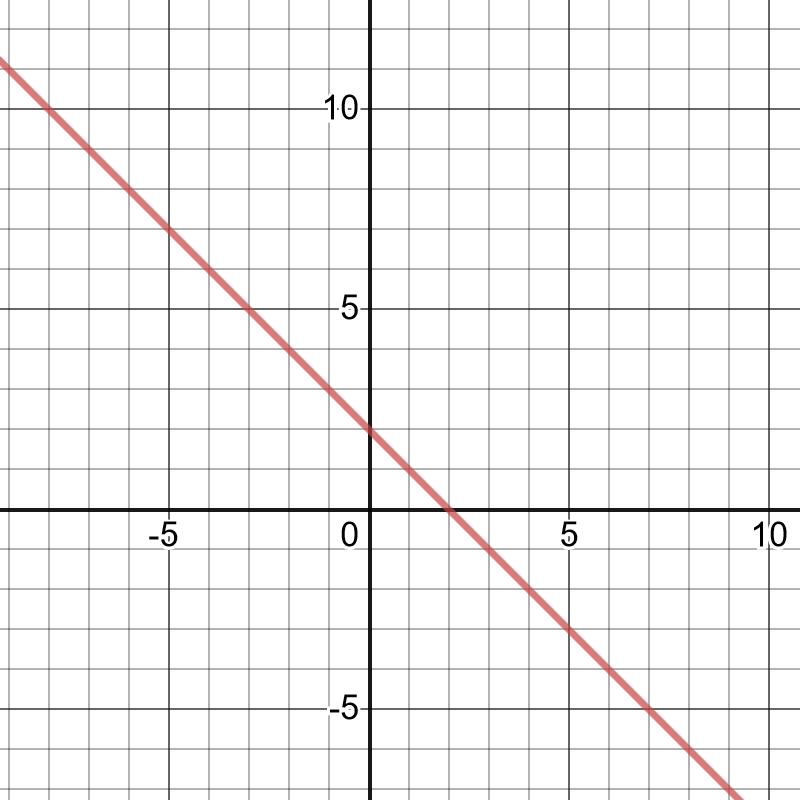
one $x$-value and one number value next to each other.

We would like to write a simplified algebraic expression for the tiles collection as follows:

$$
x^2+y+y+xy+x+x^2+x+y+y+x^2+y^2+x^2+xy+x+x+y+xy+y+x^2+x^2
$$

$$
color{#4257b2}6x^2++y^2+3xy++4x+6y
$$

$$
color{#4257b2}6x^2++y^2+3xy++4x+6y
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{Group like terms}\
&y^2+3y+2y+y+5\\
&=boxed{{color{#c34632} y^2+6y+5 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&color{#c34632} text{Not Supported}\
end{align*}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{Group like terms}\
&3xy+5x+x+3y+2+4\\
& =3xy+6x+3y+2+4 \
&=boxed{{color{#c34632} 3xy+6x+3y+6 } }
end{align*}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{Group like terms}\
&m^2+3m^2+4m+2mn+m\\
& =m^2+3m^2+5m+2mn \
&=boxed{{color{#c34632} 4m^2+5m+2mn } }
end{align*}
$$

$$
color{#4257b2} text{a)} y^2+6y+5
$$

$$
color{#4257b2} text{b) Not Supported}
$$

$$
color{#4257b2} text{c)}3xy+6x+3y+6
$$

$$
color{#4257b2} text{d)}4m^2+5m+2mn
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{For d=-1 we solve this}\
&-4left(-1right)+3\\
&= 4cdot :1+3 \
&=4+3 tag{Multiply the numbers}\
&=boxed{{color{#c34632} 7 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:-left(-aright)=a
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{For k=4 and m=-10 we solve this}\
&4-left(-10right)\\
&= 4+10 \
&=boxed{{color{#c34632} 14 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:-left(-aright)=a
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{For t=6 and w=-3 we solve this}\
&frac{6}{-3}\\
&= -frac{6}{3} \
&=boxed{{color{#c34632} -2 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{a}{-b}=-frac{a}{b}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{For x=7 and y=5 we solve this}\
&7^2+5^2\\
&= 49+25 tag{Calculate exponents} \
&=boxed{{color{#c34632} 74 } }
end{align*}
$$

$$
color{#4257b2} text{a)}7
$$

$$
color{#4257b2} text{b)}14
$$

$$
color{#4257b2} text{c)}-2
$$

$$
color{#4257b2} text{d)}74
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
&text{Adjust fractions}\
&-frac{1cdot :2}{4}+frac{3}{4}\\
&=frac{-1cdot :2+3}{4} \
&=boxed{{color{#c34632} frac{1}{4} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
&text{Adjust fractions}\
&-frac{1cdot :2}{6}-frac{1}{6}\\
&=frac{-1cdot :2-1}{6} \
&=frac{-3}{6} \
&=-frac{3}{6}\
&=boxed{{color{#c34632} -frac{1}{2} } }
end{align*}
$$

$$
color{#c34632} text{} mathrm{Since:the:denominators:are:equal,:combine:the:fractions}:quad frac{a}{c}pm frac{b}{c}=frac{apm :b}{c}
$$

$$
color{#c34632} mathrm{Apply:the:fraction:rule}:quad frac{-a}{b}=-frac{a}{b} text{}
$$

$$
text{}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
&text{Convert element to fraction}\
&frac{2}{3}cdot frac{12}{1}\\
&=-frac{2cdot :12}{3cdot :1} \
&=-frac{2cdot :12}{3} \
&=-frac{24}{3} tag{Multiply the numbers}\
&=boxed{{color{#c34632} -8 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Multiply:fractions}:quad frac{a}{b}cdot frac{c}{d}=frac{a:cdot :c}{b:cdot :d}
$$

$$
color{#c34632} text{} mathrm{Apply:rule}:1cdot :a=a
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
&-frac{4}{frac{1}{2}}\\
&=-frac{4cdot :2}{1} \
&=-left(-frac{8}{1}right) \
&=frac{8}{1} \
&=boxed{{color{#c34632} 8 } }
end{align*}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{a}{-b}=-frac{a}{b}
$$

$$
color{#c34632} text{}mathrm{Apply:the:fraction:rule}:quad frac{a}{frac{b}{c}}=frac{acdot :c}{b}
$$

$$
color{#c34632} text{} mathrm{Apply:rule}:-left(-aright)=a
$$

$$
color{#c34632} text{}mathrm{Apply:rule}:frac{a}{1}=a
$$

$$
color{#4257b2} text{a)}frac{1}{4}
$$

$$
color{#4257b2} text{b)}-frac{1}{2}
$$

$$
color{#4257b2} text{c)}-8
$$

$$
color{#4257b2} text{d)}8
$$

If you drew the line accurately, you will find two points with integer coordinates which are $color{#c34632} (-7,7)$ and $color{#c34632} (5,-2)$. The point between the two given points that lie on the line is $color{#c34632}(-1,2.5)$.

Possible answers: $(-7,7)$, $(-1,2.5)$, $(5,-2)$

Write an equation which represent this problem.

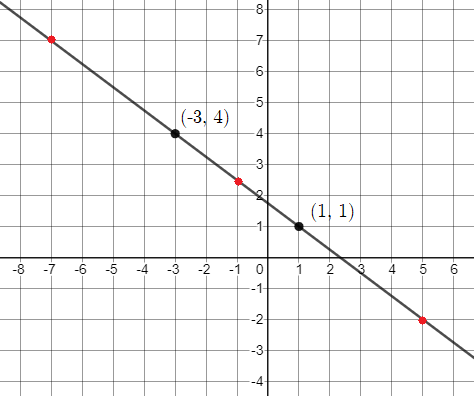
We know that,

Red tiles $+$ blue tiles $+$ beige tiles $=435$

$$
107+3b+b=435
$$

$$
107+4b=435
$$

Isolate variables on the left side as follows:

$$
4b=435-107=328
$$

$$
b=dfrac{328}{4}=82
$$

Remember that $107=82+25$

$$
color{#4257b2}435=(b+25)+3b+b
$$

$$
color{#4257b2}435=(b+25)+3b+b
$$

In all described situations, all actors lose what they have.

They do not get or lose anything at the end.

This can be represented using math symbols

as the following expression:

$$
x-x
$$

$$
x-x
$$

#### (a)

There is a built collection of tiles and written its value:

$$
5x+8y-3+4x=9x+8y-3
$$

#### (b)

You can use a different number of tiles using online tile algebra tools in order to represent

Gretchen’s expression without changing the value of the expression.

#### (c)

(i) On the following picture, there is graphed $3x+5+y$

(ii) On the following picture, there is graphed $-(3-4x)$.

a) $9x+8y-3$; b) Use different number of tiles;

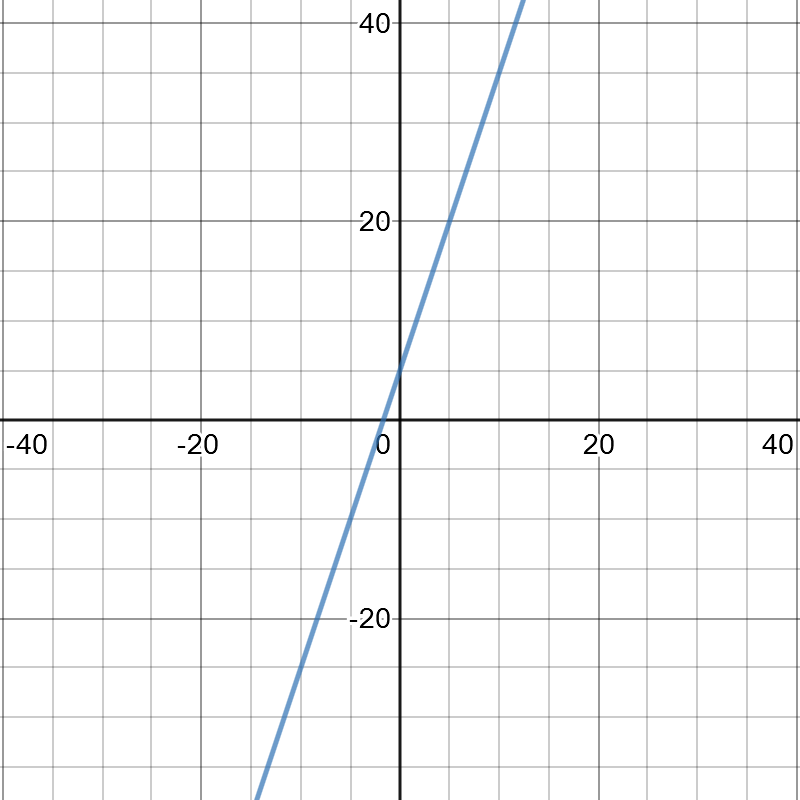
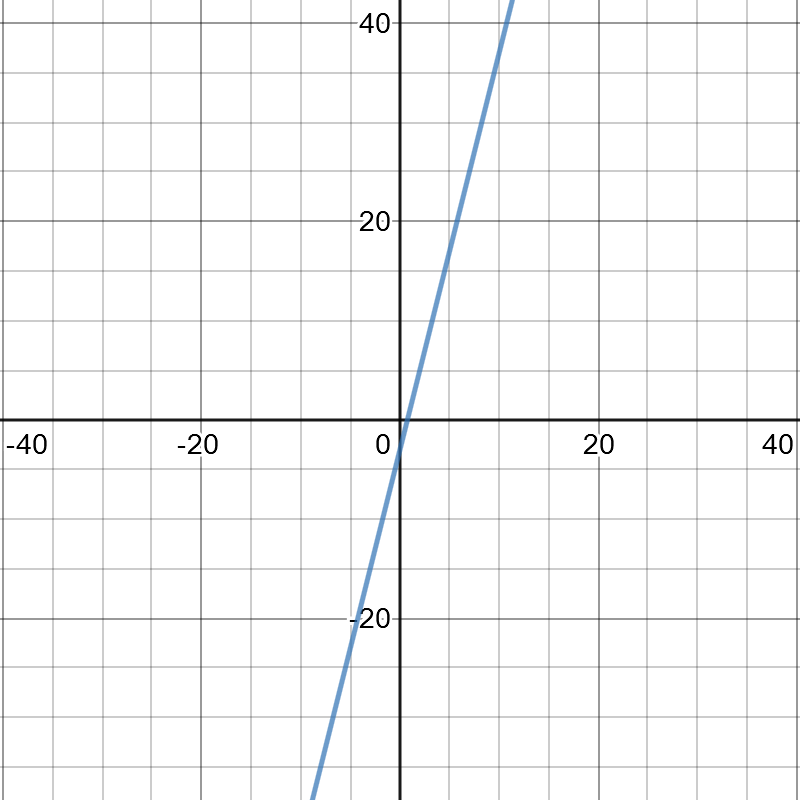
c) Use a graphing calculator

We need to explain what wade did in each step.

In the first step: he write the expression represent the first photo as,
$$
2x+1-(2)
$$

In the second step: he transfer the two tiles from negative side to positive side and he change the signs for it as,
$$
2x+1+(-2)
$$

In the third step: he simplify the expression in the positive side to be represent as
$$
2x-1
$$

$$
text{color{#4257b2}Its allowed what he made to simplify the expression.}
$$

We need to write the simplified algebraic expression for the following terms:

$$
largecolor{#4257b2}text{(a)}
$$

$$
x-2x-2-(-2)=x-2x-2+2=largecolor{#4257b2}-x
$$

$$
largecolor{#4257b2}text{(b)}
$$

$$
x-x+1-2-(x-3)x-x+1-2-x+3=largecolor{#4257b2}-x+2
$$

(a) $largecolor{#4257b2}-x$

(b) $largecolor{#4257b2}-x+2$

We would like to simplify each of the following expression as follows:

$$
text{(a)} 3x-(2x+4)
$$

Simplify,

$$
3x-2x-4=largecolor{#4257b2}x-4
$$

$$
text{(b)} 7-(4y-3)+2y-4
$$

Simplify,

$$
7-4y+3+2y-4=largecolor{#4257b2}6-2y
$$

(a) $largecolor{#4257b2}x-4$

(b) $largecolor{#4257b2}6-2y$

You need to know that a mathematical expression is a combination

of numbers, variables, and operation symbols.

Zero pairs are some kind of parts of mathematical expression but

with opposite sign, and together, they are equal to $0$.

For example, this can be explained in the following expression:

$$
8x+y-5-y=8x-5
$$

$8x+y-5-y=8x-5$

We would like to write and simplify algebraic expression for each mat as follows:

$$
color{#4257b2}text{(a)} 2x-3-(x+1)
$$

$$
=2x-3-x-1=large x-4
$$

$$
color{#4257b2}text{(b)} y-y+3-1=large2
$$

$$
color{#4257b2}text{(c)} -x-(x+2)
$$

$$
=-x-x-2=large-2x-2
$$

(a) $large x-4$
(b) $large 2$

(c) $large -2x-2$

We would like to write and simplify algebraic expression for the following expressions:

$$
color{#4257b2}text{(a)} 2x-3x-3+4x^2+10+x
$$

Rearrange the tiles to groups like terms as follows:

$$
4x^2+(2x-3x+x)+(-3+10)=4x^2+0+7 large4x^2+7
$$

$$
color{#4257b2}text{(b)} -4x+y^2-9+10-x+3x-4y^2
$$

Rearrange the tiles to groups like terms as follows:

$$
4y^2+(-4x-x+3x)+(-9+10) large4y^2-2x+1
$$

$$
color{#4257b2}text{(c)} 2x^2+30y+3x^2+4x^2-y-x
$$

Rearrange the tiles to groups like terms as follows:

$$
(2x^2+4x^2+3x^2)+(30y-y)-x large9x^2+29y-x
$$

$$
color{#4257b2}text{(d)} 0-20-5xy+4y^2+10-y+xy
$$

Rearrange the tiles to groups like terms as follows:

$$
4y^2-y+(-5xy+xy)+(0-20+10) large4y^2-y-4xy-10
$$

(a) $large4x^2+7$

(b) $large4y^2-2x+1$

(c) $large9x^2+29y-x$

(d) $large4y^2-y-4xy-10$

We need to evaluate each expression below by using the following function ads follows:

$$
color{#4257b2}f(x)=2x+3
$$

$$
{color{#4257b2}text{(a)} f(-5)}=2(-5)+3=-10+3=largecolor{#4257b2}-7
$$

$$
{color{#4257b2}text{(b)} f(-dfrac{1}{2})}=2(-dfrac{1}{2})+3=-1+3=largecolor{#4257b2}2
$$

$$
{color{#4257b2}text{(c)} f(4)}=2(4)+3=8+3=largecolor{#4257b2}11
$$

$$
{color{#4257b2}text{(d)} f(-2)}=2(-2)+3=-4+3=largecolor{#4257b2}-1
$$

(a) $largecolor{#4257b2}-7$ (b) $largecolor{#4257b2}2$

(c) $largecolor{#4257b2}11$ (d) $largecolor{#4257b2}-1$

We would like to compute the value for each expression below.

$$
color{#4257b2}text{(a)} 7-2 cdot-5
$$

Multiply from the left to right as follows:

$$
=7-(2 cdot-5)=7-(-10)=7+10=color{#4257b2}large17
$$

$$
color{#4257b2}text{(b)} 6+3(7-3 cdot2)^2
$$

Multiply from the left to the right then evaluate exponents as follows:

$$
=6+3 (7-6)^2=6+3 (1)^2=6+3=color{#4257b2}large9
$$

$$
color{#4257b2}text{(c)} 5 (-3)^2
$$

Multiply from the left to the right then evaluate exponents as follows:

$$
=5 (9)=color{#4257b2}large45
$$

$$
color{#4257b2}text{(d)} 35 div(16-3^2) cdot2
$$

Multiply and divided from the left to the right as follows:

$$
=35 div(16-9) cdot2=35div7cdot2=5cdot2=color{#4257b2}large10
$$

$$
color{#4257b2}text{(e)} -3 cdot4+5 (-2)
$$

Multiply from the left to the right then adding and subtracting terms from left to right as follows:

$$
=-12+(-10)=-12-10=color{#4257b2}large-22
$$

$$
color{#4257b2}text{(f)} 7-6 (10-4 cdot2)div4
$$

Multiply and divided from the left to the right as follows:

$$
=7-6 (10-8)div4=7-(6cdot2)div4=7-12div4=7-3=color{#4257b2}large4
$$

(a) $color{#4257b2}large17$ (b) $color{#4257b2}large9$

(c) $color{#4257b2}large45$ (d) $color{#4257b2}large10$

(e) $color{#4257b2}large-22$ (f) $color{#4257b2}large4$

We would like to calculate the area and perimeter for each figure in the text book.

$$
color{#4257b2}text{The left figure}
$$

The perimeter of figure that mean the total lengths of figure as follows:

$$
=16+12+19+13+35+25=color{#4257b2}large120text{ units}
$$

Area of the figure can be calculated as follows:

$$
=(25cdot35)-(19cdot12)=875-228=color{#4257b2}large647text{ sq. unit}
$$

$$
color{#4257b2}text{The right figure}
$$

The perimeter of figure that mean the total lengths of figure as follows:

$$
=12+8+7+8+12+8+7+8=color{#4257b2}large70text{ units}
$$

Area of the figure can be calculated as follows:

$$
=(8+8 cdot 12+7)-(8 cdot7)-(8 cdot7)=(16cdot19)-2 cdot 56=304-112=color{#4257b2}large192text{ sq. unit}
$$

The left figure,

$$
text{Perimeter}=120text{ units} text{Area}=647text{ sq unit}
$$

The right figure,

$$
text{Perimeter}=70text{ units} text{Area}=192text{ sq unit}
$$

Scientific notation of the given expression would be the following:

$$
1.75times6.01times10^{20+14}=1.75times6.01times10^{34}
$$

But, the calculator displayed the following:

$$
1.05175times10^{35}
$$

$1.75times6.01times10^{34}$; $1.05175times10^{35}$

We need to simplify and write algebraic expression for each side, then noticed the largest one.

$$
color{#4257b2}text{(a) The left figure}
$$

$$
x+2-2-3=largecolor{#4257b2}x-3
$$

$$
color{#4257b2}text{The right figure}
$$

$$
x+2-3-(-2)=x+2-3+2=largecolor{#4257b2}x+1
$$

(b) The right figure has a largest value so, its greater than the left figure.

$text{(a) The left figure}=x-3 text{The right figure}=x+1$

$$
text{(b) The right figure is greater than the left figure.}
$$

#### (a)

Left expression is the following:

$$
1-1+1-1+1-1+1=1
$$

Right expression is the following:

$$
1-1+1+1=2
$$

We can conclude that $2>1$, which means that expression

on the left side is greater.

#### (b)

Left expression is the following:

$$
-(-1-1)-1=1+1-1=1
$$

Right expression is the following:

$$
-(x)-x-1-1+1=x-x-1=-1
$$

We can conclude that $1>-1$, which means that expression

on the right is greater.

#### (c)

Left expression is the following:

$$
x-x+1-1-1=-1
$$

Right expression is the following:

$$
x-x+1+1-1-1=0
$$

We can conclude that $0>-1$, which means that expression

on the right side is greater.

a) Left$=1-1=$right; c) left$=-1<0=$right

#### (a)

Expression on the left side is:

$$
1+1+1+1+1-1-1-1-(1-1-1)=5-3-1+1+1=3
$$

Expression on the right side is:

$$
1+1+1-1-1-(1-1-1-1)=3-2-1+1+1+1=3
$$

We can conclude that those expression are equal.

#### (b)

Expression on the left side is:

$$
x+1+1+1+1-1-1-(-1+1+1)=x+4-2+1-1-1=x+1
$$

Expression on the right side is:

$$
x+1-1-1-(-1-1-1-1)=x-1+1+1+1+1=x+3
$$

We can conclude that $x+3>x+1$, which means that

the expression on the right side is greater.

a) left$=3=3=$right; b) left$=x+1<x+3=$right

#### (a)

Expression on the left side is:

$$
1-1-1-1-1-(-1+1)=1-4+1-1=-3
$$

Expression on the right side is:

$$
-1-1-1-(1+1+1)=-3-1-1-1=-6
$$

We can conclude that $-3>-6$, which means that expression

on the left side is greater.

#### (b)

Expression on the left side is:

$$
x+1+1+1-1-(x-x)=x+2-x+x=x+2
$$

Expression on the right side is:

$$
x-1-1-(1-1-1)=x-2-1+1+1=x-1
$$

We can conclude that $x+2>x-1$, which means that expression

on the left side is greater.

#### (c)

Expression on the left side is:

$$
y+1+1-1-1-1-(y+y+1+1-1)=y-1-2y-1=-y-2
$$

Expression on the right side is:

$$
1-y-1-1-(1+1+1+1-1-1)=-y-1-2=y-3
$$

We can conclude that $-y-2>-y-3$, which means that expression

on the left side is greater.

#### (d)

Expression on the left side is:

$$
x^2+1+1+1-(x+x-1)=x^2+3+1=x^2+4
$$

Expression on the right side is:

$$
x+1+1+1-(x^2+x-1-1)=x+3-x^2-x+2=-x^2+5
$$

We can conclude that $x^2+4>-x^2+5$, which means that expression

on the left side is greater.

#### (e)

Expression on the left side is:

$$
x-x+1-1-1-(x+y+y)=-2-x-2y
$$

Expression on the right side is:

$$
-1-y-(y+x+1)=-1-y-y-x-1=-2y-x-2
$$

We can conclude that $-2-x-2y=-2-x-2y$, which means that those
expressions are equivalent.

#### (f)

Expression on the left side is:

$$
1+1+1-1-1-(x^2+1+1+1-1-1)=1-x^2-1=-x^2
$$

Expression on the right side is:

$$
x+x+x-x+1-(x^2+x+x+x-x-1-1)=2x+1-x^2-2x+2=-x^2+3
$$

We can conclude that $-x^2+3>-x^2$, which means that expression

on the right side is greater.

a) left$=-3>6=$right; b) left$=x+2>x-1=$right;

c) left$=-y-2>-y-3=$right

d) left$=x^2+4>-x^2+4>-x^2+5=$right; e) left$=$right;

f) left$=-x^2<-x^2+3=$right

We need to write the simplified algebraic expression for each expression mat in the text book:

$$
large{color{#4257b2}text{(a)}} 2x+2-1-2=largecolor{#4257b2}2x-1
$$

$$
large{color{#4257b2}text{(b)}} x+3-x-(-1)=x+3-x+1= largecolor{#4257b2}4
$$

$$
large{color{#4257b2}text{(c)}} x^2-2-(y+2)=x^2-2-y-2= largecolor{#4257b2}x^2-y-4
$$

(a) $color{#4257b2}Large 2x-1$ (b) $color{#4257b2}Large 4$

(c) $color{#4257b2}Large x^2-y-4$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{ Group like terms}\
&=4x^2+x+x+2x-x-3\\
&=boxed{{color{#c34632} 4x^2+3x-3 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{ Group like terms}\
&=8x^2-13x^2+10x^2+3x-25x-x\\
&=8x^2-13x^2+10x^2-23x tag{Add similar elements}\
&=boxed{{color{#c34632} 5x^2-23x } }
end{align*}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
color{#c34632}text{ Not Supported}\
end{align*}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{ Group like terms}\
&=4y^2-2y^2+3xy+20-3+10\\
&=2y^2+3xy+20-3+10tag{Add similar elements}\
&=boxed{{color{#c34632} 2y^2+3xy+27 } }
end{align*}
$$

$$
color{#4257b2}text{a)}4x^2+3x-3
$$

$$
color{#4257b2}text{b)}5x^2-23x
$$

$$
color{#4257b2}text{c) Not Supported}
$$

$$
color{#4257b2} text{d)}2y^2+3xy+27
$$

We would like to evaluate the following expression for the given values $x$ and $y$.

$$
text{(a)} dfrac{6}{x}+9 x=3
$$

$$
dfrac{6}{x}+9=dfrac{6}{3}+9=2+9=Largecolor{#4257b2}11
$$

$$
text{(b)} -x^2+y x=2, y=1
$$

$$
-x^2+y=-(2)^2+1=-4+1=Largecolor{#4257b2}-3
$$

$$
text{(c)} -2 x y x=5, y=-3
$$

$$
-2 x y=-2 cdot 5 cdot-3=Largecolor{#4257b2}30
$$

$$
text{(d)} 2x^2-y x=-3, y=8
$$

$$
2x^2-y=2 (-3)^2-8=2 cdot9 -8=Largecolor{#4257b2}10
$$

(a) $color{#4257b2}Large11$ (b) $color{#4257b2}Large-3$

(c) $color{#4257b2}Large30$ (d) $color{#4257b2}Large10$

#### (a)

Expression on the left side is:

$$
1-1-1-1-(1+1+1+1-x)=-2-4+x=x-6
$$

Expression on the right side is:

$$
x+1+1-1-(1+1+1)=x+1-3=x-2
$$

We can conclude that $x-2>x-6$, which means that

expression on the right side is greater.

#### (b)

Expression on the left side is:

$$
x+x-1-1-(1+1)=2x-2-2=2x
$$

Expression on the right side is:

$$
x+x-x-(x)=x-x=0
$$

We can conclude that $2xgeq0$, which means that

expression on the left side is greater if $x$ is positive.

a) left$=x-6<x-2=$right; b) left$=2xgeq0=$right, $x$ is positive

We need to solve the following items:

(a) Is this a proportional situation?

Yes, there is a proportional situation because when the fuel of gasoline increase the distance traveled is increasing too.

(b) calculate the distance when she used $18$ gallons.

Distance $=dfrac{18cdot90}{4}=405$ miles

So she used $color{#4257b2}18$ gallons of fuel to travel $color{#4257b2}405$ miles

(a) Yes, there is a proportional situation

(b) $color{#4257b2}405$ miles

#### (a)

We can conclude that the line which is upper

at the $y$-axes represent company $A$ and

the other one represents the company $B$.

#### (b)

We can conclude that the profits of the company

$A$ are nonproportional situation.

#### (c)

We can conclude that for value $3$ of $x$ those

lines are intercept, so, in $3$ years those companies

will have the same profit.

#### (d)

That profit will be about $7$ thousands of dollars.

#### (e)

We can notice that profits of the company $B$ are growing

more quickly because that line has a greater slope.

a) Upper line represent Company $A$; b) Are not proportional;

c) In $3$ years; d) About $7$ thousands of dollars;

e) Profits of the Company $B$

We need to write which of the following expression is greater.

$$
text{(a)} 3x-(2-x)+1 text{or} -5+4x+4
$$

$$
3x-2+x+1 text{or} 4x-1
$$

$$
4x-1 text{or} 4x-1
$$

$$
text{color{#4257b2}Two sides are equal.}
$$

$$
text{(b)} -1+6y-2+4x-2y text{or} x+5y-(-2+y)+3x-6
$$

$$
-3+4y+4x text{or} x+5y+2-y+3x-6
$$

$$
-3+4y+4x text{or} -4+4y+4x
$$

$$
-3 text{or} -4
$$

$text{color{#4257b2}The left side is greater than the right side}$.

$$
text{(c)} 2x^2-2x+6-(-3x) text{or} -(3-2x^2)+5+2x
$$

$$
2x^2-2x+6+3x text{or} -3+2x^2+5+2x
$$

$$
2x^2+x+6 text{or} 2x^2+2x+2
$$

$$
x+6 text{or} x+x+2
$$

$$
6 text{or} x+2
$$

$text{color{#4257b2}Not enough information}$.

The first is actually flipping a tile to move it out of the region

into the opposite region.

The second is zero pairs or removing an equal number of

opposite tiles that are in the same region.

The third is removing an equal number of identical tiles from

both, $”-”$ and the $”+”$ region.

And fourth is taking away from both sides.

Actually, when you are comparing expressions if you have

the same part then you can take it away.

Whatever you do to one side, you can do to the other.

We need to write which of the following expression is greater to prove that the right side is greater.

$$
-2x-3+1-(3-x) text{or} 2-3-(x-2)
$$

$$
-2x-3+1-3+x text{or} 2-3-x+2
$$

$$
-x-5 text{or} -x+1
$$

$$
-5 text{or} 1
$$

$text{color{#4257b2}The right side is greater than the left side}$.

$text{color{#4257b2}The right side is greater than the left side}$.

She added tiles from the first $”+”$ region and then

subtract that one from $”-“$ region and then from

both expressions she removed the same parts and

then simplified it and again removed same parts and

on that way, she gets the result.

Added tiles from $”+”$ and $”-”$ region, then removed

same parts of both expressions and simplified.

We need to write which of the following expression is greater.

$$
text{(a)} x^2-x^2+2x-(x^2-1+1) text{or} x+3-1-(x^2+1)
$$

$$
x^2-x^2+2x-x^2+1-1 text{or} x+3-1-x^2-1
$$

$$
2x-x^2 text{or} x-x^2+1
$$

$$
2x text{or} x+1
$$

$$
x+x text{or} x+1
$$

$$
x text{or} 1
$$

$text{color{#4257b2}Not enough information}$.

$$
text{(b)} 5x+1-2-(3x+2) text{or} 2x+3-1-(2)
$$

$$
5x+1-2-3x-2 text{or} 2x+3-1-2
$$

$$
2x-3 text{or} 2x+0
$$

$$
-3 text{or} 0
$$

$text{color{#4257b2}The right side is greater than the left side}$.

$$
text{(c)} 5-(2y-4)-2 text{or} -y-(1+y)+4
$$

$$
5-2y+4-2 text{or} -y-1-y+4
$$

$$
-2y+7 text{or} -2y+3
$$

$$
7 text{or} 3
$$

$text{color{#4257b2}The left side is greater than the right side}$.

$$
text{(d)} 3xy+9-4x-7+x text{or} -2x+3xy-(x-2)
$$

$$
3xy-3x+2 text{or} -2x+3xy-x+2
$$

$$
3xy-3x+2 text{or} 3xy-3x+2
$$

$text{color{#4257b2}The two sides are equals}$.

(a) $text{color{#4257b2}Not enough information}$.

(b) $text{color{#4257b2}The right side is greater than the left side}$.

(c) $text{color{#4257b2}The left side is greater than the right side}$.

(d) $text{color{#4257b2}The two sides are equal}$.

We need to write which of the following expression is greater.

$$
text{(a)} 2x+1-2-(x+1) text{or} x+1-3-(6)
$$

$$
2x+1-2-x-1 text{or} x+1-3-6
$$

$$
x-2 text{or} x-8
$$

$$
-2 text{or} -8
$$

$text{color{#4257b2}The left side is greater than the right side}$

$$
text{(b)} 2x+1-3-(x-x+4) text{or} x+3-1-(4-2-x)
$$

$$
2x+1-3-x+x-4 text{or} x+3-1-4+2+x
$$

$$
2x-6 text{or} 2x+0
$$

$$
-6 text{or} 0
$$

$text{color{#4257b2}The right side is greater than the left side}$.

(a) $text{color{#4257b2}The left side is greater than the right side}$.

(b) $text{color{#4257b2}The right side is greater than the left side}$.

We need to evaluate each equation below.

$color{#4257b2}text{(a)} f(x)=2+3x x=4$

Substitute value of $x$ in the function as follows:

$$
f(4)=2+3 cdot4=2+12=Large14
$$

$$
f(4)=14
$$

$color{#4257b2}text{(b)} a=4-5 c c=-dfrac{1}{2}$

$text{Substitute value of $c$ as follows}$:

$$
a =4-5 cdotdfrac{-1}{2}=4-dfrac{-5}{2}=4+dfrac{5}{2}
$$

$$
a =dfrac{8+5}{2}=dfrac{13}{2}=6.5
$$

$$
a=6.5
$$

$color{#4257b2}text{(c)} n=3 d^2 d=-5$

Substitute value of $d$ as follows:

$$
begin{align*}
n &=3 cdot(-5)^2=3 cdot25
\ \
n &=Large75
end{align*}
$$

$color{#4257b2}text{(d)} h(x)=-4(x-2) x=-1$

Substitute value of $x$ in the function as follows:

$$
f(-1)=-4 (-1-2)=-4 cdot-3=Large12
$$

$$
f(-1)=12
$$

$color{#4257b2}text{(e)} 3+k=t t=14$

Substitute value of $t$ as follows:

$$
3+k=14 k=14-3
$$

$$
k=Large11
$$

(a) $f(4)=14$ (b) $a=6.5$

(c) $n=75$ (d) $h(-1)=12$

(e) $k=11$

We need to calculate the number of students attended the play.

Assume the number of adults is $color{#4257b2}x$ and number of student is $color{#4257b2}150+x$

Total of people attended the play is $color{#4257b2}1220$

$$
1220=150+x+x=150+2x
$$

Isolate the variables on the left side as follows:

$$
2x=1220-150=1070
$$

$$
x=dfrac{1070}{2}=535
$$

The number of adults is $535$

The number of student is $535+150=color{#4257b2}685$

The number of student is $color{#4257b2}685$

First, expression on the left side is:

$$
x+x-1-(1)=2x-2
$$

On the right side, expression is:

$$
x+x+1-1-(1)=2x-1
$$

We can conclude that $2x-2<2x-1$, so, expression on the right side is greater.

We need to solve the following items:

(a) Is this a proportional situation?

Yes, there is a proportional situation because when he read more pages, so he will take more time.

(b) calculate the time which needed to read entire novels?

Time $=dfrac{350cdot2}{75}=9.33$ hours

So he read the entire novels which contains $color{#4257b2}350$ pages in $color{#4257b2}9.33$ hours.

(a) Yes there is a proportional situation.

(b) $color{#4257b2}9.33$ hours.

We would like to calculate the following items.

(a) The perimeter of the large outer rectangle.

$$
=5+7+6+8+7+5+8+6=color{#4257b2}large52text{ units}
$$

(b) Total area of the figure can be calculated as follows:

$$
=30+40+(7cdot8)+(6cdot7)=30+40+56+42=color{#4257b2}large168text{ sq. unit}
$$

(a) $color{#4257b2}52$ units

(b) $color{#4257b2}168$ sq. unit

We need to write which of the following expression is greater.

$$
x+1-(1-2x) text{or} 3+x-1-(x-4)
$$

$$
x+1-1+2x text{or} 3+x-1-x+4
$$

$$
3x text{or} 6
$$

$text{color{#4257b2}Not enough information}$.

In this case the left side has a variable and the right side has a constant number, so that it is not possible to determine which side is greater.

$text{color{#4257b2}Not enough information}$.

We need to write which of the following expression is greater, then answer of the following question.

$$
x text{or} 5
$$

(a) If the left expression is smaller than the right expression, what about value of $x$.

The value of $x$ should be less than $5$ to make the left side is less than the right side.

$$
text{color{#4257b2}(b) If the left expression is greater than the right expression, what about value of $x$.
\
\
The value of $x$ should be more than $5$ to make the left side is greater than the right side.}
$$

(c) If the left expression is equal the right expression, what about value of $x$.

The value of $x$ should be equal $5$ to make the left side is equal the right side.

$$
text{color{#4257b2}(a) $xleq5$ (b) $xgeq5$ (c) $x=5$}
$$

#### (a)

Here we get following equation which is needed to be solved for $x$:

$$
begin{align*}
x+1+1+1-1-1-(-x-x+1)&=1+1+1+1+1+1-(-x+1)\
x+1+2x-1&=7+x-1\
3x=&x+6\
2x=&6\
x=&3\
end{align*}
$$

#### (b)

Here we have following tiles:

Rewrited equation where $x$ is alone on one side is:

$$
-3x=6
$$

(a) $x=3$; (b) $-3x=6$

We need to simplify and solving the following equations

to get the value of $x$.

$$
color{#4257b2}text{(a)} 1+2x-x=x-5+x
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
2x-x-x-x &=-5-1 2x-3-x=-6
\ \
-x &=-6 x=6
end{align*}
$$

$$
color{#4257b2}text{(b)} 3x-7=2
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
3x &=2+7 3x=9
\ \
x &=dfrac{9}{3} x=3
end{align*}
$$

$$
color{#4257b2}text{(c)} 3+2x-(x+1)=3x-6
$$

$$
3+2x-x-x=3x-6
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
2x-x-x-3x &=-6-3 -3x=-9
\ \
x &=dfrac{-9}{-3} x=3
end{align*}
$$

$$
color{#4257b2}text{(d)} 3-2x=2x-5
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
-2x-2x &=-5-3 -4x=-8
\ \
x &=dfrac{-8}{-4} x=2
end{align*}
$$

$$
color{#4257b2}text{(e)} -(x+3-x)=2x-7
$$

$$
-x-3+x=2x-7
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
-x+x-2x &=-7+3 -2x=-4
\ \
x &=dfrac{-4}{-2} x=2
end{align*}
$$

$$
color{#4257b2}text{(f)} -4+2x+2=x+1+x
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
2x-x-x &=1+4-2 0=3
\ \
text{color{#4257b2}Not supported}
end{align*}
$$

(a) $x=6$ (b) $x=3$ (c) $x=3$

(d) $x=2$ (e) $x=2$ (f) Not supported

We need to write which of the following expression is greater.

$$
text{(a)} 4-3-(x+2-2) text{or} 3-2-x-(1-3)
$$

$$
4-3-x-2+2 text{or} 3-2-x-1+3
$$

$$
1-x text{or} 3-x
$$

$$
1 text{or} 3
$$

$text{color{#4257b2}The right side is greater than the left side}$.

$$
text{(b)} -2x+2-4-(1-1) text{or} -x+2-2-(x+2-1)
$$

$$
-2x+2-4-1+1 text{or} -x+2-2-x-2+1
$$

$$
-2x-2 text{or} -2x-1
$$

$$
-2 text{or} -1
$$

$text{color{#4257b2}The right side is greater than the left side}$.

We need to write the expression represent this situation.

Assume the second number is $color{#4257b2}x$ and the first number is $color{#4257b2}x-14$

When adds is $x+x-14=40$

$$
2x-14=40
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
2x=40+14=54 x=dfrac{54}{2}
$$

$$
x=27
$$

The second number is $color{#4257b2}27$

The first number is $27-14=color{#4257b2}13$

$$
text{color{#4257b2}$$13 text{and} 27$$}
$$

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{Group like terms}\
&=3y-y+5x-7x+3\\
&=2y+5x-7x+3 tag{Add similar elements} \
&=boxed{{color{#c34632} 2y-2x+3 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{Remove parentheses}\
&=-1+5x-2x+2x^2+7\\
&=-1+3x+2x^2+7 tag{Add similar elements} \
&=2x^2+3x-1+7tag{Group like terms}\
&=boxed{{color{#c34632} 2x^2+3x+6 } }
end{align*}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{Group like terms}\
&=6x-4x-2x+2-1-3+2\\
&=2-1-3+2 tag{Add similar elements} \
&=boxed{{color{#c34632} 0 } }
end{align*}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{Group like terms}\
&=frac{2}{3}x+frac{1}{3}x-3y+2y\\
&=1cdot :x-3y+2y tag{Add similar elements} \
&=1cdot :x-y tag{Add similar elements} \
&=boxed{{color{#c34632} x-y } }
end{align*}
$$

$$
color{#4257b2} text{a)} 2y-2x+3
$$

$$
color{#4257b2} text{b)} 2x^2+3x+6
$$

$$
color{#4257b2} text{c)} 0
$$

$$
color{#4257b2} text{d)}x-y
$$

$$
{color{#4257b2}text{a)}}
$$

$$
begin{align*}
-frac{2}{3}+frac{4}{5}& {=}quad : -frac{2cdot :5}{15}+frac{4cdot :3}{15}\
&=frac{-2cdot :5+3cdot :4}{15} \
&={color{#c34632}frac{2}{15}}
end{align*}
$$

$$
{color{#4257b2}text{b)}}
$$

$$
begin{align*}
2-frac{3}{8}& {=}quad :frac{2}{1}-frac{3}{8}\
&=frac{2cdot :8}{8}-frac{3}{8} \
&=frac{2cdot :8-3}{8} \
&={color{#c34632}frac{13}{8}}
end{align*}
$$

$$
{color{#4257b2}text{c)}}
$$

$$
begin{align*}
-frac{3}{5}cdot :10& {=}quad : frac{3}{5}cdot frac{10}{1}\
&=-frac{3cdot :10}{5cdot :1} \
&=-frac{3cdot :10}{5} \
&=-frac{30}{5} \
&={color{#c34632}-6}
end{align*}
$$

$$
{color{#4257b2}text{d)}}
$$

$$
begin{align*}
mathrm{frac{2}{3}div :-2}& {=}quad : -frac{2}{2cdot :3}\
&=-frac{2}{6} \
&={color{#c34632}-frac{1}{3}}
end{align*}
$$

$$
color{#4257b2}text{ a) } frac{2}{15}
$$

$$
color{#4257b2}text{ b) } frac{13}{8}
$$

$$
color{#4257b2} text{ c) }-6
$$

$$
color{#4257b2} text{ d) } -frac{1}{3}
$$

$$
text{ }
$$

$$
text{ }
$$

$$
text{ }
$$

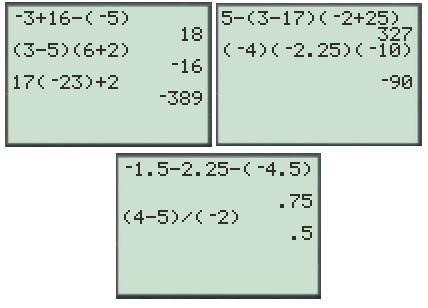
$$
begin{align*}
&text{a. }-3+16-(-5) & &to & &text{4. 18}\
&text{b. }(3-5)(6+2) & &to & &text{1. $-16$}\
&text{c. }17(-23)+2 & &to & &text{7. $389$}\
&text{d. }5-(3-17)(-2+25) & &to & &text{2. $327$}\
&text{e. }(-4)(-2.25)(-10) & &to & &text{5. $-90$}\
&text{f. }-1.5-2.25-(-4.5) & &to & &text{6. $0.75$}\
&text{g. }dfrac{4-5}{-2} & &to & &text{3. $0.5$}
end{align*}
$$

We need to calculate each equation below.

$color{#4257b2}text{(a)} y=2+4 cdot 3x x=-6$

$text{Substitute value of $x$ as follows}$:

$$
y =2+(4 cdot3 cdot -6)=2+(-72)=2-72
$$

$$
y=-70
$$

$color{#4257b2}text{(b)} g(x)=(x-3)^2 g (-9)$

Substitute value of $x$ in the function as follows:

$$
f(-9)=(-9-3)^2=(-12)^2=Large144
$$

$$
f(-9)=144
$$

$color{#4257b2}text{(c)} c(x)=x-2 c(x)=3.5$

Substitute value of $c(x)$ in the function as follows:

$$
3.5=x-2=
$$

Isolate the variables on the left side as follows:

$$
-x=-2-3.5=-5.5
$$

$$
x=5.5
$$

$color{#4257b2}text{(d)} y=5x^2-4 x=-2$

$text{Substitute value of $x$ as follows}$:

$$
y =5 (-2)^2-4=5 cdot4-4=20-4
$$

$$
y=16
$$

(a) $y=-70$ (b) $g(-9)=144$

(c) $x=5.5$ (d) $y=16$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 1-2-1=4+2x-(x-2x-2)
$$

$$
1-2-1=4+2x-x+2x+2
$$

Isolate the variables on the left side as follows:

$$
-2x-2x+x=4+2-1+2+1
$$

$$
-3x=8 x=dfrac{8}{-3} x=dfrac{-8}{3} x=-2.66
$$

$$
color{#4257b2}text{(b)} 2x-(y-2)=-2-(-y)
$$

$$
2x-y+2=-2+y
$$

Isolate the variables on the left side as follows:

$$
2x-y-y=-2-2 2x-2y=-4
$$

Divided the entire equation by $2$ as follows:

$$
x-y=-4
$$
Not supported

(a) $x=-dfrac{8}{3}$ (b) Not supported

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} x^2+2x-(-2x)=x-2-(-1-x^2)
$$

$$
x^2+2x+2x=x-2+1+x^2
$$

Isolate the variables on the left side as follows:

$$
x^2+2x+2x-x-x^2=2+1
$$

$$
3x=3 x=dfrac{3}{3} x=1
$$

$$
color{#4257b2}text{(b)} x+1-1-(-2)=x+3-(1-x)
$$

$$
x+1-1+2=x+3-1+x
$$

Isolate the variables on the left side as follows:

$$
x-x-x=3-1-2+1-1 -x=0 x=0
$$

$$
color{#4257b2}text{(c)} 1-4-x-(4-1)=-x-2-(4)
$$

$$
1-4-x-4+1=-x-2-4
$$

Isolate the variables on the left side as follows:

$$
-x+x=-2-4+4+4-1-1 0=0
$$

No variables value in the equation to be calculated, because the left side and right side are equals zero.

(a) $x=1$ (b) $x=0$ (c) Not supported

$$
{color{#4257b2}text{ a) }}
$$

$$
begin{align*}
& text{Subtract 2 from both sides}\
&-x+2-2=4-2\\
&-x=2 tag{Simplify} \
&frac{-x}{-1}=frac{2}{-1} tag{Divide both sides by -1}\
&boxed{{color{#c34632} x=-2 } }
end{align*}
$$

$$
{color{#4257b2}text{ b) }}
$$

$$
begin{align*}
& text{Group like terms}\
&4x+x-2=2x+8+3x\\
&5x-2=2x+8+3x tag{Add similar elements} \
&5x-2=2x+3x+8 tag{Group like terms}\
&5x-2=5x+8 tag{Add similar elements}\
&5x-2+2=5x+8+2 tag{Add 2 to both sides}\
&5x=5x+10 tag{Simplify}\
&5x-5x=5x+10-5x tag{Subtract 5x from both sides}\
& 0=10 tag{Simplify}\
&color{#c34632} text{No Solution}\
end{align*}
$$

$$
{color{#4257b2}text{ c) }}
$$

$$
begin{align*}
& text{Group like terms}\
&4y+y-9=6\\
&5y-9+9=6+9tag{Add 9 to both sides}\
&5y=15 tag{Simplify}\
&frac{5y}{5}=frac{15}{5}tag{Divide both sides by 5}\
&boxed{{color{#c34632} y=3 } }
end{align*}
$$

$$
{color{#4257b2}text{ d) }}
$$

$$
begin{align*}
& text{Expand}\
&3y+7=y+1\\
&3y+7-7=y+1-7tag{Subtract 7 from both sides}\
&3y=y-6 tag{Simplify}\
&3y-y=y-6-ytag{Subtract y from both sides}\
&2y=-6 tag{Simplify}\
&frac{2y}{2}=frac{-6}{2} tag{Divide both sides by 2}\
&boxed{{color{#c34632} y=-3 } }
end{align*}
$$

$$
color{#4257b2} text{a)}x=-2
$$

$$
color{#4257b2} text{b) No Solution}
$$

$$
color{#4257b2} text{c)}y=3
$$

$$
color{#4257b2} text{d)}y=-3
$$

First step is flipping a tile to move it out of the region into the opposite region.

Second one is zero pairs, or, removing an equal number of oppposite tiles that are in the same region.

Third is removing an equal number of identical tiles from both, the $”-”$ and the $”+”$ region.

And fourth is taking away from both sides. Actually, when you are comparing expressions, if you have the same part then you can take it away. Whatever you do to one side, you can do to the other.

#### (a)

Here we get the following equation which is needed

to be solved for $x$:

$$
begin{align*}
-1-1+1+x-(1+1+1-x)&=1+1+1+1+1+1-(1-1)\
-1+x-3+x&=6\
2x&=10\
x&=5\
end{align*}
$$

So, the solution of this equation is $x=5$.

#### (b)

We will solve the given equation moving $x$ to the one side of equality:

$$
begin{align*}
4x&=-8\
x&=-2\
end{align*}
$$

#### (c)

Here, $-$ in front of the expression $(x-3)$ means that in that case,

the expression is equal to:

$$
-(x-3)=-x+3
$$

The previous part actually explains the required equality.

(a) $x=5$; (b) $x=-2$; (c) Use distributivity

We need to write which of the following expression is greater.

$$
text{(a)} x-x+1-3-(2-1-x) text{or} x+2-2-(-3)
$$

$$
x-x+1-3-2+1+x text{or} x+2-2+3
$$

$$
x-x+x+1-3-2+1 text{or} x+2-2+3
$$

$$
x-3 text{or} x+3
$$

$$
-3 text{or} 3
$$

$text{color{#4257b2}The right side is greater than the left side}$

$$
text{(b)} x+2-2-(-2) text{or} 2-3-(2-x-1)
$$

$$
x+2-2+2 text{or} 2-3-2+x+1
$$

$$
x+2 text{or} x-2
$$

$$
2 text{or} -2
$$

$text{color{#4257b2}The left side is greater than the right side}$.

(a) $text{color{#4257b2}The right side is greater than the left side}$.

(b) $text{color{#4257b2}The left side is greater than the right side}$.

We would like to evaluate the following expression for the given values.

$$
text{(a)} 6m+2n^2 m=7, n=3
$$

$$
(6 cdot7)+(2 cdot3^2)=42+(2 cdot9)=42+18=Largecolor{#4257b2}60
$$

$$
text{(b)} dfrac{5x}{3}-2 x=1
$$

$$
dfrac{5 cdot1}{3}-2=dfrac{5}{3}-dfrac{2}{1}=dfrac{5-6}{3}=Largecolor{#4257b2}-dfrac{1}{3}
$$

$$
text{(c)} 6x^2-dfrac{x}{5} x=10
$$

$$
(6 cdot 10^2)-dfrac{10}{5}=(6 cdot100)-dfrac{2}{1}=600-2=Largecolor{#4257b2}598
$$

$$
text{(d)} (k-3)(k+2) k=1
$$

$$
(1-3)(1+2)=-2 cdot3=Largecolor{#4257b2}-6
$$

(a) $60$ (b) $-dfrac{1}{3}$

(c) $598$ (d) $-6$

We need to simplify each expression below.

$$
color{#4257b2}text{(a)} 4x+7+3y-(1+3y+2x)
$$

$$
4x+7+3y-1-3y-2x
$$

Add similar items to groups as follows:

$$
4x-2x-3y+3y+7-1
$$

$$
2x+6
$$

$$
color{#4257b2}text{(b)} 16x^2-4x+5-(16x^2-8x)+1
$$

$$
16x^2-4x+5-16x^2+8x+1
$$

Add similar items to groups as follows:

$$
16x^2-16x^2-4x+8x+5+1
$$

$$
4x+6
$$

$$
color{#4257b2}text{(c)} (32x-7y)-(28x-11y)
$$

$$
32x-7y-28x+11y
$$

Add similar items to groups as follows:

$$
32x-28x+11y-7y
$$

$$
4x+4y
$$

$$
color{#4257b2}text{(d)} y+2+2y+2+2y-2x+y
$$

Add similar items to groups as follows:

$$
y+2y+2y+y-2x+4
$$

$$
6y-2x+4
$$

$$
text{color{#4257b2}(a) $2x+6$ (b) $4x+6$
\
\
(c) $4x+4y$ (d) $6y-2x+4$}
$$

We need to answer of the following questions.

$$
text{color{#4257b2}(a) How much does one gallon of gas cost?}
$$

Let one gallon of gas has cost of $n$ so,

$$
12 cdot n=39.48 n= dfrac{39.48}{12}=3.29text{ dollars}
$$

$therefore$ One gallon of gas has cost of $3.29text{ dollars}$

$$
text{color{#4257b2}(b) How much will it cost if he needed $15$ gallons of gas?}
$$

Let one gallon of gas has cost of $3.29text{ dollars}$ so,

$$
15 cdot 3.29=49.35text{ dollars}
$$

$$
text{color{#4257b2}(c) How much gas it mopped needed if it cost $13.16$ dollars}
$$

Let one gallon of gas has cost of $3.29text{ dollars}$ so,

$$
x cdot 3.29=13.16 x= dfrac{13.16}{3.29}=4text{ gallons}
$$

(a) $3.29text{ dollars.}$ (b) $49.35text{ dollars.}$

(c) $4text{ gallons.}$

#### (a)

On the following picture there are graphed figures $4$ and $5$:

#### (b)

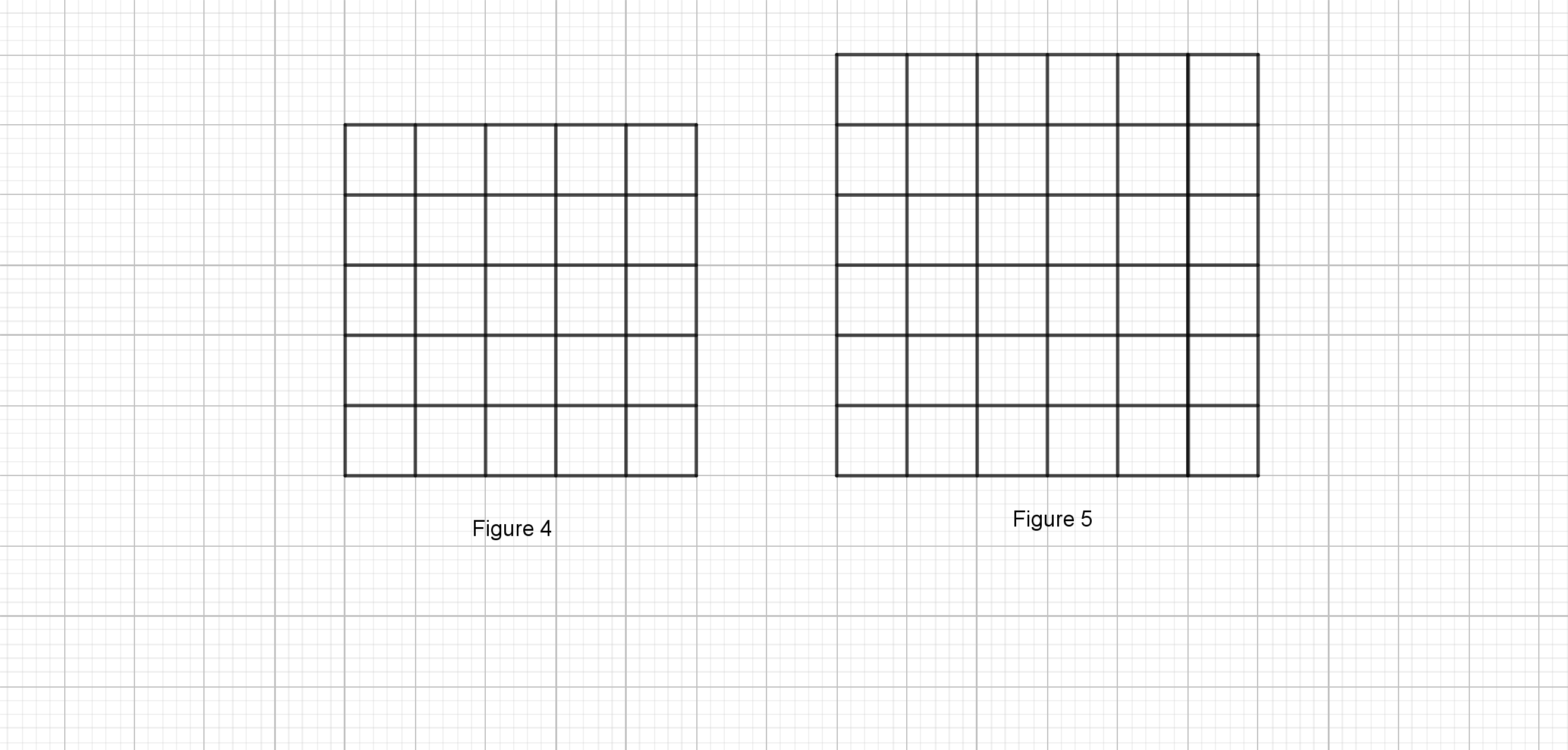
Conclusion is that Figure $10$ will have $11$ tiles on each side, while Figure $100$ will have $101$ tile on each side.

#### (c)

Here, each following figure has $4$ more patterns than previous, which means that Figure $5$ will have $21$ tiles, while Figure $8$ will have $33$ tiles.

(a) Use GeoGebra; (b) $11$ and $101$ tiles; (c) $21$ and $33$ tiles

#### (a)

Required equation is following:

$$
1+1+1+1+1+1-(x+x+x+1)=-x-x-3
$$

#### (b)

We will solve previous equation putting $x$ on one side of it and get:

$$
6-3x-1=-2x-3
$$

$$
-x=-8
$$

$$
x=8
$$

So, solution is $x=8$.

#### (c)

Here, Luke actually got follwing:

$$
-x=-8
$$

All he need to do is to multiply both sides by $-1$ and then get solution, $x=8$.

#### (d)

You need to add this move to the solution of task $60$.

#### (e)

You can substitute $8$ for $x$ in original equation from part (a) and check if both sides are equal in this case.

(a) $1+1+1+1+1+1-(x+x+x+1)=-x-x-3$; (b) $x=8$; (c) multiply by $-1$ both sides; (c) add this to the solution of task $60$; (d) substitute $8$ for $x$

#### (a)

We can substitute $100$ for $x$ in the given

equation and check it, and get:

$$
3cdot100-2=8
$$

$$
298=8
$$

But, $298ne8$, so, the conclusion is that Preston

is not correct.

#### (b)

We can substitute $4$ for $x$ in the given equation

and check it, so, we get:

$$
2cdot4+3-4=3cdot4-5
$$

$$
7=7
$$

So, the conclusion is that Edwin is correct.

#### (c)

We will solve the equation from part a) on the

following way:

$$
3x=10
$$

$$
x=dfrac{10}{3}
$$

So, the solution for this part is $x=dfrac{10}{3}$.

a) $x=100$ is not a solution; b) $x=4$ is a solution;

c) $x=dfrac{10}{3}$ is a solution.

We need to simplify and solving the following equations

to get the value of $x$.

$$
color{#4257b2}text{(a)} 3x+4=x+8
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
3x-x&=8-4 2x=4
\ \
x &=dfrac{4}{2} x=2
\
end{align*}
$$

$$
color{#4257b2}text{(b)} 4-2y=y+10
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
-2y-y &=10-4 -3y=6
\ \
y &=dfrac{6}{-3} y=dfrac{-6}{3} y=-2
end{align*}
$$

$$
color{#4257b2}text{(c)} 2x-4-5x=-(x+8)
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
2x-5x-x &=-8+4 -4x=-4
\ \
x &=dfrac{-4}{-4} x=1
\
end{align*}
$$

$$
color{#4257b2}text{(d)} -2-3k-2=-2k+8-k
$$

Isolate the variables on the left side and the numbers on the right side as follows:

$$
begin{align*}
-3k+2k+k &=8+2+2 0=12
\ \
text{No solution}
end{align*}
$$

(a) $x=2$ (b) $y=-2$

(b) $x=1$ (d) No solution

We will solve this equation in the following way:

$$
-2x=-4
$$

$$
x=2
$$

We got that solution is $x=2$.

We put $x$ on the one side of the equation,

and on that way we solved it.

$x=2$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 2x+3-(x-1)=2x-2-(-x)
$$

Change subtraction to adding the opposite as follows:

$$
2x+3-x+1=2x-2+x
$$

Isolate the variables on the left side as follows:

$$
2x-x-2x-x=-2-1-3
$$

$$
-2x=-6 x=dfrac{-6}{-2} x=3
$$

$$
color{#4257b2}text{(b)} 2x-(x-2)=-2-(x-1)
$$

Change subtraction to adding the opposite as follows:

$$
2x-x+2=-2-x+1
$$

Isolate the variables on the left side as follows:

$$
2x-x+x=-2+1-2 2x=-3
$$

$$
x=dfrac{-3}{2} x=-1.5
$$

$$
color{#4257b2}text{(c)} 3c-7=-c+1
$$

Isolate the variables on the left side as follows:

$$
3c+c=1+7
$$

$$
4c=8 c=dfrac{8}{4} c=2
$$

$$
color{#4257b2}text{(d)} -2+3x=2x+6+x
$$

Isolate the variables on the left side as follows:

$$
3x-2x-x=6+2 0=8
$$

No solution

(a) $x=3$ (b) $x=-1.5$

(c) $c=2$ (d) Not solution

We want to check the following equations to see if the given solution is correct or not.

$$
color{#4257b2}text{(a)} 3x+7=x-1 text{When} x=-4
$$

Substitute the value of $x=-4$ in the equation as follows:

$$
(3 cdot-4)+7=-4-1 -12+7=-5 -5=-5
$$

The left side is equal the right side, so the given solution is correct.

$$
color{#4257b2}text{(b)} -2x-4=-4x+3 text{When} x=3
$$

Substitute the value of $x=3$ in the equation as follows:

$$
(-2 cdot3)-4=(-4 cdot3)+3 -6-4=-12+3 -10=-9
$$

The left side is not equal the right side, so the given solution is not correct.

$$
color{#4257b2}text{(c)} -3x+5+5x-1=0 text{When} x=2
$$

Substitute the value of $x=2$ in the equation as follows:

$$
(-3 cdot2)+5+(5 cdot2)-1=0 -6+5+10-1=0 8=0
$$

The left side is not equal the right side, so the given solution is not correct.

$$
color{#4257b2}text{(d)} f(x)=-(x-1) text{When} f(-2)=3
$$

Substitute the value of $x=-2$ in the equation as follows:

$$
f(-2)=-(-2-1) f(-2)=-(-3) f(-2)=3
$$

The left side is equal the right side, so the given solution is correct.

#### (a)

Let $x$ be the price of the one-pound package of meat,

we get the following equation which we will solve for $x$:

$$
10x=27.50
$$

$$
x=2.75
$$

So, for $25$ pounds of meat, Ms. Hamm will pay:

$$
25cdot2.75=68.75text{ dollars}
$$

#### (b)

Let $y$ be required pounds, we will solve the following

equation for $y$:

$$
2.75y=55
$$

$$
y=20
$$

Ms. Hamm will buy $20$ pounds of meat.

a) $$68.75$; b) $20$ pounds

We need to get the answer for the following questions.

$$
text{color{#4257b2}(a) What are the dimension of the bathroom?}
$$

Area of bedroom is $90$ ft and its width is $10$ ft so,

Length $=dfrac{90}{10}=9$ ft

Area of kitchen is $105$ ft and its length is $15$ ft so,

Width $=dfrac{105}{15}=7$ ft

Length of bathroom $=$ length of bedroom $=9$ ft and,

Width of bathroom $=$ width of kitchen $=7$ ft

$$
text{color{#4257b2}(b) How much area will he have a clean?}
$$

He wont clean the bedroom so, adds other three areas to get the rest area of house as follows:

Area of kitchen $=15 cdot7=105$ sq.ft

Area of living room $=15 cdot10=150$ sq.ft

Area of bathroom $=9 cdot7=63$ sq.ft

Total area $=105+150+63=318$ sq.ft

$$
text{color{#4257b2}(a) Dimensions are $9$ ft and $7$ ft
\ \
(b) $318$ sq.ft}
$$

#### (a)

On the following picture there is given graph:

We have following matching:

$1$-D, $2$-A, $3$-C, $4$-B

We can notice that point $5$ is not matched.

#### (b)

For unmatched point, base is $6$ and height is $4$, so, the area is $6cdot4=24$ square units.

#### (c)

This point should not be on Cairo’s graph because its area is not $36$ square units.
#### (d)

The dimensions of three more rectangles are:

$1$ unit by $36$ units

$2$ units by $18$ units

$5$ units by $7.2$ units
Those points are on the following picture:

(a) $5$ is not matched; (b) $6, 4, 24$; (c) Its area is not $36$; (d) $(1,36), (2,18), (5,7.2)$; (e) It has $7$ vertics

We need to rewrite the following expressions as an equivalent expression.

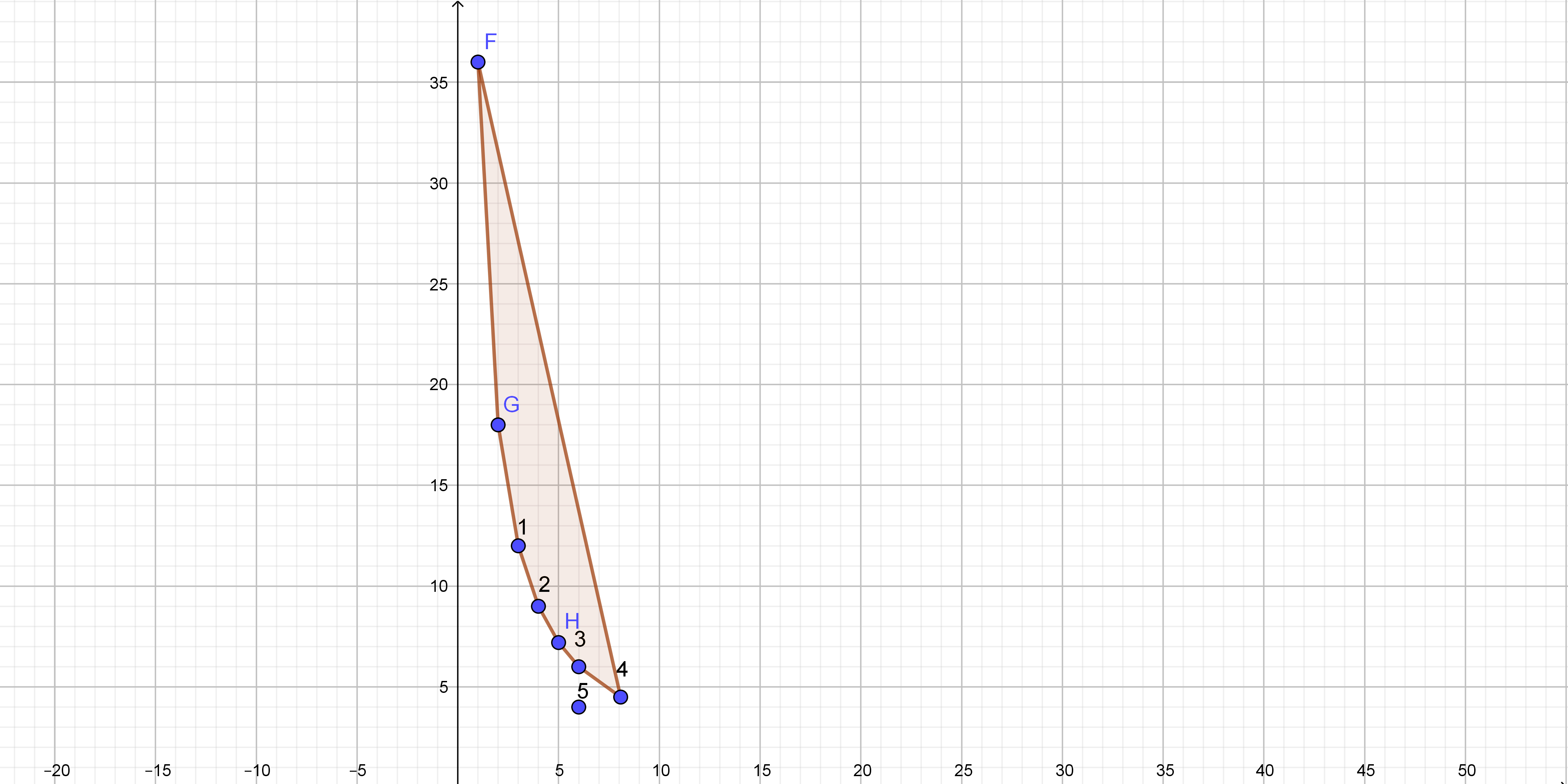
$$
Largecolor{#4257b2}text{(a)} x^3 x^-2
$$

$$
Large x^3 x^{-2}=x^{[3+(-2)]}=x^{(3-2)}=x^1=x
$$

$$
Largecolor{#4257b2}text{(b)} dfrac{y^5}{y^-2}
$$

$$
Large dfrac{y^5}{y^{-2}}=y^5 cdot y^{-(-2)}=y^5 cdot y^2=y^{(5+2)}=y^7
$$

$$
Largecolor{#4257b2}text{(c)} 4^{-1}
$$

$$
Large 4^{-1}=dfrac{1}{4}=0.25
$$

$$
Largecolor{#4257b2}text{(d)} (4x^2)^3
$$

$$
Large (4x^2)^3=4^3 cdot (x^2)^3=64 cdot x^2cdot x^2cdot x^2=64 x^{(2+2+2)}=64 x^6
$$

(a) $x$ (b) $y^7$

(c) $0.25$ (d) $64 x^6$

Here, you can ask if that number is even or odd, is it greater than $10$, for example.

Ask if it is even or odd, greater or less than $10$…

#### (a)

The equation which express the information in the game is following:

That is even number, between $0$ and $10$, divisible by $3$.

#### (b)

Between $0$ and $10$: $0, 1, 2, 3, 4, 5$…

Even number: $2, 4, 6, 8$

Divisible by $3$: $6$

So, solution is number $6$.

#### (c)

You can repeat all those steps in order to analyze Game $#4$ algebraically.

(a) Between $0$ and $10$, divisible by $3$; (b) $6$; (c) Repeat all steps

How many solutions does each equation blow have.

$$
color{#4257b2}text{(a)} 4x-5=x-5+3x
$$

Isolate the variables on the left side as follows:

$$
4x-3x-x=-5+5 4x-4x=-5+5
$$

$$
0=0 text{No solution}
$$

$$
color{#4257b2}text{(b)} -x-4x-7=-2x+5
$$

Isolate the variables on the left side as follows:

$$
-x-4x+2x=5+7 -3x=12
$$

$$
x=dfrac{12}{-3} x=-4
$$

$$
color{#4257b2}text{(c)} 3+5x-4-7x=2x-4x+1
$$

Isolate the variables on the left side as follows:

$$
5x-7x-2x+4x=1+4-3
$$

$$
0=2 text{No solution}
$$

$$
color{#4257b2}text{(d)} 4x-(-3x+2)=7x-2
$$

Change subtraction to adding the opposite as follows:

$$
4x+3x-2=7x-2
$$

Isolate the variables on the left side as follows:

$$
4x+3x-7x=-2+2 7x-7x=-2+2
$$

$$
0=0 text{No solution}
$$

$$
color{#4257b2}text{(e)} x+3+x+3=-(x+4)+(3x-2)
$$

Change subtraction to adding the opposite as follows:

$$
x+3+x+3=-x-4+3x-2
$$

Isolate the variables on the left side as follows:

$$
x+x+x-3x=-4-2-3-3 3x-3x=-12
$$

$$
0=-12 text{No solution}
$$

$$
color{#4257b2}text{(f)} x-5-(2-x)=-3
$$

Change subtraction to adding the opposite as follows:

$$
x-5-2+x=-3
$$

Isolate the variables on the left side as follows:

$$
x+x=-3+5+2 2x=4
$$

$$
x=dfrac{4}{2} x=2
$$

(a) No solution (b) $x=-4$

(c) No solution (d) No solution

(e) No solution (f) $x=2$

For example, let imagine number $12$. It is between $10$ and $15$, even number and divisible by $6$.

For example, imagine number $12$

For example, equation $0x=0$ has infinitely many solutions because any value of $x$ multiplied by $0$ is equal to $0$. But, equation $8x-2=8x+2$ has no solution because, after simplifying, we get $0=4$, which is not true.

$0x=0, 8x-2=8x+2$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 2-2x-(4-x)=2-3-(2x-2)
$$

Change subtraction to adding the opposite as follows:

$$
2-2x-4+x=2-3-2x+2
$$

Isolate the variables on the left side as follows:

$$
-2x+x+2x=2-3+2+4-2 x=3
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=3$ in the equation as follows:

$$
2-(2cdot3)-(4-3)=2-3-(2 cdot3-2) 2-6-1=2-3-4 -5=-5
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(b)} x+1-2-(3-x)=6-(1+2x-1)
$$

Change subtraction to adding the opposite as follows:

$$
x+1-2-3+x=6-1-2x+1
$$

Isolate the variables on the left side as follows:

$$
x+x+2x=6-1+1+3+2-1 4x=10
$$

$$
x=dfrac{10}{4} x=dfrac{5}{2} x=2.5
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=dfrac{5}{2}$ in the equation as follows:

$$
2.5+1-2-(3-2.5)=6-(1+2 cdot2.5-1) 2.5+1-2-0.5=6-5 1=1
$$

Since the left side is equal the right side, so the answer is correct.

$$
text{color{#4257b2}(a) $x=3$ (b) $x=2.5$}
$$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 3x-7+9-2x=x+2
$$

Isolate the variables on the left side as follows:

$$
3x-2x-x=2-9+7 -3x+3x=-7+7
$$

$$
0=0 text{No solution}
$$

$$
color{#4257b2}text{(b)} -2m+8+m+1=0
$$

Isolate the variables on the left side as follows:

$$
-2m+m=-1-8 -m=-9 m=9
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=9$ in the equation as follows:

$$
(-2cdot9)+8+9+1=0 -18+8+9+1=0 0=0
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(c)} 2=x+6-2x
$$

Isolate the variables on the left side as follows:

$$
-x+2x=6-2 x=4
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=4$ in the equation as follows:

$$
2=4+6-(2cdot4) 2=4+6-8 2=10-8 2=2
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(d)} 0.5p=p+5
$$

Isolate the variables on the left side as follows:

$$
0.5p-p=5 -0.5p=5 p=dfrac{5}{-tfrac{1}{2}}
$$

$$
p=5 cdot-2 p=-10
$$

$text{color{#4257b2}Check:}$ substitute the value of $p=-10$ in the equation as follows:

$$
0.5 cdot(-10)=-10+5 -5=-5
$$

Since the left side is equal the right side, so the answer is correct.

(a) No solution (b) $x=9$

(c) $x=4$ (d) $p=-10$

$$
text{color{#4257b2}We need to know how many students attend east high school?}
$$

Let Assume that the student at east high school is $x$ and student

in west high school is $x-250$

Total students can be represented by $color{#4257b2}2858=x-250+x$

$$
2x-250=2858
$$

Isolate the variables on the left side as follows:

$$
2x=2858+250 2x=3108 x=dfrac{3108}{2}
$$

$$
x=1554
$$

The student in the east high school is $color{#4257b2}1554$ students.

$color{#4257b2}1554$ students

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} -3+2x=-x+6
$$

Isolate the variables on the left side as follows:

$$
2x+x=6+3 3x=9
$$

$$
x=dfrac{9}{3} x=3
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=3$ in the equation as follows:

$$
-3+(2cdot3)=-3+6 -3+6=-3+6 3=3
$$

Since the left side is equal the right sidem, so the answer is correct.

$$
color{#4257b2}text{(b)} 5-3x=x+1
$$

Isolate the variables on the left side as follows:

$$
-3x-x=1-5 -4x=-4
$$

$$
x=dfrac{-4}{-4} x=1
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=1$ in the equation as follows:

$$
5-(3cdot1)=1+1 5-3=2 2=2
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(c)} -2x=4x+9
$$

Isolate the variables on the left side as follows:

$$
-2x-4x=9 -6x=9
$$

$$
x=dfrac{9}{-6} x=dfrac{-3}{2} x=-1.5
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=-1.5$ in the equation as follows:

$$
-2cdot-1.5=(4cdot-1.5)+9 3=-6+9 3=3
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(d)} 4x+3=x
$$

Isolate the variables on the left side as follows:

$$
4x-x=-3 3x=-3
$$

$$
x=dfrac{-3}{3} x=-1
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=-1$ in the equation as follows:

$$
(4cdot-1)+3=-1 -4+3=-1 -1=-1
$$

Since the left side is equal the right side, so the answer is correct.

(a) $x=3$ (b) $x=1$

(c) $x=-1.5$ (d) $x=-1$

Simplify the following expression.

$$
color{#4257b2}text{(a)} dfrac{5}{4}+dfrac{7}{16}
$$

$$
=dfrac{(5cdot16)+(4cdot7)}{16cdot4}=dfrac{80+28}{64}=dfrac{108}{64}=1.6875
$$

$$
color{#4257b2}text{(b)} -dfrac{10}{13} cdot dfrac{5}{11}
$$

$$
=dfrac{(5cdot-10)}{11cdot13}=dfrac{-50}{143}=-0.3496
$$

$$
color{#4257b2}text{(c)} dfrac{9}{11}+dfrac{-20}{21}
$$

$$
=dfrac{(9cdot21)+(11cdot-20)}{21cdot11}=dfrac{189-220}{231}=dfrac{-31}{231}=-0.1342
$$

$$
color{#4257b2}text{(d)} dfrac{-8}{3}+dfrac{-5}{18}
$$

$$
=dfrac{(-8cdot18)+(3cdot-5)}{18cdot3}=dfrac{-144-15}{54}=dfrac{-159}{54}=-2.9444
$$

(a) $1.6875$ (b) $-0.3496$

(c) $-0.1342$ (d) $-2.9444$

$textbf{(a)}$ It can be observed that length of each side of quadrilateral is equal and perpendicular to each other.

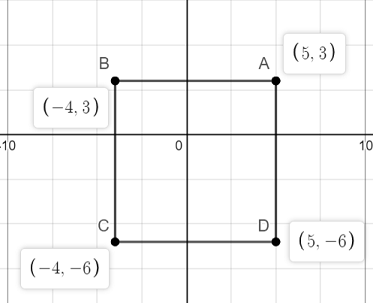
Therefore, it is a $text{textcolor{#4257b2}{square}}$.

$textbf{(b)}$ Length of each side of quadrilateral is $|3-(-6)|=textcolor{#4257b2}{9 textrm{ units}}$

$textbf{(c)}$ Area of square is square of the side, therefore area($A$) of quadrilateral is:

$$
A=(9)^2=81textrm{ unit}^2
$$

$textbf{(d)}$ Perimeter of square is 4 times the side, therefore perimeter($P$) of quadrilateral is:

$$
P=4 times 9=36textrm{ units}
$$

(a) Square (b) 9 units (c) 81 unit$^2$ (d) 36 units

In order to find how many tiles will be in Figure $50$, we need to substitute $50$ for $x$ in pattern and solve it for $y$, so, we will get:

$$
y=6cdot50+3
$$

$$
y=303
$$

Conclusion is that there will be $303$ tiles in Figure $50$.

$303$ tiles

#### (a)

Conclusion is that we suppose to supstitute $45$ for $y$ in order to solve Lew’s problem.

#### (b)

An equation which is needed to be solved for $x$ is following:

$$
45=6x+3
$$

We will solve it on that way we will isolate $x$ and get:

$$
6x=42
$$

$$
x=7
$$

So, conclusion is that “Big $7$’s” figure is made up of $45$ tiles.

#### (c)

We can check it substituting $7$ for $x$ in original equation:

$$
y=6cdot7+3
$$

$$
y=45
$$

We got $y=45$, which is supposed to be gotten, our solution is correct.

(a) Substitute $45$ for $y$; (b) $x=7$; (c) Substitute $7$ for $x$

We will substitute $84$ for $y$ in equation from previous task and solve it for $x$:

$$
84=6x+3
$$

$$
6x=81
$$

$$
x=13.5
$$

Conclusion is that this solution has no sense because it is not an integer.

$x=13.5$, it is not integer and has no sense

In order to determine how many tickets girls bought, we will substitute $824.5$ for $y$ in equation and solve it for $x$, so, we will get the following:

$$
824.5=8.5+68x
$$

$$
68x=816
$$

$$
x=12
$$

Girls bought $12$ tickets.

In order to check our solution, we will substitute $12$ for $x$ and get:

$$
824.5=8.5+68.12
$$

$$
824.5=824.5
$$

So, our solution is correct.

$12$ tickets

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} dfrac{1}{2} x-2=x-4
$$

Isolate the variables on the left side as follows:

$$
dfrac{1}{2}x-x=-4+2 -dfrac{1}{2}x=-2
$$

Multiply both sides of equation by $-2$ as follows.

$$
left(-dfrac{1}{2} cdot -2right)x=-2cdot-2 x=4
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=4$ in the equation as follows:

$$
dfrac{1}{2}cdot4-2=4-4 2-2=4-4 0=0
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(b)} 8-0.25x=0.5x+2
$$

Isolate the variables on the left side as follows:

$$
-0.25x-0.5x=2-8 -0.75x=-6
$$

$$
x=dfrac{-6}{-0.75} x=8
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=8$ in the equation as follows:

$$
8-(0.25cdot8)=(0.5cdot8)+2 8-2=4+2 6=6
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(c)} x+2-0.5x=1+0.5x+1
$$

Isolate the variables on the left side as follows:

$$
x-0.5x-0.5x=1+1-2 x-x=2-2
$$

$$
0=0 text{No solution}
$$

$$
color{#4257b2}text{(d)} 7x-0.15=2x+0.6
$$

Isolate the variables on the left side as follows:

$$
7x-2x=0.6+0.15 5x=0.75
$$

$$
x=dfrac{0.75}{5} x=0.15
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=0.15$ in the equation as follows:

$$
(7cdot0.15)-0.15=(2cdot0.15)+0.6 1.05-0.15=0.3+0.6 0.9=0.9
$$

Since the left side is equal the right side, so the answer is correct.

(a) $x=4$ (b) $x=8$

(c) No solution (d) $x=0.15$

subsection*{(a)}
We will solve this equation on following way:\

$$1.6x=4$$\
$$x=2.5$$\

Now, substitute $2.5$ for $x$ in equation and get:\

$$5=1.6cdot2.5+1$$\
$$5=5$$\
So, our solution is correct.\
subsection*{(b)}
Completed table for given rule is following:\

begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $y$ \
hline
$-1$ & $-0.6$\
hline
$0$ & $1$\
hline
$1$ & $2.6$\
hline
$2$ & $4.2$\
hline
end{tabular}
end{center}

On the following picture there is graphed the line $y=1.6x+1$:\

#### (c)

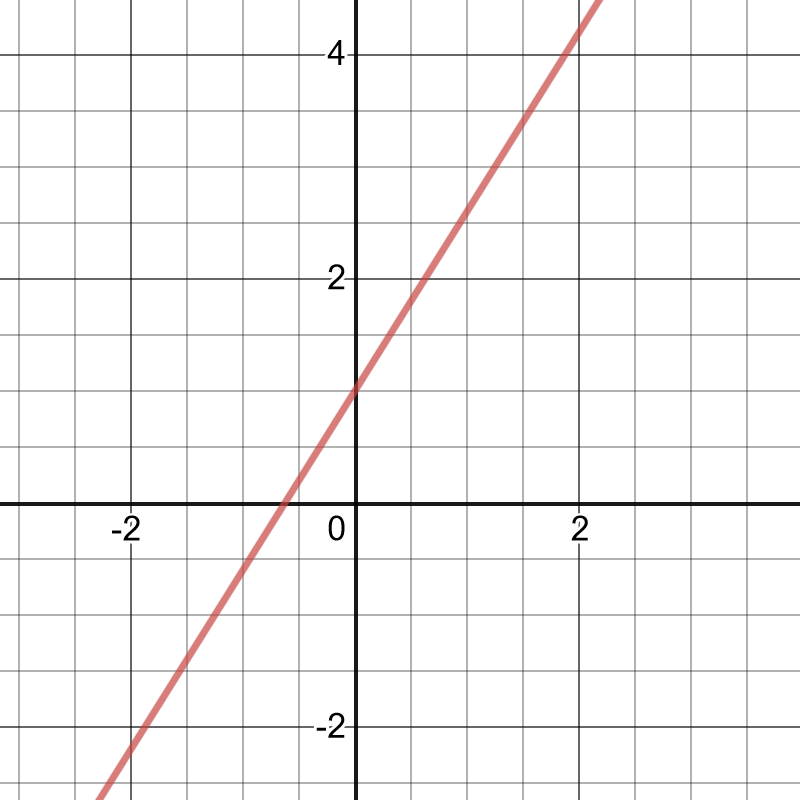
From previous picture, we can notice that required value of $x$ is $2.5$ and it is the same result as in part (a).

(a)$x=2.5$; (b) Make table for $-1, 0, 1, 2$; (c) $x=2.5$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 3x-7=3x+1
$$

Isolate the variables on the left side as follows:

$$
3x-3x=1+7 0=8 text{ No solution}
$$

$$
color{#4257b2}text{(b)} -2x-5=-4x+2
$$

Isolate the variables on the left side as follows:

$$
-2x+4x=2+5 2x=7
$$

$$
x=dfrac{7}{2} x=3.5
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=3.5$ in the equation as follows:

$$
(-2cdot3.5)-5=(-4cdot3.5)+2 -7-5=-14+2 -12=-12
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(c)} 2+3x=x+2+2x
$$

Isolate the variables on the left side as follows:

$$
3x-x-2x=2-2 0=0 text{ No solution}
$$

$$
color{#4257b2}text{(d)} -(x-2)=x+2
$$

Change subtraction to adding the opposite as follows:

$$
-x+2=x+2
$$

Isolate the variables on the left side as follows:

$$
-x-x=2-2 -2x=0 x=0
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=0$ in the equation as follows:

$$
-(0-2)=0+2 -(-2)=2 2=2
$$

Since the left side is equal the right side, so the answer is correct.

(a) No solution (b) $x=3.5$

(c) No solution (d) $x=0$

We need to solve the following equations as follows:

$$
color{#4257b2}text{(a)} 1-3-(-2x)=-x-3-(2+x)
$$

Change subtraction to adding the opposite as follows:

$$
1-3+2x=-x-3-2-x
$$

Isolate the variables on the left side as follows:

$$
2x+x+x=-3-2+3-1 4x=-3
$$

$$
x=dfrac{-3}{4} x=-0.75
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=0.75$ in the equation as follows:

$$
1-3-(-2cdot-0.75)=-(-0.75)-3-(2-0.75) 1-3-1.5=0.75-3-1.25 -3.5=-3.5
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(b)} 1+y-1-(-2)=3+y-(1-y)
$$

Change subtraction to adding the opposite as follows:

$$
1+y-1+2=3+y-1+y
$$

Isolate the variables on the left side as follows:

$$
y-y-y=3-1-2+1-1 -y=0 y=0
$$

$text{color{#4257b2}Check:}$ substitute the value of $x=0$ in the equation as follows:

$$
1+0-1-(-2)=3+0-(1-0) 1-1+2=3-1 2=2
$$

Since the left side is equal the right side, so the answer is correct.

$$
color{#4257b2}text{(c)} 1-4-x-(4-1)=-x-2-(4)
$$

Change subtraction to adding the opposite as follows:

$$
1-4-x-4+1=-x-2-4
$$

Isolate the variables on the left side as follows:

$$
-x+x=-2-4-1+4+4-1 0=-8+8 0=0
$$

No solution

$$
text{color{#4257b2}(a) $x=-0.75$ (b) $y=0$
\ \
(c) No solution}
$$

Completed table is following:\

begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$text{Left Expression}$ & $text{Right Expression}$ & $text{Explanation}$ \
hline
$3x^2-(2x-4)$ & $3+3x^2+1$ & $text{Starting expression}$ \
hline
$3x^2+(-2x)+4$ & $3+3x^2+1$ & $text{Distributive rule}$ \
hline
$-2x+4$ & $4$ & $text{Remove $3x^2$ from both sides}$ \
hline
$-2x$ & $0$ & $text{Remove $4$ from both sides}$ \
hline
$x$ & $0$ & $text{Divide both sides by $-2$}$ \
hline
end{tabular}
end{center}

So, we got that solution of the equation is $x=0$.\

$x=0$

We want to evaluate the following expression for the given values.

$$
color{#4257b2}text{(a)} 30-2x text{When} x=-6
$$

Substitute the value of $x=-6$ in the equation as follows:

$$
30-(2cdot-6)=30-(-12)=30+12=42
$$

$$
color{#4257b2}text{(b)} x^2+2x text{When} x=-3
$$

Substitute the value of $x=-3$ in the equation as follows:

$$
(-3)^2+(2cdot-3)=9+(-6)=9-6=3
$$

$$
color{#4257b2}text{(c)} – dfrac{1}{2} x+9 text{When} x=-6
$$

Substitute the value of $x=-6$ in the equation as follows:

$$
-dfrac{1}{2}cdot-6+9=-dfrac{-6}{2}+9=-(-3)+9=3+9=12
$$

$$
color{#4257b2}text{(d)} sqrt{k} text{When} k=9
$$

Substitute the value of $x=9$ in the equation as follows:

$$
sqrt{9}=sqrt{3cdot3}=3
$$

(a) $42$ (b) $3$

(c) $12$ (d) $3$

Determine how long and how wide the rectangle.

Assume the width of rectangle is $color{#4257b2}x$ and length is $color{#4257b2}3+2x$

Total perimeter is $78$ cm. $78=x+3+2x+x+3+2x$

Add similar group like terms as follows:

$$
6x+6=78 6x=78-6 6x=72
$$

Divide the both side by $6$ as follows:

$$
x=dfrac{72}{6}=12 x=12
$$

Width of the rectangle is $12$ cm, and length is $3+(2cdot12)=3+24=27$ cm.

$text{color{#4257b2}Check:}$ Substitute the value of $x$ in the perimeter equation as follows:

$$
78=12+3+(2cdot12)+12+3+(2cdot12) 78=12+3+24+12+3+24=78
$$

Since the left side is equal the right side, so the answer is correct.

$$
text{color{#4257b2}Width $=12$ cm Length $=27$ cm}
$$

Let $x$ represent number of Schnauzers. Number of Scotties is $x+3$ and number of Wirehaired Terriers is $2x-5$. So, according to previous, we get following equation which we will solve for $x$:

$$
x+x+3+2x-5=78
$$

$$
4x-2=78
$$

$$
4x=80
$$

$$
x=20
$$

So, there were $20$ Schnauzers, $23$ Scotties and $35$ Wirehaired Terriers.

$20$ Schnauzers, $23$ Scotties and $35$ Wirehaired Terriers