
All Solutions
Page 495: Questions
For this inequality, stand up if your number is greater than or equal to $-2$.
$textbf{b.}$
For this inequality, stand up if your number is less than or equal to $1$.
$textbf{c.}$
For this equation, stand up if your number is 3.
$textbf{d.}$
For this inequality, stand up if your number is greater than or equal to $0$.
$textbf{e.}$
For this equation, stand up if your number is $-2$.
$textbf{f.}$
For this inequality, stand up if your number is between $-1$ and $4$, inclusive.
$textbf{g.}$
For this inequality, stand up if your number is less than or equal to $-2$ or if it is greater than or equal to 2.
$textbf{h.}$
For this inequality, stand up if your number is less than $-3$.

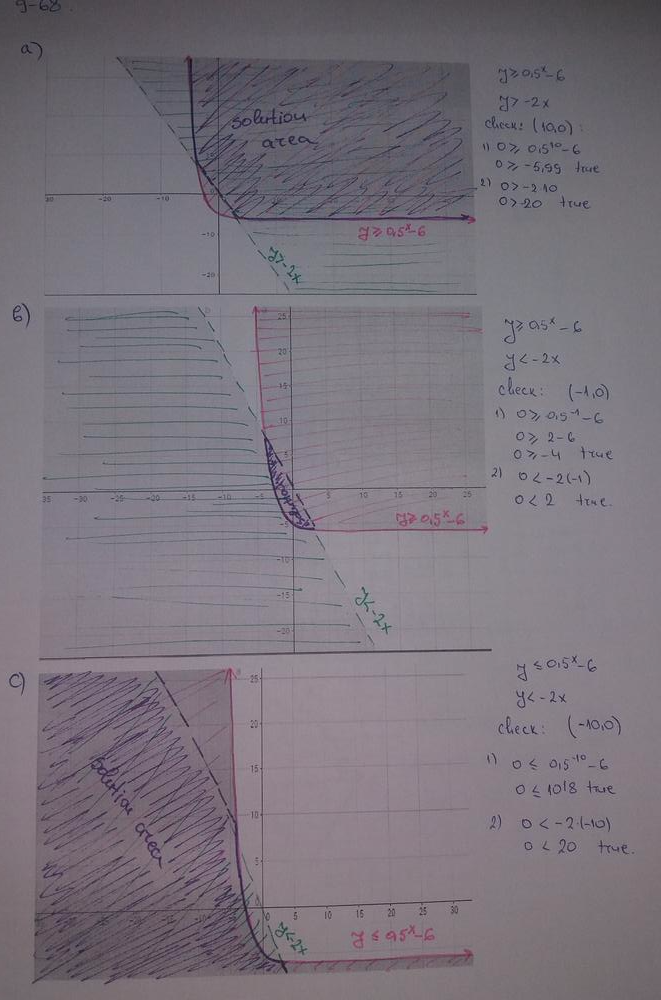
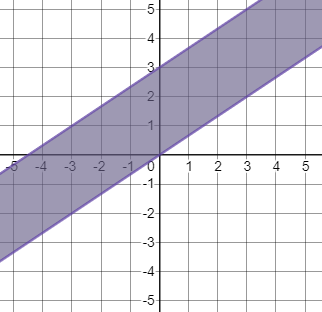
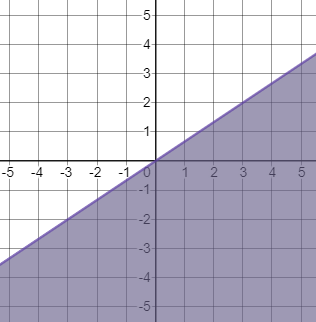
b) The inequality $xleq1$ have infinitely many solutions which are less than or equal to 1.
c) The inequality $-1leq x leq 4$ have solutions which are interval of $-1$ and $4$. It is a bounded solution. The inequality $x^2geq 4$ has solutions $xleq -2$ and $xgeq 2$.
$textbf{a.}$
The filled circle at 1 indicates that it is part of the solution. So, the inequality is represented by:
$$
color{#c34632}xgeq 1
$$
$textbf{b.}$
The open circle at 1 indicates that it is not part of the solution. So, the inequality is represented by:
$$
color{#c34632}x<1
$$
$textbf{c.}$
The filled circle at 3 indicates that it is part of the solution. So, the inequality is represented by:
$$
color{#c34632}xleq 3
$$
$textbf{d.}$
The open circle at $-4$ indicates that it is not part of the solution while the filled circle at 2 indicates that it is part of the solution. So, the inequality is represented by:
$$
color{#c34632}-4<xleq 2
$$
b. $x<1$
c. $xleq 3$
d. $-4<xleq 2$
(a) $xge1$ (b) $x<-1$
(c) $2le x<-3$ (d) $-4<xle2$
(c) $2le x<-3$ (d) $-4<xle2$
Five possible $x$-values that make the inequality true are:
$$
x={4,5,6,7,8}
$$
We can see that there are infinitely many solutions as all numbers greater than or equal to 4 are possible solutions.
$textbf{b.}$
The smallest solution for $x$ is $color{#c34632}4$, our boundary point.
$textbf{c.}$
The boundary point is the indicator where the solution of the given inequality. It is the solution of the corresponding equation of the inequality if we replaced $geq$ with $=$.
$textbf{d.}$
Using the results from parts (a) and (b), the solution of the inequality is:
$$
color{#c34632}xgeq 4
$$
To graph this on a number line, draw a filled circle at 4 and an arrow pointing to the right.

b. 4
c. The boundary point is the indicator where the solution of the given inequality. It is the solution of the corresponding equation of the inequality if we replaced $geq$ with $=$.
d. $xgeq 4$
We can replace $<$ with $=$ then solve for the corresponding equation:
$$
begin{align*}
3-2x&=1\
-2x&=-2\
color{#c34632}x&color{#c34632}=1
end{align*}
$$
$textbf{b.}$
The boundary point is not a solution because the inequality symbol used is $<$. So, we draw an open circle at $1$:

Choose a test point, say $x=0$:
$$
begin{align*}
3-2(0)&<1\
3-0&<1\
3&1$. So, draw an arrow pointing to the right:

b. Not part of the solution so draw an open circle at 1.
c. The solution is $x>1$.
$$
begin{align*}
3x+1&=7\
3x&=6\
x&=2
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
3(0)+1&<7\
0+1&<7\
1&<7
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}x<2
$$
On a number line, use an open circle for the boundary point 2 then draw an arrow pointing to the left:

x<2
$$
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
2(3p+1)&=-4\
3p+1&=-2\
3p&=-3\
p&=-1
end{align*}
$$
Next, pick a test point except for the boundary point, say $p=0$ to substitute to the inequality:
$$
begin{align*}
2(3(0)+1)&>-4\
2(0+1)&>-4\
2&>-4
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the right of it:
$$
color{#c34632}p>-1
$$
On a number line, use an open circle for the boundary point $-1$ then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
9k-2&=3k+10\
9k&=3k+12\
6k&=12\
k&=2
end{align*}
$$
Next, pick a test point except for the boundary point, say $k=0$ to substitute to the inequality:
$$
begin{align*}
9(0)-2&<3(0)+10\
0-2&<0+10\
-2&<10
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}k<2
$$
On a number line, use an open circle for the boundary point 2 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
5-h&=4\
-h&=-1\
h&=1
end{align*}
$$
Next, pick a test point except for the boundary point, say $h=0$ to substitute to the inequality:
$$
begin{align*}
5-0&geq 4\
5&geq 4
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}hleq 1
$$
On a number line, use a filled circle for the boundary point 1 then draw an arrow pointing to the left:

b. $k<2$
c. $hleq 1$
The statement is $text{textcolor{#c34632}{always true}}$ since $-4$ is less than 9.
$textbf{b.}$
The statement is $text{textcolor{#c34632}{sometimes true}}$ because if $xgeq 1$, the statement is false.
$textbf{c.}$
The statement is $text{textcolor{#c34632}{never true}}$ since $-5$ is less than $-2$.
$textbf{d.}$
The statement is $text{textcolor{#c34632}{sometimes true}}$ because if $xne -1$, the statement is false.
$textbf{e.}$
The statement is $text{textcolor{#c34632}{always true}}$ since a number is equal to itself.
$textbf{f.}$
The statement is $text{textcolor{#c34632}{never true}}$ since a number cannot be less than itself.
b. sometimes true
c. never true
d. sometimes true
e. always true
f. never true
(a) $-4le9$ Always true.
(b) $x-2$ Not true
(d) $3x+5=2 3x=2-5 3x=-3 x=-1$
(e) $61=61$ Always true
(f) $-6<-6$ Not true
(d) $x=-1$ (e) Always true. (f) Not true.
$$
color{#4257b2}text{(a)} 2x+y=-7y y=x+10
$$
For first equation isolate the variables on the left side as follows:
$$
2x=-7y-y 2x=-8y x=-dfrac{8}{2} y x=-4y
$$
Substitution the value of $x=-4y$ for second equation as follows:
$$
y=-4y+10 y+4y=10 5y=10
$$
Divide both of sides by $5$ as follows:
$$
y=dfrac{10}{5} y=2
$$
Substitution the value of $y=2$ for second equation as follows:
$$
2=x+10 x=2-10 x=-8
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-8, y=2$ in the equation as follows:
$$
2=-8+10 2=2
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} 3x=-5y 6x-7y=17
$$
Multiply the first equ. by $-2$ to get $-6x=10y$
Rearrange the equation to be like that $ax+by=c$ as follows:
$$
-6x=10y -6x-10y=0
$$
Using elimination property for the new equations as follows:
$$
(6x-6x)+(-7y-10y)=(17+0) -17y=17
$$
Divide both sides by $-17$ as follows:
$$
y=-dfrac{17}{17} y=-1
$$
Substitution the value of $y=-1$ for first equation as follows:
$$
3x=(-5cdot-1) 3x=5 x=dfrac{5}{3}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=dfrac{5}{3}, y=-1$ in the equation as follows:
$$
left(3cdotdfrac{5}{3}right)=(-5cdot-1) 5=5
$$
Since the left side is equal the right side, so the answer is correct.
(b) $x=dfrac{5}{3} y=-1$
$$
color{#4257b2}(2, 48) (5, 750)
$$
The exponent function form is $y=a b^x$. Substitution values of $(x, y)$ in the exponential form as follows:
$$
48=a b^2 750=a b^5
$$
$$
a=dfrac{48}{b^2}
$$
Substitution value of $a$ in the second equation as follows:
$$
750=dfrac{48}{b^2}cdot b^5 750=48 b^3
$$
Divide both of sides by $48$ as follows:
$$
b^3=dfrac{750}{48} b^3=15.625
$$
$$
sqrt[3]{b^3}=sqrt[3]{15.625} b=2.5
$$
Substitution value of $b=2.5$ in the first equation as follows:
$$
48=a (2.5)^2 48=6.25 a
$$
Divide both of sides by $6.25$ as follows:
$$
a=dfrac{48}{6.25} a=7.68
$$
$$
y=a b^x y=7.68 (2.5)^x
$$
text{color{#4257b2}$a=7.68 b=2.5$ $y=7.68 (2.5)^x$}
$$
On the following picture, there is graphed the given data.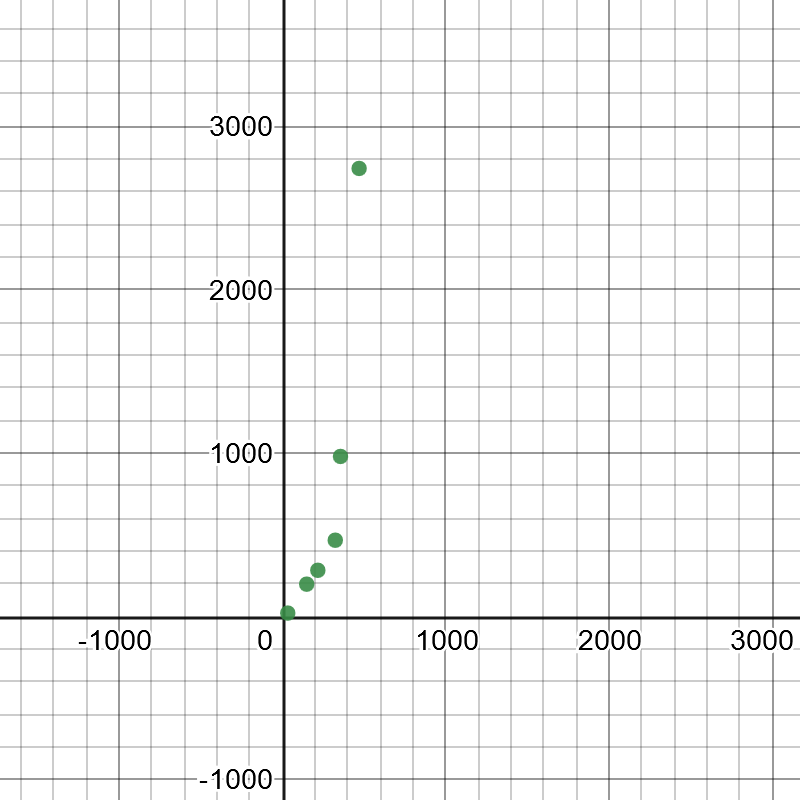
$$
text{Residual}=text{observed} text{ y-value}-text{Predicted y-value}
$$
#### (b)
On the following picture, there is graphed residual plot.
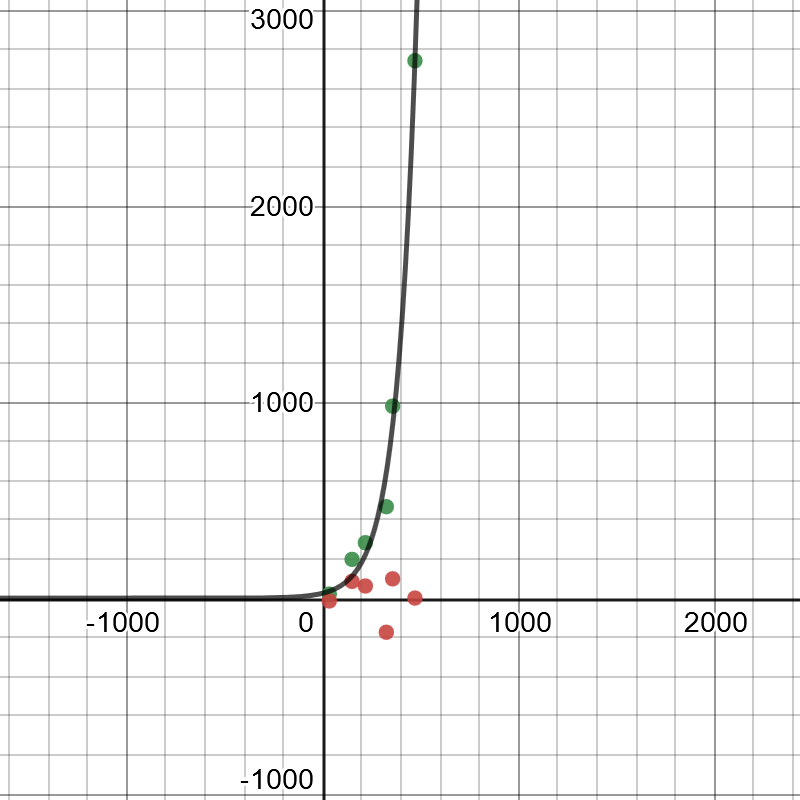
#### (c)
From the previous parts, we can conclude that we can fit our data using exponential model.
The equation of the required model will be the following:
$$
y=25.1879(1.01001)^x
$$
#### (d)
On the following picture, there is a graphed residual plot.
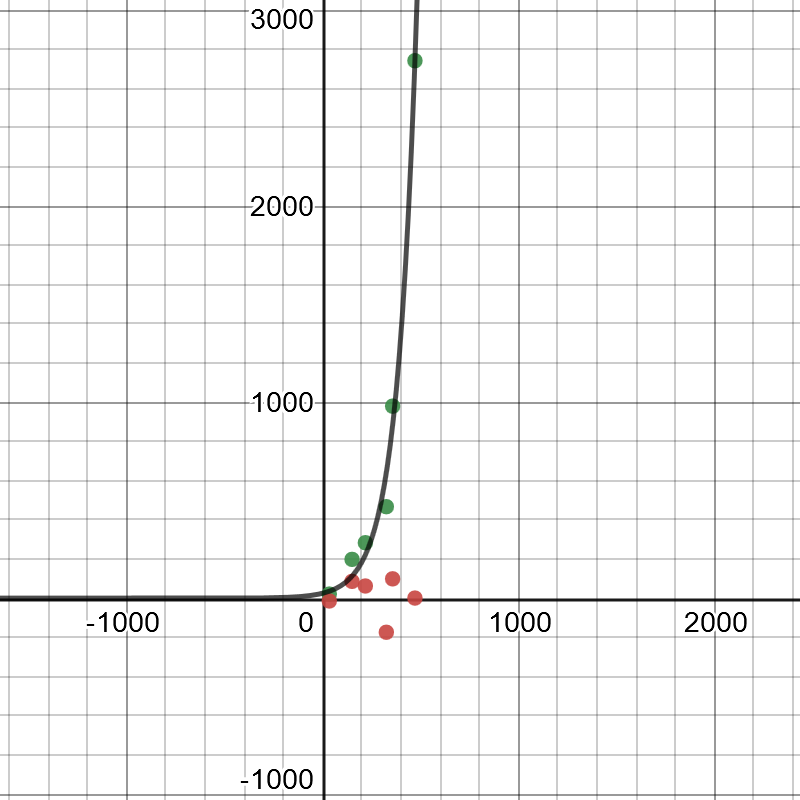
$$
color{#4257b2}text{(a) in the left figure}
$$
Since the small triangles are congruent, so :
$$
6x+6=8x+2
$$
Isolate the variables on left side as foloows:
$$
6x-8x=2-6 -2x=-4
$$
Divide both of sids by $-2$ as follows:
$$
x=dfrac{-4}{-2} x=2
$$
Substitute the value of $x=2$ in the side lengths as follows:
$$
6x+6=(6cdot2)+6=12+6=18
$$
$$
8x+2=(8cdot2)+2=16+2=18
$$
$$
12-2=(12cdot2)-2=24-2=22
$$
color{#4257b2}text{(b) in the right figure}
$$
Since the small triangles are congruent, so :
In the upper triangle, third length can be calculated as follows:
$$
=40^2+9^2=1600+81=1681
$$
Use square root property as follows:
$$
sqrt{1681}=41
$$
In the lower triangle, third length can be calculated as follows:
$$
=41^2-40^2=1681-1600=81
$$
Use square root property as follows:
$$
sqrt{81}=9
$$
$$
x=41-9=32
$$
text{color{#4257b2}(a) $x=2$ (b) $x=32$}
$$
$color{#4257b2}text{(a)} (5 a^{-2} b^3)^8 cdot (5 a b^{-2})^{-6}$
$(5^8 a^{-16} b^{24}) cdot (5^{-6} a^{-6} b^{12})$
$dfrac{5^8 b^{24}}{a^{16}} cdot dfrac{b^{12}}{5^6 a^6}=dfrac{5^8 b^{24} b^{12}}{5^6 a^{16} a^6}=dfrac{5^2 b^{36}}{a^{22}}=dfrac{25 b^{36}}{a^{22}}$
$color{#4257b2}text{(b)} dfrac{15 x^{-5} y^2}{(3x^2)^2 y^{-3}}$
$$
dfrac{15 x^{-5} y^2}{3^2 x^4 y^{-3}}=dfrac{15 y^2 y^3}{3^2 x^4 x^5}=dfrac{15 y^5}{9 x^9}=dfrac{5 y^5}{3 x^9}
$$
text{color{#4257b2}(a) $dfrac{25 b^{36}}{a^{22}}$ (b) $dfrac{5 y^5}{3 x^9}$}
$$
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
x-7&=-2\
x&=5
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
0-7&<-2\
-7&<-2
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}x<5
$$
On a number line, use an open circle for the boundary point 5 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
3m+2&=8m-8\
3m&=8m-10\
-5m&-10\
m&=2
end{align*}
$$
Next, pick a test point except for the boundary point, say $m=0$ to substitute to the inequality:
$$
begin{align*}
3(0)+2&leq 8(0)-8\
0+2&leq 0-8\
2¬{leq} -8\
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the left of it. So, the solution is to the right of the boundary point:
$$
color{#c34632}mgeq 2
$$
On a number line, use a filled circle for the boundary point 2 then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
dfrac{2}{3}p-2&=-4\
dfrac{2}{3}p&=-2\
p&=-3
end{align*}
$$
Next, pick a test point except for the boundary point, say $p=0$ to substitute to the inequality:
$$
begin{align*}
dfrac{2}{3}(0)-2&>-4\
0-2&>-4\
-2&>-4
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the right of it:
$$
color{#c34632}p>-4
$$
On a number line, use an open circle for the boundary point $-4$ then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
2-3(x-1)&=x-7 \
2-3x+3&=x-7 \
-3x+5&=x-7 \
-3x&=x-12 \
-4x&= -12 \
x&=3
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
2-3(0-1)&geq 0-7 \
2-3(-1)&geq -7 \
2-3&geq -7 \
-1&geq -7
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}xleq 3
$$
On a number line, use a filled circle for the boundary point 3 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
9k-4+1&= 2k-3+7k \
9k-3&= 9k-3
end{align*}
$$
The resulting equation is true for all values of $k$. However, it is only true for $k=0$ for the inequality $leq$ since a number cannot be less than the number itself. So, the solution is:
$$
color{#c34632}k=0
$$
Represent this as a filled circle at 0 on a number line:

When you replace the inequality symbol with $=$, the resulting equation is true for all values of $y$. However, it is false for the inequality $<$ since a number cannot be less than the number itself. So, the solution is the empty set (no solution):
$$
color{#c34632}{text{O}}
$$
Represent this as simply the number line:

d. $xleq 3$
e. $k=0$
f. ${text{O}}$
The total population of Turkey is 66 million so we can write:
$$
t+k=66tag{1}
$$
There are 4 times more Turks than Kurds so we can write:
$$
t=4ktag{2}
$$
Solve the system using Substitution Method. Substitute eq. (2) to eq. (1) and solve for $k$:
$$
begin{align*}
4k+k=&66\
5k=&66\
k=&13.2
end{align*}
$$
So, there are $text{color{#c34632}13.2 million Kurds that live in Turkey.}$
For this situation, it is appropriate an inequality. On that way, we will find how old must be at least a tree in order to flower this year.
#### (b)
Using information, we actually need to solve the following inequality for $x$:
$$
6+9xgeq150
$$
$$
9xgeq144
$$
$$
xgeq16
$$
So, the tree must be at least $16$ year old.
#### (c)
In this case, we actually need to solve and the following inequality for $x$ and make a union of this and the previous set of the solution:
$$
6+9x<240
$$
$$
9x<234
$$
$$
x<26
$$
So, the conclusion is that trees must be between $16$ and $26$ years old.
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
3(2k-1)&=9 \
6k-3&=9 \
6k&=12 \
k&=2
end{align*}
$$
Next, pick a test point except for the boundary point, say $k=0$ to substitute to the inequality:
$$
begin{align*}
3(2(0)-1)&<9 \
3(0-1)&<9 \
3(-1)&<9 \
-3&<9
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}k<2
$$
On a number line, use an open circle for the boundary point 2 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
dfrac{2p}{5}&=6 \
p&=6 cdot dfrac{5}{2}\
p&=15
end{align*}
$$
Next, pick a test point except for the boundary point, say $p=0$ to substitute to the inequality:
$$
begin{align*}
dfrac{2(0)}{5}&leq 6 \
0&leq 6
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}pleq 15
$$
On a number line, use a filled circle for the boundary point 15 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
-2+8n&=2\
8n&=4\
n&=dfrac{1}{2}
end{align*}
$$
Next, pick a test point except for the boundary point, say $n=0$ to substitute to the inequality:
$$
begin{align*}
-2+8(0)&>2\
-2+0&>2\
-2¬{>}2
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the left of it. So, the solution is the points to the right of the boundary point:
$$
color{#c34632}n>dfrac{1}{2}
$$
On a number line, use an open circle for the boundary point $dfrac{1}{2}$ then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
7t-4&=2t-4\
7t&=2t\
5t&=0\
t&=0
end{align*}
$$
Next, pick a test point except for the boundary point, say $t=1$ to substitute to the inequality:
$$
begin{align*}
7(1)-4&>2(1)-4\
7-4&>2-4\
3&>-2
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the right of it:
$$
color{#c34632}t>0
$$
On a number line, use an open circle for the boundary point $0$ then draw an arrow pointing to the right:

d. $t>0$
$$
2n-1-5
$$
Isolate the variables on the left side as follows:
$$
2n-5+1
$$
$$
2n-4
$$
Divide both of sides by $2$ as folows:
$$
n-dfrac{4}{2}
$$
$$
n-2
$$
The correct answer is forth one. (d)
text{color{#4257b2}(d) $n-2$}
$$
From graph, there are two points which equals $(0, 3) (1, 1)$
$$
y=a b^x 3=a b^0 3=acdot1= a=3
$$
$$
y=a b^x 1=a b^1 1=a b
$$
Substitution value of $a=3$ in the second equation as follows:
$$
1=a b 1=3 b
$$
Divide both of sides by $3$ as follows:
$$
b=dfrac{1}{3}
$$
Substitution value of $a=3, b=dfrac{1}{3}$ in the second equation as follows:
$$
3=3 (dfrac{1}{3})^0 1=3 (dfrac{1}{3})^1
$$
text{color{#4257b2}$a=3 b=dfrac{1}{3}$}
$$
Assume the number of kurds live in turkey is $x$
Assume the number of turkey live in turkey is $4x$
Total population is $66,000,000$
$$
4x+x=66,000,000
$$
Isolate the variables on left side as follows:
$$
5x=66,000,000
$$
Divide both sides by $5$ as follows:
$$
x=dfrac{66,000,000}{5}=13,200,000
$$
The number of kurds live in turkey is $13,200,000$ peoples.
The number of turkey live in turkey is $4cdot13,200,000=52,800,000$ peoples.
text{color{#4257b2}$13,200,000$ peoples}
$$
We know that the one miles is equal $1760$ yard, so:
When he run $8$ miles which equal:
$$
8cdot1760=14080text{ yard}
$$
The length of football field is $100$ yard, so:
$$
dfrac{14080}{100}=140.80text{ times}
$$
Griffin run the length of football field $140.80$ times.
text{color{#4257b2}$$140.80text{ times}$$}
$$

Replacing $<$ with $=$, we solve for $x$ to find the boundary point:
$$
begin{align*}
2x+7&=12\
2x&=5\
color{#c34632}x&color{#c34632}=2.5
end{align*}
$$
This is not part of the solution because it makes the inequality false (since $12not{<}12$).
$textbf{b.}$
Like what we did in part (a), we replace the inequality symbol with the equal symbol then solve for the variable to find the boundary point. To find the solutions, assign a test point (except for the boundary point itself) to the given inequality. If the point satisfies the inequality, shade the region where it is a part of. Otherwise, shade the other part.
b. Replace the inequality symbol with the equal symbol then solve for the variable to find the boundary point. To find the solutions, assign a test point to the given inequality. If the point satisfies the inequality, shade the region where it is a part of. Otherwise, shade the other part.
color{#4257b2} |3x-5|=16
$$
Equal $3x-5=16$ as follows:
$$
3x=16+5 3x=21
$$
Divide both of sides by $3$ as follows:
$$
x=dfrac{21}{3} x=7
$$
Equal $-3x+5=16$ as follows:
$$
-3x=16-5 -3x=11
$$
Divide both of sides by $-3$ as follows:
$$
x=dfrac{11}{-3} x=-dfrac{11}{3}
$$
The values of $x$ are equal
$$
x=7 text{ when} 3x-5ge0 3xge5 xgedfrac{5}{3}
$$
$$
x=-dfrac{11}{3} text{ when} 3x-5<0 3x<5 x<dfrac{5}{3}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-dfrac{11}{3}, x=7$ in the equation as follows:
$$
|3x-5|=16 |(3cdot7)-5|=16 |21-5|=16 16=16
$$
$$
|3x-5|=16 |(3cdot-dfrac{11}{3})-5|=16 |-11-5|=16 16=16
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}$x=7 x=-dfrac{11}{3}$}
$$
On the following picture, there is drawn a number line.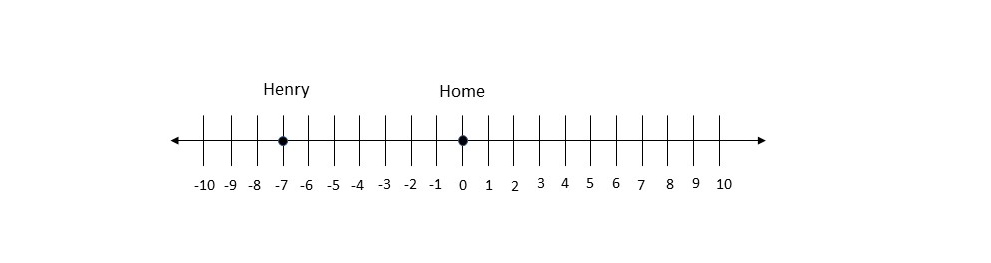
Henry’s possible location would be the following:
$$
text{location}=|0-7|
$$
On the following picture, there are possible Henry’s and Emerson’s positions: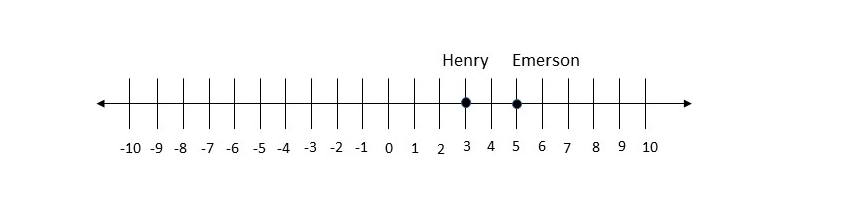
In equation which can be solved in order to determine where Emerson could be is the following:
$$
text{Emerson}=|3+2|
$$
#### (c)
Emerson’s possibly location is at $5$, which matches with the number line at part a).
On the following number line, there are Amanda’s possible positions.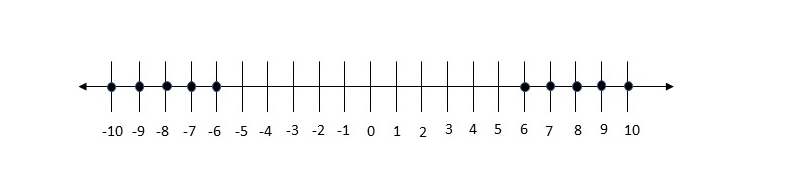
$$
|0-x|>5
$$
#### (b)
Amanda’s possible positions for this situation are:
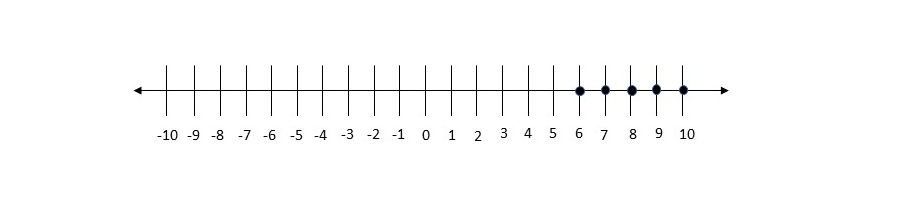
$$
x-0>5
$$
#### (c)
Solution for part a) would be:
$$
|x|>5
$$
$$
x5
$$
Solution for part b) would be:
$$
x>5
$$
$$
|x-3|<2
$$
$$
-2<x-3<2
$$
$$
1<x<5
$$
On the following picture, there are graphed all possible Emerson's positions:
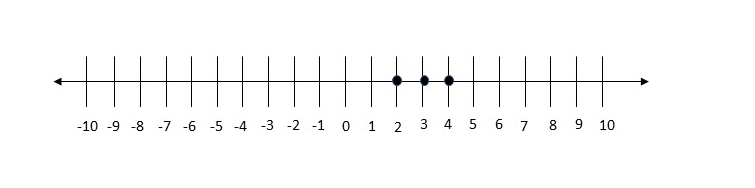


The final solution includes a combination of solutions from both cases.
$$
color{#4257b2}text{(a)} |x|=7
$$
Equal $x=7$
Equal $-x=7$ $x=-7$
The values of $x$ are equal
$$
x=7 text{ when} xge0
$$
$$
x=-7 text{ when} x<0
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=7, x=-7$ in the equation as follows:
$$
|x|=7 |7|=7 7=7
$$
$$
|x|=7 |-7|=7 7=7
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(b)} |2x|=32
$$
Equal $2x=32$ as follows:
$$
x=dfrac{32}{2} x=16
$$
Equal $-2x=32$ as follows:
$$
x=dfrac{32}{-2} x=-16
$$
$$
x=16 text{ when} 2xge0 xge0
$$
$$
x=-16 text{ when} 2x<0 x<0
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=16, x=-16$ in the equation as follows:
$$
|2x|=32 |2cdot16|=32 |32|=32 32=32
$$
$$
|2x|=32 |2cdot-16|=32 |-32|=32 32=32
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(c)} |x+7|=10
$$
Equal $x+7=10$ as follows:
$$
x=10-7 x=3
$$
Equal $-x-7=10$ as follows:
$$
-x=10+7 -x=17 x=-17
$$
The values of $x$ are equal
$$
x=3 text{ when} x+7ge0 xge-7
$$
$$
x=-17 text{ when} x+7<0 x<-7
$$
$$
|x+7|=10 |3+7|=10 |10|=10 10=10
$$
$$
|x+7|=10 |-17+7|=10 |-10|=10 10=10
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(d)} 5|x|=35
$$
Divide both of sides by $5$ as follows:
$$
|x|=dfrac{35}{5} |x|=7
$$
Equal $x=7$
Equal $-x=7$ $x=-7$
The values of $x$ are equal
$$
x=7 text{ when} xge0
$$
$$
x=-7 text{ when} x<0
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=7, x=-7$ in the equation as follows:
$$
|x|=7 |7|=7 7=7
$$
$$
|x|=7 |-7|=7 7=7
$$
Since the left side is equal the right side, so the answer is correct.
(c) $x=3$ or $x=-17$ (d) $x=7$ or $x=-7$
{color{#4257b2}text{ a) }}
$$
$$
begin{align*}
&text{This example is solved in the following way}\
&6<4\\
&color{#c34632} text{FALSE} \
end{align*}
$$
{color{#4257b2}text{ b) }}
$$
$$
begin{align*}
&text{This example is solved in the following way}\
&2>2.5\\
&color{#c34632} text{FALSE} \
end{align*}
$$
{color{#4257b2}text{ c) }}
$$
$$
begin{align*}
&text{This example is solved in the following way}\
&4ge :0\\
&color{#c34632} text{TRUE} \
end{align*}
$$
{color{#4257b2}text{ d) }}
$$
$$
begin{align*}
&text{This example is solved in the following way}\
&1>1\\
&color{#c34632} text{FALSE} \
end{align*}
$$
color{#4257b2} text{a)FALSE}
$$
$$
color{#4257b2} text{b)FALSE}
$$
$$
color{#4257b2} text{c)TRUE}
$$
$$
color{#4257b2} text{d)FALSE}
$$
Let:
$$
begin{align}
3x-2y&=14\
-2x+2y&=-10
end{align}
$$
The equations have opposite terms so we can use the Elimination Method to solve it. Add each side of eq. (1) and eq. (2) to eliminate $y$ then solve for $x$:
$$
x=4
$$
Solve for $y$ using eq. (2):
$$
begin{align*}
-2(4)+2y&=-10\
-8+2y&=-10\
2y&=-2\
y&=-1
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(4,-1)
$$
Let:
$$
begin{align}
y&=5x+3\
-2x-4y&=10
end{align}
$$
Since $y$ is already isolated in eq. (1), we use Substitution Method. Substitute eq. (1) to eq. (2) then solve for $x$:
$$
begin{align*}
-2x-4(5x+3)&=10\
-2x-20x-12&=10\
-22x-12&=10\
-22x&=22\
x&=-1
end{align*}
$$
Solve for $y$ using eq. (1):
$$
begin{align*}
y&=5(-1)+3\
y&=-5+3\
y&=-2
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(-1,-2)
$$
$textbf{c.}$
The system in part (b).
$textbf{d.}$
The system in part (a).
b. $(-1,-2)$
c. System in part (b)
d. System in part (a)
$$
color{#4257b2}text{(a)} 3x-2y=14 -2x+2y=-10
$$
Using elimination property for the new equations as follows:
$$
(3x-2x)+(-2y+2y)=(14-10) x=4
$$
Substitution the value of $x=4$ for first equation as follows:
$$
(3cdot4)-2y=14 12-2y=14 -2y=14-12
$$
$$
-2y=2 y=dfrac{2}{-2} y=-1
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=4, y=-1$ in the equation as follows:
$$
(3cdot4)-(2cdot-1)=14 12+2=14 14=14
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(a)} y=5x+3 -2x-4y=10
$$
$$
-5x+y=3 -2x-4y=10
$$
Multiply the first equ. by $4$ to get $-20x+4y=12$
Using elimination property for the new equations as follows:
$$
(-2x-20x)+(-4y+4y)=(10+12) -22x=22
$$
Divide both of sides by $-22$ as follows:
$$
x=dfrac{22}{-22} x=-1
$$
Substitution the value of $x=-1$ for first equation as follows:
$$
y=(5cdot-1)+3 y=-5+3 y=-2
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-1, y=-2$ in the equation as follows:
$$
-2=(5cdot-1)+3 -2=-5+3 -2=-2
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $x=4 y=-1$
\ \
(b) $x=-1 y=-2$}
$$
$$
3=ab^2tag{1}
$$
Using point $left(5,dfrac{1}{9}right)$, we write another equation:
$$
dfrac{1}{9}=ab^5tag{2}
$$
Using eq. (1), solve for $a$ to obtain the equation:
$$
a=dfrac{3}{b^2} tag{3}
$$
Substitute eq. (3) to eq. (2) then solve for $b$:
$$
begin{align*}
dfrac{1}{9}&=dfrac{3}{b^2}cdot b^5\
dfrac{1}{9}&=3b^3\
dfrac{1}{27}&=b^3\
sqrt[3]{dfrac{1}{27}}&=b\
dfrac{1}{3}&=b
end{align*}
$$
Solve for $a$ using eq. (3):
$$
begin{align*}
a&=dfrac{3}{(1/3)^2}\
a&=27
end{align*}
$$
So, the exponential function is:
$$
color{#c34632}y=27 left(dfrac{1}{3}right)^x
$$
y=27 left(dfrac{1}{3}right)^x
$$
$$
color{#4257b2}(2, 3) left(5, dfrac{1}{9}right)
$$
The exponent function form is $y=a b^x$ . Substitution values of $(x, y)$ in the exponential form as follows:
$$
3=a b^2 dfrac{1}{9}=a b^5
$$
Divide by $b^5$ in the second equation for both sides as follows:
$$
a=dfrac{1}{9 b^5}
$$
Substitution value of $a$ in the first equation as follows:
$$
3=dfrac{1}{9 b^5} cdot b^2 3=dfrac{1}{9 b^3}
$$
$$
3cdot 9 b^3=1 27 b^3=1 b^3=dfrac{1}{27}
$$
$$
sqrt[3]{b^3}=sqrt[3]{27} b=3
$$
Substitution value of $b=3$ in the first equation as follows:
$$
3=a (3)^2 3=9 a
$$
Divide both of sides by $9$ as follows:
$$
a=dfrac{3}{9} a=dfrac{1}{3}
$$
y=dfrac{1}{3}(3)^x
$$
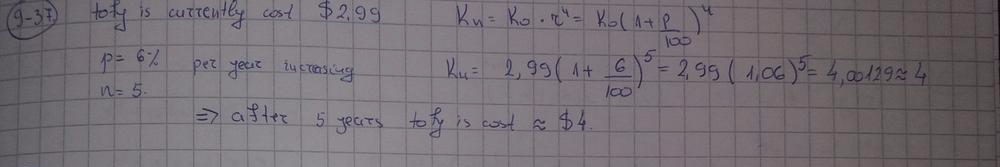
On the following picture, there is graphed quadrilateral $QUOP$.

$$
overline{QU}=sqrt{(2-5)^2+(4-4)^2}=3
$$
$$
overline{UO}=sqrt{(-1-2)^2+(10-4)^2}=sqrt{45}=3sqrt{15}
$$
$$
overline{OP}=sqrt{(6+1)^2+(10-10)^2}=7
$$
$$
overline{PQ}=sqrt{(6-5)^2+(10-4)^2}=sqrt{37}
$$
So, the perimeter is:
$$
O=3+3sqrt{15}+7+sqrt{37}
$$
$$
O=10+3sqrt{15}+sqrt{37}
$$
#### (b)
On the following picture, there is original and rotated quadrilateral.
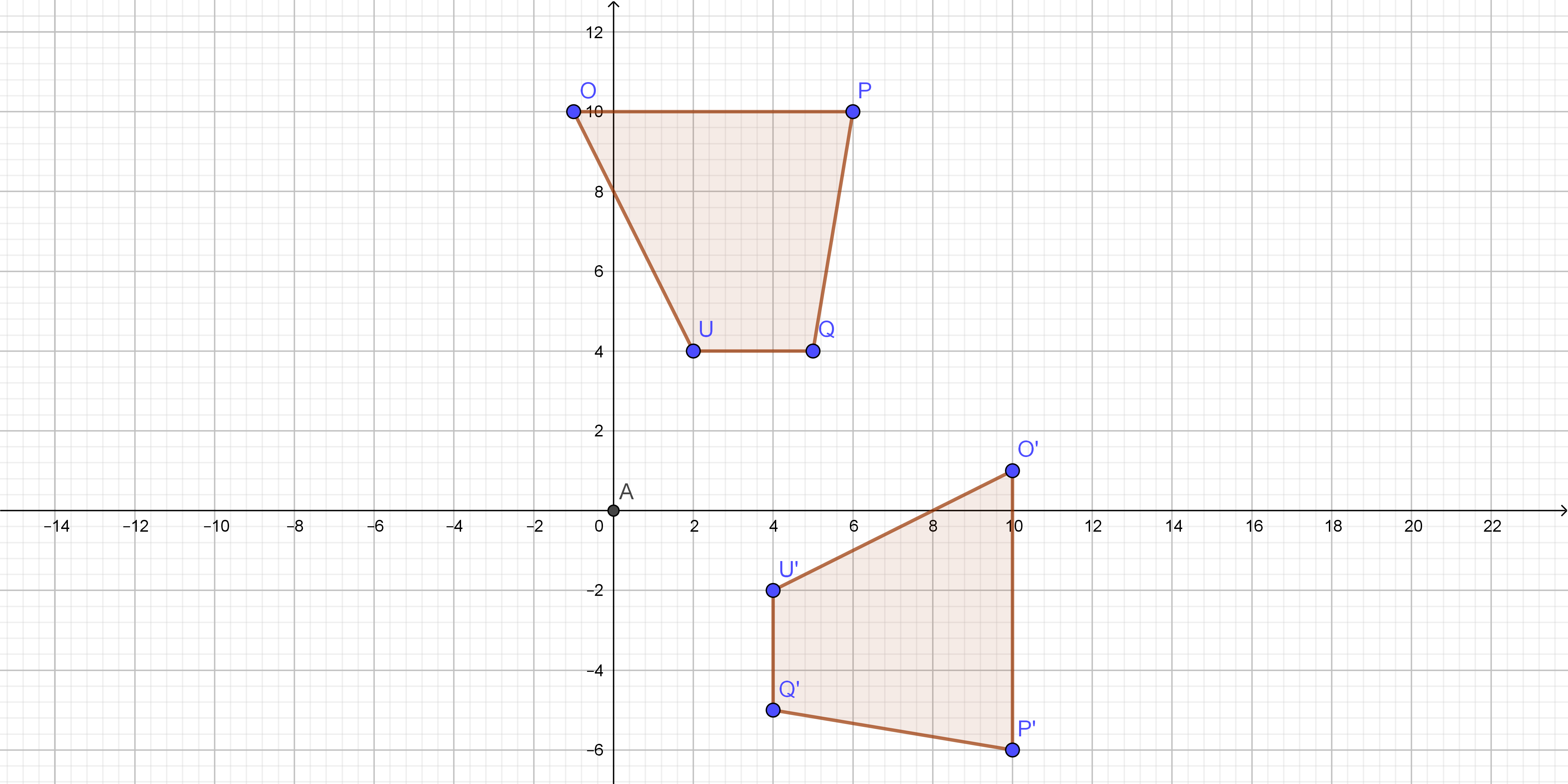
$$
text{slope}=dfrac{-6+5}{10-4}=-dfrac{1}{6}
$$

Yes, because $(-1.5)$ lies on the graph of the line. Using the equation, we can find check of it is satisfied by the point:
$$
begin{align*}
5&stackrel{?}{=}-2(-1)+3\
5&stackrel{?}{=}2+3\
5&=5
end{align*}
$$
$textbf{b.}$
$(2,-1)$ is a solution while $(0,0)$ is not. Graphically, $(2,-1)$ lies on the line while $(0,0)$ does not. Using the equation,
$$
begin{align*}
-1&stackrel{?}{=}-2(2)+3 & 0&stackrel{?}{=}-2(0)+3\
-1&stackrel{?}{=}-4+3 & 0&stackrel{?}{=}0+3\
-1&=-1 & 0&ne 3
end{align*}
$$
$textbf{c.}$
Graphically, a point lies on the line if the line passes through it. Algebraically, the point lies on the line of it satisfies its equation.
Points on the line make up the line itself while points not on the line lie on either side of the line.
b. $(2,-1)$ is a solution while $(0,0)$ is not.
c. Graphically, a point lies on the line if the line passes through it. Algebraically, the point lies on the line of it satisfies its equation. Points on the line make up the line itself while points not on the line lie on either side of the line.
For example, let’s test point $(8,-4)$, we will substitute $8$ for $y$ and $-4$ for $x$ in the inequality and get:
$$
8geq-2(-4)+3
$$
$$
8geq11
$$
So, we can see that this inequality is not true, so, this point is not one of the solutions to this inequality.
On that way can be tested all the points that your team is given.
#### (b)
On the following picture, there is graphed inequality $ygeq-2x+3$.
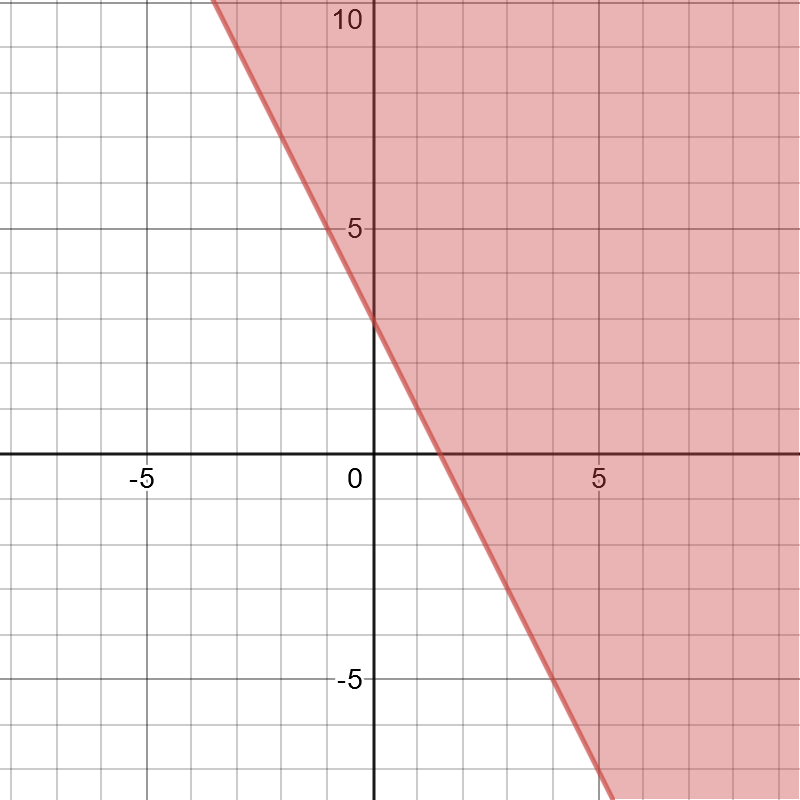
From the graph, we can see that these are infinite solutions.
Only points on the shaded side of the line satisfy given inequality, because of that there are no solutions on the other side of the line.
b) Points on the line are included, there are infinite solutions.
The equation for the line is $y=-2x+3$ (this is the given that we already graphed). Since the line is solid, the points on the line itself are solutions in the inequality. So, either use $leq$ or $geq$.
We can then assign a point that is on the shaded region, say $(0,0)$ and determine what inequality to use:
$$
begin{align*}
y&=-2x+3\
0&stackrel{?}{=}-2(0)+3\
0&stackrel{?}{=}0+3\
0&stackrel{?}{=}3
end{align*}
$$
The appropriate inequality to use is $leq$ since $0<leq 3$. Hence, the inequality for the graph is:
$$
color{#c34632}yleq -2x+3
$$
$textbf{b.}$
If we change $leq$ to $<$, this means that we have the same shaded region but points on the line are not part of the solution. Hence, a solid line for the boundary line cannot be used. So, we use another representation which is a dashed line as shown:
b. Same shaded region but points on the line are not part of the solution. Change the boundary line from solid to dashed.
The conclusion is that inequality which would correspond with the given graph is:
$$
y<-2x+3
$$
#### (b)
Because we conclude in part a) that corresponding inequality is $y<-2x+3$ with given graph, so, given graph is exactly required graph in this part.
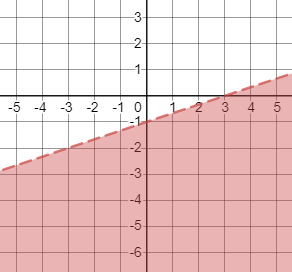
First, we graph the boundary line $y=-dfrac{1}{3}x-1$. To graph it, you can use the intercepts by solving when $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
0&=-dfrac{1}{3}x-1 & y&=-dfrac{1}{3}(0)-1\
dfrac{1}{3}x&=-1 & y&=0-1\
x&=-3 & y&=-1
end{align*}
$$
So, the intercepts are $(-3,0)$ and $(0,-1)$. Plot these two points and connect them with a dashed line since $>$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{>}-dfrac{1}{2}(0)-1 \
0&stackrel{?}{>}0-1 \
0¬{>}-1
end{align*}
$$
Since the inequality is false, shade the region where $(0,0)$ is not a part of.
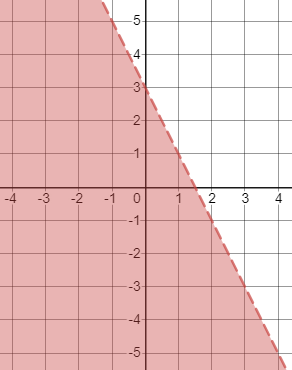
First, we graph the boundary line $y=4x+2$. To graph it, you can use the intercepts by letting $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
0&=4x+2 & y&=4(0)+2 \
-4x&=2 & y&=0+2\
x&=-0.5 & y&=2
end{align*}
$$
So, the intercepts are $(-0.5,0)$ and $(0,2)$. Plot these two points and connect them with a solid line since $leq$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{leq}4(0)+2 \
0&stackrel{?}{leq}0+2 \
0&leq 2
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
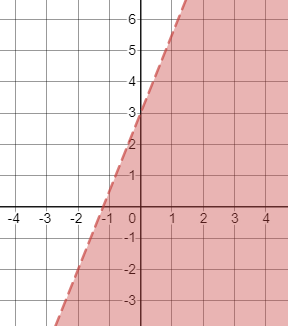
First, we graph the boundary line $y=dfrac{5}{2}x+3$. To graph it, you can use the intercepts by solving when $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
0&=dfrac{5}{2}x+3 & y&=dfrac{5}{2}(0)+3\
-dfrac{5}{2}x&=3 & y&=0+3\
x&=-1.2 & y&=3
end{align*}
$$
So, the intercepts are $(-1.2,0)$ and $(0,3)$. Plot these two points and connect them with a dashed line since $<$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{<}dfrac{5}{2}(0)+3 \
0&stackrel{?}{<}0+3 \
0&< 3
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
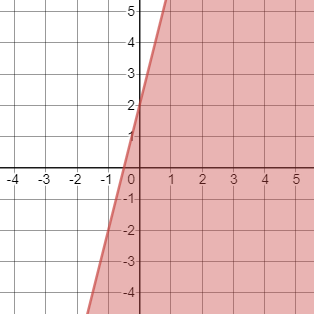
First, we graph the boundary line $2x-y=5$. To graph it, you can use the intercepts by letting $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
2x-0 &=5 & 2(0)-y &=5\
2x&=5 & -y &=5\
x&=2.5 & y&=-5
end{align*}
$$
So, the intercepts are $(-0.5,0)$ and $(0,2)$. Plot these two points and connect them with a solid line since $leq$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
2(0)-0&stackrel{?}{leq}5\
0-0&stackrel{?}{leq}5\
0&leq 5
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
Then we need to graph actually an equation of the same expression and then, depends what is the sign of inequality, decide which side of the line is needed to be shaded.
The point which is easiest to test is point $(0,0)$, testing this point, it is very easy to calculate which side of the line need to be shaded.
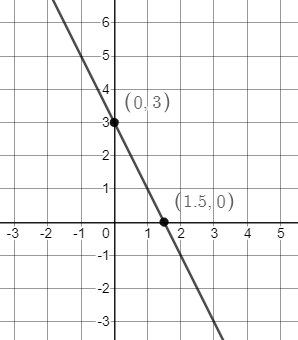
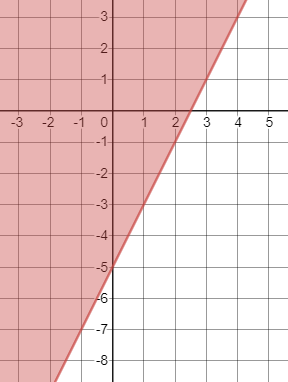
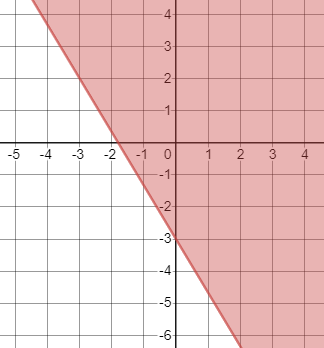
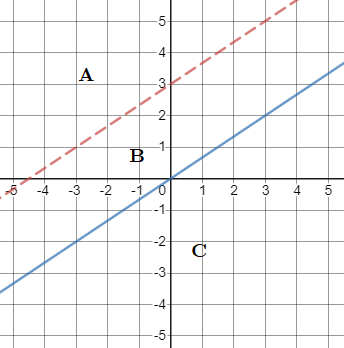
By replacing the inequality symbol with $=$ symbol, the boundary line is $y=-x+2$ which has intercepts $(2,0)$ and $(0,2)$. From this alone, the matching graph is $text{textcolor{#c34632}{graph 3}}$. We can also check by using a test point from the graph, say $(3,0)$:
$$
begin{align*}
0&stackrel{?}{>}-3+2\
0&>-1hspace{5mm}checkmark
end{align*}
$$
$textbf{b.}$
By replacing the inequality symbol with $=$ symbol, the boundary line is $y=2x-3$ which has intercepts $(1.5,0)$ and $(0,3)$. From this alone, the matching graph is $text{textcolor{#c34632}{graph 1}}$. We can also check by using a test point from the graph, say $(3,0)$:
$$
begin{align*}
0&stackrel{?}{<}2(3)-3 \
0&<3hspace{5mm}checkmark
end{align*}
$$
By replacing the inequality symbol with $=$ symbol, the boundary line is $y=dfrac{1}{2}x$ which passes the origin, or point $(0,0)$. From this alone, the matching graph is $text{textcolor{#c34632}{graph 4}}$. We can also check by using a test point from the graph, say $(0,1)$:
$$
begin{align*}
1&stackrel{?}{geq}dfrac{1}{2}(0)\
1&geq 0hspace{5mm}checkmark
end{align*}
$$
$textbf{d.}$
By replacing the inequality symbol with $=$ symbol, the boundary line is $y=-dfrac{2}{3}x+2$ which has intercepts $(3,0)$ and $(0,2)$. From this alone, the matching graph is $text{textcolor{#c34632}{graph 2}}$. We can also check by using a test point from the graph, say $(0,0)$:
$$
begin{align*}
0&stackrel{?}{leq}-dfrac{2}{3}(0)+2 \
0&leq 2hspace{5mm}checkmark
end{align*}
$$
b. graph 1
c. graph 4
d. graph 2
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
3x-2&=10 \
3x&=12 \
x&=4
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
3(0)-2&<10 \
0-2&<10 \
-2&<10
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it:
$$
color{#c34632}x<4
$$
On a number line, use an open circle for the boundary point 4 then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
5x-1-3x&=4x+5 \
2x-1&=4x+5 \
2x&=4x+6 \
-2x&=6 \
x&=-3
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
5(0)-1-3(0)&geq 4(0)+5 \
0-1-0&geq 0+5 \
-1&geq 5
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the right of it. So, the solution is to the left of the boundary point:
$$
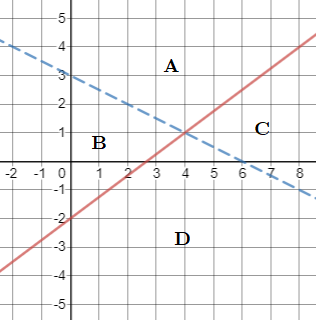
color{#c34632}xleq -3
$$
On a number line, use a filled circle for the boundary point $-3$ then draw an arrow pointing to the left:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
2(x+2)&=10-x \
2x+4&=10-x \
3x+4&=10 \
3x&=6 \
x&=2
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
2(0+2)&>10-0 \
2(2)&>10 \
4&>10
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the left of it. So, the solution is to the right of the boundary point:
$$
color{#c34632}x>2
$$
On a number line, use an open circle for the boundary point $2$ then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
4(x-3)+5&=-7 \
4x-12+5&=-7 \
4x-7&=-7 \
4x&=0 \
x&=0
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=1$ to substitute to the inequality:
$$
begin{align*}
4(0-3)+5&geq -7 \
4(-3)&geq -7\
12&geq -7
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the right of it.
$$
color{#c34632}xgeq 0
$$
On a number line, use a filled circle for the boundary point $0$ then draw an arrow pointing to the right:

d. $xgeq 0$
The absolute value of the difference of the salary and $$24000$ (since this can be a negative difference) is less than or equal $$1575$ so we write:
$$
color{#c34632}|s-24000|leq 1575
$$
Replace the inequality symbol with $=$ so we have the equation:
$$
|s-24000|=1575
$$
Since the right side is positive, then there are two solutions. We write and solve the two equations:
$$
begin{align*}
s-24000&=-1575 & s-24000&=1575\
s&=22425 & s&=25575
end{align*}
$$
Hence, the number line will be divided into 3 regions:
$$
sleq 22425, 22425leq sleq 25575,text{ and }sgeq 25575
$$
For each region, assign a test point. If the test point satisfies the inequality, the region it belongs to is a solution.
For $sleq 22425$, I used $s=0$:
$$
begin{align*}
| 0-24000|&stackrel{?}{leq}1575\
24000¬{leq} 1575
end{align*}
$$
For $22425leq sleq 25575$, I used $s=24000$:
$$
begin{align*}
|24000-24000|&stackrel{?}{leq}1575\
0&leq 1575hspace{5mm}checkmark
end{align*}
$$
For $sgeq 25575$, I used $s=26000$:
$$
begin{align*}
| 26000-24000|&stackrel{?}{leq}1575\
2000¬{leq} 1575
end{align*}
$$
So, the solution of the inequality is:
$$
color{#c34632}22425leq sleq 25575
$$
Starting annual salary is $24,000$
Average salary differ from $1575$
Maximum annual salary is represented as follows:
$$
24,000+1575=25,575text{ dollars}
$$
Minimum annual salary is represented as follows:
$$
24,000-1575=22,425text{ dollars}
$$
Range of salaries is $ge22,425$ dollars or $le25,575$ dollars.
text{color{#4257b2}Range of salaries is $ge22,425$ dollars or $le25,575$ dollars.}
$$
$$
color{#4257b2}(0, 0.2) (1, 1.6)
$$
The exponent function form is $y=a b^x$.
Substitution values of $(x, y)$ in the exponential form as follows:
$$
0.2=a b^0 a=0.2
$$
$$
1.6=a b^1 1.6=a b
$$
Substitution value of $a$ in the second equation as follows:
$$
1.6=0.2 b
$$
Divide both of sides by $0.2$ as follows:
$$
b=dfrac{1.6}{0.2} b=8
$$
$$
y=a b^x 0.2=0.2cdot8^x
$$
$$
y=a b^x 1.6=0.3cdot8^1
$$
text{color{#4257b2}$a=0.2 b=8$}
$$
We know that the equation form for the line is $y=a x+b$
$$
0=(acdot4)+b 4a+b=0
$$
$$
-3=(acdot0)+b -3=b
$$
Substitute the value of $b=-3$ in the first equation as follows:
$$
4a-3=0 4a=3
$$
Divide bothe of sides by $4$ as follows:
$$
a=dfrac{3}{4} a=0.75
$$
$$
y=a x+b y=0.75 x-3
$$
text{color{#4257b2}$a=0.75 b=-3$ $y=0.75 x-3$}
$$
$because angle ABC=angle DCB$
$because angle ACB=angle CBD$
$BC$ is the same length in both of triangles.
$therefore$ The two triangles are congruent
text{color{#4257b2}$Large$ The two triangles are congruent}
$$
Points of Coryn working are $(2, 4) (3, 5)$
Points of Leah working are $(3, 2) (0, 3)$
We know that the equation form for the line is $y=a x+b$
$$
text{color{#4257b2}For Coryn points. $(2, 4) (3, 5)$}
$$
$$
4=(acdot2)+b 2a+b=4
$$
$$
5=(acdot3)+b 3a+b=5
$$
Subtract two equations as follows:
$$
(3a-2a)+(b-b)=(5-4) a=1
$$
Substitute the value of $a=1$ as follows:
$$
(2cdot1)+b=4 2+b=4
$$
$$
b=4-2 b=2
$$
$$
y=a x+b y=x+2
$$
text{color{#4257b2}For Leah points. $(3, 2) (0, 3)$}
$$
$$
2=(acdot3)+b 3a+b=2
$$
$$
3=(acdot0)+b b=3
$$
Substitute the value of $b=3$ as follows:
$$
3a+3=2 3a=2-3 3a=-1
$$
Divide both of sides by $3$ as follows:
$$
a=-dfrac{1}{3}
$$
$$
y=a x+b y=-dfrac{1}{3} x+3
$$
text{color{#4257b2}$a=1 b=2 y=x+2$
\ \
$a=-dfrac{1}{3} b=3 y=-dfrac{1}{3} x+3$}
$$
You only need 1 since the point can represent all the other points in the region it belongs to.
$textbf{b.}$
Because computation using 0 is very easy to do.
$textbf{c.}$
Using the point $(-3,2)$,
$$
begin{align*}
2&leq -dfrac{5}{3}(-3)-3\
2&leq 5-3\
2&leq 2
end{align*}
$$
Although the inequality is true, this does not help Anita to decide which side to shade since the point is on the boundary line itself (as $2=2$).
b. Because computation using 0 is very easy to do.
c. No, because the point is on the boundary line itself.
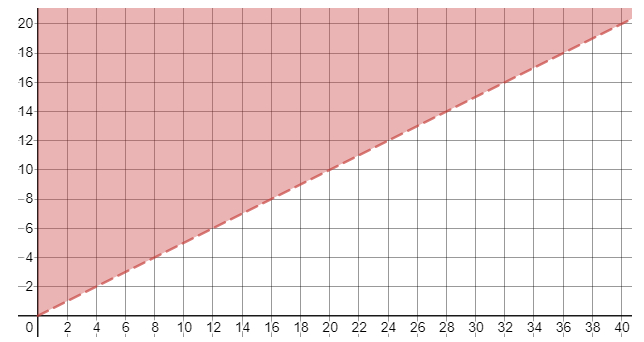
The term “more than” implies “greater than” so we use the inequality symbol $>$:
$$
color{#c34632}y>dfrac{1}{2}x
$$
$textbf{b.}$
Your line will start at $(0,0)$ and end at $(40,20)$. The solution of the inequality is all points above the boundary line.
$$
color{#c34632}text{Honduras, Rwanda, Zambia, Madagascar, and Uganda}color{white}tag{1}
$$
b. Honduras, Rwanda, Zambia, Madagascar, and Uganda
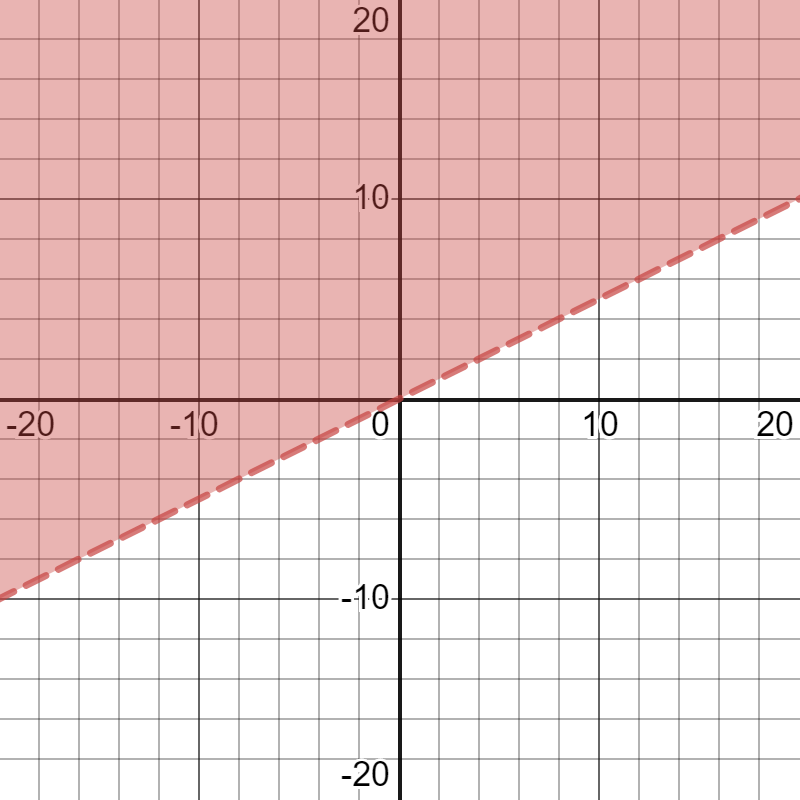
An inequality which represents the constraints on receiving foreign aid is the following:
$$
y>dfrac{1}{2}x
$$
#### (b)
For this, you can use the graphing calculator. On the following picture, there is graphed inequality from the previous part.
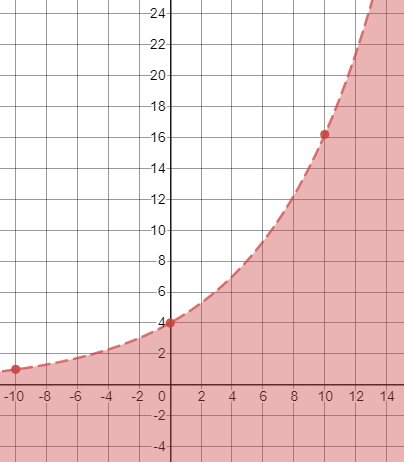
First, we graph the boundary line $y=4(1.15)^x$. Using $x=-10,0,$ and 10, three points on the exponential graph are $approx (-10,1)$, $(0,4)$, and $approx (10,16.2)$. Connect them with a smooth dashed curve since $<$ is used with the $x$-axis as the horizontal asymptote.
To find which region to be shaded, assign a test point not on the graph, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{<}4(1.15)^0\
0&stackrel{?}{<}4(1) \
0&<4
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
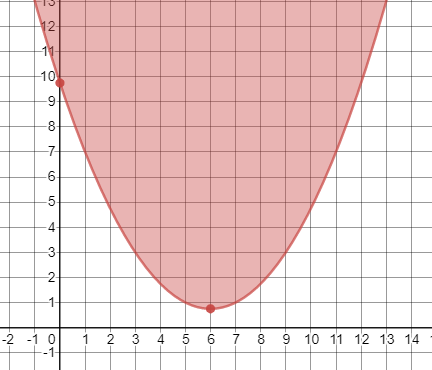
First, we graph the boundary line $y=dfrac{1}{4}(x-6)^2+dfrac{3}{4}$. This is in graphing form $y=a(x-h)^2+k$ where $(h,k)$ is the vertex. In this case, the vertex is at $left(6,dfrac{3}{4}right)$. When $x=0$, $y=9.75$ so the $y$-intercept is at $(0,9.75)$. Since $a=dfrac{1}{4}>0$, the parabola opens up. Graph the parabola using symmetry with a solid curve since $geq$ is used.
To find which region to be shaded, assign a test point not on the graph, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{geq}dfrac{1}{4}(0-6)^2+dfrac{3}{4}\
0&stackrel{?}{geq }9+dfrac{3}{4} \
0&geq dfrac{39}{4}
end{align*}
$$
Since the inequality is false, shade the region where $(0,0)$ is not a part of.
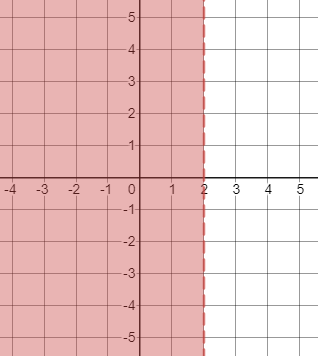
First, we graph the boundary line $x=2$. We know that this is a vertical line and it is drawn as a dashed line since $<$ is used. The inequality is true for $x<2$ so shade the left side of the boundary line:
$$
m=dfrac{Delta y}{Delta x }=dfrac{-1-0}{0-(-3)}=dfrac{-1}{3}=-dfrac{1}{3}
$$
Since $b=-1$, then the equation is:
$$
y=-dfrac{1}{3}x-1
$$
Since the line is dashed, the points on the line itself are not solutions in the inequality. So, either use $$.
We can then assign a point that is on the shaded region, say $(0,-2)$ and determine what inequality to use:
$$
begin{align*}
y&=-dfrac{1}{3}x-1\
-2&stackrel{?}{=}-dfrac{1}{3}(0)-1\
-2&stackrel{?}{=}0-1\
-2&stackrel{?}{=}-1
end{align*}
$$
The appropriate inequality to use is $<$ since $-2< -1$. Hence, the inequality for the graph is:
$$
color{#c34632} y<-dfrac{1}{3}x-1
$$
y<-dfrac{1}{3}x-1
$$
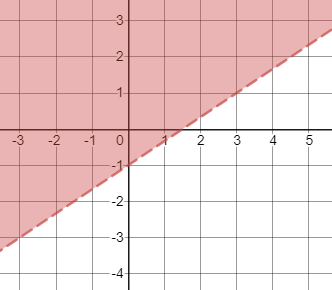
First, we graph the boundary line $y=-x+5$. To graph it, you can use the intercepts by letting $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
0&=-x+5 & y&=-0+5\
x&=5 & y&=5
end{align*}
$$
So, the intercepts are $(5,0)$ and $(0,5)$. Plot these two points and connect them with a solid line since $leq$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{leq}-0+5 \
0&leq 5
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
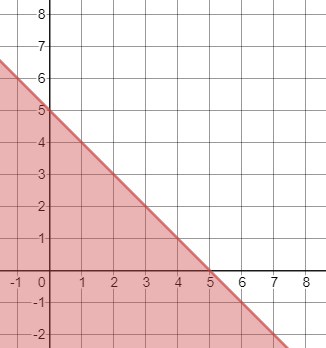
First, we graph the boundary line $y=dfrac{2}{3}x-1$. To graph it, you can use the intercepts by letting $y=0$ for the $x$-intercept and $x=0$ for the $y$-intercept:
$$
begin{align*}
0&=dfrac{2}{3}x-1 & y&=dfrac{2}{3}(0)-1\
-dfrac{2}{3}x&=-1 & y&=0-1\
x&=1.5 & y&=-1
end{align*}
$$
So, the intercepts are $(1.5,0)$ and $(0,01)$. Plot these two points and connect them with a dashed line since $>$ was used.
To find which region to be shaded, assign a test point not on the line, say $(0,0)$, and check if it satisfies the inequality:
$$
begin{align*}
0&stackrel{?}{>}dfrac{2}{3}(0)-1\
0&stackrel{?}{>}0-1\
0&> -1
end{align*}
$$
Since the inequality is true, shade the region where $(0,0)$ is a part of.
$$
color{#4257b2}text{(a)} |9+3x|=39
$$
Equal $9+3x=39$ as follows:
$$
3x=39-9 3x=30
$$
Divide both of sides by $3$ as follows:
$$
x=dfrac{30}{3} x=10
$$
Equal $-9-3x=39$ as follows:
$$
-3x=39+9 -3x=48
$$
Divide both of sides by $-3$ as follows:
$$
x=dfrac{48}{-3} x=-16
$$
The values of $x$ are equal
$$
x=10 text{ when} 9+3xge0 3xge-9 xge-dfrac{9}{3} xge-3
$$
$$
x=-16 text{ when} 9+3x<0 3x<-9 x<-dfrac{9}{3} x<-3
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=10, x=-16$ in the equation as follows:
$$
|9+3x|=39 |9+(3cdot10)|=39 |9+30|=39 |39|=39 39=39
$$
$$
|9+3x|=39 |9+(3cdot-16)|=39 |9-48|=39 |39|=39 39=39
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} |-3x+9|=10
$$
Equal $-3x+9=10$ as follows:
$$
-3x=10-9 -3x=1
$$
Divide both of sides by $-3$ as follows:
$$
x=dfrac{1}{-3} x=-dfrac{1}{3}
$$
Equal $3x-9=10$ as follows:
$$
3x=10+9 3x=19
$$
Divide both of sides by $3$ as follows:
$$
x=dfrac{19}{3}
$$
The values of $x$ are equal
$$
x=-dfrac{1}{3} text{ when} -3x+9ge0 -3xge-9 xledfrac{9}{3} xle3
$$
$$
x=dfrac{19}{3} text{ when} -3x+9<0 -3xdfrac{9}{3} x>3
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-dfrac{1}{3}, x=dfrac{19}{3}$ in the equation as follows:
$$
|-3x+9|=10 |(-3cdot-dfrac{1}{3}+9)|=10 |1+9|=10 |10|=10 10=10
$$
$$
|-3x+9|=10 |(-3cdotdfrac{19}{3}+9)|=10 |-19+9|=10 |-10|=10 10=10
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(c)} |x+3|=-2
$$
Equal $x+3=-2$ as follows:
$$
x=-2-3 x=-5
$$
Equal $-x-3=-2$ as follows:
$$
-x=-2+3 -x=1 x=-1
$$
The values of $x$ are equal
$$
x=-5 text{ when} x+3ge0 xge-3
$$
$$
x=-1 text{ when} x+3<0 x<-3
$$
There is no solution
text{color{#4257b2}(a) $x=10$ or $x=-16$
\ \
(b) $x=-dfrac{1}{3}$ or $x=dfrac{19}{3}$
\ \
(c) No solution}
$$
$$
1200+300xleq 2700
$$
Find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
1200+300x&=2700 \
300x&=1500 \
x&=5
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
1200+300(0)&leq 2700\
1200+0&leq 2700\
1200&leq 2700
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it.
$$
color{#c34632}xleq 5
$$
Hence, Algeria can order an advertisement up to 5 inches in height.
Assume the height of the ad is $x$
Total cost is $2700$ dollars.
Additional cost for every inch is $300$ dollars
Base fee is $1200$ dollars.
Total cost =base fee$+$additional cost
$$
2700=1200+(300 x)
$$
$$
2700-1200=300 x
$$
$$
300 x=1500
$$
Divide both of side by $300$ as follows:
$$
x=dfrac{1500}{300}
$$
$$
x=5text{ inch}
$$
The height of ad is $5$ inch
text{color{#4257b2}$5$ inch}
$$
$$
color{#4257b2}(1, 6) (4, 48)
$$
The exponent function form is $y=a b^x$ . Substitution values of $(x, y)$ in the exponential form as follows:
$$
6=a b^1 6=a b a=dfrac{6}{b}
$$
Substitution value of $a$ in the second equation as follows:
$$
48=a b^4
$$
$$
48=dfrac{6}{b}cdot b^4 48=6 b^3
$$
Divide both of sides by $6$ as follows:
$$
b^3=dfrac{48}{6} b^3=8
$$
$$
sqrt[3]{b^3}=sqrt[3]{8} b=2
$$
Substitution value of $b=2$ in the first equation as follows:
$$
a=dfrac{6}{b} a=dfrac{6}{2} a=3
$$
$$
y=a b^x y=3 (2)^x
$$
text{color{#4257b2}$a=3 b=2 y=3 (2)^x$}
$$
On the following picture, there is graphed given data.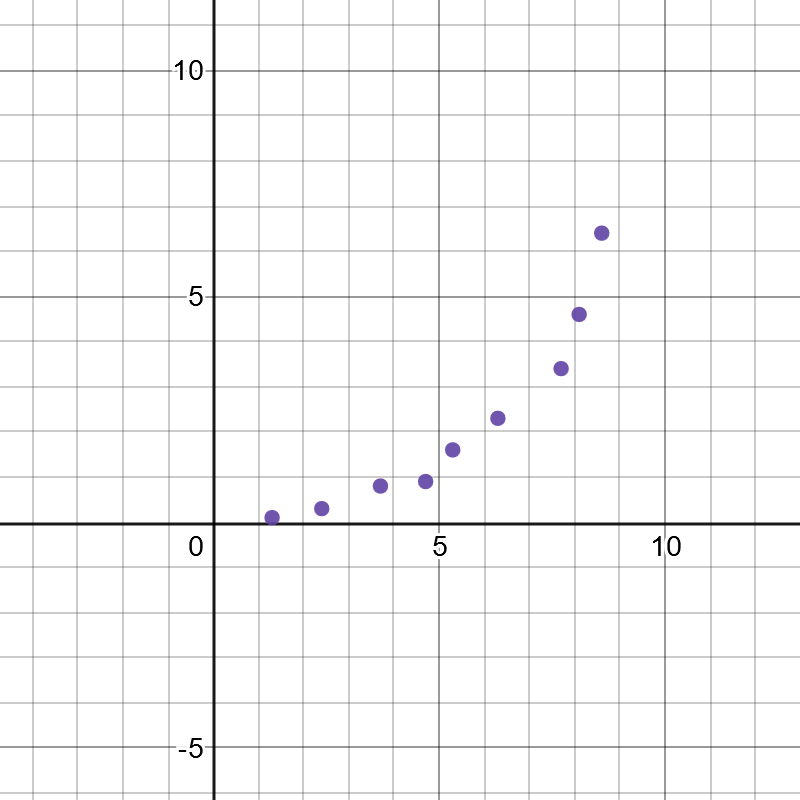
Using the given information, the corresponding equation which might model this data is $y=a(b)^x$.
#### (c)
On the following picture, there is graphed corresponding the best fit line. Equation of this line is:
$$
y=0.109603(1.5937)^x
$$
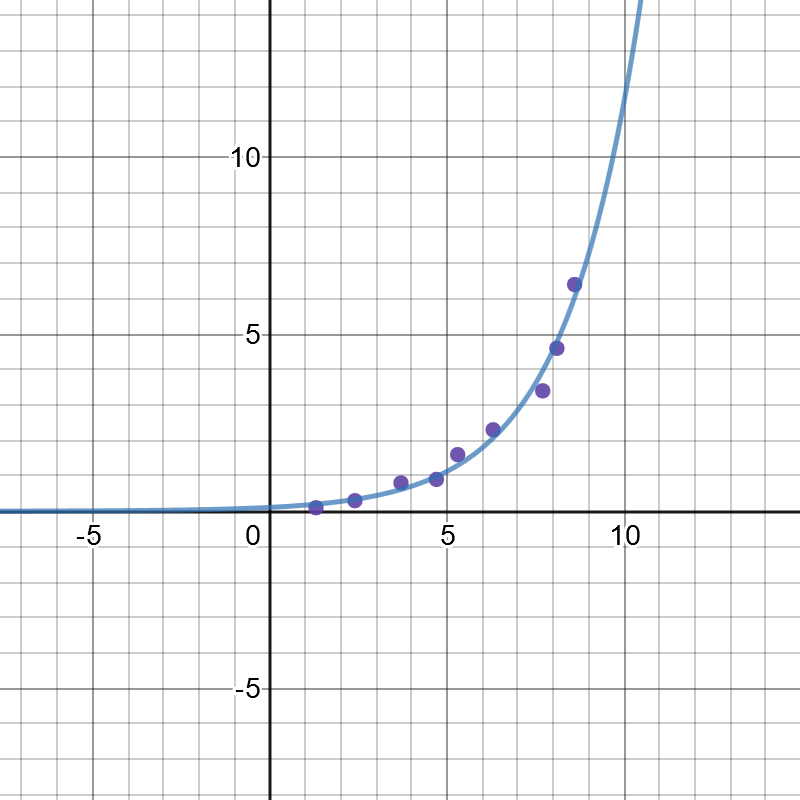
We will substitute $8$ for $x$ in equation from the previous part and solve it for $y$:
$$
y=0.109603(1.5937)^8
$$
$$
y=4.56
$$
So, an $8$-day old muschroom will weight $4.56$g.
The length of $overline{AB}$is the following:
$$
overline{AB}=sqrt{(-1+3)^2+(-6+4)^2}=2sqrt{2}
$$
#### (b)
On the following picture, there is reflected $triangle ABC$.
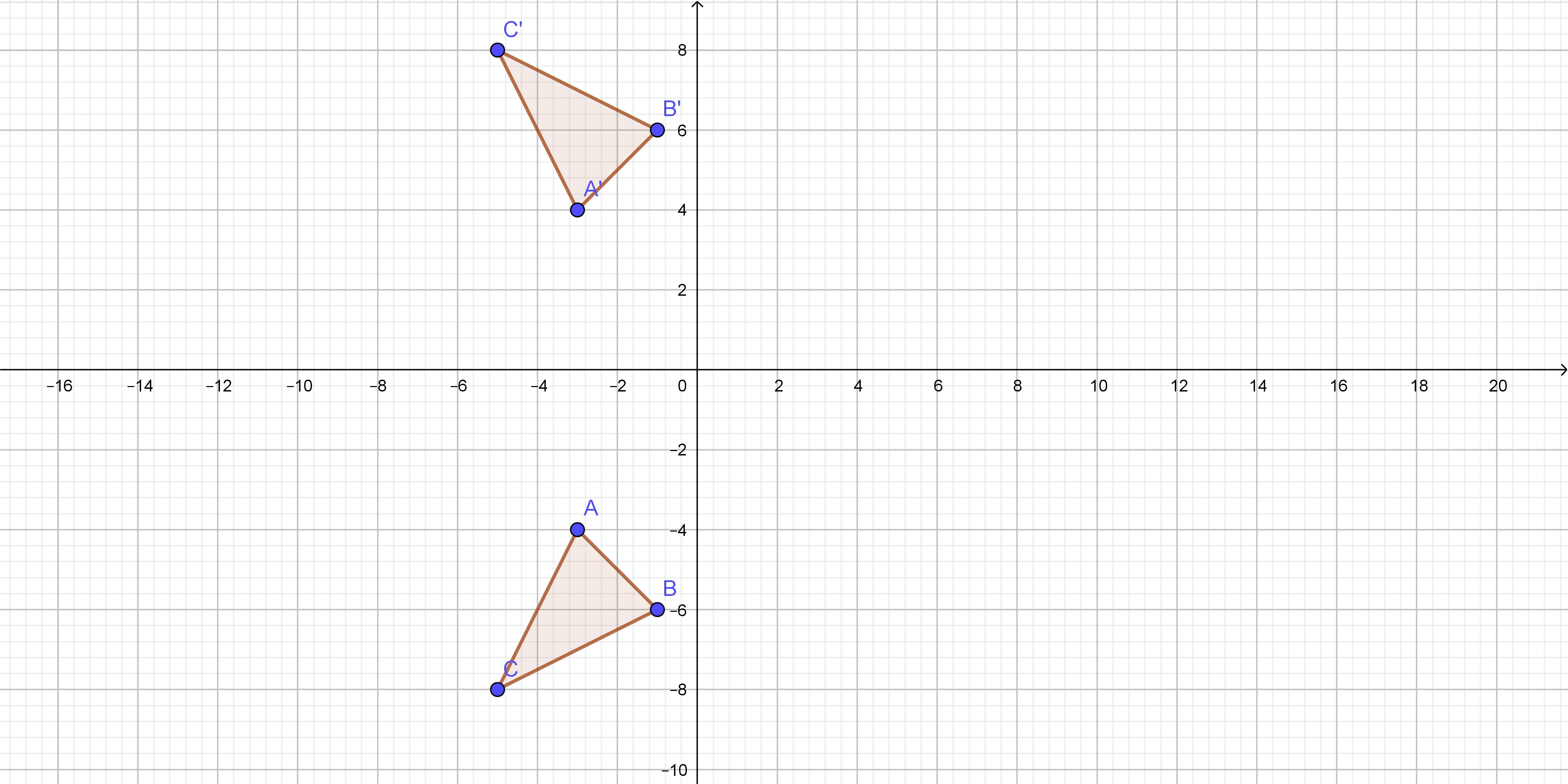
The function that would change the coordinates of $triangle ABC$ to $triangle A’B’C’$ would be:
$$
(x,y)rightarrow(x,-y)
$$
#### (c)
On the following picture there is rotated $triangle A’B’C’$.
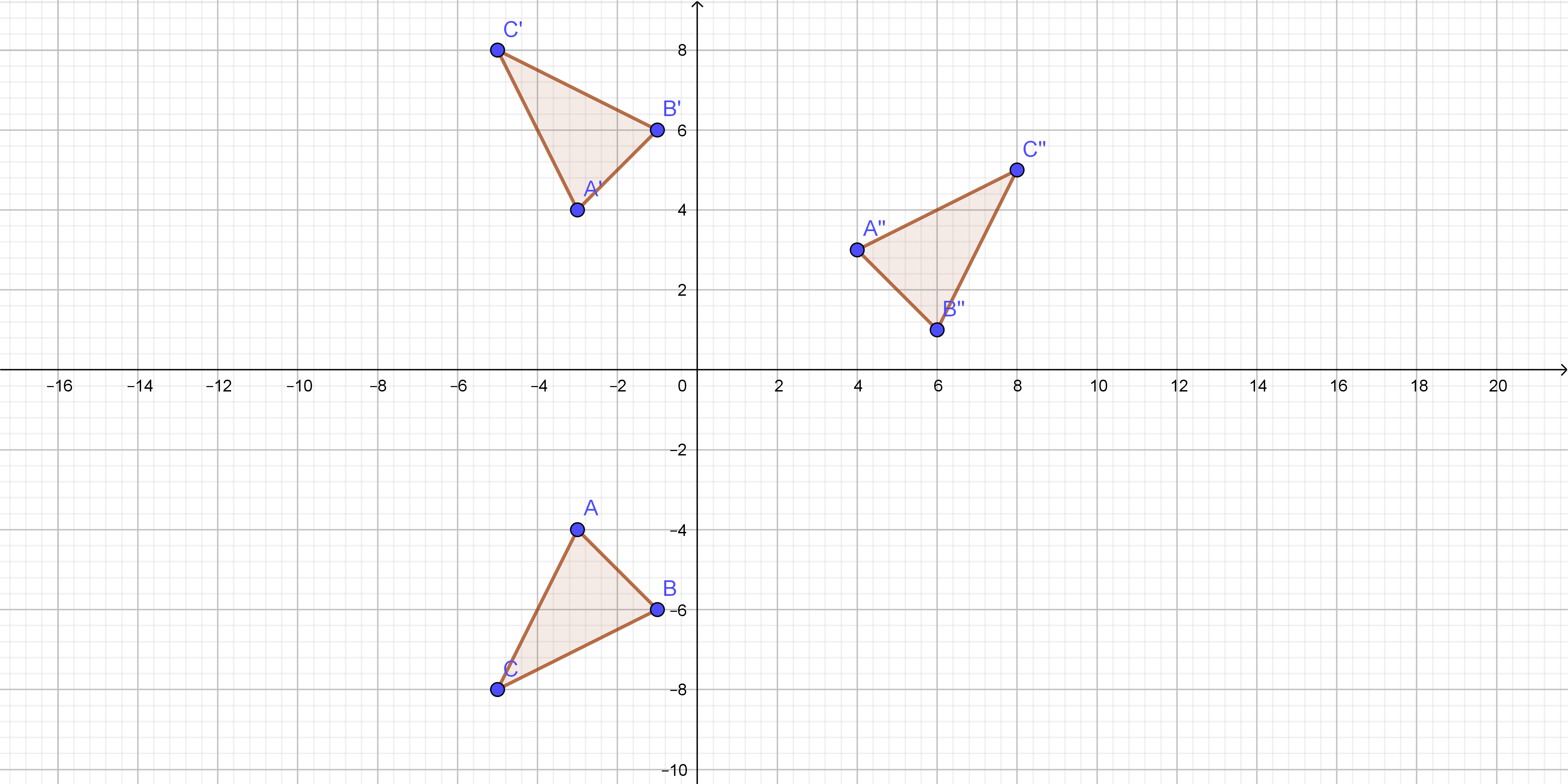
#### (d)
On the following picture, there is translated $triangle ABC$.
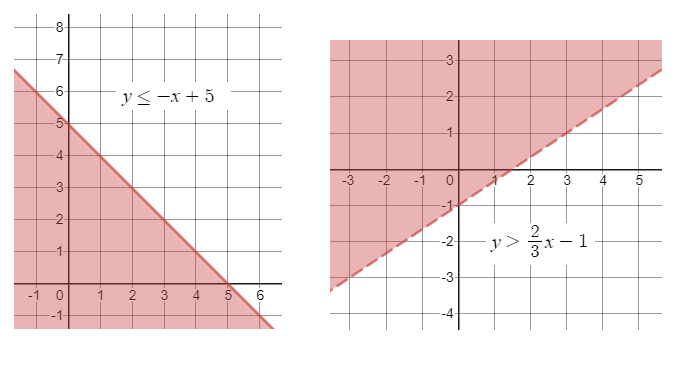
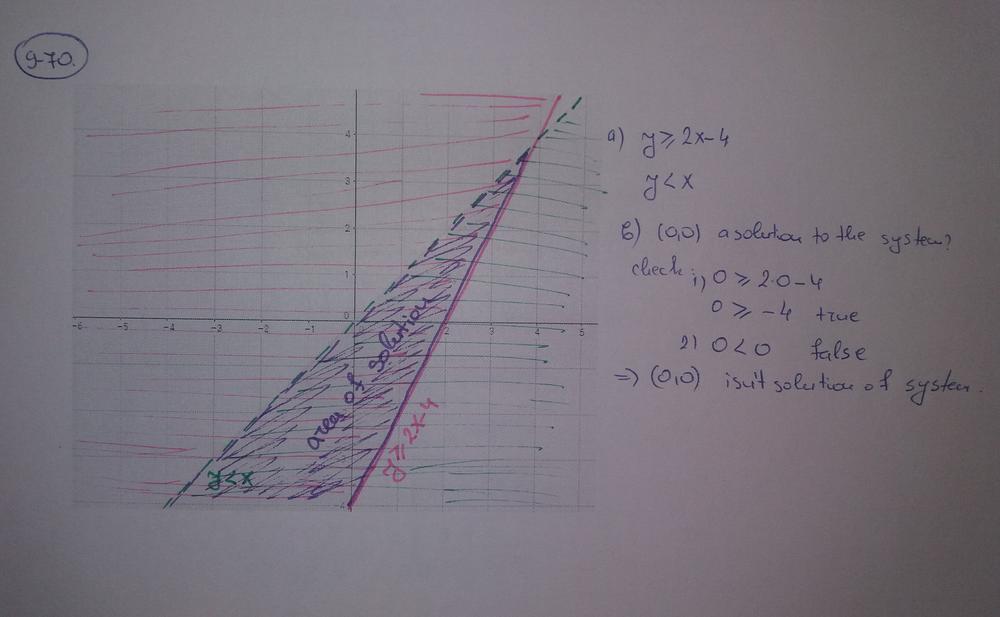
Use the results from the previous problem as shown. In the first inequality, the boundary line is included in the solution while it is not for the second inequality.
The graph of the system would have overlapping regions where it is the solution of the system. Using the graphs from part (a), the overlapping regions are shown on the left with the simplified region on the right.
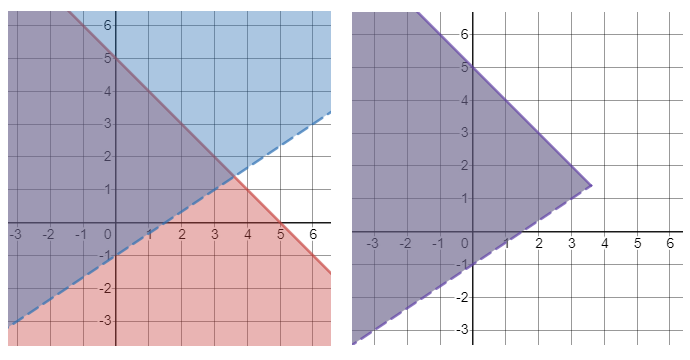
A possible point is $(0,0)$. Using the two inequalities, we have:
$$
begin{align*}
0&stackrel{?}{leq}-0+5 & 0&stackrel{?}{>}dfrac{2}{3}(0)-1\
0&stackrel{?}{leq}0+5 & 0&stackrel{?}{>}0-1\
0&leq 5hspace{5mm}checkmark & 0&>-1hspace{5mm}checkmark
end{align*}
$$
Both inequalities are true so $(0,0)$ is a solution of the system of inequalities.
$textbf{d.}$
You can try out the different points outside the regions and check if they satisfy both the inequalities.
b. Solutions in the overlapping region are solutions.
c. Possible point to use: $(0.0)$
d. You can try out the different points outside the regions.
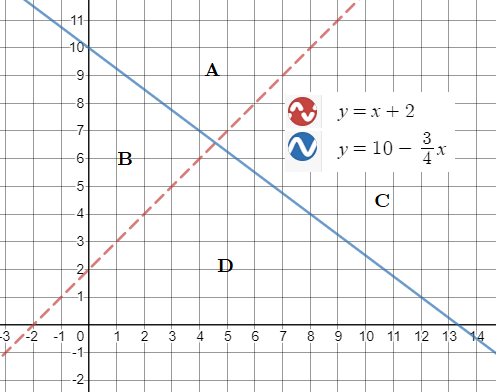
For region A, I used $(0,11)$:
$$
begin{align*}
11&stackrel{?}{<}0+2 & 11&stackrel{?}{leq}10-dfrac{3}{4}(0) \
11¬{<}2 & 11¬{leq}10
end{align*}
$$
Both inequalities are not satisfied so region A should not be shaded.
For region B, I used $(0,3)$:
$$
begin{align*}
3&stackrel{?}{<}0+2 & 3&stackrel{?}{leq}10-dfrac{3}{4}(0) \
3¬{<}2 & 3&leq 10hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region B should not be shaded.
$$
begin{align*}
6&stackrel{?}{<}8+2 & 6&stackrel{?}{leq}10-dfrac{3}{4}(8) \
6&<10hspace{5mm}checkmark & 6¬{leq} 4
end{align*}
$$
Only one inequality is satisfied so region C should not be shaded.
For region D, I used $(0,0)$:
$$
begin{align*}
0&stackrel{?}{<}0+2 & 0&stackrel{?}{leq}10-dfrac{3}{4}(0) \
0&<2hspace{5mm}checkmark & 0&leq 10hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region D should be shaded.
$$
color{white}tag{1}
$$
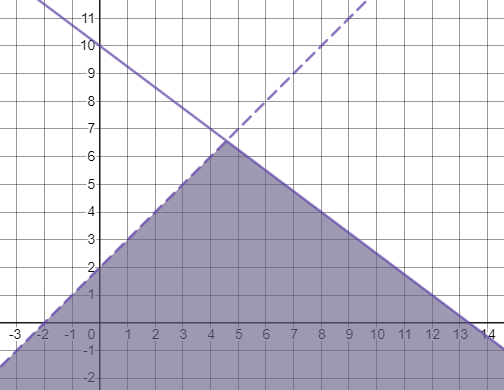
The solution of the system of inequalities is shown:
The line is dashed because the points from that line are not solutions to that inequality.
#### (b)
The conclusion is that there are $8$ possible solution regions.
#### (c)
On the following picture, there is a double shaded region which satisfies both inequalities.
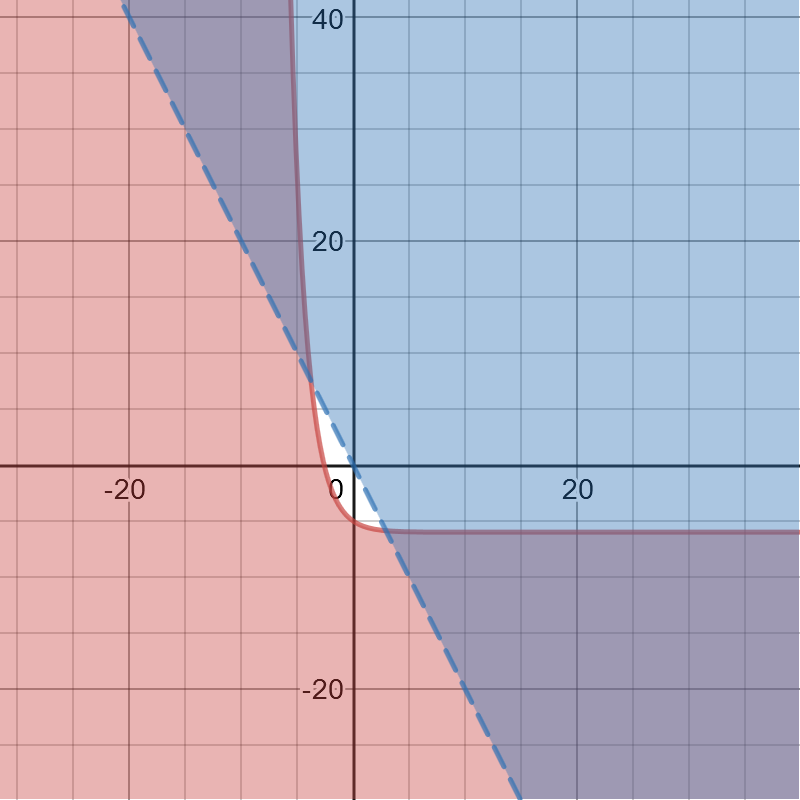
It is not good to test this point because it is on the line.
$textbf{color{#4257b2}For the 1st inequality:}$
The boundary line is $y=x+3$ which has intercepts $(-3,0)$ and $(0,3)$. Substitute the test point:
$$
begin{align*}
0&stackrel{?}{=}0+3\
0&stackrel{?}{=}3
end{align*}
$$
We use $leq$ since $0leq 3$. Hence, the 1st inequality is:
$$
color{#c34632}yleq x+3
$$
$textbf{color{#4257b2}For the 2nd inequality:}$
The boundary line is $y=2$ is a horizontal line. Since the shaded region is below this line, then the 2nd inequality is:
$$
color{#c34632}yleq 2
$$
The boundary line is $y=-dfrac{2}{3}x-1$ which has intercepts $(-1.5,0)$ and $(0,-1)$. Substitute the test point:
$$
begin{align*}
0&stackrel{?}{=}-dfrac{2}{3}(0)-1\
0&stackrel{?}{=}-1
end{align*}
$$
We use $geq$ since $0geq -1$. Hence, the 3rd inequality is:
$$
color{#c34632}ygeq -dfrac{2}{3}x-1
$$
$textbf{color{#4257b2}For the 4th inequality:}$
The line with a slope of $dfrac{1}{2}$ has a $y$-intercept of $(0,-1)$. Hence, the 4th inequality is:
$$
color{#c34632}ygeq dfrac{1}{2}x-1
$$
$textbf{color{#4257b2}For the 5th inequality:}$
The boundary line is $y=-dfrac{2}{3}x+4$ which has intercepts $(6,0)$ and $(0,4)$. Substitute the test point:
$$
begin{align*}
0&stackrel{?}{=}-dfrac{2}{3}(0)+4\
0&stackrel{?}{=}4
end{align*}
$$
We use $leq$ since $0leq 4$. Hence, the 5th inequality is:
$$
color{#c34632}yleq -dfrac{2}{3}x+4
$$
$yleq 2$
$ygeq -dfrac{2}{3}x-1$
$ygeq dfrac{1}{2}x-1$
$$
yleq -dfrac{2}{3}x+4
$$
Using choice a, $(2,1)$
$$
begin{align*}
1&stackrel{?}{<}|2-3|\
1&stackrel{?}{<}|-1|\
1¬{<}1
end{align*}
$$
So, $(2,1)$ is not a solution.
Using choice b, $(-4,5)$
$$
begin{align*}
5&stackrel{?}{<}|-4-3|\
5&stackrel{?}{<}|-7|\
5&<7hspace{5mm}checkmark
end{align*}
$$
So, $(-4,5)$ is a solution.
Using choice c, $(-2,8)$
$$
begin{align*}
8&stackrel{?}{<}|-2-3|\
8&stackrel{?}{<}|-5|\
8¬{<}5
end{align*}
$$
So, $(-2,8)$ is not a solution.
Using choice d, $(0,3)$
$$
begin{align*}
3&stackrel{?}{<}|0-3|\
3&stackrel{?}{<}|-3|\
3¬{<}3
end{align*}
$$
So, $(0,3)$ is not a solution.
The total cost is $$1.25$, plus $$0.75$ per game times the number of games. Since Charlie has $$20$, he can spend less than or equal to $$20$ so we write the inequality:
$$
1.25+0.75xleq 20
$$
Find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
1.25+0.75x &=20 \
0.75x&=18.75 \
x&=25
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
1.25+0.75(0)&leq 20\
1.25+0&leq 20\
1.25&leq 20
end{align*}
$$
The test point is a solution which means all points on this side of the boundary point are part of the solution, which is to the left of it.
$$
color{#c34632}xleq 25
$$
Hence, Charlie can bowl at most 25 games.
Total cost is $20$ dollars.
Shoes rent for $1.25$ dollars.
Assume number of games is $x$
Each game rent for $0.75$ dollars
Total cost$=$ shoes rent $+$ game rent
$$
20=1.25+(0.75cdot x)
$$
$$
0.75x=20-1.25 0.75x=18.75
$$
Divide both of sides by $0.75$ as follows:
$$
x=dfrac{18.75}{0.75}
$$
$$
x=25text{ games}
$$
The number of games needed is $25$ games.
text{color{#4257b2}$25$ games}
$$
$$
color{#4257b2} 2x-3y=12 y+x=-9
$$
Multiply the second equ. by $-2$ to get $-2x-2y=18$
Using elimination property for the new equations as follows:
$$
(2x-2x)+(-3y-2y)=(12+18) -5y=30
$$
Divide both of sides by $-5$ as follows:
$$
y=dfrac{30}{-5} y=-6
$$
Substitution the value of $y=-6$ for first equation as follows:
$$
2x-(3cdot-6)=12 2x+18=12 2x=12-18 2x=-6
$$
Divide both of sides by $2$ as follows:
$$
x=-dfrac{6}{2} x=-3
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-3, y=-6$ in the equation as follows:
$$
(2cdot-3)-(3cdot-6)=12 -6+18=12 12=12
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}$x=-3 y=-6$}
$$
$$
color{#4257b2}text{(a)} 4x-6y=20
$$
Isolate the variable $x$ on the left side as follows:
$$
4x=20+6y
$$
Divide both of sides by $4$ as follows:
$$
x=dfrac{20}{4}+dfrac{6}{4} y
$$
$$
x=5+dfrac{3}{2} y
$$
$$
color{#4257b2}text{(b)} dfrac{1}{2} (x-6)=9
$$
Multiply both of sides by $2$ as follows:
$$
x-6=9cdot2 x-6=18
$$
Isolate the variable $x$ on the left side as follows:
$$
x=18+6 x=24
$$
color{#4257b2}text{(c)} dfrac{4}{5}+dfrac{18}{x}=8
$$
Isolate the variable on the left side as follows:
$$
dfrac{18}{x}=8-dfrac{4}{5} dfrac{18}{x}=dfrac{(5cdot8)-(4cdot1)}{5}
$$
$$
dfrac{18}{x}=dfrac{40-4}{5} dfrac{18}{x}=dfrac{36}{5}
$$
$$
36 x=18cdot5 36 x=90
$$
Divide both of sides by $36$ as follows:
$$
x=dfrac{90}{36} x=2.5
$$
color{#4257b2}text{(d)} 2+|2x-3|=5
$$
$$
|2x-3|=5-2 |2x-3|=3
$$
Equal $2x-3=3$ as follows:
$$
2x=3+3 2x=6
$$
Divide both of side by $2$ as follows:
$$
x=dfrac{6}{2} x=3
$$
Equal $-2x+3=3$ as follows:
$$
-2x=3-3 -2x=0 x=0
$$
The values of $x$ are equal
$$
x=3 text{ when} 2x-3ge0 2xge3 xgedfrac{3}{2}
$$
$$
x=0 text{ when} 2x-3<0 2x<3 x<dfrac{3}{2}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=3, x=0$ in the equation as follows:
$$
2+|(2cdot3)-3|=5 2+|6-3|=5 2+|3|=5 2+3=5 5=5
$$
$$
2+|(2cdot0)-3|=5 2+|0-3|=5 2+|-3|=5 2+3=5 5=5
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $x=5+dfrac{3}{2} y$ (b) $x=24$
\ \
(c) $x=2.5$ (d) $x=3$ or $x=0$}
$$
$because$ $angle ABD=angle CDB$
$because$ AB=DC
$because$ BD is common between two triangles
$therefore$ The two triangles are congruent
text{color{#4257b2}The two triangles are congruent}
$$
For region A, I used $(0,6)$:
$$
begin{align*}
6&stackrel{?}{leq}|0|+4 & -0+4(6)&stackrel{?}{geq}4\
6¬{leq} 4 & 24&geq 4hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region A should not be shaded.
For region B, I used $(0,2)$:
$$
begin{align*}
2&stackrel{?}{leq}|0|+4 & -0+4(2)&stackrel{?}{geq}4\
2&leq 4hspace{5mm}checkmark & 8&geq 4hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region B should be shaded.
For region C, I used $(0,0)$:
$$
begin{align*}
0&stackrel{?}{leq}|0|+4 & -0+4(0)&stackrel{?}{geq}4\
0&leq 4hspace{5mm}checkmark & 0¬{geq} 4
end{align*}
$$
Only one inequality is satisfied so region C should not be shaded.
$$
color{white}tag{1}
$$
The region to be shaded is region B as shown:
$$
y>0
$$
$$
y<0.25x+1250
$$
y>0
$$
$$
y<0.25x+1250
$$
$textbf{a.}$
For region A, I used $(0,4)$:
$$
begin{align*}
4&stackrel{?}{leq}dfrac{2}{3}(0)+3 & 4&stackrel{?}{geq}dfrac{2}{3}(0)\
4¬{leq}3 & 4&geq 0hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region A should not be shaded.
For region B, I used $(0,1)$:
$$
begin{align*}
1&stackrel{?}{leq}dfrac{2}{3}(0)+3 & 1&stackrel{?}{geq}dfrac{2}{3}(0)\
1&leq 3hspace{5mm}checkmark & 1&geq 0hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region B should be shaded.
For region C, I used $(0,-1)$:
$$
begin{align*}
-1&stackrel{?}{leq}dfrac{2}{3}(0)+3 & -1&stackrel{?}{geq}dfrac{2}{3}(0)\
-1&leq 3hspace{5mm}checkmark & -1¬{geq} 0
end{align*}
$$
Only one inequality is satisfied so region C should not be shaded.
The solution of the system is shown:
For region A, I used $(0,4)$:
$$
begin{align*}
4&stackrel{?}{leq}dfrac{2}{3}(0)+3 & 4&stackrel{?}{leq}dfrac{2}{3}(0)\
4¬{leq}3 & 4¬{leq} 0
end{align*}
$$
Both inequalities are not satisfied so region A should not be shaded.
For region B, I used $(0,1)$:
$$
begin{align*}
1&stackrel{?}{leq}dfrac{2}{3}(0)+3 & 1&stackrel{?}{leq}dfrac{2}{3}(0)\
1&leq 3hspace{5mm}checkmark & 1¬{leq} 0
end{align*}
$$
Only one inequality is satisfied so region B should not be shaded.
For region C, I used $(0,-1)$:
$$
begin{align*}
-1&stackrel{?}{leq}dfrac{2}{3}(0)+3 & -1&stackrel{?}{leq}dfrac{2}{3}(0)\
-1&leq 3hspace{5mm}checkmark & -1&leq 0hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region C should be shaded.
The solution of the system is shown:
For region A, I used $(0,4)$:
$$
begin{align*}
4&stackrel{?}{geq}dfrac{2}{3}(0)+3 & 4&stackrel{?}{leq}dfrac{2}{3}(0)\
4&geq 3hspace{5mm}checkmark & 4¬{leq} 0
end{align*}
$$
Only one inequality is satisfied so region A should not be shaded.
For region B, I used $(0,1)$:
$$
begin{align*}
1&stackrel{?}{geq}dfrac{2}{3}(0)+3 & 1&stackrel{?}{leq}dfrac{2}{3}(0)\
1¬{geq} 3 & 1¬{leq} 0
end{align*}
$$
Both inequalities are not satisfied so region B should not be shaded.
For region C, I used $(0,-1)$:
$$
begin{align*}
-1&stackrel{?}{geq}dfrac{2}{3}(0)+3 & -1&stackrel{?}{leq}dfrac{2}{3}(0)\
-1¬{geq} 3 & -1&leq 0hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region C should not be shaded.
None of the regions are shaded since the test points do not satisfy the system of inequalities. So, the system has no solution.
b. The solution is the region below $yleq dfrac{2}{3}x$
c. No solution
We can graph both inequalities and those parts which are shaded for both of them is a set of solutions.
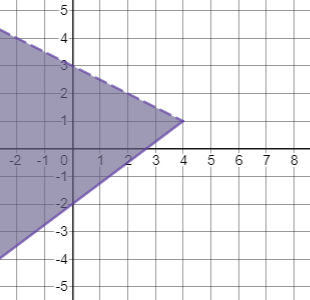
For region A, I used $(0,4)$:
$$
begin{align*}
4&stackrel{?}{geq}dfrac{3}{4}(0)-2 & 4&stackrel{?}{<}-dfrac{1}{2}(0)+3 \
4&geq -2hspace{5mm}checkmark & 4¬{<}3
end{align*}
$$
Only one inequality is satisfied so region A should not be shaded.
For region B, I used $(0,0)$:
$$
begin{align*}
0&stackrel{?}{geq}dfrac{3}{4}(0)-2 & 0&stackrel{?}{<}-dfrac{1}{2}(0)+3 \
0&geq -2hspace{5mm}checkmark & 0&<3hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region B should be shaded.
$$
begin{align*}
0&stackrel{?}{geq}dfrac{3}{4}(8)-2 & 0&stackrel{?}{<}-dfrac{1}{2}(8)+3 \
0¬{geq} 4 & 0¬{<}-1
end{align*}
$$
Both inequalities are not satisfied so region C should not be shaded.
For region D, I used $(0,-3)$:
$$
begin{align*}
-3&stackrel{?}{geq}dfrac{3}{4}(0)-2 & -3&stackrel{?}{<}-dfrac{1}{2}(0)+3 \
-3¬{geq} -2 & -3&<3hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region D should not be shaded.
$$
color{white}tag{1}
$$
The solution of the system of inequalities is shown:

The total amount of trash is 3280 homes times the amount of trash in each household, plus the other sources of trash which is 1500 lbs which must be less than 50000 lbs. Hence, the inequality is:
$$
color{#c34632}3280x+1500<50000
$$
Solve for the inequality. Subtract 1500 from both sides:
$$
3280x<48500
$$
Divide both sides by 3280:
$$
x<14.8
$$
So, each household is limited to less than 14.8 pounds of trash.
The exponent function form is $y=a b^x$.
Substitution values are given in the exponential form as follows:
$$
y=2.75 (1.05)^{10}
$$
$$
y=2.75cdot 1.6288
$$
$$
y=4.479
$$
After $10$ years the cost will be $4.479$ dollars.
text{color{#4257b2}$4.479$ dollars.}
$$
begin{align*}
&text{Let’s check if Clifford is right}\
&text{ For x=7 we solve this}\
&3left(7-2right)le :4\\
&3(5)le :4 \
&15le4 \\
&boxed{color{#c34632} text{False}}\ \
&color{#965501}text{Clifford was wrong} \
end{align*}
$$
color{#4257b2} text{False}
$$
Bernie’s rate is $dfrac{9}{4}=2.25$ meters per second so his distance is represented by:
$$
y=2.25xtag{1}
$$
Wendel’s rate is $dfrac{2}{1}=2$ meters per second and got a 9-meter head start so his distance is represented by:
$$
y=2x+9tag{2}
$$
First, we find when the two runners will have the same distance. By Equal Values Method, we equate eq. (1) and eq. (2) then solve for $x$:
$$
2.25x=2x+9
$$
Subtract $2x$ from both sides:
$$
0.25x=9
$$
Divide both sides by 0.25:
$$
x=36
$$
This corresponds to a time of 36 seconds. Solving for $y$ using $x=36$ on either equation, we have $y=2.25(36)=81$ which corresponds to a distance of 81 meters. Since the race is only 70 meters long, Bernie will never catch up with Wendel along the race.

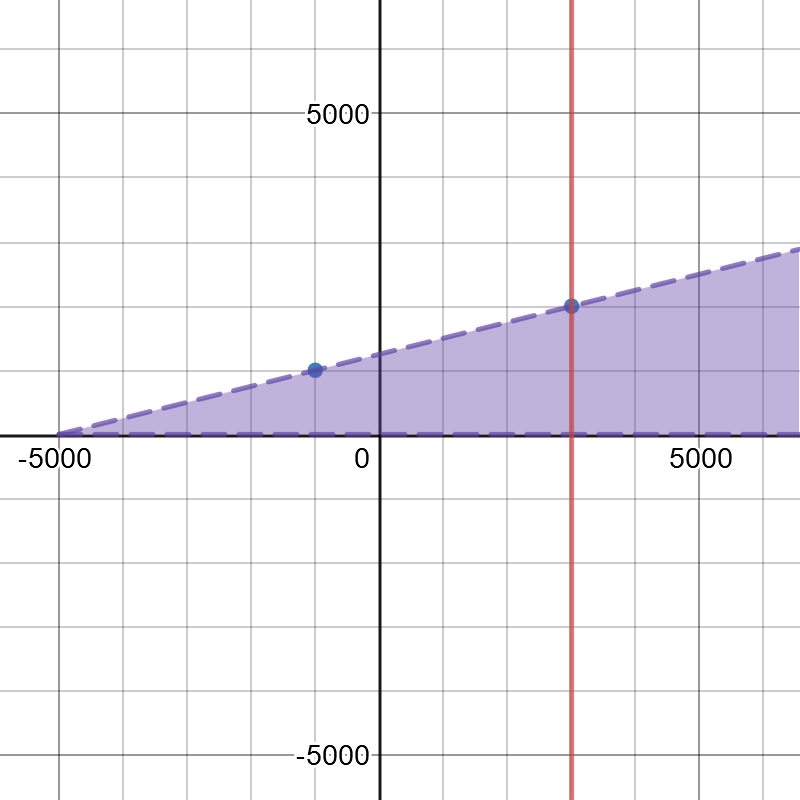
The following inequality represents the number of medicine and food packets that can be donated by a country:
$$
1000000>200x+800y
$$
On the following picture, there is graphed the solution of the previous inequality:
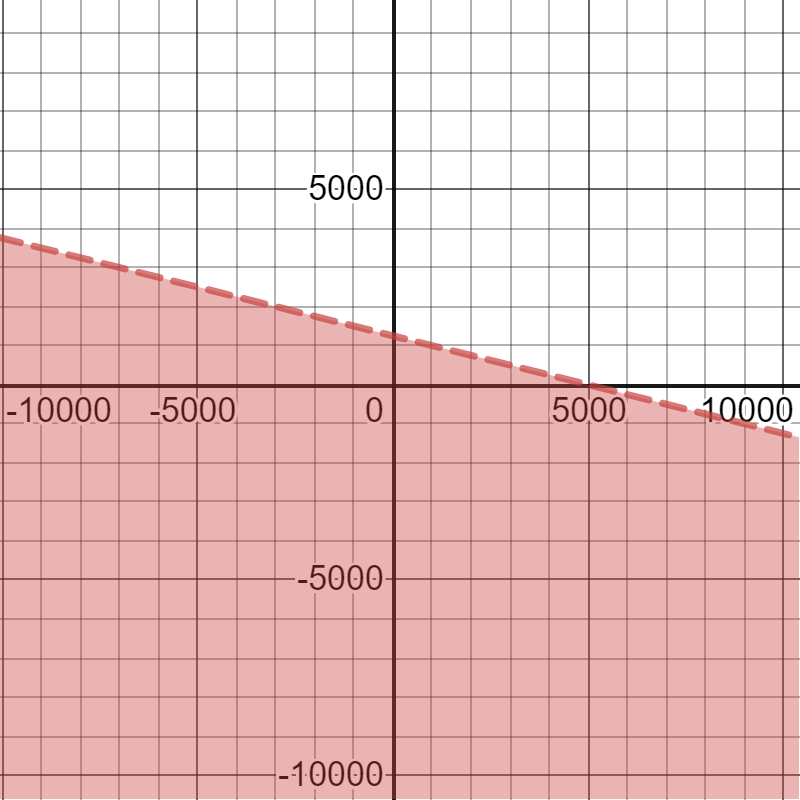
1000000>200x+800y
$$
There first we need to find how many food packages can give the country with the smallest budget, and then, the number of packages should donate each country.
#### (b)
There first we need to find how many medicine packages can donate the country with the smallest budget, and then, the number of packages should donate each country.
b) Find how many medicine packages can donate the country with the smallest budget.
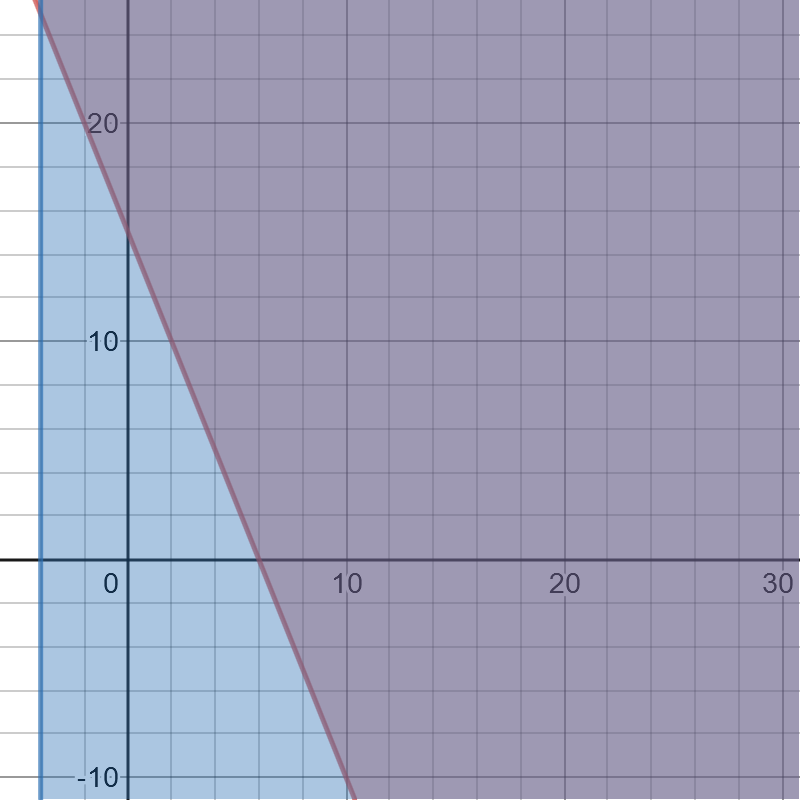
Let $y$ represent number of sold rulers and $x$ represent number of sold compasses, we get the following inequality:
$$
y+2.5xgeq15
$$
#### (b)
We will substitute $25$ for $x$ in the previous inequality and get the following:
$$
25+2.5xgeq15
$$
$$
2.5xgeq-10
$$
#### (c)
On the following picture, there are graphed both inequalities and double shaded region is set of points which are solutions to both of them.
#### (d)
There are not all points in the solution region possible combinations because some big numbers are not appropriate combinations in real life.
$text{(a)} xle6 text{(b)} x>1$
$text{(c)} xle2 text{or} x1
$$
text{color{#4257b2}$text{(a)} xle6 text{(b)} x>1$ \ \
$text{(c)} xle2 text{or} x1$}
$$
$$
color{#4257b2}text{(a)} 3(x-2)=-6
$$
Divide both of sides by $3$ as follows:
$$
x-2=-dfrac{6}{3} x-2=2
$$
Isolate the variables on the left sides as follows:
$$
x=2+2 x=4
$$
$$
color{#4257b2}text{(b)} (x+2)(x+3)=(x+1)(x+5)
$$
Use distributive property as follows:
$$
(xcdot x)+(xcdot3)+(2cdot x)+(2cdot3)=(xcdot x)+(xcdot5)+(1cdot x)+(1cdot5)
$$
$$
x^2+3x+2x+6=x^2+5x+x+5
$$
Use zero product property as follows:
$$
x^2+3x+2x+6-x^2-5x-x-5=0
$$
Add similar tiles to group like terms as follows:
$$
(x^2-x^2)+(3x+2x-5x-x)+(6-5)
$$
$$
-x+1=0 x=1
$$
color{#4257b2}text{(c)} |2x-5|=17
$$
Equal $2x-5=17$ as follows:
$$
2x=17+5 2x=22
$$
Divide both of sides by $2$ as follows:
$$
x=dfrac{22}{2} x=11
$$
Equal $-2x+5=17$ as follows:
$$
-2x=17-5 -2x=12
$$
Divide both of sides by $-2$ as follows:
$$
x=dfrac{12}{-2} x=-6
$$
The values of $x$ are equal
$$
x=11 text{ when} 2x-5ge0 2xge5 xgedfrac{5}{2}
$$
$$
x=-6 text{ when} 2x-5<0 2x<5 x<dfrac{5}{2}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=11, x=-6$ in the equation as follows:
$$
|2x-5|=17 |(2cdot11)-5|=17 |22-5|=17 |17|=17 17=17
$$
$$
|2x-5|=17 |(2cdot-6)-5|=17 |-12-5|=17 |-17|=17 17=17
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(d)} dfrac{2}{9} x=dfrac{14}{5}
$$
Multiply both of sides by $dfrac{9}{2}$ as follows:
$$
x=dfrac{14}{5}cdotdfrac{9}{2} x=dfrac{7cdot9}{5}
$$
$$
x=dfrac{63}{5} x=12.6
$$
(c) $x=11$ or $x=-6$
(d) $x=12.6$
$$
left|x-dfrac{3}{10} right|<dfrac{1}{64}
$$
$$
-dfrac{1}{64}<x-dfrac{3}{16}<dfrac{1}{64}
$$
$$
dfrac{3}{64}<x<dfrac{5}{64}
$$
So, the width suppose to be between $dfrac{3}{64}$ and $dfrac{5}{64}$ of an inch.
On the following picture, there is graphed solution.
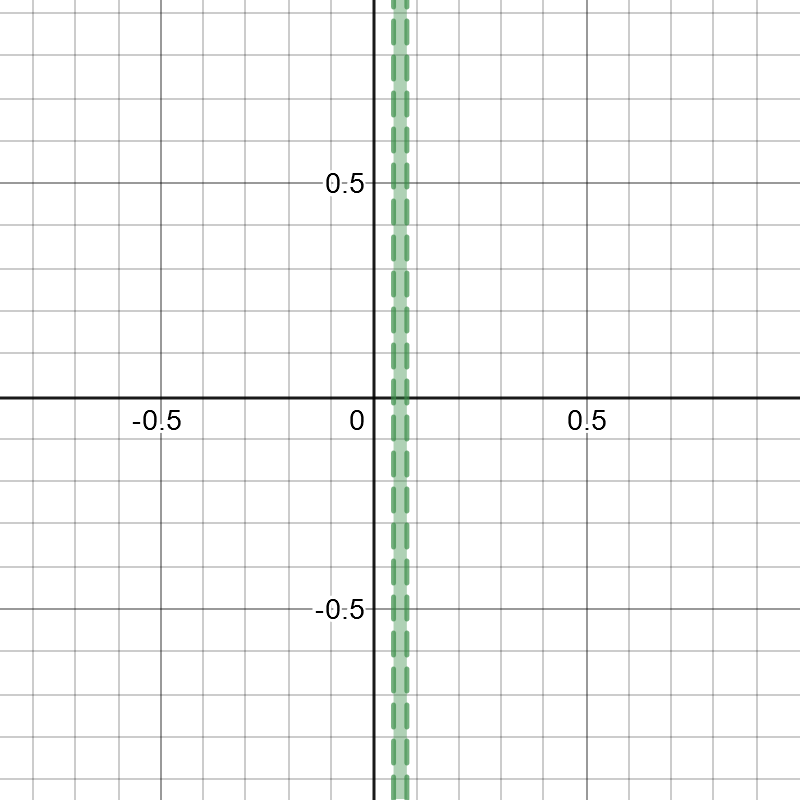
dfrac{3}{64}<x<dfrac{5}{64}
$$
Let:
$$
begin{align}
y&=3x+11\
x+y&=3
end{align}
$$
Since $y$ is already isolated in eq. (1), use Substitution Method. Substitute eq. (1) to eq. (2) then solve for $x$:
$$
begin{align*}
x+(3x+11)&=3\
4x+11&=3\
4x&=-8\
x&=-2
end{align*}
$$
Solve for $y$ using eq. (1):
$$
begin{align*}
y&=3(-2)+11\
y&=-6+11\
y&=5
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(-2,5)
$$
Let:
$$
begin{align}
y&=2x+3\
x-y&=-4
end{align}
$$
Since $y$ is already isolated in eq. (1), use Substitution Method. Substitute eq. (1) to eq. (2) then solve for $x$:
$$
begin{align*}
x-(2x+3)&=-4\
x-2x-3&=-4\
-x-3&=-4\
-x&=-1\
x&=1
end{align*}
$$
Solve for $y$ using eq. (1):
$$
begin{align*}
y&=2(1)+3\
y&=2+3\
y&=5
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(1,5)
$$
Let:
$$
begin{align}
x+2y&=16\
x+y&=2
end{align}
$$
Since both equations have the term $x$, use Elimination Method. Subtract each side of eq. (1) and eq. (2) to eliminate $x$ then solve for $y$:
$$
y=14
$$
Solve for $x$ using either eq. (1) or eq. (2). I used eq. (2):
$$
begin{align*}
x+14&=2\
x&=-12
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(-12,14)
$$
Let:
$$
begin{align}
2x+3y&=10\
3x-4y&=-2
end{align}
$$
I chose to use Elimination Method but first, we must have one variable having the same or opposite coefficients. I decided to eliminate $y$ so we multiply eq. (1) by 4 and eq. (2) by 3 to obtain the equations:
$$
begin{align}
8x+12y&=40\
9x-12y&=-6
end{align}
$$
Add eq. (3) and eq. (4) to eliminate $y$ and solve for $x$:
$$
begin{align*}
17x&=34\
x&=2
end{align*}
$$
Solve for $y$ using eq. (1):
$$
begin{align*}
2(2)+3y&=10\
4+3y&=10\
3y&=6\
y&=2
end{align*}
$$
So, the solution of the system is:
$$
color{#c34632}(2,2)
$$
b. $(1,5)$
c. $(-12,14)$
d. $(2,2)$
$$
text{color{#4257b2}(a) Find the equation which represent the following sequence.}
$$
$$
-3, 1, 5, 9, ……..
$$
$$
a_{0}=-3 a_{1}=1=-3+4=a_{0}+4
$$
$$
a_{2}=5=a_{1}+4=a_{0}+(2cdot4) a_{3}=9==a_{2}+4=a_{0}+(2cdot4)+4=a_{0}+(3cdot4)
$$
$$
color{#4257b2}a_{n}=-3+(ncdot4)=-3+4 n
$$
$$
text{color{#4257b2}(b) Write the equation in standard form.}
$$
$$
a_{n}=-3+4 n
$$
$$
text{color{#4257b2}(c) What is the {50} term of sequences.}
$$
$$
a_{n}=-3+4 n
$$
$$
a_{50}=-3+(4cdot50)=-3+200=197
$$
text{color{#4257b2}(a) $a_{n}=-3+4 n$ (b) $a_{n}=-3+4 n$
\ \
(c) $a_{50}=197$}
$$

