
All Solutions
Page 634: Closure Activity
In the exponential function $y=ab^x$, $a$ is the $y$-intercept and $b$ is the multiplier. In this case, the $y$-intercept is $(0,20)$ and the multiplier is $1.06$.
Using a table, plotting the points, and connecting them, the graph will look like:
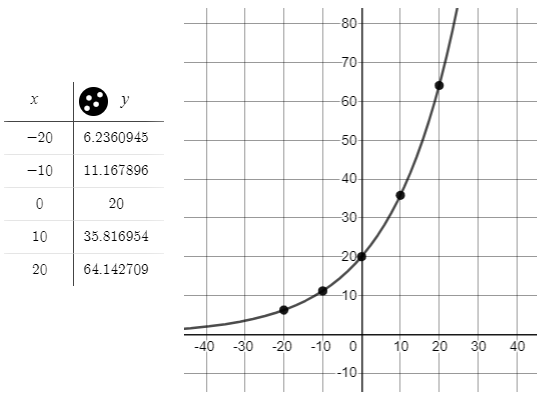
From the equation, the initial investment is $$20$. The multiplier is 1.06 which means that the percent interest per year is:
$$
1.06-1=0.06=color{#c34632}6%
$$
b. $6%$
equation $y=ab^x$ and get:
$$
24=ab^3
$$
$$
48=ab^4=ab^3cdot b=24cdot bRightarrow b=2
$$
From the first equation:
$$
a=dfrac{24}{2^3}=3
$$
So, the required function has an equation:
$$
y=3cdot2^x
$$
$$
dfrac{1}{235}nedfrac{9}{1792}nedfrac{12}{431}nedfrac{8}{120}
$$
,
Which means that there is an association between weight
in high school and developing diabetes.
From the two points, $Delta x=1-(-1)=2$ and $Delta y=2-18=-16$. So, the slope is:
$$
m=dfrac{Delta y }{Delta x}=dfrac{-16}{2}=-8
$$
Use the equation of the line in the form $y=mx+b$. Substituting any of the two points and the slope, we can solve for $b$. I used $(x,y)=(1,2)$:
$$
begin{align*}
y&=mx+b\
2&=-8 (1)+b\
2&=-8+b\
10&=b
end{align*}
$$
So, the equation of the line is:
$$
color{#c34632}y=-8x+10
$$
Use the exponential function equation:
$$
y=ab^x
$$
Using $(-1,18)$, we write one equation:
$$
18=ab^{-1}tag{1}
$$
Using $(1,2)$, we write another equation:
$$
2=abtag{2}
$$
Using eq. (1), solve for $a$ to obtain the equation:
$$
a=dfrac{18}{b^{-1}} tag{3}
$$
Substitute eq. (3) to eq. (2) then solve for $b$:
$$
begin{align*}
2&=dfrac{18}{b^{-1}}cdot b\
2&=18b^2\
dfrac{1}{9}&=b^2\
sqrt{dfrac{1}{9}}&=b\
b&=dfrac{1}{3}
end{align*}
$$
Solve for $a$ using eq. (2):
$$
begin{align*}
2&=acdot dfrac{1}{3}\
6&=a
end{align*}
$$
So, the exponential function is:
$$
color{#c34632}y=6left(dfrac{1}{3}right)^x
$$
b. $y=6left(dfrac{1}{3}right)^x$
An equation of the required line is the following:
$$
y-18=dfrac{2-18}{1+1}(x+1)
$$
$$
y=-8(x+1)+18
$$
$$
y=-8x+10
$$
#### (b)
We will substitute the corresponding values of $x$ and $y$
in the equation $y=ab^x$ and get:
$$
18=ab^{-1}=ab^2b^{-3}=2b^{-3}Rightarrow b^{-3}=9Rightarrow b=dfrac{1}{sqrt[3]{9}}=9^{-3}
$$
$$
2=ab^2
$$
From the second equation we get:
$$
a=dfrac{2}{b^2}=dfrac{2}{9^{-6}}
$$
So, the required function has an equation.
$$
y=dfrac{2}{9^{-6}}(9^{-3})^x
$$
Here, we can conclude that angles in those triangles are $62^{circ}$, $48^{circ}$ and $72^{circ}$.
They have one pair of sides with equal length and the included angles are equal in measurement, which means that those triangles are congruent according to the ASA condition.
#### (b)
Those triangles have two equal sides in the length and a non-included angle, which means that those triangles are congruent according to the SSA condition.
#### (c)
Those triangles have three pairs of sides which are equal in the length, which means that those triangles are congruent according to the $SSS$ condition.
$$
color{#4257b2}text{(a)} 2x+3y=7 -3x-5y=-13
$$
Multiply the first equ. by $3$ to get $6x+9y=21$
Multiply the second equ. by $2$ to get $-6x-10y=-26$
Using elimination property for the new equations as follows:
$$
(6x-6x)+(9y-10y)=(21-26) -y=-5 y=5
$$
Substitution the value of $y=5$ for first equation as follows:
$$
2x+3cdot5=7 2x+15=7 2x=7-15
$$
$$
2x=-8 x=-dfrac{8}{2} x=-4
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-4, y=5$ in the equation as follows:
$$
2cdot-4+3cdot5=7 -8+18=7 7=7
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} 8-y=3x 2y+3x=5
$$
Rearrange the equation as form $ax+by=c$ as follows:
$$
3x+y=8 3x+2y=5
$$
Multiply the second equ. by $-1$ as follows:
$$
3x+y=8 -3x-2y=-5
$$
Using elimination property for the new equations as follows:
$$
(3x-3x)+(y-2y)=(8-5) -y=3 y=-3
$$
Substitution the value of $y=-3$ for first equation as follows:
$$
8-(-3)=3x 8+3=3x 11=3x x=dfrac{11}{3}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=tfrac{11}{3}, y=-3$ in the equation as follows:
$$
8-(-3)=3tfrac{11}{3} 11=11
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $x=-4 y=5$
\ \
(b) $x=dfrac{11}{3} y=-3$}
$$
Here, we can notice that this is a geometric sequence where the first term is $a_{1}=20$ and the common ratio is $q=dfrac{1}{10}$, so, its equation is the following:
$$
a_{n}=20left( dfrac{1}{10}right)^{n-1}
$$
Where $a_{n}$ is $n$th term.
#### (b)
Here, we can notice that this is an arithmetic sequence where first term is $a_{1}=5$ and constant difference is $d=3$, so, its
equation is the following:
$$
a_{n}=5+3(n-1)
$$
,
Where $a_{n}$ is $n$th term.
On the following picture, there is graphed the figure
$ABCDE$ and rotated $ABCDE$.
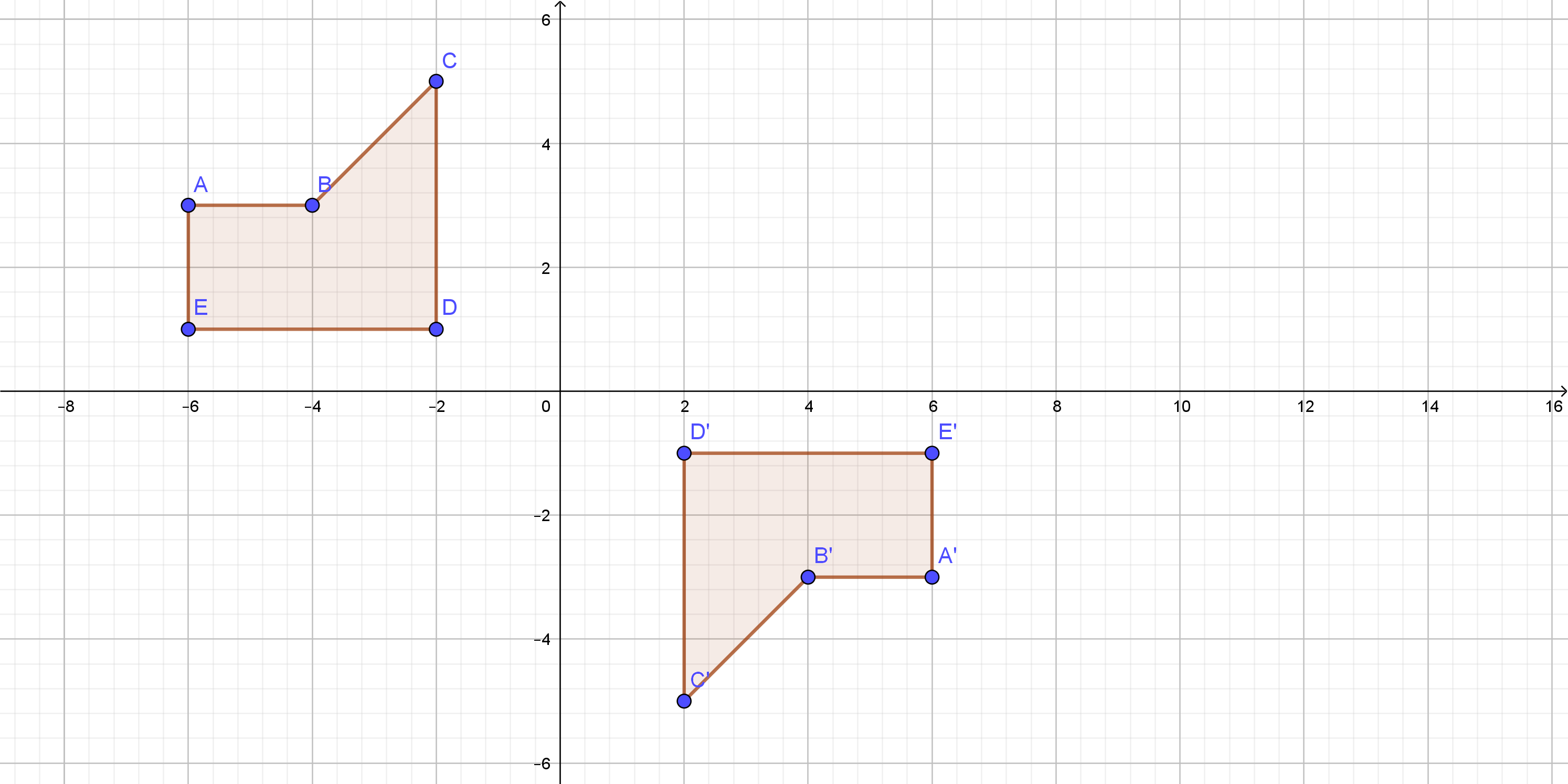
On the following picture, there is rotated $ABCDE$ around the origin.
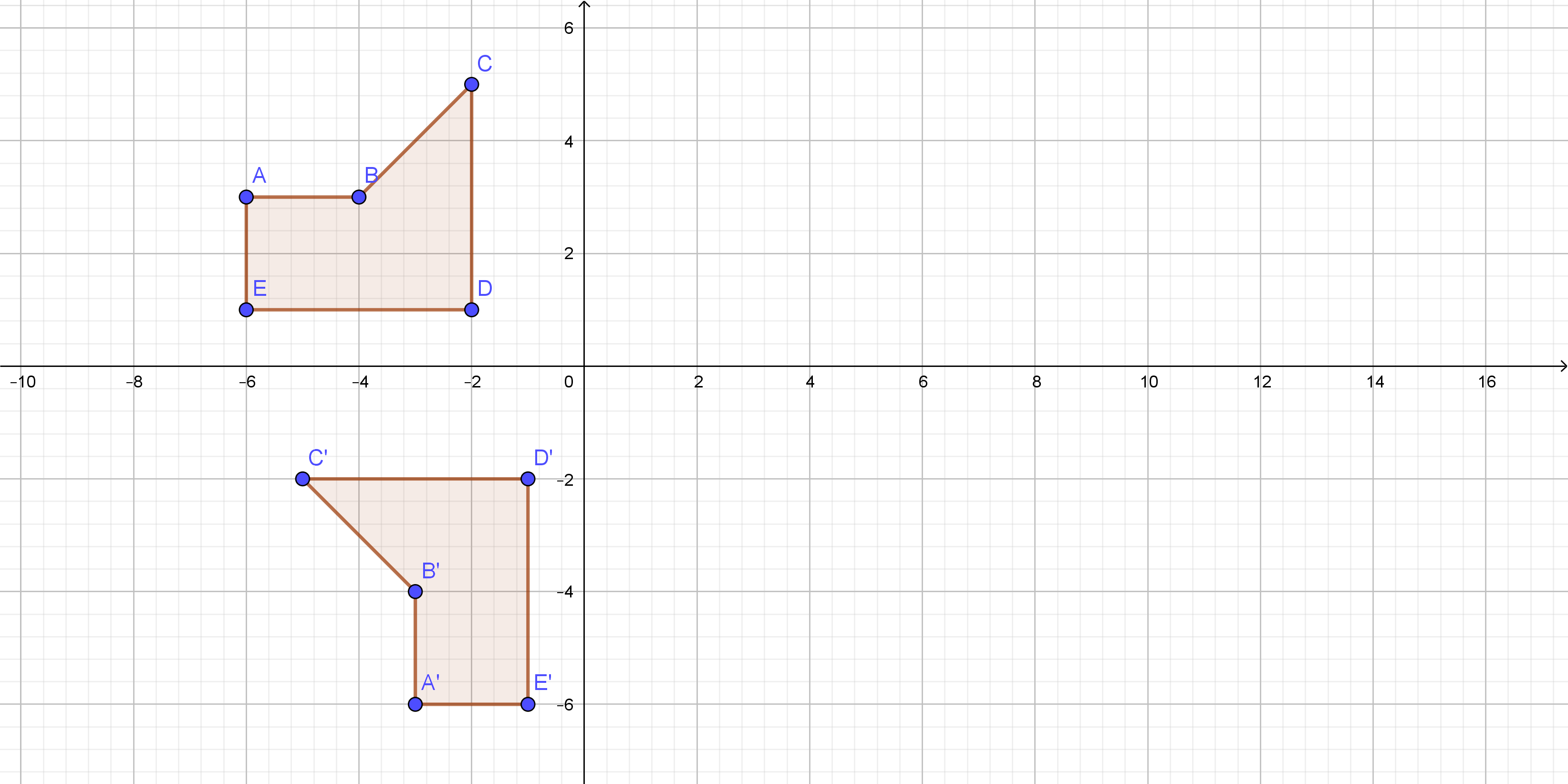
On the following picture, there is reflected $ABCDE$ across the $y$-axis.
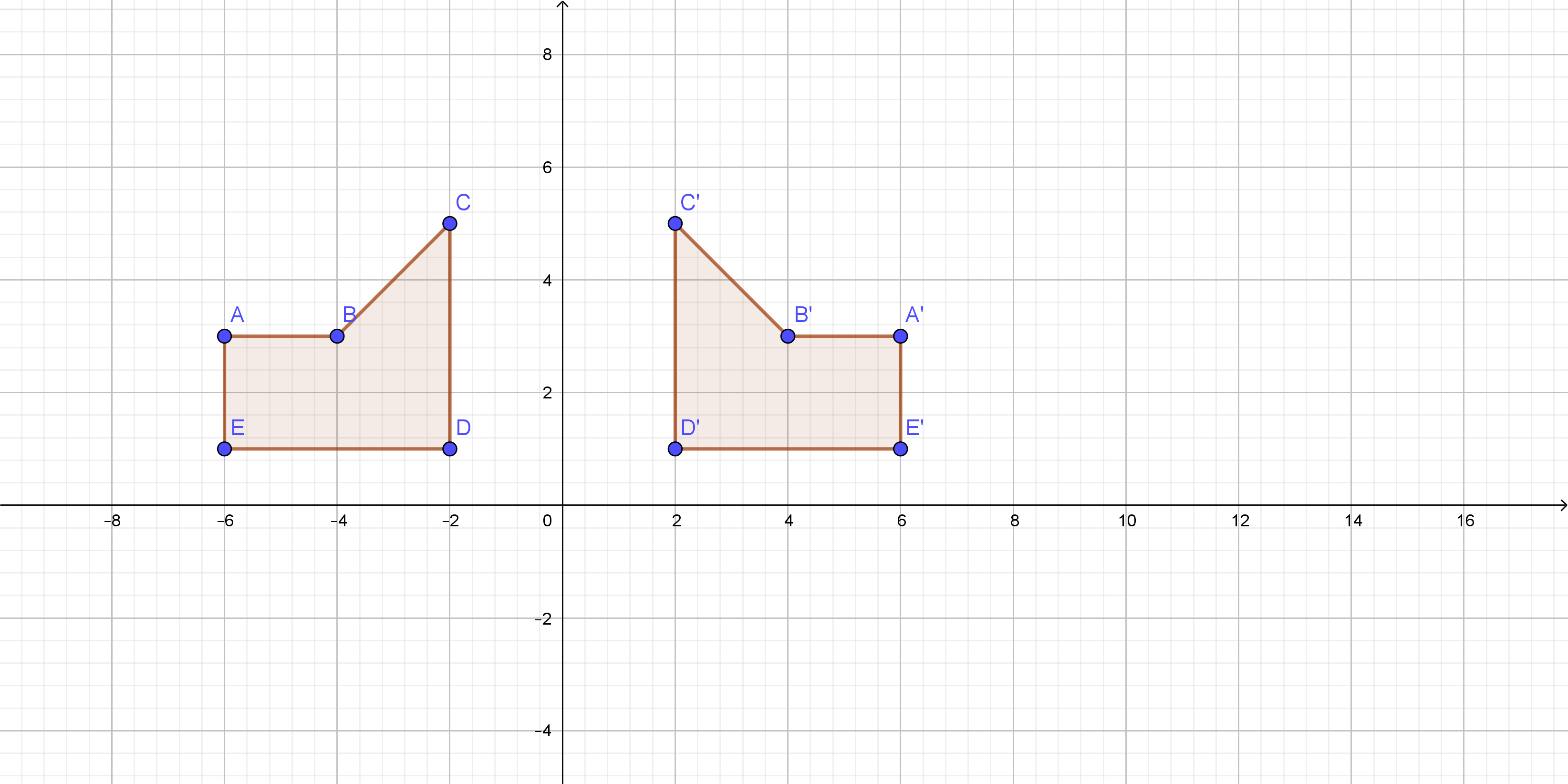
On the following picture, there is translated $ABCDE$.
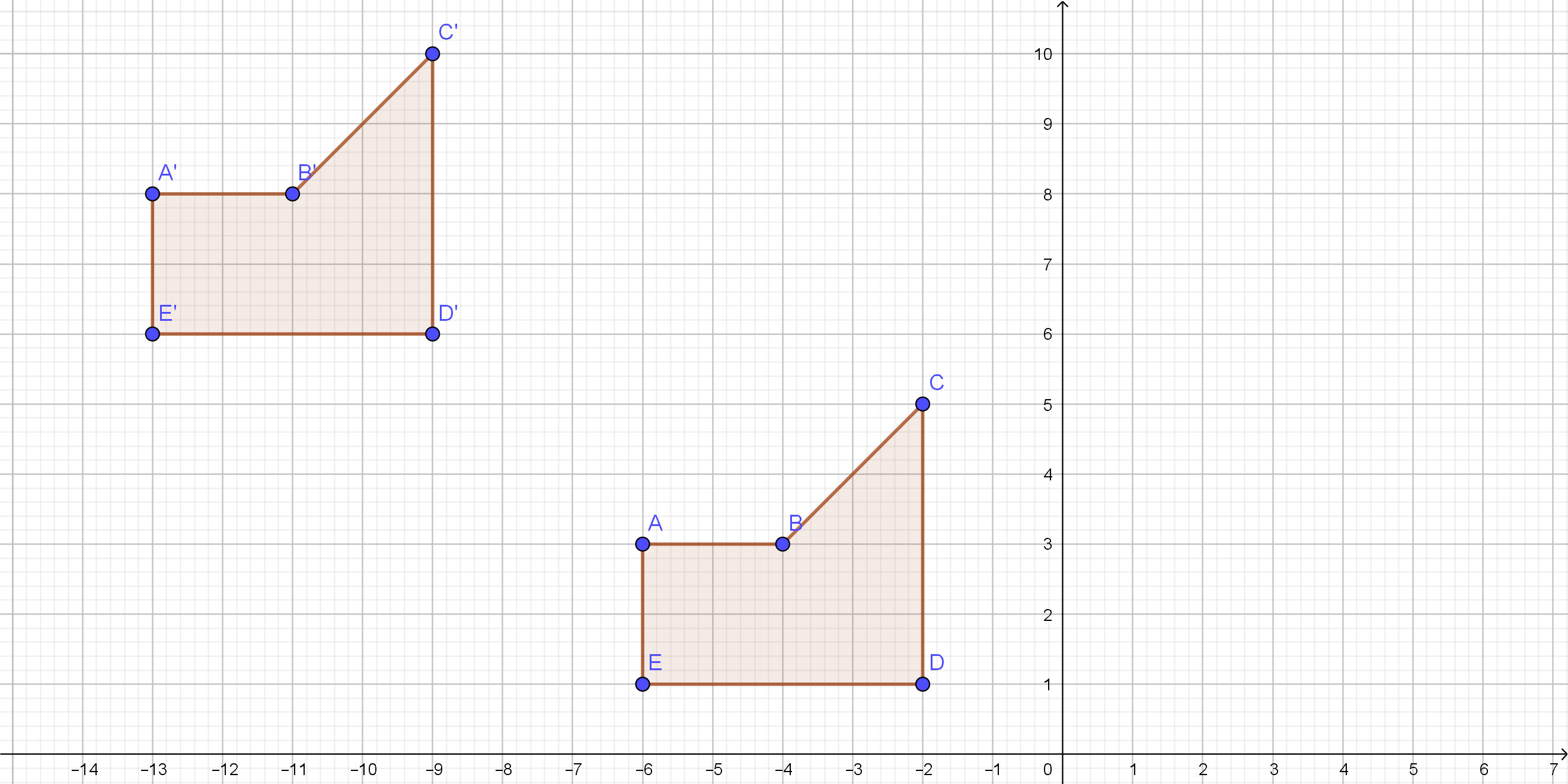
$$
color{#4257b2}text{(a)} |2x+9|=31
$$
Equal $2x+9=31$ as follows:
$$
2x+9=31 2x=31-9 2x=22
$$
$$
x=dfrac{22}{2} x=11
$$
Equal $-2-9=31$ as follows:
$$
-2-9=31 -2x=31+9 -2x=40
$$
$$
x=dfrac{40}{-2} x=-20
$$
The values of $x$ are equal
$$
x=11 text{ when} 2x+9ge0 2xge-9 xge-dfrac{9}{2}
$$
$$
x=-20 text{ when} 2x+9<0 2x<-9 x<-dfrac{9}{2}
$$
color{#4257b2}text{(b)} (x+14)^2=36
$$
Use square root property for both side as follows:
$$
sqrt{(x+14)^2}=sqrt{36} x+14=pm6
$$
Isolate the variables on the left side as follows:
$$
x=6-14 x=-8
$$
$$
x=-6-14 x=-20
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-8, x=-20$ in the equation as follows:
$$
(-8+14)^2=36 6^2=36 36=36
$$
$$
(-20+14)^2=36 -6^2=36 36=36
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(c)} sqrt{4x-6}+18=42
$$
$$
sqrt{4x-6}=42-18 sqrt{4x-6}=24
$$
Use square property for both side as follows:
$$
(sqrt{(4x-6)})^2=24^2 4x-6=576
$$
Isolate the variables on the left side as follows:
$$
4x=576+6 4x=582 x=dfrac{582}{4}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=dfrac{582}{4}$ in the equation as follows:
$$
sqrt{4cdotdfrac{582}{4}-6}+18=42 sqrt{576}+18=42
$$
$$
24+18=36 36=36
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(d)} dfrac{x}{5}+dfrac{x}{4}=1
$$
$$
dfrac{5x+4x}{20}=1 dfrac{9x}{20}=1
$$
Isolate the variables on the left side as follows:
$$
9x=20 x=dfrac{20}{9}
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=dfrac{20}{9}$ in the equation as follows:
$$
dfrac{20}{5cdot9}+dfrac{20}{4cdot9}=1 dfrac{4}{9}+dfrac{5}{9}=1
$$
$$
dfrac{9}{9}=1 1=1
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $x=11$ or $x=-20$ (b) $x=-8$ or $x=-20$
\ \
(c) $x=dfrac{582}{4}$ (d) $x=dfrac{20}{9}$}
$$
Assume length of each one of two pieces of string is $x$
The first one length is $15+x$
Total length of string can be represented by:
$$
15+x+x+x=42 15+3x=42
$$
Isolate the variables on the left side as follows:
$$
3x=42-15 3x=27
$$
Divide both of sides by $3$ as follows :
$$
x=dfrac{27}{3} x=9
$$
Length of first piece is $15+9=24$ meters
Length of two pieces which are equals are $9$ meters
text{color{#4257b2}Large Lengths are: $24, 9 text{and} 9$ meters}
$$
your answers using the table at the end of the section.
There, you can see what are your problems.

