
All Solutions
Page 585: Questions
You can align one side of tracking paper with a given line.
Because, tracing paper is square, and the square has parallel lines,
you can draw a line aligned with the opposite side.
#### (b)
You can find a midpoint of the given line and align that point with
a corner of tracing paper.
Because tracing paper is square and the square has right angles,
the conclusion is that the line through midpoint aligned with one side
of tracing paper is actually perpendicular bisector.
#### (c)
On the following picture, there is formed a triangle $ABC$.
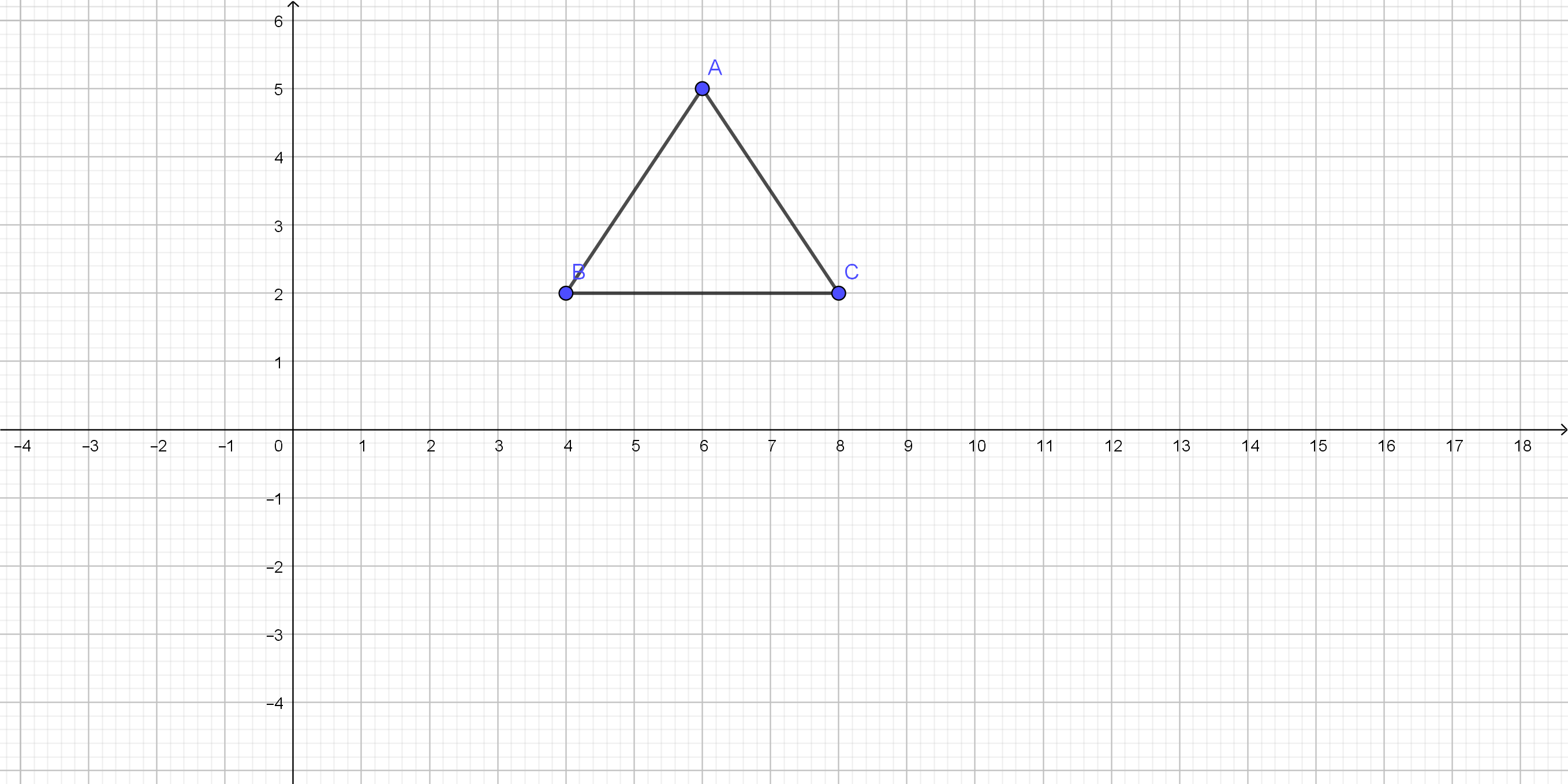
$overline{AC}$ and $overline{AB}$.
#### (d)
First, you need to use a compass and graph semicircle from point $A$ to lines $overline{AC}$ and $overline{AB}$.
Then, from points of intersecting with a semicircle and lines,
$overline{AC}$ and $overline{AB}$ graph circle bends
inside the angle.
Through their point of intersection and point $A$, graph
a line using a ruler and that line will represent the angle bisector.
b) Find midpoint first;
c) Triangle with two equal sides;
d) Use compass and a ruler.
concentric circles.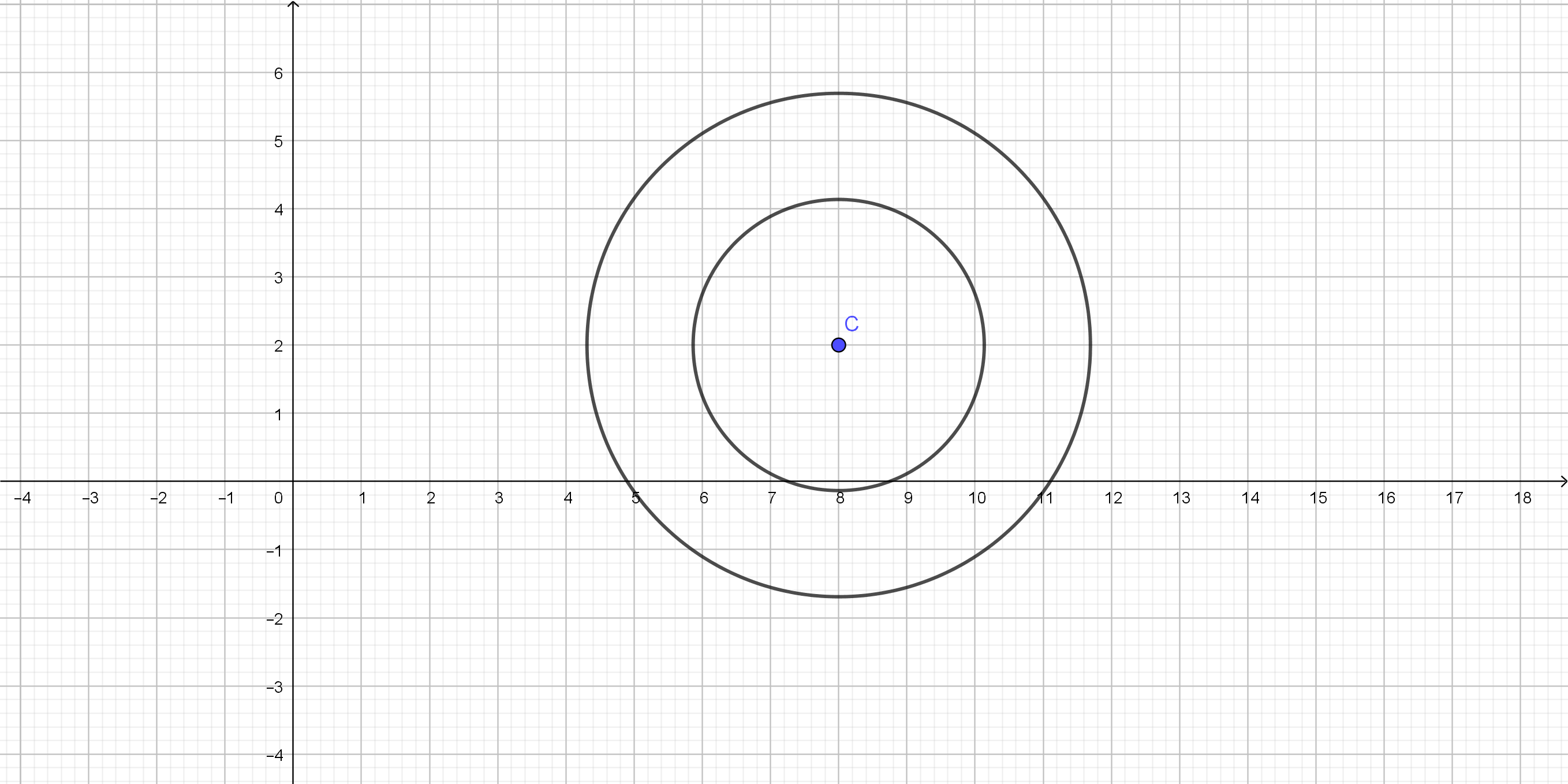
You can measure the same distance with
a straightedge from points $A$ and $B$ on
the right side and on that way mask that points
as $C$ and $D$ and then draw a line through them.
#### (c)
You can use a compass for this. You can measure
how long is $overline{AB}$ and then put on paper
twice that measure and draw a line through
the beginning and final point and that line is
$overline{EF}$ which is twice longer than $overline{AB}$.
Draw a line and on that line put circle bend from the angle
$measuredangle X$ and then graph another line at the end
of that circle bend.
That is angle $Y$.
b) You can use only a straight angle;
c) Use a compass;
d) Use a compass and a ruler.
On the following picture, there is graphed a circle
with radius $r$ and center $H$.

On the following picture, there is graphed the regular
hexagon from the previous circle.
On the following picture, there is graphed an equilateral
triangle that is inscribed in a circle $H$.

b) Perform indicated transformations. Use technology to help you if needed;
c) Perform indicated transformations. Use technology to help you if needed;
side of the triangle $overline{AB}$.
Then you need to place a compass point
on $A$ and measure the distance to the point $B$.
Then, swing an arc of this size above the segment.
After that, without changing the span on the compass,
place the compass point on $B$ and swing the same arc,
intersecting with the first arc.
Finally, label the point of intersection as the third vertex
of the equilateral triangle.
$$
y=ab^x
$$
where $a$ is the initial value and $b$ is the constnt multiplier.
From the given, $a=2.79$ (current cost of $$2.79$) and $b=100%+8%=108%=1.08$ (increased 8% per year). With $x$ as the number of years and $y$ as the cost of a loaf in dollars, the equation is:
$$
y=2.79(1.08)^x
$$
$textbf{a.}$
$x=5$ represents 5 years later, so the cost will be:
$$
begin{align*}
y&=2.79(1.08)^{ 5}\
&approx 4.10to color{#c34632}$4.10
end{align*}
$$
$textbf{b.}$
5 years ago is represented by $x=-5$. So, the cost then was:
$$
begin{align*}
y&=2.79(1.08)^{-5}\
&approx 1.90to color{#c34632}$1.90
end{align*}
$$
b. $$1.90$
Percentage of students who do not carry a backpack at school is:
$$
p=dfrac{39}{100}=39%
$$
#### (b)
The probability that a junior is carring a backpack is following:
$$
p=dfrac{14}{100}=0.14
$$
The required probability is the following:
$$
p=dfrac{14+16}{100}=dfrac{30}{100}=0.3
$$
#### (d)
We can notice that:
$$
dfrac{8}{11}nedfrac{16}{22}nedfrac{18}{22}nedfrac{19}{35}
$$
The conclusion is that there is a relationship between graduating class and carrying a backpack.
Since two triangles are similar, so :
$$
dfrac{AB}{AD}=dfrac{BC}{DE} text{Where},
$$
$$
because AB=5 AD=AB+BD=5+4=9 BC=7
$$
$$
therefore dfrac{AB}{AD}=dfrac{BC}{DE} therefore dfrac{5}{9}=dfrac{7}{DE}
$$
$$
therefore DE=dfrac{7cdot9}{5}=dfrac{63}{5}=12.6
$$
text{color{#4257b2}$$DE=12.6$$}
$$
$$
color{#4257b2}text{(a)} 8a+a-3=6a-2a-3
$$
Isolate the variables on the left side as follows:
$$
8a+a-6a+2a=-3+3 5a=0
$$
Divid both sides of equation by $5$ as follows.
$$
dfrac{5a}{5}=dfrac{0}{5} a=0
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=0$ in the equation as follows:
$$
((8cdot0)+0-3=(6cdot0)-(2cdot0)-3 0+0-3=0-0-3 -3=-3
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} 8(3m-2)-7m=0
$$
Multiply from the left to the right as follows:
$$
24m-16-7m=0
$$
Isolate the variables on the left side as follows:
$$
24m-7m=16 17m=16
$$
Divid both sides of equation by $17$ as follows.
$$
dfrac{17m}{17}=dfrac{16}{17} m=0.9411
$$
$text{color{#4257b2}Check:}$ substitute the value of $m=0.9411$ in the equation as follows:
$$
8((3cdot0.9411)-2)-(7cdot0.9411)=0 6.58-6.58=0
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(c)} dfrac{x}{2}+1=6
$$
Isolate the variables on the left side as follows:
$$
dfrac{x}{2}=6-1 dfrac{x}{2}=5
$$
Multiply both sides of equation by $2$ as follows.
$$
dfrac{x}{2} cdot2=5cdot2 x=10
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=10$ in the equation as follows:
$$
dfrac{10}{2}+1=6 5+1=6 6=6
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(d)} |x-3|+5=11
$$
Isolate the variables on the left side as follows:
$$
|x-3|=11-5 |x-3|=6
$$
$$
x-3=6 x=6+3 x=9
$$
$text{color{#4257b2}Check:}$ substitute the value of $m=9$ in the equation as follows:
$$
|9-3|+5=11 |6|+5=11 11=11
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}(a) $0$ (b) $m=0.9411$
\ \
(c) $x=10$ (d) $x=9$}
$$
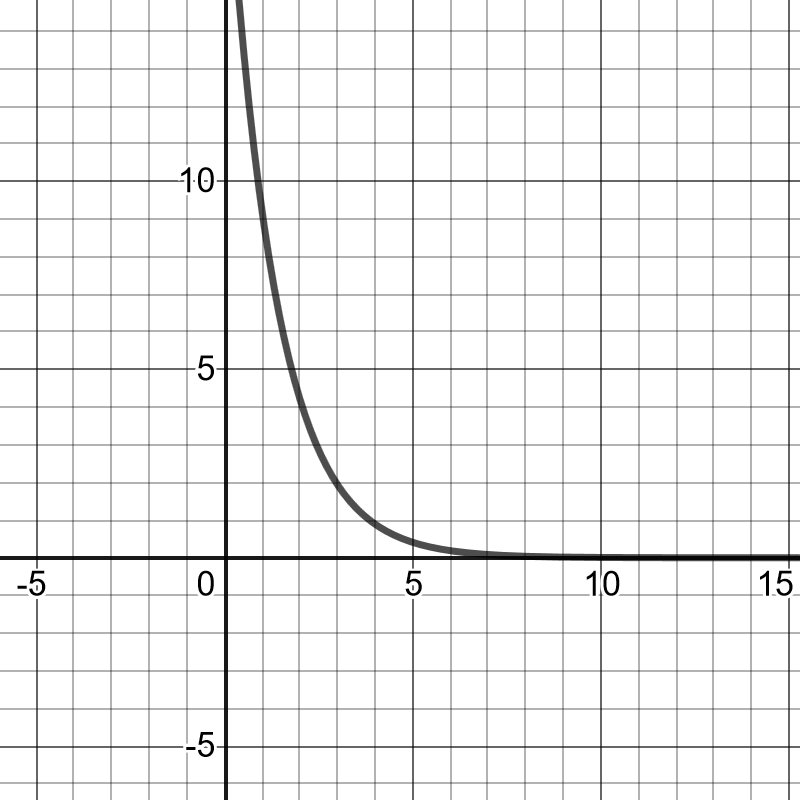
The horizontal line represents that the temperature of a cup never gains that value or being less than it.
#### (b)
The graph will be more like a straight line at the beginning until to asymptote, than this curve.
b) It will be more like a straight line at the beginning.
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
2&=2m-8 \
10&=2m \
5&=m
end{align*}
$$
Next, pick a test point except for the boundary point, say $m=0$ to substitute to the inequality:
$$
begin{align*}
2&<2(0)-8 \
2&<0-8 \
2¬{5
$$
On a number line, use an open circle for the boundary point 5 then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
dfrac{1}{3}x-1&=-3 \
dfrac{1}{3}x&=-2 \
x&=-6
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
dfrac{1}{3}(0)-1&leq -3 \
0-1&leq -3\
-1&leq -3
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the right of it. So, the solution is to the left of the boundary point:
$$
color{#c34632}xleq -6
$$
On a number line, use a filled circle for the boundary point $-6$ then draw an arrow pointing to the left:
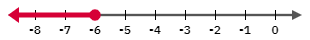
First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
5(2x-8)+24&=3(4+2x) \
10x-40+24&=12+6x \
10x-16&=12+6x\
10x&=28+6x\
4x&=28\
x&=7
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
5(2(0)-8)+24&>3(4+2(0)) \
5(-8)+24&>3(4) \
-40+24&>12 \
-16¬{>}12
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the left of it. So, the solution is to the right of the boundary point:
$$
color{#c34632}x>7
$$
On a number line, use an open circle for the boundary point 7 then draw an arrow pointing to the right:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
5+2k&=k-2+k \
5+2k&=2k-2 \
5&=-2
end{align*}
$$
The variable was eliminated and the resulting equation is false for all $k$-values. The corresponding inequality $5<-2$ is also false so the solution is the empty set (no solution):
$$
color{#c34632}{text{O}}
$$
Represent this as simply the number line:
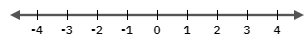
b. $xleq -6$
c. $x>7$
d. No solution
$$
color{#4257b2}text{(a)} 2 geq 2m-8
$$
Isolate the variables on the left side as follows:
$$
2+8 geq2m 2mgeq10
$$
Divide both sides of inequality by $2$ as follows.
$$
mgeq dfrac{10}{2} mgeq5
$$
$$
color{#4257b2}text{(b)} dfrac{x}{3}-1leq-3
$$
Isolate the variables on the left side as follows:
$$
dfrac{x}{3}leq-3+1 dfrac{x}{3}leq-2
$$
Multiply both sides of inequality by $3$ as follows.
$$
xleq -2cdot3 xleq-6
$$
color{#4257b2}text{(c)} 5(2x-8)+24geq3(4+2x)
$$
Multiply from the left to the right as follows:
$$
10x-40+24geq12+6x 2m geq10
$$
Isolate the variables on the left side as follows:
$$
10x-6x geq12-24+40 4x geq28
$$
Divide both sides of inequality by $4$ as follows.
$$
x geqdfrac{28}{4} xgeq7
$$
$$
color{#4257b2}text{(d)} 5+2k leq k-2+k
$$
Isolate the variables on the left side as follows:
$$
2k-k-k leq -2-5 0leq-7
$$
No solution
(c) $x geq7$ (d) No solution
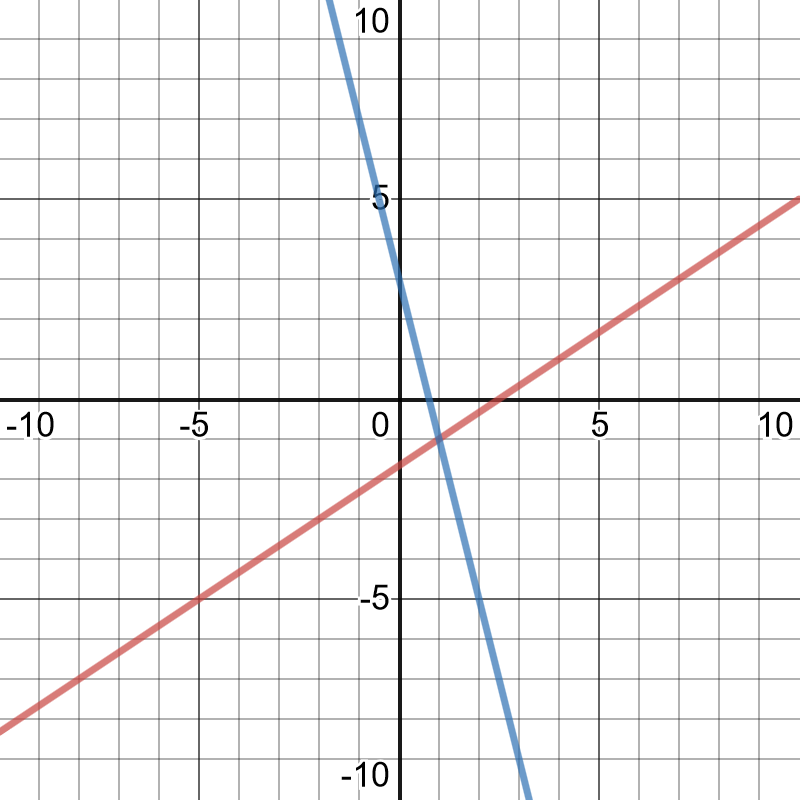
We can use a graph method. On the following picture,
there are graphed both equations and solution is their
point of intersecting, we can notice that the solution
is point $(1,-1)$, or $x=1$ and $y=-1$.
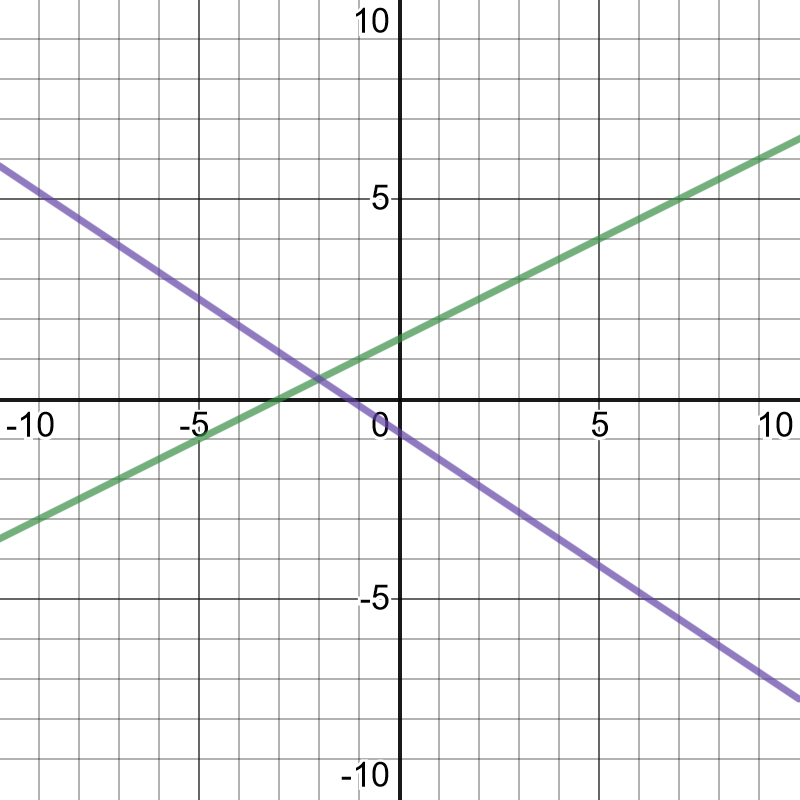
We can use the graph method. On the following picture,
there are graphed both equations and solution is their
point of intersection, we can notice that the solution is point
$left(-2,dfrac{1}{2} right)$, or $m=-2$ and $n=dfrac{1}{2}$.
$$
y=mx+b
$$
or in this case,
$$
t(n)=mn+t(0)
$$
The two terms represent the two points$(8,1056)$ and $(13,116)$ so the slope (sequence generator) is:
$$
m=dfrac{Delta y}{Delta x }=dfrac{116-1056}{13-8}=dfrac{-940}{5}=-188
$$
Using any point, say $(13,116)$, solve for $t(0)$:
$$
begin{align*}
116&=-188(13)+t(0)\
116&=-2444+t(0)\
2560&=t(0)
end{align*}
$$
So, the equation for the arithmetic sequence is:
$$
color{#c34632}t(n)=-188n+2560
$$
Find $t(5)$ using the equation we found:
$$
begin{align*}
t(5)&=-188(5)+2560\
&=-940+2560\
&=color{#c34632}1620
end{align*}
$$
$$
t(5)= 1620
$$
sequence is the following:
$$
a_{n}=a_{1}(n-1)d
$$
Where $a_{1}$ is a first term, $d$ is constant difference.
Using that $t(8)=1056$ and $t(13)=116$, we will get system
of equations which we will solve for $t(1)$ and $d$ and on that
way find $t(5)$:
$$
t(8)=1056=t(1)+(8-1)d
$$
$$
t(13)=116=t(1)+(13-1)d
$$
After simplifying, we get:
$$
t(1)+7d=1056
$$
$$
t(1)+12d=116Leftrightarrow t(1)+7d+5d=116
$$
we will substitute $1056$ for $t(1)+7d$ in the second equation
and on that way we will get $d$:
$$
1056+5d=116
$$
$$
5d=-940
$$
$$
d=-188
$$
Now, substitute $-188$ for $d$ in some of equation, and get $t(1)$:
$$
t(1)+7(-188)=1056
$$
$$
t(1)=2372
$$
So, explicit formula for this sequence is:
$$
t(n)=2372+(n-1)(-188)
$$
Now, substitute $5$ for $n$ in order to find $t(5)$:
$$
t(5)=2372+(5-1)(-188)
$$
$$
t(5)=1620
$$
$bigodot A$ and $bigodot B$ have the same radius because of each of them passes through the center of the other circle.
#### (b)
On the following picture, there are graphed described circles.

On the following picture, there is graphed required quadrilateral $ABCD$.
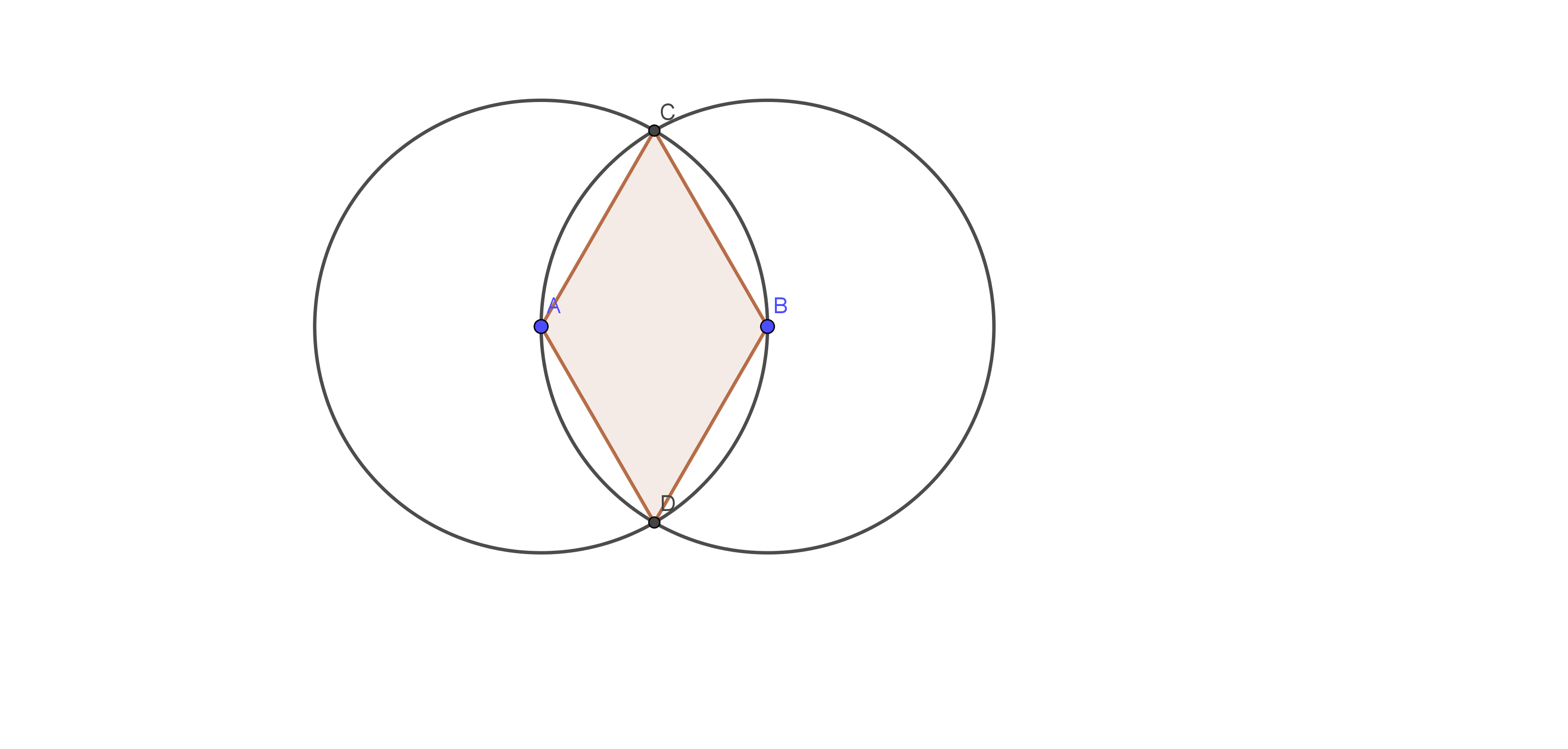
those are circles with the same radius and because
points $C, D$ are on circles, their distances from points
$A$ and $B$ are equal because of $A$ and $B$ are centers
of circles.
From the following picture, we can conclude that a triangle $triangle ACD$
is a triangle with equal sides, while $triangle ACD$ has two equal sides,
$overline{AC}$ and $overline{AD}$.
#### (e)
We can conclude that the line segments $overline{CD}$ and $overline{AB}$
are perpendicular line and their point of intersect is
a midpoint of both segments.
b) You can use GeoGebra;
c) $ABCD$ is a rhombus;
d) $triangle ACD$ is equilateral and $triangle ACD$ has two equal sides;
e) they are perpendicular lines and their point of intersect is a midpoint of both of them.
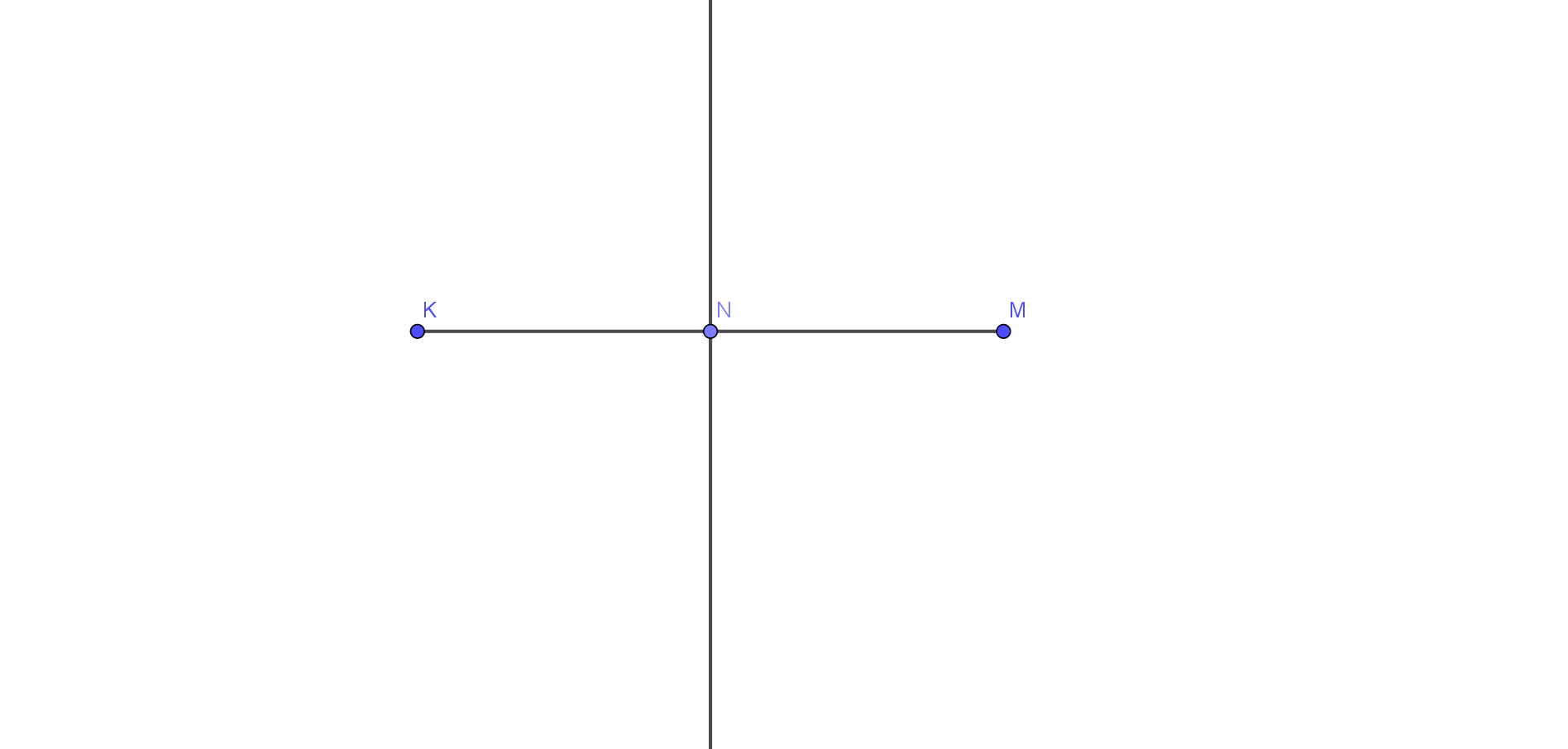
If you are already given a length of the segment $overline{AB}$,
next thing is to fix the compass opening to a distance somewhat
bigger than $dfrac{1}{2}$ the length of the segment $AB$, but not
more than the length of $AB$. After that put the needle of compass
at $A$ and draw an arc, then put the needle at $B$ and also draw an arc.
Finally, draw the line joining the two points where the two arcs intersect.
The point of intersection of the line and the segment is required midpoint.
Now, through the midpoint, using a straightedge, it is possible to construct
the perpendicular line on that way you align one side of straightedge with the segment.
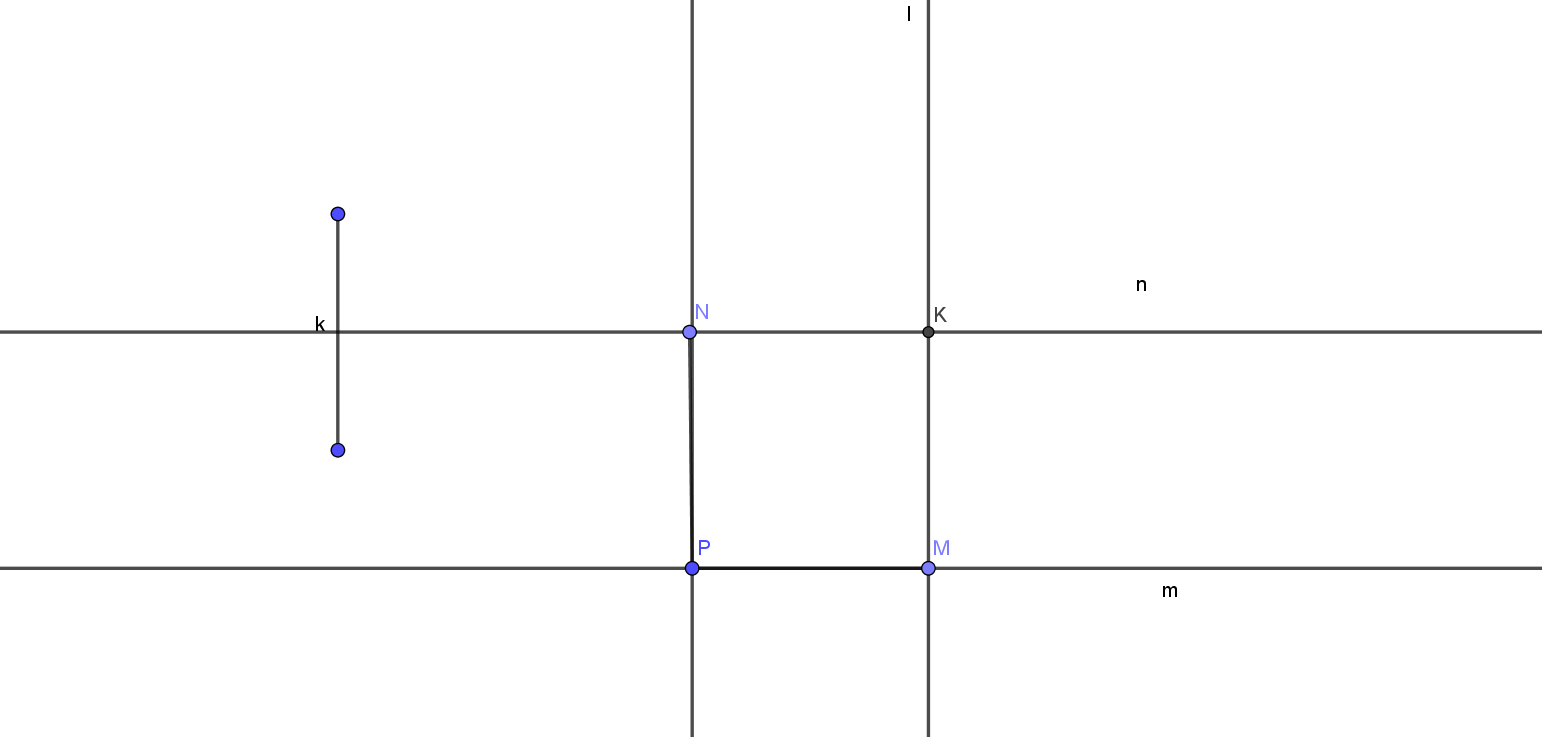
On the following picture, there is constructed a perpendicular bisector of $overline{KM}$ using previous steps.
According to $SSS$, those triangles are congruent
because it is already given that they have two equivalent
sides and $BD$ is a side of both triangles.
#### (b)
The conclusion is that $overline{BD}$ splits $measuredangle ABC$
on two equal angles.
First place the compasses point on the angle’s vertex $R$, then adjust the compasses to a median wide setting. The exact width is not important. After that, without changing the compasses width, draw an arc across each leg of the angle, place the compasses on the point where one are crosses a leg and draw an are in the interior of an angle.
Repeat this for the other leg so that the two are cross.
Finally, using a ruler draw a line from the vertex to the point where the areas cross, that line is the angle bisector.
b) It splits $measuredangle ABC$ into two equal angles;
c) Use a compass and a ruler
You can use a ruler and compass to construct a triangle $triangle ACE$.

That two points of intersecting arcs and lines $m$ and $n$ are two vertexes $M$ and $N$ of the square, the first vertex is in $P$.
Then, construct a perpendicular line through point $M$ on the line $m$ and through the point $N$ on line $n$.
Point of intersect of those perpendicular lines is the fourth vertex of a square and label it as $K$.
On that way, we get square $PMKN$.
The multiplier for the geometric sequence in this situation is $3$.
#### (b)
If $y$ represents the number of all students in this school who
heard the rumor at $3$ p.m, then, $dfrac{y}{3}$ will represent
the number of students who heard the rumor at $2$ p.m.
An equation for a geometric sequence that represents the fraction
of students that have heard the rumor after $n$ hours is:
$$
a_{n}=a(3)^n
$$
#### (d)
Number of students who heard about the rumor at $3$ p.m. is:
$$
a_{8}=a(3)^7
$$
So, required fraction will be:
$$
dfrac{a_{8}}{3^7}=dfrac{acdot3^7}{3^7}=a
$$
#### (e)
We will substitute $3$ for $a$ in the previous equation and get:
$$
a_{8}=3(3^7)=6561
$$
Conclusion is that Kenny should use columns.
#### (b)
For, example, let’s examine flavor Fudgy Fantasy.
$$
dfrac{5883}{2240}nedfrac{2771}{5446}nedfrac{672}{985}nedfrac{519}{1302}
$$
We can conclude that there is an association between
celebration and cupcake flavor to Kenny.
$$
f(x)=8(x-3)+4
$$
$$
{color{#4257b2}f(-2)}=8(-2-3)+4=8(-5)+4=-40+4={color{#4257b2}-36}
$$
$$
{color{#4257b2}f(-0.5)}=8(-0.5-3)+4=8(-3.5)+4=-28+4={color{#4257b2}-24}
$$
$$
{color{#4257b2}f(8)}=8(8-3)+4=8(5)+4=40+4={color{#4257b2}44}
$$
$$
{color{#4257b2}fleft(dfrac{3}{4}right)}=8left(dfrac{3}{4}-3right)+4=8left(dfrac{3-12}{4}right)+4=8left(dfrac{-9}{4}right)+4
$$
$$
=left(dfrac{8cdot-9}{4}right)+4=(2cdot-9)+4=-18+4={color{#4257b2}-14}
$$
(c) $f(8)=44$ (d)$fleft(dfrac{3}{4}right)=-14$
$$
color{#4257b2}text{(a)} 4x-1geq7
$$
Isolate the variables on the left side as follows:
$$
4xgeq7+1 4xgeq8
$$
divide both sides of inequality by $4$ as follows.
$$
xgeq dfrac{8}{4} xgeq2
$$
$$
color{#4257b2}text{(b)} 3-2xleq x+6
$$
Isolate the variables on the left side as follows:
$$
-2x-xleq6-3 -3xleq3
$$
Divide both sides of inequality by $-3$ as follows.
$$
xgeqdfrac{3}{-3} xgeq-1
$$
color{#4257b2}text{(c)} 2(x-5)leq8
$$
Multiply from the left to the right as follows:
$$
2x-10leq8
$$
Isolate the variables on the left side as follows:
$$
2xleq8+10 2xleq18
$$
divide both sides of inequality by $2$ as follows.
$$
xleq dfrac{18}{2} xleq9
$$
$$
color{#4257b2}text{(d)} dfrac{1}{2} xgeq5
$$
Multiply both sides of inequality by $2$ as follows.
$$
dfrac{2}{2} xgeq5cdot2 xgeq10
$$
text{color{#4257b2}(a) $xgeq2$ (b) $xgeq-1$
\ \
(c) $xleq9$ (d) $xgeq10$}
$$
In this case, graph of $f(x)$ will be translated $3$ units down.
#### (b)
In this case, graph of $f(x)$ will be translated $2$ units up.
$$
color{#4257b2}text{(a)} 3x+5=16
$$
Isolate the variables on the left side as follows:
$$
3x=16-5 3x=11
$$
Divid both sides of equation by $3$ as follows.
$$
dfrac{3x}{3}=dfrac{11}{3} x=3.6667
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=3.6667$ in the equation as follows:
$$
(3cdot3.6667)+5=16 11+5=16 16=16
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(b)} 3x+5=-16
$$
Isolate the variables on the left side as follows:
$$
3x=-16-5 3x=-21
$$
Divid both sides of equation by $3$ as follows.
$$
dfrac{3x}{3}=dfrac{-21}{3} x=-7
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=-7$ in the equation as follows:
$$
(3cdot-7)+5=-16 -21+5=-16 -16=-16
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}How many kind of fruit did he but?}
$$
Assume the number of apples is $color{#4257b2}x$ and number of pairs is $color{#4257b2}11-x$
Total cost of fruit can be represented as follows:
$$
0.6x+0.35(11-x)=5.6
$$
Multiply from left to right as follows:
$$
0.6x+3.85-0.35x=5.6
$$
Isolate the variables on th left side as follows:
$$
0.6x-0.35x=5.6-3.85 0.25x=1.75
$$
Divide both side by $0.25$ as follows:
$$
dfrac{0.25x}{0.25}=dfrac{1.75}{0.25} x=7
$$
Number of apples is $color{#4257b2}7$ pieces.
Number of pairs is $11-7=color{#4257b2}4$ pieces
Largecolor{#4257b2}7text{ and} 4
$$
$$
6(m-2)
$$
Because, after applying the Distributive property, we get:
$$
6(m-2)=6m-12
$$
6(m-2)
$$
If $l$ and $m$ are parallel, that means that $measuredangle a$ and $measuredangle c$ are angles
with equal measure.
Also, $measuredangle b$ and $measuredangle c$ are cross angles and they are equal,
so and $measuredangle a$ and $measuredangle b$ are equal angles.
#### (b)
On the following picture, there is constructed a line parallel to $l$ through
the point $P$ using transversal $f$.

In this case, you need to construct the angle with vertex $P$
which is equal to the angle made of lines $f$ and $l$, where
one leg is $f$ and the other is actually lining parallel to $l$.
b) Use GeoGebra;
c) The second leg of the angle $measuredangle P$ will be required parallel line.
Square is a geometric figure with four equal sides and all straight angles.
#### (b)
First, start with a given line segment $AB$, that will be one side of the square.
Then, extend the line $AB$ to the right and set the compasses on $B$ and any
convenient width scribe an arc on each side of $B$, creating the two points $F$ and $G$.
With the compasses on $G$ and any convenient width, draw an arc above the point $B$.
Then, without changing the compasses width, place the compasses on $F$ and draw
an arc above $B$, crossing the previous arc and creating point $H$.
After that, draw a line from $B$ through $H$, $BH$ will become the second side.
Set the compasses on $A$ and set its width to $AB$.
This width will be held unchanged as we create the square’s other three sides.
Then draw an arc above point $A$. Without changing the width, move the compasses
to the point $B$.
Draw an arc across $BA$ creating point $C$- a vertex of the square.
Without changing the width, move the compasses to $C$. Draw an arc to the left of $C$
across the existing arc, creating point $D$- a vertex of the square.
Draw the lines $CD$ and $AD$ and we got square $ABCD$.
On the following picture, there is a constructed square.
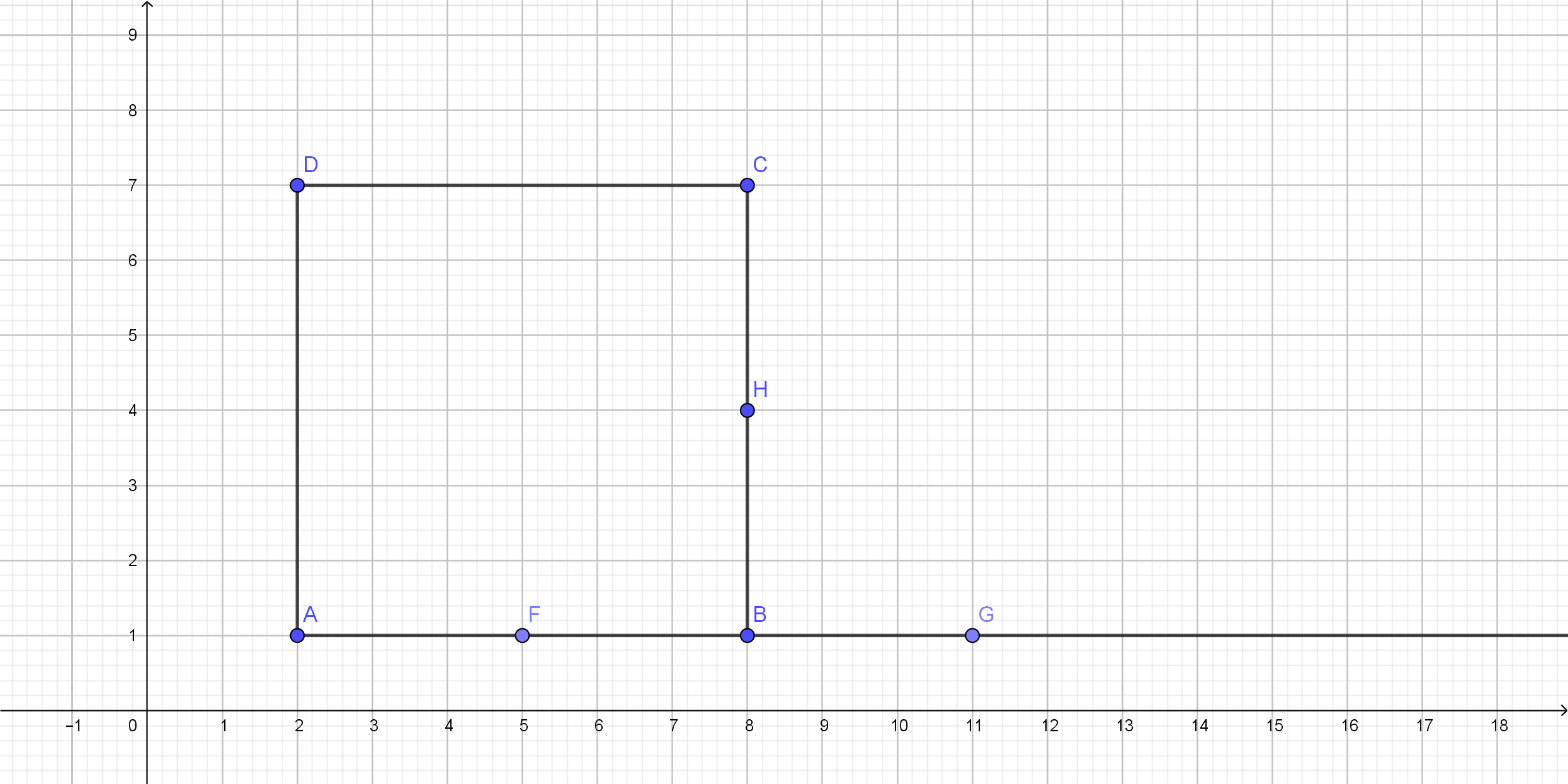
Then, segments $BC$, $CD$ and $DA$ are the same length as $AB$
because they were drawn with the same compass width-$AB$.
So, $ABCD$ is a square.
b) Use the compass and a ruler;
c) According to construction, $ABCD$ is a square.
Draw a line and on that line pick two points, $K$ and $M$.
Then, set the compasses width to be equal to the length of $overline{AB}$.
After that, from both points, we picked on the line draw two arcs without changing the width.
Their point of intersecting will be the third vertex of the required triangle,
while two others will be the first two points packed on the line.
First, draw a segment whose length is $3$ units, $overline{AB}$.
From the point, $B$ draw an arc with compasses whose width is $4$ units.
Point of intersect of those two arcs will be $C$, the third vertex.
On the same way construct the triangle with side lengths $2$, $3$ and $6$ units.
$2,3$ and $6$ units
We can notice that the center of the smaller circle
is $B$ and its radius is $overline{BC}$.
We can notice that the center of a larger circle is point
$A$ and its radius is $overline{AC}$.
Because of triangles $triangle ABC$ and $triangle GHJ$
have all equal sides, we conclude
that they are congruent, according to the $SSS$.
On the following picture, there are graphed $triangle ABC$ and $triangle GHJ$.
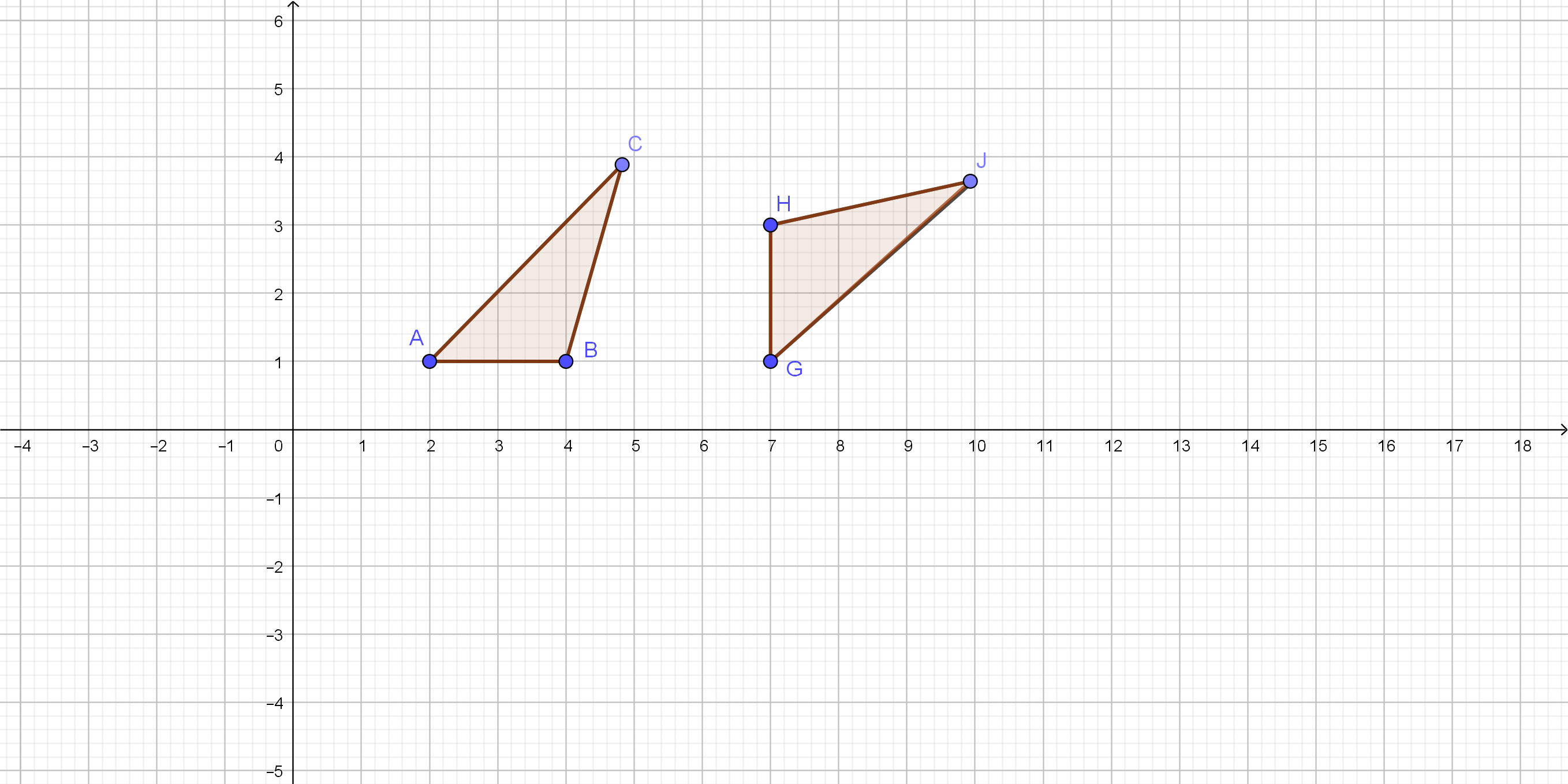
about the point with a given angle.
#### (d)
The transformation which maps point $J$ to the point $C$ is
a translation by the vector.
#### (e)
According to the previous transformation, we can confirm that those
triangles are congruent according to the $SSS$.
b) They are congruent;
c) rotation about point;
d) Translation by vector;
e) It is demonstrated.
We can conclude that the annual multiplier is $0.46$ and annual percent decrease is $46%$.
#### (b)
The equation of a function that describes this situation is the following, where $x$
represent the time in years.
$$
y=20(0.46)^x
$$
There is the following table of the first $5$ values.\
begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $y$ \
hline
$1$ & $9.2$ \
hline
$2$ & $4.232$ \
hline
$3$ & $1.95$ \
hline
$4$ & $0.897$ \
hline
$5$ & $0.41$ \
hline
end{tabular}
end{center}
On the following picture,there is a sketch of a previous function.\
On the following picture, there are graphed points $A$ and $B$ and $M$, the midpoint.
Its coordinates are $M(1.5,5)$.

The equation of the line that passes through points $A$ and $B$ is the following:
$$
y+1=dfrac{11+1}{6+3}(x+3)
$$
$$
y=dfrac{12}{9}(x+3)-1
$$
$$
y=dfrac{4}{3}x+3
$$
#### (c)
The distance between points $M$ and $B$ is the following:
$$
MB=sqrt{(11-5)^2+(sqrt{a}6-1.5)^2}=7.5
$$
is $-8$, explicit formula for calculating $n$th term of this sequence is following:
$$
a_{n}=15+(n-1)(-8)
$$
Now, we will substitute $-225$ for $a_{n}$ and find $n$ on the following way:
$$
-225=15-8n+8
$$
$$
8n=248
$$
$$
n=31
$$
So, the conclusion is that there are shown $31$ terms
of the arithmetic sequence.
$$
color{#4257b2}text{(a)} 3x-5le7+2x
$$
Isolate the variables on the left side as follows:
$$
3x-2xle7+5 xle12
$$
$$
color{#4257b2}text{(b)} |x|-3le7
$$
Isolate the variables on the left side as follows:
$$
|x|le7+3 |x|le10
$$
$$
xle10
$$
color{#4257b2}text{(c)} 5(2-x)+6ge16
$$
Multiply from left to right as follows:
$$
10-5x+6ge16
$$
Isolate the variables on the left side as follows:
$$
-5xge16-6-10 -5xge16-16 -5xge0
$$
Divide both sides by$-5$as follows:
$$
dfrac{-5x}{-5}ledfrac{0}{-5} xle0
$$
$$
color{#4257b2}text{(d)} |x+2|ge3
$$
Isolate the variables on the left side as follows:
$$
x+2ge3 xge3-2 xge1
$$
(c) $xle0$ (d) $xge1$
$$
f(x)=2^x -3
$$
$$
{color{#4257b2}f(-2)}=2^{(-2)}-3=dfrac{1}{2^2}-3=dfrac{1}{4}-3=dfrac{1-12}{4}={color{#4257b2}dfrac{-11}{4}}
$$
$$
{color{#4257b2}f(-0.5)}=2^{(-0.5)}-3=dfrac{1}{2^{0.5}}-3=dfrac{1}{sqrt{2}}-3={color{#4257b2}dfrac{1-3sqrt{2}}{sqrt{2}}}
$$
$$
{color{#4257b2}f(8)}=2^{(8)}-3=256-3={color{#4257b2}253}
$$
$$
{color{#4257b2}fleft(dfrac{3}{4}right)}=2^{(0.75)}-3=1.682-3={color{#4257b2}-1.318}
$$
(c) $f(8)=253$ (d)$fleft(dfrac{3}{4}right)=-1.318$
$$
color{#4257b2}text{(a)} |x-3|+3=4
$$
Isolate the variables on the left side as follows:
$$
|x-3|=4-3 |x-3|=1 x-3=1
$$
Add both sides of equation by $3$ as follows.
$$
x-3+3=1+3 x=4
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=4$ in the equation as follows:
$$
|4-3|+3=4 |1|+3=4 4=4
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(b)} (x-5)^3=8
$$
Evaluate the exponent as follows:
$$
(x-5)^3=2^3
$$
Since the power of the left side is equal the power in the right side, so:
$$
x-5=2
$$
Isolate the variables on the left side as follows:
$$
x=2+5 x=7
$$
$$
(7-5)^3=8 2^3=8 8=8
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(c)} dfrac{5}{9}-dfrac{x}{3}=dfrac{4}{9}
$$
Subtract both sides of equation by $dfrac{5}{9}$ as follows.
$$
dfrac{5}{9}-dfrac{5}{9}-dfrac{x}{3}=dfrac{4}{9}-dfrac{5}{9} -dfrac{x}{3}=dfrac{-1}{9}
$$
Multiply both sides of equation by $-3$ as follows.
$$
-3 cdot-dfrac{x}{3}=-3 cdot -dfrac{1}{9} x=dfrac{1}{3}
$$
$text{color{#4257b2}Check:}$ substitute the value of $x=dfrac{1}{3}$ in the equation as follows:
$$
dfrac{5}{9}-dfrac{dfrac{1}{3}}{3}=dfrac{4}{9} dfrac{5}{9}-dfrac{1}{9}=dfrac{4}{9}
$$
$$
dfrac{4}{9}=dfrac{4}{9}
$$
Since the left side is equal the right side, so the answer is correct.
On the following picture, there are graphed both equations and we can notice
that they have no solution because there is no point of intersecting.
We can conclude that the lines are parallel.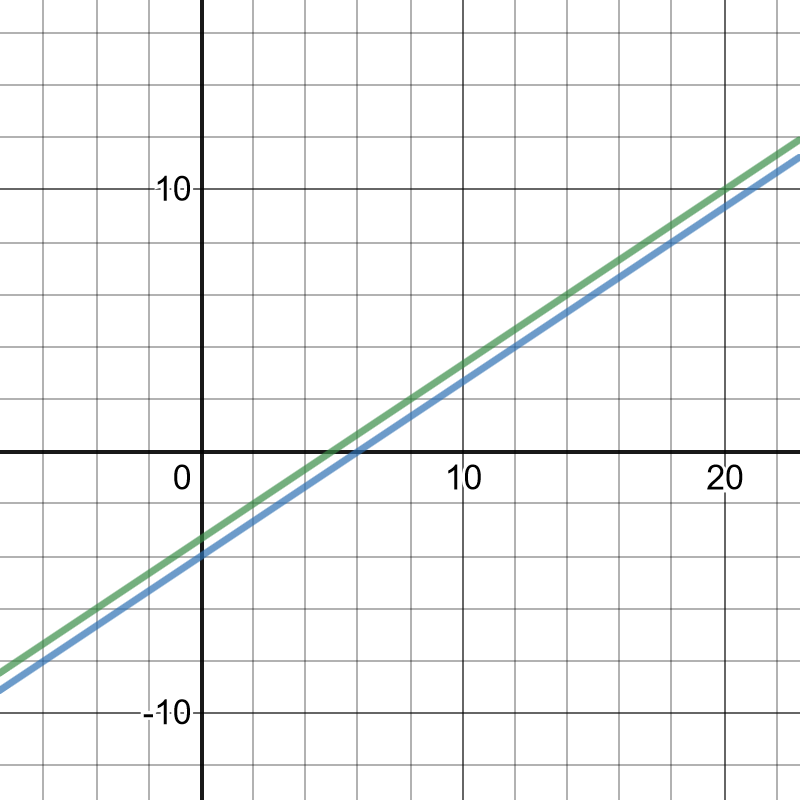
Solution for $y$ is the following:
$$
3y=2x-10
$$
$$
y=dfrac{2x-10}{3}
$$
#### (c)
Yes, the slope of each line is $dfrac{2}{3}$ and it confirms our statement
that those lines are parallel.
$$
y=acdot b^x
$$
where $a$ is the initial value (at $x=0$) and $b$ is the multiplier.
$textbf{a.}$
Let $x$ be the number of years and $y$ be the value of the car, in dollars. From the given, $a=23500$ and $b=100%-15%=85%=0.85$, so the equation is:
$$
color{#4257b2}y=23500cdot (0.85)^x
$$
Substitute $x=15$ for 15 years old and solve for $y$
$$
begin{align*}
y&=23500cdot (0.85)^{15} \
&approx 2052.82tocolor{#c34632}$2052.82
end{align*}
$$
Let $x$ be the number of years and $y$ be the population. From the given, $a=14365112$ and $b=100%+12%=112%=1.12$, so the equation is:
$$
color{#4257b2}y=14365112cdot (1.12)^x
$$
Substitute $x=20$ for 20 years from now and solve for $y$
$$
begin{align*}
y&=14365112cdot (1.12)^{20} \
&approx color{#c34632}138570081
end{align*}
$$
b. about 138570081
The rate for the first team is $dfrac{1}{10}$ and the rate for the second team is $dfrac{1}{15}$.
We need to solve the following equation for $x$ in order to find $x$:
$$
dfrac{1}{10}+dfrac{1}{15}=dfrac{1}{x}
$$
$$
dfrac{3+2}{30}=dfrac{1}{x}
$$
$$
5x=30
$$
$$
x=6
$$
So, it will take $6$ hours to both teams to mow the entire lawn.
dfrac{1}{x}=dfrac{1}{10}+dfrac{1}{15}
$$
$x$=the amount of time (in hours) they need to mow the lawn if they work together.
We write the equation:
$dfrac{1}{x}=dfrac{5}{30}$
$dfrac{1}{x}=dfrac{1}{6}$
$$
x=6
$$
$x$=the amount of time (in minutes) they need to staple the programs if they work together
dfrac{1}{x}=dfrac{1}{30}+dfrac{1}{10}
$$
$dfrac{1}{x}=dfrac{4}{30}$
$4x=30$
$x=dfrac{30}{4}=dfrac{15}{2}=7.5$ minutes
$x$=the amount of time (in minutes) his sister needs to wash the truck alone
dfrac{1}{6}=dfrac{1}{8}+dfrac{1}{x}
$$
$dfrac{1}{x}=dfrac{4}{24}-dfrac{3}{24}$
$dfrac{1}{x}=dfrac{1}{24}$
$x=24$ minutes
of students in $8$th grade.
We get the following system of equations which we need to solve for $x$ and $y$ and get:
$$
dfrac{40}{100}x+dfrac{90}{100}y=dfrac{72}{100}cdot1000
$$
$$
x+y=1000
$$
We got the following:
$$
40x+90y=72000
$$
$$
x+y=1000Rightarrow x=1000-y
$$
Now, substitute $x$ from the second equation in the first and get:
$$
40(1000-y)+90y=72000
$$
$$
50y=32000
$$
$$
y=640Rightarrow x=360
$$
The conclusion is that there are $360$ students in $7$th grade and $640$ in $8$th grade.
We will have the following:
$$
15cdotdfrac{50}{6}=125
$$
So, the conclusion is that $5$ students will hang $125$ streamers for $3$ hours.
Required system of equations in this situation is following:
$$
3.15g+1.85r=4.50
$$
$$
g+r=12
$$
#### (d)
A new system of equations for described situation in this part is following:
$$
3.15g+1.85r=3
$$
$$
g+r=15
$$
You need a $15%$ acid solution for a certain test, but your supplier only ships a $10%$ solution and a $30%$ solution. Rather than pay the hefty surcharge to have the supplier make a $15%$ solution, you decide to mix $10%$ solution with $30%$ solution, to make your own $15%$ solution. You need $10$ liters of the $15%$ acid solution. How many liters of $10%$ solution and $30%$ solution should you use?
$y$ represent the sum of money invested in bonds.
Using the information in the task, we get the following system
of equations and we will solve it for $x$ and $y$:
$$
x+y=10000Rightarrow x=x=1000-y
$$
$$
0.03x+0.05y=430
$$
We will substitute $x$ from the first equation in the second
and solve it for $y$:
$$
0.03(10000-y)+0.05y=430
$$
$$
0.02y=130
$$
$$
y=6500
$$
$$
x=10000-6500=3500
$$
So,
$$
3,500$ is invested is stocks and
$$
6,500$ is invested
in bonds.
3,500$;
$$
6,500$
We get the following equation, which we will solve for $x$:
$$
6x+3cdot4=4.75(3+x)
$$
$$
6x+12=14.25+4.75x
$$
$$
1.25x=2.25
$$
$$
x=1.8
$$
So, the conclusion is that there should be mixed $1.8$ pound of
coffee costing $$6$ per pound.
On the following picture, there are graphed given points
and the best fit line.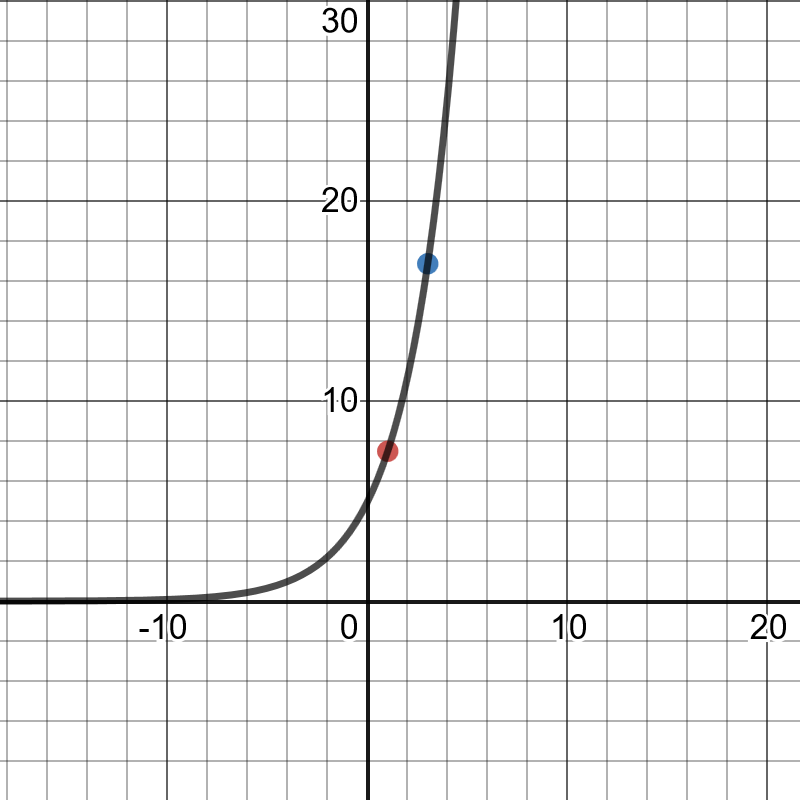
$$
y=5(1.5)^x
$$
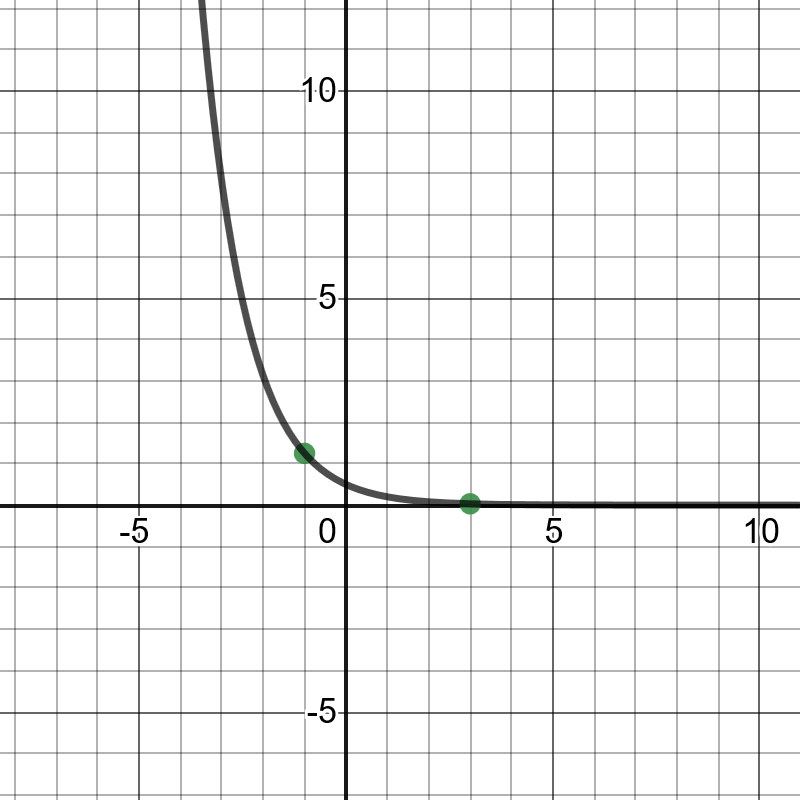
#### (b)
On the following picture, there are graphed given points and the best
fit line:
$$
y=0.5(0.4)^x
$$
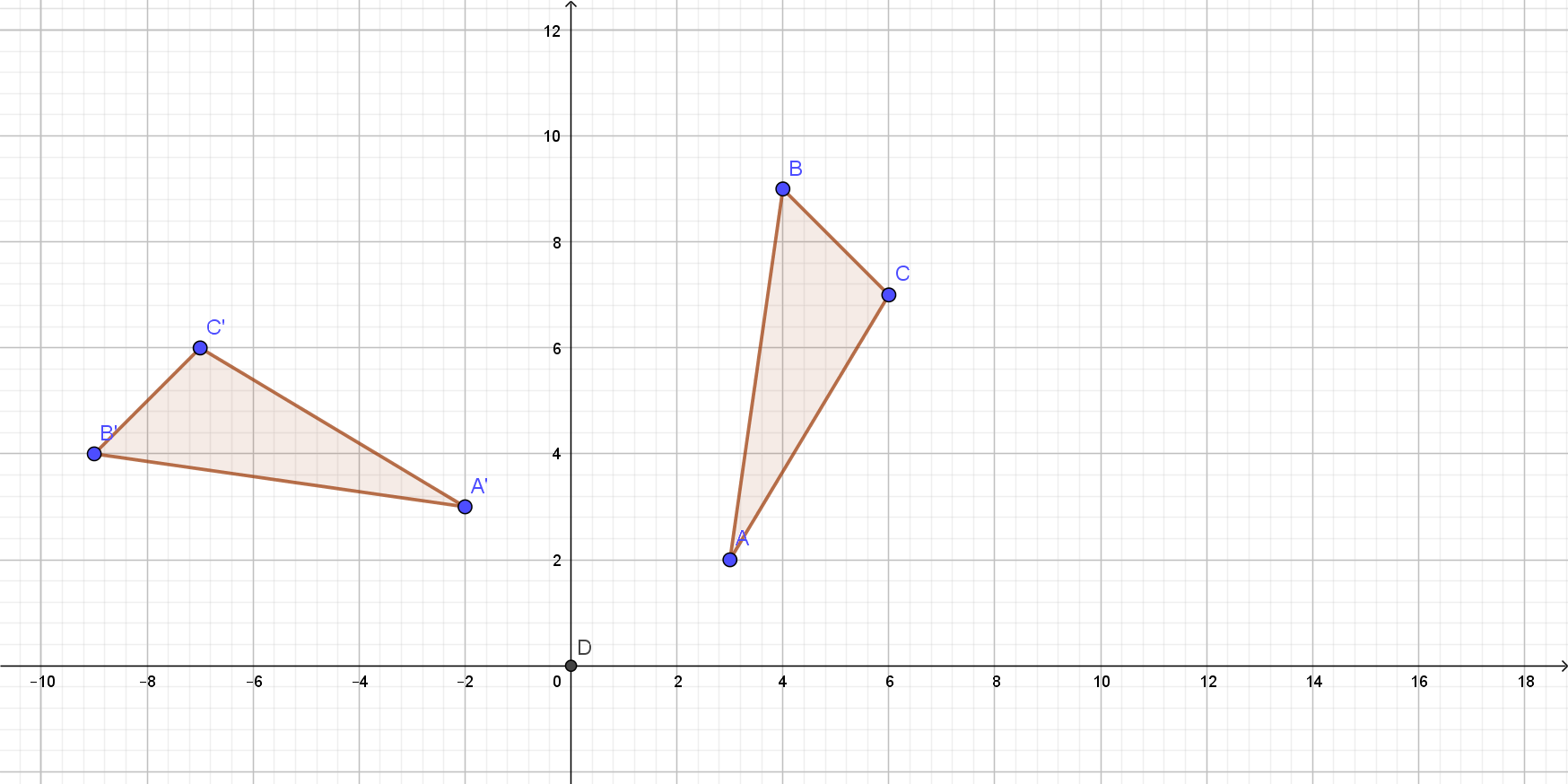
$$
A'(-2,3), B'(-9,4), C'(-7,6)
$$
Which means that the correct answer is $textbf{a)}$.
$$
m=dfrac{Delta y}{Delta x }=dfrac{-1-0}{0-0.5}=dfrac{-1}{-0.5}=2
$$
Since $b=-1$, then the equation is:
$$
y=2x-1
$$
Since the line is dashed, the points on the line itself are not solutions in the inequality. So, either use $$.
We can then assign a point that is on the shaded region, say $(0,0)$ and determine what inequality to use:
$$
begin{align*}
y&=2x-1\
0&stackrel{?}{=}2(0)-1\
0&stackrel{?}{=}0-1\
0&stackrel{?}{=}-1
end{align*}
$$
The appropriate inequality to use is $>$ since $0>-1$. Hence, the inequality for the graph is:
$$
color{#c34632} y>2x-1
$$
y>2x-1
$$
through points $left( dfrac{1}{2},0right)$ and $(0,-1)$ is $y=2left(x-dfrac{1}{2} right)$.
So, according to the picture, the conclusion is that the required inequality is:
$$
y>2left(x-dfrac{1}{2} right)
$$
y>2left(x-dfrac{1}{2} right)
$$
Graphically, the $x$-intercepts are where the graph intersects the $x$-axis:
$$
color{#c34632}(-2,0)text{ and }(0,0)
$$
and the $y$-intercept is where the graph intersects the $y$-axis:
$$
color{#c34632} (0,0)
$$
$textbf{b.}$
Graphically, the $x$-intercepts are where the graph intersects the $x$-axis:
$$
color{#c34632}(-3,0)text{ and }(5,0)
$$
and the $y$-intercept is where the graph intersects the $y$-axis:
$$
color{#c34632} (0,3)
$$
$textbf{c.}$
Using a table, the $x$-intercepts are where $y=0$:
$$
color{#c34632}(-1,0)text{ and }(1,0)
$$
and the $y$-intercept is where $x=0$:
$$
color{#c34632} (0,-1)
$$
b. $x$-intercepts: $(-3,0)$ and $(5,0)$ ; $y$-intercept: $(0,3)$
c. $x$-intercepts: $(-1,0)$ and $(1,0)$ ; $y$-intercept: $(0,-1)$
Find the boundary point(s). Replace the inequality symbol with $=$ so we have the equation:
$$
|x|+3=5
$$
Subtract 3 from both sides:
$$
|x|=2
$$
Since the right side is positive, then there are two solutions: $x=-2$ and $x=2$. These are the boundary points. Hence, the number line will be divided into 3 regions:
$$
x< -2,-2<x2
$$
For each region, assign a test point. If the test point satisfies the inequality, the region it belongs to is a solution.
For $x< -2$, I used $x=-3$:
$$
begin{align*}
|-3|+3&stackrel{?}{<}5\
6¬{<}5
end{align*}
$$
For $-2<x<2$, I used $x=0$:
$$
begin{align*}
|0|+3&stackrel{?}{<}5\
3&2$, I used $x=3$:
$$
begin{align*}
|3|+3&stackrel{?}{<}5\
6¬{<}5
end{align*}
$$
So, the solution of the inequality is:
$$
color{#c34632}-2<x<2
$$
On a number line, use open circles for both $-2$ and $2$ since they are not part of the solution:

First, we find the boundary point by replacing the inequality symbol with $=$ then solve for the corresponding equation:
$$
begin{align*}
5(2x+1)&=30\
2x+1 &=6\
2x&=5\
x&=2.5
end{align*}
$$
Next, pick a test point except for the boundary point, say $x=0$ to substitute to the inequality:
$$
begin{align*}
5(2(0)+1) &geq 30\
5(1) &geq 30\
5&geq 30
end{align*}
$$
The test point is not a solution which means all points on this side of the boundary point are not part of the solution, which is to the left of it. So, the solution is to the right of the boundary point:
$$
color{#c34632}xgeq 2.5
$$
On a number line, use a filled circle for 2.5 since it is part of the solution:

Multiply both sides by the LCD which is $2x$:
$$
2-5x=3xcolor{white}tag{1}
$$
Add $5x$ to both sides:
$$
2=8x
$$
Divide both sides by 8:
$$
dfrac{1}{4}=x
$$
or
$$
color{#c34632}x=dfrac{1}{4}
$$
On a number line, represent the solution as a point:
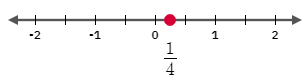
Adding $x$ to both sides, we obtain:
$$
-5>3
$$
which is false for all values of $x$. Hence, we can conclude that the inequality has $text{textcolor{#c34632}{no solution}}$. The graph is simply the number line itself:
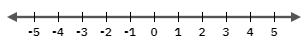
Subtract 1 from both sides:
$$
3sqrt{4-x}=12
$$
Divide both sides by 3:
$$
sqrt{4-x}=4
$$
Square both sides:
$$
4-x=16
$$
Subtract 4 from both sides:
$$
-x=12
$$
Multiply both sides by $-1$:
$$
color{#c34632}x=-12
$$
On a number line, represent the solution as a point:
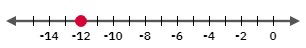
Find the boundary point(s). Replace the inequality symbol with $=$ so we have the equation:
$$
|x+1|=4
$$
Since the right side is positive, then there are two solutions. We write and solve the two equations:
$$
begin{align*}
x+1&=-4 & x+1&=4\
x&=-5 & x&=3
end{align*}
$$
So, the boundary points are $x=-5$ and $x=3$. Hence, the number line will be divided into 3 regions:
$$
xleq -5,-5 leq xleq 3,text{ and }xgeq 3
$$
For each region, assign a test point. If the test point satisfies the inequality, the region it belongs to is a solution.
For $xleq -5$, I used $x=-6$:
$$
begin{align*}
| -6+1 |&stackrel{?}{leq}4\
5¬{leq} 4
end{align*}
$$
For $-5 leq xleq 3$, I used $x=0$:
$$
begin{align*}
|0+1 |&stackrel{?}{leq}4\
1&leq 4hspace{5mm}checkmark
end{align*}
$$
For $xgeq 3$, I used $x=4$:
$$
begin{align*}
| 4+1 |&stackrel{?}{leq}4\
5¬{leq} 4
end{align*}
$$
So, the solution of the inequality is:
$$
color{#c34632}-5 leq xleq 3
$$
On a number line, use filled circles for both $-5$ and $3$ since they are part of the solution:

b. $xgeq 2.5$
c. $x=-2$, $x=dfrac{1}{3}$
d. no solution
e. $x=-12$
f. $-5 leq xleq 3$
$$
color{#4257b2}text{(a)} |x|+3<5
$$
Isolate the variables on the left side as follows:
$$
|x|<5-3 |x|<2 x<2
$$
$$
x-2
$$
$$
color{#4257b2}text{(b)} 5(2x+1)ge30
$$
Use distributive property to simplify as follows:
$$
5cdot2x+5cdot1ge30 10x+5ge30
$$
Isolate the variables on the left side as follows:
$$
10xge30-5 10xge25
$$
Divid both sides of equation by $10$ as follows.
$$
dfrac{10x}{10}gedfrac{25}{10} xge2.5
$$
$$
color{#4257b2}text{(c)} dfrac{1}{x}-dfrac{5}{2}=dfrac{3}{2}
$$
Add $dfrac{5}{2}$ to both sides as follows:
$$
dfrac{1}{x}-dfrac{5}{2}+dfrac{5}{2}=dfrac{3}{2}+dfrac{5}{2} dfrac{1}{x}=dfrac{8}{2}
$$
$$
x=dfrac{2}{8} x=dfrac{1}{4}
$$
color{#4257b2}text{(d)} -5-x>3-x
$$
Isolate the variables on the left side as follows:
$$
-x+x>3+5 0>8
$$
No solution
$$
color{#4257b2}text{(e)} 3 sqrt{4-x}+1=13
$$
Subtract both sides of equation by $-1$ as follows.
$$
3 sqrt{4-x}=13-1 3 sqrt{4-x}=12
$$
Divide both sides of equation by $3$ as follows.
$$
sqrt{4-x}=dfrac{12}{3}=4
$$
Square both of sides as follows:
$$
(sqrt{4-x})^2=(4)^2 4-x=16
$$
Isolate the variables on the left side as follows:
$$
x=4-16 x=-12
$$
color{#4257b2}text{(f)} |x+1|le 4
$$
Isolate the variables on the left side as follows:
Equal $x+1le4$ as follows:
$$
x+1le4 xle4-1 xle3
$$
Equal $-x+1le4$ as follows:
$$
-x+1le4 -xle4-1 -xle3 xge-3
$$
The value of $x$ is equal all real numbers $(-infty, infty)$
text{color{#4257b2}(a) $2> x>-2$ (b) $xge2.5$ (c) $x=dfrac{1}{4}$
\ \
(d) No solution (e) $x=-12$ (f) $(-infty, infty)$}
$$
text{color{#4257b2}How many toppings did he get?}
$$
Assume the number of toppings is $x$, so:
$$
(3 cdot 1.19)+(0.49 cdot x)=4.55 3.57+0.49 x=4.55
$$
Isolate the variables on the left side as follows:
$$
0.49 x=4.55-3.57 0.49 x=0.98
$$
Divide both of side by $0.49$ as follows:
$$
x=dfrac{0.98}{0.49} x=2
$$
The number of toppings did he get is $2$ toppings.
text{color{#4257b2}Large$Large2$ toppings.}
$$
$$
color{#4257b2}text{(a)} (2a+b)(a-3b)
$$
Use distributive property to simplify as follows:
$$
{color{#4257b2}2a}(a)+{color{#4257b2}2a}(-3b)+{color{#4257b2}b}(a)+{color{#4257b2}b}(-3b)
$$
$$
2a^2-6ab+ab-3b^2
$$
Rearrange the tiles to group like terms as follows:
$$
2a^2-3b^2+(ab-6ab)
$$
$$
2a^2-3b^2-5ab
$$
$$
color{#4257b2}text{(b)} (x+2)(x^2-2x+5)
$$
Use distributive property to simplify as follows:
$$
{color{#4257b2}x}(x^2)+{color{#4257b2}x}(-2x)+{color{#4257b2}x}(5)+{color{#4257b2}2}(x^2)+{color{#4257b2}2}(-2x)+{color{#4257b2}2}(5)
$$
$$
x^3-2x^2+5x+2x^2-4x+10
$$
Rearrange the tiles to group like terms as follows:
$$
x^3+(2x^2-2x^2)+(5x-4x)+10
$$
$$
x^3+0+x+10
$$
$$
color{#4257b2}x^3+x+10
$$
The conclusion is that the equation has only one solution because,
it represent $x$-intercept on the graph.
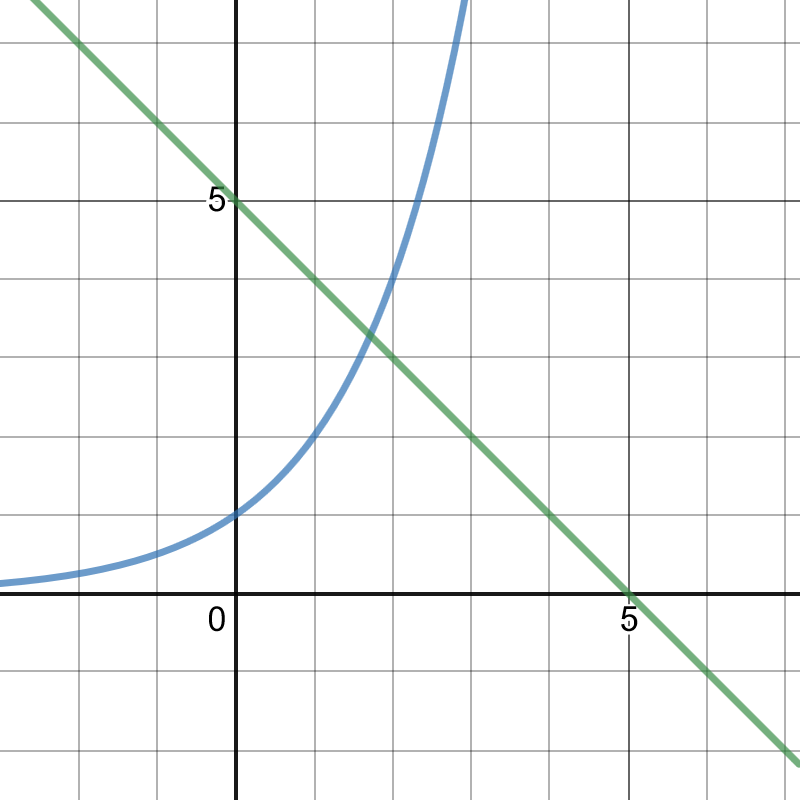
#### (b)
On the following picture, there are graphed functions $y=1$ and $y=0.5^x-3$.
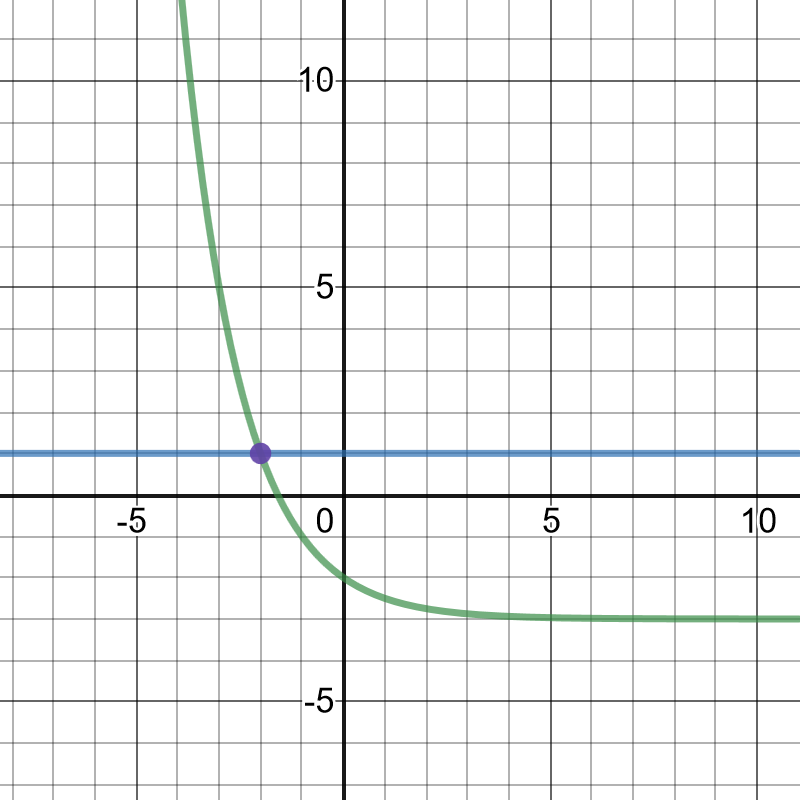
that point has coordinates $(-2,1)$, which means that solution is $x=-2$.
#### (c)
You can substitute $-2$ for $x$ and $1$ for $y$ in order to verify answer:
$$
1=(0.5)^{-2}-3
$$
$$
1=1
$$
So, the conclusion is that the solution is correct.
On the following picture, there are graphed functions
$y=20x+1$ and $y=3^x$.
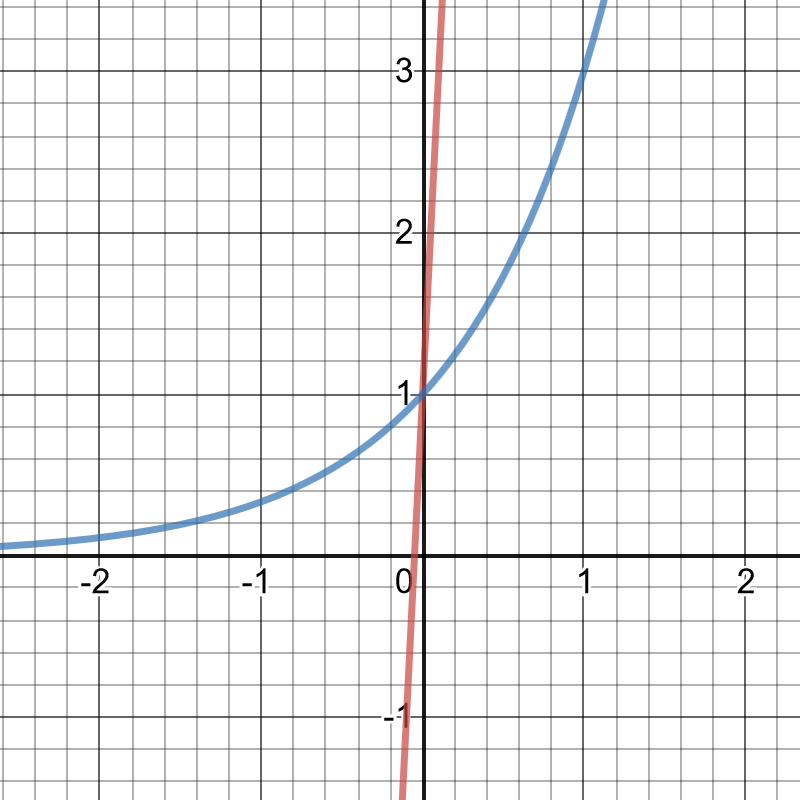
which means that there is a solution for $x=0$ and $y=1$.
If we substitute $0$ for $x$ and $1$ for $y$ in the previous
equations, we get:
$$
1=10cdot0+1=1
$$
$$
1=3^{circ}=1
$$
So, we proved that they are solutions.
#### (b)
It must be coordinates of a point because it can be
solved using graph, solution will be the point of intersection.
On the following picture, there are graphed functions:
$y=20x$ and $y=3^x-1$.
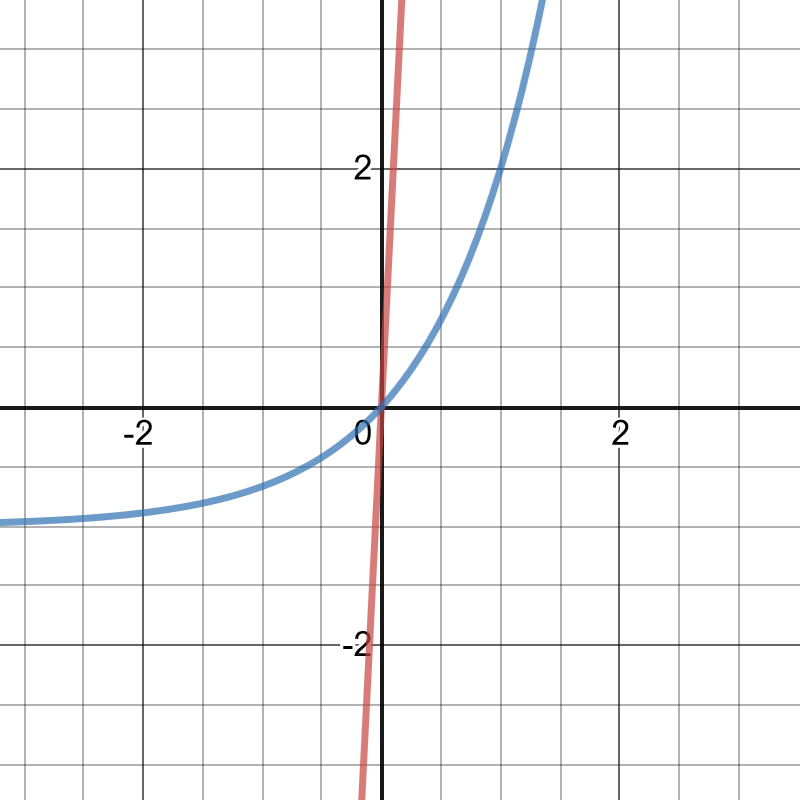
as before, here solution is a point $(0,0)$, or $x=0$ and $y=0$.
#### (d)
Karen could not solve the system algebraically because of one equation
is linear and the second one is exponential.
The conclusion is that $y=3.5-dfrac{1}{2}x$ also has infinitely
many solutions.
#### (b)
If Mason graph both functions, point of their intersect will be
the solution, on that way a graph will help Mason to solve
the equation.
#### (c)
On the following picture, there are graphed functions $y=3.5-dfrac{1}{2}x$ and $y=0.5^x-3$.
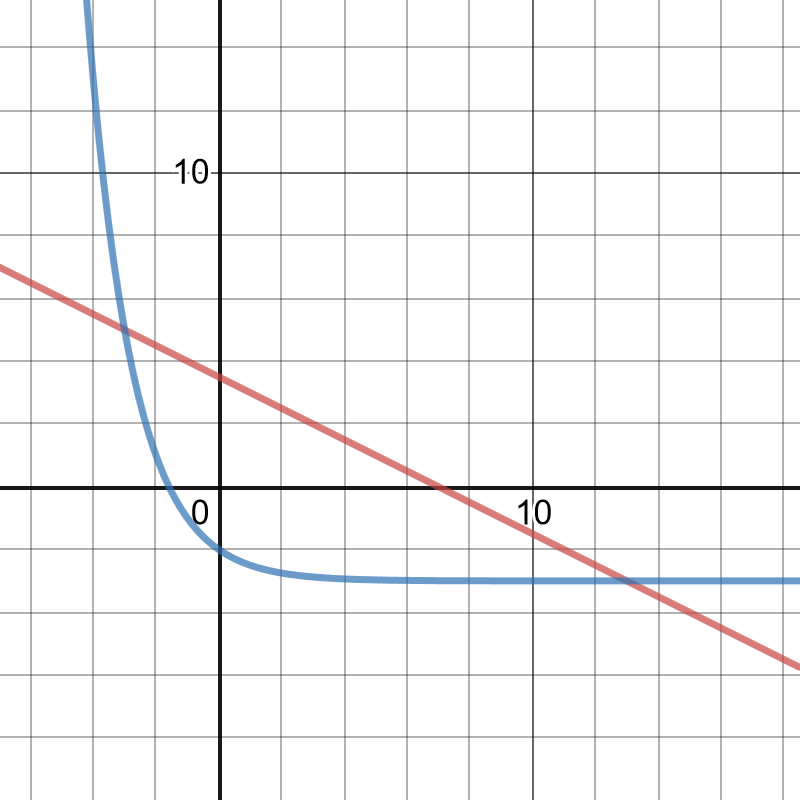
of intersect $(-3,5)$ and $(13,-3)$.
$y=2cdotleft(dfrac{3}{4} right)^x+7$ and $y=0.7(4x+38)-6$.
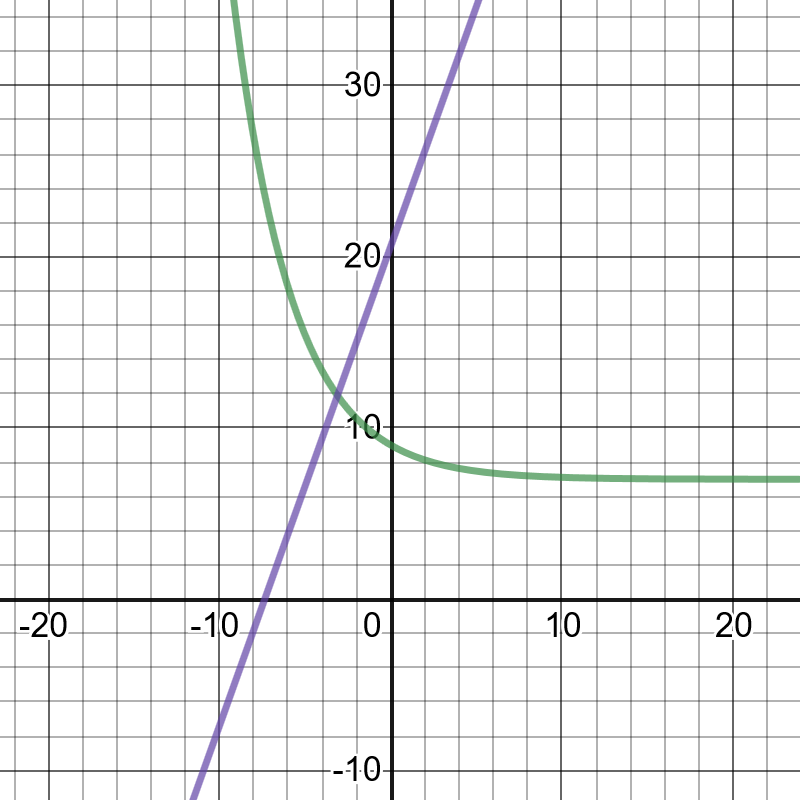
or $x=-3.11$ and $y=11.893$ are solutions.
On the following picture, there are graphed functions
$y=2^x-3$ and $y=2x+1$.
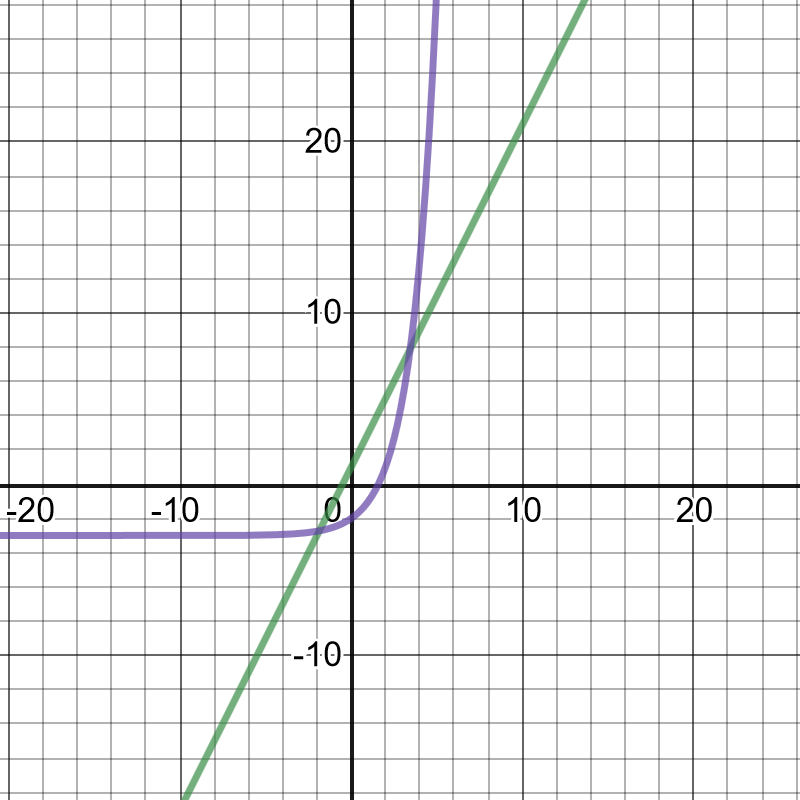
of intersecting $(3.445, 7.89)$ and $(-1.863,-2.725)$.
On the following picture, there are graphed functions
$f(x)$ and $g(x)$:
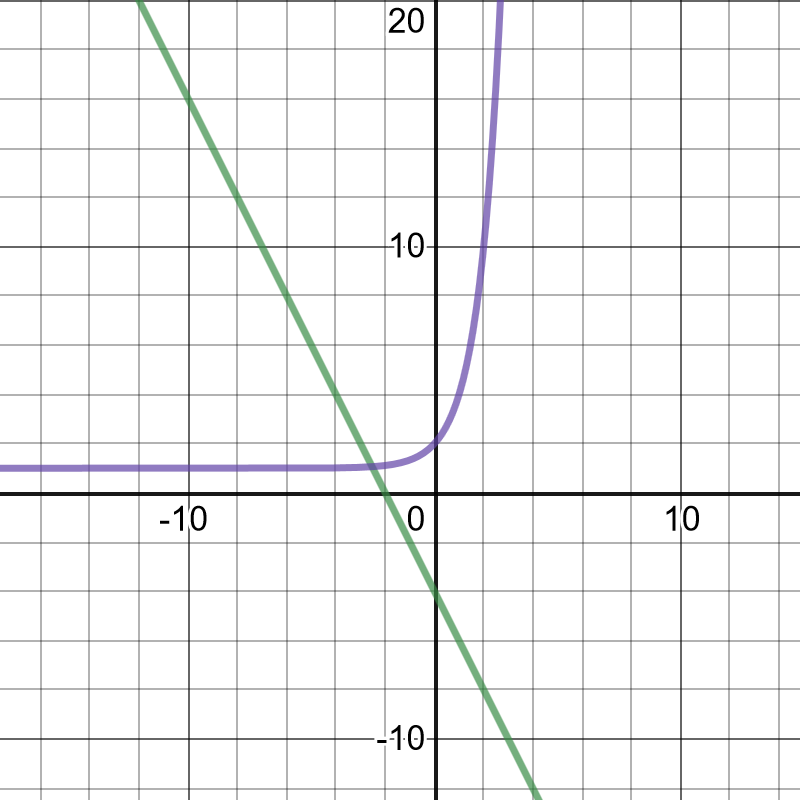
From the previous graph, we can notice that the estimated
point of intersection is $(-2,1)$, so, we will make a table of
values to prove this.
The following table is a table of values for $f(x)$.
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $f(x)$ \
hline
$-3$ & $1.04$ \
hline
$-2$ & $1.11$ \
hline
$-1$ & $1.33$ \
hline
$0$ & $1$ \
hline
$1$ & $4$ \
hline
end{tabular}
end{center}
The following table is a table of values for $g(x)$.\
begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $g(x)$ \
hline
$-3$ & $2$ \
hline
$-2$ & $0$ \
hline
$-1$ & $-2$ \
hline
$0$ & $-4$ \
hline
$1$ & $-6$ \
hline
end{tabular}
end{center}
Based on the previous part, the approximate solution to the original equation is $(-2,1)$.
Let $b$ be the multiplier. There are 5 years from 2005 to 2010 so we can write the equation:
$$
60b^5=45
$$
Divide both sides by 60:
$$
b^5=0.75
$$
Take the fifth root of both sides (or raise them by $1/5$):
$$
b=sqrt[5]{0.75}approx color{#c34632}0.944
$$
To find the percent decrease, subtract the multiplier from 1, then convert to percent:
$$
1-0.944=0.056to color{#c34632}5.6%
$$
$textbf{b.}$
Let $x$ be the number of years since 2005 and $y$ be the value of the stock.
Use the exponential equation:
$$
y=ab^x
$$
where $a=60$ (the initial value in 2005, or $x=0$) and $b=0.944$ (constant multiplier). So, the equation is:
$$
y=60(0.944)^x
$$
or
$$
color{#c34632}f(x)=60(0.944)^x
$$
$textbf{c.}$
Year 2020 is represented by $x=15$. Using the function from part (b),
$$
begin{align*}
f(15)&=60(0.944)^{15}\
&approx 25.28to color{#c34632}$25.28
end{align*}
$$
b. $f(x)=60(0.944)^x$
c. $$25.28$
On the following picture there are graphed points $(60,2005)$ and $(45,2010)$, and the best fit line whose equation is $y=2025.07(0.99)^x$.
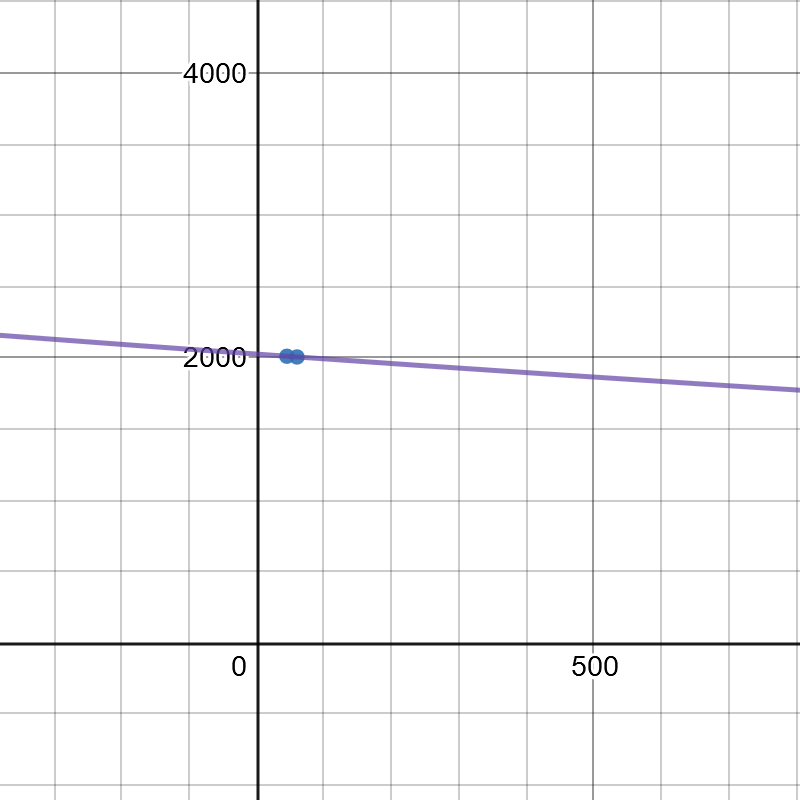
#### (b)
An exponential function that models the value of the stock starting from $2005$ is:
$$
y=2025.07(0.99)^x
$$
#### (c)
Now, substitute $2020$ for $y$ and solve equation for $x$:
$$
2020=2025.07(0.99)^x
$$
$$
x=0.25
$$
So, it will cost $$0.25$.
So $60r^4=45$
Solving, we get r= 0.931
Hence, multiplier , r =0.931
percentage decrease = $(1-0.931)times 100%=6.9%$
From part (a), we find multiplier = 0.931
Hence amount in $n^{th}$ year from 2005 is given by
$$
y=60(0.931)^{n-1}
$$
Putting n=15 in the equation obtained in part (b), we get the amount in the year 2020 = $60(0.931)^{14} = $22.05$
$a-iv$; $b-ii$; $c-v$; $d-i$; $e-iii$
Those answers are because $b$ is the only histogram with narrow
range, $c$ has a uniform distribution, $d$ has a lot of data at the edges,
those are reasons for the previous answers.
$$
40=2cdot3cdot x
$$
$$
x=dfrac{40}{6}=dfrac{20}{3}
$$
So, now we get the following equation, where $n$ is a number
of employees:
$$
dfrac{20}{3}cdot ncdot1=60
$$
$$
n=dfrac{180}{20}
$$
$$
n=9
$$
So, $9$ employees would be needed to build $60$ planters
in one day.
$$
color{#4257b2}text{(a)} 6x-1<11
$$
Isolate the variables on the left side as follows:
$$
6x<11+1 6x<12
$$
Divide both sides of inequality by $6$ as follows.
$$
x< dfrac{12}{6} x<2
$$
$$
color{#4257b2}text{(b)} dfrac{1}{3} xgeq2
$$
Multiply both sides of inequality by $3$ as follows.
$$
xgeq 2cdot3 xgeq6
$$
color{#4257b2}text{(c)} 9(x-2)>18
$$
divide both sides of inequality by $9$ as follows.
$$
x-2>dfrac{18}{9} x-2>2
$$
Divide both sides of inequality by $2$ as follows.
$$
x>2+2 x>4
$$
$$
color{#4257b2}text{(d)} 5-dfrac{x}{4}leqdfrac{1}{2}
$$
Subtract both sides of inequality by $5$ as follows.
$$
-dfrac{x}{4}leqdfrac{1}{2}-5 -dfrac{x}{4}leqdfrac{1-10}{2} -dfrac{x}{4}leqdfrac{-9}{2}
$$
Multiply both sides of inequality by $-4$ as follows.
$$
xgeqdfrac{-9}{2} cdot -4 xgeq9cdot2 xgeq18
$$
text{color{#4257b2}(a) $x 4$ (d) $xge18$}
$$
When $x=0$, $y=2^0=1$ for the first piece so $(0,1)$ should be a filled circle since $geq$ was used. When $x=0$, $y=|0|=0$ for the second piece so $(0,0)$ should be an open circle since $<$ was used. So, the piecewise function should look like:
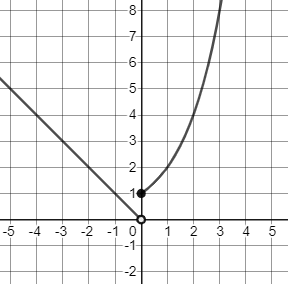
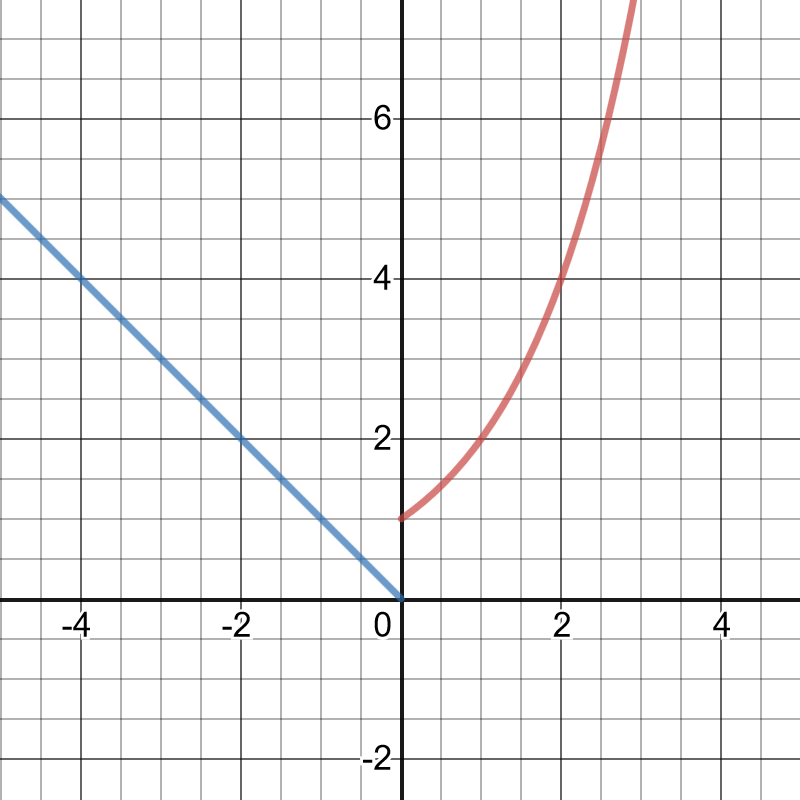
$$
color{#4257b2}text{(a)} dfrac{1}{8}=dfrac{x}{12}
$$
Multiply both of sides by $12$ as follows:
$$
dfrac{1}{8} cdot 12=x x=dfrac{12}{8}
$$
$$
x=dfrac{3}{2} x=1.5
$$
$$
color{#4257b2}text{(b)} dfrac{x}{10}=dfrac{12}{15}
$$
Multiply both of sides by $10$ as follows:
$$
x=dfrac{12}{15} cdot 10 x=dfrac{120}{15}
$$
$$
x=dfrac{24}{3} x=8
$$
text{color{#4257b2}Large(a) $x=1.5$ (b) $x=8$}
$$
text{color{#4257b2}How far away from her house does he live?}
$$
Since she traveled $(40)$ miles after $(10)$ minutes from grandmothers house, and traveled $(34)$ miles after $(22)$ minutes from her house at constant rate, so she traveled $(6)$ miles with $(12)$ minute at constant rate.
$$
dfrac{text{Distance}}{text{Time}}=dfrac{6}{12}=dfrac{x}{90}
$$
$$
x=dfrac{90cdot6}{12}=dfrac{540}{12}=45text{ miles}
$$
text{color{#4257b2}$x=45$ miles}
$$
text{color{#4257b2}We need to get the width and area of rectangle.}
$$
Assume that the length of rectangle is $x$ which equal$=11$ mm, and the width is $y$, and diagonal is $k$ which equal $=61$ mm
$$
k^2=x^2+y^2 y^2=k^2-x^2
$$
$$
y^2=(61)^2-(11)^2 y^2=3721-121 y^2=3600
$$
Use square root for both sides to get the value of $y$ as follows:
$$
sqrt{y^2}=sqrt{3600} y=60text{ mm}
$$
The width of rectangle is $60$ mm.
$text{color{#4257b2}Area}$ $=$ length $cdot$ width $=11cdot60=660$ sq.mm.
text{color{#4257b2}Width $=60$ mm Area $=660$ sq. mm}
$$
show how long one special candle last.\
begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$x$ & $y$ \
hline
$1$ & $3$ \
hline
$2$ & $3.25$ \
hline
$3$ & $4$ \
hline
$4$ & $3.70$ \
hline
end{tabular}
end{center}
On the following picture, there is graphed data from\
the table and a best fit line.\
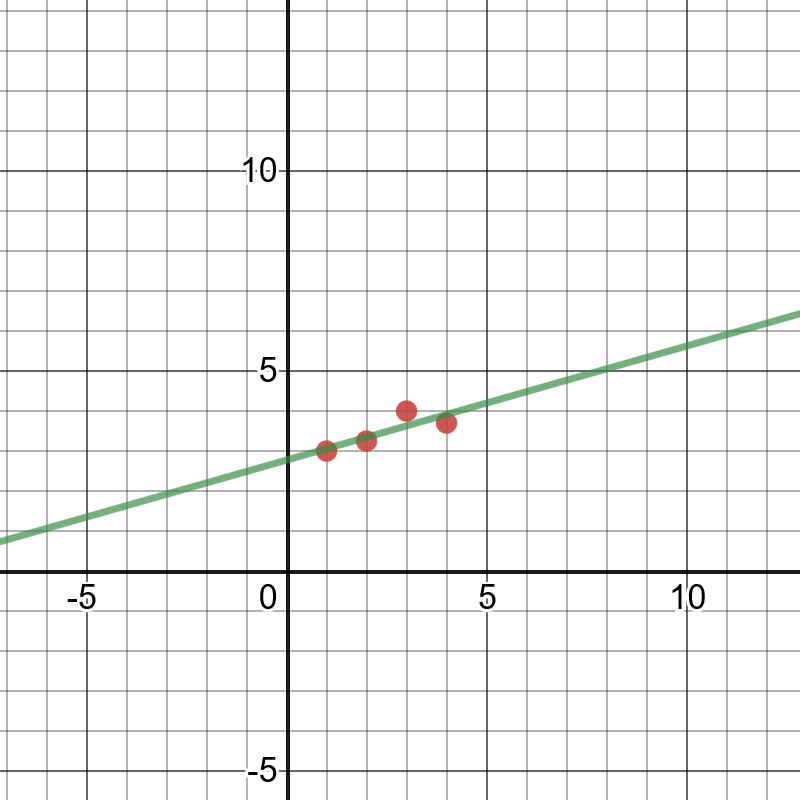
Here, we can conclude that special candle will last
between $3$ and $4$ hours.
Here, we can notice that data is increasing and there are several
points which are outliers.
#### (b)
Here, we can notice that the required slope is $14.65$.
#### (c)
We got that $R^2=0.863041$ and it shows how strong is linear
relationship between
$x$ and $y$ values.
#### (d)
$y$-intercept represents actually coefficient $b$ in linear
equation $y=ax+b$.
We will substitute $80, 150$ and $200$ for $x$ in equation of
best fit line and get that required costs are:
$2567$, $3592.5$ and $4325$, respectively.
#### (f)
We will substitute $80$ for $x$ in equation of a best fit line
and get that predicted value is $2567$, which means that
the actual cost of the well was $2567+363=2930$, because
the residual is difference between observed and predicted value.
#### (g)
We can see from the graph, because of graphed data, that a linear
model was the best choice for predicting well cost using well depth.
d) it represents coefficient $b$ in $y=ax+b$; e) $2567$, $3592.5$, $4325$;
f) $2930$; g) It was the best choice
{color{#4257b2}text{ a) }}
$$
$$
begin{align*}
& text{ For x=2 we solve this}\
&frac{2-4}{3}=frac{2}{15}\\
&frac{-2}{3}=frac{2}{15}\\
&boxed{color{#c34632}text{The sides are not equal}}\
end{align*}
$$
{color{#4257b2}text{ b) }}
$$
$$
begin{align*}
& text{ For x=2 we solve this}\
&left(2-2right)^2<0\\
&0<0\\
&boxed{color{#c34632}text{False}}\
end{align*}
$$
{color{#4257b2}text{ c) }}
$$
$$
begin{align*}
& text{ For x=2 we solve this}\
&left|3cdot :2-8right|ge :-1\\
&|6-8|ge-1\
&|-2|ge-1 \
&2ge-1 \
&boxed{color{#c34632}text{True}}\
end{align*}
$$
{color{#4257b2}text{ d) }}
$$
$$
begin{align*}
& text{ For x=2 we solve this}\
&sqrt{2+2}=16\\
&sqrt{4}=16\
&2=16 \\
&boxed{color{#c34632}text{The sides are not equal}}\
end{align*}
$$
color{#4257b2} text{a)The sides are not equal}
$$
$$
color{#4257b2} text{b)False}
$$
$$
color{#4257b2} text{c)True}
$$
$$
color{#4257b2} text{d)The sides are not equal}
$$
have the right angle and the same side, $AB$, so,
according to the $SSA$ condition, those
triangles are congruent.
According to the given information, we get the following
inequality with absolute value:
$$
|x-2.5|leq0.03cdot2.5
$$
$$
-0.03cdot2.5leq x-2.5leq0.03cdot2.5
$$
$$
2.5-0.03cdot2.5leq xleq2.5+0.03cdot2.5
$$
$$
2.425leq xleq2.575
$$
We can notice that $2.35inleft[2.425,2.575 right]$,
which means that the coin is legitimate.
$y=-left(dfrac{1}{3} right)^x$ and $y=-2.5x+3$.
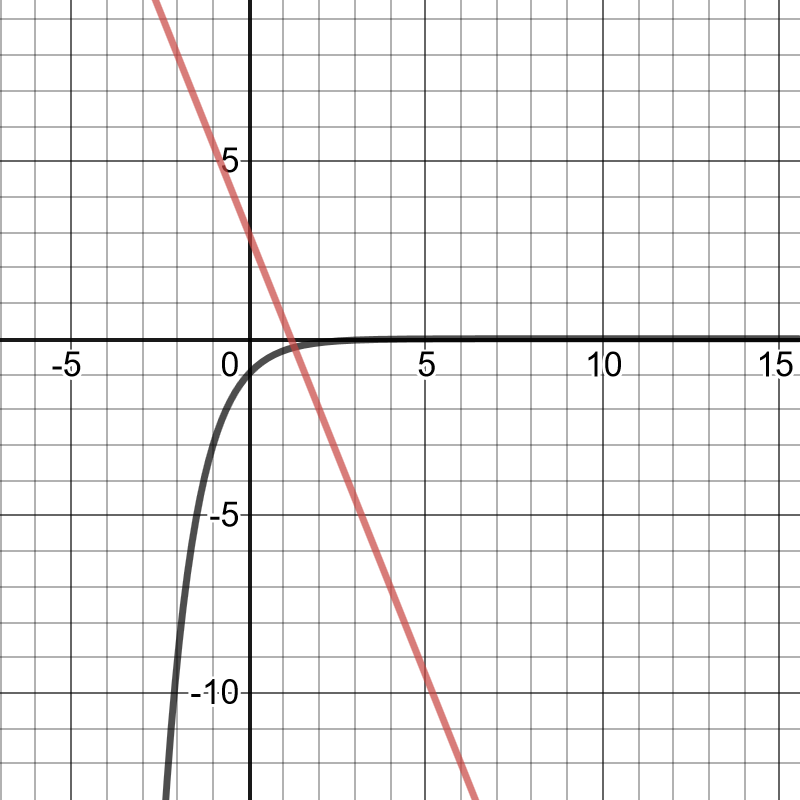
intersection, it is $(1.296,-0.241)$, so, this is exact values which
are solutions for $x$ and $y$.
text{color{#4257b2}We need to get the time needed to paint the room together.}
$$
Assume Susan paint $dfrac{1}{2}$ room per hour, and Jaime paint $dfrac{1}{3}$ room per hour.
Let represent rate together as follows:
$$
dfrac{1}{2}+dfrac{1}{3}=dfrac{1}{x}
$$
$$
dfrac{1}{x}=dfrac{2+3}{6}=dfrac{5}{6}
$$
$$
dfrac{1}{x}=dfrac{5}{6} x=dfrac{6}{5}=1.2
$$
The time needed to paint the room together is $1.2$ hour
Since the hour $=60$ minutes, so the time needed is equal:
$$
1.2 cdot (60)=72text{ Minutes}
$$
72text{ Minutes}
$$
$$
text{color{#4257b2}We need to resolve the following equation}
$$
$$
4x=8(2x-3)
$$
Use distributive property to simplify the equation as follows:
$$
4x=(8cdot2x)-(8cdot3) 4x=16x-24
$$
Isolate the variables on the left side as follows:
$$
4x-16x=-24 -12x=-24 12x=24
$$
Divide both sides by $12$ as follows:
$$
x=dfrac{24}{12} x=2
$$
On the following picture, there is a graphed given function.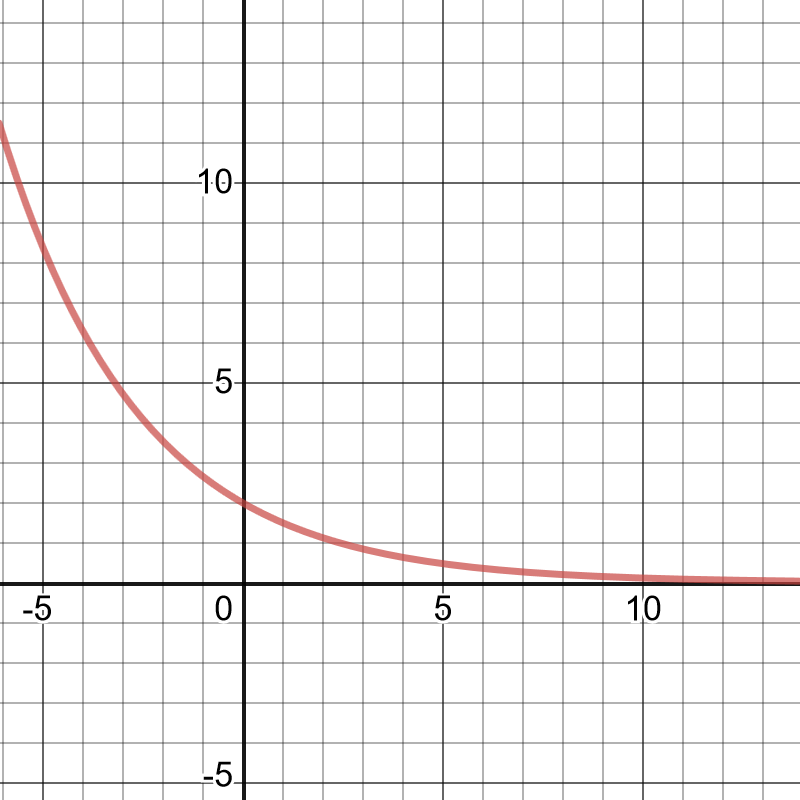
The conclusion is that the required equation is:
$$
y=10(2.3)^x
$$
We can see it from the following picture.
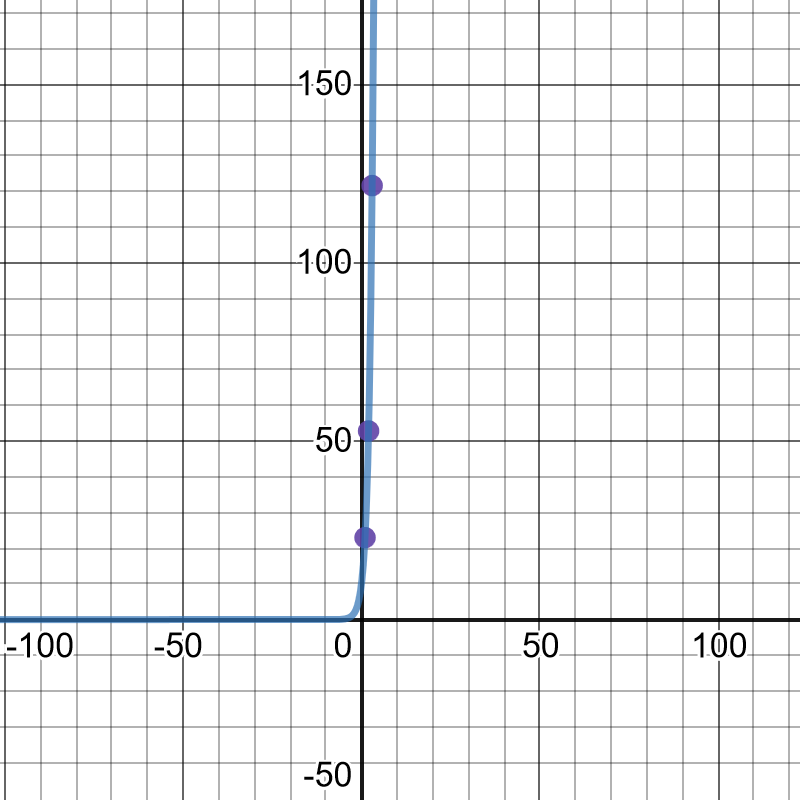
First, the exponential function which describes this situation is the following:
$$
y=42000(1.25)^x
$$
Now, we will substitute $5$ for $x$ in the previous equation and get:
$$
y=42000(1.25)^5
$$
$$
y=128173.83
$$
So, in five years, population will be $128173.83$.
#### (d)
On the following picture, there are graphed points $(2000,25)$ and $(2010,60)$ and the best fit line.
We can notice that annual multiplier is $1.09$ and percent increase is $9%$ every year.
c) $128173.83$; d) $1.09, 9%$
text{color{#4257b2}How many student attended the play?}
$$
Assume number of adults is $x$ and number of students is $150+x$
and total cost is $=4730$ dollars.
$$
4730=5 x+3(150+x) 4730=5x+450+3x
$$
Isolate the variables on the left side as follows:
$$
8x=4730-450 8x=4280
$$
Divide both of sides by $8$ as follows:
$$
x=dfrac{4280}{8} x=535
$$
The number of students attended the play is
$$
150+x=150+535={color{#4257b2}685text{ students}}
$$
Large{color{#4257b2}685text{ students}}
$$
Since the $FG$ is mid segment in triangle $ADE$, So $FG=dfrac{1}{2} DE$
$$
FG=dfrac{1}{2} cdot7=dfrac{7}{2} FG=3.5text{ cm}
$$
Since the $DE$ is mid segment in triangle $ABC$, So $DE=dfrac{1}{2} BC$
$$
BC=2 DE=2cdot7=14 BC=14text{ cm}
$$
text{color{#4257b2}$$FG=3.5text{ cm} BC=14text{ cm} $$}
$$
text{color{#4257b2}We need to get the time needed to paint the wall together.}
$$
Assume RJ rate in paint is $dfrac{1}{45}$ wall per hour, and Delaney rate in paint is $dfrac{1}{30}$ wall per hour.
Let represent rate together as follows:
$$
dfrac{1}{45}+dfrac{1}{30}=dfrac{1}{x}
$$
$$
dfrac{1}{x}=dfrac{30+45}{30cdot45}=dfrac{75}{1350}
$$
$$
dfrac{1}{x}=dfrac{75}{1350} x=dfrac{1350}{75}=18
$$
The time needed to paint the wall together is $18$ minutes
text{color{#4257b2}Large$18$ minutes}
$$
Here we have two pairs of sides which are equal in the length and the
included angles are equal in measurement, which means that those
triangles are congruent according to the $SAS$ condition.
#### (b)
Here, we can conclude that angles in those triangles are $62^{circ}$, $45^{circ}$ and $73^{circ}$.
They have and one pair of sides equal length and the included angles
are equal in measurement, which means that those triangles are
congruent according to the $ASA$ condition.
We can notice that this is an arithmetic sequence where the first term is
$a_{1}=7$ and the constant difference is $d=-3$, so, its equation is following:
$$
a_{n}=7+(n-1)(-3)
$$
#### (b)
We can notice that this is a geometric sequence where first term
$a_{1}=2000$ and common ration is $q=3$, so, its equation is following:
$$
a_{n}=2000(3)^{n-1}
$$
Shu Min : $1980 + 30x$
Wei : $2590 + 20x$
Add the expressions and set them equal to 5000.
$$
1980+30x + 2590 + 20x = 5000
$$
$$
50x = 5000-1980-2590
$$
$$
50x = 430
$$
$$
x = 8.6text{ months}
$$
$$
dfrac{1}{2}(6x-14)+5x=2-3x+8
$$
Use distributive property to simplify as follows:
$$
left(dfrac{1}{2} cdot 6xright)-left(dfrac{1}{2} cdot 14right)+5x=2-3x+8
$$
$$
3x-7+5x=10-3x
$$
The equivalent expression is first one (a).
text{color{#4257b2}(a) $3x-7+5x=10-3x$}
$$
On the following picture, there are graphed given points and the best fit line.
We can notice that the required equation is:
$$
y=-6(3)^x
$$
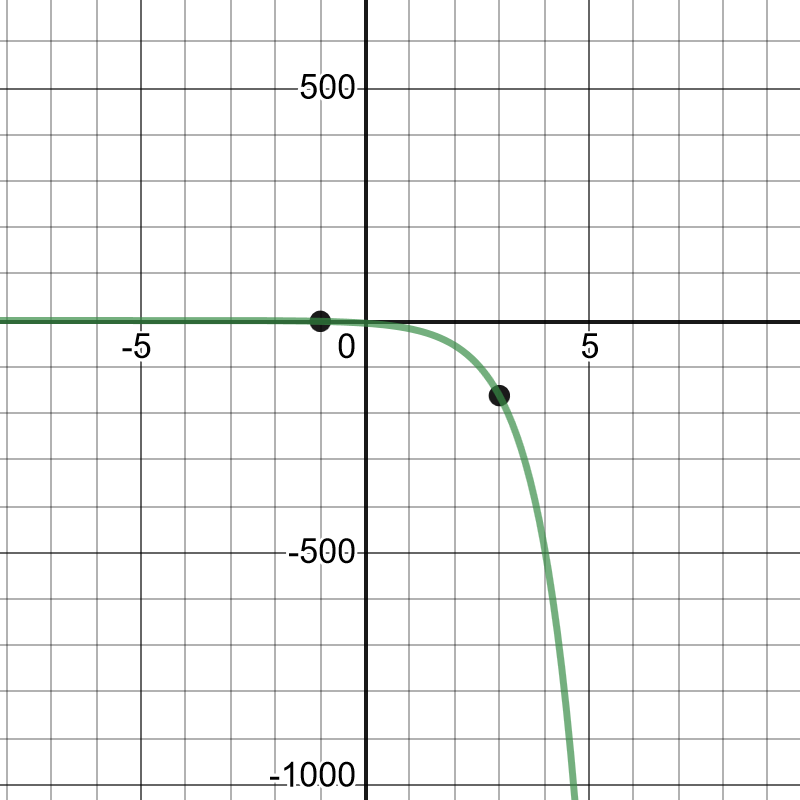
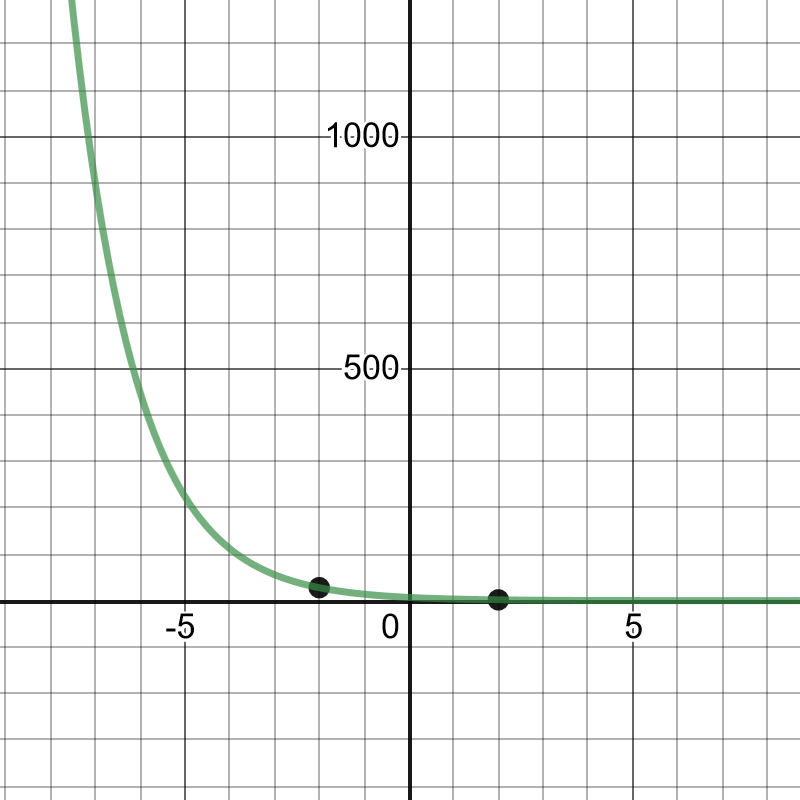
On the following picture, there are graphed given points and the best fit line.
We can notice that the required equation is:
$$
y=7(0.5)^x
$$
On the following picture, there is graphed transformed function: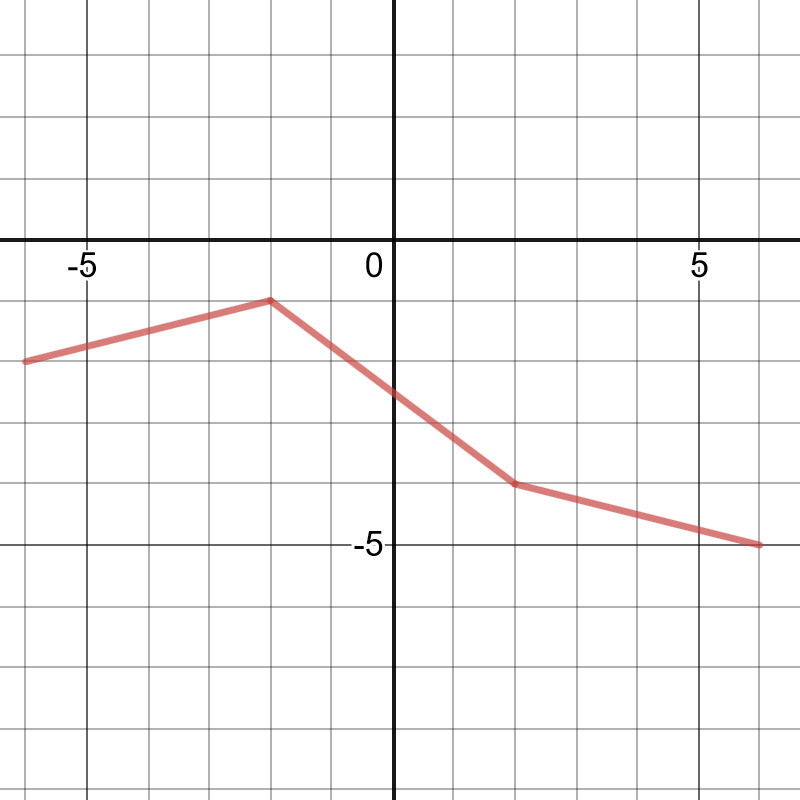
On the following picture, there is graphed transformed function: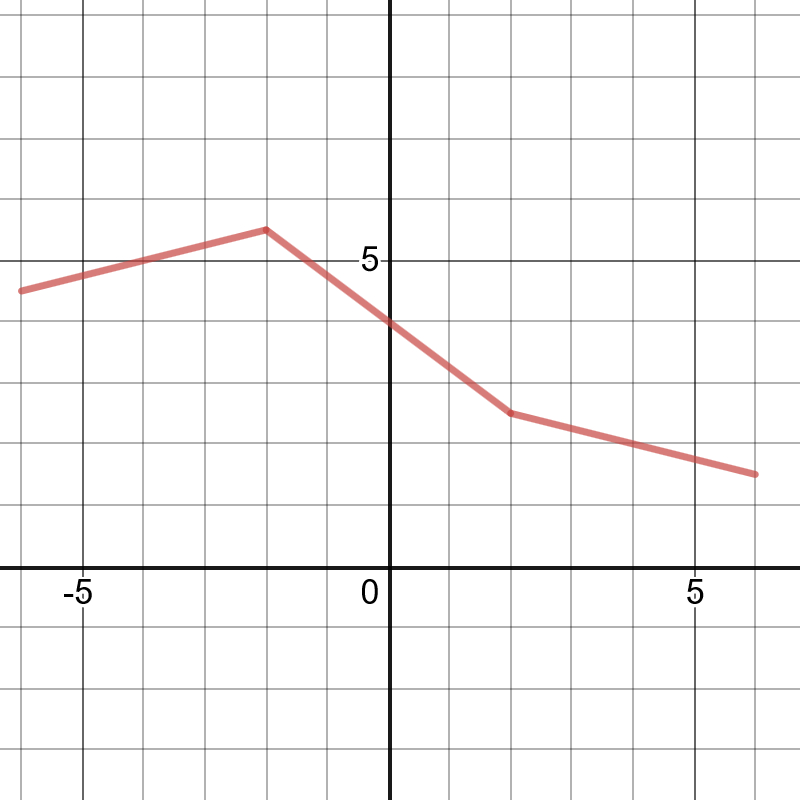
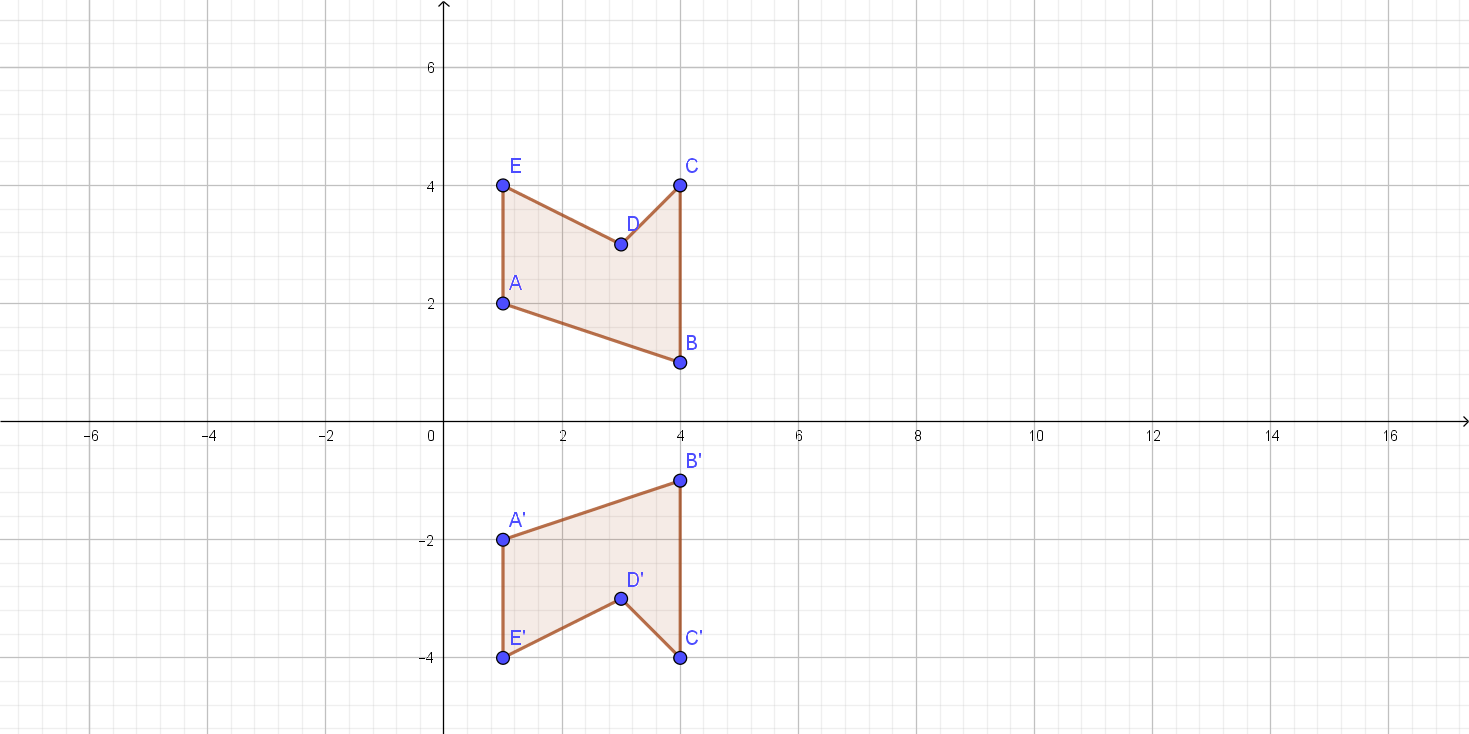
On the following picture, there is rotated $ABCDE$.
We can notice that coordinates of the point $A’$ are $A'(-1,-2)$.
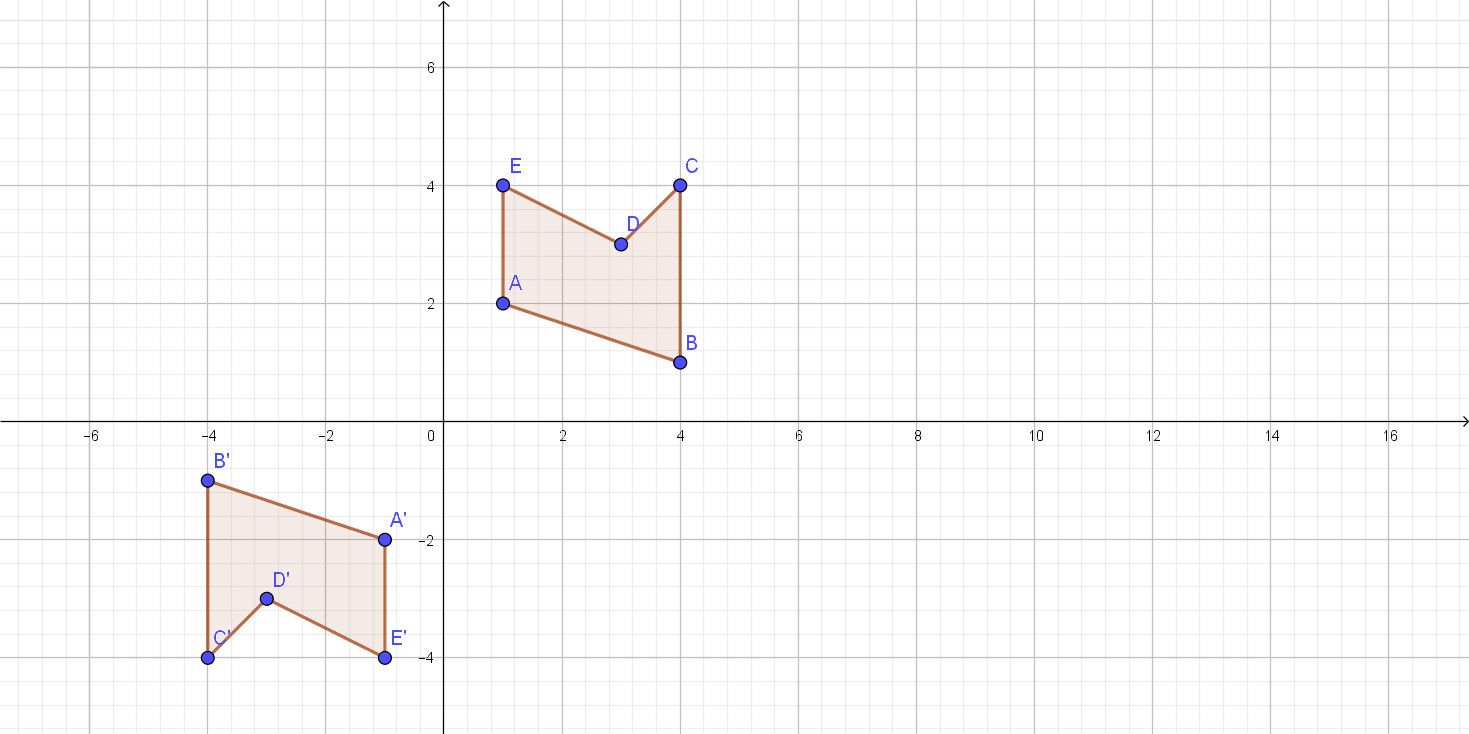
On the following picture, there is reflected $ABCDE$.
We can notice that coordinates of the point $C’$ are $C’ (4,-4)$.
Point $B$ has coordinates $B(4,1)$, which means $x=4$, $y=1$.
Now, we have the following:
$$
x-1=4-1=3
$$
$$
y+3=1+3=4
$$
So, the coordinates which correspond to the point $B’$ are $B'(3,4)$.
of functions and their properties.
Teams need to find which property corresponds to which function and
on that way find a match for each of eight dues.
Here, for this relationship, the domain is set $D=[-2,2]$ while
the range is $R=[-4,4]$.
We can conclude that this relationship is not a function because
for the same value of $x$ from the domain there are two corresponding
values of $y$ from the range.
#### (b)
Here, for this realtionship the domain is set of all real numbers
while range is set $R=left{4 right}$.
We can conclude that this relationship is a function because for
every value of $x$ from the domain there is exactly one correspond point on graph, or $y$-value, and this is constant function.
#### (c)
Here, for this realtionship, the domain is set $D=[0,4]$ while
the range is set $R=[1,5]$.
We can conclude that this relationship is a function because for
every value of $x$ from the domain there is exactly one correspond point on graph, or $y$-value, and this is constant function.
#### (d)
Here, for this realtionship, the domain is set $D=(0,+infty)$, while
the range is set $R=Bbb/{R}left{ 0right}$.
We can conclude that this relationship is a function because for
every value of $x$ from the domain there is exactly one correspond point on graph, or $y$-value, and this is constant function.
c) $D=[0,4]$, $R=[1,5]$, it is not a function;
d) $D=(0,+infty)$, $R=Bbb{R}/left{ 40right}$, it is not a function.
and $(-1,15)$, so, we will sibstitute those values for $x$ and $y$
in the equation $y=ab^x$ and find $a$ and $b$ on that way:
$$
1=ab^{circ}Rightarrow a=1
$$
$$
15=ab^{-1}Rightarrowdfrac{1}{15}
$$
So, the required equation of this function is $y=left( dfrac{1}{15}right)^x$.
calculate the median and $IQR$ as the mean and standard
deviation.
So, we got that mean is $50.6913$ and the standard deviation
is $2.63$.
$$
2(12x+7)=30x-4
$$
Use distributive property to simplify as follows:
$$
(2cdot12x)+(2cdot7)=30x-4 24x+14=30x-4
$$
Isolate the variables on the left side as follows:
$$
24x-30x=-4-14 -6x=-18
$$
Divide both sides by $-6$ as follows:
$$
x=dfrac{-18}{-6} x=3
$$
text{color{#4257b2}Large$$x=3$$}
$$
$y$ represent a number of gallons of spring blue.
We get the following system of equations which we will
solve for $x$ and $y$:
$$
0.02x+0.1y=0.04
$$
$$
0.98x+0.9y=0.96
$$
We will solve it using a graph.
On the following picture, there are graphed both equations
and the solution is a point of intersection.
which means that Antoine should use $0.75$ gallons of powder
blue and $0.25$ gallons of spring blue.
$$
color{#4257b2}text{(a)} 5x-7ge2x+5
$$
Isolate the variables on the left side as follows:
$$
5x-2xge5+7 3xge12
$$
Divide both sides of inequality by $3$ as follows.
$$
xgedfrac{12}{3} xge4
$$
$$
color{#4257b2}text{(b)} 6x-29>4x+12
$$
Isolate the variables on the left side as follows:
$$
6x-4x>12+29 2x>41
$$
Divide both sides of inequality by $2$ as follows.
$$
x>dfrac{41}{2} x>20.5
$$
color{#4257b2}text{(c)} x+6le6
$$
Isolate the variables on the left side as follows:
$$
xle6-6 xle0
$$
$$
color{#4257b2}text{(d)} |2x-7|>31
$$
Equal $2x-7>31$ as follows:
$$
2x-7>31 2x>31+7 2xdfrac{38}{2} x>19
$$
Equal $-2x+7>31$ as follows:
$$
-2x+7>31 -2x>31-7 -2x>24 x19$ or $x<-12$
(c) $x leq0$ (d) $x>19$ or $x<-12$
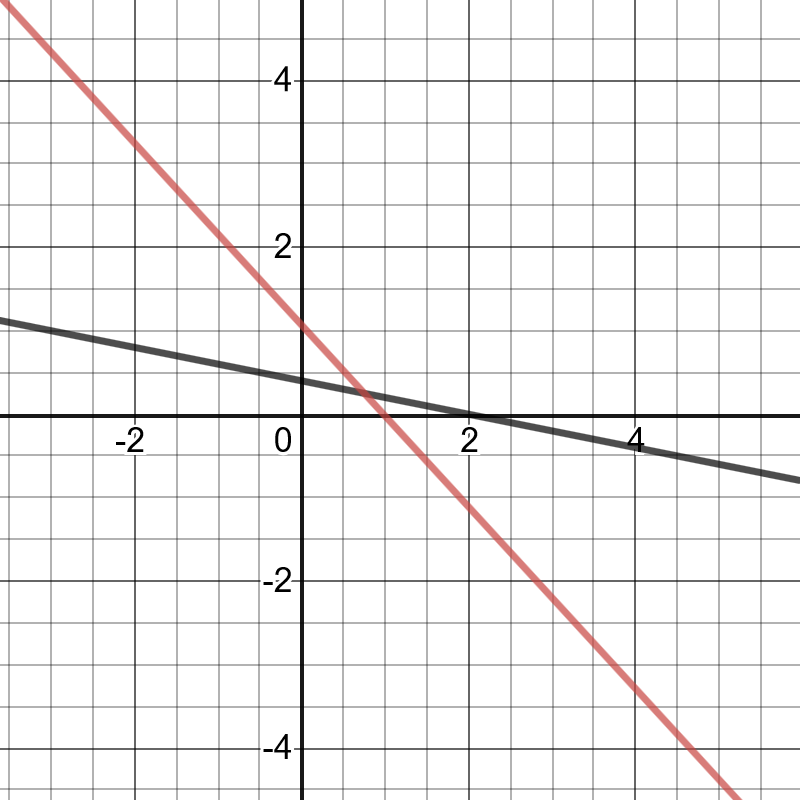
$y=2^x$ and $y=5-x$.
of the previous function.
So, using the previous picture, we can notice that the point
of an intersection, the solution is a point $(1.7,3.3)$.
Let represent total amount of Zachary money by $718-14x$
Let represent total amount of Christian money by $212+32x$
Where their have the same amount of money, so the two equations are equals as follows:
$$
718-14x=212+32x
$$
Isolate the variables on the left side as follows:
$$
-14x-32=212-718 -64x=-506
$$
Divide both sides of equation by $-64$ as follows.
$$
x=dfrac{-506}{-64} x=11text{ months}
$$
They have the same amount of money in their accounts after $11$ months.
text{color{#4257b2}After $11$ months}
$$
$$
begin{align*}
3x+2y&=10\
2y&=-3x+10\
y&=-dfrac{3}{2}x+5
end{align*}
$$
So, the slope of the parallel line is $m=-dfrac{3}{2}$. Since it goes through $(4,-7)$, we solve for the $y$-intercept $b$:
$$
begin{align*}
y&=mx+b\
-7&=-dfrac{3}{2}(4)+b\
-7&=-6+b\
-1&=b
end{align*}
$$
So, the equation of the line is:
$$
color{#c34632}y=-dfrac{3}{2}x-1
$$
y=-dfrac{3}{2}x-1
$$
line which is parallel to it has the same slope:
$$
2y=10-3x
$$
$$
y=-dfrac{3}{2}x+5
$$
So, the slope of the required line is $-dfrac{3}{2}$ and it passes
through point $(4,-7)$, so, its equation is the following:
$$
y+7=-dfrac{3}{2}(x-4)
$$
$$
dfrac{a}{b}=-dfrac{3}{2}x+6+7
$$
$$
y=-dfrac{3}{2}x+13
$$
Let $x$ represents the figure number.
Equation: $y – 11 = 2 left( x – 3right)$
$$
begin{align*}
y – 11 & = 2x – 6 && {text {equation for the situation}} \
y – 11 + 11 & = 2x – 6 + 11 && {text {add 11 to both sides of the equation}} \
y & = 2x + 5 && {text {equation for the value of $y$}} \\
y & = 2 left(50right) + 5 && {text {substitute for the value of $x$}} \
& = 100 + 5 && {text {evaluate}} \
y & = 105 text { tiles} && {text {number of tiles for the figure}}
end{align*}
$$
text{color{#4257b2}(a) What the relation between $DE$ and $AB$?}
$$
$DE$ is mid segment of $AB$ $DE=dfrac{1}{2}AB$
$$
text{color{#4257b2}(b) What the relation between $angle CDE$ and $angle DAB$?}
$$
$angle CDE$ is equal $angle DAB$ $CD=AD CE=BE DE||AB$
$$
text{color{#4257b2}(c) What the value of $x$ if $DE=4x+7$ and $AB=34$?}
$$
$$
because DE=dfrac{1}{2}AB therefore 2(4x+7)=34
$$
Use distributive property to simplify as follows:
$$
(2cdot4x)+(2cdot7)=34 8x+14=34
$$
Isolate the variables on the left side as follows:
$$
8x=34-14 8x=20
$$
Divide both of sides by $8$ as follows:
$$
x=dfrac{20}{8} x=2.5
$$
Prediction about Quinn’s resulting quadrilateral is that it
will have sides whose lengths are less than lengths of the
original quadrilateral.
#### (b)
On the following picture, there is repeated Quinn’s
experiment and the conclusion is that prediction from
part a) is correct and also, the shape of a new figure is
same as the shape of the original figure.

On the following picture, there is graphed a non-convex
quadrilateral and repeated Quinn’s experiment.
is not the same shape as an original quadrilateral.
c) New quadrilateral is not the same shape as original.
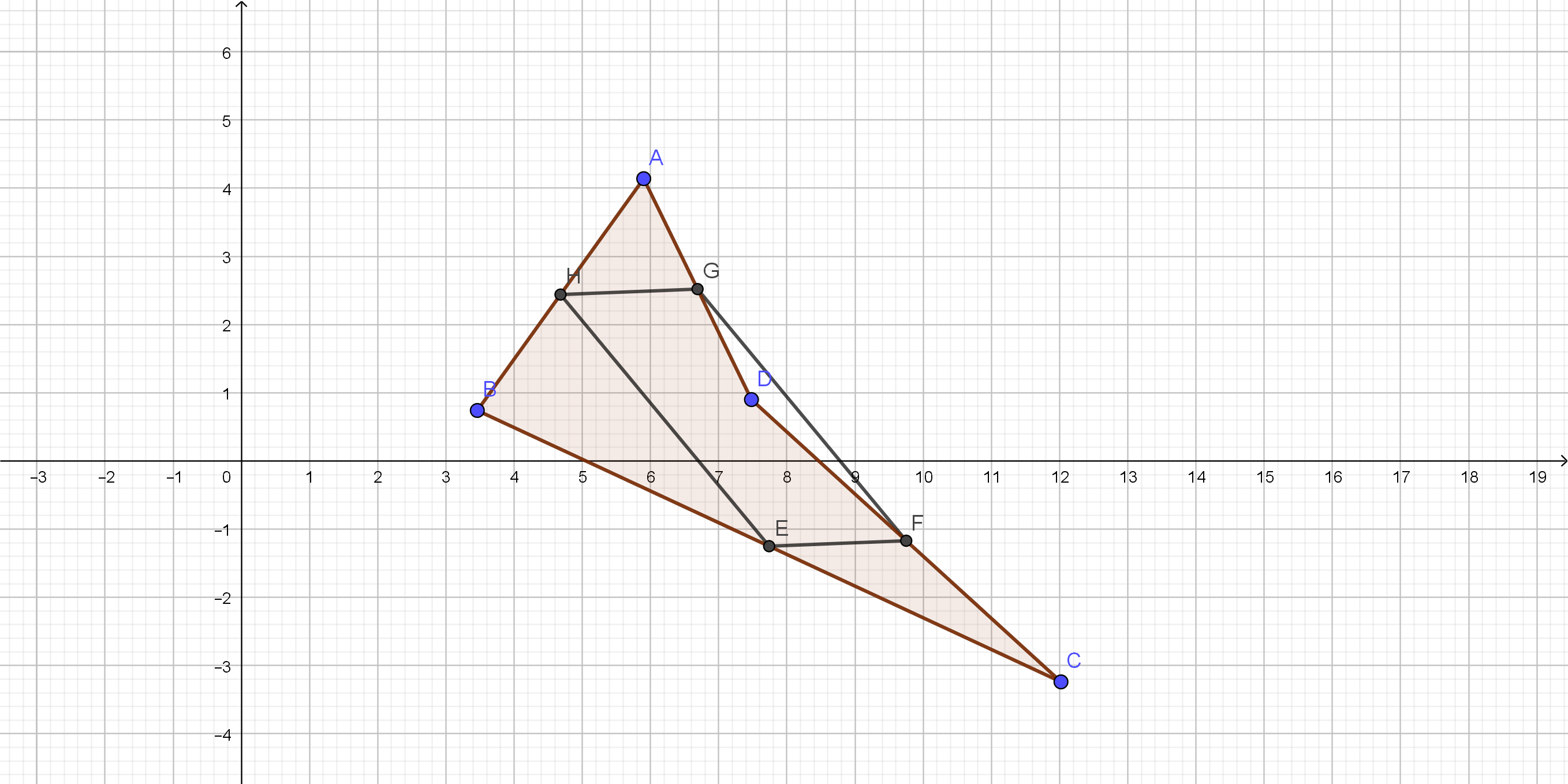
On the following picture, there is graphed quadrilateral $ABCD$.

On the following picture, there are labeled points $E, F, G$ and $H$ on $ABCD$.

On the following picture, there are connected midpoints
of the sides from the previous part.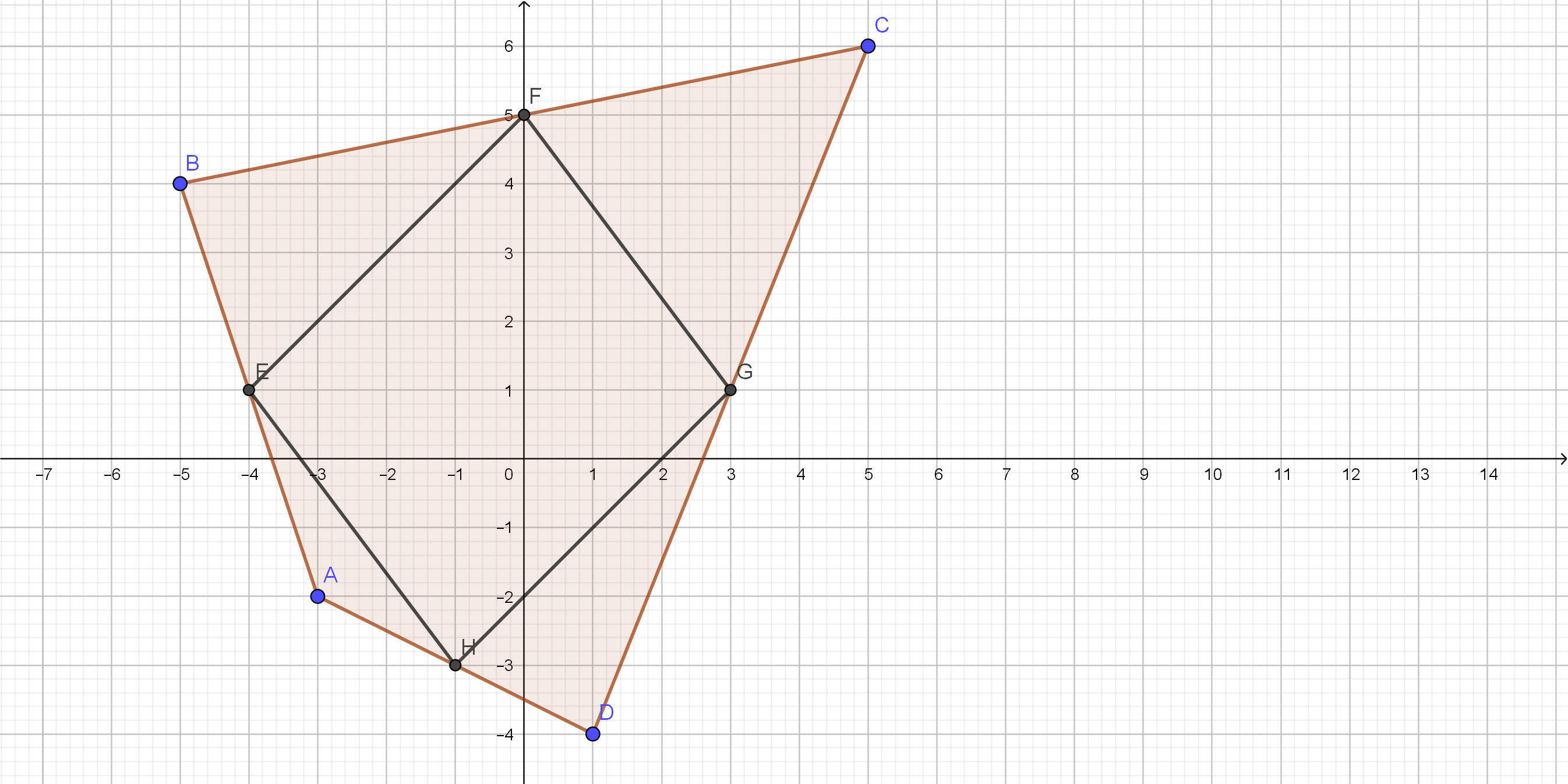
Now, we will find the slopes:
$$
text{slope }EF=dfrac{3-1}{0+4}=1
$$
$$
text{slope }FG=dfrac{1-5}{3-0}=-dfrac{4}{3}
$$
$$
text{slope }GH=dfrac{-3-1}{-1-3}=1
$$
$$
text{slope }EH=dfrac{-3-1}{-1+4}=-dfrac{4}{3}
$$
We can notice that slope $EF=$slope $GH$ and slope $FG=$ slope $EH$, which means
that those sides are parallel, so, $EFGH$ is a parallelogram.
We will calculate $EF$ and $FG$:
$$
EF=sqrt{(0+4)^2+(5-1)^2}=sqrt{32}
$$
$$
FG=sqrt{(3-0)^2+(1-5)^2}=sqrt{25}=5
$$
We got that $EFne FG$, which means that $EFGH$ is not a rhombus.
d) $EFGH$ is not a rhombus
$HE$ is parallel to $DB$.
$GF$ is also a midsegment of triangle $BCD$, so, $GF$ is parallel
to $BD$.
$HE$ is parallel to $BD$ and $BD$ is parallel to $GF$,
by transitivity, $HE$ is parallel to $GF$.
On the same way, $HG$ is parallel to $EF$, which means that
$EFGH$ is parallelogram.
begin{center}
begin{tabular}{ |c|c| c| c| c| c |c| }
hline
$$ & $text{Taco shack}$ & $text{competitor}$ \
hline
$25text{ grams cheese}$ & $30%$ & $29%$ \
hline
end{tabular}
end{center}
We can notice that there is almost no difference between\
the amount of cheese at Taco Shack and at the competitor.\
So, there is no association.\
The conclusion is that the Taco Shack owner does not need\
to adjust the amount of cheese.\
to adjust the amount of cheese.
Steven can look up $27$ words per hour .
Mary Lu can look up $35$ words per hour.
Total words look up together per hour is $27+35= 62$
The time needed to look up $100$ words is represented by
$$
dfrac{100}{62}=1.613text{ hours} text{ Where, hour}=60text{ minutes}
$$
$$
text{The time needed}=1.613cdot (60)=96.78text{ minutes}
$$
text{color{#4257b2}$$96.78text{ minutes}$$}
$$
From the original equation, use the Distributive Property:
$$
12x-4+3x=9x+5
$$
This matches equation a and not equation b. Combining like terms on the left side,
$$
15x-4=9x+5
$$
This matches equation d.
Equation c cannot be obtained from the last equation so it is not an equivalent equation of the given.
So, the equivalent equations of the given are: $text{$text{color{#c34632}a and d.\}$}$
{color{#4257b2}text{ a) }}
$$
$$
begin{align*}
& text{Group like terms} \
&12x+3x-4=9x+5\\
&15x-4=9x+5 tag{Add similar elements} \
&15x-4+4=9x+5+4 tag{Add 4 to both sides} \
&15x=9x+9tag{Simplify} \
&15x-9x=9x+9-9x tag{Subtract 9x from both sides}\
&6x=9tag{Simplify}\
&frac{6x}{6}=frac{9}{6} tag{Divide both sides by 6} \\
&boxed{color{#c34632}x=frac{3}{2}} \\
&color{#965501}text{This equation is equal to the given equation}\
end{align*}
$$
{color{#4257b2}text{ b) }}
$$
$$
begin{align*}
& text{Group like terms} \
&12x+3x-1=9x+5\\
&15x-1=9x+5 tag{Add similar elements} \
&15x-1+1=9x+5+1 tag{Add 1 to both sides} \
&15x=9x+6tag{Simplify} \
&15x-9x=9x+6-9x tag{Subtract 9x from both sides}\
&6x=6tag{Simplify}\
&frac{6x}{6}=frac{6}{6} tag{Divide both sides by 6} \\
&boxed{color{#c34632}x=1 } \\
&color{#965501}text{This equation is not equal to the given equation}\
end{align*}
$$
{color{#4257b2}text{ c) }}
$$
$$
begin{align*}
&text{Subtract 14x from both sides}\
&11x-14x=14x-14x\\
&-3x=0 \
&frac{-3x}{-3}=frac{0}{-3} tag{Divide both sides by -3}\\
&boxed{{color{#c34632} x=0 } }\\
&color{#965501}text{This equation is not equal to the given equation}\
end{align*}
$$
{color{#4257b2}text{ d) }}
$$
$$
begin{align*}
& text{Add 4 to both sides}\
&15x-4+4=9x+5+4 \ \
&15x=9x+9tag{Simplify} \
&15x-9x=9x+9-9x tag{Subtract 9x from both sides}\
&6x=9tag{Simplify}\
&frac{6x}{6}=frac{9}{6} tag{Divide both sides by 6} \\
&boxed{color{#c34632}x=frac{3}{2}} \\
&color{#965501}text{This equation is equal to the given equation}\
end{align*}
$$
color{#4257b2} text{a)}x=frac{3}{2}
$$
$$
color{#4257b2} text{b)} x=1
$$
$$
color{#4257b2} text{c)}x=0
$$
$$
color{#4257b2} text{d)}x=frac{3}{2}
$$
We can notice that this is a geometric sequence where the first term
is $a_{1}=dfrac{1}{2}$ and common ratio is $q=dfrac{1}{2}$, so,
its equation is the following:
$$
a_{n}=dfrac{1}{2}left(dfrac{1}{2} right)^{n-1}
$$
Where $a_{n}$ is $n$th term.
#### (b)
We can notice that this is an arithmetic sequence where the first term is $a_{1}=-7.5$ and constant difference is $d=-2$,
so, its equation is the following:
$$
a_{n}=-7.5+(n-1)(-2)
$$
Where $a_{n}$ is $n$th term.
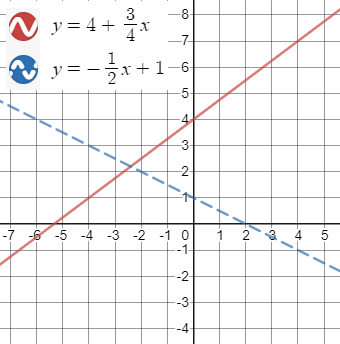
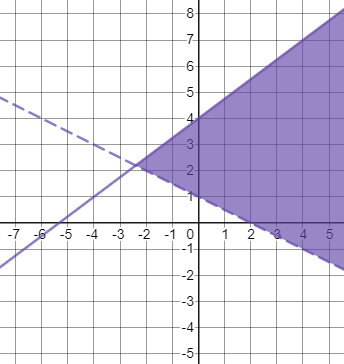
For region A, I used $(0,5)$:
$$
begin{align*}
5&stackrel{?}{leq}4+dfrac{3}{4}(0) & 5&stackrel{?}{>}-dfrac{1}{2}(0)+1 \
5¬{leq}4 & 5&>1hspace{5mm}checkmark
end{align*}
$$
Only one inequality is satisfied so region A should not be shaded.
For region B, I used $(-8,0)$:
$$
begin{align*}
0&stackrel{?}{leq}4+dfrac{3}{4}(-8) & 0&stackrel{?}{>}-dfrac{1}{2}(-8)+1 \
0¬{leq}-2 & 0¬{>}5
end{align*}
$$
Both inequalities are not satisfied so region B should not be shaded.
$$
begin{align*}
2&stackrel{?}{leq}4+dfrac{3}{4}(0) & 2&stackrel{?}{>}-dfrac{1}{2}(0)+1 \
2&leq 4hspace{5mm}checkmark & 2&>1hspace{5mm}checkmark
end{align*}
$$
Both inequalities are satisfied so region C should be shaded.
For region D, I used $(0,0)$:
$$
begin{align*}
0&stackrel{?}{leq}4+dfrac{3}{4}(0) & 0&stackrel{?}{>}-dfrac{1}{2}(0)+1 \
0&leq 4hspace{5mm}checkmark & 0¬{>}1
end{align*}
$$
Only one inequality is satisfied so region D should not be shaded.
$$
color{white}tag{1}
$$
The solution of the system of inequalities is shown:
We can conclude that $f(0)$ is equal to value of $3$ from the graph.
#### (b)
We can conclude that $g(4)$ is equal to value of $2$ from the graph.
#### (c)
We can conclude that $f(2)$ is equal to value of $1$ from the graph.
#### (d)
We can conclude that $g(0)$ is equal to the value of $0$ from the graph.
#### (e)
We can conclude that $g(2)$ is equal to value of $1$ from the graph.
#### (f)
We can conclude that $f(5)$ does not exist because for this value
function $f$ is not defined.
#### (g)
We can conclude that the required value of $x$ is $x=2$ because
for this value of $x$, those function has intercept.
f) $f(5)$ does not exist; g) $x=2$
$$
color{#4257b2}text{(a)} 6|x|>18
$$
Divide both sides of inequality by $6$ as follows:
$$
|x|>dfrac{18}{6} |x|>3
$$
$$
x>3 text{ and} x<-3
$$
$$
color{#4257b2}text{(b)} |3x-2|le2
$$
Equal $3x-2le2$ as follows:
$$
3x-2le2 3xle2+2 3xle4 xledfrac{4}{3}
$$
Equal $-3x+2le2$ as follows:
$$
-3x+2le2 -3xle2-2 -3xle0 xge0
$$
The value of $x$ is equal $0le xledfrac{4}{3}$
color{#4257b2}text{(c)} (4x-2)^2=100
$$
Use square root for two sides as follows.
$$
(4x-2)^2=10^2 4x-2=10
$$
Isolate the variables on the left side as follows:
$$
4x=10+2 4x=12
$$
Divide both sides by $4$ as follows:
$$
x=dfrac{12}{4} x=3
$$
$$
color{#4257b2}text{(d)} (x-1)^3=8
$$
$$
(x-1)^3=2^3
$$
Since the power of two sides are equal so,
$$
x-1=2
$$
Isolate the variables on the left side as follows:
$$
x=2+1 x=3
$$
text{color{#4257b2}(a) $3le xle-3$ (b) $0le xledfrac{4}{3}$
\ \
(c) $x=3$ (d) $x=3$}
$$
$$
color{#4257b2}5u+6v=2 2v=u-10
$$
Multiply the second equation by $3$ to be
$$
6v=3u-30 3u-6v=30
$$
Adding the new equation to the first equation as follows:
$$
(5u+3u)+(6v-6v)=(2+30) 8u+0=32 8u=32
$$
Divide both of sides by $8$ as follows:
$$
u=dfrac{32}{8} u=4
$$
Substitute the value of $u=4$ in the second equation as follows:
$$
2v=4-10 2v=-6
$$
Divide both of sides by $2$ as follows:
$$
v=dfrac{-6}{2} v=-3
$$
$text{color{#4257b2}Check:}$ Substitute values of $u, v$ as follows:
$$
2v=u-10=(2cdot-3)=4-10 -6=-6
$$
Since the left side is equal the right side, so the answer is correct.
text{color{#4257b2}$ u=4 v=-3$}
$$
$$
{color{#4257b2}text{(a)} left(dfrac{3x}{y^2}right)^2}=left(dfrac{3^2cdot x^2}{y^4}right)= left(dfrac{9x^2}{y^4}right)
$$
$$
{color{#4257b2}text{(b)} (6x^3) (3x y)^{-1}}=dfrac{6x^3}{3x y}=dfrac{2x^2}{y}
$$
$$
{color{#4257b2}text{(c)} dfrac{(2x)^{-2}}{(2x^3)^{-1}}}=left(dfrac{1}{2xcdot2x}right)cdot 2x^3=left(dfrac{2x^3}{2xcdot2x}right)=dfrac{x}{2}
$$
The equation which model this situation is the following:
$$
y=133(1.19)^x
$$
Where $x$ is a number of hours.
Between $8$ a.m. and $4$ p.m. there are $8$ hours, so,
we will substitute $8$ for $x$ in the previous equation and get:
$$
y=133(1.19)^8
$$
$$
y=534.84
$$
So, about $535$ cars pass the bridge in this interval of hours.
Here, we will substitute $534.84$ for $V$ in the model and get:
$$
n=(1.005)^{534.84}
$$
$$
n=14.41
$$
So, they should have about $14$ officers on duty at $4$ p.m.
The percent increase of number of officers in the model is $0.5%$.
Here, factor $k$ means that at any moment, there should
not be less than $k$ officers on duty.
In this case, an appropriate $k$ factor is between $26$ and $36$
if the Highway Patrol wants to have between $40$ and $50$
officers at $4$ p.m.
c) between $26$ and $36$
we will solve the following equation for $b$:
$$
992=15500b^3
$$
$$
b^3=0.064
$$
$$
b=0.4
$$
We can conclude that percent of decreasing is $40%$.
An equation that models the number of rooms remaining for
any number of months is the following:
$$
y=15500(0.4)^x
$$
Where $x$ represents the number of months.
Now, we will calculate after how many months there were
less than $5$ rooms on the following way:
$$
5=15500(0.4)^x
$$
$$
(0.4)^x=0.00032
$$
$$
x=8.78
$$
So, about after $9$ months there were less than $5$ rooms.
Exponential function the director of food should use to model
the number of tacos sold each hour.
#### (b)
On the following picture, there is graphed data from the table
and the best fit line.
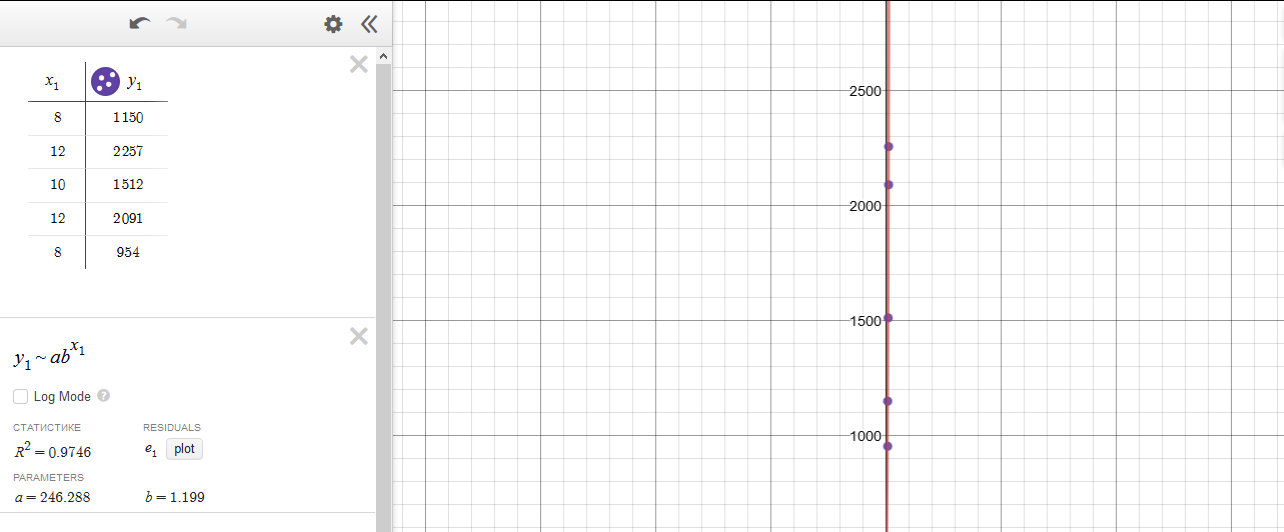
$$
y=246.288(1.199)^x
$$
We will substitute $19$ for $x$ and get:
$$
y=246.288(1.199)^{19}
$$
$$
y=5610.69
$$
So, about $5610$ tacos will be sold during the $7$ p.m.hour.
#### (c)
Here, the number of sold tacos is unreal, it does not fit
to the real situation.
c) It does not fit to the real situation.
Let $x$ represent available trams, we get following inequaltiy:
$$
xleq8
$$
Let $y$ represent available shuttle buses, we get following inequaltiy:
$$
yleq30
$$
An equation which represent the third situation is following:
$$
4x+8yleq50
$$
An equation which represent the fourth situation is following:
$$
10000+1000x-1000yleq15000
$$
On the following picture there are graphed all four inequalities and the solution region:
We have that maximum value for $x$ is 8 and maximum value for $y$ is $30$, so, according to informations in this part, we conclude that $8$ trams and $30$ buses should the organizers lease in order to shuttle the most people.
On the following picture there are graphed data from the table and the best fit line. The equation of the best fit line is follwing:
$$
y=-616857x+125297
$$
In order to find when Jeremiah should expect to be out of coins, we will substitute $0$ for $y$ in previous equation and solve it for $x$:
$$
0=-616857x+125297
$$
$$
x=2031.22
$$
So, conclusion is that Jeremiah should expect to be out of coins in $2031$.
For one minute Robby robot can working $dfrac{1}{7}$ from job
For one minute together can working $dfrac{1}{4}$ from job
$$
dfrac{1}{7}+x=dfrac{1}{4} x=dfrac{1}{4}-dfrac{1}{7}
$$
$$
x=dfrac{7-4}{28} x=dfrac{3}{28}
$$
For one minute Roger robot can working $dfrac{3}{28}$ from job.
Roger robot can working alone for $dfrac{28}{3}=9.33$ minute.
text{color{#4257b2}$9.33$ minute.}
$$
On the following picture, there are graphed given triangles.
$7, 5.4$ and $5$
In this case, first term is $t(1)=4$ and the constant difference is $d=4$, so, its equation is :
$$
t(n)=4+4(n-1)
$$
The first four terms are: $4,8,12,16$.
#### (b)
In this case, first term is $t(1)=4$ and common ration is $q=2$, so, its equation is:
$$
t(n)=4cdot2^{n-1}
$$
The first four terms are: $4,8,16,32$.
#### (c)
Another sequence that is neither arithmetric nor geometric is: $4,8,6,7,10..$
The amount sold is $$0.50$ times the number of cookies, plus $$0.75$ times the number of brownies. This must be “at least” or “greater than or equal to” $$100$ so we can write:
$$
color{#c34632}0.50c+0.75bgeq 100
$$
0.50c+0.75bgeq 100
$$
$$
begin{align*}
a&totext{price of adult ticket}\
c&totext{price of child ticket}\
end{align*}
$$
Set up the equations.
Two adults and three children paid a total of $$27.75$:
$$
2a+3c=27.75tag{1}
$$
Two children and three adults paid a total of $$32.25$:
$$
3a+2c=32.25tag{2}
$$
The equations do not have the same or opposite terms. Multiply eq. (1) by 2 and eq. (2) by 3 to obtain the equations:
$$
4a+6c=55.50tag{3}
$$
$$
9a+6c=96.75tag{4}
$$
Use the Elimination Method. Subtract each side of eq. (3) and eq. (4) to eliminate $c$ then solve for $a$:
$$
begin{align*}
-5a&=-41.25\
a&=8.25
end{align*}
$$
Solve for $c$ using eq. (2):
$$
begin{align*}
3(8.25)+2c&=32.25\
24.75+2c&=32.25\
2c&=7.5\
c&=3.75
end{align*}
$$
So, $text{color{#c34632}the price of an adult ticket is $$8.25$ and the price of a child ticket is $$3.75$.}$
Find the equations of the line using the slope-intercept form:
$$
y=mx+b
$$
where $m$ is the slope and $b$ is the $y$-intercept.
For the top line, two points are $(0,10)$ and $(4,9)$ so its slope is $m=dfrac{9-10}{4-0}=-dfrac{1}{4}$. With $b=10$, the equation is:
$$
y=-dfrac{1}{4}x+10
$$
For the bottom line, two points are $(0,3)$ and $(3,4)$ so its slope is $m=dfrac{4-3}{3-0}=dfrac{1}{3}$. With $b=3$, the equation is:
$$
y=dfrac{1}{3}x+3
$$
$$
-dfrac{1}{4}x+10=dfrac{1}{3}x+3
$$
Multiply both sides by the LCD which is 12:
$$
-3x+120=4x+36
$$
Subtract 120 from both sides:
$$
-3x=4x-84
$$
Subtract $4x$ from both sides:
$$
-7x=-84
$$
Divide both sides by $-7$:
$$
x=12
$$
Using either equation, I used the second, the corresponding $y$-value is:
$$
y=dfrac{1}{3}(12)+3=4+3=7
$$
So, the point of intersection is:
$$
color{#c34632}(12,7)
$$
which confirms our prediction that the lines will intersect.
To find the $x$-intercept, set $y=0$ and solve for $x$. To find the $y$-intercept, set $x=0$ and solve for $y$.
The equation of the top line is $y=-dfrac{1}{4}x+10$ so we have:
$$
begin{align*}
0&=-dfrac{1}{4}x+10 & y=-dfrac{1}{4}(0)+10\
dfrac{1}{4}x &=10 & y=0+10\
x &=40 & y=10
end{align*}
$$
So, the $x$-intercept is $(40,0)$ and the $y$-intercept is $(0,10)$.
The equation of the bottom line is $y=dfrac{1}{3}x+3$ so we have:
$$
begin{align*}
0&=dfrac{1}{3}x+3 & y=dfrac{1}{3}(0)+3\
-dfrac{1}{3}x &=3 & y=0+3\
x &=-9 & y=10
end{align*}
$$
So, the $x$-intercept is $(-9,0)$ and the $y$-intercept is $(0,3)$.
bottom line: $x$-intercept $=(-9,0)$ and $y$-intercept $=(0,3)$
Here we have translation of graph of $f(x)$ $1$ unit up.
#### (b)
Here we have translation of the given graph of $f(x)$ for $3dfrac{1}{3}$
units down.
b) Translation $3dfrac{1}{3}$ units down
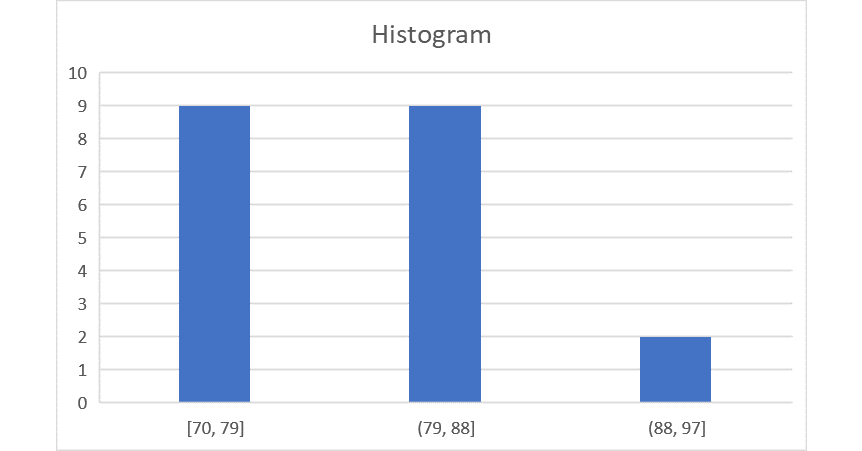
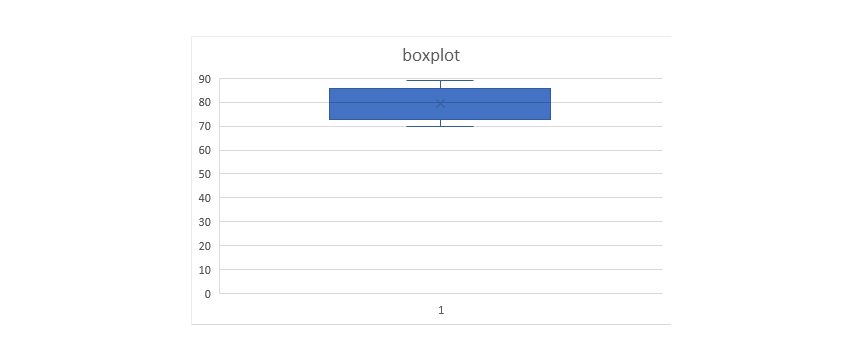
way to describe the spread is to use standard deviation.
The standard deviation for this data is $6.98$ and the mean is $79.5$.
$$
8x+6cdot10=(6+x)cdot8.5
$$
$$
8x+60=51+8.5x
$$
$$
0.5x=9
$$
$$
x=18
$$
So, the conclusion is that there should be mixed $18$ pounds
of candy which cost $$8$ a pound.
included angles are equal in measurement, which means that those
triangles are congruent according to the $ASA$ condition.
$$
f(x)=|x-3|+5
$$
$$
{color{#4257b2}text{(a)} f(-1)}=|-1-3|+5=|-4|+5=4+5=9
$$
$$
{color{#4257b2}text{(b)} f(sqrt[3]{-8})}=f(sqrt[3]{(-2)^3})|-2-3|+5=|-5|+5=5+5=10
$$
$$
{color{#4257b2}text{(c)} 10}=|x-3|+5=|x-3|=10-5=5 |x-3|=5
$$
Equal $x-3=5$ as follows:
$$
x-3=5 x=5+3 x=8
$$
Equal $-x+3=5$ as follows:
$$
-x+3=5 -x=5-3 -x=2 x=-2
$$
The values of $x$ are equal
$$
x=8 text{ when} x-3ge0 xge3
$$
$$
x=-2 text{ when} x-3<0 x<3
$$
(c) $x=8$ or $x=-2$
they are $(-2.9, 2.1)$ and $(3.7, 15.5)$.
$$
color{#4257b2}text{(a)} 300x-1500=2400
$$
Isolate the variables on the left side as follows:
$$
300x=2400+1500 300x=3900
$$
Divide both of side by $300$ as follows:
$$
x=dfrac{3900}{300} x=13
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=13$ in the equation as follows:
$$
300x-1500=2400 (300cdot13)-1500=2400
$$
$$
3600-1500=2400 2400=2400
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(b)} dfrac{3}{2} x=dfrac{5}{6} x+2
$$
Isolate the variables on the left side as follows:
$$
dfrac{3}{2} x-dfrac{5}{6} x=2 dfrac{18-10}{12} x=2 dfrac{8}{12} x=2
$$
Multiply both of side by $dfrac{12}{8}$ as follows:
$$
x=dfrac{12}{8} cdot2 x=dfrac{24}{8} x=3
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=3$ in the equation as follows:
$$
dfrac{3}{2}cdot3=dfrac{5}{6}cdot3+2 dfrac{9}{2}=dfrac{15}{6}+2
$$
$$
dfrac{9}{2}=dfrac{15+12}{6} dfrac{9}{2}=dfrac{27}{6} dfrac{9}{2}=dfrac{9}{2}
$$
Since the left side is equal the right side, so the answer is correct.
color{#4257b2}text{(c)} |3x-2|>4
$$
Equal $3x-2>4$ as follows:
$$
3x-2>4 3x>4+2 3x>6 x>dfrac{6}{3} x>2
$$
Equal $-3x+2>2$ as follows:
$$
-3x+2>4 -3x>4-2 -3x>2 x<-dfrac{2}{3}
$$
Charlie’s great-grandfather started in 1905 and Charlie received the family heirloom in 1999 so the collection is in existence for :
$$
1999-1905=color{#c34632}94text{ years}
$$
$textbf{b.}$
Since the same number of marbles were added each year, then the total number of marbles have a linear relationship and the slope is the number of marbles added each year. Using the two data points $(1966,810)$ and $(1999,1239)$, we have:
$$
dfrac{1239-810}{1999-1966}=dfrac{429}{33}=13
$$
So, $text{textcolor{#c34632}{13 marbles}}$ are added to the collection each year.
$textbf{c.}$
From the start (1905) to the year when Charlie’s father received the collection (1966), there are $1966-1905=61$ years. So, $13times 61=793$ marbles were added in these years. Since there were 810 marbles when Charlie’s father inherited the collection, then there were $810-793=color{#c34632}17$ marbles in the original collection.
The relationship is linear so we use the function:
$$
f(n)=mn+b
$$
From part b, $m=13$ and from part c, $b=17$. Hence, the function is:
$$
color{#c34632}f(n)=13n+17
$$
$textbf{e.}$
When $f(n)=2000$,
$$
begin{align*}
13n+17&=2000\
13n&=1983\
n&approx 152.5
end{align*}
$$
Rounding up, the collection is $text{textcolor{#c34632}{153 years old}}$ when it has more than 2000 marbles. (Note: 152 makes the collection 1993 marbles so it is not the correct answer.) This corresponds to the year $1905+153=color{#c34632}2058$.
b. 13 marbles
c. 17
d. $f(n)=13n+17$
e. 153 years old ; 2058
$$
color{#4257b2}text{(a)} |3x-3|=0
$$
Equal $3x-3=0$ as follows:
$$
3x-3=0 3x=3 x=dfrac{3}{3} x=1
$$
Equal $-3x+3=0$ as follows:
$$
-3x+3=0 -3x=-3 x=dfrac{-3}{-3} x=1
$$
$$
color{#4257b2}text{(b)} x^2-3(2x+3)=x^2-3
$$
Use distributive property to simplify as follows:
$$
x^2-6x-9=x^2-3
$$
Rearrange the tiles to group like terms as follows:
$$
(x^2-x^2)+-6x+(-9+3)=0 0-6x-6=0 -6x-6=0
$$
Isolate the variables on the left side as follows:
$$
-6x=6 x=dfrac{6}{-6} x=-1
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=-1$ in the equation as follows:
$$
(-1)^2-3((2cdot-1)+3)=(-1)^2-3 1-3(-2+3)=1-3
$$
$$
1+6-9=1-3 -2=-2
$$
Since the left side is equal the right side, So the answer is correct.
color{#4257b2}text{(c)} 0=(p-3)^2
$$
Use square root property for both side as follows:
$$
sqrt{(p-3)^2}=sqrt{0} p-3=0 p=3
$$
$text{color{#4257b2}Check:}$ Substitute the value of $x=3$ in the equation as follows:
$$
(3-3)^2=0 (0)^2=0 0=0
$$
Since the left side is equal the right side, so the answer is correct.
$$
color{#4257b2}text{(d)} u=dfrac{v+2}{w}
$$
$$
w=dfrac{v+2}{u}
$$
(c) $p=3$ (d) $w=dfrac{v+2}{u}$
function, its equation is:
$$
y=6x-2
$$
y=6x-2
$$

