Since the graph of an arithmetic sequence is a line when the terms are connected, then we can find an equation for the arithmetic sequence using the slope-intercept form of a line:

$$
y=mx+b
$$

or in this case,

$$
t(n)=mn+t(0)
$$

Representing the two terms as points, we have $(1,8)$ and $(7,512)$ so the slope is:

$$
m=dfrac{Delta y}{Delta x }=dfrac{512-8}{7-1}=dfrac{504}{6}=84
$$

This is also the sequence generator.

To find $t(0)$, use the slope and either of the two points. I used $(1,8)$:

$$
begin{align*}
8&=84 (1)+t(0)\
8&=84+t(0)\
-76&=t(0)\
end{align*}
$$

So, the equation for the arithmetic sequence is:

$$
color{#c34632}t(n)=84n-76
$$

Since the graph of a geometric sequence is an exponential graph when the terms are connected, then we can use the exponential equation:

$$
y=acdot b^x
$$

or in this case,

$$
t(n)= t(0)cdot b^n
$$

Using $t(1)=8$, we write one equation:

$$
8=t(0)btag{1}
$$

Using $t(7)=512$, we write another equation:

$$
512=t(0)b^7tag{2}
$$

Solve for $t(0)$ using eq. (1) to obtain:

$$
dfrac{8}{b}=t(0) tag{3}
$$

Substitute eq. (3) to eq. (2) then solve for $b$:

$$
begin{align*}
512&=dfrac{8}{b}cdot b^7\
512&=8 b^6\
64&=b^6\
2^6&=b^6\
2&=b
end{align*}
$$

Solve for $t(0)$ using eq. (3):

$$
t(0)=dfrac{8}{2}=4
$$

So, the equation for the geometric sequence is:

$$
color{#c34632}t(n)= 4(2)^n
$$

geometric: $t(n)=4(2)^n$

Divide the domain in intervals of 1. For $0leq xleq 1$, $y=2$. For $1< xleq 2$, $y=2+0.50=2.50$. For $2< xleq 3$, $y=2.50+0.50=3$. Continue this pattern for the other intervals. For $leq$, use a closed circle at the endpoint and for $<$, use an open circle at the endpoint. The step graph should look like:

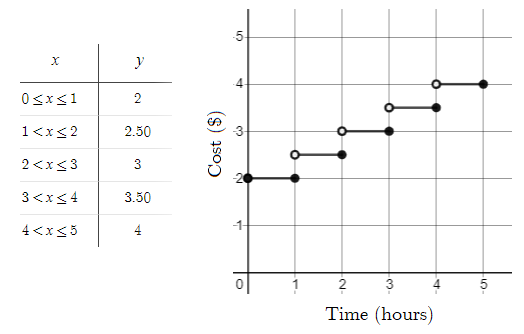
$textbf{a.}$

There is an annual (or yearly) appreciation so the appropriate unit of time is $text{textcolor{#c34632}{Years}}$.

An annual appreciation is an increase so the multiplier is:

$$
b=100%+6%=106%=color{#c34632}1.06
$$

The initial value is $a=color{#c34632}120000$ (dollars).

Let $x$ be the number of years and $y$ (or $f(x)$) be the price of the house in dollars. Using the values of $a$ and $b$, the exponential equation is:

$$
color{#c34632}f(x)= 120000(1.06)^x
$$

$textbf{b.}$

The rate is per hour so the appropriate unit of time is $text{textcolor{#c34632}{Hours}}$.

The number of bacteria increases so the multiplier is:

$$
b=100%+22%=122%=color{#c34632}1.22
$$

The initial value is $a=color{#c34632}180$.

Let $x$ be the number of hours after noon and $y$ (or $f(x)$) be the number of bacteria. Using the values of $a$ and $b$, the exponential equation is:

$$
color{#c34632}f(x)= 180(1.22)^x
$$

The rate is per year so the appropriate unit of time is $text{textcolor{#c34632}{Years}}$.

A depreciation is a decrease so the multiplier is:

$$
b=100%-11%=89%=color{#c34632}0.89
$$

The initial value is $a=color{#c34632}12250$ (dollars).

Let $x$ be the number of years and $y$ (or $f(x)$) be the price of the value of the car. Using the values of $a$ and $b$, the exponential equation is:

$$
color{#c34632}f(x)= 12250 (0.89)^x
$$

$textbf{d.}$

Since the compounding is monthly, the appropriate unit of time is $text{textcolor{#c34632}{Months}}$.

First, we find the monthly interest rate: $6%div 12=0.5%$. The investment increases so the multiplier is:

$$
b=100%+0.5%=100.5%=color{#c34632}1.005
$$

The initial value is $a=color{#c34632}1000$ (dollars).

Let $x$ be the number of months and $y$ (or $f(x)$) be the amount of investment in dollars. Using the values of $a$ and $b$, the exponential equation is:

$$
color{#c34632}f(x)= 1000 (1.005)^x
$$

b. Hours ; 1.22 ; 180 ; $f(x)=180(1.22)^x$

c. Years ; 0.89 ; 12250 ; $f(x)=12250 (0.89)^x$

d. Months ; 1.005 ; 1000 ; $f(x)=1000(1.005)^x$

$$
begin{align*}
&text{Subtract 3y from both sides}\
&2x+3y-3y=6-3y\\
&2x=6-3y tag{Simplify} \
&frac{2x}{2}=frac{6}{2}-frac{3y}{2} tag{Divide both sides by 2}\\
&boxed{{color{#c34632} x=frac{6-3y}{2} } }
end{align*}
$$

$$
begin{align*}
&text{Add 3 to both sides}\
&FM-3+3=Q+3\\
&FM=Q+3 tag{Simplify} \
&frac{FM}{M}=frac{Q}{M}+frac{3}{M};quad :Mne :0 tag{Divide both sides by M}\\
&boxed{{color{#c34632} F=frac{Q+3}{M} } }
end{align*}
$$

$$
begin{align*}
&text{Subtract a from both sides}\
&frac{r}{s}+a-a=2b-a\\
&frac{r}{s}=2b-a tag{Simplify} \
&frac{rs}{s}=2bs-as;quad :sne :0 tag{Multiply both sides by s}\\
&boxed{{color{#c34632} r=2bs-as } }
end{align*}
$$

$$
color{#4257b2} text{b)} F=frac{Q+3}{M}
$$

$$
color{#4257b2} text{c)}r=2bs-as
$$

$$
color{#4257b2}text{(a)} (-3, 11) (5, 6)
$$

Midpoint means the midpoint for $x, y$ as follows:

Midpoint for $x$ axis as follows:

$$
dfrac{-3+5}{2}=dfrac{2}{2}=1
$$

Midpoint for $y$ axis as follows:

$$
dfrac{11+6}{2}=dfrac{17}{2}=8.5
$$

The midpoint for the above points is $(1, 8.5)$.

Find the coordinate of mid point for the following points.

$$
color{#4257b2}text{(b)} (-4, -1) (8, 9)
$$

Midpoint means the midpoint for $x, y$ as follows:

Midpoint for $x$ axis as follows:

$$
dfrac{-4+8}{2}=dfrac{4}{2}=2
$$

Midpoint for $y$ axis as follows:

$$
dfrac{-1+9}{2}=dfrac{8}{2}=4
$$

The midpoint for the above points is $(2, 4)$.

On the following picture, there is graphed quadrilateral $MNPQ$.

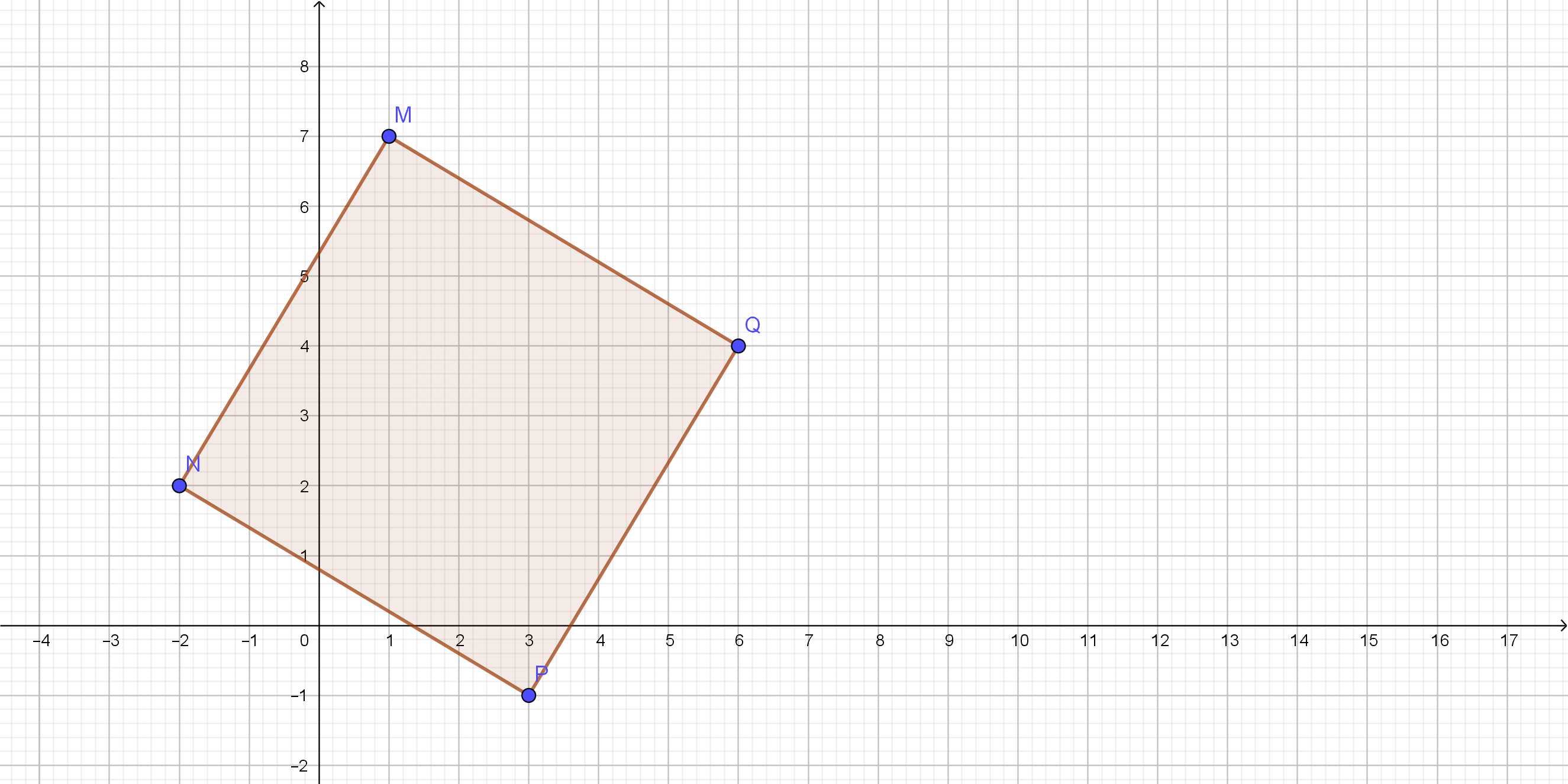
$$
text{slope}overline{MN}=dfrac{-2-1}{2-7}=dfrac{3}{5}
$$

$$
text{slope}overline{NP}=dfrac{3+2}{-1-2}=-dfrac{5}{3}
$$

Because slope $overline{MN}cdottext{slope}overline{NP}=-1$, we can conclude that $measuredangle MNP=90^{circ}$.

#### (b)

We can conclude that all angles are $90^{circ}$, so, $MNPQ$ is actually rectangle.

#### (c)

We will find first the length of diagonal $overline{NQ}$:

$$
overline{NQ}=sqrt{(6+2)^2+(4-2)^2}=sqrt{68}
$$

Now, we will calculate the length of diagonal $overline{MP}$.

$$
overline{MP}=sqrt{(3-1)^2+(-1-7)^2}=sqrt{68}
$$

We can notice that lengths of those diagonals are equal.

From the following picture, we can notice that midpoint of $overline{MN}$ is $A(-0.5,4.5)$.

Because of this rectangle with all equal sides, or square, it is enough to find the length of one side in order to calculate its perimeter an area.

$$
overline{MN}=sqrt{(-2-1)^2+(2-7)^2}=5
$$

So, the perimeter is:

$$
O=4cdot5=20
$$

The area is:

$$
P=5^2=25
$$

In order to calculate does more than half the drug remain after $4$ hours, we will substitute $4h=240$ minutes for $t$ in the equation and solve it for $y$:

$$
y=120(0.997)^{240}
$$

$$
y=58.35
$$

The conclusion is that after $4$ hours there is less than half the drug remain in the bloodstream.

Put the given information in standard form of exponent equation as follows:

$$
y=a b^x y=3.89 (1.05)^x
$$

$$
y=3.89(1.05)^10 y=3.89cdot1.6288 y=6.3364
$$

Cost it in $10$ years will be $6.3364$ dollars.

$$
text{color{#4257b2}(b) What did it cost $5$ years ago?}
$$

Put the given information in standard form of exponent equation as follows:

$$
y=a b^x y=3.89 (1.05)^x
$$

$$
y=3.89(1.05)^{-5} y=dfrac{3.89}{1.05^5} y=dfrac{3.89}{1.2763}
$$

$$
y=3.0478
$$

Cost it in $5$ years ago was $3.0478$ dollars.

$$
begin{align*}
a&totext{number of adult tickets sold}\
s&totext{number of student tickets sold}\
end{align*}
$$

Set up the equations.

There were 10 people so we write:

$$
a+s=10tag{1}
$$

A total of $$186.50$ were paid:

$$
24.95a+15.95s=186.50tag{2}
$$

Using eq. (1), solve for $s$ to obtain the equation:

$$
s=10-atag{3}
$$

Use the Substitution Method by substituting eq. (3) to eq. (2) and solve for $a$:

$$
begin{align*}
24.95a+15.95(10-a)&=186.50\
24.95a+159.5-15.95a&=186.50\
9a+159.5&=186.50\
9a&=27\
a&=3
end{align*}
$$

So, there were $text{color{#c34632}3 adults.}$

$color{#4257b2}text{(a) First figure}$.

The upper triangle

$$
text{The third length}=8^+6^=64+36=100
$$

Use square root property as follows:

$$
=sqrt{100}=10
$$

The lower triangle

$$
text{The third length}=10^2-8^2=100-36=64
$$

Use square root property as follows:

$$
=sqrt{64}=8
$$

$because$ The all sides in the triangles are equals.

$therefore$ The two triangles are congruent.

$color{#4257b2}text{(b) Second figure}$.

$because$ There are two angles in both of triangles are equals.

$because$ There is one side length in both of triangles is equal.

$therefore$ The two triangles are congruent.

$because$ There is one angle in both of triangles is equal.

$because$ There is two side lengths in both of triangles are equals.

$therefore$ The two triangles are congruent.

$color{#4257b2}text{(d) Forth figure$$}$.

$because$ There is one angle in both of triangles is equal.

$because$ There is two side lengths in both of triangles are equals.

$therefore$ The two triangles are congruent.